A Novel Tribometer and a Comprehensive Testing Method for Rolling-Sliding Conditions
Abstract
:1. Introduction
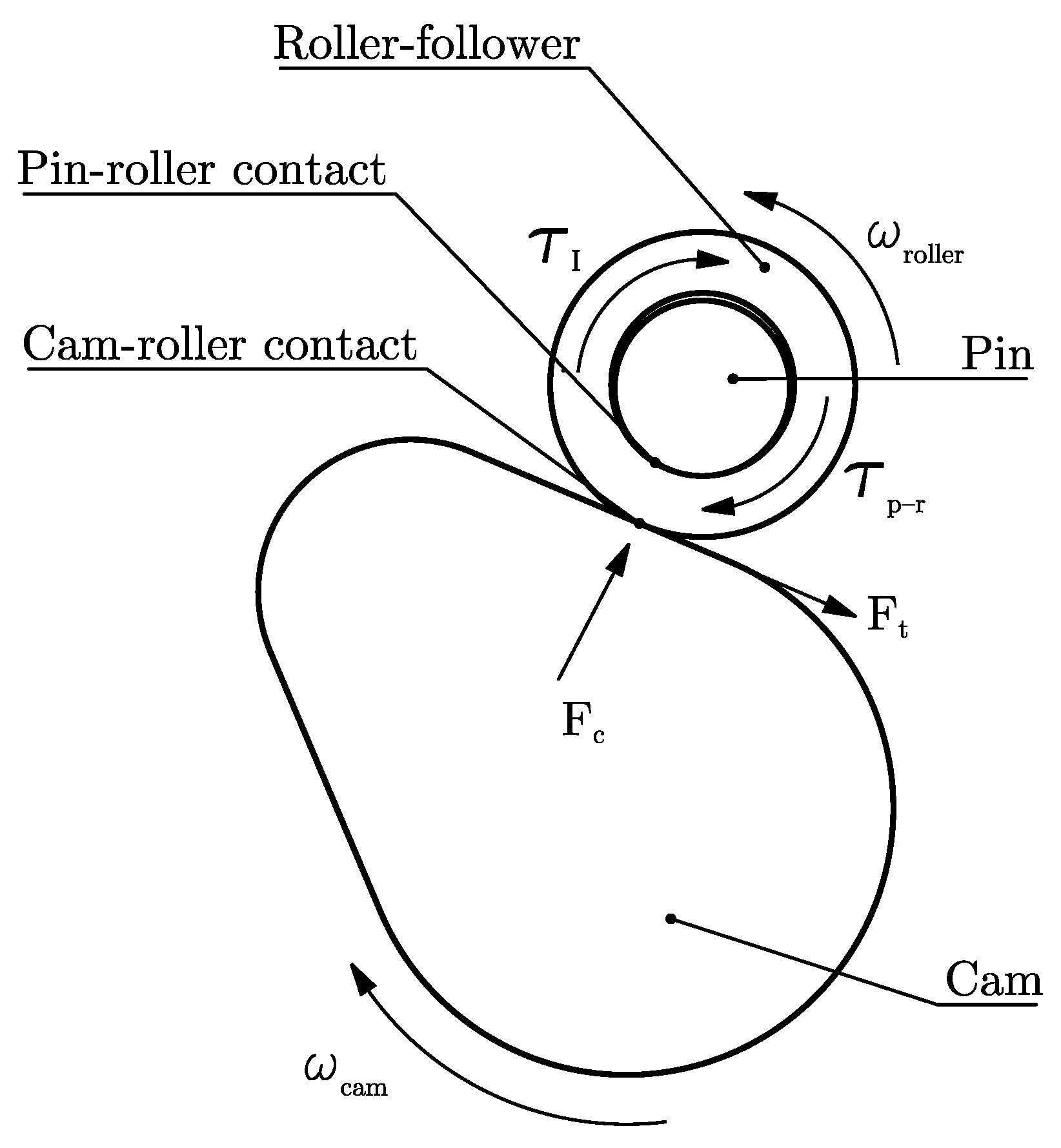
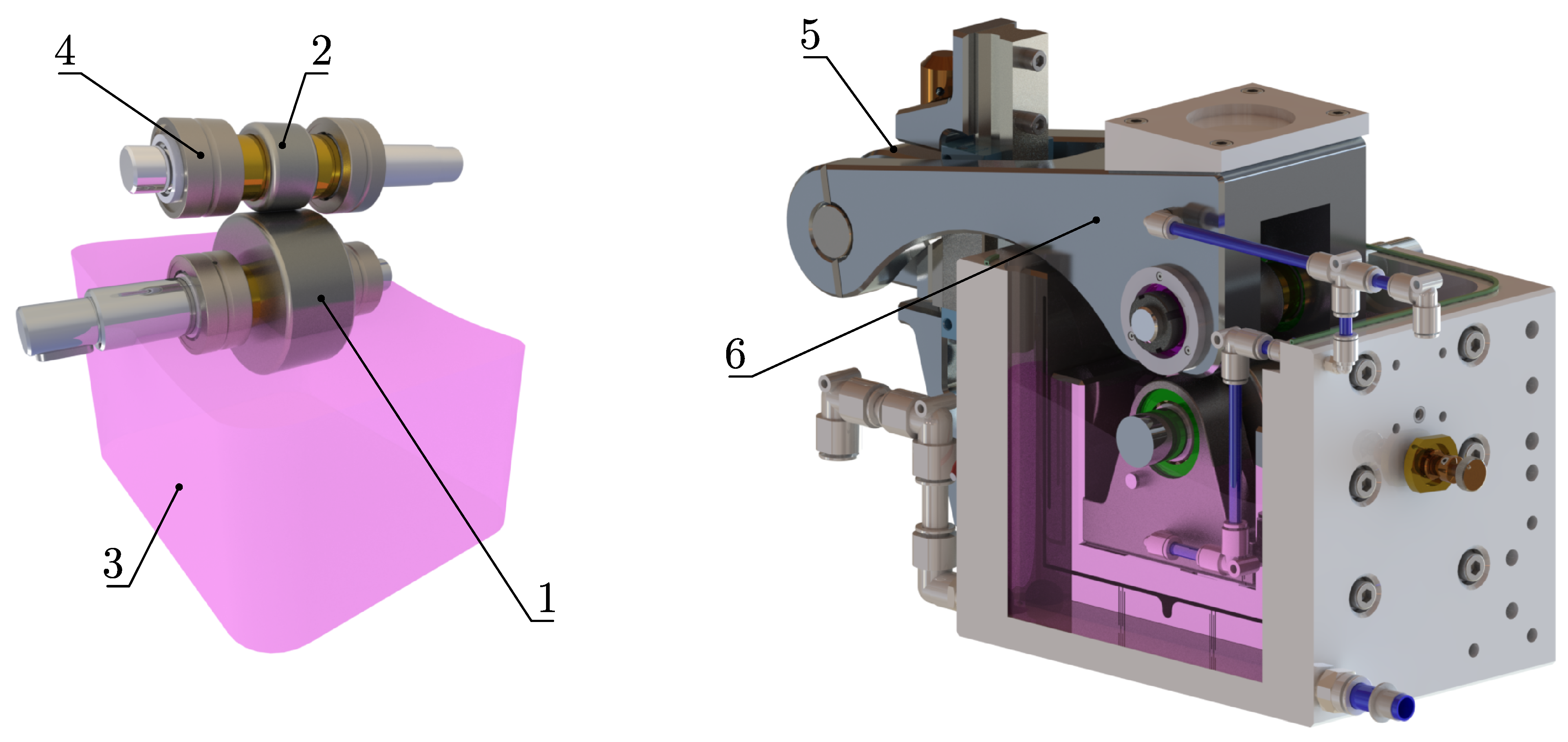
2. The Cam–Roller Tribotester (CRT)
2.1. Self-Tracking and Traction Force Measurement
2.2. CRT System Partition
2.3. Force and Torque Measurement Principle
2.4. Torque Balancing
2.5. Frictional Torque
3. Testing Method
3.1. Traction Decay Tests
3.2. Torque-Mode Traction Tests
3.3. Roughness Measurements
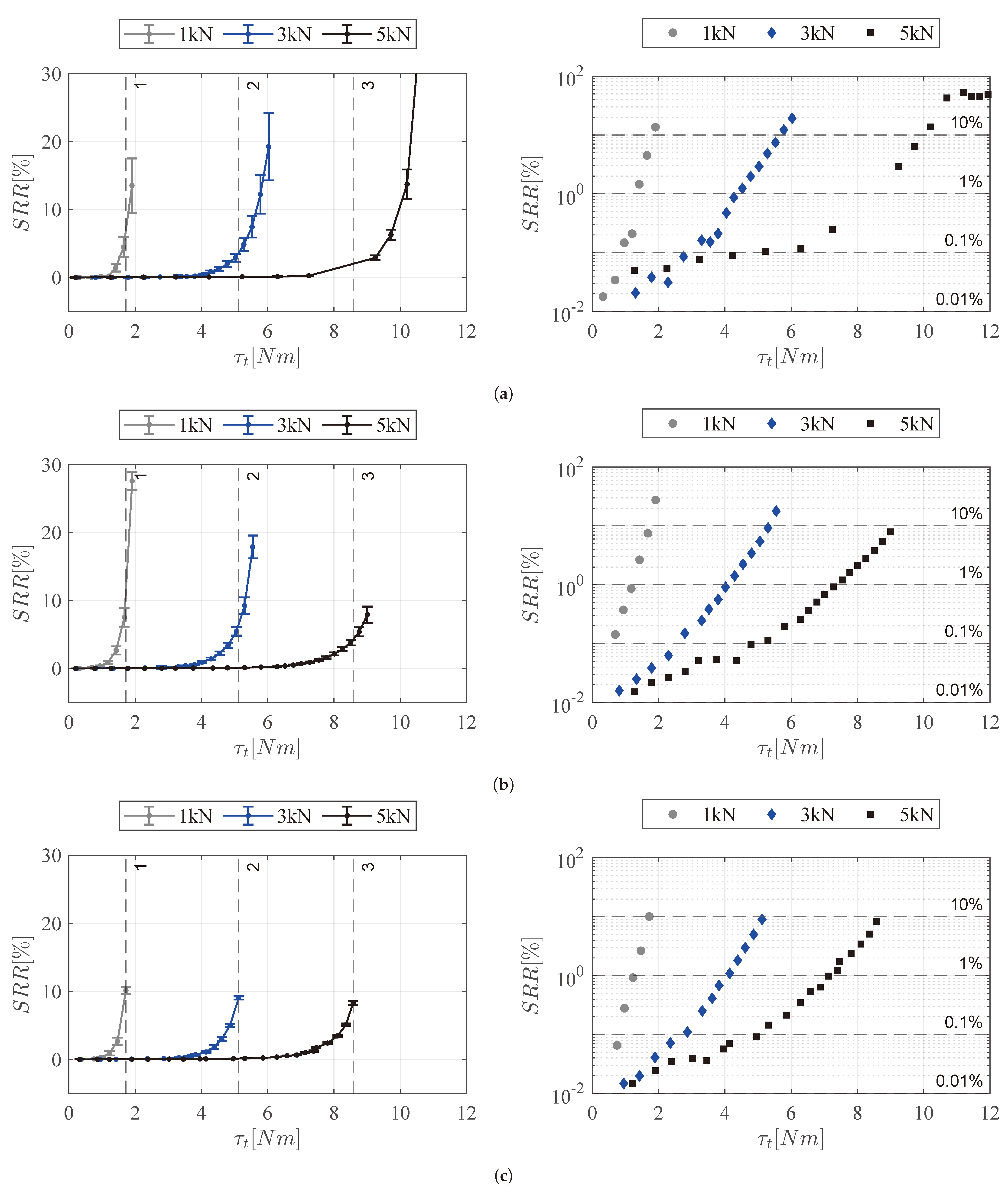
4. Results and Discussion
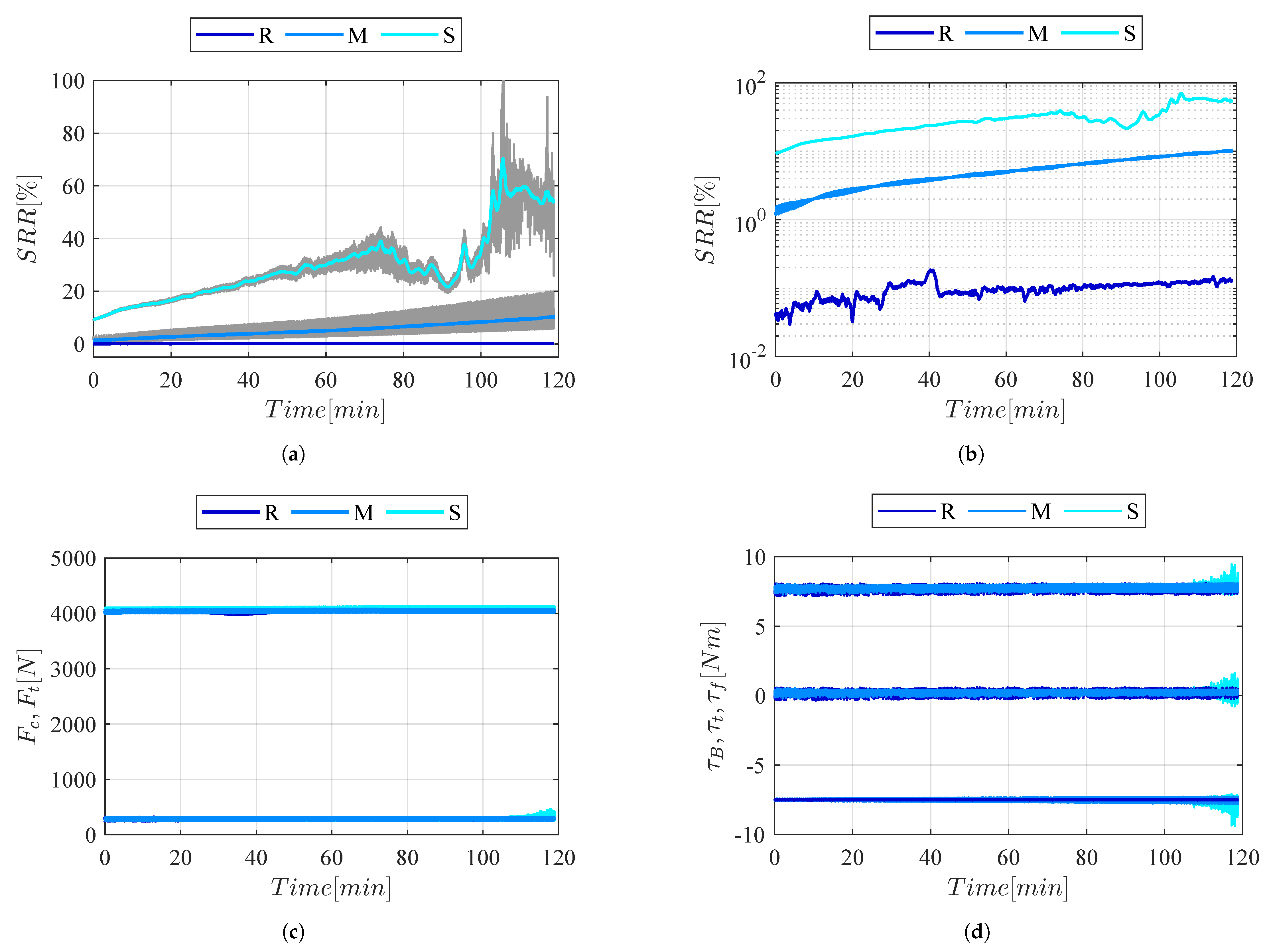
4.1. Traction Decay Tests
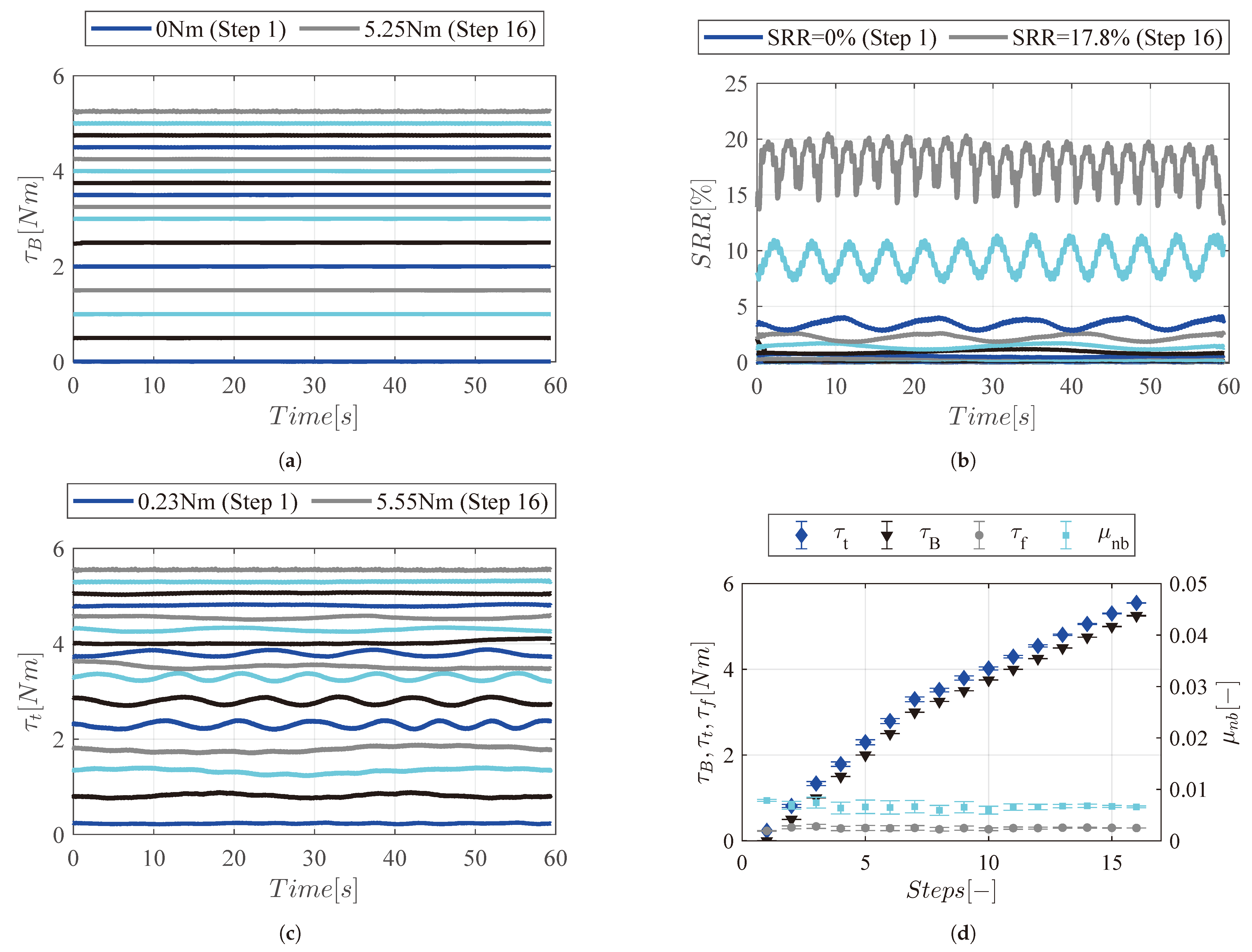
4.2. Torque-Mode Traction Tests
5. Conclusions
- The incorporation of a roller self-tracking system leads to excellent contact alignment.
- By integrating flexure-based linear guides into the design, direct measurement of the traction force without introducing parasitic friction forces can be achieved.
- The addition of a magnetic hysteresis brake, operating in a closed loop with a high-precision torque sensor and a high-speed controller, enables the precise, stable, and repeatable application of torques to the top roller.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| c | Constant | − |
| Mean bearing diameter | ||
| E | Elastic modulus | |
| Contact force | ||
| Total radial force | ||
| Traction force | ||
| Minimum film thickness | ||
| Hardness | ||
| I | Inertia | |
| Straight contact length | ||
| n | Driving roller () rotational speed | |
| Driving roller () radius | ||
| Driven roller () radius | ||
| R1 surface velocity | ||
| R2 surface velocity | ||
| Mean entrainment velocity | ||
| Pressure–viscosity coefficient | ||
| Dynamic viscosity | ||
| Traction coefficient | − | |
| Poisson’s ratio | − | |
| Kinematic viscosity | ||
| Film parameter | − | |
| Standard deviation of surface heights | ||
| Driving roller () rotational speed | ||
| Braking torque | ||
| Driving torque | ||
| Inertia torque | ||
| Frictional torque | ||
| Tractive torque | ||
| Slide-to-roll ratio | − |
References
- Baek, K.S.; Kyogoku, K.; Nakahara, T. An experimental investigation of transient traction characteristics in rolling-sliding wheel/rail contacts under dry-wet conditions. Wear 2007, 263, 169–179. [Google Scholar] [CrossRef]
- Gallardo-Hernandez, E.A.; Lewis, R. Twin disc assessment of wheel/rail adhesion. Wear 2008, 265, 1309–1316. [Google Scholar] [CrossRef]
- Wang, W.J.; Shen, P.; Song, J.H.; Guo, J.; Liu, Q.Y.; Jin, X.S. Experimental study on adhesion behavior of wheel/rail under dry and water conditions. Wear 2011, 271, 2699–2705. [Google Scholar] [CrossRef]
- Salas Vicente, F.; Pascual Guillamón, M. Use of the fatigue index to study rolling contact wear. Wear 2019, 436–437, 203036. [Google Scholar] [CrossRef]
- Rodríguez-Arana, B.; San Emeterio, A.; Panera, M.; Montes, A.; Álvarez, D. Investigation of a relationship between twin-disc wear rates and the slipping contact area on R260 grade rail. Tribol. Int. 2022, 168, 107456. [Google Scholar] [CrossRef]
- Kang, J.J.; Xu, B.S.; Wang, H.D.; Wang, C.B. Investigation of a novel rolling contact fatigue/wear competitive life test machine faced to surface coating. Tribol. Int. 2013, 66, 249–258. [Google Scholar] [CrossRef]
- Alakhramsing, S.S.; de Rooij, M.B.; Akchurin, A.; Schipper, D.J.; van Drogen, M. A mixed-TEHL analysis of cam-roller contacts considering roller slip: On the influence of roller-pin contact friction. J. Tribol. 2019, 141, 011503. [Google Scholar] [CrossRef]
- John, S.; El-Ghoul, Z.; Dimkovski, Z.; Lööf, P.J.; Lundmark, J.; Mohlin, J. Friction between pin and roller of a truck’s valvetrain. Surf. Topogr. Metrol. Prop. 2019, 7, 014001. [Google Scholar] [CrossRef]
- Johnson, K.L.; Cameron, R. Fourth Paper: Shear Behaviour of Elastohydrodynamic Oil Films at High Rolling Contact Pressures. Proc. Inst. Mech. Eng. 1967, 182, 307–330. [Google Scholar] [CrossRef]
- Masjedi, M.; Khonsari, M.M. Theoretical and experimental investigation of traction coefficient in line-contact EHL of rough surfaces. Tribol. Int. 2014, 70, 179–189. [Google Scholar] [CrossRef]
- Hu, Y.; Zhou, L.; Ding, H.; Tan, G.; Lewis, R.; Liu, Q.; Guo, J.; Wang, W. Investigation on wear and rolling contact fatigue of wheel-rail materials under various wheel/rail hardness ratio and creepage conditions. Tribol. Int. 2020, 143, 106091. [Google Scholar] [CrossRef]
- Liu, H.C.; Zhang, B.B.; Bader, N.; Venner, C.H.; Poll, G. Scale and contact geometry effects on friction in thermal EHL: Twin-disc versus ball-on-disc. Tribol. Int. 2021, 154, 106694. [Google Scholar] [CrossRef]
- Merritt, H.E.; Mech, M.I.E. Worm Gear Performance. Proc. Inst. Mech. Eng. 1935, 219, 127–194. [Google Scholar] [CrossRef]
- Moder, J.; Grün, F.; Stoschka, M.; Gódor, I. A Novel Two-Disc Machine for High Precision Friction Assessment. Adv. Tribol. 2017, 2017, 8901907. [Google Scholar] [CrossRef]
- Handschuh, M.J.; Kahraman, A.; Anderson, N.E. Development of a High-Speed Two-Disc Tribometer for Evaluation of Traction and Scuffing of Lubricated Contacts. Tribol. Trans. 2020, 63, 509–518. [Google Scholar] [CrossRef]
- Kleemola, J.; Lehtovaara, A. Experimental evaluation of friction between contacting discs for the simulation of gear contact. Tribotest 2007, 13, 13–20. [Google Scholar] [CrossRef]
- Akbarzadeh, S.; Khonsari, M.M. Experimental and theoretical investigation of running-in. Tribol. Int. 2011, 44, 92–100. [Google Scholar] [CrossRef]
- Meneghetti, G.; Terrin, A.; Giacometti, S. A twin disc test rig for contact fatigue characterization of gear materials. Procedia Struct. Integr. 2016, 2, 3185–3193. [Google Scholar] [CrossRef]
- Chiu, Y.P. Lubrication and slippage in roller finger follower systems in engine valve trains. Tribol. Trans. 1992, 35, 261–268. [Google Scholar] [CrossRef]
- Lee, J.; Patterson, D.J. Analysis of Cam/Roller Follower Friction and Slippage in Valve Train Systems; SAE Technical Paper 951039; SAE International: Warrendale, PA, USA, 1995. [Google Scholar]
- Amoroso, P.; Ostayen, R.A.J.V. Rolling-Sliding Performance of Radial and Offset Roller Followers in Hydraulic Drivetrains for Large Scale Applications: A Comparative Study. Machines 2023, 11, 604. [Google Scholar] [CrossRef]
- Masjedi, M.; Khonsari, M.M. Film thickness and asperity load formulas for line-contact elastohydrodynamic lubrication with provision for surface roughness. J. Tribol. 2012, 134, 011503. [Google Scholar] [CrossRef]
- ISO 21920-1:2021(en); Geometrical product specifications (GPS)—Surface texture: Profile—Part 1: Indication of surface texture. International Organization for Standardization, 2021. Available online: https://www.iso.org/obp/ui/#iso:std:iso:21920:-1:ed-1:v1:en (accessed on 9 October 2023).








| Parameter | Value | Unit |
|---|---|---|
| Distance between shafts | 54 | |
| Roller length (min./max.) | 20/35 | |
| Contact length (min./max.) | 4/35 | |
| Contact pressure (min./max.) | 0/2.1 | |
| Motor speed (max.) | 500 | rpm |
| Brake torque (max.) | 12 | |
| Load (min./max.) | 0/6.7 | |
| Oil temperature (max.) | 50 | |
| Pancake load cell rated force | 8.8 | |
| Compression load cell rated force | 2.2 | |
| Torque sensor rated torque | 20 | |
| Pancake load cell accuracy | 0.1 | % of rated load |
| Compression load cell accuracy | 0.25 | % of rated load |
| Torque sensor accuracy | 0.05 | % of the rated torque |
| Speed measurement accuracy | 0.01 | % of the reading |
| Lubrication type (rollers) | Oil bath | − |
| Lubrication type (bearings) | Forced lubrication | − |
| Parameter | Description | Value | Unit |
|---|---|---|---|
| E | Elastic modulus | 209 | |
| Hardness | 1.49 | ||
| Driving roller () radius | 27 | ||
| Driven roller () radius | 27 | ||
| Straight contact length | 10 | ||
| Poisson’s ratio | 0.33 | − | |
| Pressure–viscosity coefficient | |||
| Kinematic viscosity | 67 | ||
| Kinematic viscosity | 7.9 | ||
| Dynamic viscosity | 0.058 |
| Parameter | Description | Value | Unit |
|---|---|---|---|
| Contact force | 4 | ||
| Maximum contact pressure | 1 | ||
| n | Driving roller () rotational speed | 100 | rpm |
| Driving roller () rotational speed | 10.47 | ||
| Braking torque | 7.5 |
| Speed/Load | 1 kN (0.52 GPa) | 3 kN (0.91 GPa) | 5k N (1.17 GPa) |
|---|---|---|---|
| 450 rpm | (1) | (2) | (3) |
| 150 rpm | (4) | (5) | (6) |
| 50 rpm | (7) | (8) | (9) |
| Surface Finish | (m) | (m) | (%) | (%) | / | ||
|---|---|---|---|---|---|---|---|
| Smooth | 0.32 | 1.44 | 0.22 | 0.44 | 8.14 | 54.6 | 6.7 |
| Medium | 1 | 0.24 | 4.16 | 0.28 | 0.57 | 10.2 | 17.9 |
| Rough | 2.7 | 1.3 | 2.07 | 0.25 | 0.019 | 0.13 | 6.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amoroso, P.; Vrček, A.; de Rooij, M. A Novel Tribometer and a Comprehensive Testing Method for Rolling-Sliding Conditions. Machines 2023, 11, 993. https://doi.org/10.3390/machines11110993
Amoroso P, Vrček A, de Rooij M. A Novel Tribometer and a Comprehensive Testing Method for Rolling-Sliding Conditions. Machines. 2023; 11(11):993. https://doi.org/10.3390/machines11110993
Chicago/Turabian StyleAmoroso, Pedro, Aleks Vrček, and Matthijn de Rooij. 2023. "A Novel Tribometer and a Comprehensive Testing Method for Rolling-Sliding Conditions" Machines 11, no. 11: 993. https://doi.org/10.3390/machines11110993
APA StyleAmoroso, P., Vrček, A., & de Rooij, M. (2023). A Novel Tribometer and a Comprehensive Testing Method for Rolling-Sliding Conditions. Machines, 11(11), 993. https://doi.org/10.3390/machines11110993







