Analysis of Hydraulic Losses in Vortex Rope Inside the Draft Tube of Francis Pump-Turbine Based on Entropy Production Theory

Abstract

The existence of vortex ropes inside the draft tube significantly impacts hydraulic efficiency and operational stability, and few studies on the formation mechanism of vortex ropes and hydraulic loss problems have been explored. Hence, in this paper, we build an inherent correlation between the local entropy production rate (LEPR) in the draft tube and the dynamics of vortex motion, by incorporating the vortex identification method ${\tilde{\Omega }}_R$ with entropy production theory, using the OpenFOAM-v2212 software. From the analysis of the entropy production theory, the entropy production rate caused by turbulence dissipation (EPTD) is responsible for the majority of energy loss in the form of entropy production rate, accounting for about 87% of the total entropy production rate (TEPR) in different load operations. Comparatively, the entropy production rate caused by wall shear stress (EPWS) can account for up to 12%, while the entropy production rate due to direct dissipation (EPDD) plays a minor role in TEPR. The rotating vortex rope movement of the unit at part load conditions leads to more intense LEPR. Therefore, to determine the hydraulic loss caused by the vortex rope, the TEPR at the cross-section can be used to assess the hydraulic characteristics of the draft tube.

1. Introduction

As part of the development strategy for clean green energy, wind and solar energy have become increasingly mature. However, due to inherent instability and temporary character, they serve as supplementary forms of power generation. Hence, hydropower is gaining importance in national green economy initiatives due to its flexibility and efficiency. Within this framework, pumped storage power stations are a crucial component of multi-energy generation, requiring a focus on stable unit operation and efficient power conversion to prevent power fluctuations in the overall system. Given the operational flexibility of pumped storage power stations, which allows them to respond to different stages of grid scheduling commands in real-time, the majority of the units operate in off-design conditions. During these periods, limited guide vane opening may lead to an unstable condition [1] of the turbine. This instability can lead to the emergence of severe vortex phenomena [2,3] within the draft tube. And under the influence of vortex-induced vibration, the hydraulic unit may experience abnormal overall deflection [4,5]. Therefore, investigating the hydraulic characteristic distribution in the internal flow field of the pump-turbine and analyzing the energy loss quantitatively due to different types of vortex ropes under part load conditions [6] are of vital importance.

The hydraulic losses and vortex generation processes of pump-turbines are the focus of numerous studies by academics both locally and abroad, utilizing techniques like computational fluid dynamics (CFD) and model experiments. Clarifying the fundamental connection between vortex motion and the spread of pressure pulsations [7,8,9] as well as figuring out the processes behind the movement of vortices and the distribution of hydraulic losses are the primary challenges. Recently, the third-generation vortex identification method [10] presented by Liu et al. had been successfully applied in multiple fields [11,12,13], thereby paving the way for the future of vortex identification methodologies. This method presents an approach based on the R-NR method for decomposing the velocity gradient tensor and uses the R-S decomposition [14,15,16] method to separate the vortex vector into rotational and shear components. Through combining local vectors and vortex strength, it can efficiently represent the distribution and structure of vortices within the flow, enabling the Liutex method to accurately capture various forms of vortex structures. Zhang et al. [17] applied the omega vortex identification method to numerically simulate reversible pump-turbines and captured various blade vortex structures with different intensity levels in flow passages. Zhan et al. [18] compared the performance of the Q-criterion and Liutex methods applied to the in-stream structure and found that the Liutex method is more advantageous. Zhao et al. [19] further developed this innovation by implementing the Liutex vector model in multiphase flow numerical simulations of airfoils, revealing more elaborate cavitation vortex cores.

It is commonly acknowledged that the movement of vortex ropes [20,21] in draft tubes results in considerable hydraulic losses [22,23]. These losses have an impact not only on the overall hydraulic efficiency of the unit but also lead to low-frequency pulsations [24,25] that present risks to the operation of power plants. In recent years, many scholars have embraced a perspective based on the second law of thermodynamics, establishing a link between the distribution of entropy production and hydraulic losses. This method facilitates a quantitative assessment of the distribution of hydraulic characteristics [26] in over-current elements, producing outcomes that correspond with experimental parameters. Consequently, an increasing number of scholars are using entropy production theory more and more to foretell energy conversion in hydraulic units under a range of operational conditions. Gong et al. [27] utilized entropy production theory to scrutinize pump-turbine flow fields, exhibiting the technique’s benefits in evaluating internal energy losses within the units. Effectively validating the rationality of the entropy production method, Yu et al. [28] used thermodynamic entropy production to investigate the distribution of hydraulic losses in turbines under various loading conditions. Yan et al. [29] utilized numerical simulations to determine the distribution of hydraulic losses during pump-turbine operation under pumping conditions as analyzed from the perspective of entropy production. The approach of Qin et al. [30] used a multi-objective optimization strategy to improve the hydraulic performance of pump-turbine impellers under different conditions, leading to notable advances in both hydraulic losses and entropy production distribution. Similarly, Kan et al. [31] used an energy loss intensity model to study the head loss distribution of axial flow pumps operating under both turbine and pumping conditions, providing new insights into the design of related hydraulic machines.

Based on the theory of entropy production and a third-generation vortex identification method, this study analyses hydraulic losses due to vortex rope movement in pump-turbines under different load conditions and derives different distributions of entropy production, linking the energy loss due to vortex rope motion to the local entropy production rate (LEPR). The overall structure of this paper is as follows: Section 2 introduces governing equations and the turbulence model, explaining the vortex identification method and the application of entropy production theory to numerical simulation. Section 3 gives the computational domain model and relevant solution setup. The results of the calculations are validated and discussed in Section 4. Finally, Section 5 is a summary of results in the paper.

2. Numerical Simulation Methodology

2.1. Governing Equations and Turbulence Model

In this study, the Scale-Adaptive Simulation (SAS)-SST turbulence model is used to calculate the transient numerical simulation of pump-turbines. For incompressible turbulence calculations, the unsteady Reynolds-Averaged Navier–Stokes (URANS) equation is mainly composed of the continuity equation and momentum equation:

$$\nabla ·\mathit{u}=0$$

(1)

$$\frac{\partial \mathit{u}}{\partial t}+\nabla ·(\mathit{u}\mathit{u})=-\frac{\nabla p}{\rho }+\nabla ·(\nu \nabla \mathit{u})$$

(2)

In contrast to the SST k-ω turbulence model, the SAS-SST turbulence model incorporates a Q_SAS source term based on the ω transport equation, which has higher accuracy in the calculation of flows with large-scale separated states. Hence, the SAS-SST turbulence model in OpenFOAM consists of the following equations.

Where the turbulence specific dissipation rate equation is given by

$$\frac{\partial \rho \omega }{\partial t}=S_{\omega }+\nabla ·(\rho D_{\omega }\nabla \omega )+\frac{\rho \gamma G}{\nu }-\frac{2}{3}\rho \gamma \omega (\nabla ·\mathit{u})-\rho \beta {\omega }^2-\rho (F_1-1)C{D}_{k\omega }+Q_{SAS},$$

(3)

$$Q_{SAS}=\max \left[\rho \xi S^2{\left(\frac{L_1}{L_{vk}}\right)}^2-C·\frac{2\rho k}{{\sigma }_{\varphi }}\max \left(\frac{{\left|\nabla \omega \right|}^2}{{\omega }^2},\frac{{\left|\nabla k\right|}^2}{k^2}\right),0\right],$$

(4)

$$L_l=\sqrt{k}/(C_{\mu }{}^{1/4}\omega ),$$

(5)

$$L_{\mathit{vk}}=\kappa S/\left|{\nabla }^2\mathit{U}\right|.$$

(6)

The turbulence kinetic energy is given by:

$$\frac{\partial \rho k}{\partial t}=S_k+\nabla ·(\rho D_k\nabla k)+\rho G-\frac{2}{3}\rho k(\nabla ·\mathit{u})-\rho {\beta }^{*}\omega k.$$

(7)

The turbulence viscosity can be obtained by:

$${\nu }_t=a_1\frac{k}{\max (a_1\omega ,b_1{F}_2{S}_2)}.$$

(8)

Then, the closure coefficients are:

$$F_1=\tanh \left\{{\left\{\min \left[\max \left(\frac{\sqrt{k}}{{\beta }^{*}\omega y},\frac{500\nu }{y^2\omega }\right),\frac{4{\sigma }_{\omega 2}k}{C{D}_{k\omega }{y}^2}\right]\right\}}^4\right\},$$

(9)

$$C{D}_{k\omega }=\max (2\rho {\sigma }_{\omega 2}\frac{\nabla k·\nabla \omega }{\omega },{10}^{-10}),$$

(10)

$$G=2{\nu }_t·(\mathit{S}:\nabla \mathit{U}),$$

(11)

where u represents the velocity (m/s), p is the pressure (Pa), ρ is the fluid density (kg/m³), t is the time (s), $\nabla$ signifies the Hamilton operator, ν indicates the kinematic viscosity, L_l represents the turbulent length scale, and L_vk is the von Karman length scale used as a threshold for distinguishing between RANS and LES flow regimes, with the constants α₁ = 5/9, α₂ = 0.44, β₁ = 3/40, β₂ = 3/40, β* = 0.09, C = 2.0, ξ = 3.51, κ = 0.41, σ_φ = 0.67, σ_ω1 = 0.5, σ_ω2 = 0.856, and C_μ =0.09.

2.2. Vortex Identification Method

${\tilde{\Omega }}_R$ is a new generation of vortex identification method. In contrast to conventional techniques like vorticity, Q-criterion, λ_i, and λ₂ criteria, this method builds upon $\Omega$ and incorporates the definition of local fluid rotation axis and rotation strength from the Liutex vector. By decomposing vorticity into rotational and shear components, it becomes possible to distinguish vortex core structures of varying intensities. The $\Omega$ vortex identification method is defined through Equations (5) and (6):

$$\Omega =\frac{B_F^2}{B_F^2+A_F^2+\epsilon },$$

(12)

$$\epsilon =b_0{(B_F^2-A_F^2)}_{\max }.$$

(13)

In the equations, $B_F^2$ represents the square of Frobenius norm of the anti-symmetric matrix in the velocity gradient tensor, and $A_F^2$ is the square of Frobenius norm of the symmetric matrix in the velocity gradient tensor. The parameter b₀ can be adjusted based on actual condition, often chosen as 0.001. Moreover, the vortex identification method ${\tilde{\Omega }}_R$ is further refined based on the foundation of $\Omega$, by introducing adjustments and modifications.

$${\tilde{\Omega }}_R=\frac{{\beta }^2}{{\beta }^2+{\alpha }^2+{\lambda }_{cr}^2+\frac{1}{2}{\lambda }_r^2+\epsilon },$$

(14)

$$\alpha =\frac{1}{2}\sqrt{{(\frac{\partial \mathit{V}}{\partial Y}-\frac{\partial \mathit{U}}{\partial X})}^2+{(\frac{\partial \mathit{V}}{\partial X}+\frac{\partial \mathit{U}}{\partial Y})}^2},$$

(15)

$$\beta =\frac{1}{2}(\frac{\partial \mathit{V}}{\partial X}-\frac{\partial \mathit{U}}{\partial Y}),$$

(16)

$$\epsilon =b_0{({\beta }^2-{\alpha }^2)}_{\max },$$

(17)

where ${\lambda }_{cr}$ represents the real part of the complex eigenvalues of the velocity gradient tensor, and ${\lambda }_r$ denotes the real eigenvalues of the velocity gradient tensor. In the subsequent analysis of vortex identification in the draft tube, b₀ is set to 1e⁻⁶.

2.3. Entropy Production Theory Model

According to the second law of thermodynamics, the energy dissipation within the internal flow field caused by turbulent shear and heat exchange can be quantified using the integral of entropy production. When a pump-turbine operates, irreversible energy transformations occur, with hydraulic losses leading to suboptimal operational efficiency. Therefore, incorporating entropy production theory analysis into numerical simulations is a prime method for predicting energy conversion within the turbine. The specific entropy production transport model, derived from the Fourier heat conduction equation, is expressed as Equation (18):

$$\rho (\frac{\partial s}{\partial t}+u\frac{\partial s}{\partial x}+v\frac{\partial s}{\partial y}+w\frac{\partial s}{\partial z})=\nabla ·(\frac{\overrightarrow{q}}{T})+\frac{\Phi }{T}+\frac{{\Phi }_{\theta }}{T^2}$$

(18)

In the equation, $\frac{\Phi }{T}$ represents viscous entropy production, while $\frac{{\Phi }_{\theta }}{T^2}$ represents heat transfer entropy production and T is thermodynamic temperature. Kock et al. [32,33] further extended turbulent viscous entropy production based on this foundation. In time-averaging numerical simulations, the source of viscous dissipation can be decomposed into two major directions: one part from the time-averaged velocity and the other part from the fluctuation velocity. Therefore, each type of entropy production is defined by the following equation.

$$\dot{S}={\dot{S}}_{\overline{D}}+{\dot{S}}_{D^{\prime }},$$

(19)

$${\dot{S}}_{\overline{D}}=\frac{{\mu }_{eff}}{T}\left[2\left({(\frac{\partial \overline{u}}{\partial x})}^2+{(\frac{\partial \overline{v}}{\partial y})}^2+{(\frac{\partial \overline{w}}{\partial z})}^2\right)+{(\frac{\partial \overline{u}}{\partial y}+\frac{\partial \overline{v}}{\partial x})}^2+{(\frac{\partial \overline{u}}{\partial z}+\frac{\partial \overline{w}}{\partial x})}^2+{(\frac{\partial \overline{v}}{\partial z}+\frac{\partial \overline{w}}{\partial y})}^2\right],$$

(20)

$${\dot{S}}_{D^{\prime }}=\frac{{\mu }_{eff}}{T}\left[2\left({(\frac{\partial u^{\prime }}{\partial x})}^2+{(\frac{\partial v^{\prime }}{\partial y})}^2+{(\frac{\partial w^{\prime }}{\partial z})}^2\right)+{(\frac{\partial u^{\prime }}{\partial y}+\frac{\partial v^{\prime }}{\partial x})}^2+{(\frac{\partial u^{\prime }}{\partial z}+\frac{\partial w^{\prime }}{\partial x})}^2+{(\frac{\partial v^{\prime }}{\partial z}+\frac{\partial w^{\prime }}{\partial y})}^2\right],$$

(21)

$${\mu }_{eff}=\mu +{\mu }_t,$$

(22)

where ${\dot{S}}_{\overline{D}}$ represents the direct dissipation, which is the direct entropy production rate caused by time-averaged movement (EPDD); ${\dot{S}}_{D^{\prime }}$ represents the indirect dissipation or turbulent dissipation, which is the indirect entropy production rate caused by velocity fluctuation (EPTD); μ_eff is the effective dynamic viscosity; μ_t is the eddy viscosity.

However, it is difficult to derive the velocity fluctuation components in the Reynolds-averaged equations. Hence, these components can be transformed using the Formula (23) for k-ω turbulence model proposed by Kock et al. [32]

$${\dot{S}}_{D^{\prime }}=\beta \frac{\rho \omega k}{T}$$

(23)

where β is 0.09; k represents turbulent kinetic energy; ω is turbulent dissipation rate.

Furthermore, Duan et al. [34] established a wall energy dissipation model in the near-wall region to obtain the entropy production rate caused by wall shear stress (EPWS), enhancing the accuracy of entropy production prediction. Therefore, the wall entropy production can be acquired by Equation (24):

$$S_w={\displaystyle \underset{A}{\int }\frac{\tau ·v_p}{T}dA}$$

(24)

Finally, the total entropy production rate (TEPR) within the computational domain encompasses the sum of direct dissipation, turbulent dissipation, and wall friction. The total entropy production is obtained through the volume integration using Equation (25).

$$S={\displaystyle \underset{V}{\int }{\dot{S}}_{\overline{D}}}dV+{\displaystyle \underset{V}{\int }{\dot{S}}_{D^{\prime }}}dV+S_W$$

(25)

3. Numerical Simulation Subject

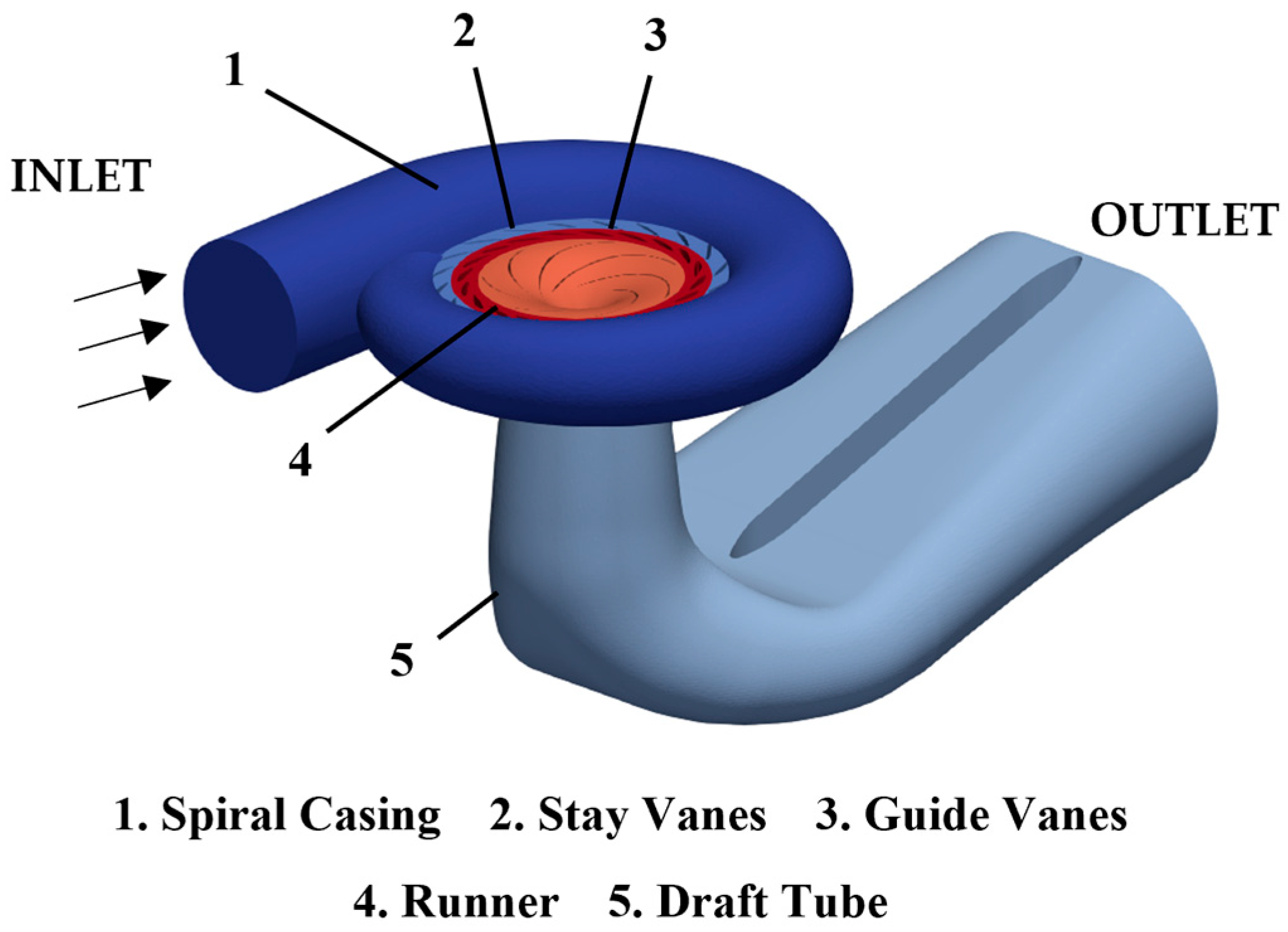
3.1. Computational Domain Model

As shown in Figure 1, the turbine model that this paper is discussing is a prototype pump-turbine located inside a pumped-storage power plant, including parts like spiral casing (SC), guiding vanes (GVs), stay vanes (SVs), runner, draft tube, and extended pipes. The detailed parameter of the pump-turbine is shown in

Table 1. Detailed parameters of the pump-turbine.

Parameter	Value
Rated head Hr (m)	105.8
Rated flow Qr (m3/s)	148.7
Rated rotate speed n (rpm)	200
Number of runner blades Nr	7
Rated power of turbine Pr (MW)	139
Runner inlet diameter D1 (m)	5.22
Number of guide/stay vanes Nv	20

.

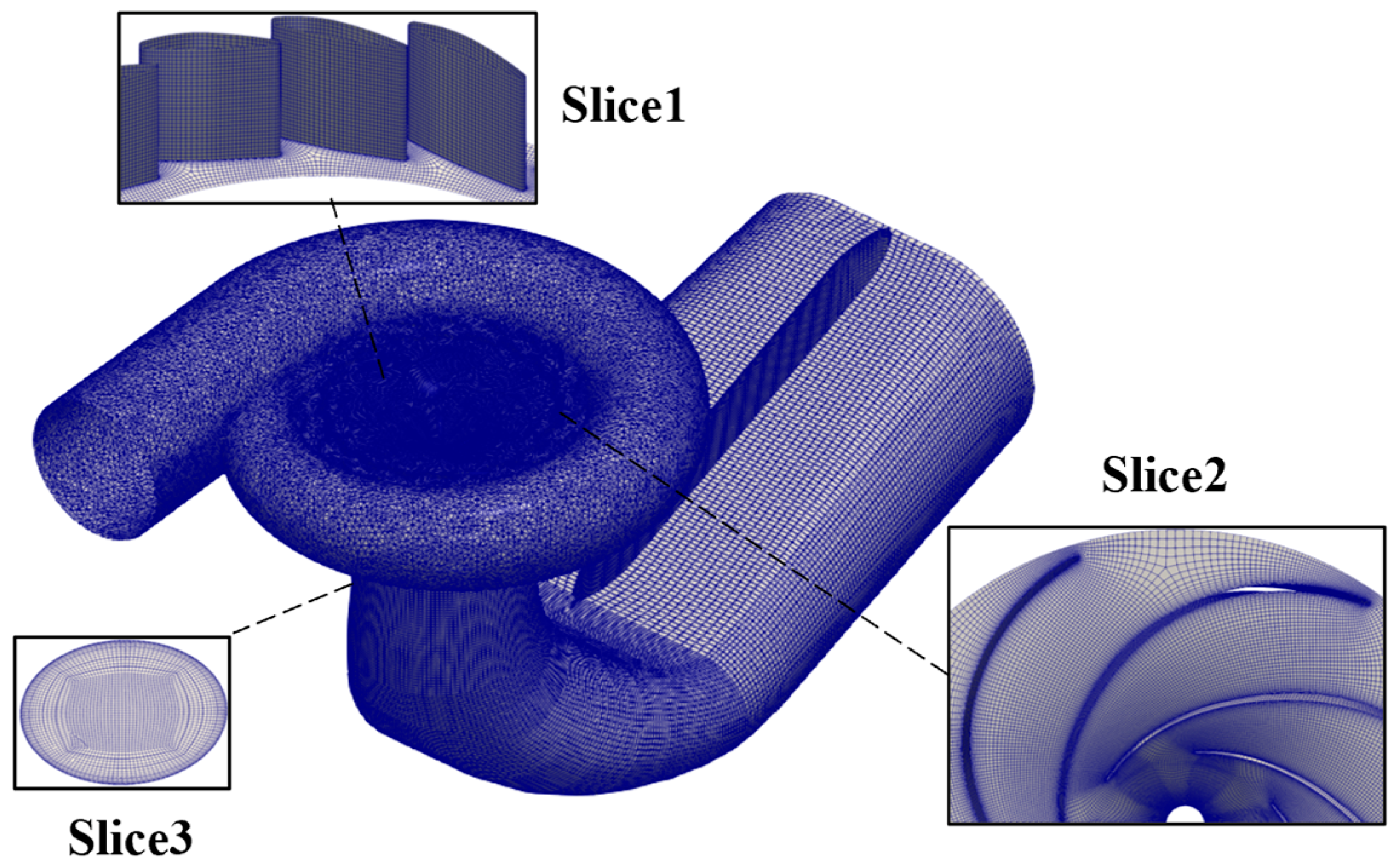
3.2. Mesh Generation and Convergence Assessment

The ANSYS-TurboGrid software is utilized for the structural meshes generation of the runner. The parts of the spiral casing and stay vanes, due to the complexity of their structure, are generated using tetrahedral unstructured meshes. Other sections are generated using the ANSYS-ICEM software to create hexahedral structured meshes.

Convergence assessment is performed using Richardson extrapolation for grid quantities of 2.76 million, 4.65 million, and 7.86 million. The Grid Convergence Index (GCI) [35] is used to assess grid discretization errors [36], in addition to the flow and efficiency parameters under Q_r conditions for determining convergence criteria. As indicated in

Table 2. Verification of mesh convergence.

N (Million)	Q (m3/s)	H (%)	h	r	e1	e2	$\mathit{G}\mathit{C}{\mathit{I}}_1^{21}$	$\mathit{G}\mathit{C}{\mathit{I}}_2^{21}$
7.864	148.92	91.5	0.0091	1.297	0.4%	0.33%	0.5%	1.12%
4.651	148.62	91.2	0.0118
2.766	148.04	90.8	0.0153	1.300	0.34%	0.44%

, the external parameters, flowrate and efficiency, show deviations of 0.5% and 1.12%, respectively, across different grid sizes, satisfying grid convergence requirements.

$$GC{I}^{21}=\frac{F_S{e}_a^{21}}{r_{21}^p-1},$$

(26)

$${\varphi }^{21}=\frac{r_{21}^p{\varphi }_1-{\varphi }_2}{r_{21}^p-1},$$

(27)

$$e_a^{21}=\left|\frac{{\varphi }_1-{\varphi }_2}{{\varphi }_1}\right|,$$

(28)

$$h={\left[\frac{1}{N_S}{\displaystyle \sum _{i=1}^{N_S}(\Delta A_I)}\right]}^{\frac{1}{2}},$$

(29)

$$r=\frac{h_2}{h_1},$$

(30)

$$J=\frac{1}{\ln (r_{21})}\left|\ln \left|\frac{{\epsilon }_{32}}{{\epsilon }_{21}}\right|+z(J)\right|,$$

(31)

$$z(J)=\ln (\frac{r_{21}^J-s}{r_{32}^J-s}),$$

(32)

$$s=\frac{{\epsilon }_{32}/{\epsilon }_{21}}{\left|{\epsilon }_{32}/{\epsilon }_{21}\right|},$$

(33)

where F_s is a security factor which takes the value of 1.25; $e_a^{21}$ is the extrapolate relative error; h represents the grid size parameter.

The grid distributions for various regions are depicted in Figure 2, in which Slice1, Slice2, and Slice3 illustrate detailed grid views at locations of the guide vanes, runner, and draft tube, respectively. At least ten boundary layers are positioned in high Reynolds number locations, such as the near-wall zones of the runner, guiding vanes, and draft tube. Ultimately, a grid quantity of 7.86 million is chosen, with an average y+ value for the primary flow components near walls conforming to the requirements of turbulence model solving.

3.3. Calculation Condition Setting

In this paper, numerical simulations of the pump-turbine under various operating circumstances are carried out using the OpenFOAM software. The pressure–velocity coupled field is calculated for the steady-state and transient operating conditions of the turbine using the SIMPLEC and PIMPLE algorithms. The PIMPLE algorithm combines SIMPLE (Semi-Implicit Method for Pressure-Linked Equations) [37] and PISO (Pressure Implicit with Splitting of Operator) [38], embedding an inner PISO algorithm loop inside an outer SIMPLE algorithm loop, which has improved stability when handling the more complex internal field. The associated variables in divergence are implemented using the second-order linear upwind scheme, while the gradient term is solved using a second-order central linear differencing scheme.

The totalPressure boundary condition is applied at the turbine’s inlet, while the fixedValue boundary condition is imposed at the turbine’s outlet. Under varied working conditions, the pump-turbine operates at a rated speed of 200 rpm. The boundary condition for cyclic arbitrary mesh interfaces (cyclicAMI) is used at the interfaces within the differential mesh domain. For the velocity and pressure fields of the wall, the zeroGradient boundary condition and no-slip boundary condition are applied individually.

4. Analysis of Numerical Simulation Results

4.1. Verification of Computational Accuracy

To obtain more accurate computational results of the flow field, the mesh orthogonal correction and PIMPLE algorithm’s inner PISO loop iterations are set to 2. The outer SIMPLE loop iterations are set to 40. For transient simulations, a time step of 0.000833 s is chosen, which corresponds to one degree of rotation. For pressure, velocity, and turbulence variables, the permitted final residual is 10⁻⁵. The simulation results of the exterior characteristic parameters of the pump-turbine under various load circumstances are shown in

Table 3. Calculated parameters for operating condition.

Operating Condition		Q11/L·s−1	N11/kW	η/%
0.43QN	OP1	226.87	1.47	66.2
0.54QN	OP2	287.96	2.29	81.2
0.66QN	OP3	351.39	3.04	88.3
0.75QN	OP4	395.96	3.49	89.9
0.8QN (QBEP)	OP5	429.31	3.89	92.3
0.92QN	OP6	489.92	4.41	91.7
QN	OP7	536.87	4.72	89.7

below. As shown in Figure 3, the calculated findings are compared with the experimental data. At various operating conditions, the average errors in the torque and efficiency external characteristic parameters are all less than 7%.

The unit flow rate and unit speed are shown by Equations (34) and (35).

$$Q_{11}=\frac{Q}{D_1^2\sqrt{H}}$$

(34)

$$N_{11}=\frac{N}{D_1^2{H}^{3/2}}$$

(35)

where Q is the flow of the turbine (m³/s); Q₁₁ is unit flow of the turbine (L/s); D₁ is the diameter of the runner (m); H is the head of the turbine (m); N is the power of the turbine (W); N₁₁ is the unit power (W).

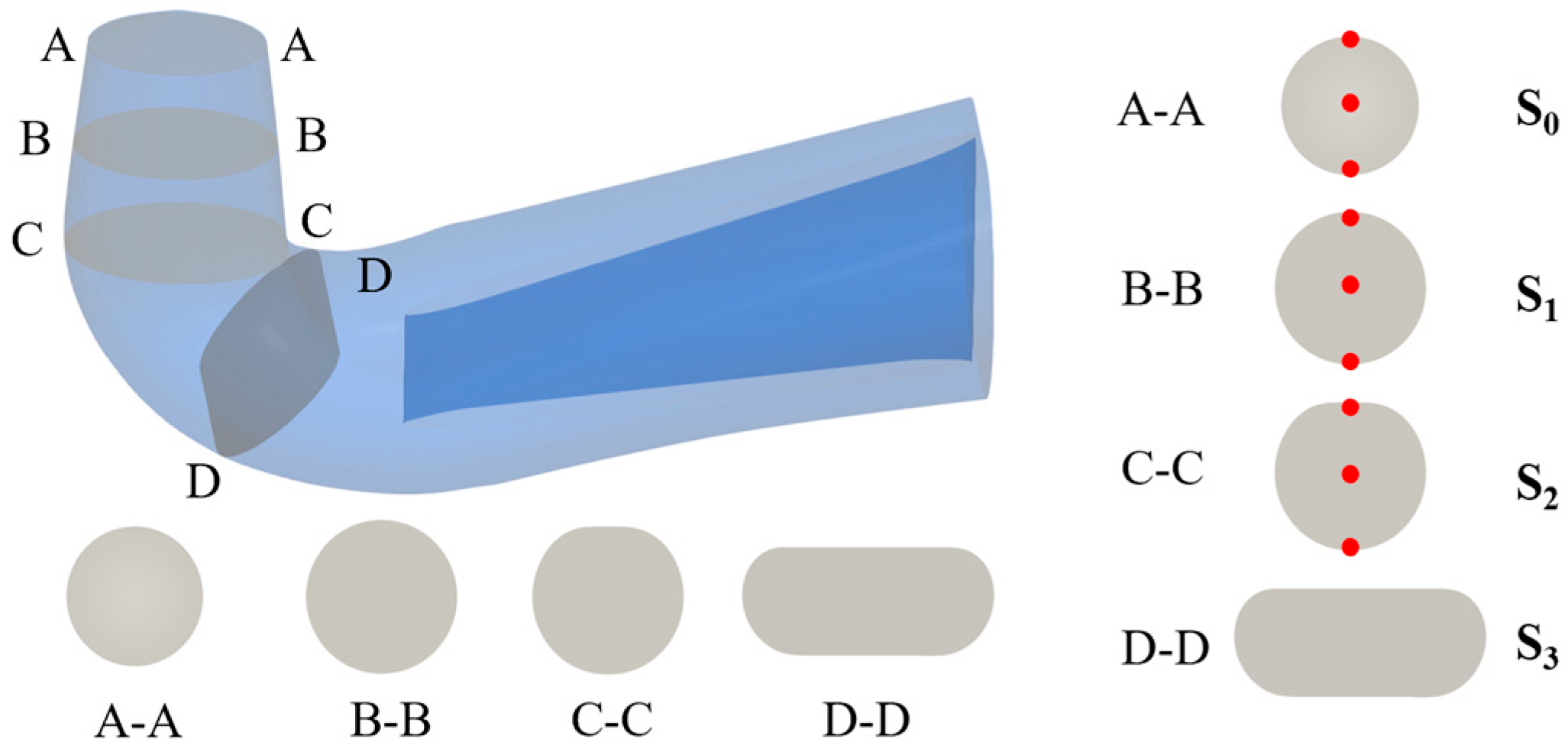
4.2. Monitoring Points and Cross-Sectional Planes

To explore the internal flow distribution, as shown in Figure 4, four sets of monitoring sections, denoted as S₀, S₁, S₂, and S₃, are arranged at the inlet of the draft tube and at positions 0.5D₁ and D₁ downstream from the inlet, as well as in the curved section. On sections S₀, S₁, and S₂, three monitoring points are uniformly arranged along the radial direction. In the subsequent text, the notation S*-* will be used to represent the monitoring points at various positions on these sections.

4.3. Analysis of Internal Flow Field of the Draft Tube

Currently, the Q-criterion vortex identification method is widely applied [20,21,22], defined as shown in Equation (36):

$$Q=\frac{1}{2}({‖B‖}_F^2-{‖A‖}_F^2).$$

(36)

In this equation, B represents the skew-symmetric tensor component obtained from the Cauchy–Stokes decomposition of the velocity gradient tensor, and A represents the symmetric tensor component after the decomposition. ‖ ‖_F denotes the Frobenius norm of the tensor. However, the threshold of Q-criterion needs adjustment for different practical conditions. Furthermore, this method treats both stretching and shear deformation of the fluid as vortex components, making vortex structures susceptible to shear force contamination and leading to inaccurate identification.

Therefore, the third-generation method is needed to mitigate the influence of wall shear stress and further differentiate various vortex components present in the flow field. The comparison between the ${\tilde{\Omega }}_R$ method and Q-criterion used in the runner and draft tube is shown in Figure 5. It is evident that the iso-surface of ${\tilde{\Omega }}_R$ = 0.52 can capture distinct vortex patterns, with more complete radial and longitudinal distribution and clearer internal structures within the vortex core. By efficiently lowering the effect of the wall vortex on the precision of vortex detection, the runner’s channel vortex may be clearly recognized. The vortex core near the inlet and wall are relatively weakened. Thus, this method can partially replace the Q-criterion. Conversely, the Q-criterion requires threshold adjustment to obtain a complete vortex distribution and cannot fully capture the intricate vortex ring transition structures.

Figure 6 illustrates the vortex ropes identified using the ${\tilde{\Omega }}_R$ method under various load conditions. At part load conditions (OP₃ and OP₄), the flow exiting the runner carries the higher tangential velocity component, resulting in spiral vortex ropes rotating in the same direction as the runner. As the turbine flow rate increases, the axial velocity component at the inlet of the draft tube dominates, diminishing the eccentric rotational velocity component. Ultimately, the phenomenon of concentric cylindrical vortex rope appears under the OP₅ condition, while no vortex structures are observed under the OP₆ condition.

Figure 7 depicts variations in the radial sectional velocity components within the draft tube under different load conditions. Under the OP₃ and OP₄ conditions, the vortex ropes within the draft tube exhibit an eccentric spiral distribution. These structures primarily disturb the axial main flow at the inlet of the draft tube, constituting the main reason for the deviation in flow direction. However, their impact on the elbow section is relatively minor. Thus, it can be observed that the axial velocity U_a and tangential velocity U_t at the conical section exhibit more pronounced fluctuations, while the velocity changes are relatively small near the D-D section close to the elbow section. Consequently, the spiral vortex ropes cause more noticeable disruption within the draft tube’s internal flow. Additionally, phenomena such as backflow vortices and secondary flows tend to occur around the vortex patterns, serving as key factors leading to hydraulic losses within the draft tube. Under the OP₅ condition, concentric cylindrical vortex structures emerge, resulting in less disturbance to the internal flow state of the draft tube. Radial velocity components at various sections do not exhibit significant fluctuations. Therefore, under this condition, hydraulic losses within the draft tube are relatively minor.

Figure 8 illustrates the variations in the pressure fluctuation coefficient at different operating conditions for the monitoring points. The pressure fluctuation coefficient is defined by Equation (37):

$$C_P=\frac{\overline{p}}{g\overline{H}}$$

(37)

where $\overline{p}$ represents the mean pressure at the monitoring point (Pa); g is the acceleration due to gravity (m/s²); and $\overline{H}$ signifies the mean head for the given operating condition (m).

Table 4. Summary of pressure pulsation monitoring points.

Operating Condition	f	S0-1	S0-2	S0-3	S1-1	S1-2	S1-3	S2-1	S2-2	S2-3
OP1	0.168fn	0.0267	0.0268	0.0193	0.0242	0.0262	0.0169	0.0128	0.0075	0.0072
OP2	0.168fn	0.03	0.0274	0.0128	0.0276	0.0387	0.0239	0.016	0.0169	0.0157
OP3	0.168fn	0.0128	0.0128	0.0036	0.0159	0.019	0.011	0.0106	0.0092	0.009
OP4	0.168fn	0.0016	0.0016	0.0032	0.0072	0.0063	0.0027	0.0073	0.0068	0.0047

presents the distribution of dominant frequencies and pressure amplitudes at different operating conditions for the pressure monitoring points. It is observed that the motion of vortices within the draft tube induces low-frequency pressure pulsations at 0.168fn. This phenomenon is particularly significant in the straight conical section of the draft tube, affecting the pressure measurement points along this region. The variation in pressure amplitude in the elbow section is less noticeable. Under the OP₂ operating conditions, the pressure amplitude exhibits significant fluctuations, mainly attributed to the oscillations of vortices leading to an eccentric displacement of the main flow direction within the draft tube. Furthermore, the impact of vortices hitting the walls contributes to higher amplitude occurrences. Particularly under the OP₃ conditions, the spiral vortex rope causes substantial disturbances in the radial flow component, resulting in higher pressure fluctuations at certain monitoring points compared to the central point. For instance, the pressure amplitude at monitoring point S₂ in section S₂ is approximately 15% higher than the other points. This discrepancy is mainly attributed to the instability of the vortex tail, which might lead to periodic shedding during its rotation.

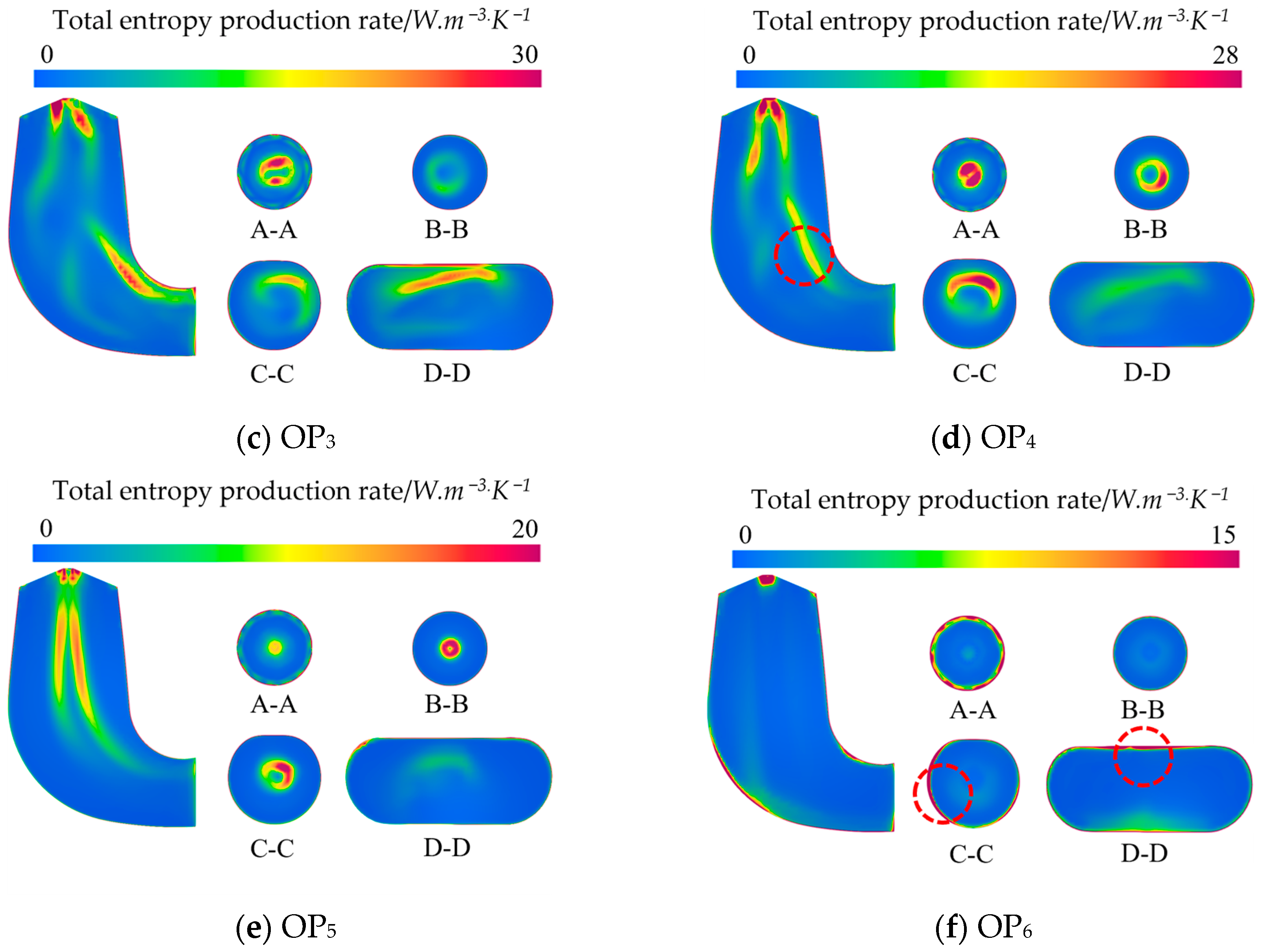
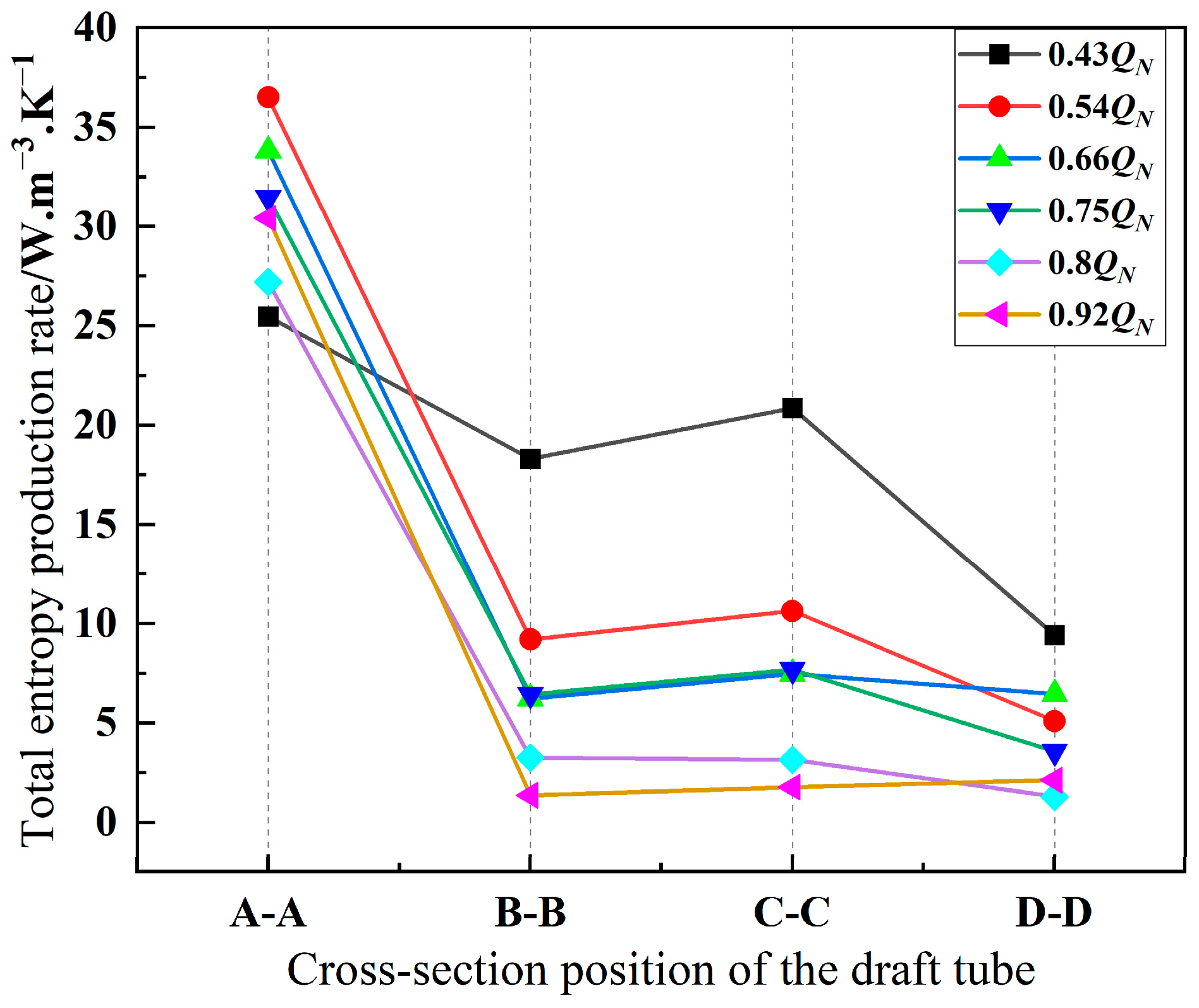
4.4. Analysis of Entropy Production Results

In order to investigate the energy loss produced by the pump-turbine under different loading conditions, the hydraulic loss calculated by the entropy production method is transformed through Equation (38):

$$h_s=\frac{T·S_D}{\rho gQ}$$

(38)

where T is the temperature (K); S_D is the total entropy production of the calculation domain (W/K); Q is the flow (m³/s).

As demonstrated in Figure 9, the distribution of hydraulic losses is predominantly concentrated around the runner and draft tube, with losses at the spiral casing accounting for quite a relatively small percentage. In the part load operation condition OP₁, the unit produces a more intense hydraulic loss phenomenon. In this condition, the hydraulic loss at the runner parts can reach 2.78 m, the hydraulic loss inside the draft tube is 2.13 m, and the sum of the hydraulic loss of both can reach 83.6% of the total hydraulic loss of the calculation domain. The remaining hydraulic loss is caused by the head loss of the guide vane at 0.96 m. With the increase in the unit flow, the distribution of the h_s inside the unit shows a trend of decreasing and then rising steadily, which is mainly manifested in the fact that when the unit operates near the Q_BEP, the internal flow field is relatively smooth, so the hydraulic loss at each component is small. And as the guide vane opening (GVO) increases and the flow rate reaches the rated flow rate Q_N, the overall hydraulic loss of the unit is in a relatively stable state, as shown in the OP₆ and OP₇ operating conditions in Figure 9. The main source of hydraulic loss is the interaction between the water and the wall inside the runner.

As shown in Figure 10, under different operating load conditions, for the hydraulic loss calculated by the total entropy production distribution inside the draft tube and the quantitative analysis of each type of entropy production, it can be seen that the indirect entropy production (EPTD) occupies a significant portion of the operating conditions up to 85%; secondly, for the wall entropy production (EPWS), under the influence of the wall shear force, it accounts for up to 12%. Under the OP₁ part load condition, the hydraulic loss caused by indirect entropy production occupies a dominant position, and the hydraulic loss can reach 1.91 m. While under the OP₅ condition, the actual operation of the unit is close to the optimal condition point, so the hydraulic loss inside the unit is relatively small, and the total entropy head loss inside the draft tube is 0.26 m, of which the indirect entropy head loss is 0.22 m; in this condition, hydraulic efficiency reaches its peak.

Figure 11 shows the local total entropy production rate (TEPR) distribution at each cross-section inside the draft tube under different operating conditions, and it can be found that the TEPR is gradually decreased as the flow rate increases, and the entropy distribution is shifted from the internal flow field to the wall surface. Under the part load condition of OP₁, the flow inside the unit is subject to the friction of the GVs and runner components, thus generating more wall energy loss, and at the same time, the flow direction of the internal flow field in the inlet of the draft tube is normal to the outflow. At the simultaneous action on the wall of the draft tube, it is also subjected to the vortex reflux at the inlet and the action of the eccentric helical vortex rope, and the entropy is mostly concentrated in the wall of the bent elbow of the draft tube, as the distribution of the high entropy production area is in the cross-section of C-C. As the distribution of the high entropy production area in the C-C cross-section shows, most of the entropy production is concentrated in the elbow wall of the draft tube, while the distribution of entropy production at the cross-section is mainly affected by the wall shear force and velocity gradient. In addition, the vortex rope will produce reverse gradient vortex flow in the surrounding area during the movement process, so it will produce more obvious energy loss. Combining this with the analysis of the TEPR value of the cross-section can produce a more accurate internal flow distribution. In Figure 12, the relationship between the vortex rope and the TEPR is demonstrated in the cross-section of the draft tube. EPTD is mostly distributed around the vortex rope. With the increase in the guide vanes opening (GVO), the high magnitude area of the TEPR is concentrated in the wall area, as shown in the red circle area at the cross-section under the OP₆ condition, and the main energy loss comes from the wall shear effect when the unit operates near the rated operating condition.

5. Conclusions

In this paper, we employ OpenFOAM software to conduct a three-dimensional numerical simulation of the Francis pump-turbine. The hydraulic loss of vortex ropes is performed in conjunction with the entropy production theory and ${\tilde{\Omega }}_R$ method. The key findings are summarized as follows:

(1)

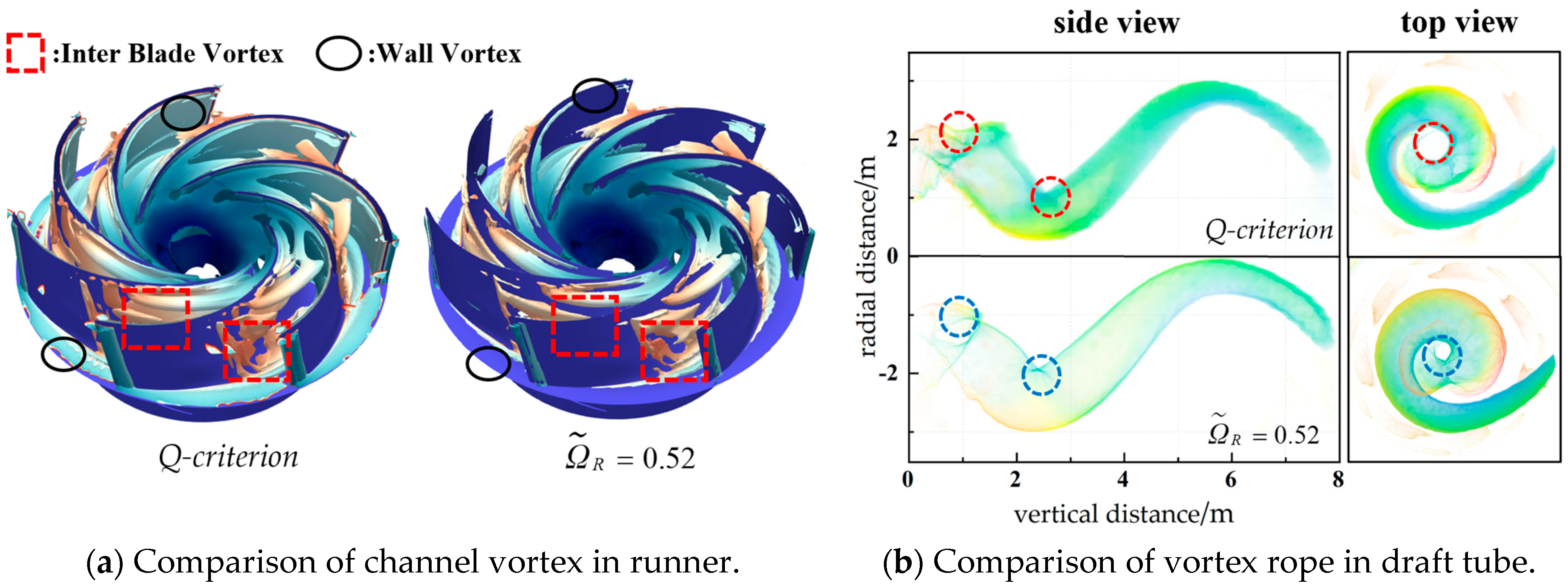
By comparing different vortex identification methods applied in the runner and draft tube, the ${\tilde{\Omega }}_R$ method can precisely identify different types of strong and weak vortex structures and reduce the interference of wall shear stress on the accuracy of vortex identification to obtain distinct and thorough vortex rope outlines.

(2)

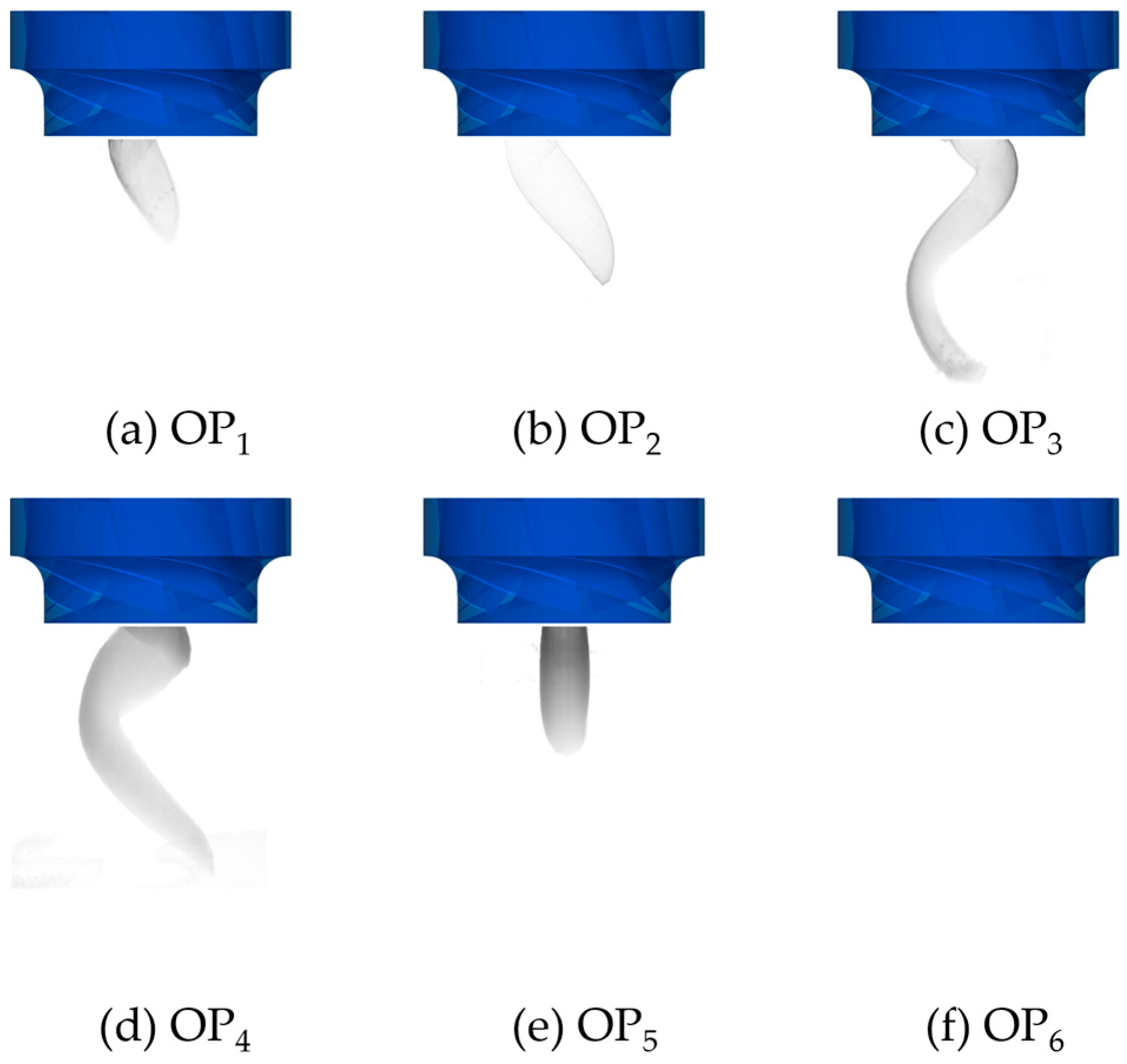
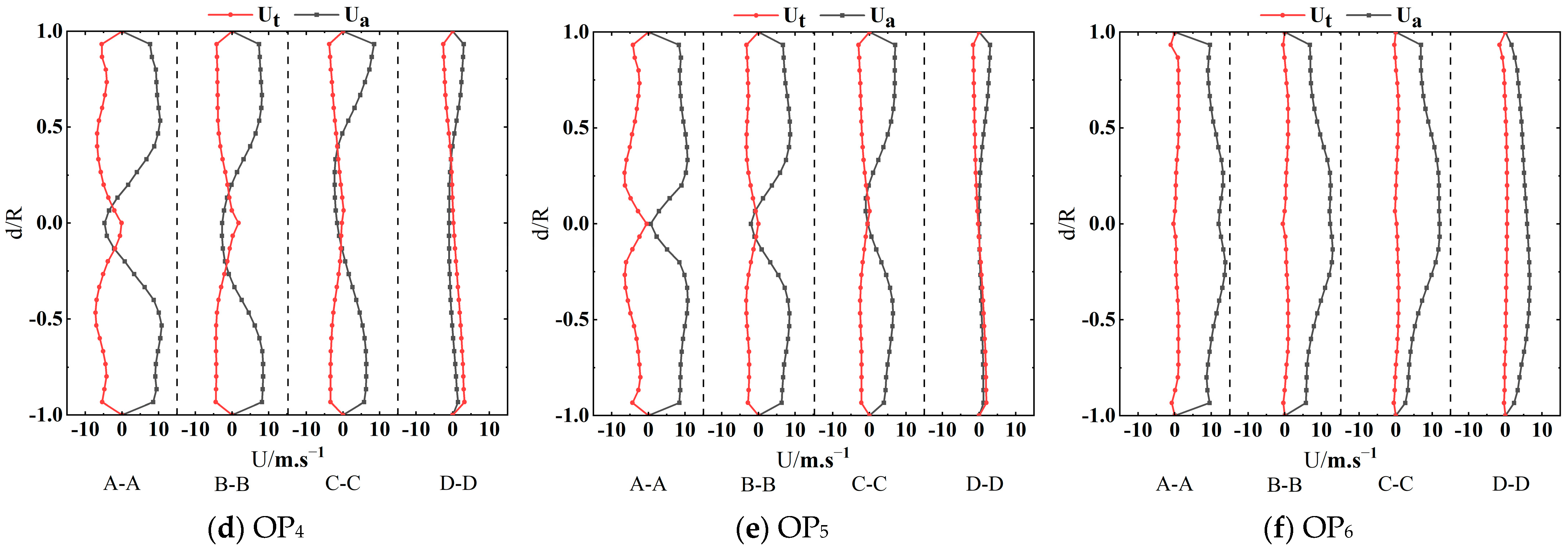
The spiral vortex rope inside the draft tube is primarily caused by the circumferential velocity component at the runner outlet. Furthermore, the low-frequency pulsation phenomenon of 0.168fn at each cross-section can be observed, and the motion of the rotating vortex rope induces significant amplitude fluctuations of both tangential and axial velocity. However, as the flow rate increases, the flow pattern within the draft tube gradually improves. The vortex rope developed is less disruptive to the flow field.

(3)

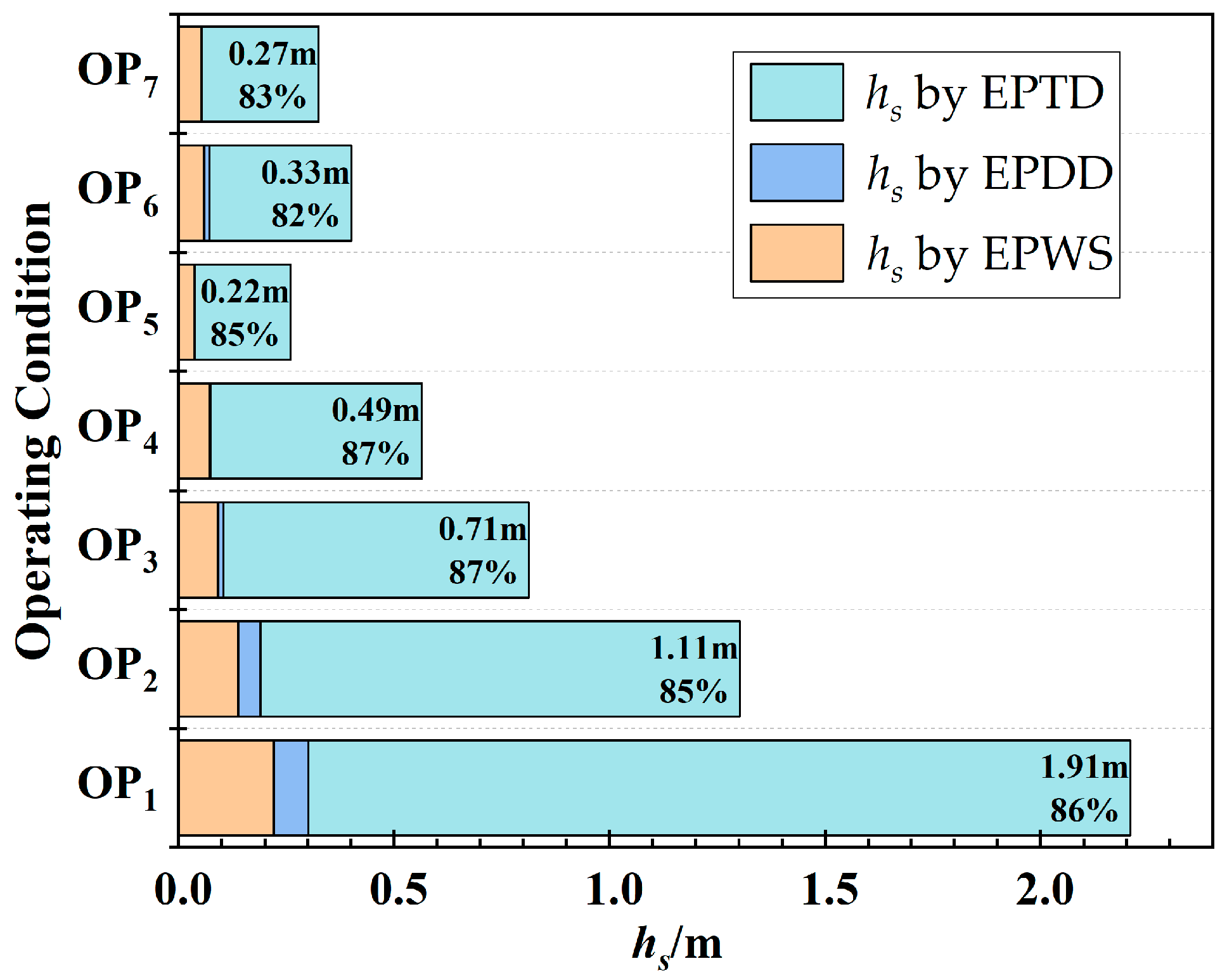
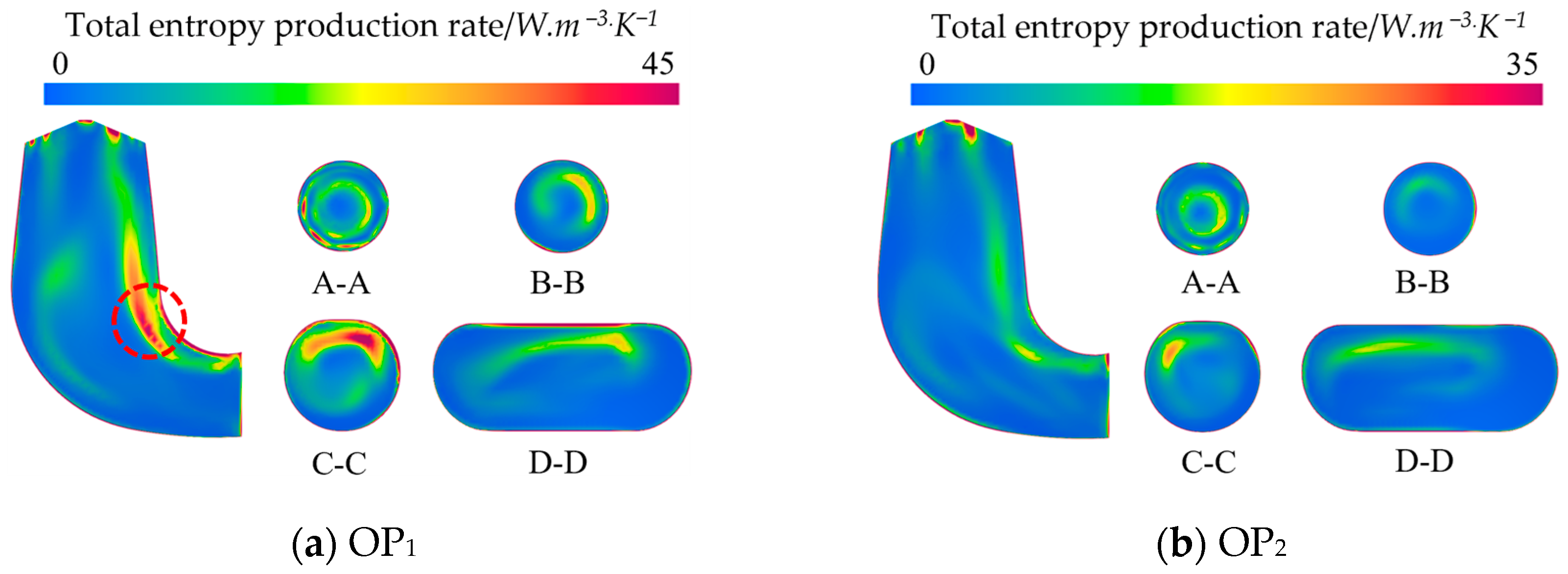
The dispersion of the vortex ropes substantially correlates with the local entropy production rate (LEPR) inside the draft tube. Since the vortex rope would drastically change the internal flow field distribution during movements, it may cause hydraulic excitation phenomena including large-scale vortex and backflow, which would result in more hydraulic losses. Nevertheless, the hydraulic loss in the flow field inside the draft tube steadily decreases towards the Q_N conditions, and TEPR is mostly spread along the wall of the draft tube.

In future research, we will use this paper as a basis for further numerical simulations and experimental studies on vortex rope suppression methods, such as optimization of the structure of the rotor blades and draft tube sections, air injection in the draft tube, the introduction of vortex suppression devices, etc.