Fault Diagnosis of Autonomous Underwater Vehicle with Missing Data Based on Multi-Channel Full Convolutional Neural Network
Abstract
:1. Introduction
2. Missing Data Estimation with Multiple Imputation
2.1. Random Forest Algorithm
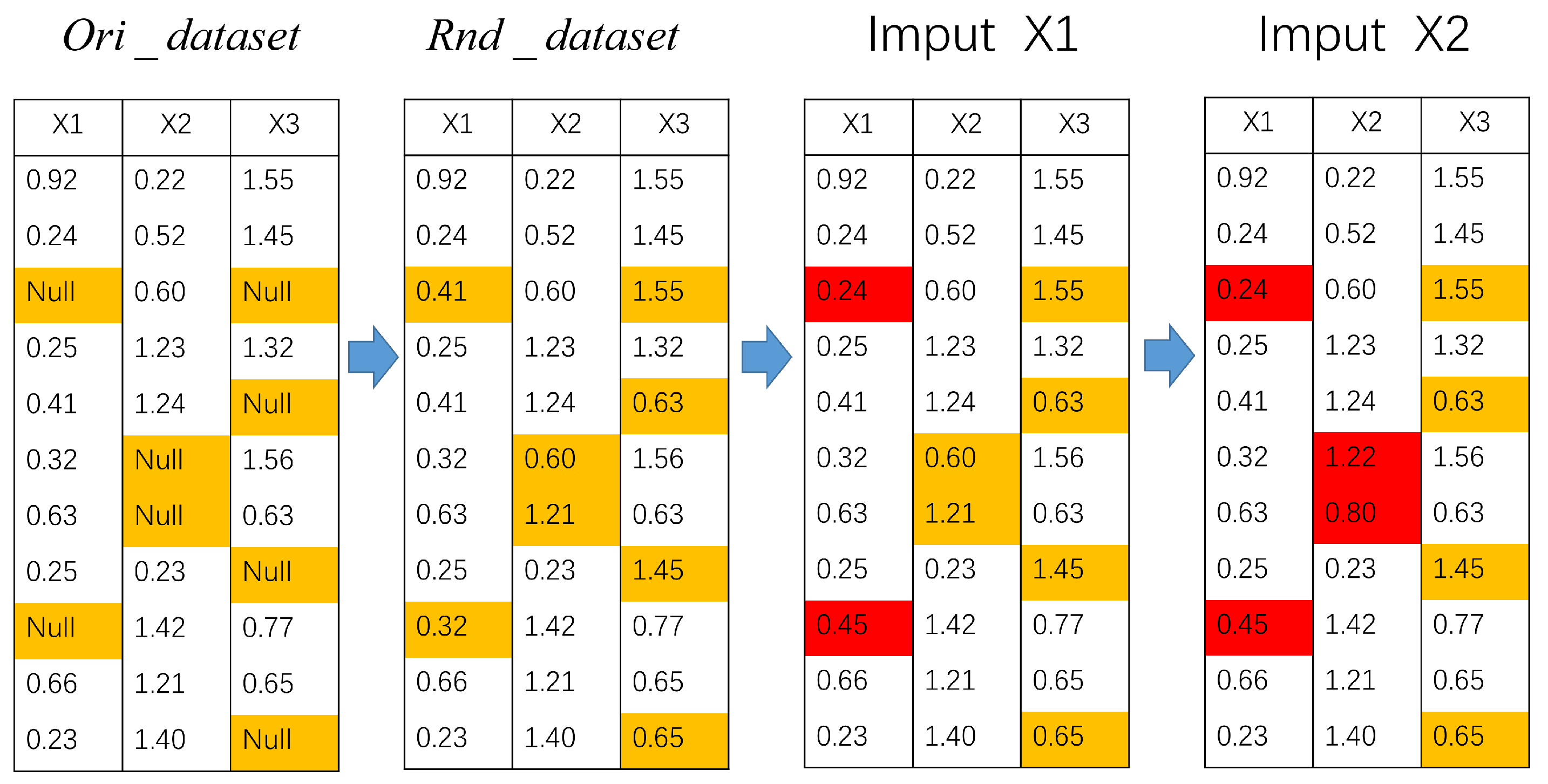
2.2. RF-MICE Technique
3. CNN Architecture Design
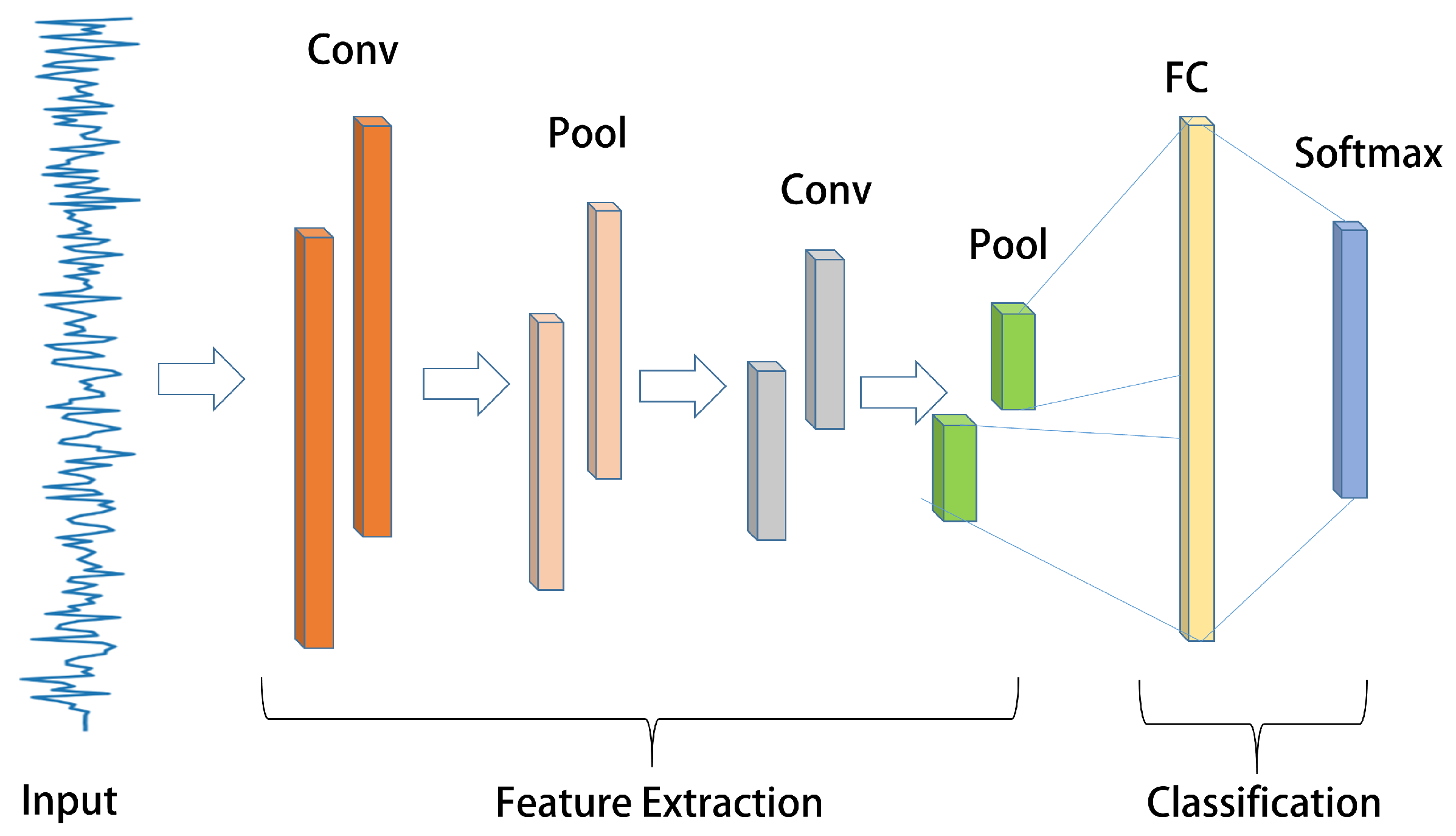
3.1. Typical Model of CNN
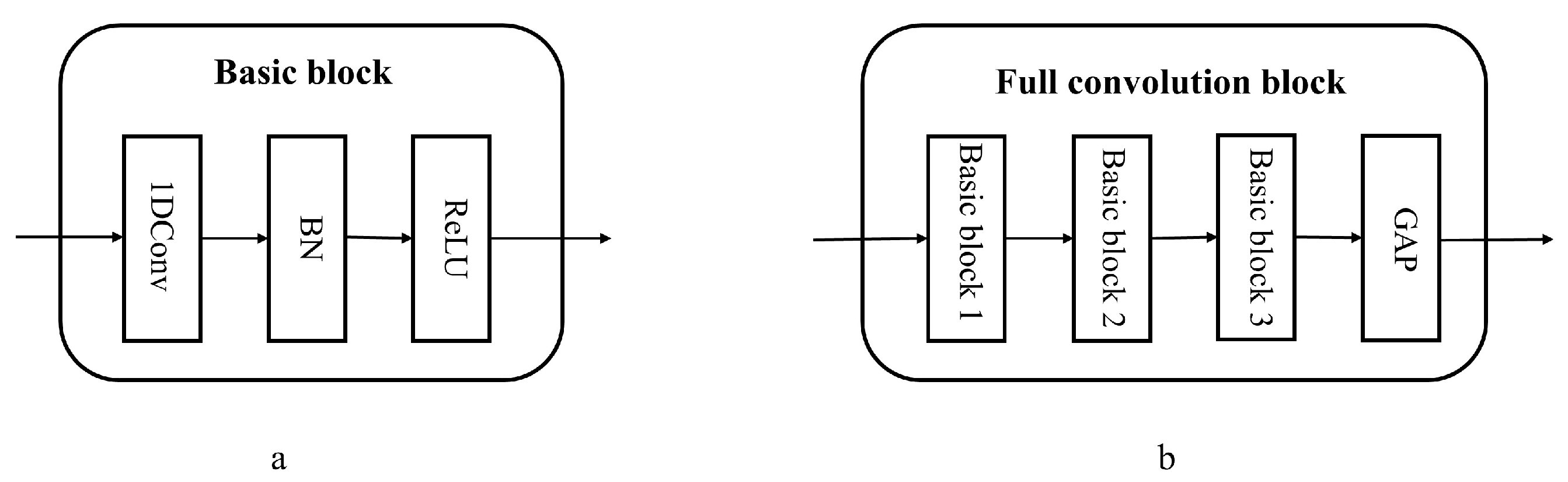
3.2. 1D-CNN Model
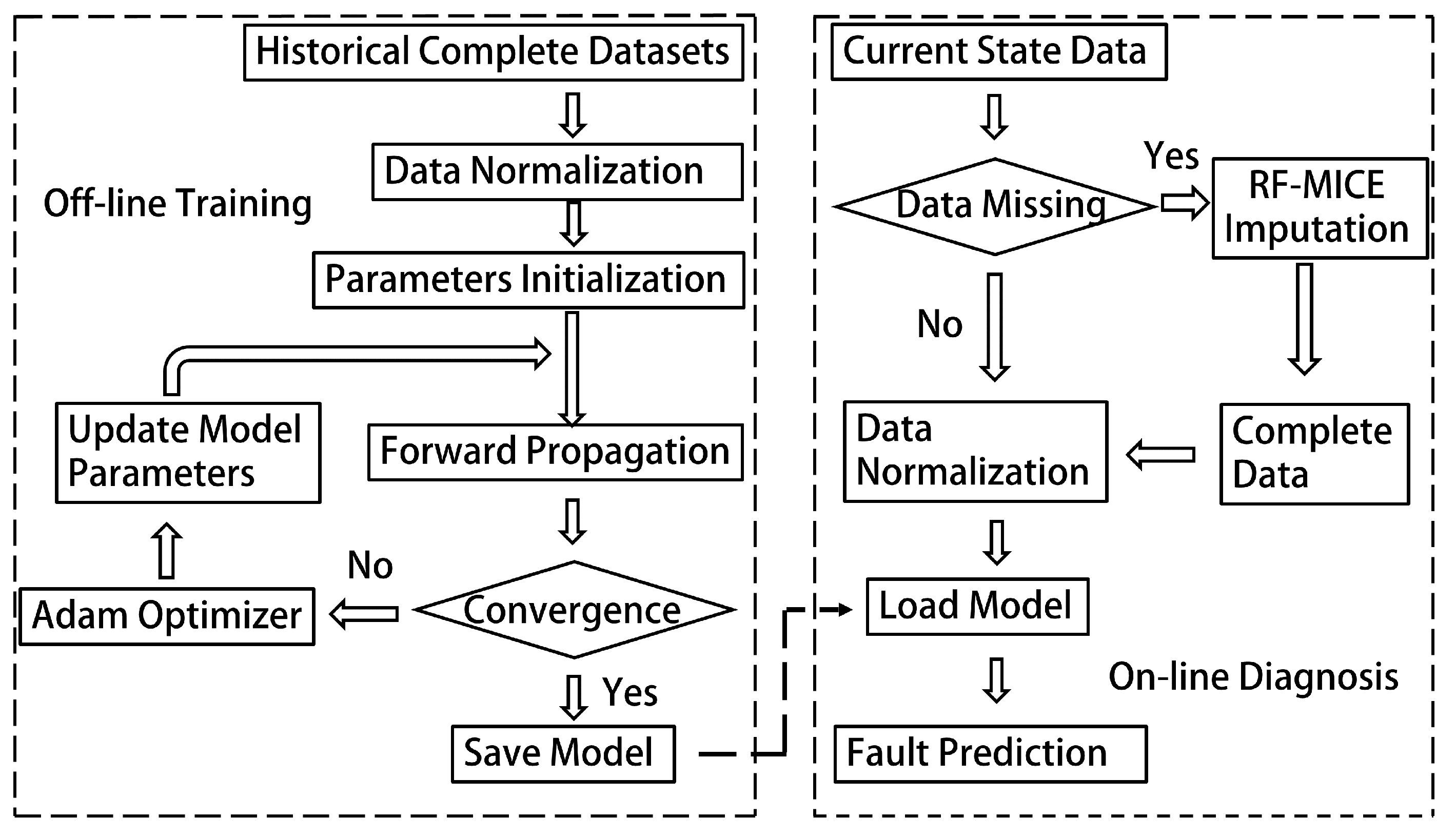
4. MC-FCNN-Based Fault Diagnosis
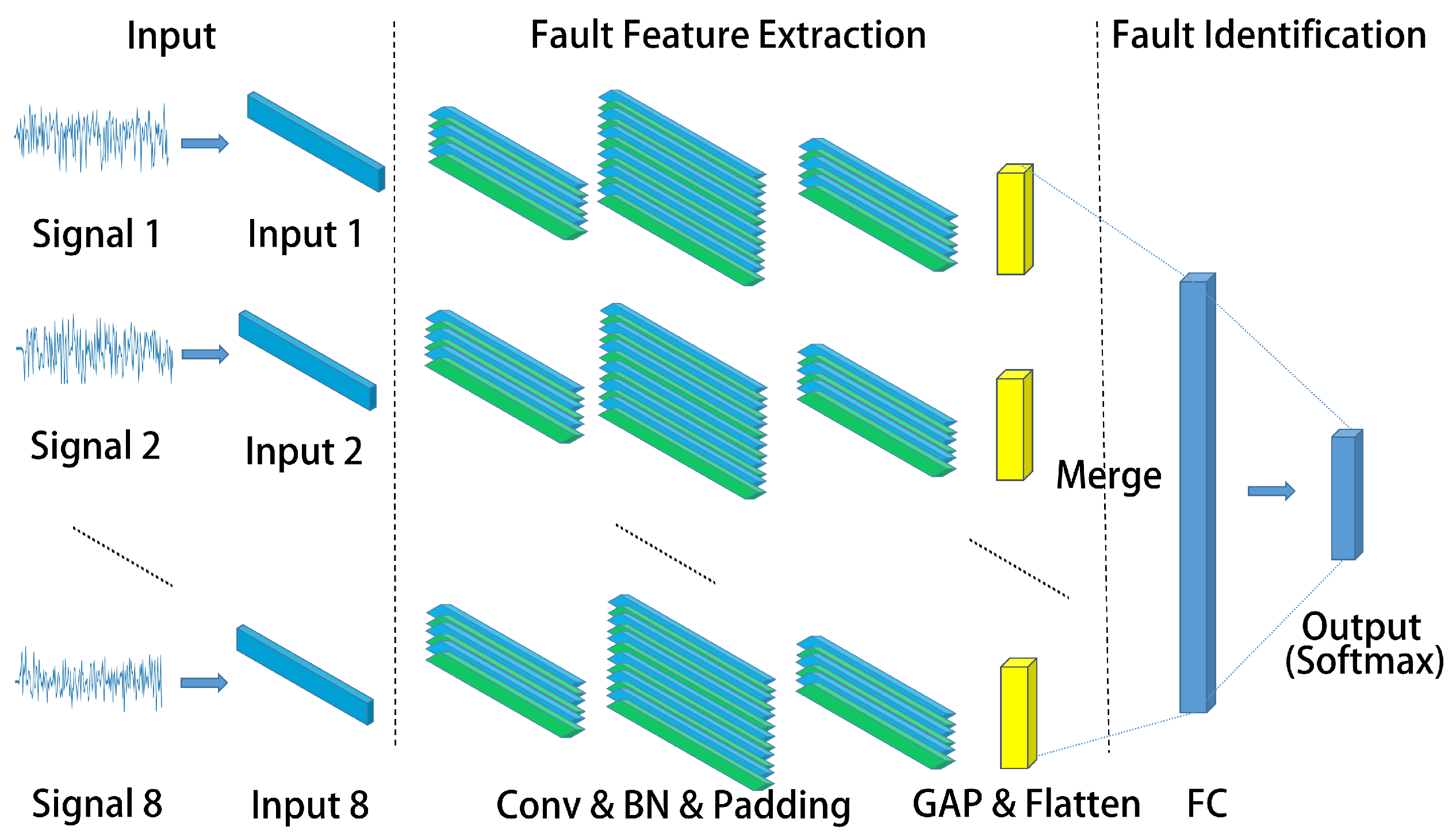
4.1. MC-FCNN Architecture
4.2. Fault Diagnosis Scheme
5. Experimental Results and Analysis
5.1. Experimental Data of AUVs
5.2. Data Pre-Processing
5.3. Comparisons
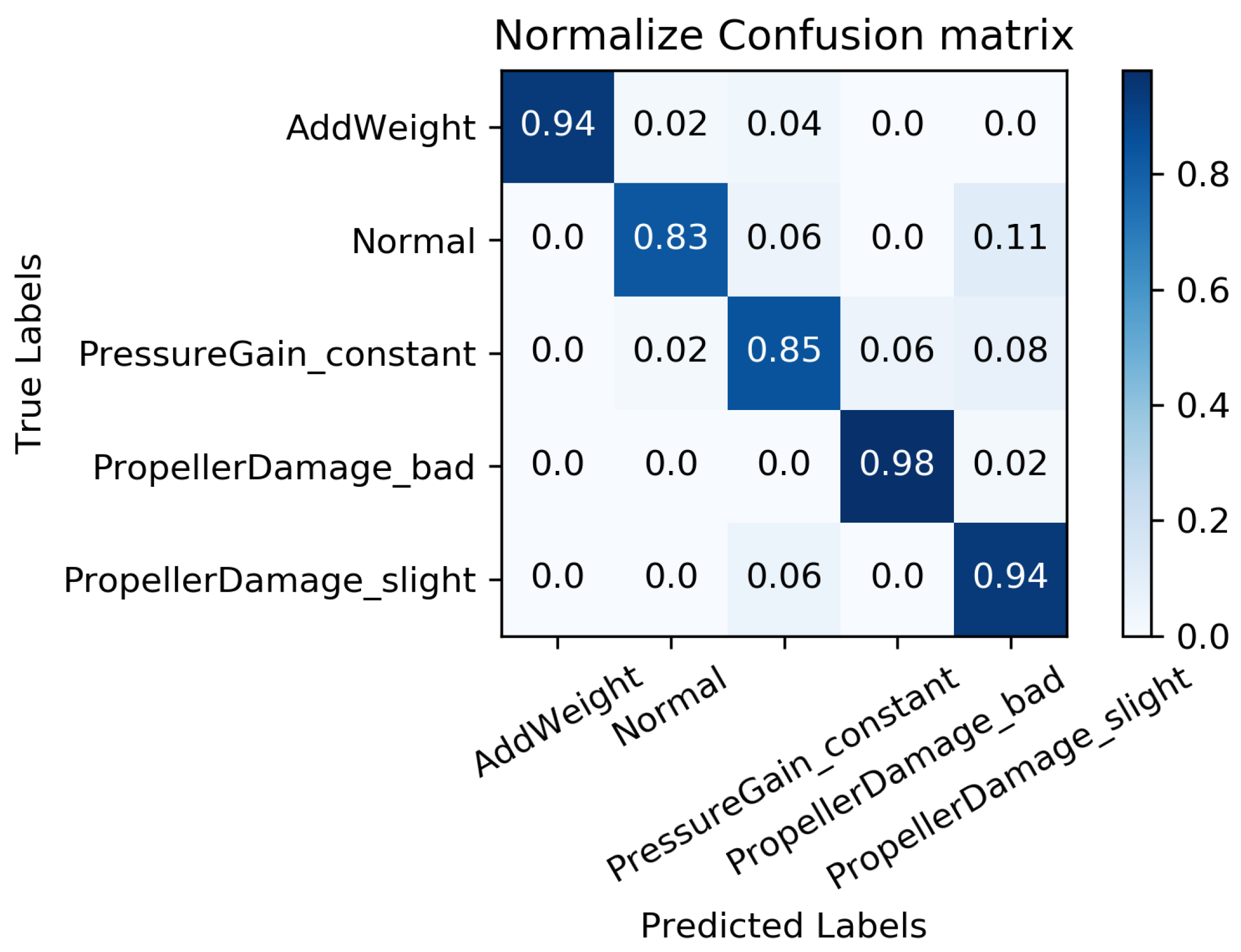
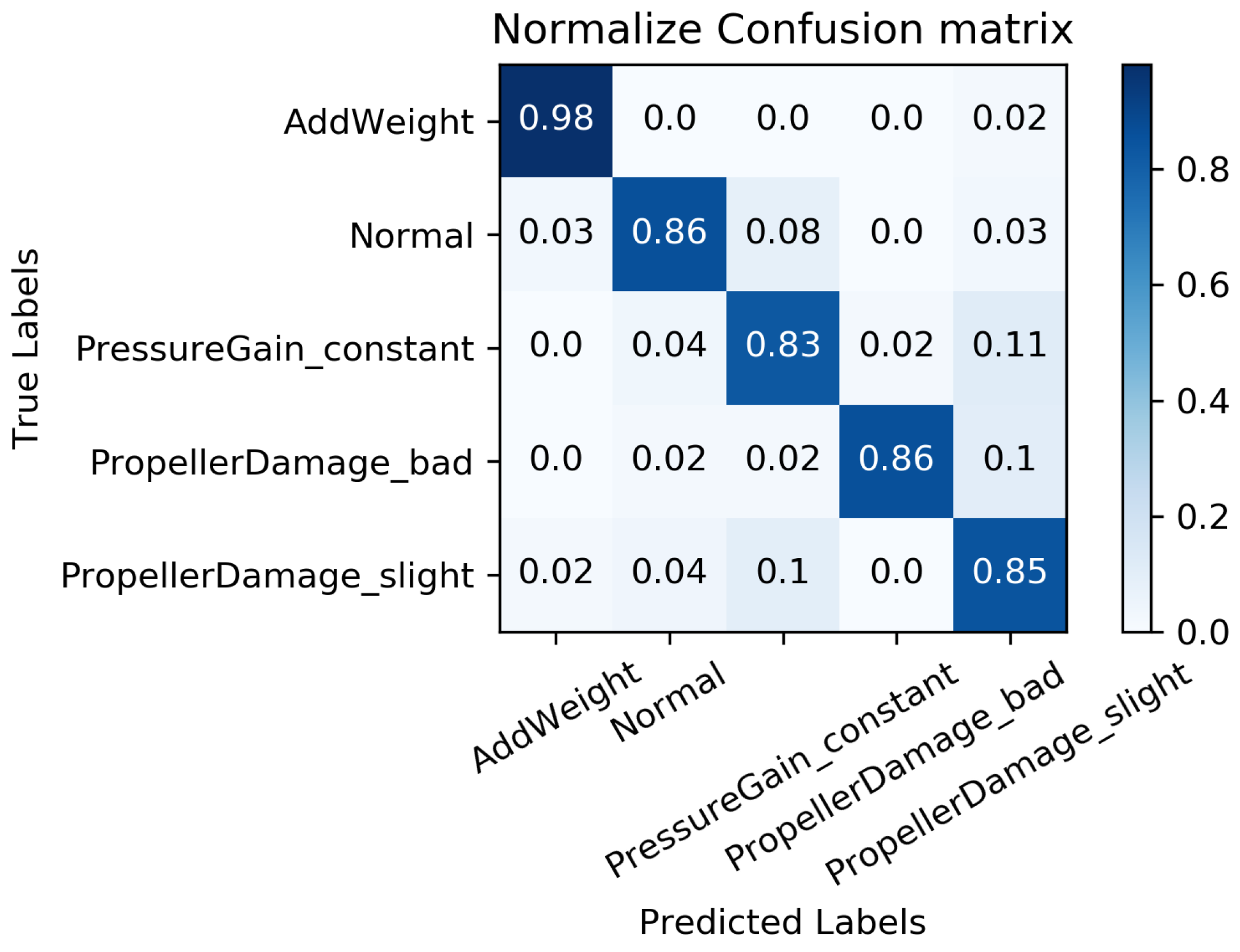
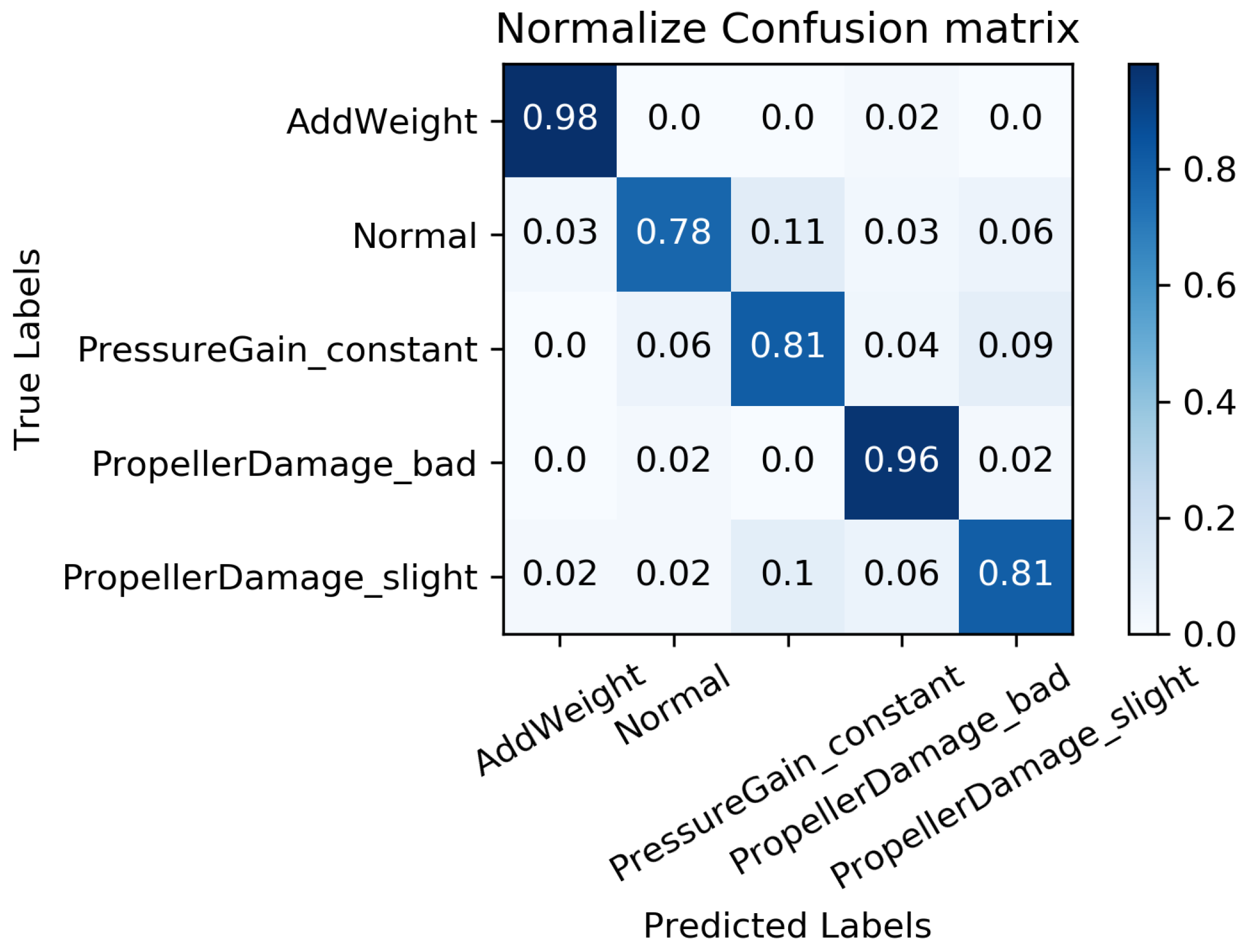
5.4. MC-FCNN-Based Fault Diagnosis Analysis with Different Missing Data
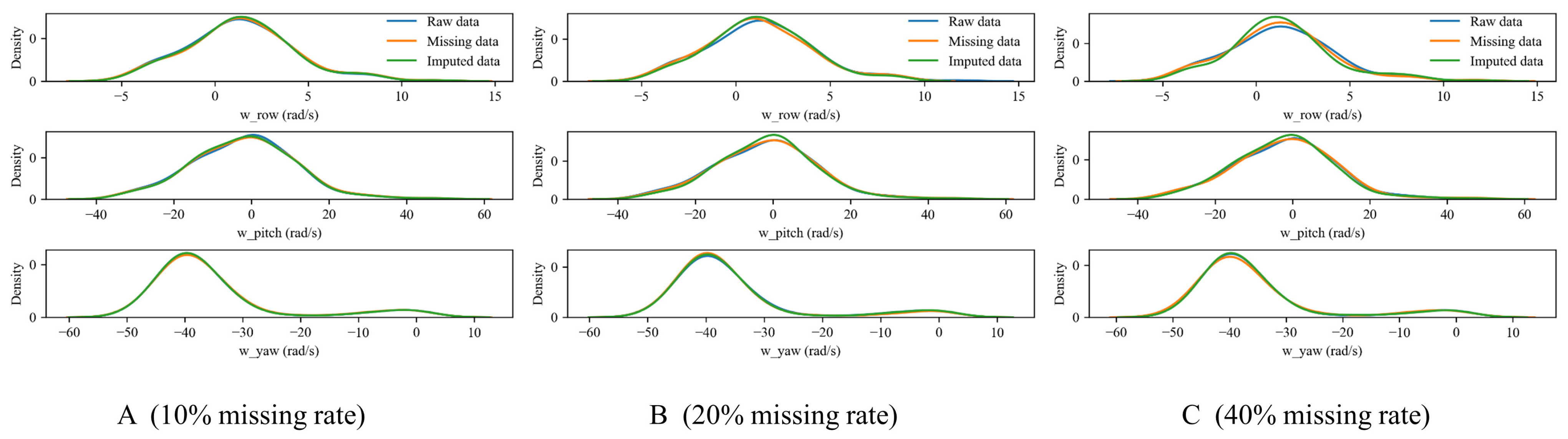
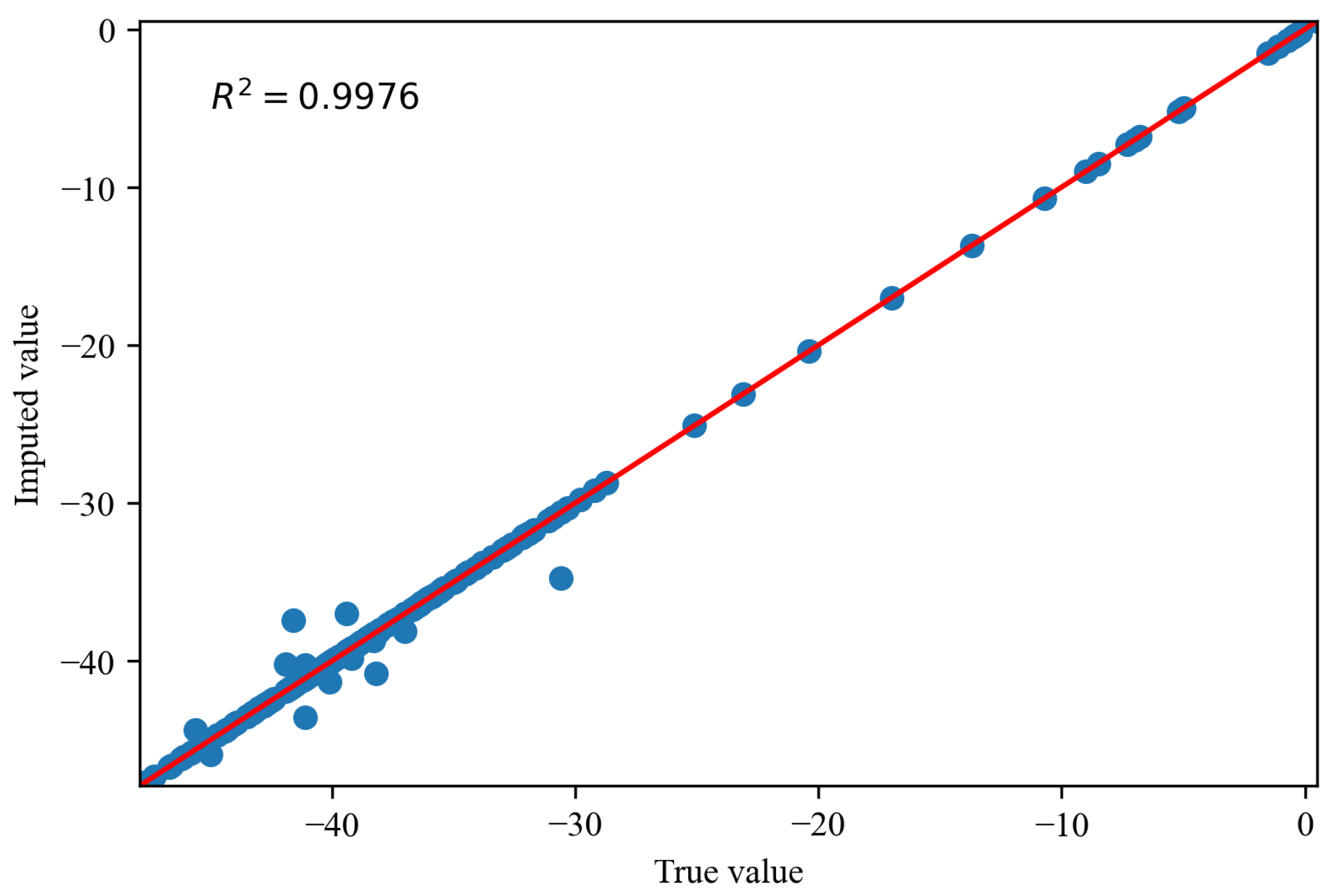
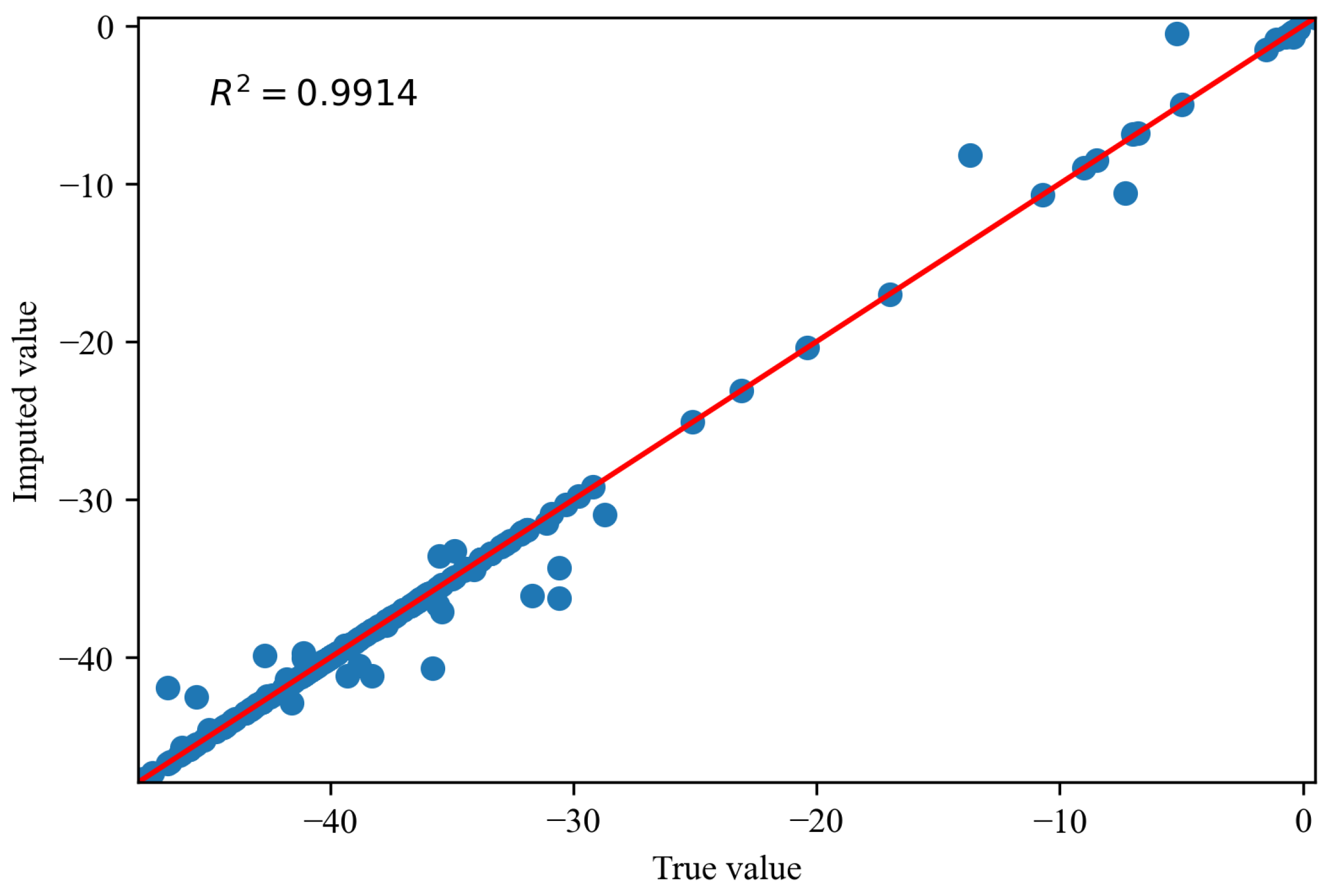
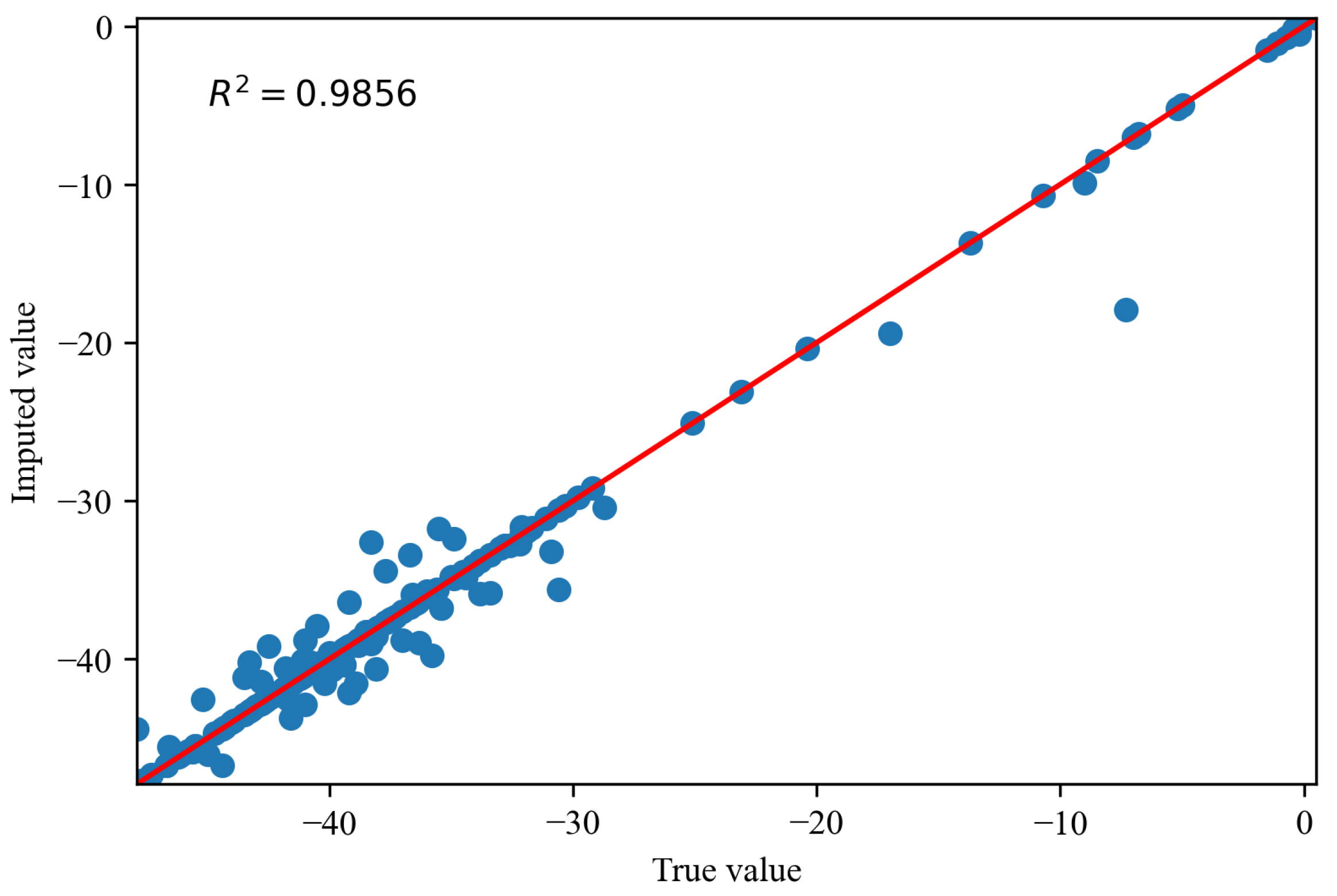
5.4.1. Evaluation of Missing Data Imputation Based on RF-MICE
5.4.2. Fault Diagnosis Result with Different Missing Data
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| MLP | Multilayer Perception |
| MC-FCNN | Multi Channel Full Convolutional Neural Network |
| AUV | Autonomous Underwater Vehicle |
| RF-MICE | Random Forest Multiple Imputation by Chained Equations |
| MAR | Missing At Random |
References
- Freeman, P.; Pandita, R.; Srivastava, N.; Balas, G.J. Model-based and data-driven fault detection performance for a small UAV. IEEE ASME Trans. Mechatron. 2013, 18, 1300–1309. [Google Scholar] [CrossRef]
- Chen, H.T.; Liu, Z.G.; Alippi, C.; Huang, B.; Liu, D. Explainable intelligent fault diagnosis for nonlinear dynamic systems: From unsupervised to supervised learning. IEEE Trans. Neural Netw. Learn. 2022, 8, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.T.; Luo, H.; Huang, B.; Jiang, B.; Kaynak, O. Transfer Learning-Motivated Intelligent Fault Diagnosis Designs: A Survey, Insights, and Perspectives. IEEE Trans. Neural Netw. Learn. 2023, 7, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Abed, W.; Sharma, S.; Sutton, R. Neural network fault diagnosis of a trolling motor based on feature reduction techniques for an unmanned surface vehicle. Proc. Inst. Mech. Eng. H 2015, 229, 738–750. [Google Scholar] [CrossRef]
- Zhang, M.J.; Yin, B.J.; Liu, W.X.; Wang, Y.J. Fault feature extraction and fusion of AUV thruster under random interference. J. Huazhong Univ. Sci. Technol. 2015, 43, 22–54. [Google Scholar]
- Chauhan, V.K.; Dahiya, K.; Sharma, A. Problem formulations and solvers in linear SVM: A review. Artif. Intell. Rev. 2019, 52, 803–855. [Google Scholar] [CrossRef]
- Zhang, M.J.; Wu, J.; Chu, Z. Multi-fault diagnosis for autonomous underwater vehicle based on fuzzy weighted support vector domain description. China Ocean Eng. 2014, 28, 599–616. [Google Scholar] [CrossRef]
- Zhao, R.; Yan, R.Q.; Chen, Z.H.; Mao, K.Z.; Wang, P.; Gao, R.X. Deep learning and its applications to machine health monitoring. Mech. Syst. Signal Process. 2019, 115, 213–237. [Google Scholar] [CrossRef]
- Lei, Y.G.; Yang, B.; Jiang, X.W.; Jia, F.; Li, N.P.; Nandi, A.K. Applications of machine learning to machine fault diagnosis: A review and roadmap. Mech. Syst. Signal Process. 2020, 138, 106587. [Google Scholar] [CrossRef]
- Tang, S.N.; Yuan, S.Q.; Zhu, Y. Deep learning-based intelligent fault diagnosis methods toward rotating machinery. IEEE Access 2019, 8, 9335–9346. [Google Scholar] [CrossRef]
- Zhu, D.Q.; Sun, B. Information fusion fault diagnosis method for unmanned underwater vehicle thrusters. IET Electr. Syst. Transp. 2013, 3, 102–111. [Google Scholar] [CrossRef]
- Nascimento, S.; Valdenegro-Toro, M. Modeling and soft-fault diagnosis of underwater thrusters with recurrent neural networks. IFAC-PapersOnLine 2018, 51, 80–85. [Google Scholar] [CrossRef]
- Ren, H.; Qu, J.F.; Chai, Y.; Tang, Q.; Ye, X. Deep learning for fault diagnosis: The state of the art and challenge. J. Control Decis. 2017, 32, 1345–1358. [Google Scholar]
- Jiang, Y.; Feng, C.; He, B.; Guo, J.; Wang, D.R.; PengFei, L.V. Actuator fault diagnosis in autonomous underwater vehicle based on neural network. Sens. Actuators A 2021, 324, 112668. [Google Scholar] [CrossRef]
- Yeo, S.J.; Choi, W.S.; Hong, S.Y.; Song, J.H. Enhanced convolutional neural network for in Situ AUV thruster health monitoring using acoustic signals. Sensors 2022, 22, 7073. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.M.; Wang, Y.Z.; Yu, Y.; Wang, J.R.; Gao, J. A Fault Diagnosis Method for the Autonomous Underwater Vehicle via Meta-Self-Attention Multi-Scale CNN. J. Mar. Sci. Eng. 2023, 11, 1121. [Google Scholar] [CrossRef]
- Ji, D.X.; Yao, X.; Li, S.; Tang, Y.G.; Tian, Y. Model-free fault diagnosis for autonomous underwater vehicles using sequence convolutional neural network. Ocean Eng. 2021, 232, 108874. [Google Scholar] [CrossRef]
- Jinn, J.H.; Sedransk, J. Effect on secondary data analysis of common imputation methods. Sociol. Methodol. 1989, 19, 213–241. [Google Scholar] [CrossRef]
- Khatibisepehr, S.; Huang, B. Dealing with Irregular Data in Soft Sensors: Bayesian Method and Comparative Study. Ind. Eng. Chem. Res. 2008, 47, 8713–8723. [Google Scholar] [CrossRef]
- Thomas, T.; Rajabi, E. A systematic review of machine learning-based missing value imputation techniques. Data Technol. Appl. 2021, 55, 558–585. [Google Scholar] [CrossRef]
- Kokla, M.; Virtanen, J.; Kolehmainen, M.; Paananen, J.; Hanhineva, K. Random forest-based imputation outperforms other methods for imputing LC-MS metabolomics data: A comparative study. BMC Bioinf. 2019, 20, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Feng, R.; Grana, D.; Balling, N. Imputation of missing well log data by random forest and its uncertainty analysis. Comput. Geosci. 2021, 152, 104763. [Google Scholar] [CrossRef]
- Van, B.S.; Groothuis, O.K. mice: Multivariate imputation by chained equations in R. J. Stat. Softw. 2011, 45, 1–67. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Azur, M.J.; Stuart, E.A.; Frangakis, C.; Leaf, P.J. Multiple imputation by chained equations: What is it and how does it work? Int. J. Methods Psychiatr. Res. 2011, 20, 40–49. [Google Scholar] [CrossRef] [PubMed]
- Gu, J.X.; Wang, Z.H.; Kuen, J.; Ma, L.Y.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.X.; Wang, G.; Cai, J.F. Recent advances in convolutional neural networks. Pattern Recognit. 2018, 77, 354–377. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Avci, O.; Abdeljaber, O.; Ince, T.; Gabbouj, M.; Inman, D.J. 1D convolutional neural networks and applications: A survey. Mech. Syst. Signal Process. 2021, 151, 107398. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 11–12 June 2015; pp. 3431–3440. [Google Scholar]
- Lin, M.; Chen, Q.; Yan, S. Network In Network. arXiv 2013, arXiv:1312.4400. [Google Scholar]
- Ji, D.X.; Yao, X.; Li, S.; Tang, Y.G.; Tian, Y. Autonomous underwater vehicle fault diagnosis dataset. Data Brief. 2021, 39, 107477. [Google Scholar] [CrossRef]
- Ji, D.X.; Wang, R.; Zhai, Y.Y.; Gu, H.T. Dynamic modeling of quadrotor AUV using a novel CFD simulation. Ocean Eng. 2021, 237, 1096501. [Google Scholar] [CrossRef]
- Wang, Z.; Yan, W.; Oates, T. Time series classification from scratch with deep neural networks: A strong baseline. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 1578–1585. [Google Scholar]





| Layer1 | Kernel Size | Stride | Channel | Padding | Output |
|---|---|---|---|---|---|
| 1DConv1 | 8 | 1 | 16 | SAME | 196 |
| 1DConv2 | 5 | 1 | 32 | SAME | 196 |
| 1DConv3 | 3 | 1 | 16 | SAME | 196 |
| GAP | 196 | - | 16 | - | 1 |
| Working Conditions | Size | Label |
|---|---|---|
| Load increase | 268 | 0 |
| Normal | 182 | 1 |
| Depth sensor failure | 266 | 2 |
| Propeller severe damage | 249 | 3 |
| Propeller slight damage | 260 | 4 |
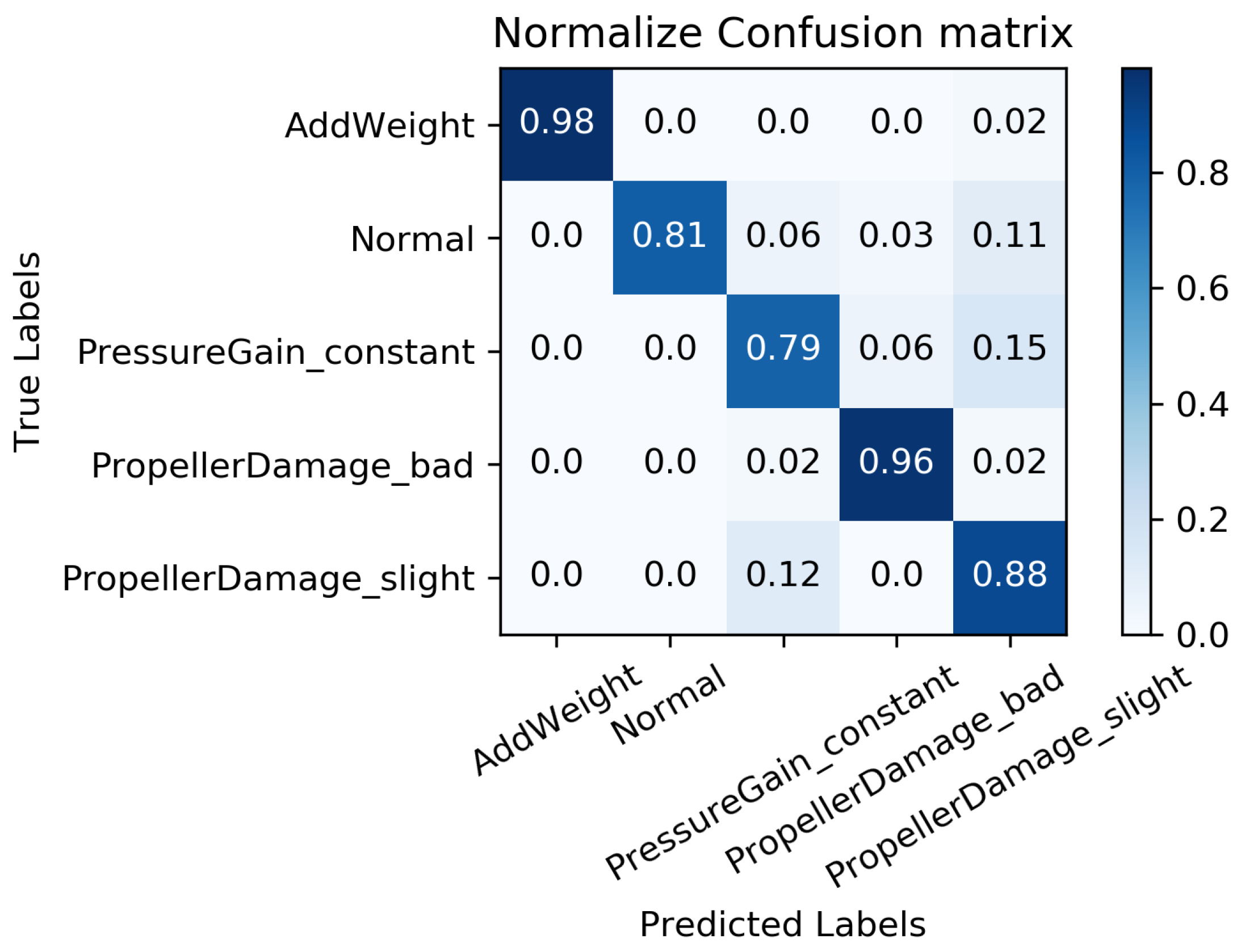
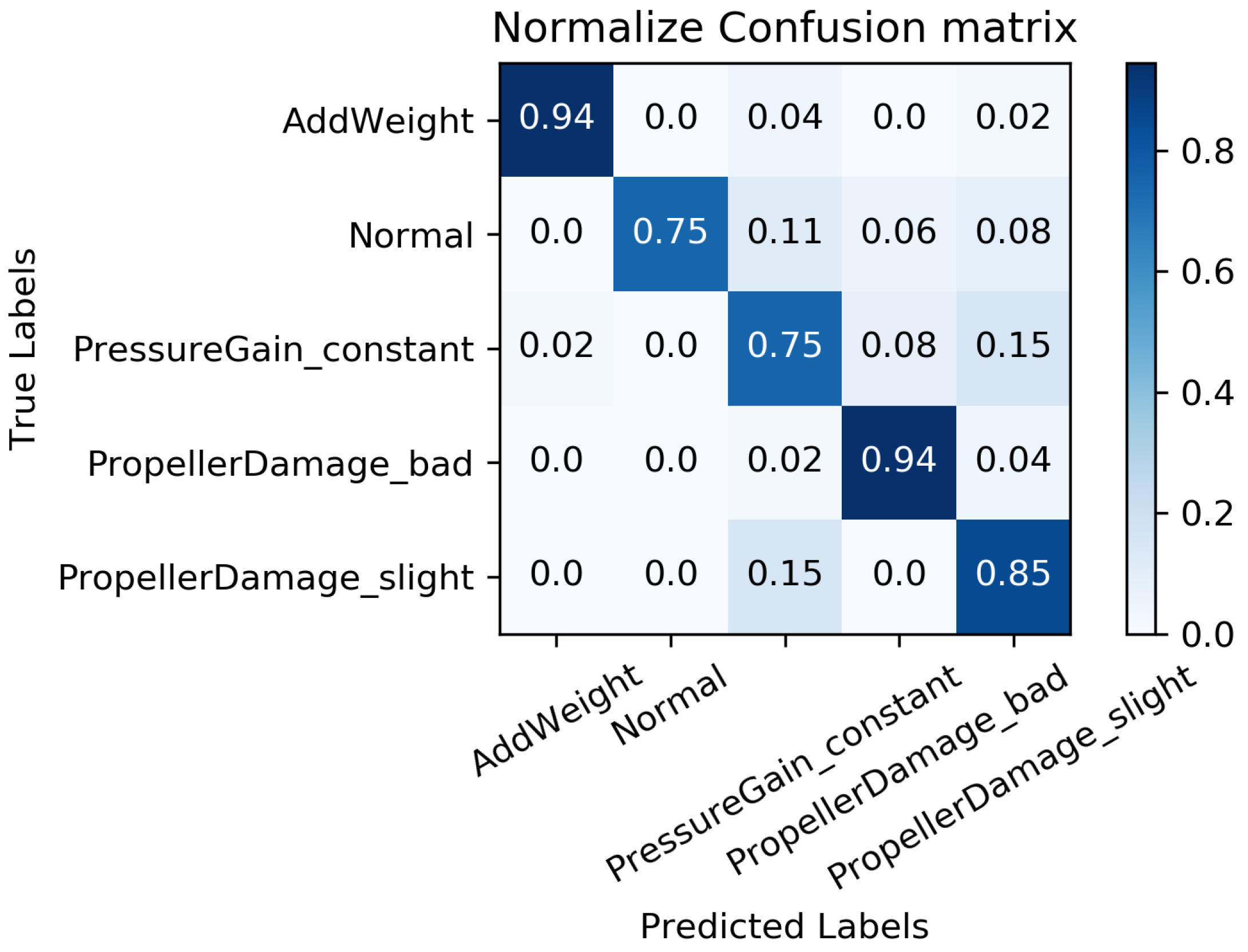
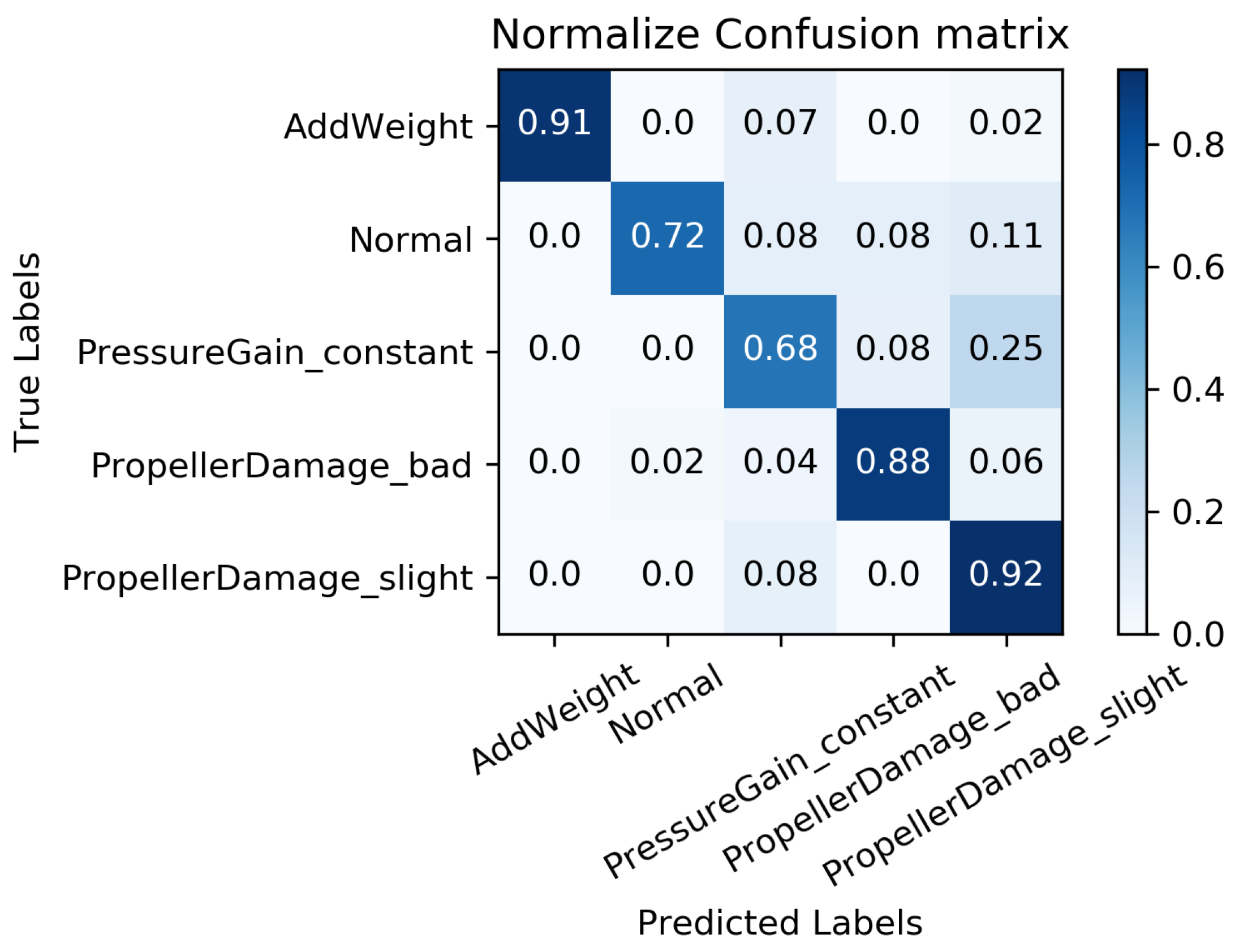
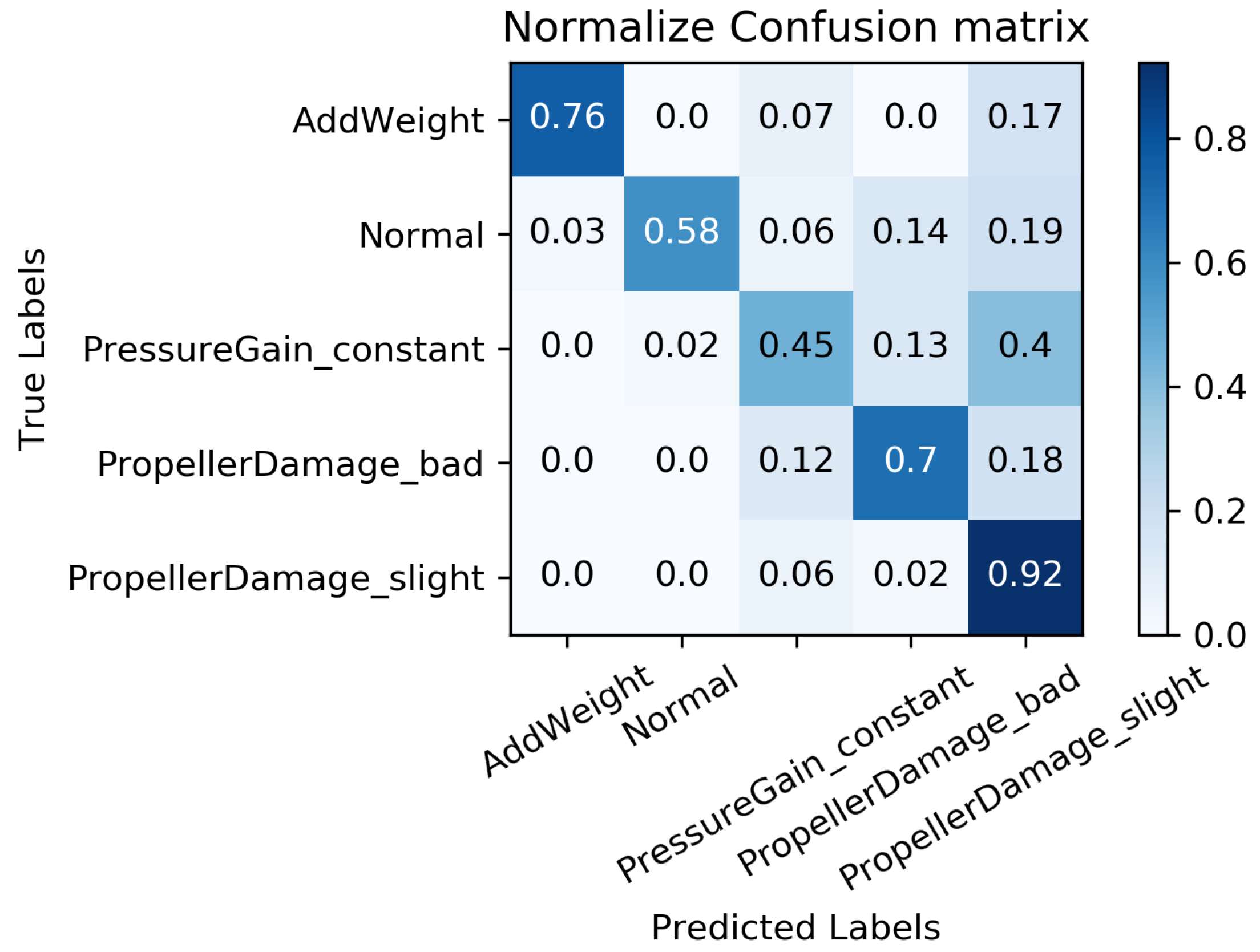
| Missing Rate | Working Conditions | Accuracy | ||||
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | ||
| 0.98 | 0.81 | 0.79 | 0.96 | 0.88 | 0.884 | |
| 0.94 | 0.75 | 0.75 | 0.94 | 0.85 | 0.846 | |
| 0.91 | 0.72 | 0.68 | 0.88 | 0.92 | 0.822 | |
| 0.81 | 0.69 | 0.58 | 0.84 | 0.88 | 0.760 | |
| 0.76 | 0.58 | 0.45 | 0.70 | 0.92 | 0.682 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Wang, A.; Zhou, Y.; Zhu, Z.; Zeng, Q. Fault Diagnosis of Autonomous Underwater Vehicle with Missing Data Based on Multi-Channel Full Convolutional Neural Network. Machines 2023, 11, 960. https://doi.org/10.3390/machines11100960
Wu Y, Wang A, Zhou Y, Zhu Z, Zeng Q. Fault Diagnosis of Autonomous Underwater Vehicle with Missing Data Based on Multi-Channel Full Convolutional Neural Network. Machines. 2023; 11(10):960. https://doi.org/10.3390/machines11100960
Chicago/Turabian StyleWu, Yunkai, Aodong Wang, Yang Zhou, Zhiyu Zhu, and Qingjun Zeng. 2023. "Fault Diagnosis of Autonomous Underwater Vehicle with Missing Data Based on Multi-Channel Full Convolutional Neural Network" Machines 11, no. 10: 960. https://doi.org/10.3390/machines11100960
APA StyleWu, Y., Wang, A., Zhou, Y., Zhu, Z., & Zeng, Q. (2023). Fault Diagnosis of Autonomous Underwater Vehicle with Missing Data Based on Multi-Channel Full Convolutional Neural Network. Machines, 11(10), 960. https://doi.org/10.3390/machines11100960









