Abstract
Disc pumps have obvious advantages in dealing with difficult-to-pump media. Energy efficiency and sustainable energy management are important topics with regard to reducing costs and promoting carbon neutrality. Though the concept of the disc pump was proposed in the 1850s, development was slow and limited by its initial model. However, with the development of industries such as petrochemicals and food, the efficient pumping of difficult-to-pump media is much needed, but facing challenges. Therefore, research on energy-efficient disc pumps is particularly important moving forward. In this paper, the available information from the open literature about the research and development of the disc pump will be thoroughly reviewed. It focuses on the historical development, energy efficiency and physical model application of the disc pump. The review ends with a proposal for the direction of future development, and in this aspect, it is proposed that the energy efficiency prediction model based on velocity slip theory, the energy management system based on multi-scenarios and the design method based on energy conversion theory are important. The latest achievements in energy conversion are given. This review also provides a new perspective for the development of energy-efficient disc pumps.
1. Introduction
Energy-efficient equipment design and energy system management are key to promoting the transition from carbon-peak to carbon-neutral [1,2,3,4], as well as the aim of reducing costs and increasing efficiency in various industries to improve their competitiveness [5,6,7,8]. The pump, as an important piece of mechanical equipment for conveying fluid or pressurizing fluid [9,10,11], is widely used in conveying water, oil, mud, jam, suspension emulsion, liquid metal and other media. The power consumption of the pumping system accounts for about 20% of the overall power consumption of society [12,13]. Therefore, the energy management and energy efficiency design of pumping equipment will profoundly affect the advancement in energy saving and emission reduction. To meet the energy efficiency requirement and energy consumption optimization, new physical models and theoretical methods are needed [14,15,16].
Although the energy efficiency of conventional centrifugal pumps has been greatly improved, their development in applications to deal with difficult-to-pump multiphase media has been slow, leading it to have not only poor adaptability and low reliability, but also poor energy efficiency. Therefore, it is important to develop energy-efficient pumping equipment to cope with difficult-to-pump multiphase viscous media.
For multiphase viscous media containing particles, the disc pump has excellent performance with its unique impeller structure. Compared with traditional centrifugal pumps, the blades on the impeller of a disc pump are discontinuous, and the flow channel inside the impeller is divided into a bladed area and a bladeless area. The pumping principle is based on boundary layer flow and—for higher Reynolds numbers—on eddy viscosity. The boundary layers adhering to the discs induce a tangential velocity in the fluid, which allows centrifugal forces to carry the fluid outwards. Due to the boundary layer effect, the wear and cavitation of the flow passage components inside the pump are relatively small, and the media are only subjected to slight shear damage. Although disc pumps have less efficiency in conveying media such as water compared to classical rotating pumps, they have higher energy efficiency, excellent reliability and good passability for pumping viscous and difficult-to-pump mixed media, such as mud, heavy oil, lotion, fiber and other mixtures, and are especially suitable for complex media with viscous and large particles. Energy consumption is reduced and operational reliability is increased through the use of energy-efficient disc pumps in petrochemical, medical devices, food and bioengineering industries. Among them, in the field of the petrochemical industry, disc pumps have attracted more attention and achieved rapid development [17].
This paper focuses on a systematic review and in-depth summary of the historical development of the disc pump, the application of physical models, the development of energy efficiency models and the analysis of energy characteristics. Then, considering the development needs of the industry and the technical requirements of low carbon and energy saving, it innovatively points out the direction of the development and future prospects of the energy-efficient physical model, the energy efficiency model and energy characteristic theory. In addition, the latest achievements of the energy efficiency prediction model and the energy characteristic theory applicable to disc pumps for deep-sea energy development are also discussed, which provides a new perspective for the development of high energy efficiency and energy system management of the disc pump.
2. Historical Development of Disc Pump
2.1. First-Generation Disc Pump
The original concept of the disc pump was attributed to Sargent [18] in 1850. The pump was constructed by connecting multiple parallel discs, as shown in Figure 1a. The disc spacing of the prototype disc pump is large. The outlet of the disc pump is composed of multiple groups of discs forming a semi-closed annular surface with multiple holes where the fluid is discharged. Because the disc surface is relatively flat, the fluid in the impeller is completely driven out by centrifugal force and viscous drag. Such a pump does not provide good energy efficiency.
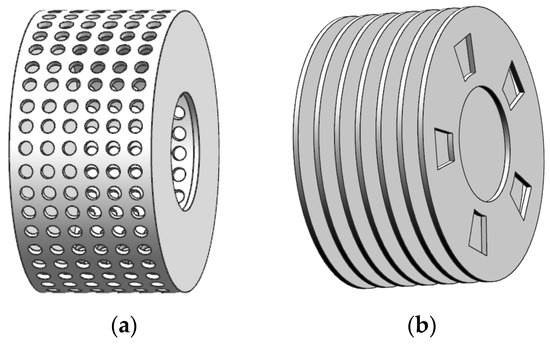
Figure 1.
Preliminary model of disc pump impeller. (a) Initial model; (b) Tesla’s friction ‘disc pump’.
Around 1900, Nikola Tesla, proposed to remove the annular, partially perforated ring cover disc of the initial design to form an open outlet so as to expand the application of the pump, as shown in Figure 1b. Although the open outlet design improved the trafficability of media, the viscous dragging force (henceforth referred to as binding force) caused by the boundary was also reduced. Therefore, he subsequently reduced the spacing between the discs as much as possible, while improving the expansibility of the disc pump, and promoting its overall energy efficiency. The improved design solved the two shortcomings of the initial conceptual model to a certain extent; it improved the pumping energy efficiency characteristics, and had acceptance in America and Europe. In the early stage, researchers mainly focused on the passability and reliability of this type of pump in conveying difficult-to-pump media, with an efficiency of generally less than 35%.
However, the improved model was faced with new problems. Although the narrow disc spacing was suitable for pumping clean water to a certain extent, it also limited the ability to pump viscous fluid or solid–liquid mixed media. Although the open impeller outlet improved the trafficability of media, it also faced the reduction of binding force. The above factors led to very low efficiency after improvement.
In addition, the same design can also be used as a turbine expander. After Nikola Tesla further developed the concept of the disc turbine in 1913, due to the emergence of the gas turbine and its development in large power plants in the following decades, the expander had poor performance in high-power applications. The technology was not commercially successful and was not evaluated until 1950. This paper focuses on the application and development of the design as a pump [19,20,21,22,23].
In summary, the first-generation disc pump development faced various problems such as application scalability and poor energy efficiency. However, the introduction of the new concept provided a new direction for the development of pumps for difficult-to-pump media. At the same time, the centrifugal pump developed rapidly, and the overall performance was far better than Nikola Tesla’s model. In addition, the demand for pumps for difficult-to-pump media was not so high at that time. Therefore, the development of Nikola Tesla’s model at that time was almost at a standstill.
2.2. Second-Generation Disc Pump
Until the 1970s, Max I. Gurth [24], an inventor from Southern California of the United States, carried out experimental research on the disc pump, as shown in Figure 2a. It was found that when the disc spacing was expanded to twenty inches (500 mm), the flow pattern between the discs still met the boundary layer and viscous resistance principle, and the flow between the discs maintained no pulsation and laminar flow, so that the disc pump could maintain higher efficiency at higher viscosity. This characteristic was different from that of the conventional centrifugal pump. When the viscosity of the pumped media increased to a certain extent (the fluid viscosity was higher than 250 cP), the energy efficiency characteristic of the disc pump was better than that of conventional centrifugal pump of the same size, and the maximum viscosity of the flow media could reach 100,000 cP. The discovery of the law between the structural parameters and energy efficiency characteristics greatly enriched the application scope of the disc pump and provided a new perspective for further structural development of it.
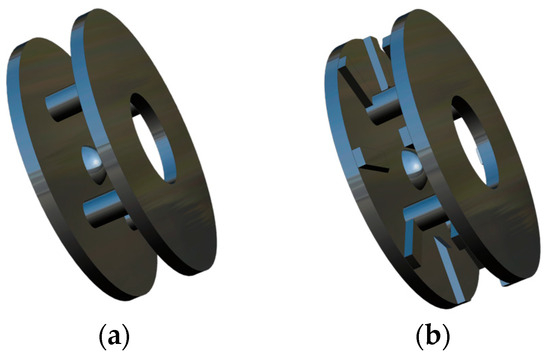
Figure 2.
Improved impeller of second-generation disc pump. (a) Improved design; (b) second generation.
Based on the above findings, Max I. Gurth applied for the first patent [24]. In 1982, a factory was established in California to produce and market the pump. The pumping mechanism was named Discpac at the time, which originally used a flat disc. Until 1988 [25,26], Max I. Gurth developed a new generation of Discpac, as shown in Figure 2b, and obtained a patent. The new generation of disc pump adopted the design of discontinuous blades, and the energy efficiency was greatly improved. At this time, the improved disc pump was called a high-lift disc pump or the second-generation disc pump.
The disc pump with discontinuous blades was more suitable than the disc pump with a smooth disc surface for conveying difficult-to-pump media containing solid particles and clotted suspended solids, as well as viscous difficult-to-pump media [25,26]. The solid particles in the media could reach 200 mm, and the efficiency of the disc pump could reach 60%. This improved disc pump opened up the new development and application of the second-generation disc pump, provided more space for further development of comprehensive energy efficiency and multi-scenario applicability of the pump, and also provided a new dawn for the development of the disc pump.
2.3. New-Generation Disc Pump
From the initial design concept of the disc pump to what it is today, there is no unified understanding of the definition and name of the disc pump. In particular, the differences in terms of names make it more difficult for scholars to communicate and share relevant research results, preventing them from forming effective collaborative development and research, which also seriously restricts the exploration of the internal flow mechanism and the development of the disc pump with a new blade structure.
As the development of the disc pump continues, its applications are mainly in petrochemical, medical devices, food and biological industries. At present, it can be referred to as the “Disc pump”, “Disk pump”, “Tesla pump” or “Discpac pump”. There are also names in accordance with its applications such as “Disk-Shape Boundary-Layer Pump”, “Tesla-Based Blood Pump”, “Centrifugal Blood Pump”, “Multiple Disk Centrifugal Blood Pump“, “Visual Pump”, “Shear Force Pump”, etc. Through the analysis of the available literature, most scholars use the term “disc” or “disk” in the name. In this paper, “Disc Pump” is used throughout for ease of identification. It is believed that a common form of naming eases the identification of the subject and is more conducive to collaborative development and research on the disc pump.
Regarding the structural characteristics, the disc pump mainly includes discs with a smooth surface or a discontinuous blade. The latter version is a new type with good scalability, wider application and better performance [27,28,29,30]. In addition, the new pump design adapts and improves the performance characteristics based on different application conditions. The characteristics include energy efficiency, reliability, particle passability and the protection of special media [31,32,33,34,35]. Presently, new pump designs are still explored and optimized, such as the design of similar blades, composite blades, composite disc, etc, as shown in Figure 3.
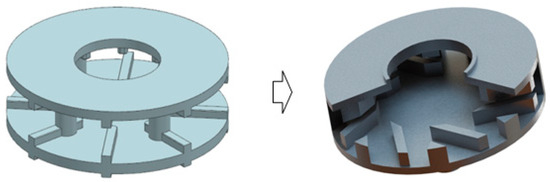
Figure 3.
A model for the new-generation disc pump.
3. Reviewing the Studies on Energy-Efficient Disc Pump
3.1. Physical Model and Optimization
3.1.1. Representative Physical Model Development
Exploring the relationship between geometrical parameters and performance characteristics has been the focus of the research in disc pumps that accounts for most of the development leading to pump energy efficiency. Table 1 summarizes the developments associated with the disc pump that are available in the open literature.

Table 1.
Representative physical model development timeline.
Based on the open literature, there are more research works on the second-generation disc pump than on the first, and the former accounts for about 87% of the energy efficiency-related work. In addition, the research is mainly concentrated on the last decade. It indirectly shows that the disc pump has been receiving more attention both in pumping and energy recovery application.
In 2012, Charles David Gilliam and Baton Rouge et al. invented a disc pump patent. The front and rear covers of the disc pump had pits or bulges with a height of half the thickness of the disc cover, as shown in Figure 4. A thick boundary layer can be generated to improve efficiency. In the 1990s, Hebei Institute of Mechanical Science successfully developed the 80 MP disc friction pump. At present, disc pumps are mainly produced by the companies such as Discflo in the Southern California, USA (Figure 5) and HUATUO Pump Industry in Hebei province, China [50].
Figure 4.
Diagram of a disc pump invented by Charles David Gilliam and Baton Rouge.

Figure 5.
Schematic diagram of the current applied disc pump structure.
The first generation of the disc pump can also be used as a turbine, such as in the Rankine cycle power system, the transcritical carbon dioxide heat pump cycle system, the intelligent water network system and the waste gas energy recovery system [51,52,53,54], etc. In recent years, with regard to the development of typical renewable energy low-temperature resources and a large number of waste heat resources generated by industrial processes or prime movers, the organic Rankine cycle power system (ORC) has been in a leading position with its good thermodynamic characteristics and high flexibility. The Tesla turbine, as a new expander for small and micro power applications, has attracted more and more attention in the scientific community because of its low cost and high reliability [19,55,56,57,58,59]. It is a bladeless turbine composed of one or more nozzles that inject the working fluid tangentially into the rotor. It is made of multiple stacked parallel discs, which are assembled very closely to each other to form a very close gap, and the fluid exchange is carried out through the viscous effect [60,61,62,63,64]. At present, two kinds of Tesla turbines are mainly of concern, and these are the nozzle Tesla turbine and the volute Tesla turbine, classified according to turbine inlet geometry [65,66,67,68,69].
3.1.2. Flow Characteristic and Optimization
Based on the investigation and analysis of pumping technology and its working principle, John Pacella focused on the operation and design characteristics of disc pumps for application in environments containing difficult-to-pump media, as well as the application experience in refineries [39]. José Leonardo Pérez mainly analyzed the pressure and velocity distribution through numerical simulation and revealed the fluidynamic behavior of the entrance–impeller interaction of the disc pump [70]. Dmitry Eskin established an engineering model of a laminar flow in a disc pump stage. Through simulation analysis, it was found that the head and efficiency of the disc stage increased with the increase in fluid viscosity, a multichannel rotor had better characteristics than a single-channel one, and the optimal number of channels was three or four. It was proposed that the disc pump was more suitable for pumping high viscosity oil with high solid content than the conventional blade centrifugal pump [71]. Laura Dodsworth explored the relationship between disc spacing and efficiency, as well as the relationship between speed and energy efficiency. The smaller the spacing, the higher the overall energy efficiency. Under the condition of large disc spacing, high speed had little impact on the overall energy efficiency. However, this study was a clean water experiment and lacked the comparison of viscous media conditions [72].
A summary of the study development of flow characteristics and optimization of the first-generation disc pump is shown in Table 2.

Table 2.
Flow characteristic and optimization of first-generation disc pump.
In 1988, Max Gurth developed the second-generation disc pump, which greatly improved the energy efficiency and expanded application scalability [74,75,76]. Due to the development gap in the initial stage, the research on the flow characteristics and optimization of the second-generation disc pump was mainly carried out in recent years [77,78,79,80].
Li Bin [44] established a set of numerical simulation methods for calculating the multiphase flow inside the disc pump and improved the structure of the impeller. The relationship of different solid-phase particle concentrations, different gas-phase concentrations and the head and pump efficiency were obtained. As a result, the energy efficiency was significantly improved. V Cheremushkin and V Lomakin [46] comprehensively discussed the influence of some of the basic parameters of the disc impeller on its energy efficiency characteristics through measurement and simulation. Under the conditions of low viscosity and the addition of ribs equivalent to discontinuous blades, the increase in head and energy efficiency was up to 20 m and 30%, respectively. Leonel Martínez-Díaz [81] designed four types of turbulizers in the interdisc channel output to improve the pump performance. The measured results showed that the square section turbulizer had the best pump efficiency, and each impeller with a different diameter had an optimal number of turbulizers to obtain the most energy-efficient design. Regressions obtained for head and efficiency (φ1 = 183 s−1) are shown in Table 3. When the disc pump operates with an angular velocity (φ1) of 183 s−1 in the range of flows (Q) between Q = 0 and Q = 0.78 l/s), the use of square turbulizers achieves a load increase in the range of 1.72 to 2.30 m in relation to the use of circular turbulizers.

Table 3.
Regression model for head and efficiency (φ1 = 183 s−1).
Since 2010, Zhou Changjing [42,43] has carried out systematic analysis of measurement and theoretical studies for the second-generation pump. The studies mainly include single-phase flow, solid–liquid two-phase flow, impeller cutting and structure matching performance, focusing on its applicability in petroleum exploration and development fields. Qi Hao [82] improved the pump design by adding several radial blades with different shapes on both sides of the disc. The results show that in gas–liquid two-phase flow, the liquid phase is mainly concentrated on the working surface of the blade, and the corresponding gas phase is mainly concentrated on the back of the blade. The head and efficiency were up to 43 m and 30%, respectively, when the gas volume content was 5%. Pei Yingju [48] systematically analyzed the characteristics of the disc pump under the conditions of clean water and viscous media with and without particles. The flow and energy efficiency characteristics of the blade area and bladeless area in the inner channel of the impeller were analyzed.
A summary of the study on the development of flow characteristics and optimization of the second-generation pump is shown in Table 4.

Table 4.
Flow characteristic and optimization of second-generation disc pump.
The research of the disc pump in medical devices has also made great progress. It has been used as an alternative blood pump, and the adaptability analysis has also been gradually deepened [84,85,86]. Due to the special requirements in the blood pumping application, the bladeless disc pump has been used and researched [87,88,89,90].
Valentin Izraelev [91] introduced the suspended Tesla type LAVD blood pump with satisfactory results. From 1990 to 1999 [92,93,94,95], Gerald E. Miller and Nobuyuki Kabei improved the multi disc centrifugal pump based on the Tesla turbine. They compared it with the Harvard Apparatus pulsed piston pump to explore its adaptability for use as an artificial ventricle or ventricular assist device. They found that the device could produce a wider range of pressure and flow at a various speeds. The pump could produce a higher flow without the risk of dissolving blood at a lower speed. Unlike Harvard pumps, disc pumps do not use valves to avoid backflow. It was proved that the Tesla pump operating in pulsatile mode could produce physiological pressure and flow similar to that of Harvard and other pulsatile pumps. Se Myong Chang [41] designed a disc boundary layer pump widely used in artificial heart, biological fluid and marine biological transportation. The research data were converted into dimensionless parameters, which could be useful as references for future new designs. Medvedev, A.E. [96] designed and built the physical model of the LVAD disc pump and analyzed the correlation, which could be used to optimize the hydraulic parameters.
Chernyavskiy, A.M. [96,97] pointed out that one of the new research directions was the viscous friction disc pump for liquid transportation based on the Tesla pump principle, put forward the shortcomings of the current research based on the published data, and introduced the current model of disc pump. The test results showed that the pressure characteristics of the disc pump could provide necessary blood circulation parameters.
A summary of the research carried out on disc pumps used in the medical industry is shown in Table 5.

Table 5.
Research studies on disc pump used in medical industry.
3.1.3. Physical Model with Extended Application
The working principle of the micro viscous pump is similar to that of the disc pump. It also uses the friction and centrifugal actions of the rotating disc to drive the media [102,103,104,105]. The impeller structure of the two is obviously different, but the research results of the flow mechanism and flow characteristics also provide a reference for the design and development of the disc pump [106,107,108,109,110]. Therefore, typical cases and results are also reviewed in this study.
Danny Blanchard [111,112] introduced and tested a single-disc viscous pump and found that the pressure rise through the pump chamber could be increased by increasing the pumping speed, the fluid viscosity, or the circumferential span of the shear channel, or by decreasing the flow passage height. The flow rate could be increased by increasing the flow passage height or the speed, or by decreasing the width of the pumping chamber. Ala’aldeen Al-Halhouli [40] reviewed the latest progress in the development of helical channel, single-disc and double-disc micropumps, as shown in Figure 6. An analytical solution was proposed to estimate the combined effects of operating and geometric parameters on its performance. In addition, it was carried out to change the induced slip by using different levels of surface roughness on the rotating disc [113]. The micro viscous disc pump (VDP) was used to characterize and quantify the elastic turbulence effect of non-Newtonian fluid relative to Newtonian fluid behavior [114,115], as shown in Figure 7.
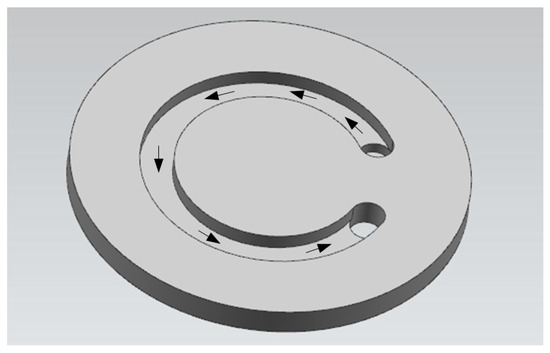
Figure 6.
Single and double disc viscous micropumps.
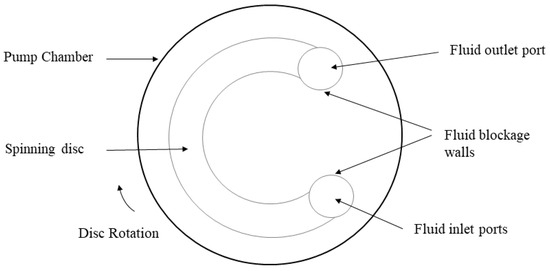
Figure 7.
Viscous Disc Pump.
A summary on the quantitative comparison of key parameters of typical micro viscous disc pumps is shown in Table 6.

Table 6.
Quantitative comparison of micro viscous disc pumps.
3.1.4. Design Theory
The key design parameters of the disc pump impeller include impeller diameter (impeller external diameter), disc spacing, disc number, blade number, blade height and inlet diameter. The parameters that affect energy consumption include theoretical head, efficiency and particle passing rate. At the same time, the design and calculation of some of the structural parameters and energy efficiency parameters of the disc pump need to be modified in combination with its applicable special environment. For example, when a disc pump is used for lifting the multiphase media containing solid particles in deep water, the settlement velocity of particles should be fully considered.
At present, the theoretical calculation method of disc pump structural parameters is still in the preliminary exploration stage, and more directly draws on the design method of the key structural parameters of the conventional blade centrifugal pump. Chen Guoming’s team has carried out relevant targeted research. Zhou Changjing, a member of the team, obtained the impeller outlet diameter through the theoretical head calculation method in 2012 and introduced the head coefficient CH. The impeller disc spacing, that is, the impeller outlet width of the blade disc pump, is the main factor affecting the flow of the disc pump. The disc spacing can be obtained using the similarity law of pump [118]. Yin Shumeng, another team member, also introduced the head coefficient CH in 2012, obtained the impeller outlet diameter using the theoretical head calculation method, and provided a similar formula for calculating disc spacing. However, the difference between the two is that the specific expression of CH is different. In addition, on the basis of Zhou Changjing’s research, Yin Shumeng referred to the excellent disc pump hydraulic model data of DiscfloTM, and drew the curve of the relevant design coefficient using the least square method, which was convenient for practical calculation and application [119]. In 2015, Zhang Ye conducted numerical calculation on nearly sixty hydraulic models of disc pumps of various sizes, analyzed the best energy efficiency characteristics of those disc pumps, selected the models of twenty-seven disc pumps with the highest energy efficiency, and designed the disc pump parameters using the empirical coefficient method. The empirical formulas of the key structural parameters of the disc pump were obtained using regression analysis and functional relationship expression [50].
The summary of the calculation methods for the key structural parameters of the disc pump impeller is shown in Table 7.

Table 7.
Key structural parameters for the impeller of disc pump.
3.2. Energy Efficiency Model
Energy efficiency models mainly include pump efficiency models and matching energy efficiency models. At present, whether concerning a disc pump or a conventional blade centrifugal pump, the theoretical calculation and analysis methods of energy efficiency models are immature and lag behind simulation and experiment.
At present, there are few theoretical calculation research results on the energy efficiency prediction model of the disc pump in the open literature. Naumov, I.E. carried out experimental research on centrifugal the disc pump. By introducing dimensionless parameters to summarize the experimental data of the pump, it was helpful to express the energy efficiency of the disc pump, which proved that the method had high calculation accuracy [99]. Saima Naz pointed out that the effective design of the Tesla pump was still the focus of experimental and numerical research. Based on simulation analysis, the performance parameters of the pump were evaluated by considering dimensionless flow coefficient and efficiency [101]. From 2012 to 2016, Zhou Changjing, Zhang Ye and Xie Yongchao carried out relevant research on the correction of the key parameters separately. The discontinuous blade structure of the disc pump made the velocity distribution at the impeller outlet uneven. Therefore, the average coefficient of impeller outlet circumferential velocity was introduced, but the calculation method of average circumferential velocity was not given [50,118,120].
Moreover, Pei Yingju et al. [48,121] proposed two calculation methods of average circumferential velocity of the blade disc pump. One is the calculation method that uses the axial dimensions of the blade area and bladeless area in the impeller, as shown in Figure 8 and Equation (1). The other is the calculation method that uses the velocity coefficient through the micro flow law, momentum conservation and energy saving, as shown in Figure 9 and Equation (2). The theoretical and simulation errors of the two methods are 12.6% and 10.7%, respectively, and the relative error considering slip is significantly smaller than that without considering slip (nearly 39.4%). However, the above two methods need to be further considered for validation in extended applications.
where is the average circumferential velocity, m/s; uA and uB are the circumferential velocities at the inner wall surfaces of the two discs at the impeller outlet, respectively, m/s; and h1 to h4 are the height coefficients of different axial sections of the disc pump.
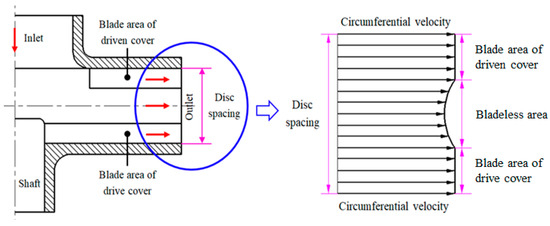
Figure 8.
Circumferential velocity at outlet of discontinuous blade passage.
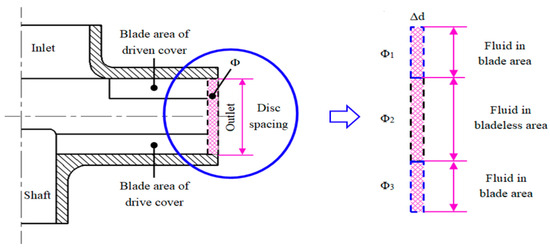
Figure 9.
Different areas at the outlet of discontinuous blade passage.
The summary of the efficiency parameters of the disc pump for predicting the efficiency and improving energy efficiency is shown in Table 8.

Table 8.
Efficiency parameters for the impeller of disc pump.
3.3. Energy Conversion Characteristics
At present, the internal flow field analysis of the disc pump is mainly focused on single-phase and two-phase research, mainly with the help of streamlines, velocity vectors and pressure fields.
Khaled M. Bataineh gave the numerical solution of Navier–Stokes equations coupled with the energy equation for gaseous slip flow between two micro disc pumps and revealed the effects of the Knudsen number, the rotational Reynolds number and the gap height on the head, flow, and torque coefficients and the overall efficiency of the micro disc pump [122]. Wang Baotong studied the internal flow dynamics and the loss mechanisms of a complete shear force pump device, and evaluated the achievable isentropic efficiency and pressure coefficient. The shear force pump test bed was designed and built, and the energy loss law of each part under different working conditions was revealed [123]. Chenhui Hu and Wei Wu proposed a design scheme of a micro viscous pump with different inlet and outlet areas, and discussed in detail the mass flow and driving power under different inlet opening angles, flow field structure and vortex evolution, so as to improve the performance [124]. Diego Hayashi Alonso proposed a topology optimization formula to optimize Tesla pumps by using a two-dimensional eddy current model, and defined a multi-objective function to minimize energy dissipation and vorticity [73]. Zharkovsky, A.A. and Ivanov, O.A. analyzed the pressure and energy characteristics of the impeller, studied the influence of impeller geometric parameters on the pump characteristics, and compared the energy characteristics of the disc centrifugal pump and electric centrifugal pump [47]. Pei Yingju studied the turbulent kinetic energy of the discontinuous blade disc pump at different speeds through simulation, and revealed the distribution law of turbulent kinetic energy and energy change along the radial and axial direction in the blade area and bladeless area of the impeller [48].
In summary, although mature energy analysis theory and design theory have not yet been formed, the hydrodynamics and kinematics analysis based on energy characteristics and design optimization based on energy theory are new perspectives for current pump research.
4. Result and Discussion
4.1. Physical Model Development and Prospects
At present, the disc pump has developed two generations, including the first generation of bladeless disc pumps and the second generation of blade disc pumps. However, the two generations of disc pumps have their own application scenarios, and the second generation of disc pumps is not a substitute for the first generation. The first generation of bladeless disc pumps has more advantages than the second generation of blade disc pumps in some cases with high media protection [125,126,127,128].
Due to the wider application of the second-generation disc pump, such as the development of marine energy, there are more research results in the development of the physical model than the first-generation disc pump. It mainly focuses on the optimization of blade shape, blade number, disc shape and disc number. At the same time, a new-generation physical model of the disc pump has been explored. The summary on the development of the physical model of the disc pump is shown in Table 9 and Figure 10.

Table 9.
Innovative development of physical model.
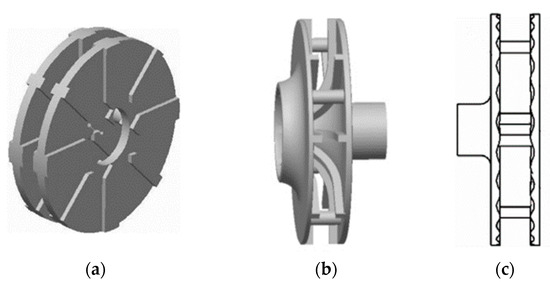
Figure 10.
Innovative physical model of disc pump. (a) Main and auxiliary blade models; (b) curved disc model; (c) ripple model.
Although the disc pump has undergone two generations of development, and has carried out structural innovation and adaptive development in special applications, the energy efficiency has also been improved to a certain extent. However, it is still facing problems such as poor energy efficiency and immature design methods, and the innovative design of energy-efficient physical models is still facing greater challenges. Due to the special structure of the disc pump, it has unique advantages in pumping difficult-to-pump media and is an indispensable piece of equipment. In future development, the application is still very much anticipated.
As shown in Table 9, some ideas for improving the physical model have been given. In the future development of the physical model, while maintaining the unique structural advantages of the disc pump, it is necessary to fully learn from the excellent model design experience of the vortex pump, micro flow disc pump and multiphase centrifugal pump. Focusing on the discontinuous composite blade structure, composite disc surface structure and multi-stage pump structure fused with other types of pumps would help to obtain an excellent disc pump physical model. Due to the wide application of the disc pump in various industries, and the large differences in the requirements of different application scenarios, the development of the physical model needs to fully consider the requirements of specific application scenarios and make full use of the structural advantages of the first- and second-generation disc pumps to obtain wider and more efficient applications.
Regarding the selection of the volute for the disc pump, Zhou Changjing conducted modeling and numerical calculation research on spiral volutes, quasi-spiral volutes, and annular volutes, respectively. The results show that the relative loss rate of energy conversion in the quasi-spiral volute is lower than the other two under various operating conditions. The energy loss rate of the annular volute is the smallest with flow rate changes, and it is the least sensitive to changes in the operating conditions. The energy loss rate of the spiral volute is the most sensitive to changes in flow rate [132]. In the selection of volutes, viscosity and particle size should be fully considered. While ensuring passability and reliability, efficiency should be considered.
4.2. Energy Efficiency Model Development and Prospects
The energy efficiency model has always been a difficulty in pumping equipment, especially in the special impeller structure of the disc pump, which will become more difficult.
As summarized in Table 7, for disc pumps used for marine energy development, Zhou Changjing et al. put forward the average circumferential velocity at the impeller outlet [130]. Pei Yingju et al. gave a variety of calculation methods for the average circumferential velocity at the impeller outlet, tried to promote the research and application of the energy efficiency model, and obtained phased results, which also laid a foundation for the development of energy efficiency models in the future.
At present, the research of matching energy efficiency models (MEEM) has attracted more and more attention. For example, in the process of riserless dual-gradient drilling of mud for offshore oil and gas exploration, it is necessary to consider both mud lifting and pressure regulation. At this point, MEEM has great practical value. The matching energy efficiency model is closely related to specific application scenarios. Therefore, the development of the matching energy efficiency model under different application scenarios becomes more difficult. Establishing top-level logic and top-level design for matching energy efficiency is an important development direction for the future. Pei Yingju fully combined the application environment of disc pumps in deep-sea oil and gas development, and established a targeted, system-matching energy efficiency prediction model based on the pump efficiency prediction model (PEPM), as shown in Figure 11. By considering the non-uniform velocity slip at the outlet, the average circumferential velocity was obtained. When the deviation was within the range of about 20% of the rated speed, the prediction error was less than 5%. When the deviation from the rated speed was more than 20%, the calculation accuracy of PEPM was improved by about 4%. The full combination of PEPM and MEEM opens up a new idea for the development and application of the energy efficiency model.
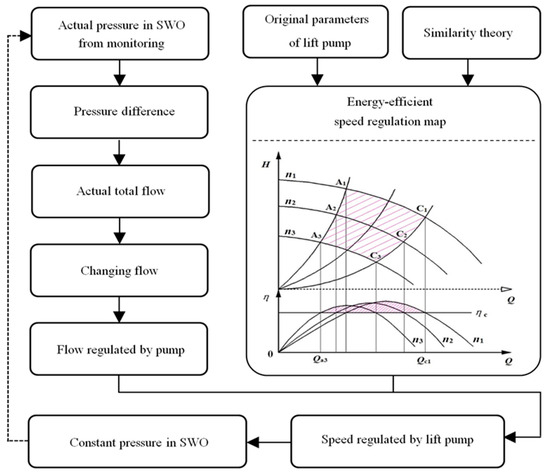
Figure 11.
Energy-efficient pressure regulation model (EPRM) diagram.
The development of the energy-efficient model is one of the most important goals of pump physical model improvement and technological innovation. Micro parameter modification and system section matching need to complement each other and develop collaboratively. For example, focusing on parameter modification such as the impeller outlet circumferential velocity to improve the calculation accuracy of theoretical head. Furthermore, establishing the energy-efficient self-prediction model and integrating it into the specific application system to obtain the system-matching energy efficiency model, so as to achieve the goal of low carbon production and energy saving.
4.3. Energy Conversion Theory Development and Prospects
Energy conversion theory is an important method to characterize the flow pattern in pump equipment. It mainly includes the analysis of the stability of the pump flow field considering the idea of energy balance. Through the research on the effect of factors such as pressure gradient, rotation effect and viscous dissipation, the formation, development and evolution process of energy in the pump flow field and the distribution characteristics in different hydraulic components are analyzed in detail, and the energy conversion characteristics of the flow field are explored in combination with energy factors. At present, the research results of energy conversion theory have appeared in the research of the conventional centrifugal pump, such as analyzing the internal energy distribution and energy loss by entropy and enthalpy.
There are fluid mass and energy transfer, as well as vortex motion and evolution in the blade and bladeless areas of the disc pump impeller. It is very necessary to analyze the energy characteristics. However, there are few studies of the disc pump. In future research, on the one hand, the energy analysis methods that have appeared in conventional centrifugal pump research can be used for reference. On the other hand, a new energy transport characteristic analysis method in the rotating coordinate system can be established. The dynamic energy distribution law of rotating fluid is an effective way to explore the internal flow pattern and hydraulic characteristics of disc pumps with a discontinuous blade. The dynamic evolution of the flow pattern in the impeller channel of the disc pump can be comprehensively analyzed by the viscous dissipated energy, velocity gradient and pressure gradient in the flow field. Then, the characterization model of internal flow characteristics and the internal flow mechanism based on energy elements and energy gradient can be established [130]. The idea of eddy energy analysis is given below.
The N–S equation of incompressible fluid in the rotating reference system can be expressed as:
where V is the speed; fc is the Coriolis force; fcf is the centrifugal force; f is the body force per unit mass; p is the pressure; and μ is the viscosity coefficient. Bold symbols represent vectors.
The simplified N–S equation is:
In the simplified N–S Equation (5), the left term can be decomposed into the following expression:
where ω is the vorticity; Ω is the curl; and g is the gravity.
Substituting the above Formula (6) into the simplified N–S Equation (5), the following N–S equation of rotating fluid can be obtained:
According to the energy transport equation of Newtonian fluid, the absolute value of the kinetic energy equation of unit mass media is , and the energy transport equation of rotating fluid can be obtained.
When the fluid flows in the internal passage of hydraulic machinery, it is generally high-velocity flow, and the flow Reynolds number in the flow field is relatively high, so the turbulence and viscous effects in the flow field must be considered. In this paper, the eddy viscosity hypothesis in the turbulence theory and the fluid viscosity are combined to form a viscosity coefficient consistent with the above. Let ; the energy transport equation of the rotating fluid can be expressed as the following formula:
The energy transport equation of rotating fluid is shown in Formula (9). The left side of the equation represents the local total energy, and the right side of the equation is mainly composed of five parts. The first and second terms on the right of the equation represent the buoyancy power and kinetic energy power generated by the micro element fluid, respectively. Since the rising height of the fluid micro mass of the disc pump during the high-velocity rotating movement in the impeller and the change of potential energy are very small, these two items can be ignored. The third term on the right of the equation can be expressed as pressure push work or pressure energy. The fourth term on the right of the equation represents the work carried out by the tangential viscous force, which can also be called the divergence of the lamb vector. The fifth term on the right of the equation represents the viscous dissipation rate of kinetic energy in the flow field, which is called vortex quasi “energy” [132].
As seen in Table 10, Table 11 and Table 12, in ref. [132], the contribution of pressure propulsion power to increase the energy gain by the media is more than 90%, and that of lamb vector divergence is less than 10%. The contribution of enstrophy is low except for 0.4 Qd (designed flow rate, m3/h) which shows more than 10% enstrophy part in the rise in media energy. This energy method can clearly identify the position and size of energy generation and loss in the flow field of the impeller, and summarize the law of multi parameter influence in the energy transport process. It is also based on the energy transfer theory to study new design methods and optimization methods.

Table 10.
Pressure propulsion power.

Table 11.
Lamb vector divergence.

Table 12.
Enstrophy.
In summary, it can be seen that pressure energy, lamb vortex energy and vortex pseudo “energy” are the main influencing factors of the rotating vortex energy transport characteristics in the impeller flow field. Therefore, based on the above analysis, the study of the energy change law and the distribution characteristics of the rotating fluid flow field in the disc pump is carried out to obtain the laws of energy migration, distribution and evolution in the internal flow field of the impeller under different working conditions and different media physical properties. Furthermore, this study promotes the research on the optimal design of the physical model and the energy-efficient development of the disc pump based on the energy theory.
The summary of the historical development, research development and prospects of the disc pump is shown in Figure 12.
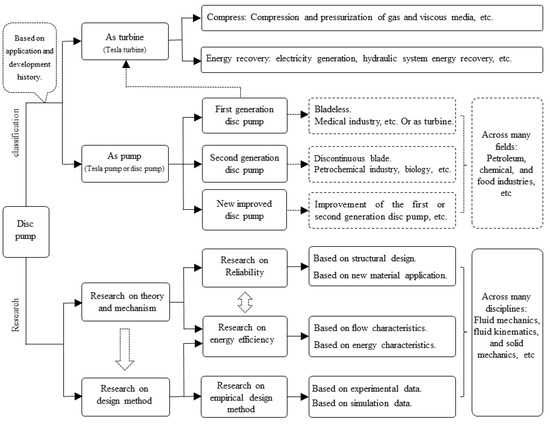
Figure 12.
Review on the development and future outlook of the disc pump.
5. Conclusions
Taking the development of energy-efficient disc pumps as the main line of inquiry, this paper traces the development history, as well as the opportunities and problems faced by disc pumps at each stage of development. It comprises a systematic review and exploration of the development of the physical model, energy efficiency model and energy conversion theory, and puts forward some future research directions and new ideas. The main conclusions are as follows:
- (1)
- In the technical innovation of the disc pump, the first-generation disc pump and the second-generation disc pump were developed. Both generations of disc pumps have their own application environment, and the second-generation disc pump is not a substitute for the first generation. The first-generation bladeless disc pump has more advantages than the second-generation blade disc pump in some application environments with higher media protection. However, the discontinuous blade design of the second-generation disc pump has higher energy efficiency and wider expansibility and application. Therefore, in future developments, making full use of the advantages of the two generation pumps will aid the development of energy-efficient physical models for different application environments.
- (2)
- In promoting the development and applicability of the energy-efficient disc pump, the current research mainly focuses on the optimization of the physical model based on the analysis results of internal fluid flow characteristics. There is huge potential in the development of the energy efficiency model and energy conversion characteristics. The published information shows that the existing design method is the empirical design method combined with data statistics, and the design theory of the multiphase pump needs to be further excavated. Therefore, the energy characteristic perspective can be used to explore the design theory in future development.
- (3)
- In the application environment of particle-containing viscous pumping, there are currently few studies on the particle motion characteristics in the blade and bladeless areas of the disc pump. Research on the anti-wear mechanism of the impeller based on the energy conversion characteristics and particles will also be a new direction. At the same time, considering the viscosity of the media, the study of energy conversion laws under gas–liquid two-phase and gas–liquid-solid three-phase flow conditions is a future research difficulty and focus.
Therefore, in order to better meet the needs of society and various industries for energy-efficient pumping equipment, especially the development of disc pumps for marine energy development, in addition to the conventional flow characteristic analysis method and an innovative energy theoretical design method, it is possible to fully integrate materials science, computer science and other disciplines, so as to realize the greater development potential of a “green” disc pump in the future.
Author Contributions
Conceptualization, Y.P. and Q.L.; software Y.P.; validation, Y.P.; methodology, Y.P. and K.T.O.; investigation, Y.P.; resources, Y.P., Q.L. and K.T.O.; writing—original draft, Y.P; writing and editing, Y.P. and K.T.O.; review and editing, K.T.O.; supervision, Q.L. and K.T.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key R&D Program of China [2018YFC0310200], CHINA SCHOLARSHIP COUNCIL [202009225033], National Natural Science Youth Fund of China [52304004], Key R&D projects in Sichuan Province [2023YFG0093], International Science and Technology Innovation Cooperation funded projects (Sichuan Province) [2023YFH0033].
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wei, X.; Qiu, R.; Liang, Y.; Liao, Q.; Klemeš, J.J.; Xue, J.; Zhang, H. Roadmap to carbon emissions neutral industrial parks: Energy, economic and environmental analysis. Energy 2022, 238, 121732. [Google Scholar] [CrossRef]
- Yao, J.; Dou, P.; Zheng, S.; Zhao, Y.; Dai, Y.; Zhu, J.; Novakovic, V. Co-generation ability investigation of the novel structured PVT heat pump system and its effect on the “Carbon neutral” strategy of Shanghai. Energy 2022, 239, 121863. [Google Scholar] [CrossRef]
- Fortes, P.; Simoes, S.G.; Amorim, F.; Siggini, G.; Sessa, V.; Saint-Drenan, Y.; Carvalho, S.; Mujtaba, B.; Diogo, P.; Assoumou, E. How sensitive is a carbon-neutral power sector to climate change? The interplay between hydro, solar and wind for Portugal. Energy 2022, 239, 122106. [Google Scholar] [CrossRef]
- Franke, K.; Sensfuß, F.; Bernath, C.; Lux, B. Carbon-neutral energy systems and the importance of flexibility options: A case study in China. Comput. Ind. Eng. 2021, 162, 107712. [Google Scholar] [CrossRef]
- Cui, Q.; Li, X. Investigating the Profit Pollution Abatement Costs difference before and after the “Carbon neutral growth from 2020” strategy was proposed. Res. Transp. Econ. 2021, 90, 101120. [Google Scholar] [CrossRef]
- Carvalho, F.; Müller-Casseres, E.; Poggio, M.; Nogueira, T.; Fonte, C.; Wei, H.K.; Portugal-Pereira, J.; Rochedo, P.R.R.; Szklo, A.; Schaeffer, R. Prospects for carbon-neutral maritime fuels production in Brazil. J. Clean. Prod. 2021, 326, 129385. [Google Scholar] [CrossRef]
- Matsuda, C.; Mino, Y. Study on power-saving effects in direct-use of geothermal energy for datacenter cooling systems. In Proceedings of the 2016 IEEE International Telecommunications Energy Conference (INTELEC), Austin, TX, USA, 23–27 October 2016. [Google Scholar]
- Stump, P.; Keller, N.; Vacca, A. Energy Management of Low-Pressure Systems Utilizing Pump-Unloading Valve and Accumulator. Energies 2019, 12, 4423. [Google Scholar] [CrossRef]
- Morales, S.; Culman, M.; Acevedo, C.; Rey, C. Quality evaluation of energy consumed in flow regulation method by speed variation in centrifugal pumps. IOP Conf. Ser. Mater. Sci. Eng. 2014, 59, 12011. [Google Scholar] [CrossRef]
- Luo, Y.; Xiong, Z.; Sun, H.; Guo, Y. Research on energy-saving operation control model of the multi-type configuration centrifugal pump system with single invert. Adv. Mech. Eng. 2017, 9, 2071939853. [Google Scholar] [CrossRef]
- Dmitriev, A.; Gerasimov, V. To the issue of energy efficiency of using frequency-controlled centrifugal pump units. MATEC Web Conf. 2018, 170, 3017. [Google Scholar] [CrossRef][Green Version]
- Arun Shankar, V.K.; Umashankar, S.; Paramasivam, S.; Hanigovszki, N. A comprehensive review on energy efficiency enhancement initiatives in centrifugal pumping system. Appl Energ. 2016, 181, 495–513. [Google Scholar] [CrossRef]
- Kocak, G.; Durmusoglu, Y. Energy efficiency analysis of a ship’s central cooling system using variable speed pump. J. Mar. Eng. Technol. 2018, 17, 43–51. [Google Scholar] [CrossRef]
- Petrochenkov, A.B.; Mishurinskikh, S.V. Development of a Method for Optimizing Power Consumption of an Electric Driven Centrifugal Pump. In Proceedings of the 2021 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (ElConRus), Moscow, Russia, 26–29 January 2021. [Google Scholar]
- Hieninger, T.; Goppelt, F.; Schmidt-Vollus, R.; Schlücker, E. Energy-saving potential for centrifugal pump storage operation using optimized control schemes. Energ. Effic. 2021, 14, 23. [Google Scholar] [CrossRef]
- Šavar, M.; Kozmar, H.; Sutlović, I. Improving centrifugal pump efficiency by impeller trimming. Desalination 2009, 249, 654–659. [Google Scholar] [CrossRef]
- Xupeng, H.; Wenbin, S.; Hang, Z.; Yanni, Z.; Qiao, H.; Chaohui, W. Research of the hydrostatic transmission for deep-sea current energy converter. Energ. Convers. Manag. 2020, 207, 112544. [Google Scholar] [CrossRef]
- Available online: https://www.unit-pump.dk/disc-his.htm (accessed on 15 October 2021).
- Talluri, L.; Dumont, O.; Manfrida, G.; Lemort, V.; Fiaschi, D. Geometry definition and performance assessment of Tesla turbines for ORC. Energy 2020, 211, 118570. [Google Scholar] [CrossRef]
- Pacini, L.; Ciappi, L.; Talluri, L.; Fiaschi, D.; Manfrida, G.; Smolka, J. Computational investigation of partial admission effects on the flow field of a tesla turbine for ORC applications. Energy 2020, 212, 118687. [Google Scholar] [CrossRef]
- Qi, W.; Deng, Q.; Jiang, Y.; Yuan, Q.; Feng, Z. Disc Thickness and Spacing Distance Impacts on Flow Characteristics of Multichannel Tesla Turbines. Energies 2019, 12, 44. [Google Scholar] [CrossRef]
- Huynh, N.D.; Lin, Z.; Choi, D. Dynamic balanced hybridization of TENG and EMG via Tesla turbine for effectively harvesting broadband mechanical pressure. Nano Energy 2021, 85, 105983. [Google Scholar] [CrossRef]
- Galindo, Y.; Reyes-Nava, J.A.; Hernández, Y.; Ibáñez, G.; Moreira-Acosta, J.; Beltrán, A. Effect of disc spacing and pressure flow on a modifiable Tesla turbine: Experimental and numerical analysis. Appl. Therm. Eng. 2021, 192, 116792. [Google Scholar] [CrossRef]
- Gurth, M.I. Method and Apparatus for Pumping Large Solid Articles. U.S. Patent 4,335,994, 22 June 1982. [Google Scholar]
- Gurth, M.I. Method for Pumping Fragile or Other Article in a Liquid Medium. U.S. Patent 4,624,320, 6 September 1988. [Google Scholar]
- Gurth, M.I. Rotary Disc Slurry Pump. U.S. Patent 4,773,819, 27 September 1988. [Google Scholar]
- Ladouani, A.; Nemdili, A. Influence of Reynolds number on net positive suction head of centrifugal pumps in relation to disc friction losses. Forsch. Ing. 2009, 73, 173–182. [Google Scholar] [CrossRef]
- Gorkin, R.; Clime, L.; Madou, M.; Kido, H. Pneumatic pumping in centrifugal microfluidic platforms. Microfluid. Nanofluid 2010, 9, 541–549. [Google Scholar] [CrossRef]
- Feng, H.; Chen, L.; Xie, Z.; Sun, F. Constructal optimization of a disc-shaped body with cooling channels for specified power pumping. Int. J. Low-Carbon Technol. 2015, 10, 229–237. [Google Scholar] [CrossRef]
- Liu, B.; Ba, D.C.; Fan, L.H.; Zhou, L.N. The Numerical Simulation Research of Disk-Type Molecular Pump Based on DSMC Method. Appl. Mech. Mater. 2013, 423–426, 2054–2058. [Google Scholar] [CrossRef]
- Skrzypacz, J. Numerical modelling of flow phenomena in a pump with a multi-piped impeller. Chem. Eng. Process. Process Intensif. 2014, 75, 58–66. [Google Scholar] [CrossRef]
- Koroteeva, E.; Ščepanskis, M.; Bucenieks, I.; Platacis, E. Numerical modeling and design of a disk-type rotating permanent magnet induction pump. Fusion Eng. Des. 2016, 106, 85–92. [Google Scholar] [CrossRef]
- Torabi, R.; Nourbakhsh, S.A. The Effect of Viscosity on Performance of a Low Specific Speed Centrifugal Pump. Int. J. Rotat. Mach. 2016, 2016, 3878357. [Google Scholar] [CrossRef]
- Liu, B.; Zheng, Y.; Chen, M.; Chen, X.; Jin, Z. CFD simulation of the mixing and dispersing of floating particles in a viscous system. Braz. J. Chem. Eng. 2017, 34, 1175–1189. [Google Scholar] [CrossRef]
- Figueira Júnior, E.A.; de Freitas Oliveira, C.H.; Borges, V.L.; de Carvalho, S.R. Design of bladeless impellers for abrasive fluid pumping. J. Braz. Soc. Mech. Sci. 2021, 43, 225. [Google Scholar] [CrossRef]
- Rice, W. An Analytical and Experimental Investigation of Multiple Disk Pumps and Compressors.: ASME Tram. J. Eng. Power 1963, 85, 191–198. [Google Scholar] [CrossRef]
- Crawford, M.E.; Rice, W. Calculated Design Data for the Multiple-Disk Pump Using Incompressible Fluid.: ASME Tram. J. Eng. Power 1974, 96, 274–282. [Google Scholar] [CrossRef]
- Available online: https://discflo.com/ (accessed on 15 October 2021).
- Pacella, J.; Hanas, P. Disc Pump-Type Pump Technology for Hard-to-Pump Applications. In Proceedings of the 17th Pump User Symposium, Houston, TX, USA, 17–19 February 2000. [Google Scholar]
- Al-Halhouli, A.T. Recent Advances in On-disk Viscous Micropumps. J. Microelectron. Electron. Packag. 2009, 6, 240–249. [Google Scholar] [CrossRef]
- Jeong, S.Y.; Chang, S.M.; Yang, J.S. Computational Design of a Disk-Shape Boundary-Layer Pump. J. Fluid Mach. 2010, 13, 12–17. [Google Scholar] [CrossRef]
- Zhou, C.; Chen, G.; Xu, Q.; Xu, L. Research on Flow Mechanismin Disc Pump. Fluid Mach. 2010, 38, 44–47. (In Chinese) [Google Scholar]
- Zhou, C.; Chen, G.; Tan, H. Numerical simulation of Flow in Solid-Liquid Blade Disc Pump Volute. Chem. Eng. Mach. 2014, 41, 501–504. (In Chinese) [Google Scholar]
- Li, B.; Qi, H. The Numerical Simulation of Gas-Liquid-Solid Three-Phase Flow in the Disc Pump. Adv. Mater. Res. 2011, 320, 434–440. [Google Scholar] [CrossRef]
- Chernyavskiy, A.M.; Ruzmatov, T.M.; Fomichev, A.V.; Medvedev, A.E.; Prikhodko, Y.M.; Fomin, V.M.; Vladislav, F.; Chekhov, V.P. The Experimental Model of Disc-Pump for Mechanical Circulatory Support. Russ. J. Transp. Artif. Organs 2017, 18, 93–101. [Google Scholar] [CrossRef]
- Cheremushkin, V.; Lomakin, V. Development and research of hydraulic disk pump. IOP Conf. Ser. Mater. Sci. Eng. 2019, 492, 12039. [Google Scholar] [CrossRef]
- Zharkovsky, A.A.; Ivanov, O.A.; Klyuev, A.S.; Myshlyavtsev, A.V.; Likholobov, V.A.; Yusha, V.L. On the possibility of using disk impellers in low-flow oil pumps. AIP Conf. Proc. 2020, 2285, 030008. [Google Scholar]
- Pei, Y.; Liu, Q.; Wang, C.; Wang, G. Energy efficiency prediction model and energy characteristics of subsea disc pump based on velocity slip and similarity theory. Energy 2021, 229, 120690. [Google Scholar] [CrossRef]
- Pei, Y.; Liu, Q.; Wang, C.; Wang, G. Energy-efficient pressure regulation model and experiment of lift pump system in deepwater dual-gradient drilling. J. Pet. Sci. Eng. 2021, 203, 108621. [Google Scholar] [CrossRef]
- Zhang, Y. Study on Design Application Method for Subsea Mudlift Disc Pump. Master’s Thesis, China University of Petroleum (East China), Qingdao, China, 2015. (In Chinese). [Google Scholar]
- Placco, G.M.; Guimarães, L.N.F. Power Analysis on a 70-mm Rotor Tesla Turbine. J. Energy Resour. Technol. 2020, 142, 031202. [Google Scholar] [CrossRef]
- Han, K.; Luo, J.; Chen, J.; Chen, B.; Xu, L.; Feng, Y.; Tang, W.; Wang, Z. Self-powered ammonia synthesis under ambient conditions via N2 discharge driven by Tesla turbine triboelectric nanogenerators. Microsyst. Nanoeng. 2021, 7, 7. [Google Scholar] [CrossRef] [PubMed]
- Aghagoli, A.; Sorin, M. CFD modelling and exergy analysis of a heat pump cycle with Tesla turbine using CO2 as a working fluid. Appl. Therm. Eng. 2020, 178, 115587. [Google Scholar] [CrossRef]
- Rusin, K.; Wróblewski, W.; Strozik, M. Comparison of methods for the determination of Tesla turbine performance. J. Theor. Appl. Mech-Pol. 2019, 57, 563–575. [Google Scholar] [CrossRef]
- Ali Kamran, M.; Manzoor, S. Effect of nozzle angle, turbine inlets and mass flow rate on the performance of a bladeless turbine. Proc. Inst. Mech. Eng. Part A J. Power Energy 2020, 234, 1101–1107. [Google Scholar] [CrossRef]
- Rusin, K.; Wróblewski, W.; Rulik, S. Efficiency based optimization of a Tesla turbine. Energy 2021, 236, 121448. [Google Scholar] [CrossRef]
- Sheikhnejad, Y.; Simões, J.; Martins, N. Energy Harvesting by a Novel Substitution for Expansion Valves: Special Focus on City Gate Stations of High-Pressure Natural Gas Pipelines. Energies 2020, 13, 956. [Google Scholar] [CrossRef]
- Talluri, L.; Dumont, O.; Manfrida, G.; Lemort, V.; Fiaschi, D. Experimental investigation of an Organic Rankine Cycle Tesla turbine working with R1233zd(E). Appl. Therm. Eng. 2020, 174, 115293. [Google Scholar] [CrossRef]
- Sengupta, S.; Guha, A. Inflow-rotor interaction in Tesla disc turbines: Effects of discrete inflows, finite disc thickness, and radial clearance on the fluid dynamics and performance of the turbine. Proc. Inst. Mech. Eng. Part A J. Power Energy 2018, 232, 971–991. [Google Scholar] [CrossRef]
- Qi, W.; Deng, Q.; Chi, Z.; Hu, L.; Yuan, Q.; Feng, Z. Influence of Disc Tip Geometry on the Aerodynamic Performance and Flow Characteristics of Multichannel Tesla Turbines. Energies 2019, 12, 572. [Google Scholar] [CrossRef]
- Sheikhnejad, Y.; Simões, J.; Martins, N. Introducing Tesla turbine to enhance energy efficiency of refrigeration cycle. Energy Rep. 2020, 6, 358–363. [Google Scholar] [CrossRef]
- Klingl, S.; Lecheler, S.; Pfitzner, M. Linear stability investigations on the inward flow between closely spaced co-rotating disks. Eur. J. Mech.—B/Fluids 2020, 84, 455–469. [Google Scholar] [CrossRef]
- Niknam, P.H.; Talluri, L.; Ciappi, L.; Fiaschi, D. Numerical assessment of a two-phase Tesla turbine: Parametric analysis. Appl. Therm. Eng. 2021, 197, 117364. [Google Scholar] [CrossRef]
- Rusin, K.; Wróblewski, W.; Rulik, S.; Majkut, M.; Strozik, M. Performance Study of a Bladeless Microturbine. Energies 2021, 14, 3794. [Google Scholar] [CrossRef]
- Hoya, G.P.; Guha, A. The design of a test rig and study of the performance and efficiency of a Tesla disc turbine. Proc. Inst. Mech. Eng. Part A J. Power Energy 2009, 223, 451–465. [Google Scholar] [CrossRef]
- Rusin, K.; Wróblewski, W.; Rulik, S. The evaluation of numerical methods for determining the efficiency of Tesla turbine operation. J. Mech. Sci. Technol. 2018, 32, 5711–5721. [Google Scholar] [CrossRef]
- Guha, A.; Sengupta, S. The fluid dynamics of work transfer in the non-uniform viscous rotating flow within a Tesla disc turbomachine. Phys Fluids 2014, 26, 33601. [Google Scholar] [CrossRef]
- Osintsev, K.V. Using the organic Rankine cycle for heat supply of greenhouses at agricultural enterprises. IOP Conf. Ser. Mater. Sci. Eng. 2020, 941, 12056. [Google Scholar] [CrossRef]
- Qi, W.; Deng, Q.; Jiang, Y.; Feng, Z.; Yuan, Q. Aerodynamic performance and flow characteristics analysis of Tesla turbines with different nozzle and outlet geometries. Proc. Inst. Mech. Eng. Part A J. Power Energy 2019, 233, 358–378. [Google Scholar] [CrossRef]
- Pérez, J.L.; Espinoza, L.P.C.Y. Three-dimensional simulation of the entrance-impeller interaction of a hydraulic disc pump. Rev. Téc. Fac. Ing. Univ. Zulia 2006, 29, 49–57. [Google Scholar]
- Eskin, D. An Engineering Model of a Disc Pump Stage for Heavy Oil. Chem. Eng. Technol. 2009, 32, 1245–1251. [Google Scholar] [CrossRef]
- Dodsworth, L.; Groulx, D. Operational Parametric Study of a Tesla Pump: Disk Pack Spacing and Rotational Speed. In Proceedings of the Fluids Engineering Division Summer Meeting, Seoul, South of Korea, 26–31 July 2015; American Society of Mechanical Engineers: New York, NY, USA, 2015. [Google Scholar]
- Alonso, D.H.; de Sá, L.F.N.; Saenz, J.S.R.; Silva, E.C.N. Topology optimization based on a two-dimensional swirl flow model of Tesla-type pump devices. Comput. Math. Appl. 2019, 77, 2499–2533. [Google Scholar] [CrossRef]
- Yu, S.C.M.; Ng, B.T.H.; Chan, W.K.; Chua, L.P. The flow patterns within the impeller passages of a centrifugal blood pump model. Med. Eng. Phys. 2000, 22, 381–393. [Google Scholar] [CrossRef] [PubMed]
- Cheng, X.X.; Wu, S. Discussion on Bearing Matching Principles of Balancing Disc-Type Centrifugal Pumps. Adv. Mater. Res. 2012, 479–481, 1453–1456. [Google Scholar] [CrossRef]
- Wu, W.; Xiong, Z.; Hu, J.; Yuan, S. Application of CFD to model oil–air flow in a grooved two-disc system. Int. J. Heat Mass Tranf. 2015, 91, 293–301. [Google Scholar] [CrossRef]
- Siddique, M.H.; Samad, A.; Husain, A. Combined effects of viscosity and surface roughness on electric submersible pump performance. Proc. Inst. Mech. Eng. Part A J. Power Energy 2017, 231, 303–316. [Google Scholar] [CrossRef]
- Amjad, S.N.; Shah, S.I.A. Estimation of velocity and pressure profiles to design an optimum Von Karman Viscous Pump. In Proceedings of the 2017 14th International Bhurban Conference on Applied Sciences and Technology (IBCAST), Islamabad, Pakistan, 10–14 January 2017. [Google Scholar]
- Li, W.; Zhang, Y. The Vortex Pump Under Highly Viscous Liquid Flow Conditions. Arab. J. Sci. Eng. 2018, 43, 4739–4761. [Google Scholar] [CrossRef]
- Heng, Y.; Han, Y.; Zhang, H.; Zhang, W.; Bois, G.; Jiang, Q.; Wang, Z.; Liu, X. Tesla Bladed Pump (Disc Bladed Pump) Preliminary Experimental Performance Analysis. Energies 2020, 13, 4873. [Google Scholar] [CrossRef]
- Martínez-Díaz, L.; Herrera, H.H.; González, L.M.C.; Izquierdo, N.V.; Carvajal, T.R. Effects of turbulization on the disc pump performance. Alexandria Eng. J. 2019, 58, 909–916. [Google Scholar] [CrossRef]
- Qi, H.; Li, B. Numerical simulation of gas-liquid two-phase flow in mixed transport disc pump. J. China Pet. Mach. 2009, 37, 34–37. (In Chinese) [Google Scholar]
- Zhou, C.; Chen, G.; Xu, C. Numerical simulation of gas-liquid two-phase flow in mixed transport disc pump. J. China Univ. Pet. 2010, 34, 147–151+158. (In Chinese) [Google Scholar]
- Mochizuki, S.; Abe, Y.; Chinzei, T.; Isoyama, T.; Ono, T.; Saito, I.; Guba, P.; Karita, T.; Sun, Y.P.; Kouno, A.; et al. Results of Animal Experiments Using an Undulation Pump Total Artificial Heart: Analysis of 10 Day and 19 Day Survival. ASAIO J. 2000, 46, 500–504. [Google Scholar] [CrossRef]
- Abi-Samra, K.; Clime, L.; Kong, L.; Gorkin, R.; Kim, T.; Cho, Y.; Madou, M. Thermo-pneumatic pumping in centrifugal microfluidic platforms. Microfluid Nanofluid 2011, 11, 643–652. [Google Scholar] [CrossRef]
- Jhun, C.S.; Newswanger, R.; Cysyk, J.; Lukic, B.; Weiss, W.; Rosenberg, G. Tesla-Based Blood Pump and Its Applications. J. Med. Device 2013, 7, 409171–409172. [Google Scholar] [CrossRef]
- Medvedev, A.E.; Fomin, V.M.; Prikhodko, Y.M.; Cherniavskiy, A.M.; Fomichev, V.P.; Fomichev, A.V.; Chekhov, V.P.; Ruzmatov, T.M. Circular pump support of blood circulation in the human body. AIP Conf. Proc. 2016, 1770, 030084. [Google Scholar]
- Chernyavskiy, A.M.; Ruzmatov, T.M.; Fomichev, A.V.; Medvedev, A.E.; Prikhodko, Y.M.; Fomin, V.M.; Fomichev, V.P.; Lomanovich, K.A.; Karaskov, A.M. Experimental evaluation of mechanical heart support system based on viscous friction disc pump. Russ. J. Transp. Artif. Organs 2017, 19, 28–34. [Google Scholar] [CrossRef][Green Version]
- Medvedev, A.E.; Fomin, V.M.; Chernyavskiy, A.M.; Prikhodko, Y.M.; Zhulkov, M.O.; Golovin, A.M.; Prikhodko, Y.M.; Zhulkov, M.O.; Golovin, A.M. Implanted system of mechanical support of the disk-based heart pump viscous friction. AIP Conf. Proc. 2018, 2027, 030149. [Google Scholar]
- Zhulkov, M.O.; Golovin, A.M.; Golovina, E.O.; Grenadyorov, A.S.; Fomichev, A.V.; Alsov, S.A.; Chernyavskiy, A.M. Study of haemolytic properties of a disk-type pump. Patol. Krovoobrashcheniya Kardiokhirurgiya 2020, 24, 87–93. [Google Scholar] [CrossRef]
- Izraelev, V.; Weiss, W.J.; Fritz, B.; Newswanger, R.K.; Paterson, E.G.; Snyder, A.; Medvitz, R.B.; Cysyk, J.; Pae, W.E.; Hicks, D.; et al. A Passively Suspended Tesla Pump Left Ventricular Assist Device. ASAIO J. 2009, 55, 556–561. [Google Scholar] [CrossRef]
- Miller, G.E.; Etter, B.D.; Dorsi, J.M. A multiple disk centrifugal pump as a blood flow device. IEEE Trans. Biomed. Eng. 1990, 37, 157–163. [Google Scholar] [CrossRef] [PubMed]
- Miller, G.E.; Sidhu, A.; Fink, R.; Etter, B.D. Evaluation of a multiple disk centrifugal pump as an artificial ventricle. Artif. Organs 1993, 17, 590–592. [Google Scholar] [CrossRef]
- Kabei, N.; Tuichiya, K.; Sakurai, Y. Concept Designs of Nonrotating-type Centrifugal Blood Pump and Basic Study on Output Characteristics of the Oscillating Disk-type Centrifugal Pump. Artif. Organs 1994, 18, 657–663. [Google Scholar] [CrossRef]
- Miller, G.E.; Fink, R. Analysis of optimal design configurations for a multiple disk centrifugal blood pump. Artif. Organs 1999, 23, 559–565. [Google Scholar] [CrossRef] [PubMed]
- Medvedev, A.E.; Fomin, V.M.; Prikhodko, Y.M.; Cherniavskiy, A.M.; Fomichev, V.P.; Fomichev, A.V.; Chekhov, V.P.; Ruzmatov, T.M. Mathematical modelling of flow in disc friction LVAD pump. AIP Conf. Proc. 2017, 1893, 020019. [Google Scholar]
- Chernyavskiy, A.M.; Fomichev, A.V.; Ruzmatov, T.M.; Medvedev, A.E.; Prikhodko, Y.M.; Fomin, V.M.; Vladislav, F.; Chekhov, V.P. Prospects of Disk Pump for Mechanical Circulatory Support in Cardiac Surgery (Review). Russ. J. Transp. Artif. Organs 2016, 18, 68–73. [Google Scholar] [CrossRef][Green Version]
- Medvitz, R.B.; Boger, D.A.; Izraelev, V.; Rosenberg, G.; Paterson, E.G. Computational Fluid Dynamics Design and Analysis of a Passively Suspended Tesla Pump Left Ventricular Assist Device. Artif. Organs 2011, 35, 522–533. [Google Scholar] [CrossRef] [PubMed]
- Naumov, I.E.; Prikhodko, Y.M.; Chekhov, V.P.; Fomichev, V.P. On dimensionless parameters for generalization pressure head and flow rate characteristics of centrifugal disk pumps. Thermophys Aeromech. 2012, 19, 77–82. [Google Scholar] [CrossRef]
- Habhab, M.; Ismail, T.; Lo, J. A Laminar Flow-Based Microfluidic Tesla Pump via Lithography Enabled 3D Printing. Sensors 2016, 16, 1970. [Google Scholar] [CrossRef]
- Naz, S.; Lockhart, D.; Harwood, P.; Komrakova, A.E. Numerical Study of Turbulent Rotating Flow in a Tesla Disc Pump. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Tampa, FL, USA, 3–9 November 2017; American Society of Mechanical Engineers: New York, NY, USA, 2017. [Google Scholar]
- Zhai, L.; Han, B.; Zhang, Y.; Ye, X.; Sun, M. A Modal Analysis Method for Turbomolecular Pump Rotor Assembly with Separable Thrust Disk. In Proceedings of the 2018 21st International Conference on Electrical Machines and Systems (ICEMS), Jeju, South of Korea, 7–10 October 2018. [Google Scholar]
- Wilk, A. Laboratory Measurements the Rise in Power Consumption Resulting from the Use of a Finned Rotating Disc at a Centrifugal Water Flow. Iran. J. Sci. Technol. Trans. Mech. Eng. 2019, 43 (Suppl. S1), 773–782. [Google Scholar] [CrossRef]
- Guan, D.; Jing, L.; Gong, J.; Yang, Z.; Shen, H. Friction and wear modeling of rotary disc in spherical pump. Ind. Lubr. Tribol. 2019, 71, 420–425. [Google Scholar] [CrossRef]
- Zhulkov, M.O.; Golovin, A.M.; Golovina, E.O.; Grenaderov, A.S.; Fomichev, A.V.; Alsov, S.A.; Chernyavsky, A.M. First experience in implantation of a mechanical circulatory support device based on a disk-type pump: An acute experiment. Vestn. Transp. Iskusstv. Org. 2020, 22, 113–116. [Google Scholar] [CrossRef]
- Yang, F.; Sun, H.; Zhang, C. Gas-Liquid Mixing in a Grid-Disc Impeller Stirred Tank. Chem. Eng. Technol. 2020, 43, 1297–1307. [Google Scholar] [CrossRef]
- Zhang, H.; Tang, L.; Zhao, Y. Influence of Blade Profiles on Plastic Centrifugal Pump Performance. Adv. Mater. Sci. Eng. 2020, 2020, 6665520. [Google Scholar] [CrossRef]
- Huang, W.; Lai, L.; Chen, X.; Chen, Z.; Huang, Z.; Tang, M.; Bao, Q.; Zhang, J. Influence of disc parameters on output performance of elastic valve piezoelectric pump. Microsyst. Technol. 2021, 27, 3049–3057. [Google Scholar] [CrossRef]
- Zhao, F.; Kong, F.; Duan, X.; Wu, H.; Wang, J. Numerical Investigation on the Transient Flow of a Boiler Circulating Pump Based on the Shear Stress Transport Turbulence Model. Processes 2020, 8, 1279. [Google Scholar] [CrossRef]
- Wang, Z.; Shi, H.; Wang, S.; Wang, Z.; Hao, M.; Wang, J. Study on the operating characteristic of disc seal single screw pump used in energy recovery systems. Int. J. Refrig. 2020, 118, 336–344. [Google Scholar] [CrossRef]
- Blanchard, D.; Ligrani, P.; Gale, B. Miniature Single-Disk Viscous Pump (Single-DVP), Performance Characterization. J. Fluids Eng. 2006, 128, 602–610. [Google Scholar] [CrossRef]
- Blanchard, D.; Ligrani, P.; Gale, B. Single-disk and double-disk viscous micropumps. Sensors Actuators A Phys. 2005, 122, 149–158. [Google Scholar] [CrossRef]
- Ligrani, P.; Blanchard, D.; Gale, B. Slip due to surface roughness for a Newtonian liquid in a viscous microscale disk pump. Phys. Fluids 2010, 22, 52002. [Google Scholar] [CrossRef]
- Lund, B.; Brown, M.; Jennerjohn, M.; Ligrani, P.; Fatemi, A. Elastic Turbulence Effects on the Performance of a Miniature Viscous Disk Pump. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Houston, TX, USA, 13–19 November 2015; American Society of Mechanical Engineers: New York, NY, USA, 2015. [Google Scholar]
- Ligrani, P.; Lund, B.; Fatemi, A. Miniature Viscous Disk Pump: Performance Variations from Non-Newtonian Elastic Turbulence. J. Fluids Eng. 2017, 139, 021104. [Google Scholar] [CrossRef]
- Kilani MI, Galambos PC, Haik YS, Chen CJ Design and analysis of a surface micro-machined spiral-channel viscous pump. ASME J. Fluids Eng. 2003, 125, 339–344. [CrossRef]
- Haik, Y.; Kilani, M.; Hendrix, J.; Al Rifai, O.; Galambos, P. Flow field analysis in a spiral viscous micropump. Microfluidics and Nanofluidics 2007. 3, 527–535. [CrossRef]
- Zhou, C. Research on the Blade Disk Pump for Subsea Mudlifl Drilling. Ph.D. Thesis, China University of Petroleum (East China), Qingdao, China, 2012. (In Chinese). [Google Scholar]
- Yin, S. The Optimization of Subsea Mudlift Disc Pump and the Development of Its Multi-stage Pump. Master’s Thesis, China University of Petroleum (East China), Qingdao, China, 2012. (In Chinese). [Google Scholar]
- Xie, Y. Study on Design and Configuration of Subsea Mudlift Drilling for Marine Natural Gas Hydrate System. Master’s Thesis, China University of Petroleum (East China), Qingdao, China, 2016. (In Chinese). [Google Scholar]
- Pei, Y.; Liu, Q.; Wang, C.; Wang, G. Analytical Methods and Verification of Impeller Outlet Velocity Slip of Solid–Liquid Disc Pump with Multi-Type Blades. Arab. J. Sci. Eng. 2021, 46, 6835–6847. [Google Scholar] [CrossRef]
- Bataineh, K.M.; Al-Nimr, M.D.A.; Kiwan, S.M. Double-disk rotating viscous micro-pump with slip flow. Microsyst. Technol. 2010, 16, 1811–1819. [Google Scholar] [CrossRef]
- Wang, B.; Okamoto, K.; Yamaguchi, K.; Teramoto, S. Loss Mechanisms in Shear-Force Pump with Multiple Corotating Disks. J. Fluids Eng. 2014, 136, 081101. [Google Scholar] [CrossRef]
- Hu, C.; Wu, W.; Hu, J.; Yuan, S. Flow dynamical behavior and performance of a micro viscous pump with unequal inlet and outlet areas. Eng. Appl. Comput. Fluid 2016, 10, 441–451. [Google Scholar] [CrossRef]
- Schima, H.; Schmallegger, H.; Huber, L.; Birgmann, I.; Reindl, C.; Schmidt, C.; Roschal, K.; Wieselthaler, G.; Trubel, W.; Losert, U.; et al. An implantable seal-less centrifugal pump with integrated double-disk motor. Artif. Organs 1995, 19, 639–643. [Google Scholar] [CrossRef] [PubMed]
- Atencia, J.; Beebe, D.J. Steady flow generation in microcirculatory systems. Lab Chip 2006, 6, 567. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.X.; Egusquiza, E.; Valero, C.; Presas, A. Dynamic behaviour of pump-turbine runner: From disk to prototype runner. IOP Conf. Ser. Mater. Sci. Eng. 2013, 52, 22036. [Google Scholar] [CrossRef]
- Zhenyu, X.; Xuhong, M.; Hai, Z. The Research on Pulsation of Pump Pressure in Water Mist System. Energy Procedia 2015, 66, 73–76. [Google Scholar] [CrossRef][Green Version]
- Yin, S.; Chen, G.; Zhou, C. New-type Impeller Design and Performance Prediction for Disc Pump. Fluid Mach. 2012, 40, 19–23. (In Chinese) [Google Scholar]
- Yin, S.; Chen, G.; Zhou, C.; Chen, Y. Numerical analysis of solid-liquid two-phase flow and external characteristics of conical disc pump. China Pet. Mach. 2011, 39, 26–28. (In Chinese) [Google Scholar]
- Chen, Y.; Chen, G.; Li, W.; Zhou, C. Structure Design for a Multi-stage Disc Pump with High Wear-Resistance. Oil Field Equip. 2013, 42, 25–28. (In Chinese) [Google Scholar]
- Jin, Y.; Zhang, D.; Song, W.; Shen, X.; Shi, L.; Lu, J. Numerical study on energy conversion characteristics of molten salt pump based on energy transport theory. Energy 2022, 244, 122674. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).