Multi-Objective Optimization of Process Parameters in Longitudinal-Torsional Ultrasonic Vibration Face Grinding CFRP
Abstract
:1. Introduction
2. Experimental Conditions and Methods
2.1. Experimental Set-Up and Conditions
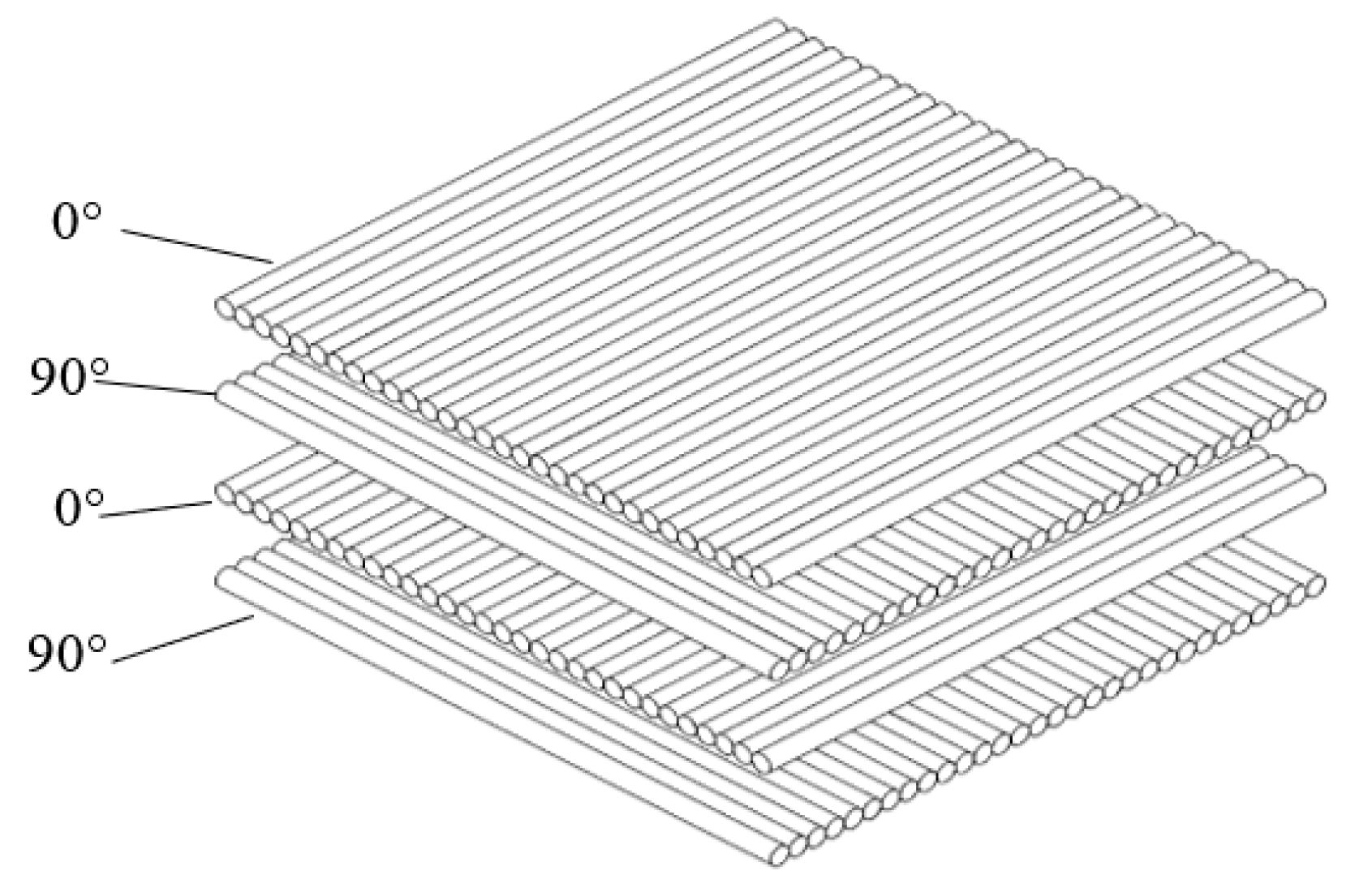
2.2. Materials
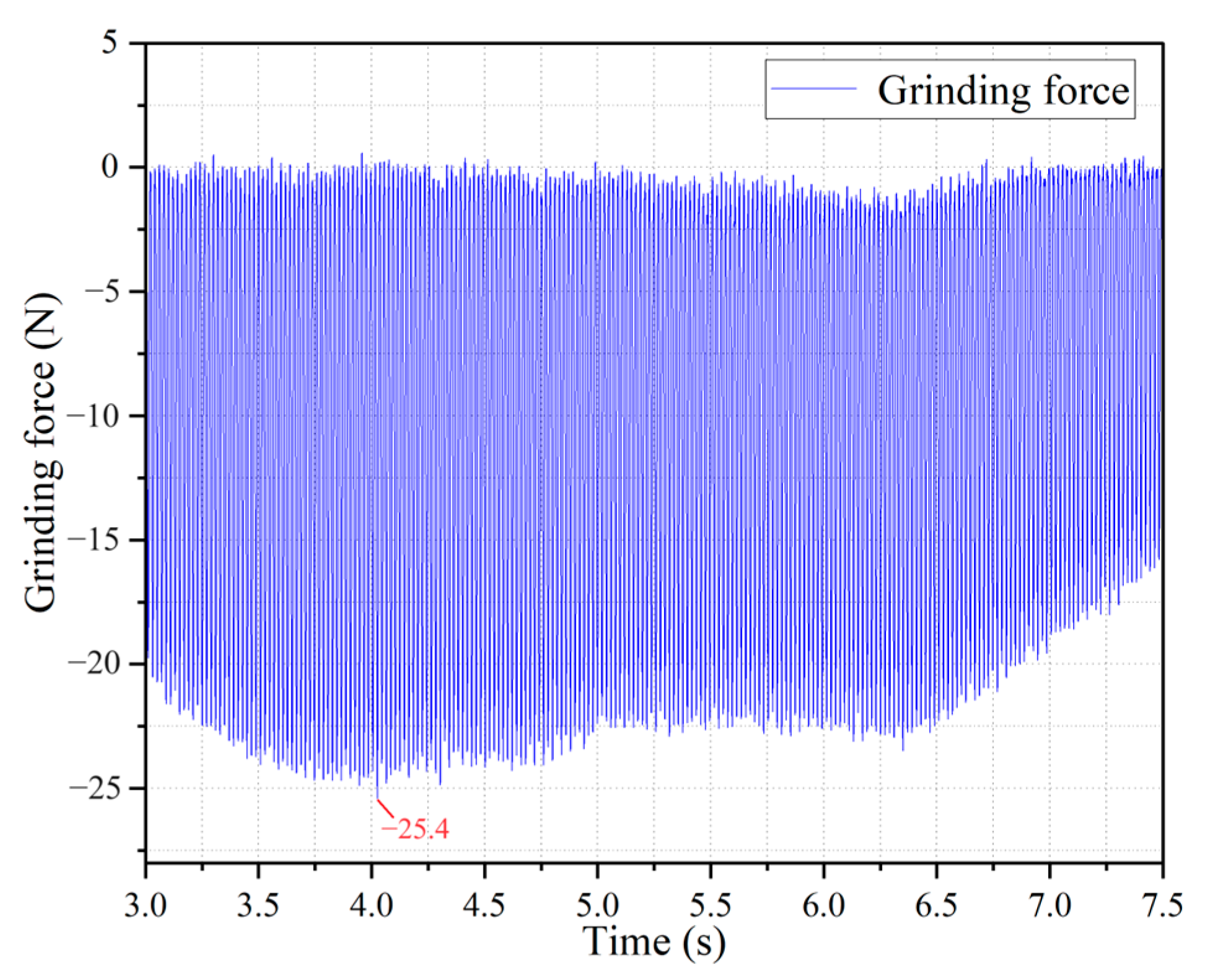
2.3. Material Measurement Procedures for Output Variables
2.4. Experimental Design
3. Results and Discussions
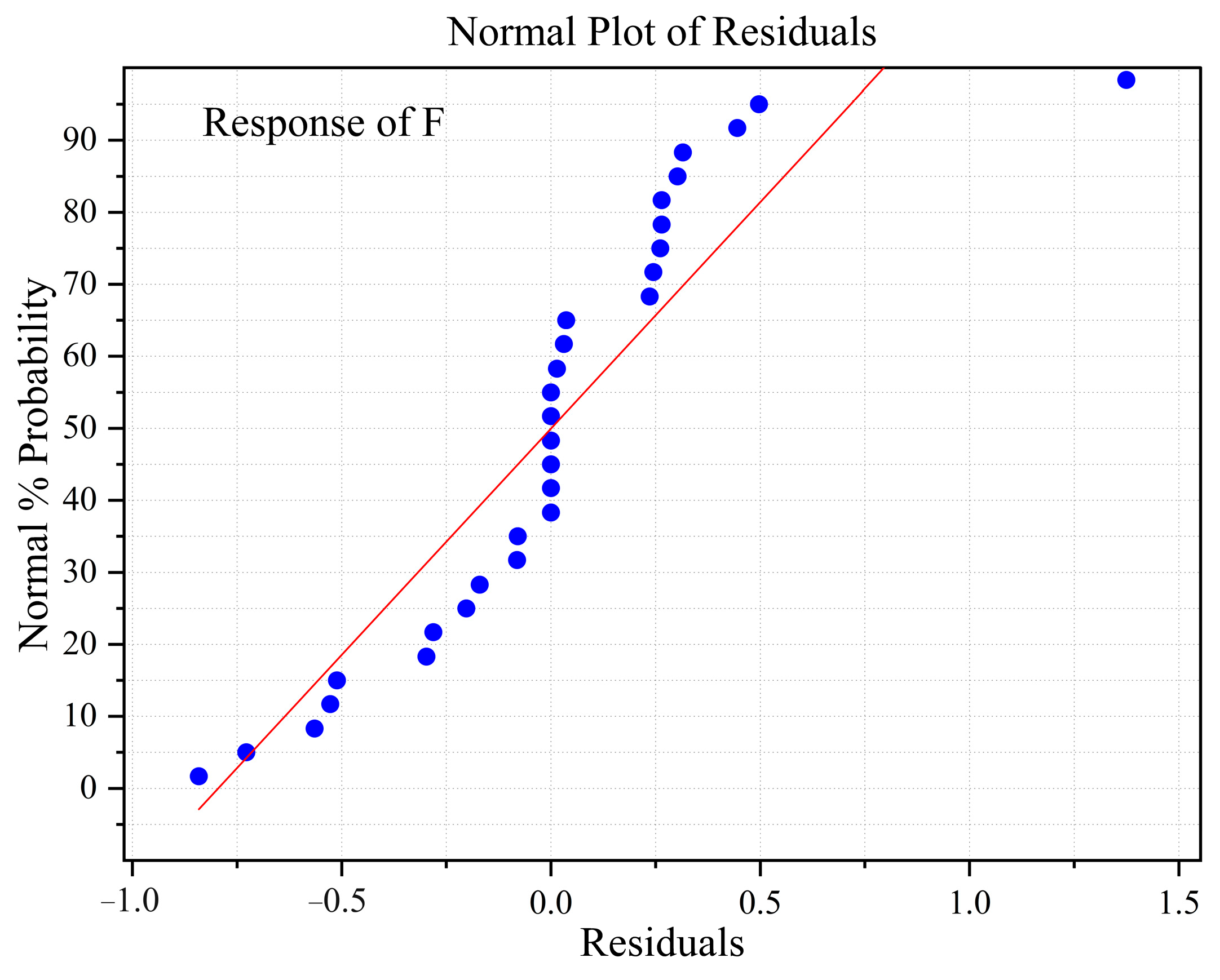
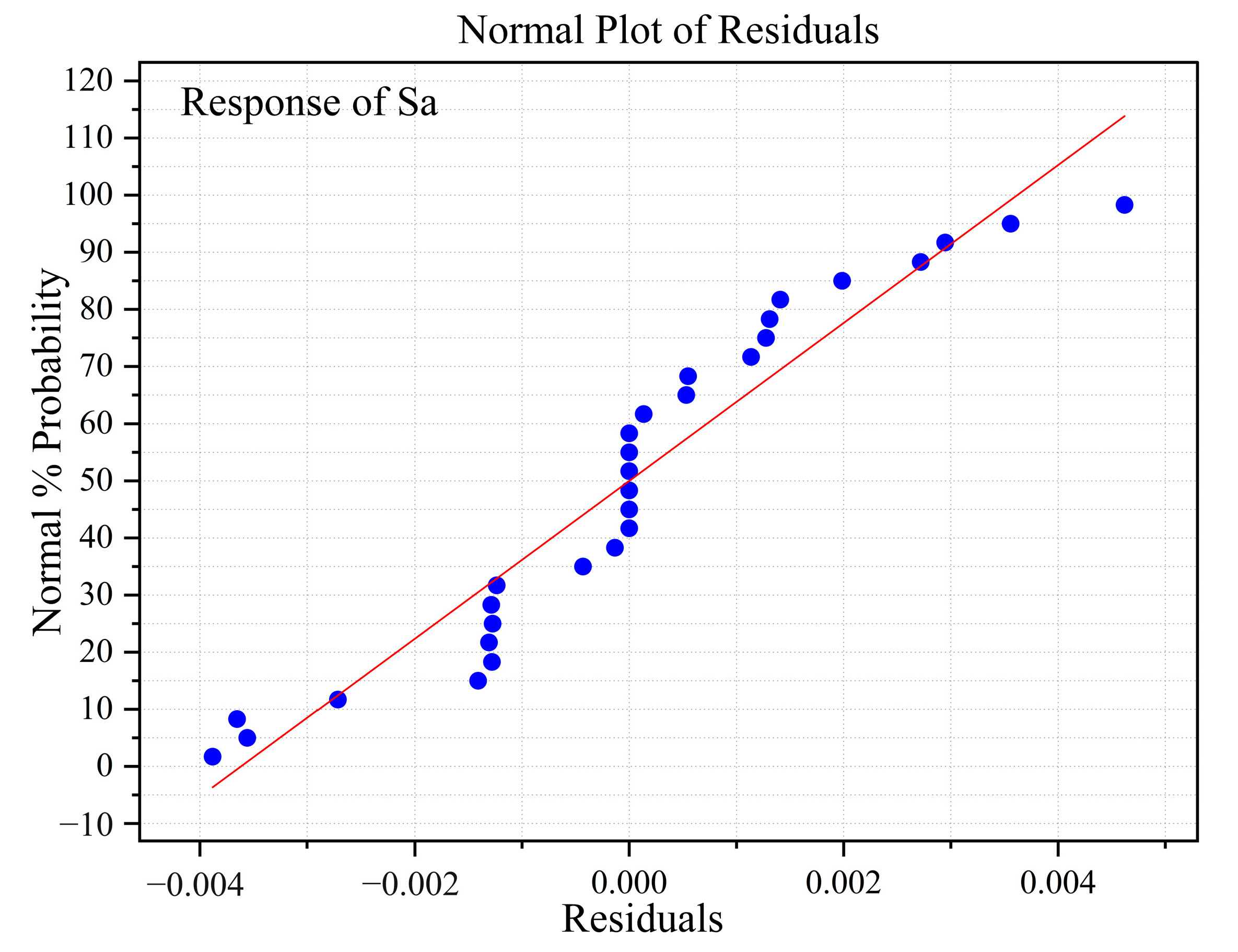
3.1. ANOVA
3.1.1. Grinding Force Analysis and Prediction
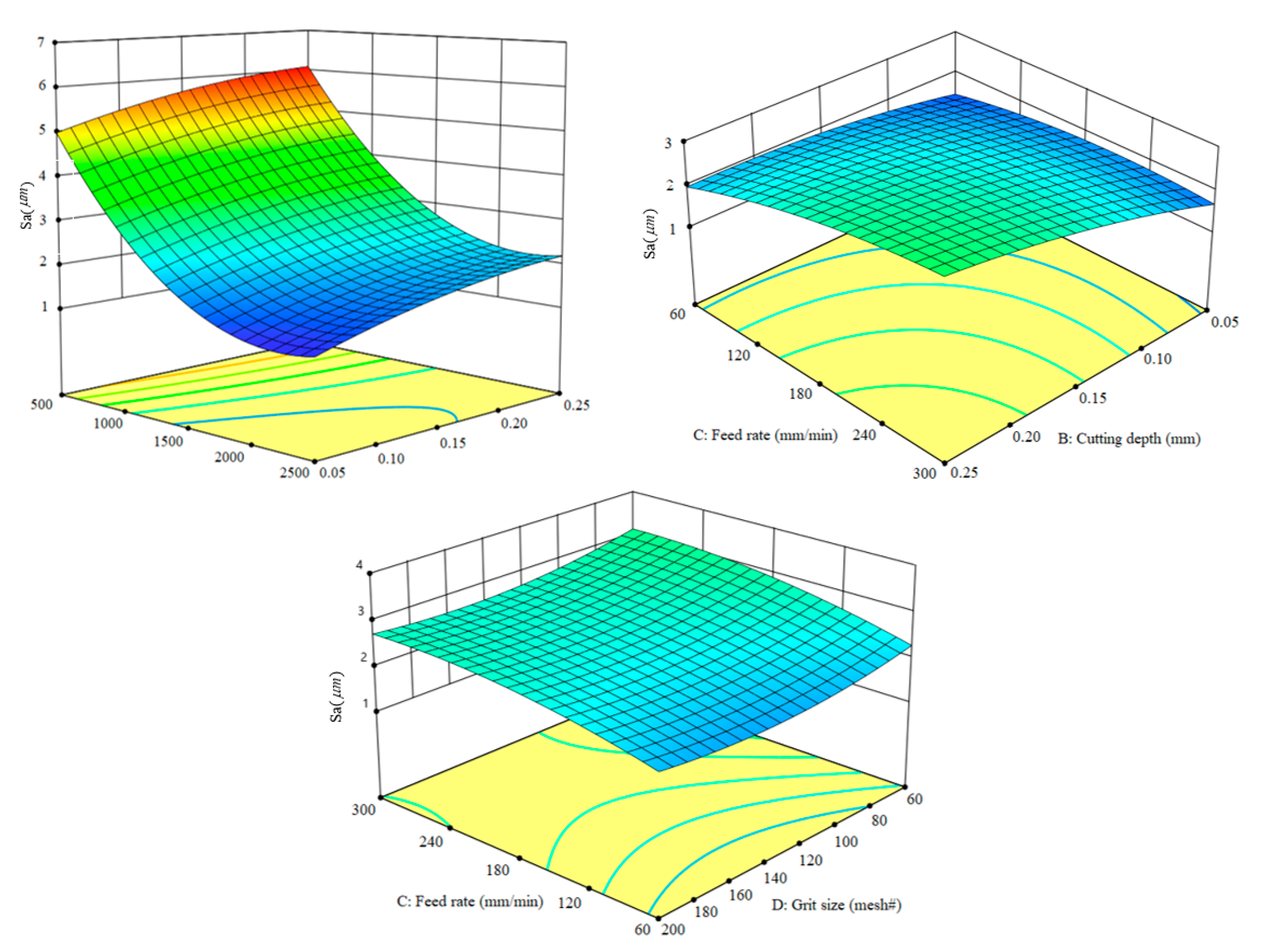
3.1.2. Surface Roughness Analysis and Prediction
3.2. Multi-Objective Optimization via NSGA-II
- Find the Pareto optimal solution set.
- Compare the evaluation results of all elements in the Pareto optimal solution set and select the best solution that is closest to the optimal level (with two objectives simultaneously optimal).
3.2.1. Models of Multi-Objective Optimization
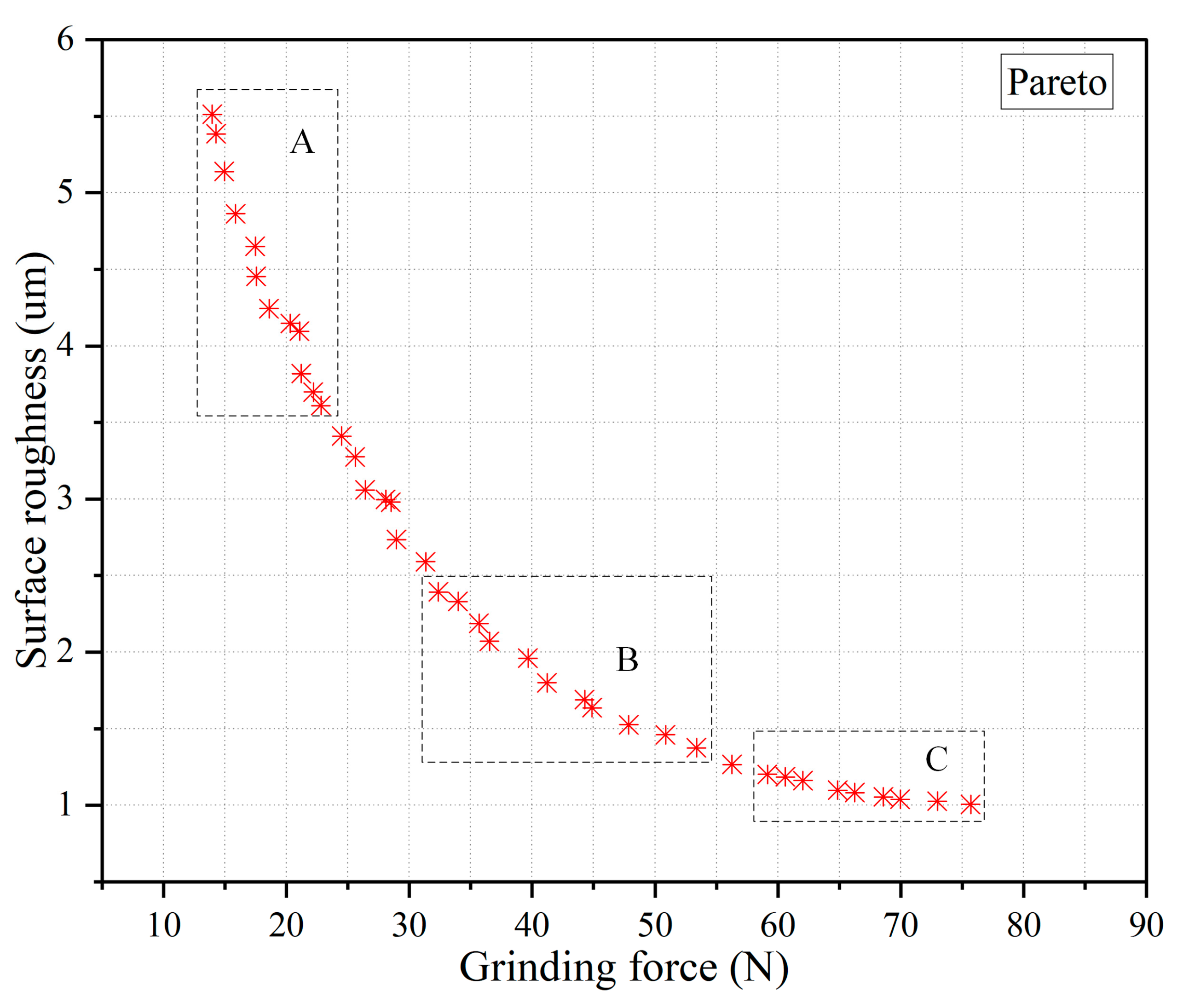
3.2.2. Optimization Results Discussion
4. Conclusions
- Using the Box—Behnken design method in RSM to analyze the influence of various cutting parameters on the machining results, it was concluded that the spindle speed had a marked impact on the cutting force and the surface roughness. The influence of the cutting depth, grit size and feed rate on the machining results decreased in sequence.
- Regression equations obtained through general full factorial design of parameters affecting the surface roughness and the cutting forces were obtained. A statistical mathematical model with high predictive power was created, which effectively predicted the grinding force and surface roughness during the L&T ultrasonic vibration face grinding process.
- With the purpose of minimizing the grinding force and surface roughness, the NSGA-II algorithm was used for multi-objective optimization. Compared with the initial experimental parameters, the optimized results significantly improved surface roughness and reduced cutting force. Moreover, this optimization model has a high level of accuracy and application value, and can provide optimization solutions for different industrial requirements.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Aamir, M.; Tolouei-Rad, M.; Giasin, K.; Nosrati, A. Recent advances in drilling of carbon fiber–reinforced polymers for aerospace applications: A review. Int. J. Adv. Manuf. Technol. 2019, 105, 2289–2308. [Google Scholar] [CrossRef]
- Asmael, M.; Safaei, B.; Zeeshan, Q.; Zargar, O.; Nuhu, A.A. Ultrasonic machining of carbon fiber–reinforced plastic composites: A review. Int. J. Adv. Manuf. Technol. 2021, 113, 3079–3120. [Google Scholar] [CrossRef]
- Liu, J.; Che, G.; Ji, C.; Qin, X.; Li, H.; Ren, C. An investigation of workpiece temperature variation of helical milling for carbon fiber reinforced plastics (CFRP). Int. J. Mach. Tools Manuf. 2014, 86, 89–103. [Google Scholar] [CrossRef]
- Rodríguez, A.; Calleja, A.; de Lacalle, L.L.; Pereira, O.; Rubio-Mateos, A.; Rodríguez, G. Drilling of CFRP-Ti6Al4V stacks using CO2-cryogenic cooling. J. Manuf. Process. 2021, 64, 58–66. [Google Scholar] [CrossRef]
- Lopez de Lacalle, N.; Lamikiz, A.; Campa, F.J.; Valdivielso, A.F.; Etxeberria, I. Design and test of a multitooth tool for CFRP milling. J. Compos. Mater. 2009, 43, 3275–3290. [Google Scholar] [CrossRef]
- Suárez, A.; Veiga, F.; de Lacalle, L.N.L.; Polvorosa, R.; Lutze, S.; Wretland, A. Effects of ultrasonics-assisted face milling on surface integrity and fatigue life of Ni-Alloy 718. J. Mater. Eng. Perform. 2016, 25, 5076–5086. [Google Scholar] [CrossRef]
- Shamoto, E.; Moriwaki, T. Study on Elliptical Vibration Cutting. CIRP Ann. -Manuf. Technol. 1994, 43, 35–38. [Google Scholar] [CrossRef]
- Celaya, A.; Lopez de Lacalle, L.N.; Campa, F.J.; Lamikiz, A. Ultrasonic Assisted Turning of mild steels. Int. J. Mater. Prod. Technol. 2010, 37, 60–70. [Google Scholar] [CrossRef]
- Geng, D.; Lu, Z.; Yao, G.; Liu, J.; Li, Z.; Zhang, D. Cutting temperature and resulting influence on machining performance in rotary ultrasonic elliptical machining of thick CFRP. Int. J. Mach. Tools Manuf. 2017, 123, 160–170. [Google Scholar] [CrossRef]
- Pujana, J.; Rivero, A.; Celaya, A.; De Lacalle, L.L. Analysis of ultrasonic-assisted drilling of Ti6Al4V. Int. J. Mach. Tools Manuf. 2009, 49, 500–508. [Google Scholar] [CrossRef]
- Geng, D.; Teng, Y.; Liu, Y.; Shao, Z.; Jiang, X.; Zhang, D. Experimental study on drilling load and hole quality during rotary ultrasonic helical machining of small-diameter CFRP holes. J. Mater. Process. Technol. 2019, 270, 195–205. [Google Scholar] [CrossRef]
- Cao, S.; Li, H.N.; Huang, W.; Zhou, Q.; Lei, T.; Wu, C. A delamination prediction model in ultrasonic vibration assisted drilling of CFRP composites. J. Mater. Process. Technol. 2022, 302, 117480. [Google Scholar] [CrossRef]
- Yashiro, T.; Ogawa, T.; Sasahara, H. Temperature measurement of cutting tool and machined surface layer in milling of CFRP. Int. J. Mach. Tools Manuf. 2013, 70, 63–69. [Google Scholar] [CrossRef]
- Amin, M.; Yuan, S.; Israr, A.; Zhen, L.; Qi, W. Development of cutting force prediction model for vibration-assisted slot milling of carbon fiber reinforced polymers. Int. J. Adv. Manuf. Technol. 2018, 94, 3863–3874. [Google Scholar] [CrossRef]
- Ning, F.; Cong, W.; Wang, H.; Hu, Y.; Hu, Z.; Pei, Z. Surface grinding of CFRP composites with rotary ultrasonic machining: A mechanistic model on cutting force in the feed direction. Int. J. Adv. Manuf. Technol. 2017, 92, 1217–1229. [Google Scholar] [CrossRef]
- Shi, H.; Yuan, S.; Zhang, C.; Chen, B.; Li, Q.; Li, Z.; Qian, J. A cutting force prediction model for rotary ultrasonic side grinding of CFRP composites considering coexistence of brittleness and ductility. Int. J. Adv. Manuf. Technol. 2020, 106, 2403–2414. [Google Scholar] [CrossRef]
- Wang, J.; Feng, P.; Zhang, J.; Guo, P. Reducing cutting force in rotary ultrasonic drilling of ceramic matrix composites with longitudinal-torsional coupled vibration. Manuf. Lett. 2018, 18, 1–5. [Google Scholar] [CrossRef]
- Geng, D.; Liu, Y.; Shao, Z.; Zhang, M.; Jiang, X.; Zhang, D. Delamination formation and suppression during rotary ultrasonic elliptical machining of CFRP. Compos. Part B Eng. 2020, 183, 107698. [Google Scholar] [CrossRef]
- Chen, Y.; Liang, Y.; Xu, J.; Hu, A. Ultrasonic vibration assisted grinding of CFRP composites: Effect of fiber orientation and vibration velocity on grinding forces and surface quality. Int. J. Lightweight Mater. Manuf. 2018, 1, 189–196. [Google Scholar] [CrossRef]
- Wang, H.; Pei, Z.J.; Cong, W. A feeding-directional cutting force model for end surface grinding of CFRP composites using rotary ultrasonic machining with elliptical ultrasonic vibration. Int. J. Mach. Tools Manuf. 2020, 152, 103540. [Google Scholar] [CrossRef]
- Niu, Y.; Jiao, F.; Zhao, B.; Wang, D. Multiobjective optimization of processing parameters in longitudinal-torsion ultrasonic assisted milling of Ti-6Al-4V. Int. J. Adv. Manuf. Technol. 2017, 93, 4345–4356. [Google Scholar] [CrossRef]
- Sindhu, D.; Thakur, L.; Chandna, P. Multiobjective optimization of rotary ultrasonic machining parameters for quartz glass using Taguchi-Grey relational analysis (GRA). Silicon 2019, 11, 2033–2044. [Google Scholar] [CrossRef]
- Banerjee, B.; Mondal, K.; Adhikary, S.; Paul, S.N.; Pramanik, S.; Chatterjee, S. Optimization of process parameters in ultrasonic machining using integrated AHP-TOPSIS method. Mater. Today Proc. 2022, 62, 2857–2864. [Google Scholar] [CrossRef]
- Singh, R.P.; Singhal, S. Experimental study on rotary ultrasonic machining of alumina ceramic: Microstructure analysis and multi-response optimization. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2018, 232, 967–986. [Google Scholar] [CrossRef]
- Singh, M.; Singh, S. Multiple response optimization of ultrasonic assisted electric discharge Machining of Nimonic 75: A Taguchi-Grey relational analysis approach. Mater. Today Proc. 2021, 45, 4731–4736. [Google Scholar] [CrossRef]
- Kumar, V.; Singh, H. Rotary ultrasonic Drilling of Silica Glass BK-7: Microstructural investigation and process optimization through TOPSIS. Silicon 2019, 11, 471–485. [Google Scholar] [CrossRef]
- Choi, S.J.; Lee, C.M.; Kim, D.H. Experimental investigation for multiresponse optimization in rotary ultrasonic side milling of quartz. Int. J. Adv. Manuf. Technol. 2022, 122, 1583–1597. [Google Scholar] [CrossRef]


| Tool No. | Grit Size (mesh #) | Diameter of the Tool Shank | ) | Wheel Diameter D (mm) |
|---|---|---|---|---|
| 1 | 60# | 6 | 88 | 8 |
| 2 | 100# | 6 | 41 | 8 |
| 3 | 120# | 6 | 30 | 8 |
| 4 | 150# | 6 | 40 | 8 |
| 5 | 200# | 6 | 20 | 8 |
| Fiber Orientations | Fiber Diameter | Layer Thickness | Tensile Strength | Elastic Modulus | Density |
|---|---|---|---|---|---|
| 0°/90° | 6~8 μm | 125 μm | 3500 MPa | 235 GPa | 1.78 g/cm3 |
| Parameters (Code Unit) | −1 | 0 | 1 |
|---|---|---|---|
| Spindle speed (rpm) | 500 | 1500 | 2500 |
| Cutting depth (mm) | 0.05 | 0.15 | 0.25 |
| Feed rate (mm/min) | 60 | 180 | 300 |
| Grit size (mesh#) | 60 | 120 | 300 |
| Run Order | Spindle Speed (rpm) | Cutting Depth (mm) | Feed Rate (mm/min) | Grit Size (mesh#) | Grinding Force F (N) | ) |
|---|---|---|---|---|---|---|
| 1 | 2500 | 0.15 | 60 | 120 | 68.4 | 1.43 |
| 2 | 2500 | 0.05 | 180 | 120 | 68.6 | 1.13 |
| 3 | 1500 | 0.15 | 180 | 120 | 25.4 | 2.55 |
| 4 | 1500 | 0.05 | 180 | 60 | 27 | 2.1 |
| 5 | 1500 | 0.15 | 300 | 60 | 20.1 | 3.16 |
| 6 | 1500 | 0.25 | 60 | 120 | 21.8 | 2.02 |
| 7 | 500 | 0.15 | 60 | 120 | 4.1 | 4.94 |
| 8 | 1500 | 0.15 | 60 | 60 | 24.9 | 2.28 |
| 9 | 2500 | 0.25 | 180 | 120 | 66.1 | 2.23 |
| 10 | 1500 | 0.15 | 180 | 120 | 25.4 | 2.55 |
| 11 | 1500 | 0.15 | 300 | 200 | 27.2 | 2.74 |
| 12 | 1500 | 0.05 | 180 | 200 | 28.9 | 2.02 |
| 13 | 1500 | 0.15 | 60 | 200 | 21.7 | 2.04 |
| 14 | 1500 | 0.25 | 180 | 60 | 24.4 | 3.42 |
| 15 | 500 | 0.15 | 300 | 120 | 13.3 | 6.12 |
| 16 | 1500 | 0.15 | 180 | 120 | 25.4 | 2.55 |
| 17 | 1500 | 0.05 | 300 | 120 | 24.7 | 1.7 |
| 18 | 2500 | 0.15 | 180 | 60 | 67.2 | 2.25 |
| 19 | 1500 | 0.15 | 180 | 120 | 25.4 | 2.55 |
| 20 | 2500 | 0.15 | 180 | 200 | 65.2 | 1.97 |
| 21 | 500 | 0.15 | 180 | 60 | 7.7 | 6.18 |
| 22 | 1500 | 0.25 | 180 | 200 | 26.3 | 2.85 |
| 23 | 500 | 0.15 | 180 | 200 | 13.6 | 5.81 |
| 24 | 1500 | 0.15 | 180 | 120 | 25.4 | 2.55 |
| 25 | 1500 | 0.05 | 60 | 120 | 27.2 | 1.44 |
| 26 | 500 | 0.05 | 180 | 120 | 13.2 | 5 |
| 27 | 500 | 0.25 | 180 | 120 | 10.6 | 6.14 |
| 28 | 2500 | 0.15 | 300 | 120 | 63.2 | 1.84 |
| 29 | 1500 | 0.15 | 180 | 120 | 25.4 | 2.55 |
| 30 | 1500 | 0.25 | 300 | 120 | 25 | 3.35 |
| Source | Sum of Squares | DF | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 10,867.88 | 14 | 776.28 | 2240.03 | <0.0001 |
| A-Spindle speed | 9049.73 | 1 | 9049.73 | 26,113.91 | <0.0001 |
| B-Cutting depth | 19.25 | 1 | 19.25 | 55.56 | <0.0001 |
| C-Feed rate | 5.54 | 1 | 5.54 | 15.97 | 0.0012 |
| D-Grit size | 11.21 | 1 | 11.21 | 32.36 | <0.0001 |
| AC | 51.84 | 1 | 51.84 | 149.59 | <0.0001 |
| AD | 15.94 | 1 | 15.94 | 45.98 | <0.0001 |
| BC | 8.12 | 1 | 8.12 | 23.44 | 0.0002 |
| CD | 25.37 | 1 | 25.37 | 73.22 | <0.0001 |
| A² | 1206.89 | 1 | 1206.89 | 3482.60 | <0.0001 |
| B² | 8.17 | 1 | 8.17 | 23.58 | 0.0002 |
| C² | 19.43 | 1 | 19.43 | 56.07 | <0.0001 |
| Residual | 5.20 | 15 | 0.3465 | ||
| Lack of Fit | 5.20 | 10 | 0.5198 | ||
| Pure Error | 0.0000 | 5 | 0.0000 | ||
| Cor Total | 10,873.08 | 29 |
| Source | Sum of Squares | DF | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 64.80 | 14 | 4.63 | 5.785 × 105 | <0.0001 |
| A-Spindle speed | 44.11 | 1 | 44.11 | 5.513 × 106 | <0.0001 |
| B-Cutting depth | 3.41 | 1 | 3.41 | 4.258 × 105 | <0.0001 |
| C-Feed rate | 1.80 | 1 | 1.80 | 2.249 × 105 | <0.0001 |
| D-Grit size | 0.3201 | 1 | 0.3201 | 40,009.21 | <0.0001 |
| AB | 0.0004 | 1 | 0.0004 | 49.99 | <0.0001 |
| AC | 0.1482 | 1 | 0.1482 | 18,524.67 | <0.0001 |
| AD | 0.0021 | 1 | 0.0021 | 257.67 | <0.0001 |
| BC | 0.2862 | 1 | 0.2862 | 35,771.46 | <0.0001 |
| BD | 0.0612 | 1 | 0.0612 | 7647.60 | <0.0001 |
| CD | 0.0081 | 1 | 0.0081 | 1009.32 | <0.0001 |
| A² | 10.97 | 1 | 10.97 | 1.371 × 106 | <0.0001 |
| B² | 0.2475 | 1 | 0.2475 | 30,937.09 | <0.0001 |
| C² | 0.3707 | 1 | 0.3707 | 46,325.29 | <0.0001 |
| D² | 0.4611 | 1 | 0.4611 | 57,631.92 | <0.0001 |
| Residual | 0.0001 | 15 | 8.001 × 10−6 | ||
| Lack of Fit | 0.0001 | 10 | 0.0000 | ||
| Pure Error | 0.0000 | 5 | 0.0000 | ||
| Cor Total | 64.80 | 29 |
| Run Order | Spindle Speed (rpm) | Cutting Depth (mm) | Feed Rate (mm/min) | Grit Size (mesh#) | Grinding Force F (N) | ) |
|---|---|---|---|---|---|---|
| Center point level | 1500 | 0.15 | 180 | 120 | 25.4 | 2.55 |
| 1 | 1600 | 0.055 | 60 | 80 | 47.868 | 1.527 |
| 2 | 1360 | 0.055 | 60 | 80 | 39.673 | 1.960 |
| 3 | 1600 | 0.055 | 60 | 100 | 50.870 | 1.460 |
| 4 | 1360 | 0.055 | 60 | 60 | 36.536 | 2.071 |
| 5 | 1220 | 0.055 | 60 | 60 | 32.369 | 2.392 |
| 6 | 1280 | 0.055 | 60 | 70 | 35.683 | 2.188 |
| 7 | 1220 | 0.055 | 60 | 70 | 33.976 | 2.331 |
| 8 | 1500 | 0.055 | 60 | 80 | 44.271 | 1.690 |
| 9 | 1600 | 0.055 | 60 | 60 | 44.866 | 1.636 |
| 10 | 1500 | 0.055 | 60 | 60 | 41.213 | 1.800 |
| 11 | 1120 | 0.055 | 60 | 70 | 31.340 | 2.591 |
| 12 | 1810 | 0.055 | 60 | 60 | 53.383 | 1.374 |
| 13 | 1500 | 0.055 | 60 | 60 | 41.213 | 1.800 |
| 14 | 1120 | 0.055 | 60 | 70 | 31.340 | 2.591 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Zheng, K.; Li, H.; Cao, Z.; Zhao, S. Multi-Objective Optimization of Process Parameters in Longitudinal-Torsional Ultrasonic Vibration Face Grinding CFRP. Machines 2023, 11, 935. https://doi.org/10.3390/machines11100935
Liu S, Zheng K, Li H, Cao Z, Zhao S. Multi-Objective Optimization of Process Parameters in Longitudinal-Torsional Ultrasonic Vibration Face Grinding CFRP. Machines. 2023; 11(10):935. https://doi.org/10.3390/machines11100935
Chicago/Turabian StyleLiu, Shuliang, Kai Zheng, Hongcheng Li, Zhengfeng Cao, and Shuang Zhao. 2023. "Multi-Objective Optimization of Process Parameters in Longitudinal-Torsional Ultrasonic Vibration Face Grinding CFRP" Machines 11, no. 10: 935. https://doi.org/10.3390/machines11100935
APA StyleLiu, S., Zheng, K., Li, H., Cao, Z., & Zhao, S. (2023). Multi-Objective Optimization of Process Parameters in Longitudinal-Torsional Ultrasonic Vibration Face Grinding CFRP. Machines, 11(10), 935. https://doi.org/10.3390/machines11100935






