Comparative Analysis of Data-Driven Models for Marine Engine In-Cylinder Pressure Prediction
Abstract
:1. Introduction
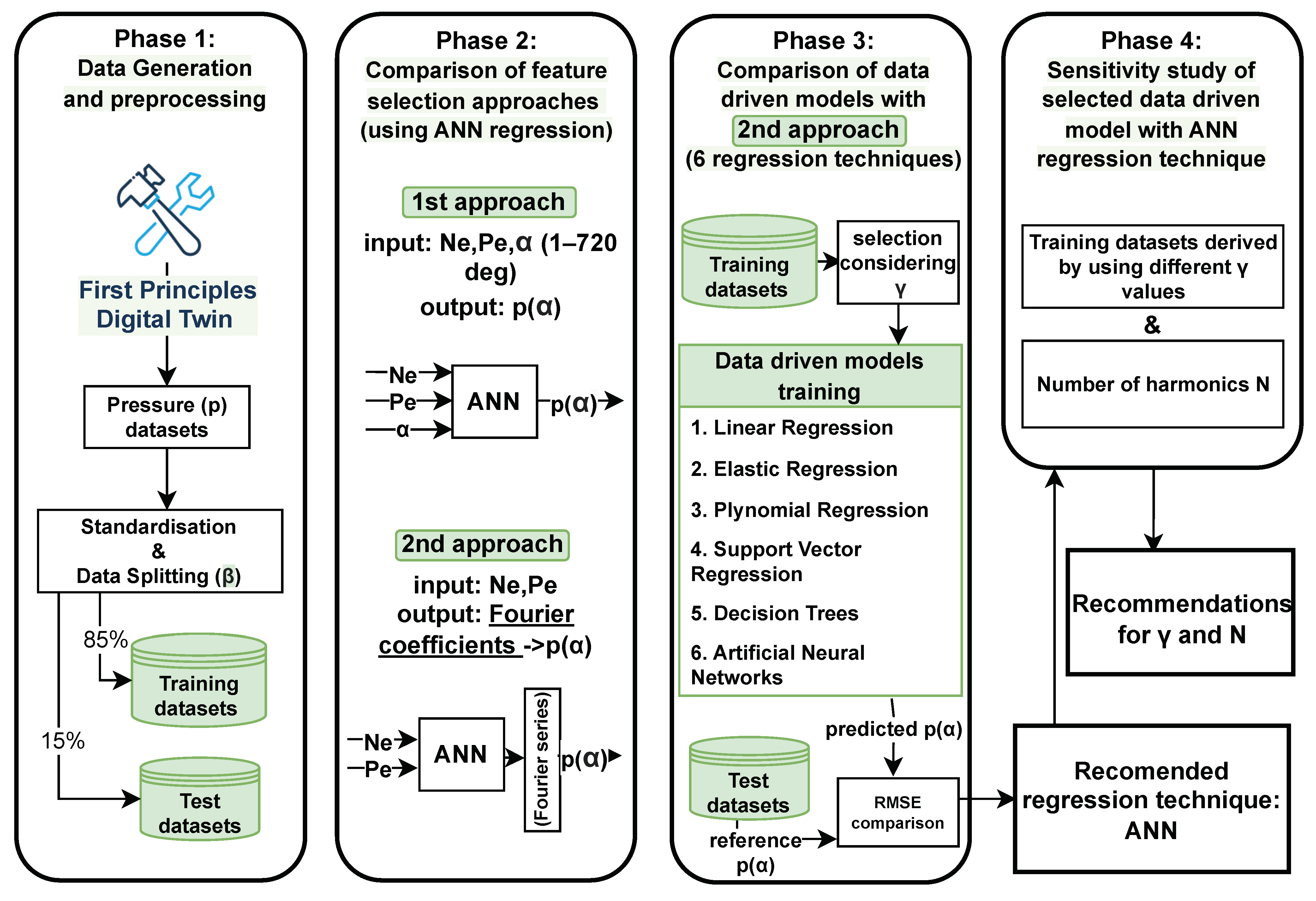
2. Methodology
- Phase 1 generates the required datasets using a first-principle digital twin for the training and testing (validation) of the data-driven models. It additionally focuses on these datasets’ pre-processing, which includes standardisation and splitting into training and testing datasets.
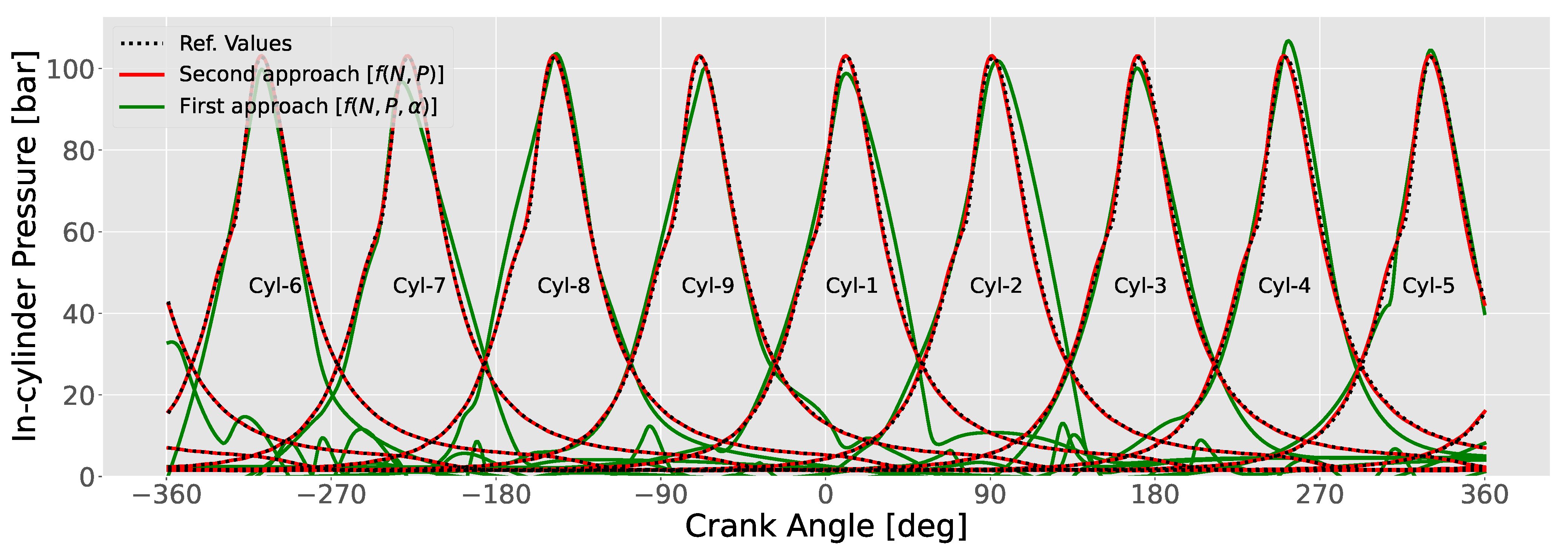
- Phase 2 includes the comparison of two approaches and their input features. The first approach considers the engine speed, power, and crank angle as input to directly predict the in-cylinder pressure for all cylinders via ANN regression. The second approach considers the engine speed and power as input to predict the harmonics coefficients via ANN regression, and subsequently uses a Fourier series function to reconstruct the in-cylinder pressure for all cylinders.
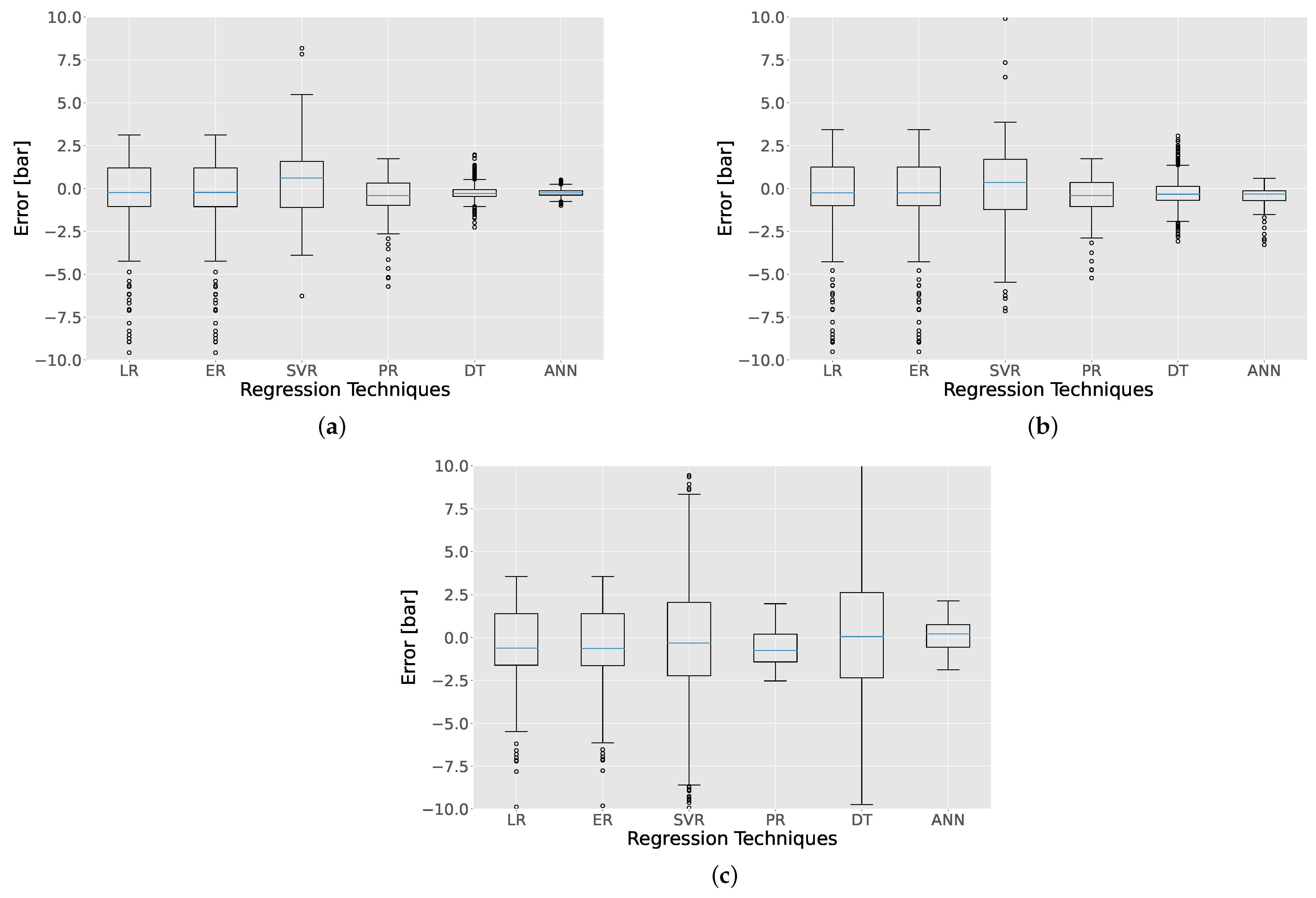
- Phase 3 focuses on the comparative assessment of the data-driven models based on the second approach and six regression techniques, namely, linear regression, elastic regression, polynomial regression, support vector regression, decision tree regression, and ANN regression. The training datasets (from Phase 1) are further split by considering the ratio (explained in Section 2.3.1) and the derived datasets are employed to train the data-driven models. A parametric study is performed considering several values of (0.9, 0.95, 0.995) to comparatively assess the data-driven models’ performance on predicting the in-cylinder pressure with minimum amount of training datasets. The test datasets (Phase 1) are employed to assess the data-driven models’ accuracy considering the root mean square error (RMSE) on the in-cylinder pressure prediction, as well as errors on predicting the mean effective pressure (MEP) and maximum in-cylinder pressure. Recommendations on the most effective regression technique are provided.
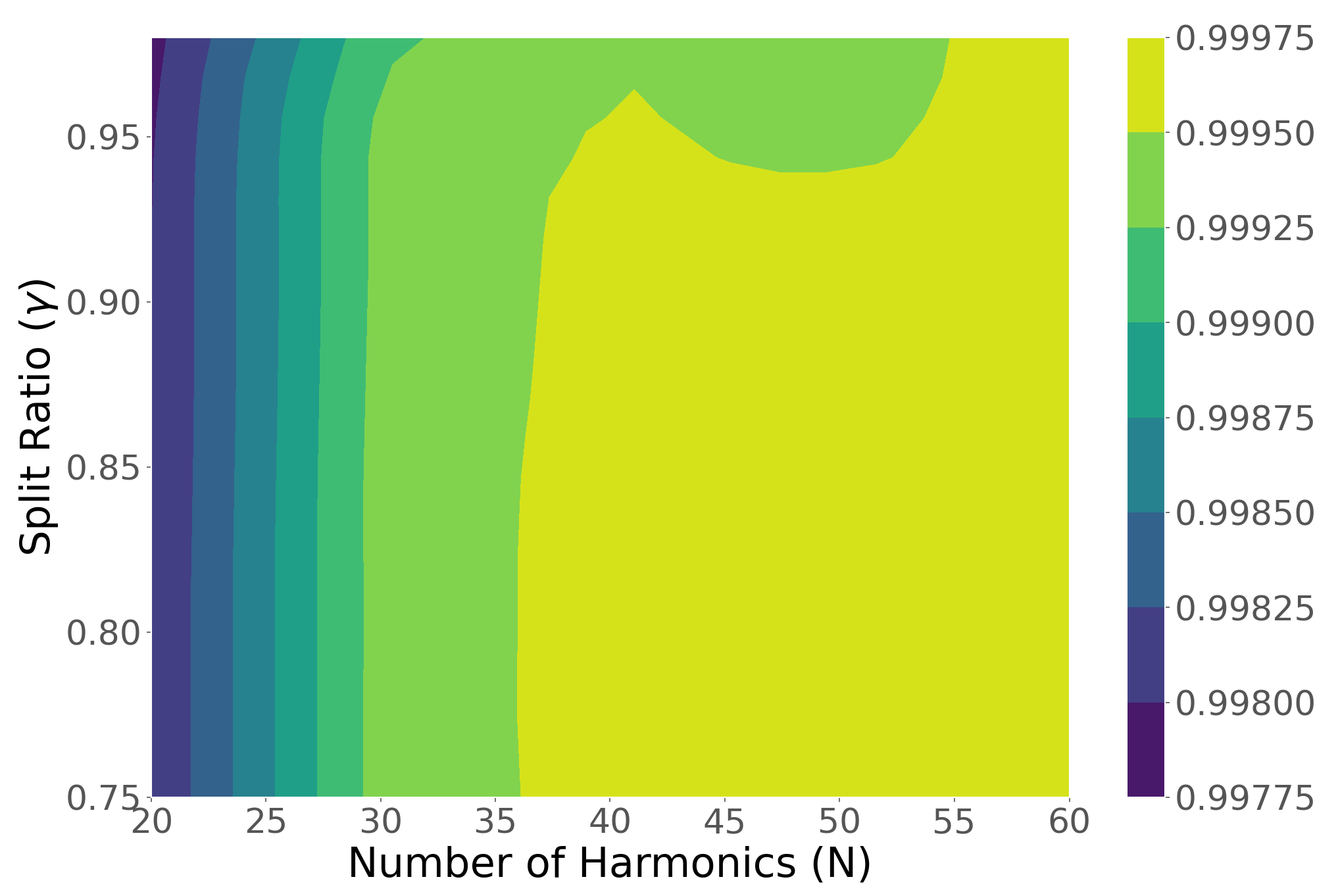
- Phase 4 includes the sensitivity study of the data-driven model based on the second approach and the ANN regression, considering different training datasets and harmonics numbers, to derive recommendations for these parameters’ values.
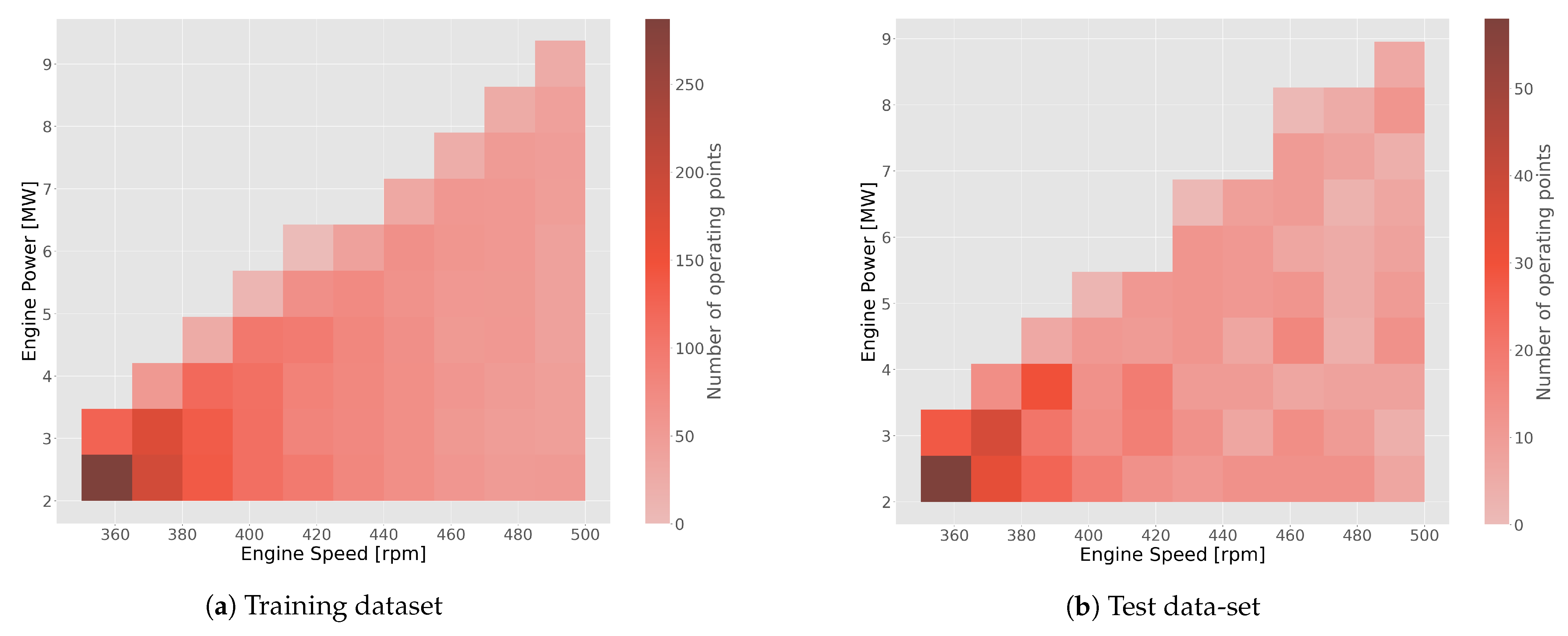
2.1. Data Generation and Pre-Processing
2.1.1. Feature Standardisation
2.1.2. Data Splitting
2.2. Feature Selection Approaches
2.3. Data-Driven Models Based on Regression
2.3.1. Parametric Study
2.3.2. Multiple Linear Regression (LR)
2.3.3. Elastic Regression (ER)
2.3.4. Polynomial Regression (PR)
2.3.5. Support Vector Regression (SVR)
2.3.6. Decision Tree Regression (DT)
2.3.7. Artificial Neural Networks (ANN)
2.4. Metrics Selection
3. Results and Discussion
4. Conclusions
- The second approach with ANN regression and 50 harmonics (corresponding to 101 Fourier coefficients per cylinder) was proved the most effective, exhibiting percentage errors for the in-cylinder pressure prediction within and RMSE within bar when trained with only 20 datasets.
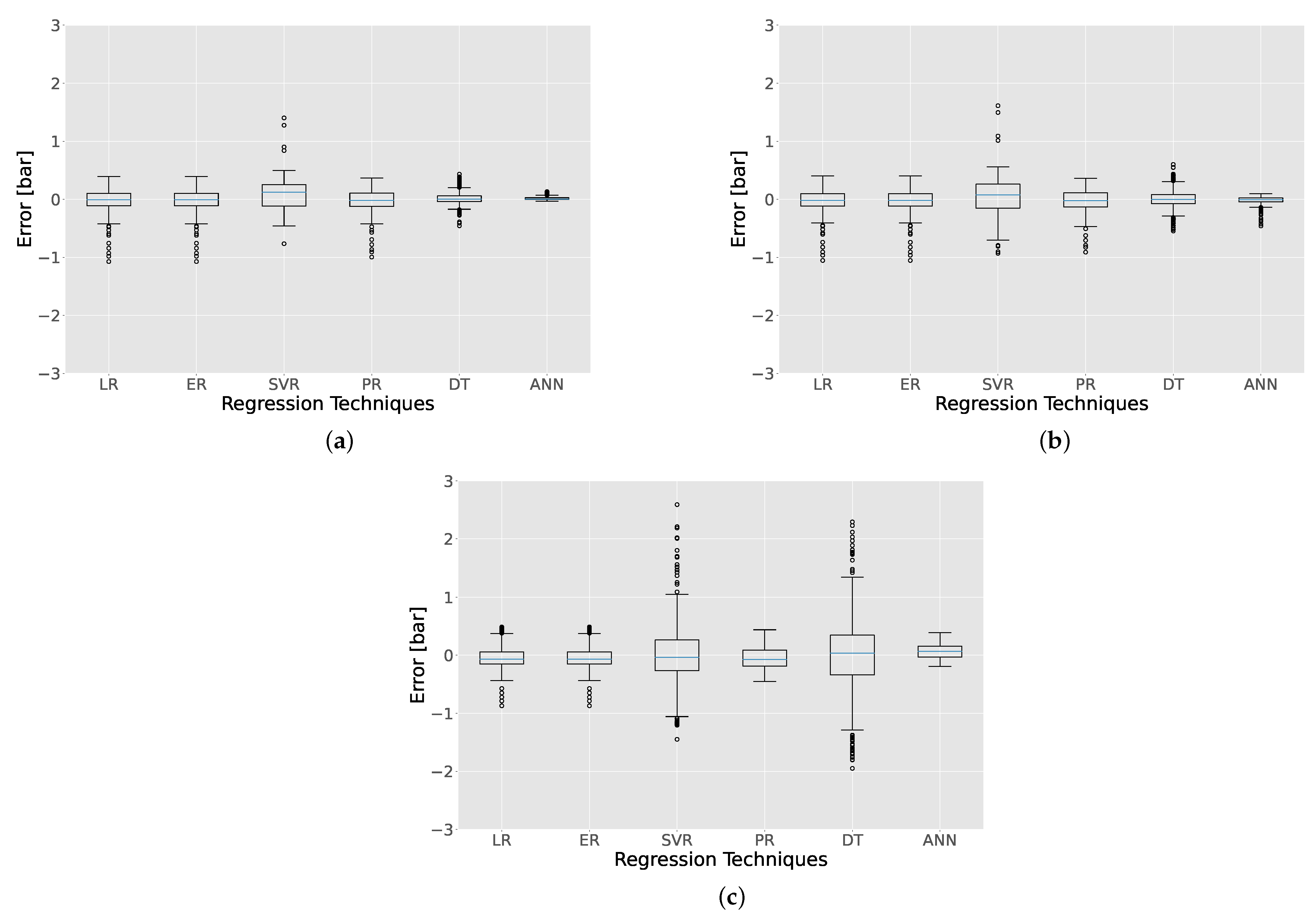
- Simple linear regression techniques exhibited an overall root mean square error for the in-cylinder pressure prediction up to 0.65 bar with only 20 training samples.
- ANN demonstrated the best performance on predicting the mean effective pressure and maximum in-cylinder pressure with minimum outliers compared to other methods.
- A higher training dataset number led to higher accuracy of SVR, DT and ANN regression techniques, whereas linear regression techniques exhibited saturation in the predicted parameters error with the increase in the training dataset number.
- The sensitivity study revealed that minimum of the training datasets (1000 samples) along with 45 harmonics led to RMSE values ranging 0.04–0.05 bar corresponding to ) close to .
- ANN regression is therefore recommended for use in data-driven models for the prediction of marine engine in-cylinder pressure.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Engine speed (rev/m) | |
| n | Number of samples (-) |
| Engine power (kW) | |
| p | Reference in-cylinder pressure (bar) |
| Predicted in-cylinder pressure (bar) | |
| Crank angle (°CA) | |
| Split ratio for separating test data (-) | |
| Split ratio (-) | |
| Hyperparameters (-) | |
| Mean value of parameter (unit of parameter) | |
| Standard deviation of parameter (unit of parameter) |
References
- Mauro, F.; Kana, A. Digital twin for ship life-cycle: A critical systematic review. Ocean Eng. 2023, 269, 113479. [Google Scholar] [CrossRef]
- Coraddu, A.; Oneto, L.; Cipollini, F.; Kalikatzarakis, M.; Meijn, G.J.; Geertsma, R. Physical, data-driven and hybrid approaches to model engine exhaust gas temperatures in operational conditions. Ships Offshore Struct. 2022, 17, 1360–1381. [Google Scholar] [CrossRef]
- Mihai, S.; Yaqoob, M.; Hung, D.V.; Davis, W.; Towakel, P.; Raza, M.; Karamanoglu, M.; Barn, B.; Shetve, D.; Prasad, R.V.; et al. Digital twins: A survey on enabling technologies, challenges, trends and future prospects. IEEE Commun. Surv. Tutorials 2022, 24, 2255–2291. [Google Scholar] [CrossRef]
- Venkatesh, K.; Murugesan, S. Prediction of Engine Emissions using Linear Regression Algorithm in Machine Learning. Int. J. Innov. Technol. Explor. Eng. 2020, 9, 7. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Q.; Chen, X.; Yan, Y.; Yang, R.; Liu, Z.T.; Fu, J. The Prediction of Spark-Ignition Engine Performance and Emissions Based on the SVR Algorithm. Processes 2022, 10, 312. [Google Scholar] [CrossRef]
- Alexiou, K.; Pariotis, E.G.; Leligou, H.C.; Zannis, T.C. Towards data-driven models in the prediction of ship performance (speed—power) in actual seas: A comparative study between modern approaches. Energies 2022, 15, 6094. [Google Scholar] [CrossRef]
- Liu, J.; Ulishney, C.; Dumitrescu, C.E. Application of Random Forest Machine Learning Models to Forecast Combustion Profile Parameters of a Natural Gas Spark Ignition Engine. Des. Syst. Complex. 2020, 6, V006T06A003. [Google Scholar]
- Yu, Z.J.; Haghighat, F.; Fung, B.C.M.; Yoshino, H. A decision tree method for building energy demand modeling. Energy Build. 2010, 42, 1637–1646. [Google Scholar] [CrossRef]
- Bhatt, A.N.; Shrivastava, N. Application of Artificial Neural Network for Internal Combustion Engines: A State of the Art Review. Arch. Comput. Methods Eng. 2022, 29, 897–919. [Google Scholar] [CrossRef]
- Wang, R.; Chen, H.; Guan, C. A self-supervised contrastive learning framework with the nearest neighbors matching for the fault diagnosis of marine machinery. Ocean Eng. 2023, 270, 113437. [Google Scholar] [CrossRef]
- Panda, J. Machine learning for naval architecture, ocean and marine engineering. J. Mar. Sci. Technol. 2023, 28, 1–26. [Google Scholar] [CrossRef]
- Noor, C.M.; Mamat, R.; Najafi, G.; Yasin, M.M.; Ihsan, C.; Noor, M. Prediction of marine diesel engine performance by using artificial neural network model. J. Mech. Eng. Sci. 2016, 10, 1917–1930. [Google Scholar] [CrossRef]
- Raptodimos, Y.; Lazakis, I. Application of NARX neural network for predicting marine engine performance parameters. Ships Offshore Struct. 2020, 15, 443–452. [Google Scholar] [CrossRef]
- Johnsson, R. Cylinder pressure reconstruction based on complex radial basis function networks from vibration and speed signals. Mech. Syst. Signal Process. 2006, 20, 1923–1940. [Google Scholar] [CrossRef]
- Saraswati, S.; Chand, S. Reconstruction of cylinder pressure for SI engine using recurrent neural network. Neural Comput. Appl. 2010, 19, 935–944. [Google Scholar] [CrossRef]
- Solmaz, O.; Gurbuz, H.; Karacor, M. Comparison of artificial neural network and fuzzy logic approaches for the prediction of in-cylinder pressure in a spark ignition engine. J. Dyn. Syst. Meas. Control. Trans. ASME 2020, 142, 091005. [Google Scholar] [CrossRef]
- Tsitsilonis, K.M.; Theotokatos, G. A novel method for in-cylinder pressure prediction using the engine instantaneous crankshaft torque. Proc. Inst. Mech. Eng. Part M: J. Eng. Marit. Environ. 2022, 236, 131–149. [Google Scholar] [CrossRef]
- Tsitsilonis, K.M.; Theotokatos, G.; Patil, C.; Coraddu, A. Health assessment framework of marine engines enabled by digital twins. Int. J. Engine Res. 2023, 24, 3264–3281. [Google Scholar] [CrossRef]
- Tsitsilonis, K.M.; Theotokatos, G. Engine malfunctioning conditions identification through instantaneous crankshaft torque measurement analysis. Appl. Sci. 2021, 11, 3522. [Google Scholar] [CrossRef]
- Khurana, U.; Samulowitz, H.; Turaga, D.S. Feature Engineering for Predictive Modeling using Reinforcement Learning. arXiv 2017, arXiv:1709.07150. [Google Scholar] [CrossRef]
- Maldonado, S.; Weber, R. A wrapper method for feature selection using Support Vector Machines. Inf. Sci. 2009, 179, 2208–2217. [Google Scholar] [CrossRef]
- Zeng, P.; Assanis, D.N. Cylinder Pressure Reconstruction and Its Application to Heat Transfer Analysis; SAE Technical Peper; SAE: Atlanta, GA, USA, 2004. [Google Scholar]
- Zhang, Z. Improved Adam Optimizer for Deep Neural Networks. In Proceedings of the 2018 IEEE/ACM 26th International Symposium on Quality of Service (IWQoS), Banff, AB, Canada, 4–6 June 2018; pp. 1–2. [Google Scholar]
- Bishop, C.M.; Nasrabadi, N.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006; Volume 4. [Google Scholar]
- Townsend, W. ELASTICREGRESS: Stata Module to Perform Elastic Net Regression, Lasso Regression, Ridge Regression; Research Papers in Economics; Boston College Department of Economics: Boston, MA, USA, 2017. [Google Scholar]
- Yang, X.S. Support vector machine and regression. In Introduction to Algorithms for Data Mining and Machine Learning; Academic Press: Cambridge, MA, USA, 2019. [Google Scholar]
- Basak, D.; Pal, S.; Patranabis, D.C. Support Vector Regression. Neural Inf. Process. Lett. Rev. 2007, 11, 203–224. [Google Scholar]
- Czajkowski, M.; Kretowski, M. The role of decision tree representation in regression problems—An evolutionary perspective. Appl. Soft Comput. 2016, 48, 458–475. [Google Scholar] [CrossRef]
- Loh, W.Y. Classification and regression trees. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2011, 1, 14–23. [Google Scholar] [CrossRef]
- Szoplik, J. Forecasting of natural gas consumption with artificial neural networks. Energy 2015, 85, 208–220. [Google Scholar] [CrossRef]



| Maximum Continuous Rating (MCR) power | 9450 kW |
| MCR speed | 500 rpm |
| Cylinders No. | 9 |
| Cylinder Bore | 460 mm |
| Turbocharger | ABB TPL 77-A30 |
| Operating Point | BSFC (% error) | (% error) |
|---|---|---|
| 4.725 MW @ 500 RPM | 2.7 | 2.5 |
| 7.088 MW @ 500 RPM | 1.2 | 3.0 |
| 8.033 MW @ 500 RPM | –0.1 | 0.0 |
| 9.450 MW @ 500 RPM | –0.5 | –0.4 |
| 1.0395 MW @ 500 RPM | –1.2 | –0.1 |
| 6.143 MW @ 440 RPM | 1.04 | 1.2 |
| 4.725 MW @ 400 RPM | 0.1 | 0.1 |
| Layer (Type) | Output Shape | Parameters |
|---|---|---|
| Input layer | (None, 4) | 0 |
| Hidden layer (dense) | (None, 10) | 50 |
| Hidden layer (dense) | (None, 10) | 110 |
| Output layer | (None, 1) | 11 |
| Layer (Type) | Output Shape | Parameters |
|---|---|---|
| Input layer | (None, 3) | 0 |
| Hidden layer (dense) | (None, 10) | 30 |
| Hidden layer (dense) | (None, 10) | 110 |
| Output layer | (None, 909) | 999 |
| Split Ratio () | Training Datasets Percentage | Training Datasets Number |
|---|---|---|
| 0.9 | 10% | 425 |
| 0.95 | 5% | 212 |
| 0.995 | 0.5% | 20 |
| Regression Technique | Abr. | Error Minimisation | Hyperparameters |
|---|---|---|---|
| Multiple Linear Regression | LR | Mean Squared Error | – |
| Elastic Regression | ER | Mean Squared Error | – |
| Polynomial Regression | PR | Mean Squared Error | Degrees: 2 |
| Support Vector Regression | SVR | Mean Squared Error | Kernel: ’rbf’ |
| 1 | |||
| 2 | |||
| 3 | |||
| Decision Tree Regression | DT | Mean Squared Error | Splitter: ’best’ minimum sample split: 2 |
| Artificial Neural Networks | ANN | Mean Squared Error | Hidden layers No: 2 (exponential linear unit activation) |
| Output layers No: 1 (linear activation) | |||
| Neurons No per hidden layer: 10 | |||
| Epochs No: 200 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Patil, C.; Theotokatos, G. Comparative Analysis of Data-Driven Models for Marine Engine In-Cylinder Pressure Prediction. Machines 2023, 11, 926. https://doi.org/10.3390/machines11100926
Patil C, Theotokatos G. Comparative Analysis of Data-Driven Models for Marine Engine In-Cylinder Pressure Prediction. Machines. 2023; 11(10):926. https://doi.org/10.3390/machines11100926
Chicago/Turabian StylePatil, Chaitanya, and Gerasimos Theotokatos. 2023. "Comparative Analysis of Data-Driven Models for Marine Engine In-Cylinder Pressure Prediction" Machines 11, no. 10: 926. https://doi.org/10.3390/machines11100926
APA StylePatil, C., & Theotokatos, G. (2023). Comparative Analysis of Data-Driven Models for Marine Engine In-Cylinder Pressure Prediction. Machines, 11(10), 926. https://doi.org/10.3390/machines11100926







