Test and Simulation Study on the Static Load and Pure Longitudinal Slip Characteristics of Non-Pneumatic Tire

Abstract

Compared with pneumatic tires, non-pneumatic tires have incomparable performance, in terms of load bearing and safety. In this paper, the static load characteristics and pure longitudinal slip characteristics of the non-pneumatic tire are studied by combining experiments and simulations. The test results show that the radial stiffness of the original structure is nonlinear, the pure longitudinal sliding characteristics are seriously inconsistent, the brakes are very sensitive, and the driving is slightly soft. A series of designs have been carried out from the aspects of load-bearing mode and anti-symmetry of the structure, and numerical simulations have been carried out. The results show that the radial secant stiffness of the optimized structure II is increased by 58.8%, and the radial tangent stiffness is increased by 2.96 times, under the premise of ensuring the mass reduction. Additionally, the R square is 0.9932, and the linearity of the radial stiffness curve is greatly improved. The braking and driving conditions under pure longitudinal sliding characteristics are more antisymmetric, which greatly improves the braking sensitivity, but the driving performance is not as good as the original structure. In addition, this paper establishes the evaluation index of the non-pneumatic tire carrying mode, which lays the foundation for further exploration of the non-pneumatic tire carrying mechanism.

1. Introduction

New energy vehicles development will also be more intelligent, especially in the field of unmanned driving, which requires safer tires. Because non-pneumatic tires have enough safety, no air leakage or puncture will occur, which is far safer than pneumatic tires, and the NPT (abbreviation of non-pneumatic tire) has a higher degree of freedom in its design, so it can achieve higher load bearing through a wider range of design performances [1].

The study of non-pneumatic tires is mainly designed from two aspects, one is the design of the support structure, and the other is the design of the shear band. Considering the high degree of design freedom of non-pneumatic tires, the shape of the support also varies, for instance, the spoke-type, honeycomb-type, mechanical-type, etc. For spoke-type wheels, we have to say that Michelin developed a Tweel. For example, some scholars established a Tweel mainly to analyze the static radial characteristics of NPT, mainly the radial stiffness and ground pressure distribution and deflection distribution of the spokes [2,3]. Rugsaj built the Tweel model based on the transient dynamics method and performed a drum analysis, which can evaluate the dynamic response [4]. Sim et al. designed a branch-shaped spoke structure, mainly to explore the impact of spoke shape, asymmetric spoke division, and symmetric spoke division on NPT bearing [5]. Jang et al. used topology optimization to design support structures and obtained three representative structures, one of which was similar to Tweel, and the design freedom of support structures could be greatly improved by topology optimization [6]. Kumar developed a 3D FE model of aperiodic rhombi tessellated NPT, which mainly analyzed the spoke deformation and ground pressure distribution under static conditions, and proposed the design concepts of bottom bearing and top bearing [7]. Meng designed two supporting spoke structures, cross arcs cell and rectangular cell, to enhance the load-bearing performance of the two structures by optimizing the geometric parameters [8]. In addition to the spoke-type, there is also a mechanical NPT. For example, Zhao et al. studied the various mechanical properties of the mechanical elastic wheel [9,10,11,12,13,14,15,16], not only the static mechanical properties, but also the dynamic analysis. This snap-on mechanism can only withstand tension, but not pressure. This is completely top bearing, and its shear band is composed of several groups of steel rings. The buffering and shock absorption effect of this structure may be poor, and the mechanical snap-in structure is unstable. However, this structure has an outstanding advantage in that it is very resistant to impact damage, which is its biggest advantage. Stowe et al. mainly designed a LUNAR WHEEL, which is also a completely top-loaded mechanical structure. In general, the shear band is a very important design parameter, and a reasonable design can make the ground pressure of the lunar rover more uniform [17].

There are also many NPT supports for honeycomb structures or honeycomb-like structures [18,19,20,21,22]. Some researchers have studied honeycomb-like NPT with different cell types (square, hexagonal, triangular, mixed square and triangle, and rhombus). Some scholars have carried out numerical simulations on the static and dynamic behaviors of NPTs with different honeycomb spokes, respectively [18,19,20], and improved the bearing performance of NPT by optimizing the honeycomb structure parameters. The NPT structure designed using the bionic principle has significant advantages in bearing capacity. The Fibonacci spiral designed in this paper is also a bionic structure, and its bearing performance is different from that of the honeycomb structure. Wu et al. proposed a new type of non-pneumatic tire based on a gradient anti-tetrachirality structure and studied its deformation law and mechanical properties, which is a negative Poisson’s ratio structure, which also has a certain degree of bearing performance advantage [21].

In addition, there are many studies on shear bands, which are important structures for top-loaded NPT. Researchers from Clemson University employed innovative homogenization and topology optimization methods to determine the locally optimal geometric design of the shear band, with the novelty being that the shear band uses a linear elastic material to eliminate rolling losses, due to hysteresis [22,23]. Gasmi et al. mainly carried out theoretical analysis on shear beams and discussed the contact between the ring and the plane rigid ground. Most of the important characteristics of non-pneumatic tires are described by relating the structural stiffness of the wheel to the contact conditions. This theoretical analysis has important implications for the shear band design of NPT [24,25]. Aboul-Yazid et al. analyzed the influence of tire shape on NPT performance with a composite ring and without a composite ring, especially when NPTs with a composite ring can reduce the impact of spokes on the ground contact pressure [26].

Based on the above investigation, it can be seen that there are not many designs that combine shear band and support design, and most of the studies are only based on static bearing studies. This paper will focus on the design of the combination of shear band and support structure and analyze the rolling characteristics of NPT pure longitudinal slip. In the second part of the article, a non-pneumatic tire based on the Fibonacci spiral structure is designed, and the static load test and the pure longitudinal slip test are carried out after the trial production of NPT. The Fibonacci spiral designed in this paper is also a bionic structure, and its bearing performance is different from that of the honeycomb structure. The third part is to establish the finite element model of the original structure, and the accuracy of the model is verified by comparison tests. The fourth part is to optimize the design of the original structure based on the finite element model. The results show that the optimized NPT performance is significantly improved.

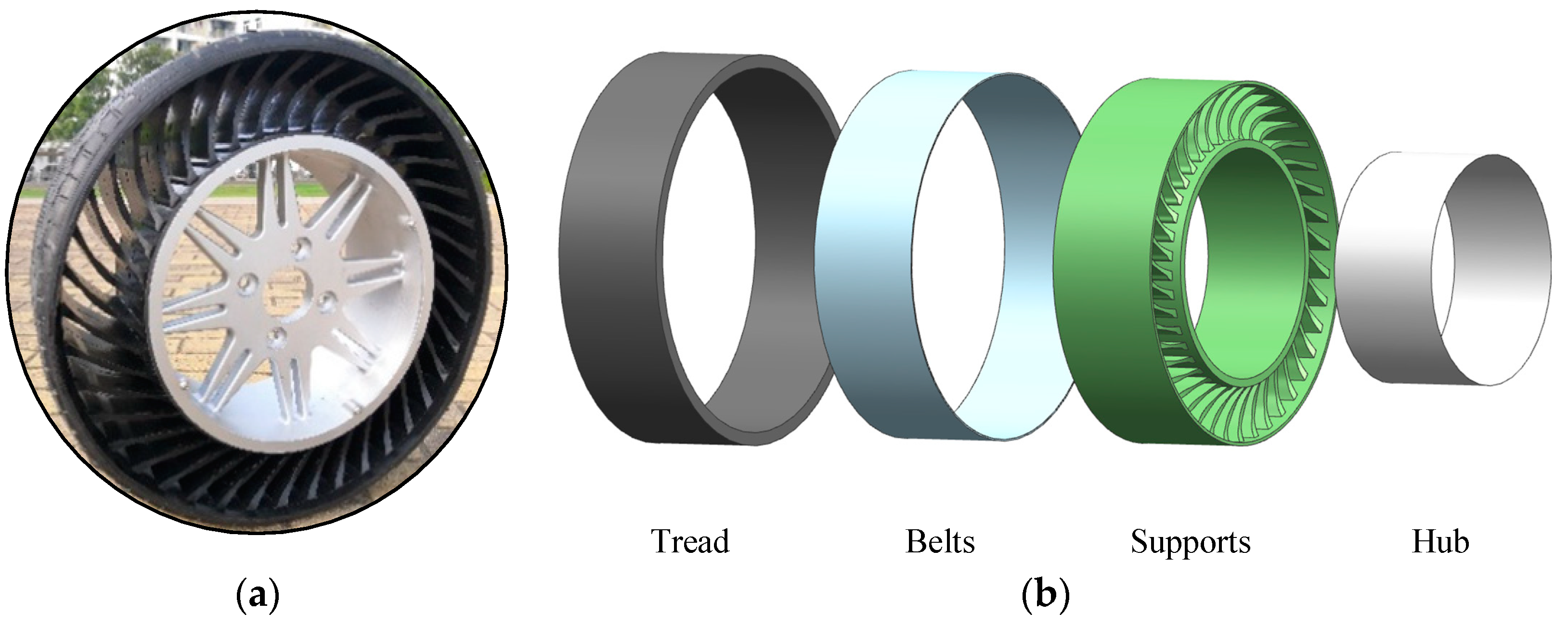
2. Design and Test Procedure

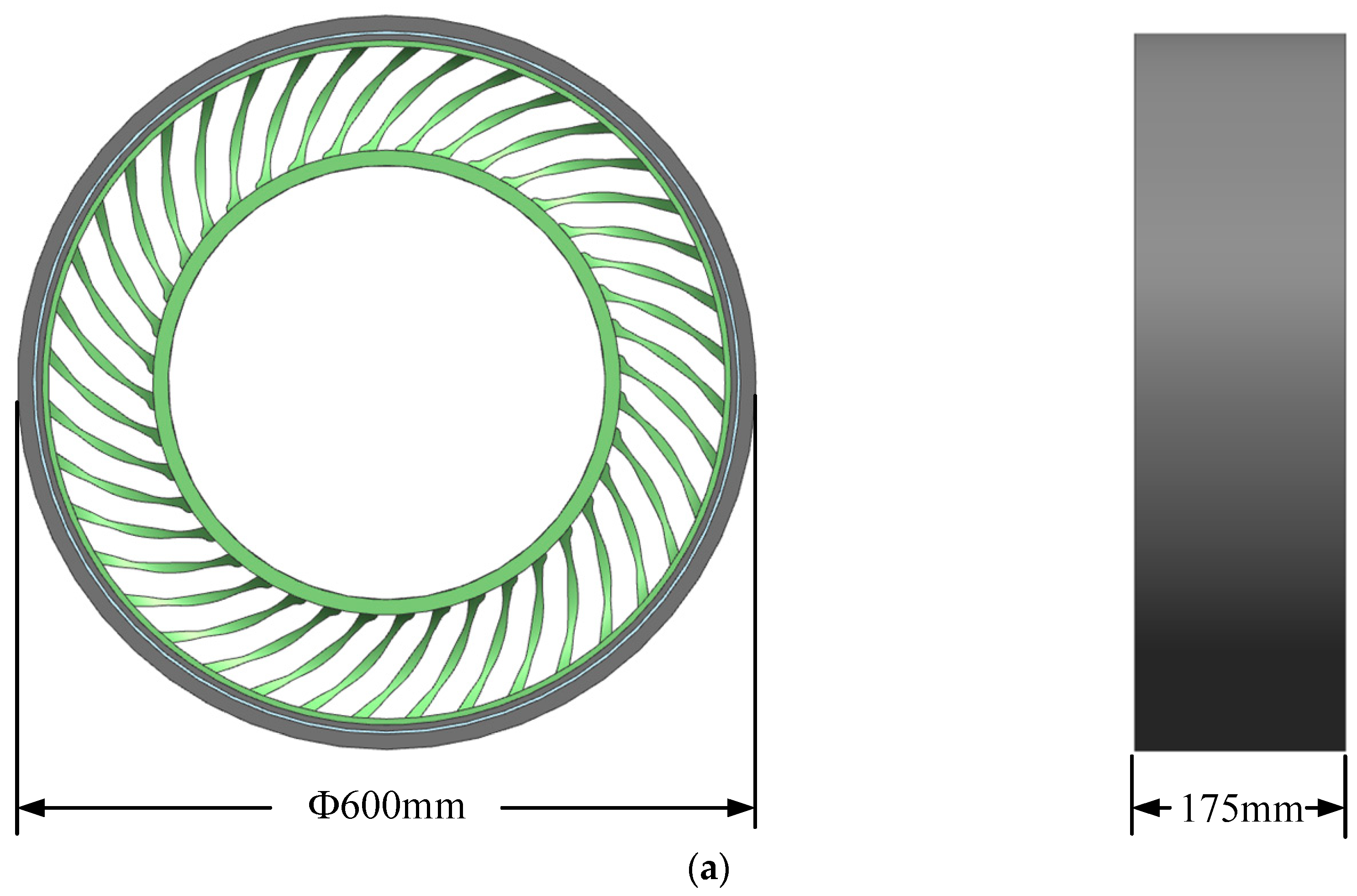
2.1. Geometric Design Dimensions

Non-pneumatic tires mainly consist of four parts, as shown in Figure 1, including the hub, support, belt, and tread. The support structure is a Fibonacci spiral, which improves the cushioning and vibration reduction performance of the non-pneumatic tire. Considering that the tread pattern has little effect on the load bearing, the tread pattern is ignored. The overall structure size is shown in Figure 2. The spoke structure is two continuous Fibonacci curves, and the reinforcing belt layer is embedded in the tread, which mainly plays the role of tightening the non-pneumatic tire and ensuring the overall circumferential stiffness of the non-pneumatic tire.

2.2. Material Properties

Since polyurethane has a stronger modulus and better mechanical properties than rubber, NPT mainly uses polyurethane materials. However, considering the poor wear resistance of polyurethane materials, it is not suitable for treads, and rubber materials are more suitable for treads. Through the uniaxial tensile test of the polyurethane material, the mechanical properties of the material can be obtained. Figure 3 shows the process and results of the polyurethane uniaxial tensile test. The width and thickness of the sample were 6.28 mm and 2 mm, respectively. The uniaxial tensile test of polyurethane under quasi-static loading was completed on a universal tensile testing machine. The experiment adopted a displacement control mode, and the nominal strain rate of loading was selected as 0.001 s⁻¹. The engineering stress–strain curve was obtained by averaging the tensile results of the five groups of samples.

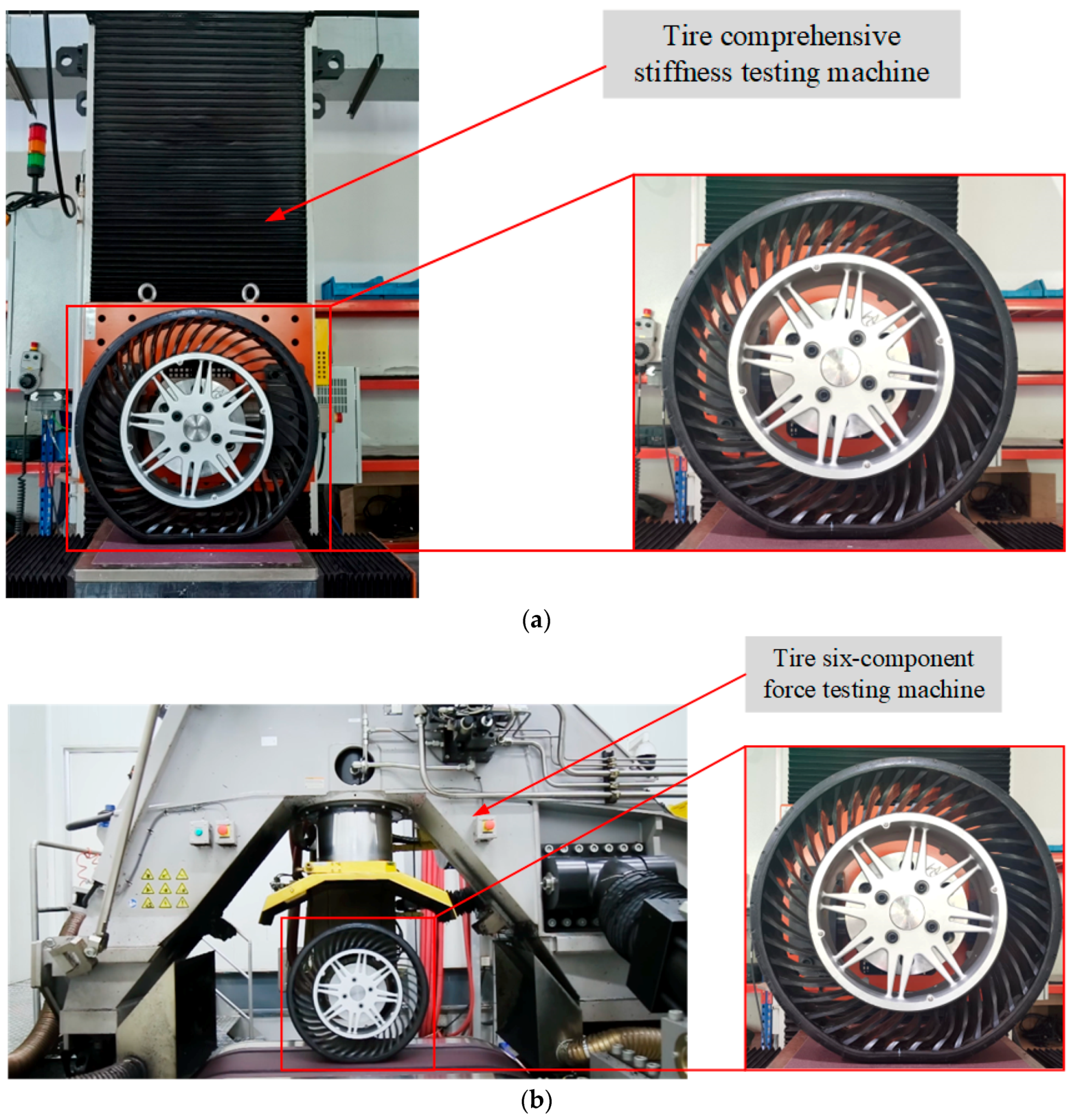
2.3. Test Program

After the trial production of the non-pneumatic tires, the static load test and the pure longitudinal sliding test were mainly carried out. The testing equipment used were a stiffness testing machine and a six-component force testing machine. The stiffness testing machine was used for the stiffness test of the tire, and the six-component force testing machine was used for the pure longitudinal sliding test of the tire. The test process and test results are briefly described below.

2.3.1. Test Procedures

The two experimental schemes are shown in Figure 4. For the tire static load test, since the designed NPT benchmark model was a pneumatic tire of 175/70 R14, the test standard for pneumatic tires was adopted here. This test standard is HG/T 2443-2012 “Tire static load performance test method”, which does not have to consider the inflation pressure. The loading rate of the test was 50 mm/min, the standard load was 3000 N, and the maximum load was 5000 N. For the longitudinal stiffness of the static load test, the radial force was 2400 N, and the friction coefficient was 0.9. For the pure longitudinal slip test, the purpose of this test was to study the driving and braking performance of NPT. The tire speed was 40 km/h, the slip angle and the roll angle were both 0 degrees, and the rated load was 3000 N. The friction coefficient of the road surface was 1.1. During the test, the driving and braking process of NPT could be realized by adjusting the rotating speed of the testing machine and the speed of the pulley.

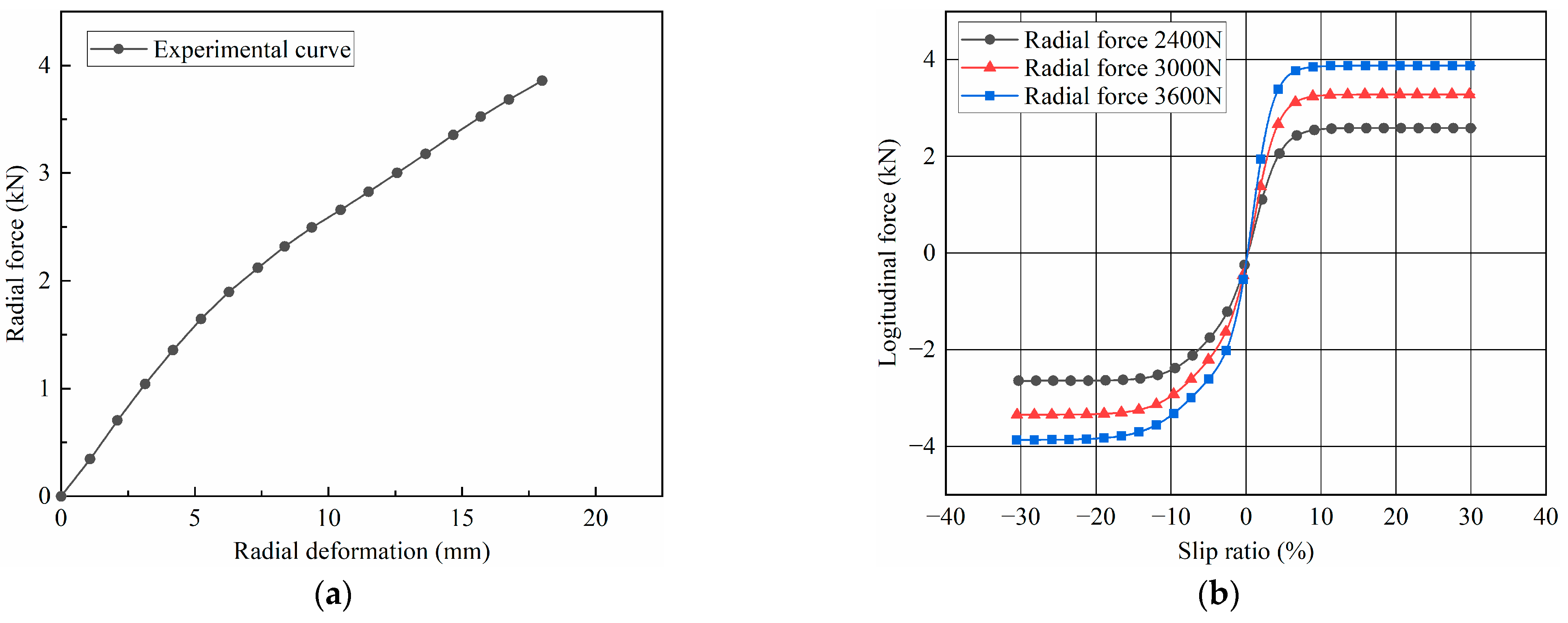
2.3.2. Test Results

The test results are shown in Figure 5. When the NPT was loaded in static load, the stiffness curve was non-linear, which is unfavorable. Usually, the pneumatic tires were linear during the loading process, and even the stiffness would increase as the air pressure increases. The root cause was that its internal air pressure was connected, and the NPT had no air pressure. The current NPT load almost completely relied on the support structure at the bottom. The non-linearity of the bottom structure led to the non-linearity of the carrying performance. In order to improve the NPT stiffness, the next step was to weaken the carrying effect of the spokes at the bottom and replace the loading method of the NPT from the bottom load to the top load.

The results of the pure longitudinal slip test show the curve of the longitudinal force and sliding rate. It can be seen that, when the NPT was driven, the corresponding slip rate of the maximum longitudinal friction was 8%, and when the NPT braked, the corresponding slip rate of the maximum longitudinal friction was 20%. Obviously, the drive was more sensitive, and the braking was softer. The basic reason for the soft braking is the counterclockwise rotation of the global supports structure, which will inevitably lead to different force states when the NPT rolls forward and backward. Therefore, the next step was to pay attention to the consistency of the supports structure.

3. FE Modeling and Validation

3.1. FE Modeling of NPT

3.1.1. Material Constitutive Model

In order to shorten the product design cycle and reduce the cost, numerical simulation is an efficient way. This paper uses SIMULIA/ABAQUS software for numerical simulation. Before numerical simulation, it is very important to obtain accurate material parameters of each component, which directly affects the accuracy of simulation results. NPT is mainly composed of two parts of hyperelastic materials, namely polyurethane and rubber, in addition to the steel cord of the belt layer. Hyperelastic materials are described in terms of a “strain energy potential”, which defines the strain energy stored in the material per unit of reference volume as a function of the strain at that point in the material. There are several forms of strain energy potentials available in Abaqus to approximately model incompressible isotropic elastomers: the Marlow form, the Mooney–Rivlin form, the neo-Hookean form, the Ogden form, the Yeoh form, etc.

In order to select an accurate constitutive model, the polyurethane nominal stress–strain curve obtained earlier was imported into the software and evaluated by the software’s own identification tool. The obtained results are shown in Figure 6. When only one set of test data (uniaxial, equibiaxial, or planar test data) is available, the Marlow form is recommended.

It is necessary to explore the strain energy of the Marlow model [27], the form of the Marlow strain energy potential, as follows:

$$U=U_{\mathrm{dev}}(I_1)+U_{vol}\left(J_{\mathrm{el}}\right)$$

(1)

$$I_1={\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2$$

(2)

where U is the strain energy per unit of reference volume, with U_dev as its deviatoric part and U_vol as its volumetric part; J_el is the elastic volume ratio, I₁ is the first deviatoric strain invariant defined as Equation (2), and λ_i are the principal stretches.

The hyperelastic constitutive model adopted by rubber is the Mooney–Rivlin model, and its expression is as follows:

$$U=C_{10}(I_1-3)+C_{01}(I_2-3)$$

(3)

In Equation (3), C₁₀ and C₀₁ are the Rivlin coefficients. I₁ and I₂ are the first and second strain invariants. The specific parameters are shown in

Table 1. Material parameters of NPT.

Component	Density (kg/m3)	Young’s Modulus (MPa)	Poisson’s Ratio	C10	C01
PU	1200	-	0.49	-	-
Rubber	920	-	0.49	0.88	−0.18
Steel	7850	2.05 × 105	0.29	-	-

.

Since the hub hardly deforms, the hub can be used as an analytical rigid body. The belt was steel wire, and the tread was rubber, which are very common materials, obtained through references [10,26]. The material parameters of each component of NPT are shown in the table below.

3.1.2. FE Model

As shown in Figure 7, the finite element model of NPT is shown. In order to improve the accuracy of the simulation, the refined mesh size was 4 mm, which ensured that there were at least four layers of elements in the thickness direction of the spokes. There were a total of 359,424 meshes, of which, 340,160 linear hexahedral elements were of type C3D8RH, and 19,264 linear quadrilateral elements were of type S4R. The penalty function contact was used between the tread and the ground, and the friction coefficient was 1.1, which was consistent with the test. In addition, the belt was embedded in the tread. For the pure longitudinal slip simulation process, the rolling angular velocity of the tire was gradually changed by keeping the translational speed of the tire unchanged, which can simulate the process of the tire changing from braking to driving. At the moment when the equilibrium solution was obtained, it was in a steady state, so that a series of steady state solutions between braking s.

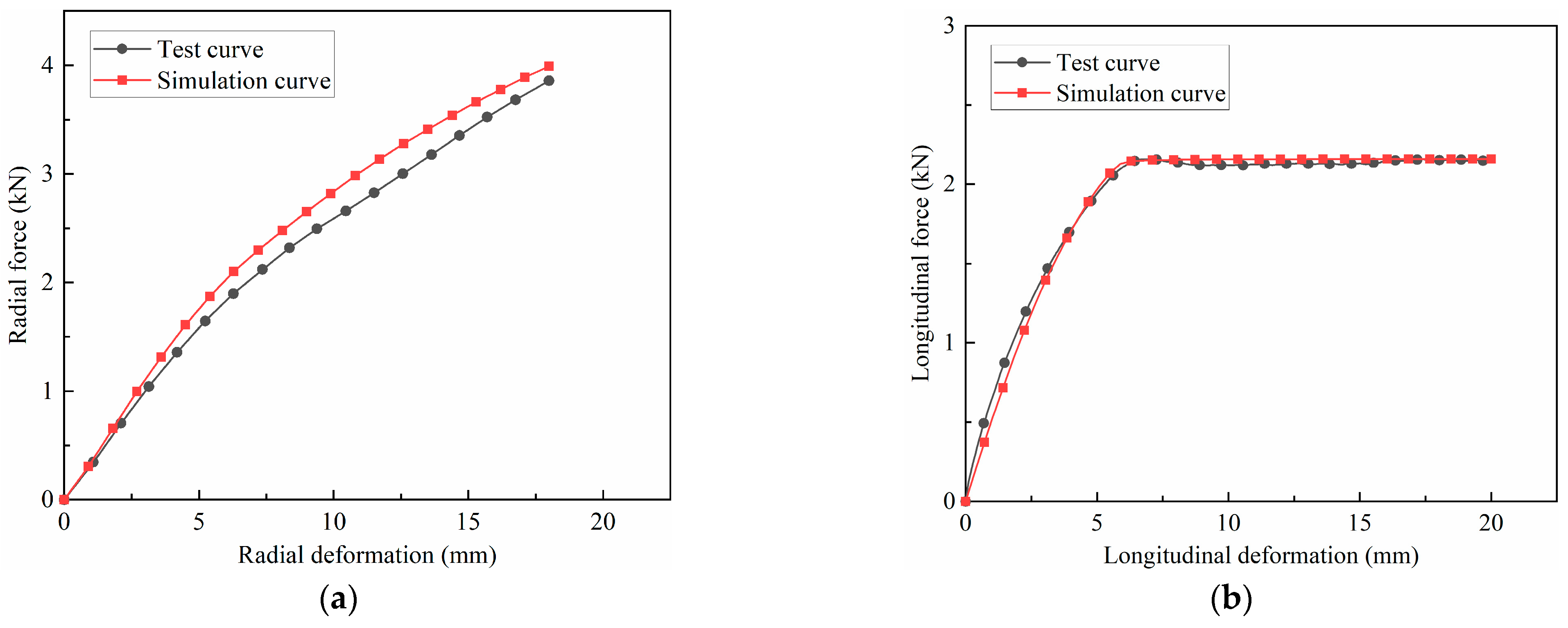
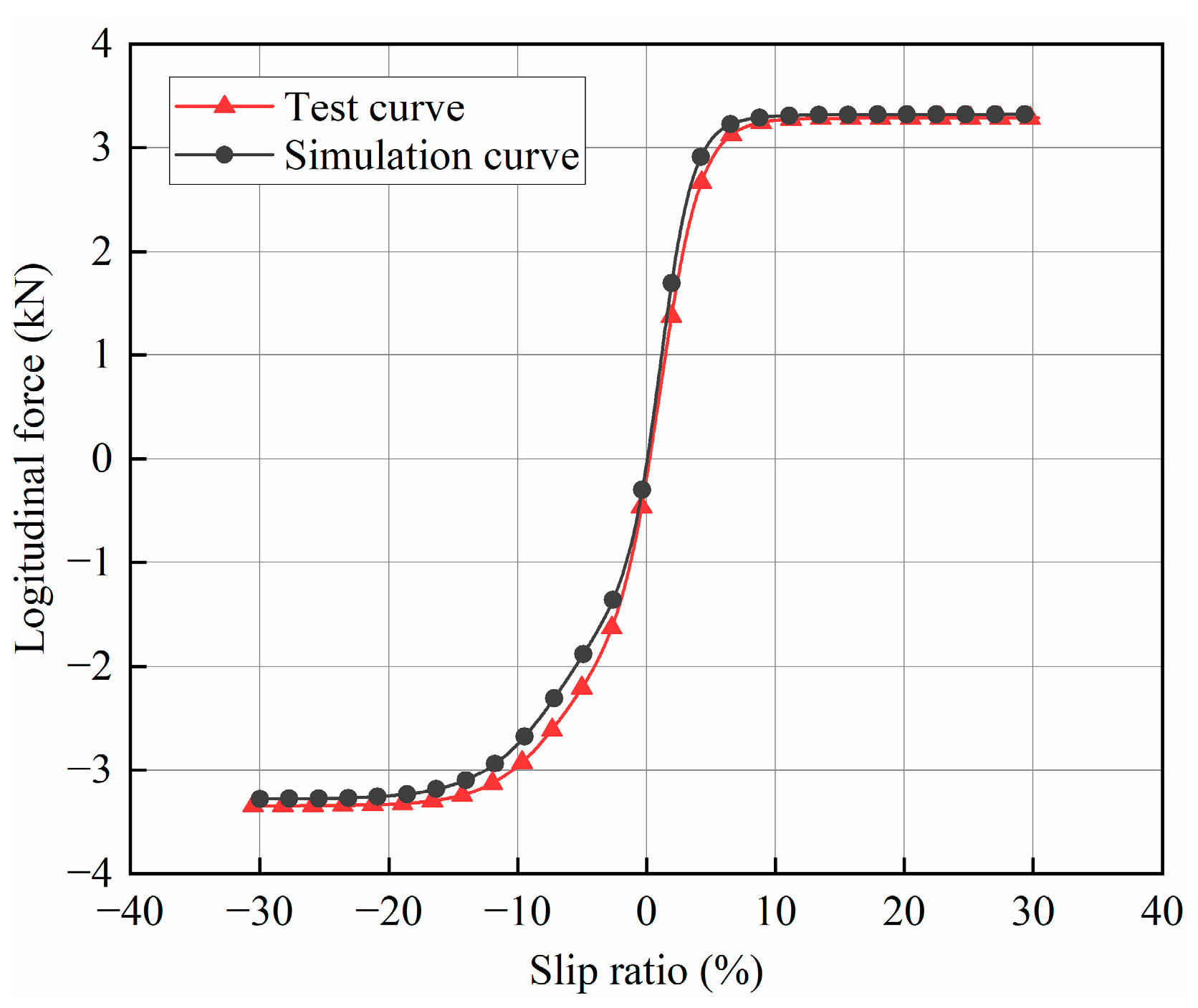
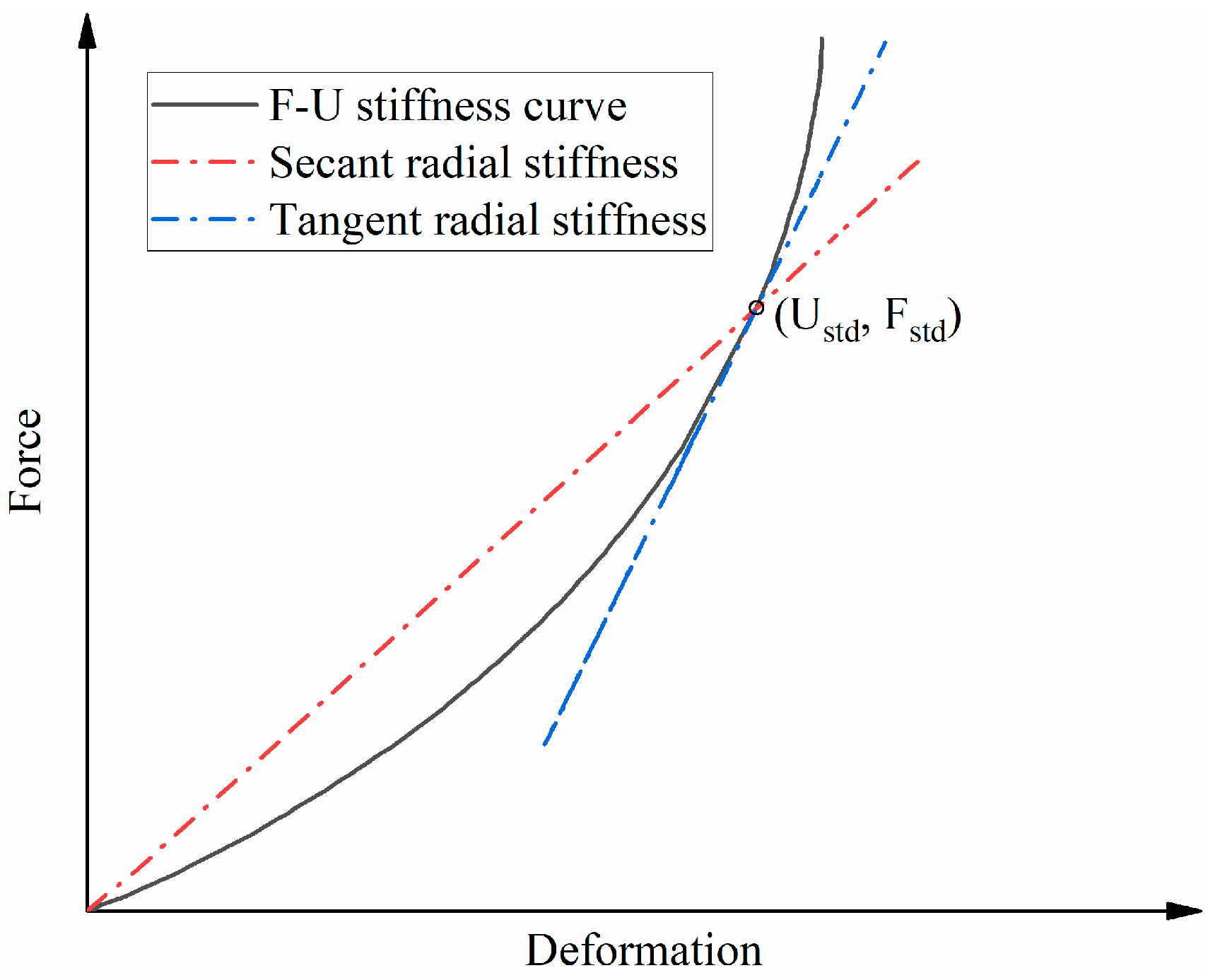
3.2. Validation of FE Models

Figure 8 shows the test and simulation results of the static load simulation. From the radial stiffness results of static load simulation, although there was a certain error in the middle of the curve, the overall nonlinear change trend was still consistent, and from the perspective of equivalent stiffness (secant stiffness), the simulation accuracy could reach below 5%, which is reliable. From the longitudinal stiffness results, the simulation and test results were basically consistent. Figure 9 shows the simulation results of the pure longitudinal slip, and the simulation results were almost consistent with the experimental results. In the braking condition, the simulation data lagged slightly behind the experimental data, and in the driving condition, the simulation data were slightly ahead of the test data. From the simulation curve, it can be seen, once again, that the NPT had the characteristics of slightly soft braking, although the driving was very sensitive.

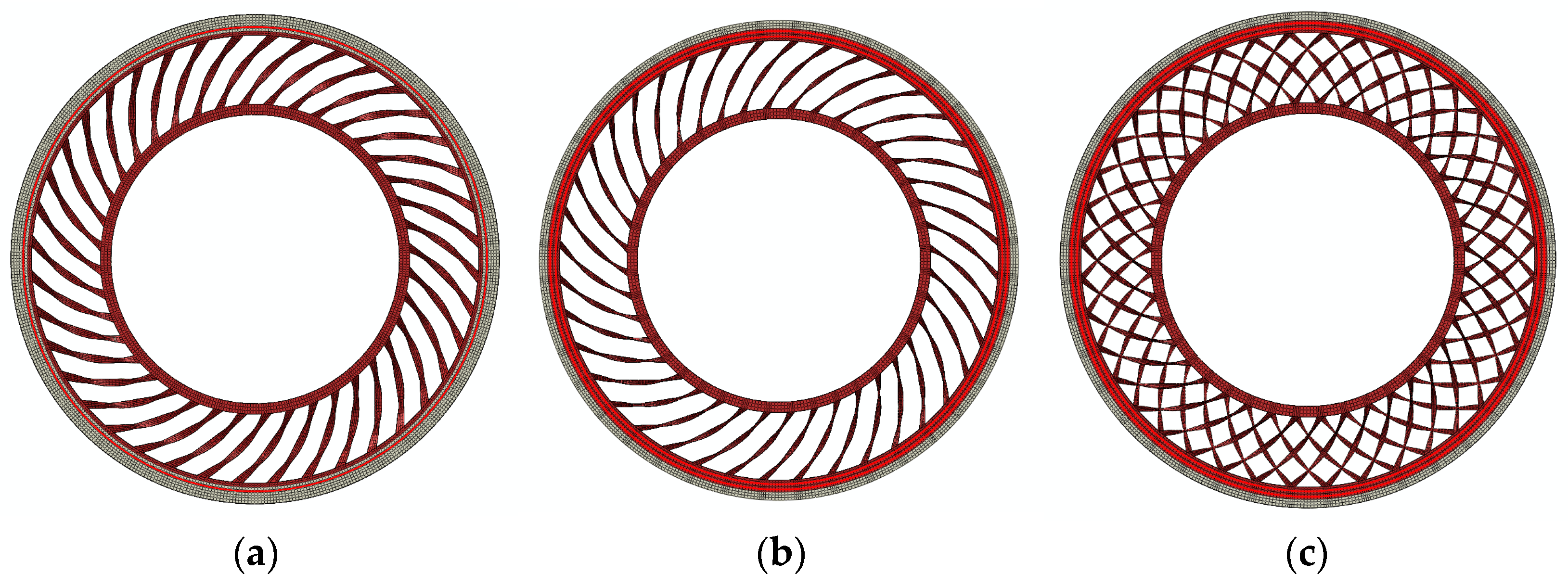
4. Improved Design of NPT

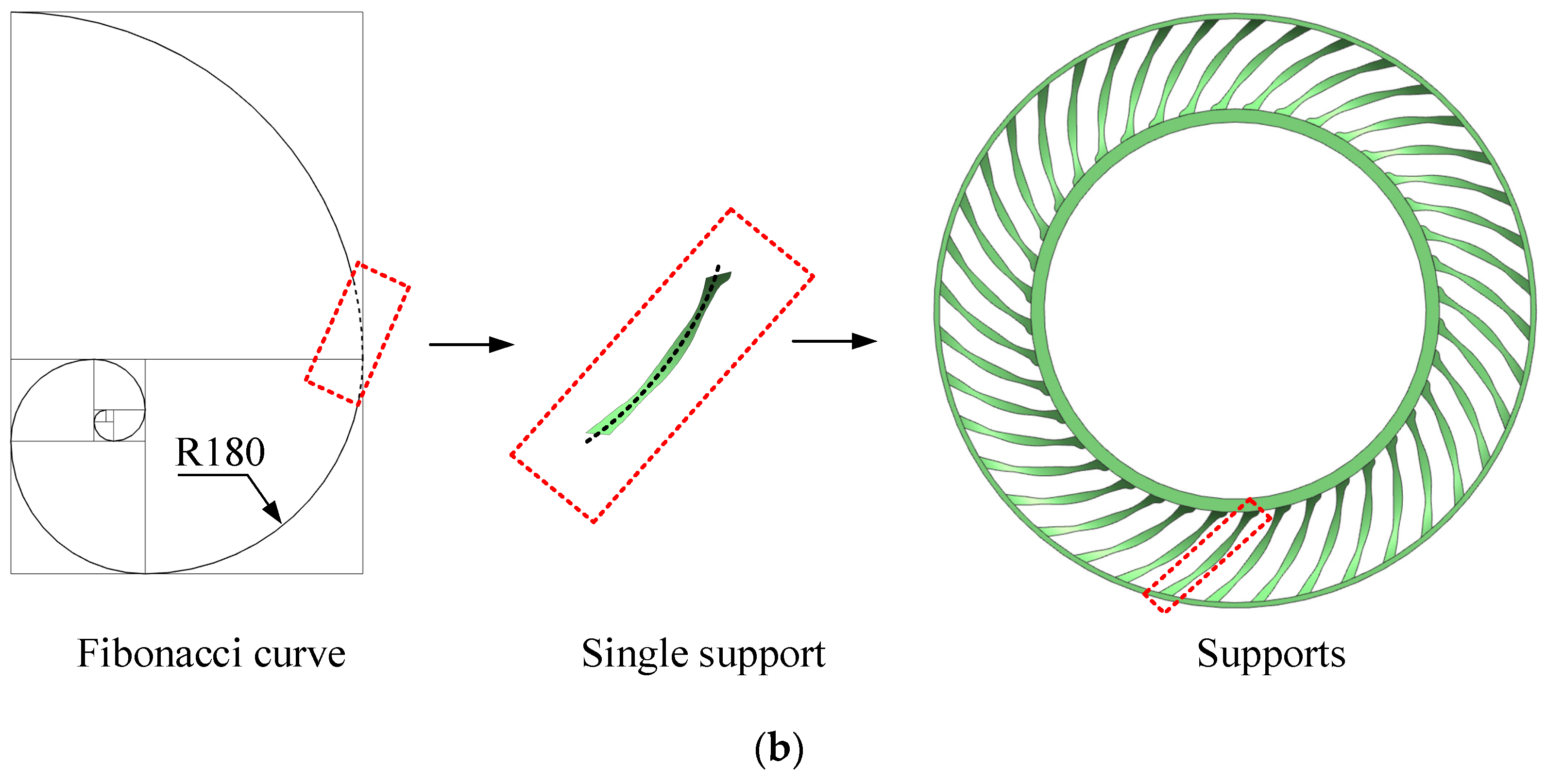
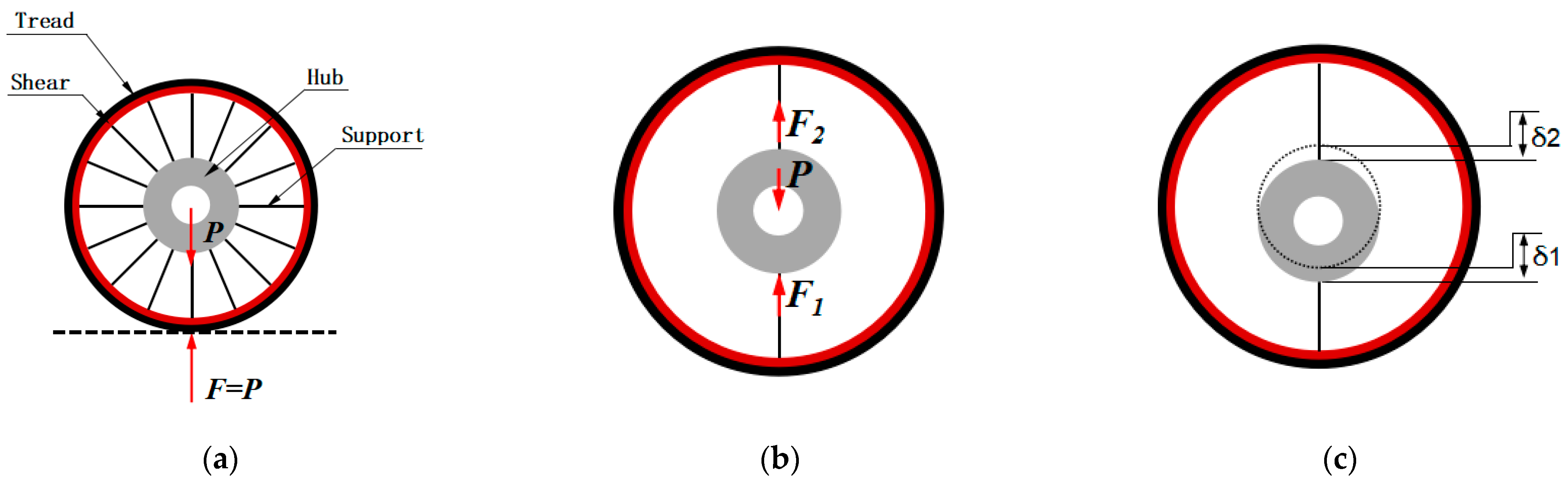
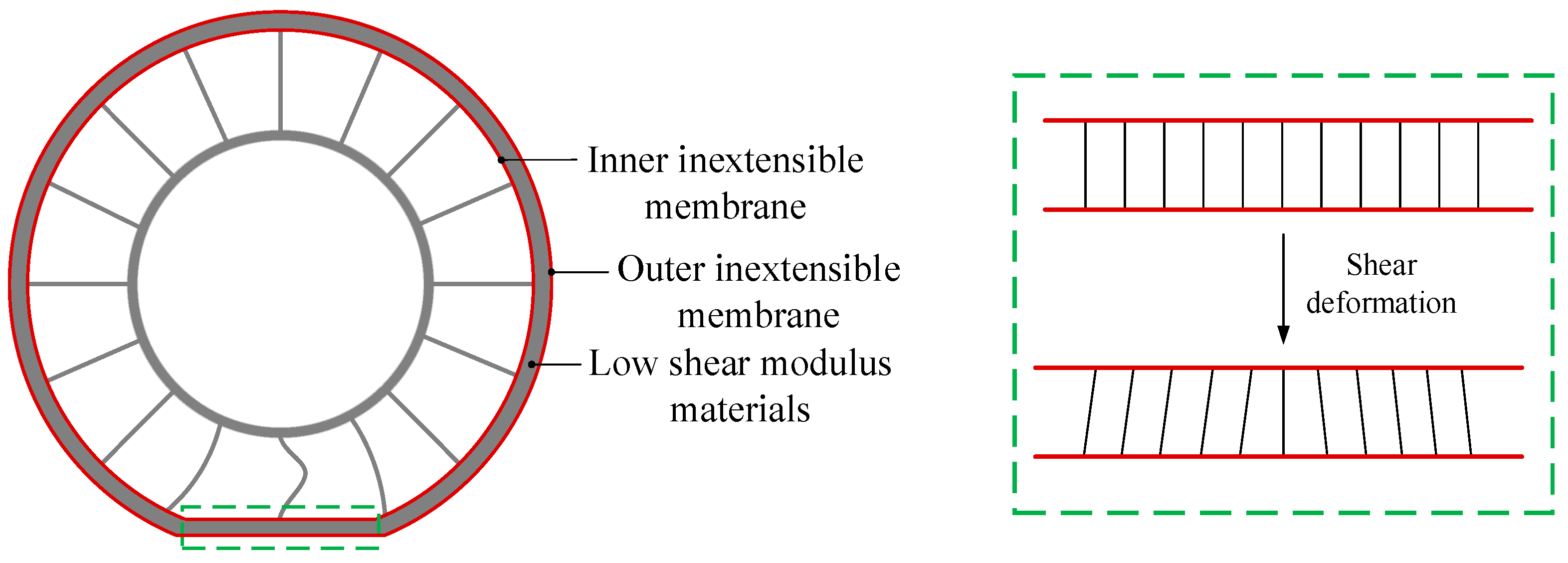
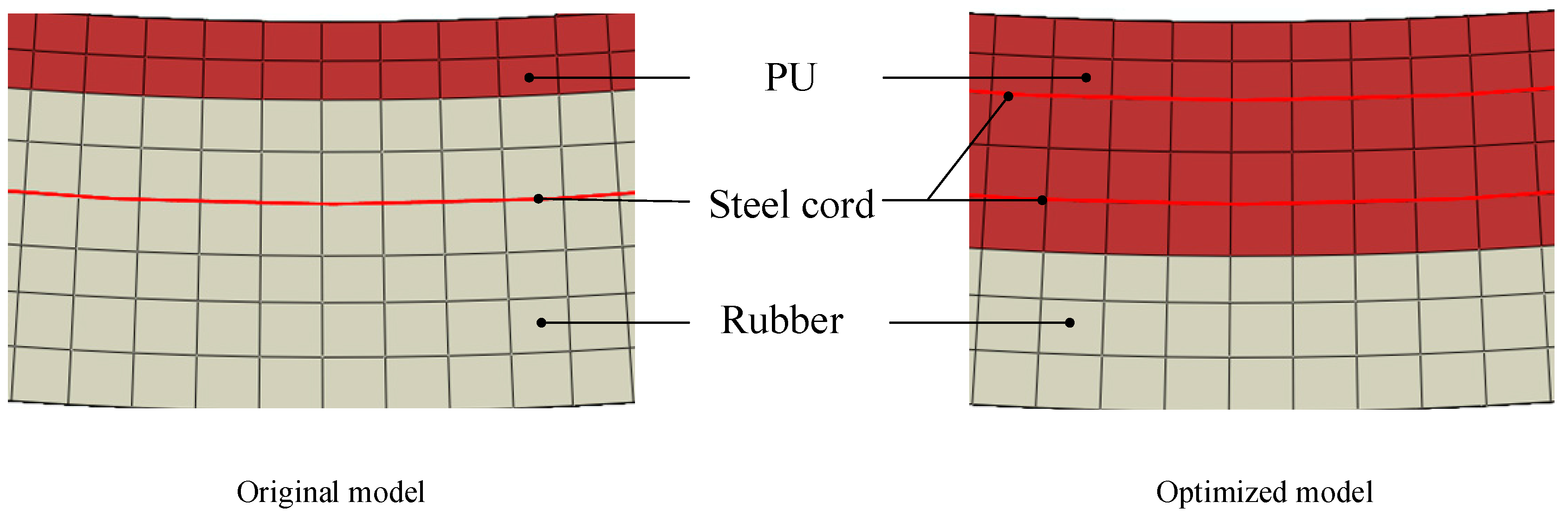
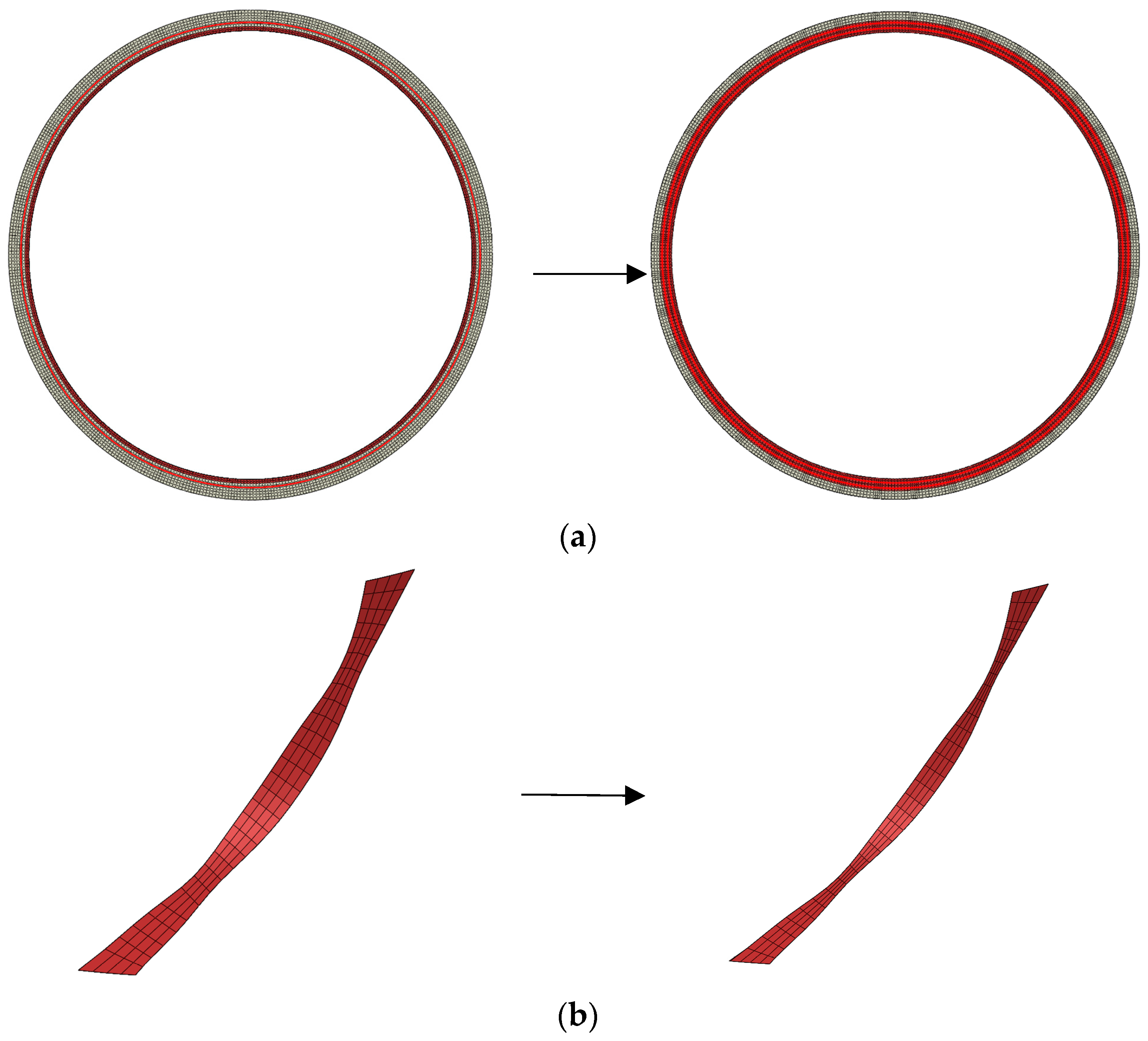
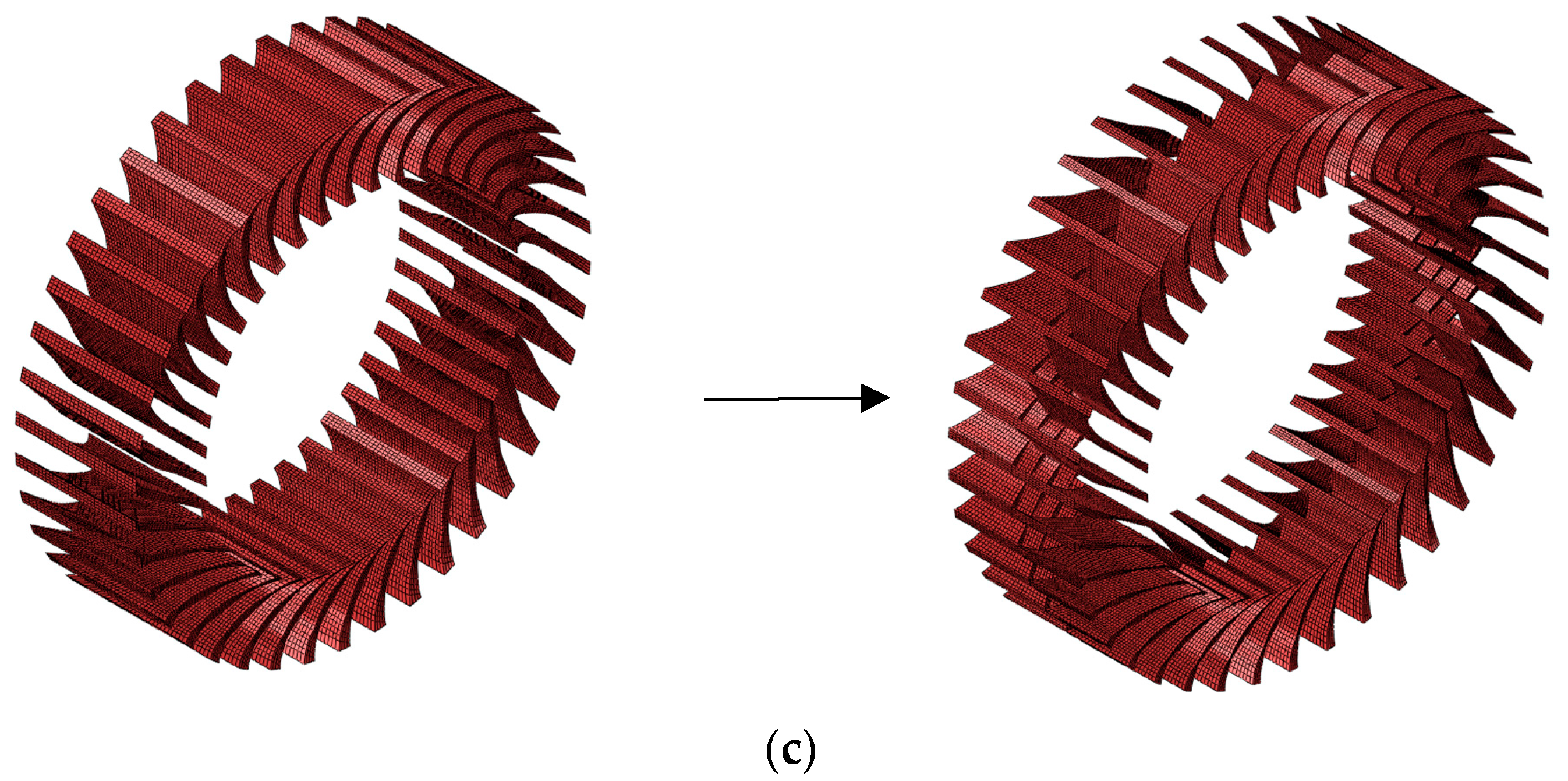
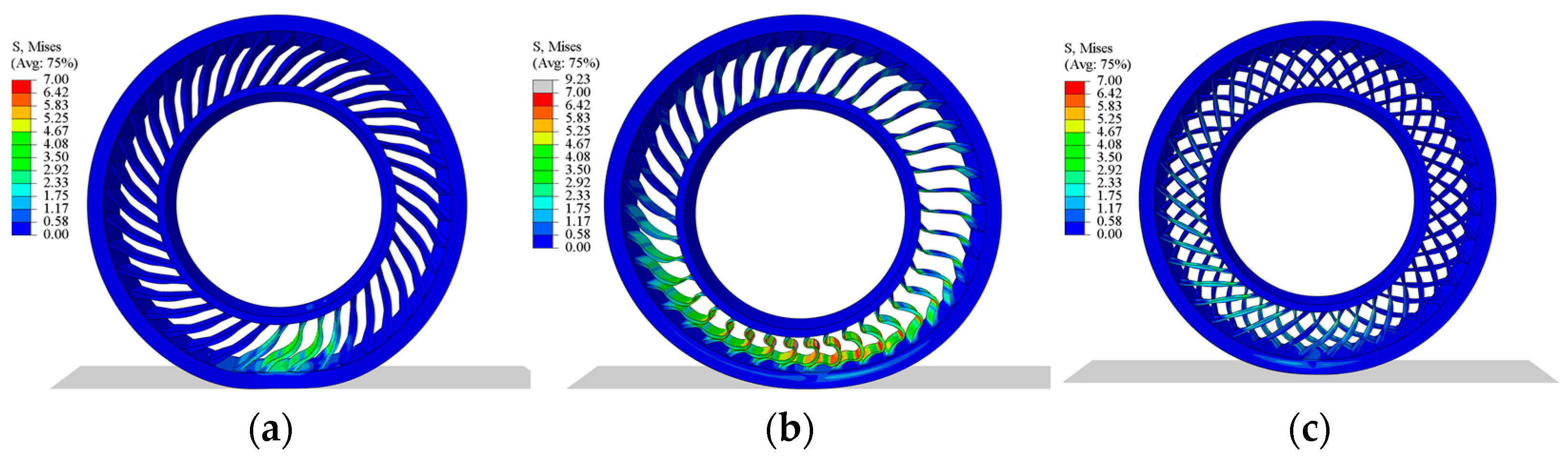
4.1. Mechanism Analysis and Structural Design

Before optimizing the design, a mechanism analysis was performed first. Generally, radial tire forces are essential for vehicle modeling and dynamic control, so it is necessary to analyze the radial force of the tire in detail [28]. It can be seen that the load-bearing modes of non-pneumatic tires were bottom loading and top loading [29]. The original structure was almost completely bottom loading. The load-bearing performance of the original structure was determined by several supports at the bottom. The nonlinearity of the stiffness of the bottom support structure lead to the nonlinearity of the overall load bearing. This nonlinearity will increase with the increase of load, and the instantaneous stiffness cannot meet the stiffness requirement under rated load. Therefore, it is necessary to change the way of the bottom bearing and adopt the top bearing, so that the role of the global support structure can be exerted as much as possible. In order to judge the top load and bottom load more clearly, the following is a simplified force analysis of NPT.

As shown in Figure 10, this is the force analysis diagram of the wheel, in which Figure 10a is the balance between the gravity of the wheel and the reaction force of the ground. In order to better analyze the force of the support, the ground is ignored, and then the force analysis is shown in the Figure 10b—when the wheel is stable, the following formula must be satisfied:

$$P=F_1+F_2=K\times {\delta }_1+K\times {\delta }_2$$

(4)

$$P=F_1\to {\delta }_2=0$$

(5)

$$P=F_2\to {\delta }_1=0$$

(6)

$$\alpha ={\delta }_2/{\delta }_1$$

(7)

The bottom support is subjected to the resultant compression force F₁, the top support is subjected to the resultant tensile force F₂, P is the total radial load of the wheel, and δ₁ and δ₂ are the compressive deformation and tensile deformation, as shown in Figure 10c. Assuming that the tensile and compressive stiffness of the isotropic material are the same, represented by K here, the equation in the equilibrium state is shown in Formula (4). When Formula (5) is satisfied, it is a full bottom load, and when Formula (6) is satisfied, it is a full top load. α is the bearing coefficient, as shown in Formula (7). When α is close to 10% or even much larger than 10%, it tends to be loaded at the top. When α is close to 1%, or even much less than 1%, it tends to be loaded at the bottom.

In order to achieve top load bearing, not only the bottom support must be weakened, but also the shear straps that increase a certain stiffness. Sandwich shear tape is a good choice, as shown in Figure 11—sandwich shear tape consists of an inner inextensible membrane, an outer inextensible membrane, and a low shear modulus material in the middle; due to the inextensible membrane, the inner reinforcement layer is shorter than the outer reinforcement layer, and when the NPT is grounded, the intermediate layer material must be sheared to accommodate the difference in length.

The simulation experience shows that the strength of the sandwich shear band is related to the shear modulus and volume of the middle material. The larger the shear modulus of the middle material or the larger the volume, the stronger the shear effect will be. Therefore, the material of the intermediate layer was polyurethane, and the thickness of the intermediate layer was as large as possible. The specific improvement is shown in Figure 12. The single-layer steel cord was increased to two layers to form a sandwich structure. In addition, the rubber on the inner edge of the tread was replaced with polyurethane, which can significantly improve the stiffness of the sandwich shear belt.

In order to reduce the thickness of the supporting spokes and ensure the variable thickness characteristics of the supporting structure and the Fibonacci spiral structure, the supporting spokes were designed to be offset by 40% of the thinnest dimension. The mass of the optimized structure was smaller than that of the original structure, because the mass increases by 0.74 kg after adding a layer of steel wire belt. Although the weight increased by 0.74 kg after adding a layer of steel wire, after the single support spoke was thinned by 40%, the mass of all supports was reduced by 1.74 kg. This means that the weight of the optimized structure was reduced by 1 kg, which is beneficial to the lightweight property of the NPT.

Through the previous mechanism analysis, a series of improvements will be made to the original structure. The optimized structure should achieve a top-bearing property, while maintaining the original Fibonacci spiral structure. There are three main improvement schemes, as shown in Figure 13: the first, sandwich shear band; second, support thinning; third, antisymmetric. The optimized structures are shown in Figure 14.

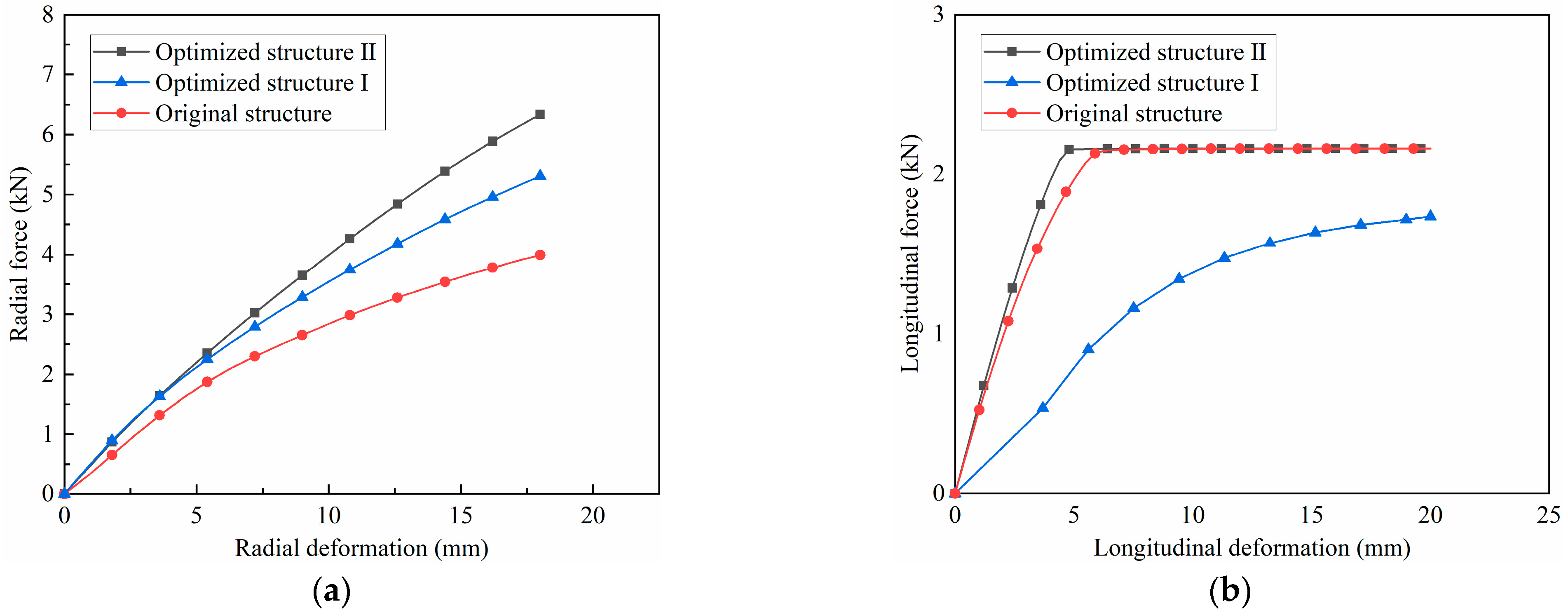
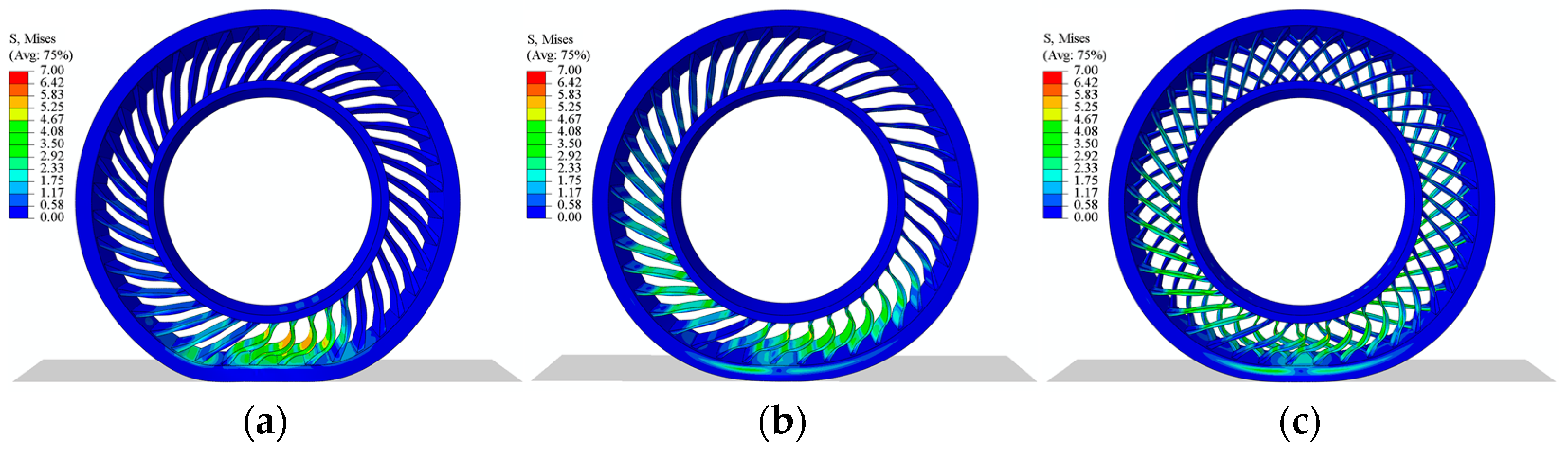
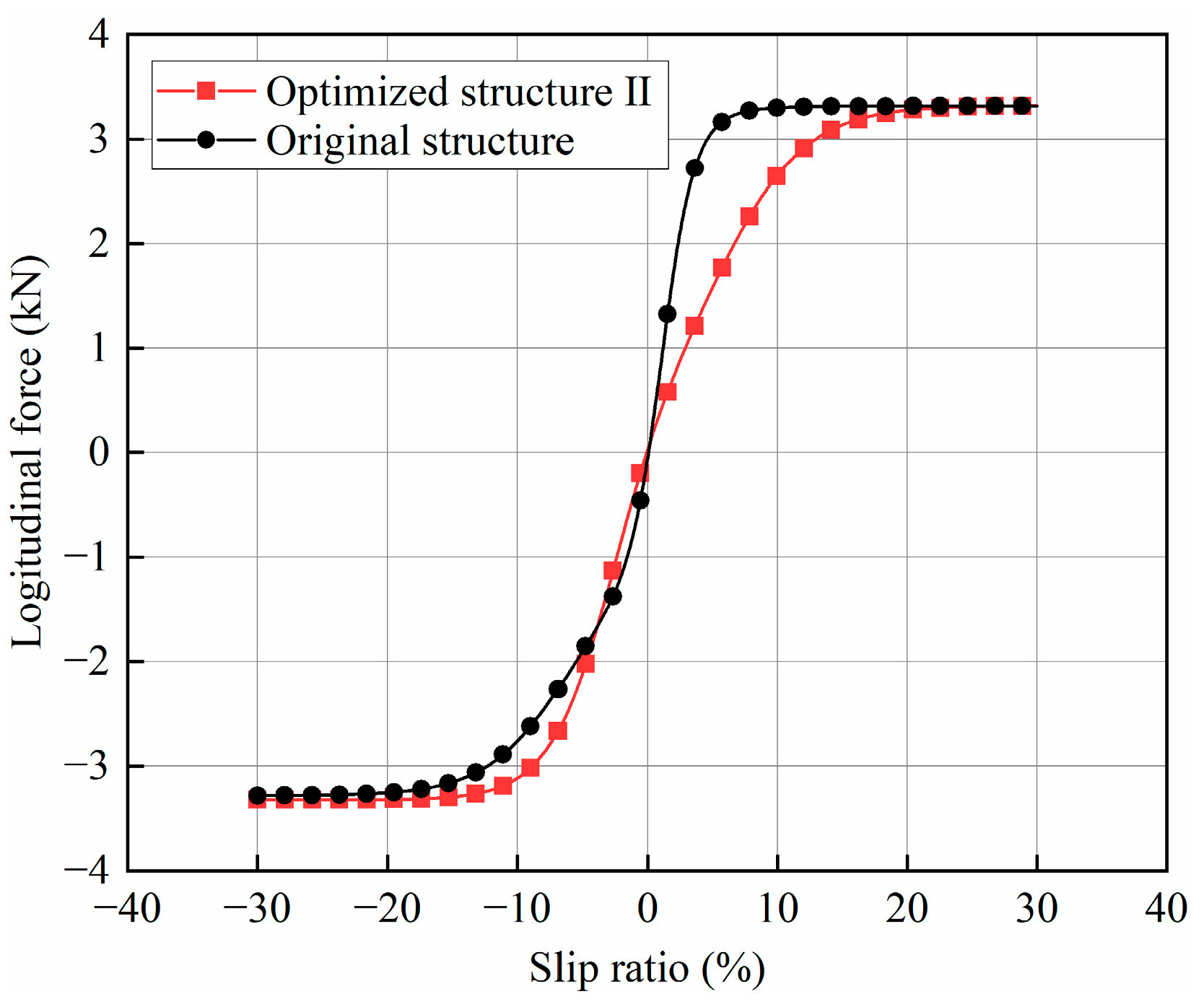
4.2. Simulation Results and Analysis

For nonlinear NPT, its stiffness curve is nonlinear, and the simple equivalent stiffness cannot reasonably evaluate the bearing index. The three-dimensional stiffness evaluation index of NPT is established below. For the radial stiffness, there are two ways to judge: the first is the secant stiffness, and the second is the tangential stiffness. As shown in Figure 15, the tangential stiffness of a general pneumatic tire was larger than the secant stiffness, but the radial stiffness of NPT was opposite, and its tangential stiffness gradually decreased and was smaller than the secant stiffness.

The three-dimensional stiffness standard formula for non-pneumatic tires is established here, and the radial stiffness is characterized by two formulas.

Equations (8) and (9) represent the radial secant stiffness and the radial tangential stiffness, respectively. Equation (10) expresses the longitudinal stiffness.

$$S{R}_1=F_{\mathrm{s}td}/U_{std}$$

(8)

$$S{R}_2=F^{\prime }(U_{std})$$

(9)

$$SL=\frac{500}{U_{30\%F_{std}+250}-U_{30\%F_{std}-250}}$$

(10)

Here, SR₁ and SR₂ represent the secant stiffness and tangential stiffness under standard load, respectively, where F_std is standard load, U_std is radial deformation under standard load, and SL is the longitudinal stiffness.

Figure 16a shows that the static load bearings of the three structures were quite different. At the same time, as shown in

Table 2. Radial stiffness and longitudinal stiffness of NPT.

Structures	Secant Radial Stiffness (N/mm)	Tangent Radial Stiffness (N/mm)	Longitudinal Stiffness (N/mm)
Original	221.7	61.3	465.6
Optimized I	294.8	145.3	142.6
Optimized II	352.0	242.9	533.9

, the secant stiffness of the optimized structure I was increased by 33%, compared with the original structure, while the optimized structure II was increased by 58.8%, which were achieved with the global mass reduction. Compared with the original structure, the tangent stiffness of optimized structure II and optimized structure I increased by 1.37 times and 2.96 times, respectively, so it can be seen that the top bearing can greatly improve the radial bearing stiffness of NPT. The optimized structure I was weaker than the optimized structure II because the support of optimized structure I was thin and rotated in one direction, which lead to the torsion of the whole support and the sliding of the grounding part.

It can be seen from the longitudinal stiffness curve in Figure 16b and Table 2 that the longitudinal force of optimized structure I was seriously non-linear, and even could not reach the maximum driving force. The original structure and optimized structure II were normal, and the longitudinal stiffness of the original structure was slightly smaller than that of optimized structure II, but both were better than optimized structure I. If the optimization structure I is improved, it may be necessary to abandon the Fibonacci spiral structure, and it is best to directly adopt a design similar to Tweel. On the basis of ensuring the Fibonacci spiral structure, it is reasonable to optimize structure II. After all, the Fibonacci spiral structure has good advantages, in terms of cushioning and shock absorption.

The stress distribution of the three structures under static load conditions is shown in Figure 17. The stress distribution of the original structure is mainly concentrated at the bottom, which is almost completely bottom bearing, which brings certain challenges to the fatigue durability of the supports. The stress distribution of the optimized structure I was slightly better than that of the original structure, but this resulted in a stress distribution with distinct characteristics in the direction of rotation, due to the unidirectional rotation of the spokes. The optimized structure II was the best, and the stress distribution was symmetrical when the tire rolled forward and backward. In addition, it can be seen from the legend color that the stress value was much smaller, which greatly improved the fatigue durability of the support. It is also shown that top loading can greatly improve the global spoke stress analysis, compared to bottom loading, and the degree of improvement is also related to the distribution of the spokes.

Figure 18 shows the stress distribution diagram for the longitudinal loading condition. Since the spokes of the optimized structure I were too thin and rotated in one direction, the bottom support was significantly deformed, which causes severe hysteresis in the pure longitudinal sliding driving condition.

Considering that the longitudinal stiffness of the optimized structure I is not ideal and there is a serious driving hysteresis, it is not necessary to consider the optimized structure I in the next pure longitudinal slip simulation. Figure 19 shows the pure longitudinal slip curves of the original structure and the optimized structure II. It can be seen that the driving of the original structure was very sensitive, which is favorable, but the braking was very soft—the slip ratio corresponding to the maximum braking force was close to 20%, and the drive was about 8%. It can be seen that the bottom load also had certain advantages, and its drive sensitivity was much higher. The pure longitudinal slip curve of the optimized structure II was more balanced, and the slip ratio corresponding to the maximum driving force or the maximum braking force was about 15%, which was mainly determined by the symmetry of the bottom spokes in the front and rear directions. However, the bearing method had a certain influence on the pure longitudinal sliding condition.

It is also biased to use only the slip ratio corresponding to the maximum braking force and driving force to characterize the consistency. Here, the following formula (11) was used to calculate the degree of antisymmetry between the braking and driving conditions.

$$\beta =\sqrt{\frac{1}{n}{\displaystyle \sum _{s=0}^1{\left[G\left(s\right)-\left|W(-s)\right|\right]}^2}}$$

(11)

β is the antisymmetric ratio, s is the slip ratio, the value range of s is (0,1), n is the number of points, G is a series of driving forces, and W is a series of braking forces. The antisymmetric ratio of the whole pure longitudinal sliding process can be obtained by calculation. The smaller the β value, the better the consistency of braking and driving.

In addition, to characterize the linearity of the stiffness curve, R-squared is a reasonable indicator. As shown in

Table 3. Characteristic parameters of three NPT structures.

Structures	Bearing Coefficient α	Linearity R-Square	Anti-Symmetric Ratio β
Original	1.1%	0.9625	642.9
Optimized I	11.1%	0.9818	-
Optimized II	8.2%	0.9932	379.7

, the original structure, optimized structure I, and optimized structure II were 0.9625, 0.9818, and 0.9932, respectively, and the closer the value was to 1, the better the linearity. It can be seen that the optimized structure improved the load-bearing linearity. At the same time, according to Formulas (7) and (11), Table 3 also summarizes the load-bearing coefficients and antisymmetric ratios of different structures. It can be seen that the load-bearing coefficients α of optimized structure I and optimized structure II were around 10%, which tended to be the top load-bearing mode. At the same time, it can be seen from the stress cloud diagrams in Figure 17b,c that the global stress distribution was relatively uniform. The load-bearing factor of the original structure was only 1.1%, which tended to be loaded at the bottom. From Figure 17a, it can be clearly seen that the stress was concentrated at the bottom support position. In addition, the linearity of the stiffness curve of the top-loaded structure was very good, which was more beneficial to the load-bearing form. The degree of antisymmetry of the optimized structure II was significantly lower than that of the original structure, which further indicated that the consistency of braking and driving was better. It can be seen that the different bearing coefficients will play a key role in the stiffness linearity and braking–driving consistency.

5. Conclusions

This paper mainly studies the static load characteristics and pure longitudinal sliding characteristics of NPT. After carrying out static load and pure longitudinal sliding tests on the original structure NPT, the results show that the static load stiffness curve is nonlinear, and the tangential stiffness gradually decreases. There are obvious differences in the pure longitudinal slip curve in the braking and driving conditions. In order to optimize the original structure, numerical simulation and verification are carried out in the third part, and an accurate model is obtained. In the fourth part, two optimization designs are carried out for NPT. The results show that, under the premise of reducing the overall NPT mass, the secant radial stiffness of the optimized structure II is increased by 58.8%, the tangent stiffness is increased by 2.96 times, the R-square is 0.9932, and the linearity is greatly improved. For the pure longitudinal slip simulation, the braking performance is improved and becomes more sensitive, but the driving performance is not as good as the original structure, and the consistency of driving and braking conditions is improved.

The non-pneumatic tires designed in this paper will be of guiding significance for practical applications. When designing non-pneumatic tires, attention should be paid to the load-bearing performance and the combined design of the shear band and the support. In addition, the non-pneumatic tire stiffness index, bearing coefficient, and analysis process of braking and driving established in this paper will provide a theoretical design basis for scholars in this field.

In addition, this paper uses the bearing coefficient to characterize the bearing form, and the design of the best bearing method needs to be further balanced. The next step is to explore how to balance the way NPT is carried. Bottom bearing will inevitably require a stronger bottom support, which is more conducive to the responsiveness of vehicle braking and driving and is more suitable for designing a high-speed, low-load NPT. The top load needs to weaken the support strength, so that the brake drive has a certain hysteresis effect. However, the stress distribution is more uniform, and it is more suitable for designing low-speed and heavy-load anti-fatigue NPT. However, extreme top load or excessive bottom load will bring some advantages and disadvantages; therefore, determining how to balance the top load and bottom load is more important.