Abstract
A feedforward strap-down control with a compensator base on the linear extended state observer (LESO) is proposed for a miniaturized camera stabilized platform, which reduces the influence of the dead zone in speed regulation and uncertainties in parameters to reduce the level of angular bias to the field of vision (FOV) in a low-cost stabilized platform. Firstly, the feedforward control is inspired by an approximate linear model proposed for the dead zone to improve the response velocity of the system when tracking the varying reference. Then, the compensator, combining the LESO and proportional differential (PD) law, is designed to eliminate the disturbances including the model bias in the dead zone, inaccuracy in the plant model, and external disturbance. Moreover, the observation performance of the LESO is improved by a preprocessor based on a tracking differentiator (TD) to deal with the time delay and nonlinearities in sampling the state variables. Meanwhile, the complex and uncertain control plant is also simplified by an approximate model combining a disturbance compensator for practical application. Finally, the feasibility of the proposed controller is verified and analyzed by the simulation, and its effectiveness is simultaneously validated by the 2-DOF camera stabilized platform.
1. Introduction
Actuators driven by motors with reduction gears or belts are widely used in machine tools, pan–tilt control, and industrial robots. Generally, they can provide a large output torque by the reducer and be controlled by a position loop with an integrated encoder. As actuators with inner controllers, they can be modularized at a small size, and re increasingly being applied in multiaxial platforms for miniaturized intelligent devices such as unmanned aerial vehicles (UAV), remotely operated vehicles (ROV), and quadruped robots. However, the backlash and buffer of the reducer mechanism cause many problems to the control system, such as the dead zone and parameter uncertainties. With the increasing demand for control performances of intelligent devices, these problems caused by the above elements should be solved as soon as possible.
Many adaptive derivative strategies have been researched to optimize the actuator dead-zone model and to compensate the disturbances, such as the adaptive fuzzy controller in [1,2,3], in which when the dead zone is unknown and changed in time varying, fuzzy logic can be used to identify parameters and smooth functions. In the control system of flexible spacecraft attitude tracking [4] and multiple flexible manipulators [5], the external disturbance and the input dead zone of the actuator are considered simultaneously. To deal with that situation, the adaptive sliding mode control law is proposed to ensure that the disturbance, nonlinearity, and errors can be simultaneously compensated via the adaptive mechanism. Synchronous control for dual-electro-hydraulic actuators [6], or the master–slave manipulator [7] has been influenced by the asymmetric dead-zone characteristics. An adaptive controller with the inverse dead-zone model was proposed to compensate the time delay of the actuator response caused by the unknown dead zone and guarantee synchronous performance. Then, an adaptive neural network controller was discussed and applied to deal with dead-zone influence in nonlinear quantized systems in a finite-time control problem [8], multiagent systems [9] and multiple-input–multiple-output (MIMO) switched nonlinear systems [10]. Actually, most of the low-cost systems have model inaccuracy and low precision in actuators and sensors, which means more random disturbance and uncertainty in the dead zone. For these reasons, the disturbance observer (DOB) was utilized in the system, which contributes the above influence to the inner disturbance that can be observed and compensated. Ref. [11] developed an infinite dimensional observer associated with coupled parameter update laws to consider the actuator and sensor faults with a dead-zone nonlinearity, which can be taken into account and accommodated completely. Refs. [12,13] proposed a fixed-time disturbance observer to deal with actuator dead zones and disturbances, improving the performance of unmanned ground vehicle (UGV) control systems in yaw angle and velocity tracking. Furthermore, many other control methods have also been introduced into the DOB. A back-stepping-based fault-tolerant controller was proposed for a robotic manipulator system [14] and a hydroturbine governing system [15]; when considering the actuator input saturation, asymmetric dead-zone characteristics, and the external disturbance, the DOB was embedded to compensate those impacts. Considering the effect of unpredictable factors in active vehicle suspension systems, such as actuator imperfections, uncertainties in suspension parameters, and unknown road profiles, a method based on a disturbance observer combined with sliding mode control was proposed for compensating [16]. However, the model of the dead zone is unknown in some control systems. Moreover, the system works with a random external disturbance. Many researchers have placed emphasis on active disturbance rejection control (ADRC) in recent years, which considers the internal and external disturbance and the nonlinear characteristics as the total disturbance. Then, the total disturbance can be observed and compensated by the extended state observer (ESO) before influencing the feedback loop. Moreover, the model is unnecessary when processing the effect of the dead zone. Ref. [17] proposed a linear active disturbance rejection optimal controller based on a proportional-derivative (PD) control law to eliminate the negative effects of the dead zone and improve the dynamic and steady-state control performances. Ref. [18] utilized an ESO with a switched dynamic parameter estimation law to estimate the effect of the external disturbance, the uncertain nonlinearity, the unknown dead-zone model, and the unmeasurable states. To deal with the influence of the valve dead zone, the parametric uncertainties, and the unmodeled disturbance in the hydraulic actuator system, Ref. [19] proposed a composite parameter adaptation law combined with the ESO, and [20] proposed a model-free linear ADRC (LADRC) integrating dead-zone inverse compensation. To improve the performance of the missile in the ascent phase, Ref. [21] utilized the ADRC to simplify the complex nonlinear time-varying process, including nonlinear dynamics of the actuator and wind disturbance into a linear time-invariant one, which can be compensated directly.
The dead zone is inevitable in the actuator with the reducer mechanism. With the increasing development of control strategies and precision machining, the influences of the dead zone have been decreased greatly. Actuators with stepping motors and belt transmission have been gradually used as a low-cost scheme in recent years. This type of actuator can obtain high precision in the position control with an integrated encoder, and has been widely used in facilities such as robot arms, pan–tilt control, and antenna mounts. Due to the particularity in driving the stepping motor, it can work with a step speed regulation (SSR) mode in the velocity loop control only. The dead zone of the SSR mode affects the accuracy in the velocity loop, especially in a low-speed output situation by the reducer mechanism [22]. Although it presents good performance in the position loop control, the actuator causes many problems in the application of the inertial stabilized control system when working in the SSR mode, such as the great enlargement of the level of angular bias to the field of vision (FOV) on the camera stabilized platform for virtual reality (VR) navigation systems. As the miniaturized camera stabilization platform seeks performance improvement and cost reduction simultaneously, these problems are common in low-cost actuator systems and affect the control precision, which needs to be solved immediately. To deal with the problems mentioned above, a feedforward strap-down control with an LESO compensator is proposed.
Therefore, the main contributions of this research are concluded as follows:
1. The dead zone of the actuator in speed regulation is modeled as an approximate linear model combining a bounded disturbance function that is compensated preferentially. The innovative manner that describes the dead zone in speed regulation could optimize the control scheme during the application.
2. A feedforward control based on the approximate linear model of the dead zone is proposed, then the compensator with LESO is designed, by which the total disturbance, including the model bias, can be compensated. Moreover, the response time could be improved by the feedforward control when the reference input changes rapidly.
3. Considering the time delay and nonlinearities in sampling the state variables from the actuator module by communication, a preprocessor based on a tracking differentiator (TD) is proposed to optimize the signal and provide smooth-state variables to the LESO. The preprocessor could greatly improve the observation performance of the LESO.
The rest of this paper is organized as follows. In Section 2, the definitions of the kinematics of the camera stabilized platform are introduced, and the model of the dead zone is proposed. Then, the influences of the dead zone on the typical inertial stabilized control system are analyzed. In Section 3, the implementation of the feedforward control with the compensator is designed and analyzed in detail. Moreover, the preprocessor with the TD is derived. In Section 4, the simulation of the proposed controller is studied, the feasibility of which is verified. In Section 5, the experiments are implemented with a high-precision turntable to verify the improvement in control performance. Finally, the conclusions are presented in Section 6.
2. Models and Definitions of System
2.1. The Kinematic Model
The camera stabilized platform for VR navigation consists of dual-axial gimbals in the pitch and roll rotations. The definitions of the frames are shown in Figure 1. The rotations of the base, the roll, and the pitch are represented by the frames OB, OO, and OI, respectively. The angular velocity of each frame is represented by triads of vectors, as shown in (1). The base rotation is transformed into the inner pitch gimbal by matrixes (2), which are shown in Equation (3). The derivative process is expressed by [23] in detail.
ωI = (ωIx, ωIy, ωIz)T, ωO = (ωOx, ωOy, ωOz)T, ωB = (ωBx, ωBy, ωBz)T
ωO = ROB·ωB + (α′, 0, 0) T, ωI = RIO·ωO + (0, β′, 0)T
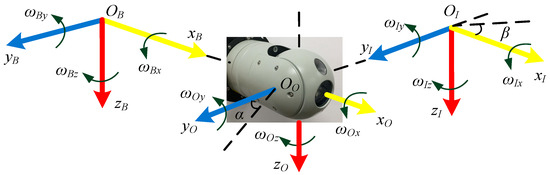
Figure 1.
The coordinates of the camera stabilized platform.
The platform is installed on a rack, as shown in Figure 2. The roll and pitch gimbals are driven by the actuators with angles α and β, which can counteract the motions from the base. The variables σ and μ represent the angles of LOS in roll and pitch rotations. The angular velocities of the LOS and the actuators are represented by triads of vectors ωm = (α′, β′, 0)T, and ωL = (σ′, μ′, 0)T. The relationship of the angular velocities between the LOS and the actuators can be represented by Equation ωL = RIB·ωB + ωm, where the transition matrix is expressed by (4).
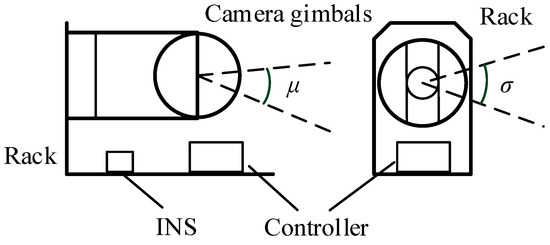
Figure 2.
The structure of the camera stabilized platform.
2.2. The Dead-Zone Model
The actuator dead zone with the stepping motor exists with input order in speed regulation, as shown in Figure 3, which can be expressed by Equation (5).
where the input order r = u(t) is the output signal of the controller, ds(r) is the value of the speed in a step function, and the variable l is width of the dead zone. According to (5), the function expresses continuous dead zones that are different from the conventional model. The speed exists in the dead-zone with the input order r in each step, which is expressed by sequence number n, and is regulated by steps with the control signal u(t). However, the dead zone causes deviations in the angular velocity tracking process, resulting in the angular bias to the FOV. The speed jitter in the threshold of the dead zone can induce nonlinear disturbance to the sensors in the feedback during the angular velocity tracking.
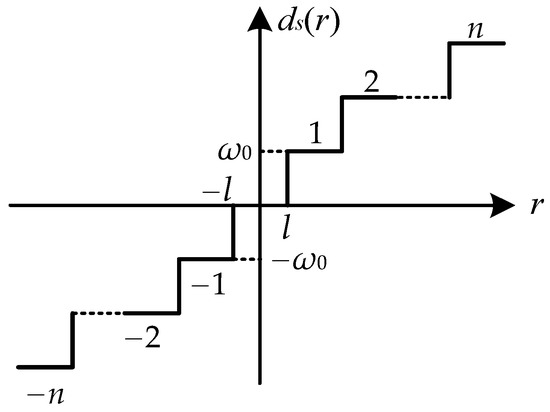
Figure 3.
The actuator dead zone in speed regulation.
As an innovation, the dead zone in speed regulation is described by an approximate linear function via a bounded unknown disturbance by Equation (6).
where the approximate linear function d(r) = k·r, let k = ω0/2l. The disturbance ωs(r) includes the model bias from the variable ω0, l, which cannot be acquired accurately in a practical system, and the wide of the dead-zone in each step of the speed are not uniform in coefficient.
ds(r) = d(r) + ωs(r)
2.3. Camera Stabilized Control System
Typically, the system is designed as an angular velocity loop control in inertia, as shown in Figure 4. The motions from the base acting on the camera are expressed by RIBωB, which can be counteracted by the actuators with the gimbal velocity ωm. The reference input should be set as ωs= (0, 0, 0)T to keep the LOS stable. The variables in the vector ωL are detected by the MEMS gyroscope installed on the inner gimbal. The C(s) is the transfer function of the controller for the angular velocity loop, and kg is the gain in the feedback.
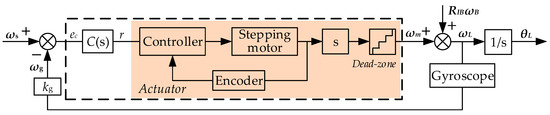
Figure 4.
Typical inertial stabilized control by the angular velocity loop.
The roll gimbal control, for example, can be illustrated in Equation (7). The angular velocity of the LOS is derived as:
σ′ = ωBx + d(r) + ωs(r)
Then, the motion of the LOS detected by the MEMS gyroscope as feedback is shown in Equation (8).
where the function fg(ωs(r), t) is the random disturbance in the MEMS gyroscope during the detection, which is related to the dead zone of the actuator and the sampling frequency of the sensor. Therefore, the input signal of the controller in Equation (9) is affected by the disturbance from the actuator and the sensor.
ωgx = σ′ + fg(ωs(r), t)
ec = −kg·ωgx = −kg·[(ωBx + d(r)) − (ωs(r) + fg(ωs(r), t))]
Although the disturbance of the dead zone is bounded, it can be amplified by the controller C(s) continuously in the feedback loop control. Let ωr = ωs(r) + fg(ωs(r), t), and u = ωBx + d(r), then the system can be expressed as a typical two-order system in Equation (10).
where the total disturbance is modeled as f0, which depends on the state variable x1, x2, and internal time-varying disturbance. The output y is the angle of the gimbal.
3. Design of the Proposed Controller
In this scheme, the inertial angular variables for stabilization are from the inertial navigation system (INS) on the ship instead of the angular velocity variables from the gyroscope on the inner gimbal. Therefore, the platform is designed as a strap-down system for stabilization. The differences to the typical scheme are discussed in [24]. The methods and definitions of the strap-down system in an inertial stabilized platform are discussed by [25,26] in detail.
Considering the strap-down system in this research, the approximate linear model is used with the feedforward to implement the stabilized control of the camera platform in Figure 5, and deservedly caused angular bias to the level of the FOV. Then, the compensator is designed to deal with that problem, which is caused by the dead zone and nonlinearity of the actuator in the control process. Moreover, a preprocessor for the state variables with the tracking differentiator (TD) is proposed to modify the LESO, which has the advantages of simple design, fewer parameters, and suitability in engineering applications [27,28]. These modifications can solve problems during communication and data sampling from the actuator module, which introduces the time delay and nonlinearities to the state variables.
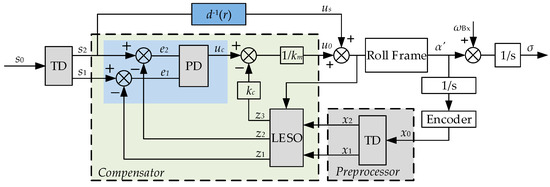
Figure 5.
The scheme of the proposed controller in the roll frame.
3.1. The LESO with TD Preprocessor
Considering the time delay in data sampling and communication when acquiring the angular variables from the actuator module, the variable content step signal causes an overshoot in the differential process. A preprocessor with a TD is proposed to deal with that problem. The TD can track the input signal and generate a smooth and continuous tracking trajectory. A discrete two-order TD is expressed in Equation (11).
The state variable x0 is the angle data from the actuator module, which contains nonlinear disturbance and is processed by the fast optimal control synthesis function fst(x1(k) − x0(k + 1), x2(k), r1, h1). The variables x1 and x2 are the outputs of the TD. The process is expressed in Equation (12).
where sign(a) is a limiting sign function, and the function can be described in Equations (13) and (14).
where the variable r1 is the speed factor of the tracking speed of x0 to x1. The variable h1 is the step length of the integration, which can be adjusted to eliminate the overshoot in x0 and avoid the noise amplify in the differential process. To provide a fast and accurate response to the input signal, the proposed TD parameters can be turned online, as explained in [29]. In those parameters, the variables r1 and h1 should be turned first. Then, the other variables such as d, d0, y, a0, and a1 can be determined.
The total disturbance, including the dead zone, nonlinear uncertainties, and external disturbances, can be extended to a state variable in Equation (15).
where x3 is the state of the total disturbance. The state vector is x = [x1, x2, x3]T, which can be observed by the LESO in Equation (16).
The vector z = [z1, z2, z3]T is the output of the LESO for the estimation of the state variables, and the variables β1, β2, and β3 are the gains for adjusting. The LESO is improved by adding the observation error for the two-order state variable correction. The vector z is expressed by the observed errors ε1 and ε2. It can improve the accuracy in the observation of the high-order state variables when ε1 is too small to estimate z2 and z3.
3.2. The Compensator for the Feedforward Control
As a strap-down system, the input of the controller s0 is the reference angle, which is detected from the INS. To coordinate the following process, the variable s0 is tracked by the TD. Then, a smooth angular variable s1 and a differential variable s2 are acquired. The input TD is expressed as discrete and two-order in Equation (17):
The output of the feedforward is expressed by us = kf·s2, which is the inverse function of the linear part in the dead-zone model. Although it presents good performance in rapid response with the feedforward control, the disturbance part of the dead-zone model can influence the control precision. Considering the dead zone and the model inaccuracy, a compensator with the LESO is designed. Different from other strategies to compensate for the dead zone directly, the compensator is committed to correcting the output angle of the system, which can coordinate the feedforward control.
Then, z1 is the observed variable of the output angle, and z2 is the observed variable of the angular velocity. The reference signals of the PD controller s1, s2 are the outputs of the TD. Based on this, e1 = s1 − z1, and e2 = s2 − z2 are defined as tracking errors. The PD control law is employed to provide a control signal, with kp, and kd being proportional and derivative gains.
The purpose of the compensator is to correct the angular bias to the FOV that is caused by the dead zone. The PD controller makes the compensator more effective, and the total disturbance observed variable kc·z3 can suppress the overshoot during the compensation. Finally, the control signal of the actuator can be expressed by Equation (18).
In order to analyze the stabilization of the control scheme, the feedforward with the compensator can be equated to a high-gain control with a disturbance observer. The method derived in [30] defines the tracking error variable of the angular velocity as es = s2 − x2. Then, the angular velocity tracking can be equivalently depicted by es′ = −(kf + kd)·es − de, where the variable de is the disturbance of the model inaccuracy in the dead zone and the external disturbance. To make the analysis of the system in stabilization, the error function can be transformed as:
In Equation (19), the output will track the input reference as time goes to infinity in the absence of the disturbance. Considering the presence of the disturbance, it is supposed that the disturbance of the dead zone is bounded and satisfies |de(t)| < d* with d* > 0. Equation (21) is derived from (20) and gives Equation (22) by taking the limits of both sides of the inequality.
In Equation (23), the disturbance in model inaccuracy can be supposed as the errors between the actual and observed angular velocity of the actuator output, that is, de = ωs −kmz3 − kpe1. Due to the LESO being modified by the TD preprocessor, the variables for observations z1 and z3 can be observed accurately. The base motions are detected by the high-precision INS, which is adopted by the input signal of the strap-down system. Guaranteed by the above conditions, the disturbance ωs can be observed and compensated accurately. Consequently, the control gains have to be designed such that kf + kd > 0, and with the continuous state, that is, de(∞) = 0, the tracking function is implemented.
4. Simulation and Verification
4.1. Performance of the Feedforward Control
To analyze the performance of the feedforward control with the approximate linear model of the dead zone, the simulation scheme of the proposed controller is implemented in the environment of MATLAB/Simulink. Taking the roll gimbal, for example, let kc, kp, and kd be zero. The control signal r = us is obtained, which controls the actuator by the feedforward independently. The reference input of TD is set as s0 = −ωBx, which is derived from the INS on the base. The parameters of TD are turned online that r2 = 3, h2 = 5, then the equation can be expressed as (24).
The simulation result is demonstrated in Figure 6. s1 is the base angle and s2 is the base velocity, which is the input of the feedforward control. The gain of the feedforward is kf = 1/4.52, which is the inverse of the linear part of the dead-zone model. With the control signal us = kf·s2, the output velocity of the actuator is α′, in which the influence of the dead zone is expressed as α′ = d(r) + ωs(r), r = us. Obviously, the output velocity α′ cannot track the base velocity s2 accurately due to the disturbance ωs(r). As shown in the result, the disturbance in the angular velocity is integrated and leads to an angular bias. There is about a −11° bias in angle when finishing the simulation at 10 s. Moreover, the feedforward input s2 changes rapidly from 1.2 s to 2.5 s in the tracking process, and can be tracked by the actuator velocity accurately, with an angular bias of less than 3°. In contrast, the angular bias increases after 3 s when the base velocity s2 changes moderately. It is concluded that the feedforward control presents a better time response performance when the input reference changes rapidly.
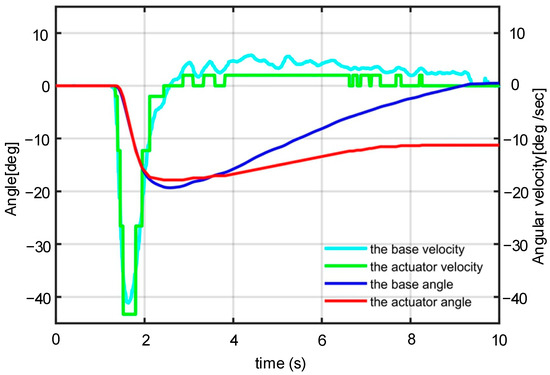
Figure 6.
The influence of the dead zone in feedforward velocity tracking.
4.2. Analysis of the Compensator
The control signal of the actuator r is affected by the sum of the PD controller, the feedforward control, and the fast correction with z3. To analyze and verify the feasibility of the proposed scheme, the process of the analysis is described in two steps:
Step 1: In this section, the actuator is controlled by the feedforward and compensated with the angular variable in observation. The initial parameters of the LESO are set as shown in Table 1. The control signal is r = kf·s2 + kpe1, and kp = 0 to 0.95 is a contrast. It means that the feedforward control is compensated by the observed variable z1. Then, the state variable z1 = ∫(z1 − β1ε1) dt, ε1 = z1 − x1. The error between the reference and variable observed is e1 = s1 − z1.

Table 1.
Initial parameters in step 1.
The performance of the LESO on observing the angle of the actuator with z1 is shown in Figure 7. It is implemented at 5 s to track the angle α and obtain a stable trajectory after 9 s. The overshoot of z1 is within 5° during the tracking process. Figure 7a illustrates the performance of the feedforward control based on the approximate linear model solitary. At the end of the process, the angular bias in tracking is about −11° for lagging. As a contrast in Figure 7b, the compensator is implemented with the control signal uc = kpe1. The angular bias is −7°at the end with the compensation.

Figure 7.
The effect of the compensation by the angular observation: (a) controlled by the feedforward solitary; (b) adding the compensation by z1.
Step 2: The compensator is implemented with the PD controller, the parameters of which are turned, as shown in Table 2. The reference inputs s1 and s2 are the variables of the angle and the angular velocity, which are the outputs of the TD. The state variables in feedback are observed by the LESO. Then, z2 = uo + us + ∫(z3 − β2ε2) dt, which is improved by ε2 = z2 − x2. It can obtain a better performance in precision when z1 is tracking x1 accurately. The control signal is r = kp·e1 + kd·e2, e2 = s2 − z2, and kp = 0.7, kd = 0.04. The performance of the compensator is illustrated in Figure 8a. The PD controller is implemented at 5 s and obtains a stable trajectory in tracking after 9 s. At the end of the process, the bias angle caused by the dead zone is compensated entirely. Then, the maxim angular overshoot is within 8°at 6.2 s during the process.

Table 2.
Initial parameters in step 2.
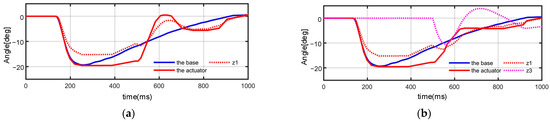
Figure 8.
The effect of the correction by z3 in suppressing the overshoot: (a) compensated by PD; (b) adding the correction by z3.
To improve the stability of the system, the disturbance correcting variable z3 is involved in the compensator; z3 = ∫(−β3ε2) dt, and kc = 0.25. The overshoots are regarded as the inner disturbance of the system, which can be estimated and corrected by the total disturbance observed variable kc·z3. As shown in Figure 8b, the correction of the maxim angular overshoot is within 3° during the tracking process. It is concluded that the derivative element of the PD controller has improved the effectiveness of the compensator; meanwhile, the stability of which has been enhanced by correcting with z3.
4.3. Simulation of the Stabilized System
In order to verify and demonstrate the effectiveness of the proposed control scheme, a simulation experiment of the stabilized platform is carried out. Considering the typical control scheme with an inertial velocity loop in the roll gimbal, the base motion is set as ωBx = Asin(ωt + τ), and A = 30, ω = 0.4π, τ = 0.25π, which is a sine signal in velocity and simulates the attitude data from the MEMS gyroscope installed on the inner gimbal. The input of the controller C(s) is ec = ωs − ωg, and ωs = 0. The controller C(s) is set as a PD scheme, which is widely used in practice. Therefore, the control signal is r = k1ec + k2ec’, where ec = −kg·[(ωBx + d(r)) − ωr]. To analyze the influence of the dead zone in the actuator independently, the disturbance from the sensor fg(ωs(r), t) is filtered by an ideal low-pass filter, that is, ωr = ωs(r). Let kg = 0.25, k1 = 0.7, and k2 = 0.05. Due to the influence of the dead-zone, errors exist throughout the velocity tracking process, as shown in Figure 9a. It is even worse at the peak of the input signal, which has a low accelerated velocity. Finally, the angular bias is within ±5°.
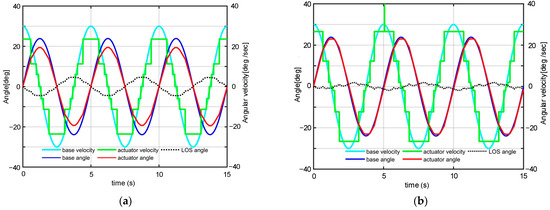
Figure 9.
The performance of the stabilized control in simulation: (a) the typical controller; (b) the proposed scheme.
In contrast in Figure 9b, the input reference is s0 = Asin(ωt), which is the attitude angle that can be acquired from the INS on the base. Let A = 25, ω = 0.4π. The parameters of the compensator are set in Table 3, which are turned online with the method in [27]. With the compensator, the actuator can track the input order accurately, even if errors of velocity between the actuator and the base exist. The roll angular trajectory of the LOS illustrates that the maxim angular bias is within ±2°. Obviously, the better performance of the control schema can be approved by the results of the simulation.

Table 3.
Parameters of the compensator.
As a whole, the superiorities of the proposed camera stabilized system are as follows: firstly, the advantage of the high-gain loop is reserved by the feedforward with the approximate linear model, which can improve the response time of the system. Secondly, the angular bias to the level of the FOV caused by the dead zone and the model inaccuracy has been corrected by the compensator, in which the PD controller and disturbance observation can obviously enhance the stability and the robustness in the control process.
4.4. Simulation of the Preprocessor
The acquisition of the state variables is implemented by the communication and the digital sampling between different modules. Therefore, the disturbances from time lagging and nonlinearities in discrete sampling generally exist, and are even worse in the low-cost modularized hardware system. As shown in Figure 10a, the angle data x0 are sampled from the actuator module with about 0.3 s delay to the real actuator angle, which is stepped and nonlinear. Then, the state variables are observed by the LESO independently. It illustrates that the observed variable z1 is delayed by almost 0.6 s to the actuator angle, and z2 contains high-frequency disturbance that can influence the performance of the compensator.

Figure 10.
The state variables observed: (a) LESO; (b) LESO + TD.
To deal with the problem above, the TD is implemented to preprocess the data from the module, which can track the disturbance signal rapidly and provide a smooth high-order output signal without overshoots. Let r1 = 1.2, h1 = 3.5, which are the tracking speed and the filter factors. The testing results are shown in Figure 10b and Table 4. As a contrast, the proposed preprocessor decreases the delay time in the observed variable z1, and makes the observed variable z2 smoother.

Table 4.
The results of the observation.
5. Experimental Verification
5.1. System for Experimens
In order to verify the effectiveness of the proposed control scheme further, the devices for the experiment are constructed, as shown in Figure 11. The camera is installed in the pan–tilt platform with roll and pitch axis gimbals, and the image is displayed by the displayer. The control module and the INS are on the base of the rack. The control strategy for the stabilized platform is programed in the computer, by which the data of the platform during the experiment can be displayed and saved. The communication is used to transmit the data between the modules above. The detailed parameters of the hardware are shown in Table 5 and Table 6.

Figure 11.
Devices of the camera stabilized platform experiment for testing.

Table 5.
The elements and interface of the modules that compose the camera stabilized platform.

Table 6.
Range of the parameters in the control system.
5.2. Analyses of the Results
The verification experiments are implemented on the high-precision turntable, as shown in Figure 12. To simulate the swaying movement on the ship, the turntable is set as ±15° in the angular range and 0.2 Hz on the frequency of swing. Let kp = 0.03, kd = 0.005, and kg = 0.9, which are the parameters of the typical scheme with the PD controller. Then, the proposed controller is set in Table 7.

Figure 12.
Experiments on the high-precision turntable.

Table 7.
Parameter settings of the proposed scheme.
The sequence of the parameters in the controller to be turned is the TD for the preprocessor, the TD for input, the LESO, and the PD controller. The experimental results are illustrated as follows. In Figure 13a, the controller is designed as a typical scheme, which is based on the PD law in the inertial angular velocity loop. The bias of the trajectory in the angle between the actuator and the input order increases after 20 s. The maxim error is almost 19° at the end of the test. The dead zone in the velocity control and the model inaccuracy of the actuator lead to problems, and the mechanical deviation makes that serious. In contrast, in Figure 13b, the results of the proposed controller show that the trajectory of the angular bias of the LOS is within ±3.5°. The performance is obviously improved, and the average value of the angular bias is almost 0°. Although there are fluctuations in low frequency in the angular trajectory of the LOS, the shakes caused in the FOV are within the limits of the ability of the image stabilization algorithm in the camera.

Figure 13.
The contrast of the stability performance of the LOS: (a) the typical controller; (b) the proposed scheme.
6. Conclusions
The performance of the camera stabilized platform can be influenced by the actuator dead zone, uncertainties in parameters, and nonlinearities in data transmission. To solve these problems, the feedforward strap-down control with the LESO compensator is proposed to compensate the angular bias of the LOS caused by the dead zone. Moreover, this simplifies the dead-zone model and can be implemented on a low-cost hardware system, as well as being more suitable for a modularized camera stabilized platform. Firstly, the dead zone is modeled by an approximate linear model via a bounded disturbance function, which is utilized to the feedforward control and ensures dynamic performance in the strap-down system. Secondly, the scheme based on the angular observation is proposed to compensate for the uncertain disturbance, which is implemented by the LESO and the PD controller. The compensator combines the robustness and stability to the control process, which is attributed to the angular velocity and the total disturbance observation by the LESO. Thirdly, the preprocessor for the LESO is designed by the TD to solve the nonlinearities and time delay in the state variable data during the communications between different modules. Meanwhile, the mathematical model of the control system is established, and the feasibility of the method is verified by simulation. Finally, contrastive experiments with the typical scheme verify the superior performance of the controller.
The camera stabilized platform with the feedforward strap-down system will be applied for a VR navigation system and implemented in actual experiments on a moving ship in the future.
Author Contributions
T.F. and Y.G. conceived the idea; T.F. designed the software, collected the data, and analyzed the experimental data; L.G. collected the related resources and supervised the experiment; T.F. prepared the original draft and final article; C.Q. proposed the comment for the paper and experiment. All authors have read and agreed to the published version of the manuscript.
Funding
This work is sponsored by the key project of the “High-level Guidance Special Project of Scientific Research” of Harbin Engineering University (No. 3072022QBZ0404), the Department of Science and Technology of Heilongjiang Province (LH2021F018), the Science and Technology Research Program of Chongqing Municipal Education Commission (KJZD-K202104701), and the National Natural Science Foundation of China (NSFC.61803118).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lu, K.; Liu, Z.; Lai, G.; Zhang, Y.; Chen, C.L.P. Adaptive Fuzzy Tracking Control of Uncertain Nonlinear Systems Subject to Actuator Dead Zone with Piecewise Time-varying Parameters. IEEE Trans. Fuzzy Syst. 2019, 27, 1493–1505. [Google Scholar] [CrossRef]
- Lan, J.; Liu, Y.J.; Liu, L.; Tong, S. Adaptive Output Feedback Tracking Control for a Class of Nonlinear Time-Varying State Constrained Systems with Fuzzy Dead-Zone Input. IEEE Trans. Fuzzy Syst. 2020, 29, 1841–1852. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, Z.; Wang, J.; Liu, Z.; Chen, C.L.P. Fuzzy Adaptive Two-Bit-Triggered Control for a Class of Uncertain Nonlinear Systems with Actuator Failures and Dead-Zone Constraint. IEEE Trans. Cybern. 2021, 51, 210–221. [Google Scholar] [CrossRef] [PubMed]
- Li, A.; Liu, M.; Cao, X.B.; Liu, R.X. Adaptive quantized sliding mode attitude tracking control for flexible spacecraft with input dead-zone via Takagi-Sugeno fuzzy approach. Inf. Sci. 2022, 587, 746–773. [Google Scholar] [CrossRef]
- Chen, T.; Shan, J.J. Distributed Control of Multiple Flexible Manipulators with Unknown Disturbances and Dead-Zone Input. IEEE Trans. Ind. Electron. 2020, 67, 9937–9947. [Google Scholar] [CrossRef]
- Wang, L.X.; Zhao, D.X.; Liu, F.C.; Liu, Q.; Zhang, Z. Active Disturbance Rejection Position Synchronous Control of Dual-Hydraulic Actuators with Unknown Dead-Zones. Sensors 2020, 20, 6124. [Google Scholar] [CrossRef]
- Jung, D.; Jeon, J. Synchronous Control of 2-DOF Master-Slave Manipulators Using Actuators with Asymmetric Nonlinear Dead-Zone Characteristics. IEEE Access 2022, 10, 22782–22794. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, F.; Wang, J.; Huang, Y. Adaptive Finite Time Control of Nonlinear Quantized Systems with Actuator Dead-Zone. IEEE Access 2019, 7, 117600–117611. [Google Scholar] [CrossRef]
- Liu, D.C.; Liu, Z.; Chen, C.L.P.; Zhang, Y. Distributed adaptive neural control for uncertain multi-agent systems with unknown actuator failures and unknown dead zones. Nonlinear Dyn. 2020, 99, 1001–1017. [Google Scholar] [CrossRef]
- Xie, K.; Lyu, Z.; Liu, Z.; Zhang, Y.; Chen, C.L.P. Adaptive Neural Quantized Control for a Class of MIMO Switched Nonlinear Systems with Asymmetric Actuator Dead-Zone. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 1927–1941. [Google Scholar] [CrossRef]
- Xu, X.D.; Dubljevic, S. Robust State Estimation for Positive Real Infinite-Dimensional Systems with Actuator and Sensor Faults. IEEE Syst. J. 2021, 15, 4887–4894. [Google Scholar] [CrossRef]
- Zhang, P.F.; Chen, Q.Y.; Yang, T.T. Trajectory Tracking of Autonomous Ground Vehicles with Actuator Dead Zones. Int. J. Comput. Games Technol. 2022, 2021, 2914190. [Google Scholar] [CrossRef]
- Guo, G.; Zhang, P.F. Asymptotic Stabilization of USVs with Actuator Dead-Zones and Yaw Constraints Based on Fixed-Time Disturbance Observer. IEEE Trans. Veh. Technol. 2020, 69, 302–316. [Google Scholar] [CrossRef]
- Zhang, Z.; Peng, L.X.; Zhang, J.N.; Wang, X.W. Finite-Time Neural Network Fault-Tolerant Control for Robotic Manipulators under Multiple Constraints. Electronics 2022, 11, 1343. [Google Scholar] [CrossRef]
- Yi, Y.P.; Chen, D.Y. Disturbance observer-based backstepping sliding mode fault-tolerant control for the hydro-turbine governing system with dead-zone input. ISA Trans. 2019, 88, 127–141. [Google Scholar] [CrossRef] [PubMed]
- Pusadkar, U.S.; Chaudhari, S.D.; Shendge, P.D.; Phadke, S.B. Linear disturbance observer based sliding mode control for active suspension systems with non-ideal actuator. J. Sound Vib. 2019, 442, 428–444. [Google Scholar] [CrossRef]
- Zhang, Z.; Cheng, J.; Guo, Y. PD-Based Optimal ADRC with Improved Linear Extended State Observer. Entropy 2021, 23, 888. [Google Scholar] [CrossRef]
- He, K.H.; Dong, C.Y.; Wang, Q. Active disturbance rejection adaptive control for uncertain nonlinear systems with unknown time-varying dead-zone input. Asian J. Control 2021, 24, 1209–1222. [Google Scholar] [CrossRef]
- Yang, F.B.; Zhou, H.P.; Deng, W.X. Active Disturbance Rejection Adaptive Control for Hydraulic Lifting Systems with Valve Dead-Zone. Electronics 2022, 11, 1788. [Google Scholar] [CrossRef]
- Wang, L.X.; Zhao, D.X.; Zhang, Z.X.; Liu, Q.; Liu, F.; Jia, T. Model-free Linear Active Disturbance Rejection Output Feedback Control for Electro-Hydraulic Proportional System with Unknown Dead-zone. IET Control Theory Appl. 2021, 15, 2081–2094. [Google Scholar] [CrossRef]
- Fu, B.S.; Qi, H.; Xu, J.T.; Yang, Y.; Wang, S.; Gao, Q. Attitude Control in Ascent Phase of Missile Considering Actuator Non-Linearity and Wind Disturbance. Appl. Sci. 2020, 9, 5113. [Google Scholar] [CrossRef]
- Kondo, D.; Yashiro, D.; Yubai, K.; Komada, S. Load torque control of an electromagnetic motor with a reduction gear and motor/load-side encoders using a spring model including a dead zone. Electr. Eng. Jpn. 2021, 214, 4. [Google Scholar] [CrossRef]
- Ekstrand, B. Equations of motion for a two-axes gimbal system. IEEE Trans. Aerosp. Eelctron. Syst. 2001, 37, 1083–1091. [Google Scholar] [CrossRef]
- Kennedy, P.J.; Kennedy, R.L. Direct Versus Indirect Line of Sight (LOS) Stabilization. IEEE Trans. Control Syst. Technol. 2003, 11, 3–15. [Google Scholar] [CrossRef]
- Hilkert, J.M. Inertially stabilized platform technology—Concepts and principles. IEEE Control Syst. Mag. 2008, 2, 26–46. [Google Scholar]
- Masten, M.K. Inertially stabilized platforms for optical imaging systems—Tracking dynamic targets with mobile sensors. IEEE Control Syst. Mag. 2008, 28, 47–64. [Google Scholar]
- Gao, Z. Scaling and bandwidth-parameterization based controller tuning. In Proceedings of the 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003; pp. 4989–4996. [Google Scholar]
- Wang, X.; Pan, T.H. A structure-improved extended state observer for active disturbance rejection control. In Proceedings of the 2020 Chinese Automation Congress, Shanghai, China, 6–8 November 2020; pp. 2798–2801. [Google Scholar]
- Han, J.Q. Active Disturbance Rejection Control Technique—The Technique for Estimating and Compensating the Uncertainties, 1st ed.; National Defense Industry Press: Beijing, China, 2008. [Google Scholar]
- Khalil, H.K. High-gain Observers in Feedback Control—Application to Permanent Magnet Synchronous Motors. IEEE Control Syst. Mag. 2017, 5, 25–41. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).