Enhanced Reaching-Law-Based Discrete-Time Terminal Sliding Mode Current Control of a Six-Phase Induction Motor
Abstract
1. Introduction
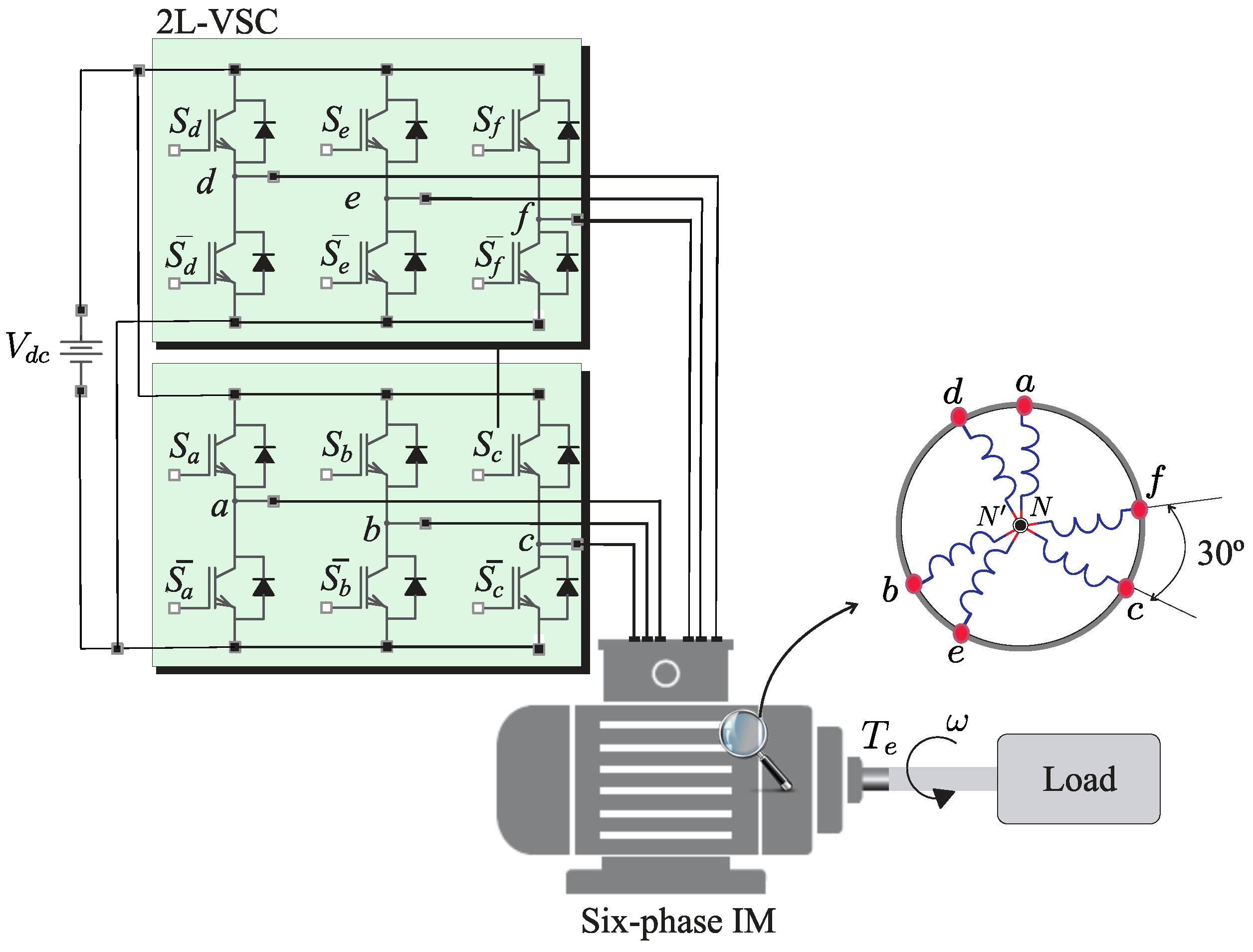
2. System Modelling
- are the unmeasurable rotor currents,
- are the stator currents,
- are the stator input voltages,
- are the uncertain dynamics caused by uncertain parameters and the disturbances acting on the stator currents,
- ,
- is the inductance of the stator,
- is the leakage inductance of the stator,
- is the inductance of the rotor,
- and are, respectively, the resistances of the stator and the rotor,
- P is the number of pole pairs,
- is the mechanical speed,
- is the rotor’s electrical speed,is the generated torque, is the load torque, B and J are the coefficients of the friction and the inertia, and , are the stator fluxes.
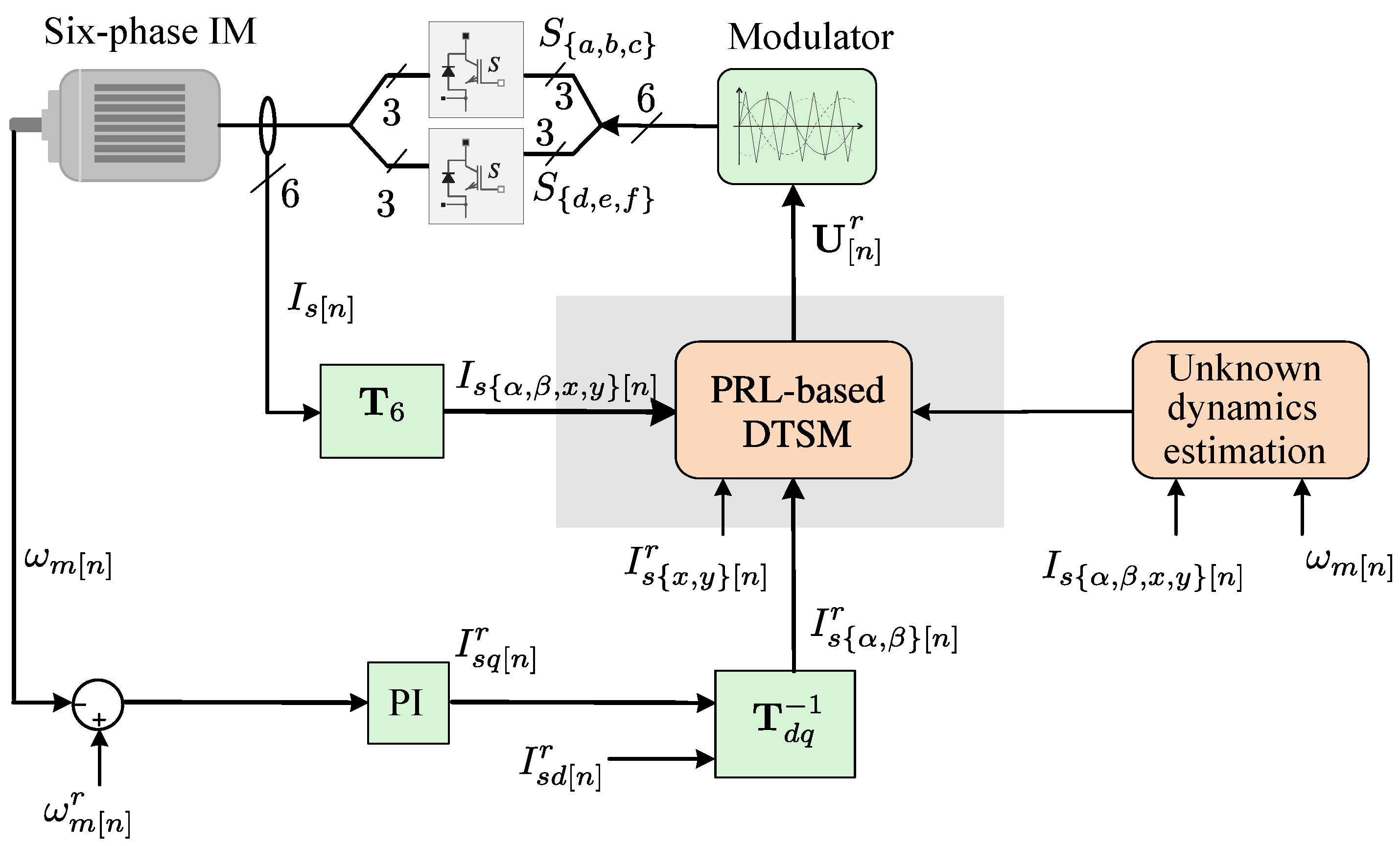
3. Proposed Discrete-Current Controller Conception
3.1. Outer Control Loop
3.2. Inner Control Loop
- is the vector of stator current tracking errors;
- is the vector of stator current references;
- and are diagonal matrices with positive elements;
- where for , and:
- is the identity matrix;
- , where for ;
- , and are diagonal positive-definite matrices that will be fixed in the proof of stability;
- for with , for , and, finally, .
- Let us start with the case where . Then:Choosing to satisfy (21) ensures that .Otherwise, can be expressed as follows:Hence:In this case, is positive definite, and it is obvious that the right side of the inequality is negative definite, which implies that is always true.
- Now, let us consider the case where . On one hand, let us rewrite the inequality as:This is always true, since . On the other hand, can be expressed as follows:It is clear that the above inequality is always true because and .
- Finally, let us consider the last case, where , then:
- a.
- If is positive definite, then this third case becomes:andwhere . Moreover, if (21) is verified, then:andThis implies that:
- b.
- if is negative definite, then this third case becomes:Using the same methodology for , it can be easily demonstrated that:
- Firstly, let us assume that and are both strictly positive definite and for all . Then,Hence, one can notice that ensures thatIt follows that:which is contradictory to the fact that .
- Secondly, let us assume that and are both strictly negative definite and for all . Then,Once again, we can clearly notice that verifies thatIt follows thatwhich is contradictory to the fact that .
4. Experimental Results
4.1. Analysis Criteria
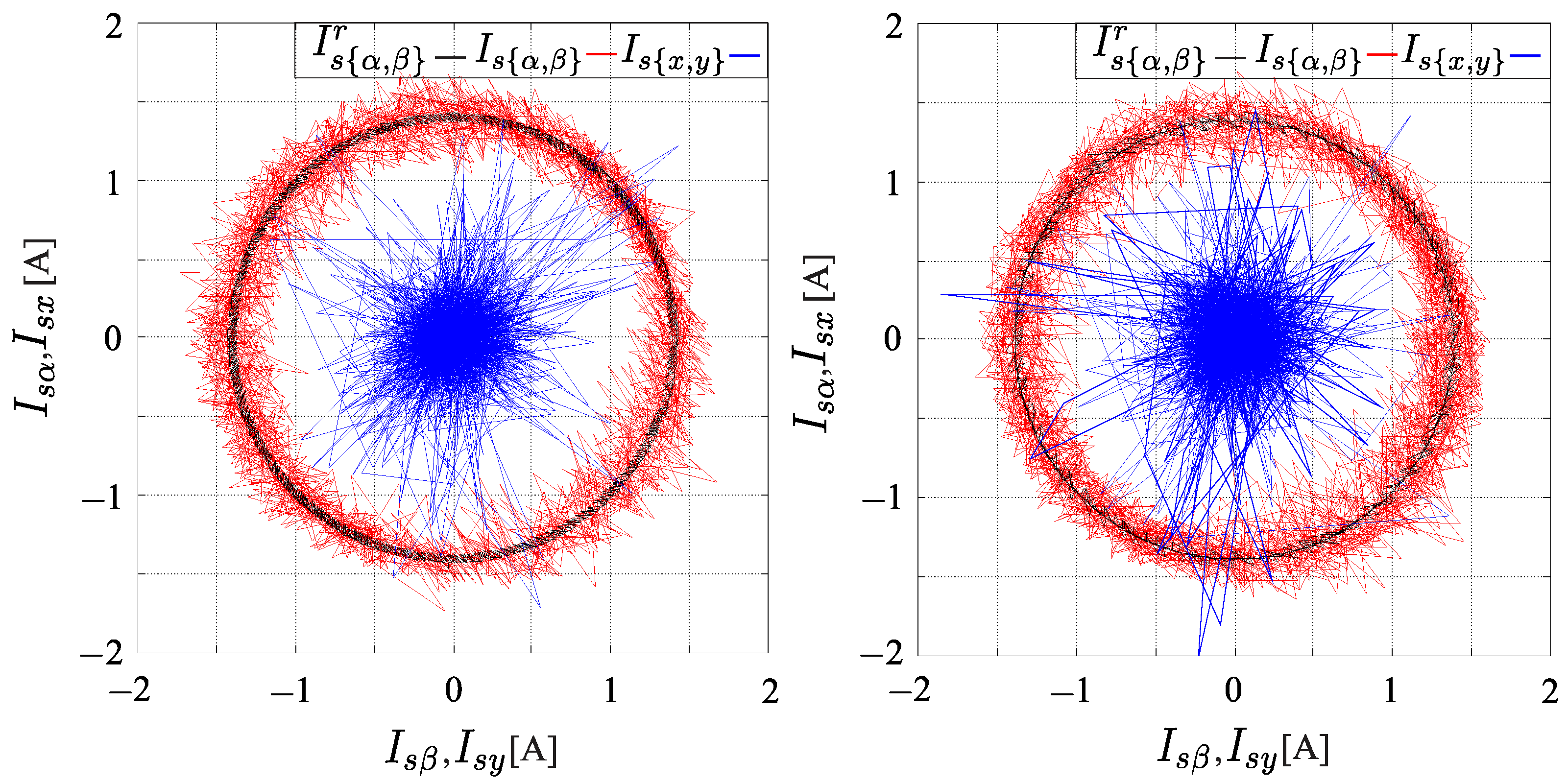
4.2. Steady-State Results
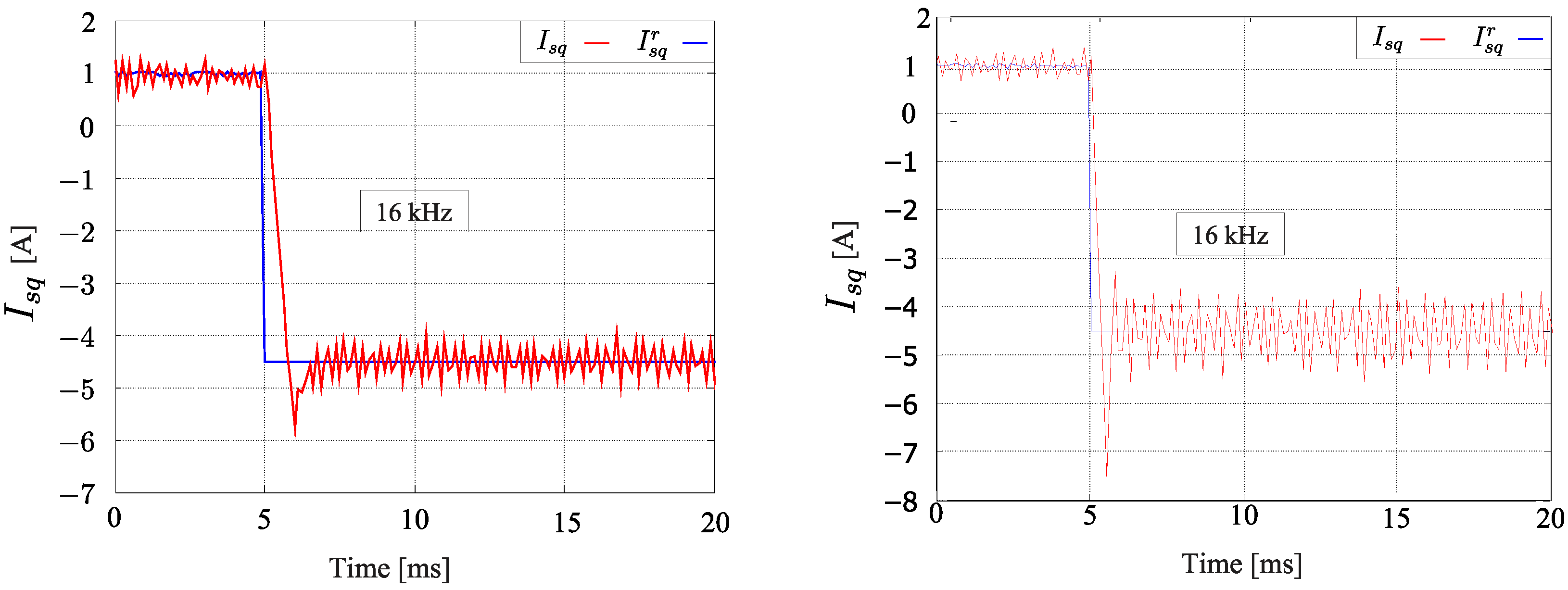
4.3. Transient Condition Results
4.4. Parameter Mismatch Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 2L-VSC | Two-level voltage course converter |
| IM | Induction motor |
| DSMC | Discrete-time sliding mode control |
| DTSMC | Discrete-time terminal sliding mode control |
| ERL | Exponential reaching law |
| FCS-MPC | Finite-control-set MPC |
| MPC | Model predictive control |
| MSE | Mean squared error |
| PI | Proportional–integral |
| PC | Personal computer |
| PRL | Power-reaching law |
| TDE | Time delay estimation |
| TSM | Terminal sliding mode |
| SMC | Sliding mode control |
References
- Gonzalez, O.; Ayala, M.; Romero, C.; Delorme, L.; Rodas, J.; Gregor, R.; Gonzalez-Prieto, I.; Durán, M.J. Model Predictive Current Control of Six-Phase Induction Motor Drives Using Virtual Vectors and Space Vector Modulation. IEEE Trans. Power Electron. 2022, 37, 7617–7628. [Google Scholar] [CrossRef]
- Salem, A.; Narimani, M. A Review on Multiphase Drives for Automotive Traction Applications. IEEE Trans. Transp. Electrif. 2019, 5, 1329–1348. [Google Scholar] [CrossRef]
- Pantea, A.; Yazidi, A.; Betin, F.; Carrière, S.; Sivert, A.; Vacossin, B.; Henao, H.; Capolino, G.A. Fault-Tolerant Control of a Low-Speed Six-Phase Induction Generator for Wind Turbines. IEEE Trans. Ind. Appl. 2019, 55, 426–436. [Google Scholar] [CrossRef]
- Levi, E. Advances in Converter Control and Innovative Exploitation of Additional Degrees of Freedom for Multiphase Machines. IEEE Trans. Ind. Electron. 2016, 63, 433–448. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Y.; Zheng, Z. A review of drive techniques for multiphase machines. CES Trans. Electr. Mach. Syst. 2018, 2, 243–251. [Google Scholar] [CrossRef]
- Rodas, J.; Gonzalez-Prieto, I.; Kali, Y.; Saad, M.; Doval-Gandoy, J. Recent Advances in Model Predictive and Sliding Mode Current Control Techniques of Multiphase Induction Machines. Front. Energy Res. 2021, 9, 729034. [Google Scholar] [CrossRef]
- Rodas, J. A Brief Survey of Model Predictive Current Control Techniques for Six-Phase Induction Machines. In Proceedings of the 2021 IEEE CHILEAN Conference on Electrical, Electronics Engineering, Information and Communication Technologies (CHILECON), Valparaiso, Chile, 6–9 December 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Gonçalves, P.; Cruz, S.; Mendes, A. Finite Control Set Model Predictive Control of Six-Phase Asymmetrical Machines—An Overview. Energies 2019, 12, 4693. [Google Scholar] [CrossRef]
- Duran, M.; Gonzalez-Prieto, I.; Gonzalez-Prieto, A.; Aciego, J.J. The Evolution of Model Predictive Control in Multiphase Electric Drives: A Growing Field of Research. IEEE Ind. Electron. Mag. 2022, 16, 29–39. [Google Scholar] [CrossRef]
- Habib, A.; Shawier, A.; Mamdouh, M.; Samy Abdel-Khalik, A.; Hamad, M.S.; Ahmed, S. Predictive current control based pseudo six-phase induction motor drive. Alex. Eng. J. 2022, 61, 3937–3948. [Google Scholar] [CrossRef]
- Kali, Y.; Ayala, M.; Rodas, J.; Saad, M.; Doval-Gandoy, J.; Gregor, R.; Benjelloun, K. Current Control of a Six-Phase Induction Machine Drive Based on Discrete-Time Sliding Mode with Time Delay Estimation. Energies 2019, 12, 170. [Google Scholar] [CrossRef]
- Kali, Y.; Saad, M.; Doval-Gandoy, J.; Rodas, J.; Benjelloun, K. Discrete sliding mode control based on exponential reaching law and time delay estimation for an asymmetrical six-phase induction machine drive. IET Electr. Power Appl. 2019, 13, 1660–1671. [Google Scholar] [CrossRef]
- Latosiński, P. Sliding mode control based on the reaching law approach—A brief survey. In Proceedings of the 2017 22nd International Conference on Methods and Models in Automation and Robotics (MMAR), Miedzyzdroje, Poland, 28–31 August 2017; pp. 519–524. [Google Scholar] [CrossRef]
- Ma, H.; Wu, J.; Xiong, Z. A Novel Exponential Reaching Law of Discrete-Time Sliding-Mode Control. IEEE Trans. Ind. Electron. 2017, 64, 3840–3850. [Google Scholar] [CrossRef]
- Ma, H.; Li, Y.; Xiong, Z. Discrete-Time Sliding-Mode Control with Enhanced Power Reaching Law. IEEE Trans. Ind. Electron. 2019, 66, 4629–4638. [Google Scholar] [CrossRef]
- Gao, W.; Wang, Y.; Homaifa, A. Discrete-time variable structure control systems. IEEE Trans. Ind. Electron. 1995, 42, 117–122. [Google Scholar] [CrossRef]
- Zheng, L.; Jiang, F.; Song, J.; Gao, Y.; Tian, M. A Discrete-Time Repetitive Sliding Mode Control for Voltage Source Inverters. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 1553–1566. [Google Scholar] [CrossRef]
- Kali, Y.; Ayala, M.; Rodas, J.; Saad, M.; Doval-Gandoy, J.; Gregor, R.; Benjelloun, K. Time Delay Estimation Based Discrete-Time Super-Twisting Current Control for a Six-Phase Induction Motor. IEEE Trans. Power Electron. 2020, 35, 12570–12580. [Google Scholar] [CrossRef]
- Kali, Y.; Saad, M.; Doval-Gandoy, J.; Rodas, J. Discrete Terminal Super-Twisting Current Control of a Six-Phase Induction Motor. Energies 2021, 14, 1339. [Google Scholar] [CrossRef]
- Du, H.; Chen, X.; Wen, G.; Yu, X.; Lü, J. Discrete-Time Fast Terminal Sliding Mode Control for Permanent Magnet Linear Motor. IEEE Trans. Ind. Electron. 2018, 65, 9916–9927. [Google Scholar] [CrossRef]
- Xiong, X.; Chu, Y.; Udai, A.D.; Kamal, S.; Jin, S.; Lou, Y. Implicit Discrete-Time Terminal Sliding Mode Control for Second-Order Systems. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 2508–2512. [Google Scholar] [CrossRef]
- Wang, Y.; Jiang, S.; Chen, B.; Wu, H. Trajectory Tracking Control of Underwater Vehicle-Manipulator System Using Discrete Time Delay Estimation. IEEE Access 2017, 5, 7435–7443. [Google Scholar] [CrossRef]
- Levi, E. Power Electronics and Motor Drives, Chapter: FOC: Field Oriented Control, United States. In The Industrial Electronics Handbook, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Kali, Y.; Saad, M.; Benjelloun, K.; Fatemi, A. Discrete-time second order sliding mode with time delay control for uncertain robot manipulators. Robot. Auton. Syst. 2017, 94, 53–60. [Google Scholar] [CrossRef]
- Delorme, L.; Ayala, M.; Rodas, J.; Gregor, R.; Gonzalez, O.; Doval-Gandoy, J. Comparison of the Effects on Stator Currents Between Continuous Model and Discrete Model of the Three-phase Induction Motor in the Presence of Electrical Parameter Variations. In Proceedings of the 2020 IEEE International Conference on Industrial Technology (ICIT), Buenos Aires, Argentina, 26–28 February 2020; pp. 151–156. [Google Scholar] [CrossRef]
- Bermudez, M.; Arahal, M.R.; Duran, M.J.; Gonzalez-Prieto, I. Model predictive control of six-phase electric drives including ARX disturbance estimator. IEEE Trans. Ind. Electron. 2020, 68, 81–91. [Google Scholar] [CrossRef]




| Description | Characteristics |
|---|---|
| Current sensor | LA 55-P, frequency bandwidth from 0 to 200 kHz |
| A/D converter | 16-bit |
| Speed sensor | 1024 ppr incremental encoder |
| Variable load | 5 HP eddy current brake |
| Six-phase IM | 2 kW |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Rotor resistance | Inertia coefficient | kg·m | |
| Leakage stator inductance | mH | Friction coefficient | kg·m |
| Mutual inductance | mH | DC-link voltage | V |
| Rotor inductance | mH | Pole pairs |
| Sampling | Frequency | 16 kHz | ||||
|---|---|---|---|---|---|---|
| MSE | MSE | MSE | MSE | MSE | MSE | |
| 1000 rpm | 0.1595 | 0.1639 | 0.2706 | 0.2808 | 0.1609 | 0.1625 |
| 1500 rpm | 0.1796 | 0.1827 | 0.2789 | 0.2991 | 0.1741 | 0.1880 |
| Sampling | Frequency | 16 kHz | ||||
|---|---|---|---|---|---|---|
| MSE | MSE | MSE | MSE | MSE | MSE | |
| 1000 rpm | 0.1860 | 0.1808 | 0.2032 | 0.2026 | 0.1766 | 0.1860 |
| 1500 rpm | 0.1655 | 0.1716 | 0.1969 | 0.1999 | 0.1708 | 0.1664 |
| Sampling | Frequency | 16 kHz | ||||
|---|---|---|---|---|---|---|
| MSE | MSE | MSE | MSE | MSE | MSE | |
| 1000 | 0.1703 | 0.1696 | 0.2937 | 0.3130 | 0.1669 | 0.1729 |
| 1500 | 0.1855 | 0.1894 | 0.2742 | 0.3005 | 0.1797 | 0.1950 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kali, Y.; Rodas, J.; Doval-Gandoy, J.; Ayala, M.; Gonzalez, O. Enhanced Reaching-Law-Based Discrete-Time Terminal Sliding Mode Current Control of a Six-Phase Induction Motor. Machines 2023, 11, 107. https://doi.org/10.3390/machines11010107
Kali Y, Rodas J, Doval-Gandoy J, Ayala M, Gonzalez O. Enhanced Reaching-Law-Based Discrete-Time Terminal Sliding Mode Current Control of a Six-Phase Induction Motor. Machines. 2023; 11(1):107. https://doi.org/10.3390/machines11010107
Chicago/Turabian StyleKali, Yassine, Jorge Rodas, Jesus Doval-Gandoy, Magno Ayala, and Osvaldo Gonzalez. 2023. "Enhanced Reaching-Law-Based Discrete-Time Terminal Sliding Mode Current Control of a Six-Phase Induction Motor" Machines 11, no. 1: 107. https://doi.org/10.3390/machines11010107
APA StyleKali, Y., Rodas, J., Doval-Gandoy, J., Ayala, M., & Gonzalez, O. (2023). Enhanced Reaching-Law-Based Discrete-Time Terminal Sliding Mode Current Control of a Six-Phase Induction Motor. Machines, 11(1), 107. https://doi.org/10.3390/machines11010107










