Author Contributions
Conceptualization, X.Z. and S.Y.; methodology, S.Y.; software, S.Y.; validation, S.Y., M.X. and Y.Z.; formal analysis, S.H.; investigation, S.Y.; resources, X.Z.; data curation, Y.Z.; writing—original draft preparation, S.Y.; writing—review and editing, T.G.; visualization, S.Y.; supervision, J.Z.; project administration, M.X.; funding acquisition, X.Z. All authors have read and agreed to the published version of the manuscript.
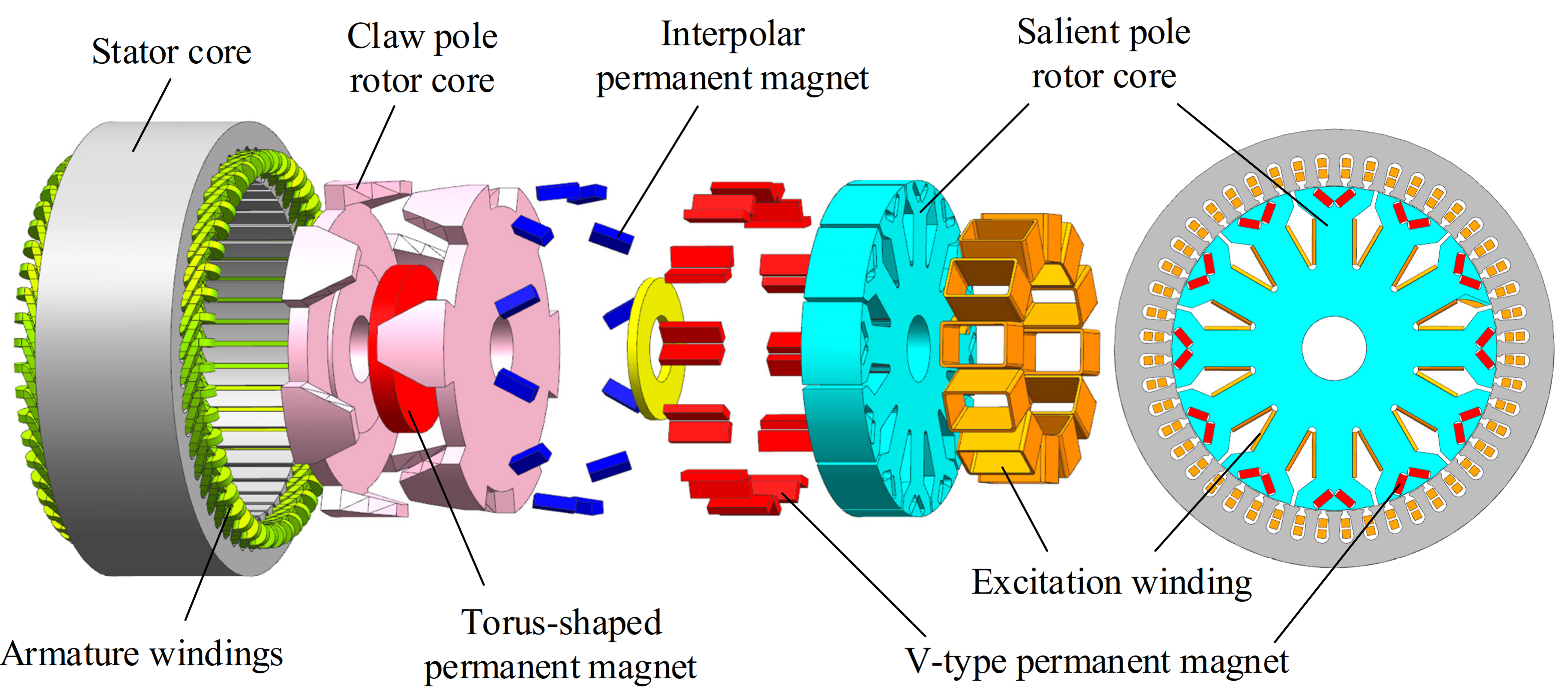
Figure 1.
The structure of the new compound excitation generator.
Figure 1.
The structure of the new compound excitation generator.
Figure 2.
Air-gap flux density of different built-in permanent magnet salient pole rotors.
Figure 2.
Air-gap flux density of different built-in permanent magnet salient pole rotors.
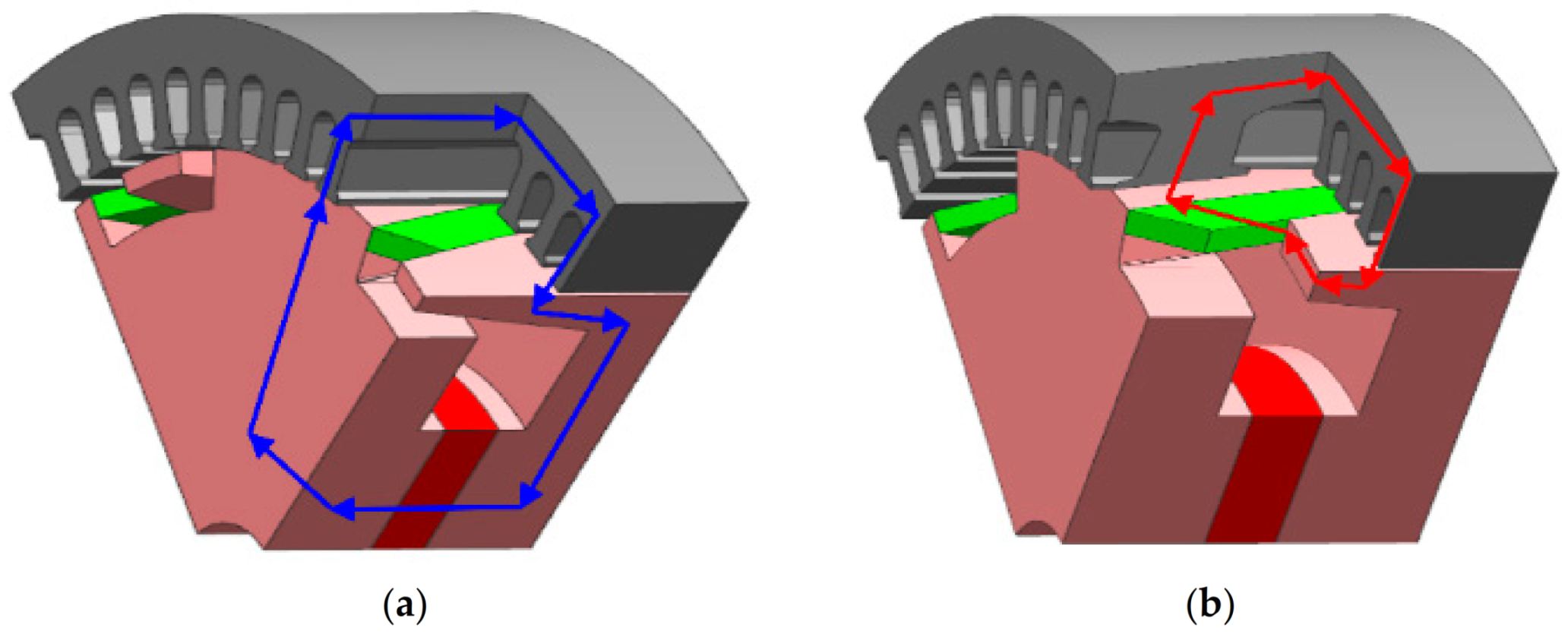
Figure 3.
Schematic diagram of the main magnetic circuit of claw pole generator. (a) The first main magnetic circuit; (b) the second main magnetic circuit.
Figure 3.
Schematic diagram of the main magnetic circuit of claw pole generator. (a) The first main magnetic circuit; (b) the second main magnetic circuit.
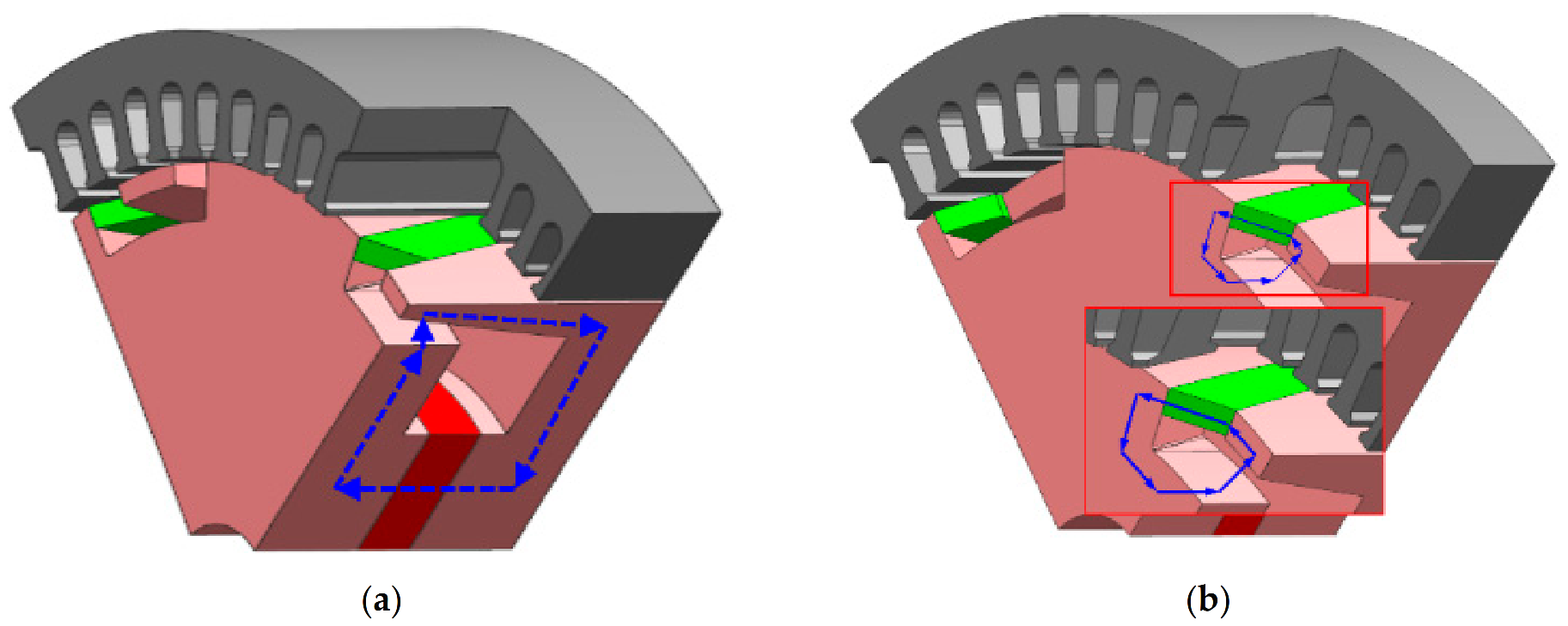
Figure 4.
Schematic diagram of the leakage flux path of claw pole generator. (a) The first main magnetic circuit; (b) the second main magnetic circuit.
Figure 4.
Schematic diagram of the leakage flux path of claw pole generator. (a) The first main magnetic circuit; (b) the second main magnetic circuit.
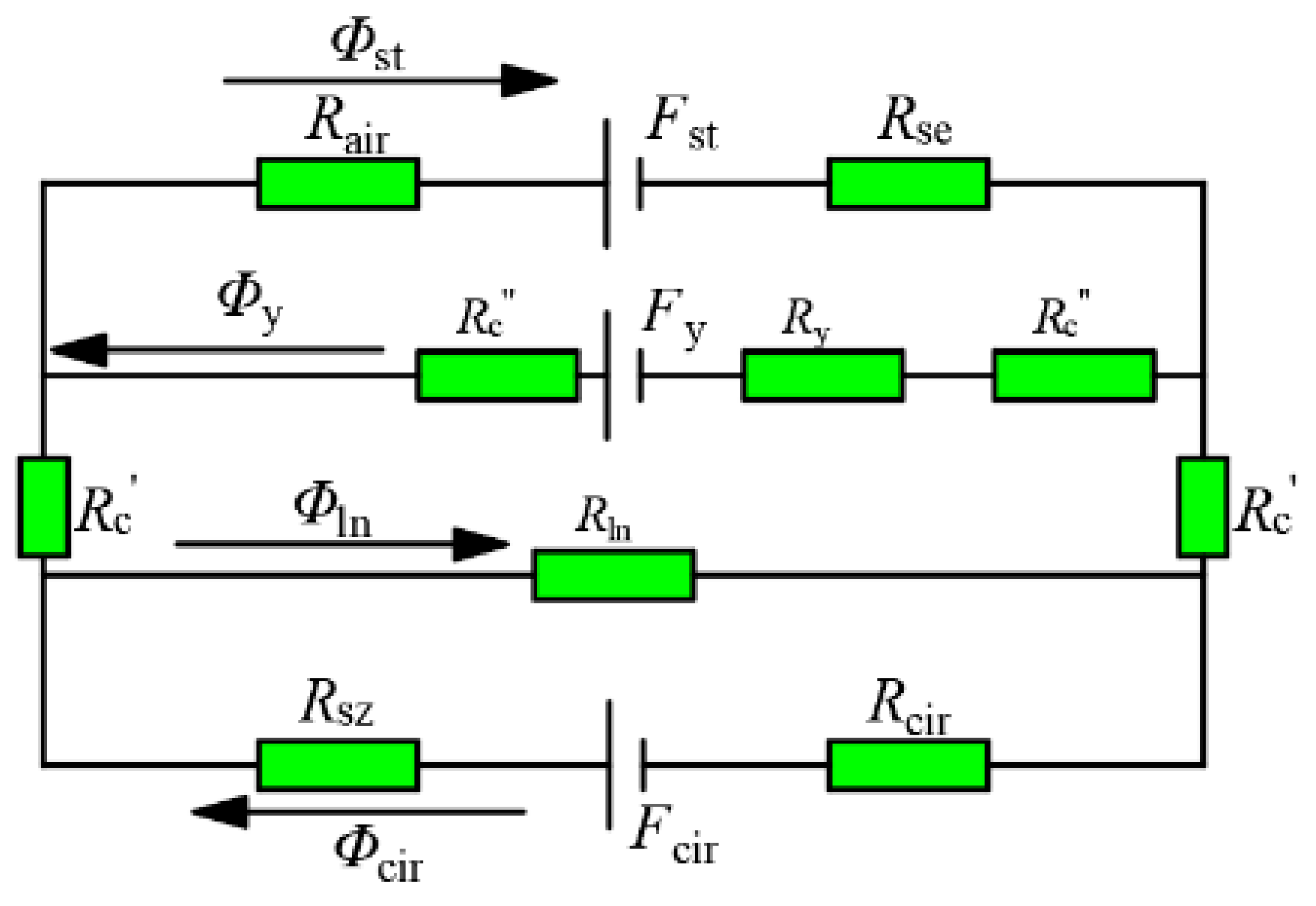
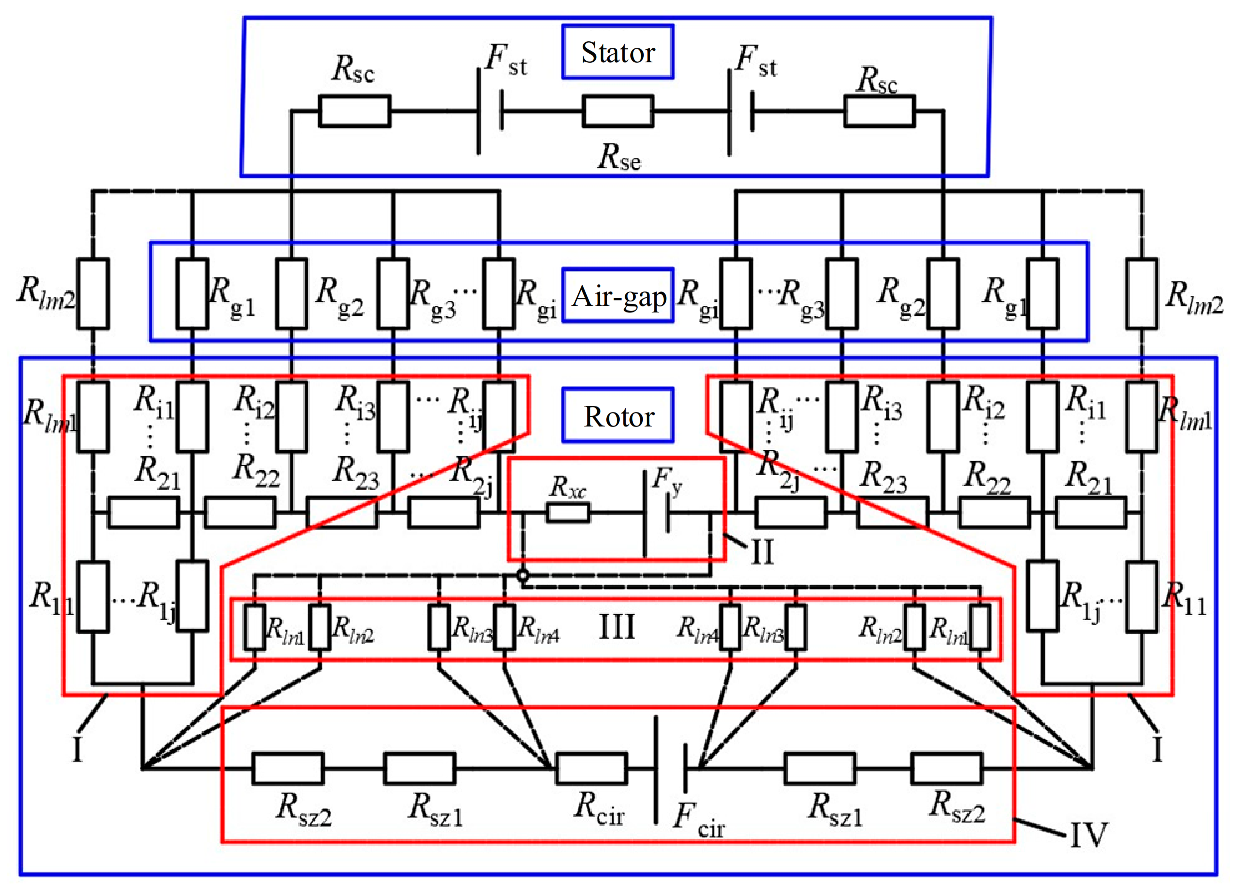
Figure 5.
Equivalent magnetic circuit diagram of claw pole generator with inter-pole PM.
Figure 5.
Equivalent magnetic circuit diagram of claw pole generator with inter-pole PM.
Figure 6.
Improved equivalent magnetic network model.
Figure 6.
Improved equivalent magnetic network model.
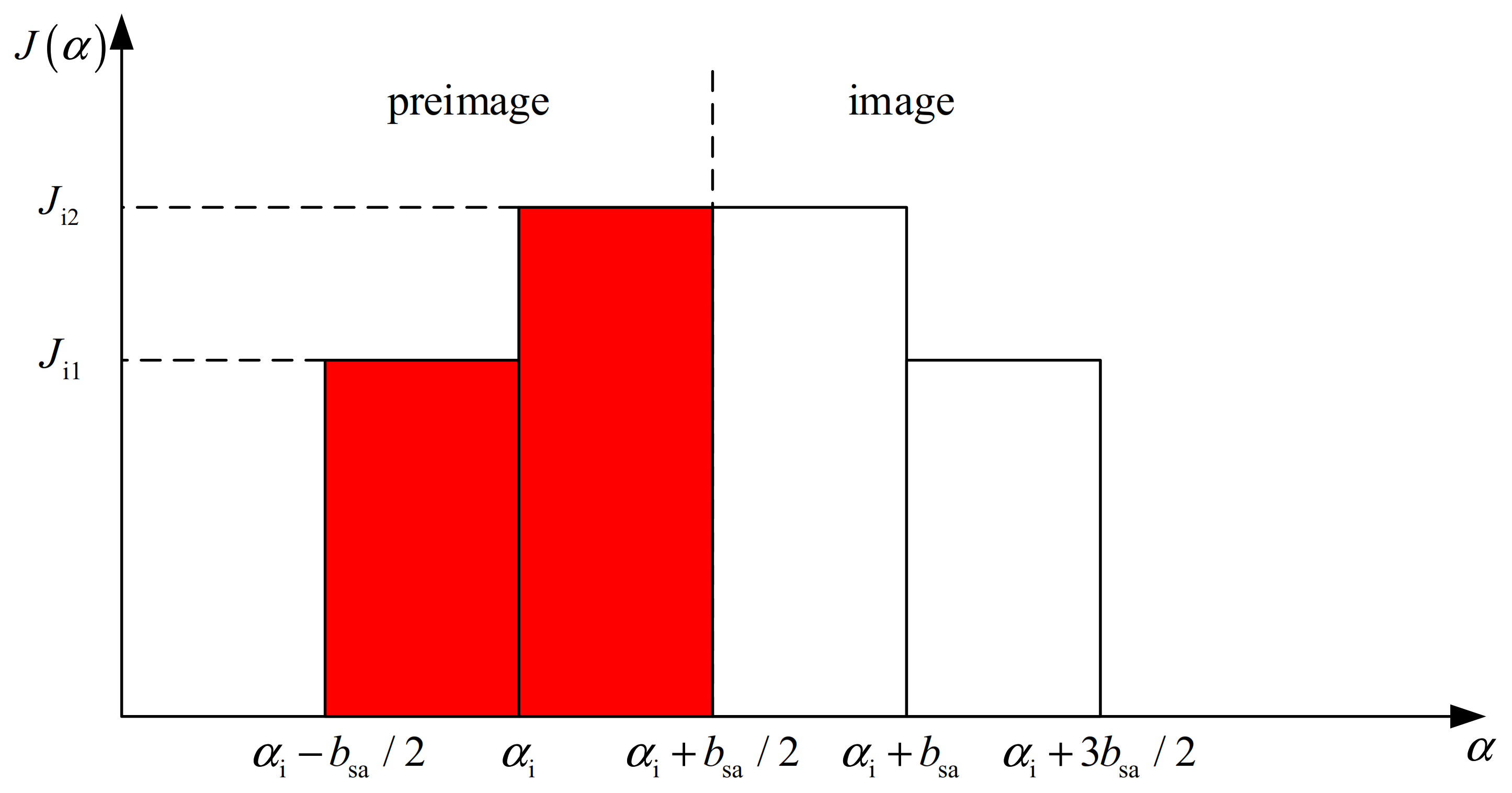
Figure 7.
The subdivision unit.
Figure 7.
The subdivision unit.
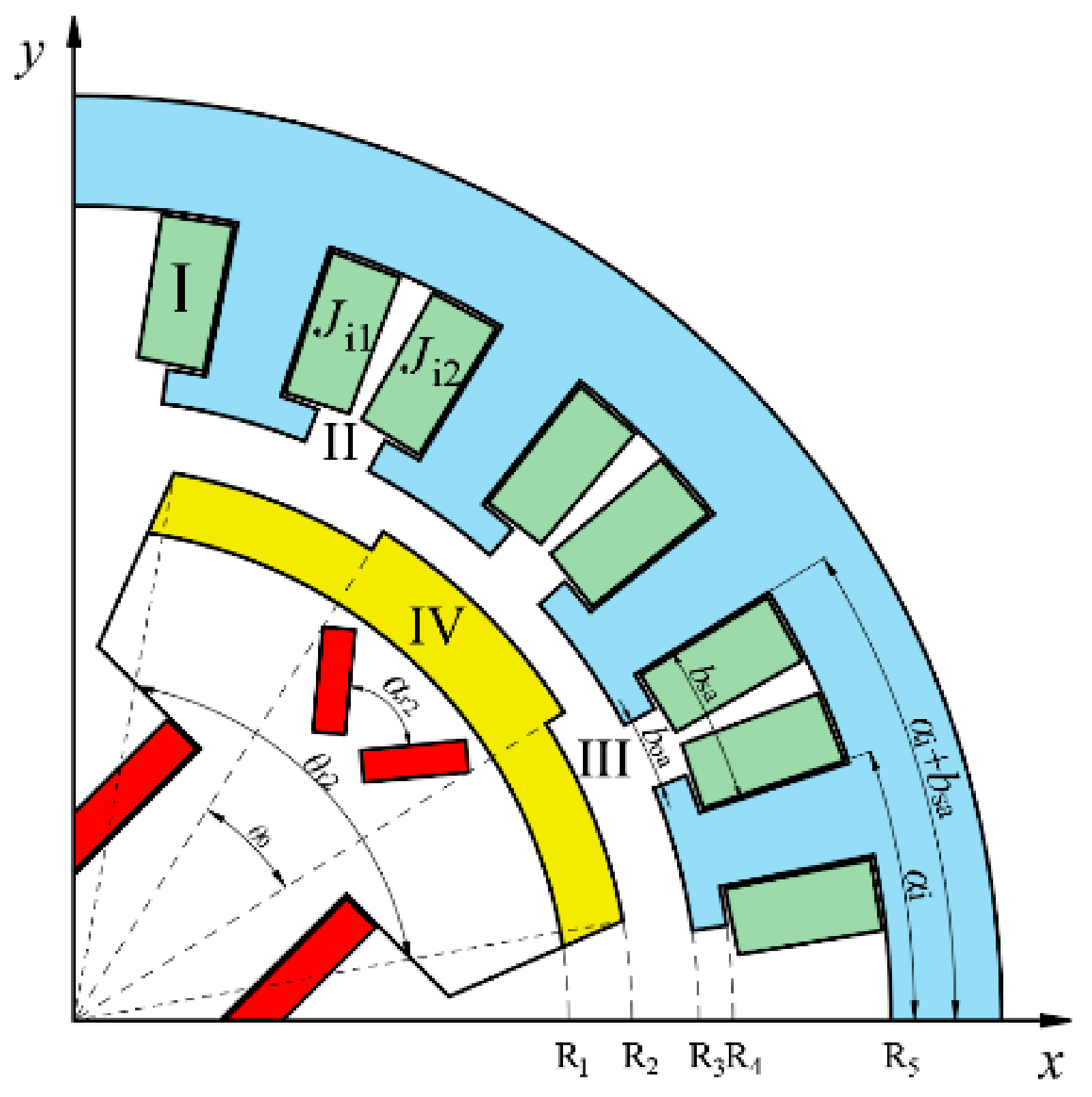
Figure 8.
Schematic diagram of the regional division of the salient-pole generator.
Figure 8.
Schematic diagram of the regional division of the salient-pole generator.
Figure 9.
Stator slot current density distribution.
Figure 9.
Stator slot current density distribution.
Figure 10.
Schematic diagram of Latin hypercube sampling.
Figure 10.
Schematic diagram of Latin hypercube sampling.
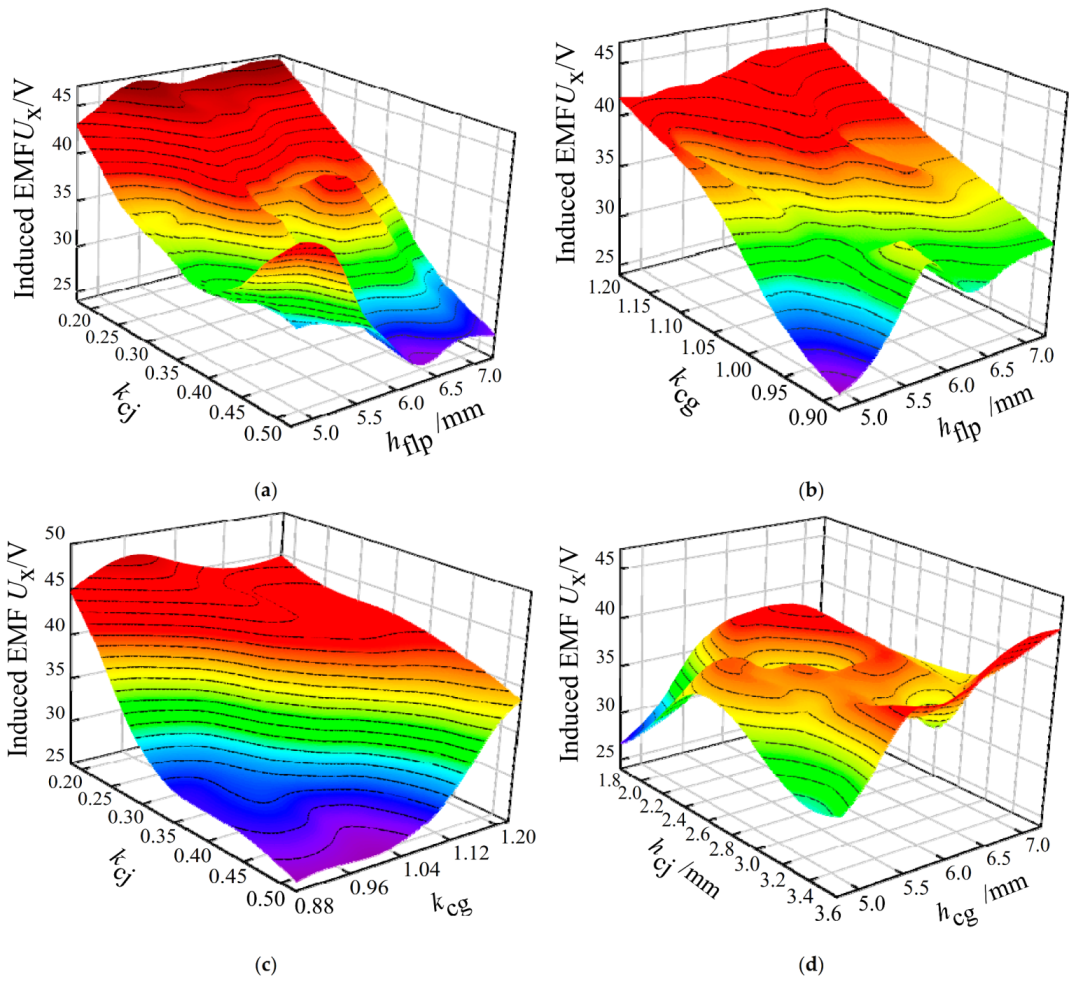
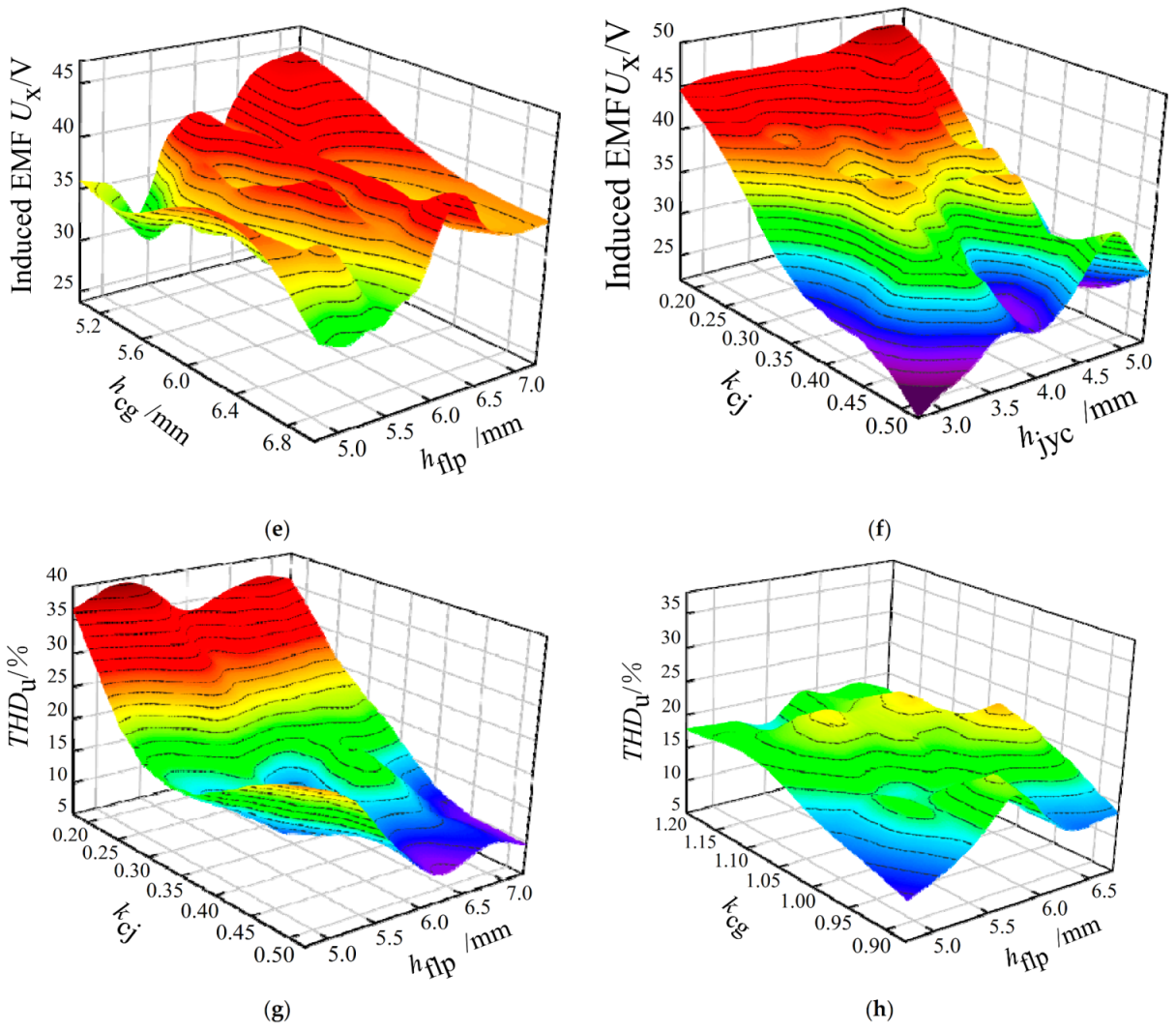
Figure 11.
Design variable and response value fitting diagram (partial). (a) kcj, hflp, and Ux; (b) kcg, hflp, and Ux; (c) kcj, kcg, and Ux; (d) hcj, hcg, and Ux; (e) hcg, hflp, and Ux; (f) kcj, hjyc, and Ux; (g) kcj, hflg, and THDu; (h) kcg, hflp, and THDu.
Figure 11.
Design variable and response value fitting diagram (partial). (a) kcj, hflp, and Ux; (b) kcg, hflp, and Ux; (c) kcj, kcg, and Ux; (d) hcj, hcg, and Ux; (e) hcg, hflp, and Ux; (f) kcj, hjyc, and Ux; (g) kcj, hflg, and THDu; (h) kcg, hflp, and THDu.
Figure 12.
The sensitivity of optimization objective. (a) Sensitivity of each design variable to Ux; (b) sensitivity of each design variable to THDu.
Figure 12.
The sensitivity of optimization objective. (a) Sensitivity of each design variable to Ux; (b) sensitivity of each design variable to THDu.
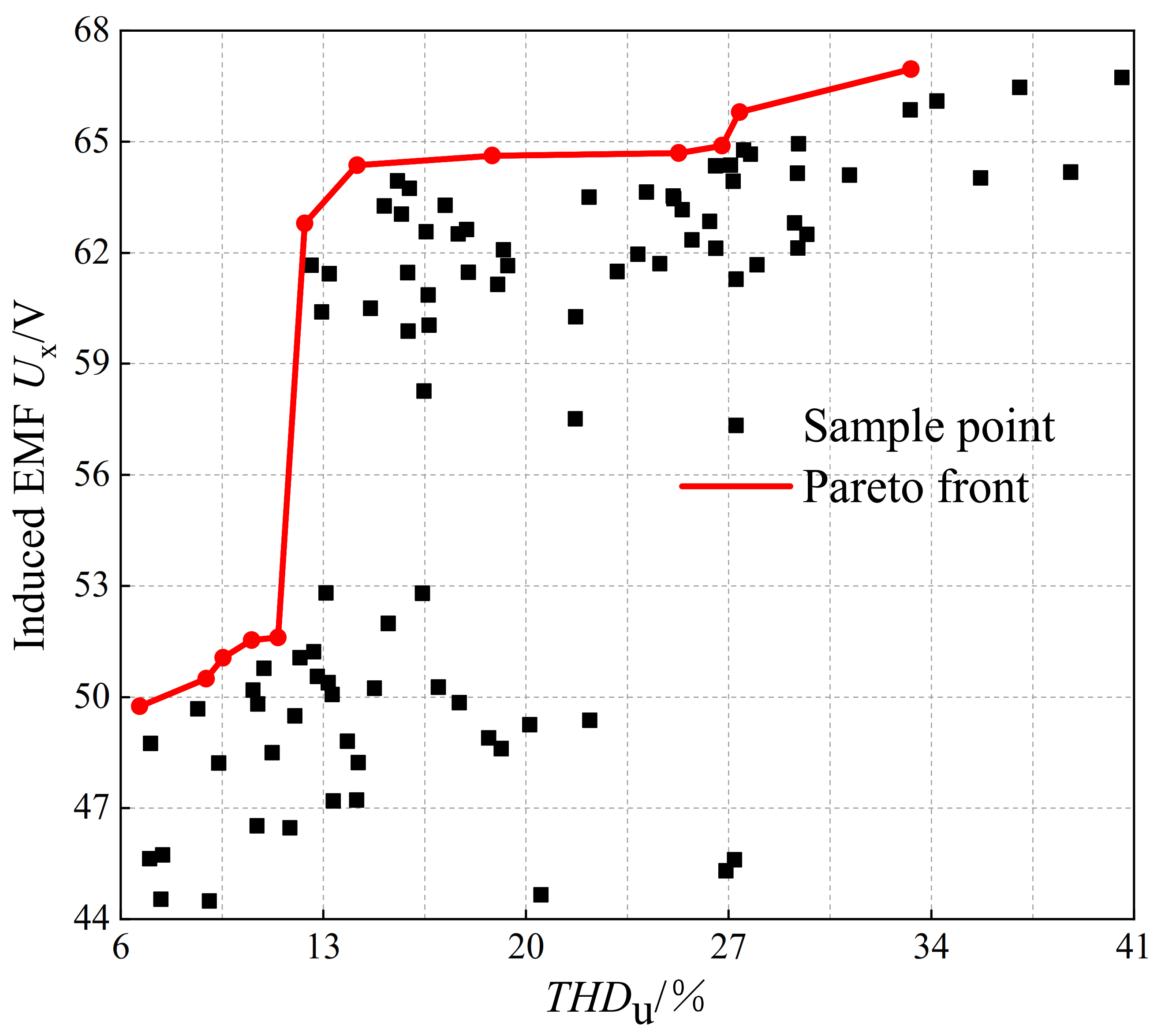
Figure 13.
Pareto frontier distribution map.
Figure 13.
Pareto frontier distribution map.
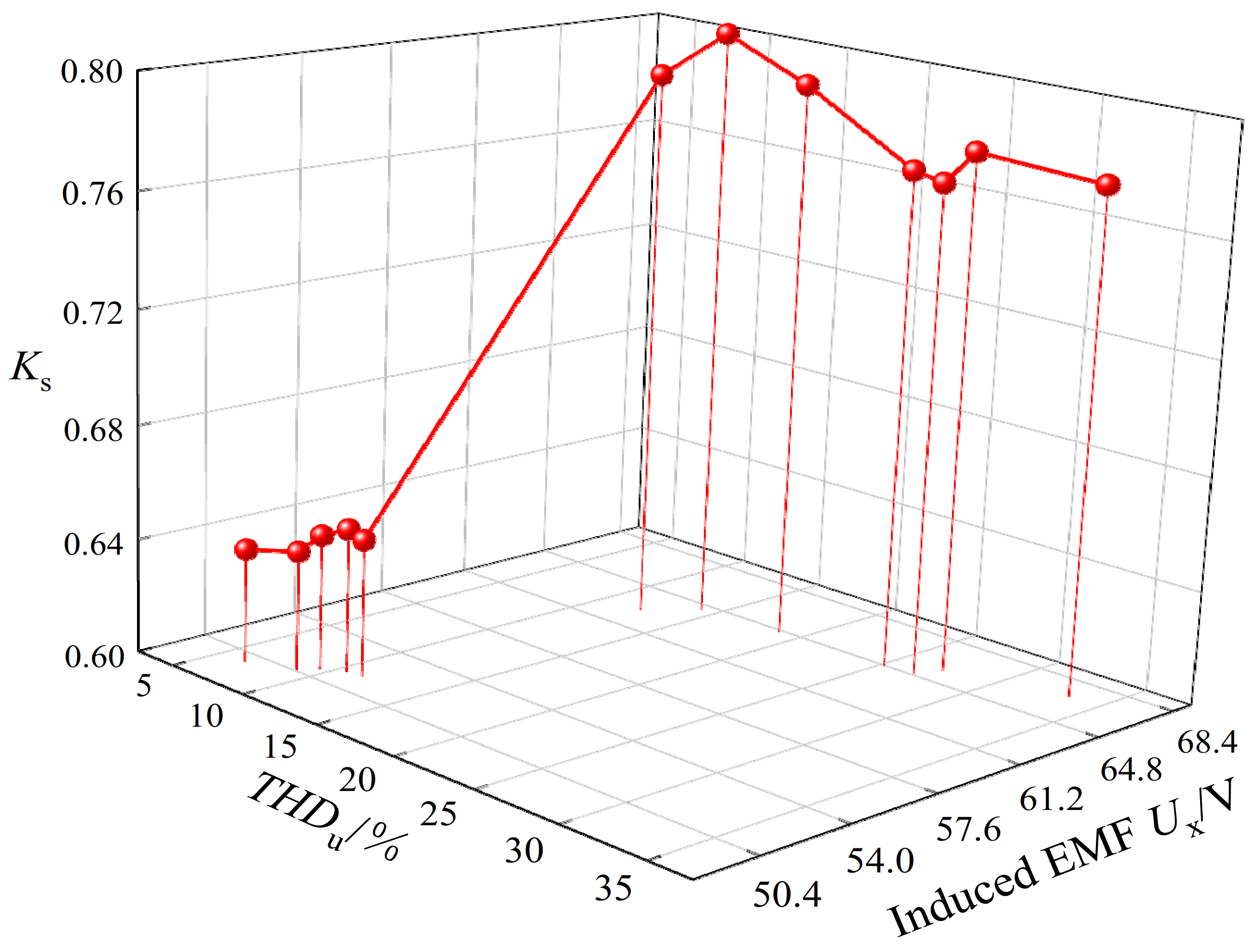
Figure 14.
Relationship between two optimization goals and matching coefficients.
Figure 14.
Relationship between two optimization goals and matching coefficients.
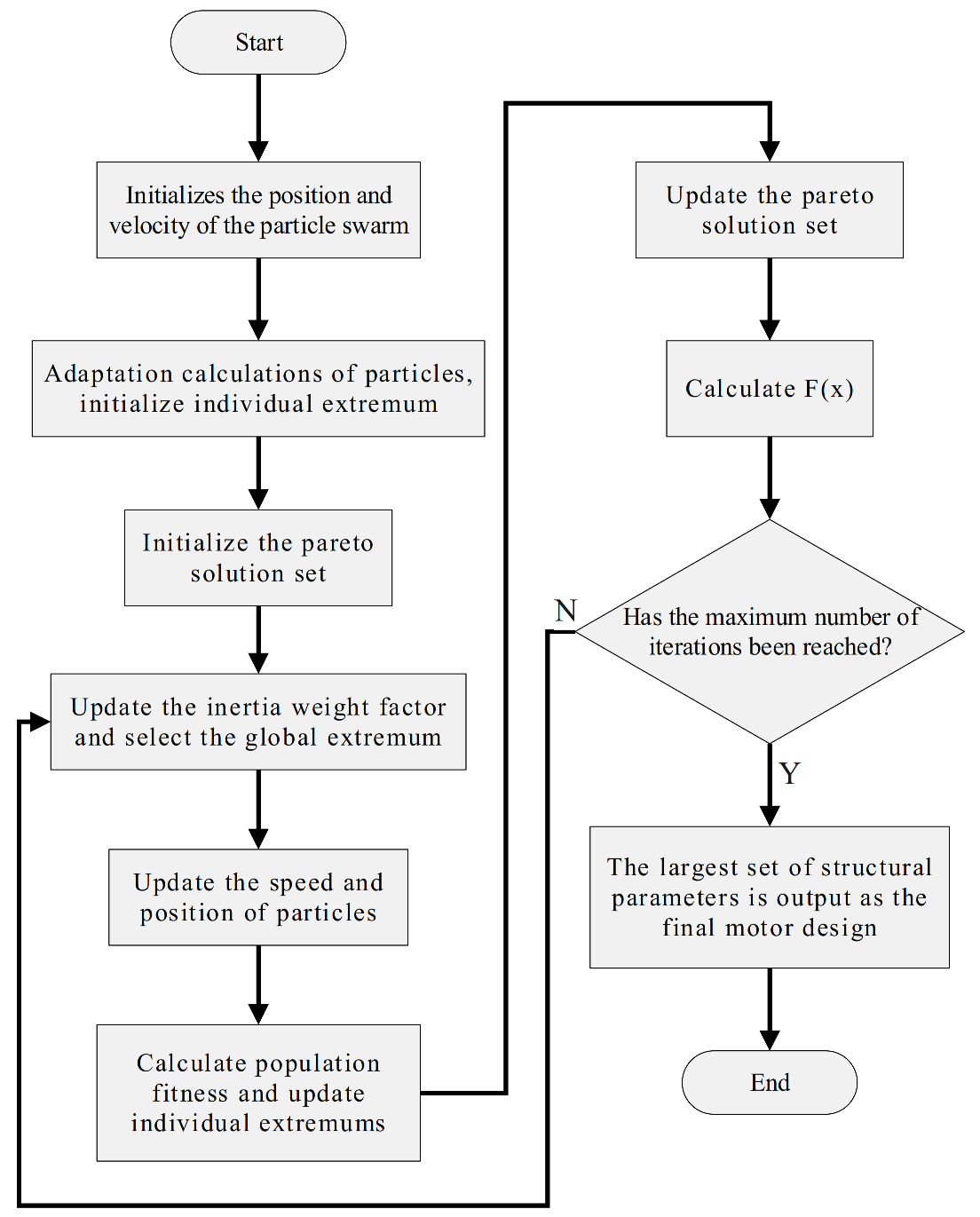
Figure 15.
Flow block diagram of the particle swarm optimization algorithm.
Figure 15.
Flow block diagram of the particle swarm optimization algorithm.
Figure 16.
Diagram of the relationship between evolutionary algebra and optimal individual values.
Figure 16.
Diagram of the relationship between evolutionary algebra and optimal individual values.
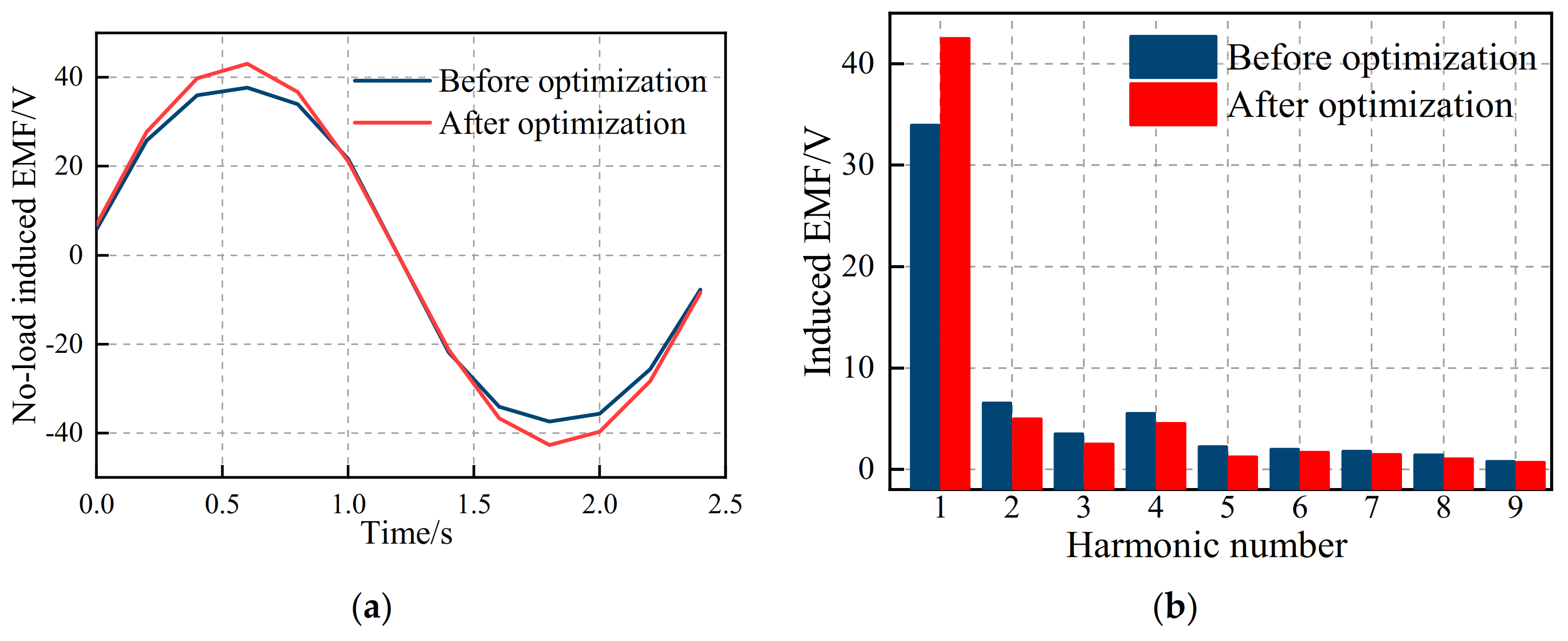
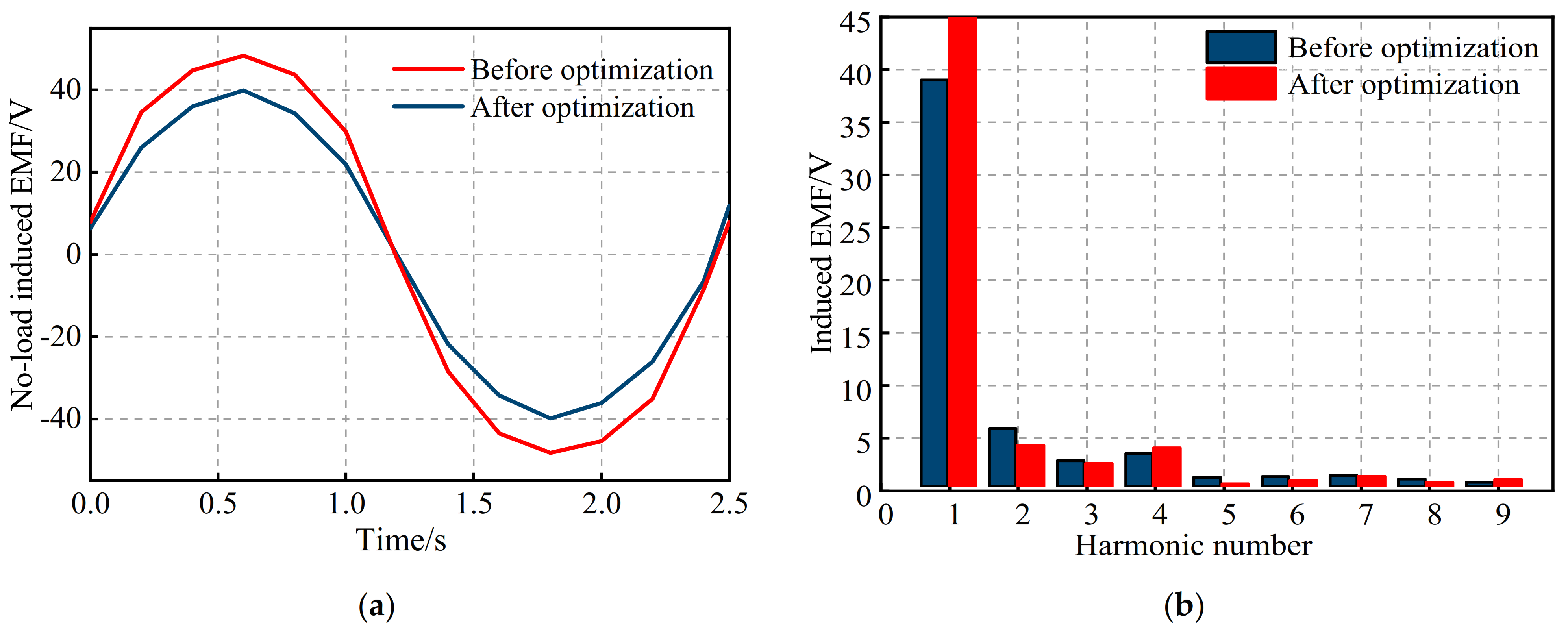
Figure 17.
Comparison of the no-load induced EMF of claw pole rotor before and after optimization. (a) Comparison of the no-load induced EMF curves; (b) comparison of the no-load induced EMF harmonic distribution.
Figure 17.
Comparison of the no-load induced EMF of claw pole rotor before and after optimization. (a) Comparison of the no-load induced EMF curves; (b) comparison of the no-load induced EMF harmonic distribution.
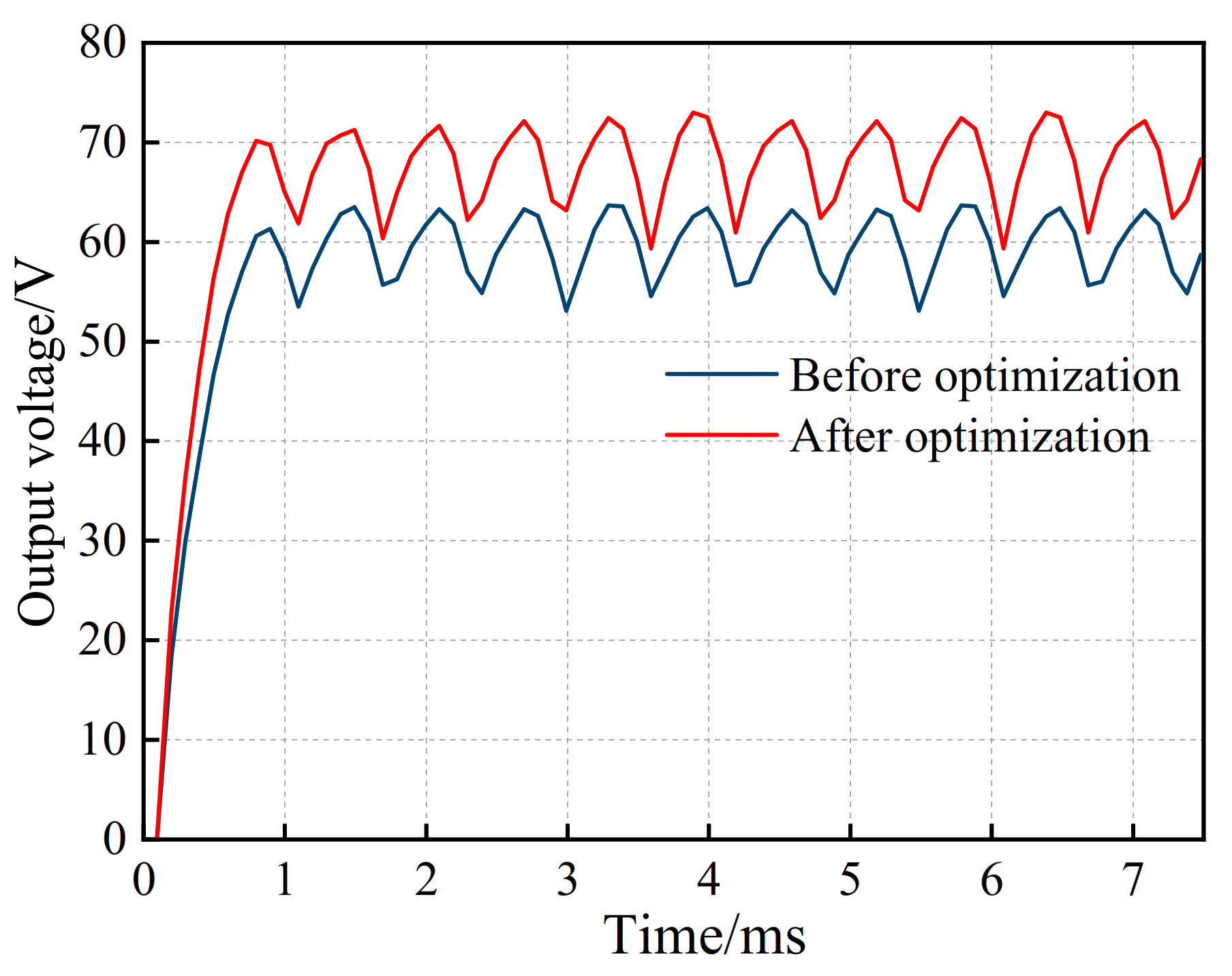
Figure 18.
Comparison of the output voltage of the claw pole rotor before and after optimization.
Figure 18.
Comparison of the output voltage of the claw pole rotor before and after optimization.
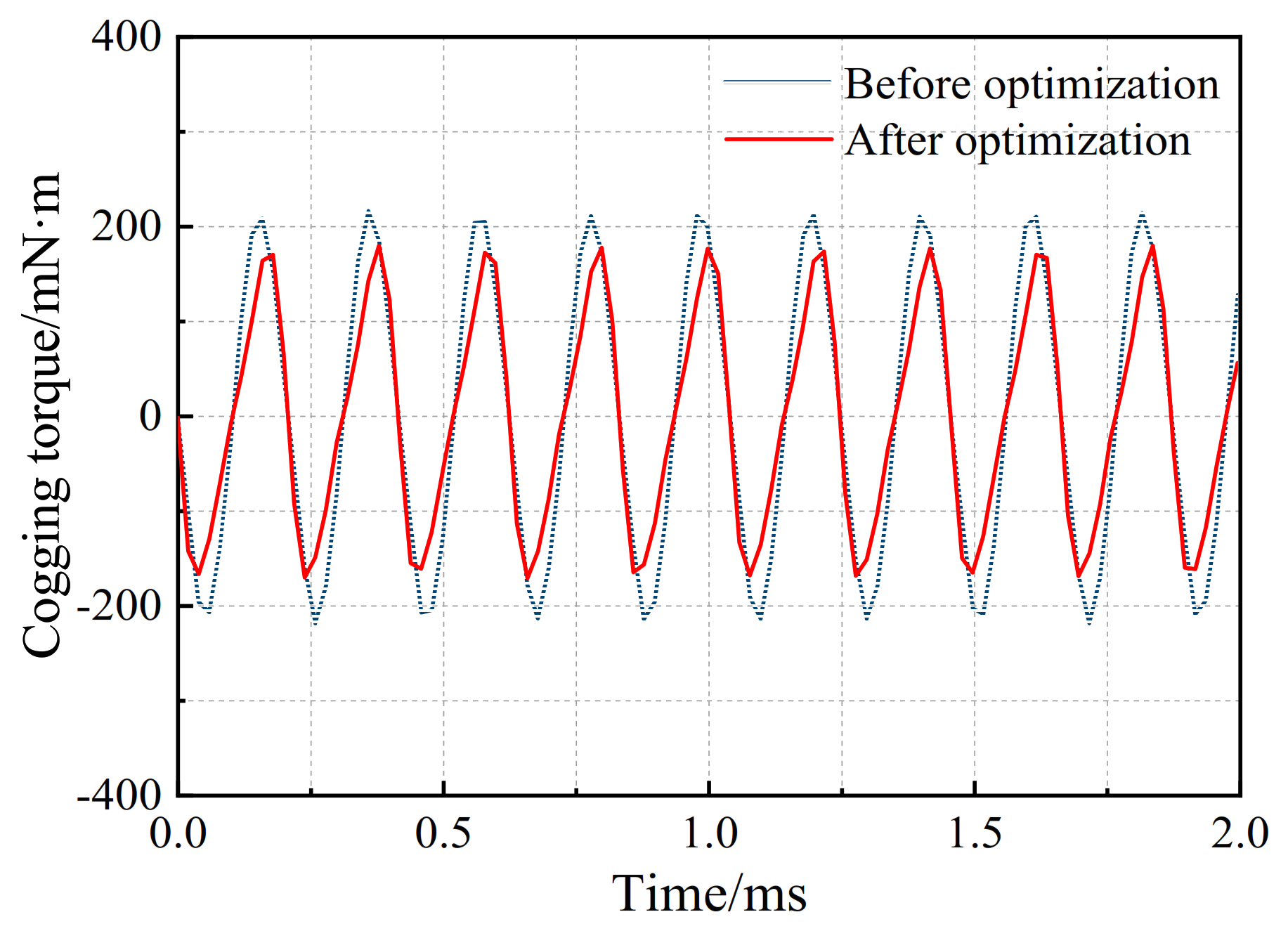
Figure 19.
Comparison of cogging torque of claw pole rotor before and after optimization.
Figure 19.
Comparison of cogging torque of claw pole rotor before and after optimization.
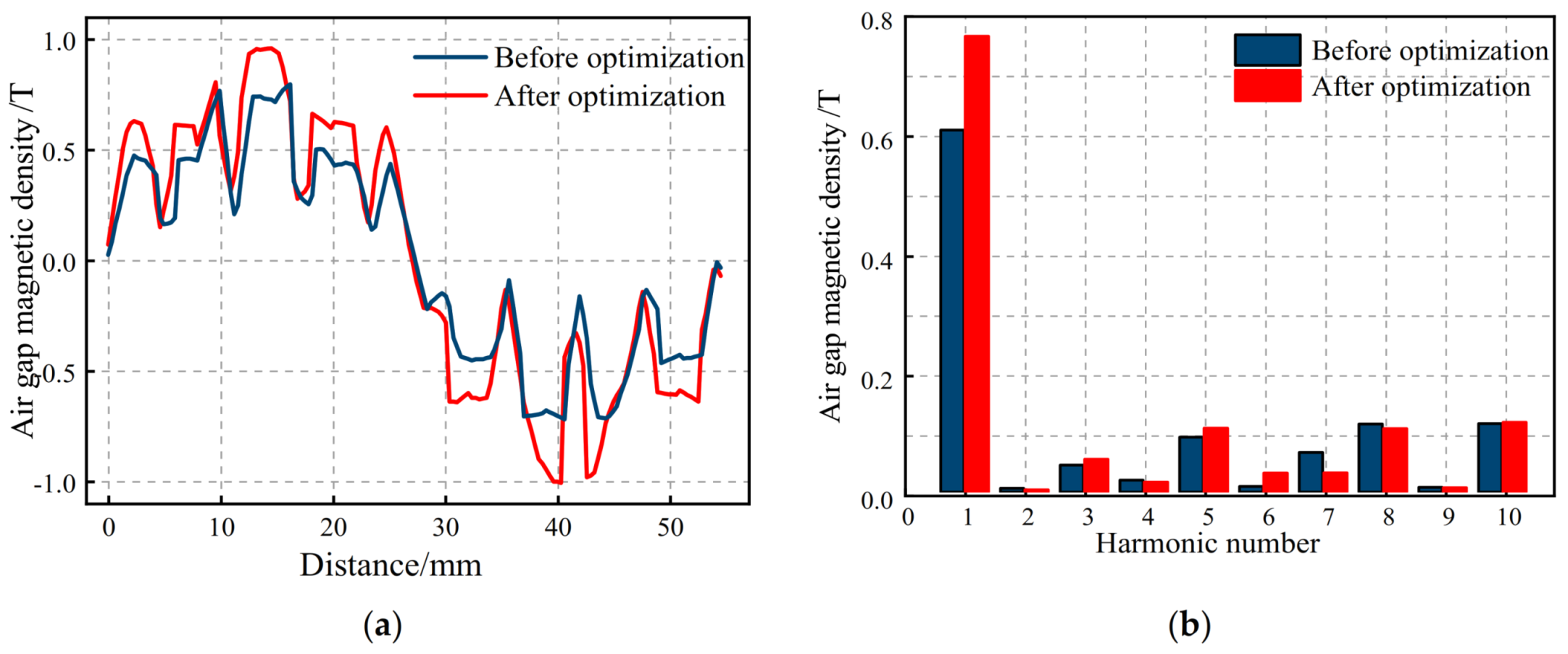
Figure 20.
Comparison of the air gap magnetic flux density of the salient-pole rotor before and after optimization. (a) Comparison of the air gap magnetic flux density curves; (b) comparison of the air gap magnetic flux density harmonic distribution.
Figure 20.
Comparison of the air gap magnetic flux density of the salient-pole rotor before and after optimization. (a) Comparison of the air gap magnetic flux density curves; (b) comparison of the air gap magnetic flux density harmonic distribution.
Figure 21.
Comparison of induced EMF of the generator before and after optimization. (a) Comparison of induced EMF curves; (b) comparison of induced EMF harmonic distribution.
Figure 21.
Comparison of induced EMF of the generator before and after optimization. (a) Comparison of induced EMF curves; (b) comparison of induced EMF harmonic distribution.
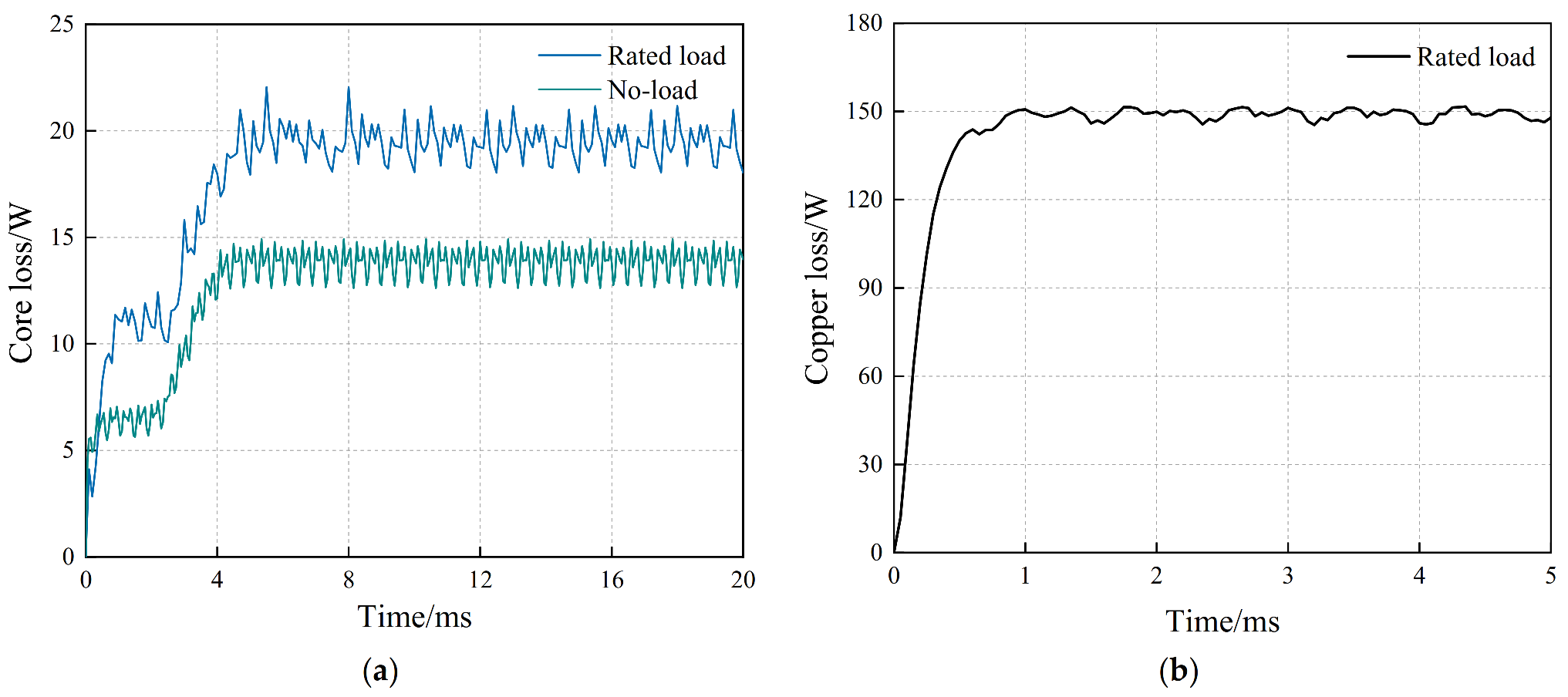
Figure 22.
Loss of the hybrid excitation generator. (a) Core loss of the generator; (b) copper loss of the generator.
Figure 22.
Loss of the hybrid excitation generator. (a) Core loss of the generator; (b) copper loss of the generator.
Figure 23.
Compound excitation generator prototype. (a) Salient-pole rotor core; (b) PM claw pole rotor core; (c) stator; (d) generator.
Figure 23.
Compound excitation generator prototype. (a) Salient-pole rotor core; (b) PM claw pole rotor core; (c) stator; (d) generator.
Figure 24.
Compound excitation generator prototype experimental platform.
Figure 24.
Compound excitation generator prototype experimental platform.
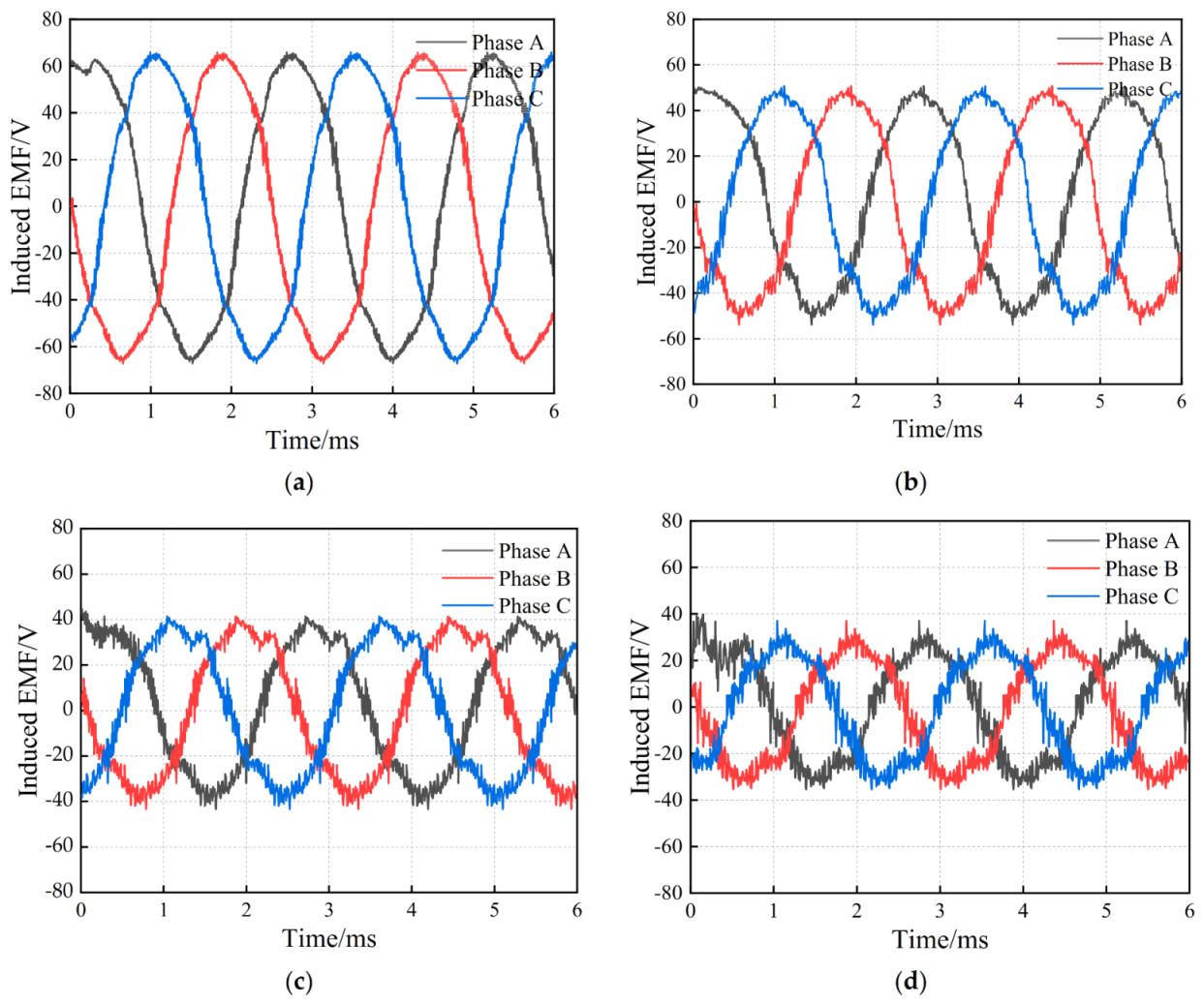
Figure 25.
Induced EMF of the compound excitation generator prototype under different loads. (a) Load 10 Ω; (b) Load 5 Ω; (c) Load 3 Ω; (d) Load 1.5 Ω.
Figure 25.
Induced EMF of the compound excitation generator prototype under different loads. (a) Load 10 Ω; (b) Load 5 Ω; (c) Load 3 Ω; (d) Load 1.5 Ω.
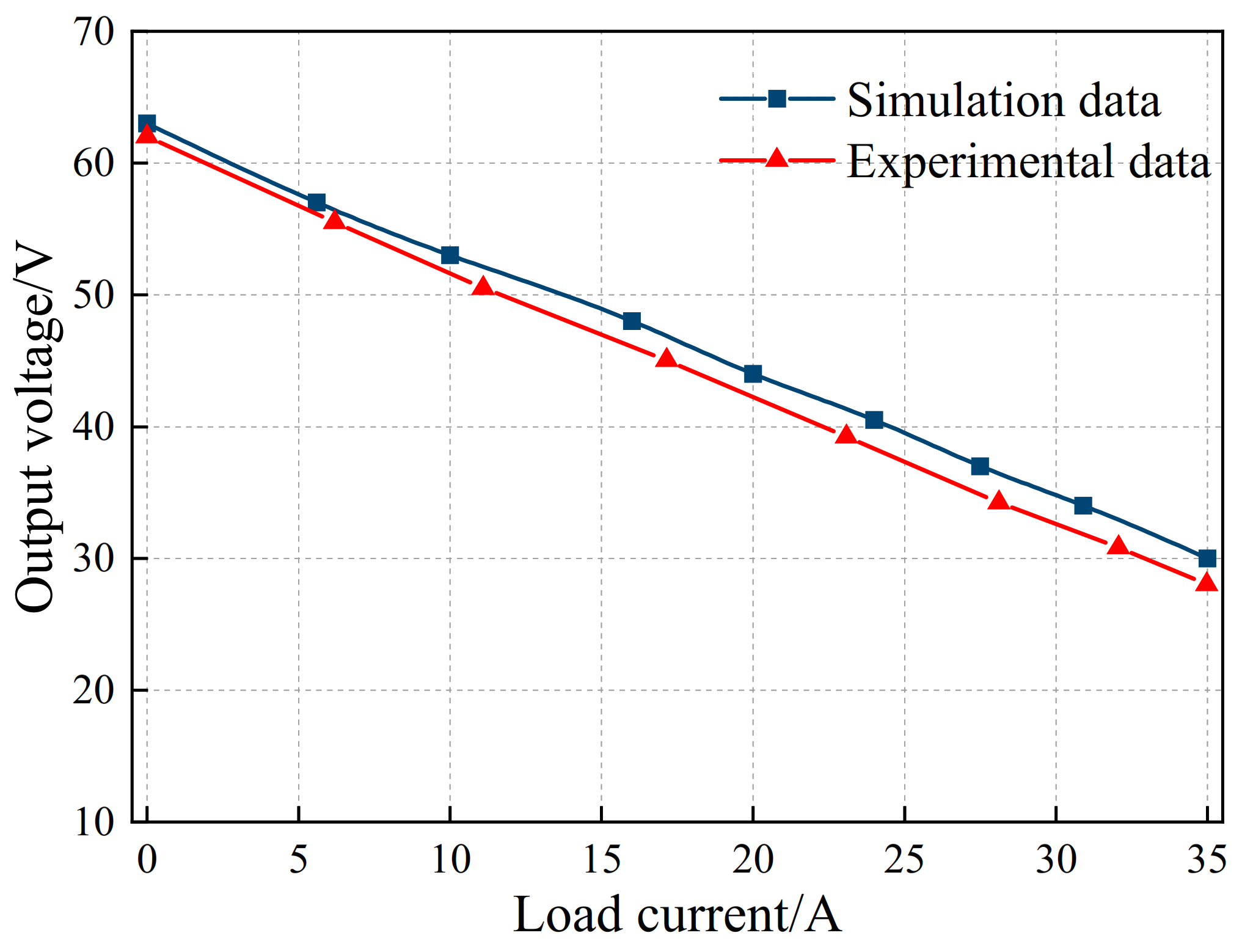
Figure 26.
Compound excitation generator external characteristic curve.
Figure 26.
Compound excitation generator external characteristic curve.
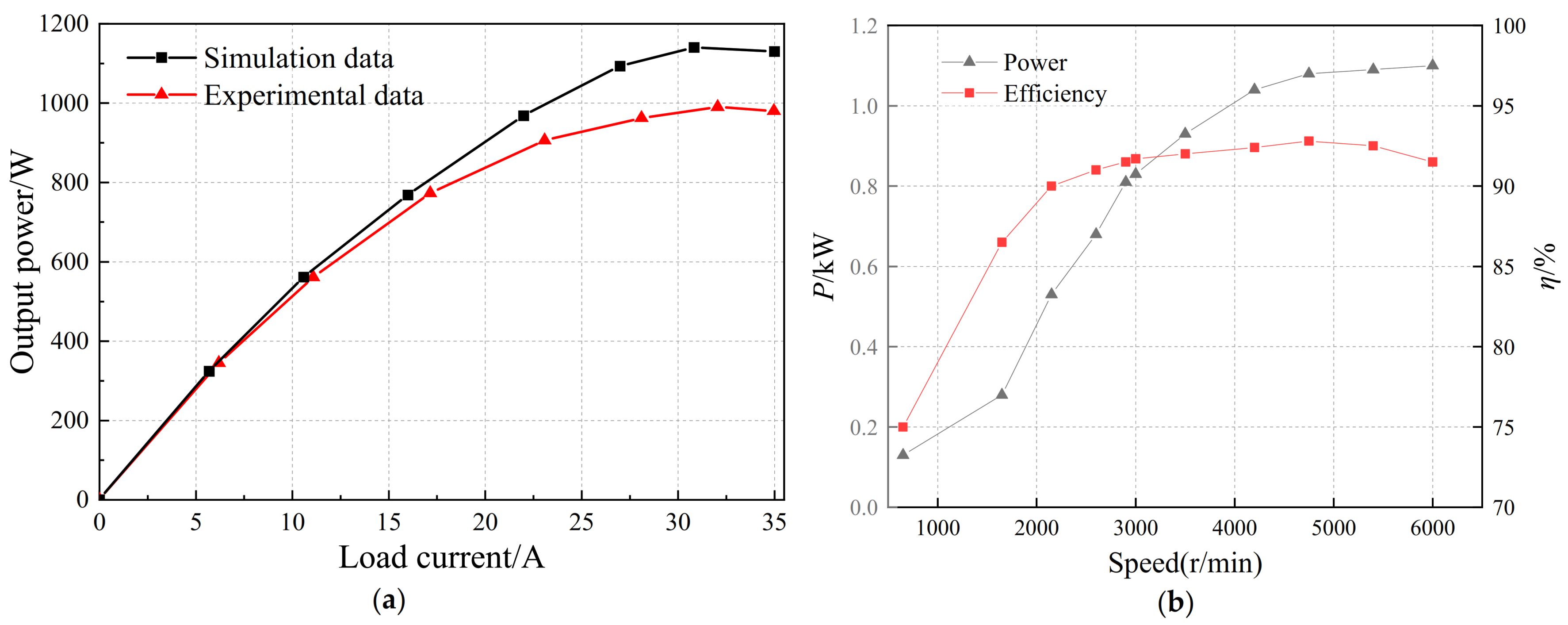
Figure 27.
Generator output power and efficiency change curve. (a) The output power varies with the load current; (b) curve of power and efficiency with generator speed.
Figure 27.
Generator output power and efficiency change curve. (a) The output power varies with the load current; (b) curve of power and efficiency with generator speed.
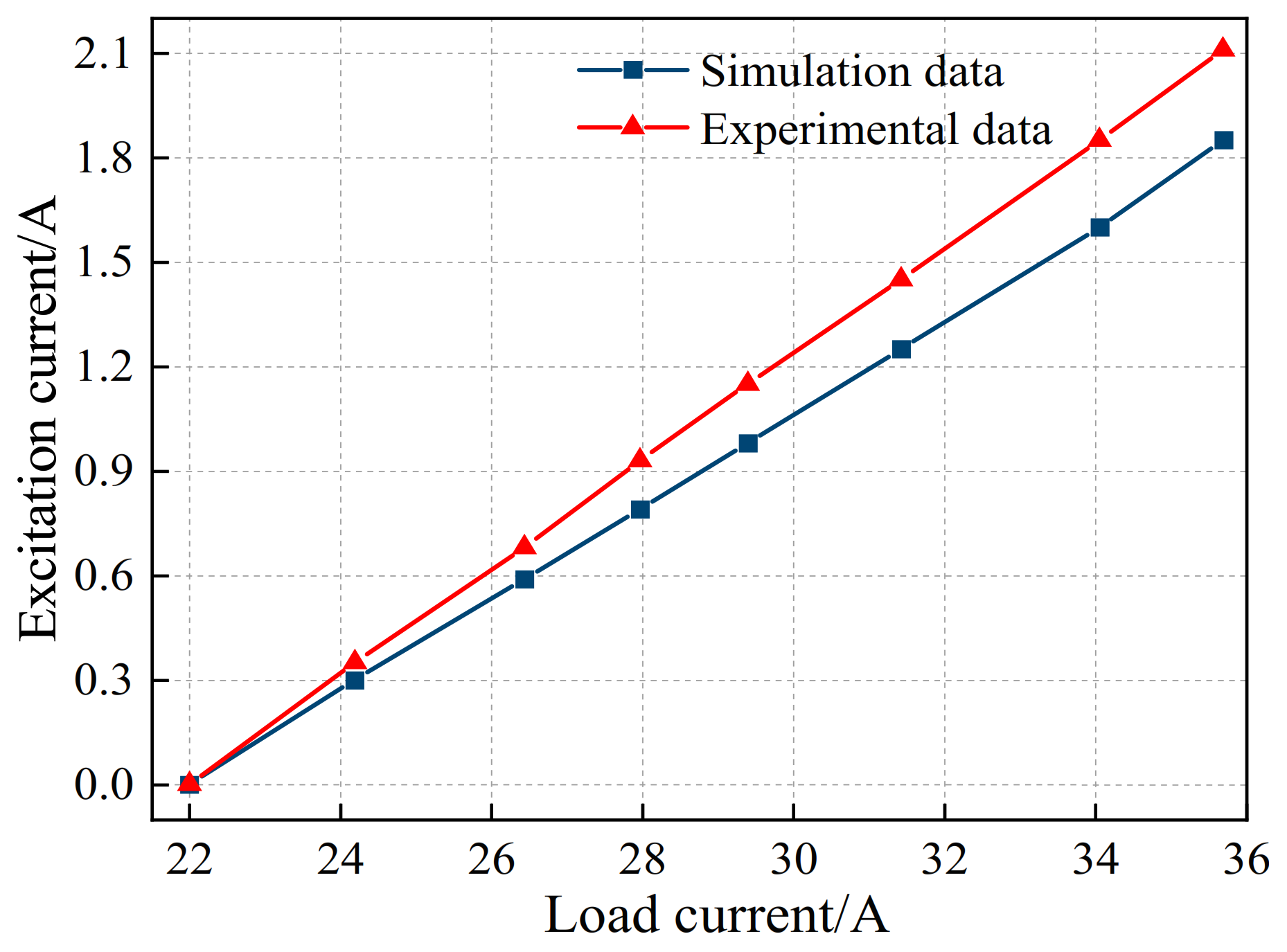
Figure 28.
The compound excitation generator regulates the characteristic curve.
Figure 28.
The compound excitation generator regulates the characteristic curve.
Table 1.
Optimization constraints for each design variable.
Table 1.
Optimization constraints for each design variable.
| Design Variables | Initial Value | Constraints |
|---|
| The arc coefficient of the claw tooth cusp pole kcj | 0.3 | 0.2 ≤ kcj ≤ 0.5 |
| The arc coefficient of the root of the claw tooth kcg | 1.1 | 0.9 ≤ kcg ≤ 1.2 |
| Claw pole tooth tip thickness hcj/mm | 2.5 | 2 ≤ hcj ≤ 3.5 |
| Claw tooth root thickness hcg/mm | 6 | 5 ≤ hcg ≤ 7 |
| Flange thickness hflp/mm | 5 | 5 ≤ hflp ≤ 6.5 |
| The radial thickness of the inter-pole PM hjyc/mm | 4 | 3 ≤ kjyc ≤ 5 |
Table 2.
Sensitivity of design variables concerning response values.
Table 2.
Sensitivity of design variables concerning response values.
| Design Variables | Sensitivity for Ux | Sensitivity for THDu |
|---|
| kcj | 0.55276 | 0.56532 |
| kcg | 0.38321 | 0.15872 |
| hflp | 0.09483 | 0.02394 |
| hcj | 0.05397 | 0.07471 |
| hcg | 0.05216 | 0.03763 |
| hjyc | 0.02274 | 0.08146 |
Table 3.
The concrete values of design variables and optimization goals in valid solutions.
Table 3.
The concrete values of design variables and optimization goals in valid solutions.
| Serial Number | kcg | kcj | hcj/mm | hcg/mm | hflp/mm | hjyc/mm | THDu/% | Ux/V |
|---|
| 48 | 1.0245 | 0.3815 | 2.0375 | 6.0875 | 5.29 | 4.73 | 6.66 | 34.747 |
| 74 | 0.9885 | 0.3485 | 2.0225 | 5.5025 | 6.69 | 3.31 | 8.96 | 35.488 |
| 24 | 1.0485 | 0.4805 | 3.0875 | 6.4025 | 6.79 | 4.51 | 9.54 | 36.059 |
| 37 | 1.0305 | 0.3935 | 3.4325 | 6.4625 | 5.93 | 3.03 | 10.52 | 36.534 |
| 8 | 0.9615 | 0.3665 | 2.9075 | 5.9675 | 6.05 | 4.55 | 11.44 | 36.608 |
| 34 | 1.1745 | 0.3245 | 3.1025 | 5.3375 | 6.03 | 4.31 | 12.36 | 40.793 |
| 68 | 1.1445 | 0.3395 | 2.0975 | 6.3125 | 5.85 | 4.91 | 14.16 | 42.482 |
| 18 | 1.0335 | 0.3365 | 2.6375 | 5.7425 | 6.61 | 4.41 | 18.84 | 42.620 |
| 35 | 0.9945 | 0.2645 | 3.4775 | 6.2225 | 6.53 | 4.29 | 25.28 | 42.685 |
| 38 | 1.0215 | 0.2825 | 2.9975 | 5.3675 | 6.75 | 4.75 | 26.78 | 42.887 |
| 90 | 1.0815 | 0.2585 | 2.9675 | 5.6675 | 6.31 | 4.99 | 27.38 | 43.796 |
| 98 | 0.9315 | 0.2405 | 3.4175 | 5.5625 | 6.17 | 4.57 | 33.3 | 44.960 |
Table 4.
The optimal solution and the final value of each response variable.
Table 4.
The optimal solution and the final value of each response variable.
| Parameter | Optimal Solution | Final Value |
|---|
| kcj | 1.1445 | 1.14 |
| kcg | 0.3395 | 0.34 |
| hflp/mm | 5.85 | 6 |
| hcj/mm | 2.0975 | 2.1 |
| hcg/mm | 6.3125 | 6.3 |
| hjyc/mm | 4.91 | 3 |
Table 5.
The constraint scope of the design variable.
Table 5.
The constraint scope of the design variable.
| Design Variables | Initial Value | Constraints |
|---|
| Magnetization thickness of PM ar2/mm | 2 | 2 ≤ ar2 ≤ 3 |
| Tangential length of PM br2/mm | 6 | 5 ≤ br2 ≤ 7.5 |
| PM angle αr2/° | 55 | 50 ≤ αr2 ≤ 100 |
| Pole-arc coefficient kr2 | 0.85 | 0.8 ≤ kr2 ≤ 0.9 |
| Eccentricity hpx/mm | 11 | 5 ≤ hpx ≤ 20 |
Table 6.
The constraint scope of the design variable.
Table 6.
The constraint scope of the design variable.
| Design Variables | Initial Value | Optimal Value |
|---|
| Magnetization thickness of PM ar2/mm | 2 | 2.39129 |
| Tangential length of PM br2/mm | 6 | 6.68317 |
| PM angle αr2/° | 55 | 61.6139 |
| Pole-arc coefficient kr2 | 0.85 | 0.809997 |
| Eccentricity hpx/mm | 11 | 12.5815 |
Table 7.
Compound excitation generator output performance experimental results.
Table 7.
Compound excitation generator output performance experimental results.
| Speed (r/min) | Load Power (W) | Output Voltage (V) |
|---|
| 2000 | 980 | 27.6 |
| 1000 | 27.1 |
| 1020 | 26.5 |
| 4000 | 980 | 28.3 |
| 1000 | 28.4 |
| 1020 | 28.2 |
| 4800 | 980 | 28.6 |
| 1000 | 28.6 |
| 1020 | 28.5 |