Abstract
Numerous path-planning studies have been conducted in past decades due to the challenges of obtaining optimal solutions. This paper reviews multi-robot path-planning approaches and decision-making strategies and presents the path-planning algorithms for various types of robots, including aerial, ground, and underwater robots. The multi-robot path-planning approaches have been classified as classical approaches, heuristic algorithms, bio-inspired techniques, and artificial intelligence approaches. Bio-inspired techniques are the most employed approaches, and artificial intelligence approaches have gained more attention recently. The decision-making strategies mainly consist of centralized and decentralized approaches. The trend of the decision-making system is to move towards a decentralized planner. Finally, the new challenge in multi-robot path planning is proposed as fault tolerance, which is important for real-time operations.
1. Introduction
Robot applications have been widely implemented in various areas, including industry [1], agriculture [2], surveillance [3], search and rescue [4], environmental monitoring [5], and traffic control [6]. A robot is referred to as an artificial intelligence system that integrates microelectronics, communication, computer science, and optics [7]. Due to the development of robotics technology, mobile robots have been utilized in different environments, such as Unmanned Aerial Vehicles (UAVs) for aerospace, Automated Guided Vehicles (AGVs) for production, Unmanned Surface Vessels (USVs) for water space, and Autonomous Underwater Vehicles (AUVs) for underwater.
To perform tasks, employing a set of vehicles cooperatively and simultaneously has gained interest due to the increased demand. Multiple robots can execute tasks in parallel and cover larger areas. The system continues working even with the failure of one robot [8], and it has the advantages of robustness, flexibility, scalability, and spatial distribution [9]. Each robot has its coordinates and independent behavior for a multi-robot system, and it can model the cooperative behavior of real-life situations [10]. For reliable operation of the robot, the robotics system must address the path/motion planning problem. Path planning aims to find a collision-free path from the source to the target destination.
Path planning is an NP-hard problem in optimization, and it involves multiple objectives, resulting in its solution being polynomial verified [11]. The robots are aimed to accomplish the tasks in the post-design stage with higher reliability, higher speed, and lower energy consumption [12]. Task allocation, obstacle avoidance, collision-free execution, and time windows are considered [13]. Multi-robot path planning has high computational complexity, which results in a lack of complete algorithms that offer solution optimality and computational efficiency [14].
Substantial optimality criteria have been considered in path planning, such as the rendezvous and operation time, path length, velocity smoothness, safety margin, and heading profiles for generating optimal paths [15]. During missions, the robot systems have limitations, such as limited communication with the center or other robots, stringent nonholonomic mission constraints, and limited mission length because of weight, size, and fuel constraints [16]. The planned path must be a smooth curve due to nonholonomic motion constraints and support kinematic constraints with geometric continuity. Furthermore, the path’s continuity is significant for collaborative transport [17].
Path-planning approaches can be divided into offline and real-time implementation. Offline generation of a multi-robot path cannot exploit the cooperative abilities, as there is little or no interaction between robots, leading to the multi-robot system not ensuring that the robots are moving along a predefined path or formation [18]. Real-time systems have been proposed to overcome the problems created by offline path generation, and these can maximize the efficiency of algorithms. The chart of offline/real-time implementation included in the literature review is exhibited in the discussion section.
Decision-making strategies can be classified as centralized and decentralized approaches. The centralized system has the central decision-maker, and thus the degree of cooperation is higher than in the decentralized approach. All robots are treated as one entity in the high-dimensional configuration space [19]. A central planner assigns tasks and plans schedules for each robot, and the robots start operation after completion of the planning [20]. The algorithms used in the centralized structure are without limitation because the centralized system has better global support for robots.
However, the decentralized approach is more widely employed in real-time implementation. Decentralized methods are typical for vehicle autonomy and distributed computation [21]. These have the robots communicate and interact with each other and have higher degrees of flexibility, robustness, and scalability, thereby, supporting dynamic changes. The robots execute computations and produce suboptimal solutions [20]. The decentralized approach includes task planning and motion planning, and it reduces computational complexity with limited shared information [22].
Many surveys have been conducted for the mobile robot path planning strategies [23,24,25]; however, these papers only focus on single robot navigation without cooperative planning. This review’s motivation is to introduce the state-of-art path-planning algorithms of multi-robot systems and provide an analysis of multi-robot decision-making strategies, considering real-time performance. This paper not only investigates 2D or ground path planning but also the 3D environment.
We review the recent literature and classify the path-planning approaches based on the main principles. The paper is organized as follows. Section 2 presents the multi-robot path-planning approaches with classification. Section 3 provides the decision-making strategies for the multi-robot system. Section 4 discusses the mentioned path-planning algorithms and concludes the paper.
2. Multi-Robot Path Planning Approaches
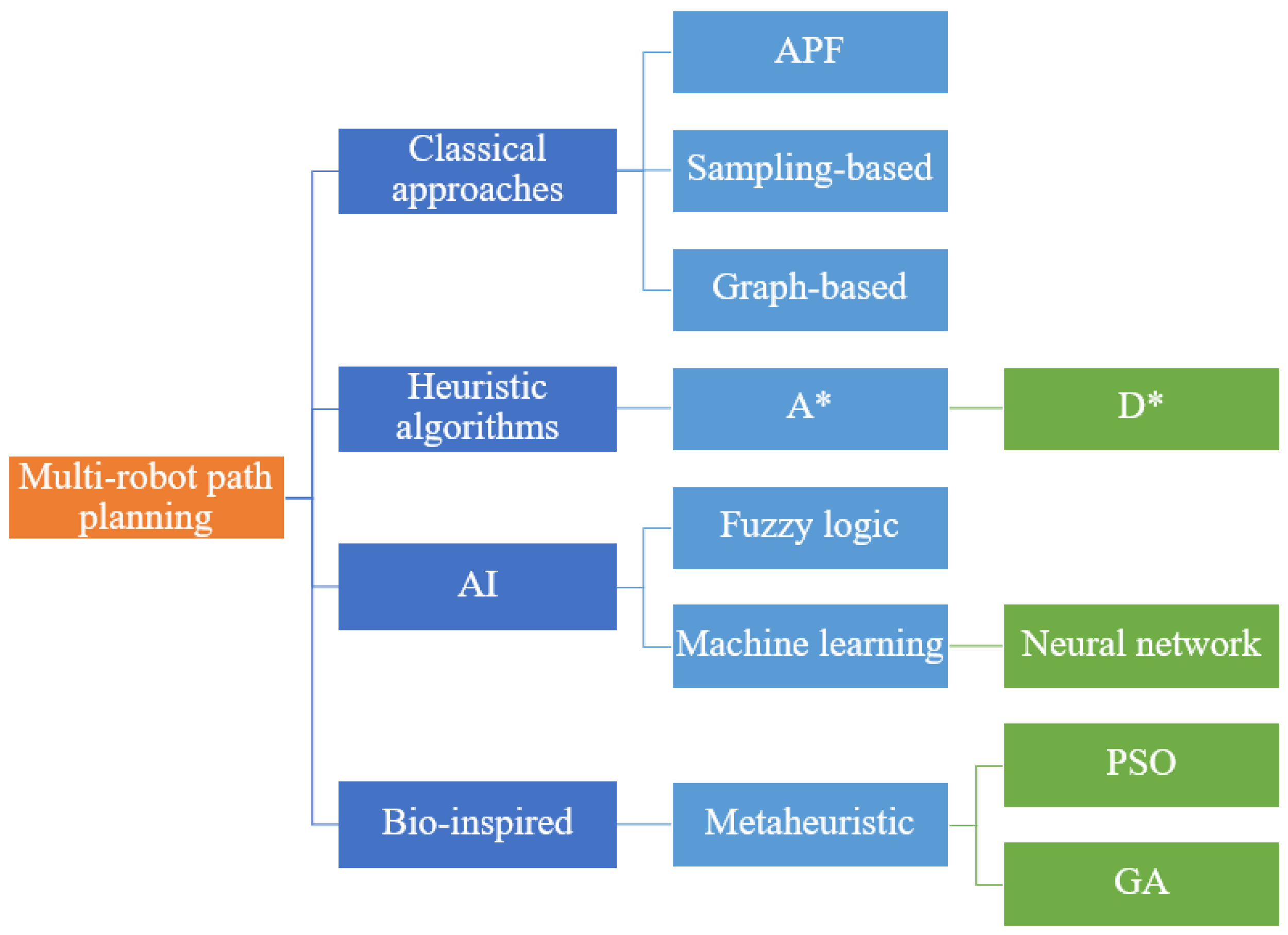
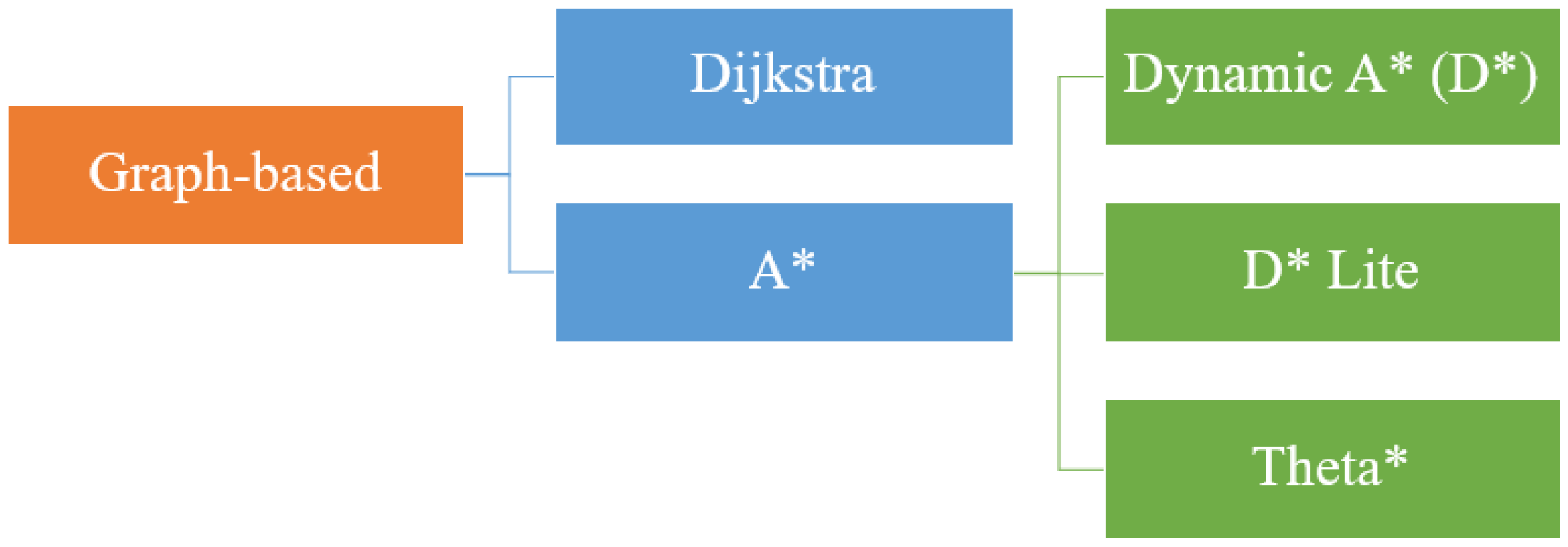
Figure 1 presents the classification of multi-robot path-planning algorithms, and it is divided into three categories: classical approaches, heuristic algorithms, and artificial intelligence (AI)-based approaches. The subcategories are linked to the primary categories and only display the significant subcategories. The classical approaches include the Artificial potential field, sampling-based, and graph-based approaches. The heuristic algorithms mainly consist of A* and D* search algorithms. The AI-based approaches are the most common algorithms for multi-robot systems, and the bio-inspired approaches take most of the attention. Metaheuristic has been applied to most of the research, and the famous algorithms are PSO and GA. From [26], GA and PSO are the most commonly used approaches.
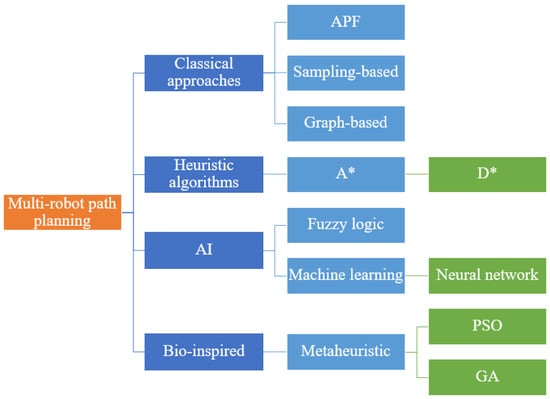
Figure 1.
Classification of multi-robot path planning approaches.
2.1. Classical Approaches
2.1.1. Artificial Potential Field (APF)
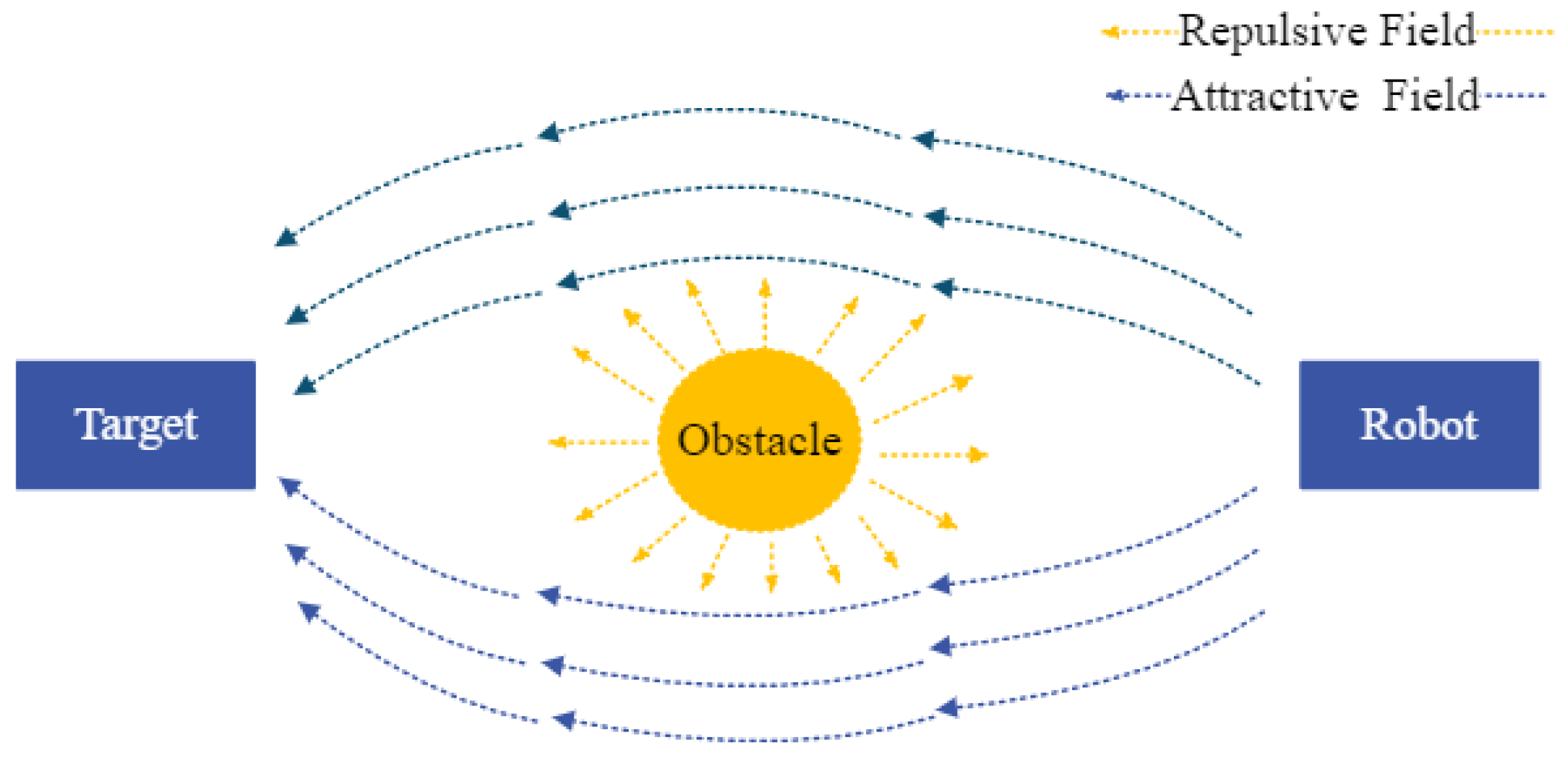
The APF uses its control force for path planning, and the control force sums up the attractive and the repulsive potential field. The illustration of APF is shown in Figure 2; the blue force indicates the attractive field, and the yellow force represents the repulsive field. The APF establishes path-planning optimization and dynamic particle models, and the additional control force updates the APF for multi-robot formation in a realistic and known environment [27]. Another APF-based approach is presented for a multi-robot system in a warehouse.
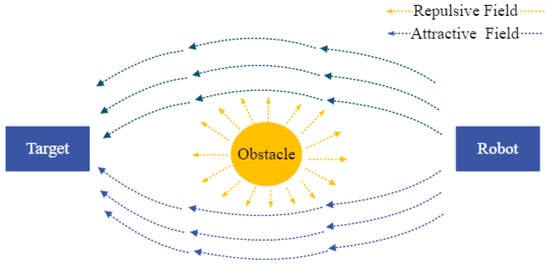
Figure 2.
Illustration of the APF algorithm.
It uses the priority strategy and solves the drawbacks of traffic jams, local minima, collisions, and non-reachable targets [28]. An innovative APF algorithm is proposed to find all possible paths under a discrete girded environment. It implements a time-efficient deterministic scheme to obtain the initial path and then uses enhanced GA to improve it [29]. A potential field-based controller in [30] supports robots to follow the designed path, avoid collision with nearby robots, and distribute the robots stochastically across different paths in topologically distinct classes.
An improved APF is proposed to overcome the traditional APF’s shortcomings, including target unreachable and local minimum in [31] for real-time performance with dynamic obstacles for realizing local path planning. A collision avoidance strategy and risk assessment are proposed based on the improved APF and the fuzzy inference system for multi-robot path planning under a completely unknown environment [32].
APF is applied in the approximate cost function in [33], and integral reinforcement learning is developed for the minimum time-energy strategy in an unknown environment, converting the finite horizon problem with constraints to an infinite horizon optimal control problem. APF is introduced for the reward functions and integrates Deep Deterministic Policy Gradient and Model Predictive Control to address uncertain scenes [34].
2.1.2. Sampling-Based
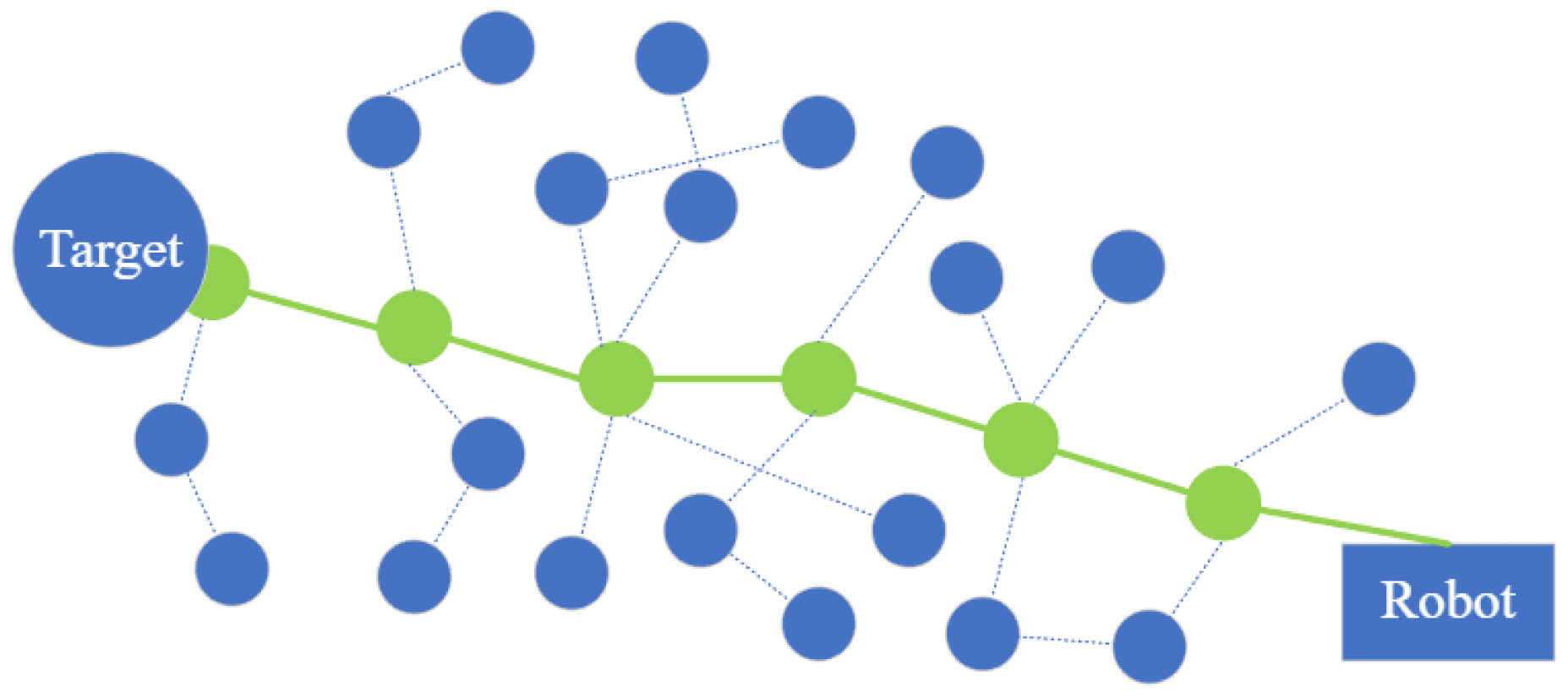
The rapidly exploring random tree (RRT) searches high-dimensional and nonconvex space by using a space-filling tree randomly, and the tree is built incrementally from samples to grow towards unreached areas. The sampling-based approach’s outline is demonstrated in Figure 3, and the generated path is highlighted in green. For a multi-robot centralized approach, multi-robot path-planning RRT performs better in optimizing the solution and exploring search space in an urban environment than push and rotate, push and swap, and the Bibox algorithm [35]. The discrete-RRT extends the celebrated RRT algorithm in the discrete graph with a speedy exploration of the high-dimensional space of implicit roadmaps [36].
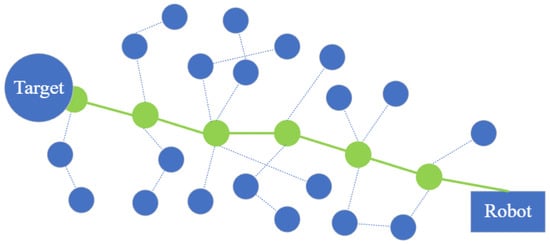
Figure 3.
Demonstration of the RRT algorithm.
2.1.3. Other Classical Approaches
Tabu search keeps searching the solutions in the neighborhood and records the solutions in the Tabu list. The classic Tabu search is integrated with particle swarm optimization (PSO) to enhance optimization ability in [37], and it is aimed at the decision-making of routing and scheduling. It is based on the PSO and Tabu search algorithm with a “minimum ring” for obtaining the dynamic path planning for adapting the online requirements for a dynamic environment.
A polygon area decomposition strategy is applied to explore a target area with located waypoints. It analyzes the effect of the partition of the area, and the number of robots [38]. Planar graphs are used to solve optimal multi-robot path planning problems with computational complexity and establish the intractability of the problems on the graphs to reduce the sharing of paths in opposite directions [39]. The grid pattern map decomposition is developed for coverage path planning and employing multiple UAVs for collecting the images and creating a response map to obtain helpful information [40].
For remote sensing and area coverage with multi-robot, graph-based task modeling is proposed with mixed-integer linear programming to route the multiple robots [41]. A mixed-integer linear programming model is presented based on the hexagonal grid-based decomposition method [42]. It can be applied for multi-UAV coverage path planning in rescue and emergency operations. The biconnected graph, user input, and small critical benchmark are controlled by a path planner as presented in [43] to solve the multi-AGV path planning problems of AGV planetary exploration, automatic packages, and robotics mining.
A multi-robot informative path-planning approach transforms the continuous region into Voronoi components, and the robots are allocated free regions [44]. The multi-robot navigation strategy with path priority is presented in [45]; a generalized Voronoi diagram divides the map according to the robot’s path-priority order and finds the path-priority order for each robot.
For the cited papers, the classical approaches consist of APF and sampling-based algorithms. The classical algorithms usually involve the predefined graph, requiring high computational space. The trend of implementing the classical algorithms is combined with other state-of-art algorithms. The heuristic algorithms are proposed for complete and fast path planning.
2.2. Heuristic Algorithms
2.2.1. A* Search
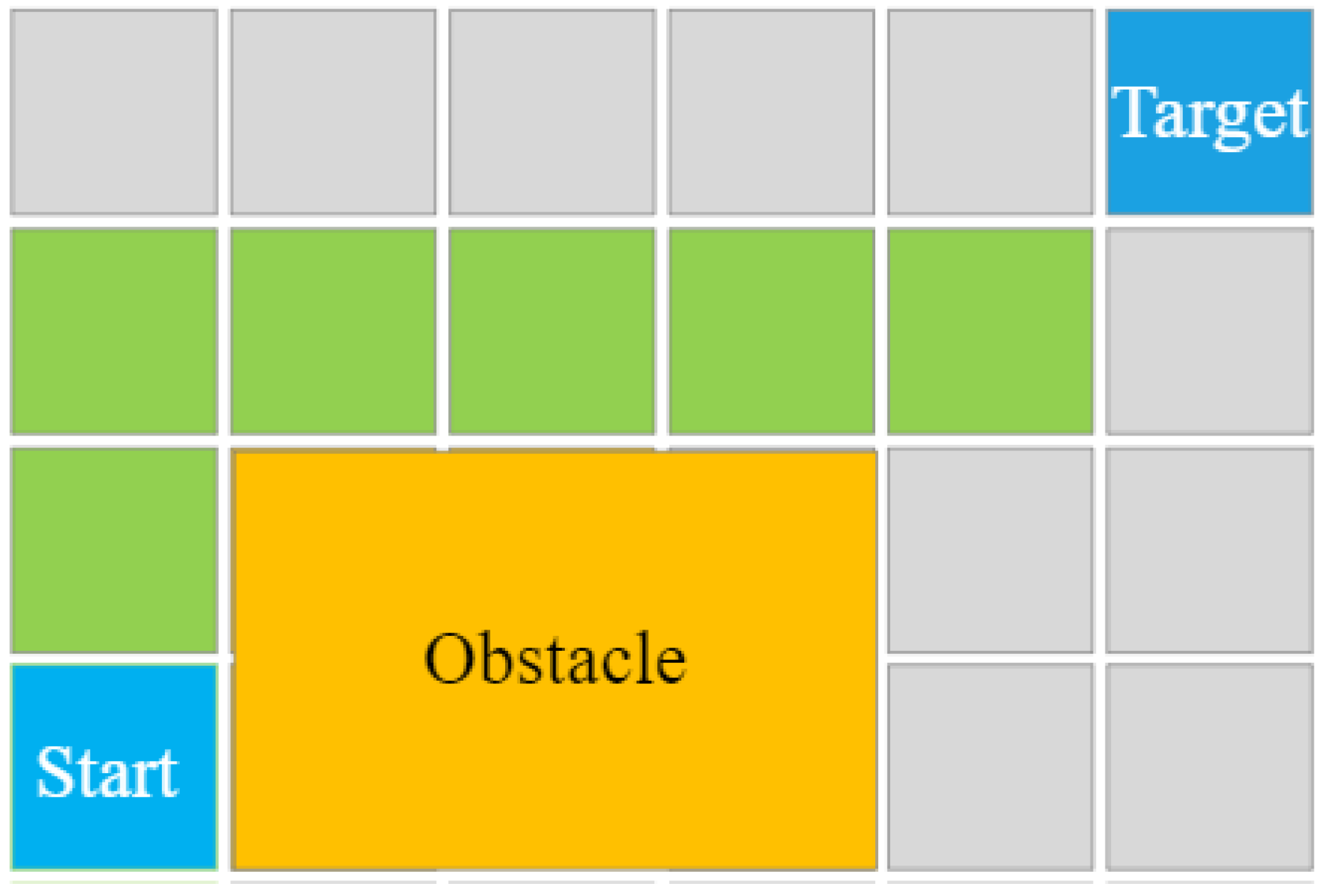
The A* search algorithm is one of the most common heuristic algorithms in path planning. Figure 4 shows the simple example of the gird-based A* algorithm, and the path is highlighted in green. It uses the heuristic cost to determine the optimal path on the map. The relaxed-A* is used to provide an optimal initial path and fast computation, and Bezier-splines are used for continuous path planning to optimize and control the curvature of the path and restrict the acceleration and velocity [17].
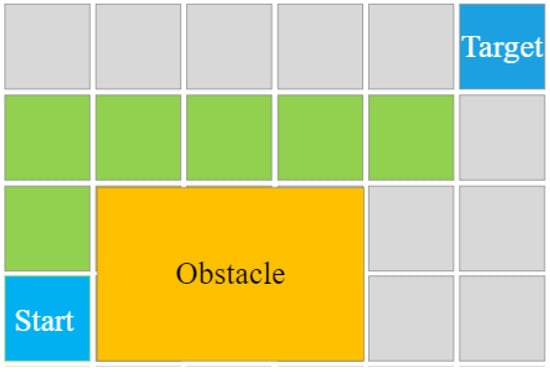
Figure 4.
Simple example of the A* algorithm.
A two-level adaptive variable neighborhood search algorithm is designed to be integrated with the A* search algorithm for the coupled mission planning framework. It models the path planning problem and the integrated sensor allocation to minimize travel costs and maximize the task profit [46]. For the multi-AGV routing problem, the improved A* algorithm plans the global path and uses a dynamic RRT algorithm to obtain a passable local path with kinematic constraints, avoiding collisions in the grid map [47].
Additionally, Ref. [48] utilized the A* algorithm for the predicted path and generated a flyable path by cubic B-spline in real-time for guidance with triple-stage prediction. With the computational efficiency of cluster algorithms and A*, the proposed planning strategy supports online implementation. An optimal multi-robot path-planning approach is proposed with EA* algorithm with assignment techniques and fault-detection algorithm for the unknown environment based on the circle partitioning concept in [49]. A proposed navigation system integrates a modified A* algorithm, auction algorithm, and insertion heuristics to calculate the paths for multiple responders. It supports connection with a geo-database, information collection, path generation in dynamic environments, and spatio-temporal data analysis [50].
The D* algorithm is employed for multi-robot symbiotic navigation in a knowledge-sharing mechanism with sensors [8]. It allows robots to inform other robots about environmental changes, such as new static obstacles and path blockage, and it can be extended for real-time mobile applications. Additionally, D* Lite is applied with artificial untraversable vertex to avoid deadlocks and collisions for real-time robot applications, and D* Lite has fast re-planning abilities [9].
A cloud approach is developed with D* Lite and multi-criteria decision marking to offer powerful processing capabilities and shift computation load to the cloud from robots in the multi-robot system with a high level of autonomy [51]. An integrated framework is proposed based on D* Lite, A*, and uniform cost search, and it is used for multi-robot dynamic path-planning algorithms with concurrent and real-time movement [52].
2.2.2. Other Heuristic Algorithms
A constructive heuristic approach is presented to perceive multiple regions of interest. It aims to find the robot’s path with minimal cost and cover target regions with heterogeneous multi-robot settings [6]. Conflict-Based Search is proposed for multi-agent path planning problems in the train routing problem for scheduling multiple vehicles and setting paths in [53]. For multi-robot transportation, a primal-dual-based heuristic is designed to solve the path planning problem as the multiple heterogeneous asymmetric Hamiltonian path problem, solving in a short time [54]. The linear temporal logic formula is applied to solve the multi-robot path planning by satisfying a high-level mission specification with Dijkstra’s algorithm in [55].
A modified Dijkstra’s algorithm is introduced for robot global path planning without intersections, using a quasi-Newton interior point solver to smooth local paths in tight spaces [56]. Moreover, cognitive adaptive optimization is developed with transformed optimization criteria for adaptively offering the accurate approximation of paths in the proposed real-time reactive system; it takes into account the unknown operation area and nonlinear characteristics of sensors [18].
The Grid Blocking Degree (GBD) is integrated with priority rules for multi-AGV path planning, and it can generate a conflict-free path for AGV to handle tasks and update the path based on real-time traffic congestion to overcome the problems caused by most multi-AGV path planning is offline scheduling [57]. Heuristic algorithms, minimization techniques, and linear sum assignment are used in [58] for multi-UAV coverage path and task planning with RGB and thermal cameras. [59] designed the extended Angular-Rate-Constrained-Theta* for a multi-agent path-planning approach to maintaining the formation in a leader–follower formation.
Figure 5 displays the overview of the mentioned heuristic algorithms. The heuristic algorithms are widely used in path planning, and the heuristic cost functions are developed to evaluate the paths. The algorithms can provide the complete path in a grid-like map. However, for the requirement of flexibility and robustness, bio-inspired algorithms are proposed.
Figure 5.
Search algorithms.
2.3. Bio-Inspired Techniques
2.3.1. Particle Swarm Optimization (PSO)
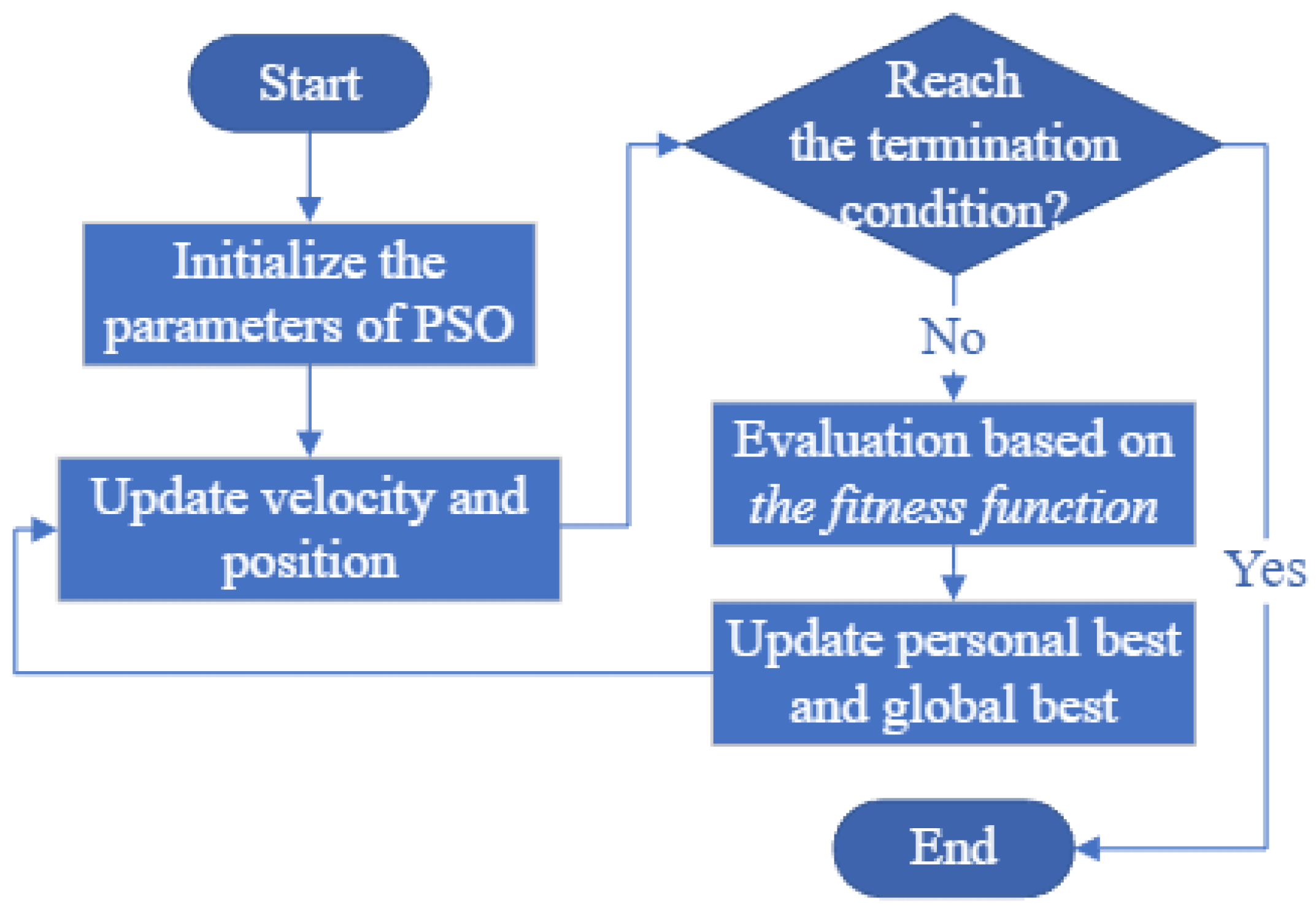
PSO is one of the most common metaheuristic algorithms in multi-robot path planning problems and formation. The flowchart of PSO is shown in Figure 6. It is a stochastic optimization algorithm based on the social behavior of animals, and it obtains global and local search abilities by maintaining a balance between exploitation and exploration [60]. Ref. [61] presents an interval multi-objective PSO using an ingenious interval update law for updating the global best position and the crowding distance of risk degree interval for the particle’s local best position. PSO is employed for multiple vehicle path planning to minimize the mission time, and the path planning problem is formulated as a multi-constrained optimization problem [62], while the approach has low scalability and execution ability.
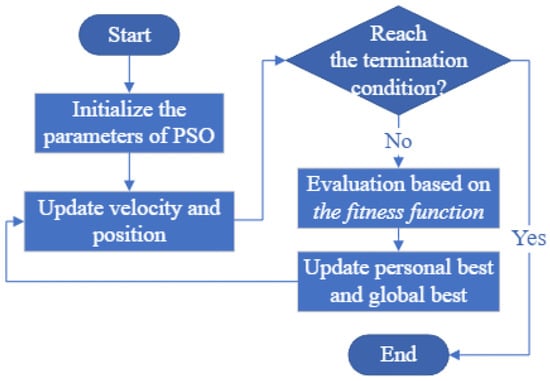
Figure 6.
Flowchart of the PSO algorithm.
An improved PSO is developed with differentially perturbed velocity, focusing on minimizing the maximum path length and arrival time with a multi-objective optimization problem [63]. The time stamp segmentation model handles the coordination cost. Improved PSO is combined with modified symbiotic organisms searching for multi-UAV path planning, using a B-spline curve to smooth the path in [64]. For a non-stationary environment, improved PSO and invasive weed optimization are hybrids for planning a path for each robot in the multi-robot system, balancing diversification and intensification, and avoiding local minima [65].
PSO is adapted for a leader–follower strategy in multi-UAV path planning with obstacle avoidance [60]. A distributed cooperative PSO is proposed for obtaining a safe and flyable path for a multi-UAV system, and it is combined with an elite keeping strategy and the Pythagorean hodograph curve to satisfy the kinematic constraints in [66]. The enhanced PSO is improved by greedy strategy and democratic rule in human society inspired by sine and cosine algorithms. The projected algorithm can generate a deadlock-free path with preserving a balance between intensification and diversification [67].
For the multi-robot path planning issue, a coevolution-based PSO is proposed to adjust the local and goal search abilities and solve the stagnation problem of PSO with evolutionary game theory in [68]. An improved gravitational search algorithm is integrated with the improved PSO for a new methodology for multi-robot path planning in the clutter environment, and it updates the particle positions and gravitational search algorithm acceleration with PSO velocity simultaneously [69].
A hybrid algorithm of democratic robotics PSO and improved Q-learning is proposed to balance exploitation and exploration, and it is fast and available for a real-time environment. However, it cannot guarantee the completeness of the path, and it is hard to achieve robot cooperation [70]. PSO-based and a B-Spline data frame solver engine is developed for uninterrupted collision-free path planning. It is robust to deal with current disturbances and irregular operations and provides quick obstacle avoidance for real-time implementation [15].
A wireless sensor network is presented for locating obstacles and robots in a dynamic environment. It combines a jumping mechanism PSO algorithm and a safety gap obstacle avoidance algorithm for multi-robot path planning [7]. The jumping mechanism PSO estimates the inertia weight based on fitness value and updates the particles. The safety gap obstacle avoidance algorithm focuses on robots struck when avoiding obstacles. Ref. [71] designed the hybrid GA and PSO with fuzzy logic controller for multi-AGV conflict-free path planning with rail-mounted gantry and quay cranes; however, it is inapplicable to real-time scheduling.
2.3.2. Genetic Algorithm (GA)
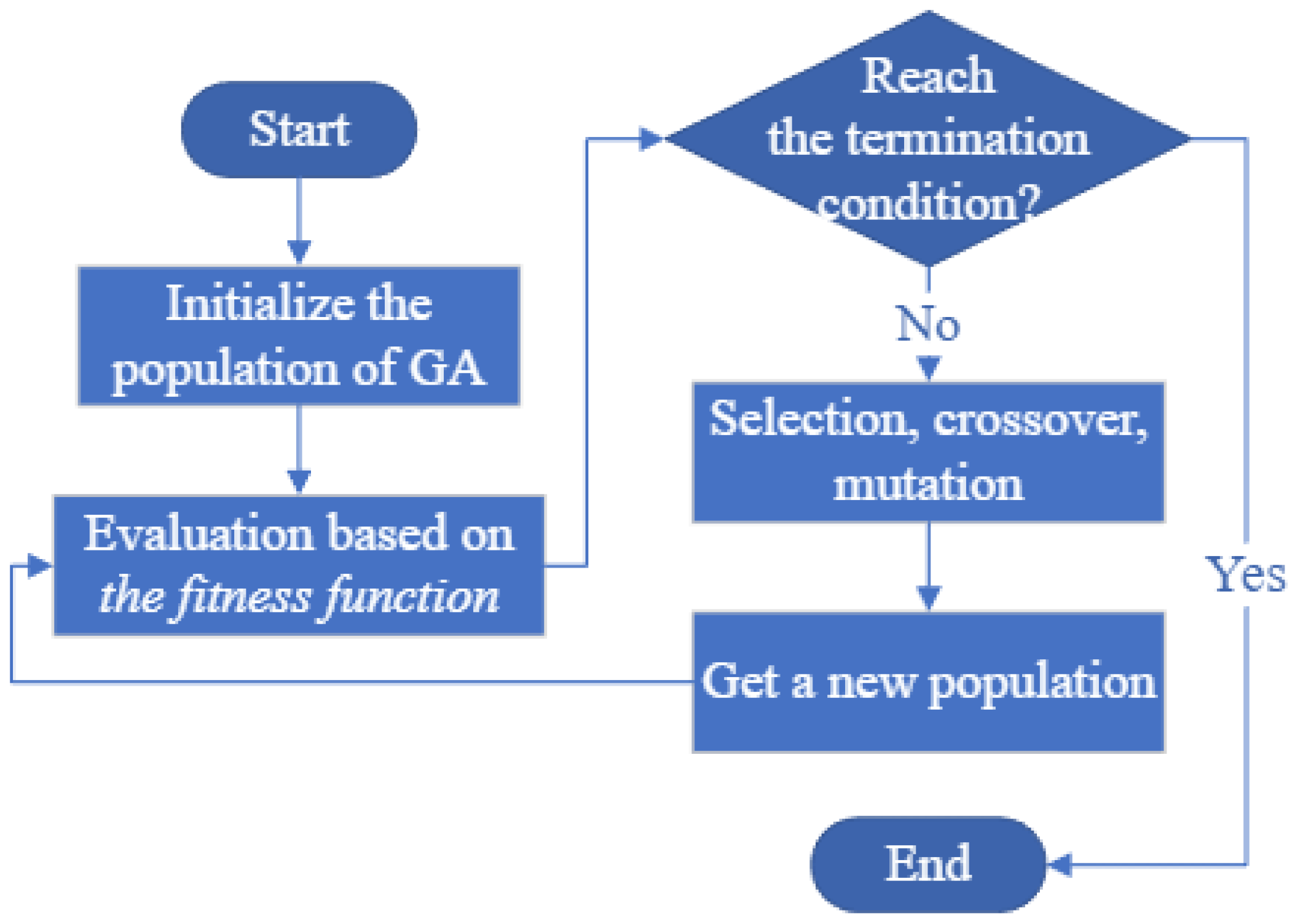
GA is widely utilized for solving optimization problems as an adaptive search technique, and it is based on a genetic reproduction mechanism and natural selection [72]. The flowchart of GA is indicated in Figure 7. Ref. [73] uses GA and reinforcement learning techniques for multi-UAV path planning, considers the number of vehicles and a response time, and a heuristic allocation algorithm for ground vehicles. GA solves the Multiple Traveling Sales Person problem with the stop criterion and the cost function of Euclidean distance, and Dubins curves achieve geometric continuity while the proposed algorithm cannot avoid the inter-robot collision or support online implementation [16].
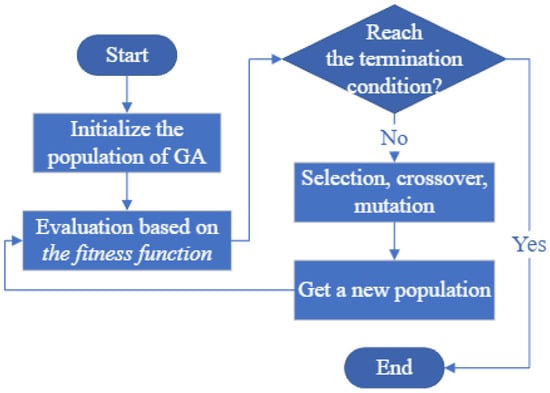
Figure 7.
Flowchart of the GA algorithm.
A 3D sensing model and a cube-based environment model are involved in describing a complex environment, and non-dominated sorting GA is modified to improve the convergence speed for the Pareto solution by building a voyage cost map by the R-Dijkstra algorithm in [74] as an omnidirectional perception model for multi-robot path planning. Ref. [75] applies the sensors in the area to obtain a minimal cost and solves the traveling salesman, and GA is adapted for persistent cooperative coverage.
Efficient genetic operators are developed to generate valid solutions on a closed metric graph in a reasonable time and are designed for multi-objective GA for multi-agent systems [76]. GA assigns the regions to each robot, sets the visiting orders, and uses simultaneous localization and mapping to create the global map in [77] for coverage path planning. Ref. [78] presents GA to optimize the integration of motion patterns that represent the priority of the neighbor cell and divides the target environment into cell areas, and then uses a double-layer strategy to guarantee complete coverage.
A domain knowledge-based operator is proposed to improve GA by obtaining the elite set of chromosomes, and the proposed algorithm can support robots that have multiple targets [79]. For intelligent production systems, the improved GA is aimed at complicated multi-AGV path planning and maneuvering scheduling decision with time-dependent and time-independent variables. It first addresses AGV resource allocation and transportation tasks, and then solves the transportation scheduling problem [80].
An improved GA was presented with three-exchange crossover heuristic operators than the traditional two-exchange operators, which consider double-path constraints for multi-AGV path planning [81]. Ref. [72] proposed a boundary node method with a GA for finding the shortest collision-free path for 2D multi-robot system and using a path enhancement method to reduce the initial path length. Due to the short computational time, it can be used for real-time navigation, while it can only be implemented in a known environment without dynamic obstacles.
A high degree of GA is employed for optimal path planning under a static environment at offline scheduling, and online scheduling is aimed to solve conflicts between AGVs for the two-stage multi-AGV system [82]. The evolution algorithm is used for planning a real-time path for multi-robot cooperative path planning with a unique chromosome coding method, redefining mutation and crossover operator in [83].
2.3.3. Ant Colony Optimization (ACO)
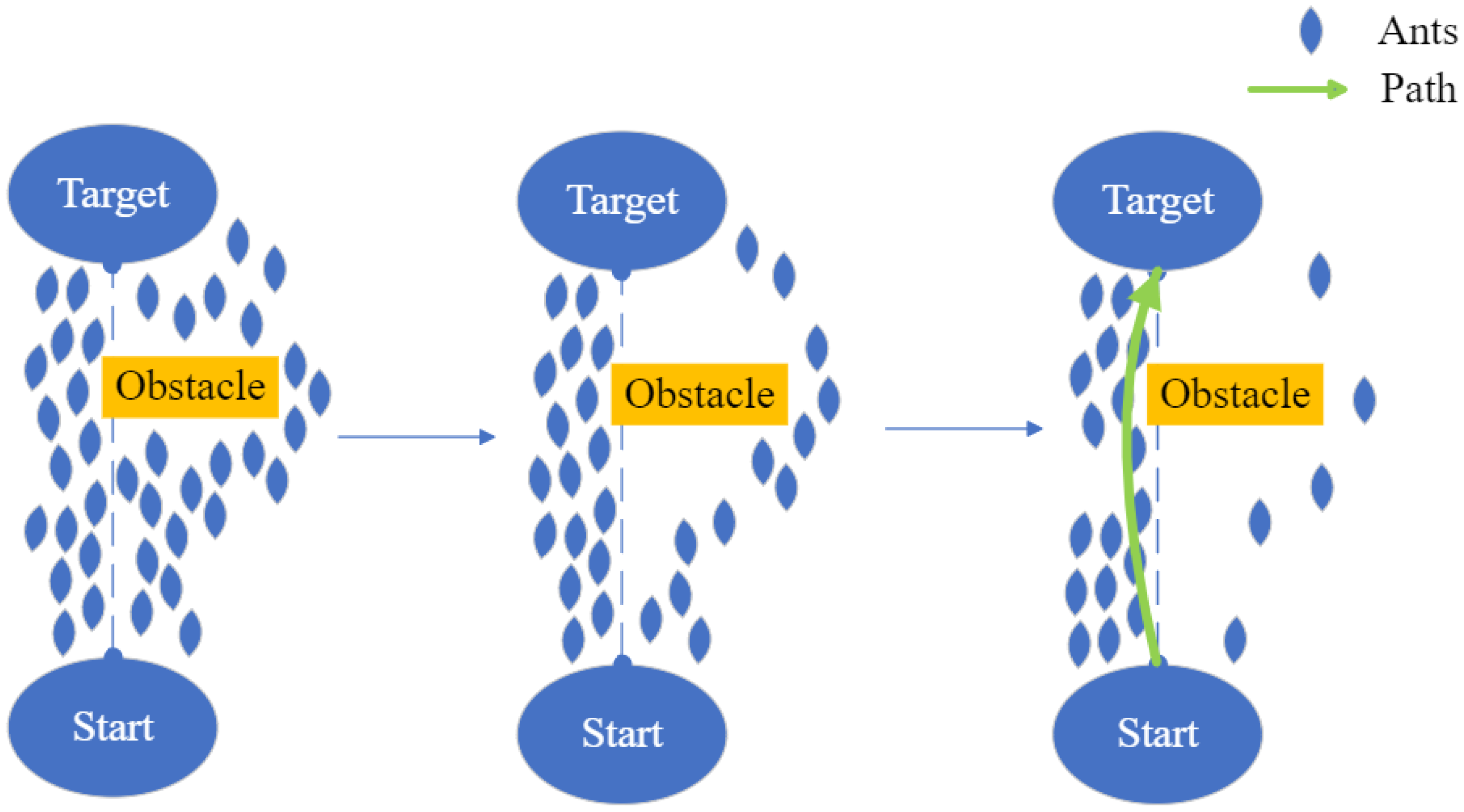
Ants will move along the paths and avoid the obstacle, marking available paths with pheromone, and the ACO treats the path with higher pheromone as the optimal path. The principle of ACO is demonstrated in Figure 8, and the path with a higher pheromone is defined as the optimal path marked by green. For collision-free routing and job-shop scheduling problems, an improved ant colony algorithm is enhanced by multi-objective programming for a multi-AGV system [84].
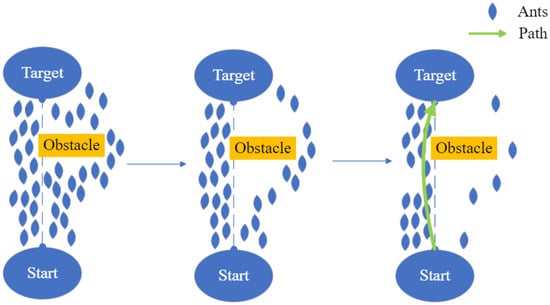
Figure 8.
Changes of the ACO algorithm with different timeslots.
For multi-UGVs, a continuous ACO-based path planner focuses on coordination and path planning. It is integrated with an adaptive waypoint-repair method and a probability-based random-walk strategy to balance exploration and exploitation and improve the algorithm’s performance, resolving the coordination with a velocity-shifting optimization algorithm [85].
K-degree smoothing and the improved ACO are integrated as a coordinated path planning strategy for the multi-UAV control and precise coordination strategy in [86]. Voronoi models the environment by considering various threats, and the improved ACO’s pheromone update method and heuristic information are redefined for path planning, then using a k-degree smoothing method for the path smoothing problem. For precision agriculture and agricultural processes, ACO, Bellman–Held–Karp, Christofides, and Nearest Neighbor based on K-means clustering are used for the optimization path of multi-UAV [87].
2.3.4. Pigeon-Inspired Optimization (PIO)
Pigeon navigation tools inspired PIO, and it uses two operators for evaluating the solutions. Social-class PIO is proposed to improve the performances and convergence capabilities of standard PIO with inspiring by the inherent social-class character of pigeons [88], and it is combined with time stamp segmentation for multi-UAV path planning. Ref. [89] analyzing and comparing the changing trend of fitness value of local and global optimum positions to improve the PIO algorithm as Cauchy mutant PIO method, and the plateau topography and wind field, control constraints of UAVs are modeled for cooperative strategy and better robustness.
2.3.5. Grey Wolf Optimizer (GWO)
GWO is inspired by the hunting behavior and leadership of grey wolves, and it obtain the solutions by searching, encircling, and attacking prey. An improved grey wolf optimizer is employed for the multi-constraint objective optimization model for multi-UAV collaboration under the confrontation environment. It considers fuel consumption, space, and time [90]. The improvements of the grey wolf optimizer are individual position updating, population initialization, and decay factor updating. An improved hybrid grey wolf optimizer is proposed with a whale optimizer algorithm in a leader–follower formation and fuses a dynamic window approach to avoid dynamic obstacles [91].
The leader–follower formation controls the followers to track their virtual robots based on the leader’s position and considers the maximum angular and linear speed of robots. Ref. [92] proposed a hybrid discrete GWO to overcome the weakness of traditional GWO, and it updates the grey wolf position vector to gain solution diversity with faster convergence in discrete domains for multi-UAV path planning, using greedy algorithms and the integer coding to convert between discrete problem space and the grey wolf space.
2.3.6. Other Bio-Inspired Techniques
The fruit fly optimization approach usually solves the nonlinear optimization problem. The multiple swarm fruit optimization algorithm is presented for the coordinated path planning for multi-UAVs, and it improves the global convergence speed and reduces the possibilities of local optimum [93].
An improved gravitational search algorithm is proposed for multi-robot path planning under the dynamic environment based on a cognitive factor, social, memory information of PSO, and deciding the population for the next generation based on greedy strategy [94]. The simulated annealing is integrated with the Dijkstra algorithm for calculating the optimal path based on the Boolean formula and the global map for a high-level specification for multi-robot path planning [13].
The hybrid algorithm of sine-cosine and kidney-inspired is developed for multi-robot in a complex environment. It selects the optimal positions for each robot to avoid conflicts with teammates and dynamic obstacles [95]. The hybridization of invasive weed optimization and firefly algorithm is employed to adjust the movement property of the firefly algorithm and spatial dispersion property of invasive weed optimization for exploration and exploitation [96]. The Differential Evolution algorithm tunes the differential weight, population size, generation number, and crossover for multi-UAV path planning in [97]. It defines the minimum generation’s weighting required between the computational and the path cost.
Physarum is a bio-inspired method for path planning, and it can take a quick response to external change. Ref. [12] proposed a Physarum-based algorithm for multi-AGV for model-based mission planning in dynamic environments, with an adaptive surrogate modeling method. A novel swarm intelligence algorithm is developed as an Anas platyrhynchos optimizer for multi-UAV cooperative path planning.
The Anas platyrhynchos optimizer simulates the swarm’s moving process and warning behavior [98]. It proposes low-communication cooperation and heterogeneous strategies for online path planning based on differential evolution-based path planners [99]. It summarizes local measurements with the sparse variation Gaussian process, sharing information even in a weak communication environment. Ref. [100] developed a multi-task multi-robot framework for challenging industrial problems. It proposes Large Neighbor Search as a new coupled method to make task assignment choices by actual delivery costs.
The artificial immune network algorithm is improved with the position tracking control method for providing the abilities of diversity and self-recognition for multi-robot formation path planning with leader robots, and it overcomes the shortcomings of immature convergence and local minima [101]. Differential evolution algorithm is improved in [102] for calculating collision-free optimal path with multiple dynamic obstacle constraints in a 2D map. An efficient artificial bee colony algorithm is proposed for online path planning, selecting the appropriate objective function for collision avoidance, target, and obstacles [103].
Bio-inspired techniques mainly include PSO, GA, ACO, PIO, and GWO. They are inspired by animals’ natural behaviors and employ particles for path generation. As of computational efficiency and powerful implementation, they are popular in multi-robot path planning. AI-based approaches are proposed due to the development of intelligent systems and the requirements of adapting to changing environments.
2.4. Artificial Intelligence
2.4.1. Fuzzy Logic
Fuzzy logic uses the principle of “degree of truth” for computing the solutions. It can be applied for controlling the robot without the mathematical model but cannot predict the stochastic uncertainty in advance. As a result, a probabilistic neuro-fuzzy model is proposed with two fuzzy level controllers and an adaptive neuro-fuzzy inference system for multi-robot path planning and eliminating the stochastic uncertainties with leader–follower coordination [104]. The fuzzy C-means or the K-means methods filter and sort the camera location points, then use A* as a path optimization process for the multi-UAV traveling salesman problem in [5].
For collision avoidance and autonomous mobile robot navigation, Fuzzy-wind-driven optimization and a singleton type-1 fuzzy logic system controller are hybrids in the unknown environment in [105]. The wind-driven optimization algorithm optimizes the function parameters for the fuzzy controller, and the controller controls the motion velocity of the robot by sensory data interpretation. Ref. [106] proposed a reverse auction-based method and a fuzzy-based optimum path planning for multi-robot task allocation with the lowest path cost.
2.4.2. Machine Learning
Machine learning simulates the learning behavior to obtain the solutions. It is used for path planning, embracing mobile computing, hyperspectral sensing, and rapid telecommunication for the rapid agent-based robust system [107]. Kernel smooth techniques, reinforcement learning, and the neural network are integrated for greedy actions for multi-agent path planning in an unknown environment [10] to overcome the shortcomings of traditional reinforcement learning, such as high time consumption, slow learning speed, and disabilities of learning in an unknown environment.
The self-organizing neural network has self-learning abilities and competitive characteristics for the multi-robot system’s path planning and task assignment. Ref. [108] combined it with Glasius Bio-inspired neural network for obstacle avoidance and speed jump while the environment changes have not been considered in this approach. The biological-inspired self-organizing map is combined with a velocity synthesis algorithm for multi-robot path planning and task assignment. The self-organizing neural network supports a set of robots to reach multiple target locations and avoid obstacles autonomously for each robot with updating weights of the winner by the neurodynamic model [109].
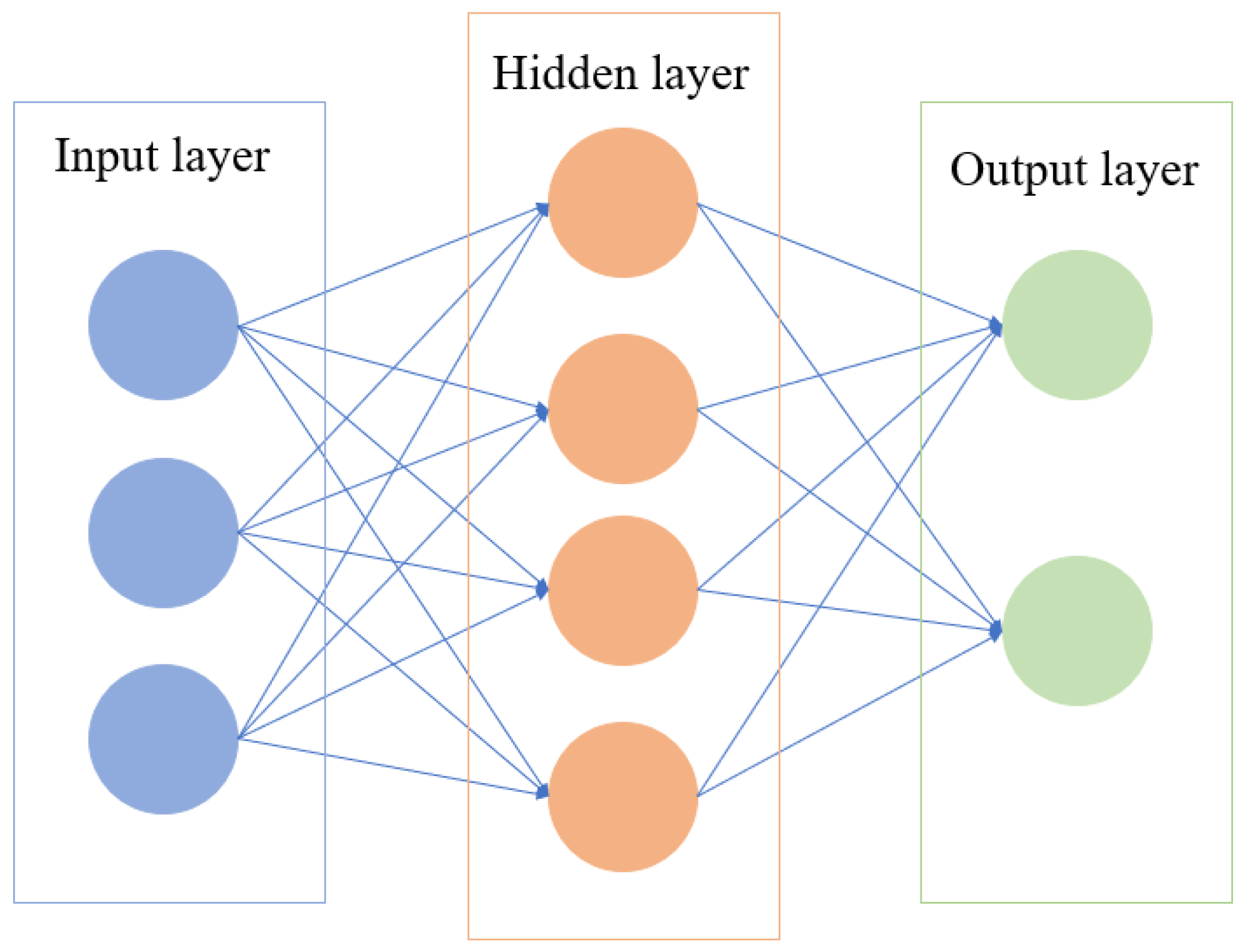
Convolution Neural networks analyze image information to find the exact situation in the environment, and Deep q learning achieves robot navigation in a noble multi-robot path-planning algorithm [110]. This algorithm learns the mutual influence of robots to compensate for the drawback of conventional path-planning algorithms. In an unknown environment, a bio-inspired neural network is developed with the negotiation method, and each neuron has a one-to-one correspondence with the position of the grid map [111]. A biologically inspired neural network map is presented for task assignment and path planning, and it is used to calculate the activity values of robots in the maps of each target and select the winner with the highest activity value, then perform path planning [112]. The simple neural network diagram is exhibited in the following Figure 9.
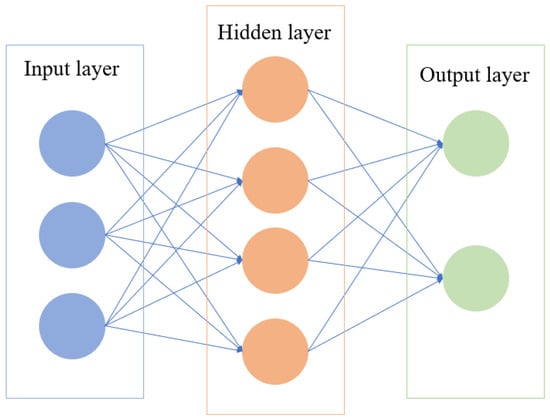
Figure 9.
Diagram of a three-layer neural network.
Moreover, a multi-agent path-planning algorithm based on deep reinforcement learning is proposed, providing high efficiency [113]. Another multi-agent reinforcement learning is developed in [114], and it constructs a node network and establishes an integer programming model to extract the shortest path. The improved Q-learning plans the collision-free path for a single robot in a static environment and then uses the algorithm to achieve collision-free motion among robots based on prior knowledge in [115]. The reinforcement learning framework is applied to optimize the quality of service and path planning, describe the users’ requirements, and consider geometric distance and risk by reinforcement learning reward matrix with a sigmoid-like function [116].
An attention neural network is used for generating the multimachine collaborative path planning as attention reinforcement learning, and it can meet high real-time requirements [117]. A deep Q-network is implemented with a Q-learning algorithm in a deep reinforcement learning algorithm for a productive neural network to handle multi-robot path planning with faster convergence [118]. The meta-reinforcement learning is designed based on transfer learning in [119], and it improves proximal policy optimization by covariance matrix adaptation evolutionary strategies to avoid static and dynamic obstacles.
Multi-agent reinforcement learning is improved by an iterative single-head attention mechanism for multi-UAV path planning, and it calculates robot interactions for each UAV’s control decision-making [120]. Fuzzy reinforcement learning is proposed for the continuous-time path-planning algorithm, combining a modified Wolf-PH and fuzzy Q-iteration algorithm for cooperative tasks [121].
2.5. Others
The algorithms based on mathematical principles or other unclassified systems are listed in this session. These principles of algorithms are not typically classified into four classifications: classical, heuristic, bio-inspired, and AI-based approaches.
A multi-robot path planning system is developed with Polynomial-Time for solutions with optimality constant-factor in [14], and it provides efficient implementations and adapted routing subroutines. A multi-robot path-planning algorithm for industrial robots is presented based on the first low polynomial-time algorithm on grids [122]. An innovative method based on Fast Marching Square is proposed in [123] for simple priority-based speed control, the planning phase, and conflict resolution in 3D urban environments. The fast Marching Square algorithm is also used in a triangular deformable leader–follower formation for multi-UAV coverage path planning [124].
Ref. [125] combined polynomial time with Push and spin algorithm for multi-robot path-planning algorithm and enhances the performance of choosing the best path. A first low-polynomial running time algorithm is proposed for multi-robot path planning in grid-like environments and solves average overall problem instances by constant factors make-span optimal solutions [126]. For optimal multi-robot coverage path planning, spanning tree coverage is proposed, and it divides the surface into many equal areas for each robot to guarantee minimum coverage path, complete coverage, and a non-backtracking solution [127].
For multi-UAV coverage path planning, a metric Cartesian system is proposed, and it transforms the coordinates into Cartesian and splits the field to assign to each robot, then forms the path with minimizing the time [2]. Probability Hypothesis Density representation is used to optimize the number of observed objects in multi-agent informed path planning, and it can represent unseen objects [128]. An iterative min–max improvement algorithm is designed to make span-minimized multi-agent path planning to solve the constrained optimization problem using a local search approach in discrete space [129].
The new route-based optimization model is presented for multi-UAV coverage path planning with column generation, and it can generate feasible paths and trace energy required for mission phases [130]. A multi-agent collaborative path-planning algorithm is provided in [131] to guarantee complete area coverage and exploration and use a staying alive policy to consider battery charge level limitation in the indoor environment.
Integer linear programming models the path planning problem for three objectives with task due times, including minimizing total unit penalties, tardiness, and maximum lateness [132]. Integer linear programming solves the multi-robot association path planning problem for optimizing the path and robots’ access points associations in industrial scenarios [133]. For finding the optimal path for robots to perform tasks, the optimal problem is transformed into integer linear programming with the Petri net model in [134]. One-way multi-robot path planning is proposed for the warehouse-like environment, and it is based on Integer programming to reduce the robots’ configuration costs [135].
A mixed-integer linear programming formulation is designed for multi-robot discrete path planning, and it extends the single robot decision model to multi-robot settings with anticipated feedback data [4]. It supports real-time action based on modeling extension.
For multi-agent navigation, the reciprocal velocity obstacles (RVO) model is used for collision detection and prevention and uses an agent-based high-level path planner [136]. A cooperative cloud robotics architecture is developed as a cooperative data fusion system to gather data from various sensing sources and renew the global view to extend the field of view for each AGV in the industrial environment and uses flexible global and local path planning to avoid unexpected obstacles and congestion zones [1].
The hybrid approach is presented in [137] based on the improved Interfered Fluid Dynamical System and the Lyapunov Guidance Vector Field for multi-UAV cooperative path planning. It introduces a vertical component for target tracking and uses the improved Interfered Fluid Dynamical System to resolve local minimum problems and avoid obstacles. Cooperative sensing and path planning for multi-vehicle is transformed as a partially observable decision-making problem, and it uses Markov decision processes as a decision policy and deploys a multi-vehicle communication framework [138].
2.6. Discussion of Path Planning Classification
The classical approaches include APF and sampling-based algorithms, such as RRT. The classical techniques usually require more computational time and space, especially for the sampling-based methods. Furthermore, the classical techniques cannot ensure completeness or capability, and it requires a predefined graph and is difficult for them to re-plan the path during implementation.
A* and dynamic A* (D*) algorithms are standard applications for heuristic algorithms. The heuristic algorithms primarily consist of the graph search algorithm, and they are easy to apply for path planning problems and evaluate the path by the developed cost function. The heuristic algorithms can successfully provide the globally optimal path with lower required runtime and space than the classical approaches in a graph.
The bio-inspired approaches have been widely researched in recent years as the primary algorithms used in multi-robot path planning, especially metaheuristic algorithms. This paper discusses PSO, GA, ACO, PIO, and GWO. They are inspired by nature, such as the social behavior of animals. The bio-inspired approaches use various particles to generate the optimal solution for the defined problem.
The AI-based approaches based on fuzzy logic or machine learning have gained more attention recently. They have fast computation abilities, and the models are usually adapted for online path planning. The AI-based strategies learn from the previous data to train the models. The neural network is the primary application of machine learning for multi-robot path planning, which consists of multiple layers for learning. The detailed analysis refers to Section 4.1.
Path planning is part of the multi-robot system’s consideration, and the structure of the multi-robot system can be classified as centralized or decentralized based on the planner. The multi-robot system is centralized if the system has supervisory control or a central planner. For robots making their decisions, the system is decentralized. The details of the decision-making of the multi-robot system refer to Section 3.
3. Decision Making
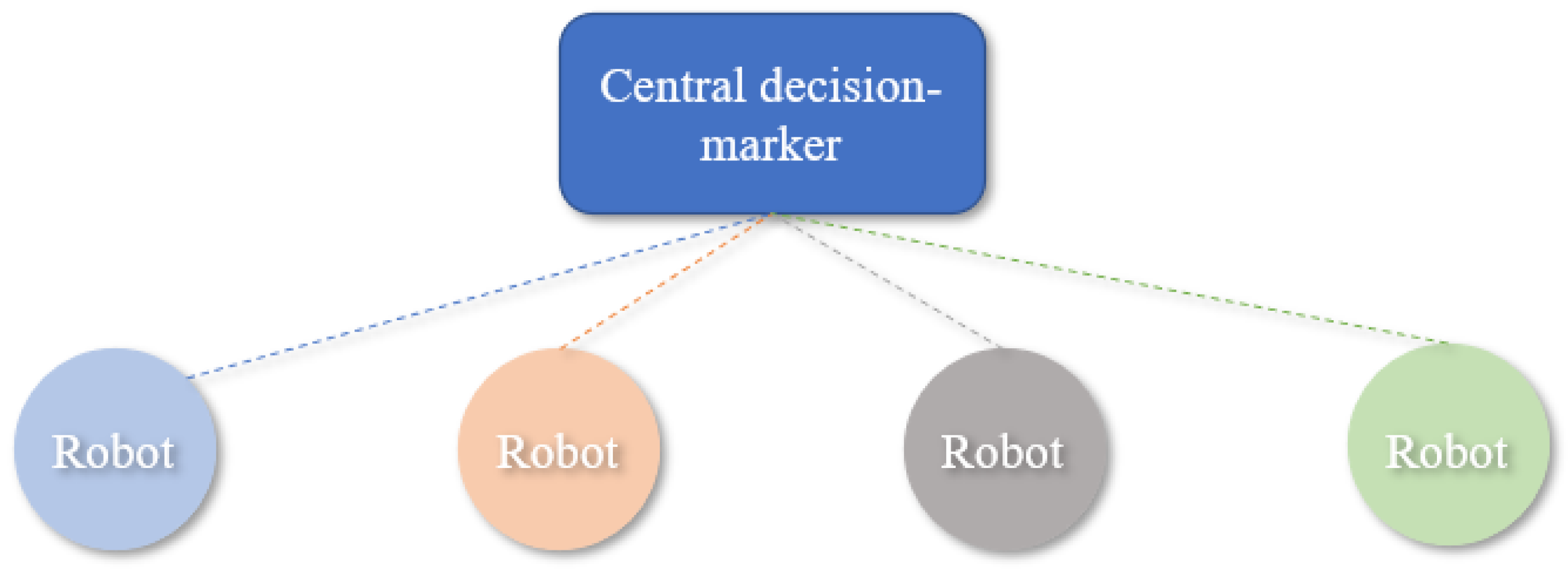
A Multi-robot system can be a centralized or decentralized structure. A centralized system is controlled by the central decision-maker, while a decentralized multi-robot system has no supervisory control. Figure 10 exhibits a centralized framework. Decentralized architecture has more vital fault-tolerant ability with poor global ability. Figure 11 indicates a decentralized framework in which robots use the neighbors’ information.
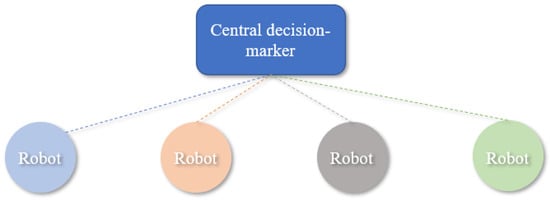
Figure 10.
Structure of a centralized framework.
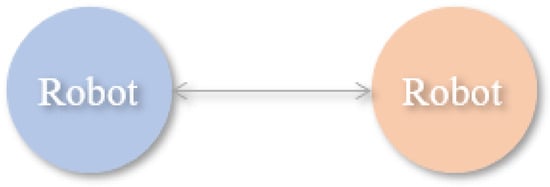
Figure 11.
Structure of a decentralized framework.
3.1. Centralized
A centralized framework for an industrial robot is proposed in [139], which combines GA and A* algorithms for 2D multi-robot path planning. GA is utilized for task allocation, and the A* algorithm is for path planning, and this approach addresses collision avoidance. A two-stage centralized framework solves multi-agent pickup and delivery problems, and it achieves path and action planning with orientation under non-uniform environments by heuristic algorithms, detecting, and resolving conflicts by a synchronized block of information [140].
A practical centralized framework is developed based on an integer linear programming model, and it operates time expansion in the discrete roadmap to obtain the space-time model with dived and conquer heuristic and reachability analysis [19]. In grid graphs, a centralized and decoupled algorithm is proposed for multi-robot path planning in automated and on-demand warehouse-like settings, and it explores optimal sub-problem solutions and path diversification databases for resolving local path conflicts [141]. It uses a decoupling-based planner with two heuristic attack phases and goal configuration adjustments.
Ref. [142] uses a centralized controller for multi-target multi-sensor tracking for environmental data acquisition for path planning and feedback control for sending the path to the system. The optimal bid valuation is proposed with the Dijkstra algorithm to find the shortest path, and the proposed centralized model supports an alternative sampling-based method to reduce the computation time with achieving optimality [20]. A self-organizing map is used for data collection tasks and active perception for online multi-robot path planning, and it jointly picks and allocates nodes and finds sequences of sensing positions [143].
A mixed-integer programming formulation is adapted for a discrete centralized multi-agent path planning problem, and a two-phase fuzzy programming technique gains the Pareto optimal solution in [144]. The centralized simultaneous inform and connect (SIC) strategy is applied for multi-objective path planning by GA, and it uses SIC to optimize search, communicate and find the best path, and monitor tasks with quality of service [145].
A developed synthesized A* algorithm is used for path planning through a centralized meta-planner based on Bag of Tasks, and it runs on distributed computing platforms to avoid dynamic obstacles [146]. A wireless network is proposed for commutation among the robots in APF links, and it uses the Software Defined Network technique to update the network architecture and employ the topology and APF to establish a network control model [147].
A centralized architecture has a high degree of coordination, while dynamic and real-time actions are weak [148]. The decentralized structure is proposed to overcome the drawback of the centralized structure, thereby, providing a higher level of flexibility.
3.2. Decentralized
Task assignment for multi-robot is essential during path planning. The decentralized heuristic path-planning algorithm is proposed as Space utilization optimization for multi-robot structures, and it reduces computation time and the number of conflicts to gain the solution for one-shot and life-long problems [149]. An offline time-independent approach is developed with deadlock-based search and conflict-based search to assign the path to each robot when agents cannot share information [150].
The distributed multi-UAV system utilizes an insertion-based waypoint for path planning and its reconfiguration in [151]. The roadmap algorithm receives near-optimal paths in a decentralized coordination strategy to maximize connectivity and redundancy, while the global path planning utilizes shared information for the proposed two-layer control architecture [152].
The coordinated locomotion of a multi-robot system is divided into sub-problems, such as homogenous prioritized multi-robot path planning and task planning, and it uses prioritized reinforcement learning for these problems [22]. For a swarm of UAVs, PSO is adapted as a planner for distributed full coverage path planning in a dynamic and stochastic environment, minimizing the cost function and maximizing the fitness function [3].
The enhanced A* algorithm referred to as the MAPP algorithm, is delivered in [153] as the decentralized planner for task assignment and cooperative path planning for multi-UAV in urban environments. Free-ranging motion scheme is implemented in autonomous multi-AGV path planning and motion coordination. It considers nonholonomic vehicle constraints for path planning and reliable detection and resolution of conflicts for motion coordination based on a priority scheme [154].
A sampling-based motion planning paradigm is developed for decentralized multi-robot belief space planning in an unknown environment for high-dimensional state spaces in [21], and it calculates the utility of each path based on incremental smoothing of efficient inference and insights from the factor graph. A fully completed distributed algorithm is developed for considering plan restructuring, individual path planning, and priority decision-making for a distributed multi-agent system in [155].
Graph search algorithm and APF are mixed for multi-robot delivery service in different environments, and it uses a strongly connected digraph to simplify the path planning problem and use APF to prove flexibly [156].
A cluster-based decentralized task assignment is proposed for real-time missions [48]. It generates a path, assigns tasks for each robot in the initial planning stage, and adds the popup tasks into the task list to be considered in the next planning stage. A novel smooth hypocycloidal path is developed for multi-robot motion planning with local communication, and it maintains safe clearances with obstacles [157].
A multi-agent distributed framework formulates the path planning problem as a centralized linear program and then uses a framework for each agent while only communicating with its neighbors as the distributed algorithms [158]. The proposed model in [159] integrates decision-making policies and local communication for multi-robot navigation in constrained workspaces, and it uses a convolutional neural network to extract features from observations with a graph neural network to achieve robot communication.
A localized path planning and a task allocation module are combined into a decentralized task and path planning framework, and it models each task as a mixed observed Markov Decision Process or Markov Decision Process, using the max-sum algorithm for task allocation and the localized forward dynamic programming scheme for conflict resolution [160].
A Graph Neural Network is utilized to combine with a key-query-like mechanism to evaluate the relative importance of messages and learn communication policies in a decentralized multi-robot system [161]. The path planning problem is formulated as a decentralized partially observable Markov decision process in [162], and the multi-agent reinforcement learning approach is proposed for multi-robot path planning to harvest data from distributed end devices. It can support non-communicating, cooperative, and homogenous UAVs, and the control policy can be used for challenging urban environments without prior knowledge.
A genetic programming approach is proposed in a decentralized framework, and the robots conduct the learning program to determine the following action in real-time until they reach their respective destinations [163]. A decentralized multi-robot altruistic coordination is improved for cooperative path planning and resolves deadlock situations [164]. APF is adapted in a proposed decentralized space-based potential field algorithm for a group of robots to explore an area quickly and connect with the team by dispersion strategy, using a monotonic coverage factor for a map exchange protocol, avoiding minima, and realistic sensor bounds [165].
Another study [166] proposed APF with the notion of priority, the neighborhood system, and the non-minimum speed algorithm to resolve the intersection of robots and minimum local problems for the multi-robot system. The multi-agent Rapidly exploring Pseudo-random Tree is developed for real-time multi-robot motion planning and control based on the classical Probabilistic Road Map (PRM) algorithm. It extends PRM as a deterministic planner with probabilistic completeness, simplicity, and fast convergence [167].
3.3. Discussion of Decision-Making Strategies
The centralized framework has higher control abilities for robots, and the actions are directly sent from the center controller to the robots, making decisions for each robot. It provides better support and task assignment scheduling, and the algorithms applied in the centralized framework have no restrictions. The cited papers use the classical approaches, the heuristic algorithms, bio-inspired, and AI-based techniques for the centralized framework, in particular the heuristic algorithms.
However, centralized frameworks are weak in dynamic applications. The decentralized structure is proposed to overcome the drawbacks of the centralized frameworks, and it makes robots can communicate with others and share information. The algorithms used in the decentralized structure involve heuristic algorithms, optimization metaheuristic algorithms, neural networks, APF, sampling-based approaches, and AI-based algorithms. For more discussion of decision-making strategies, refer to Section 4.2.
4. Discussion and Conclusions
4.1. Multi-Robot Path Planning
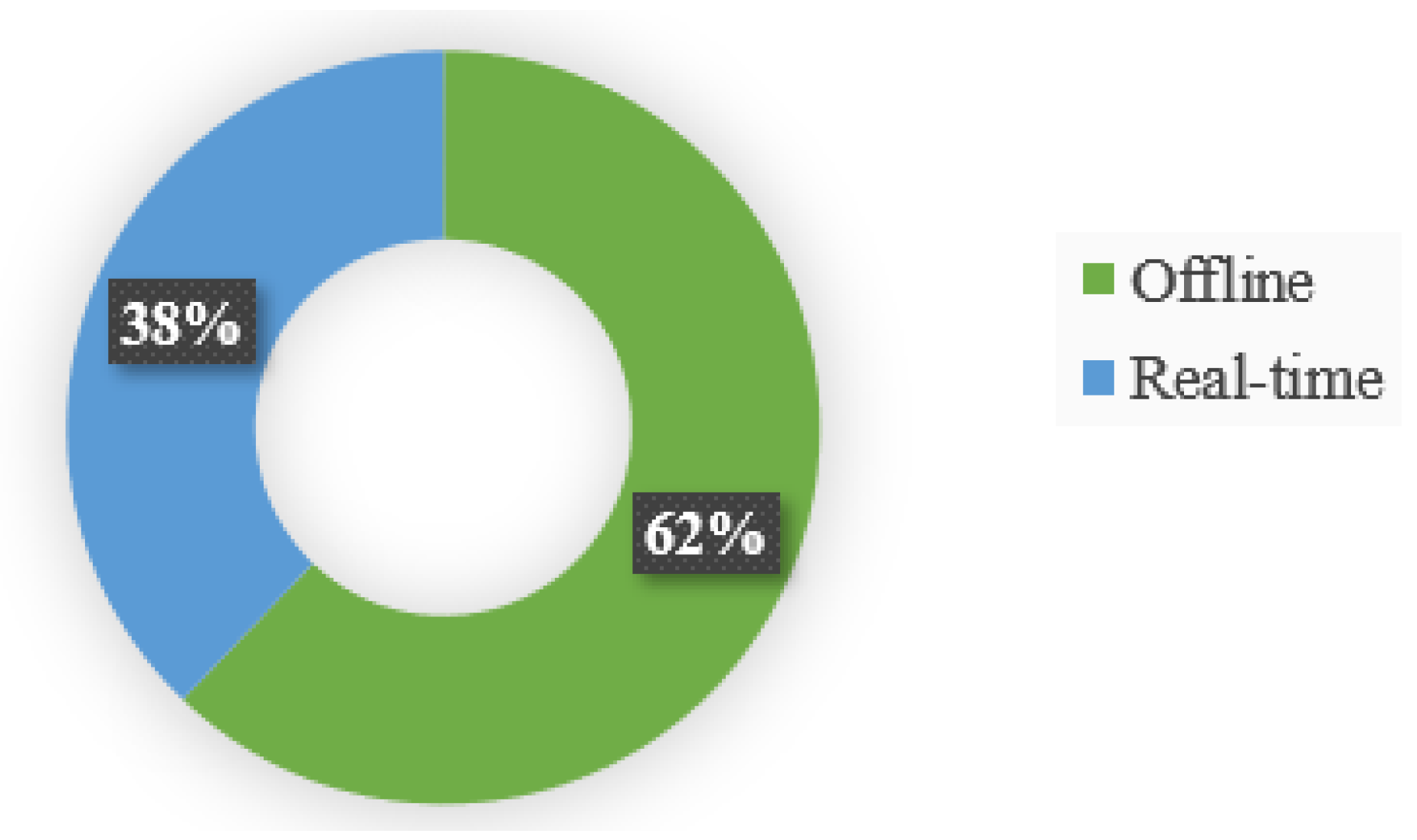
From the literature, the multi-robot path-planning approaches are classified into four primary categories: classical approaches, heuristic approaches, bio-inspired techniques, and artificial-intelligence-based approaches. Table 1 summarizes the main algorithms used in the categories, focusing on real-time implementation. The online/offline implementation percentage is indicated in Figure 12. The offline executions occupy 62% of the multi-robot path-planning approaches, and real-time operation reaches 38%.

Table 1.
Comparison of multi-robot path planning algorithms.
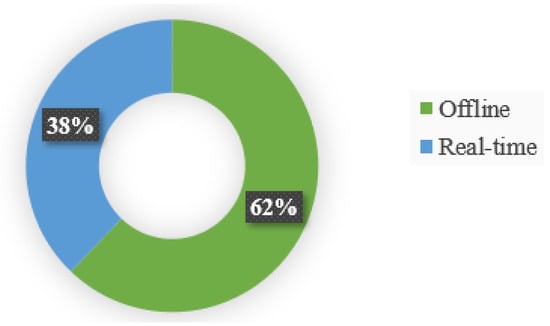
Figure 12.
Offline/real-time implementation.
The classical approach requires huge computational space to save the predefined map and generated nodes, and thus they are mainly implemented in offline strategies. In the mentioned papers, only 36.36% of the classical approaches can be employed for online performance. The hybridization of the classical approach is adapted to solve the mentioned problem and achieve real-time implementation by other algorithms with developed algorithms or functions. 72.73% of papers are improved as hybrid algorithms to overcome the drawbacks of the classical approaches.
The heuristic algorithms require less computation space than the classical approaches, and they can produce complete solutions. It is typical for the heuristic algorithms to be integrated with other algorithms, and the percentage of the hybrid approaches reaches 88.89%. Furthermore, 66.67% of the papers indicate they can be applied for online path planning and are achieved by computational efficiency. The power heuristic algorithms or the approaches involved in interactive robots can be used for online processing but with poor convergence performance.
The bio-inspired techniques are proposed for simple but powerful and robust solutions. They can consider multiple constraints during path planning, even for a complex or dynamic environment. From the cited literature, PSO and GA are mainly involved in path optimization. High computational efficiency and fast convergence ensure real-time performance in dealing with dynamic obstacles, and 19.44% of metaheuristic algorithms demonstrate real-time abilities. The hybrid coevolutionary algorithms are usually proposed to overcome the drawbacks of a single evolutionary algorithm, such as trapping in local optima and uncertainly scenes. The percentage of the hybrid approaches reaches 66.67%.
The AI-based approaches are developed to satisfy the dynamic environmental changes, especially with machine learning. Machine learning for multi-robot path planning mainly includes neural network and reinforcement learning. They can usually achieve dynamic operation according to the environmental changes with the designed model or sensors, reaching 75% cited in AI-based papers. 60% of AI-based algorithms are combined with other approaches to improve learning abilities and reduce the consumed time.
4.2. Decision-Making
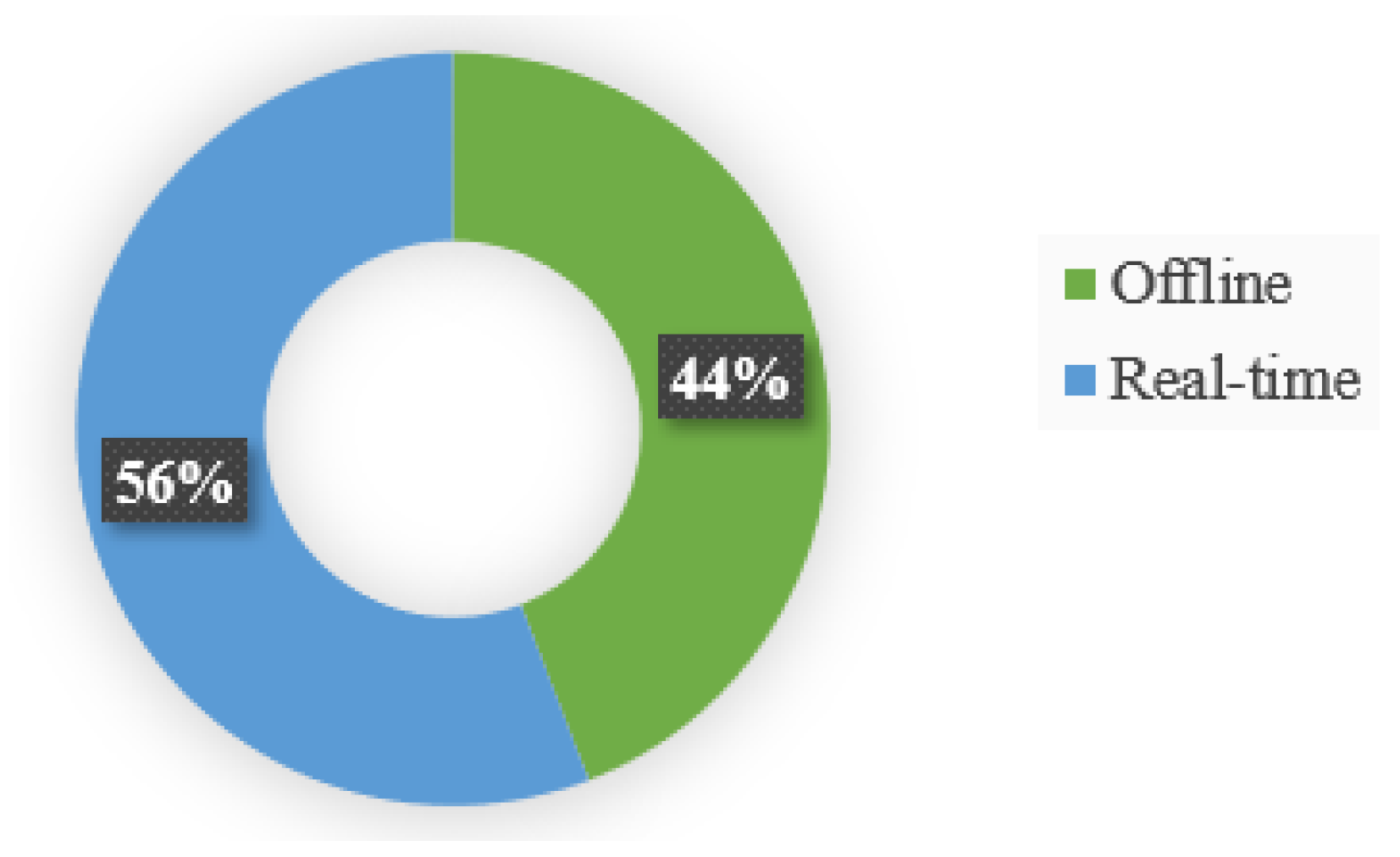
Additionally, the decision-making strategies can be divided into two categories, centralized and decentralized. Table 2 compares the decision-making approaches for algorithms, real-time application, and hybrid techniques. Figure 13 indicates the partitions of the real-time implementation; the percentage of real-time performance reaches 56%, and the portion of the offline techniques is 44%. The real-time implementation has a higher rate due to the cited literature on the decentralized framework.

Table 2.
Comparison of decision-making approaches.
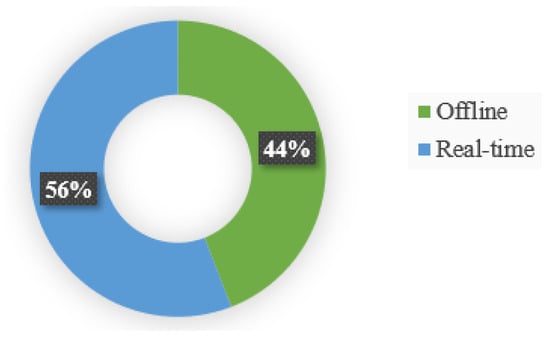
Figure 13.
Offline/real-time implementation of the decision-making strategies.
For the centralized framework, the implemented algorithms include classical, bio-inspired, heuristic, and AI-based approaches. It is general for an algorithm to combine with other algorithms for improvement, and 72.73% of the cited centralized papers propose hybrid strategies. The heuristic techniques or the classical methods are integrated with the bio-inspired algorithms or network communications. The rate of real-time operation in the centralized framework reaches 54.55%.
The centralized framework achieves real-time implementation by an online network/system, the algorithm with fast speed, or data generation from the sensors.
The decentralized framework has more real-time applications than the centralized framework. The robots gain information from the neighbors’ robots to determine the next step and operate the local communication system immediately. A total of 57.14% of the decentralized approaches support the online operations. The algorithms with fast convergence, simplicity, excellent robustness or little computational time and space are widely implemented in the structure. Only 23.81% of the cited decentralized papers involve the hybrid approaches.
Moreover, the hybrid structure has been developed recently to combine the advantages of centralized and decentralized approaches. It uses centralized problem formation while the robots can make their decisions during task operations. Robots can gain information from other robots or accomplish tasks under distributed structure. The employed techniques have no restrictions because the hybrid method combines the benefits of centralized and decentralized methods as [141,158,168].
4.3. Challenge
From the review of multi-robot path planning and decision-making strategies, the traditional challenges involved in multi-robot path planning can be considered local optima, ungranted completeness, and slow convergence. Many papers aim to solve these problems by integrating the different algorithms or by using a developed controller. Nevertheless, this paper discovered a new challenge, as the multi-robot path-planning approaches have not considered fault tolerance. The proposed papers mention real-time implementation; however, most articles mainly focus on computational efficiency or model simplicity to provide faster convergence for online computation.
However, in real-time performance, the update of the robots’ status and the backup of robots’ failures are essential. The robots can send positions or motions to the controller or the neighbors to update their status immediately rather than entirely relying on the predefined path, which can be achieved by localization or vision sensors. The multi-robot system’s fault tolerance is aimed to support the system operating as expected, even if a robot fails.
For actual applications, a multi-robot system should detect the failure immediately and broadcast the information to avoid collisions with other robots or path congestion. Furthermore, the other robots should adjust their defined task plans or paths in real-time to achieve the tasks if necessary. This has no limitations of the system framework for fault tolerance because the centralized framework can inform all robots quickly, and the decentralized framework can send the fault signs to the neighbor robots.
Author Contributions
Conceptualization, S.L.; methodology, S.L.; software, S.L.; validation, S.L.; formal analysis, S.L.; investigation, S.L.; resources, S.L.; data curation, S.L.; writing—original draft preparation, S.L.; writing—review and editing, S.L., A.L. and J.W.; visualization, S.L.; supervision, J.W. and X.K.; project administration, S.L., J.W. and X.K.; funding acquisition, J.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| UAV | Unmanned Aerial Vehicle |
| AGV | Automated Guided Vehicle |
| USV | Unmanned Surface Vessel |
| AUV | Autonomous Underwater Vehicle |
| AI | Artificial Intelligence |
| APF | Artificial Potential Field |
| RRT | Rapidly exploring Random Tree |
| PSO | Particle Swarm Optimization |
| GBD | Grid Blocking Degree |
| GA | Genetic Algorithm |
| PIO | Pigeon-Inspired Optimization |
| GWO | Grey Wolf Optimizer |
| RVO | Reciprocal Velocity Obstacles |
| SIC | Simultaneous Inform and Connect |
| PRM | Probabilistic Road Map |
| D* | Dynamic A* |
References
- Cardarelli, E.; Digani, V.; Sabattini, L.; Secchi, C.; Fantuzzi, C. Cooperative cloud robotics architecture for the coordination of multi-AGV systems in industrial warehouses. Mechatronics 2017, 45, 1–13. [Google Scholar] [CrossRef]
- Tevyashov, G.K.; Mamchenko, M.V.; Migachev, A.N.; Galin, R.R.; Kulagin, K.A.; Trefilov, P.M.; Onisimov, R.O.; Goloburdin, N.V. Algorithm for Multi-drone Path Planning and Coverage of Agricultural Fields. In Agriculture Digitalization and Organic Production; Smart Innovation, Systems and Technologies; Springer: Berlin/Heidelberg, Germany, 2022; Chapter 25; pp. 299–310. [Google Scholar] [CrossRef]
- Ahmed, N.; Pawase, C.J.; Chang, K. Distributed 3-D Path Planning for Multi-UAVs with Full Area Surveillance Based on Particle Swarm Optimization. Appl. Sci. 2021, 11, 3417. [Google Scholar] [CrossRef]
- Berger, J.; Lo, N. An innovative multi-agent search-and-rescue path-planning approach. Comput. Oper. Res. 2015, 53, 24–31. [Google Scholar] [CrossRef]
- Nagasawa, R.; Mas, E.; Moya, L.; Koshimura, S. Model-based analysis of multi-UAV path planning for surveying postdisaster building damage. Sci. Rep. 2021, 11, 18588. [Google Scholar] [CrossRef]
- Pereira, T.; Moreira, A.P.G.M.; Veloso, M. Multi-Robot Planning for Perception of Multiple Regions of Interest. In ROBOT 2017: Third Iberian Robotics Conference; Advances in Intelligent Systems and Computing; Springer: Berlin/Heidelberg, Germany, 2018; Chapter 23; pp. 275–286. [Google Scholar] [CrossRef]
- Tian, S.; Li, Y.; Kang, Y.; Xia, J. Multi-robot path planning in wireless sensor networks based on jump mechanism PSO and safety gap obstacle avoidance. Future Gener. Comput. Syst. 2021, 118, 37–47. [Google Scholar] [CrossRef]
- Ravankar, A.; Ravankar, A.A.; Kobayashi, Y.; Emaru, T. Symbiotic Navigation in Multi-Robot Systems with Remote Obstacle Knowledge Sharing. Sensors 2017, 17, 1581. [Google Scholar] [CrossRef]
- Li, H.; Zhao, T.; Dian, S. Prioritized planning algorithm for multi-robot collision avoidance based on artificial untraversable vertex. Appl. Intell. 2021, 52, 429–451. [Google Scholar] [CrossRef]
- Cruz, D.L.; Yu, W. Path planning of multi-agent systems in unknown environment with neural kernel smoothing and reinforcement learning. Neurocomputing 2017, 233, 34–42. [Google Scholar] [CrossRef]
- Kyprianou, G.; Doitsidis, L.; Chatzichristofis, S.A. Towards the Achievement of Path Planning with Multi-robot Systems in Dynamic Environments. J. Intell. Robot. Syst. 2021, 104, 15. [Google Scholar] [CrossRef]
- Liu, Y.; Jiang, C.; Zhang, X.; Mourelatos, Z.P.; Barthlow, D.; Gorsich, D.; Singh, A.; Hu, Z. Reliability-Based Multivehicle Path Planning Under Uncertainty Using a Bio-Inspired Approach. J. Mech. Des. 2022, 144, 091701. [Google Scholar] [CrossRef]
- Shi, W.; He, Z.; Tang, W.; Liu, W.; Ma, Z. Path Planning of Multi-Robot Systems With Boolean Specifications Based on Simulated Annealing. IEEE Robot. Autom. Lett. 2022, 7, 6091–6098. [Google Scholar] [CrossRef]
- Han, S.D.; Rodriguez, E.J.; Yu, J. SEAR: A Polynomial-Time Multi-Robot Path Planning Algorithm with Expected Constant-Factor Optimality Guarantee. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 1–9. [Google Scholar] [CrossRef]
- MahmoudZadeh, S.; Abbasi, A.; Yazdani, A.; Wang, H.; Liu, Y. Uninterrupted path planning system for Multi-USV sampling mission in a cluttered ocean environment. Ocean. Eng. 2022, 254, 111328. [Google Scholar] [CrossRef]
- Cai, W.; Zhang, M.; Zheng, Y.R. Task Assignment and Path Planning for Multiple Autonomous Underwater Vehicles Using 3D Dubins Curves (dagger). Sensors 2017, 17, 1607. [Google Scholar] [CrossRef] [PubMed]
- Lurz, H.; Recker, T.; Raatz, A. Spline-based Path Planning and Reconfiguration for Rigid Multi-Robot Formations. Procedia CIRP 2022, 106, 174–179. [Google Scholar] [CrossRef]
- Kapoutsis, A.C.; Chatzichristofis, S.A.; Doitsidis, L.; de Sousa, J.B.; Pinto, J.; Braga, J.; Kosmatopoulos, E.B. Real-time adaptive multi-robot exploration with application to underwater map construction. Auton. Robot. 2015, 40, 987–1015. [Google Scholar] [CrossRef]
- Yu, J.; Rus, D. An Effective Algorithmic Framework for Near Optimal Multi-robot Path Planning. In Robotics Research; Springer Proceedings in Advanced Robotics; Springer: Berlin/Heidelberg, Germany, 2018; Chapter 30; pp. 495–511. [Google Scholar] [CrossRef]
- Öztürk, S.; Kuzucuoğlu, A.E. Optimal bid valuation using path finding for multi-robot task allocation. J. Intell. Manuf. 2014, 26, 1049–1062. [Google Scholar] [CrossRef]
- Regev, T.; Indelman, V. Decentralized multi-robot belief space planning in unknown environments via identification and efficient re-evaluation of impacted paths. Auton. Robot. 2017, 42, 691–713. [Google Scholar] [CrossRef]
- Veeramani, S.; Muthuswamy, S. Hybrid type multi-robot path planning of a serial manipulator and SwarmItFIX robots in sheet metal milling process. Complex Intell. Syst. 2021, 8, 2937–2954. [Google Scholar] [CrossRef]
- Gul, F.; Mir, I.; Abualigah, L.; Sumari, P.; Forestiero, A. A Consolidated Review of Path Planning and Optimization Techniques: Technical Perspectives and Future Directions. Electronics 2021, 10, 2250. [Google Scholar] [CrossRef]
- Patle, B.K.; Babu, L.G.; Pandey, A.; Parhi, D.R.K.; Jagadeesh, A. A review: On path planning strategies for navigation of mobile robot. Def. Technol. 2019, 15, 582–606. [Google Scholar] [CrossRef]
- Sanchez-Ibanez, J.R.; Perez-Del-Pulgar, C.J.; Garcia-Cerezo, A. Path Planning for Autonomous Mobile Robots: A Review. Sensors 2021, 21, 7898. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.Y.; Lin, W.M.; Chen, A.X. Path Planning for the Mobile Robot: A Review. Symmetry 2018, 10, 450. [Google Scholar] [CrossRef]
- Chen, Y.; Yu, J.; Su, X.; Luo, G. Path Planning for Multi-UAV Formation. J. Intell. Robot. Syst. 2014, 77, 229–246. [Google Scholar] [CrossRef]
- Chen, H.; Wang, Q.; Yu, M.; Cao, J.; Sun, J. Path Planning for Multi-robot Systems in Intelligent Warehouse. In Internet and Distributed Computing Systems; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2018; Chapter 13; pp. 148–159. [Google Scholar] [CrossRef]
- Nazarahari, M.; Khanmirza, E.; Doostie, S. Multi-objective multi-robot path planning in continuous environment using an enhanced genetic algorithm. Expert Syst. Appl. 2019, 115, 106–120. [Google Scholar] [CrossRef]
- Wang, X.; Sahin, A.; Bhattacharya, S. Coordination-free Multi-robot Path Planning for Congestion Reduction Using Topological Reasoning. arXiv 2022. [Google Scholar] [CrossRef]
- Wang, B.; Zhou, K.; Qu, J. Research on Multi-robot Local Path Planning Based on Improved Artificial Potential Field Method. In Proceedings of the Fifth Euro-China Conference on Intelligent Data Analysis and Applications, Xian, China, 12–14 October 2018; Advances in Intelligent Systems and Computing. Springer: Berlin/Heidelberg, Germany, 2019. Chapter 77. pp. 684–690. [Google Scholar] [CrossRef]
- Zhao, T.; Li, H.; Dian, S. Multi-robot path planning based on improved artificial potential field and fuzzy inference system. J. Intell. Fuzzy Syst. 2020, 39, 7621–7637. [Google Scholar] [CrossRef]
- He, C.; Wan, Y.; Gu, Y.; Lewis, F.L. Integral Reinforcement Learning-Based Multi-Robot Minimum Time-Energy Path Planning Subject to Collision Avoidance and Unknown Environmental Disturbances. IEEE Control. Syst. Lett. 2021, 5, 983–988. [Google Scholar] [CrossRef]
- Xue, J.; Kong, X.; Dong, B.; Xu, M. Multi-Agent Path Planning based on MPC and DDPG. arXiv 2021. [Google Scholar] [CrossRef]
- Turki, E.; Al-Rawi, H. Multi-Robot Path-Planning Problem for a Heavy Traffic Control Application: A Survey. Int. J. Adv. Comput. Sci. Appl. 2016, 7, 179–188. [Google Scholar] [CrossRef]
- Solovey, K.; Salzman, O.; Halperin, D. Finding a needle in an exponential haystack: Discrete RRT for exploration of implicit roadmaps in multi-robot motion planning. Int. J. Robot. Res. 2016, 35, 501–513. [Google Scholar] [CrossRef]
- Shen, L.; Wang, Y.; Liu, K.; Yang, Z.; Shi, X.; Yang, X.; Jing, K. Synergistic path planning of multi-UAVs for air pollution detection of ships in ports. Transp. Res. Part E Logist. Transp. Rev. 2020, 144, 102128. [Google Scholar] [CrossRef]
- Pintado, A.; Santos, M. A First Approach to Path Planning Coverage with Multi-UAVs. In Proceedings of the 15th International Conference on Soft Computing Models in Industrial and Environmental Applications (SOCO 2020), Burgos, Spain, 16–18 September 2020; Advances in Intelligent Systems and Computing. Springer: Berlin/Heidelberg, Germany, 2021. Chapter 64. pp. 667–677. [Google Scholar] [CrossRef]
- Yu, J. Intractability of Optimal Multirobot Path Planning on Planar Graphs. IEEE Robot. Autom. Lett. 2016, 1, 33–40. [Google Scholar] [CrossRef]
- Nedjati, A.; Izbirak, G.; Vizvari, B.; Arkat, J. Complete Coverage Path Planning for a Multi-UAV Response System in Post-Earthquake Assessment. Robotics 2016, 5, 26. [Google Scholar] [CrossRef] [Green Version]
- Avellar, G.S.; Pereira, G.A.; Pimenta, L.C.; Iscold, P. Multi-UAV Routing for Area Coverage and Remote Sensing with Minimum Time. Sensors 2015, 15, 27783–27803. [Google Scholar] [CrossRef]
- Cho, S.W.; Park, J.H.; Park, H.J.; Kim, S. Multi-UAV Coverage Path Planning Based on Hexagonal Grid Decomposition in Maritime Search and Rescue. Mathematics 2021, 10, 83. [Google Scholar] [CrossRef]
- Turki, E.; Al-Rawi, H. MRPPSim: A Multi-Robot Path Planning Simulation. Int. J. Adv. Comput. Sci. Appl. 2016, 7, 145–155. [Google Scholar] [CrossRef]
- Dutta, A.; Bhattacharya, A.; Kreidl, O.P.; Ghosh, A.; Dasgupta, P. Multi-robot informative path planning in unknown environments through continuous region partitioning. Int. J. Adv. Robot. Syst. 2020, 17, 1729881420970461. [Google Scholar] [CrossRef]
- Huang, S.K.; Wang, W.J.; Sun, C.H. A Path Planning Strategy for Multi-Robot Moving with Path-Priority Order Based on a Generalized Voronoi Diagram. Appl. Sci. 2021, 11, 9650. [Google Scholar] [CrossRef]
- Zheng, H.; Yuan, J. An Integrated Mission Planning Framework for Sensor Allocation and Path Planning of Heterogeneous Multi-UAV Systems. Sensors 2021, 21, 3557. [Google Scholar] [CrossRef]
- Yuan, Z.; Yang, Z.; Lv, L.; Shi, Y. A Bi-Level Path Planning Algorithm for Multi-AGV Routing Problem. Electronics 2020, 9, 1351. [Google Scholar] [CrossRef]
- Sun, X.; Liu, Y.; Yao, W.; Qi, N. Triple-stage path prediction algorithm for real-time mission planning of multi-UAV. Electron. Lett. 2015, 51, 1490–1492. [Google Scholar] [CrossRef]
- Singh, A.K. Fault-Detection on Multi-Robot Path Planning. Int. J. Adv. Res. Comput. Sci. 2017, 8, 539–543. [Google Scholar] [CrossRef]
- Wang, Z.; Zlatanova, S. Multi-agent based path planning for first responders among moving obstacles. Comput. Environ. Urban Syst. 2016, 56, 48–58. [Google Scholar] [CrossRef]
- Zagradjanin, N.; Pamucar, D.; Jovanovic, K. Cloud-Based Multi-Robot Path Planning in Complex and Crowded Environment with Multi-Criteria Decision Making using Full Consistency Method. Symmetry 2019, 11, 1241. [Google Scholar] [CrossRef]
- Serpen, G.; Dou, C. Automated robotic parking systems: Real-time, concurrent and multi-robot path planning in dynamic environments. Appl. Intell. 2014, 42, 231–251. [Google Scholar] [CrossRef]
- Salerno, M.; E-Martín, Y.; Fuentetaja, R.; Gragera, A.; Pozanco, A.; Borrajo, D. Train Route Planning as a Multi-agent Path Finding Problem. In Advances in Artificial Intelligence; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2021; Chapter 23; pp. 237–246. [Google Scholar] [CrossRef]
- Bae, J.; Chung, W. Efficient path planning for multiple transportation robots under various loading conditions. Int. J. Adv. Robot. Syst. 2019, 16, 1729881419835110. [Google Scholar] [CrossRef]
- Gujarathi, D.; Saha, I. MT*: Multi-Robot Path Planning for Temporal Logic Specifications. arXiv 2021. [Google Scholar] [CrossRef]
- Modi, V.; Chen, Y.; Madan, A.; Sueda, S.; Levin, D.I.W. Multi-Agent Path Planning with Asymmetric Interactions In Tight Spaces. arXiv 2022. [Google Scholar] [CrossRef]
- Yu, N.N.; Li, T.K.; Wang, B.L.; Yuan, S.P.; Wang, Y. Reliability oriented multi-AGVs online scheduling and path planning problem of automated sorting warehouse system. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1043, 22035. [Google Scholar] [CrossRef]
- Luna, M.A.; Ale Isaac, M.S.; Ragab, A.R.; Campoy, P.; Flores Pena, P.; Molina, M. Fast Multi-UAV Path Planning for Optimal Area Coverage in Aerial Sensing Applications. Sensors 2022, 22, 2297. [Google Scholar] [CrossRef]
- Kim, H.; Kim, D.; Kim, H.; Shin, J.U.; Myung, H. An extended any-angle path-planning algorithm for maintaining formation of multi-agent jellyfish elimination robot system. Int. J. Control. Autom. Syst. 2016, 14, 598–607. [Google Scholar] [CrossRef]
- Mobarez, E.N.; Sarhan, A.; Ashry, M.M. Obstacle avoidance for multi-UAV path planning based on particle swarm optimization. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1172, 12039. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, H.; Chen, Y.; Cheng, L.; Zhang, B. Patrol robot path planning in nuclear power plant using an interval multi-objective particle swarm optimization algorithm. Appl. Soft Comput. 2022, 116, 108192. [Google Scholar] [CrossRef]
- Chen, Y.; Ren, S.; Chen, Z.; Chen, M.; Wu, H. Path Planning for Vehicle-borne System Consisting of Multi Air–ground Robots. Robotica 2019, 38, 493–511. [Google Scholar] [CrossRef]
- Das, P.K.; Behera, H.S.; Das, S.; Tripathy, H.K.; Panigrahi, B.K.; Pradhan, S.K. A hybrid improved PSO-DV algorithm for multi-robot path planning in a clutter environment. Neurocomputing 2016, 207, 735–753. [Google Scholar] [CrossRef]
- He, W.; Qi, X.; Liu, L. A novel hybrid particle swarm optimization for multi-UAV cooperate path planning. Appl. Intell. 2021, 51, 7350–7364. [Google Scholar] [CrossRef]
- Panda, M.R.; Das, P.; Pradhan, S. Hybridization of IWO and IPSO for mobile robots navigation in a dynamic environment. J. King Saud Univ. Comput. Inf. Sci. 2020, 32, 1020–1033. [Google Scholar] [CrossRef]
- Shao, Z.; Yan, F.; Zhou, Z.; Zhu, X. Path Planning for Multi-UAV Formation Rendezvous Based on Distributed Cooperative Particle Swarm Optimization. Appl. Sci. 2019, 9, 2621. [Google Scholar] [CrossRef]
- Paikray, H.K.; Das, P.K.; Panda, S. Optimal Multi-robot Path Planning Using Particle Swarm Optimization Algorithm Improved by Sine and Cosine Algorithms. Arab. J. Sci. Eng. 2021, 46, 3357–3381. [Google Scholar] [CrossRef]
- Tang, B.; Xiang, K.; Pang, M.; Zhanxia, Z. Multi-robot path planning using an improved self-adaptive particle swarm optimization. Int. J. Adv. Robot. Syst. 2020, 17, 1729881420936154. [Google Scholar] [CrossRef]
- Das, P.K.; Behera, H.S.; Panigrahi, B.K. A hybridization of an improved particle swarm optimization and gravitational search algorithm for multi-robot path planning. Swarm Evol. Comput. 2016, 28, 14–28. [Google Scholar] [CrossRef]
- Sahu, B.; Kumar Das, P.; Kabat, M.R. Multi-robot cooperation and path planning for stick transporting using improved Q-learning and democratic robotics PSO. J. Comput. Sci. 2022, 60, 101637. [Google Scholar] [CrossRef]
- Zhong, M.; Yang, Y.; Dessouky, Y.; Postolache, O. Multi-AGV scheduling for conflict-free path planning in automated container terminals. Comput. Ind. Eng. 2020, 142, 106371. [Google Scholar] [CrossRef]
- Saeed, R.A.; Reforgiato Recupero, D.; Remagnino, P. The boundary node method for multi-robot multi-goal path planning problems. Expert Syst. 2021, 38, e12691. [Google Scholar] [CrossRef]
- Song, J.; Liu, L.; Liu, Y.; Xi, J.; Zhai, W.; Yang, G. Path Planning for Multi-Vehicle-Assisted Multi-UAVs in Mobile Crowdsensing. Wirel. Commun. Mob. Comput. 2022, 2022, 9778188. [Google Scholar] [CrossRef]
- Ru, J.; Yu, S.; Wu, H.; Li, Y.; Wu, C.; Jia, Z.; Xu, H. A Multi-AUV Path Planning System Based on the Omni-Directional Sensing Ability. J. Mar. Sci. Eng. 2021, 9, 806. [Google Scholar] [CrossRef]
- Sun, G.; Zhou, R.; Di, B.; Dong, Z.; Wang, Y. A Novel Cooperative Path Planning for Multi-robot Persistent Coverage with Obstacles and Coverage Period Constraints. Sensors 2019, 19, 1994. [Google Scholar] [CrossRef]
- Yanes Luis, S.; Peralta, F.; Tapia Córdoba, A.; Rodríguez del Nozal, Á.R.; Toral Marín, S.; Gutiérrez Reina, D. An evolutionary multi-objective path planning of a fleet of ASVs for patrolling water resources. Eng. Appl. Artif. Intell. 2022, 112, 104852. [Google Scholar] [CrossRef]
- Sun, R.; Tang, C.; Zheng, J.; Zhou, Y.; Yu, S. Multi-robot Path Planning for Complete Coverage with Genetic Algorithms. In Intelligent Robotics and Applications; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2019; Chapter 29; pp. 349–361. [Google Scholar] [CrossRef]
- Xu, M.; Xin, B.; Dou, L.; Gao, G. A Cell Potential and Motion Pattern Driven Multi-robot Coverage Path Planning Algorithm. In Bio-inspired Computing: Theories and Applications; Communications in Computer and Information Science; Springer: Berlin/Heidelberg, Germany, 2020; Chapter 36; pp. 468–483. [Google Scholar] [CrossRef]
- Sarkar, R.; Barman, D.; Chowdhury, N. A Cooperative Co-evolutionary Genetic Algorithm for Multi-Robot Path Planning Having Multiple Targets. In Computational Intelligence in Pattern Recognition; Advances in Intelligent Systems and Computing; Springer: Berlin/Heidelberg, Germany, 2020; Chapter 63; pp. 724–740. [Google Scholar] [CrossRef]
- Farooq, B.; Bao, J.; Raza, H.; Sun, Y.; Ma, Q. Flow-shop path planning for multi-automated guided vehicles in intelligent textile spinning cyber-physical production systems dynamic environment. J. Manuf. Syst. 2021, 59, 98–116. [Google Scholar] [CrossRef]
- Han, Z.; Wang, D.; Liu, F.; Zhao, Z. Multi-AGV path planning with double-path constraints by using an improved genetic algorithm. PLoS ONE 2017, 12, e0181747. [Google Scholar] [CrossRef]
- Xu, W. Path Planning for Multi-AGV Systems based on Two-Stage Scheduling. Int. J. Perform. Eng. 2017, 13, 1347–1357. [Google Scholar] [CrossRef]
- Huang, H.; Zhuo, T. Multi-model cooperative task assignment and path planning of multiple UCAV formation. Multimed. Tools Appl. 2017, 78, 415–436. [Google Scholar] [CrossRef]
- Yi, G.; Feng, Z.; Mei, T.; Li, P.; Jin, W.; Chen, S. Multi-AGVs path planning based on improved ant colony algorithm. J. Supercomput. 2019, 75, 5898–5913. [Google Scholar] [CrossRef]
- Liu, J.; Anavatti, S.; Garratt, M.; Abbass, H.A. Modified continuous Ant Colony Optimisation for multiple Unmanned Ground Vehicle path planning. Expert Syst. Appl. 2022, 196, 116605. [Google Scholar] [CrossRef]
- Huang, L.; Qu, H.; Ji, P.; Liu, X.; Fan, Z. A novel coordinated path planning method using k-degree smoothing for multi-UAVs. Appl. Soft Comput. 2016, 48, 182–192. [Google Scholar] [CrossRef]
- Botteghi, N.; Kamilaris, A.; Sinai, L.; Sirmacek, B. Multi-Agent Path Planning of Robotic Swarms in Agricultural Fields. ISPRS Ann. Photogramm. Remote. Sens. Spat. Inf. Sci. 2020, 1, 361–368. [Google Scholar] [CrossRef]
- Zhang, D.; Duan, H. Social-class pigeon-inspired optimization and time stamp segmentation for multi-UAV cooperative path planning. Neurocomputing 2018, 313, 229–246. [Google Scholar] [CrossRef]
- Wang, B.H.; Wang, D.B.; Ali, Z.A. A Cauchy mutant pigeon-inspired optimization–based multi-unmanned aerial vehicle path planning method. Meas. Control 2020, 53, 83–92. [Google Scholar] [CrossRef]
- Xu, C.; Xu, M.; Yin, C. Optimized multi-UAV cooperative path planning under the complex confrontation environment. Comput. Commun. 2020, 162, 196–203. [Google Scholar] [CrossRef]
- Zhou, M.; Wang, Z.; Wang, J.; Dong, Z. A Hybrid Path Planning and Formation Control Strategy of Multi-Robots in a Dynamic Environment. J. Adv. Comput. Intell. Intell. Inform. 2022, 26, 342–354. [Google Scholar] [CrossRef]
- Huang, G.; Cai, Y.; Liu, J.; Qi, Y.; Liu, X. A Novel Hybrid Discrete Grey Wolf Optimizer Algorithm for Multi-UAV Path Planning. J. Intell. Robot. Syst. 2021, 103, 49. [Google Scholar] [CrossRef]
- Shi, K.; Zhang, X.; Xia, S. Multiple Swarm Fruit Fly Optimization Algorithm Based Path Planning Method for Multi-UAVs. Appl. Sci. 2020, 10, 2822. [Google Scholar] [CrossRef]
- Das, P.K.; Behera, H.S.; Jena, P.K.; Panigrahi, B.K. Multi-robot path planning in a dynamic environment using improved gravitational search algorithm. J. Electr. Syst. Inf. Technol. 2016, 3, 295–313. [Google Scholar] [CrossRef]
- Das, P.K. Hybridization of Kidney-Inspired and Sine–Cosine Algorithm for Multi-robot Path Planning. Arab. J. Sci. Eng. 2019, 45, 2883–2900. [Google Scholar] [CrossRef]
- Panda, M.R.; Dutta, S.; Pradhan, S. Hybridizing Invasive Weed Optimization with Firefly Algorithm for Multi-Robot Motion Planning. Arab. J. Sci. Eng. 2017, 43, 4029–4039. [Google Scholar] [CrossRef]
- Kok, K.Y.; Rajendran, P. Differential-Evolution Control Parameter Optimization for Unmanned Aerial Vehicle Path Planning. PLoS ONE 2016, 11, e0150558. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wang, P.; Yang, L.; Liu, Y.; Lu, Y.; Zhu, X. Novel Swarm Intelligence Algorithm for Global Optimization and Multi-UAVs Cooperative Path Planning: Anas Platyrhynchos Optimizer. Appl. Sci. 2020, 10, 4821. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, M.; Zhang, S.; Zheng, R.; Dong, S. Multi-AUV Adaptive Path Planning and Cooperative Sampling for Ocean Scalar Field Estimation. IEEE Trans. Instrum. Meas. 2022, 71, 9505514. [Google Scholar] [CrossRef]
- Chen, Z.; Alonso-Mora, J.; Bai, X.; Harabor, D.D.; Stuckey, P.J. Integrated Task Assignment and Path Planning for Capacitated Multi-Agent Pickup and Delivery. IEEE Robot. Autom. Lett. 2021, 6, 5816–5823. [Google Scholar] [CrossRef]
- Deng, L.; Ma, X.; Gu, J.; Li, Y.; Xu, Z.; Wang, Y. Artificial Immune Network-Based Multi-Robot Formation Path Planning with Obstacle Avoidance. Int. J. Robot. Autom. 2016, 31, 233–242. [Google Scholar] [CrossRef]
- Kang, Y.T.; Chen, W.J.; Zhu, D.Q.; Wang, J.H. Collision avoidance path planning in multi-ship encounter situations. J. Mar. Sci. Technol. 2021, 26, 1026–1037. [Google Scholar] [CrossRef]
- Liang, J.H.; Lee, C.H. Efficient collision-free path-planning of multiple mobile robots system using efficient artificial bee colony algorithm. Adv. Eng. Softw. 2015, 79, 47–56. [Google Scholar] [CrossRef]
- Al-Jarrah, R.; Shahzad, A.; Roth, H. Path Planning and Motion Coordination for Multi-Robots System Using Probabilistic Neuro-Fuzzy. IFAC-PapersOnLine 2015, 48, 46–51. [Google Scholar] [CrossRef]
- Pandey, A.; Parhi, D.R. Optimum path planning of mobile robot in unknown static and dynamic environments using Fuzzy-Wind Driven Optimization algorithm. Def. Technol. 2017, 13, 47–58. [Google Scholar] [CrossRef]
- K, R.; R, B.; Panchu K, P.; M, R. A novel fuzzy and reverse auction-based algorithm for task allocation with optimal path cost in multi-robot systems. Concurr. Comput. Pract. Exp. 2021, 34, e6716. [Google Scholar] [CrossRef]
- Zohdi, T.I. The Game of Drones: Rapid agent-based machine-learning models for multi-UAV path planning. Comput. Mech. 2019, 65, 217–228. [Google Scholar] [CrossRef]
- Zhu, D.; Liu, Y.; Sun, B. Task Assignment and Path Planning of a Multi-AUV System Based on a Glasius Bio-Inspired Self-Organising Map Algorithm. J. Navig. 2017, 71, 482–496. [Google Scholar] [CrossRef]
- Cao, X.; Zhu, D. Multi-AUV task assignment and path planning with ocean current based on biological inspired self-organizing map and velocity synthesis algorithm. Intell. Autom. Soft Comput. 2015, 23, 31–39. [Google Scholar] [CrossRef]
- Bae, H.; Kim, G.; Kim, J.; Qian, D.; Lee, S. Multi-Robot Path Planning Method Using Reinforcement Learning. Appl. Sci. 2019, 9, 57. [Google Scholar] [CrossRef] [Green Version]
- Zhu, D.; Lv, R.; Cao, X.; Yang, S.X. Multi-AUV Hunting Algorithm Based on Bio-inspired Neural Network in Unknown Environments. Int. J. Adv. Robot. Syst. 2015, 12, 166. [Google Scholar] [CrossRef]
- Zhu, D.; Zhou, B.; Yang, S.X. A Novel Algorithm of Multi-AUVs Task Assignment and Path Planning Based on Biologically Inspired Neural Network Map. IEEE Trans. Intell. Veh. 2021, 6, 333–342. [Google Scholar] [CrossRef]
- Çetinkaya, M. Multi-Agent Path Planning Using Deep Reinforcement Learning. arXiv 2021. [Google Scholar] [CrossRef]
- Hu, H.; Yang, X.; Xiao, S.; Wang, F. Anti-conflict AGV path planning in automated container terminals based on multi-agent reinforcement learning. Int. J. Prod. Res. 2021, ahead-of-print. 1–16. [Google Scholar] [CrossRef]
- Li, B.; Liang, H. Multi-Robot Path Planning Method Based on Prior Knowledge and Q-learning Algorithms. J. Physics. Conf. Ser. 2020, 1624, 42008. [Google Scholar] [CrossRef]
- Chang, H.; Chen, Y.; Zhang, B.; Doermann, D. Multi-UAV Mobile Edge Computing and Path Planning Platform Based on Reinforcement Learning. IEEE Trans. Emerg. Top. Comput. Intell. 2022, 6, 489–498. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, B.; Zhang, M.; Zhang, S.; Guo, D. Multi-UAV Collaborative Path Planning Method Based on Attention Mechanism. Math. Probl. Eng. 2021, 2021, 6964875. [Google Scholar] [CrossRef]
- Yang, Y.; Juntao, L.; Lingling, P. Multi-robot path planning based on a deep reinforcement learning DQN algorithm. CAAI Trans. Intell. Technol. 2020, 5, 177–183. [Google Scholar] [CrossRef]
- Wen, S.; Wen, Z.; Zhang, D.; Zhang, H.; Wang, T. A multi-robot path-planning algorithm for autonomous navigation using meta-reinforcement learning based on transfer learning. Appl. Soft Comput. 2021, 110, 107605. [Google Scholar] [CrossRef]
- Shiri, H.; Seo, H.; Park, J.; Bennis, M. Attention Based Communication and Control for Multi-UAV Path Planning. IEEE Wirel. Commun. Lett. 2022, 11, 1409–1413. [Google Scholar] [CrossRef]
- Luviano, D.; Yu, W. Continuous-time path planning for multi-agents with fuzzy reinforcement learning. J. Intell. Fuzzy Syst. 2017, 33, 491–501. [Google Scholar] [CrossRef]
- Guo, T.; Yu, J. Sub-1.5 Time-Optimal Multi-Robot Path Planning on Grids in Polynomial Time. arXiv 2022. [Google Scholar] [CrossRef]
- Lopez, B.; Munoz, J.; Quevedo, F.; Monje, C.A.; Garrido, S.; Moreno, L.E. Path Planning and Collision Risk Management Strategy for Multi-UAV Systems in 3D Environments. Sensors 2021, 21, 4414. [Google Scholar] [CrossRef] [PubMed]
- Munoz, J.; Lopez, B.; Quevedo, F.; Monje, C.A.; Garrido, S.; Moreno, L.E. Multi UAV Coverage Path Planning in Urban Environments. Sensors 2021, 21, 7365. [Google Scholar] [CrossRef] [PubMed]
- Alotaibi, E.T.S.; Al-Rawi, H. A complete multi-robot path-planning algorithm. Auton. Agents Multi-Agent Syst. 2018, 32, 693–740. [Google Scholar] [CrossRef]
- Yu, J. Average case constant factor time and distance optimal multi-robot path planning in well-connected environments. Auton. Robot. 2019, 44, 469–483. [Google Scholar] [CrossRef]
- Kapoutsis, A.C.; Chatzichristofis, S.A.; Kosmatopoulos, E.B. DARP: Divide Areas Algorithm for Optimal Multi-Robot Coverage Path Planning. J. Intell. Robot. Syst. 2017, 86, 663–680. [Google Scholar] [CrossRef]
- Olofsson, J.; Hendeby, G.; Lauknes, T.R.; Johansen, T.A. Multi-agent informed path planning using the probability hypothesis density. Auton. Robot. 2020, 44, 913–925. [Google Scholar] [CrossRef]
- Wang, W.; Goh, W.B. An iterative approach for makespan-minimized multi-agent path planning in discrete space. Auton. Agents -Multi-Agent Syst. 2014, 29, 335–363. [Google Scholar] [CrossRef]
- Choi, Y.; Choi, Y.; Briceno, S.; Mavris, D.N. Energy-Constrained Multi-UAV Coverage Path Planning for an Aerial Imagery Mission Using Column Generation. J. Intell. Robot. Syst. 2019, 97, 125–139. [Google Scholar] [CrossRef]
- Koval, A.; Sharif Mansouri, S.; Nikolakopoulos, G. Multi-Agent Collaborative Path Planning Based on Staying Alive Policy. Robotics 2020, 9, 101. [Google Scholar] [CrossRef]
- Wang, H.; Chen, W. Multi-Robot Path Planning With Due Times. IEEE Robot. Autom. Lett. 2022, 7, 4829–4836. [Google Scholar] [CrossRef]
- Tatino, C.; Pappas, N.; Yuan, D. Multi-Robot Association-Path Planning in Millimeter-Wave Industrial Scenarios. IEEE Netw. Lett. 2020, 2, 190–194. [Google Scholar] [CrossRef]
- Zhang, H.; Luo, J.; Long, J.; Huang, Y.; Wu, W. Multi-robot Path Planning Using Petri Nets. In Verification and Evaluation of Computer and Communication Systems; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2020; Chapter 2; pp. 15–26. [Google Scholar] [CrossRef]
- Huo, J.; Zheng, R.; Liu, M.; Zhang, S. Integer-Programming-Based Narrow-Passage Multi-Robot Path Planning with Effective Heuristics. arXiv 2021. [Google Scholar] [CrossRef]
- Haciomeroglu, M. Congestion-free multi-agent navigation based on velocity space by using cellular automata. Adapt. Behav. 2015, 24, 18–26. [Google Scholar] [CrossRef]
- Yao, P.; Wang, H.; Su, Z. Cooperative path planning with applications to target tracking and obstacle avoidance for multi-UAVs. Aerosp. Sci. Technol. 2016, 54, 10–22. [Google Scholar] [CrossRef]
- Melin, J.; Lauri, M.; Kolu, A.; Koljonen, J.; Ritala, R. Cooperative Sensing and Path Planning in a Multi-vehicle Environment**This work was in part (Melin, J., Ritala, R.) funded by the Academy of Finland, project “Optimization of observation subsystems in autonomous mobile machines”, O3-SAM. IFAC-PapersOnLine 2015, 48, 198–203. [Google Scholar] [CrossRef]
- Jose, K.; Pratihar, D.K. Task allocation and collision-free path planning of centralized multi-robots system for industrial plant inspection using heuristic methods. Robot. Auton. Syst. 2016, 80, 34–42. [Google Scholar] [CrossRef]
- Yamauchi, T.; Miyashita, Y.; Sugawara, T. Path and Action Planning in Non-uniform Environments for Multi-agent Pickup and Delivery Tasks. In Multi-Agent Systems; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2021; Chapter 3; pp. 37–54. [Google Scholar] [CrossRef]
- Han, S.D.; Yu, J. DDM: Fast Near-Optimal Multi-Robot Path Planning Using Diversified-Path and Optimal Sub-Problem Solution Database Heuristics. IEEE Robot. Autom. Lett. 2020, 5, 1350–1357. [Google Scholar] [CrossRef]
- Olofsson, J.; Veibäck, C.; Hendeby, G.; Johansen, T.A. Outline of a System for Integrated Adaptive Ice Tracking and Multi-Agent Path Planning. In Proceedings of the 2017 Workshop on Research, Education and Development of Unmanned Aerial Systems (RED-UAS), Linkoping, Sweden, 3–5 October 2017; p. 13. [Google Scholar] [CrossRef]
- Best, G.; Faigl, J.; Fitch, R. Online planning for multi-robot active perception with self-organising maps. Auton. Robot. 2017, 42, 715–738. [Google Scholar] [CrossRef]
- Nielsen, I.; Bocewicz, G.; Saha, S. Multi-agent Path Planning Problem Under a Multi-objective Optimization Framework. In Proceedings of the 17th International Conference on Distributed Computing and Artificial Intelligence, Special Sessions, L’Aquila, Italy, 1–19 June 2020; Advances in Intelligent Systems and Computing. Springer: Berlin/Heidelberg, Germany, 2021. Chapter 1. pp. 5–14. [Google Scholar] [CrossRef]
- Hayat, S.; Yanmaz, E.; Bettstetter, C.; Brown, T.X. Multi-objective drone path planning for search and rescue with quality-of-service requirements. Auton. Robot. 2020, 44, 1183–1198. [Google Scholar] [CrossRef]
- Kiadi, M.; Villar, J.R.; Tan, Q. Synthesized A* Multi-robot Path Planning in an Indoor Smart Lab Using Distributed Cloud Computing. In Proceedings of the 15th International Conference on Soft Computing Models in Industrial and Environmental Applications (SOCO 2020), Burgos, Spain, 16–18 September 2020; Advances in Intelligent Systems and Computing. Springer: Berlin/Heidelberg, Germany, 2021. Chapter 56. pp. 580–589. [Google Scholar] [CrossRef]
- Han, G.; Qi, X.; Peng, Y.; Lin, C.; Zhang, Y.; Lu, Q. Early Warning Obstacle Avoidance-Enabled Path Planning for Multi-AUV-Based Maritime Transportation Systems. IEEE Trans. Intell. Transp. Syst. 2022, 1–12. [Google Scholar] [CrossRef]
- Dai, X.; Fan, Q.; Li, D. Research status of operational environment partitioning and path planning for multi - robot systems. J. Phys. Conf. Ser. 2017, 887, 12080. [Google Scholar] [CrossRef]
- Han, S.D.; Yu, J. Optimizing Space Utilization for More Effective Multi-Robot Path Planning. arXiv 2021. [Google Scholar] [CrossRef]
- Okumura, K.; Bonnet, F.; Tamura, Y.; Défago, X. Offline Time-Independent Multi-Agent Path Planning. arXiv 2021. [Google Scholar] [CrossRef]
- Causa, F.; Fasano, G.; Grassi, M. Multi-UAV Path Planning for Autonomous Missions in Mixed GNSS Coverage Scenarios. Sensors 2018, 18, 4188. [Google Scholar] [CrossRef]
- Digani, V.; Sabattini, L.; Secchi, C.; Fantuzzi, C. Ensemble Coordination Approach in Multi-AGV Systems Applied to Industrial Warehouses. IEEE Trans. Autom. Sci. Eng. 2015, 12, 922–934. [Google Scholar] [CrossRef]
- Andreychuk, A.; Yakovlev, K. Applying MAPP Algorithm for Cooperative Path Finding in Urban Environments. In Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2017; pp. 1–10. [Google Scholar] [CrossRef]
- Draganjac, I.; Miklic, D.; Kovacic, Z.; Vasiljevic, G.; Bogdan, S. Decentralized Control of Multi-AGV Systems in Autonomous Warehousing Applications. IEEE Trans. Autom. Sci. Eng. 2016, 13, 1433–1447. [Google Scholar] [CrossRef]
- Chouhan, S.S.; Niyogi, R. DiMPP: A complete distributed algorithm for multi-agent path planning. J. Exp. Theor. Artif. Intell. 2017, 29, 1129–1148. [Google Scholar] [CrossRef]
- Huang, X.; Cao, Q.; Zhu, X. Mixed path planning for multi-robots in structured hospital environment. J. Eng. 2019, 2019, 512–516. [Google Scholar] [CrossRef]
- Ravankar, A.; Ravankar, A.A.; Kobayashi, Y.; Emaru, T. SHP: Smooth Hypocycloidal Paths with Collision-Free and Decoupled Multi-Robot Path Planning. Int. J. Adv. Robot. Syst. 2016, 13, 133. [Google Scholar] [CrossRef]
- Abdelkader, M.; Jaleel, H.; Shamma, J.S. A Distributed Framework for Real Time Path Planning in Practical Multi-agent Systems. IFAC-PapersOnLine 2017, 50, 10626–10631. [Google Scholar] [CrossRef]
- Li, Q.; Gama, F.; Ribeiro, A.; Prorok, A. Graph Neural Networks for Decentralized Multi-Robot Path Planning. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October–24 January 2021; pp. 11785–11792. [Google Scholar] [CrossRef]
- Chen, Y.; Rosolia, U.; Ames, A.D. Decentralized Task and Path Planning for Multi-Robot Systems. IEEE Robot. Autom. Lett. 2021, 6, 4337–4344. [Google Scholar] [CrossRef]
- Li, Q.; Lin, W.; Liu, Z.; Prorok, A. Message-Aware Graph Attention Networks for Large-Scale Multi-Robot Path Planning. IEEE Robot. Autom. Lett. 2021, 6, 5533–5540. [Google Scholar] [CrossRef]
- Bayerlein, H.; Theile, M.; Caccamo, M.; Gesbert, D. Multi-UAV Path Planning for Wireless Data Harvesting with Deep Reinforcement Learning. IEEE Open J. Commun. Soc. 2021, 2, 1171–1187. [Google Scholar] [CrossRef]
- Trudeau, A.; Clark, C.M. Multi-Robot Path Planning Via Genetic Programming. arXiv 2019. [Google Scholar] [CrossRef]
- Wei, C.; Hindriks, K.V.; Jonker, C.M. Altruistic coordination for multi-robot cooperative pathfinding. Appl. Intell. 2015, 44, 269–281. [Google Scholar] [CrossRef]
- Liu, T.M.; Lyons, D.M. Leveraging area bounds information for autonomous decentralized multi-robot exploration. Robot. Auton. Syst. 2015, 74, 66–78. [Google Scholar] [CrossRef]
- Matoui, F.; Boussaid, B.; Abdelkrim, M.N. Distributed path planning of a multi-robot system based on the neighborhood artificial potential field approach. Simulation 2018, 95, 637–657. [Google Scholar] [CrossRef]
- Neto, A.A.; Macharet, D.G.; Campos, M.F.M. Multi-agent Rapidly-exploring Pseudo-random Tree. J. Intell. Robot. Syst. 2017, 89, 69–85. [Google Scholar] [CrossRef]
- Lin, S.; Liu, A.; Kong, X.; Wang, J. Development of Swarm Intelligence Leader-Vicsek-Model for Multi-AGV Path Planning. In Proceedings of the 2021 20th International Symposium on Communications and Information Technologies (ISCIT), Tottori, Japan, 19–22 October 2021; pp. 49–54. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).