Experimental Study on the Influence of a Two-Dimensional Cosine Hill on Wind Turbine Wake
Abstract
:1. Introduction
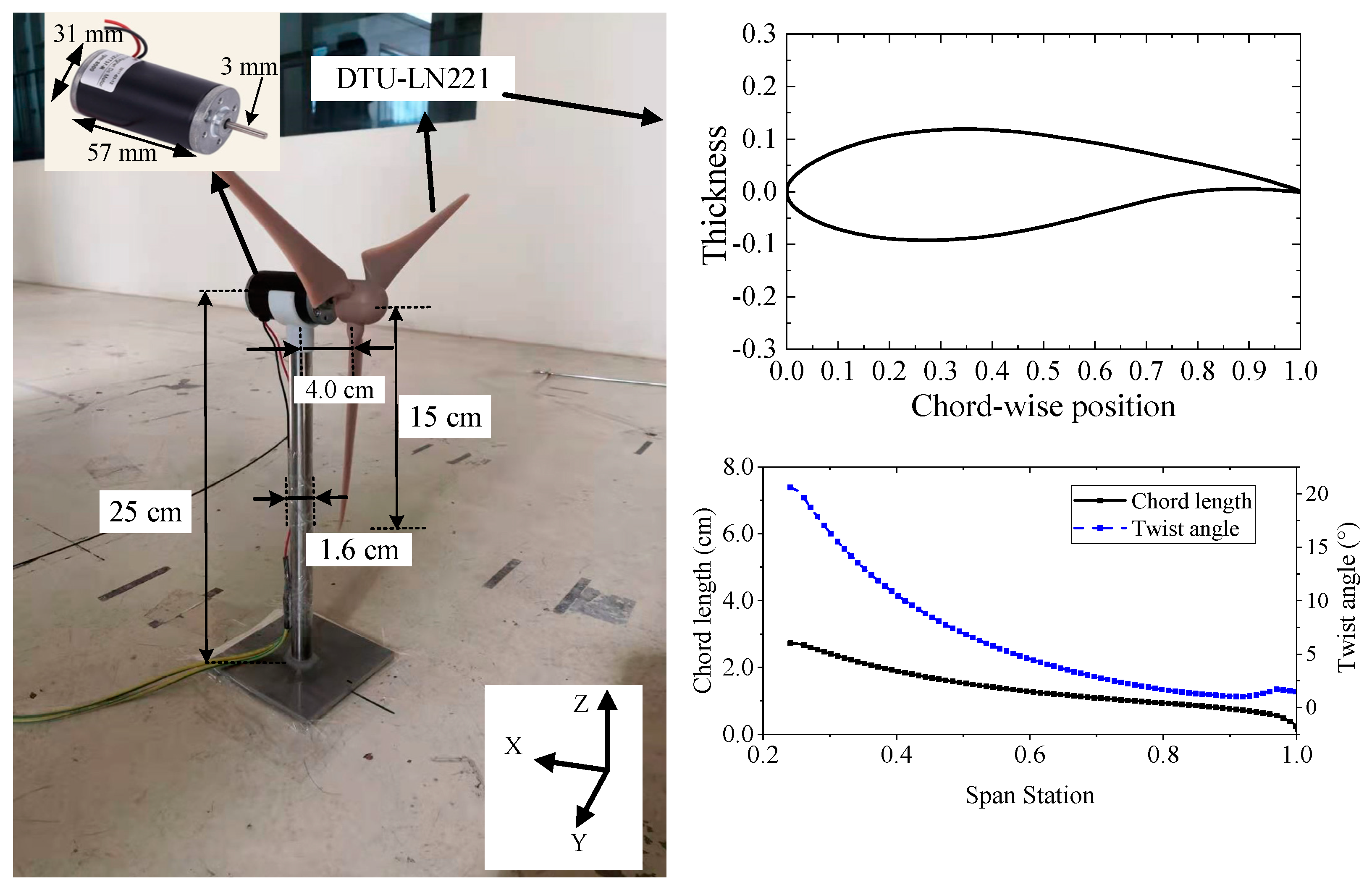
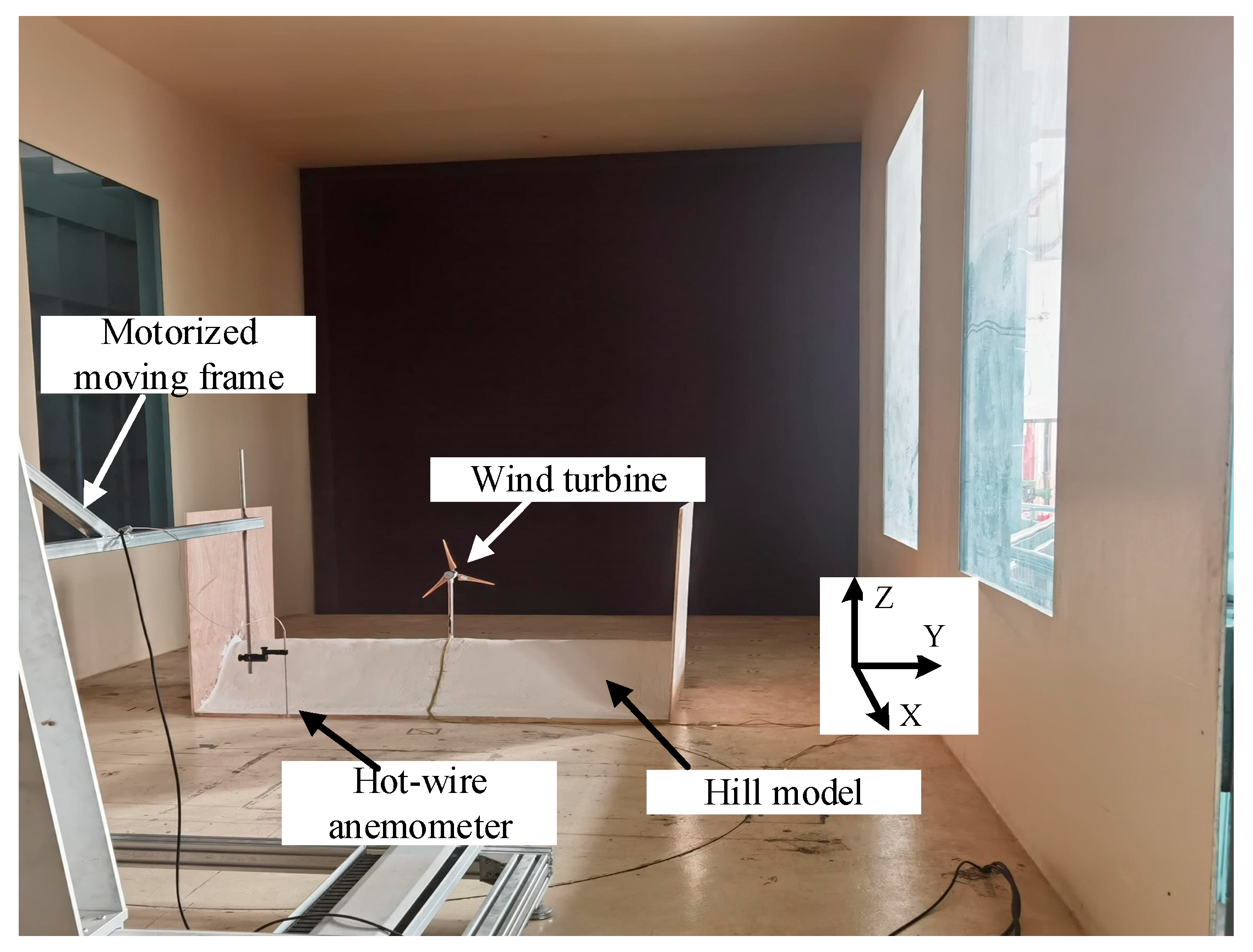
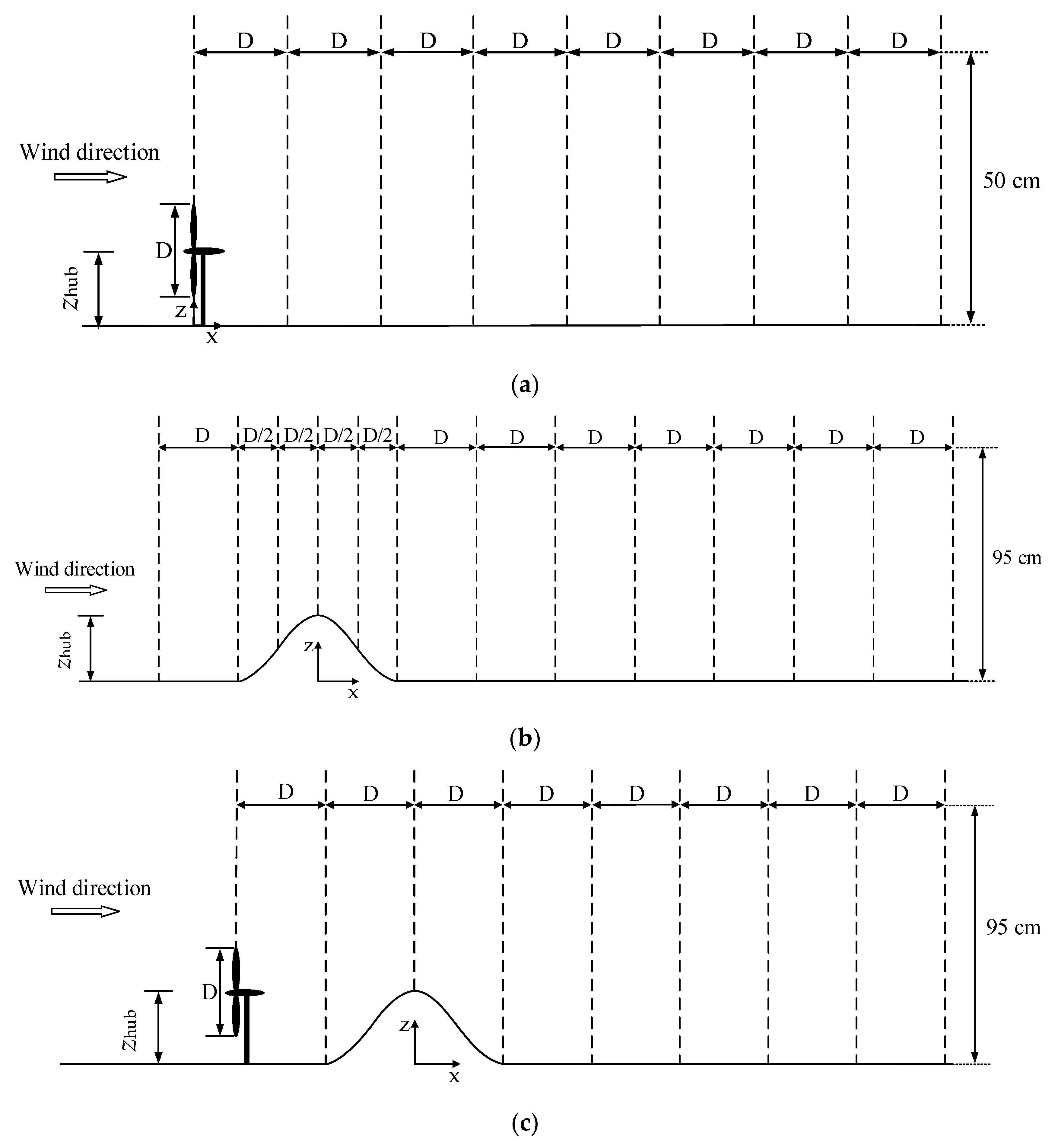
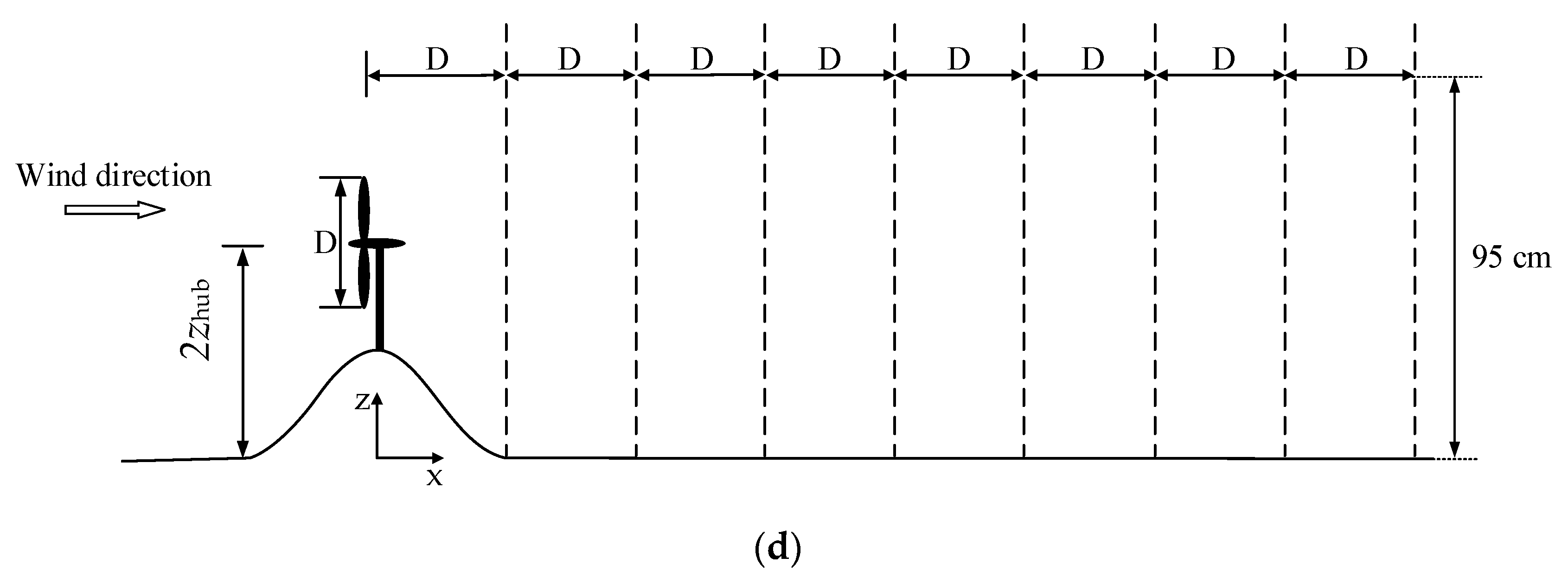
2. Experimental Setup
3. Results and Discussion
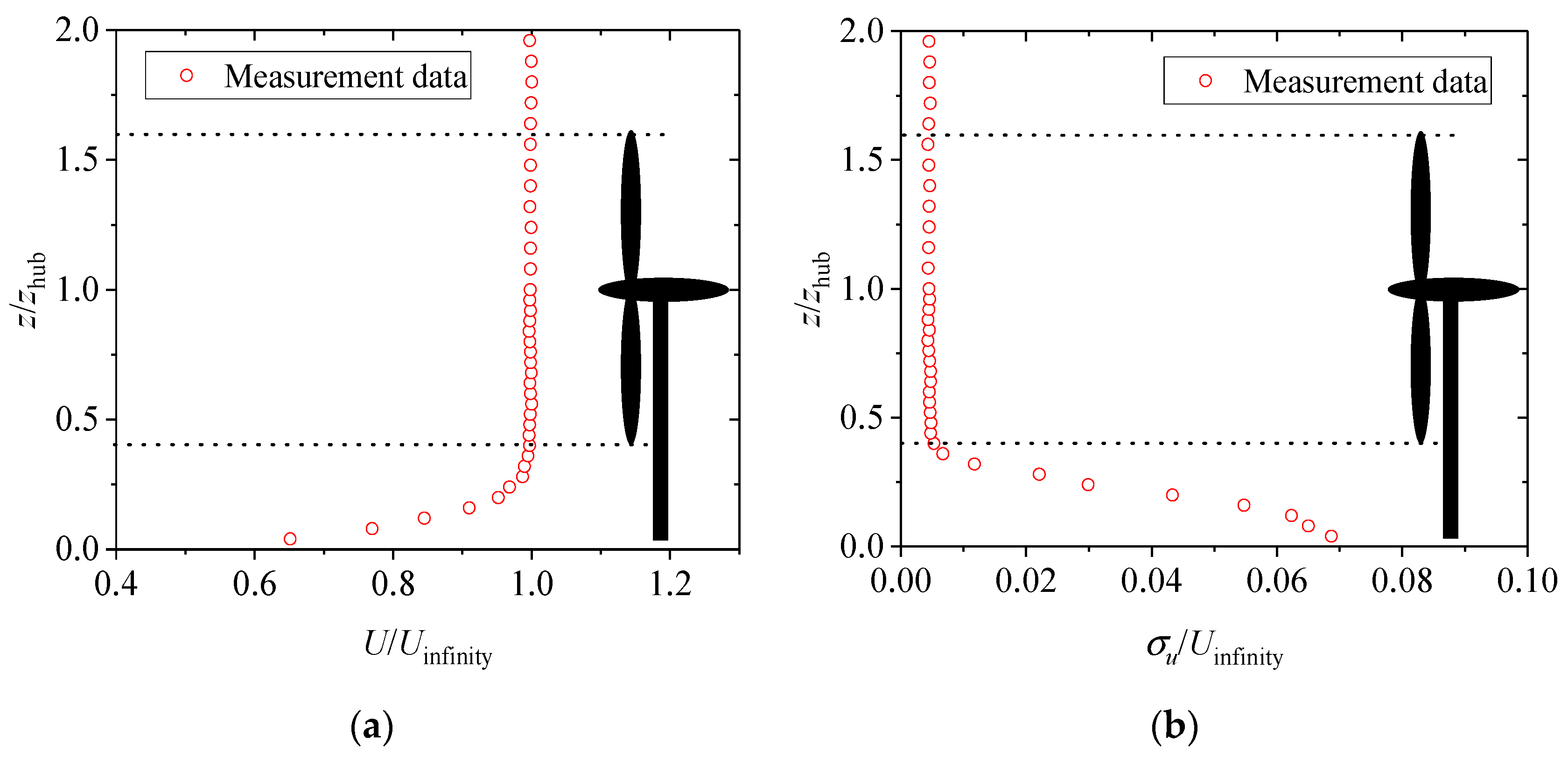
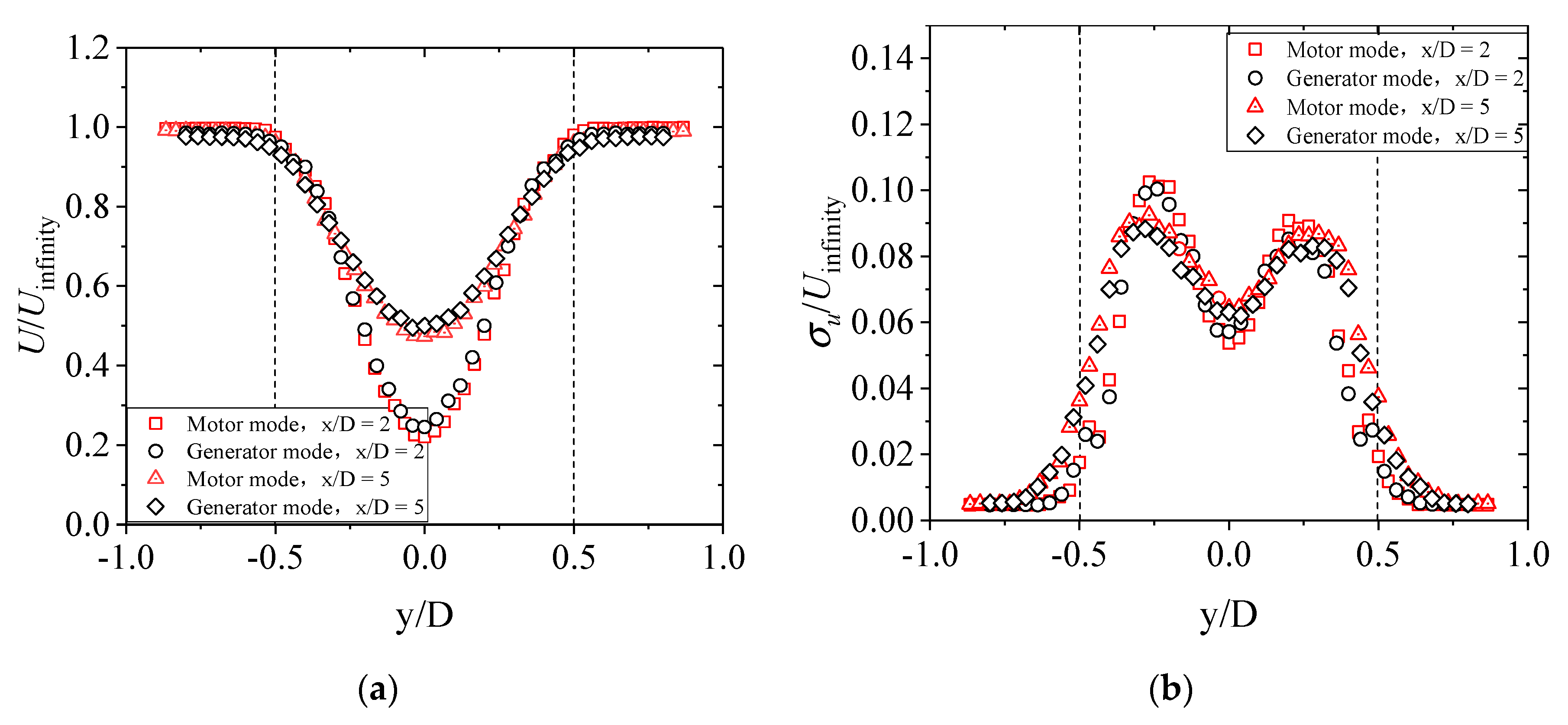
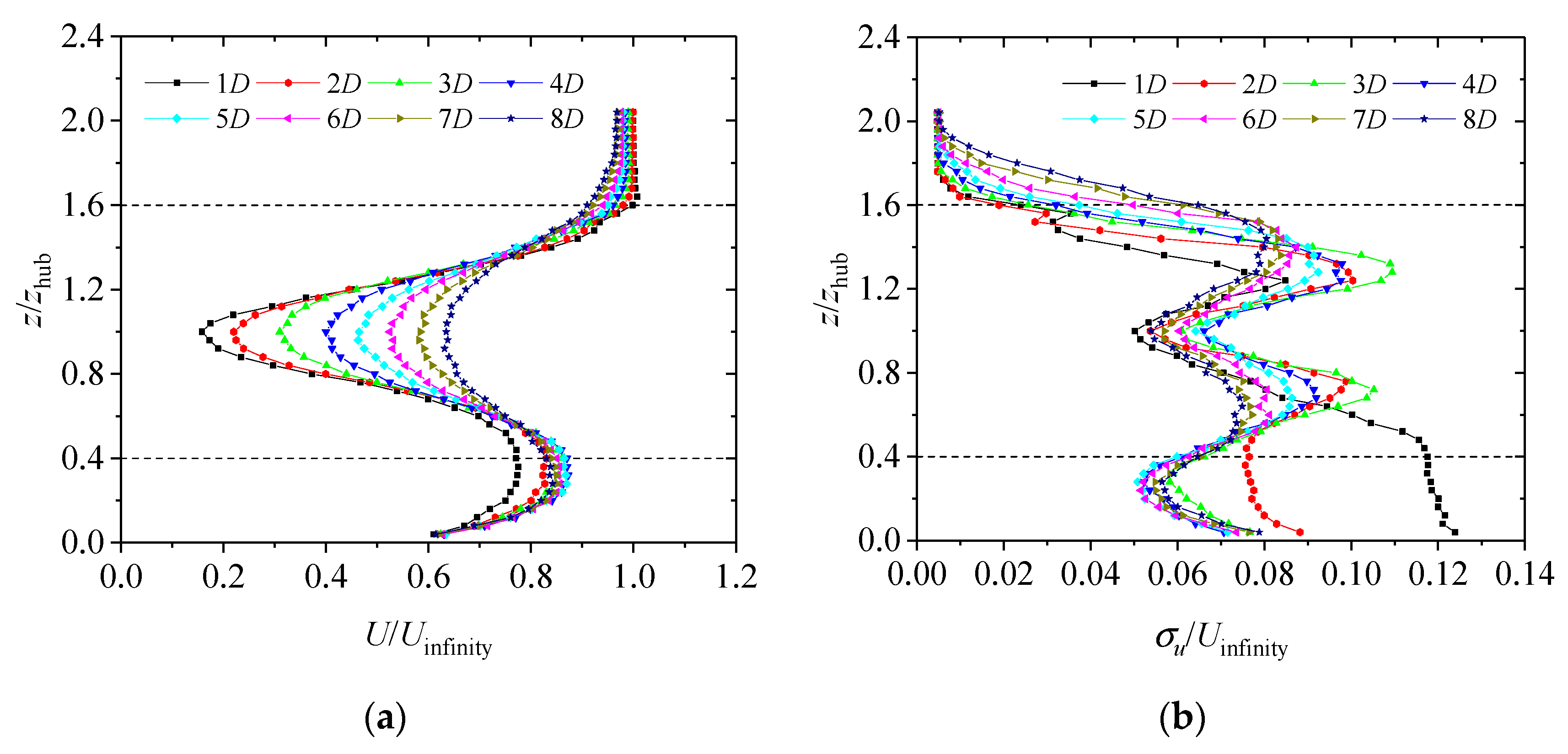
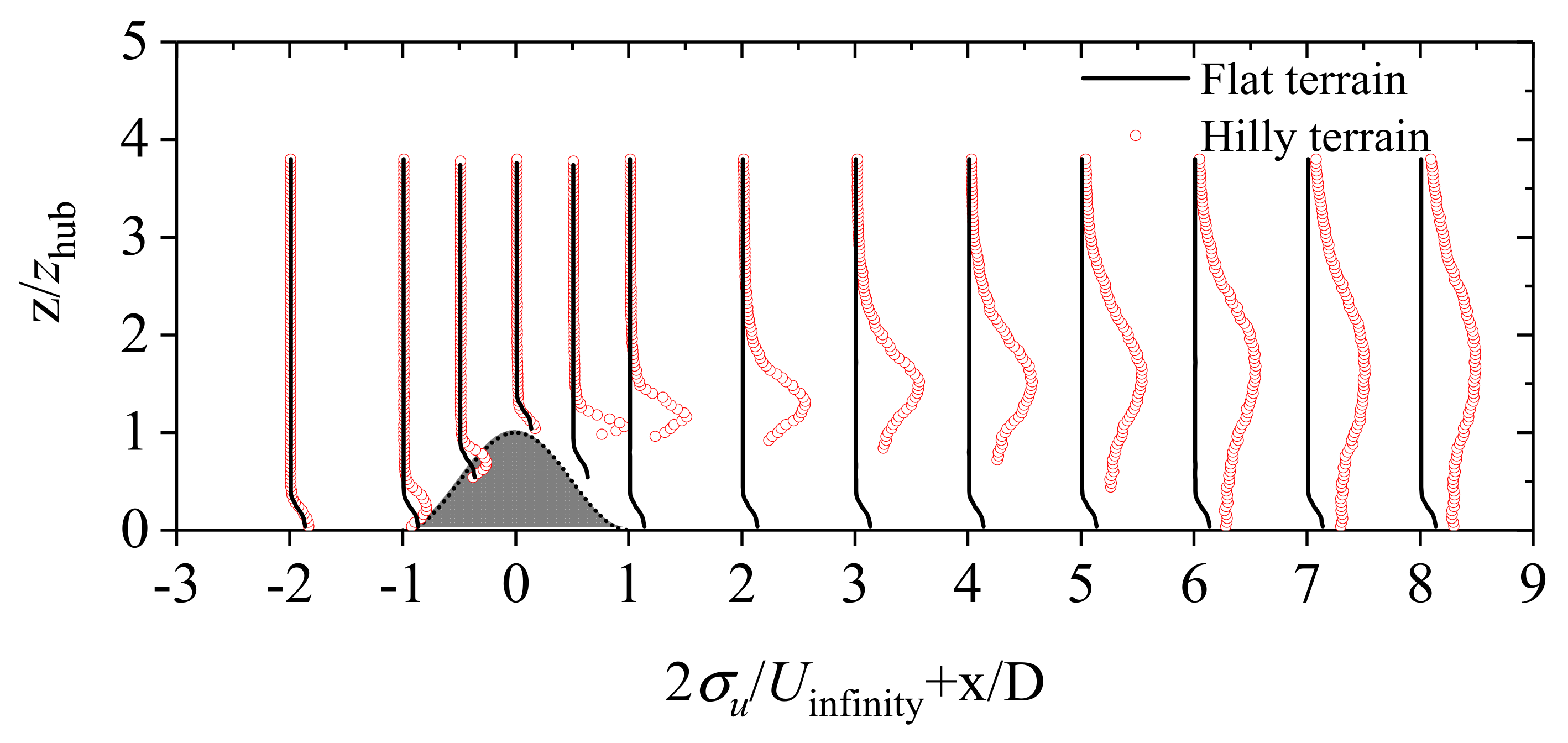
3.1. Wake Characteristics on Flat Terrain
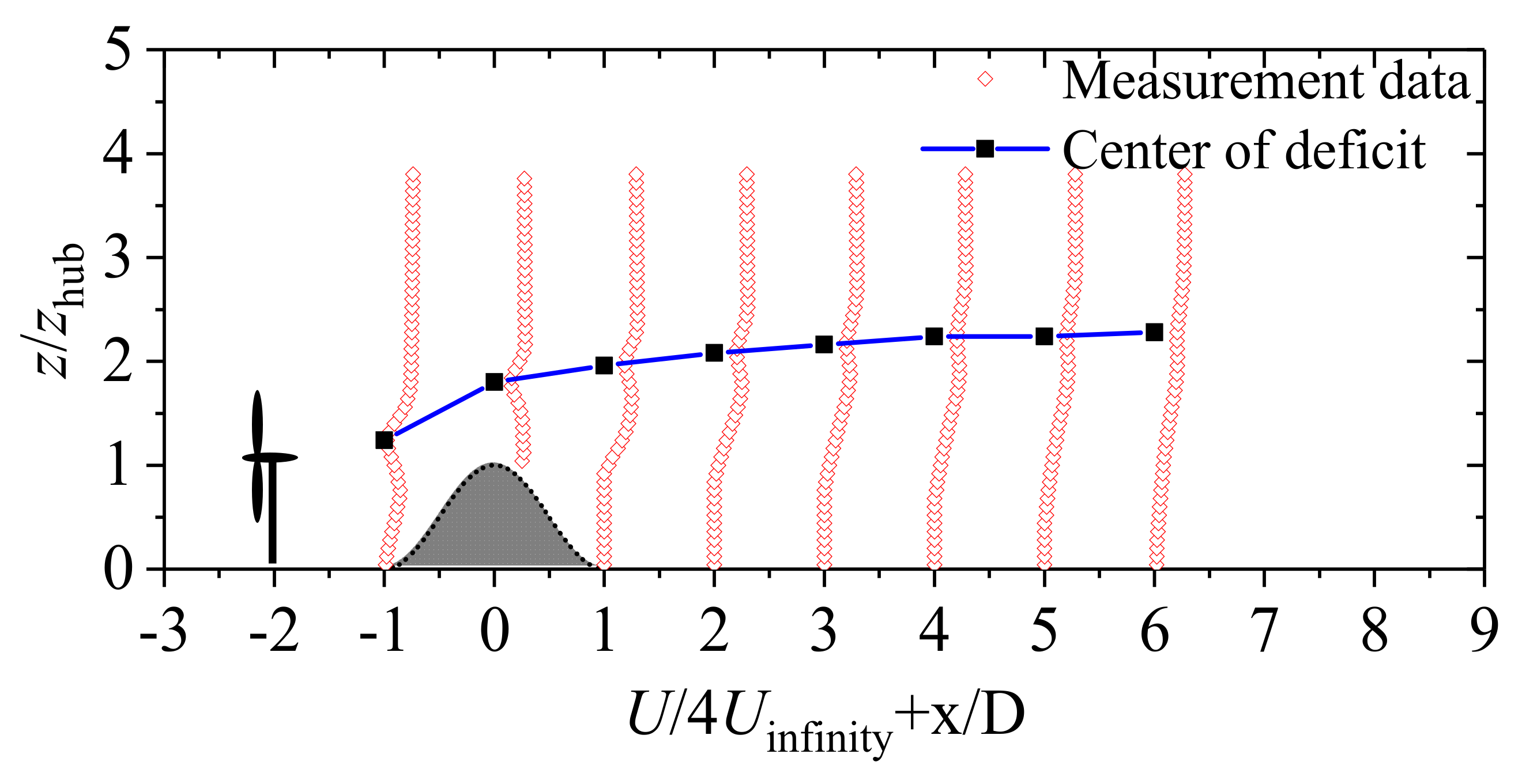
3.2. Wind Characteristics around a Cosine Hill
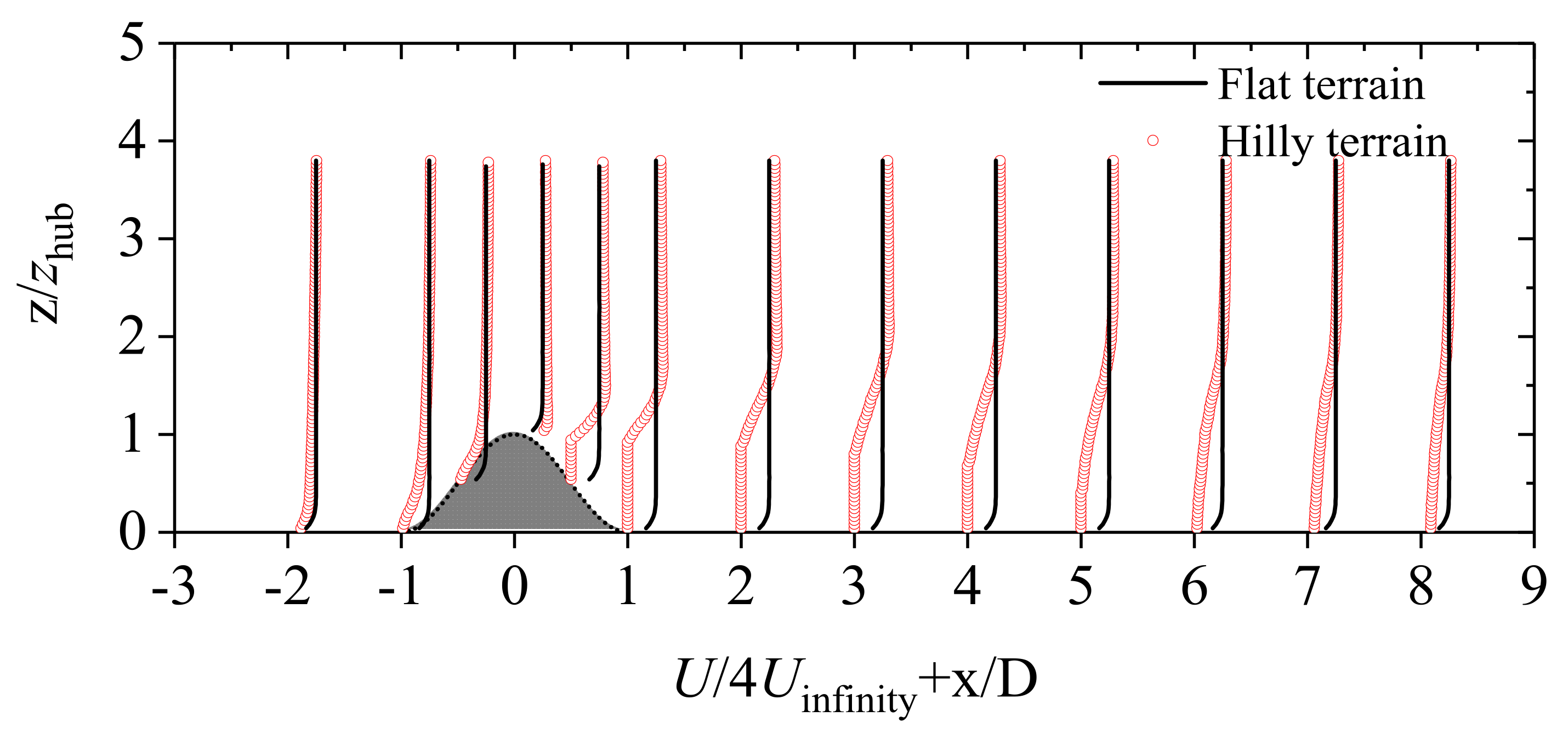
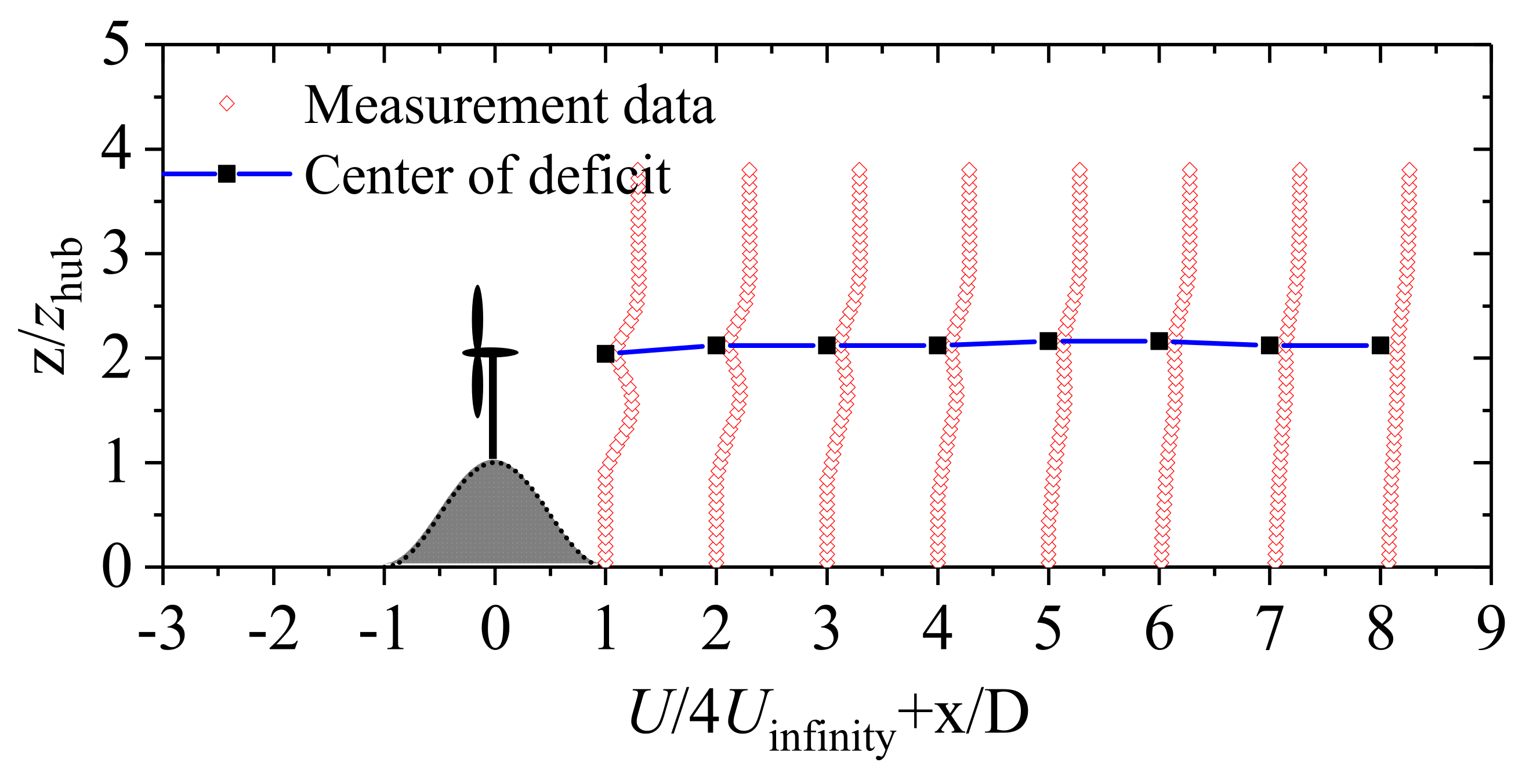
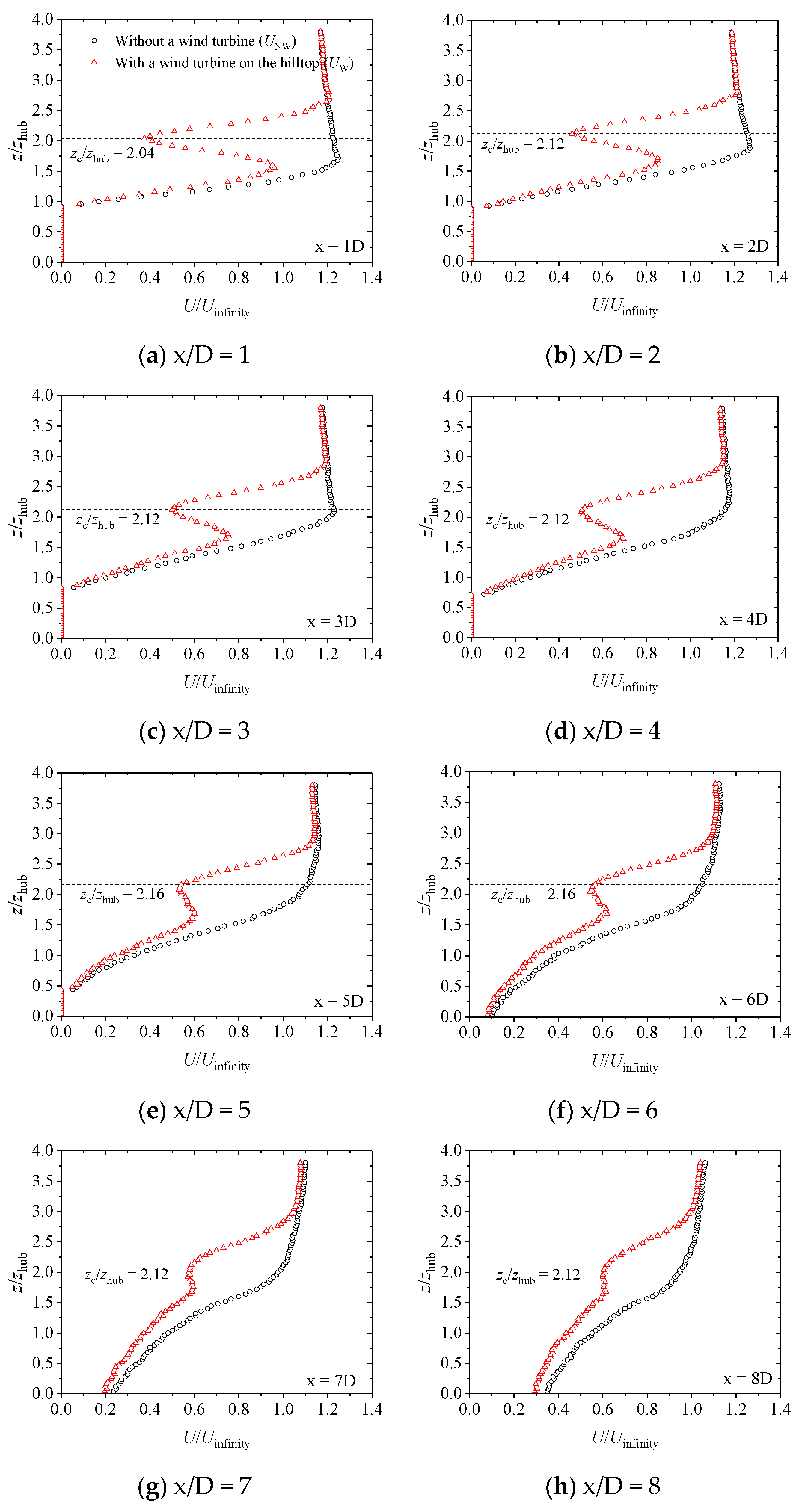
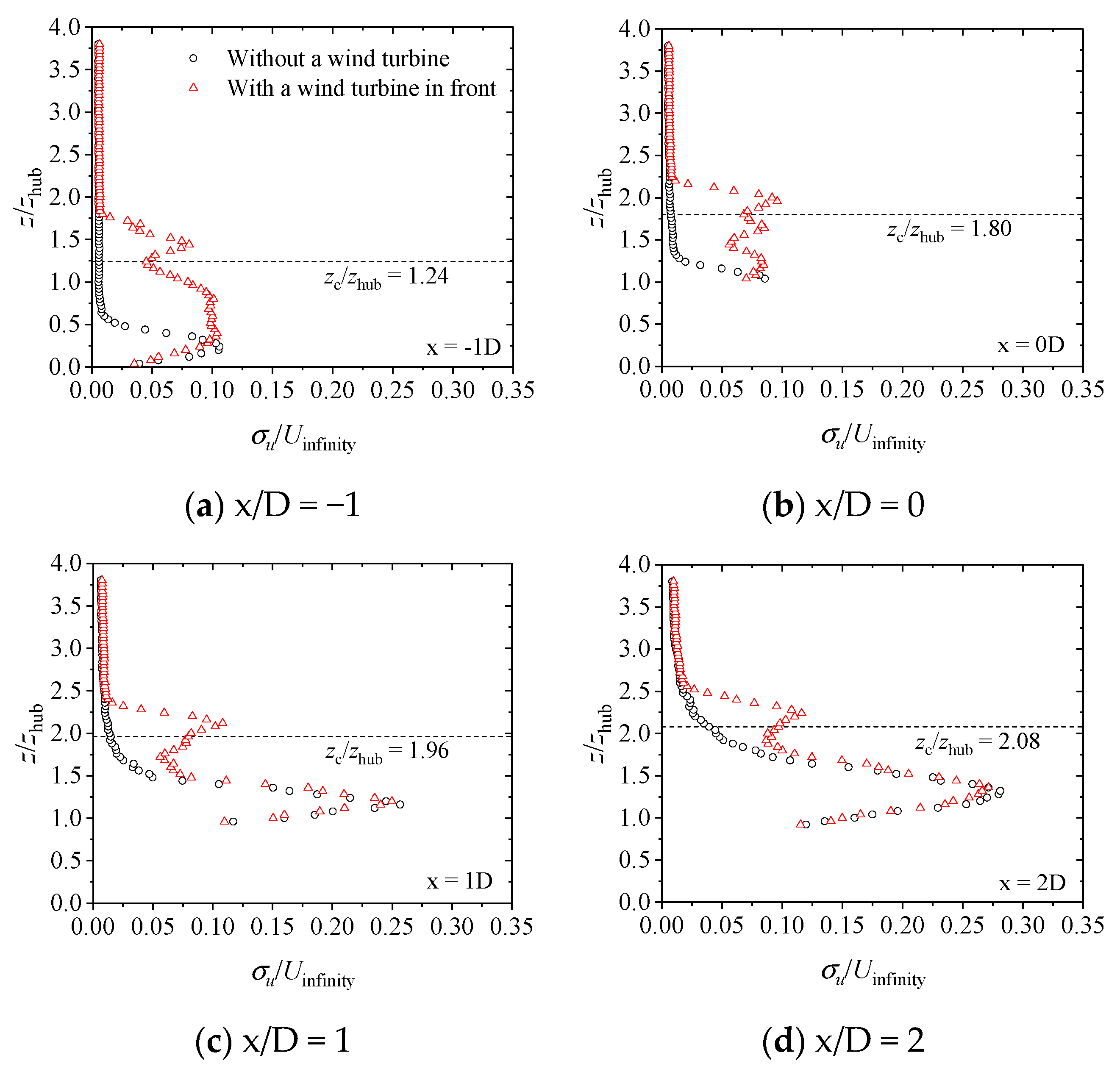
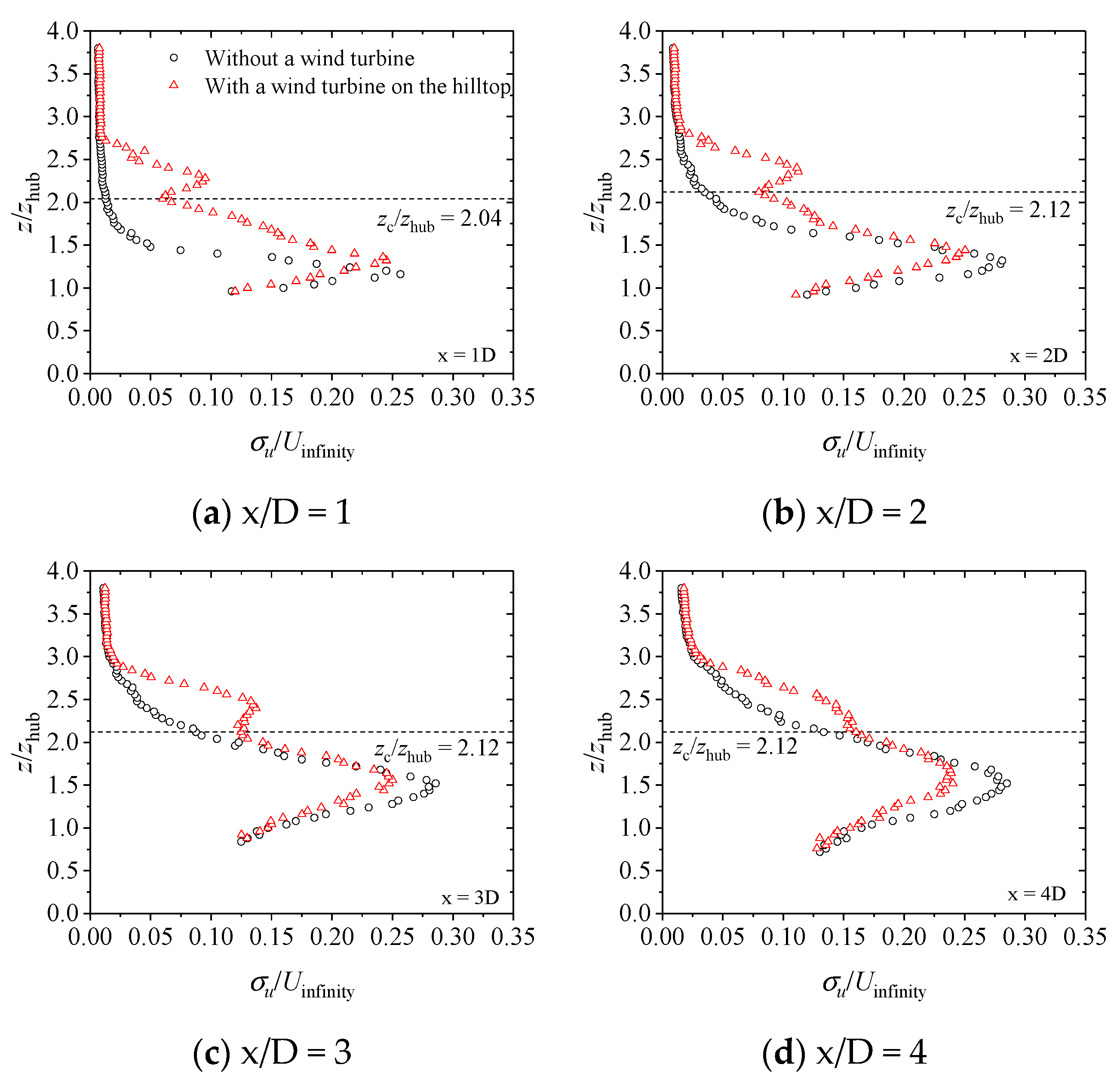
3.3. Velocity Profiles Combined with a Cosine Hill and a Wind Turbine
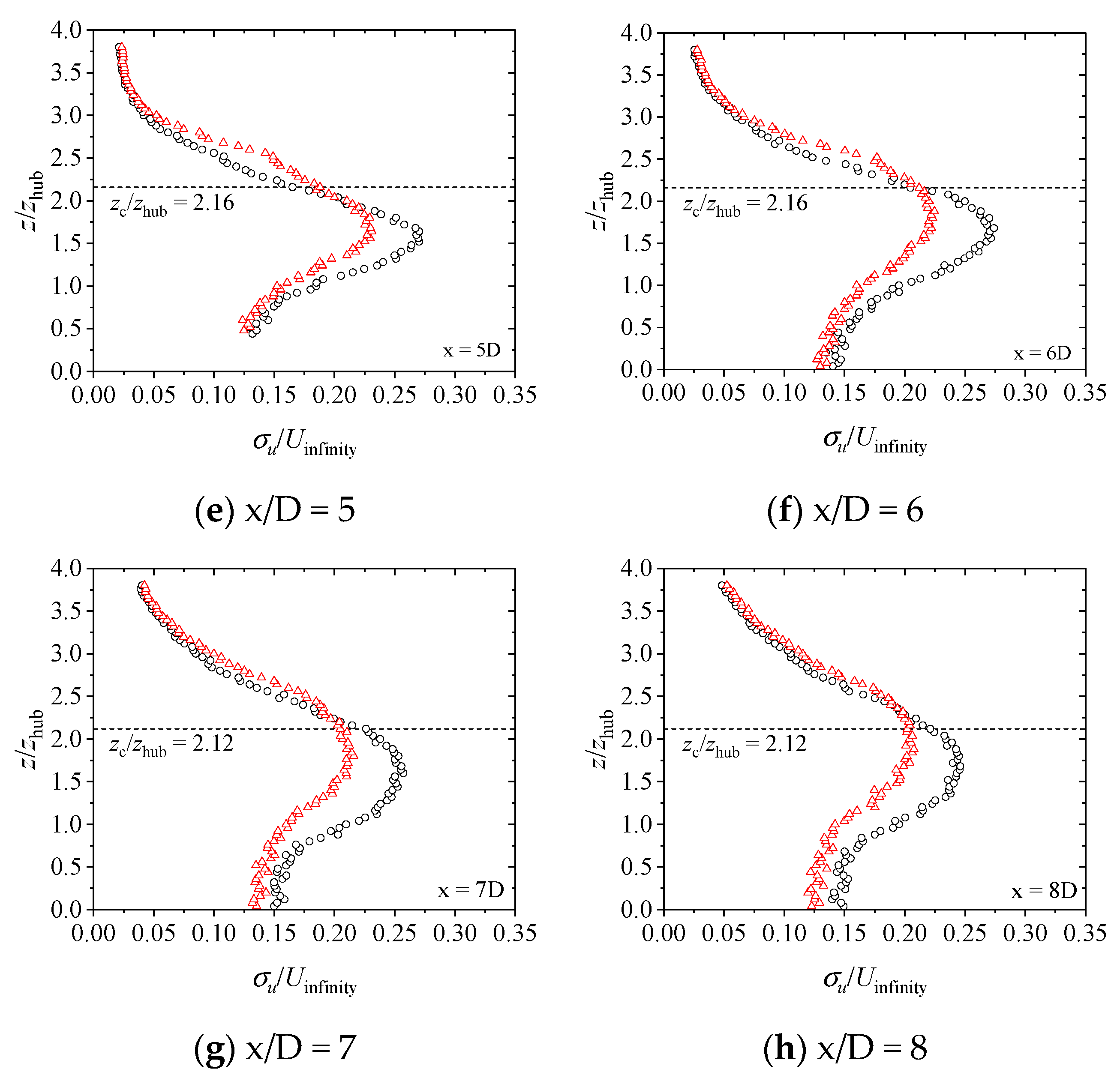
3.4. Turbulence Intensity in the Wind Turbine Wake over the Cosine Hill
4. Conclusions
- (1)
- On flat terrain, the lowest wind velocity in the same vertical position of the wake emerged in the center of the rotor, and the wind shear was formed along the vertical direction. At the position of x/D = 8, the average velocity deficit at hub height was about 63% of the inflow. Without considering the tower’s blocking effect, the turbulence intensity mainly presented a double shape in a vertical direction. The peak value tended to increase first and decrease with each successive increase in longitudinal distance. The maximum peak values of turbulence intensity occurred downstream of the turbine at the x = 3D position.
- (2)
- Based on the single test hill with a slope of 0.83, the speed-up effect existed on the upper part of the windward and leeward sides. In contrast, the wind velocity on the lower part of the windward and leeward sides decreased, and a flow separation zone was formed within the range of 6D on the leeward side. The turbulence intensity on the leeward side increased significantly and showed a single-peak shape, with the vertical height growing first and then decreasing.
- (3)
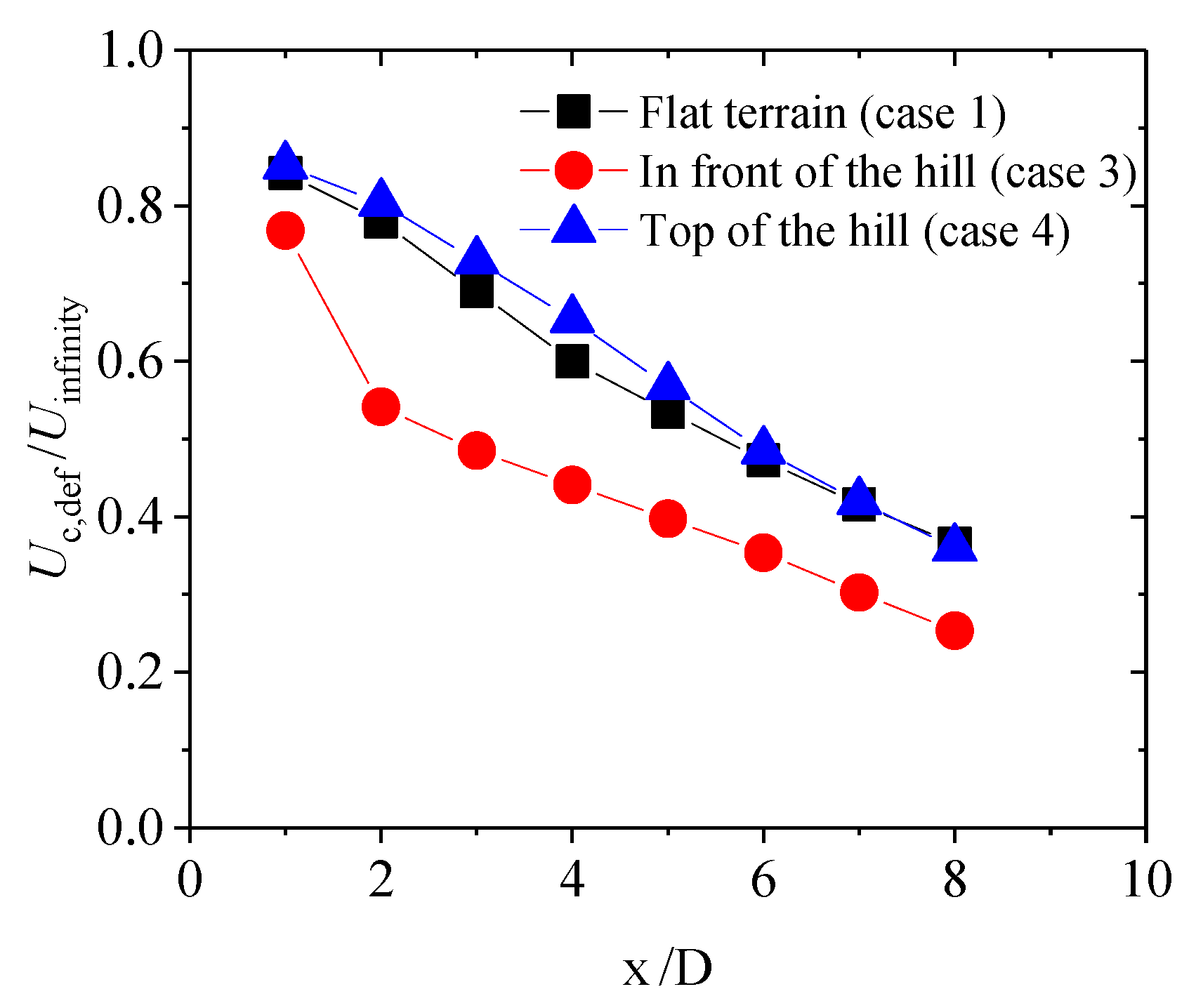
- The wake flow field was measured when the turbine was sited on the hilltop and 2D in front. The wake recovery of the wind turbine was promoted on the windward side and 4D behind the hilltop in two test cases, while it was limited within the range of 4D on the leeward side in comparison with the flat terrain. When the wind turbine was located 2D in front of the hilltop as well as on the top, values were achieved at 67% and 85% of that of the flat terrain, respectively. Furthermore, the turbulence intensity changed into a single peak shape in the x = 4D position downstream in the vertical direction. The generated peak value of turbulence intensity with a slightly higher position than the test hill with no wind turbine was smaller. However, the turbulence intensity peak was more than twice that of the flat terrain, suggesting that the wind turbine’s site selection and load calculation need to be paid attention to.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Adaramola, M.S.; Krogstad, P.-A. Experimental investigation of wake effects on wind turbine performance. Renew. Energy 2011, 36, 2078–2086. [Google Scholar] [CrossRef]
- El-Asha, S.; Zhan, L.; Iungo, G.V. Quantification of power losses due to wind turbine wake interactions through SCADA, meteorological and wind LiDAR data. Wind Energy 2017, 20, 1823–1839. [Google Scholar] [CrossRef]
- Tian, W.; Ozbay, A.; Hu, H. An experimental investigation on the aeromechanics and wake interferences of wind turbines sited over complex terrain. J. Wind Eng. Ind. Aerodyn. 2018, 172, 379–394. [Google Scholar] [CrossRef]
- Zhao, F.; Gao, Y.H.; Wang, T.Y.; Yang, J.S.; Gao, X.X. Experimental Study on Wake Evolution of a 1.5 MW wind turbine in a complex terrain wind farm based on LiDAR measurements. Sustainability 2020, 12, 2467. [Google Scholar] [CrossRef]
- Meng, H.; Lien, F.-S.; Glinka, G.; Li, L.; Zhang, J.H. Study on wake-induced fatigue on wind turbine blade based on elastic actuator line model and two-dimensional finite element model. Wind Eng. 2019, 43, 64–82. [Google Scholar] [CrossRef]
- Menke, R.; Vasiljević, N.; Hansen, K.S.; Hahmann, A.N.; Mann, J. Does the wind turbine wake follow the topography? A multi-lidar study in complex terrain. Wind Energy Sci. 2018, 67, 681–691. [Google Scholar] [CrossRef]
- Hansen, K.S.; Larsen, G.C.; Menke, R.; Vasiljevic, N.; Angelou, N.; Ju, F.; Zhu, W.J.; Vignaroli, A.; Liu, W.W.; Xu, C.; et al. Wind turbine wake measurement in complex terrain. J. Phys. Conf. Ser. 2016, 75, 032013. [Google Scholar] [CrossRef]
- Subramanian, B.; Chokani, N.; Abhari, R.S. Aerodynamics of wind turbine wakes in flat and complex terrains. Renew. Energy 2016, 85, 454–463. [Google Scholar] [CrossRef]
- Ibrahim, O.M.A.M.; Yoshida, S.; Hamasaki, M.; Takada, A. Wind turbine wake modeling in accelerating wind field: A preliminary study on a two-dimensional hill. Fluids 2019, 4, 153. [Google Scholar] [CrossRef]
- Tian, W.; Ozbay, A.; Yuan, W.; Sarakar, P.; Hu, H. An experimental study on the performances of wind turbines over complex terrains. In Proceedings of the 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, USA, 7–10 January 2013. [Google Scholar]
- Hyvärinen, A.; Segalini, A. Qualitative analysis of wind-turbine wakes over hilly terrain. J. Phys. Conf. Ser. 2017, 85, 012023. [Google Scholar] [CrossRef] [Green Version]
- Hyvärinen, A.; Segalini, A. Effects from complex terrain on wind-turbine performance. J. Energy Resour.-ASME 2017, 139, 36–48. [Google Scholar] [CrossRef]
- Howard, K.B.; Hu, J.S.; Chamorro, L.P.; Guala, M. Characterizing the response of a wind turbine model under complex inflow conditions. Wind Energy 2015, 18, 729–743. [Google Scholar] [CrossRef]
- Liu, X.; Yan, S.; Guo, Y.T.; Shi, S.P.; Chen, X.M.; Mu, Y.F. CFD simulation and Lidar experimental study on wind turbines in complex terrain. Acta Energ. Sol. Sin. 2020, 41, 1–7. [Google Scholar]
- Berg, J.; Troldborg, N.; Sørensen, N.N.; Patton, E.G.; Sullivan, P.P. Large-eddy simulation of turbine wake in complex terrain. J. Phys. Conf. Ser. 2017, 854, 012003. [Google Scholar] [CrossRef]
- Shamsoddin, S.; Fernando, P.-A. Wind turbine wakes over hills. J. Fluid Mech. 2018, 855, 671–702. [Google Scholar] [CrossRef]
- Politis, E.S.; Prospathopoulos, J.; Cabezon, D.; Hansen, K.S.; Chaviaropoulos, P.K.; Barthelmie, R.J. Modeling wake effects in large wind farms in complex terrain: The problem, the methods and the issues. Wind Energy 2012, 15, 161–182. [Google Scholar] [CrossRef]
- Yang, X.L.; Maggie, P.; Fotis, S. Large-eddy simulation of a utility-scale wind farm in complex terrain. Appl. Energy 2018, 229, 767–777. [Google Scholar] [CrossRef]
- Astolfi, D.; Castellani, F.; Terzi, L. A study of wind turbine wakes in complex terrain through RANS simulation and SCADA data. J. Sol. Energy Eng. 2018, 140, 031001. [Google Scholar] [CrossRef]
- Makridis, A.; Chick, J. Validation of a CFD model of wind turbine wakes with terrain effects. J. Wind Eng. Ind. Aerodyn. 2013, 123, 12–29. [Google Scholar] [CrossRef]
- Zhou, T.Y.; Tan, J.F.; Cai, J.G.; Shi, R.P.; Xia, Y.S. Numerical Investigation on Power Outputs of a Wind Turbine Sited over Continuous Hilly Terrain. Trans. Nanjing Univ. Aeronaut. Astronaut. 2020, 37, 120–128. [Google Scholar]
- Dar, A.S.; Berg, J.; Troldborg, N.; Patton, E.G. On the self-similarity of wind turbine wakes in a complex terrain using large eddy simulation. Wind Energy Sci. 2019, 4, 633–644. [Google Scholar] [CrossRef]
- Xu, C.; Hang, H.; Shi, C.; Duan, H.; Li, G.; Li, L. Numerical Simulation of Wind Turbine Wakes in Typical Complex Terrains Based on LBM-LES Method. Proc. CSEE 2020, 40, 4236–4242. [Google Scholar]
- Yang, J.W.; Yang, H.; Zhu, W.J.; Li, N.L.; Yuan, Y.P. Experimental study on aerodynamic characteristics of a Gurney flap on a wind turbine airfoil under high turbulent flow condition. Appl. Sci. 2020, 10, 7258. [Google Scholar] [CrossRef]
- Zhou, H.C.; Jiang, Z.; Wang, G.L.; Zhang, S.P. Aerodynamic Characteristics of Isolated Loaded Tires with Different Tread Patterns: Experiment and Simulation. Chin. J. Mech. Eng. 2021, 34, 6. [Google Scholar] [CrossRef]
- Sessarego, M.; Ramos-Garcia, N.; Yang, H.; Shen, W.Z. Aerodynamic wind-turbine rotor design using surrogate modeling and three-dimensional viscous–inviscid interaction technique. Renew. Energy 2016, 93, 620–635. [Google Scholar] [CrossRef]
- Kulak, M.; Lipian, M.; Zawadzki, K. Investigation of performance of small wind turbine blades with winglets. Int. J. Numer. Methods Heat Fluid Flow 2021, 31, 629–640. [Google Scholar] [CrossRef]
- Dou, B.Z.; Guala, M.; Zeng, P.; Lei, L.P. Experimental investigation of the power performance of a minimal wind turbine array in an atmospheric boundary layer wind tunnel. Energy Convers. Manag. 2019, 196, 906–919. [Google Scholar] [CrossRef]
- Medici, D.; Alfredsson, P.H. Measurements on a Wind Turbine Wake: 3D Effects and Bluff Body Vortex Shedding. Wind Energy 2006, 9, 219–236. [Google Scholar] [CrossRef]
- Chamorro, L.R.; Arndt, R.E.A.; Sotiropoulos, F. Reynolds number dependence of turbulence statistics in the wake of wind turbines. Wind Energy 2012, 15, 733–742. [Google Scholar] [CrossRef]
- Mason, P.J.; King, J.C. Measurements and predictions of flow and turbulence over an isolated hill of moderate slope. Q. J. Roy. Meteor. Soc. 1985, 111, 617–640. [Google Scholar] [CrossRef]
- Ryi, J.; Rhee, W.; Hwang, U.C.; Choi, J.S. Blockage effect correction for a scaled wind turbine rotor by using wind tunnel test data. Renew. Energy 2015, 79, 227–235. [Google Scholar] [CrossRef]
- Meng, H.R.; Ma, Z.; Dou, B.Z.; Zeng, P.; Lei, L.P. Investigation on the performance of a novel forward folding rotor used in a downwind horizontal axis turbine. Energy 2020, 190, 116384. [Google Scholar] [CrossRef]
- Uehara, K.; Murakami, S.; Oikawa, S.; Wakamatsu, S. Wind tunnel experiments on how thermal stratification affects flow in and above urban street canyons. Atmos. Environ. 2000, 34, 1553–1562. [Google Scholar] [CrossRef]
- Li, Q.; Murata, J.; Endo, M.; Maeda, T.; Kamada, Y. Experimental and numerical investigation of the effect of turbulent inflow on a Horizontal Axis Wind Turbine (part II: Wake characteristics). Energy 2016, 113, 1304–1315. [Google Scholar] [CrossRef]
- Dou, B.Z.; Yang, Z.P.; Guala, M.; Qu, T.M.; Lei, L.P.; Zeng, P. Comparison of Different Driving Modes for the Wind Turbine Wake in Wind Tunnels. Energies 2020, 13, 1915. [Google Scholar] [CrossRef]
- Li, Q.; Maeda, T.; Kamada, Y.; Mori, N. Investigation of wake characteristics of a Horizontal Axis Wind Turbine in vertical axis direction with field experiments. Energy 2017, 141, 262–272. [Google Scholar] [CrossRef]
- Kamada, Y.; Li, Q.; Maeda, T.; Yamada, K. Wind tunnel experimental investigation of flow field around two-dimensional single hill models. Renew. Energy 2019, 136, 1107–1118. [Google Scholar] [CrossRef]
- Zhang, W.; Markfort, C.D.; Porté-Agel, F. Near-wake flow structure downwind of a wind turbine in a turbulent boundary layer. Exp. Fluids 2012, 52, 1219–1235. [Google Scholar] [CrossRef] [Green Version]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Feng, K.; Yang, H.; Wang, X. Experimental Study on the Influence of a Two-Dimensional Cosine Hill on Wind Turbine Wake. Machines 2022, 10, 753. https://doi.org/10.3390/machines10090753
Yang J, Feng K, Yang H, Wang X. Experimental Study on the Influence of a Two-Dimensional Cosine Hill on Wind Turbine Wake. Machines. 2022; 10(9):753. https://doi.org/10.3390/machines10090753
Chicago/Turabian StyleYang, Junwei, Keru Feng, Hua Yang, and Xiangjun Wang. 2022. "Experimental Study on the Influence of a Two-Dimensional Cosine Hill on Wind Turbine Wake" Machines 10, no. 9: 753. https://doi.org/10.3390/machines10090753
APA StyleYang, J., Feng, K., Yang, H., & Wang, X. (2022). Experimental Study on the Influence of a Two-Dimensional Cosine Hill on Wind Turbine Wake. Machines, 10(9), 753. https://doi.org/10.3390/machines10090753






