A Novel MSFED Feature for the Intelligent Fault Diagnosis of Rotating Machines
Abstract
1. Introduction
2. Methodology
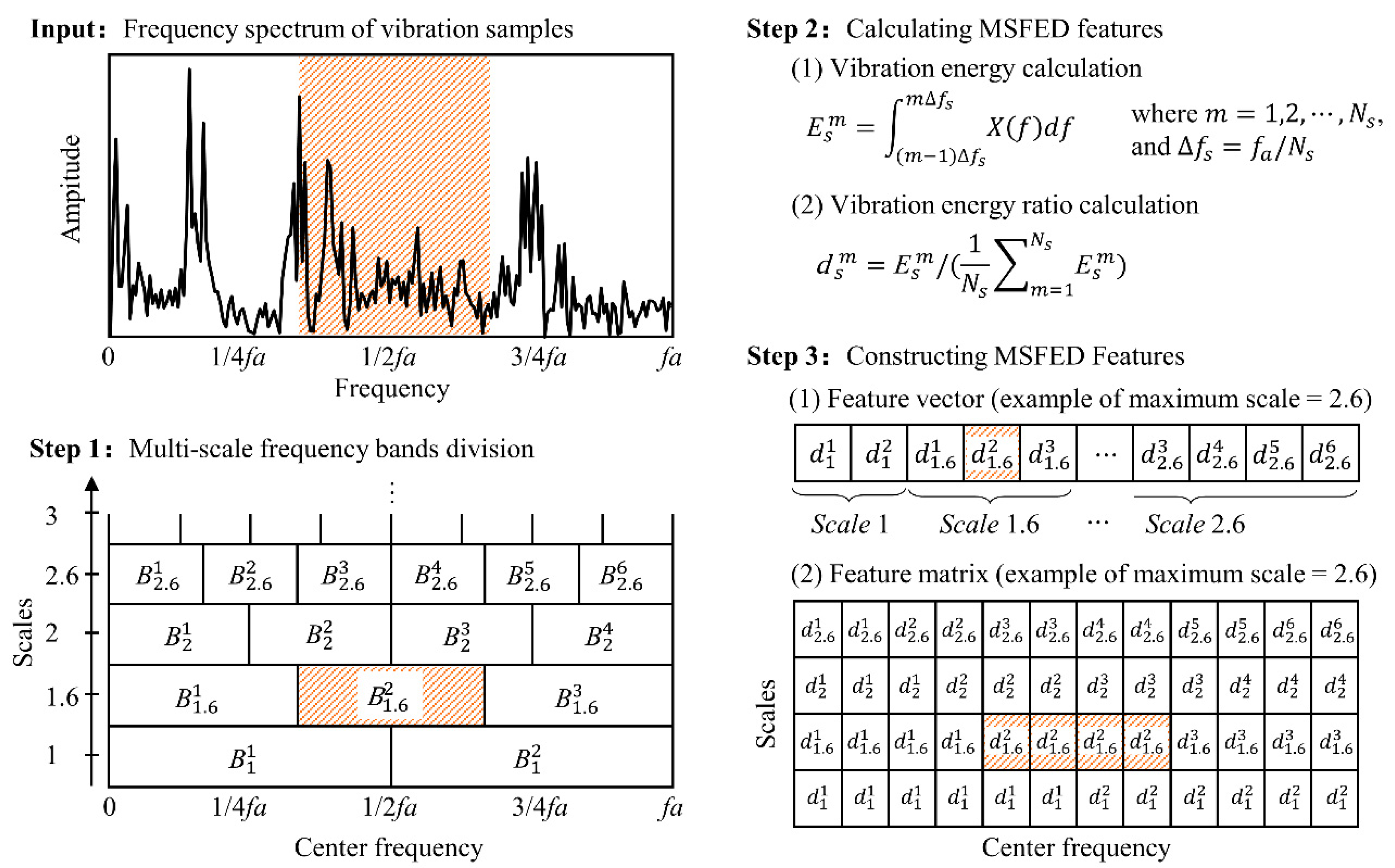
2.1. The Proposed MSFED Feature
2.1.1. Multi-Scale Frequency Bands Division
2.1.2. Construction of the MSFED Feature
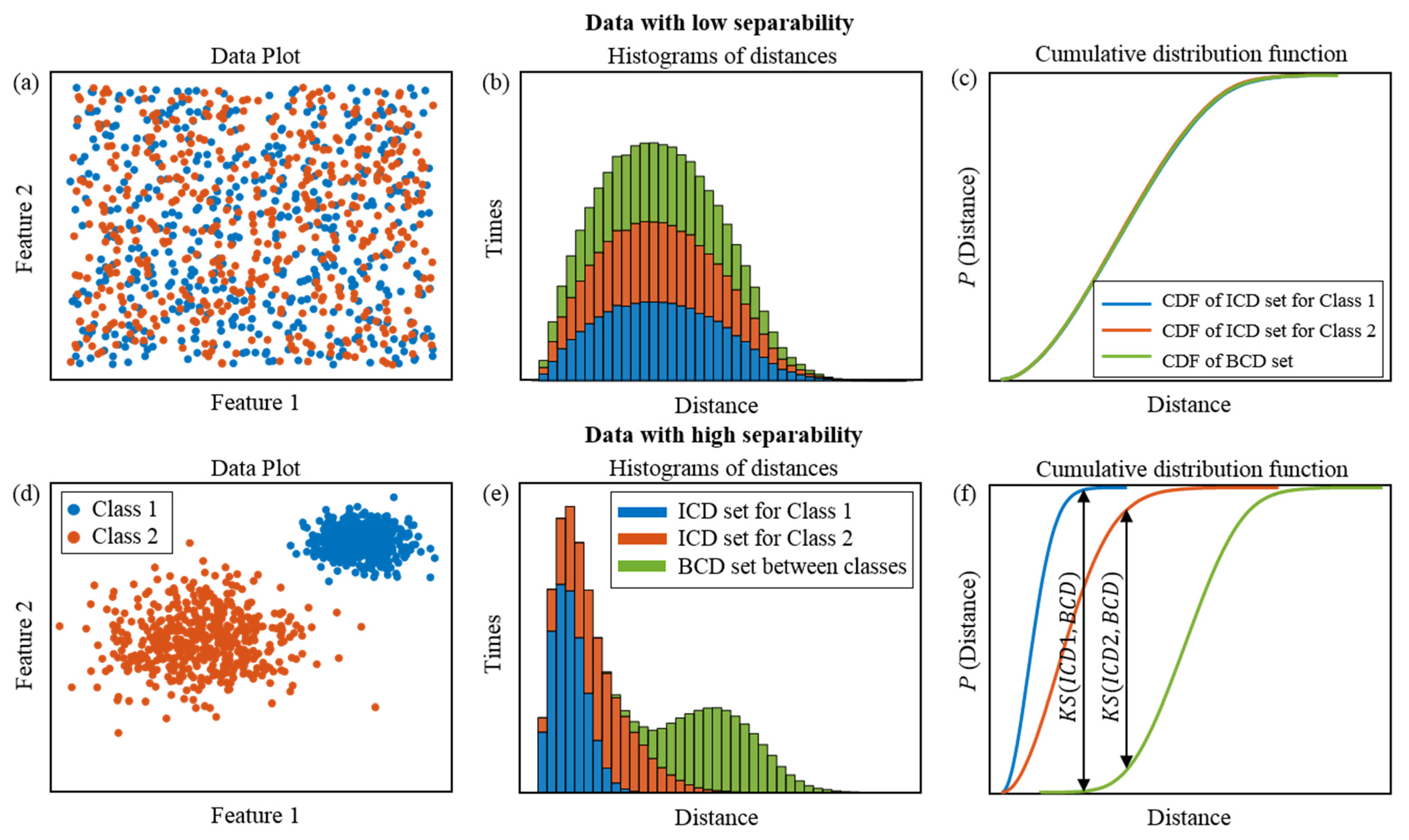
2.2. The Separability and Transferability Evaluation Metrics
2.2.1. Distance-Based Separability Index
- (1)
- Calculate the intra-class distance sets for each class: .
- (2)
- Calculate the between-class distance sets for each class: . For the n-th class, the between-class distance set is the distances between any two samples in the -th class and the class other than the -th class.
- (3)
- Calculate the DSIs of classes, and the DSI of the initial feature is the average of the DSIs of classes.
2.2.2. Distance-Based Transferability Index
- (1)
- Calculate the intra-class distance sets for each class in the testing dataset and the training dataset: , and .
- (2)
- Calculate the between-class distance sets for each class in the testing dataset: , For the -th class, the between-class distance set is the distances between any two samples in the -th class in testing dataset and the class other than the -th class in training dataset.
- (3)
- Calculate the DSIs of each class according to Equation (5) and calculate the ratios of DSIs of each class according to Equation (6). At last, the DTI between the feature set is the average of the DTIs of classes.
3. Experimental Verification on Gearbox Dataset
3.1. Gearbox Testing Rig and Data Description
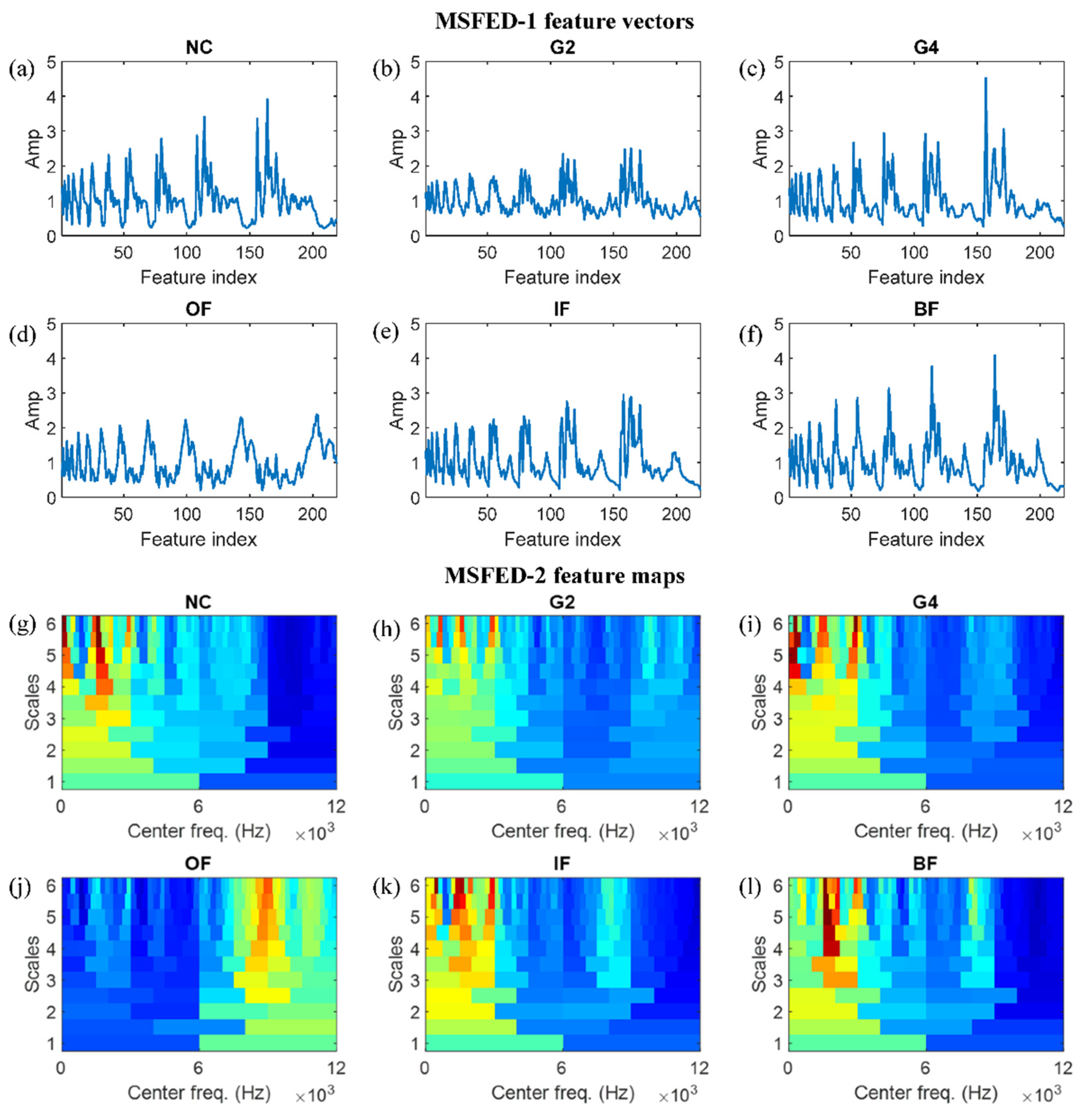
3.2. MSFED Feature Analysis
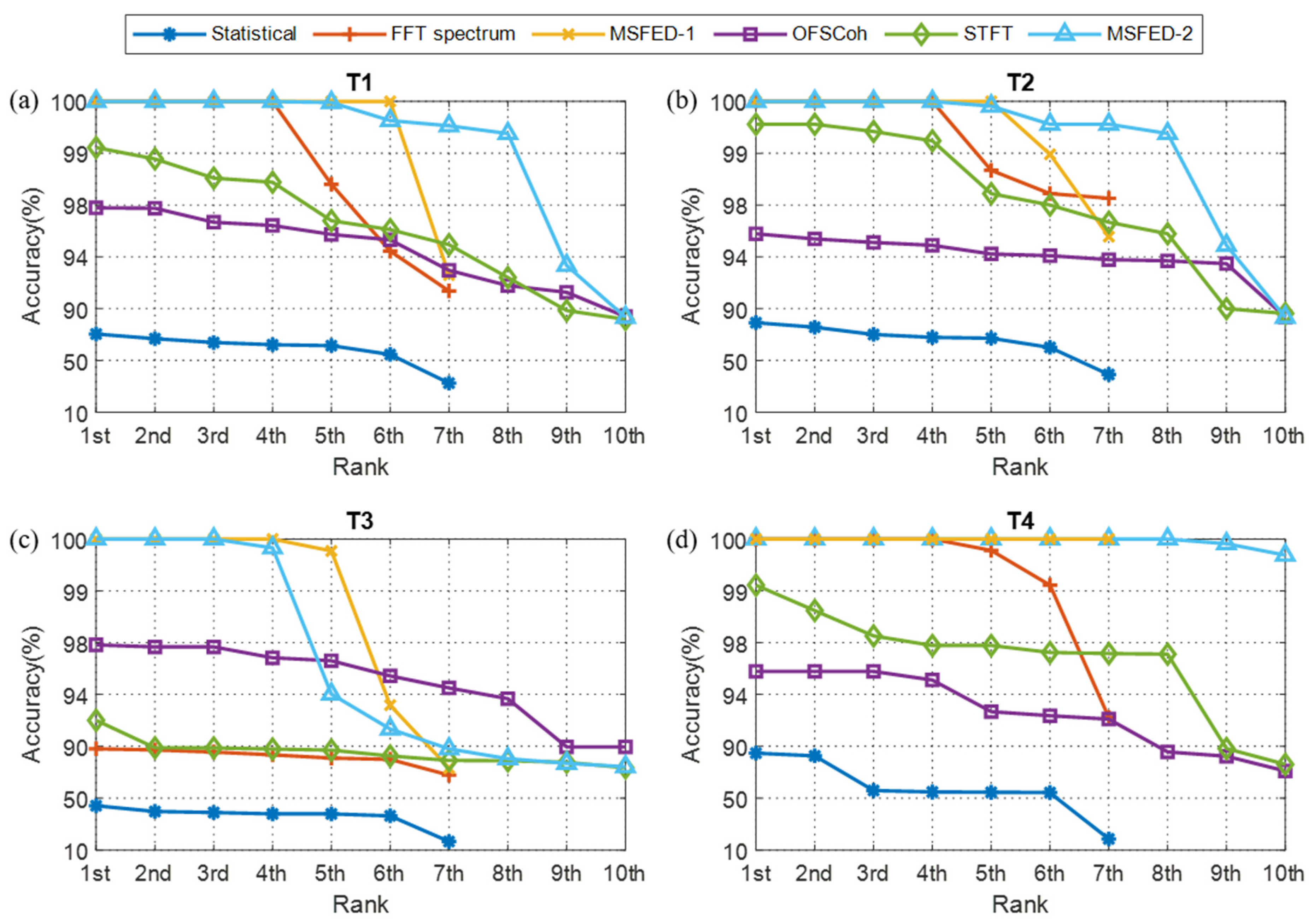
3.3. Fault Diagnosis Results Analysis
3.4. Separability and Transferability Evaluation
4. Experimental Verification on Bearing Dataset
4.1. Bearing Testing Rig and Data Description
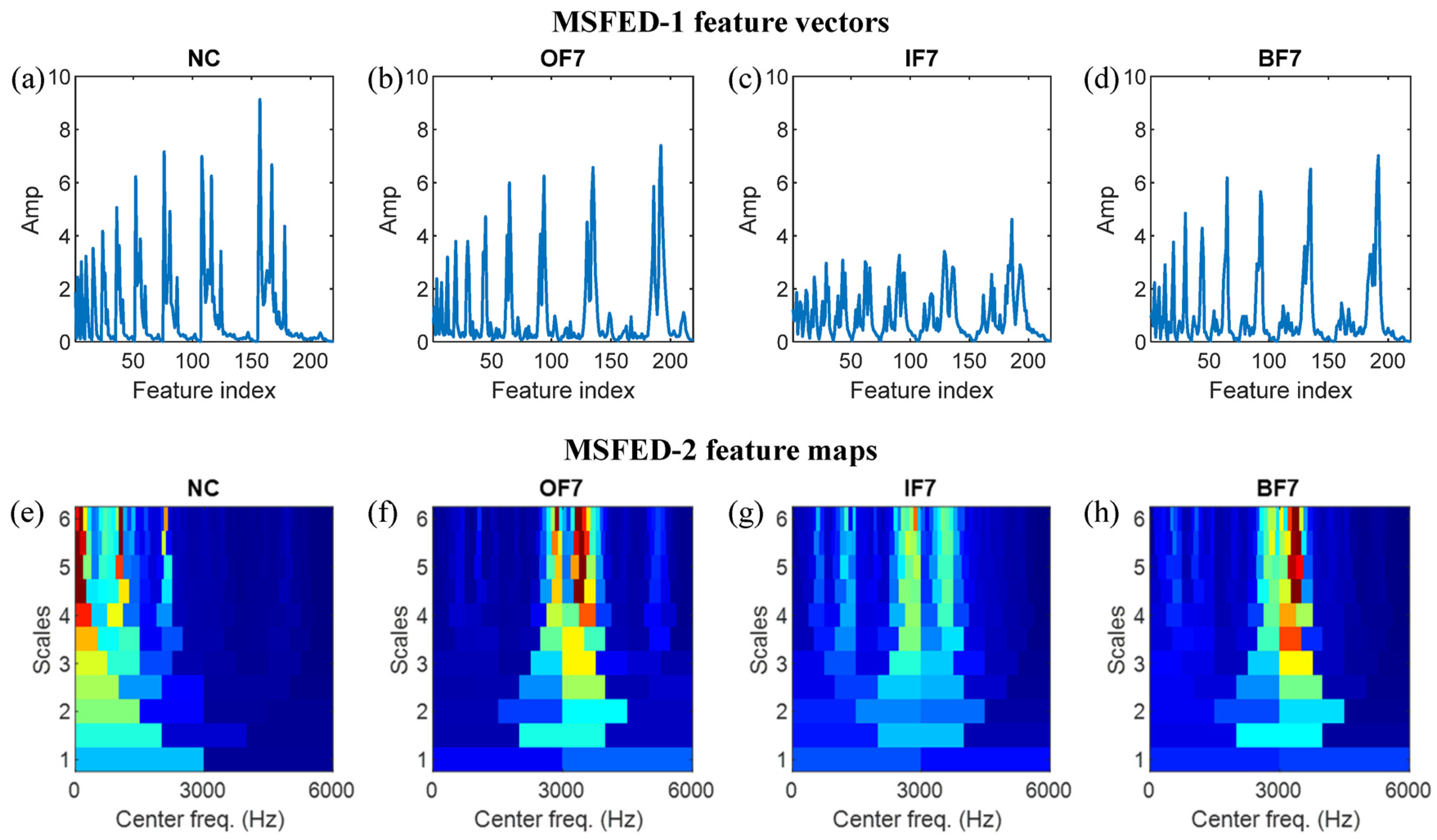
4.2. MSFED Feature Analysis
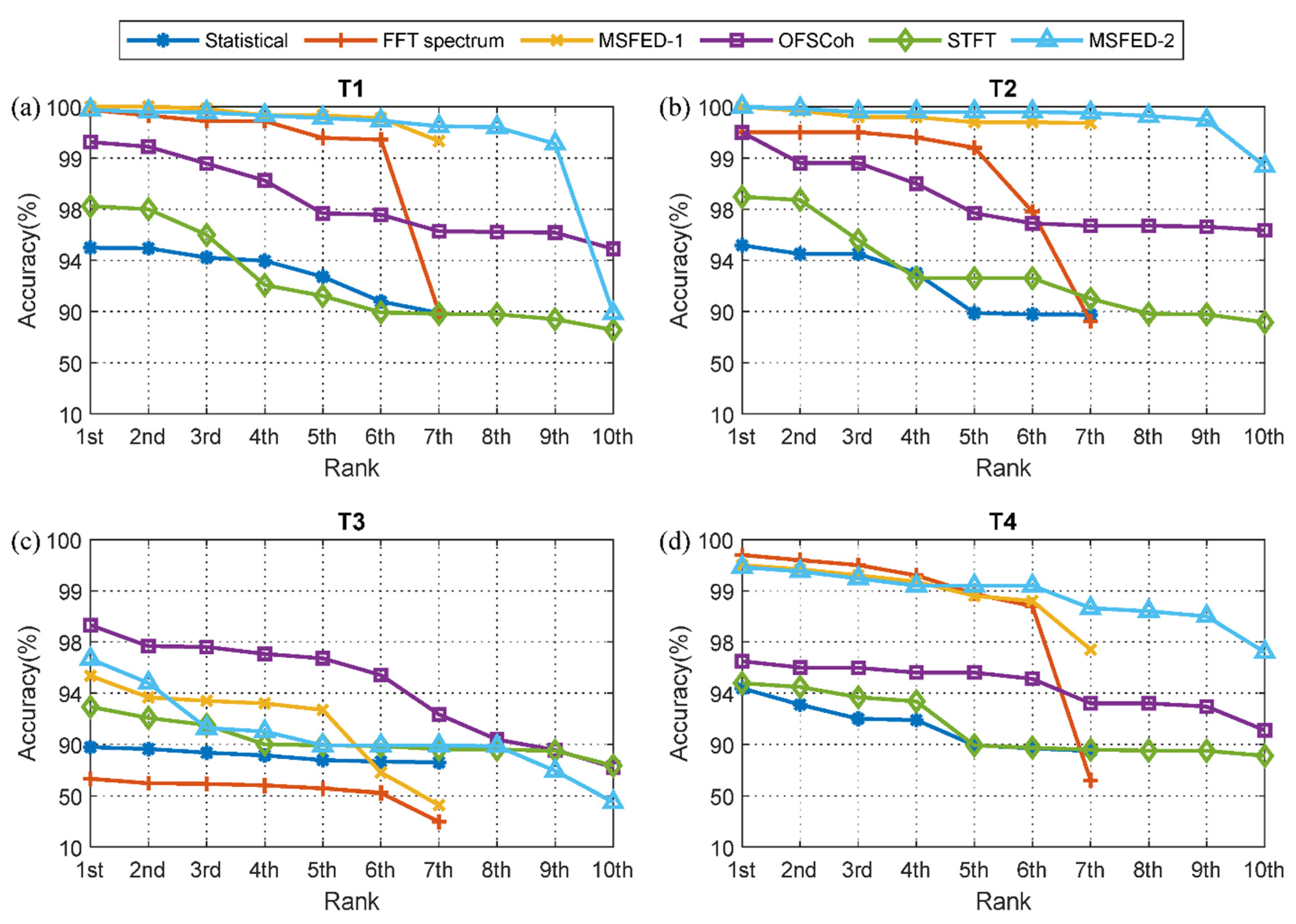
4.3. Fault Diagnosis Results Analysis
4.4. Separability and Transferability Evaluation
5. Conclusions
- (1)
- The MSFED feature revealed the vibration energy distribution pattern and generated discriminative feature vectors and maps for different fault types. In gearbox fault diagnosis, the MSFED features achieved accuracy (average accuracy of top three) of 100% in all four tasks, higher than the Statistics feature, FFT spectrum feature, STFT feature, and OFSCoh feature. In bearing fault diagnosis, the MSFED features achieved accuracies of 99.99% (MSFED-1) on the limited training data fault-diagnosis task, 99.95% (MSFED-2) on the class-imbalanced data fault-diagnosis task, 94.24% (MSFED-2) on the variable-load data fault-diagnosis task, and 99.41% (MSFED-1) on the low signal-to-noise ratio data fault-diagnosis task. The accuracy of the MSFED feature is higher than the other four features on the limited training data fault-diagnosis task and the class-imbalanced data fault-diagnosis task, while lower than the OFSCoh feature on the variable-load data fault-diagnosis task (97.87%), and a little lower than the FFT Spectrum feature on the low signal-to-noise ratio data fault-diagnosis task (99.60%).
- (2)
- The separability and transferability evaluation results of the initial features are in good agreement with the diagnostic performance of initial features. The data separability index s of the MSFED features are a little lower than that of the FFT spectrum feature, but higher than that of the Statistics feature, the OFSCoh feature, and the STFT feature, on the gearbox dataset and bearing dataset. The data transferability index s of the MSFED features is lower than the Statistics feature, the OFSCoh feature, and the STFT feature, but higher than the FFT spectrum feature.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Features of the Gearbox Dataset and Bearing Dataset
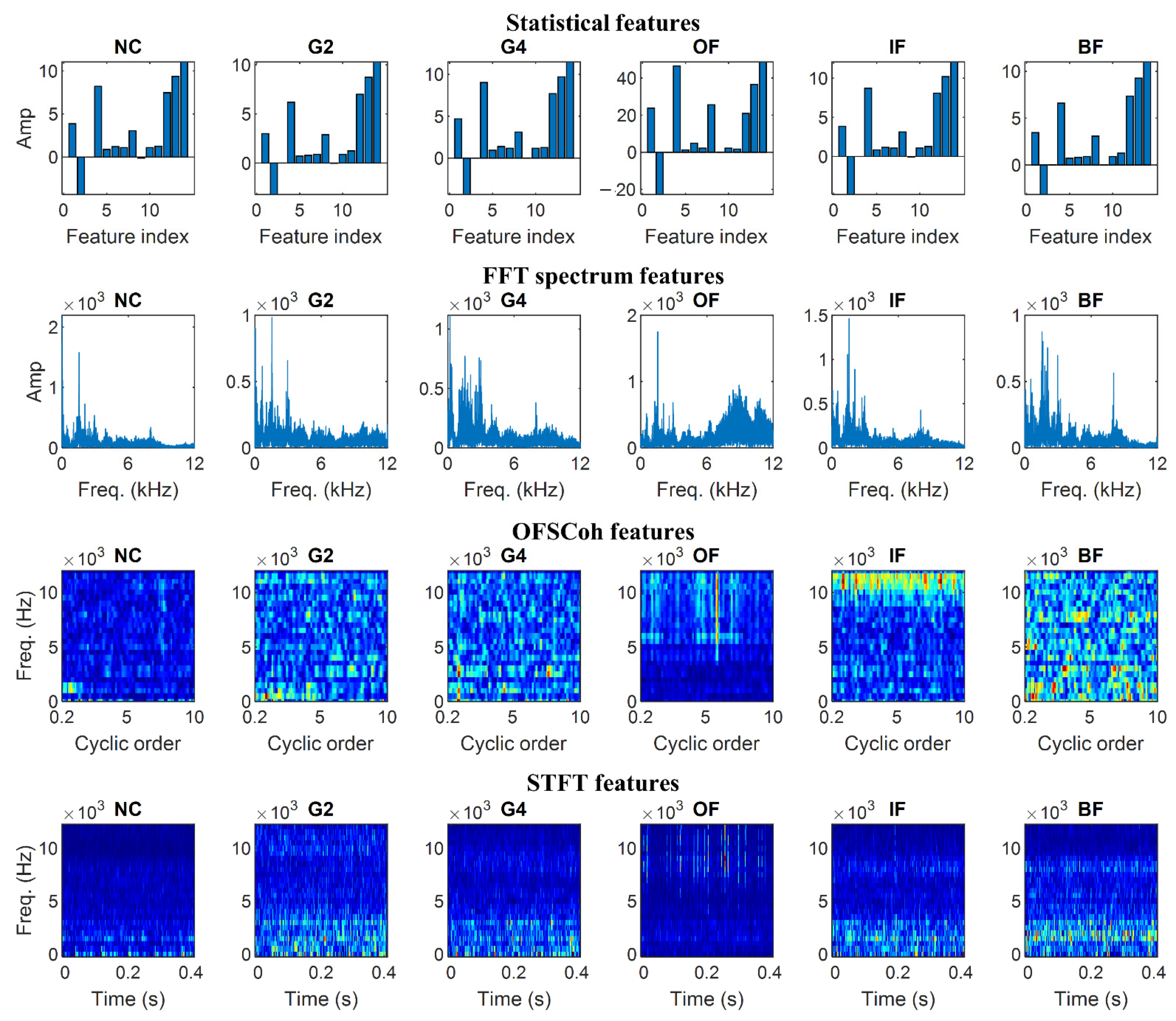
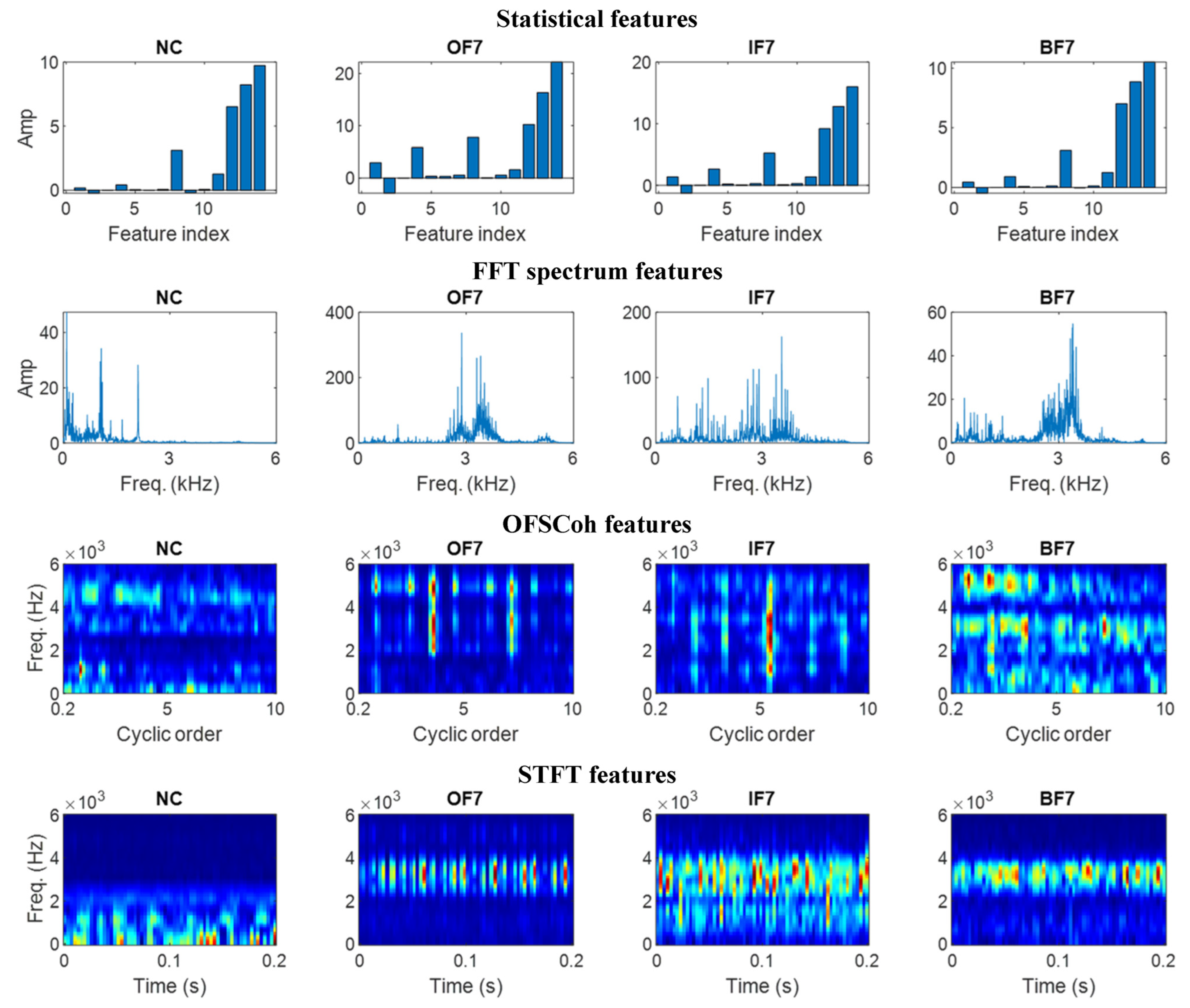
Appendix B. Diagnostic Accuracies of the Six Features and the Ten IFD Models
| Features | IFD Models | Accuracy (%) | |||
|---|---|---|---|---|---|
| T1 | T2 | T3 | T4 | ||
| Statistical | Softmax | 54.57 ± 0.00 | 60.00 ± 0.00 | 36.50 ± 0.00 | 54.22 ± 0.00 |
| KNN | 61.36 ± 0.00 | 70.00 ± 0.00 | 44.33 ± 0.00 | 55.78 ± 0.00 | |
| SVM | 32.47 ± 0.00 | 39.11 ± 0.00 | 16.67 ± 0.00 | 18.67 ± 0.00 | |
| LDA | 62.10 ± 0.00 | 67.11 ± 0.00 | 38.00 ± 0.00 | 54.67 ± 0.00 | |
| NB | 63.83 ± 0.00 | 67.78 ± 0.00 | 38.00 ± 0.00 | 54.44 ± 0.00 | |
| RF | 70.37 ± 1.40 | 79.11 ± 0.42 | 39.87 ± 0.34 | 84.67 ± 0.37 | |
| ANN | 66.79 ± 3.01 | 75.60 ± 1.77 | 39.10 ± 11.22 | 82.53 ± 1.84 | |
| FFT spectrum | Softmax | 100.00 ± 0.00 | 100.00 ± 0.00 | 85.50 ± 0.00 | 100.00 ± 0.00 |
| KNN | 98.40 ± 0.00 | 98.22 ± 0.00 | 88.00 ± 0.00 | 99.78 ± 0.00 | |
| SVM | 94.44 ± 0.00 | 100.00 ± 0.00 | 79.83 ± 0.00 | 92.22 ± 0.00 | |
| LDA | 100.00 ± 0.00 | 100.00 ± 0.00 | 83.33 ± 0.00 | 100.00 ± 0.00 | |
| NB | 91.36 ± 0.00 | 98.67 ± 0.00 | 67.67 ± 0.00 | 99.11 ± 0.00 | |
| RF | 100.00 ± 0.00 | 98.13 ± 0.39 | 80.87 ± 0.69 | 100.00 ± 0.00 | |
| ANN | 100.00 ± 0.00 | 100.00 ± 0.00 | 87.17 ± 0.00 | 100.00 ± 0.00 | |
| MSFED-1 | Softmax | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 |
| KNN | 92.59 ± 0.00 | 95.56 ± 0.00 | 73.00 ± 0.00 | 100.00 ± 0.00 | |
| SVM | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | |
| LDA | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | |
| NB | 100.00 ± 0.00 | 100.00 ± 0.00 | 93.17 ± 0.00 | 100.00 ± 0.00 | |
| RF | 100.00 ± 0.00 | 98.98 ± 0.27 | 99.77 ± 0.20 | 100.00 ± 0.00 | |
| ANN | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | |
| OFSCoh | Softmax | 97.78 ± 0.00 | 95.78 ± 0.00 | 97.83 ± 0.00 | 95.11 ± 0.00 |
| KNN | 92.96 ± 0.00 | 94.22 ± 0.00 | 93.67 ± 0.00 | 92.67 ± 0.00 | |
| SVM | 96.67 ± 0.00 | 93.78 ± 0.00 | 97.67 ± 0.00 | 95.78 ± 0.00 | |
| LDA | 96.42 ± 0.00 | 94.89 ± 0.00 | 96.83 ± 0.00 | 95.78 ± 0.00 | |
| NB | 83.83 ± 0.00 | 83.56 ± 0.00 | 94.50 ± 0.00 | 70.89 ± 0.00 | |
| RF | 95.73 ± 0.62 | 93.69 ± 0.61 | 96.60 ± 0.31 | 92.09 ± 0.56 | |
| ANN | 97.75 ± 0.05 | 95.11 ± 0.00 | 97.67 ± 0.00 | 95.78 ± 0.00 | |
| ChenCNN | 95.31 ± 0.63 | 95.38 ± 1.26 | 95.43 ± 2.13 | 92.36 ± 1.38 | |
| YangCNN | 91.78 ± 1.10 | 93.47 ± 1.65 | 89.50 ± 4.47 | 85.60 ± 2.06 | |
| IslamCNN | 91.26 ± 1.58 | 94.09 ± 1.40 | 89.47 ± 2.26 | 82.27 ± 2.60 | |
| STFT | Softmax | 96.79 ± 0.00 | 98.22 ± 0.00 | 87.00 ± 0.00 | 97.78 ± 0.00 |
| KNN | 88.52 ± 0.00 | 86.22 ± 0.00 | 79.00 ± 0.00 | 88.22 ± 0.00 | |
| SVM | 94.94 ± 0.00 | 98.00 ± 0.00 | 87.83 ± 0.00 | 97.11 ± 0.00 | |
| LDA | 98.52 ± 0.00 | 99.56 ± 0.00 | 92.00 ± 0.00 | 97.78 ± 0.00 | |
| NB | 81.73 ± 0.00 | 90.00 ± 0.00 | 78.83 ± 0.00 | 76.00 ± 0.00 | |
| RF | 96.10 ± 0.65 | 95.78 ± 0.63 | 82.47 ± 6.02 | 98.13 ± 0.30 | |
| ANN | 98.89 ± 0.00 | 99.56 ± 0.00 | 88.80 ± 0.19 | 97.16 ± 0.09 | |
| ChenCNN | 99.11 ± 0.32 | 99.42 ± 0.23 | 88.70 ± 5.41 | 98.62 ± 0.65 | |
| YangCNN | 92.40 ± 3.20 | 96.67 ± 1.36 | 77.63 ± 6.40 | 97.24 ± 0.52 | |
| IslamCNN | 98.44 ± 0.70 | 99.24 ± 0.44 | 73.30 ± 3.64 | 99.11 ± 0.54 | |
| MSFED-2 | Softmax | 100.00 ± 0.00 | 100.00 ± 0.00 | 99.83 ± 0.00 | 100.00 ± 0.00 |
| KNN | 93.33 ± 0.00 | 94.89 ± 0.00 | 74.17 ± 0.00 | 100.00 ± 0.00 | |
| SVM | 83.33 ± 0.00 | 83.33 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | |
| LDA | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | |
| NB | 99.38 ± 0.00 | 100.00 ± 0.00 | 91.33 ± 0.00 | 100.00 ± 0.00 | |
| RF | 100.00 ± 0.00 | 99.38 ± 0.29 | 87.97 ± 3.05 | 100.00 ± 0.00 | |
| ANN | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | |
| ChenCNN | 99.98 ± 0.05 | 99.91 ± 0.18 | 94.03 ± 3.52 | 100.00 ± 0.00 | |
| YangCNN | 99.53 ± 0.30 | 99.56 ± 0.28 | 80.33 ± 5.16 | 99.69 ± 0.23 | |
| IslamCNN | 99.63 ± 0.41 | 99.56 ± 0.58 | 76.83 ± 10.13 | 99.91 ± 0.11 | |
| Features | IFD Models | Accuracy (%) | |||
|---|---|---|---|---|---|
| T1 | T2 | T3 | T4 | ||
| Statistical | Softmax | 90.78 ± 0.00 | 87.50 ± 0.00 | 76.47 ± 0.00 | 89.30 ± 0.00 |
| KNN | 88.89 ± 0.00 | 88.80 ± 0.00 | 86.33 ± 0.00 | 84.80 ± 0.00 | |
| SVM | 94.94 ± 0.00 | 94.50 ± 0.00 | 77.67 ± 0.00 | 86.90 ± 0.00 | |
| LDA | 94.22 ± 0.00 | 94.50 ± 0.00 | 81.27 ± 0.00 | 92.00 ± 0.00 | |
| NB | 92.72 ± 0.00 | 93.00 ± 0.00 | 75.93 ± 0.00 | 93.10 ± 0.00 | |
| RF | 94.99 ± 0.06 | 95.18 ± 0.07 | 87.71 ± 0.69 | 94.38 ± 0.28 | |
| ANN | 93.96 ± 0.49 | 87.92 ± 0.52 | 83.44 ± 0.35 | 91.90 ± 0.11 | |
| FFT spectrum | Softmax | 99.83 ± 0.00 | 99.50 ± 0.00 | 55.53 ± 0.00 | 99.60 ± 0.00 |
| KNN | 99.39 ± 0.00 | 99.40 ± 0.00 | 57.87 ± 0.00 | 98.70 ± 0.00 | |
| SVM | 89.61 ± 0.00 | 82.30 ± 0.00 | 52.20 ± 0.00 | 61.90 ± 0.00 | |
| LDA | 99.72 ± 0.00 | 99.20 ± 0.00 | 59.07 ± 0.00 | 99.30 ± 0.00 | |
| NB | 99.72 ± 0.00 | 99.50 ± 0.00 | 29.67 ± 0.00 | 99.50 ± 0.00 | |
| RF | 99.36 ± 0.15 | 97.80 ± 0.11 | 63.11 ± 1.12 | 98.94 ± 0.20 | |
| ANN | 99.94 ± 0.00 | 99.50 ± 0.47 | 59.57 ± 4.68 | 99.70 ± 0.00 | |
| MSFED-1 | Softmax | 99.83 ± 0.00 | 99.80 ± 0.00 | 93.40 ± 0.00 | 98.80 ± 0.00 |
| KNN | 99.33 ± 0.00 | 99.70 ± 0.00 | 68.00 ± 0.00 | 97.40 ± 0.00 | |
| SVM | 99.78 ± 0.00 | 99.70 ± 0.00 | 93.20 ± 0.00 | 98.90 ± 0.00 | |
| LDA | 100.00 ± 0.00 | 100.00 ± 0.00 | 93.67 ± 0.00 | 99.30 ± 0.00 | |
| NB | 100.00 ± 0.00 | 99.80 ± 0.00 | 42.80 ± 0.00 | 99.50 ± 0.00 | |
| RF | 99.83 ± 0.05 | 99.68 ± 0.04 | 92.68 ± 0.80 | 99.18 ± 0.25 | |
| ANN | 99.96 ± 0.04 | 99.92 ± 0.07 | 95.36 ± 0.73 | 99.42 ± 0.10 | |
| OFSCoh | Softmax | 98.89 ± 0.00 | 98.90 ± 0.00 | 97.07 ± 0.00 | 95.60 ± 0.00 |
| KNN | 96.22 ± 0.00 | 96.70 ± 0.00 | 92.33 ± 0.00 | 91.10 ± 0.00 | |
| SVM | 98.56 ± 0.00 | 98.50 ± 0.00 | 97.67 ± 0.00 | 96.50 ± 0.00 | |
| LDA | 99.22 ± 0.00 | 98.90 ± 0.00 | 98.33 ± 0.00 | 96.00 ± 0.00 | |
| NB | 94.89 ± 0.00 | 96.90 ± 0.00 | 71.93 ± 0.00 | 93.20 ± 0.00 | |
| RF | 97.57 ± 0.23 | 96.62 ± 0.26 | 96.72 ± 0.73 | 95.12 ± 0.25 | |
| ANN | 99.31 ± 0.04 | 99.50 ± 0.00 | 97.61 ± 0.03 | 95.98 ± 0.12 | |
| ChenCNN | 97.67 ± 0.34 | 97.68 ± 0.38 | 95.41 ± 0.88 | 95.60 ± 0.30 | |
| YangCNN | 96.28 ± 0.53 | 96.70 ± 0.41 | 85.60 ± 1.69 | 92.96 ± 0.59 | |
| IslamCNN | 96.17 ± 0.85 | 96.36 ± 0.85 | 90.37 ± 1.69 | 93.20 ± 0.74 | |
| STFT | Softmax | 84.00 ± 0.00 | 87.80 ± 0.00 | 86.20 ± 0.00 | 85.10 ± 0.00 |
| KNN | 75.56 ± 0.00 | 81.50 ± 0.00 | 73.40 ± 0.00 | 81.00 ± 0.00 | |
| SVM | 88.17 ± 0.00 | 91.00 ± 0.00 | 84.87 ± 0.00 | 84.90 ± 0.00 | |
| LDA | 91.22 ± 0.00 | 92.60 ± 0.00 | 92.93 ± 0.00 | 89.20 ± 0.00 | |
| NB | 87.94 ± 0.00 | 92.60 ± 0.00 | 85.93 ± 0.00 | 87.40 ± 0.00 | |
| RF | 89.31 ± 0.64 | 88.32 ± 1.22 | 88.72 ± 0.44 | 85.78 ± 0.72 | |
| ANN | 92.07 ± 0.04 | 92.60 ± 0.24 | 89.35 ± 0.92 | 93.68 ± 0.27 | |
| ChenCNN | 98.00 ± 0.73 | 98.18 ± 0.44 | 91.51 ± 0.95 | 94.48 ± 0.63 | |
| YangCNN | 95.99 ± 0.24 | 95.58 ± 0.65 | 89.92 ± 1.27 | 93.36 ± 0.51 | |
| IslamCNN | 98.06 ± 0.93 | 98.24 ± 0.52 | 92.07 ± 2.20 | 94.78 ± 0.64 | |
| MSFED-2 | Softmax | 99.89 ± 0.00 | 99.90 ± 0.00 | 91.27 ± 0.00 | 98.50 ± 0.00 |
| KNN | 99.28 ± 0.00 | 99.90 ± 0.00 | 69.27 ± 0.00 | 97.20 ± 0.00 | |
| SVM | 88.56 ± 0.00 | 99.90 ± 0.00 | 89.13 ± 0.00 | 98.60 ± 0.00 | |
| LDA | 99.94 ± 0.00 | 100.00 ± 0.00 | 96.67 ± 0.00 | 99.10 ± 0.00 | |
| NB | 99.83 ± 0.00 | 99.90 ± 0.00 | 44.93 ± 0.00 | 99.10 ± 0.00 | |
| RF | 99.90 ± 0.04 | 99.96 ± 0.05 | 94.79 ± 0.60 | 99.10 ± 0.11 | |
| ANN | 100.00 ± 0.00 | 100.00 ± 0.00 | 95.07 ± 3.19 | 99.64 ± 0.05 | |
| ChenCNN | 99.78 ± 0.09 | 99.88 ± 0.04 | 91.01 ± 1.33 | 99.46 ± 0.12 | |
| YangCNN | 99.73 ± 0.06 | 98.84 ± 0.76 | 89.07 ± 2.70 | 98.66 ± 0.32 | |
| IslamCNN | 99.60 ± 0.19 | 99.82 ± 0.12 | 89.19 ± 2.02 | 99.24 ± 0.21 | |
References
- Vishwakarma, M.; Purohit, R.; Harshlata, V.; Rajput, P. Vibration analysis & condition monitoring for rotating machines: A review. In Proceedings of the 5th International Conference on Materials Processing and Characterization (ICMPC), Gokaraju Rangaraju Institute of Engineering and Technology, Hyderabad, India, 12–13 March 2016; pp. 2659–2664. [Google Scholar]
- Guan, S.Y.; Huang, D.R.; Guo, S.H.; Zhao, L.; Chen, H.T. An Improved Fault Diagnosis Approach Using LSSVM for Complex Industrial Systems. Machines 2022, 10, 443. [Google Scholar] [CrossRef]
- Peng, Y.W.; Ma, X.H. A Fault Diagnosis Method of Rolling Bearings Based on Parameter Optimization and Adaptive Generalized S-Transform. Machines 2022, 10, 207. [Google Scholar] [CrossRef]
- Raouf, I.; Lee, H.; Kim, H.S. Mechanical fault detection based on machine learning for robotic RV reducer using electrical current signature analysis: A data-driven approach. J. Comput. Des. Eng. 2022, 9, 417–433. [Google Scholar] [CrossRef]
- Rohan, A.; Raouf, I.; Kim, H.S. Rotate Vector (RV) Reducer Fault Detection and Diagnosis System: Towards Component Level Prognostics and Health Management (PHM). Sensors 2020, 20, 6845. [Google Scholar] [CrossRef]
- Gültekin, Ö.; Cinar, E.; Özkan, K.; Yazıcı, A. Multisensory data fusion-based deep learning approach for fault diagnosis of an industrial autonomous transfer vehicle. Expert Syst. Appl. 2022, 200, 117055. [Google Scholar] [CrossRef]
- He, Q. Vibration signal classification by wavelet packet energy flow manifold learning. J. Sound Vib. 2013, 332, 1881–1894. [Google Scholar] [CrossRef]
- Chen, X.; Yang, Y.; Cui, Z.; Shen, J. Vibration fault diagnosis of wind turbines based on variational mode decomposition and energy entropy. Energy 2019, 174, 1100–1109. [Google Scholar] [CrossRef]
- Javorskyj, I.; Matsko, I.; Yuzefovych, R.; Lychak, O.; Lys, R. Methods of Hidden Periodicity Discovering for Gearbox Fault Detection. Sensors 2021, 21, 6138. [Google Scholar] [CrossRef]
- Aijun, H.; Jianfeng, L.; Shangfei, S.; Ling, X. A Novel Approach of Impulsive Signal Extraction for Early Fault Detection of Rolling Element Bearing. Shock Vib. 2017, 2017, 9375491. [Google Scholar] [CrossRef]
- Peng, C.; Bo, L. Vibration Signal Analysis of Journal Bearing Supported Rotor System by Cyclostationarity. Shock Vib. 2014, 2014, 952958. [Google Scholar] [CrossRef][Green Version]
- Prasad, A.; Dantreliya, C.; Chande, M.; Chauhan, V.; Rai, A. An intelligent fault diagnosis framework based on piecewise aggregate approximation, statistical moments, and sparse autoencoder. Proc. Inst. Mech. Eng. Part O-J. Risk Reliab. 2022. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Liu, Z.; Liang, X.; Si, S. The Entropy Algorithm and Its Variants in the Fault Diagnosis of Rotating Machinery: A Review. IEEE Access 2018, 6, 66723–66741. [Google Scholar] [CrossRef]
- Zhang, X.; Cong, Y.; Yuan, Z.; Zhang, T.; Bai, X.; Rosso, C. Early Fault Detection Method of Rolling Bearing Based on MCNN and GRU Network with an Attention Mechanism. Shock Vib. 2021, 2021, 6660243. [Google Scholar] [CrossRef]
- Nguyen, V.H.; Cheng, J.S.; Yu, Y.; Thai, V.T. An architecture of deep learning network based on ensemble empirical mode decomposition in precise identification of bearing vibration signal. J. Mech. Sci. Technol. 2019, 33, 41–50. [Google Scholar] [CrossRef]
- Xu, Y.H.; Li, S.F.; Jiang, W.; Liu, W.; Zhao, K.J. A progressive fault diagnosis method for rolling bearings based on VMD energy entropy and a deep adversarial transfer network. Meas. Sci. Technol. 2022, 33, 095003. [Google Scholar] [CrossRef]
- Kumar, A.; Tang, H.S.; Vashishtha, G.; Xiang, J.W. Noise subtraction and marginal enhanced square envelope spectrum (MESES) for the identification of bearing defects in centrifugal and axial pump. Mech. Syst. Signal Process. 2022, 165, 108366. [Google Scholar] [CrossRef]
- Puche-Panadero, R.; Martinez-Roman, J.; Sapena-Bano, A.; Burriel-Valencia, J.; Pineda-Sanchez, M.; Perez-Cruz, J.; Riera-Guasp, M. New method for spectral leakage reduction in the FFT of stator currents: Application to the diagnosis of bar breakages in cage motors working at very low slip. IEEE Trans. Instrum. Meas. 2021, 70, 1–11. [Google Scholar] [CrossRef]
- Tao, H.F.; Wang, P.; Chen, Y.Y.; Stojanovic, V.; Yang, H.Z. An unsupervised fault diagnosis method for rolling bearing using STFT and generative neural networks. J. Frankl. Inst.-Eng. Appl. Math. 2020, 357, 7286–7307. [Google Scholar] [CrossRef]
- Xi, W.K.; Li, Z.X.; Tian, Z.; Duan, Z.H. A feature extraction and visualization method for fault detection of marine diesel engines. Measurement 2018, 116, 429–437. [Google Scholar] [CrossRef]
- Hu, M.T.; Wang, G.F.; Ma, K.L.; Cao, Z.H.; Yang, S. Bearing performance degradation assessment based on optimized EWT and CNN. Measurement 2021, 172, 108868. [Google Scholar] [CrossRef]
- Wang, X.L.; Zheng, J.D.; Pan, H.Y.; Liu, Q.Y.; Wang, C.J. Maximum envelope-based Autogram and symplectic geometry mode decomposition based gear fault diagnosis method. Measurement 2021, 174, 108575. [Google Scholar] [CrossRef]
- Cheng, Y.; Chen, B.Y.; Zhang, W.H. Enhanced spectral coherence and its application to bearing fault diagnosis. Measurement 2022, 188, 110418. [Google Scholar] [CrossRef]
- Schmidt, S.; Heyns, P.S.; Gryllias, K.C. A methodology using the spectral coherence and healthy historical data to perform gearbox fault diagnosis under varying operating conditions. Appl. Acoust. 2020, 158, 107038. [Google Scholar] [CrossRef]
- Chen, Z.; Mauricio, A.; Li, W.; Gryllias, K. A deep learning method for bearing fault diagnosis based on Cyclic Spectral Coherence and Convolutional Neural Networks. Mech. Syst. Signal Process. 2020, 140, 106683. [Google Scholar] [CrossRef]
- Yu, H.; Wei, H.; Li, J.; Zhou, D.; Wei, L.; Liu, H.; Concli, F. Lubrication state recognition based on energy characteristics of friction vibration with EEMD and SVM. Shock Vib. 2021, 2021, 9972119. [Google Scholar] [CrossRef]
- Wang, Y.; He, Z.; Xiang, J.; Zi, Y. Application of local mean decomposition to the surveillance and diagnostics of low-speed helical gearbox. Mech. Mach. Theory 2012, 47, 62–73. [Google Scholar] [CrossRef]
- Cheng, G.; Cheng, Y.-l.; Shen, L.-h.; Qiu, J.-b.; Zhang, S. Gear fault identification based on Hilbert–Huang transform and SOM neural network. Measurement 2013, 46, 1137–1146. [Google Scholar] [CrossRef]
- Feng, G.-H.; Pan, Y.-L. Establishing a cost-effective sensing system and signal processing method to diagnose preload levels of ball screws. Mech. Syst. Signal Process. 2012, 28, 78–88. [Google Scholar] [CrossRef]
- Randall, R.B.; Antoni, J. Rolling element bearing diagnostics-A tutorial. Mech. Syst. Signal Process. 2011, 25, 485–520. [Google Scholar] [CrossRef]
- Wen, H.; Dai, H.; Teng, Z.; Yang, Y.; Li, F. Performance comparison of windowed interpolation FFT and Quasisynchronous Sampling Algorithm for frequency estimation. Math. Probl. Eng. 2014, 2014, 745830. [Google Scholar] [CrossRef]
- Antoni, J. Fast computation of the kurtogram for the detection of transient faults. Mech. Syst. Signal Process. 2007, 21, 108–124. [Google Scholar] [CrossRef]
- Guan, S.; Loew, M. A novel intrinsic measure of data separability. Appl. Intell. 2022, 1–17. [Google Scholar] [CrossRef]
- Zheng, M.L.; Chang, Q.; Man, J.F.; Liu, Y.; Shen, Y.P. Two-Stage Multi-Scale Fault Diagnosis Method for Rolling Bearings with Imbalanced Data. Machines 2022, 10, 336. [Google Scholar] [CrossRef]
- Yang, Y.; Zheng, H.; Li, Y.; Xu, M.; Chen, Y. A fault diagnosis scheme for rotating machinery using hierarchical symbolic analysis and convolutional neural network. ISA Trans. 2019, 91, 235–252. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.M.M.; Kim, J.-M. Automated bearing fault diagnosis scheme using 2D representation of wavelet packet transform and deep convolutional neural network. Comput. Ind. 2019, 106, 142–153. [Google Scholar] [CrossRef]
- Loparo, K. Bearings Vibration Data Set; Case Western Reserve University: Cleveland, OH, USA, 2003. [Google Scholar]
- Du, Y.; Wang, A.M.; Wang, S.; He, B.M.; Meng, G.Y. Fault Diagnosis under Variable Working Conditions Based on STFT and Transfer Deep Residual Network. Shock Vib. 2020, 2020, 1274380. [Google Scholar] [CrossRef]
- Ma, S.J.; Liu, W.K.; Cai, W.; Shang, Z.W.; Liu, G. Lightweight Deep Residual CNN for Fault Diagnosis of Rotating Machinery Based on Depthwise Separable Convolutions. IEEE Access 2019, 7, 57023–57036. [Google Scholar] [CrossRef]
- Wang, X.D.; Liu, F. Triplet Loss Guided Adversarial Domain Adaptation for Bearing Fault Diagnosis. Sensors 2020, 20, 320. [Google Scholar] [CrossRef]


| Rotating Speed (rpm) | Fault Types | Number of Samples | Class Label |
|---|---|---|---|
| 800 & 1000 & 1200 | NC | 50 & 50 & 50 | 0 |
| 800 & 1000 & 1200 | G2 | 50 & 50 & 50 | 1 |
| 800 & 1000 & 1200 | G4 | 50 & 50 & 50 | 2 |
| 800 & 1000 & 1200 | OF | 50 & 50 & 50 | 3 |
| 800 & 1000 & 1200 | IF | 50 & 50 & 50 | 4 |
| 800 & 1000 & 1200 | BF | 50 & 50 & 50 | 5 |
| Features | Parameters | Size |
|---|---|---|
| Statistical | Max, Min, Mean, Peak to peak, ARV, Var, Std, Kurtosis, Skewness, rms, Form factor, Crest factor, Impulse factor, Clearance factor | 1 × 14 |
| FFT spectrum | none | 1 × 4800 |
| STFT | Analytic frequency range: 0~12,000 Hz, window length: 0.002 s, Overlap rate: 0.5 | 64 × 64 |
| OFSCoh | Analytic frequency range: 0~12,000 Hz, analytic cyclic order: 0~10 | 64 × 64 |
| MSFED-1 | Analytic frequency range: 0~12,000 Hz, scales: 1~6 | 1 × 219 |
| MSFED-2 | Analytic frequency range: 0~12,000 Hz, scales: 1~6 | 64 × 64 |
| Tasks | SNR | Training Data | Testing Data | ||
|---|---|---|---|---|---|
| Rotating Speed (rpm) | Number of Samples | Rotating Speed (rpm) | Number of Samples | ||
| T1 | No noise | 800 & 1000 & 1200 | 5 × 6 × 3 | 800 & 1000 & 1200 | 45 × 6 × 3 |
| T2 | No noise | 800 & 1000 & 1200 | (25 & 15 & 15 & 5 & 5 & 5) × 3 | 800 & 1000 & 1200 | 25 × 6 × 3 |
| T3 | No noise | 1000 | 50 × 6 × 1 | 800 & 1200 | 50 × 6 × 2 |
| T4 | 0 dB | 800 & 1000 & 1200 | 25 × 6 × 3 | 800 & 1000 & 1200 | 25 × 6 × 3 |
| Models | Fixed Parameters | Tunable Parameters | Number of HSs |
| Softmax | / | / | 1 |
| KNN |
|
| 12 |
| SVM |
|
| 90 |
| LDA |
|
| 4 |
| NB | / |
| 16 |
| RF |
|
| 54 |
| ANN |
|
| 32 |
| Chen CNN |
|
| 12 |
| Yang CNN |
|
| 8 |
| Islam CNN |
|
| 6 |
| Features | Average Accuracy of Top 3 (%) | |||
|---|---|---|---|---|
| T1 | T2 | T3 | T4 | |
| Statistical | 67.00 | 74.90 | 41.10 | 74.33 |
| FFT spectrum | 100.00 | 100.00 | 86.89 | 100.00 |
| MSFED-1 | 100.00 | 100.00 | 100.00 | 100.00 |
| OFSCoh | 97.40 | 95.42 | 97.72 | 95.78 |
| STFT | 98.84 | 99.51 | 89.83 | 98.62 |
| MSFED-2 | 100.00 | 100.00 | 100.00 | 100.00 |
| Features | DSIs | DTIs | |||||
|---|---|---|---|---|---|---|---|
| 800 rpm | 1000 rpm | 1200 rpm | Average | 1000→800 rpm | 1000→1200 rpm | Average | |
| SI | 0.45 | 0.43 | 0.44 | 0.440 | 1.37 | 0.92 | 1.145 |
| FFT spectrum | 0.70 | 0.69 | 0.71 | 0.700 | 0.89 | 0.96 | 0.925 |
| MSFED-1 | 0.68 | 0.70 | 0.71 | 0.697 | 1.12 | 0.87 | 0.995 |
| OFSCoh | 0.49 | 0.44 | 0.45 | 0.460 | 2.57 | 1.77 | 2.170 |
| STFT | 0.42 | 0.47 | 0.44 | 0.443 | 1.70 | 2.10 | 1.900 |
| MSFED-2 | 0.66 | 0.69 | 0.72 | 0.690 | 1.12 | 0.90 | 1.010 |
| Load (hp) | Fault Types | Severity (mils) | Number of Samples | Label |
|---|---|---|---|---|
| 0 & 1 & 2 & 3 | NC | / | 50 & 50 & 50 & 50 | 0 |
| 0 & 1 & 2 & 3 | OF | 7 | 50 & 50 & 50 & 50 | 1 |
| 0 & 1 & 2 & 3 | OF | 14 | 50 & 50 & 50 & 50 | 2 |
| 0 & 1 & 2 & 3 | OF | 21 | 50 & 50 & 50 & 50 | 3 |
| 0 & 1 & 2 & 3 | IF | 7 | 50 & 50 & 50 & 50 | 4 |
| 0 & 1 & 2 & 3 | IF | 14 | 50 & 50 & 50 & 50 | 5 |
| 0 & 1 & 2 & 3 | IF | 21 | 50 & 50 & 50 & 50 | 6 |
| 0 & 1 & 2 & 3 | BF | 7 | 50 & 50 & 50 & 50 | 7 |
| 0 & 1 & 2 & 3 | BF | 14 | 50 & 50 & 50 & 50 | 8 |
| 0 & 1 & 2 & 3 | BF | 21 | 50 & 50 & 50 & 50 | 9 |
| Tasks | SNR | Training Data | Testing Data | ||
|---|---|---|---|---|---|
| Load (hp) | Number of Samples | Load (hp) | Number of Samples | ||
| T1 | No noise | 0 & 1 & 2 & 3 | 5 × 10 × 4 | 0 & 1 & 2 & 3 | 45 × 10 × 4 |
| T2 | No noise | 0 & 1 & 2 & 3 | (25 & 15 & 15 & 15 & 10 & 10 & 10 & 5 & 5 & 5) × 4 | 0 & 1 & 2 & 3 | 25 × 10 × 4 |
| T3 | No noise | 0 | 50 × 10 × 1 | 1 & 2 & 3 | 50 × 10 × 3 |
| T4 | 0 dB | 0 & 1 & 2 & 3 | 25 × 10 × 4 | 0 & 1 & 2 & 3 | 25 × 10 × 4 |
| Features | Average Accuracy of Top 3 (%) | |||
|---|---|---|---|---|
| T1 | T2 | T3 | T4 | |
| Statistical | 94.72 | 94.73 | 85.83 | 93.16 |
| FFT Spectrum | 99.83 | 99.50 | 60.58 | 99.60 |
| MSFED-1 | 99.99 | 99.91 | 94.14 | 99.41 |
| OFSCoh | 99.14 | 99.10 | 97.87 | 96.16 |
| STFT | 97.35 | 97.33 | 92.17 | 94.31 |
| MSFED-2 | 99.91 | 99.95 | 94.24 | 99.36 |
| Features | DSIs | DTIs | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 hp | 1 hp | 2 hp | 3 hp | Average | 0→1 hp | 0→2 hp | 0→3 hp | Average | |
| SI | 0.49 | 0.49 | 0.51 | 0.47 | 0.490 | 6.67 | 4.77 | 3.21 | 4.883 |
| FFT spectrum | 0.67 | 0.67 | 0.68 | 0.69 | 0.678 | 0.83 | 0.86 | 0.80 | 0.830 |
| MSFED-1 | 0.62 | 0.64 | 0.65 | 0.65 | 0.640 | 1.03 | 0.93 | 0.79 | 0.917 |
| OFSCoh | 0.51 | 0.53 | 0.54 | 0.55 | 0.533 | 1.46 | 1.34 | 1.17 | 1.323 |
| STFT | 0.44 | 0.44 | 0.46 | 0.45 | 0.448 | 3.78 | 3.33 | 2.43 | 3.180 |
| MSFED-2 | 0.62 | 0.63 | 0.65 | 0.65 | 0.638 | 1.21 | 0.99 | 0.87 | 1.023 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Q.; Zhang, X.; Wu, C. A Novel MSFED Feature for the Intelligent Fault Diagnosis of Rotating Machines. Machines 2022, 10, 743. https://doi.org/10.3390/machines10090743
Zhou Q, Zhang X, Wu C. A Novel MSFED Feature for the Intelligent Fault Diagnosis of Rotating Machines. Machines. 2022; 10(9):743. https://doi.org/10.3390/machines10090743
Chicago/Turabian StyleZhou, Qi, Xuyan Zhang, and Chaoqun Wu. 2022. "A Novel MSFED Feature for the Intelligent Fault Diagnosis of Rotating Machines" Machines 10, no. 9: 743. https://doi.org/10.3390/machines10090743
APA StyleZhou, Q., Zhang, X., & Wu, C. (2022). A Novel MSFED Feature for the Intelligent Fault Diagnosis of Rotating Machines. Machines, 10(9), 743. https://doi.org/10.3390/machines10090743





