Abstract
The shearer drum undertakes the main function of coal falling and loading, and picks distributed on it have a great impact on the performance of the drum. However, few studies have optimized the pick and drum at the same time. In this paper, parameters of pick and drum are considered as design variables, and the response functions of design variables are established based on the central composite experiment method. The optimal structural and working parameters of the pick and the drum of MG500/1130-WD shearer are obtained by using the multi-objective bat algorithm and multi-objective bat algorithm with grid, respectively. Comparing results of the two algorithms, the multi-objective bat algorithm with grid is more effective in improving the comprehensive performance of the drum. According to the optimized design variables, a coal mining test is carried out to verify the optimization effect of the algorithm. The result provides some theoretical references for the design and production of the drum and has some engineering application value.
1. Introduction
A shearer is one of the major equipment pieces of fully mechanized mining equipment, which is a large complex system integrating machinery, electricity, and hydraulics [1]. Mechanized operation with a shearer can reduce manual labor, improve staff working conditions in a harsh environment, and produce coal mining with lower power consumption and higher efficiency. The drum is the main working part of the shearer, which is in charge of excavation and conveying coal. When the drum rotates, picks distributed on the drum collide with the coal periodically to realize the cutting of coal, then the coal will be thrown onto the scraper conveyor and transported out. The shearer travels according to the set traction speed, so that the coal cutting and loading processes can be carried out continuously.
The comprehensive performance of the drum has a significant impact on production efficiency, cutting energy consumption, and machine service life [2,3]. Therefore, many researchers have carried out some theoretical, experimental, and simulation works in these areas. Li [4] conducted a series of full-scale shearer drum cutting tests and built a reliable shearer drum cutting predictive models by comparing numerical simulation with the empirical results. Zhao [5] established the coupling model of the drum using the discrete element method (DEM), and focused on the impact of drum rotation speed, traction speed, and spiral angle on pick and blade wear depth. Liu [6] investigated the relationship between the drum rotation speed, traction speed, rock firmness coefficient, cutting depth, and spiral angle, and drum wear based on the single factor method, which provided a quick way to study drum wear law. Liu [7] studied the load performance of the shearer drum through the orthogonal test method. Based on the analysis of variance, it was found that the spiral blade parameters have the greatest impact on the load performance of the drum and the traction speed has the greatest impact on the cutting power of the drum. Gao [8] investigated the effects of the cutting depth, drum hub diameter, drum rotation speed, traction speed, and vane helix angle on the coal-loading rate under circumstances of coal-loading with drum ejection and pushing modes using a model test method. Sun [9] studied the effect of blade axial tilt angle on the conveying performance based on DEM. However, the above studies only pay attention to a specific performance on the pick or drum, while the multiple properties of the pick and drum affect each other and it is difficult to find a balance through the traditional mechanical design optimization method; therefore, it is necessary to use new methods to solve the problem.
In recent years, many intelligent optimization algorithms and their improved versions have emerged. NSGA-II [10] is one of the most popular genetic algorithms at present. It has the advantages of fast running speed and good convergence of solution set, and has become the benchmark of the performance of other optimization algorithms. Wu [11] adopted a new density selection and decoding method based on sorting algorithms to improve the NSGA-II, and the method was validated by an example of PFAL evolution planning for a family of similar mechanical products, which indicated that the efficiency was significantly improved. Zhang [12] introduced the selection strategy including individual importance level into the NSGA-II, so as to obtain the solution of the task of multiple targets with different importance. Based on the algorithm, the notch filter was optimized. Particle swarm optimization (PSO) [13] simulates the clustering behavior of insects, herds, and birds. These groups search for food in a cooperative way, and each member of the group constantly changes its search mode by learning its own experience and the experience of other members. The PSO provides ideas for many later algorithms that imitate animal behavior. Based on the hierarchical structure concept of control theory, Lu [14] proposed a hierarchical structure poly-particle swarm optimization (HSPPSO), which performed parallel optimization calculation on multi particle swarm and expanded the scope of particle search. After testing, the algorithm was superior to PSO in convergence speed and accuracy. Zhan [15] designed an adaptive particle swarm optimization (ASPO) which could execute a real-time evolutionary state estimation procedure according to the population distribution and particle fitness and execute the elite learning strategy when it is in the convergence state, so it had faster convergence speed and better global optimality. Dorigo [16] proposed the ant colony algorithm, which was inspired by the ant’s foraging behavior to find the shortest path from the food source to the nest, and applied it to solve the traveling salesman problem (TSP). Later, Dorigo proposed the ant colony system (ACS) [17], and global pheromone update rules were introduced to update the optimal path of each iteration in order to find the optimal solution quickly, which improved the convergence speed of the algorithm.Cao [18] carried out task assignment research based on improved ant colony algorithm in the field operation environment, and realized the management of multi state agricultural machinery cooperative operation, which avoided overloading of some agricultural machines and idling of other agricultural machines, and shortened the operation cycle. Ge [19] aimed at the shortcomings of ant colony algorithm, which is slow and easy to fall into local optimization; he dynamically improved the strength of pheromone, and applied the algorithm to cloud computing task scheduling. Inspired by various metaheuristic algorithms, Yang [20] proposed the bat algorithm (BA) based on the echolocation behavior of bats, which is also widely used in parameter optimization. Sambariya [21] adopted the bat algorithm to enhance small signal stability, which optimized the performance of the fuzzy logic-based power system stabilizer (FPSS). Wu [22] introduced the chaos search strategy into the initial algorithm to improve the uniformity and ergodicity of population and applied the modified bat algorithm to solar photovoltaic system. Qin [23] applied the bat algorithm to bearing fault diagnosis and realized the accurate extraction of fault features.
With the rapid development of algorithms, some of them have been applied to the multi-objective optimization in many fields [24]. Mendrofa [25] adopted ant colony algorithm to optimize the controller of serial manipulator and evaluated the results through experiments. Nikoo [26] used the bat algorithm-based ANN to estimate the compressive strength of concrete, and the model was compared with four compressive strength models which indicated that the model was accurate and effective. Hemeida [27] optimized the renewable distributed generators based on the manta ray foraging optimization algorithm (MRFO), and the results proved the feasibility of the optimization compared with applied technology. Sq [28] proposed a new hybrid cooperative multi-objective Drosophila optimization algorithm, which optimized the execution time and cost, and realized the reasonable scheduling of cloud resources. Zhang [29] used NSGA-II to design the structural parameters of the hinge and the thickness of the reflector, realized the multi-objective optimization design of the first to third natural frequencies, and effectively improved the control bandwidth of the two-degree-of-freedom (2-DOF) fast steering mirror (FSM) system. Singh [30] introduced the multi-objective optimization into additive manufacturing, taking laser power, laser deposition speed, and powder feed rate as input process parameters and laser energy efficiency, powder deposition efficiency, and dilution as the output response, effectively improving the friction performance of the coating. In the field of shearers, Mao [31] proposed an optimization method based on NSGA-III algorithm, and number of picks, number of picks on the same line, the leaf thickness, leaf helix angle, and install angle of picks were optimized, which improved the loading efficiency, cutting energy consumption, and load fluctuation. Zhao [32] selected the helix angle, cutting line spacing, speed, and traction speed as design variables, and the genetic algorithm was used to optimize these parameters. Xu [33] optimized the structure of the cutting part transmission system based on the genetic algorithm, and the volume of the shearer became smaller and the bearing capacity became stronger after optimization. Ren [34] introduced the fruit fly optimization algorithm (FOA) into the complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN) denoising algorithm, and the improved CEEMDAN was used to process the coal-rock cutting sound signal of the shearer, which was better than the other four typical eliminate noise signal algorithms. Wang [35] proposed a comprehensive coordinated speed planning strategy of scraper conveyor and shearer according to the load analysis of scraper conveyor. Based on the multi-objective optimization model and particle swarm optimization algorithm, the speed planning scheme was optimized, and the actual effect was verified through experiments.
After investigation, it is found that the optimization of the shear drum mostly focuses on the drum itself, and the parameters of the pick are rarely considered. In addition, bionic algorithms suitable for multi-objective optimization are rarely used in the area of shearer drums. This paper takes into account parameters of pick and drum at the same time, the response functions between the optimization objectives and design variables are established based on the central composite experiment method. Then, the multi-objective bat algorithm and multi-objective bat algorithm with grid are used to optimize respectively according to the multi-objective optimization function. Furthermore, the optimization result is verified by the coal mining test, which provides a theoretical reference for the design of the drum.
2. Determination of Optimization Objectives
2.1. Torque Acting on Drum
The drum mainly undertakes the work of cutting and loading coal, spraying cooling, and dust reduction in the coal mining process. Therefore, it is necessary to study the torque characteristics of the drum, find the factors affecting the torque characteristics of the drum. Based on the analysis results, the relevant parameters can be optimized to extend the drum life and reduce mining costs.
The torque acting on drum can be calculated using the following equation [4]:
where, is torque of the -th pick to the center of the drum, is the total number of picks.
2.2. Specific Energy
The theory of specific energy was proposed by Teale R [36], which is the amount of energy consumed by the drum to cut a unit volume of coal. This evaluation index relates the drum load to the volume of falling coal, with the reduction of specific energy, the working efficiency gets higher and the economy of shearer becomes better. Therefore, the specific energy is selected as one of the optimization objectives in this paper.
According to the definition of specific energy , the calculation formula is:
where, is the force used to destroy coal and rock, is the distance at which the force acts, is the volume of falling coal.
According to Equation (2), the specific energy is related to the structural and working parameters of the shearer and the characteristics of coal. In order to reduce the specific energy, adjustable parameters can be selected within a reasonable range.
2.3. Average Stress Acting on Pick
In the process of working, the picks will squeeze and rub with the coal, and the picks also need to withstand the sudden impact from the gangue in coal. Considering the harsh working environment of high temperature, pressure, and impact, the picks need to have characteristics of high strength, abrasion resistance, and long service life [37]. The load will cause the abrasion and failure of the pick [5], and the average stress acting on pick can reflect the load characteristics in the working process partly. Therefore, the average stress acting on the pick is chosen as one of the optimization objectives in this paper, and the calculation formula is:
where, is the instantaneous stress acting on pick at time , is total time of cutting coal with the pick.
2.4. Construction of Multi-Objective Optimization Model
The following parameters were selected as design variables: half cone angle: , taper angle of pick body: , installation angle of the pick: , carbide head diameter: , and traction speed: (Figure 1). The following parameters were selected as optimization objectives: average torque acting on drum: , specific energy: , and average stress acting on pick: .
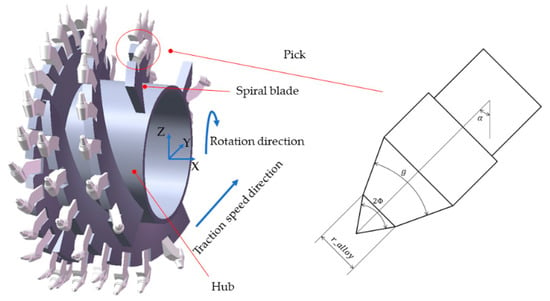
Figure 1.
Design variables of the drum and pick.
Because it takes hours to obtain the results through the numerical simulation method, the relationship between the design variables and optimization objectives are established based on the results of the simulation and the central composite experiment method.
The experimental scheme and results are shown in Table 1.

Table 1.
The scenarios and results of numerical simulations.
According to the test results, the response functions of , , and are as follows:
where, , , , , and are the code for , , , , and , respectively.
In order to verify the accuracy of fitting results, the adaptability analysis is carried out. According to Equations (7) and (8) [5], the multi-fitting coefficient and the modified multi-fitting coefficient are calculated:
According to Table 2, the values of Prob > F are less than 0.0001, indicating that the fitting results are of high importance. The models have an effective predictive ability because the multi-fitting coefficient, modified multi-fitting coefficient, and prediction fitting coefficient are higher than 0.9, which makes the result reliable and can be adopted in subsequent optimization. In order to illustrate the accuracy of the selected model intuitively, scatter plots of , , and were plotted, as shown in Figure 2. Each scatter point is distributed near the reference line: = , which indicates that the models can predict the results accurately.

Table 2.
The adaptability analysis result.
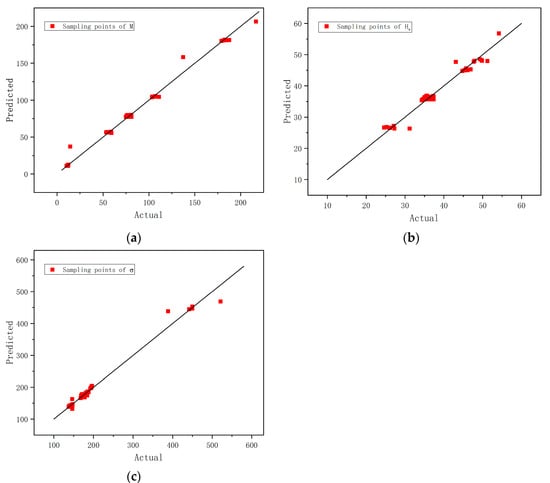
Figure 2.
Comparison of predicted and true values. (a) The (, ) scatter data points of average torque acting on drum; (b) the (, ) scatter data points of specific energy; (c) the (, ) scatter data points of average stress acting on pick.
2.5. Response Surface Analysis
The influences law of , on , , and are analyzed by using the response surface of second-order interaction [38,39]. For the analysis, all parameters except the investigation parameters are set to fixed values: is 20°, is 22.5°, and is 24 mm. The results are shown in Figure 3:
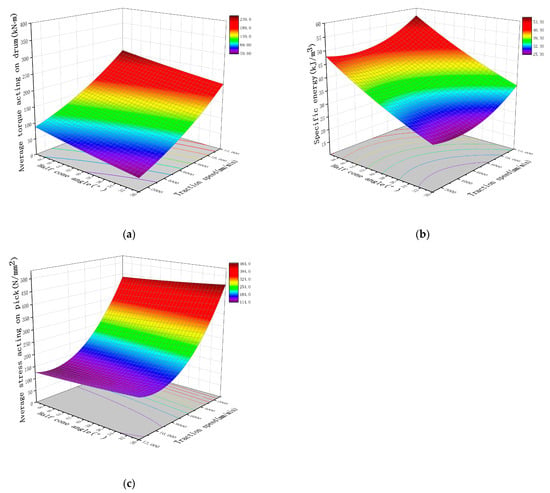
Figure 3.
Influence of and on optimization objectives. (a) Influence of and on ; (b) influence of and on ; (c) influence of and on .
As shown in Figure 3, the average torque acting on the drum increases gently with the half cone angle and increases with the traction speed. When the half cone angle increases from 30° to 50°, the average torque acting on drum decreases by 81.12%, 68.37%, 53.30%, 35.91%, and 16.21% for the traction speeds of 2000 mm/min, 4000 mm/min, 6000 mm/min, 8000 mm/min, and 10,000 mm/min, respectively. It was found that the smaller the traction speed is, the greater the effect of the half cone angle on the average torque acting on drum.
The specific energy increases with the half cone angle, while decreasing and then increasing with the traction speed. As the half cone angle increases from 30° to 50°, the specific energy decreases by 54.79%, 47.83%, 37.70%, 24.30%, and 7.62% for the traction speed of 2000 mm/min, 4000 mm/min, 6000 mm/min, 8000 mm/min, and 10,000 mm/min, respectively. It was found that the larger the half cone angle is, the greater the influence of the traction speed on the specific energy.
The average stress acting on the pick decreases with the half cone angle while decreasing and then increasing with the traction speed. When the half cone angle increases from 30° to 50°, the average stress acting on pick decreases by 14.08%, 39.51%, 58.22%, 70.19%, and 75.42% for the traction speed of 2000 mm/min, 4000 mm/min, 6000 mm/min, 8000 mm/min, and 10,000 mm/min, respectively. It was found that when the half cone angle is certain, the smaller the traction speed is, the faster the rate of increase of the average stress acting on the pick.
The selection of half cone angle needs to take into account the strength of alloy head and rock breaking ability. The smaller alloy head (such as less than 40°) will greatly improve the rock breaking ability, while high stress on the surface of the picks and less material of the picks will jointly accelerate the abrasion of picks. In contrast, the larger alloy head (such as more than 55°) can improve the abrasion resistance of picks but will greatly reduce the rock-breaking ability of picks.
The drum torque and the working efficiency of the shearer should be taken into account when making a selection of the traction speed. The torque acting on drum and the energy consumption are small when the traction speed is at a low value, which can reduce the cost of coal mining, but the volume of the cut-off coal per unit time is reduced and the working efficiency is decreased. In contrast, when a high traction speed is selected, average stress acting on the pick becomes smaller and the working efficiency is improved, but it will greatly increase the cost of shearer operation because the drum needs more torque to complete the work.
According to the analysis, and have a great impact on the optimization objectives. In order to reduce the average torque and stress acting on drum and pick, respectively, to prolong the service life of drum and pick, at the same time, the specific energy consumption should be reduced to improve the economy of mining. Several design variables mentioned above should be carefully selected after comprehensive consideration. Therefore, it is vital to make a reasonable optimization of the shearer drum structural and working parameters.
3. Optimization Method
3.1. Bat Algorithm
The bat algorithm (BA) [20] was proposed based on the particle swarm optimization (PSO) [13] and firefly algorithm [40], and combines the advantages of existing algorithms. The bat algorithm has the advantages of strong global search ability, fast convergence speed, and fewer parameter settings. Therefore, the bat algorithm was selected as the basic algorithm for multi-objective optimization in this paper. The bat algorithm assigned four attributes to each bat: position , velocity , frequency , and loudness . Each bat in the bat algorithm can have two behaviors: (1) update frequency and position; (2) fly randomly. The bat algorithm uses the following simplified rules:
- Bats use echolocation to perceive distance, and they are able to make judgments about food and obstacles;
- Bats fly randomly at position with fixed frequency , loudness , and speed to find food;
- The bat can automatically adjust the frequency according to the distance from the target, and the frequency is guaranteed to be within the range of ;
- The bat emits a positive value of loudness, varying from a larger initial value of to a smaller value of .
For the first behavior, each bat will update its frequency randomly before updating the velocity:
where is the frequency of a bat in the iteration, is the minimum value of frequency, is the maximum value of frequency, and is a uniformly distributed random number between 0 and 1.
Each bat updates its velocity based on the distance between its current position and the optimal position:
where is the speed of the bat in the iteration, is the position of the bat in the -th iteration, and is the current optimal position of the bat population in space.
Each bat will update the position as:
where is the position of the bat in the iteration.
For the second behavior of the bat, a random number will be chosen, and if the number is greater than the bat’s current rate of pulse emission, the bat will choose to fly randomly. The equation describing this behavior is:
where is a random number within and is the average loudness of all bats in the -th iteration.
After the position has been updated, the bat will fly to the new position if the new position is better than the previous position, otherwise it stays at the previous position. The bat also updates its loudness and rate of pulse emission as it flies to the new position:
where is the rate of pulse emission of the bat in the iteration, is initial rate of pulse emission, and and are constants related to loudness and rate of pulse emission, respectively.
3.2. Multi-Objective Bat Algorithm with Grid
The bat algorithm is suitable for solving single objective optimization problems. When there are multiple objective functions, these functions usually conflict with each other, and the optimal solution cannot be obtained at the same time. Therefore, the weighted sum method [41] can be used to convert the multi-objective problem into a single objective problem, and the bat algorithm can be adopted to solve it.
However, since only one optimal solution can be obtained and the selectivity is poor through the bat algorithm, the multi-objective bat algorithm with grid (MOBA/G) is proposed and used in this study. In MOBA/G, to improve the search performance of the population and ensure the diversity of the population, the Pareto dominance mechanism is used in the MOBA/G to evaluate the relationship between the solutions and constantly update the pareto solution set. Multiple solutions can be obtained, and solutions cannot be compared simply by being greater than or less than. Therefore, the concept of Pareto solution [41] is introduced to evaluate the results:
- Dominating relationship: for the two individuals and in the decision set, dominates only when the following relationship is established, which is recorded as ,where is the number of objective functions.
- Pareto solution (nondominant solution): in the feasible domain, is a Pareto solution if and only if does not exist, so that .
- Pareto front: the set of Pareto solutions is called the Pareto optimal solution set, and the set of corresponding objective functions is called the Pareto front.
For many optimization problems, the Pareto solution set may contain an infinite number of solutions; in order to limit the number of solutions, ensure the distribution of the population, and obtain better convergence, the grid [42,43] is used in the MOBA/G to deal with the retention and abandonment of individuals. First, the leader bats are randomly selected in the current Pareto solution set according to roulette algorithm, so that these leaders can cover the effective objective function space and adaptively adjust the grid boundary. Then, based on the positions of leaders in the objective function space, the bat individual can not only follow the leader for a broader search, but also conduct the careful local search, thus ensuring the diversity of the population and the convergence of the algorithm. Finally, the dominant relationship between individuals is judged and the Pareto solution set is updated.
By combining the Pareto occupancy mechanism, grid technology, and bat algorithm, the multi-objective algorithm not only retains the characteristics of fewer parameters, fast convergence speed, and excellent global search capability of the original bat algorithm, but also ensures the diversity and distribution of the solution set.
3.3. Multi-Objective Optimization Process
The flow of the optimization process of shear drum based on multi-objective bat algorithm with grid is shown in Figure 4:
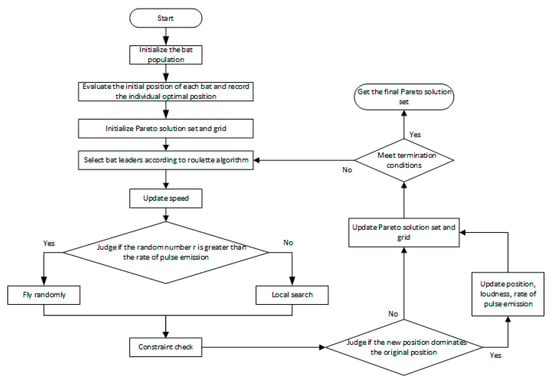
Figure 4.
Optimization flow chart of the multi-objective bat algorithm with grid.
Step 1: Set required hyperparameters and initialize the position of each bat randomly.
Step 2: Based on the objective functions, the position of each bat is evaluated in different dimensions, then the Pareto solution set and grid are initialized.
Step 3: According to the roulette algorithm, bat leaders are selected from the Pareto solution set, which can cover the objective function space.
Step 4: Update the velocity and position of each bat according to Equations (10) and (11).
Step 5: Generate a random number between 0 and 1. If , the bat generates a new position around the leader according to Equation (12).
Step 6: Compare the original position with the new position of the bat according to Equation (15). If the new position is better, the bat flies to the new position and updates its loudness and rate of pulse emission according to Equations (13) and (14), otherwise it stays at the original position.
Step 7: Update the Pareto solution set and grid, and the redundant individuals are eliminated according to the size of the solution set and grid.
Step 8: If the current number of iterations is greater than the maximum number of iterations, stop the iteration and output the Pareto solution, otherwise return to step 3.
4. Optimal Design of the Drum of MG500/1130-WD Shearer
4.1. Determination of Constraint Conditions
Based on the optimization process described above, the drum of MG500/1130-WD shearer is optimized. Before optimization, the design variables must be constrained to ensure that the final result is in a reasonable range.
The half cone angle and taper angle of pick body will both have a greater impact on the force of picks during the cutting process, thus affecting the torque acting on drum.
For a certain half cone angle, the change of the installation angle will lead to the change of front angle and cleaning angle of the picks, which will change the force and load fluctuation amplitude acting on the picks, and then will affect the service life of the picks.
When the traction speed is low, the specific energy declines, thus the cost can be reduced, but the efficiency of mining will get lower. While a high traction speed can ensure high efficiency, but it will lead to an increase of torque acting on the drum, which will make the energy consumption of the shearer higher.
The design variables are limited to the following ranges (Table 3).

Table 3.
Range of the design variables.
4.2. Multi-Objective Optimization Result and Analysis
In order to reduce the energy consumption of the shearer and improve the mining efficiency, the optimization equation of the shearer drum is defined as follows:
where is the optimization objective and is the design variable.
According to the fuzzy theory, the optimization degree of the objective function can be reflected by the membership degree, and the solution of the optimal multi-objective function can be measured by weighting each objective. In this study, each objective function has the same important position, so corresponding to Equation (18), the Pareto solution is the unbiased optimal solution [5].
where , , and are the value, minimum value, and maximum value of optimization function, respectively, is the number of optimization functions, and is the number of Pareto solutions.
In this study, the multi-objective optimization program of the drum based on the multi-objective bat algorithm with grid is realized in MATLAB software. The population size is set to 150, the size of the Pareto solution set is set to 100, the number of iterations is 200, and bat leader selection pressure and individual deletion pressure are set to 2. In order to verify the effectiveness of this method, the multi-objective bat algorithm (MOBA) is selected to optimize the parameters of the drum, and the population size, Pareto solution set size, and number of iterations are same as the MOBA/G.
In order to make the comparison impartial, 10 optimizations are performed and the initialization populations of the two algorithms are consistent. After normalization, the point closest to the origin is selected as the evaluation point (Figure 5). The average evaluation points of MOBA and MOBA/G are 0.374 and 0.373, respectively, and the variances are and , respectively. Through the analysis, the optimization result of MOBA/G is better than that of MOBA, and the fluctuation range of optimization results is smaller, which proves that the MOBA/G is effective and stable in shear drum optimization.
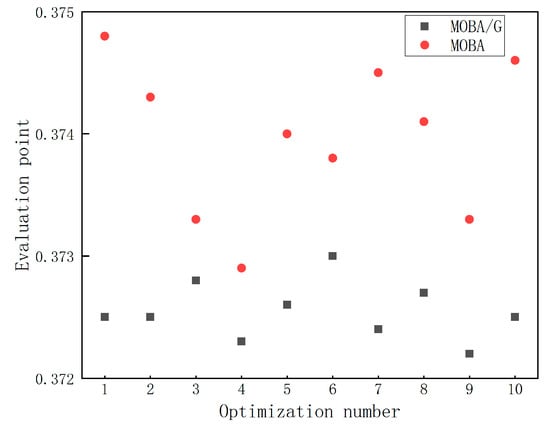
Figure 5.
Ten optimization results of MOBA and MOBA/G.
The Pareto fronts obtained by MOBA/G and MOBA are shown in Figure 6. It can be seen that the Pareto solutions obtained by MOBA are mostly distributed in clusters with poor diversity; while in the Pareto solutions obtained by MOBA/G, the arrangement between solutions is relatively loose, the population distribution is better and the front surface is smoother than that of MOBA. In order to analyze the distribution of the solution set even further, the solution set is evaluated by Equation (20) [44] after normalization. The smaller the result, the better the distribution of the solution set. The mean value of of MOBA/G in 10 tests is 0.035, while that of MOBA is 0.063, which indicates that the MOBA/G can obtain the optimal solution of shear drum with better distribution than MOBA.
where is the Pareto solution set, is the minimum distance from the -th solution to other solutions in , and is the average value of .
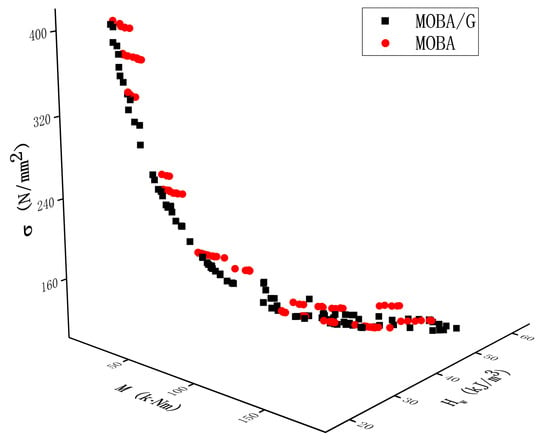
Figure 6.
Pareto fronts of MOBA/G and MOBA.
From the analysis, it can be seen that the quality and distribution of the optimal solutions of MOBA/G are better than that of MOBA. According to the actual situation, a Pareto solution of the set is selected as the optimal individual. After rounding values of the optimal individual, the values of the design variables before and after optimization are shown in Table 4. After the optimization with MOBA/G, the half cone angle and carbide head diameter decrease, while the taper angle of pick body, installation angle of the pick, and traction speed increase. The values of the optimization objectives before and after optimization are shown in Table 5, it can be seen that the average torque acting on the drum decreases by 57.69%, the specific energy decreases by 48.24%, and the average stress acting on the pick decreases by 26.39%. The result shows that all optimization objectives of the drum are improved, which promotes overall performance of the drum.

Table 4.
Design variables before and after optimization.

Table 5.
Objective functions before and after optimization.
5. Coal Mining Test
In order to verify the optimization results, the coal mining test is organized in the 15160-coal mining working face of Xin’an Coal Mine of Yimei group as shown in Figure 7. Before the test, the relevant parameters of the picks and drum were adjusted according to the optimization result, and other parameters remained unchanged. In order to obtain reliable results, the data are collected when the shearer is in a stable working state (the drum torque before and after optimization is shown in Figure 8). According to the test result, the average torque acting on drum decreases by 42.86%, the specific energy decreases by 35.57%, and the average stress acting on pick decreases by 18.62%. All objectives have been optimized, which proves the effectiveness of the optimization.

Figure 7.
Testing ground.
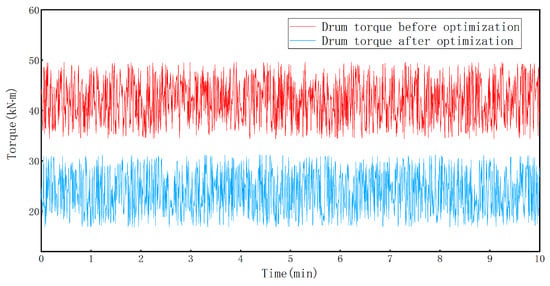
Figure 8.
The drum torque during test.
6. Conclusions
In order to prolong the working life of the drum, improve the working efficiency, and reduce the energy consumption of the shear, the response functions of average torque acting on drum, specific energy, and average stress acting on pick are established based on the central composite experiment method. Then, the half cone angle, taper angle of pick body, installation angle of the pick, carbide head diameter, and traction speed of MG500/1130-WD shearer were optimized based on MOBA and MOBA/G simultaneously. The result shows that MOBA/G has a better solution set and population distribution and achieves a quality comprehensive performance of the drum. The optimization effect is verified by the coal mining test, which provides some theoretical references for the design and production of shearer drum.
Author Contributions
Conceptualization, M.D. and Q.H.; methodology, M.D.; software, R.X.; validation, M.D. and R.X.; formal analysis, C.W.; investigation, C.W.; resources, J.X.; data curation, M.D.; writing—original draft preparation, R.X.; writing—review and editing, M.D.; visualization, C.W.; supervision, Q.H.; project administration, Q.H.; funding acquisition, J.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No. 51575201), National Natural Science Foundation of China (No. 51905229), Natural Science Foundation of Jiangsu Province (No. BK20190968).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Exclude this statement.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Du, C.L.; Liu, S.Y.; Cui, X.X.; Li, T.J. Study on pick arrangement of shearer drum based on load fluctuation. J. China Univ. Min. Technol. 2008, 18, 305–310. [Google Scholar] [CrossRef]
- Wang, J.; Huang, Z. The recent technological development of intelligent mining in China. Engineering 2017, 3, 439–444. [Google Scholar] [CrossRef]
- Wang, G.; Xu, Y.; Ren, H. Intelligent and ecological coal mining as well as clean utilization technology in China: Review and prospects. Int. J. Min. Sci. Technol. 2019, 29, 161–169. [Google Scholar] [CrossRef]
- Li, X.F.; Wang, S. A study on drum cutting properties with full-scale experiments and numerical simulations. Measurement 2018, 114, 25–36. [Google Scholar] [CrossRef]
- Zhao, L.J.; Jin, X. Numerical research on wear characteristics of drum based on discrete element method (DEM). Eng. Fail. Anal. 2020, 109, 104269. [Google Scholar] [CrossRef]
- Liu, H. Study on the wear of spiral drum cutting coal containing rock. Eng. Rep. 2022, 4, e12450. [Google Scholar] [CrossRef]
- Liu, S.; Du, C.; Zhang, J.; Jiang, H. Parameters analysis of shearer drum loading performance. Min. Sci. Technol. (China) 2011, 21, 621–624. [Google Scholar] [CrossRef]
- Gao, K.D.; Xu, W.B. Factors affecting thin coal seam shearer drum coal-loading performance by a model test method. J. Cent. South Univ. 2019, 26, 1619–1636. [Google Scholar] [CrossRef]
- Sun, L.; Zhang, X.; Zeng, Q. Application of a screw conveyor with axial tilt blades on a shearer drum and investigation of conveying performance based on DEM. Particuology 2022, 61, 91–102. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T.A.M.T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Zhao, X.; Xu, Y.; Chen, Y. A flexible planning methodology for product family assembly line based on improved NSGA_II. Assem. Autom. 2020, 40, 625–639. [Google Scholar] [CrossRef]
- Zhang, L.; Ge, H.; Ma, Y.; Xue, J.; Li, H.; Pecht, M. Multi-objective Optimization Design of a Notch Filter Based on Improved NSGA-II for Conducted Emissions. IEEE Access 2020, 8, 83213–83223. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the Icnn95—International Conference on Neural Networks, IEEE, Perth, Australia, 27 November–1 December 1995. [Google Scholar]
- Yu, Y.F.; Li, G.; Xu, C. An improved particle swarm optimization algorithm. Appl. Mech. Mater. 2013, 401, 1328–1335. [Google Scholar] [CrossRef]
- Zhan, Z.H.; Zhang, J.; Li, Y.; Chung, H.S.H. Adaptive Particle Swarm Optimization; IEEE Press: Hoboken, NJ, USA, 2009; pp. 1362–1381. [Google Scholar]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. Part B 1996, 26, 29–41. [Google Scholar] [CrossRef] [PubMed]
- Dorigo, M.; Gambardella, L.M. Ant colony system: A cooperative learning approach to the traveling salesman problem. IEEE Trans. Evol. Comput. 1997, 1, 53–66. [Google Scholar] [CrossRef]
- Cao, R.; Li, S.; Ji, Y.; Zhang, Z.; Xu, H.; Zhang, M.; Li, M.; Li, H. Task assignment of multiple agricultural machinery cooperation based on improved ant colony algorithm. Comput. Electron. Agric. 2021, 182, 105993. [Google Scholar] [CrossRef]
- Ge, J.; Yu, D.; Fang, Y. Multi-dimensional QoS Cloud Computing Task Scheduling Strategy Based on Improved Ant Colony Algorithm. J. Phys. Conf. Ser. 2021, 1848, 012031. [Google Scholar] [CrossRef]
- Yang, X. A new metaheuristic bat-inspired algorithm. In Nature Inspired Cooperative Strategies for Optimization (NICSO); Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Sambariya, D.K.; Prasad, R. Application of Bat Algorithm to Optimize Scaling Factors of Fuzzy Logic-Based Power System Stabilizer for Multimachine Power System. Int. J. Nonlinear Sci. Numer. Simul. 2016, 17, 41–53. [Google Scholar] [CrossRef]
- Wu, Z.; Yu, D. Application of improved bat algorithm for solar PV maximum power point tracking under partially shaded condition. Appl. Soft Comput. 2018, 62, 101–109. [Google Scholar] [CrossRef]
- Qin, Y.; Jin, L.; Zhang, A.; He, B. Rolling Bearing Fault Diagnosis with Adaptive Harmonic Kurtosis and Improved Bat Algorithm. IEEE Trans. Instrum. Meas. 2021, 70, 1–12. [Google Scholar] [CrossRef]
- Audet, C.; Bigeon, J. Performance indicators in multi-objective optimization. Eur. J. Oper. Res. 2021, 292, 397–422. [Google Scholar] [CrossRef]
- Mendrofa, A.H.; Muis, A. Serial Manipulator Control Optimization Using Ant Colony Algorithm. J. Phys. Conf. Ser. 2021, 1993, 012026. [Google Scholar] [CrossRef]
- Aalimahmoody, N.; Bedon, C.; Hasanzadeh-Inanlou, N.; Hasanzade-Inallu, A.; Nikoo, M. BAT Algorithm-Based ANN to Predict the Compressive Strength of Concrete—A Comparative Study. Infrastructures 2021, 6, 80. [Google Scholar] [CrossRef]
- Hemeida, M.G.; Ibrahim, A.A.; Mohamed, A.; Alkhalaf, S.; El-Dine, A.M.B. Optimal allocation of distributed generators DG based Manta Ray Foraging Optimization algorithm (MRFO). Ain Shams Eng. J. 2020, 12, 609–619. [Google Scholar] [CrossRef]
- Qin, S.; Pi, D.; Shao, Z.; Xu, Y. Hybrid Collaborative Multi-objective Fruit Fly Optimization Algorithm for Scheduling Workflow in Cloud Environment. Swarm Evol. Comput. 2022, 68, 101008. [Google Scholar] [CrossRef]
- Zhang, W.; Yuan, J.; Yan, C.; Gao, Z.; Dong, Y. Multi-Objective Optimization Design of Natural Frequency of Two-Degree-of-Freedom Fast Steering Mirror System. IEEE Access 2021, 9, 33689–33703. [Google Scholar] [CrossRef]
- Singh, A.K.; Sadhu, A.; Das, A.K.; Pratihar, D.K.; Choudhury, A.R. An approach towards energy and material efficient additive manufacturing: Multi-objective optimization of stellite-6 deposition on SS304. Opt. Laser Technol. 2022, 148, 107799. [Google Scholar] [CrossRef]
- Mao, J.; Wang, X.; Chen, H.; Zhang, K.; Bai, Y. Optimization Design and System Development of Shearer Drums Based on NSGA-Ⅲ Algorithm. Zhongguo Jixie Gongcheng/China Mech. Eng. 2018, 29, 2335–2341. [Google Scholar]
- Zhao, L.; Fan, J. Shearer’s Helical Drum Multi-objective Optimization Design Based on GA. China Mech. Eng. 2018, 29, 591. [Google Scholar]
- Xu, W. Structure optimization design of transmission system of shearer cutter based on genetic algorithm. J. Phys. Conf. Ser. 2021, 1952, 042106. [Google Scholar] [CrossRef]
- Ren, C.; Xu, J.; Xu, J.; Liu, Y.; Sun, N. Coal–Rock Cutting Sound Denoising Based on Complete Ensemble Empirical Mode Decomposition with Adaptive Noise and an improved Fruit Fly Optimization Algorithm. Machines 2022, 10, 412. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, S. Coordinated Speed Planning Strategy of Scraper Conveyor and Shearer Based on Scraper Conveyor Loads Analysis. IOP Conf. Ser. Earth Environ. Sci. 2019, 267, 042044. [Google Scholar] [CrossRef] [Green Version]
- Teale, R. The concept of specific energy in rock drilling. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1965, 2, 57–73. [Google Scholar] [CrossRef]
- Lu, Z.; Wan, L.; Zeng, Q.; Zhang, X.; Gao, K. The structural optimization of roadheader conical picks based on fatigue life. Int. J. Modeling Simul. Sci. Comput. 2018, 9, 1850013. [Google Scholar] [CrossRef]
- Kong, L.; Ma, L.; Jin, H.; Hou, J.; He, G.; Zhang, R. Synthesis of a novel oil-absorption resin and optimization of its performance parameters using response surface design. Polym. Adv. Technol. 2019, 30, 1441–1452. [Google Scholar] [CrossRef]
- Zhang, H.; Li, H.; Zhang, Z.; Hou, T. Optimization of ultrasound-assisted extraction of polysaccharides from perilla seed meal by response surface methodology: Characterization and in vitro antioxidant activities. J. Food Sci. 2021, 86, 306–318. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.S. Firefly Algorithm, Stochastic Test Functions and Design Optimisation. Int. J. Bio-Inspired Comput. 2010, 2, 78–84. [Google Scholar] [CrossRef]
- Miettinen, K. Nonlinear Multiobjective Optimization; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar] [CrossRef]
- Knowles, J.D.; Corne, D.W. Approximating the Nondominated Front Using the Pareto Archived Evolution Strategy. Evol. Comput. 2014, 8, 149–172. [Google Scholar] [CrossRef]
- Coello, C.; Pulido, G.T.; Lechuga, M.S. Handling multiple objectives with particle swarm optimization. IEEE Trans. Evol. Comput. 2004, 8, 256–279. [Google Scholar] [CrossRef]
- Schott, J. Fault Tolerant Design Using Single and Multicriteria Genetic Algorithm Optimization. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2005. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).