Abstract
AC copper loss from stator winding is one of the main losses of the high-speed permanent magnet machines (HSPMMs) and directly affects the performance of the machines. AC copper losses are influenced by many factors, including the frequency, conductor diameter, temperature performance, etc. These factors cause the AC losses to increase significantly at high frequencies due to the skin effect and proximity effect. In this paper, a comprehensive analysis of the AC copper losses of HSPMMs with round copper wire windings is presented. Firstly, the structure and parameters of a 60 kW, 30,000 rpm high-speed permanent magnet machine are provided. Then, based on this parameter, a 2D-finite element model (2D-FEM) is established to obtain the AC copper loss. Through the eddy-current field analysis, the current density distribution of the stator winding and the variation trends of AC copper losses under different frequencies are observed. In addition, by comparing the winding current density distribution and the AC copper loss value under different conditions, the influencing factors of AC winding losses are comprehensively analyzed, including the frequency, conductor diameter, number of conductors per slot, notch height of the stator slot, and working temperature. Finally, four stator coil cases are manufactured, which have different conductor diameters and wire strands. The AC losses of the four cases at different frequencies are tested, and the theoretical results are verified by measuring the AC/DC loss ratios (kac) of different conductor cases at various frequencies.
1. Introduction
High-speed permanent magnet machines (HSPMMs) have small size, high efficiency and high power density. Permanent magnet motors are the best choice for high speed in various machine types because of their high efficiency and high power density [1,2,3]. HPSMMs have been extensively researched in industrial and scientific fields [4,5,6]. HPSMMs are widely used in flywheel energy storage, air compressors, distributed power generation systems, hydrogen fuel cells, etc. [7,8,9,10]. The small inertia moment of the motor allows a fast dynamic response, which is also an important feature [11,12,13]. In addition, HSPMMs are also popular in transportation applications, where compactness and lightness are required [14,15,16].
However, the special characteristics of HSPMMs, such as high speed, high frequency, high loss density, and serious heat generation, have a great adverse effect on the performance of the motor. Under high frequency, the copper losses in the windings increase significantly, which is caused by eddy-current influences, including the skin effect and proximity effect, and the motor efficiency is affected. Therefore, it is essential to accurately calculate and predict the AC copper losses in the stator windings while designing and analyzing the motor so that the additional copper losses at high frequencies are reduced and the efficiency is improved.
Generally, to decrease copper losses, it is necessary to make the AC resistance (Rac) tend to be close to the DC resistance (Rdc), that is, Rac/Rdc ≈ 1. Therefore, the conductor diameter is adjusted to be smaller than the skin depth at the operating frequency [17,18,19]. By twisting between wires, Litz wire can be used to reduce AC copper losses at high frequencies [20,21]. To reduce the excessive losses by the skin effect and proximity effect in the windings, some solutions of Litz wires are provided in [22,23]. Recently, Litz wires have been gradually adopted in high-speed machines [24]. Another option is to twist/transpose the coil along the slot length, which is also an effective measure to reduce AC copper losses [25,26]. In addition, temperature also has a significant impact on HSPMMs, and the changing DC and AC components of copper losses are caused by the various temperatures. Some relevant analysis and research on the thermal dependence of the AC winding are given in studies [27,28,29].
In summary, there is some research on AC copper losses in HSPMMs with round copper wire. However, the research on the AC loss of round copper wire at high frequency mostly focuses on the frequency and conductor diameter. The influence of more influences on the AC loss of round copper wire is still unclear, such as the number of conductors per slot, the notch height of the stator slot, the operating temperature, etc. These effects are extremely important for the design of HSPMMs.
Therefore, in this paper, the AC losses of HSPMMs with round copper wire winding are analyzed comprehensively. In this analysis, more influencing factors are considered and summarized, including the frequency, the conductor diameter, number of conductors per slot, the notch height of the stator slot, and the working temperature. The paper is organized as follows. Firstly, the structure and parameters of a 60 kW, 30,000 rpm HSPMM are provided. Then, a 2D-finite element model (2D-FEM) is established to obtain the effect of the frequency on AC copper loss. Furthermore, the influence factors of AC winding losses at high frequencies are comprehensively analyzed, including the conductor diameter, number of conductors per slot, the notch height of the stator slot, and the working temperature. Finally, four stator coil cases are manufactured, and the AC losses at different frequencies are tested to verify the theoretical analysis of this paper.
2. HSPMM Parameters and Structure
In this paper, a 60 kW, 30,000 rpm HSPMM is designed, as shown in Figure 1. The motor is designed with 4 poles. A 5 mm carbon fiber sleeve is applied to ensure the motor-operated reliably at high speed. In addition, 24 slots and double-layer windings of round copper wire are used in the stator structure. Some key design parameters of the motor are given in Table 1.
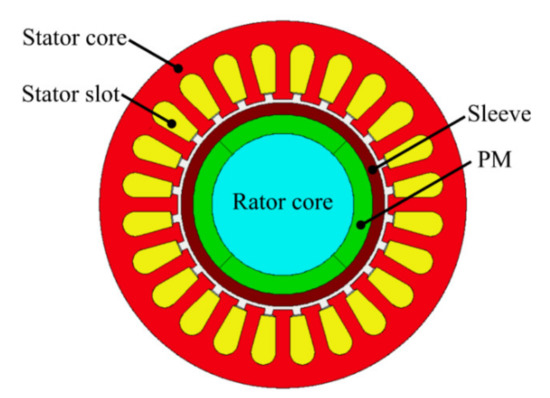
Figure 1.
Structure of HSPMM.

Table 1.
Some key design parameters of the HSPMM.
3. Influencing Factors of AC Losses at High Frequency
3.1. AC Loss Simulation Model of Round Copper Wire
This paper presents a cross-sectional view of the studied motor as well as the specific distribution of the windings in one of the slots, as shown in Figure 2. As shown in Figure 2b, a specific finite element analysis is performed for only one stator slot in this paper, which is to study the AC losses clearly and reduce the calculation time.
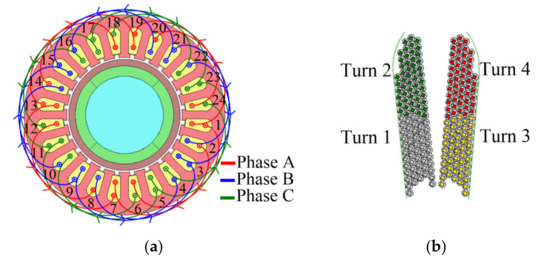
Figure 2.
AC copper loss analysis model. (a) Overall model. (b) Conductor models per slot.
3.2. AC Copper Loss with Different Frequencies
High-speed motors operate at a high frequency, and the frequency of the windings current can reach thousands of Hertz. Although the skin effect and proximity effect of windings can be ignored at low frequencies, they cannot be avoided and neglected at high frequencies. Thus, it is necessary to study the AC losses of windings at high frequencies.
Through the finite element analysis of the eddy current field, the current density distribution of the windings in the stator slot is obtained. In this analysis, the conductor parallel winding number is set to 51, and the conductor diameter is kept at 0.6 mm. Figure 3 shows the current density distribution at the end of a period under different frequencies. For example, at 1000 Hz, the current density distribution at 0.001 s is observed. The current density gradually increases with the increasing frequency because the skin effect and proximity effect are more significant at higher frequencies. During the entire period, the current of each coil varies with time, so the value of the current density at different times also changes. The maximum AC loss values over time at different frequencies are given in Figure 4. As shown in the figure, in one period, the maximum current density at 800 Hz is 57.71 A/mm2, and as the frequency increases to 2000 Hz, the maximum current density can reach 117.73 A/mm2.
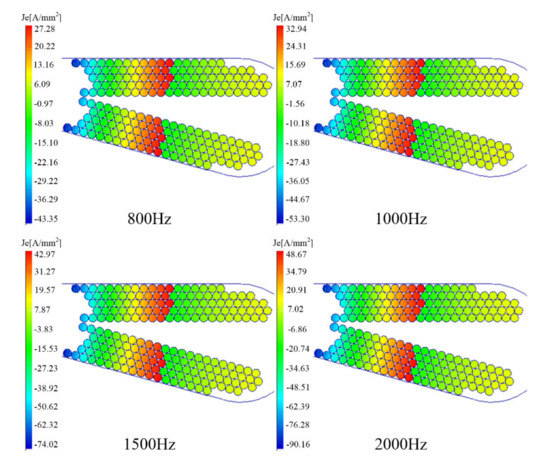
Figure 3.
Current density distribution at different frequencies.
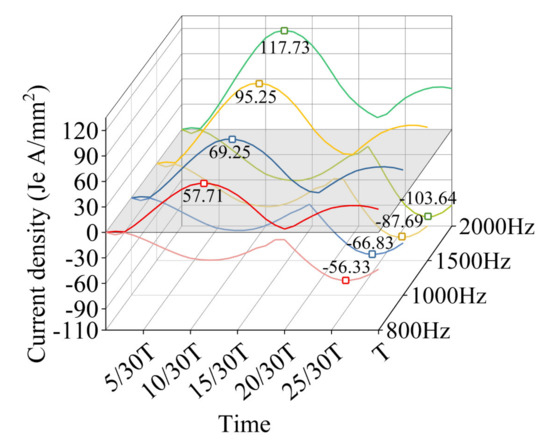
Figure 4.
Maximum current density in one period at different frequencies.
The concept of AC/DC loss ratio (kac) is defined to reflect the increasing trend of AC windings copper losses, directly. Figure 5 shows the variation of AC loss, DC loss, and AC/DC loss ratio with frequency. As shown in Figure 5, at 800 Hz, the AC loss is 406 W and the kac value is slightly greater than 1. As the frequency increases to 2000 Hz, the AC loss and kac values increase to 1232 W and 3.66, respectively. As can be seen, the AC loss increases more than twice as the frequency increases. Therefore, it can be seen that with the increase of frequency, the DC loss does not change, while the AC loss and kac value increase significantly. The rising kac curve indicates the phenomenon of increased AC loss in Figure 5.
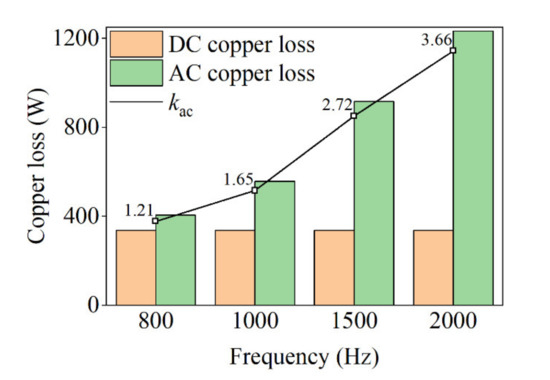
Figure 5.
Copper loss and AC/DC copper loss ratio kac with frequency.
3.3. Influence of Conductor Diameter on AC Losses
The effect of conductor diameter on AC copper losses is studied, and two cases are analyzed in this paper, described as follows. For case A, the number of strands per conductor remains the same, and when the conductor diameter changes, the copper fill rate is different. Case B is to keep the copper fill rate unchanged so the number of strands per conductor decreases as the conductor diameter increases.
For the first case (Case A), each conductor consists of 51 cross-wound wires, and the frequency is set at 1000 Hz in the simulation. The current density distribution under different conductor diameters is given in Figure 6. As can be seen, the current density initially shows an increasing trend due to the greater skin effect and proximity effect at larger conductor diameters. However, as the conductor diameter becomes bigger, the total copper area expands further; thus, the current density eventually decreases.
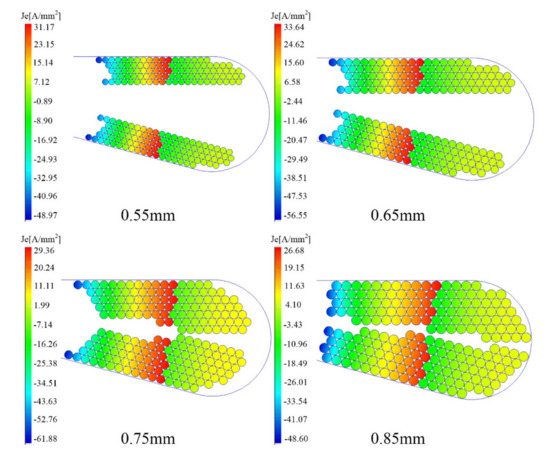
Figure 6.
Current density distribution with different conductor diameters at 1000 Hz for Case A.
Figure 7 shows the winding copper loss and the AC/DC loss ratio kac change with the frequency at 1000 Hz. On the one hand, the DC losses decrease as the conductor diameter increases, which is caused by a higher slot fill rate, that is, a higher total copper area. On the other hand, as the conductor diameter increases, the skin effect and the proximity effect of the conductors become more obvious; therefore, this leads to larger kac values at bigger conductor diameters. The combined effect of frequency and conductor diameter on AC losses is comparatively analyzed in Figure 8. At 800 Hz, when conductor diameters of 0.6 mm and 0.85 mm are used, the AC losses are 406 W and 708 W, respectively, and it can be seen that the AC loss increases by 74% as the conductor diameter increases. When the frequency is increased to 1500 Hz, the AC loss increases to 916 W and 1174 W, respectively. As can be seen, the larger the conductor diameter, the higher the AC losses, and this phenomenon is obvious at high frequencies. Figure 9 shows the variated trend of kac curve with frequency for different conductor diameters. Obviously, the kac curve rises significantly with the conductor diameter under high frequency.
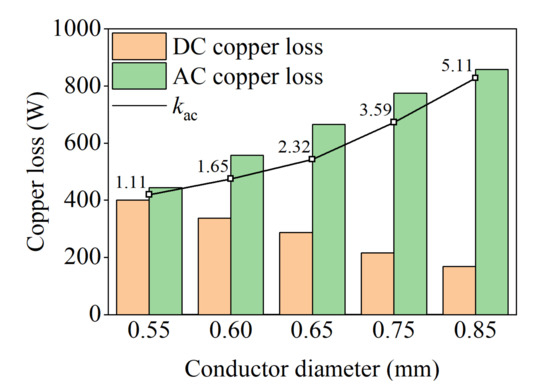
Figure 7.
Copper loss and AC/DC copper loss ratio kac with conductor diameter at 1000 Hz for Case A.
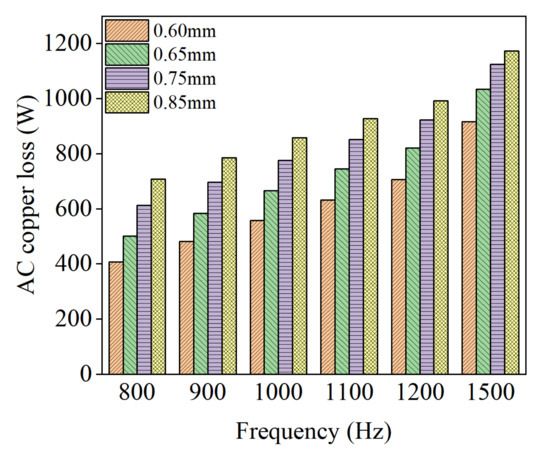
Figure 8.
AC copper loss with conductor diameter under different frequencies for Case A.
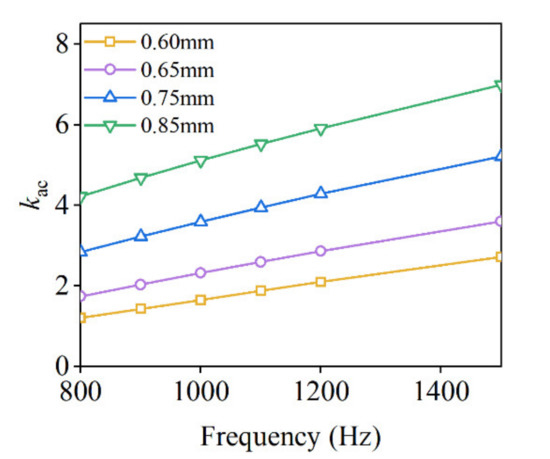
Figure 9.
AC/DC copper loss ratio kac with conductor diameter at different frequencies for Case A.
Another case (Case B) is adopted to study the influence of conductor diameter on the AC copper losses in this paper. Maintaining the same copper fill rate, the influencing law of the conductor diameter on the AC copper losses is summarized. The conductor strand number must be reduced with the conductor diameter increasing to keep the same slot full rate. The windings arrangement parameters are shown in Table 2. Similarly, the influence of conductor diameter on current density distribution, copper loss and AC/DC loss ratio kac is analyzed in Figure 10, Figure 11, Figure 12 and Figure 13.

Table 2.
Windings data in different cases.
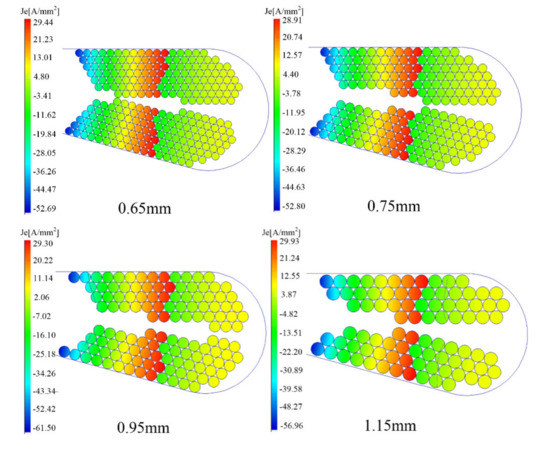
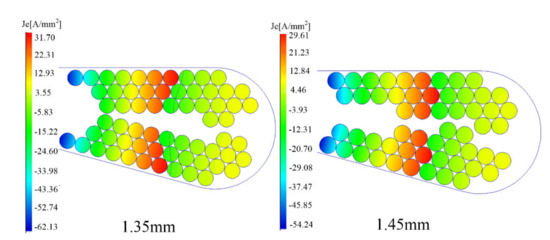
Figure 10.
Current density distribution with different conductor diameters at 1000 Hz for Case B.
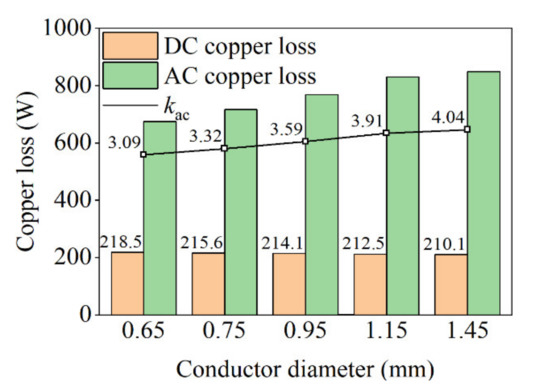
Figure 11.
Copper loss and AC/DC copper loss ratio kac with conductor diameter at 1000 Hz for Case B.
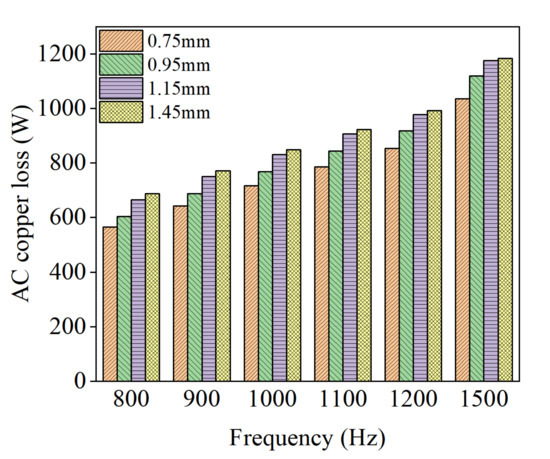
Figure 12.
AC copper loss with conductor diameter under different frequencies for Case B.
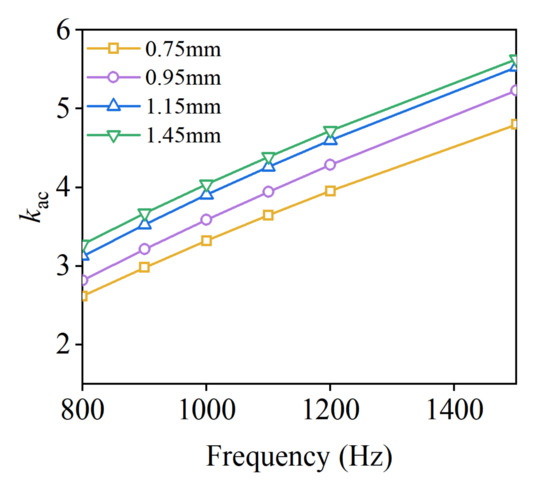
Figure 13.
AC/DC copper loss ratio kac with conductor diameter at different frequencies for Case B.
The current density is almost unchanged, as shown in Figure 10, which is because of the similar slot fill rate, so the total copper area is the same. In Figure 11, the DC losses does not change significantly because of the same slot fill rate. However, the trend of the kac curve still shows a slight rise due to the increasing AC copper loss with increasing conductor diameter. In addition, the trends of AC losses and the kac curves with frequency are shown in Figure 12 and Figure 13. It can be seen that the larger the conductor diameter, the more obvious the AC loss increases with frequency increases, and this trend agrees with the first case analyzed. Therefore, it can be concluded that for both cases, the AC/DC loss ratio and the AC loss increase as the conductor diameter increases.
Figure 14 compares the change in AC copper loss in the two cases as the conductor diameter increases at 1000 Hz. In the figure, as the conductor diameter increases from 0.65 mm to 0.85 mm, the AC copper loss in Case A increased by 31% from 655 W to 858 W, but the AC loss only increased by 12% from 674 W to 757 W in Case B. Obviously, the growth rate of AC loss in case A is significantly higher than that in case B. As can be seen, the change of the conductor diameter has a great influence on the AC loss if the copper fill rate is not maintained.
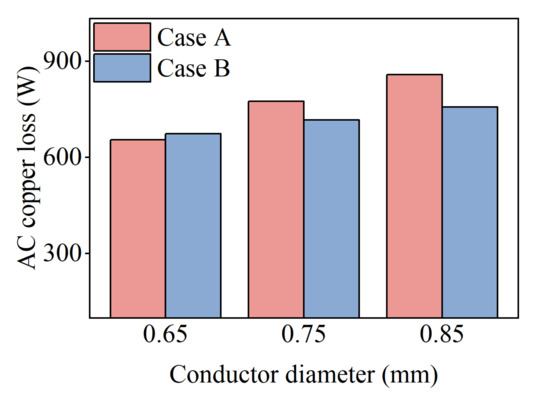
Figure 14.
AC copper loss with conductor diameter in two cases at 1000 Hz.
Based on the above analysis, the influence of varied conductor diameter on the AC copper losses cannot be ignored at high frequency. Thus, it is necessary to design a smaller conductor diameter to reduce AC losses and improve efficiency.
3.4. Influence of Number of Conductors Per Slot on AC Losses
Keeping the same number of strands per turn of the winding, the effect of the number of conductors per slot on AC copper losses is analyzed in this paper. Figure 15 shows the effect of the number of conductors per slot on the current density distribution. In the analysis of Figure 15, the wire diameter is kept at 0.6 mm and the frequency is set at 1000 Hz. As can be seen, the eddy current density is significantly raised by the increased turn number in each slot, because the skin effect and the proximity effect of the conductor become more obvious as the conductor number increases.
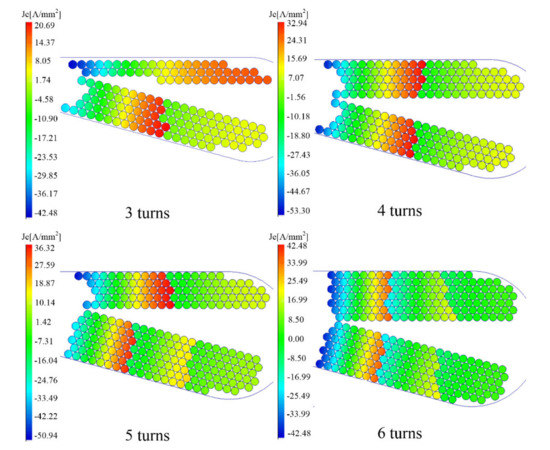
Figure 15.
Current density with conductor turns at 1000 Hz.
The effect of the number of turns per slot on the AC loss, DC loss, and AC/DC loss ratio kac is obtained, as shown in Figure 16. As can be seen, the DC losses increased by 66% as the number per slot increased from three turns to six turns because the number of turns per slot is positively correlated with the number of conductors. From Figure 16, the kac value of six turns is two times that of three turns, which means that both the AC loss and the kac curve increase sharply as the number of turns per slot increases. In addition, as the frequency increases, the influence of the conductor turns per slot on the AC losses is obvious. The changes in AC loss and kac curves at different frequencies and conductor turns per slot are analyzed in Figure 17 and Figure 18. As shown in Figure 17, at high frequencies, the AC losses of the windings with more turns per slot are much greater than those with fewer turns. At different frequencies, the rising kac curve with the increase of turns per slot is shown in Figure 18, which indicates a significant increase in AC losses at different frequencies.
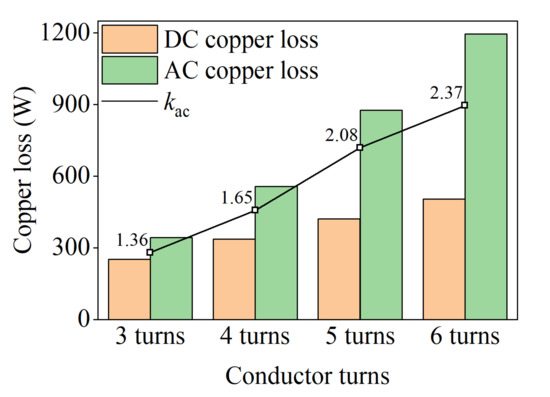
Figure 16.
Copper loss and AC/DC copper loss ratio kac with conductor turns at 1000 Hz.
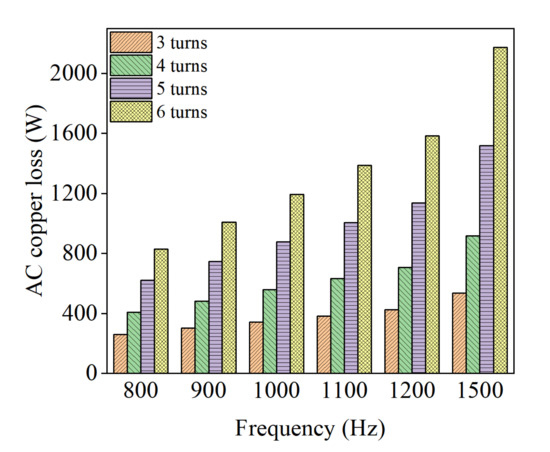
Figure 17.
AC copper loss with conductor turns at different frequencies.
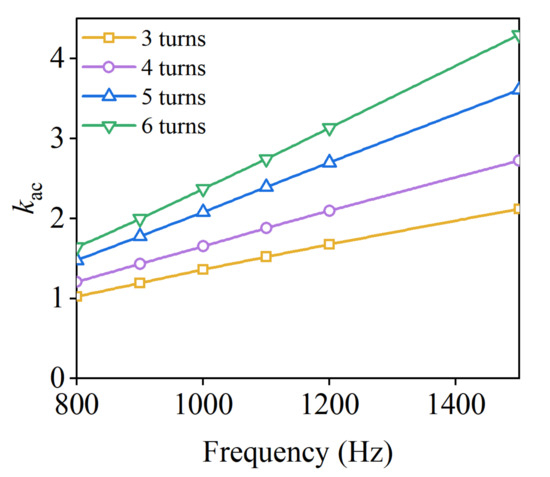
Figure 18.
AC/DC copper loss ratio kac with conductor turns at different frequencies.
3.5. Influence of the Notch Height of the Stator Slot on AC Losses
The AC losses of the windings in the slot can be affected by the magnetic field and frequency, and the magnetic field in the slot is closely related to the slot size.
At present, the effect law of slot shape on AC copper losses is discussed by many researchers. However, the research on the influence of the notch height on the AC loss is rare. The notch height is the distance between the conductor position and the slot opening, as given in Figure 19. In Table 3, the three cases with different notch heights are shown. In order to maintain the same conductor depth for placing stator windings, the depth of the slots has to be deepened as the notch height increases.
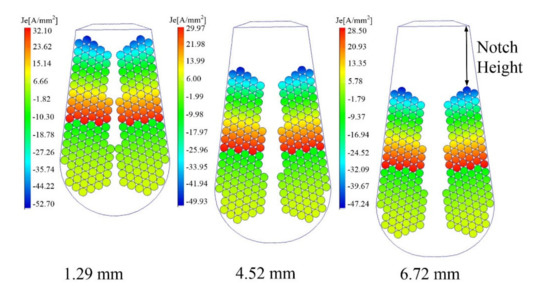
Figure 19.
Current density with notch height at 1000 Hz.

Table 3.
Slot data in different cases.
In order to obtain the current density at different slot heights, a calculation model with different stator slot depths is established in the eddy current field, as shown in Figure 19. The conductor diameter in the simulation is kept the same at 0.7 mm, and the frequency is set to 1000 Hz. The current density distribution at the end of one period is shown in Figure 19. Because the current density varies with time, Figure 20 summarizes the variation of the maximum current density amplitude over the entire period. From Figure 19 and Figure 20, it can be seen that the current density value is the largest at the notch of the stator slot. In addition, the shorter the notch height, the higher the current density value because of the larger magnetic field in the notch.
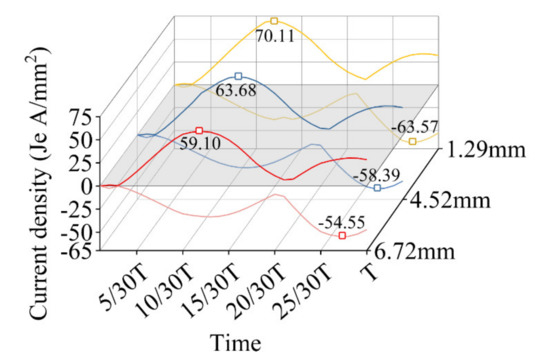
Figure 20.
Maximum current density with notch height at 1000 Hz.
Figure 21 shows the copper losses and the corresponding AC/DC loss ratio kac with different notch heights at 1000 Hz. From Figure 21, the DC losses are almost unchanged with the variation of the notch height, due to the same conductor size. However, as the notch height decreases from 6.72 mm to 1.29 mm, the AC loss increased by 20% from 608 W to 730 W. As can be seen, the AC losses of the short notch height are obviously higher than that of the long notch height. Because of the raised kac value, accordingly, the AC loss tends to increase. In order to clearly show how the notch height affects the AC loss at different frequencies, as shown in Figure 22 and Figure 23, the change trends of the AC loss and kac value with frequency and notch height are also obtained. The AC loss gradually increases as the notch height becomes shorter due to the increase of AC/DC loss ratio kac. In addition, the increasing trend of the AC losses is more significant at high frequencies.
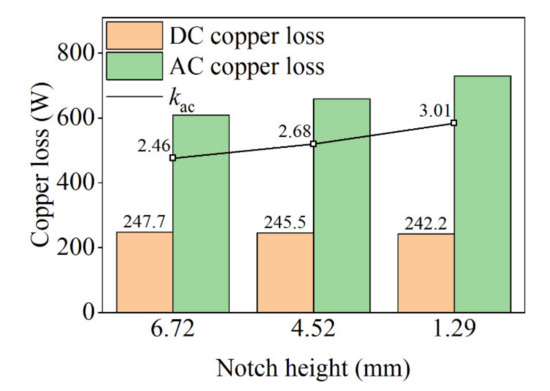
Figure 21.
Copper loss and AC/DC copper loss ratio kac with notch height at 1000 Hz.
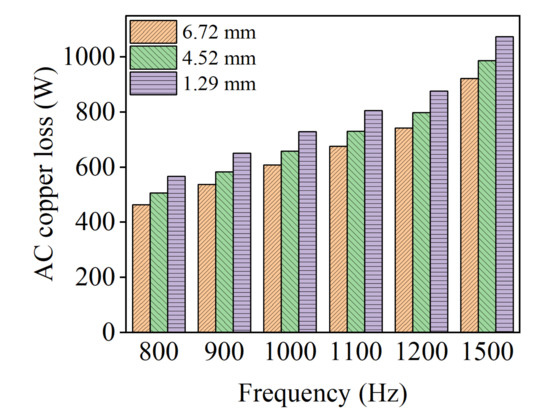
Figure 22.
AC copper loss with notch height at different frequencies.
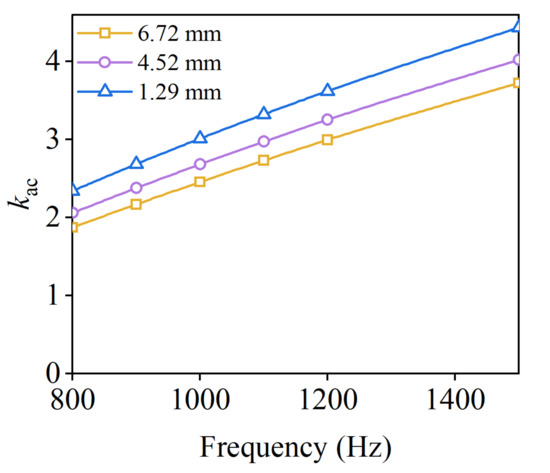
Figure 23.
AC/DC copper loss ratio kac with notch height at different frequencies.
3.6. Influence of Operating Temperature on AC Losses
As is known, different temperatures cause variable electrical conductivity of copper, which results in varying currents in the windings. In the analysis of windings AC losses, temperature performance cannot be ignored. In the analysis, the conductor diameter is set to 0.75 mm and the frequency is 1000 Hz, the current density distribution of the windings is obtained in the eddy current field. The variation of current density with temperature is given in Figure 24. As shown, the eddy current density of the conductor reduces with a raised temperature, which is due to the decrease in electrical conductivity of the copper with increasing temperature.
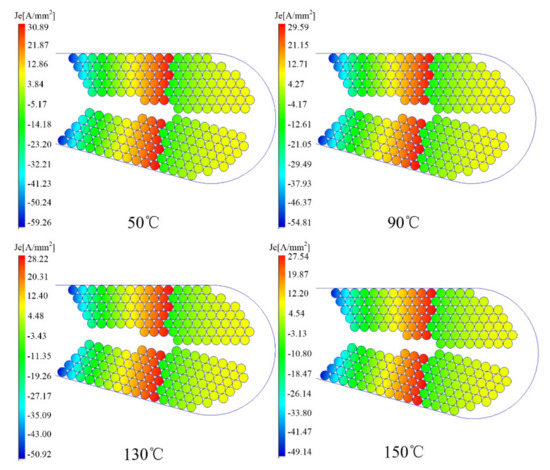
Figure 24.
Current density with temperature when the conductor diameter is 0.75 mm.
Figure 25 analyzes the trends of DC copper loss and AC/DC loss ratio kac at different temperatures and conductor diameters. As shown, the electrical conductivity of copper decreases with increasing temperature, which leads to an increase in DC losses. The decreasing kac curves with increasing temperature when different conductor diameters are adopted are given in Figure 25 and Figure 26. As can be seen, the increase in temperature leads to the opposite trend of the DC loss and the kac value. Therefore, the change of AC copper loss with temperature needs to be further analyzed because the AC loss is affected by the combination of the DC loss and the AC/DC loss ratio kac.
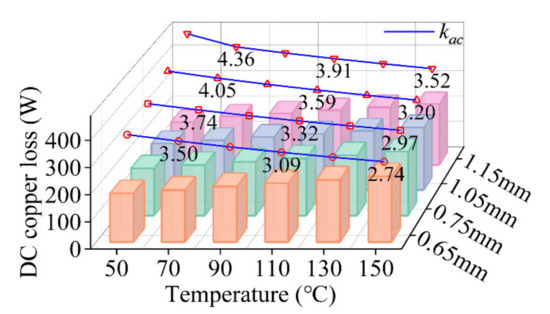
Figure 25.
DC Copper loss and AC/DC copper loss ratio kac with the temperature at different conductors.
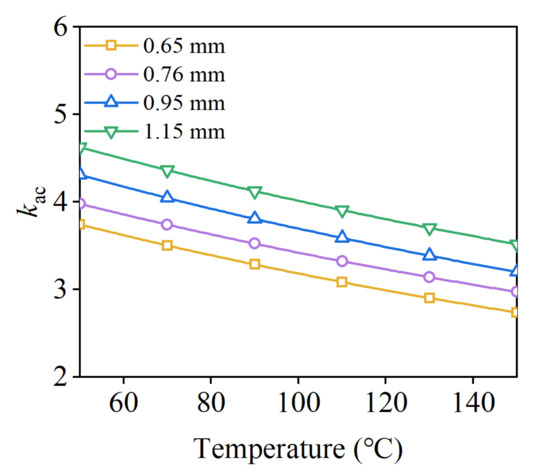
Figure 26.
AC/DC copper loss ratio kac with conductor diameter at different temperatures.
Figure 27 shows the variation of AC loss with changing temperature when different wire diameters are adopted. When the conductor diameter is small, it can be noticed that as the temperature increases, the AC losses first rise and then fall. However, the AC losses keep increasing as the temperature rises, after the diameter exceeds a specific value. Theoretically, the higher the temperature, the greater the AC losses, but when using a smaller diameter, the AC loss eventually shows a decreasing trend with the increase of temperature. It is because the reduction of the AC/DC loss ratio kac is greater than the increase of DC copper loss with the increased temperature.
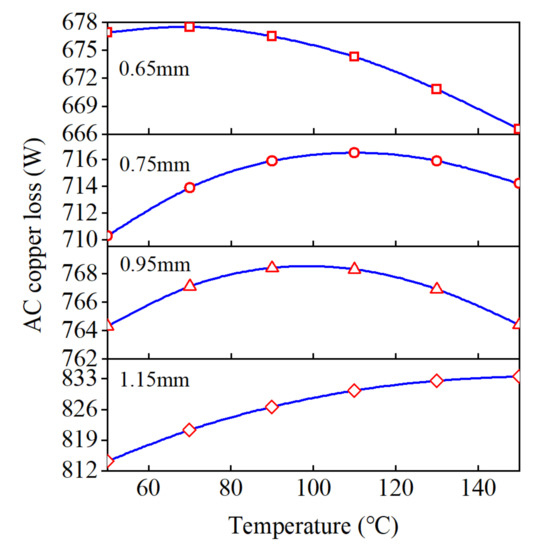
Figure 27.
AC copper loss with conductor diameter at different temperatures.
4. Prototype and Experimental Tests
In this paper, the AC/DC loss ratios kac are tested for round copper wires in different sizes, and the finite element analysis is verified by four cases. In order to better verify the theoretical analysis, a 60 kW, 30,000 rpm HSPMM is manufactured, in which 0.6 mm conductors are adopted in the windings, and each conductor consists of 51 cross-wound wires, as given in case 1 of Table 4. In addition, four coil cases are adopted in the experiments in order to obtain kac under different conductor sizes, and the different conductor diameters and their corresponding strand numbers are given in Table 4. In the experiments, the AC resistance values of the windings at different frequencies are obtained by an AC resistance measuring instrument. The experimental current is set to 1 A, and the AC resistance at different frequencies is obtained by varying the current. The experimental process for four coils is shown in Figure 28, in which case 1 is the stator of the actual prototype.

Table 4.
Test coil cases.

Figure 28.
The test processes.
The experimental and finite element simulation results of the four coils at different frequencies are compared in Figure 29. It can be seen that the increase of the frequency would lead to a larger kac value. As shown, the experimental and calculation results are similar, so the experimental and theoretical analysis are consistent. Case 1 in Figure 29 shows the comparison between the measured values of the prototype and the calculated values of the finite element simulation. Note that the measured value is slightly bigger than the calculated value, because the effect of the end windings on the loss is ignored in the simulation. As shown in the figure, the measured and simulated results become closer as the frequency increases; that is, the error becomes smaller. In general, the experimental and theoretical results are in good agreement, which verifies the correctness of the theoretical analysis.
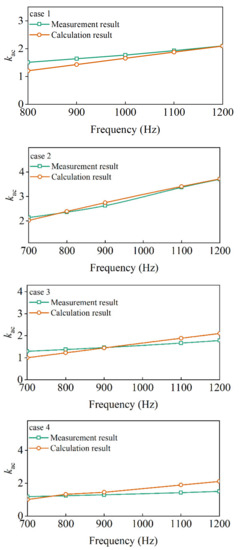
Figure 29.
Test and calculation results at different frequencies.
5. Conclusions
In this paper, the AC copper losses of HPSMMs with round copper wire windings were comprehensively studied, and the influence of different factors on the AC losses was comparatively analyzed, including the frequency, the conductor diameter, the number of conductors per slot, the notch height of the stator slot, and the working temperature. Four stator coils with round copper wire windings were fabricated and tested to verify the theoretical analysis. In summary, in this paper, the conclusions obtained are as follows.
- (1)
- Keeping the same number of parallel wires for the conductors, the value of the AC/DC loss ratio kac increased five times at 1000 Hz as the conductor diameter increased from 0.55 mm to 0.85 mm. When the slot fill rate remained the same, the kac values are 3.09 and 4.04 at 1000 Hz under conductor diameters of 0.65 mm and 1.45 mm, respectively. As can be seen, the conductor diameter has an larger impact on AC losses for both cases, and the larger the diameter, the higher the AC copper losses.
- (2)
- The AC/DC loss ratio kac value of six turns is twice that of three turns at 1000 Hz, which means that both the AC loss and the kac curve increase sharply as the number of turns per slot increases, and this phenomenon is obviously under high frequency. The effect of the number of turns per slot on AC losses cannot be ignored in the design of HSPMMs.
- (3)
- When the notch height is 6.72 mm, the AC loss is 608 W at 1000 Hz, and when the notch is 1.29 mm, the AC loss increases to 730 W. Due to the magnetic flux field change in the stator slot, the shorter the notch height, the bigger the AC copper loss. As can be seen, the notch height in the slot is also a crucial factor on AC losses at high frequency.
- (4)
- As the temperature increases, the electrical conductivity of the conductor is decreased. Therefore, the DC losses increase while the kac curve decreases with the rising temperature, which causes the trend of AC loss uncertainty. Through research, when the wire diameter is 1.15 mm, the AC loss at 1000 Hz increases from 814 W to 833 W when the temperature increases from 50 °C to 150 °C. However, when the conductor diameter is less than 1.15 mm, the AC loss of the winding does not keep increasing, which eventually shows a decreasing trend. As can be seen, the changing temperature makes a significant variation in AC losses for different conductor diameters. As the temperature rises, the AC losses increase and then decrease for smaller diameter conductors. However, the AC losses keep increasing after the diameter is larger than a specific value.
Author Contributions
Conceptualization, G.D. and Y.Z.; data curation, G.D. and W.Y.; formal analysis, W.Y.; funding acquisition, G.D.; investigation, G.D. and W.Y.; methodology, G.D. and W.Y.; project administration, G.D.; resources, G.D.; software, W.Y.; supervision, Y.Z.; validation, G.D., Y.Z., L.W. and T.P.; visualization, W.Y.; writing–original draft, W.Y.; writing–review and editing, G.D., W.Y., L.W. and T.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Nature Science Foundation of China, grant number 52177056.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ismagilov, F.R.; Uzhegov, N.; Vavilov, V.E.; Bekuzin, V.I.; Ayguzina, V.V. Multidisciplinary design of ultra-high-speed electrical machines. IEEE Trans. Energy Convers. 2018, 33, 1203–1212. [Google Scholar] [CrossRef]
- Fang, H.; Li, D.; Qu, R.; Li, J.; Wang, C.; Song, B. Rotor design and eddy-current loss suppression for high-speed machines with a solid-PM rotor. IEEE Trans. Ind. Appl. 2018, 55, 448–457. [Google Scholar] [CrossRef]
- Al-Timimy, A.; Giangrande, P.; Degano, M.; Galea, M.; Gerada, C. Investigation of AC Copper and Iron Losses in High-Speed High-Power Density PMSM. In Proceedings of the 2018 XIII International Conference on Electrical Machines (ICEM), Alexandroupoli, Greece, 3–6 September 2018; pp. 263–269. [Google Scholar]
- Gu, Y.; Wang, X.; Gao, P.; Li, X. Mechanical analysis with thermal effects for high-speed permanent-magnet synchronous machines. IEEE Trans. Ind. Appl. 2021, 57, 4646–4656. [Google Scholar] [CrossRef]
- Feng, J.; Wang, Y.; Guo, S.; Chen, Z.; Wang, Y.; Zhu, Z. Split ratio optimisation of high-speed permanent magnet brushless machines considering mechanical constraints. IET Electr. Power Appl. 2018, 13, 81–90. [Google Scholar] [CrossRef]
- Gerada, D.; Mebarki, A.; Brown, N.L.; Gerada, C.; Cavagnino, A.; Boglietti, A. High-speed electrical machines: Technologies, trends, and developments. IEEE Trans. Ind. Electron. 2013, 61, 2946–2959. [Google Scholar] [CrossRef]
- Borisavljevic, A.; Polinder, H.; Ferreira, J.A. On the speed limits of permanent-magnet machines. IEEE Trans. Ind. Electron. 2009, 57, 220–227. [Google Scholar] [CrossRef]
- Gieras, J.F.; Saari, J. Performance calculation for a high-speed solid-rotor induction motor. IEEE Trans. Ind. Electron. 2011, 59, 2689–2700. [Google Scholar] [CrossRef]
- Uzhegov, N.; Kurvinen, E.; Nerg, J.; Pyrhonen, J.; Sopanen, J.T.; Shirinskii, S. Multidisciplinary design process of a 6-slot 2-pole high-speed permanent-magnet synchronous machine. IEEE Trans. Ind. Electron. 2015, 63, 784–795. [Google Scholar] [CrossRef]
- Pechlivanidou, M.S.C.; Kladas, A.G. Litz Wire Strand Shape Impact Analysis on AC Losses of High-Speed Permanent Magnet Synchronous Motors. In Proceedings of the 2021 IEEE Workshop on Electrical Machines Design, Control and Diagnosis (WEMDCD), Modena, Italy, 8–9 April 2021; IEEE: Piscataway, NJ, USA, 2001; pp. 95–100. [Google Scholar] [CrossRef]
- Gurumurthy, S.R.; Agarwal, V.; Sharma, A. Optimal energy harvesting from a high-speed brushless DC generator-based flywheel energy storage system. IET Electr. Power Appl. 2013, 7, 693–700. [Google Scholar] [CrossRef]
- Khan, H.A.; Khan, F.; Khan, S.; Ahmad, N.; Soomro, J.B.; Sami, I. Design and performance investigation of 3-slot/2-pole high speed permanent magnet machine. IEEE Access 2021, 9, 41603–41614. [Google Scholar] [CrossRef]
- Liu, L.; Guo, Y.; Lei, G.; Zhu, J.; Jin, J. Power Loss Analysis of High Speed Permanent Magnet Machine. In Proceedings of the 2020 IEEE International Conference on Applied Superconductivity and Electromagnetic Devices (ASEMD), Tianjin, China, 16–18 October 2020. [Google Scholar]
- Tenconi, A.; Vaschetto, S.; Vigliani, A. Electrical machines for high-speed applications: Design considerations and tradeoffs. IEEE Trans. Ind. Electron. 2013, 61, 3022–3029. [Google Scholar] [CrossRef]
- Gonzalez, D.A.; Saban, D.M. Study of the Copper Losses in a High-Speed Permanent-Magnet Machine With Form-Wound Windings. IEEE Trans. Ind. Electron. 2013, 61, 3038–3045. [Google Scholar] [CrossRef]
- Bharatkar, S.S.; Yanamshetti, R.; Chatterjee, D.; Ganguli, A.K. Dual-mode switching technique for reduction of commutation torque ripple of brushless dc motor. IET Electr. Power Appl. 2011, 5, 193–202. [Google Scholar] [CrossRef]
- Wojda, R.P.; Kazimierczuk, M.K. Analytical optimization of solid-round wire-windings. IEEE Trans. Ind. Electron. 2012, 60, 1033–1041. [Google Scholar] [CrossRef]
- Sullivan, C.R. Optimal choice for number of strands in a Litz-wire transformer winding. IEEE Trans. Power Electron. 1999, 14, 283–291. [Google Scholar] [CrossRef]
- Thang, C.X.; Sullivan, R. Stranded wire with uninsulated strand as a low-cost alternative to Litz wire. In Proceedings of the IEEE 34th Annual Conference on Power Electronics Specialist, 2003. PESC’03, Acapulco, Mexico, 15–19 June 2003. [Google Scholar] [CrossRef]
- Nan, X.; Sullivan, C.R. An equivalent complex permeability model for Litz-wire windings. IEEE Trans. Ind. Appl. 2009, 45, 854–860. [Google Scholar] [CrossRef]
- Uzhegov, N.; Smirnov, A.; Park, C.H.; Ahn, J.H.; Heikkinen, J.; Pyrhonen, J. Design aspects of high-speed electrical machines with active magnetic bearings for compressor applications. IEEE Trans. Ind. Electron. 2017, 64, 8427–8436. [Google Scholar] [CrossRef]
- Bianchi, N.; Bolognani, S.; Luise, F. Potentials and limits of high-speed PM motors. IEEE Trans. Ind. Appl. 2004, 40, 1570–1578. [Google Scholar] [CrossRef]
- Bardalai, A.; Zhang, X.; Zou, T.; Gerada, D.; Li, J.; Gerada, C. Comparative Analysis of AC losses with round magnet wire and Litz wire winding of a High–Speed PM Machine. In Proceedings of the 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019. [Google Scholar] [CrossRef]
- Popescu, M.; Dorrell, D.G. Proximity Losses in the Windings of High-Speed Brushless Permanent Magnet AC Motors With Single Tooth Windings and Parallel Paths. IEEE Trans. Magn. 2013, 49, 3913–3916. [Google Scholar] [CrossRef]
- Mellor, P.; Wrobel, R.; Simpson, N. AC losses in high frequency electrical machine windings formed from large section conductors. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014. [Google Scholar] [CrossRef]
- Gyselinck, J.; Dular, P.; Sadowski, N.; Kuo-Peng, P.; Sabariego, R.V. Homogenization of Form-Wound Windings in Frequency and Time Domain Finite-Element Modeling of Electrical Machines. IEEE Trans. Magn. 2010, 46, 2852–2855. [Google Scholar] [CrossRef]
- Wrobel, R.; Salt, D.E.; Griffo, A.; Simpson, N.; Mellor, P.H. Derivation and Scaling of AC Copper Loss in Thermal Modeling of Electrical Machines. IEEE Trans. Ind. Electron. 2014, 61, 4412–4420. [Google Scholar] [CrossRef]
- Du, G.; Ye, W.; Zhang, Y.; Wang, L.; Pu, T.; Huang, N. Comprehensive Analysis of the AC Copper Loss for High Speed PM Machine With Form-Wound Windings. IEEE Access 2022, 10, 9036–9047. [Google Scholar] [CrossRef]
- Du, G.; Xu, W.; Zhu, J.; Huang, N. Power Loss and Thermal Analysis for High-Power High-Speed Permanent Magnet Machines. IEEE Trans. Ind. Electron. 2020, 67, 2722–2733. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).