A Study on the Vibration Characteristics and Damage Mechanism of Pantograph Strips in a Railway Electrification System
Abstract
:1. Introduction
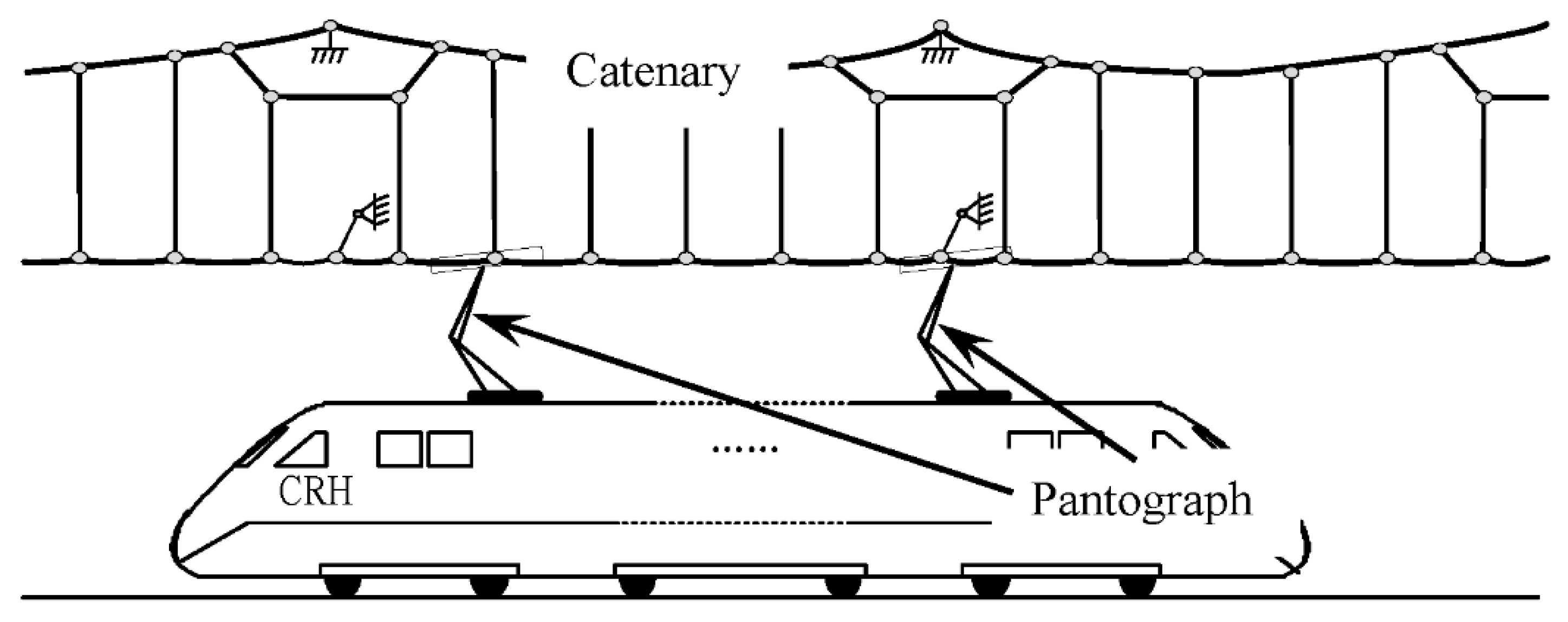
1.1. Pantograph–Catenary Interaction
1.2. Irregular Wear
2. Computational Simulation of the Pantograph–Catenary System
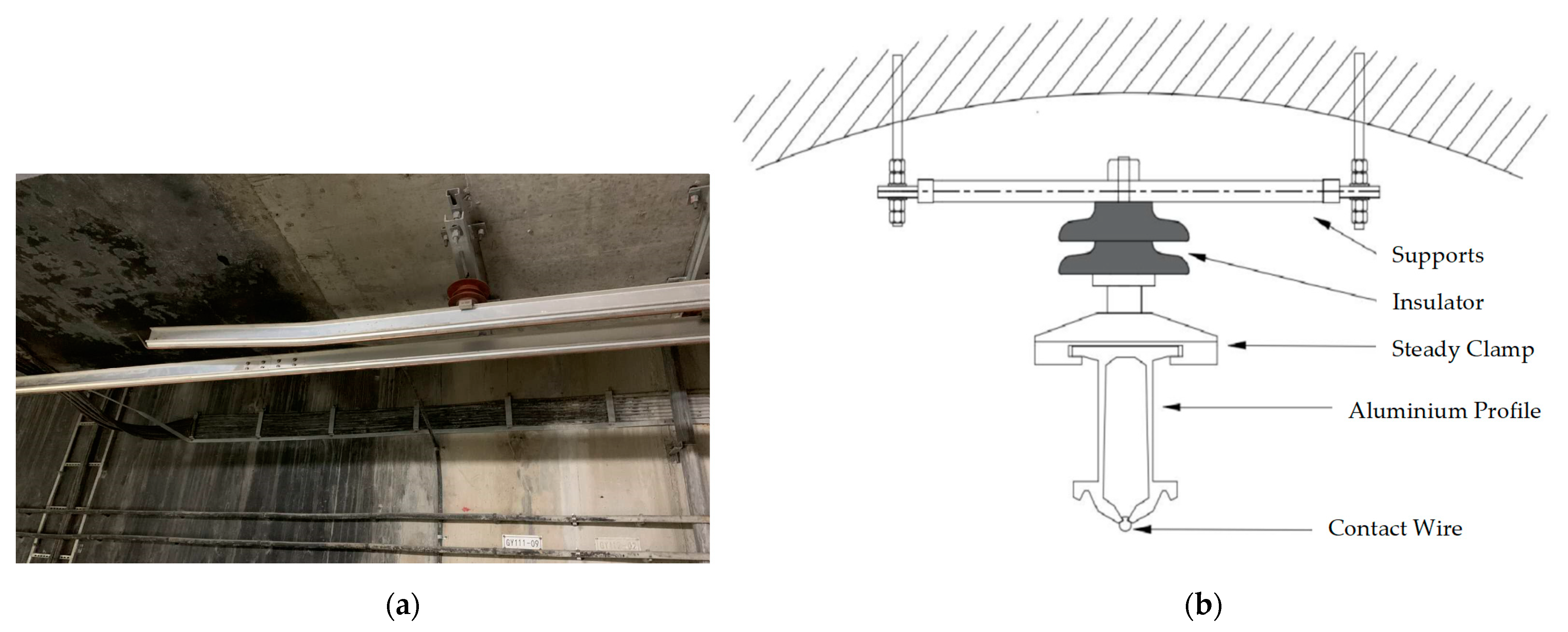
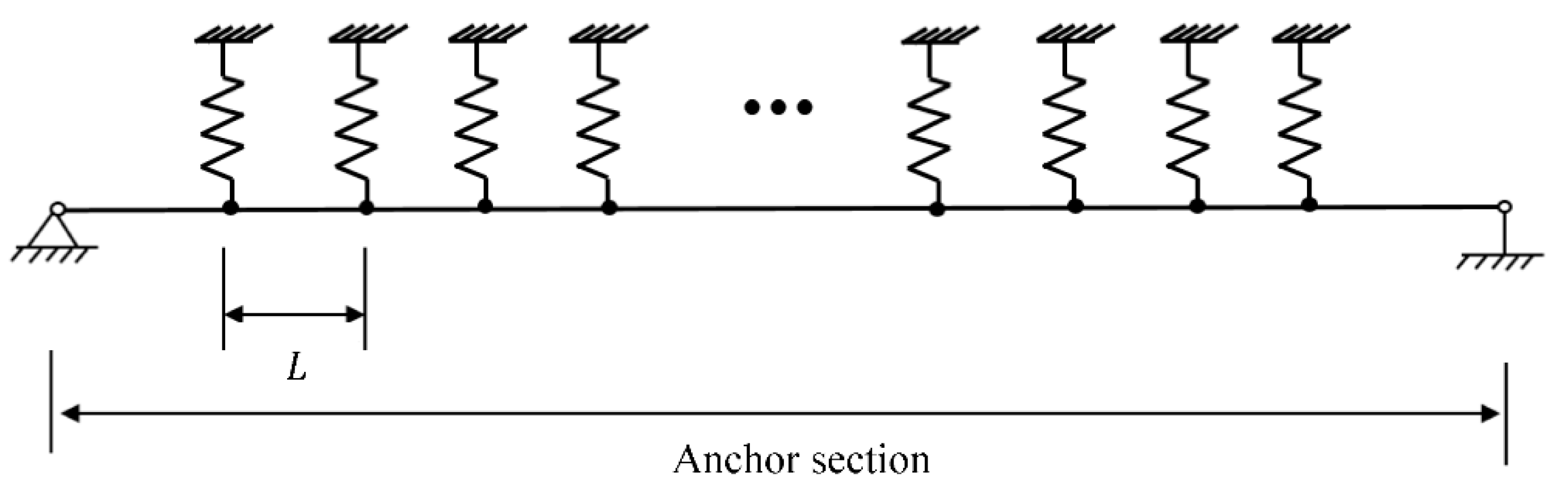
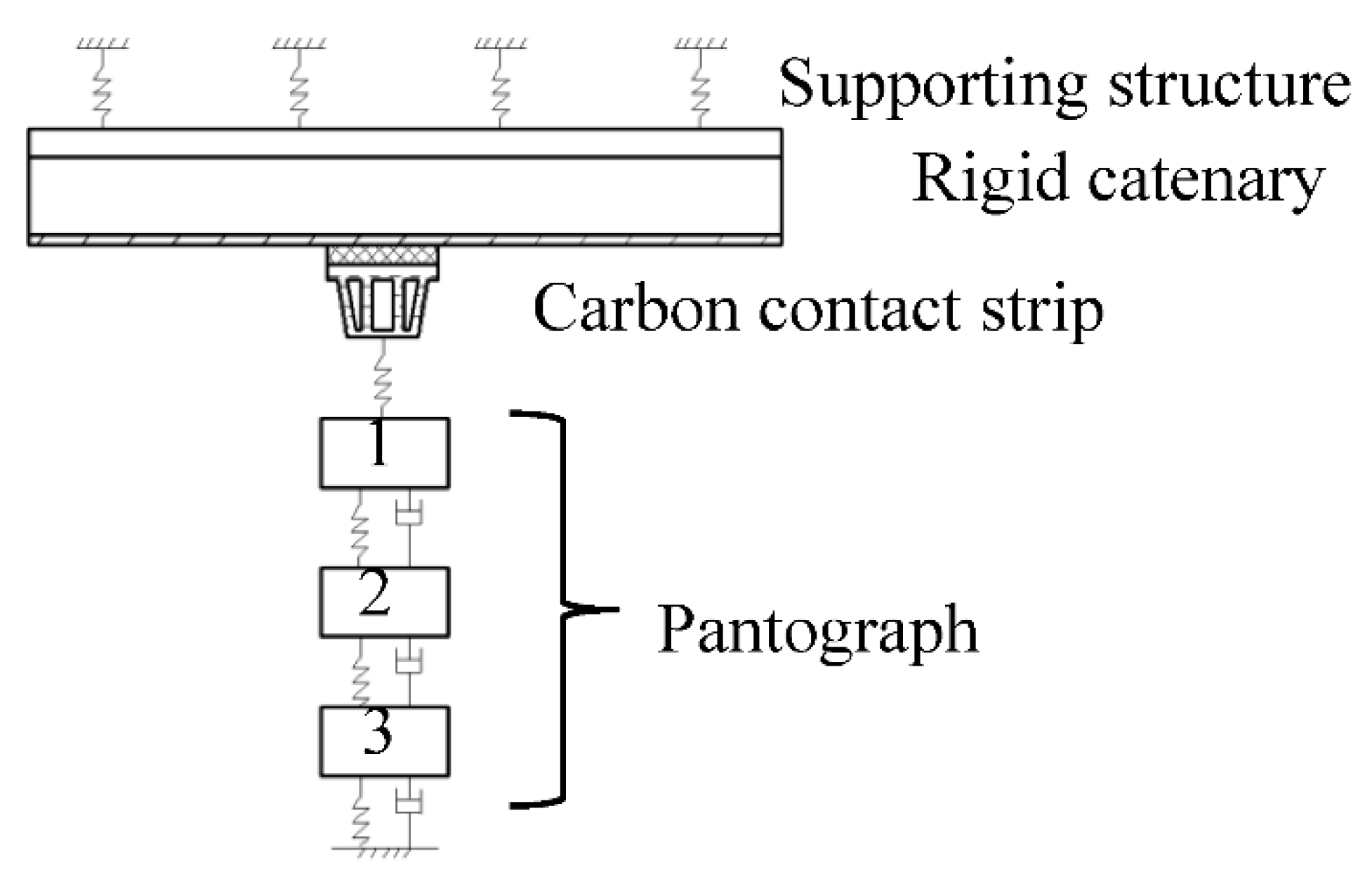
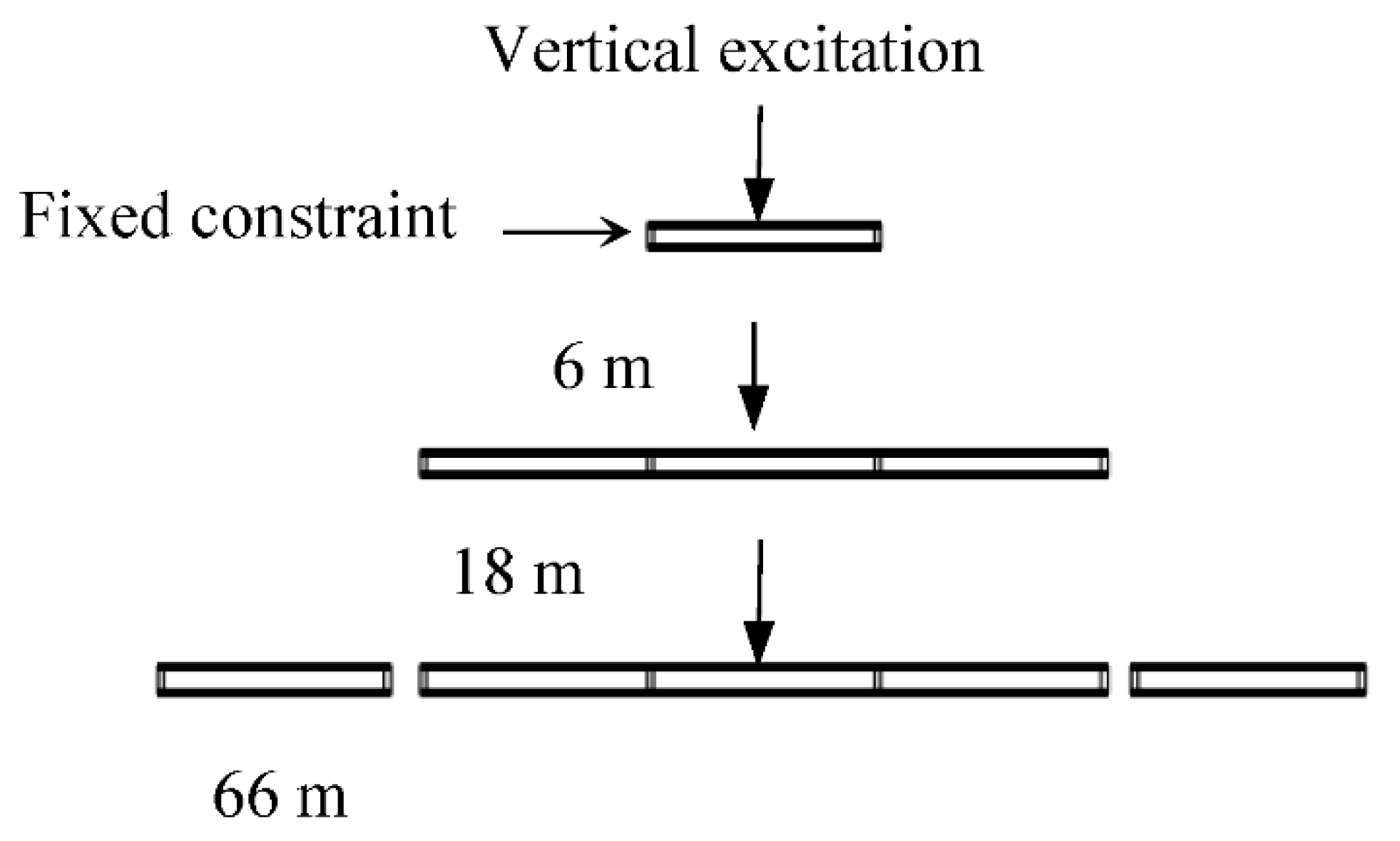
2.1. The Rigid Catenary Model
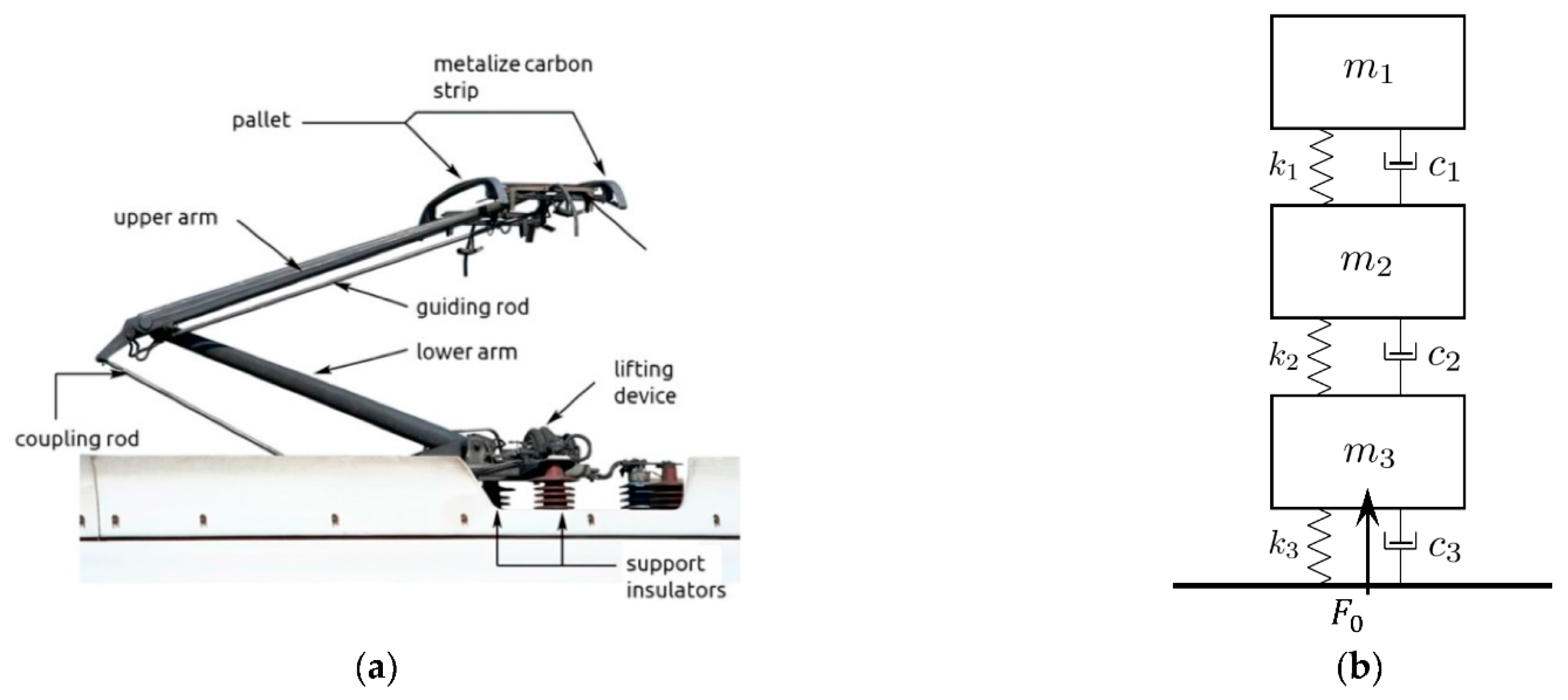
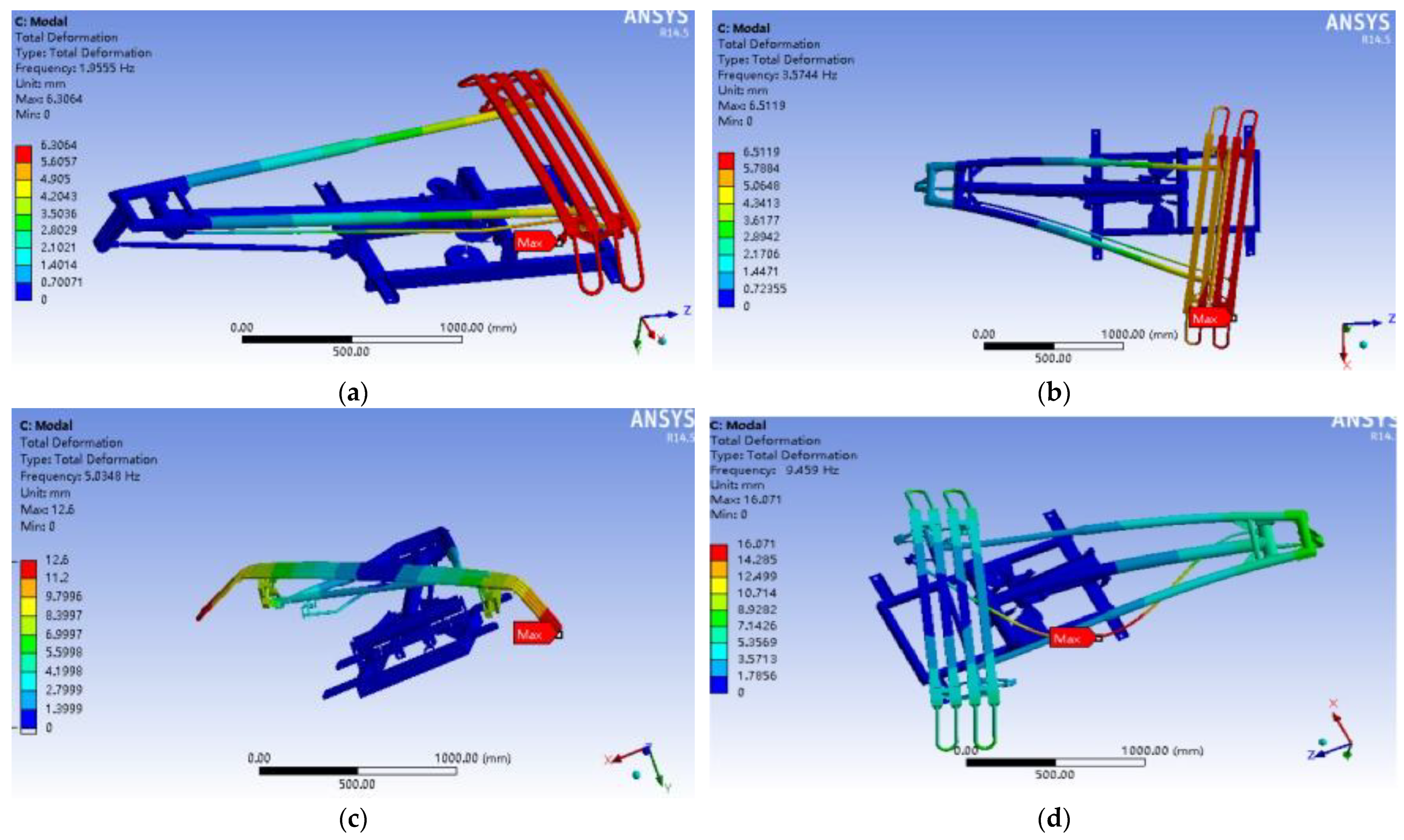
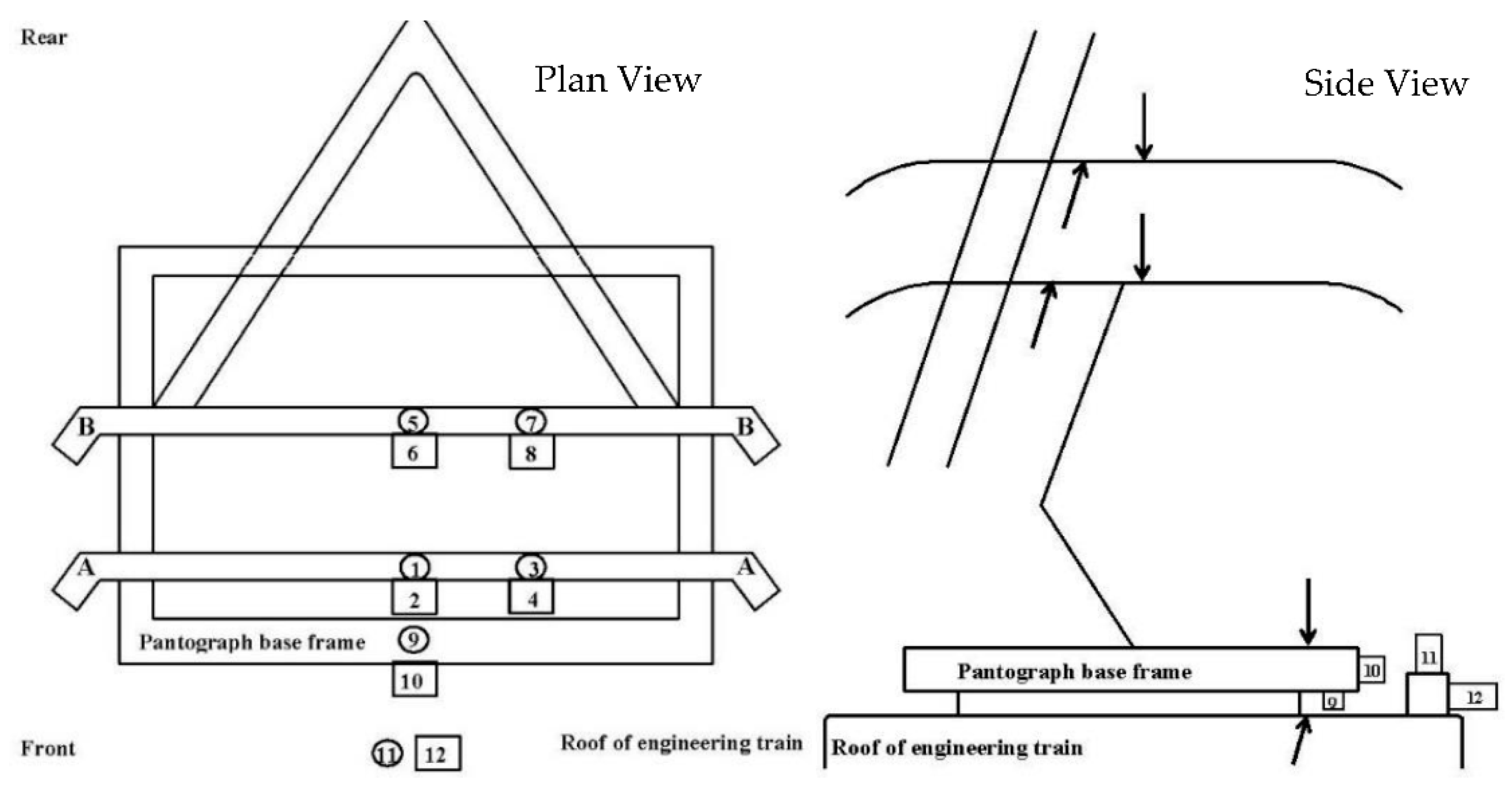
2.2. The Pantograph Model
2.3. The Pantograph–Catenary Contact Model
2.4. The Pantograph–Catenary Coupled Model
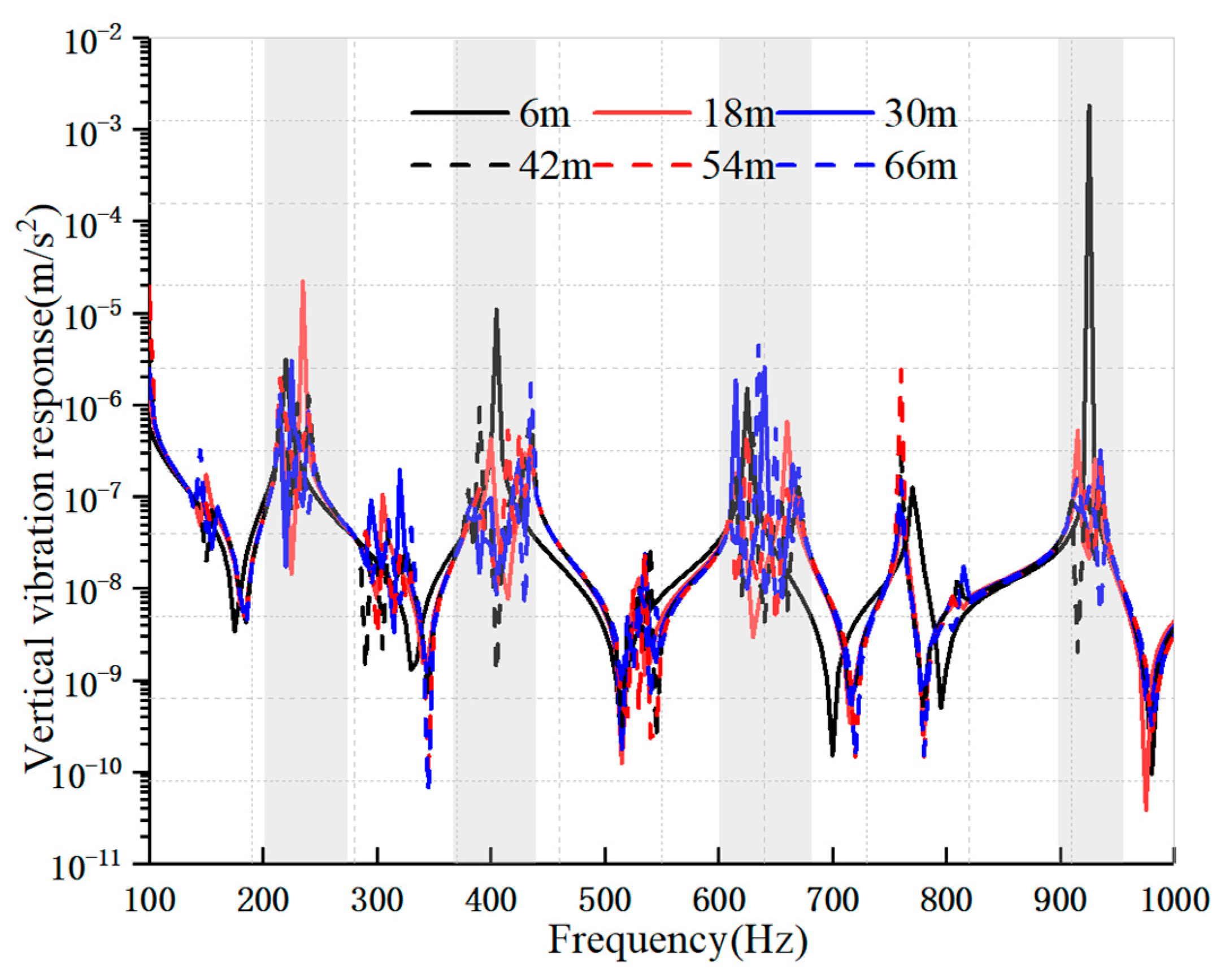
2.5. Simulation Results
3. Laboratory Tests
Test Set-Up
4. Improvement in the Damping Property of the Pantograph Strip
5. Conclusions
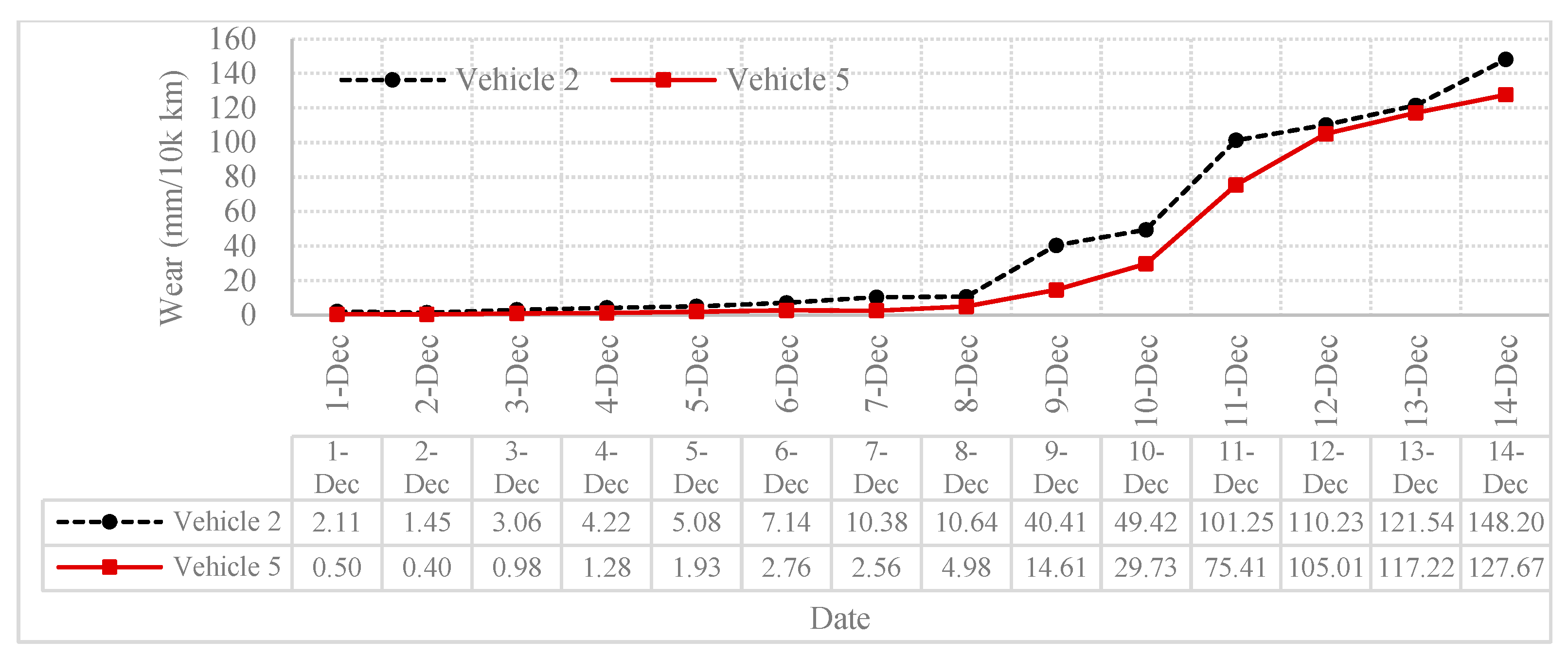
- The irregular wear problem is characterized by the consistency between the wear pattern and the mode shape of dominant modal frequencies of pantograph strips, not the pantograph as a whole. Furthermore, this is due to resonance at the pantograph strip and contact wire sliding interface in the high-frequency range;
- Improvement of damping performance is one of the most effective means to control the high-frequency vibration of the pantograph strip. Damping-treated pantograph strips can reduce vibration acceleration up to 7 dB;
- By comparing damping performance between traditional and rigid catenary system, and with varying train speeds, it was found that the worse the initial condition of the pantograph–catenary system, the more prominent the damping effects on the control of high-frequency vibration in the irregular wear problem.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Levy, S.; Bain, J.A.; Leclerc, E.J. Railway Overhead Contact Systems, Catenary-Pantograph Dynamics for Power Collection at High Speeds. J. Eng. Ind. 1968, 90, 692–699. [Google Scholar] [CrossRef]
- Klapas, D.; Benson, F.A.; Hackam, R. Simulation of Wear in Overhead Current Collection Systems. Rev. Sci. Instrum. 1985, 56, 1820–1828. [Google Scholar] [CrossRef]
- Klapas, D.; Benson, F.A.; Hackam, R.; Evison, P.R. Wear in Simulated Railway Overhead Current Collection Systems. Wear 1988, 126, 167–190. [Google Scholar] [CrossRef]
- Kang, S. A Study of Friction and Wear Characteristics of Copper- and Iron-Based Sintered Materials. Wear 1993, 162–164, 1123–1128. [Google Scholar] [CrossRef]
- Azevedo, C.R.F.; Sinatora, A. Failure Analysis of a Railway Copper Contact Strip. Eng. Fail. Anal. 2004, 11, 829–841. [Google Scholar] [CrossRef]
- Wu, T.X.; Brennan, M.J. Basic Analytical Study of Pantograph-Catenary System Dynamics. Veh. Syst. Dyn. 1998, 30, 443–456. [Google Scholar] [CrossRef]
- Wu, T.X.; Brennan, M.J. Dynamic stiffness of a railway overhead wire system and its effect on pantograph–catenary system dynamics. J. Sound Vib. 1999, 219, 483–502. [Google Scholar] [CrossRef]
- Arnold, M.; Simeon, B. Pantograph and Catenary Dynamics: A Benchmark Problem and Its Numerical Solution. Appl. Numer. Math. 2000, 34, 345–362. [Google Scholar] [CrossRef]
- Benet, J.; Cuartero, N.; Cuartero, F.; Rojo, T.; Tendero, P.; Arias, E. An Advanced 3D-Model for the Study and Simulation of the Pantograph Catenary System. Transp. Res. Part C Emerg. Technol. 2013, 36, 138–156. [Google Scholar] [CrossRef]
- Jimenez-Octavio, J.R.; Carnicero, A.; Sanchez-Rebollo, C.; Such, M. A Moving Mesh Method to Deal with Cable Structures Subjected to Moving Loads and Its Application to the Catenary–Pantograph Dynamic Interaction. J. Sound Vib. 2015, 349, 216–229. [Google Scholar] [CrossRef]
- Takemura, T. Characteristics of Overhead Rigid Conductor Line Having T-Type Cross Section. In Proceedings of the International Conference on Developments in Mass Transit Systems, London, UK, 20–23 April 1998; pp. 173–177. [Google Scholar]
- Poetsch, G.; Evans, J.; Meisinger, R.; Kortüm, W.; Baldauf, W.; Veitl, A.; Wallaschek, J. Pantograph Catenary Dynamics and Control. Veh. Syst. Dyn. 1997, 28, 159–195. [Google Scholar] [CrossRef]
- Chater, E.; Ghani, D.; Giri, F.; Rachid, A.; Chaoui, F.Z.; Haloua, M. Output Feedback Control of Pantograph-Catenary System. IFAC Proc. Vol. 2013, 46, 131–136. [Google Scholar] [CrossRef]
- Song, Y.; Ouyang, H.; Liu, Z.; Mei, G.; Wang, H.; Lu, X. Active Control of Contact Force for High-Speed Railway Pantograph-Catenary Based on Multi-Body Pantograph Model. Mech. Mach. Theory 2017, 115, 35–59. [Google Scholar] [CrossRef]
- Zhou, N.; Zhang, W. Investigation on Dynamic Performance and Parameter Optimization Design of Pantograph and Catenary System. Finite Elem. Anal. Des. 2011, 47, 288–295. [Google Scholar] [CrossRef]
- Bruni, S.; Bucca, G.; Collina, A.; Facchinetti, A.; Melzi, S. Pantograph–Catenary Dynamic Interaction in the Medium-High Frequency Range. Veh. Syst. Dyn. Suppl. 2004, 41, 697–706. [Google Scholar]
- Collina, A.; Melzi, S. Effect of Contact Strip–Contact Wire Interaction on Current Transfer at High Sliding Speed in the Mid-High Frequency Range. In Proceedings of the 5th International Conference on Tribology AITC–AIT 2006, Parma, Italy, 20–22 September 2006. [Google Scholar]
- Collina, A.; lo Conte, A.; Carnevale, M. Effect of Collector Deformable Modes in Pantograph—Catenary Dynamic Interaction. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2009, 223, 1–14. [Google Scholar] [CrossRef]
- Bouchoucha, A.; Zaidi, H.; Kadiri, E.K.; Paulmier, D. Influence of Electric Fields on the Tribological Behaviour of Electrodynamical Copper/Steel Contacts. Wear 1997, 203–204, 434–441. [Google Scholar] [CrossRef]
- Nagasawa, H.; Kato, K. Wear Mechanism of Copper Alloy Wire Sliding against Iron-Base Strip under Electric Current. Wear 1998, 216, 179–183. [Google Scholar] [CrossRef]
- Kubota, Y.; Nagasaka, S.; Miyauchi, T.; Yamashita, C.; Kakishima, H. Sliding Wear Behavior of Copper Alloy Impregnated C/C Composites under an Electrical Current. Wear 2013, 302, 1492–1498. [Google Scholar] [CrossRef]
- Kubo, S.; Kato, K. Effect of Arc Discharge on the Wear Rate and Wear Mode Transition of a Copper-Impregnated Metallized Carbon Contact Strip Sliding against a Copper Disk. Tribol. Int. 1999, 32, 367–378. [Google Scholar] [CrossRef]
- Ding, T.; Chen, G.X.; Bu, J.; Zhang, W.H. Effect of Temperature and Arc Discharge on Friction and Wear Behaviours of Carbon Strip/Copper Contact Wire in Pantograph–Catenary Systems. Wear 2011, 271, 1629–1636. [Google Scholar] [CrossRef]
- Wei, X.K.; Meng, H.F.; He, J.H.; Jia, L.M.; Li, Z.G. Wear Analysis and Prediction of Rigid Catenary Contact Wire and Pantograph Strip for Railway System. Wear 2020, 442–443, 203118. [Google Scholar] [CrossRef]





| Parameter | Definition |
|---|---|
| Density of the simplified beam section | |
| Cross sectional area of the simplified beam section | |
| Young’s modulus of the simplified beam section | |
| Moment of inertia of the simplified beam section | |
| Length of the simplified beam section between supporting points | |
| Vertical displacement of the simplified beam section | |
| Contact force between the pantograph strip and contact wire | |
| Force on the supporting arm at the supporting point | |
| Force on the simplified section at the supporting point | |
| Initial position at the sliding interface between the pantograph strip and contact wire | |
| Initial timestep at the sliding interface between the pantograph strip and contact wire | |
| Cartesian coordinate | |
| Mass of the simplified beam section | |
| Damping coefficient of the simplified beam section | |
| Stiffness of the simplified beam section |
| Parameter | Definition |
|---|---|
| Vertical displacement of the pan-head | |
| Vertical displacement of the upper arm | |
| Vertical displacement of the lower arm | |
| Mass of the pan-head | |
| Mass of the upper arm | |
| Mass of the lower arm | |
| Damping coefficient between the pan-head and the upper arm | |
| Damping coefficient between the upper arm and the lower arm | |
| Damping coefficient between the lower arm and the roof of the rail vehicle | |
| Stiffness between the pan-head and the upper arm | |
| Stiffness between the upper arm and the lower arm | |
| Stiffness between the lower arm and the roof of the rail vehicle | |
| Static uplift force | |
| Contact force between the pantograph strip and contact wire |
| Parameter | Definition |
|---|---|
| Length of the simplified beam section between supporting points | |
| Width of the contact area between the pantograph strip and contact wire | |
| Distance along the z-axis from the origin of the Cartesian coordinate | |
| Distribution of the contact stress | |
| External load | |
| Radial distance from the contact point to the middle of the contact area | |
| Young’s Modulus | |
| Equivalent Young’s Modulus | |
| Poisson’s ratio | |
| Radius of the cylinder of the contact wire | |
| Normal stress on contact wire | |
| Shear stress on contact wire |
| Components | Material | Young’s Modulus (GPa) | Density (kg/m3) | Poisson’s Ratio | |
|---|---|---|---|---|---|
| Rigid catenary | Aluminium profile | Aluminium alloy | 72.0 | 2800 | 0.33 |
| Contact Line | Copper silver alloy | 120 | 9183 | 0.3 | |
| Pantograph strip | Support | Aluminium alloy | 72.0 | 2800 | 0.33 |
| Carbon strip | Carbon | 12.7 | 2000 | 0.35 |
| Mass Block No. | m/kg | k/(N/m) | c/(N.s/m) |
|---|---|---|---|
| 1 | 11 | 13,300 | 0 |
| 2 | 10 | 7540 | 0 |
| 3 | 12 | 3500 | 120 |
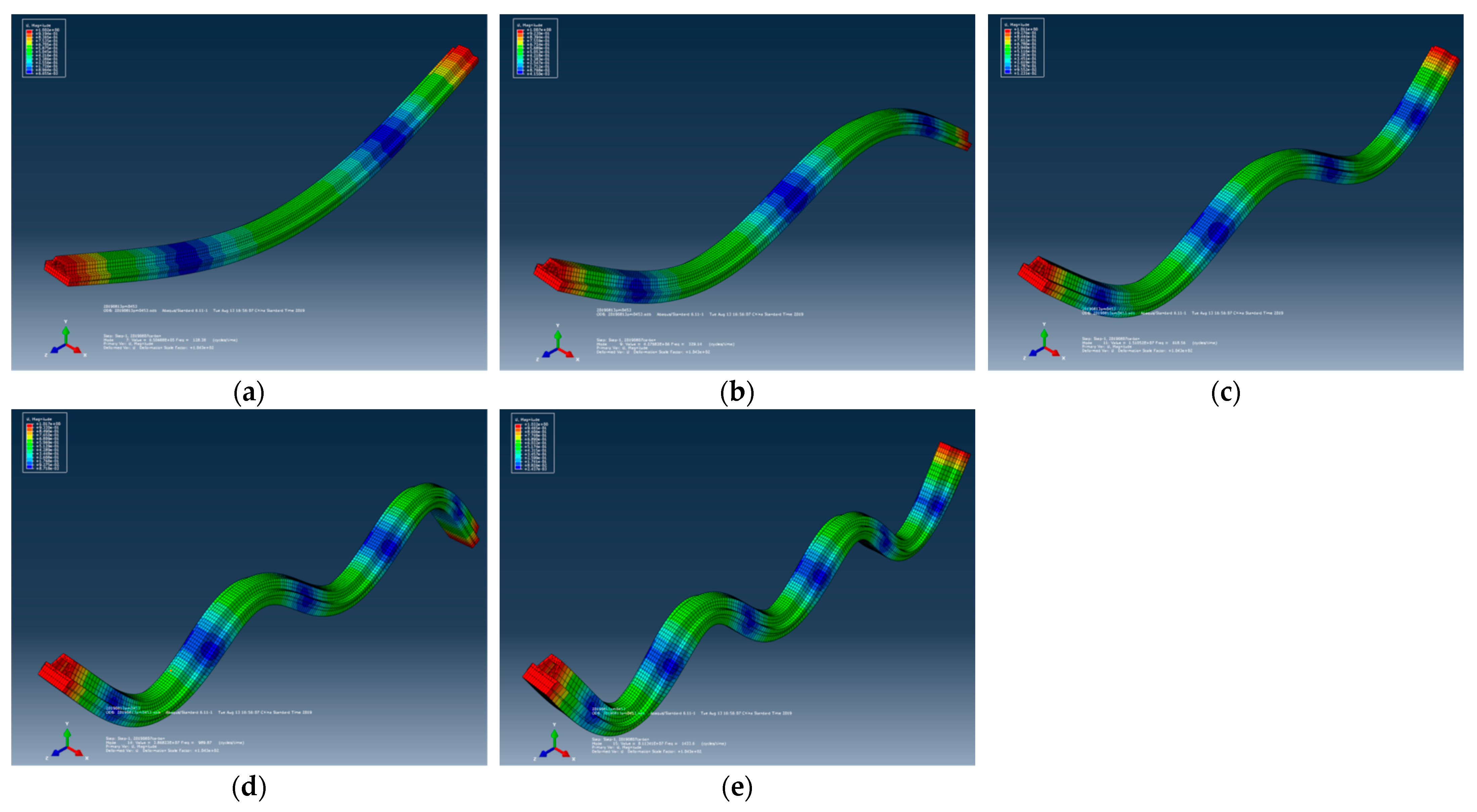
| Vibration Mode | Simulation (Hz) | Laboratory (Hz) | % Error |
|---|---|---|---|
| 1 | 116 | 121 | 4.1% |
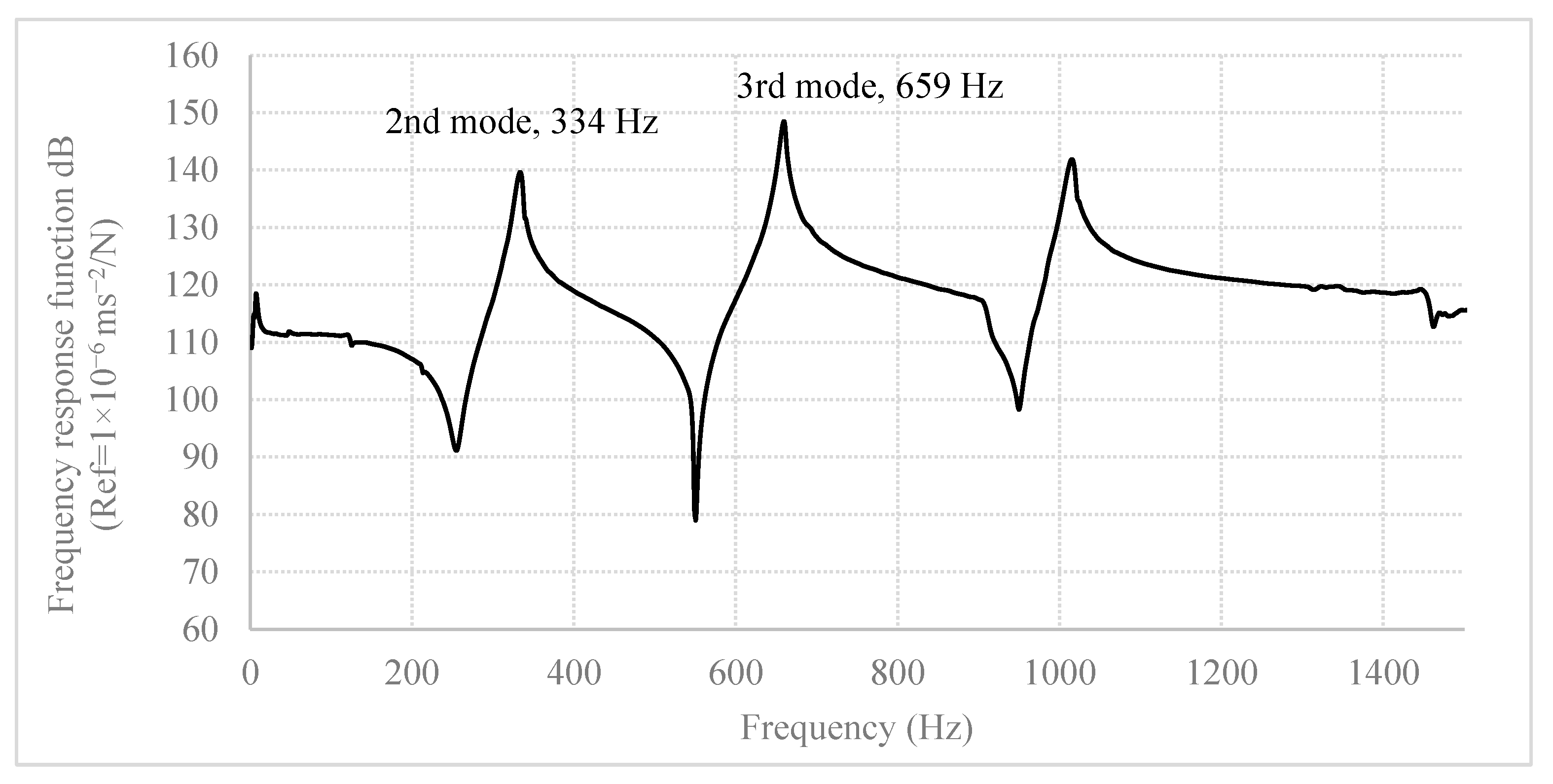
| 2 | 339 | 334 | 1.5% |
| 3 | 653 | 659 | 0.9% |
| 4 | 1005 | 1016 | 1.1% |
| 5 | 1431 | 1450 | 1.3% |
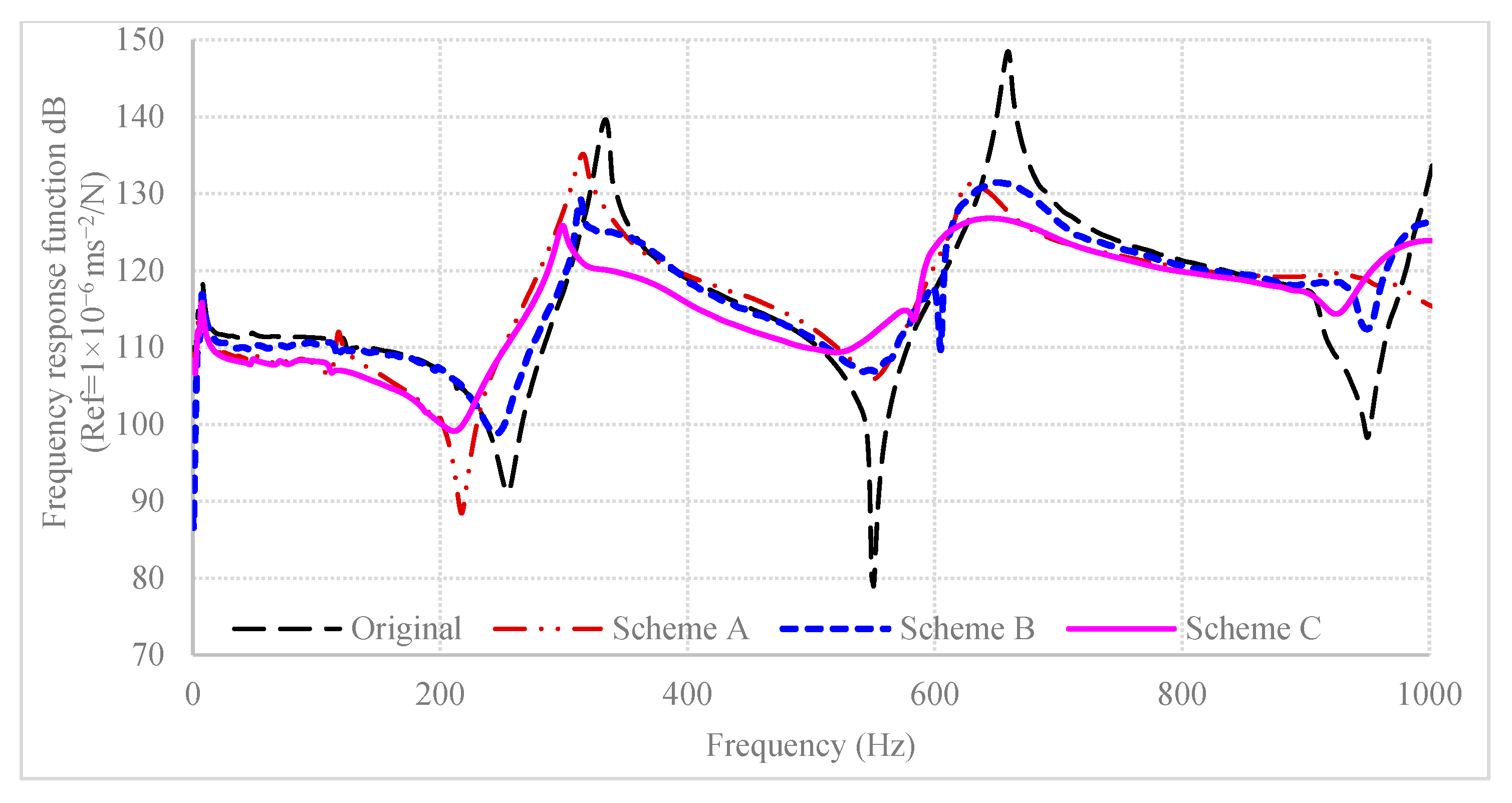
| Vibration Mode | Original | Scheme A | Scheme B | Scheme C | ||||
|---|---|---|---|---|---|---|---|---|
| F (Hz) | ζ | F (Hz) | ζ | F (Hz) | ζ | F (Hz) | ζ | |
| 2nd vertical mode | 334 | 1.05% | 315 | 1.69% | 314 | 0.96% | 299 | 1.99% |
| 3rd vertical mode | 659 | 0.39% | 625 | 2.81% | 651 | 4.86% | 644 | 7.70% |
| Train Speed (km/h) | Accelerometer Position | Reduction in Vibration Acceleration (dB) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Rigid Catenary | Traditional Catenary with Suspension Wires | ||||||||
| Upline | Downline | Upline | Downline | ||||||
| A | B | A | B | A | B | A | B | ||
| 20 | Middle | 6.6 | 2.8 | 2.8 | 2.4 | 5.7 | 2.2 | 1.4 | 3.1 |
| 1/4 position | 3.8 | 2.2 | 5.4 | 1.9 | 1.1 | 2.0 | 2.4 | 1.9 | |
| 48 | Middle | 5.9 | 7.0 | 5.5 | 1.5 | 1.9 | 2.0 | 1.0 | 2.6 |
| 1/4 position | 4.9 | 5.0 | 1.9 | 1.8 | 2.1 | 2.0 | 2.1 | 0.7 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Q.; Gu, X.P.; Ma, Z.; Wang, A. A Study on the Vibration Characteristics and Damage Mechanism of Pantograph Strips in a Railway Electrification System. Machines 2022, 10, 710. https://doi.org/10.3390/machines10080710
Wu Q, Gu XP, Ma Z, Wang A. A Study on the Vibration Characteristics and Damage Mechanism of Pantograph Strips in a Railway Electrification System. Machines. 2022; 10(8):710. https://doi.org/10.3390/machines10080710
Chicago/Turabian StyleWu, Qirui, Xiaohan Phrain Gu, Ziyan Ma, and Anbin Wang. 2022. "A Study on the Vibration Characteristics and Damage Mechanism of Pantograph Strips in a Railway Electrification System" Machines 10, no. 8: 710. https://doi.org/10.3390/machines10080710
APA StyleWu, Q., Gu, X. P., Ma, Z., & Wang, A. (2022). A Study on the Vibration Characteristics and Damage Mechanism of Pantograph Strips in a Railway Electrification System. Machines, 10(8), 710. https://doi.org/10.3390/machines10080710






