Meshing Characteristics of Spur Gears Considering Three-Dimensional Fractal Rough Surface under Elastohydrodynamic Lubrication
Abstract
:1. Introduction
2. Characterization of Gear Surface Topography
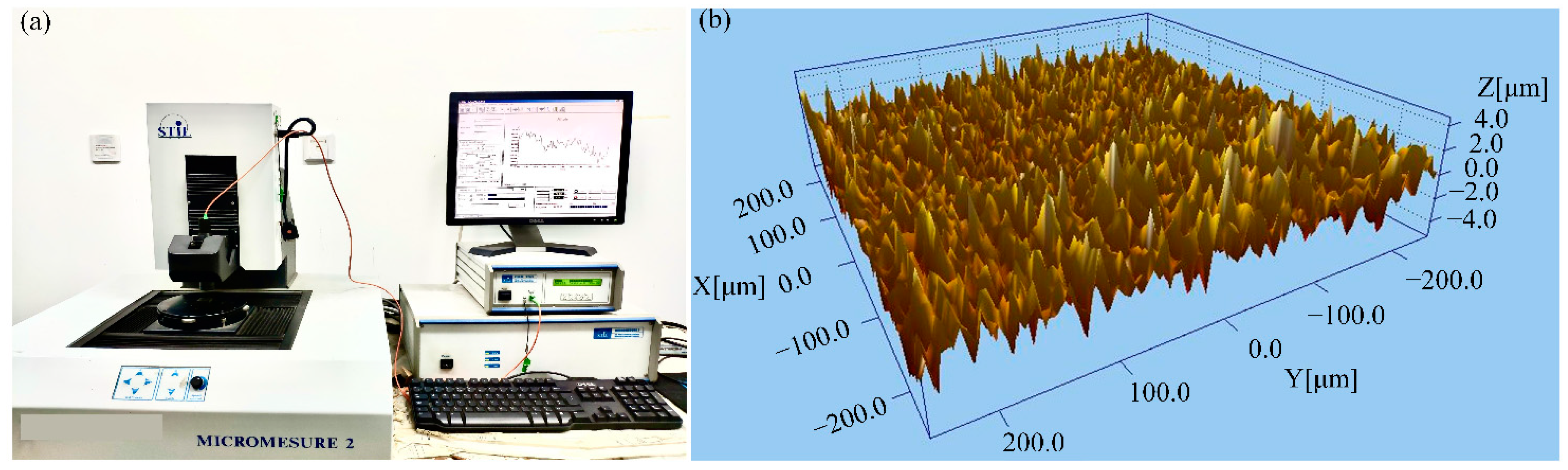
2.1. Measurement of Tooth Surface Topography
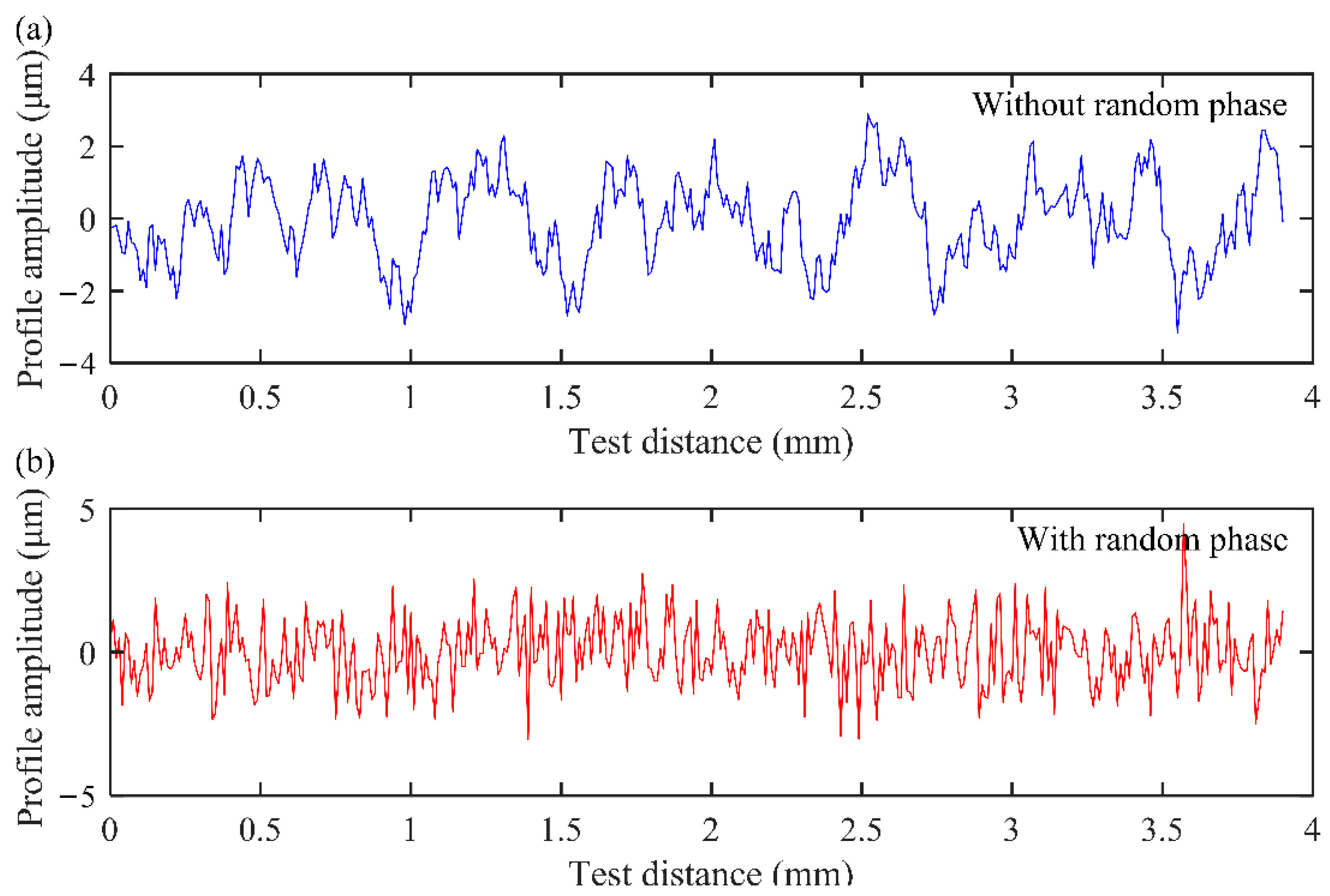
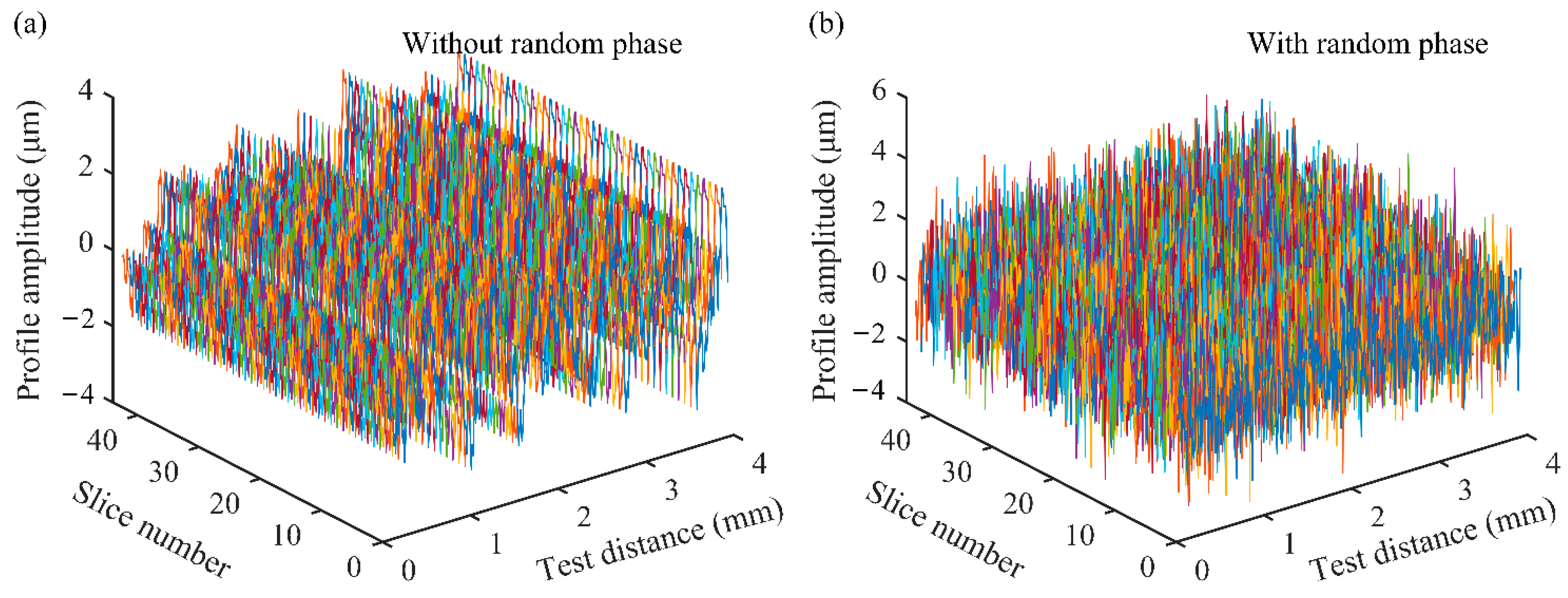
2.2. Tooth Surface Topography Characterization Based on Fractal Function
3. Model of EHL
3.1. Solution of EHL Model with Fractal Roughness
| Algorithm 1 Rough EHL solved by multi_grid |
| Input: Paras—gear conditions, rough topography, grid properties |
| Output: P—film pressure, H—film thickness |
| 1: function RoughEHL (Paras) |
| 2: while ErrW <εW && ErrP <εP do |
| 3: S(k) = 0 (k = 1∼6); k ← 6 |
| 4: while k > 1 do |
| 5: relax v1 to iterate P by Gauss–Seidel or dipole Jacobi |
| 6: S(k) = S(k) + 1 |
| 7: restrict P; k = k − 1 |
| 8: end while |
| 9: relax v0 to iterate P at Level 1 |
| 10: interpolate P; k = k + 1 |
| 11: relax v2 to iterate P |
| 12: if k ≠ 6 then |
| 13: if S(k) == 2 then |
| 14: S(k) ← 0 |
| 15: goto 10 |
| 16: else |
| 17: goto 4 |
| 18: end if |
| 19: else |
| 20: obtain P, H at Level 6 |
| 21: end if |
| 22: calculate ErrW, ErrP |
| 23: end while |
| 24: return P, H |
| 25: end function |
3.2. Calculation of OFS
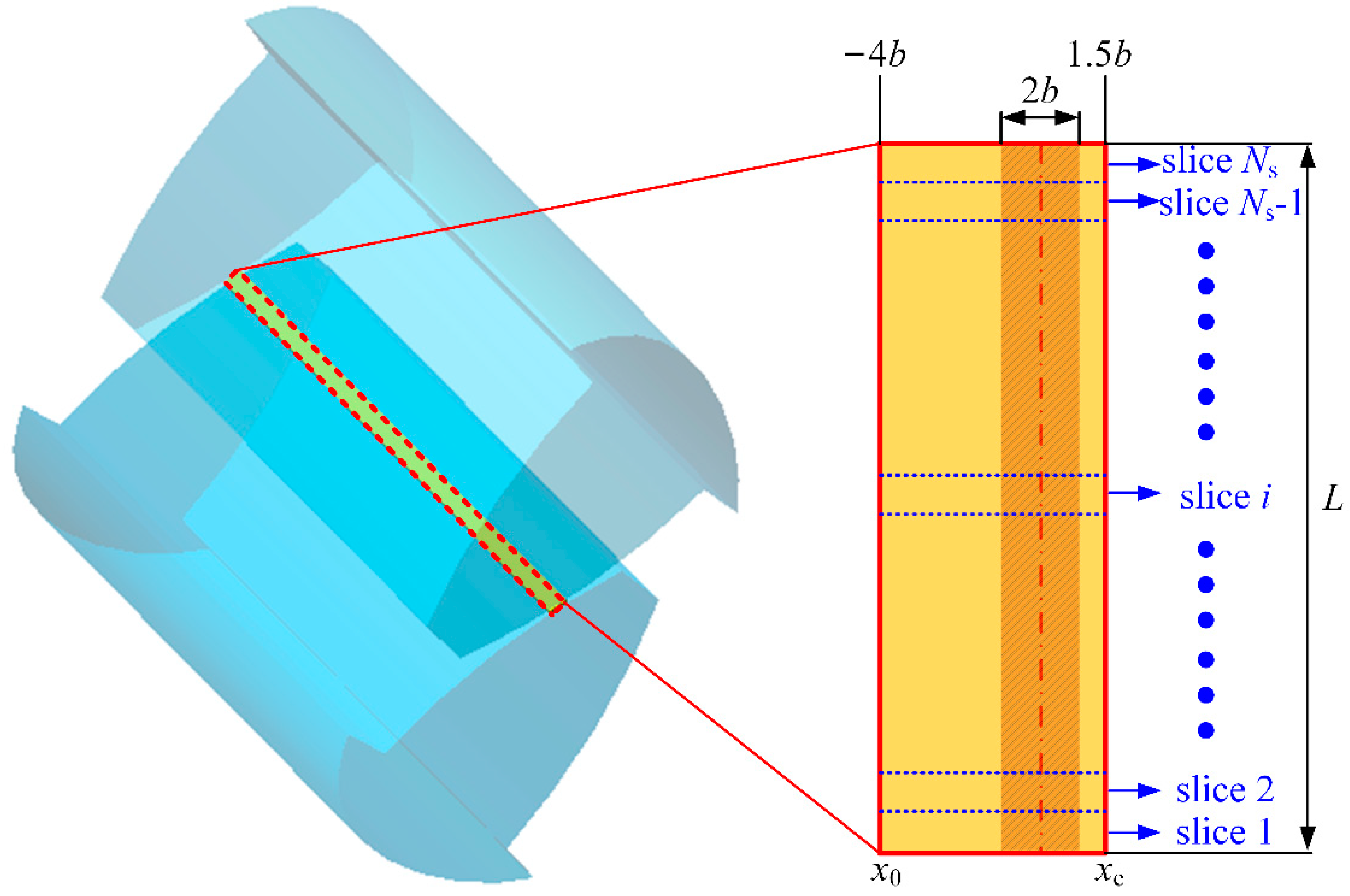
4. Mesh Stiffness Model under Fractal Rough EHL Condition
5. Results and Discussion
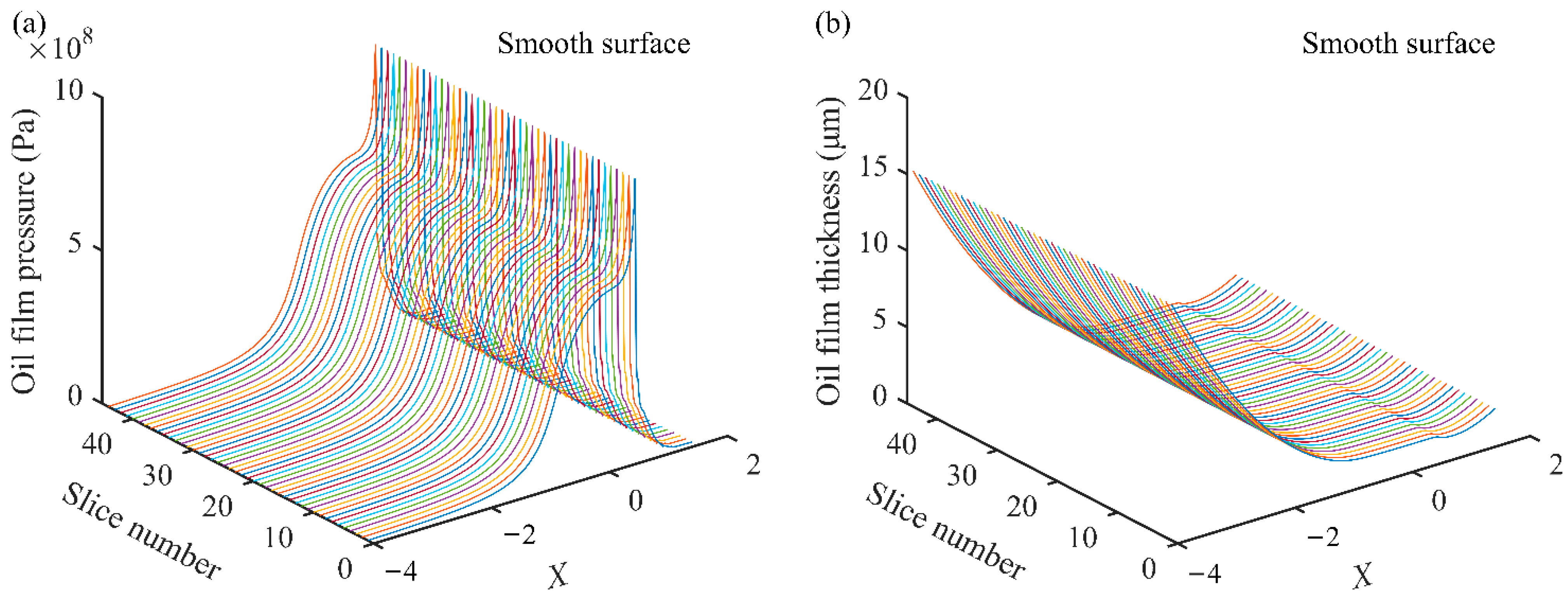
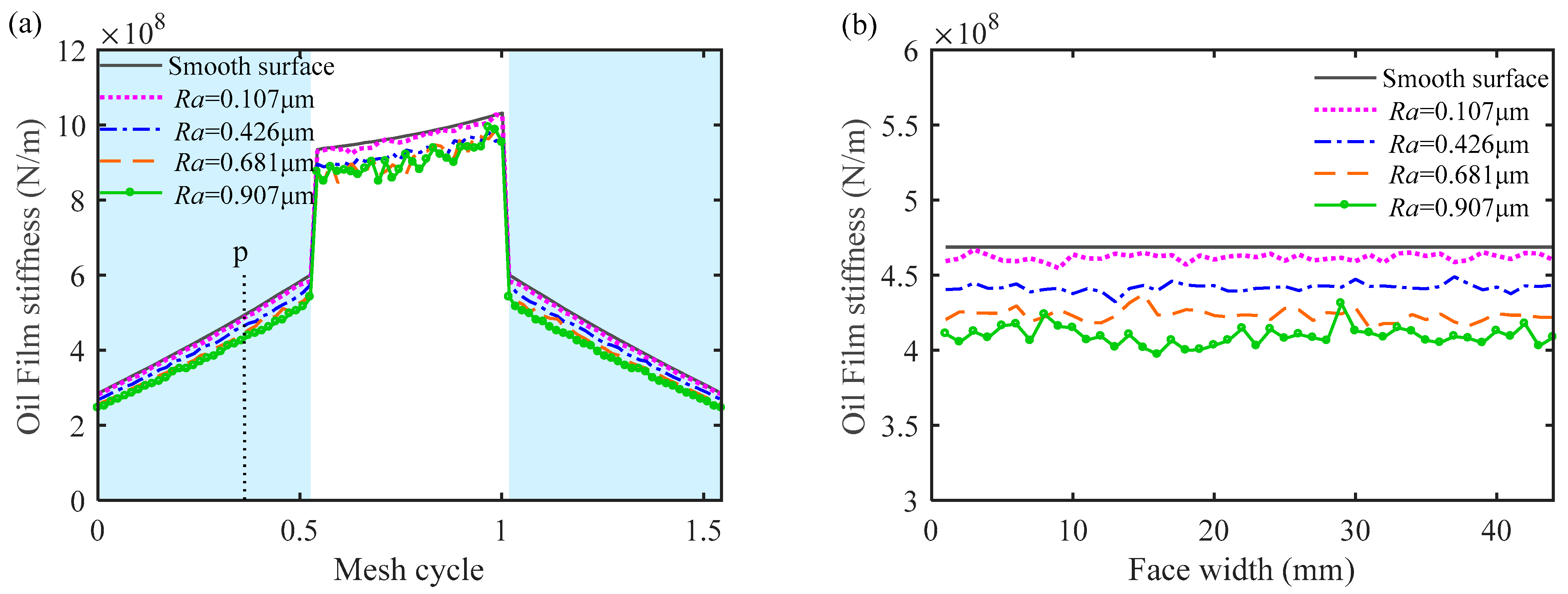
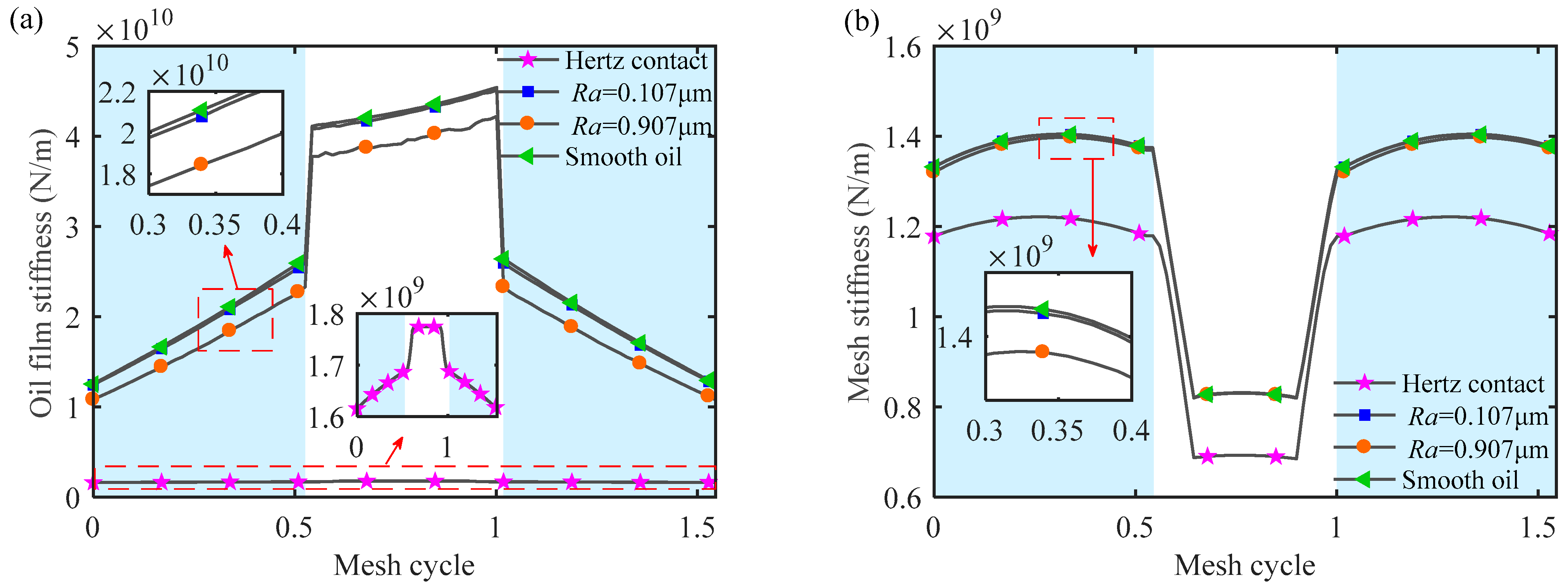
5.1. Mesh Stiffness under Different Contact States
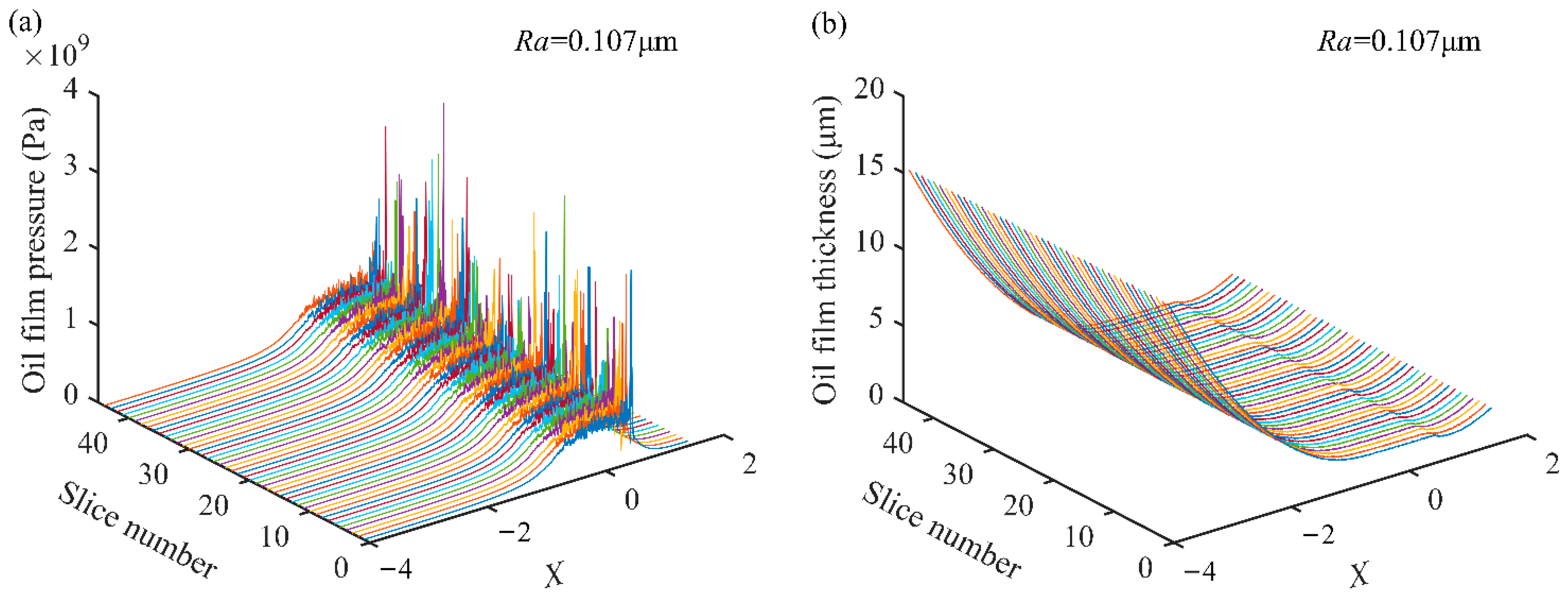
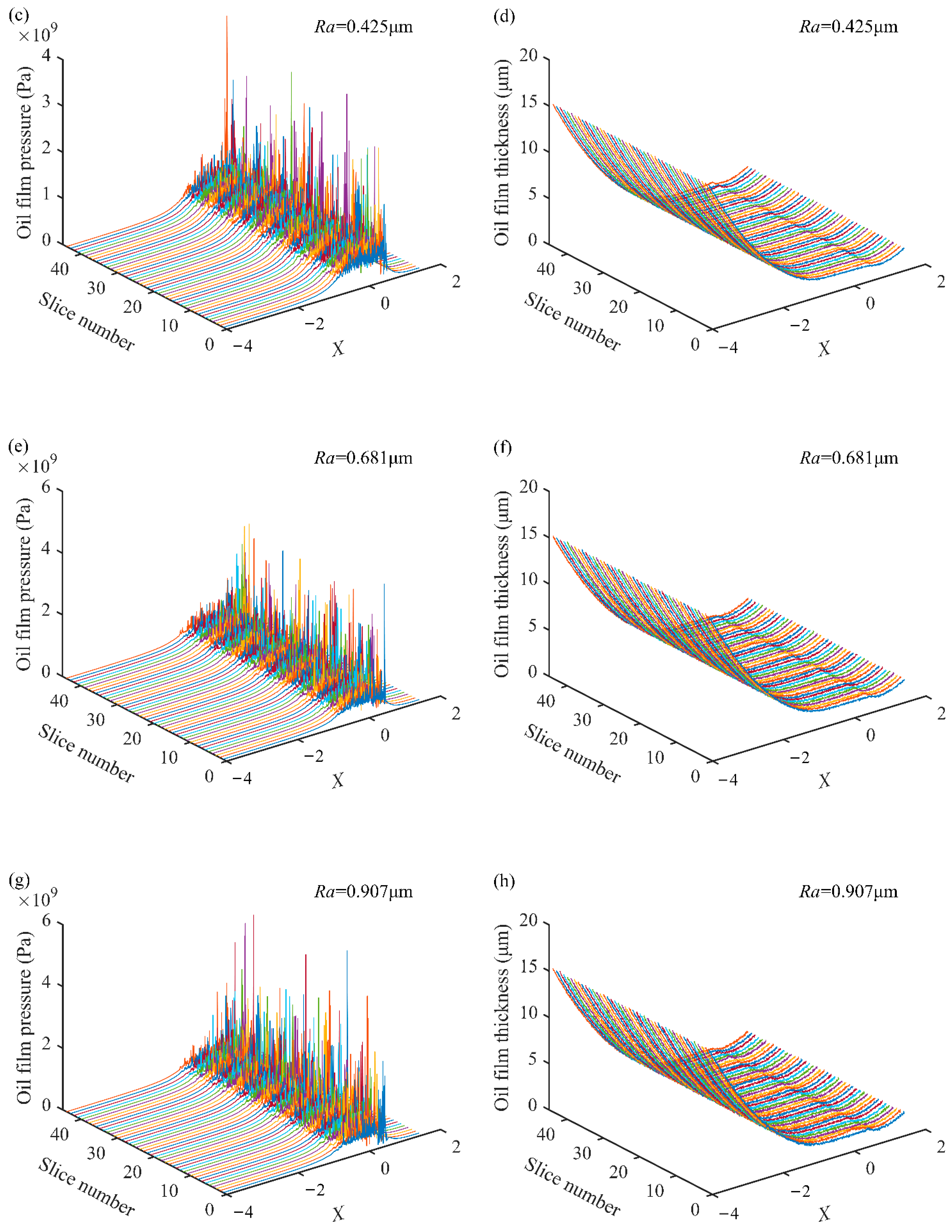
5.2. Mesh Stiffness under Different Roughness Levels
5.3. Mesh Stiffness under Different Rotational Speeds
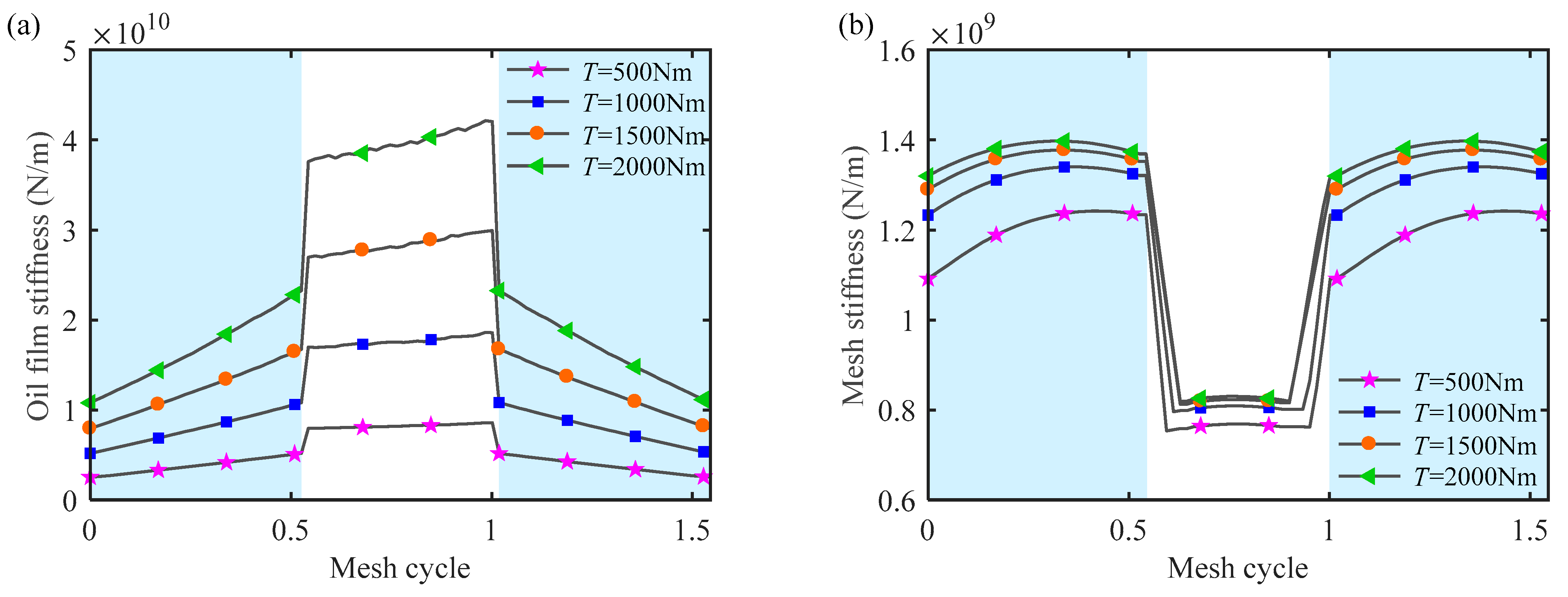
5.4. Mesh Stiffness under Different Torques
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| A | Oil film contact area |
| b | Contact half width of the gear |
| Bl | Bulk modulus of the lubrication |
| c* | Tip clearance coefficient |
| D | Fractal dimension |
| E | Equivalent modulus of elasticity |
| Total tooth profile error of the i-th tooth pair of each slice gear pair along line of action | |
| Epc | Tooth errors of each slice gear caused by lead crowning relief along face width direction |
| Fslice | External load on each slice |
| F | Total meshing force |
| G | Characteristic scale parameter of the profile |
| h | Lubricant film thickness |
| ha* | Addendum coefficient |
| h0 | Initial oil film thickness |
| hl | Oil film thickness |
| Restriction operator transferred from k level to (k−1) level | |
| Interpolation operator transferred from k level to (k- + 1) level | |
| k | Mesh stiffness |
| ka | Axial compression stiffness |
| kb | Bending stiffness |
| kfp, kfg | Foundation stiffness of pinion and gear, respectively |
| kh | Local contact stiffness |
| kl | Stiffness of the contact area of the oil film |
| kln | Oil film stiffness of the n-th slice |
| Kl | The sum of the oil film stiffness of all slices |
| kn | Mesh stiffness of each slice of gear pair |
| ks | Shear stiffness |
| ktooth | Stiffness of gear tooth |
| Tooth stiffness of the i-th tooth pair | |
| ktp, ktg | Structure stiffness of tooth of pinion and gear, respectively |
| L | Face width |
| m | Module of gear |
| n | Frequency index of the asperity |
| N | Rotational speed |
| nmax | The maximum frequency index |
| nmin | The minimum frequency index |
| Ns | Number of slices |
| p | Lubricant film pressure |
| p0 | Pressure coefficient |
| q | Number of tooth pairs involved in meshing at the same time |
| R | Equivalent radius of curvature |
| Ra | Surface roughness |
| rint | Hub radius of gear |
| T | Transmitted torque |
| u1, u2 | Rolling speed at the meshing point of the pinion and gear, respectively |
| us | Entrainment velocity |
| v(x,t) | Elastic deformation |
| v0, v1, v2 and v3 | Number of iterations in W cycle iterative process |
| wm(x,t) | Amplitude of the contour of the two-dimensional rough surface |
| x | Horizontal measuring length |
| x0 | Oil film inlet coordinate |
| xe | Oil film outlet coordinate |
| Z | Number of teeth of gear |
| z | Viscosity–pressure index |
| zn | Axial coordinate of a sliced spur gear |
| Greek symbols | |
| α | Pressure angle of pitch circle |
| γ | Sampling frequency |
| η | Lubricant viscosity |
| η0 | Initial lubricant viscosity under ambient pressure |
| λp, λg | Coefficients of the fillet-foundation stiffness of the pinion and gear, respectively |
| ν | Poisson’s ratio |
| ρ | Lubricant density |
| ρ0 | Initial lubricant density under ambient pressure |
| φn | Random phase |
| Abbreviations | |
| DTC | Double-tooth contact |
| EHL | Elastohydrodynamic lubrication |
| OFP | Oil film pressure |
| OFS | Oil film stiffness |
| OFT | Oil film thickness |
| STC | Single-tooth contact |
| TVMS | Time-varying mesh stiffness |
| 2D | Two-dimensional |
| 3D | Three-dimensional |
References
- Zhou, W.; Tang, J.; Shao, W. Study on surface generation mechanism and roughness distribution in gear profile grinding. Int. J. Mech. Sci. 2020, 187, 105921. [Google Scholar] [CrossRef]
- Chen, K.; Huangfu, Y.; Ma, H.; Xu, Z.; Li, X.; Wen, B. Calculation of mesh stiffness of spur gears considering complex foundation types and crack propagation paths. Mech. Syst. Signal Process. 2019, 130, 273–292. [Google Scholar] [CrossRef]
- Huangfu, Y.; Chen, K.; Ma, H.; Li, X.; Han, H.; Zhao, Z. Meshing and dynamic characteristics analysis of spalled gear systems: A theoretical and experimental study. Mech. Syst. Signal Process. 2020, 139, 106640. [Google Scholar] [CrossRef]
- Huangfu, Y.; Chen, K.; Ma, H.; Li, X.; Han, H.; Zhao, Z. An improved model for meshing characteristics analysis of spur gears considering fractal surface contact and friction. Mech. Mach. Theory 2021, 158, 104219. [Google Scholar]
- Wang, Q.; Xu, K.; Huai, T.; Ma, H.; Wang, K. A mesh stiffness method using slice coupling for spur gear pairs with misalignment and lead crown relief. Appl. Math. Model. 2021, 90, 845–861. [Google Scholar] [CrossRef]
- Hou, S.; Wei, J.; Zhang, A.; Zhang, C.; Yan, J.; Wang, C. A novel comprehensive method for modeling and analysis of mesh stiffness of helical gear. Appl. Sci. 2020, 10, 6695–6714. [Google Scholar] [CrossRef]
- Chen, Z.; Zhou, Z.; Zhai, W.; Wang, K. Improved analytical calculation model of spur gear mesh excitation with tooth profile deviations. Mech. Mach. Theory 2020, 149, 103838. [Google Scholar] [CrossRef]
- Jiang, L.; Deng, Z.; Gu, F.; Ball, A.D.; Li, X. Effect of friction coefficients on the dynamic response of gear systems. Front. Mech. Eng. 2017, 12, 397–405. [Google Scholar] [CrossRef]
- Gropper, D.; Wang, L.; Harvey, T.J. Hydrodynamic lubrication of textured surfaces: A review of modeling techniques and key findings. Tribol. Int. 2016, 94, 509–529. [Google Scholar] [CrossRef]
- Liu, H.; Liu, H.; Zhu, C.; Parker, R.G. Effects of lubrication on gear performance: A review. Mech. Mach. Theory 2020, 145, 103701. [Google Scholar] [CrossRef]
- Chen, S.; Yin, N.; Cai, X.; Zhang, Z. Iteration framework for solving mixed lubrication computation problems. Front. Mech. Eng. 2021, 16, 635–648. [Google Scholar] [CrossRef]
- Hu, Y.Z.; Zhu, D. A full numerical solution to the mixed lubrication in point contacts. J. Tribol. 2000, 122, 1–9. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Q.J.; Wang, W.; Hu, Y.; Zhu, D. Effects of differential scheme and mesh density on EHL film thickness in point contacts. J. Tribol. 2006, 128, 641–653. [Google Scholar] [CrossRef]
- Zhu, D. On some aspects of numerical solutions of thin-film and mixed elastohydrodynamic lubrication. Part J J. Eng. Tribol. 2007, 221, 561–579. [Google Scholar] [CrossRef]
- Akbarzadeh, S.; Khonsari, M.M. Prediction of steady state adhesive wear in spur gears using the EHL load sharing concept. ASME. J. Tribol. 2009, 131, 024503. [Google Scholar] [CrossRef]
- Li, S.; Kahraman, A. A transient mixed elastohydrodynamic lubrication model for spur gear pairs. ASME. J. Tribol. 2010, 132, 011501. [Google Scholar] [CrossRef]
- Li, S.; Kahraman, A. Prediction of spur gear mechanical power losses using a transient elastohydrodynamic lubrication model. Tribol. Trans. 2010, 53, 554–563. [Google Scholar] [CrossRef]
- Elisaus, V.; Mohammadpour, M.; Theodossiades, S.; Rahnejat, H. Effect of teeth micro-geometrical form modification on contact kinematics and efficiency of high performance transmissions. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2017, 231, 538–555. [Google Scholar] [CrossRef]
- Sivayogan, G.; Rahmani, R.; Rahnejat, H. Lubricated loaded tooth contact analysis and non-Newtonian thermoelastohydrodynamics of high-performance spur gear transmission systems. Lubricants 2020, 8, 20. [Google Scholar] [CrossRef]
- Ren, N.; Zhu, D.; Chen, W.W.; Liu, Y.; Wang, Q.J. A three-dimensional deterministic model for rough surface line-contact EHL problems. J. Tribol. 2009, 131, 011501. [Google Scholar] [CrossRef]
- Shi, X.; Sun, W.; Lu, X.; Ma, X.; Zhu, D.; Zhao, B.; He, T. Three-dimensional mixed lubrication analysis of spur gears with machined roughness. Tribol. Int. 2019, 140, 105864. [Google Scholar] [CrossRef]
- Shi, X.J.; Lu, X.Q.; He, T.; Sun, W.; Tong, Q.S.; Ma, X.; Zhao, B.; Zhu, D. Predictions of friction and flash temperature in marine gears based on a 3D line contact mixed lubrication model considering measured surface roughness. J. Cent. South Univ. 2021, 28, 1570–1583. [Google Scholar] [CrossRef]
- Liu, H.; Mao, K.; Zhu, C.; Xu, X. Mixed lubricated line contact analysis for spur gears using a deterministic model. J. Tribol. 2012, 134, 021501. [Google Scholar] [CrossRef]
- Liu, H.; Zhu, C.; Sun, Z.; Song, C. Starved lubrication of a spur gear pair. Tribol. Int. 2016, 94, 52–60. [Google Scholar] [CrossRef]
- Liu, H.; Liu, H.; Zhu, C.; Wei, P.; Tang, J. Tribological behavior of coated spur gear pairs with tooth surface roughness. Friction 2019, 7, 117–128. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhu, C.; Liu, H. A micropitting study considering rough sliding and mild wear. Coatings 2019, 9, 639–644. [Google Scholar] [CrossRef]
- Liu, H.; Liu, H.; Zhu, C.; Sun, Z.; Bai, H. Study on contact fatigue of a wind turbine gear pair considering surface roughness. Friction 2020, 8, 553–567. [Google Scholar] [CrossRef]
- Jian, G.X.; Wang, Y.Q.; Zhang, P.; Li, Y.K.; Luo, H. Thermal elastohydrodynamic lubrication of modified gear system considering vibration. J. Cent. South Univ. 2020, 27, 3350–3363. [Google Scholar] [CrossRef]
- Yin, L.; Deng, C.L.; Yu, W.N.; Shao, Y.M.; Wang, L.M. Dynamic characteristics of gear system under different micro-topographies with the same roughness on tooth surface. J. Cent. South Univ. 2020, 27, 2311–2323. [Google Scholar] [CrossRef]
- Xiao, H.; Sun, Y.; Xu, J. Investigation into the normal contact stiffness of rough surface in line contact mixed elastohydrodynamic lubrication. Tribol. Trans. 2018, 61, 742–753. [Google Scholar] [CrossRef]
- Sun, Y.; Xiao, H.; Xu, J.; Yu, W. Study on the normal contact stiffness of the fractal rough surface in mixed lubrication. Part J: J. Eng. Tribol. 2018, 232, 1604–1617. [Google Scholar] [CrossRef]
- Zhou, C.; Xiao, Z.; Chen, S.; Han, X. Normal and tangential oil film stiffness of modified spur gear with non-Newtonian elastohydrodynamic lubrication. Tribol. Int. 2017, 109, 19–327. [Google Scholar] [CrossRef]
- Cheng, G.; Xiao, K.; Wang, J.; Pu, W.; Han, Y. Gear contact stiffness under mixed lubrication status. J. Jilin Univ. Eng. Technol. Ed. 2020, 50, 494–503. [Google Scholar]
- Cheng, G.; Xiao, K.; Wang, J.; Pu, W.; Han, Y. Calculation of gear meshing stiffness considering lubrication. J. Tribol. 2020, 142, 031602. [Google Scholar] [CrossRef]
- Wang, S.; Zhu, R. An improved mesh stiffness model of helical gear pair considering axial mesh force and friction force influenced by surface roughness under EHL condition. Appl. Math. Model. 2022, 102, 453–471. [Google Scholar] [CrossRef]
- Wang, X.; Xiang, C.; Li, C.; Li, S.; Shao, Y.; Wang, L. Effect of roughness on meshing power loss of planetary gear set considering elasto-hydrodynamic lubrication. Adv. Mech. Eng. 2020, 12, 1687814020908422. [Google Scholar] [CrossRef]
- Huang, K.; Xiong, Y.; Wang, T.; Chen, Q. Research on the dynamic response of high- contact-ratio spur gears influenced by surface roughness under EHL condition. Appl. Surf. Sci. 2017, 392, 8–18. [Google Scholar] [CrossRef]
- Wei, J.; Zhang, A.; Gao, P. A study of spur gear pitting under EHL conditions: Theoretical analysis and experiments. Tribol. Int. 2016, 94, 146–154. [Google Scholar] [CrossRef]
- Huangfu, Y.; Dong, X.; Chen, K.; Tu, G.; Long, X.; Peng, Z. A tribo-dynamic based pitting evolution model of planetary gear sets: A topographical updating approach. Int. J. Mech. Sci. 2022, 220, 107157. [Google Scholar] [CrossRef]
- Wang, L.; Deng, C.; Xu, J.; Yin, L.; Yu, W.; Ding, X.; Shao, Y.; Huang, W.; Yang, X. Effects of spalling fault on dynamic responses of gear system considering three-dimensional line contact elasto-hydrodynamic lubrication. Eng. Fail. Anal. 2022, 132, 105930. [Google Scholar] [CrossRef]
- Liu, S.; Wang, Q.; Liu, G. A versatile method of discrete convolution and FFT (DC-FFT) for contact analyses. Wear 2000, 243, 101–111. [Google Scholar] [CrossRef]
- Venner, C.H.; ten Napel, W.T.; Bosma, R. Advanced multilevel solution of the EHL line contact problem. J. Tribol. 1990, 112, 426–431. [Google Scholar] [CrossRef]
- Dwyer-Joyce, R.S.; Reddyhoff, T.; Zhu, J. Ultrasonic measurement for film thickness and solid contact in elastohydrodynamic lubrication. J. Tribol. 2011, 133, 031501. [Google Scholar] [CrossRef]
- Ma, H.; Zeng, J.; Feng, R.; Pang, X.; Wen, B. An improved analytical method for mesh stiffness calculation of spur gears with tip relief. Mech. Mach. Theory 2016, 98, 64–80. [Google Scholar] [CrossRef]
- Sainsot, P.; Velex, P.; Duverger, O. Contribution of gear body to tooth deflections–a new bidimensional analytical formula. J. Mech. Des. 2004, 126, 748–752. [Google Scholar] [CrossRef]
- Sun, Y.; Ma, H.; Huangfu, Y.; Chen, K.; Che, L.; Wen, B. A revised time-varying mesh stiffness model of spur gear pairs with tooth modifications. Mech. Mach. Theory 2018, 129, 261–278. [Google Scholar] [CrossRef]


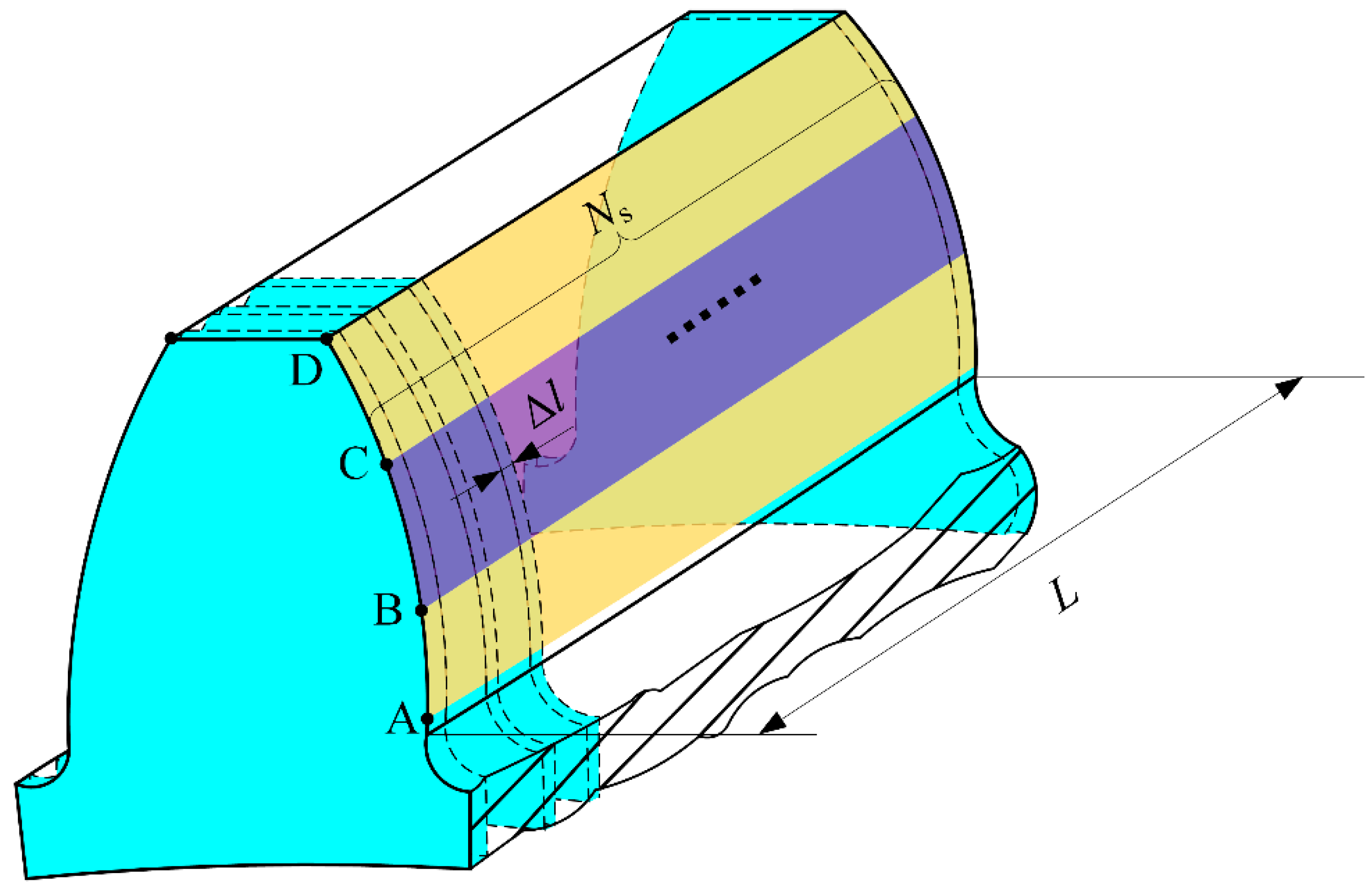



| Parameters | Pinion/Gear | Parameters | Pinion/Gear |
|---|---|---|---|
| Tooth number Z | 45/34 | Addendum modification coefficient | 0.37/0.34 |
| Module m (mm) | 6 | Addendum coefficient ha* | 1 |
| Face width L (mm) | 44 | Tip clearance coefficient c* | 0.25 |
| Hub radius rint (mm) | 81.5/80 | Elastic modulus E (GPa) | 207 |
| Pressure angle α (°) | 20 | Poisson’s ratio ν | 0.29 |
| Torque T (N·m) | 2000 | Rotational speed N (r/min) | 2000 |
| Roughness Level | Ra/μm | D | G |
|---|---|---|---|
| 1 | 0.107 | 1.692 | 1.669 × 10−6 |
| 2 | 0.425 | 1.596 | 3.528 × 10−6 |
| 3 | 0.681 | 1565 | 4.513 × 10−6 |
| 4 | 0.907 | 1.546 | 5.229 × 10−6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Z.; Yang, Y.; Han, H.; Ma, H.; Wang, H.; Li, Z. Meshing Characteristics of Spur Gears Considering Three-Dimensional Fractal Rough Surface under Elastohydrodynamic Lubrication. Machines 2022, 10, 705. https://doi.org/10.3390/machines10080705
Zhao Z, Yang Y, Han H, Ma H, Wang H, Li Z. Meshing Characteristics of Spur Gears Considering Three-Dimensional Fractal Rough Surface under Elastohydrodynamic Lubrication. Machines. 2022; 10(8):705. https://doi.org/10.3390/machines10080705
Chicago/Turabian StyleZhao, Zhifang, Yang Yang, Hongzheng Han, Hui Ma, Haixu Wang, and Zhanwei Li. 2022. "Meshing Characteristics of Spur Gears Considering Three-Dimensional Fractal Rough Surface under Elastohydrodynamic Lubrication" Machines 10, no. 8: 705. https://doi.org/10.3390/machines10080705
APA StyleZhao, Z., Yang, Y., Han, H., Ma, H., Wang, H., & Li, Z. (2022). Meshing Characteristics of Spur Gears Considering Three-Dimensional Fractal Rough Surface under Elastohydrodynamic Lubrication. Machines, 10(8), 705. https://doi.org/10.3390/machines10080705






