Multi-Physics Comparison of Surface-Mounted and Interior Permanent Magnet Synchronous Motor for High-Speed Applications
Abstract
:1. Introduction
2. Motor Structure and Parameters
- Stress-field constraints: The maximum yield strength of PM is 75 MPa. The sleeve strength yield limit is 1960 MPa. The yield strength of the rotor core is 480 MPa.
- Electromagnetic field constraints: The output power in the rated load is 60 kW. In the design, a commercial frequency converter is used, which can output a peak voltage of 600 V. Considering the voltage margin of the converter, the amplitude of the back-EMF under no load is limited between 500 V and 540 V. The amplitude of air-gap magnetic flux density is between 0.4 T and 0.6 T. The thermal load is required to be .
- Thermal field constraints: The limited working temperature of PM materials is 150 °C. The maximum temperature of the rotor is 150 °C. The maximum winding temperature is 130 °C.
3. Rotor Stress Analysis
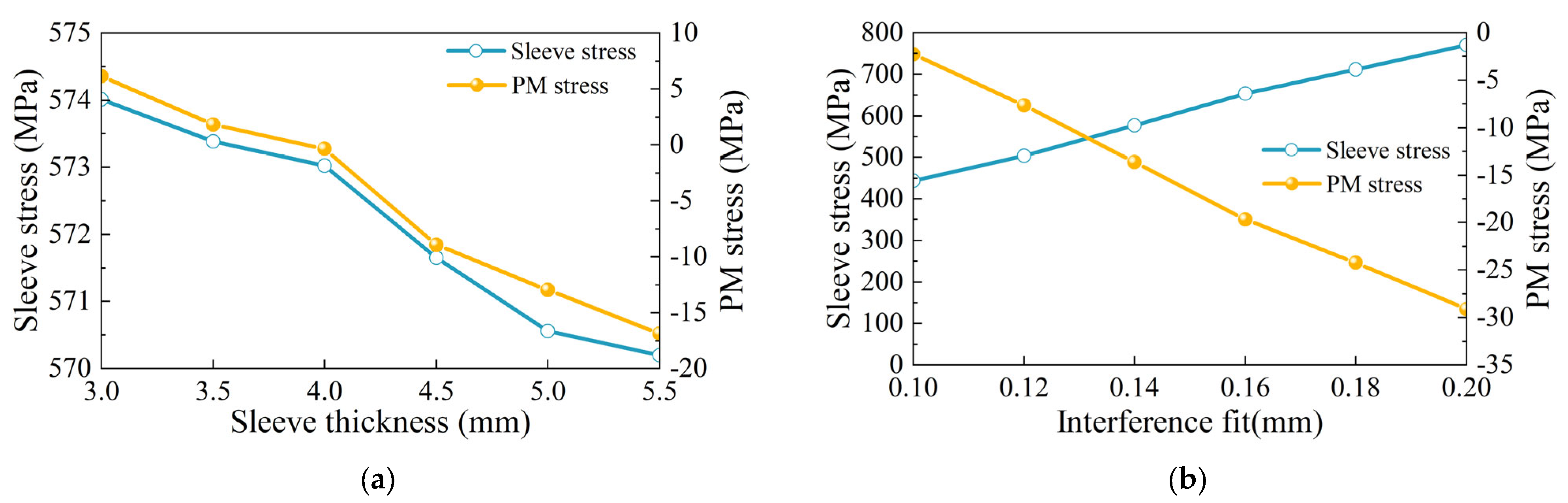
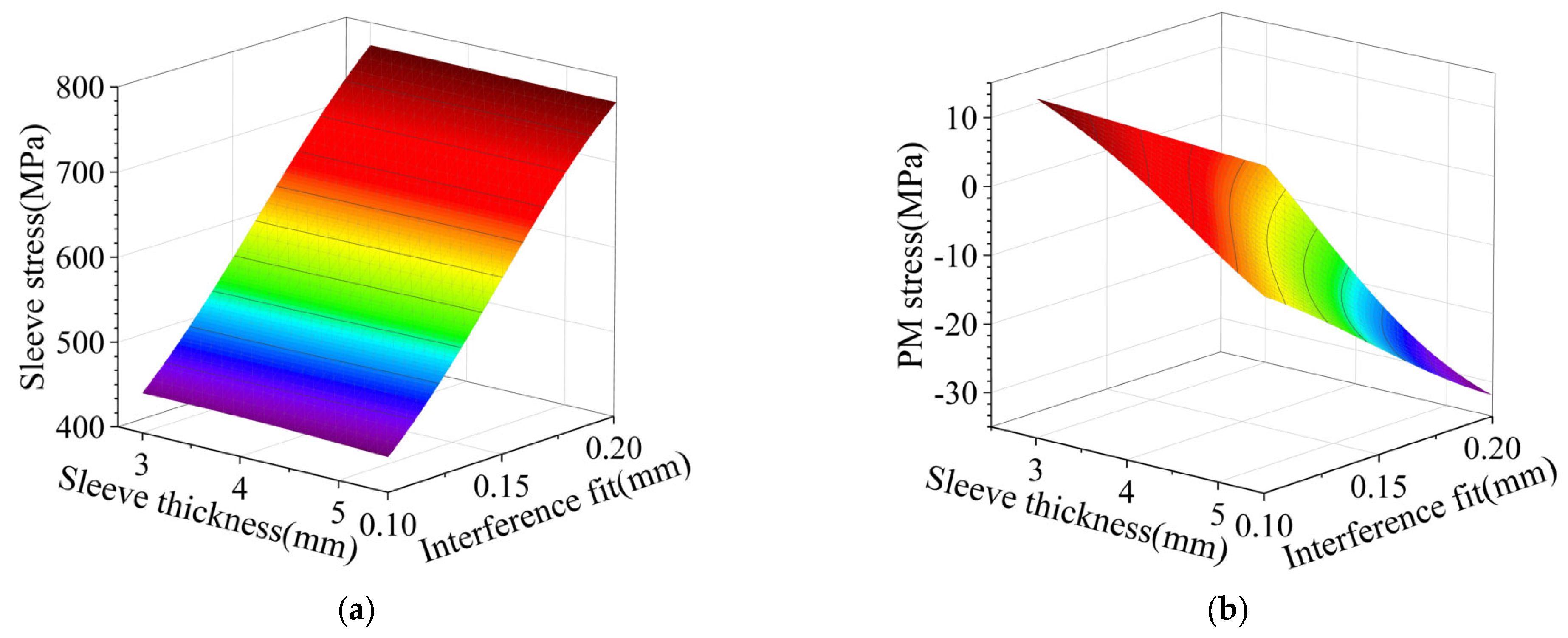
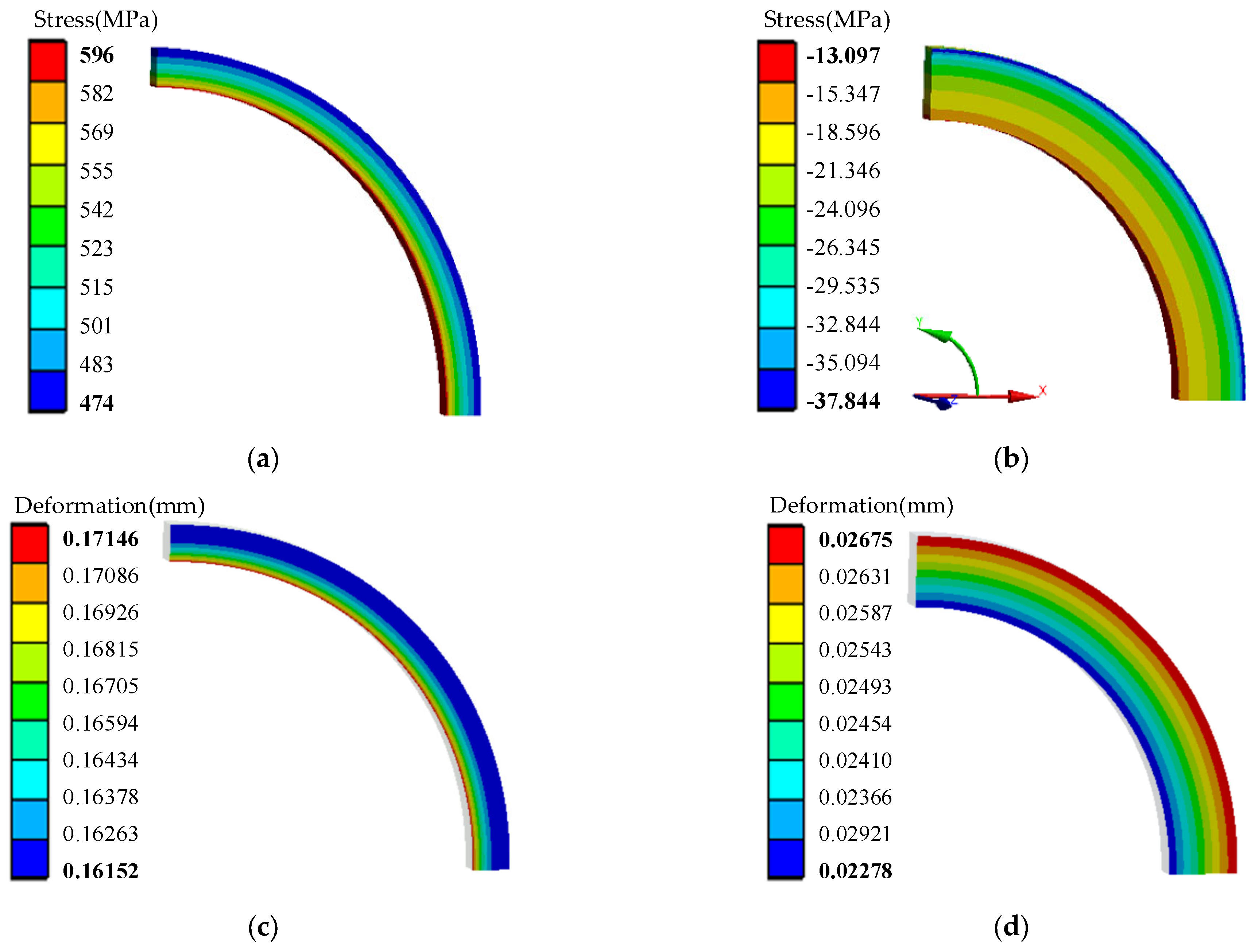
3.1. Stress Analysis of SPM Rotor
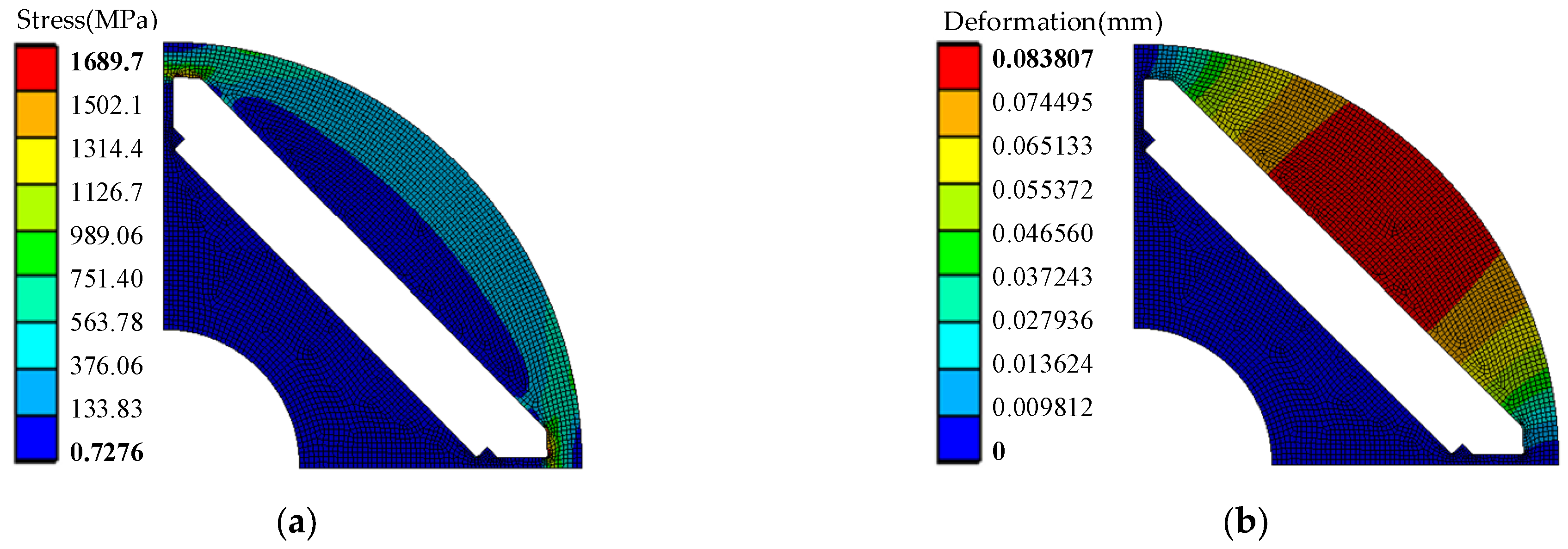
3.2. Stress Analysis of IPM Rotor
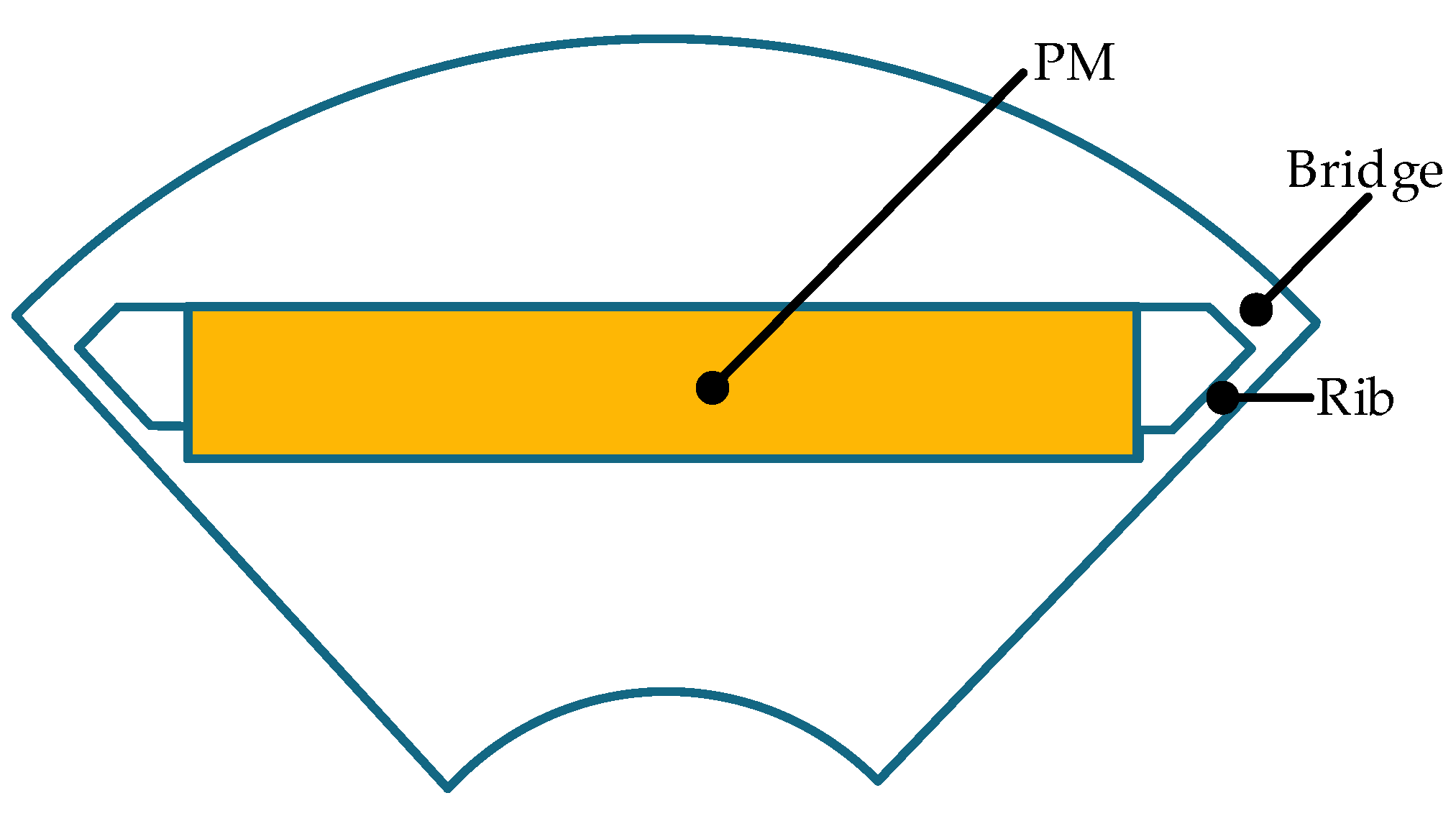
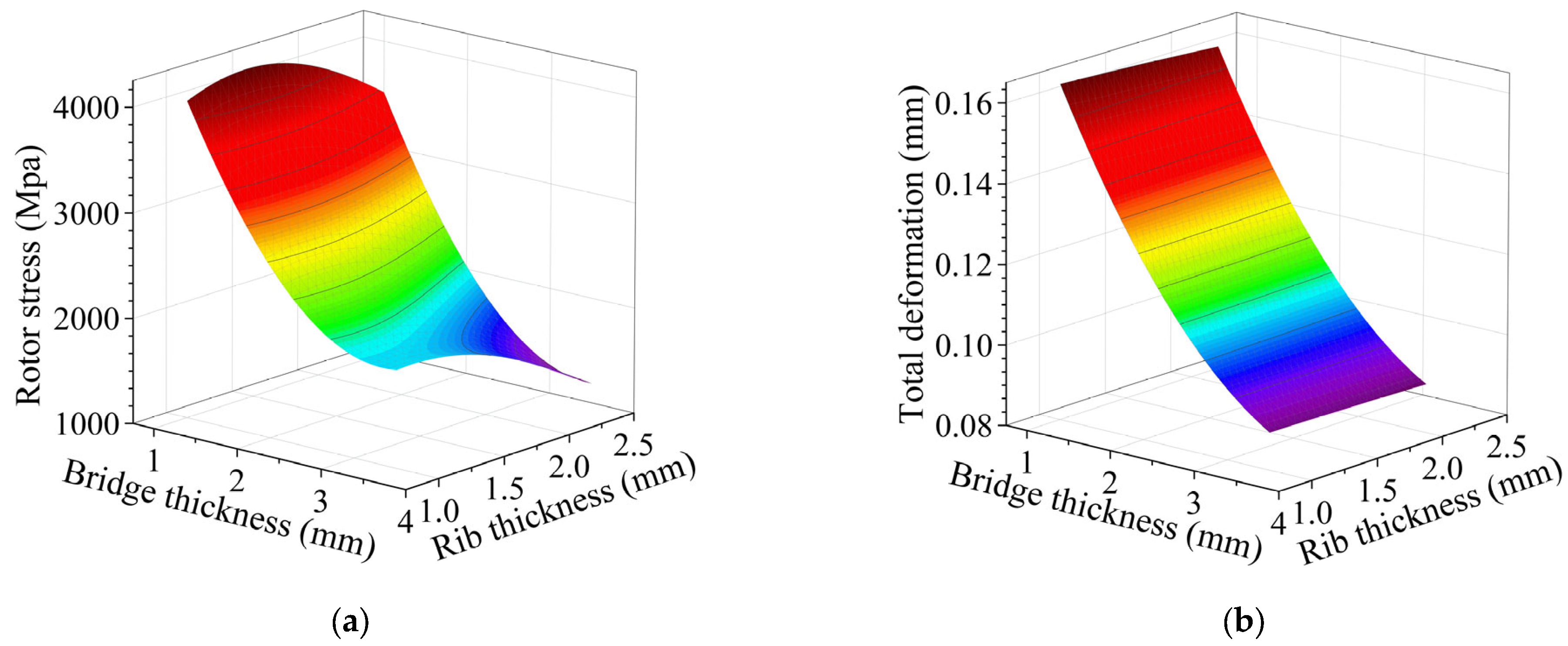
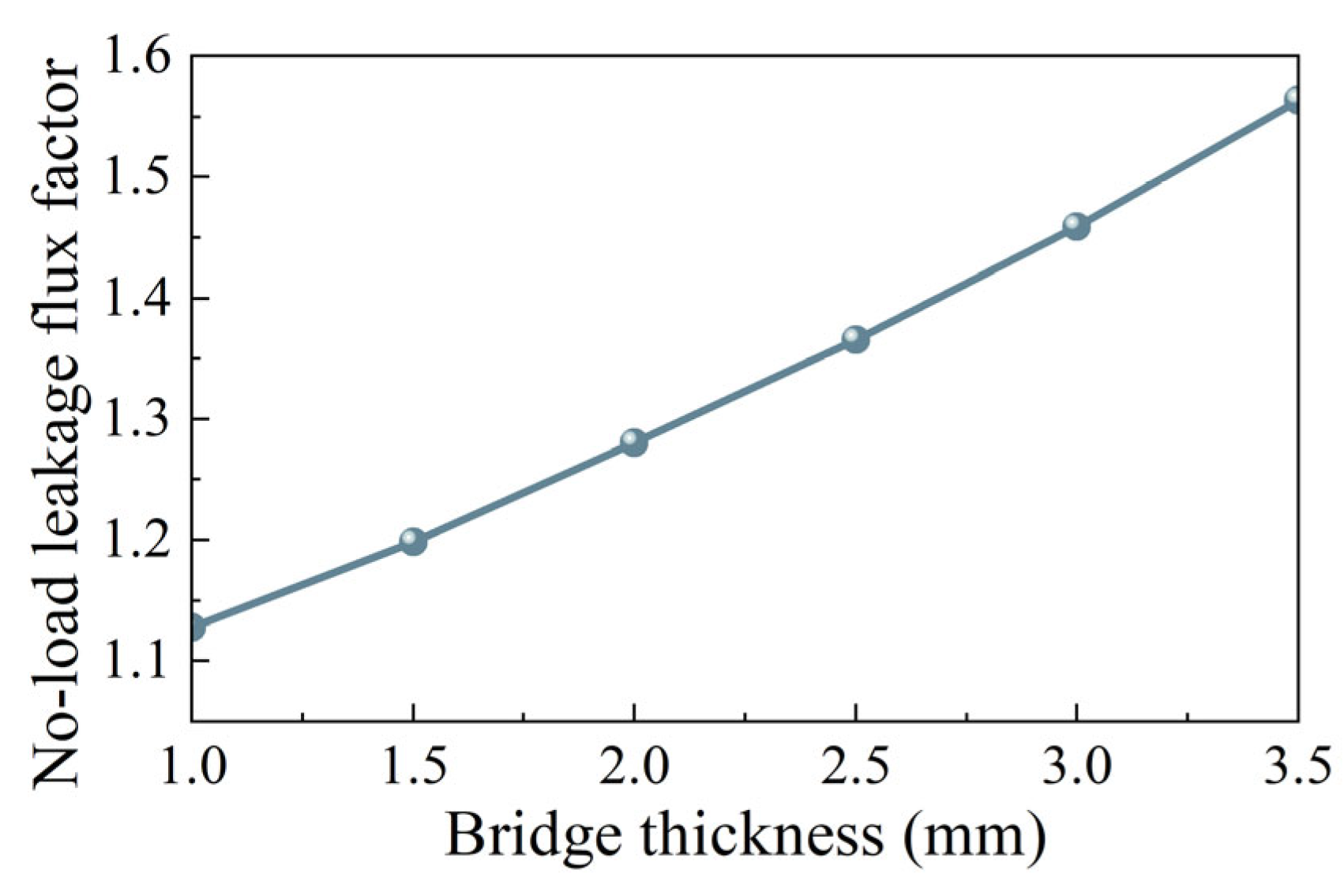
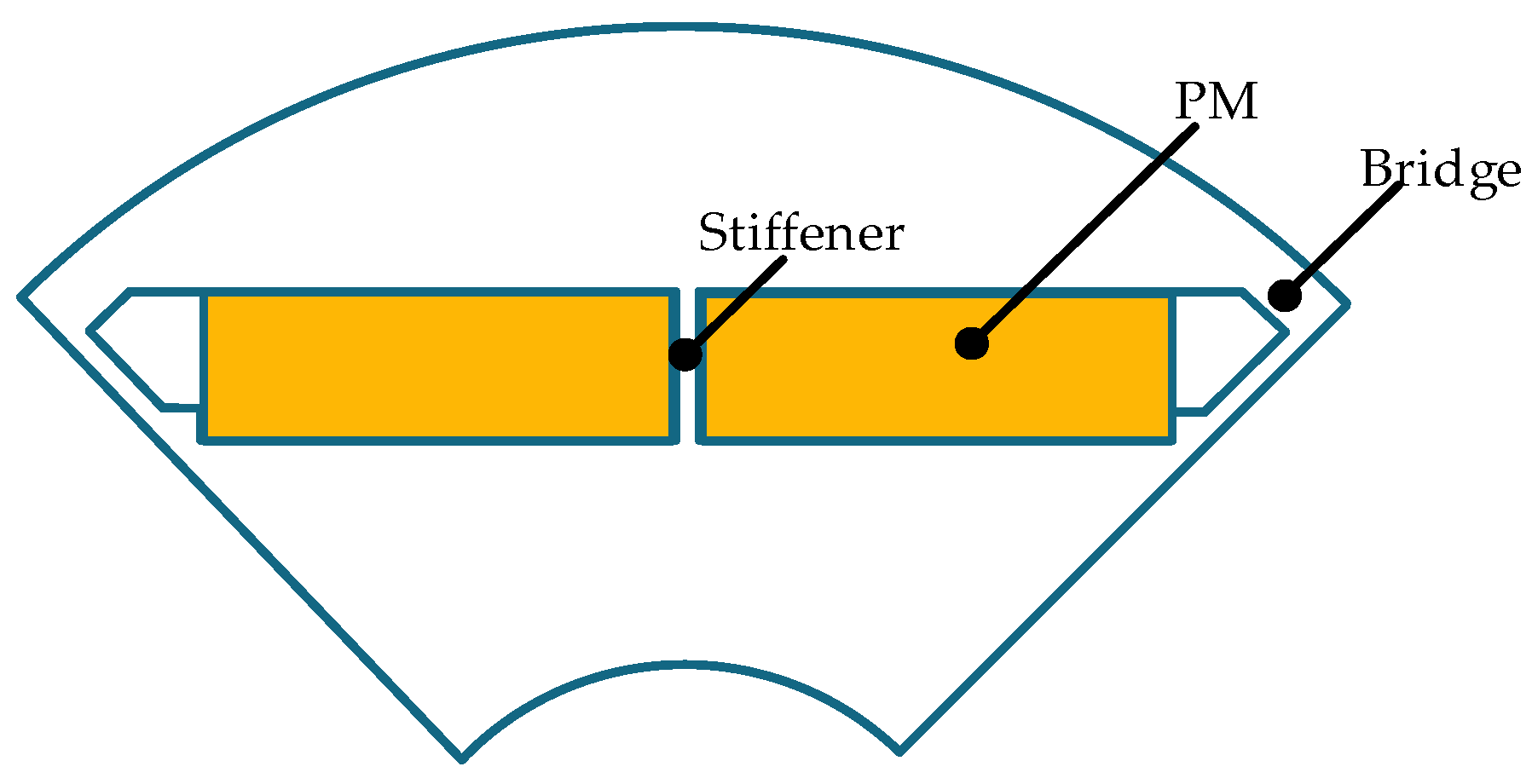
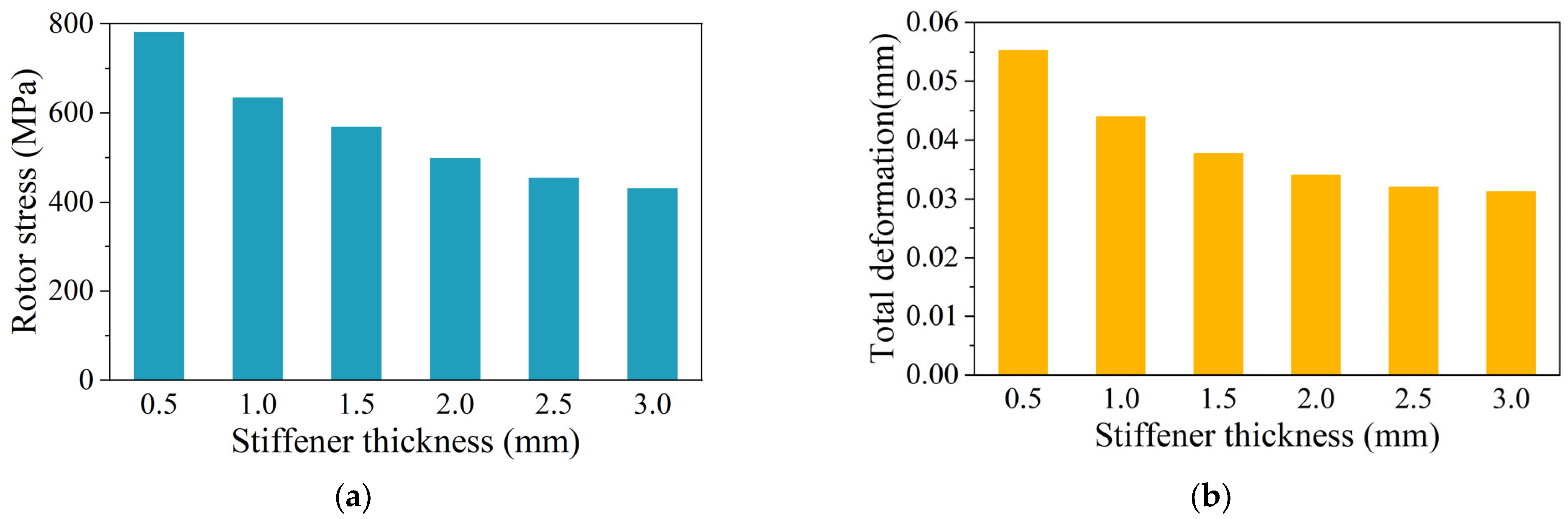
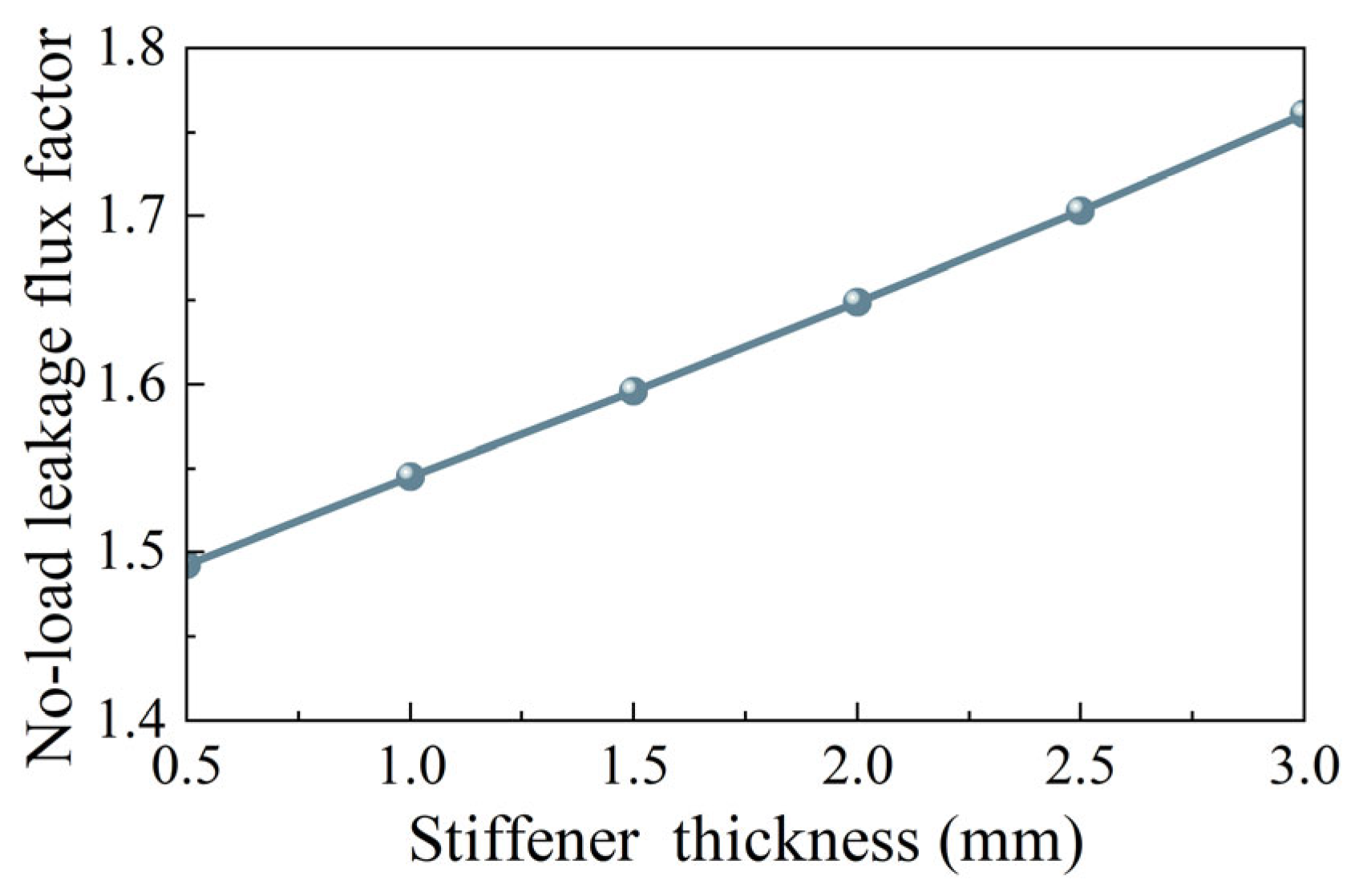
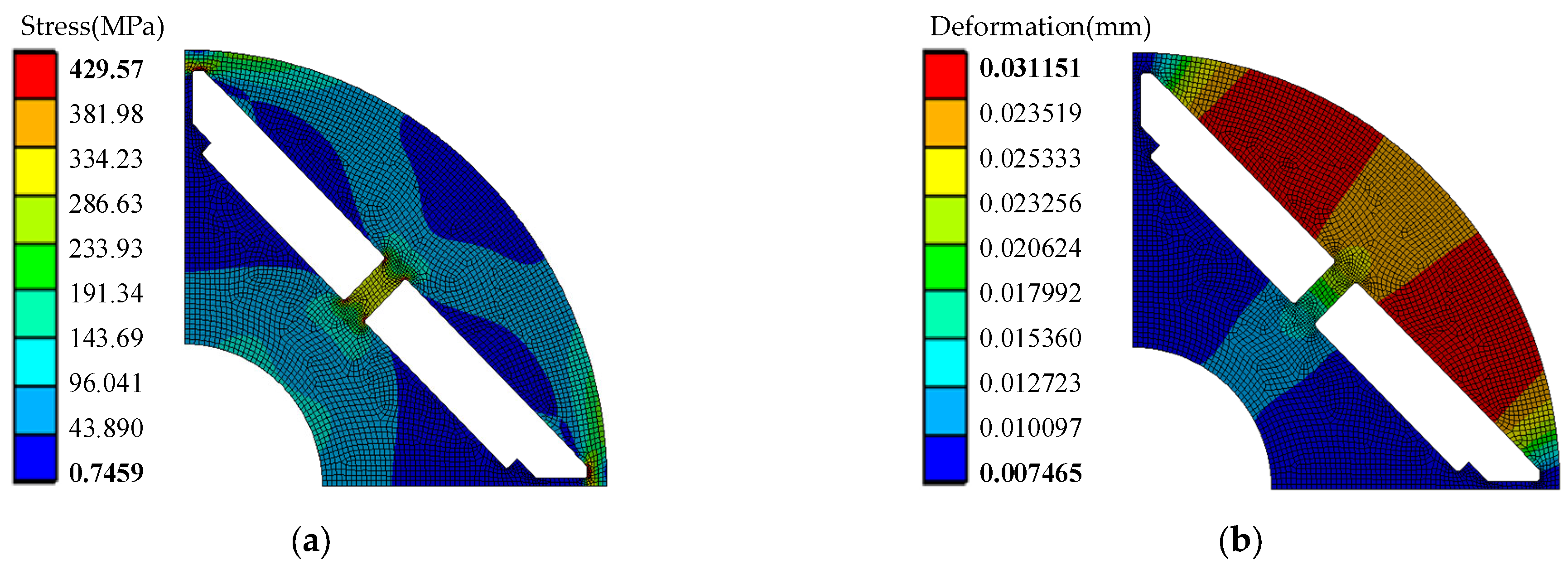
3.3. Stress Analysis of IPM Rotor with Stiffener
4. Analysis of Electromagnetic Performances of Two Different Rotor Structures
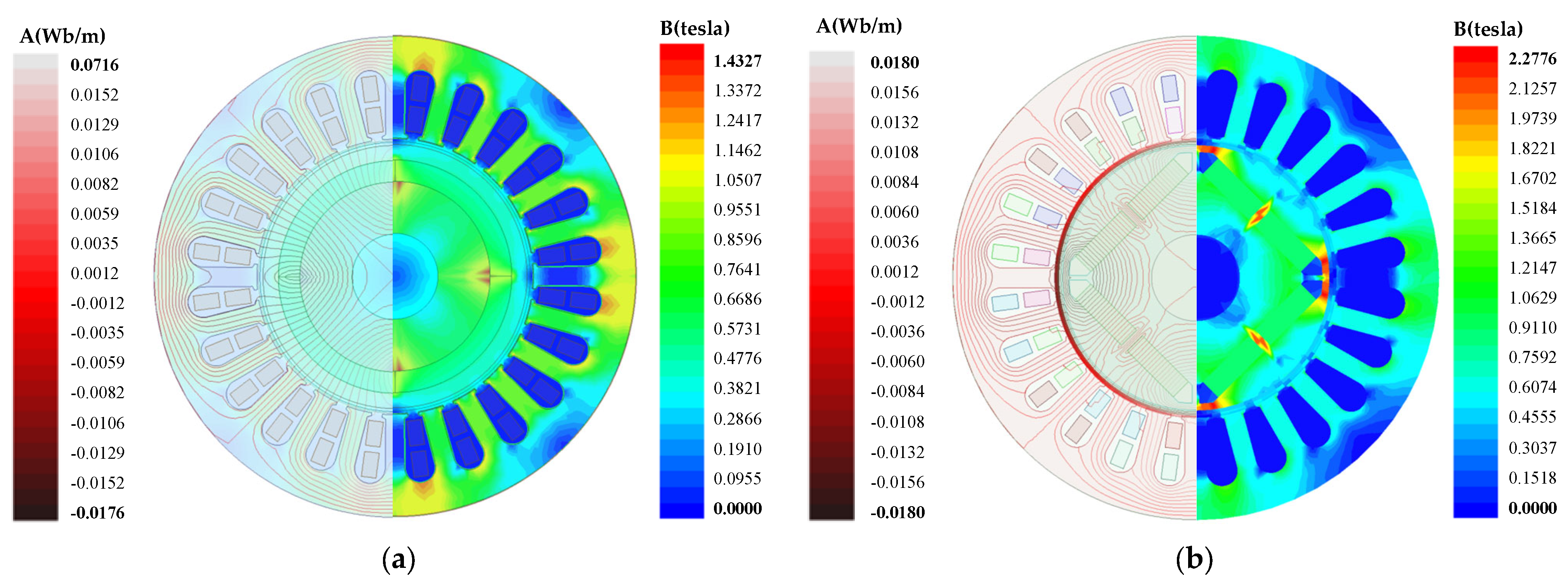
4.1. Magnetic Flux Distributions
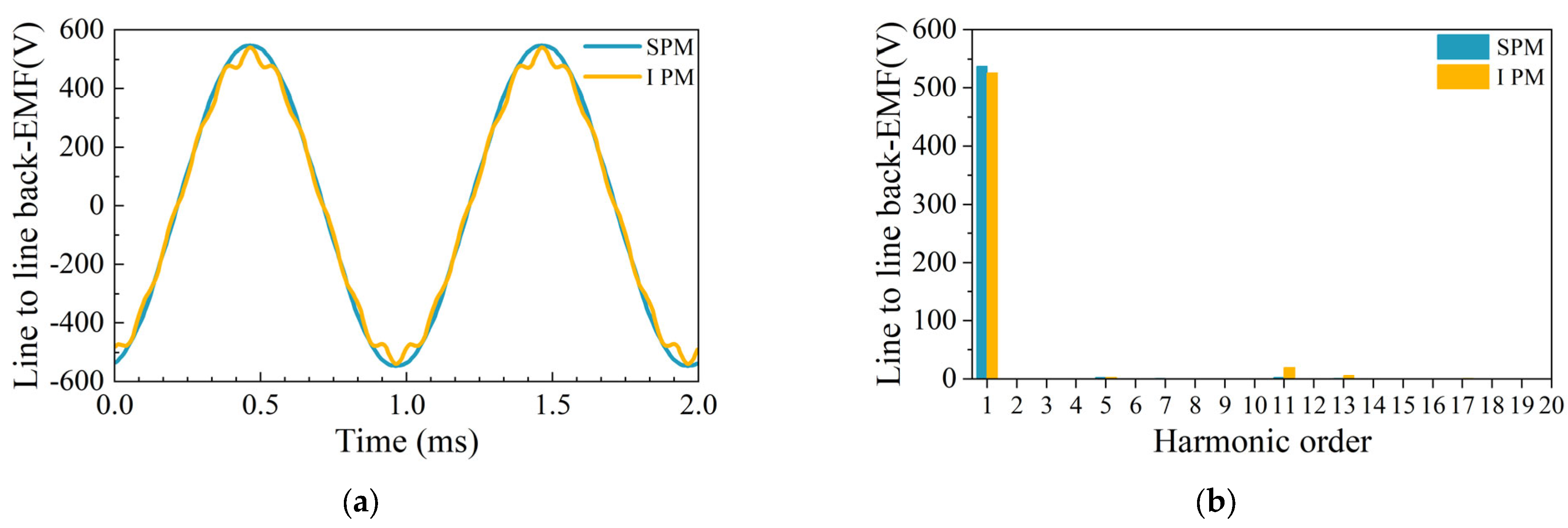
4.2. Line-to-Line Back-EMF
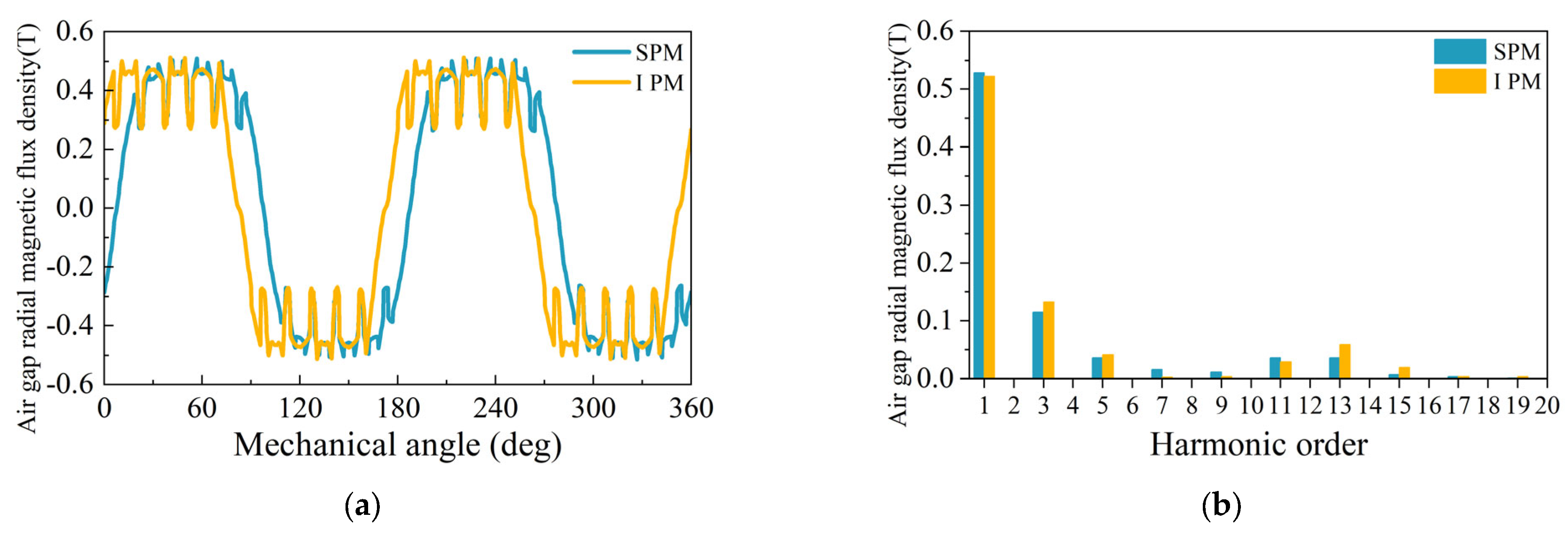
4.3. Air Gap Radial Magnetic Flux Density
4.4. Torque and Cogging Torque Characteristics
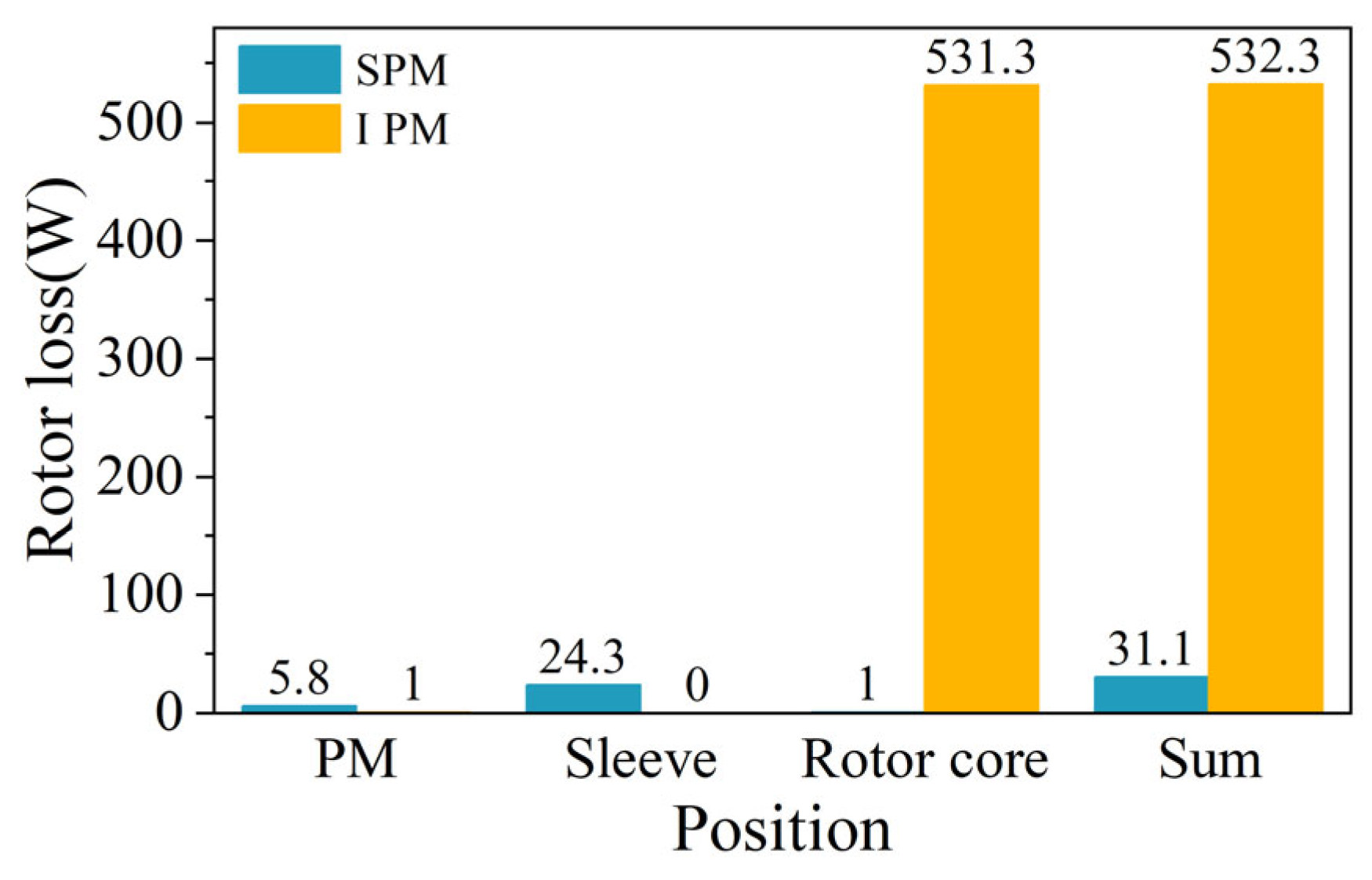
4.5. Rotor Loss Comparative Analysis
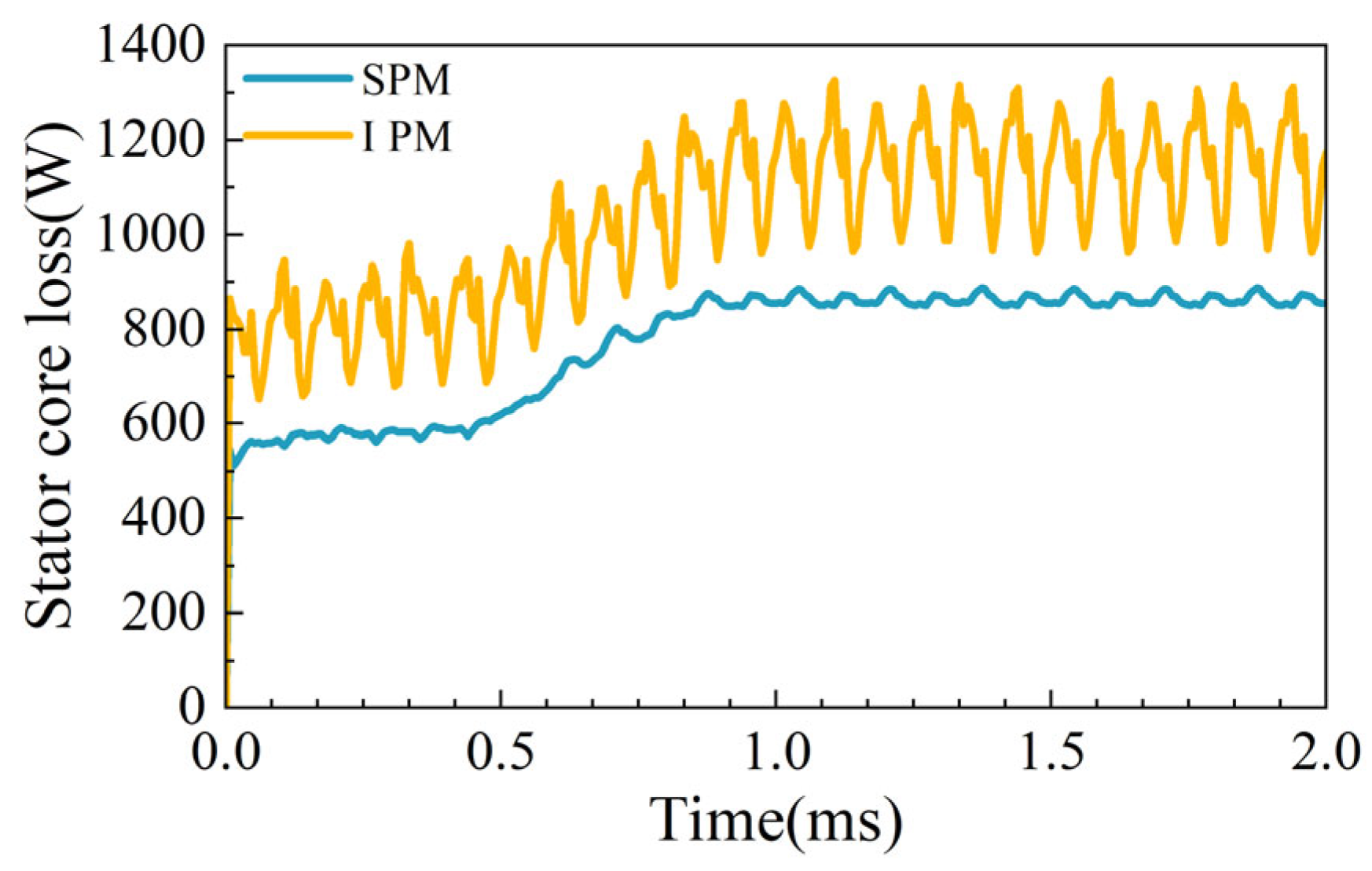
4.6. Stator Loss Comparative Analysis
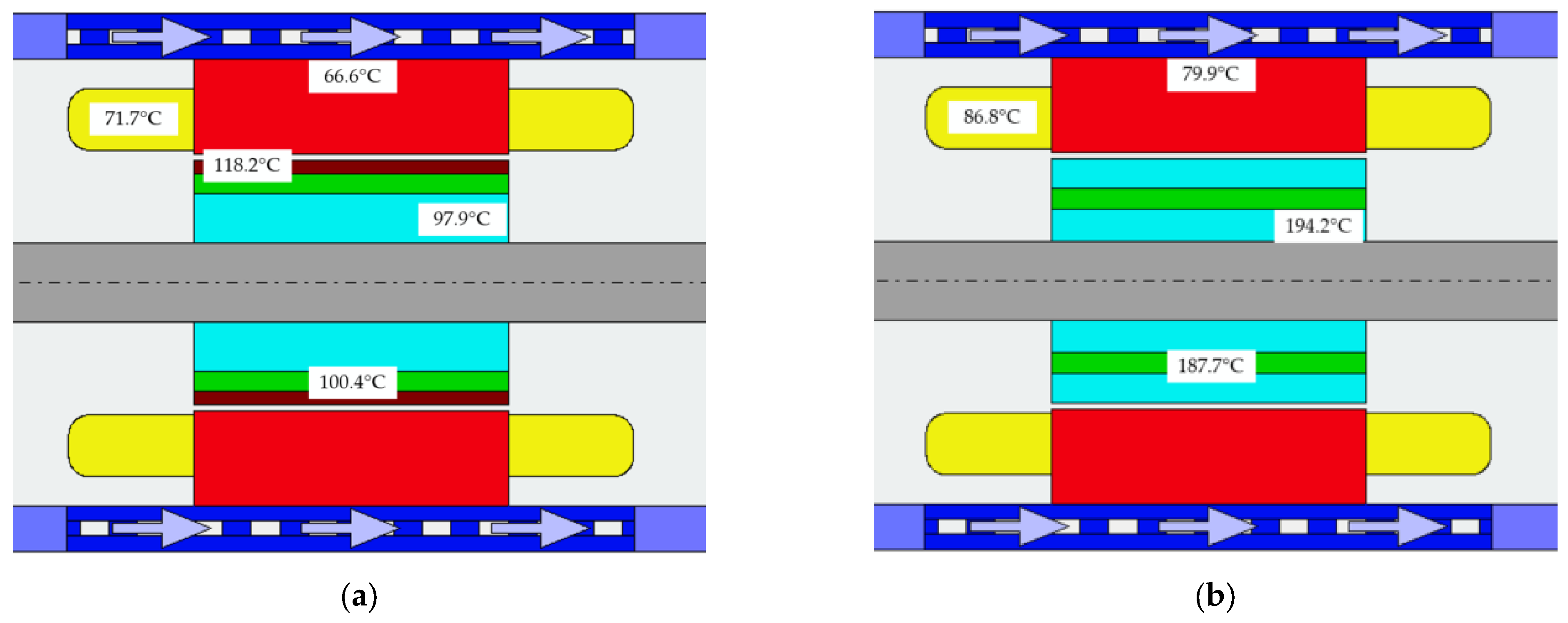
5. Temperature Distribution of Two Different Rotor Structures
5.1. Temperature Calculation Model
5.2. Temperature Comparative Analysis
6. Prototype and Experiment
6.1. Comparison Summary of Multi-Physics
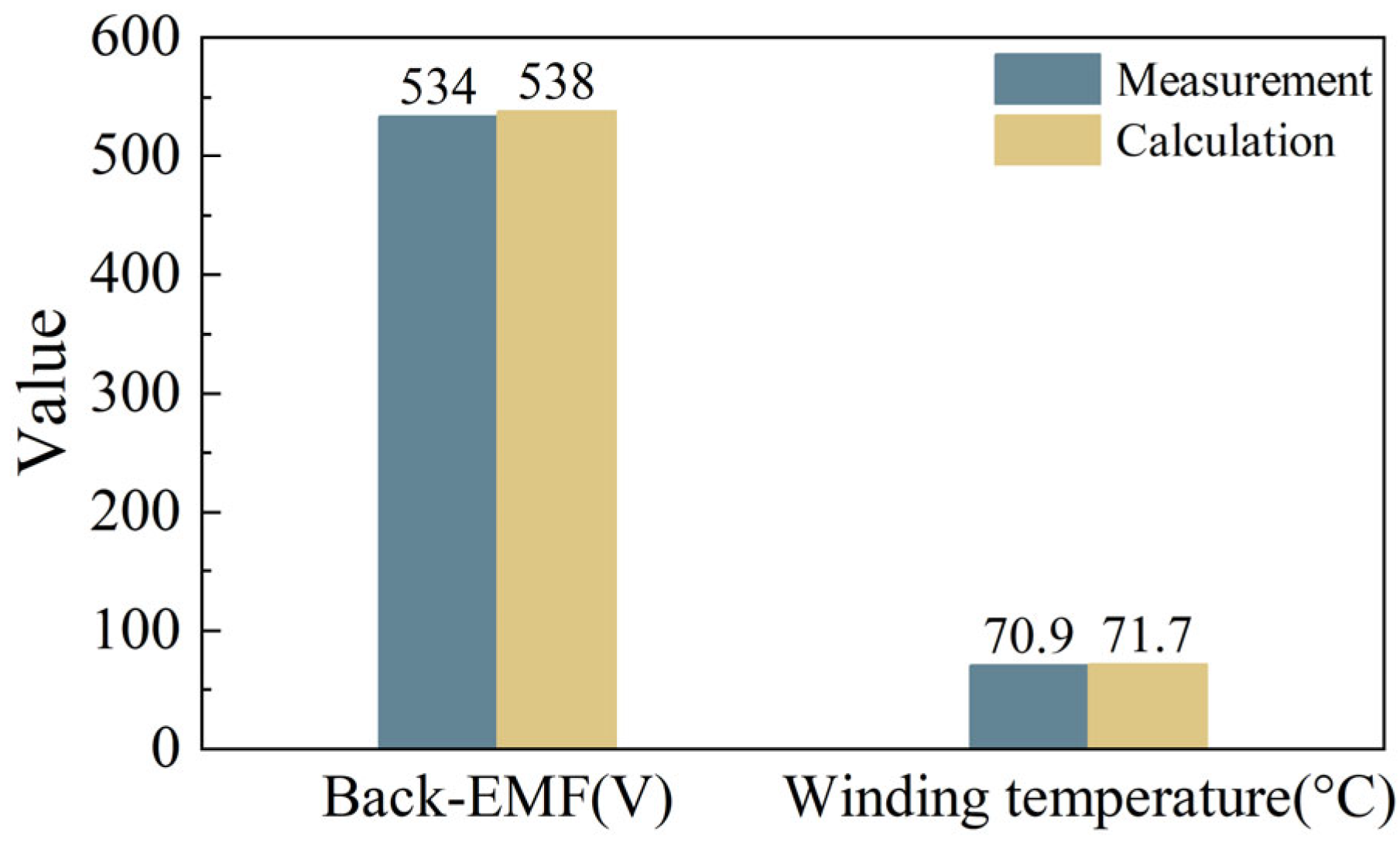
6.2. Prototype Experiment
7. Conclusions
- For the rotor stress analysis and comparison, both rotor structures meet the stress constraints, but the IPM has a small margin. As the sleeve thickness of SPM increases, the equivalent stress of the sleeve and the tangential stress of PM decrease. When the sleeve thickness is 5 mm, the sleeve stress is 596 MPa, while the yield strength of the carbon-fiber sleeve is 1960 MPa. The IPM structure has a conflict between rotor flux leakage and rotor stress. The traditional radial structure cannot meet the stress constraints. When the thickness of the magnetic bridge is 3.5 mm, the rotor stress is 1690 MPa, which is much larger than the yield strength of the rotor corn of 480 MPa. Dividing the PM into two sections and adding a stiffener can effectively reduce the rotor stress. When the stiffener thickness is 2.8 mm, the leakage flux factor is as high as 1.72, and the rotor stress is 430 MPa, which is close to the yield strength of the rotor core.
- For the electromagnetic field analysis and comparison, the loss of the two rotor structures is quite different, and the performance of other aspects is similar. Compared with IPM, the line back-EMF and air-gap flux density waveforms of SPM are closer to sine waves. The torque of SPM is slightly greater than that of IPM. In addition, the rotor loss of IPM is 532 W while the rotor loss of SPM is 31 W. The stator core loss of IPM is 1149 W while the stator core loss of SPM is 863 W.
- For the temperature-field analysis comparison, the temperature difference of the rotor part is larger than that of the stator part for the two rotor structures. The stator temperature of SPM is 66.6 °C while the stator temperature of IPM is 79.9 °C. The rotor temperature of SPM is 98 °C due to the poor thermal conductivity of the carbon-fiber sleeve. Although the IPM rotor structure has better heat dissipation performance, the rotor temperature is as high as 194 °C due to large losses. The IPM temperature distribution does not satisfy the temperature-field constraints.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Du, G.H.; Huang, N.; He, H.C.; Lei, G.; Zhu, J.G. Parameter Design for a High-Speed Permanent Magnet Machine Under Multiphysics Constraints. IEEE Trans. Energy Convers. 2020, 35, 2025–2035. [Google Scholar] [CrossRef]
- Hou, P.; Ge, B.J.; Tao, D.J.; Pan, B.; Wang, Y. Rotor Strength Analysis of FeCo-Based Permanent Magnet High Speed Motor. Machines 2022, 10, 462. [Google Scholar] [CrossRef]
- Qi, Z.N.; Zhang, Y.; Yu, S.Y.; Xu, Z.Y. Design and Analysis of a 30 KW, 30,000 r/Min High-Speed Permanent Magnet Motor for Compressor Application. Energies 2022, 15, 3923. [Google Scholar] [CrossRef]
- Lin, Y.Z.; Huang, Y.K.; Zhang, T. Comprehensive Design and Analysis of Rotor Stress for HSPMM Considering Cooling Method. Machines 2022, 10, 475. [Google Scholar] [CrossRef]
- Hong, J.F.; Wang, S.M.; Yang, Z.L. Comparison of Electromagnetic Excited Vibration for SPM and IPM Motors. In Proceedings of the 2017 19th European Conference on Power Electronics and Applications (EPE’17 ECCE Europe), Warsaw, Poland, 11–14 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–8. [Google Scholar]
- Pellegrino, G.; Vagati, A.; Guglielmi, P.; Boazzo, B. Performance Comparison Between Surface-Mounted and Interior PM Motor Drives for Electric Vehicle Application. IEEE Trans. Ind. Electron. 2012, 59, 803–811. [Google Scholar] [CrossRef]
- Ahn, J.H.; Han, C.; Kim, C.W.; Choi, J.Y. Rotor Design of High-Speed Permanent Magnet Synchronous Motors Considering Rotor Magnet and Sleeve Materials. IEEE Trans. Appl. Supercond. 2018, 28, 5201504. [Google Scholar] [CrossRef]
- Chu, G.Y.; Dutta, R.; Rahman, M.F.; Lovatt, H.; Sarlioglu, B. Analytical Calculation of Maximum Mechanical Stress on the Rotor of Interior Permanent-Magnet Synchronous Machines. IEEE Trans. Ind. Appl. 2020, 56, 1321–1331. [Google Scholar] [CrossRef]
- Du, G.H.; Xu, W.; Zhu, J.G.; Huang, N. Rotor Stress Analysis for High-Speed Permanent Magnet Machines Considering Assembly Gap and Temperature Gradient. IEEE Trans. Energy Convers. 2019, 34, 2276–2285. [Google Scholar] [CrossRef]
- Du, G.H.; Xu, W.; Huang, N.; Cheng, X.; Xiao, X.Y. Rotor Design of High Power High Speed Permanent Magnet Machine Considering Multiphysics Constraints. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019; pp. 1–5. [Google Scholar]
- Li, W.L.; Qiu, H.B.; Zhang, X.C.; Cao, J.C.; Zhang, S.N.; Yi, R. Influence of Rotor-Sleeve Electromagnetic Characteristics on High-Speed Permanent-Magnet Generator. IEEE Trans. Ind. Electron. 2014, 61, 3030–3037. [Google Scholar] [CrossRef]
- Wang, L.; Du, G.H.; Tong, J.; Huang, N.; Hu, C.S.; Xu, W. Comparation of Different Rotor Sleeves of Highspeed Permanent Magnet Synchronous Motors Based on Multi-Physics. In Proceedings of the 2021 IEEE 4th Student Conference on Electric Machines and Systems (SCEMS), Huzhou, China, 1–3 December 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–5. [Google Scholar]
- Xia, Y.; Li, J.; Qu, R.H.; Fang, H.Y. Comparison of Two Rotor Topologies for High-Speed Permanent Magnet Synchronous Machines. In Proceedings of the 2016 XXII International Conference on Electrical Machines (ICEM), Lausanne, Switzerland, 4–7 September 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1419–1425. [Google Scholar]
- Liu, X.P.; Zhang, Z.X.; Xiao, J.J.; Xu, H. Comparison and Analysis of Electromagnetic Characteristics of IPMSM with Single and Double Layer PMs. JAE 2018, 58, 483–496. [Google Scholar] [CrossRef]
- Yang, Y.Y.; Castano, S.; Yang, R.; Kasprzak, M.; Bilgin, B.; Sathyan, A.; Dadkhah, H.; Emadi, A. Design and Comparison of Interior Permanent Magnet Motor Topologies for Traction Applications. IEEE Trans. Transp. Electrif. 2017, 3, 86–97. [Google Scholar] [CrossRef]
- Kim, S.I.; Kim, Y.K.; Lee, G.H.; Hong, J.P. A Novel Rotor Configuration and Experimental Verification of Interior PM Synchronous Motor for High-Speed Applications. IEEE Trans. Magn. 2012, 48, 843–846. [Google Scholar] [CrossRef]
- Dong, J.N.; Huang, Y.K.; Jin, L.; Lin, H.Y. Comparative Study of Surface-Mounted and Interior Permanent-Magnet Motors for High-Speed Applications. IEEE Trans. Appl. Supercond. 2016, 26, 5200304. [Google Scholar] [CrossRef]
- Zhao, N.N.; Liu, W.G. Loss Calculation and Thermal Analysis of Surface-Mounted PM Motor and Interior PM Motor. IEEE Trans. Magn. 2015, 51, 8112604. [Google Scholar] [CrossRef]
- Tao, P.; Du, G.H.; Tong, J.; Huang, N.; Li, N.M.; Xu, W. Comparison of Rotor Strength of Various Rotor Structures for Ultra-High-Speed Permanent Magnet Synchronous Motor. In Proceedings of the 2021 IEEE 4th Student Conference on Electric Machines and Systems (SCEMS), Huzhou, China, 1–3 December 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Fang, H.Y.; Li, D.W.; Qu, R.H.; Li, J.; Wang, C.; Song, B. Rotor Design and Eddy-Current Loss Suppression for High-Speed Machines with a Solid-PM Rotor. IEEE Trans. Ind. Applicat. 2019, 55, 448–457. [Google Scholar] [CrossRef]
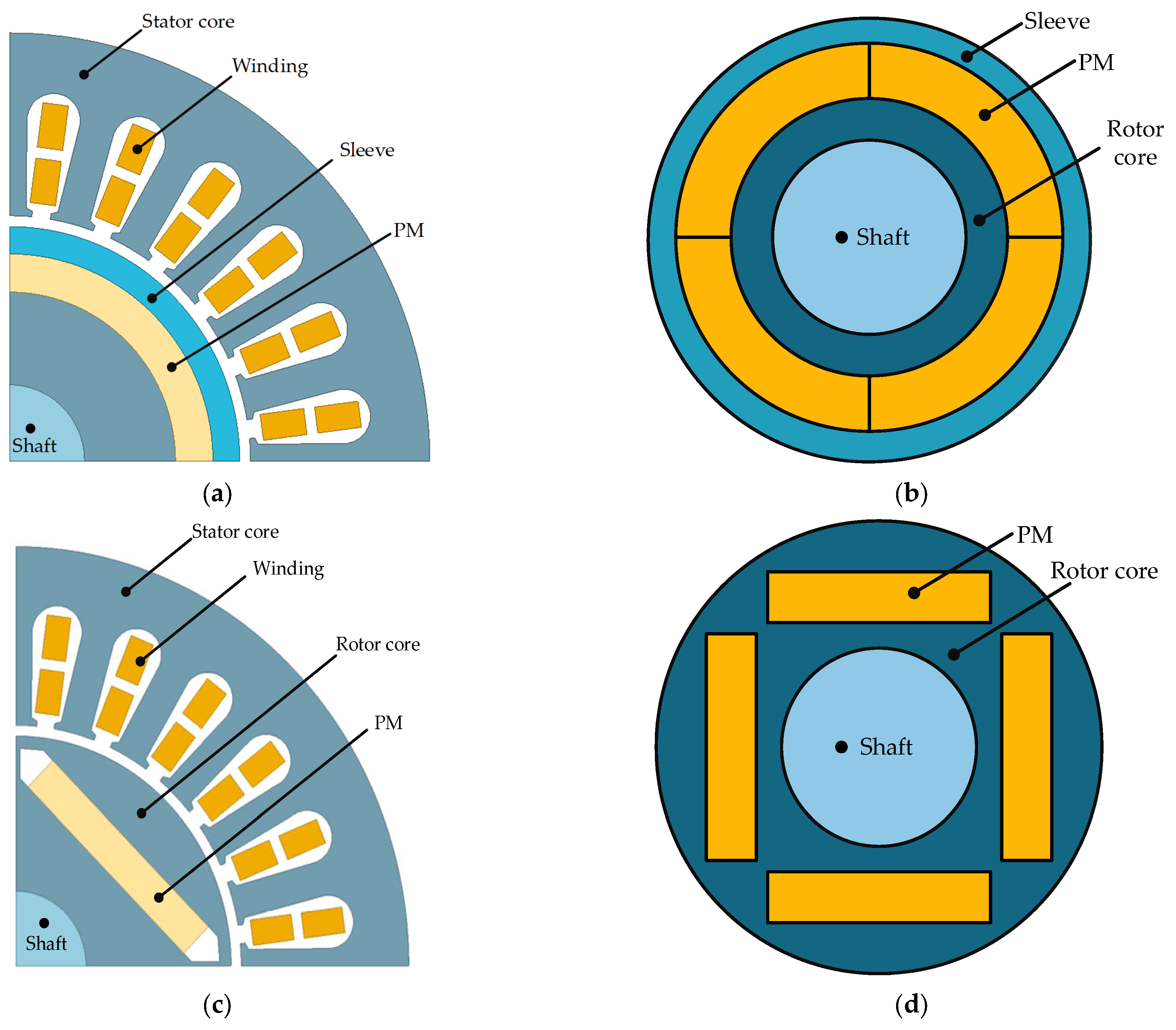







| Parameters | Values |
|---|---|
| Rated power (kW) | 60 |
| Rated speed (rpm) | 30,000 |
| Rated voltage (V) | 380 (RMS) |
| Stator slot number Pole number | 24 4 |
| Stator inner diameter (mm) Axial length (mm) | 90 110 |
| Rotor outer diameter (mm) | 86 |
| Permanent magnet thickness (mm) | 7 |
| Air-gap length (mm) | 2 |
| PM material | N38UH |
| Material Properties | Rotor Core | PM | Carbon Fiber | |
|---|---|---|---|---|
| Tangential | Radial | |||
| Density (kg/m3) | 7850 | 7400 | 1800 | |
| Elastic modulus (GPa) | 200 | 160 | 125 | 8.8 |
| Poisson’s ratio | 0.3 | 0.24 | 0.28 | 0.015 |
| CTE 1 (10−6/K) | 11 | 8 | −0.38 | 28 |
| Yield strength (MPa) | 480 | 75 | 1960 | −100 |
| Parameters | SPM | IPM |
|---|---|---|
| Embrace | 1 | 0.83 |
| Permanent magnet thickness (mm) | 7 | 7 |
| Permanent magnet width (mm) | 60 | 40 |
| Sleeve thickness (mm) | 5 | - |
| Interference fit (mm) | 0.15 | - |
| Rib thickness (mm) | - | 1.6 |
| Bridge rib thickness (mm) | - | 2.3 |
| Reinforcement thickness | - | 2.8 |
| Sleeve/rotor core stress (MPa) | 596 | 430 |
| Stress safety factor | 3.29 | 1.12 |
| Parameters | Values |
|---|---|
| Water temperature (°C) | 30 |
| Water flow rate (m3/h) | 1 |
| Spiral channel width (mm) | 10 |
| Spiral channel spacing (mm) | 10 |
| Parameters | SPM | IPM |
|---|---|---|
| Permanent magnet thickness (mm) | 7 | 7 |
| Permanent magnet width (mm) | 60 | 40 |
| No-load flux leakage factor | 1 | 1.72 |
| Sleeve/rotor core stress (MPa) | 596 | 430 |
| Stress safety factor | 3.29 | 1.12 |
| Fundamental amplitude of back-EMF (V) | 538 | 526 |
| THD of back-EMF | 0.64% | 3.20% |
| Torque (N·m) | 19.63 | 19.58 |
| Rotor Loss (W) | 31.1 | 532.3 |
| Stator Loss (W) | 863 | 1149 |
| Efficiency | 95.27% | 93.97% |
| Maximum temperature of winding (°C) | 71.7 | 86.8 |
| Maximum temperature of rotor core (°C) | 97.9 | 194.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, G.; Li, N.; Zhou, Q.; Gao, W.; Wang, L.; Pu, T. Multi-Physics Comparison of Surface-Mounted and Interior Permanent Magnet Synchronous Motor for High-Speed Applications. Machines 2022, 10, 700. https://doi.org/10.3390/machines10080700
Du G, Li N, Zhou Q, Gao W, Wang L, Pu T. Multi-Physics Comparison of Surface-Mounted and Interior Permanent Magnet Synchronous Motor for High-Speed Applications. Machines. 2022; 10(8):700. https://doi.org/10.3390/machines10080700
Chicago/Turabian StyleDu, Guanghui, Niumei Li, Qixun Zhou, Wentao Gao, Lu Wang, and Tao Pu. 2022. "Multi-Physics Comparison of Surface-Mounted and Interior Permanent Magnet Synchronous Motor for High-Speed Applications" Machines 10, no. 8: 700. https://doi.org/10.3390/machines10080700
APA StyleDu, G., Li, N., Zhou, Q., Gao, W., Wang, L., & Pu, T. (2022). Multi-Physics Comparison of Surface-Mounted and Interior Permanent Magnet Synchronous Motor for High-Speed Applications. Machines, 10(8), 700. https://doi.org/10.3390/machines10080700





