A Few-Shot Learning-Based Crashworthiness Analysis and Optimization for Multi-Cell Structure of High-Speed Train
Abstract
:1. Introduction
2. Materials and Methods
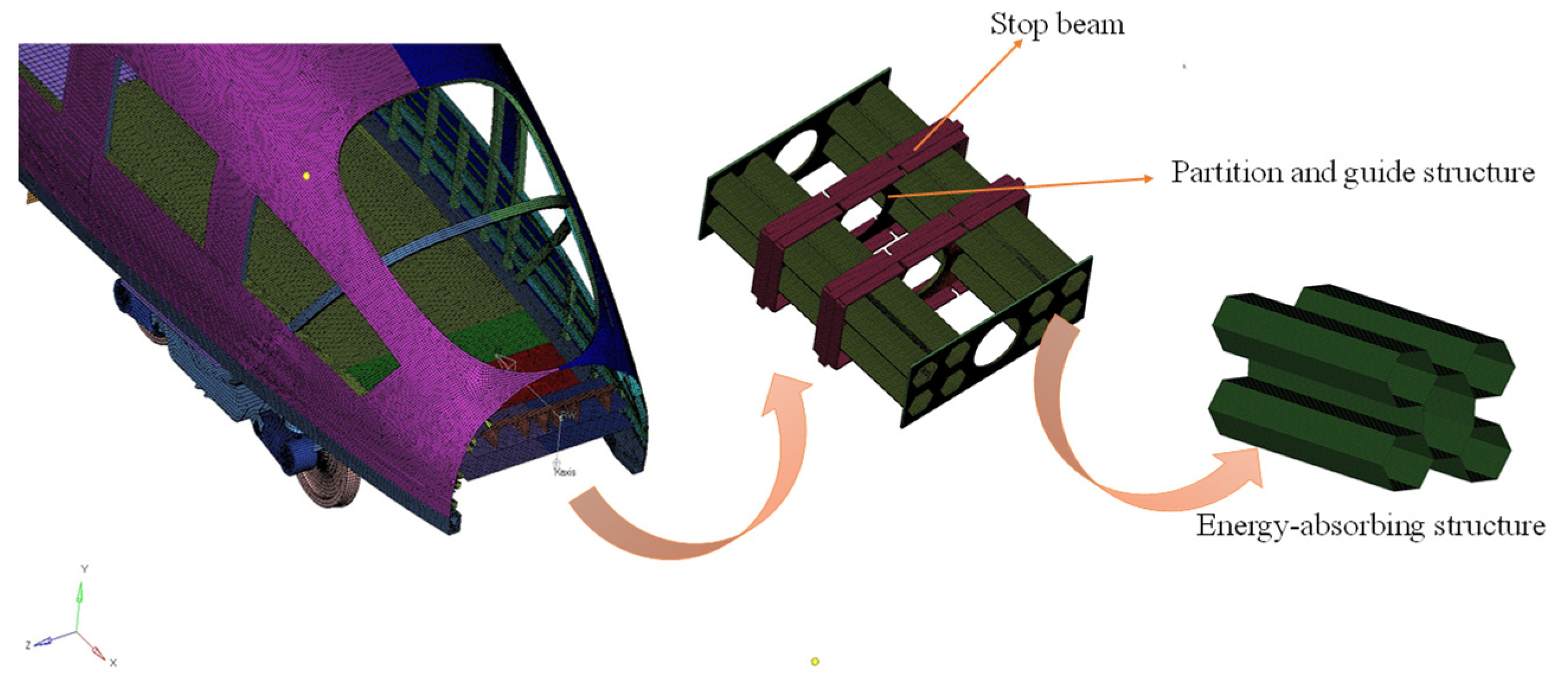
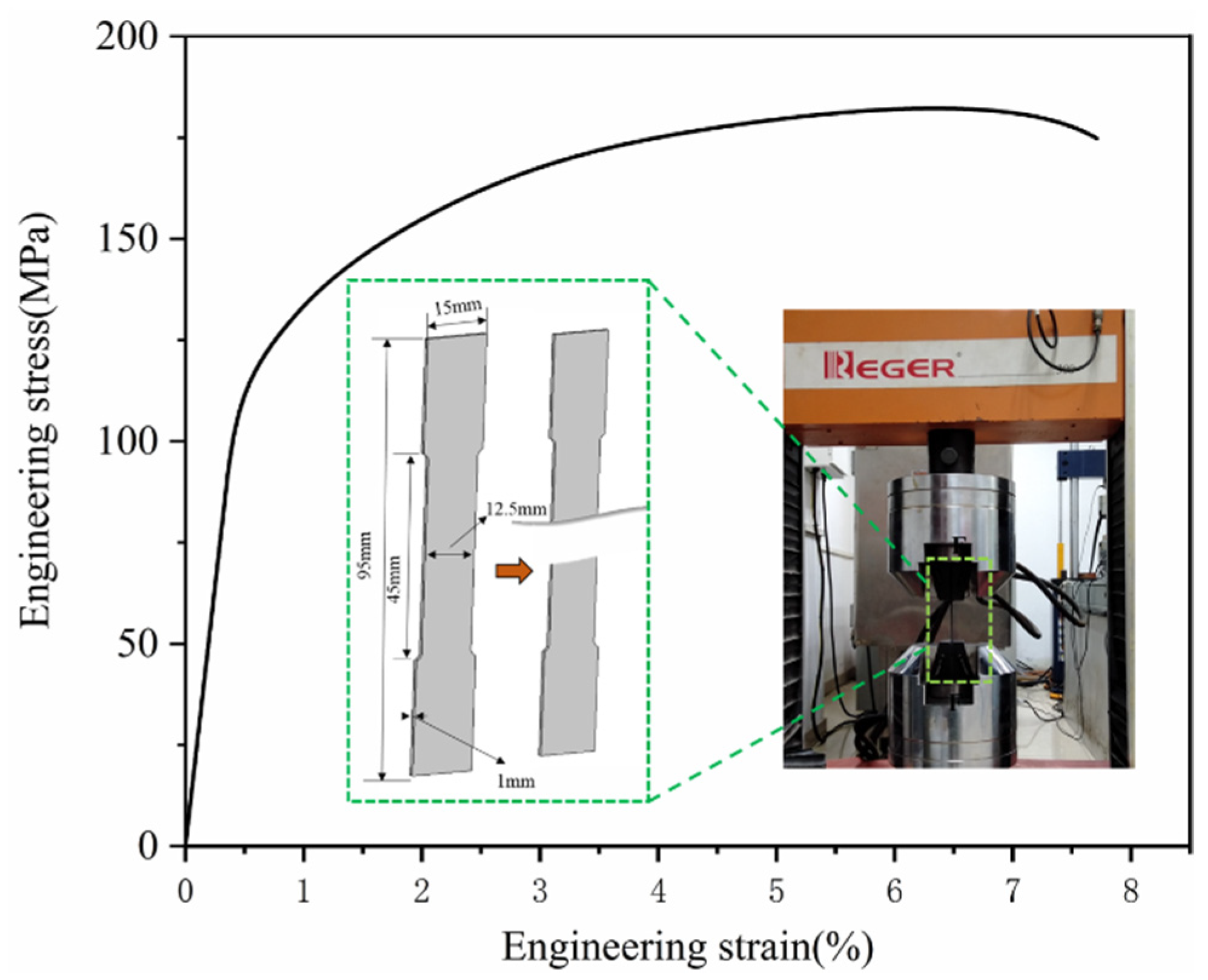
2.1. Materials
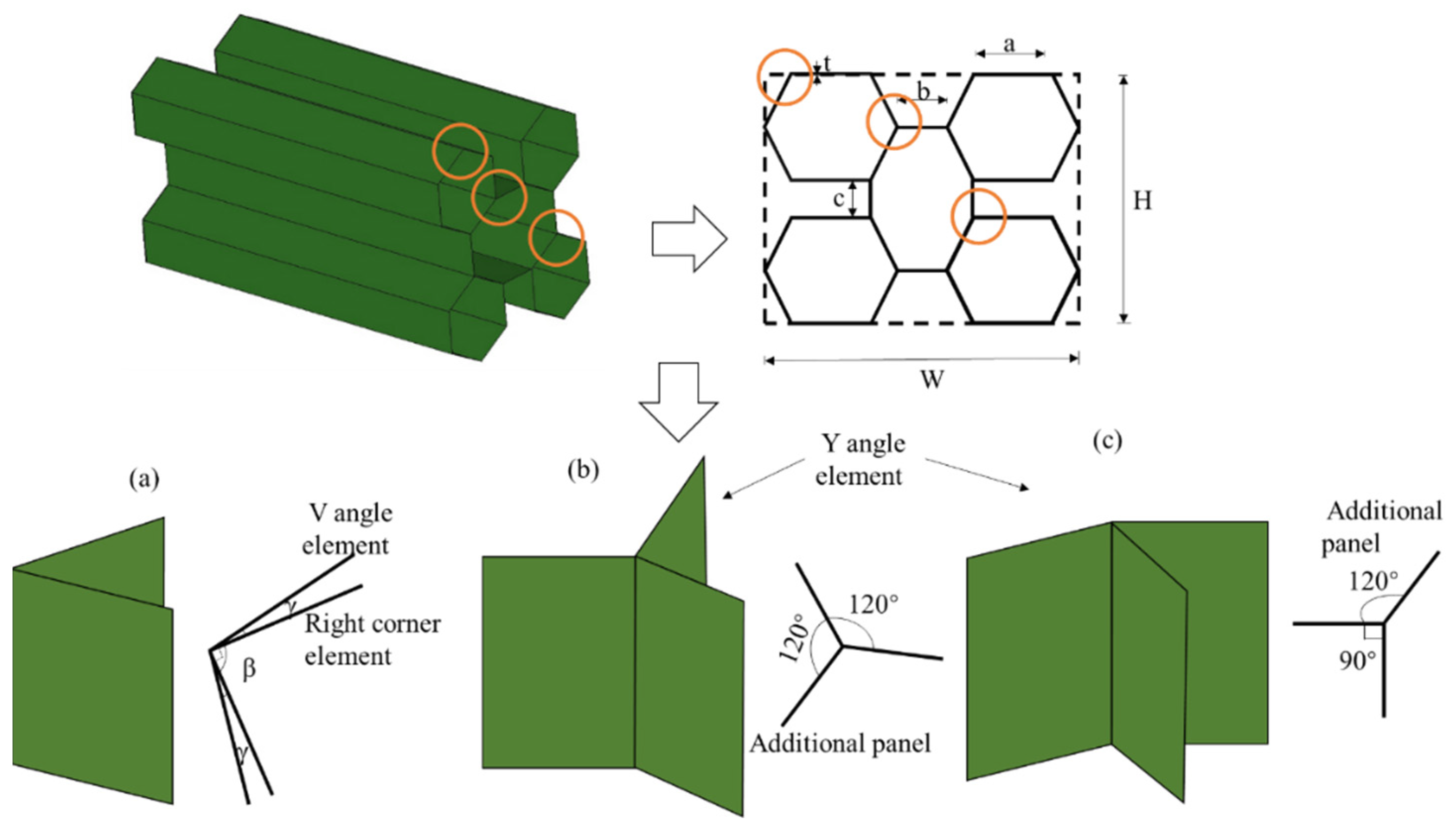
2.1.1. Theoretical Analysis
- Film deformation energy: The film deformation energy Em of each flange plate can be calculated by integrating the triangular cells of a folded wavelength.where . An energy equivalent stress σ0 can be used to approximate the flow stress for power-law hardening materialswhere , and n denote the yield strength, the ultimate strength of the material, and the exponent of the power-law, respectively. Given that a plate’s function is similar to that of a rectangular thin-film unit, the deformation energy of a thin-film unit is twice that of a plate.
- Bending deformation energy: Using the SSFE theory, where buckling wavelength L and wall thickness t are assumed to be constant, we can divide the energy absorption region of each corner unit into a thin film deformation zone and a bending deformation zone. For each of the flange plates, bending deformation energy is calculated as follows:where c, B0 and M0 is the side length, the sum lengths of the corner cell wall and the plastic bending moment of the flange plate, respectively; the four rotation angle values θi at the bent strand are π/2.
- Mean crushing forces: Five-cell structures with the cross-section configuration honeycomb tubes consist of 16 V-shaped elements, 4 Y-I-shaped elements, and 4 Y-II-shaped elements. We can then substitute Equations (5) and (7)–(9) into Equation (1) to obtain Equation (10).
2.1.2. Finite Element Model
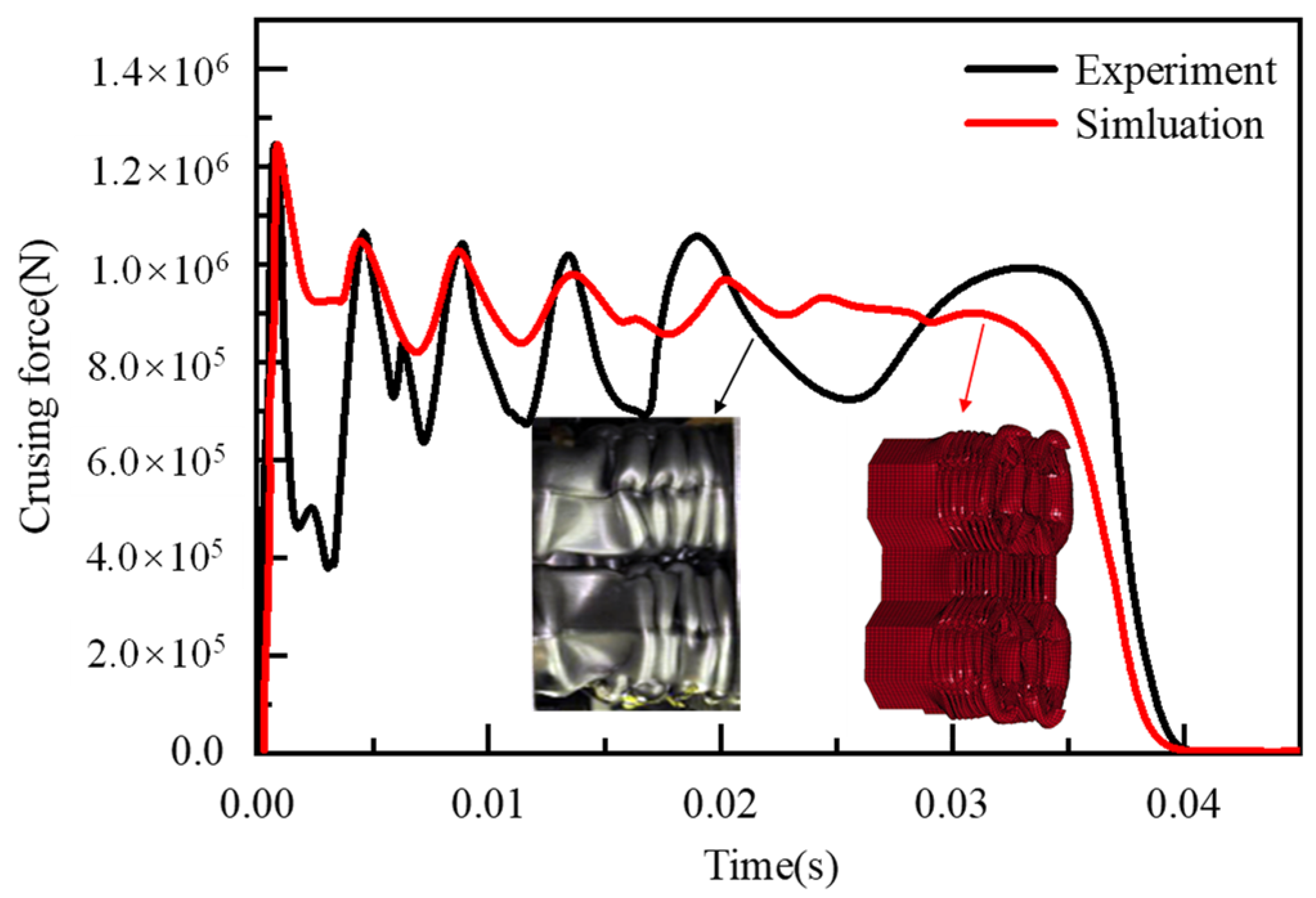
2.1.3. Test Set-Up
2.1.4. Crashworthiness Analysis
2.2. Few-Shot Learning
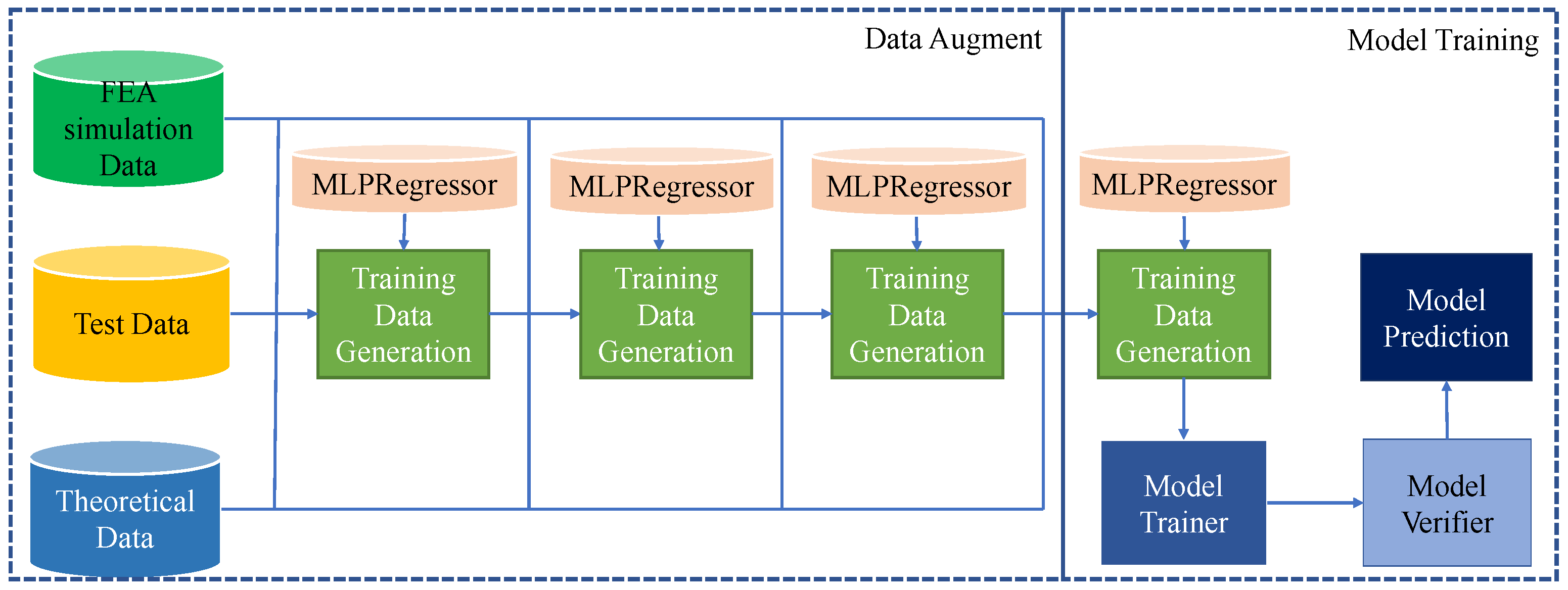
2.2.1. Data Augmentation
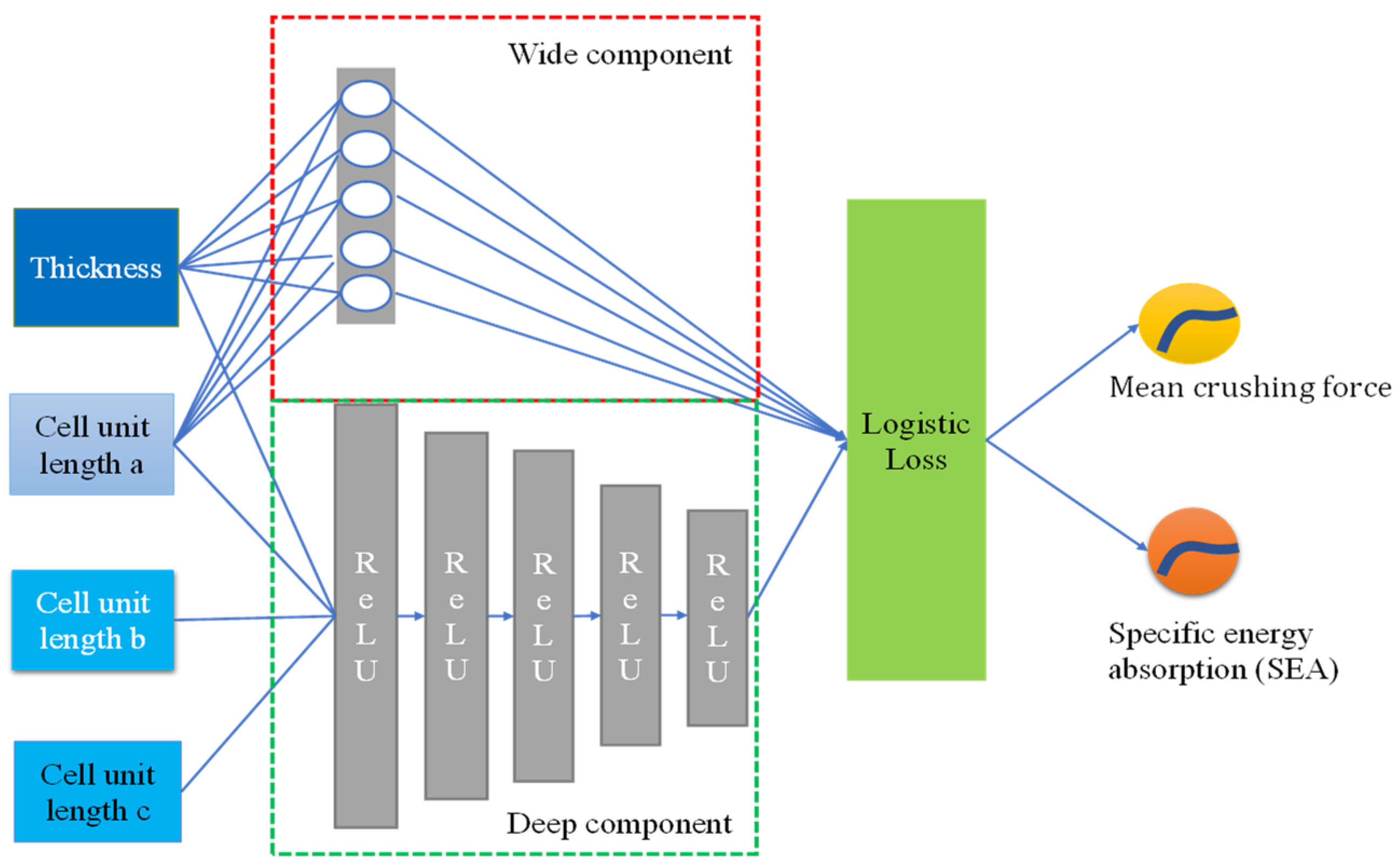
2.2.2. Model Framework
- Wide component
- 2.
- Deep component
- 3.
- Joint training
| Algorithm 1. Few-shot learning pseudo code. |
| Few-Shot Learning in This Study |
| hybrid data augmentation to obtain dataset |
| initialize all variables by the random value |
| for loop from 1 to num_epoch |
| choose xi from X data as the wide model input |
| choose xj from X data as the deep model input |
| compute the yj of the wide model output |
| compute the output of the deep model output-layer a(l+1) |
| for l = L to 5: |
| compute the a(l + 1) based on a(l) and W(l) and b(l) |
| concatenate the wide output and deep output, and compute the model output |
2.3. Problem Set-Up
2.3.1. Optimization Problem
2.3.2. Optimization Algorithm
3. Results and Discussion
3.1. Model Training
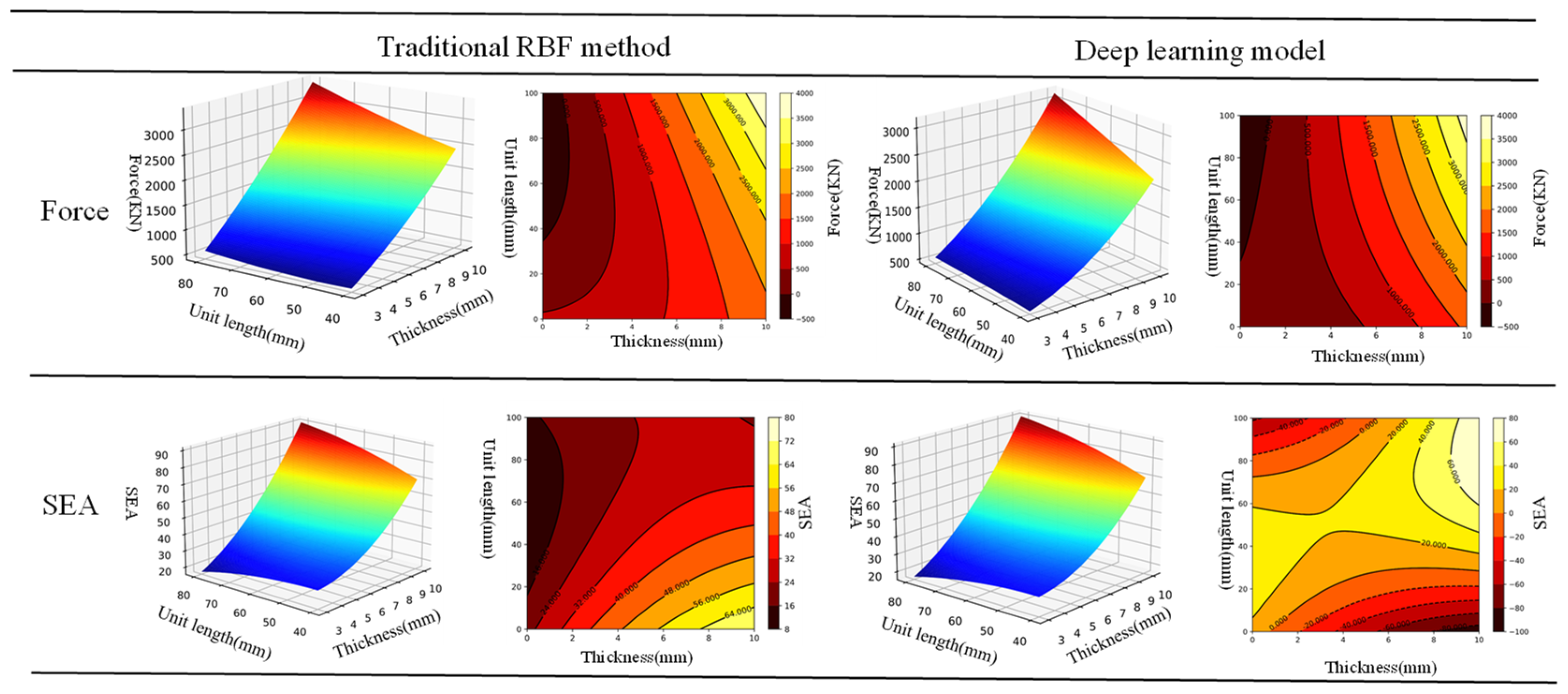
3.2. Parametric Study
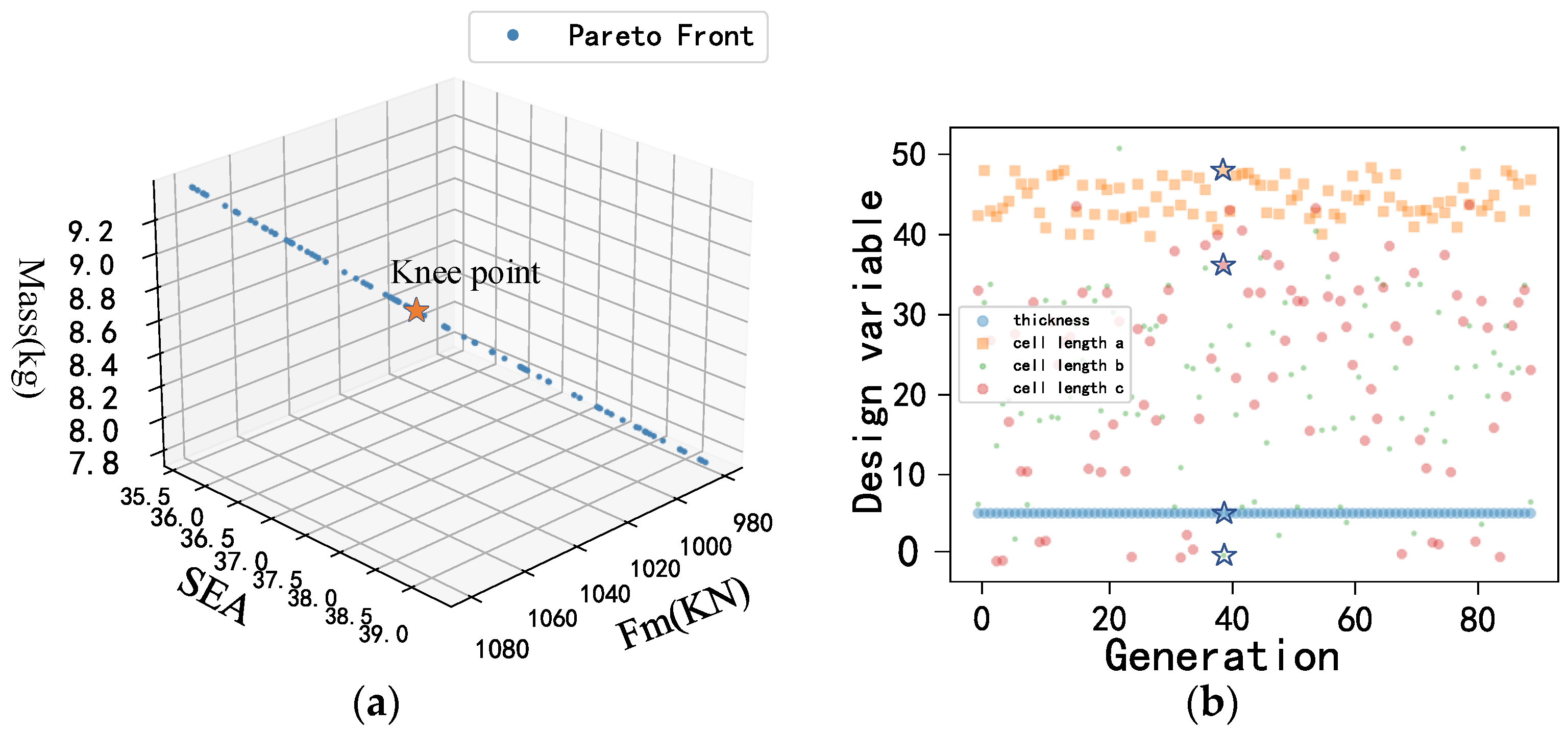
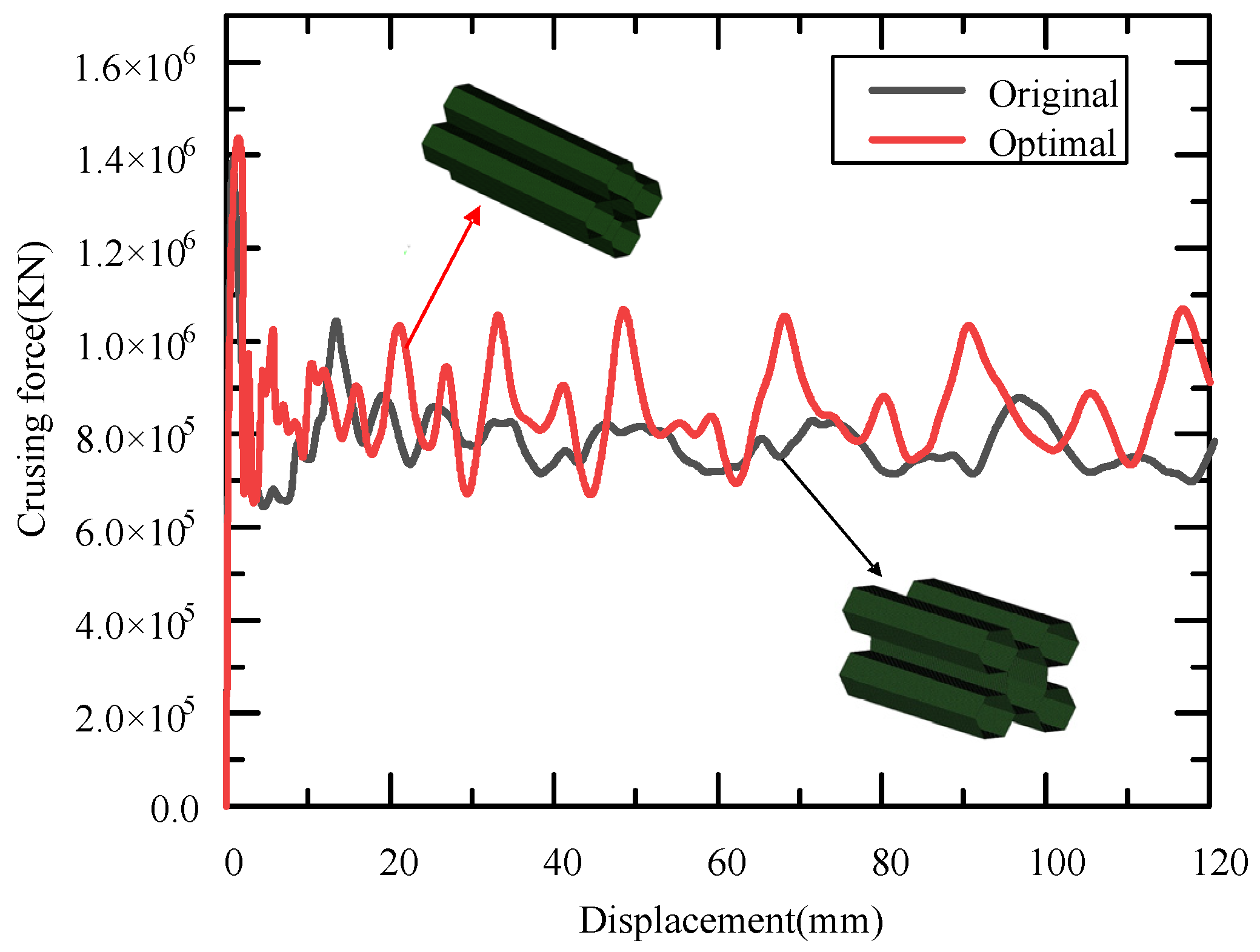
3.3. Optimisation Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chou, S.; Rhodes, J. Review and compilation of experimental results on thin-walled structures. Comput. Struct. 1997, 65, 47–67. [Google Scholar] [CrossRef]
- Bull, J.W. Finite Element Analysis of Thin-Walled Structures; CRC Press: London, UK, 1988. [Google Scholar]
- Bischoff, M.; Ramm, E.; Irslinger, J. Models and finite elements for thin-walled structures. In Encyclopedia of Computational Mechanics, 2nd ed.; John Wiley & Sons, Ltd.: Chichester, UK, 2004; Volume 2, pp. 1–86. [Google Scholar]
- Chen, W.; Wierzbicki, T. Relative merits of single-cell, multi-cell and foam-filled thin-walled structures in energy absorption. Thin-Walled Struct. 2001, 39, 287–306. [Google Scholar] [CrossRef]
- Susac, F.; Beznea, E.F.; Baroiu, N. Artificial Neural Network Applied to Prediction of Buckling Behaviour of the Thin Walled Box. Advanced Engineering Forum; Trans Tech Publications: Zurich, Switzerland, 2017; Volume 21, pp. 141–150. [Google Scholar]
- Tang, Z.; Zhu, Y.; Nie, Y.; Guo, S.; Liu, F.; Chang, J.; Zhang, J. Data-driven train set crash dynamics simulation. Veh. Syst. Dyn. 2017, 55, 149–167. [Google Scholar] [CrossRef]
- Dong, S.; Tang, Z.; Yang, X.; Wu, M.; Zhang, J.; Zhu, T.; Xiao, S. Nonlinear Spring-Mass-Damper Modeling and Parameter Estimation of Train Frontal Crash Using CLGAN Model. Shock Vib. 2020, 2020, 9536915. [Google Scholar] [CrossRef]
- Acar, E. Increasing automobile crash response metamodel accuracy through adjusted cross validation error based on outlier analysis. Int. J. Crashworthiness 2015, 20, 107–122. [Google Scholar] [CrossRef]
- Wei, Z.; Robbersmyr, K.G.; Karimi, H.R. Data-based modeling and estimation of vehicle crash processes in frontal fixed-barrier crashes. J. Frankl. Inst. 2017, 354, 4896–4912. [Google Scholar] [CrossRef]
- Karimi, H.R.; Pawlus, W.; Robbersmyr, K.G. Signal reconstruction, modeling and simulation of a vehicle full-scale crash test based on morlet wavelets. Neurocomputing 2012, 93, 88–99. [Google Scholar] [CrossRef]
- Wang, Y.; Yao, Q.; Kwok, J.T.; Ni, L.M. Generalizing from a few examples: A survey on few-shot learning. ACM Comput. Surv. 2020, 53, 1–34. [Google Scholar] [CrossRef]
- Argüeso, D.; Picon, A.; Irusta, U.; Medela, A.; San-Emeterio, M.G.; Bereciartua, A.; Alvarez-Gila, A. Few-Shot Learning approach for plant disease classification using images taken in the field. Comput. Electron. Agric. 2020, 175, 105542. [Google Scholar] [CrossRef]
- Ren, Z.; Zhu, Y.; Yan, K.; Chen, K.; Kang, W.; Yue, Y.; Gao, D. A novel model with the ability of few-shot learning and quick updating for intelligent fault diagnosis. Mech. Syst. Signal Process. 2020, 138, 106608. [Google Scholar] [CrossRef]
- Sun, X.; Wang, B.; Wang, Z.; Li, H.; Li, H.; Fu, K. Research progress on few-shot learning for remote sensing image interpretation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 2387–2402. [Google Scholar] [CrossRef]
- Nia, A.A.; Parsapour, M. Comparative analysis of energy absorption capacity of simple and multi-cell thin-walled tubes with triangular, square, hexagonal and octagonal sections. Thin-Walled Struct. 2014, 74, 155–165. [Google Scholar]
- Guler, M.A.; Cerit, M.E.; Bayram, B.; Gerceker, B.; Karakaya, E. The effect of geometrical parameters on the energy absorption characteristics of thin-walled structures under axial impact loading. Int. J. Crashworthiness 2010, 15, 377–390. [Google Scholar] [CrossRef]
- Guillow, S.; Lu, G.; Grzebieta, R. Quasi-static axial compression of thin-walled circular aluminium tubes. Int. J. Mech. Sci. 2001, 43, 2103–2123. [Google Scholar] [CrossRef]
- Fan, Z.; Lu, G.; Liu, K. Quasi-static axial compression of thin-walled tubes with different cross-sectional shapes. Eng. Struct. 2013, 55, 80–89. [Google Scholar] [CrossRef]
- Tai, Y.; Huang, M.; Hu, H.-T. Axial compression and energy absorption characteristics of high-strength thin-walled cylinders under impact load. Theor. Appl. Fract. Mech. 2010, 53, 1–8. [Google Scholar] [CrossRef]
- Shim, V.-W.; Stronge, W. Lateral crushing of thin-walled tubes between cylindrical indenters. Int. J. Mech. Sci. 1986, 28, 683–707. [Google Scholar] [CrossRef]
- Baroutaji, A.; Gilchrist, M.D.; Smyth, D.; Olabi, A.G. Crush analysis and multi-objective optimisation design for circular tube under quasi-static lateral loading. Thin-Walled Struct. 2015, 86, 121–131. [Google Scholar] [CrossRef]
- Niknejad, A.; Elahi, S.M.; Elahi, S.A.; Elahi, S.A. Theoretical and experimental study on the flattening deformation of the rectangular brazen and aluminium columns. Arch. Civ. Mech. Eng. 2013, 13, 449–464. [Google Scholar] [CrossRef]
- Tran, T.; Baroutaji, A. Crashworthiness optimal design of multi-cell triangular tubes under axial and oblique impact loading. Eng. Fail. Anal. 2018, 93, 241–256. [Google Scholar] [CrossRef]
- Ying, L.; Dai, M.; Zhang, S.; Ma, H.; Hu, P. Multiobjective crashworthiness optimisation of thin-walled structures with functionally graded strength under oblique impact loading. Thin-Walled Struct. 2017, 117, 165–177. [Google Scholar] [CrossRef]
- Alkhatib, S.E.; Tarlochan, F.; Hashem, A.; Sassi, S. Collapse behaviour of thin-walled corrugated tapered tubes under oblique impact. Thin-Walled Struct. 2018, 122, 510–528. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, H.; Wang, Z. Bending collapse of square tubes with variable thickness. Int. J. Mech. Sci. 2016, 106, 107–116. [Google Scholar] [CrossRef]
- Du, Z.; Duan, L.; Cheng, A.; Xu, Z.; Zhang, G. Theoretical prediction and crashworthiness optimisation of thin-walled structures with single-box multi-cell section under three-point bending loading. Int. J. Mech. Sci. 2019, 157, 703–714. [Google Scholar] [CrossRef]
- Duan, L.; Xiao, N.C.; Li, G.; Xu, F.; Chen, T.; Cheng, A. Bending analysis and design optimisation of tailor-rolled blank thin-walled structures with top-hat sections. Int. J. Crashworthiness 2017, 22, 227–242. [Google Scholar] [CrossRef]
- Baroutaji, A.; Sajjia, M.; Olabi, A.-G. On the crashworthiness performance of thin-walled energy absorbers: Recent advances and future developments. Thin-Walled Struct. 2017, 118, 137–163. [Google Scholar] [CrossRef]
- Chen, T.; Zhang, Y.; Lin, J.; Lu, Y. Theoretical analysis and crashworthiness optimisation of hybrid multi-cell structures. Thin-Walled Struct. 2019, 142, 116–131. [Google Scholar] [CrossRef]
- Chen, J.; Xu, P.; Yao, S.; Xing, J.; Hu, Z. The multi-objective structural optimisation design to improve the crashworthiness of a multi-cell structure for high-speed train. Int. J. Crashworthiness 2020, 27, 24–33. [Google Scholar] [CrossRef]
- Langseth, M.; Hopperstad, O.S. Static and dynamic axial crushing of square thin-walled aluminium extrusions. Int. J. Impact Eng. 1996, 18, 949–968. [Google Scholar] [CrossRef]
- Wierzbicki, T.; Abramowicz, W. On the crushing mechanics of thin-walled structures. J. Appl. Mech. 1983, 50, 727–739. [Google Scholar] [CrossRef]
- Abramowicz, W.; Wierzbicki, T. Axial crushing of multicorner sheet metal columns. J. Appl. Mech. 1989, 56, 113–120. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhai, X.; Sun, L. Test and design method for the buckling behaviours of 6082-T6 aluminium alloy columns with box-type and L-type sections under eccentric compression. Thin-Walled Struct. 2016, 100, 62–80. [Google Scholar] [CrossRef]
- Cheng, H.T.; Koc, L.; Harmsen, J.; Shaked, T.; Chandra, T.; Aradhye, H.; Anderson, G.; Corrado, G.; Chai, W.; Ispir, M.; et al. Wide & deep learning for recommender systems. In Proceedings of the 1st Workshop on Deep Learning for Recommender Systems, Boston, MA, USA, 15 September 2016; pp. 7–10. [Google Scholar]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems with Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- He, Q.; Shahabi, H.; Shirzadi, A.; Li, S.; Chen, W.; Wang, N.; Chai, H.; Bian, H.; Ma, J.; Chen, Y.; et al. Landslide spatial modelling using novel bivariate statistical based Naïve Bayes, RBF Classifier, and RBF Network machine learning algorithms. Sci. Total Environ. 2019, 663, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Douglas-Smith, D.; Iwanaga, T.; Croke, B.F.; Jakeman, A.J. Certain trends in uncertainty and sensitivity analysis: An overview of software tools and techniques. Environ. Model. Softw. 2020, 124, 104588. [Google Scholar] [CrossRef]





| Property | Units | Value |
|---|---|---|
| Density | kg/m3 | 2700 |
| Young’s modulus | MPa | 71,000 |
| Poisson’s ratio | - | 0.33 |
| Yield stress | MPa | 121 |
| Ultimate tensile strength | MPa | 183 |
| Fracture strain | % | 7.71 |
| Fracture stress | MPa | 175 |
| Methods | Fm (kN) | Displacement (mm) | EA (KJ) | SEA (KJ/kg) |
|---|---|---|---|---|
| Experimental | 874.0 | 278 | 243.0 | 26.9 |
| Simulation | 905.7 | 269 | 243.6 | 25.75 |
| Theorical | 903.3 | 279 | 252.0 | 26.6 |
| Simulation Error (%) | 3.6 | 3.2 | 0.2 | 4.2 |
| Theorical Error (%) | 3.4 | 3.5 | 3.3 | 3.1 |
| Test | t (mm) | a (mm) | b (mm) | c (mm) | Fm (kN) | SEA | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Actual | Predicted | Eror | Actual | Predicted | Error | |||||
| 1 | 4.2 | 57 | 67 | 44 | 761.11 | 749.03 | 0.015 | 26.078 | 28.034 | −0.07 |
| 2 | 5.7 | 69 | 41 | 46 | 1116.38 | 1114.536 | 0.002 | 28.729 | 31.34 | −0.09 |
| 3 | 4.7 | 70 | 67 | 68 | 931.48 | 952.34 | −0.025 | 29.2 | 32.456 | −0.111 |
| 4 | 5.7 | 47 | 48 | 69 | 1006.12 | 1007.639 | −0.001 | 33.272 | 36.299 | −0.09 |
| 5 | 3.6 | 61 | 69 | 63 | 629.65 | 651.34 | −0.034 | 23.16 | 28.67 | −0.237 |
| 6 | 5.9 | 69 | 63 | 64 | 1231.12 | 1218.28 | 0.01 | 32.29 | 34.85 | −0.08 |
| 7 | 5.4 | 69 | 98 | 67 | 1140.87 | 1134.53 | 0.006 | 35.88 | 36.5 | −0.017 |
| 8 | 3.6 | 70 | 67 | 68 | 668.87 | 700.87 | −0.047 | 21.8 | 28.82 | −0.322 |
| 9 | 4.2 | 42 | 58 | 48 | 666.69 | 668.17 | −0.002 | 29.77 | 29.16 | 0.02 |
| 10 | 3.8 | 79 | 31 | 63 | 749.89 | 776.08 | −0.03 | 21.67 | 28.35 | −0.30 |
| 11 | 4.3 | 47 | 68 | 70.5 | 741.17 | 756.45 | −0.02 | 28.07 | 32.37 | −0.15 |
| 12 | 1.33 | 11 | 4 | 82 | 71.022 | 131.23 | −0.84 | 28.02 | 30.23 | −0.07 |
| Design | t (mm) | a (mm) | b (mm) | c (mm) | Fm (kN) | EA (kJ) | SEA (kJ/kg) | M (kg) |
|---|---|---|---|---|---|---|---|---|
| Initial | 5 | 56 | 56 | 51 | 905.7 | 243.6 | 25.75 | 9.46 |
| Optimal | 6 | 49 | 0 | 37 | 1060.9 | 333.9 | 36.86 | 9.06 |
| Change | 0.20 | −0.125 | - | −0.274 | 0.171 | 0.371 | 0.301 | −0.040 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, S.; Jing, T.; Zhang, J. A Few-Shot Learning-Based Crashworthiness Analysis and Optimization for Multi-Cell Structure of High-Speed Train. Machines 2022, 10, 696. https://doi.org/10.3390/machines10080696
Dong S, Jing T, Zhang J. A Few-Shot Learning-Based Crashworthiness Analysis and Optimization for Multi-Cell Structure of High-Speed Train. Machines. 2022; 10(8):696. https://doi.org/10.3390/machines10080696
Chicago/Turabian StyleDong, Shaodi, Tengfei Jing, and Jianjun Zhang. 2022. "A Few-Shot Learning-Based Crashworthiness Analysis and Optimization for Multi-Cell Structure of High-Speed Train" Machines 10, no. 8: 696. https://doi.org/10.3390/machines10080696
APA StyleDong, S., Jing, T., & Zhang, J. (2022). A Few-Shot Learning-Based Crashworthiness Analysis and Optimization for Multi-Cell Structure of High-Speed Train. Machines, 10(8), 696. https://doi.org/10.3390/machines10080696






