Abstract
The evaluation of rolling bearing performance degradation has important implications for the prediction and health management (PHM) of rotating equipment. A method for evaluation of rolling bearing performance degradation based on comprehensive index reduction and support vector data description (SVDD) is proposed in this study. Firstly, the improved variational mode decomposition (VMD) method was used to decompose vibration signals, and the defect frequency amplitude ratio index which is sensitive to early faults is extracted. Secondly, a comprehensive feature index set of rolling bearings is constructed by combining traditional time-domain and time–frequency-domain indexes, and the main features are extracted by the dimensionality reduction algorithm of locally linear embedding (LLE). Finally, the SVDD evaluation model was utilized to characterize and evaluate the rolling bearing lifetime degradation process using the distance from the test sample to the trained hypersphere center. Results showed that the proposed comprehensive degradation index can accurately detect the occurrence of early weak fault stage of rolling bearings and objectively reveal the performance degradation process of rolling bearings.
1. Introduction
Rolling bearings are an important part of modern large rotating machinery systems. Damage in bearings can lead to catastrophic accidents in the entire mechanical system. Therefore, the performance of bearings directly affects the operational reliability of the entire machinery and equipment [1,2,3,4]. Moreover, degradation stages of bearings begin from the normal state to complete failure. If researchers can monitor the degradation process and develop appropriate maintenance strategies to prevent bearing failures, then production downtime can be significantly reduced while saving on maintenance costs [5].
Feature extraction of the bearing vibration signal is a critical step before degradation assessment of rolling bearings [6,7]. Traditional time-domain feature indicators, such as root mean square (RMS) and kurtosis, are often used for bearing degradation assessment [8,9]. Although the kurtosis index can appropriately reflect the shock signal during bearing degradation, it fails to reflect the periodicity of the shock [10]. RMS can reflect energy characteristics of data and correlate them with the development of bearing failure although its sensitivity to early failures is insufficient [11]. Hence, understanding the vibration characteristics of the bearing when a fault occurs is necessary to solve these problems. The location of the damage will come into contact with the surface of other components during operation and produce a shock that excites the resonance of the bearing system when local damage of the types of crack, pitting, spalling, and indentation occur in a rolling bearing [12]. Therefore, the resonance band caused by localized fault shocks can be band-pass filtered via resonance demodulation to remove the interference and then analyzed using envelope demodulation methods to determine the presence or absence of the fault and the type of damage. The envelope signal contains information about pulses of each cycle and the severity of each pulse. Hence, fault characteristic parameters defined by the envelope signal should accurately reflect the operating state and failure mode of the faulty equipment [13]. For example, in Ref. [14], the frequency envelope method is used to analyze the faults of rolling bearings, but it needs to be carried out by changing the motor speed for the frequency spectrum obtained for normal and defective bearings in various frequency ranges. In Ref. [15], an envelope harmonic-to-noise ratio method was proposed to characterize the periodicity of fault pulses. The harmonic energy and noise energy of the envelope signal are calculated by periodic pulses to realize the detection of the initial fault. However, locating periodic pulses triggered by faults via autocorrelation methods in signals heavily influenced by noise is difficult; hence, the true time of the detected fault onset can lag behind the actual time [16]. The defect frequency amplitude ratio indicator based on envelope spectrum analysis is sensitive to early faults and extracted and used as a degradation assessment indicator in this work while considering the influence of interference factors. Although traditional time-domain features demonstrate low sensitivity to initial faults, they present satisfactory consistency in the overall trend of degradation; the frequency-domain method is an integral transformation method that can directly extract useful frequency components from the signal despite its limited ability to extract features of nonsmooth bearing signals with statistical characteristics that change with time [17]. The time–frequency-domain method presents disadvantages of uncertainty and insensitivity to early faults as well as advantages of acceptable characterization of nonsmooth signals with statistical characteristics that change with time. Therefore, feature indicators constructed in this study are comprehensive because they consider the assessment limitations of single indicators and integrate the advantages of traditional time-, frequency-, and time–frequency-domain indicators to form a multidimensional feature space. The LLE nonlinear dimensionality reduction algorithm is used to extract main features on the basis of the original popularity given that the multi-Witt collection typically leads to computational complication problems [18].
A similarity model based on feature extraction is commonly used for the assessment of performance degradation. For example, Ref. [19] proposes a degradation assessment model based on the hidden Markov model, but the number of hidden states must be determined in advance and this scenario is unrealistic in practical applications. Refs. [20,21] put forward a performance degradation evaluation model based on the Gaussian mixture model (GMM). Although the GMM-based model can effectively address the distribution of bearing data, its computation and processing are complicated. Refs. [22,23] propose an equipment performance degradation assessment model based on fuzzy C-means clustering (FCM) for rolling bearing performance degradation assessment although its model training requires normal and completely failed data, which are inapplicable to actual situations. SVDD is an effective single-value classification algorithm that can primarily map samples to a high-dimensional inner product space through nonlinear mapping and find a minimum hypersphere in the space that contains all or the majority of normal sample points. Data that do not belong in this class are located outside the hypersphere. On the basis of this principle, the SVDD model only needs the normal state to build and distinguish normal data from data in other states. Notably, this model is widely used in the field of data outlier detection and performance degradation because of its advantages of high computational efficiency and robustness [24,25].
Accordingly, a comprehensive indicator dimensionality reduction method combined with an SVDD assessment model for performance degradation assessment is proposed in this study. The vibration signal is decomposed using an improved VMD method to extract frequency-domain indexes that can provide an evident amplitude ratio of the initial fault and are then combined with traditional time-domain and fast approximation entropy indexes in time-domain indicators to build a comprehensive feature index. The main features are extracted using the LLE dimensionality reduction algorithm and then combined with the SVDD model to achieve the performance degradation assessment of the bearing. The effectiveness and superiority of the proposed method is verified using experimental data on the full-life fatigue of rolling bearings.
2. Feature Extraction and Dimensionality Reduction
2.1. Improved Variational Mode Decomposition
VMD decomposition methods have been successfully used in fault diagnosis of rotating machinery. The VMD method can solve problems of modal mixing and endpoint effects compared with empirical mode decomposition (EMD) and ensemble empirical mode decomposition (EEMD) methods [26]. The specific decomposition steps are described in [27]. However, the requirement to set the number of decompositions before decomposition, the presence of a memory overflow problem when data are excessively large, and possible existence of over-decomposition after decomposition are limitations of the VMD method. Therefore, combining the decomposition of low frequency with the principle of modal reorganization is proposed in this work to achieve adaptive decomposition of the VMD algorithm. The flowchart of the improved VMD method is shown in Figure 1.
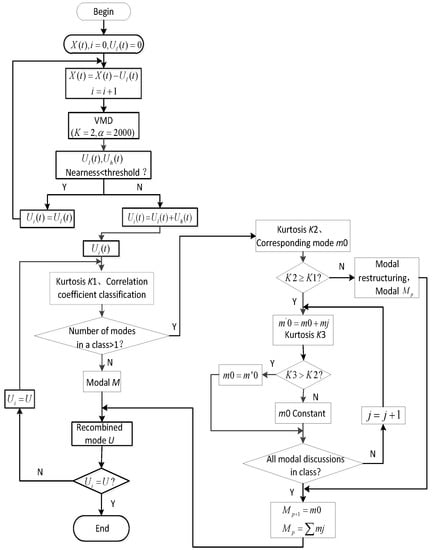
Figure 1.
Improved VMD flowchart.
- (1)
- Initialize and . Assign the original signal to , and assign the low-frequency mode to 0.
- (2)
- Remove low-frequency modes. remove the low-frequency mode from at each run as follows:
- (3)
- Perform VMD decomposition. The number of fixed decompositions K is set to 2, and the penalty factor parameter alpha is set to 2000. The relevant literature showed that the penalty factor demonstrates strong applicability when the penalty factor is set to 2000 and VMD is suitable for extracting low-frequency modal components when the penalty factor is beyond 2000. Therefore, the VMD was run one at a time to obtain both high- and low-frequency modes.
- (4)
- Iteration stop judgment. Stop the iteration when the posting progress of central frequencies of the two modes obtained from the decomposition is less than the set threshold to obtain the final decomposed mode. The posting progress is defined as follows:where and represent the posting progress of center frequencies of modes and , respectively. Step (2) is performed when is less than the set threshold; otherwise, the sum of all low- and high-frequency modes is calculated. Finally, all modes are outputted .
Modal reorganization of components obtained after the decomposition of the delowered VMD decomposition method [28] is carried out to avoid splitting of adjacent modes due to over-decomposition and extract the signal effectively.
- (5)
- Take the kurtosis. Mode is represented by , and the kurtosis is calculated for all modes . The maximum kurtosis value is denoted as .
- (6)
- Initial mode classification. Fast Fourier transform (FFT) is performed on mode to obtain the corresponding spectrum of each mode as follows:where represents the number of modal components, represents the length of the signal, and represents the amplitude spectrum of modalities. The normalization of obtains as follows:
Spectral correlation coefficients for all neighboring modes in mode are calculated as follows:
The average of all spectral coefficients obtained through Equation (5) is used as the clustering threshold and calculated as follows:
The relationship between the spectral overlap coefficient and the threshold value initially classifies the decomposed modes. Two adjacent modes may contain the same frequency components and a mixing problem may exist when . The two modes are then placed in one category; otherwise, the modes are placed in two categories, respectively.
- (7)
- Modal reorganization determination. On the basis of the kurtosis, the reorganization of the class with more than one mode is determined and the maximum kurtosis S of modes in the class is compared with the value of kurtosis . When , the modal classification in the class is considered to be dominated by noise, the modal reorganization in the class. When , all modalities in the class are combined with corresponding modalities , respectively, and, based on the above principle, the decision is made whether to reorganize or not. Finally, all modalities are outputted after regrouping.
2.2. Mode Selection Based on KCI Features
The feature selection indicator selects the modalities obtained after improving the VMD and determines the acceptability of decomposed modalities. The kurtosis index is usually used as an indicator for evaluating the fault impact strength of mechanical damage, but it relies on the distribution density of the shock. The correlation characterizes the acquaintance of two signals but is susceptible to noise during the detection of the shock signal. Therefore, advantages and disadvantages of both kurtosis and correlation are combined to construct a weighted kurtosis index as the basis for feature selection and achieve an effective selection of modes obtained from the improved VMD. KCIs are expressed as follows:
where is the kurtosis, is the signal length, is the correlation, is the covariance, and is the variance.
2.3. Defect Frequency Amplitude Ratio
Probable fault index (PFI) is used to extract a valid indicator from the envelope spectrum that can characterize the fault and evaluate the ability of the fault characteristic frequency to behave in the envelope spectrum; hence, the relative change in amplitude at the fault characteristic frequency of a certain fault type relative to the amplitude at the characteristic frequency in the normal state is examined [29]. PFI can be expressed as follows:
where is the amplitude at the fault characteristic frequency and is the average value of the amplitude at the fault characteristic frequency for that type of fault under healthy conditions.
Actual operating conditions are also considered although the fault is absent, PFI values may be large due to strong noise effects, and deviations caused by speed variations or relative sliding effects may lead to misdiagnoses. Therefore, the following indicator is introduced to solve this problem:
where is the amplitude at the fault characteristic frequency. The denominator is the average of all amplitudes in the 10 Hz band around the fault characteristic frequency.
Although the indicator is intended to address the impact due to interference factors, the indicator is limited by the overall frequency band around the defect frequency, thereby resulting in a volatile indicator and increased computational difficulty of the capture algorithm. Therefore, the indicator is proposed in this work on the basis of these indicators to highlight the influence of dominant frequency band peaks around the fault. This indicator narrows the capture range to the influence of 10 dominant peak points on the characteristic frequency of the fault to the left and right. The indicator is calculated as follows:
where the denominator is the average of the amplitude of 10 peak points to the left and right of the fault characteristic frequency (dominant peak point can be set according to the complexity of actual data).
2.4. Comprehensive Indicator Downscaling
The defect frequency amplitude ratio is proposed as a new index to assess the bearing performance degradation and sensitivity to initial bearing degradation as well as examine the bearing performance degradation as part of the frequency-domain index. Meanwhile, the traditional time-domain and fast approximate entropy indexes in the time- and frequency-domain are jointly constructed as a comprehensive characteristic parameter to consider the limitation problem of a single index for assessment and investigate the rolling bearing performance degradation and construct a comprehensive set of features.
The LLE dimensionality reduction algorithm is introduced to extract the main features on the basis of the original popular structure given that a multidimensional feature set will likely lead to computational complexity and high dimensionality may reduce the performance of the evaluation model. The specific principle of LLE is referred to in literature [18].
3. Support Vector Data Description
The main idea of the support vector data description is to find the minimum hypersphere that can cover target samples, with inner samples of the hypersphere as target sample points and outer sample points as nontarget sample points or outliers [30]. The hypersphere model is shown in Figure 2, where is the center that represents the model and is the radius of the sphere.
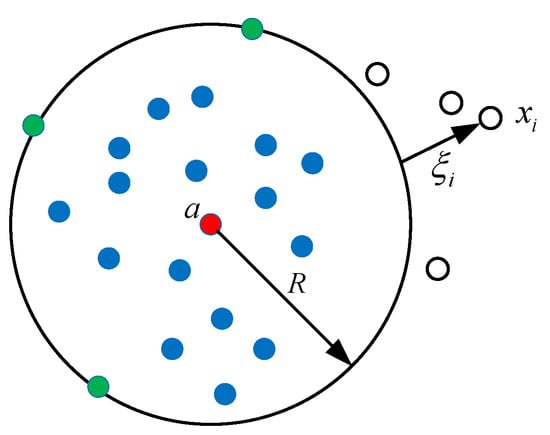
Figure 2.
Diagram of the hypersphere classification.
The model takes into account that the target sample will contain a small number of outlier points. A relaxation factor and a penalty parameter are introduced to improve the robustness of training data and allow a small number of sample points to lie outside the hypersphere. Thus, the model is transformed into the following minimization problem:
A Lagrange equation is introduced to solve the optimization problem of Equation (13) as follows:
where and are Lagrangian coefficients. Partial derivatives of , , and in Equation (14) are determined and then set to zero.
Substituting Equation (15) into Equation (14) obtains the following optimization function:
where is the kernel function instead of the inner product operation. Thus, a low-dimensional nonlinear problem is converted to a high-dimensional linear problem. The radius of the hypersphere can be calculated from the distance of an arbitrary support vector to the center as follows:
Furthermore, the distance of the new sample from the center of the sphere for an arbitrary new sample can be expressed as follows:
If , then the new sample is in the interior of the hypersphere and can be considered normal; otherwise, does not belong to the training sample category and is an outlier. Therefore, according to this principle, the SVDD model can be applied to the field of bearing performance degradation assessment.
4. Performance Degradation Assessment Based on Combined Metric Downscaling and SVDD
A performance degradation assessment method based on comprehensive index dimensionality reduction combined with the SVDD model is proposed in this study to understand the degradation process of a set of full-life data samples from the normal state to final failure. The model is divided into two parts, namely, offline and online, in which the normal-state multidimensional data are downscaled as the training sample and the trained model is evaluated online for the whole-life data, as shown in Figure 3.
Step 1: Feature extraction. Extract training samples, that is, time-, frequency-, and time–frequency-domain feature indicators in the normal state, to construct a comprehensive feature indicator set.
Step 2: Model training. Normal-state integrated feature indicators are dimensionalized, and the extracted main features are used as training samples for the SVDD model to obtain the optimal hypersphere containing normal feature samples with a hypersphere radius of .
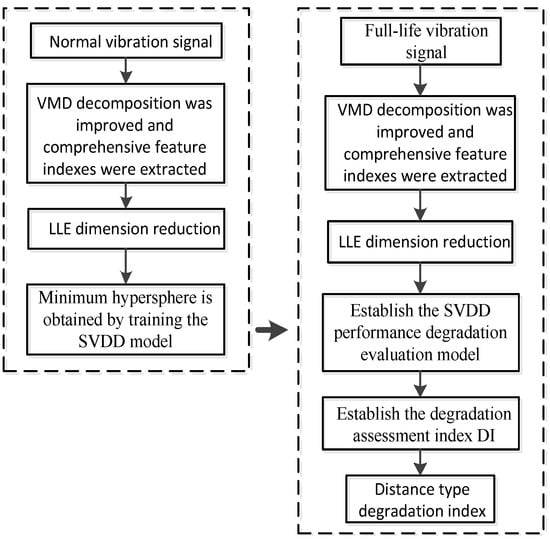
Figure 3.
Overall process of degradation assessment.
Step 3: Degradation evaluation. The degraded full-life data are inputted into the established SVDD degradation model to obtain the distance between the data and the center of the hypersphere, and the performance degradation indicator (DI) is established using the relationship between and the radius of the hypersphere [31]. The indicator is calculated as follows:
If , then the data are considered in the normal-state range. Otherwise, the data are considered abnormal values and the bearing is in the degraded state. values are normalized to solve the coordinate problem, ensure that vertical coordinates are the same, and facilitate intuitive analysis.
5. Experimental Analysis and Validation
5.1. Presentation of Experimental Data
Data 1: Publicly available experimental data from the Bearing Data Center at Casey Western Reserve University (CWRU), USA were used to verify the usefulness of the downscaling algorithm [32]. As shown in Figure 4, the test rig consists of a 2 hp drive motor, a torque transducer, and a generator connected on the right side. The bearing type at the drive end was SKF 6205 and the data were sampled at 12 kHz. The equipment was machined on bearing parts using EDM cutting to simulate different types of failures and various levels of the bearing failure. The bearing inner ring failure data were obtained at a speed of 1750 r/min and a load of 0; the four levels of failure demonstrated a failure depth of 0.007, 0.014, 0.021, and 0.028 inches; and normal-condition data were used in this study.

Figure 4.
CWRU bearing test rig.
Data 2: Full-life data were publicly available information from the Intelligent Maintenance Systems (IMS) Center at the University of Cincinnati, USA [33]. The experimental device is shown in Figure 5, it is mainly composed of an AC motor, a shaft, and four bearings (ZA-2115 double row roller bearings). The rotational speed was 2000 r/min, the sampling frequency was 20 kHz, the sampling interval was 10 min, the sampling length was 20480 points, and the bearing was subjected to a radial load of 6000 lbs.
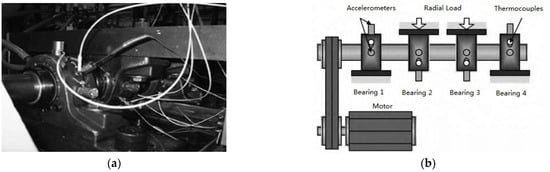
Figure 5.
The experimental equipment of the state degradation of rolling bearings; (a) bearing test rig illustration; (b) sensor placement in the test rig [34].
In this experiment, the bearing parameters are as follows: pitch diameter is 71, 5 mm, rolling element diameter is 8.4 mm, number of rolling elements per row is 16. The characteristic frequencies are as follows: outer ring defect frequency is 236 Hz, inner ring defect frequency is 297 Hz, rolling element defect frequency is 279 Hz, and shaft rotation frequency is 33.33 Hz. In this study, the outer ring fault data of bearing 1 and bearing 3 are selected for analysis, which include the process from normal to failure of the bearing outer ring. Among them, bearing 1 collected 984 data sets from 12 February 2004 10:32:39 to 19 February 2004 06:22:39. Since the last two data sets are completely invalid, only 982 data sets are analyzed here.
5.2. Effectiveness of VMD Improvements
The enhanced decomposition characteristics of the improved VMD were analyzed using a set of real laboratory signals to verify its effectiveness. The data were obtained from publicly available full-life bearing data from the University of Cincinnati in the USA. These laboratory data were used in the rolling bearing performance degradation assessment in this study. During this experiment, the simulation software was MATLAB 2019, the CPU configuration and operating system information is as follows: (1) i5-10210U CPU@1.60GHz 2.11 GHz, (2) Windows 21H2 RAM 16.0 GB.
A modified VMD analysis was performed on data sample 533, which is an early degradation point that was analyzed through degradation analysis when the performance degradation was examined. Figure 6 presents the waveform and envelope spectrum after direct processing of the original signal. Although the outer ring fault characteristic frequency in the envelope spectrum in Figure 6b was doubled, finding other octave components of the outer ring fault characteristic frequency in the envelope spectrum is difficult.
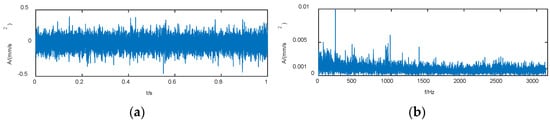
Figure 6.
Time-domain waveform and envelope spectrum of the original signal; (a) time-domain waveform; (b) spectral envelope.
The VMD method was used for the decomposition, and only the signal at 0.75 s was used here for the analysis due to the limitations of the VMD decomposition on the computer memory. Meanwhile, and VMD parameters α and K were set to 2000 and 6, respectively. The histogram was obtained via KCI calculation on the basis of KCI for the selection of decomposed modes (Figure 7). IMF3 is the optimal mode component for the envelope analysis, as shown in Figure 8.
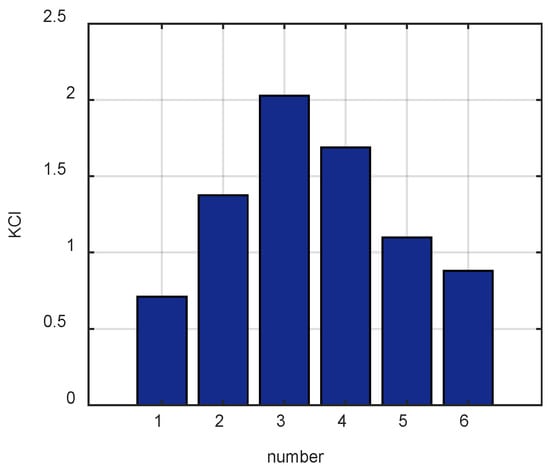
Figure 7.
Histogram of the model obtained by KCI.
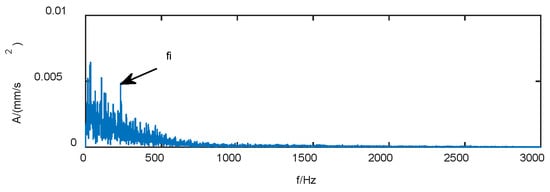
Figure 8.
The envelope spectrum of IMF3.
The envelope spectrum demonstrated that one octave of the fault characteristic frequency is only weakly highlighted by noise interference and other octave components of the fault characteristic frequency are absent in the envelope spectrum.
The data were then processed using the modified VMD, and all modes obtained by this method were subjected to the modal selection based on the weighted kurtosis index (KCI). The selected modes were subsequently subjected to envelope analysis. Figure 9 illustrates the histogram obtained via KCI for the reconstituted modes. IMF2 is the optimal mode component for the envelope analysis. The results are presented in Figure 10.
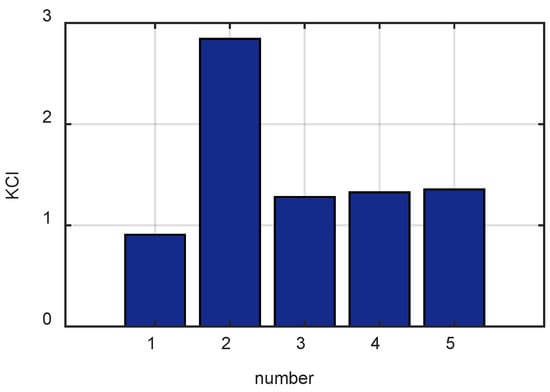
Figure 9.
Histogram of the recombination model obtained by KCI.
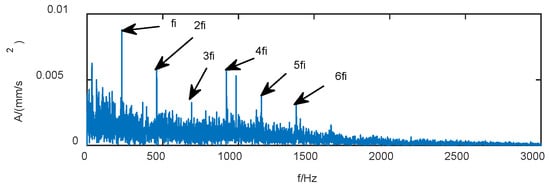
Figure 10.
The envelope spectrum of IMF2.
Figure 10 shows that the characteristic frequencies of bearing outer ring faults and their multiples can be clearly observed in the envelope spectrum of the mode selected via the improved VMD and the weighted kurtosis index. This finding indicated that the improved VMD can successfully extract fault information. Meanwhile, the peak signal-to-noise ratio of the optimal mode obtained using the VMD and the improved VMD was calculated to compare the filtering effect of these two methods quantitatively; note that a large peak signal-to-noise ratio of the mode corresponds to an enhanced filtering effect [35]. The two filtering results are shown in Table 1. The filtering effect based on the improved VMD is significantly better than that of the VMD method and beneficial to the extraction of feature indicators.

Table 1.
Filtering effect comparison.
5.3. Comparative Analysis of the Effect of LLE Downscaling
Degradation states can be denoted by representative features. An effective dimensionality reduction algorithm is essential in extracting the main degradation features and defining changes in the degradation process of the bearing because of the multidimensional input of indicators with characterization of bearing degradation.
The LLE is a principal component analysis (PCA) algorithm that was used to assess the two-dimensional visual space popularity performance of the data from data one. The data were divided into four levels of failure for the inner ring at 0.007, 0.014, 0.021, and 0.028 inches as well as the normal condition. The data for each state consisted of 20 samples, with 4096 sampling points in each sample.
Fault data were identified, and time-, frequency-, and time–frequency-domain feature indicators were extracted as multidimensional feature indicators. The LLE prevalence algorithm was used for feature dimensionality reduction, and the first two dimensions of prevalence features, namely, y1 and y2, were used as the respective horizontal and vertical coordinates of the two-dimensional spatial display, as shown in Figure 11a. The PCA method was also utilized for comparative analysis. The result of dimensionality reduction based on popular features indicated that the enhanced projection performance can improve the clustering and separation. Moreover, the data are changed according to the trend of increasing severity level, except for faults with categories 0.007 and 0.014, likely due to the small distance between these two fault levels that result in similar fault performance. Notably, the trend of the LLE-based method varies strictly according to the degree of fault. Meanwhile, the PCA-based method is a linear distribution of second-order statistical significance in nature that fails to reflect the essential nonlinear characteristics of the bearing performance degradation process clearly. Therefore, the LLE-based popular feature algorithm can improve the degradation performance to a certain extent and be used in the degradation assessment of bearings.
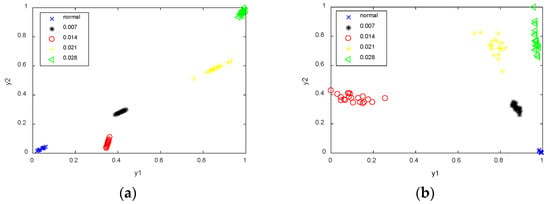
Figure 11.
Comparison of dimensionality reduction effects of different methods; (a) LLE feature dimension reduction results; (b) PCA feature dimension reduction results.
5.4. Assessment of Performance Degradation of Full-Life Rolling Bearings
The range data and calculated data points of outer ring failure data of the time-domain shape of the Cincinnati full-life cycle bearing 1 shown in Figure 12 demonstrated that the waveform amplitude suddenly increases and the bearing shows evident failure when data are located in group 703. Similarly, a significant increase in waveform amplitude occurs again and the bearing should enter a failure condition when data are located in group 970. Although the two significant locations of failure can be identified by looking at the full-life time-domain waveform, the onset of weak failures cannot be identified by direct observation until group 703. This phenomenon is not conducive to early failure maintenance. Moreover, the whole bearing degradation process requires further evaluation.
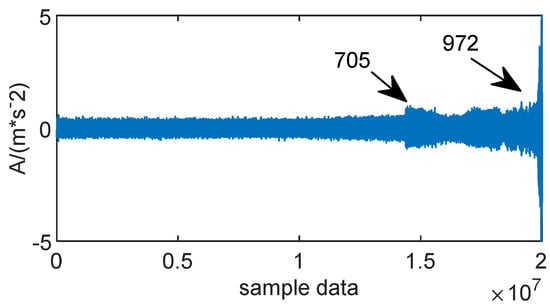
Figure 12.
Time-domain waveforms of bearing 1 outer ring failure data for the full-life cycle.
The degradation assessment process refers to the effective identification of degradation stages of a bearing. The key to degradation assessment is the extraction of degradation indicators. Indicators should be simple to calculate, sensitive to early failure detection, and able to provide consistency on the overall degradation trend. The RMS values for 982 data sets are shown in Figure 13.
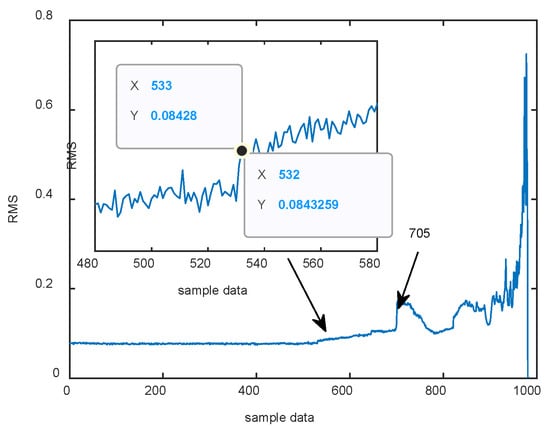
Figure 13.
RMS of original vibration signals.
According to the RMS value changes, a clear and abrupt change occurred at sample point 705. Specifically, a weak monotonic increasing trend exists between points 533 and 705, thereby indicating that observing the early failure initiation and evolution process through RMS is difficult. However, the RMS values show an overall trend of deterioration and smoothing of the bearing at various stages, and the monotonic increase in fluctuations reflects the impact strength of the signal to a certain extent. Hence, RMS values can be used as a characteristic indicator for degradation assessment because this finding is consistent with the bearing degradation process.
A characteristic indicator based on the amplitude ratio of defect frequencies is proposed due to the insensitivity of traditional time-domain indicators, such as RMS values, to the early degradation of rolling bearings. Note that the indicator concept has been introduced in the previous Section 2.3. The extraction of the defect frequency amplitude ratio indicator is achieved through the envelope capture combined with the indicator principle by improving the VMD decomposition. The extracted defect frequency amplitude ratio indicator is shown in Figure 14.
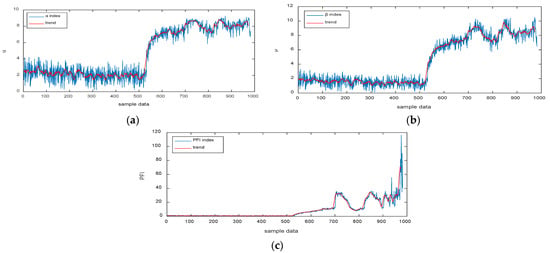
Figure 14.
α, β, and PFI indexes; (a) α index; (b) β index; (c) PFI index.
As shown in Figure 14, the indicator begins to increase significantly at around 530 sample points and the value of the indicator remains high until the end of the experiment. Therefore, the proposed indicator is more sensitive to early failures than the RMS indicator.
In addition, a comprehensive set of characteristic indicators is established in this work by considering the limitations of single indicators, the ability of time-domain indicators to be consistent with the degradation trend, the ability of time- and frequency-domain indicators to characterize nonstationary signals, and the sensitivity of the proposed defect frequency amplitude ratio to early degradation in the frequency-domain.
The extracted degradation indicators demonstrated that when the bearing operation is in the first 400 sets of data during the operation period, both from the data waveform and from each characteristic indicator are relatively stable, and the bearing can be considered to be working under normal conditions. SVDD model parameters were set to and . Feature indicators of full-life data are dimensionalized using LLE, and the first two dimensional feature vectors are inputted into the established SVDD degradation assessment model given that these vectors can appropriately characterize degradation characteristics of bearings after dimensionalization. The variation trend of the proposed method is presented in Figure 14.
The dynamic criterion is used as an adaptive alarm threshold [36]. The traditional threshold line is typically a horizontal state threshold. However, the threshold value can suffer from abnormal fluctuations that lead to fault misclassification when perturbed by external factors. Therefore, a dynamic and adaptive threshold line is used. This threshold line is different from the traditional criterion because it sets multiple consecutive indicator values beyond the value range delineated by previous indicator values as well as assumes that the current operating state of the bearing equipment has transformed from the previous stage.
As shown in Figure 15, the degradation curve exceeds the dynamic threshold line at sample 533. This finding indicated the onset of failure. The rise in the curve in a gradual increment between sample points 533 and 705 implied that the failure gradually increases. The sharp change in the curve around sample point 705 is due to the failure deepening and smoothing process, which can be considered the moderate degradation stage. The same situation occurs at around 850 points, thereby indicating that the bearing degrades to the next level again. This part is considered the severe degradation stage. A sudden drop occurs after an uncontrollable rise at around 972. This scenario indicated that the bearing has completely failed. Various stages of bearing degradation in the proposed method are clearly distinguished and the sensitivity of degradation significantly increases in the early stages, with the whole degradation process showing a monotonically rising process. This finding is consistent with the degradation trend of the bearing.
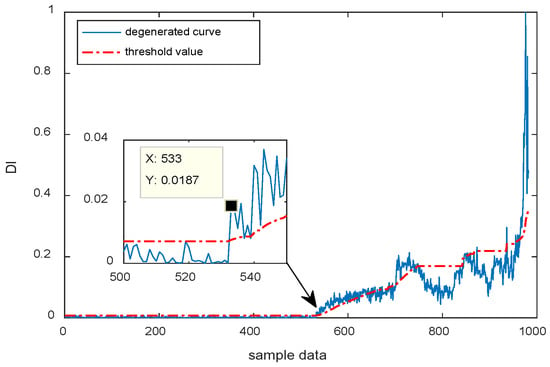
Figure 15.
Degradation index based on LLE-SVDD.
Original data were subjected to PCA dimensionality reduction to highlight the effectiveness of the method, and the contribution rate of dimensionality reduction must be more than or equal to 85% under normal circumstances to ensure that the information can approximately reduce features without losing the main data. The contribution rate in this study is set to 90%. Figure 16 presents that the contribution rate of the first two principal components is already greater than 90%. Hence, the first two dimensions after dimensionality reduction are used as the feature input in the SVDD assessment model. The obtained degradation curve is shown in Figure 17.
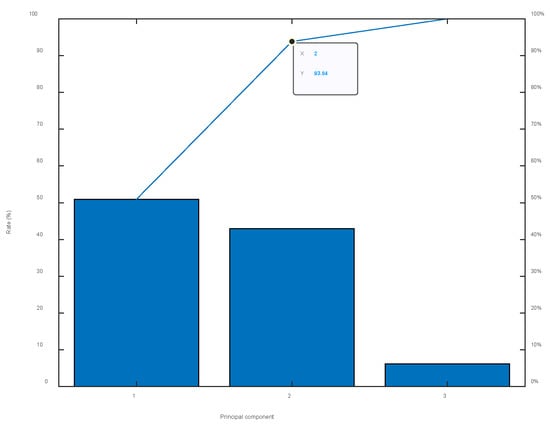
Figure 16.
Dimensionality reduction of each principal component contribution rate via PCA.
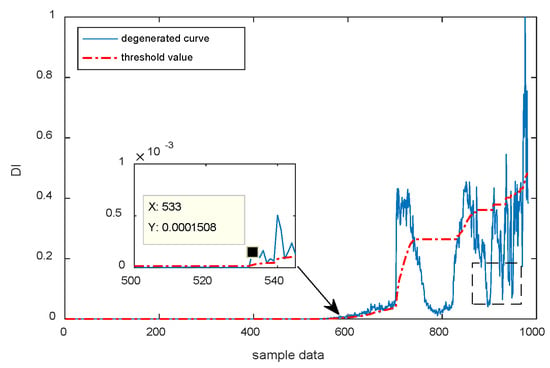
Figure 17.
Degradation index based on PCA-SVDD.
According to the results of the PCA method, the PCA-based method can also detect early faults at 533 sample points because feature indicators extracted in this study exert a strong effect on early faint faults but is not as sensitive to the initial degradation as the LLE-based method. The PCA-based method combined with SVDD fluctuates more intensively at each stage in the robustness analysis, likely due to some poor-quality influence, as shown in the black box in the figure. Failure of the PCA-based method to extract effective components results in more significant fluctuations, which are inconsistent with the monotonic variation characteristics of faults and can easily cause misdiagnosis.
Similarly, raw data were inputted directly into the SVDD model for comparative analysis. The degradation results are shown in Figure 18. The results are basically similar to those of the PCA-based method combined with SVDD, and the curve fluctuates more sharply. The influence of poor-quality feature indicators leads to a minimally robust curve, which fails to reflect the degradation trend properly in the later stages of degradation.
The SVDD assessment model was replaced with a fuzzy C-mean clustering model to highlight the superiority of the degradation assessment curve based on LLE downscaling combined with the SVDD assessment model further. The model was first trained on a number of groups of normal-state data and a number of groups of completely failed bearing characteristics, with clustering centers for both types of data. The fluctuation range of the degradation curve is set between the value of 0 and 1. The index value is 1 when the data are normal-state data, that is, the subordination degree is 1. The subordination degree is small as it approaches to 0, thereby indicating that the bearing degradation state becomes increasingly serious. The results of LLE dimensionality reduction-based features combined with the FCM assessment model are illustrated in Figure 19.
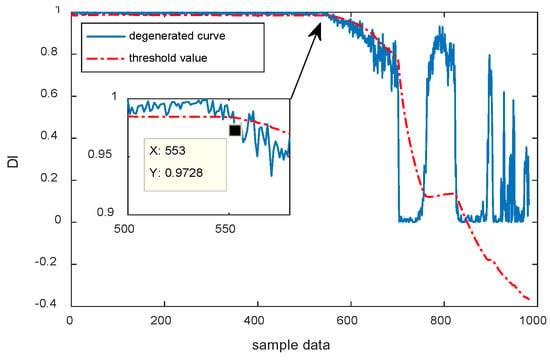
Figure 19.
Degradation index based on LLE-FCM.
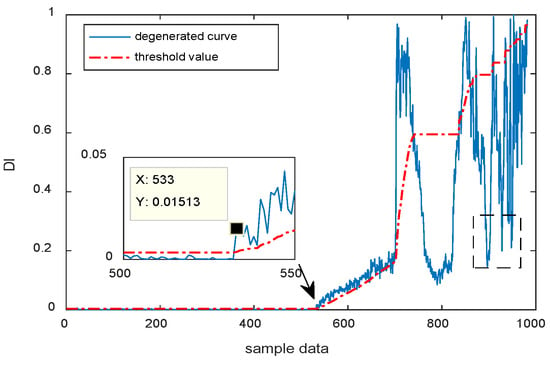
Figure 18.
Degradation index based on original features and SVDD.
As shown in Figure 19, the FCM-based assessment model demonstrates multiple consecutive samples that exceed the threshold line near sample point 553. This finding is approximately 20 sample points later than the onset of degradation detected by the proposed LLE-based reduced dimensional features combined with the SVDD assessment model. Hence, a delay of 200 min exists in the detection of the initial degradation of the bearing. This phenomenon is not conducive to the detection of early degradation as well as the detection and repair of actual failures. Furthermore, the FCM assessment model presented that the degree of affiliation reaches 0, which indicates complete failure, and begins to increase again. This phenomenon is inconsistent with the actual situation, as shown in the dashed black box. Moreover, the threshold line appears monotonically uncontrollable at the late stage of degradation due to the misleading distortion of the degradation curve.
The comprehensive analysis of this comparison showed that the proposed LLE-based method combined with SVDD for bearing degradation assessment can clearly distinguish between various stages, is clearly sensitive to early bearing degradation, and presents a monotonically increasing degradation process. These findings are consistent with the bearing degradation trend.
5.5. Fault Verification in All Stages of Bearing Degradation
Envelope analysis was conducted for key sample points 532, 533, 705, 850, and 972 in the degradation assessment curve to verify the inferences drawn from the degradation assessment results in this study for the start of each stage. Data from each key sample point were adaptively decomposed into a number of modes using the improved VMD method, and the mode with the maximum corresponding weighted kurtosis index was selected for the envelope analysis by means of the weighted kurtosis index. The envelope demodulation results for each sample point are illustrated in Figure 20.
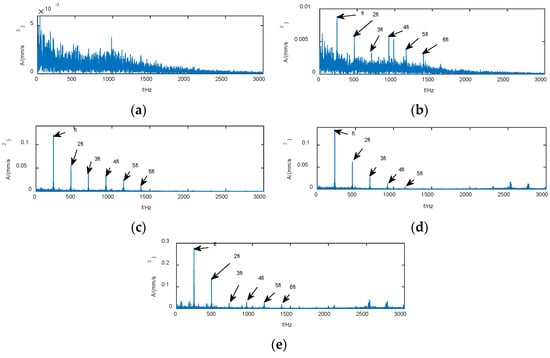
Figure 20.
Envelope demodulation of key sample points; (a) 532nd data point; (b) 533rd data point; (c) 705th data point; (d) 850th data point; (e) 972nd data point.
The analysis of envelope results demonstrated that the envelope spectrum fails to find components similar to the fault characteristic frequency at sample point 532, as shown in Figure 20a. The envelope demodulation of sample point 533 at the beginning of the early fault is presented in Figure 20b. The outer ring fault characteristic frequency and its multiplier components can be clearly observed in the envelope spectrum, and the amplitude at the fault frequency is 0.0087, thereby indicating the occurrence of early degradation. The fault characteristic frequency and its multiplier at sample point 705 in Figure 20c become increasingly clear, and the fault amplitude increases to 0.1215. The fault characteristic frequency and its multiplication frequency at sample point 850 in Figure 20d are also observed, and the amplitude increases further to 0.135. The fault characteristic frequency amplitude at sample point 972 increases abruptly to 0.2787, thereby indicating that the bearing has reached extremely severe degradation and is about to fail. The detailed analysis results are shown in Table 2. The envelope analysis showed that the results are generally consistent with the assessment results.

Table 2.
Key sample point degradation analysis.
To further verify the effectiveness of the model proposed in this paper, we have added data analysis of bearing 3 of the same type in the case of data verification of bearing 1 (the Intelligent Maintenance Systems Center at the University of Cincinnati, Cincinnati, OH, USA). In order to compare with bearing 1, one sample is drawn every seven samples from the 6324 samples, and a total of 904 samples are drawn. The full-life degradation time-domain waveform of bearing 3 is shown in Figure 21. From about the 874th sample after filtering (point 17899520 of the original data), the amplitude of the time-domain waveform rises significantly.
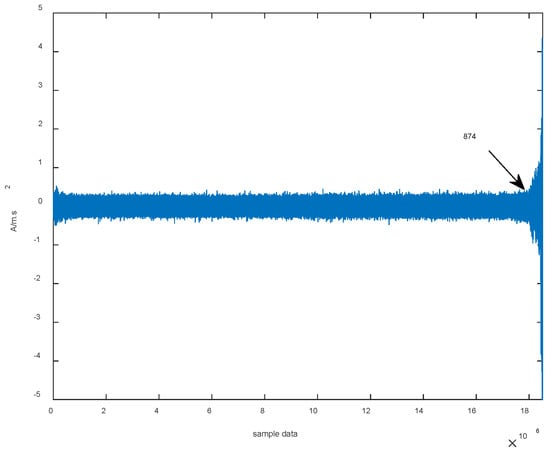
Figure 21.
Life-time degradation time-domain waveform of bearing 3.
The model proposed in this paper only uses the normal data of the rolling bearing to train the SVDD model. When the performance degradation of the rolling bearing needs to be verified, the failure or full-life cycle data of the rolling bearing can be used to obtain the performance degradation index curve. Therefore, this method cannot directly evaluate the degradation of rolling bearings that are not included in the learning process (the SVDD model is not trained with normal data). Similarly, since the normal thresholds corresponding to different bearings may vary greatly, and are prone to false alarms, the degradation threshold curve corresponding to the rolling bearing 1 cannot be directly used as the threshold curve of the rolling bearing 3. Therefore, the model still needs to be trained using the normal data of the bearing being evaluated. Bearing 3 degradation index based on LLE and SVDD is shown in Figure 22. Near the 108th sample point, the degradation index DI value exceeds the threshold line (green) of bearing 1, which is unreasonable, so the threshold line (red) trained by bearing 3 needs to be used. Similarly, at the 854th sample, the degradation index DI exceeds the threshold line. Compared with the time-domain waveform, the degradation index DI value not only clearly shows the degradation trend of bearing 3, but also earlier than the degradation point reflected by the time-domain waveform.
It can be seen from the above analysis that this method has nothing to do with the number of bearings to be learned, but is related to whether the normal data of the bearings can be obtained accurately, which is easier to realize in engineering practice.
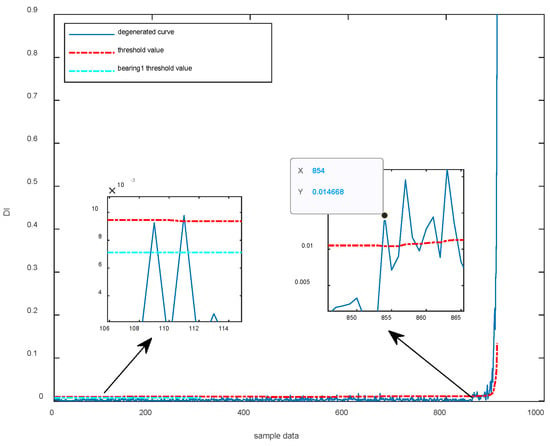
Figure 22.
Bearing 3 degradation index based on LLE and SVDD.
To verify the degradation process of bearing 3, the 854th, 872nd, and 902nd sample points after screening were selected for envelope demodulation analysis. The analysis results are shown in Figure 23. It can be seen that the fault characteristic frequency of the outer ring and its multiplier amplitude gradually increase until the bearing fails completely. It should be pointed out that the degradation point of bearing 3 is later than that of bearing 1, but the degradation speed is faster in the later stage.
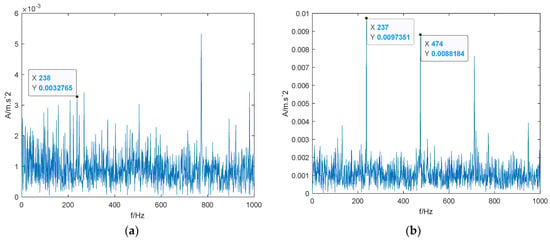
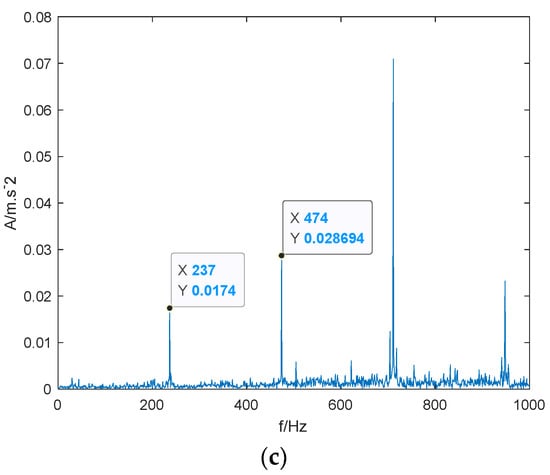
Figure 23.
Envelope pectrum of key sampling points in bearing 3; (a) 854th data point; (b) 872nd data point; (c) 902nd data point.
6. Conclusions
A comprehensive index degradation and SVDD rolling bearing performance degradation assessment method is proposed in this study. The following conclusions can be drawn from the results of this study.
- (1)
- The original vibration signal is decomposed using the improved VMD method, and modalities selected by the weighted kurtosis index are demodulated via enveloping with evident filtering effect. This effect is beneficial for separating early fault characteristics from the disturbance noise and conducive to the extraction of feature indicators.
- (2)
- Defect frequency amplitude ratio indicators, which are sensitive to early faults and more sensitive to early fault onset than traditional RMS indicators, are extracted to address the problem of strong sensitivity of effective feature indicators to the initial stage.
- (3)
- LLE dimensionality reduction is carried out on extracted comprehensive feature indicators to extract the main features, and the SVDD degradation assessment model combined with the relative distance indicator is used in the degradation assessment of the whole-life bearing. The proposed method is important for online health monitoring and early warning of bearings in practical production.
Author Contributions
Conceptualization, H.X. and H.Z.; methodology, J.W.; software, H.Z.; validation, Y.Y. and H.Z.; formal analysis, H.X.; investigation, Y.Y.; resources, H.X.; data curation, Y.Y.; writing—original draft preparation, H.X.; writing—review and editing, J.W.; visualization, Y.Y.; supervision, J.W.; project administration, J.W.; funding acquisition, J.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science and Technology Development Program of Jilin Province-Key R&D Project under Grant Number 20220203077SF.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
This research used the published rolling bearing datasets of Western Reserve University. The access of the datasets is https://engineering.case.edu/bearingdatacenter/welcome (accessed on 7 July 2022). This research used the published rolling bearing datasets of IMS, University of Cincinnati. “Bearing Data Set”, NASA Ames Prognostics Data Repository. NASA Ames Research Center, Moffett Field, CA. 2007, Available online: https://ti.arc.nasa.gov/progect/prognostic-data-repository (accessed on 7 July 2022).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, F.; Chen, Y.; Wang, J.; Zhou, X.; Tang, B. A Reinforcement Learning Unit Matching Recurrent Neural Network for The State Trend Pre-diction of Rolling Bearings. Measurement 2019, 145, 191–203. [Google Scholar] [CrossRef]
- Hu, Y.; Li, H.; Shi, P.; Chai, Z.; Wang, K.; Xie, X.; Chen, Z. A Prediction Method for The Real-time Remaining Useful Life of Wind Turbine Bearings Based on The Wiener Process. Renew. Energy 2018, 127, 452–460. [Google Scholar] [CrossRef]
- Fardin, D.; Myeongsu, K.; Satar, D.; Michael, P. Detection of Generalized-roughness and Single-Point Bearing Faults Using Linear Prediction-based Current Noise Cancellation. IEEE Trans. Ind. Electron. 2018, 65, 9728–9738. [Google Scholar] [CrossRef]
- Cao, L.; Li, J.; Peng, Z.; Han, W.; Zhang, Y. Fault Diagnosis of Rolling Bearing Based on EEMD and Fast Spectral Kurtosis. J. Mech. Eng. 2021, 38, 1311–1316. [Google Scholar]
- Qian, Y.; Yan, R.; Gao, R.X. A Multi-time Scale Approach to Remaining Useful Life Prediction in Rolling Bearing. J. Mech. Syst. Signal Process. 2017, 83, 549–567. [Google Scholar] [CrossRef] [Green Version]
- Randall, R.B.; Antoni, J. Rolling Element Bearing Diagnostics—A Tutorial. Mech. Syst. Signal Process. 2011, 25, 485–520. [Google Scholar] [CrossRef]
- Saidi, L.; Ali, J.B.; Fnaiech, F. Bi-spectrum Based-EMD Applied to The Non-stationary Vibration Signals for Bearing Faults Diagnosis. ISA Trans. 2014, 53, 1650–1660. [Google Scholar] [CrossRef]
- Li, Y.Q.; Wang, R.X.; Xu, M.Q.; Zhou, R.S. A Damage Severity Assessment Method for Bearings with Rolling Element Damage. Shock Vib. 2013, 32, 169–173. [Google Scholar] [CrossRef]
- Yang, T.; Liu, C.; Wu, X.; Liu, X.; Liu, T. Time-domain Compression Feature Extraction and Application Study of Compressed Sensing in Equipment. J. Mech. Eng. Technol. 2017, 36, 1536–1541. [Google Scholar] [CrossRef]
- Zhang, L.; Cheng, L.; Li, X.; Yang, S. Fault Quantitative Evaluation of Rolling Bearings Based on Shock Value of Selected Frequency Band. J. Vib. Shock 2018, 37, 30–38. [Google Scholar] [CrossRef]
- Zhang, L.; Song, C.; Zou, Y.; Hong, C.; Wang, C. Bearing Performance Degradation Assessment Based on Renyi Entropy and K-medoids Clustering. J. Vib. Shock 2020, 39, 24–31. [Google Scholar] [CrossRef]
- Jiang, T.; Zhang, Q. Bearing Failure Impulse Enhancement Method Using Multiple Resonance Band Centre Positioning and Envelope Integration. Measurement 2022, 200, 111623. [Google Scholar] [CrossRef]
- Zheng, J.; Cao, S.; Pan, H.; Ni, Q. Spectral Envelope-based Adaptive Empirical Fourier Decomposition Method and Its Application to Rolling Bearing Fault Diagnosis. ISA Trans. 2022, in press. [CrossRef]
- Kulkarni, V.V.; Khadersab, A. Condition Monitoring Analysis of Rolling Element Bearing Based on Frequency Envelope. Mater. Today Proc. 2021, 46, 4667–4671. [Google Scholar] [CrossRef]
- Xu, X.; Zhao, M.; Lin, J.; Lei, Y. Envelope Harmonic-to-noise Ratio for Periodic Impulses Detection and Its Application to Bearing Diagnosis. Measurement 2016, 91, 385–397. [Google Scholar] [CrossRef]
- Sachan, S.; Shukla, S.; Singh, S.K. Two Level De-noising Algorithm for Early Detection of Bearing Fault Using Wavelet Transform and Zero Frequency Filter. Tribol. Int. 2020, 143, 106088. [Google Scholar] [CrossRef]
- Yu, G.; Li, C.; Sun, J. Machine Fault Diagnosis Based on Gaussian Mixture Model and Its Application. Int. J. Adv. Manuf. Technol. 2010, 48, 205–212. [Google Scholar] [CrossRef]
- Ma, R.; Wang, J.; Song, Y. Multi-manifold Learning Using Locally Linear Embedding (LLE) Nonlinear Dimensionality Reduction. J. Tsinghua Univ. 2008, 48, 582–585. [Google Scholar] [CrossRef]
- Jiang, H.; Chen, J.; Dong, G. Hidden Markov Model and Nuisance Attribute Projection Based Bearing Performance Degradation Assessment. Mech. Syst. Signal Process. 2015, 72–73, 184–205. [Google Scholar] [CrossRef]
- Yu, J.B. Bearing Performance Degradation Assessment Using Locality Preserving Projections and Gaussian Mixture Models. Mech. Syst. Signal Process. 2011, 25, 2573–2588. [Google Scholar] [CrossRef]
- Rai, A.; Upadhyay, S.H. An Integrated Approach to Bearing Prognostics Based on EEMD-multi Feature Extraction, Gaussian Mixture Models and Jensen-Rényi Divergence. Appl. Soft Comput. 2018, 71, 36–50. [Google Scholar] [CrossRef]
- Tong, Q.; Hu, J. Bearing Performance Degradation Assessment Based on Information-theoretic Metric Learning and Fuzzy C-means Clustering. Meas. Sci. Technol. 2020, 31, 075001. [Google Scholar] [CrossRef]
- Wang, F.; Chen, X.; Yan, D.; Li, H.; Wang, L.; Zhu, H. Fuzzy C-means Using Manifold Learning and Its Application to Rolling Bearing Performance Degradation Assessment. J. Manuf. Sci. Eng. 2016, 52, 60–64. [Google Scholar] [CrossRef]
- Jiang, W.; Lei, Y.; Han, K.; Zhang, S.; Su, X. Performance Degradation Quantitative Assessment Method for Rolling Bearings Based on VMD and SVDD. J. Vib. Shock 2018, 37, 43–50. [Google Scholar] [CrossRef]
- Wang, F.; Fang, L.; Zhao, Y.; Qi, Z. Rolling Bearing Early Weak Fault Detection and Performance Degradation Assessment Based on VMD and SVDD. J. Vib. Shock 2019, 38, 224–230. [Google Scholar] [CrossRef]
- Dibaj, A.; Hassannejad, R.; Ettefagh, M.M.; Ehghaghi, M.B. Incipient Fault Diagnosis of Bearings Based on Parameter-optimized VMD and Envelope Spectrum Weighted Kurtosis Index with A New Sensitivity Assessment Threshold. ISA Trans. 2021, 114, 413–433. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Li, J.; Yao, X.; Wang, H.; Zhang, J. Periodic Impulses Extraction Based on Improved Adaptive VMD and Sparse Code Shrinkage Denoising and Its Application in Rotating Machinery Fault Diagnosis. Mech. Syst. Signal Process. 2019, 126, 568–589. [Google Scholar] [CrossRef]
- Jaskaran Singh, A.K.; Darpe, S.P. Singh. Bearing Damage Assessment Using Jensen-Rényi Divergence Based on EEMD. Mech. Syst. Signal Process. 2017, 87, 307–339. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, H.; Ren, M.; He, M.; Jin, L. Rolling Bearing Fault Diagnosis Based on Multiscale Permutation Entropy and SOA-SVM. Machines 2022, 10, 485. [Google Scholar] [CrossRef]
- Zhou, J.M.; Guo, H.J.; Zhang, L.; Xu, Q.Y.; Li, H. Bearing Performance Degradation Assessment Using Lifting Wavelet Packet Symbolic Entropy and SVDD. Shock Vib. 2016, 2016, 3086454. [Google Scholar] [CrossRef] [Green Version]
- Case Western Reserve University Bearing Data Center Website. Available online: https://engineering.case.edu/bearingdatacenter/welcome (accessed on 7 July 2022).
- Lee, J.; Qiu, H.; Yu, G.; Lin, J.; Rexnord Technical Services. IMS, University of Cincinnati. “Bearing Data Set”, NASA Ames Prognostics Data Repository. NASA Ames Research Center, Moffett Field, CA, USA. 2007. Available online: https://ti.arc.nasa.gov/progect/prognostic-data-repository (accessed on 7 July 2022).
- Qiu, H.; Lee, J.; Lin, J.; Yu, G. Wavelet Filter-based Weak Signature Detection Method and Its Application on Rolling Element Bearing Prognostics. J. Sound Vib. 2006, 289, 1066–1090. [Google Scholar] [CrossRef]
- Gu, R.; Chen, J.; Hong, R. Early Fault Diagnosis of Rolling Bearings Based on Adaptive Variational Mode Decomposition and The Teager Energy Operator. J. Vib. Shock 2020, 39, 1-7+22. [Google Scholar] [CrossRef]
- Zhang, L.; Huang, W.; Xiong, G.; Cao, Q. Assessment of Rolling Bearing Performance Degradation Using Gauss Mixture Model and Multi-domain Features. J. China Mech. Eng. 2014, 25, 3066–3072. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).