SOC Estimation Based on Hysteresis Characteristics of Lithium Iron Phosphate Battery

Abstract

In order to improve the estimation accuracy of the state of charge (SOC) of lithium iron phosphate power batteries for vehicles, this paper studies the prominent hysteresis phenomenon in the relationship between the state of charge and the open circuit voltage (OCV) curve of the lithium iron phosphate battery. Through the hysteresis characteristic test of the battery, the corresponding SOC-OCV data when the battery is charged or discharged from different SOC states are analyzed. According to the approximation trend of the hysteresis main loop curve by the data points, a differential equation model for approximately solving the charge or discharge hysteresis small loop curve under any SOC state is established, and the adjustment parameters of the model are analyzed and debugged in sections. Then, based on the second-order Thevenin equivalent circuit model, the forgetting factor recursive least squares method is used to identify the model parameters online. When deriving the relationship between the OCV and SOC, according to the state of charge and discharge and the current SOC value, the approximate model of the real hysteresis small loop curve in the current state is solved in real time, and the extended Kalman recursion algorithm is substituted to correct the corresponding relationship between the OCV and SOC. Finally, the integrated forgetting factor recursive least squares online parameter identification and extended Kalman filter to correct the SOC-OCV hysteresis relationship in real time considering the hysteresis characteristics are used to complete the real-time estimation of the SOC of the lithium iron phosphate battery. The synthesis algorithm proposed in this paper and the Kalman filter algorithm without considering the hysteresis characteristics are compared and verified under the Dynamic Stress Test (DST) data. Based on the method proposed in this paper, the maximum error of terminal voltage is 0.86%, the average error of terminal voltage is 0.021%, the root mean square error (RMSE) of terminal voltage is 0.042%, the maximum error of SOC estimation is 1.22%, the average error of SOC estimation is 0.41%, the average error of SOC estimation is 0.41%, and the RMSE of SOC estimation is 0.57%. The results show that the comprehensive algorithm proposed in this paper has higher accuracy in both terminal voltage following and SOC estimation.

1. Introduction

At present, the power battery is one of the core components of electric vehicles. The quality of its state estimation is particularly important for electric vehicles and in various state estimations of the battery management system. The accuracy of the estimation of SOC of the power battery directly affects the energy management control strategy of the whole vehicle, the performance of the electric vehicle, and the reliability and cost of the whole vehicle.

Battery SOC estimation methods include an ampere-hour integration method, open circuit voltage method, data-driven algorithm and equivalent circuit model observation method, etc. [1,2]. The ampere-hour integration method does not need to establish a model, and the calculation is simple. However, it does not have initial convergence and has a strong dependence on the initial SOC value, and in the estimation process, it is easy to produce accumulated errors and cannot self-correct [3]; the OCV method obtains the open circuit voltage by sufficient rest. The battery SOC is estimated using the relationship between the open circuit voltage and the SOC. Usually, the SOC-OCV curves measured at different resting times are slightly different. The longer the rest time, the more accurate the measurement of the open circuit voltage OCV. Therefore, it is not suitable for direct application to real vehicles. Generally, the open-circuit voltage method and the ampere-hour integration method are used in combination [4,5]; data-driven algorithms do not need to consider the internal model of the system. However, the amount of calculation for the sample training process is relatively large. It is easy to appear over-fitting and fall into local optimum, so it is difficult to apply in engineering; the equivalent circuit model observation method is based on the circuit model. The model parameters are identified first using the charge and discharge data. Finally, they are combined with various filtering algorithms to estimate the battery SOC [6]. Reference [7] developed a comprehensive equivalent circuit model for life degradation prediction based on a semi-empirical method, which can accurately predict the key degradation outputs in terms of capacity degradation and resistance increase. Reference [8] proposes an electrothermal model based on the combination of the second-order equivalent circuit model and the thermal model, and the model has high robustness. Because an extended Kalman filter (EKF) has lower algorithm complexity and faster calculation speed, it has higher estimation accuracy. Therefore, the SOC estimation algorithm based on the battery equivalent circuit is mainly based on Kalman filter algorithms such as EKF.

The accuracy of model parameter identification directly affects the accuracy of model output. This further affects the accuracy of battery SOC estimation [9,10]. At present, offline parameter identification and online parameter identification are the main research directions of battery model parameter identification methods. Reference [11] uses a simulated annealing algorithm that does not require initial parameters and has a fast convergence speed to identify parameters. The battery status has a certain relationship with the internal parameters. The offline identification is only the parameter situation in the current environment, so it is not universal. Reference [12] proposed a recursive least squares-extended Kalman filter (RLS-EKF) algorithm. The online identification of parameters can be realized by the recursive least squares method, which can be combined with an extended Kalman filter. Reference [13] uses an adaptive extended Kalman filter (AEKF) and RLS to estimate open circuit voltage. Then, the battery SOC is estimated by the relationship of SOC-OCV. The test results show that this method has a certain improvement effect. However, RLS is more suitable for the steady unknown parameter system. The battery parameters are slow time-varying systems. Therefore, the RLS method is prone to the problem of “data saturation” [14] in order to overcome the “data saturation” problem in parameter identification. Reference [15] uses recursive least squares with a forgetting factor and an adaptive volume-extended Kalman filter algorithm for joint estimation. This improved the algorithm tracking effect. However, the above studies seldom consider hysteresis characteristics.

Although the lithium iron phosphate battery and the ternary lithium battery are the same as the lithium-ion battery, the open-circuit voltage hysteresis characteristic of the former is obviously stronger than that of the latter. Moreover, most scholars do not consider its open-circuit voltage hysteresis characteristics when studying ternary lithium batteries. In recent years, lithium iron phosphate batteries have staged a strong comeback in the electric vehicle market [16]. Therefore, it is necessary to carry out more research on lithium iron phosphate batteries. The hysteresis characteristic is one of the research directions.

For example, reference [17] proposed a method of using the average SOC-OCV curve relationship after noting the open-circuit voltage difference in the main charge-discharge cycle of lithium iron phosphate. This method reduces the maximum open-circuit voltage error by half. However, the processing method is simple, which still leads to a large open-circuit voltage error. Therefore, the hysteresis characteristics of the open circuit voltage cannot be fundamentally solved; reference [18] studied the charge-discharge hysteresis voltage of lithium iron phosphate battery and found that the hysteresis voltage bias law can be approximately corrected by the difference of charge-discharge open-circuit voltage. Therefore, a correction algorithm considering the hysteresis characteristic is proposed. However, its method is relatively simple and rough, and it is difficult to adapt to the hysteresis characteristics under changing working conditions; reference [19] proposed to use the hysteresis voltage as the state quantity to construct a fourth-order state equation including the battery SOC to estimate the hysteresis voltage. However, the state space corresponding to this method is complex. The coupling relationship between each state quantity will affect the estimation accuracy; in reference [20], when studying the open-circuit voltage hysteresis main loop and hysteresis small loop data, it is found that the approximation of the main loop curve by the small loop data can be approximated by a mathematical model. Furthermore, an approximate method for solving the hysteresis small loop curve is proposed. However, it does not consider the adjustment of the hysteresis model under different SOC states in changing conditions.

Based on the above analysis, this paper takes the lithium iron phosphate battery as the research object and establishes a battery equivalent circuit model considering the battery hysteresis characteristics based on the hysteresis characteristics of the battery charge-discharge open-circuit voltage curve. Based on this model, a forgetting factor recursive least square method combined with an extended Kalman filter algorithm considering battery hysteresis characteristics is proposed to realize the online real-time joint estimation of the SOC of the lithium iron phosphate battery. In the online identification of battery-equivalent circuit model parameters, this paper adopts the recursive least squares method with the forgetting factor (FFRLS) to realize the online identification of model parameters. Among them, the recursive least squares (RLS) algorithm can identify the battery parameters online and correct the circuit model in real time. The introduction of the forgetting factor (FF) can reduce the influence of old data and increase the influence of new data. In terms of the SOC estimation of the battery, based on a large number of open-circuit voltage hysteresis small loop and hysteresis large loop tests, this paper establishes a battery hysteresis characteristic model that can correct the corresponding charge-discharge SOC-OCV relationship according to the current SOC and charge-discharge state in real time. Based on the established battery hysteresis characteristic model, a method for solving the model adjustment parameter is proposed. By determining a more suitable model parameter in different SOC intervals, a more accurate battery SOC-OCV relationship can be obtained, so as to improve the accuracy of battery SOC estimation.

2. Establishment of Battery Model Considering Hysteresis Characteristics

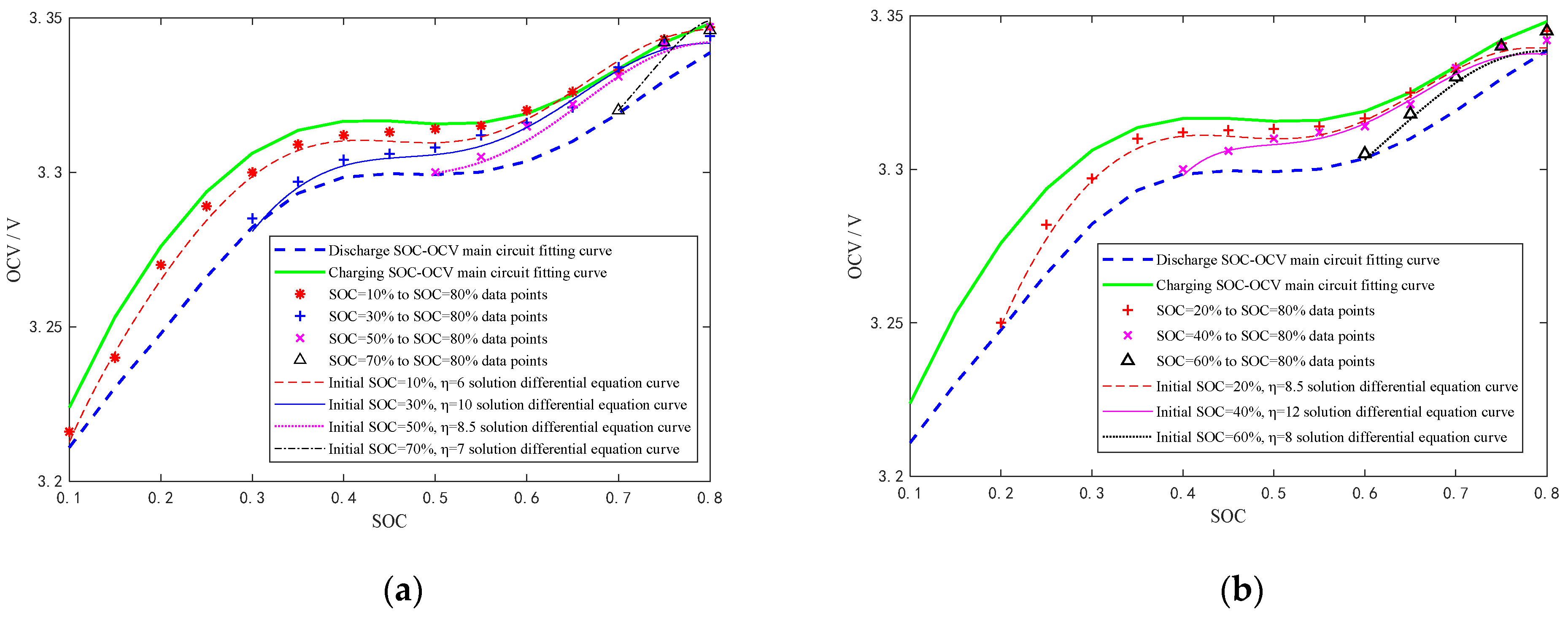
2.1. Analysis of Hysteresis Characteristics

The hysteresis characteristic of the battery means that the charge and discharge SOC-OCV curves of the battery do not overlap [21,22]. This phenomenon is more obvious in lithium iron phosphate batteries. The SOC-OCV curve is an important basis for using the equivalent circuit model to estimate the battery SOC. If the obtained relationship curve has a large error, the estimation accuracy of the battery SOC will be affected.

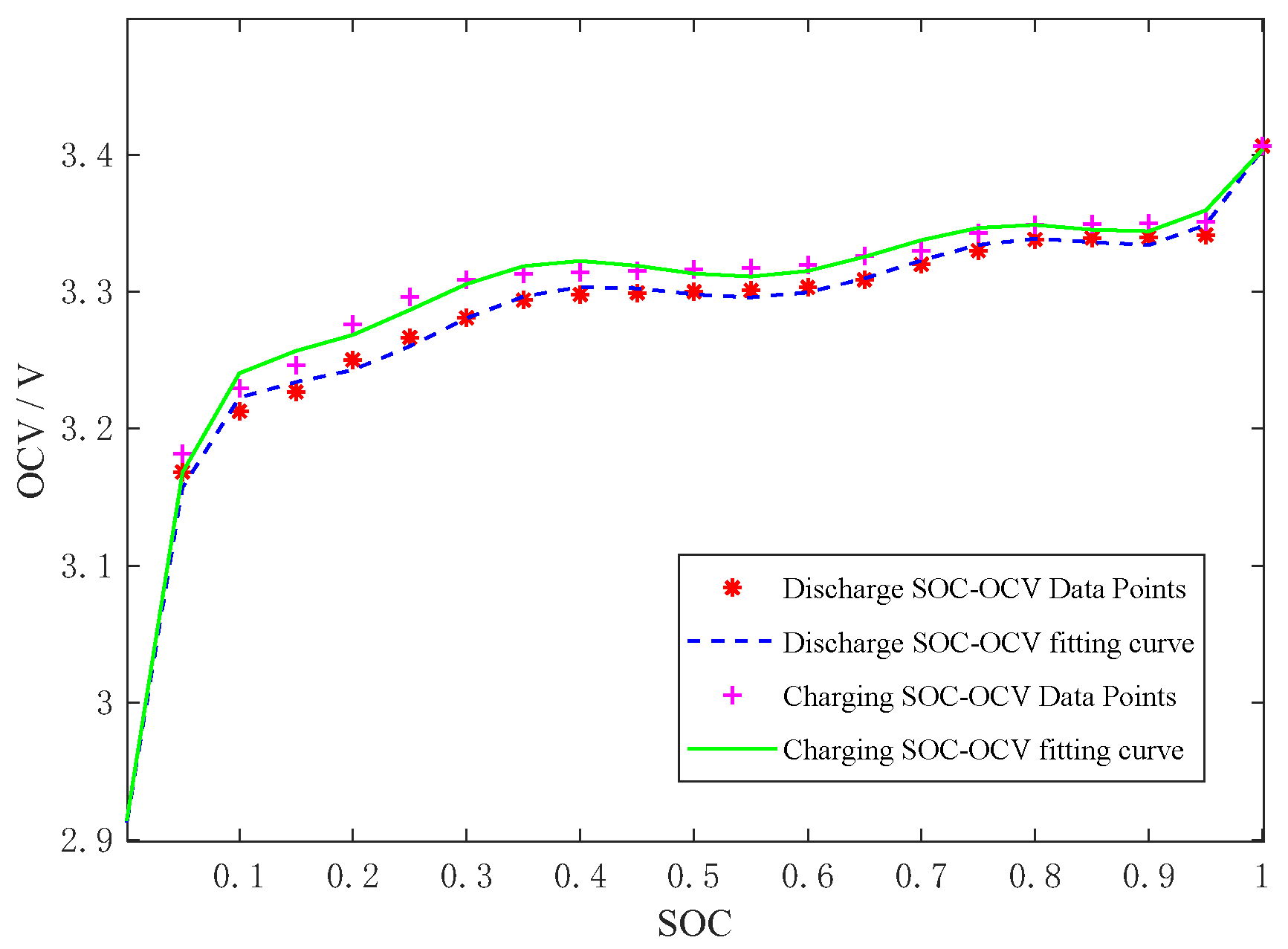
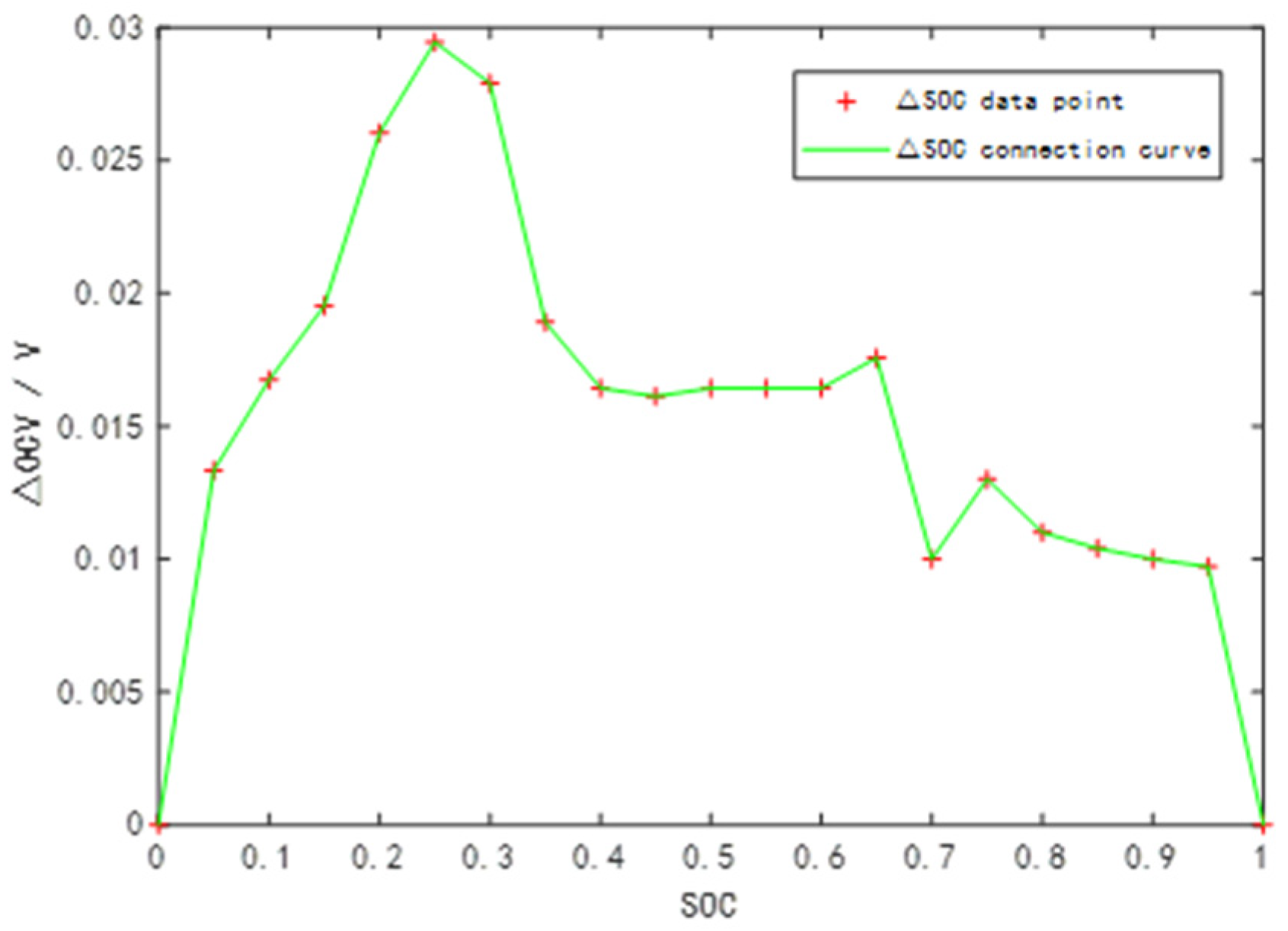
2.1.1. Analysis of Hysteresis Main Loop

The hysteresis main loop curve refers to the SOC-OCV curve relationship obtained when the SOC is from 0% to 100% and from 100% to 0% during the whole charging and discharging process of the battery. Since the open circuit voltage is the terminal voltage of the battery after standing for a period of time. Therefore, the open-circuit voltage values corresponding to all SOCs cannot be obtained accurately and in real time in both the test and the real vehicle. Therefore, the SOC-OCV relationship curve is usually fitted according to a limited number of the SOC-OCV test data points.

The test steps are as follows:

• Fully charge the test battery (SOC = 100%) with the standard charging method of constant current and then constant voltage. Then let it stand for 1 h;
• Starting from the battery SOC = 100%, discharge 5% of the capacity at a 1/3 C rate. Then the terminal voltage was recorded after standing for 1 h. Repeat the test 20 times until the battery SOC = 0%;
• Starting from the battery SOC = 0%, charge the battery with 5% capacity at 1/3 C rate. Then the terminal voltage was recorded after standing for 1 h. Repeat the test 20 times until the battery SOC = 100%.

The terminal voltage recorded during the above test is the open circuit voltage at the corresponding SOC. An eighth-order polynomial is used to fit the SOC-OCV data points obtained from the above experiments. The hysteresis main loop curve is obtained as shown in Figure 1. Use U_oc to represent the open-circuit voltage corresponding to the hysteresis main loop during charging. Use U_of to represent the open-circuit voltage corresponding to the hysteresis main loop during discharge. Z represents SOC. Then the eighth order polynomial fitting formula is:

$$U_{\mathrm{oc}}=a_1{Z}^8+a_2{Z}^7+a_3{Z}^6+a_4{Z}^5+a_5{Z}^4+a_6{Z}^3+a_7{Z}^2+a_{8}Z+a_9$$

(1)

$$U_{\mathrm{of}}=b_1{Z}^8+b_2{Z}^7+b_3{Z}^6+b_4{Z}^5+b_5{Z}^4+b_6{Z}^3+b_7{Z}^2+b_{8}Z+b_9$$

(2)

In the formula, a₁~a₉, b₁~b₉ are polynomial coefficients.

The fitted polynomial coefficients are shown in

Table 1. Fitting Polynomial Coefficients.

coefficient	a1	a2	a3	a4	a5	a6	a7	a8	a9
value	−293.2	1340.9	−2521.6	2519.4	−1442.7	477.5	−88.3	8.6	2.9
coefficient	b1	b2	b3	b4	b5	b6	b7	b8	b9
value	−245.3	1163.1	−2258.2	2321.5	−1363.3	460.4	−86.1	8.3	2.9

.

It can be seen in Figure 1 that under the same SOC, the open-circuit voltage of the charging process is higher than that of the discharging process, and the open circuit voltage difference is more obvious in the common segment when the battery SOC is 10%~80%.

During the above charging and discharging process. The corresponding open circuit voltage difference (ΔOCV) under the same SOC is shown in Figure 2.

It can be seen in Figure 2 that in the whole process of discharging or charging, the maximum voltage difference of its SOC-OCV curve is 0.0295 V. The open-circuit voltage variation range during the entire charging and discharging process is only about 0.5 V. Therefore, ignoring the battery hysteresis characteristic will lead to a large battery SOC estimation error.

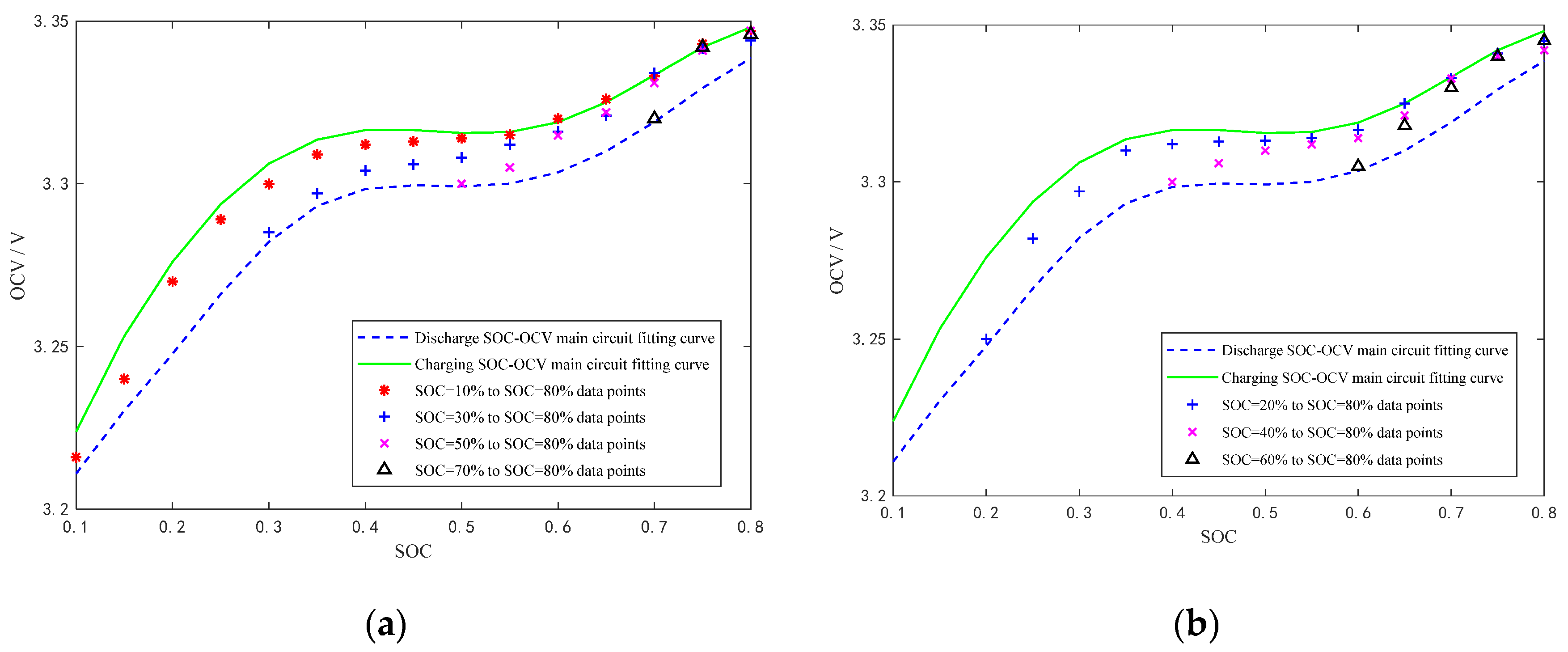
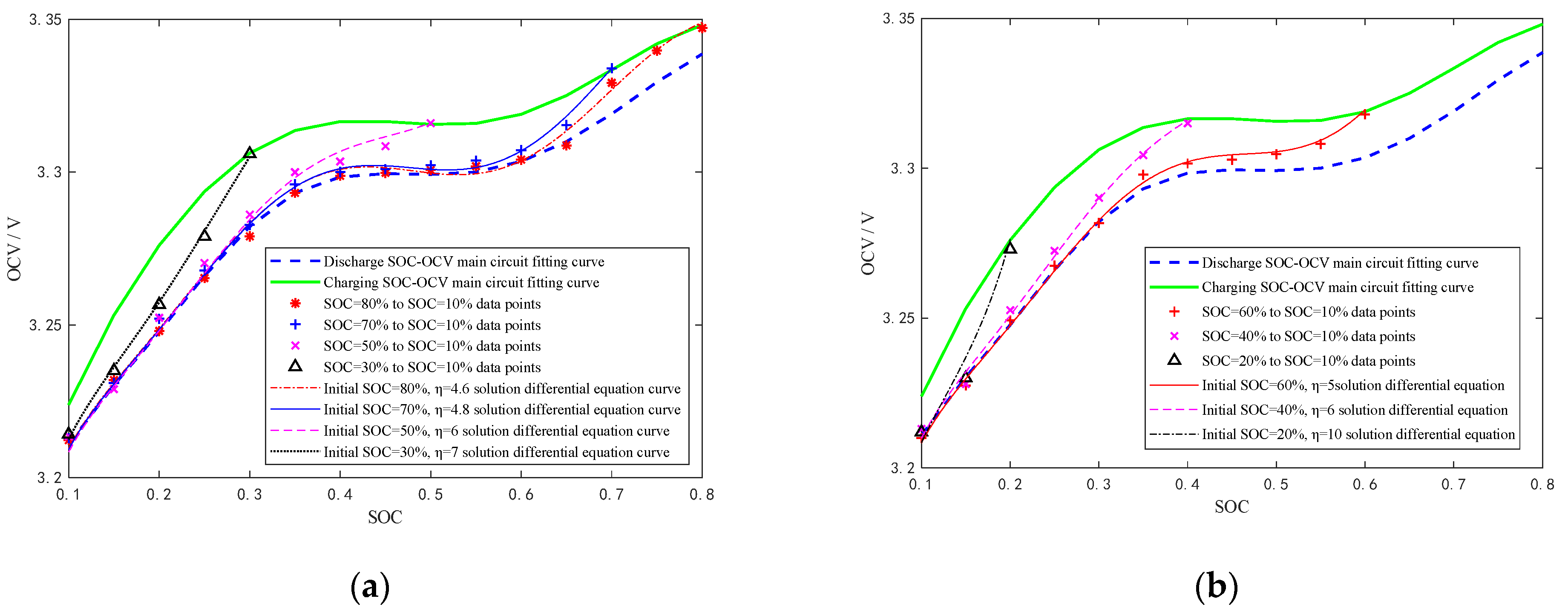
2.1.2. Hysteresis Small Loop Analysis

The hysteresis characteristics of lithium iron phosphate batteries are far more than the hysteresis main circuit characteristics. The charging and discharging state and the SOC starting point of different charging and discharging will affect the trend of the hysteresis loop, but it is included in the main loop curve [23]. This paper calls these small loops hysteretic small loops. It can be seen in Figure 1 that when the battery SOC is less than 10% and greater than 80%, the charge-discharge open-circuit voltage difference is small, and its open circuit voltage changes fast. In order to facilitate the study of the characteristics of the small hysteresis loop, the experimental scheme is designed as follows:

• Fully charge the test battery (SOC = 100%) with the standard charging method of constant current and then constant voltage. Then let it stand for 1 h;
• From SOC = 100%, discharge at 1/3 C rate to SOC = 10%. Record the terminal voltage after standing for 1 h;
• Charge 5% capacity at 1/3 C rate. The terminal voltage was recorded after standing for 1 h. Repeat the test several times until the SOC is 80%;
• In the same way, the charging hysteresis small loop data of different SOC starting points (SOC is 20%, 30%, 40%, 50%, 60%, 70%) and the endpoint of 80% SOC are obtained by testing in the a, b, and c methods;
• Put the test battery to SOC = 0 by standard discharge method. Then let it stand for 1 h;
• Starting at SOC = 0%, discharge at 1/3 C rate to SOC = 80%. Then record the terminal voltage after standing for 1 h;
• Discharge 5% capacity at 1/3 C rate. Then the terminal voltage was recorded after standing for 1 h. Repeat the test several times until SOC = 10%;
• In the same way, the charging hysteresis small loop data of different SOC starting points (SOC is 70%, 60%, 50%, 40%, 30%, 20%) and the endpoint of 10% SOC are obtained by testing in the e, f and g methods.

The partial hysteresis small loop data points obtained from the test are shown in Figure 3 and Figure 4.

It can be seen in Figure 3 that on the charge hysteresis main loop curve, the SOC-OCV relationship corresponding to the start of discharge at different SOCs gradually approaches the discharge hysteresis main loop curve.

It can be seen in Figure 4 that the SOC-OCV relationship corresponding to charging at different SOCs on the discharge hysteresis main loop curve gradually approaches the charge hysteresis main loop curve.

2.2. Equivalent Circuit Model Based on Hysteresis Characteristics

The hysteresis main circuit and hysteresis small circuit of lithium iron phosphate battery are analyzed. It can be seen that dynamically selecting the hysteresis small-cycle SOC-OCV curve in the corresponding state and substituting it into the filtering algorithm can greatly reduce the open-circuit voltage error during the battery charging and discharging process [24,25]. Therefore, the SOC estimation accuracy is improved.

Observe the hysteretic small loop test data points. It can be found that the approximation speed decreases as it approaches the main loop curve. It can be considered that its approach speed is positively related to its distance from the main loop curve [26]. From this approximation, the following model representation is selected.

$$\frac{d{U}_{\mathrm{o}}}{dZ}=\{\begin{array}{c}\frac{d{U}_{\mathrm{oc}}}{dZ}+\eta \left(U_{\mathrm{oc}}-U_{\mathrm{o}}\right),\frac{dZ}{dt}\ge 0\\ \frac{d{U}_{\mathrm{of}}}{dZ}+\eta \left(U_{\mathrm{o}}-U_{\mathrm{of}}\right),\frac{dZ}{dt}<0\end{array}$$

(3)

In the formula, Z represents the SOC, which is the variable of the differential equation; U_o represents the corresponding open-circuit voltage on the small hysteresis loop, which is the function to be solved; U_oc is the curve equation of the charging hysteresis main loop (which has been calculated from Table 1 and Formula (1); U_of is the discharge hysteresis main loop curve equation (which has been calculated from Table 1 and Formula (2)); η is the model adjustment coefficient related to the initial SOC state; dZ/dt > 0 indicates that the current moment is the charging state, otherwise it is the discharging state, and dZ/dt = 0 means standing still.

In this case, it is only necessary to specify the value of η. The corresponding charge or discharge hysteresis small loop curve can be approximately solved under any SOC initial condition.

In order to study the best value of η under different charge and discharge states, η is assigned to the experimental data in Figure 3 and Figure 4 and adjusted to find a suitable value of η to solve differential equations. The solution results are shown in Figure 5 and Figure 6.

As can be seen in Figure 5, when the battery starts to discharge from the SOC of 80%, 70%, 60%, 50%, 40%, 30%, and 20%, respectively, and the values of η are 4.6, 4.8, 5, 6, 6, 7, and 10, respectively, the model will obtain a better fitting effect on the data of the discharge hysteresis small loop.

Likewise, it can be seen in Figure 6 that when the battery starts charging from SOCs of 10%, 20%, 30%, 40%, 50%, 60%, and 70%, respectively, the values of η are 6, 8.5, 10, 12, 8.5, 8, and 7, respectively. The model will obtain a better fitting effect on the data of the charging hysteresis small loop.

The battery SOC estimation in this paper is based on the battery equivalent circuit model because the second-order Thevenin equivalent circuit model can better reflect the internal dynamic changes of lithium-ion batteries than the first-order model [27,28]. Therefore, this paper is based on the second-order Thevenin equivalent circuit model. An equivalent circuit model considering the hysteresis characteristics of the battery is proposed as shown in Figure 7.

In Figure 7: U_o is the open circuit voltage corresponding to the hysteresis small loop, which is a function of the SOC. It can be obtained by solving the differential equation of Formula (3); R₀ is the ohmic internal resistance; I is the working current, which is positive during discharge; R₁ and R₂ are the internal resistance of electrochemical polarization and concentration polarization, respectively; C₁ and C_2, respectively, are the electrochemical polarization capacitance and concentration polarization capacitance [29]; U₁ and U₂ are the terminal voltage of the electrochemical polarization ring and the terminal voltage of the concentration polarization ring, respectively; U_t is the terminal voltage of the battery.

According to Kirchhoff’s voltage and current laws, the electrical relationship of the equivalent circuit model can be obtained as:

$$\{\begin{array}{l}{\dot{U}}_1=\frac{-U_1}{R_1{C}_1}+\frac{I}{C_1}\\ {\dot{U}}_2=\frac{-U_2}{R_2{C}_2}+\frac{I}{C_2}\\ U_{\mathrm{t}}=U_{\mathrm{o}}-U_1-U_2-I\cdot R_0\end{array}$$

(4)

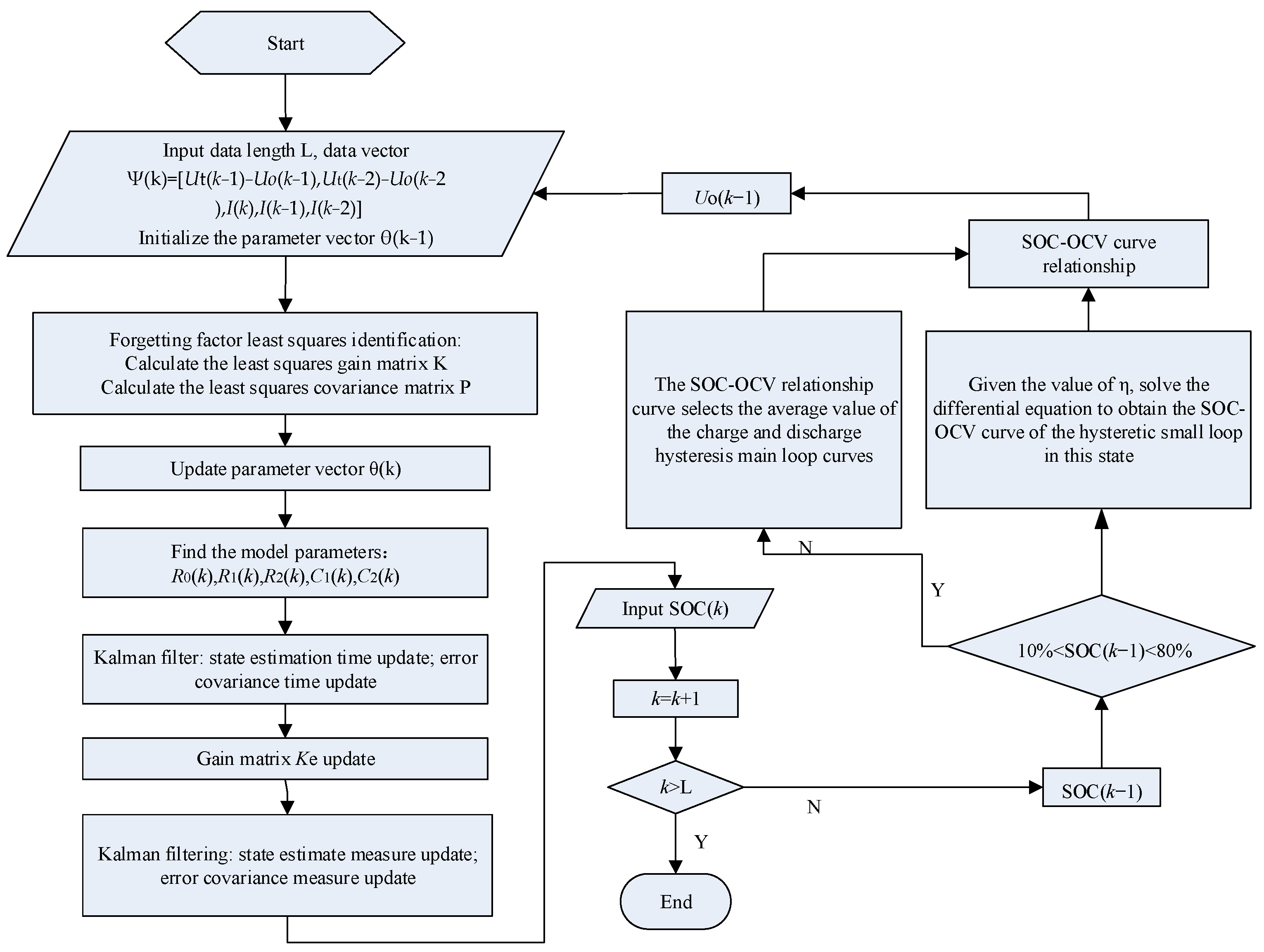
3. Online Identification of Model Parameters

Before applying the Forgetting Factor Recursive Least Squares (FFRLS) for model parameter identification, convert the discrete recurrence of the second-order equivalent circuit model into the basic form of least squares. The Laplace transform of Formula (4) is shown in Formula (5):

$$U_{\mathrm{t}}(s)-U_{\mathrm{o}}(s)=-I(s)\left(R_0+\frac{R_1}{1+s{R}_1{C}_1}+\frac{R_2}{1+s{R}_2{C}_2}\right)$$

(5)

where s is the Laplace operator on the s field.

The bilinear transformation formula is:

$$s=\frac{2}{T}\cdot \frac{1-z^{-1}}{1+z^{-1}}$$

(6)

In the formula, T is the sampling period; z is the corresponding operator on the discrete z domain. Bilinear transformation is to realize the conversion of continuous time system and discrete time system.

Use Formula (6) to map Formula (5) from the s domain to the z domain. Obtain the transfer function of the system on the z domain and simplify it to receive:

$$G\left(z^{-1}\right)=\frac{U\mathrm{t}\left(z^{-1}\right)-U_{\mathrm{o}}\left(z^{-1}\right)}{-I\left(z^{-1}\right)}=\frac{{\theta }_{3,k}+{\theta }_{4,k}{z}^{-1}+{\theta }_{5,k}{z}^{-2}}{1-{\theta }_{1,k}{z}^{-1}-{\theta }_{2,k}{z}^{-2}}$$

(7)

In the formula, θ_1,k, θ_2,k, θ_3,k, θ_4,k, θ_5,k are the simplified representative coefficients at time k, and the specific expression is:

$$\{\begin{array}{l}{\theta }_{1,k}=\frac{8b-2T^2}{4b+2cT+T^2}\hfill \\ {\theta }_{2,k}=\frac{4cT}{4b+2cT+T^2}-1\hfill \\ {\theta }_{3,k}=-\frac{4ab+2eT+d{T}^2}{4b+2cT+T^2}\hfill \\ {\theta }_{4,k}=\frac{8ab-2d{T}^2}{4b+2cT+T^2}\hfill \\ {\theta }_{5,k}=-\frac{4ab-2eT+d{T}^2}{4b+2cT+T^2}\hfill \end{array}$$

(8)

In the formula, a = R₁; b = τ1τ2; c = τ1 + τ2; d = R₀ + R₁ + R₂; e = R₀(τ1 + τ2) + R₁τ2 + R₂τ1; τ1 = R₁C₁; and τ2 = R₂C₂.

U_t(k) is the terminal voltage value recorded in the test, take y(k) = U_t(k) − U_oc(k), and discretize Formula (7) to receive:

$$y(k)=Q_{1,k}y(k-1)+Q_{2,k}y(k-2)+Q_{3,k}I(k)+Q_{4,k}I(k-1)+Q_{5,k}I(k-2)$$

(9)

Then the least square parameter vector is θ(k) = (θ_1,k,θ_2,k,θ_3,k,θ_4,k,θ_5,k)T, and the data vector is φ(k) = (y(k − 1), y(k − 2), I(k), I(k − 1), I(k − 2))T. The I(k) is the current value recorded in the test.

θ(k) is estimated in real time by recursive least squares, and then can be calculated inversely from Equation (8):

$$\{\begin{array}{l}a=\frac{{\theta }_{4,k}-{\theta }_{3,k}-{\theta }_{5,k}}{1+{\theta }_{1,k}-{\theta }_{2,k}}\hfill \\ b=\frac{T^2(1+{\theta }_{1,k}-{\theta }_{2,k})}{4(1-{\theta }_{1,k}-{\theta }_{2,k})}\hfill \\ c=\frac{T(1+{\theta }_{2,k})}{1-{\theta }_{1,k}-{\theta }_{2,k})}\hfill \\ d=\frac{-{\theta }_{3,k}-{\theta }_{4,k}-{\theta }_{5,k}}{1-{\theta }_{1,k}-{\theta }_{2,k}}\hfill \\ e=\frac{T({\theta }_{5,k}-{\theta }_{3,k})}{1-{\theta }_{1,k}-{\theta }_{2,k}}\hfill \end{array}$$

(10)

Combining the expressions of a~e, we can find:

$$\begin{array}{cc}{\tau }_1=\frac{c+\sqrt{c^2-4b}}{2},& {\tau }_2=\frac{c-\sqrt{c^2-4b}}{2}\end{array}$$

(11)

$$\{\begin{array}{l}{R}_0=a\hfill \\ R_1=[{\tau }_1(d-a)+ac-e]/({\tau }_1-{\tau }_2)\hfill \\ R_2=R_1-d+a\hfill \\ C_1={\tau }_1/R_1\hfill \\ C_2={\tau }_2/R_2\hfill \end{array}$$

(12)

The forgetting factor recursive least squares introduces forgetting factor λ to adjust the weight of new and old data. The value of λ is close to 1, generally 0.95 ≤ λ ≤ 1.00 [12]. In this paper, λ is taken as 0.99. Let the gain coefficient be K(k), the parameter estimation value is θ(k), and the covariance matrix be P(k). Then the forgetting factor least squares recurrence equation is:

$$\{\begin{array}{c}K\mathit{(}k\mathit{)}=\frac{P\mathit{(}k-\mathit{1}\mathit{)}\phi \mathit{(}k\mathit{)}}{\lambda +\phi {\mathit{(}k\mathit{)}}^{T}P\mathit{(}k-\mathit{1}\mathit{)}\phi \mathit{(}k\mathit{)}}\\ P\mathit{(}k\mathit{)}=\frac{\mathit{1}}{\lambda }\left[I\mathit{(}k\mathit{)}-K\mathit{(}k\mathit{)}\phi {\mathit{(}k\mathit{)}}^T\right]P\mathit{(}k-\mathit{1}\mathit{)}\\ \theta \mathit{(}k\mathit{)}=\theta \mathit{(}k-\mathit{1}\mathit{)}+K\mathit{(}k\mathit{)}\left[U_t\mathit{(}k\mathit{)}-U_{oc}\mathit{(}k\mathit{)}-\theta {\mathit{(}k-\mathit{1}\mathit{)}}^T\phi \mathit{(}k\mathit{)}\right]\end{array}$$

(13)

4. Joint Estimation of Battery SOC

4.1. Battery SOC Estimation by Extended Kalman Filter

Kalman filtering can only be applied to linear systems. The battery model system is nonlinear. Therefore, this paper adopts the extended Kalman filter method [30,31,32]. This method performs first-order Taylor expansion on nonlinear systems, omitting higher-order terms to achieve approximate linearization. Furthermore, the recursive formula of the linear Kalman filter theory can be used to realize the state estimation of the nonlinear system [33,34,35]. The second-order equivalent circuit extended Kalman filter estimation process of the battery SOC is as follows:

a. Let the original nonlinear state equation of the system be:

$$\{\begin{array}{c}x(k+1)=f(x(k),u(k))+\omega (k)\\ h(k)=g(x(k),u(k))+v(k)\end{array}$$

(14)

In the formula, x is the system state variable; u is the system input; h is the system output; ω is the state noise; ν is the observation noise.

b. Combined with Equation (4), the nonlinear functions f and g are linearized by the first-order Taylor expansion at the estimated point. System state quantity x = [U₁,U₂,Z]T; system input quantity u = I; system output quantity h = U_t; then the system discrete state space is:

$$\{\begin{array}{l}x(k+1)=A(k)x(k)+B(k)u(k)+\omega (k)\\ U_{\mathrm{t}}\left(k\right)=C(k)x(k)+D(k)u(k)+v(k)\end{array}$$

(15)

Among them, the expressions of A(k), B(k), C(k), D(k) are:

$$\{\begin{array}{l}A(k)={\frac{\partial f}{\partial x}|}_{x={\widehat{x}}_k}=\left[\begin{array}{ccc}{e}^{\frac{-\mathrm{T}}{R_1{C}_1}}& 0& 0\\ 0& e^{\frac{-\mathrm{T}}{R_2{C}_2}}& 0\\ 0& 0& 1\end{array}\right]\\ B(k)=\left[R_1\left(1-{\mathrm{e}}^{\frac{-\mathrm{T}}{R_1{C}_1}}\right)\hspace{0.17em},R_2\left(1-{\mathrm{e}}^{\frac{-\mathrm{T}}{R_2{C}_2}}\right),-\frac{\eta \mathrm{T}}{{\mathrm{C}}_{\mathrm{N}}}\right]\\ C(k)=\left[-1,-1,{\frac{\partial U\mathrm{o}\left(\mathrm{SOC}\right(k\left)\right)}{\partial \mathrm{SOC}(k)}|}_{\mathrm{SOC}=\mathrm{SOC}(k)}\right]\\ D(k)=R_0\end{array}$$

(16)

In the formula, ${\widehat{x}}_k$ is the estimated value of the state quantity x at time k; η is the charging and discharging efficiency; C_N is the battery capacity.

c. Kalman recursion process, where Q is the state noise covariance matrix and R is the observation noise covariance matrix.

Initialize the state variable estimates $\widehat{x}$ and the error covariance matrix Pe:

$$\{\begin{array}{l}\widehat{x}(0\mid 0)=[0,0,\mathrm{SOC}(0)];\\ P_e(0\mid 0)=E\left[\left(x(0)-\widehat{x}(0)\right){\left(x(0)-\widehat{x}(0)\right)}^{\mathrm{T}}\right]\end{array}$$

(17)

In the formula, E is the identity matrix.

Status estimate time update:

$$\widehat{x}(k|k-1)=A(k)\widehat{x}(k-1|k-1)+B(k)u(k-1)$$

(18)

Error covariance matrix time update:

$$P_e(k|k-1)=Q(k-1)+A(k-1)P_e(k-1|k-1)A^T(k-1)$$

(19)

Kalman gain matrix K_e update:

$$K_e(k)=P_e(k|k-1)C^T(k){\left[C(k)P_e(k-1|k-1)CT(k)+R(k)\right]}^{-1}$$

(20)

State estimation measurement update:

$$\widehat{x}(k|k)=\widehat{x}(k|k-1)+K_e(k)(U_t(k)-C(k)\widehat{x}(k|k-1)$$

(21)

Error covariance matrix measure update:

$$P_e(k|k)=[I(k)-K_e(k)C(k)]P_e(k|k-1)$$

(22)

4.2. A Joint Algorithm Considering Battery Hysteresis

Based on the second-order equivalent circuit model, the forgetting factor recursive least squares method is used to identify the model parameters online. After analyzing the hysteresis characteristics, taking the true hysteretic open circuit voltage into account in the SOC-OCV relationship reduces the effect of open circuit voltage error, and it is combined with extended Kalman filter algorithm to achieve battery SOC estimation. The algorithm flow is shown in Figure 8.

In the flowchart, when 10% < SOC < 80%, the most suitable η value is fitted according to the model, and the selection method is shown in

Table 2. Values of η in different SOC states during charging and discharging.

Charging Process
SOC (k − 1)	[75%, 80%)	[65%, 75%)	[55%, 65%)	[45%, 55%)	[35%, 45%)	[25%, 35%)	[10%, 25%)
value of η	4.6	4.8	5	6	6	7	10
Discharge process
SOC (k − 1)	[10%, 15%)	[15%, 25%)	[25%, 35%)	[35%, 45%)	[45%, 55%)	[55%, 65%)	[60%, 80)
value of η	6	8.5	10	12	8.5	8	7

.

Depending on the SOC state of the battery, the most suitable η value corresponding to solving the differential equation will always change. However, in the process of adjusting the η value in the experiment, it is found that in a small SOC range, the suitable η value changes little and the small range of its value has little effect on the approximation of the curve. Therefore, the above segmentation method is adopted. In the set SOC interval, the differential equation curves solved by the η value determined by the experiment are respectively substituted. It can approximately replace the hysteresis small loop SOC-OCV curve corresponding to the charge and discharge under different SOC initial states.

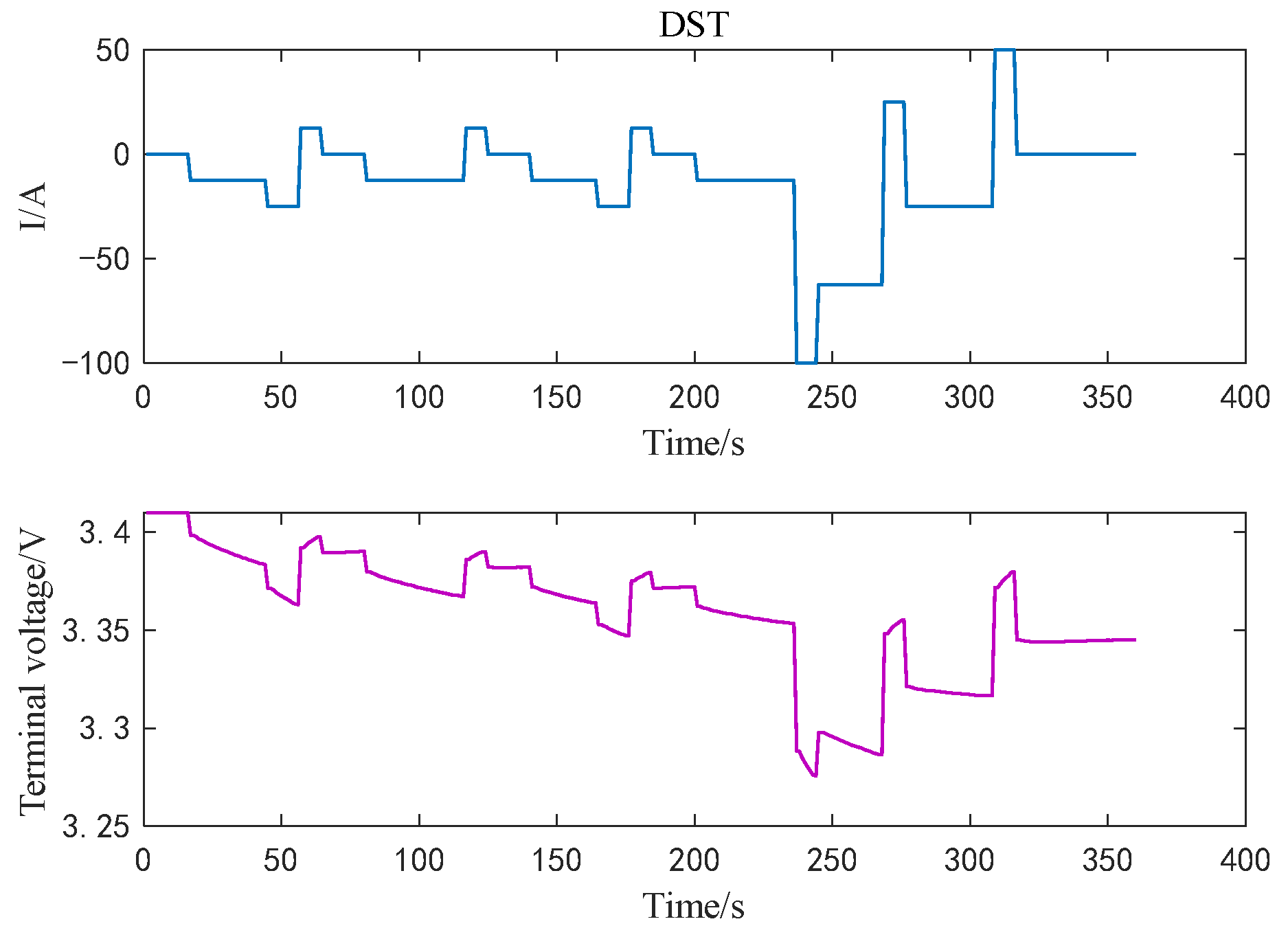
5. Experiment and Algorithm Verification Analysis

5.1. Experimental Procedure

The technical parameters of the lithium iron phosphate battery selected in this paper are: the rated capacity of 100 A·h, the rated voltage of 3.2 V, the discharge cut-off voltage of 2.5 V, and the charge cut-off voltage of 3.65 V. In the static capacity test of the battery, the average value of three tests is 100.1 A·h at an ambient temperature of 25 degrees. That is, CN = 100.1 A·h, and the sampling time T = 1 s.

The battery is subjected to a Dynamic Stress Test (DST) with reference to the Electric Vehicle Battery Test Manual. The period of the DST condition is 360 s, and 70 DST cycles are set to discharge the battery capacity from 100% to about 10%. Figure 9 shows the current and voltage data for one DST cycle in the actual test.

All the test data in this paper are obtained by the test equipment shown in Figure 10.

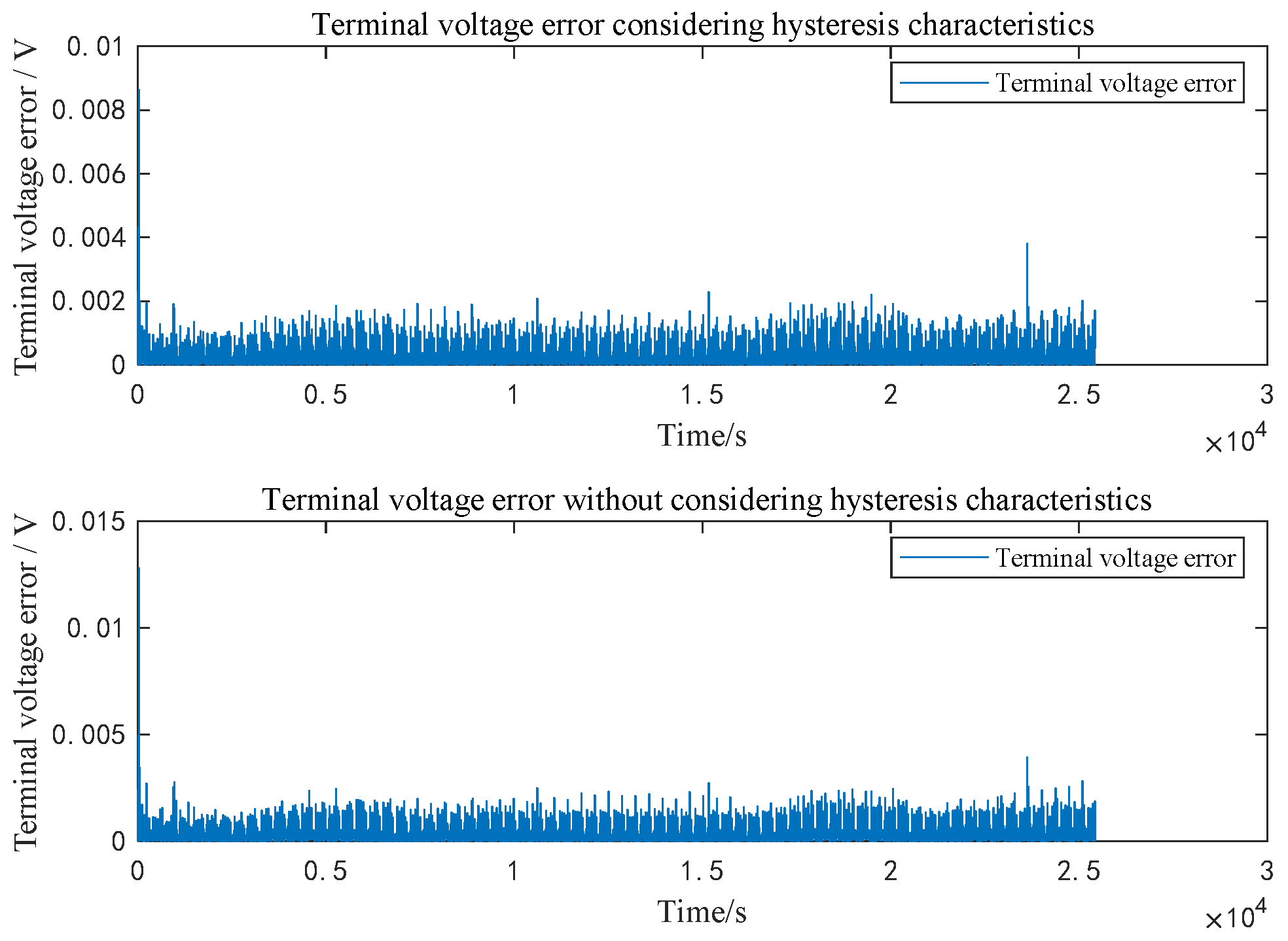
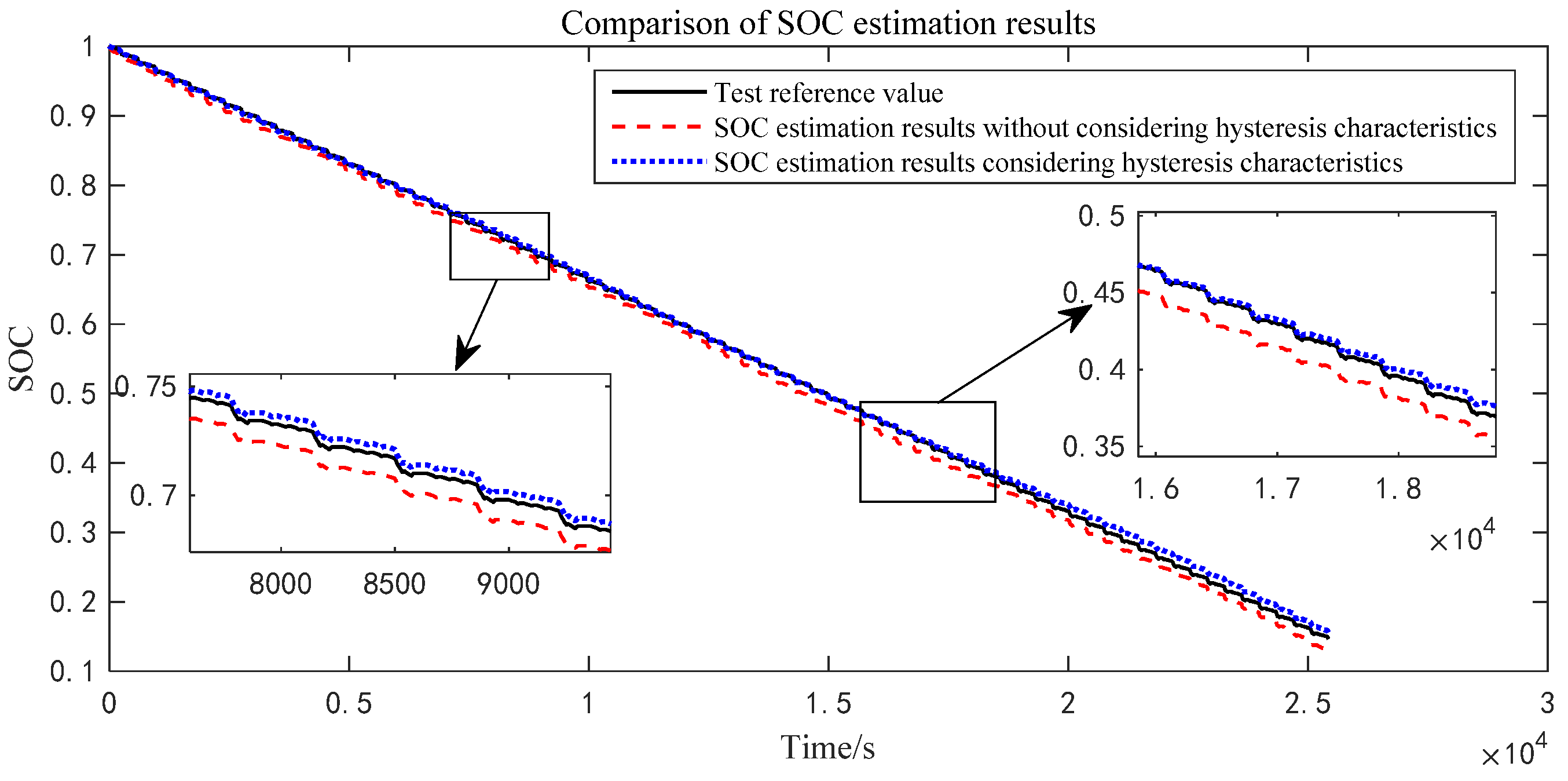
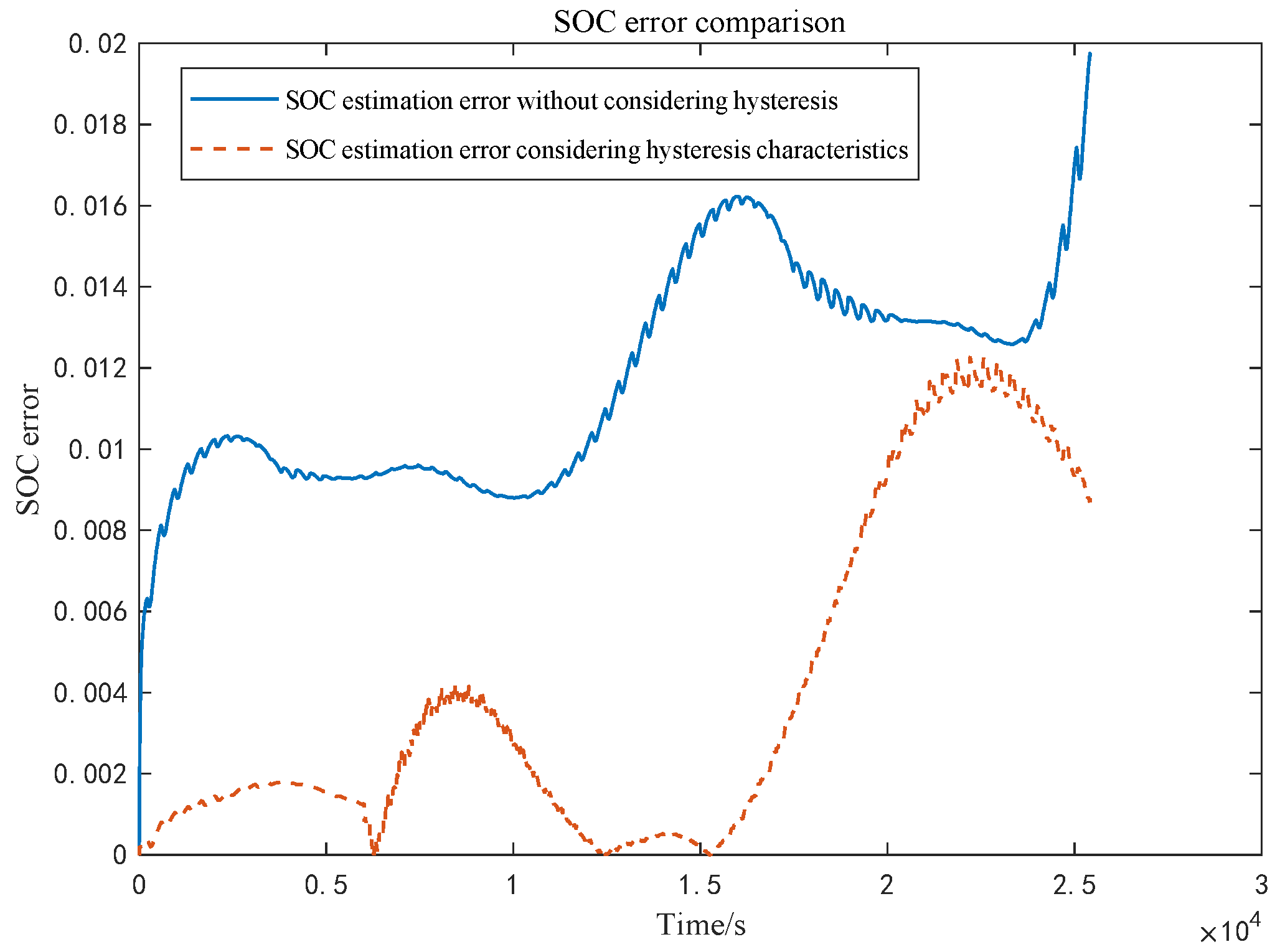
5.2. Comparative Analysis of Algorithm Results

The m language programming based on MATLAB realizes the proposed online identification of battery model parameters and SOC estimation algorithm considering hysteresis characteristics. Based on the test data of DST working conditions, the hysteresis characteristic combined with the extended Kalman filter algorithm and the Kalman filter algorithm are compared, and the verification results are shown in Figure 11, Figure 12 and Figure 13.

As shown in Figure 11, the terminal voltage errors of the two algorithms are small. However, the terminal voltage errors recorded considering the hysteresis characteristics are still significantly smaller than those of the algorithms without hysteresis characteristics. The maximum terminal voltage error of the algorithm without considering the hysteresis characteristic is 1.279%; the average terminal voltage error is 0.024%; the root mean square error is 0.056%. Considering the hysteresis characteristic algorithm, the maximum terminal voltage error is 0.86%; the average terminal voltage error is 0.021%; the root mean square error is 0.042%.

Figure 12 compares the SOC estimation results of the algorithm considering the battery hysteresis characteristics and algorithms that do not consider the hysteresis characteristics. Local magnification is used in some areas. It can be clearly seen in this that the algorithm considering the hysteresis characteristic has a good follow-up to the experimental reference value compared to the algorithm without considering the hysteresis characteristic.

Figure 13 compares the SOC estimation error of the algorithm considering the battery hysteresis characteristic and without considering the hysteresis characteristic. It can be clearly seen in the figure that the error of the algorithm considering the battery hysteresis characteristic is continuously and dynamically converged in the whole process. The error is always kept within a very small range. However, the algorithm, without considering the hysteresis characteristic, is generally in a divergent state. When there is a large SOC error in the process, the control convergence cannot be well controlled, and the whole process SOC error is too large. The maximum SOC error of the algorithm without considering the hysteresis characteristic is 1.97%; the average error is 1.11%; the root mean square error is 0.93%. Considering the hysteresis characteristic algorithm, the maximum error of the SOC is 1.22%; the average error is 0.41%; the root mean square error is 0.57%. Reference [36] uses FFRLS combined with EKF to estimate the SOC of lithium-ion batteries, and the maximum estimation error is 1.59%, while this paper considers the battery hysteresis characteristics to obtain the maximum SOC error of 1.22%. The comparison results show that the adaptive forgetting factor recursive least square method combined with the extended Kalman filter algorithm considering battery hysteresis characteristics proposed in this paper has a greater estimation accuracy for battery SOC.

6. Conclusions

In this paper, the lithium iron phosphate battery is taken as the research object. Based on the hysteresis characteristics of the open-circuit voltage curve of the battery’s charge and discharge, a battery equivalent circuit model considering the hysteresis characteristics of the battery is established, and based on this model, a forgetting factor recursive least squares combined extended Kalman filter algorithm considering battery hysteresis characteristics is proposed, which realizes the online real-time joint estimation of the SOC of lithium iron phosphate batteries. The main research work of the paper is summarized as follows:

(1)

Aiming at the hysteresis characteristics of the open-circuit voltage of LiFePO₄ battery, an equivalent circuit model considering the hysteresis characteristics of the battery is established on the basis of a large number of open-circuit voltage hysteresis small loop and hysteresis large loop tests. The model can correct the charge-discharge SOC-OCV relationship corresponding to the battery in real time according to the current SOC and charge-discharge state. Aiming at the uncertainty of variable parameters in the hysteresis characteristic model, a segmented test method is used to determine the appropriate values of model parameters in different SOC intervals, so as to achieve a more accurate correction of the battery SOC-OCV relationship and improve the battery SOC estimation accuracy.

(2)

Based on the established equivalent circuit model considering the hysteresis characteristics of lithium iron phosphate batteries, the recursive least squares method with a forgetting factor combined with the extended Kalman filter algorithm is used to realize the online identification of model parameters and the real-time online estimation of battery SOC. Finally, the estimation methods considering battery hysteresis characteristics and those without considering battery hysteresis characteristics are compared and analyzed under DST test conditions. In the estimation of the terminal voltage, the maximum terminal voltage error, average terminal voltage error, and RMSE error obtained by considering the hysteresis characteristic algorithm are 0.86%, 0.021%, and 0.042%, respectively. The maximum terminal voltage error, average terminal voltage error, and RMSE error obtained by the algorithm without considering the hysteresis characteristic are 1.279%, 0.024%, and 0.056%, respectively. In terms of the SOC estimation of the battery, the maximum error, average error, and RMSE of the SOC obtained by considering the hysteresis characteristic algorithm are 1.22%, 0.41%, and 0.57%, respectively. The maximum error, average error, and RMSE of the SOC obtained by the algorithm without considering the hysteresis characteristic are 1.97%, 1.11%, and 0.93%, respectively. The comparison results show that the forgetting factor recursive least squares method combined with the extended Kalman filter algorithm considering battery hysteresis characteristics proposed in this paper has a greater estimation accuracy for the battery SOC.

(3)

Although the method proposed in this paper has a high estimation accuracy for battery SOC, there are still shortcomings in the current research, mainly including that the parameters of the hysteresis differential equation are not given rigorously, and the battery hysteresis characteristics under different temperature environments and different aging states have not been studied. Therefore, in future work, the author will conduct further research on the optimization of the model parameter selection, battery hysteresis characteristics at different temperatures, and different battery aging states.