Design and Motion Analysis of a Magnetic Climbing Robot Applied to Ship Shell Plate
Abstract
:1. Introduction
2. Design of Mechanical Structure and Control System
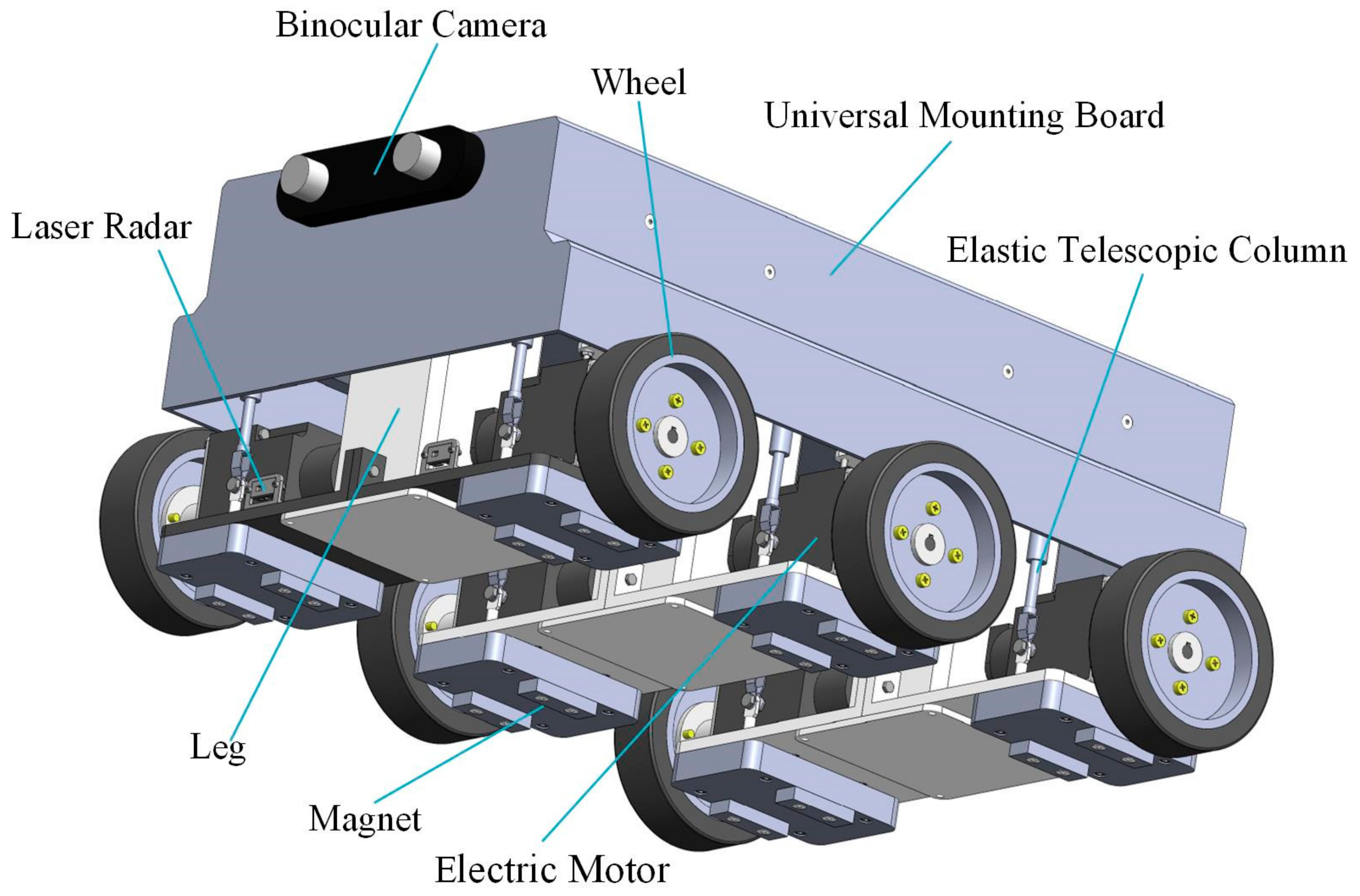
2.1. Mechanical Structure and Working Principle
- (1)
- Three legs that can complete telescopic motion were installed in the middle of the abdomen of robot.
- (2)
- A wheel was installed on each side of the foot position of each leg, and the wheel was driven by brushless DC servomotor on the inside.
- (3)
- The magnet was installed under the brushless DC servomotor, which can move up and down with the lifting and dropping of the leg to achieve the adjustment of the magnetic force.
- (4)
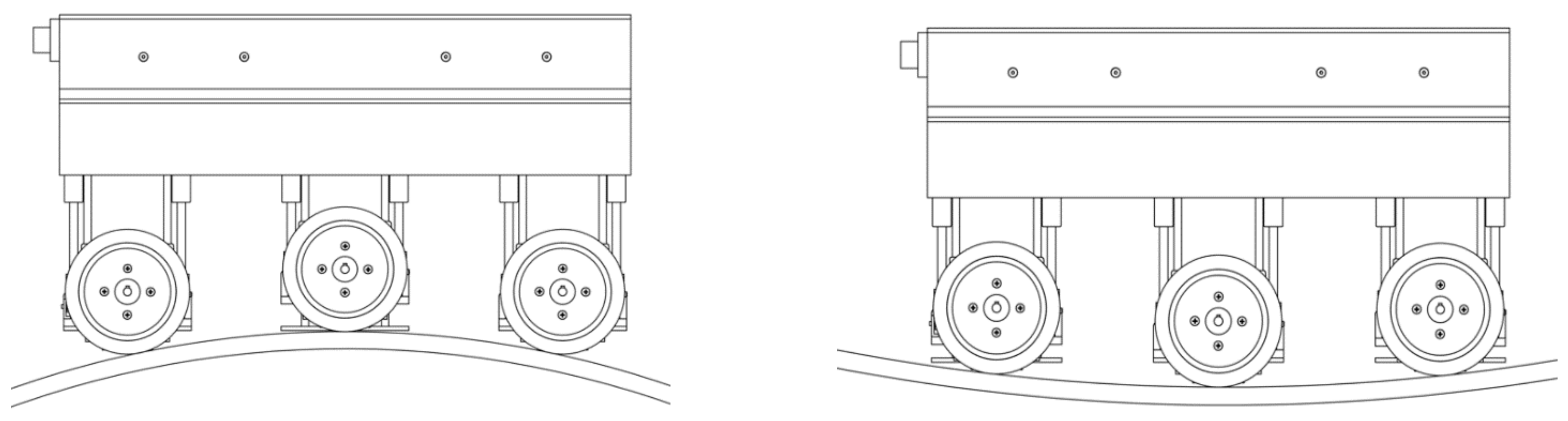
- Elastic telescopic columns connect the wheels to the robot body, and they allow the magnetic climbing robot to cope with the curvature of ship shell plate.
- (5)
- The universal mounting board was supported on the top of the magnetic climbing robot by small columns.
- (1)
- The magnet keeps a distance from ship shell plate, which can not only reduce the resistance during work but also make the magnetic climbing robot easy to adapt to the curved surface.
- (2)
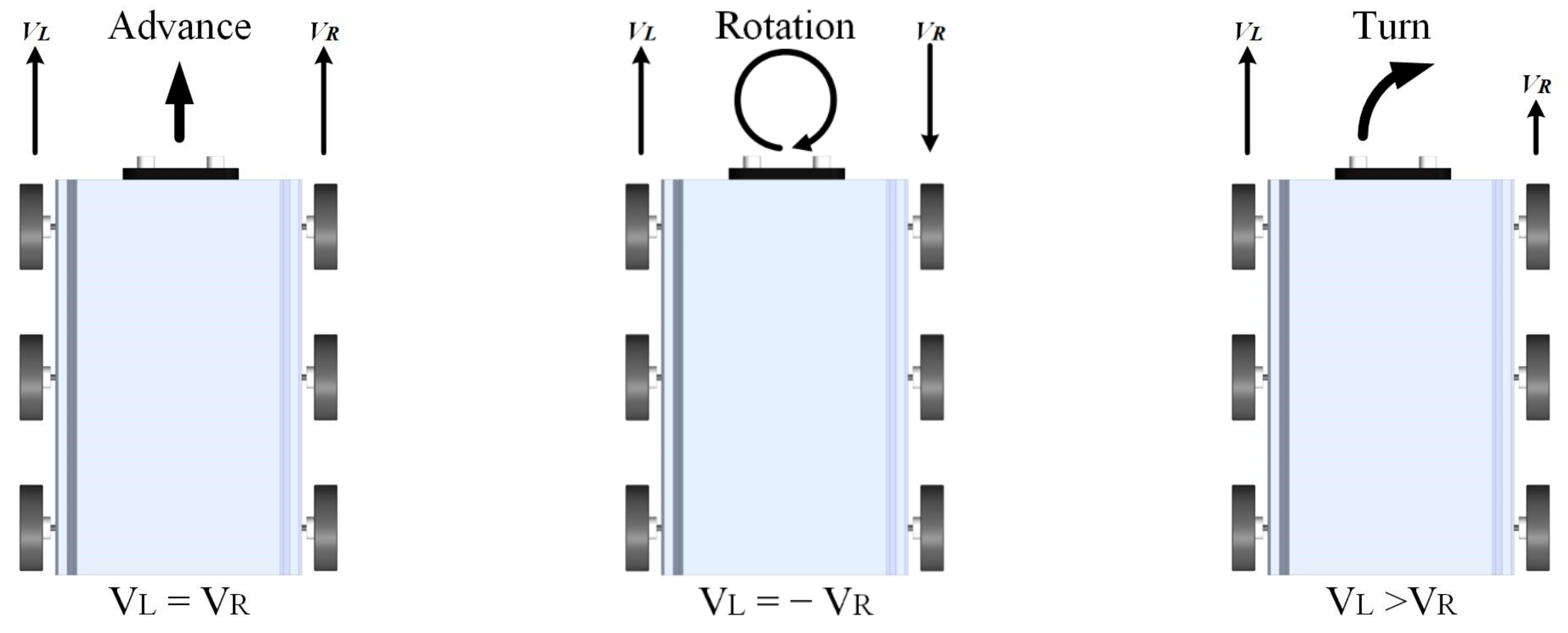
- The wheel speed of each wheel can be controlled individually, and the direction of the magnetic climbing robot can be controlled by adjusting the speed difference between the wheels on both sides.
- (3)
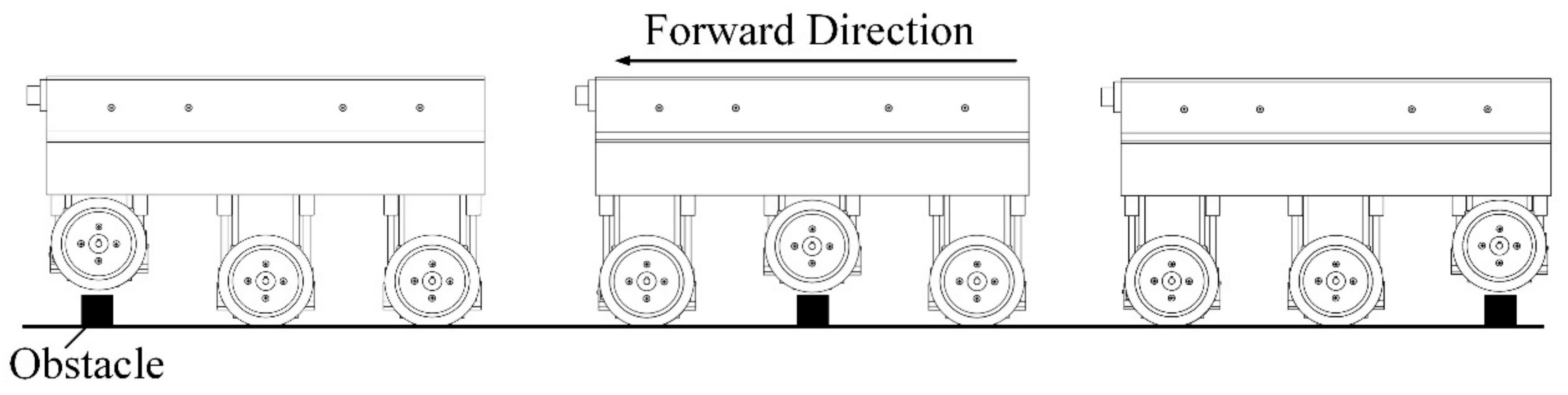
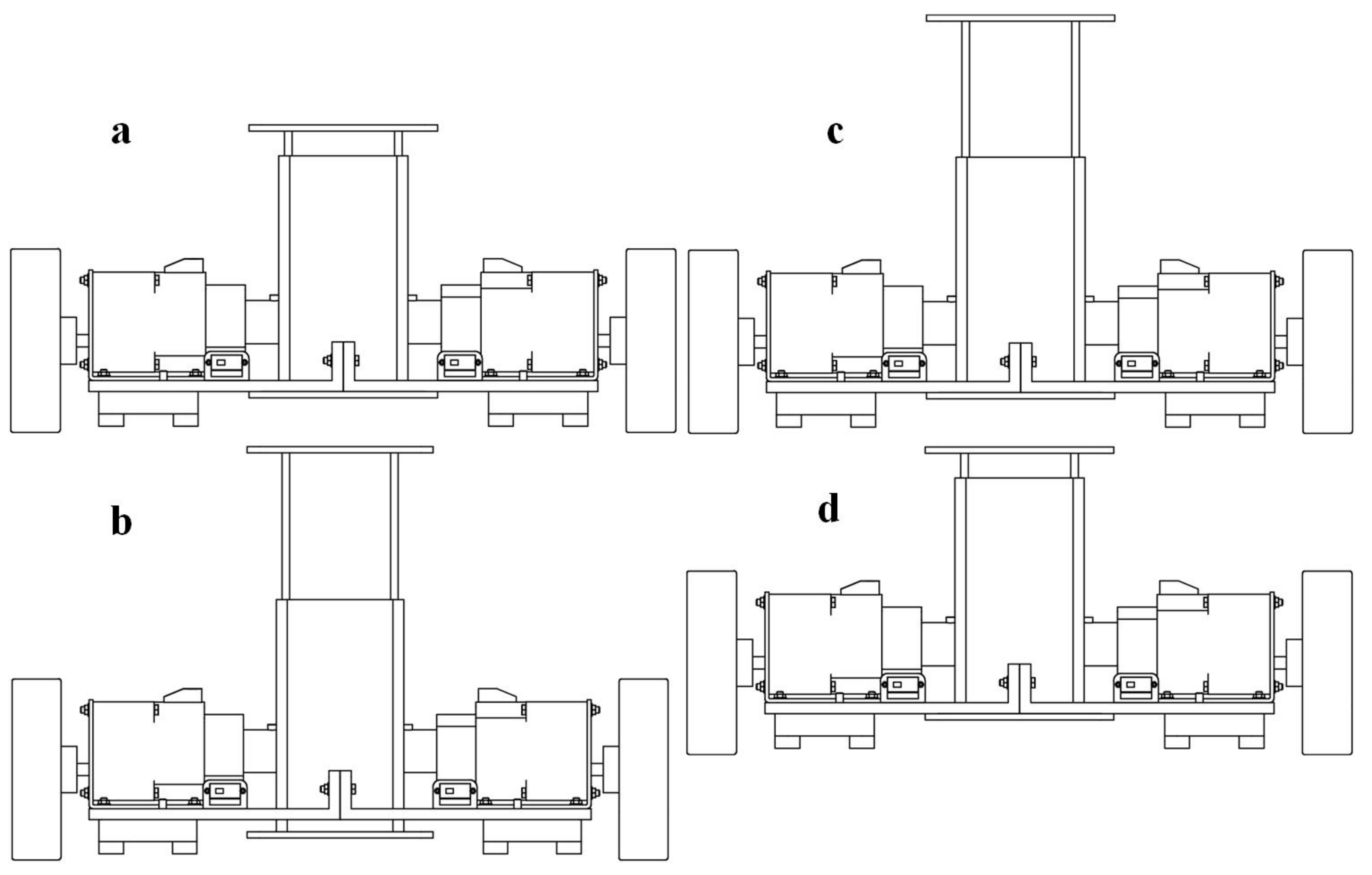
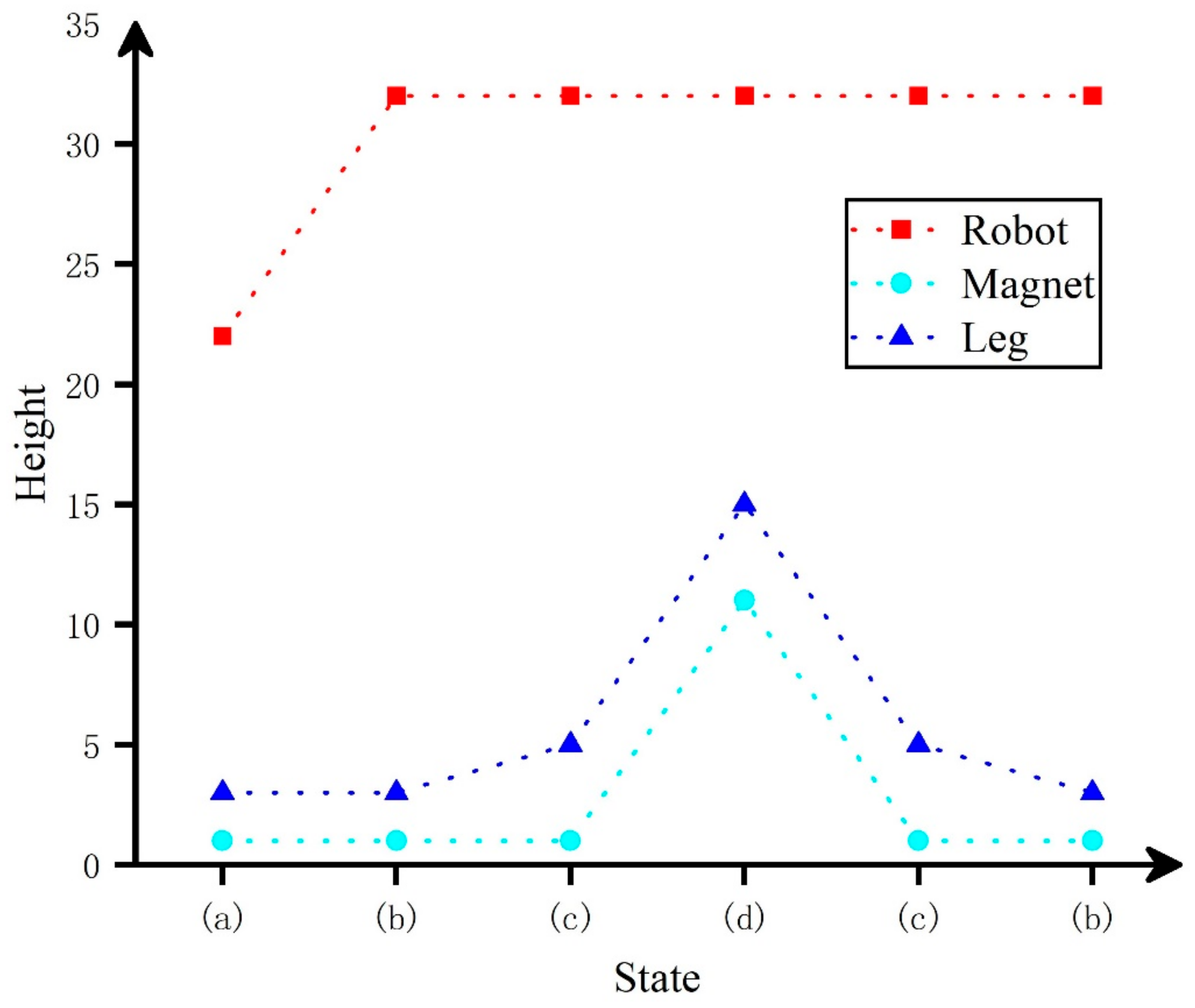
- When the laser radar detects that there was an obstacle in front of the robot, the first leg, the second leg and the third leg of the robot will be lifted in turn. After crossing the obstacle, the three legs will drop in turn, so that the robot can cross the obstacle as a whole, as shown in Figure 3.
- (4)
- The leg and wheel of the magnetic climbing robot were not in direct contact, but they were connected to the splint above. When ship shell plate has curvature, the wheel can adapt to the curved surface due to the characteristics of the elastic telescopic column, and the elastic telescopic column can be compressed when the leg is lifted, thereby driving the wheel to rise.
- (5)
- Various work equipment can be installed on the universal mounting board to increase the function of the magnetic climbing robot.
2.2. Design of Control System
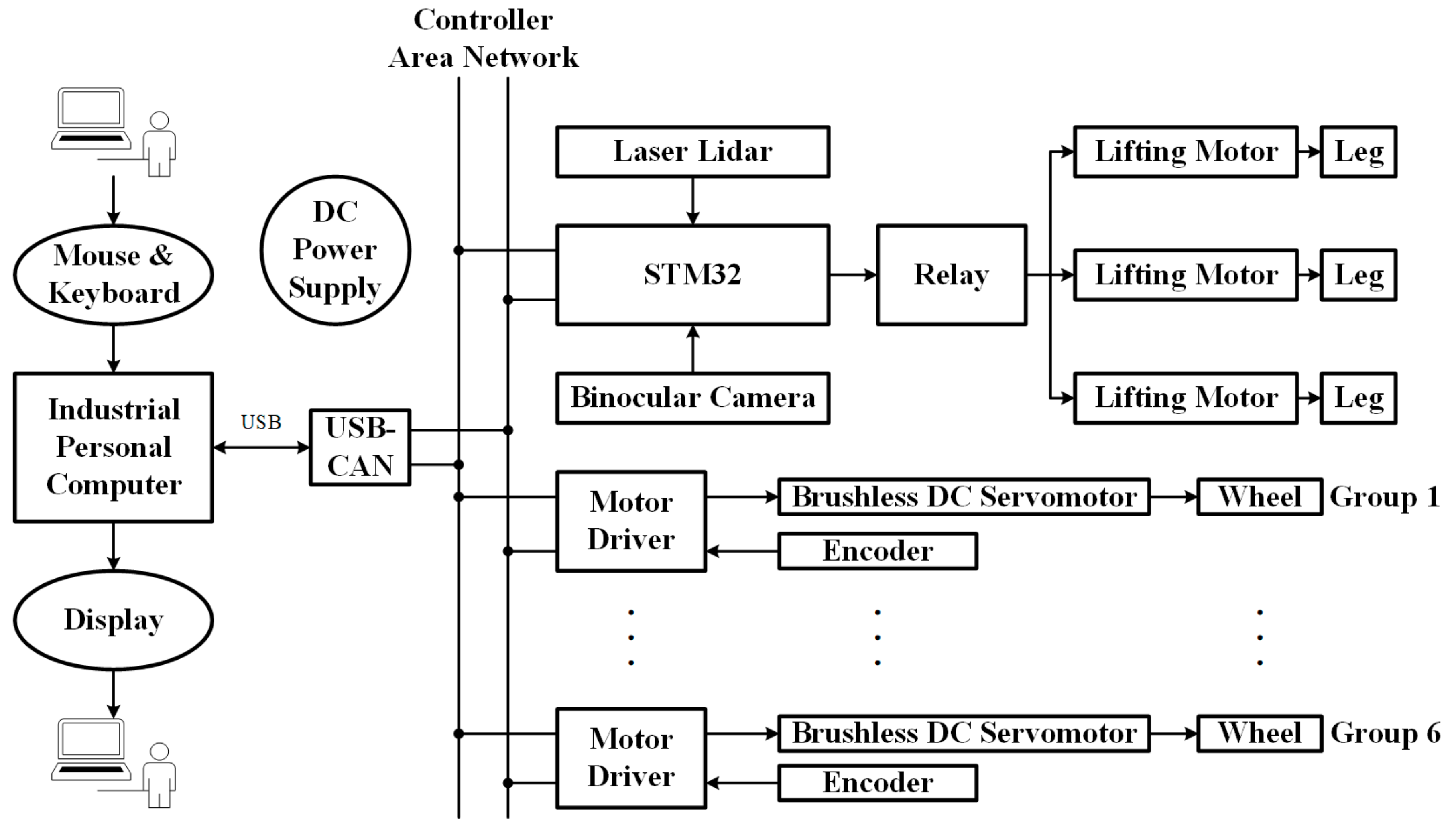
2.2.1. Hardware Design of Control System
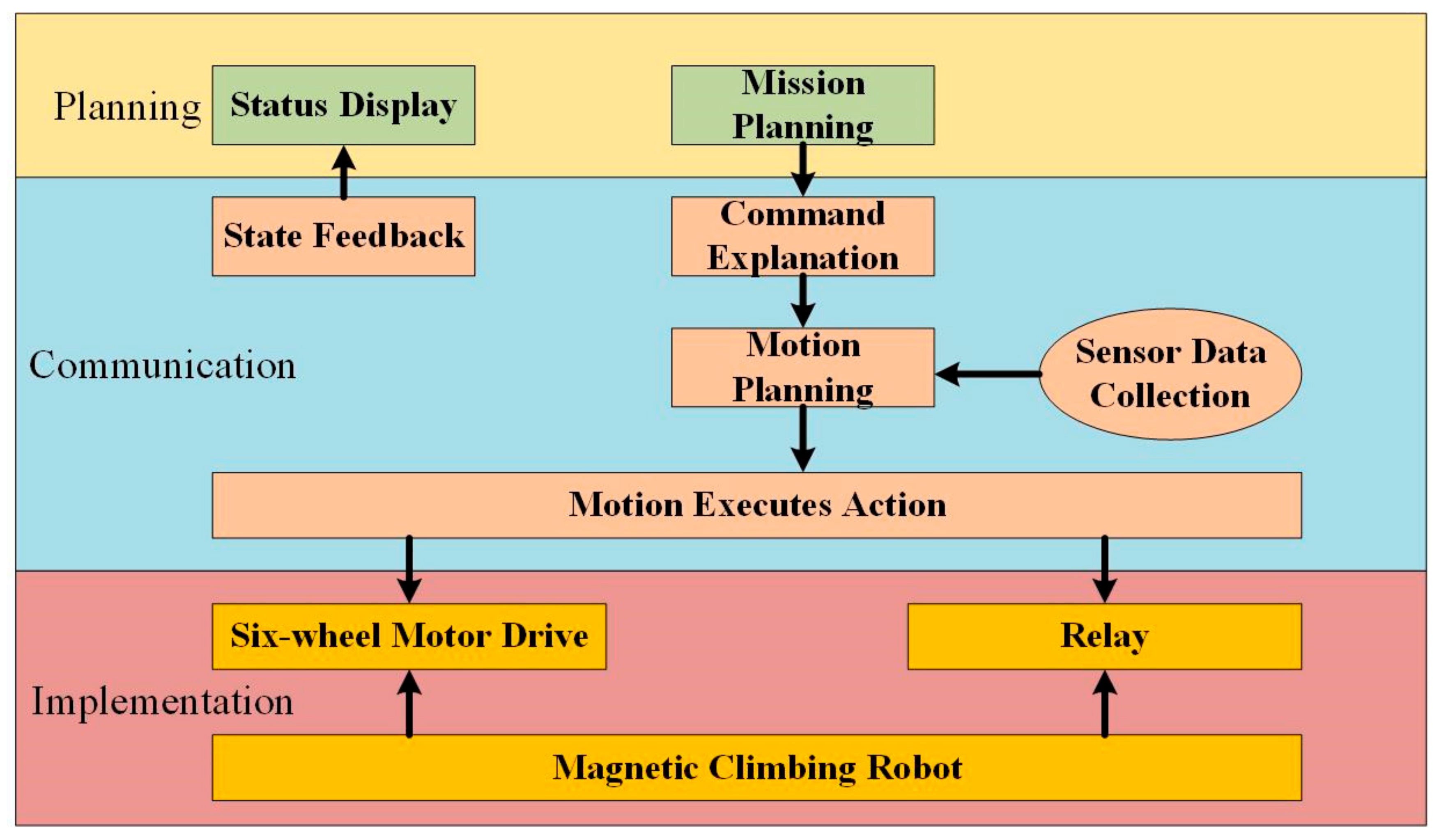
2.2.2. Software Design of Control System
3. Motion Analysis
3.1. Kinematic Analysis
3.1.1. Kinematic Analysis of Leg Motion
3.1.2. Kinematic Analysis of Chassis Motion
- (1)
- Six drive wheels were symmetrically distributed on the same plane.
- (2)
- The deformation of the wheel was negligible, and the contact with the ship shell plate was a point. The radius of the wheel was r.
- (3)
- The geometric center point C of the chassis coincided with the projection of the center of mass on the ship shell plate.
- (4)
- The wheels simply rolled on the ship shell plate, and there was no slippage.
- (5)
- Assuming that the ship shell plate was a rigid body, the deformation of the ship shell plate was ignored.
- (6)
- Longitudinal slip was not considered when turning.
- (7)
- The robot was in a state of steady motion.
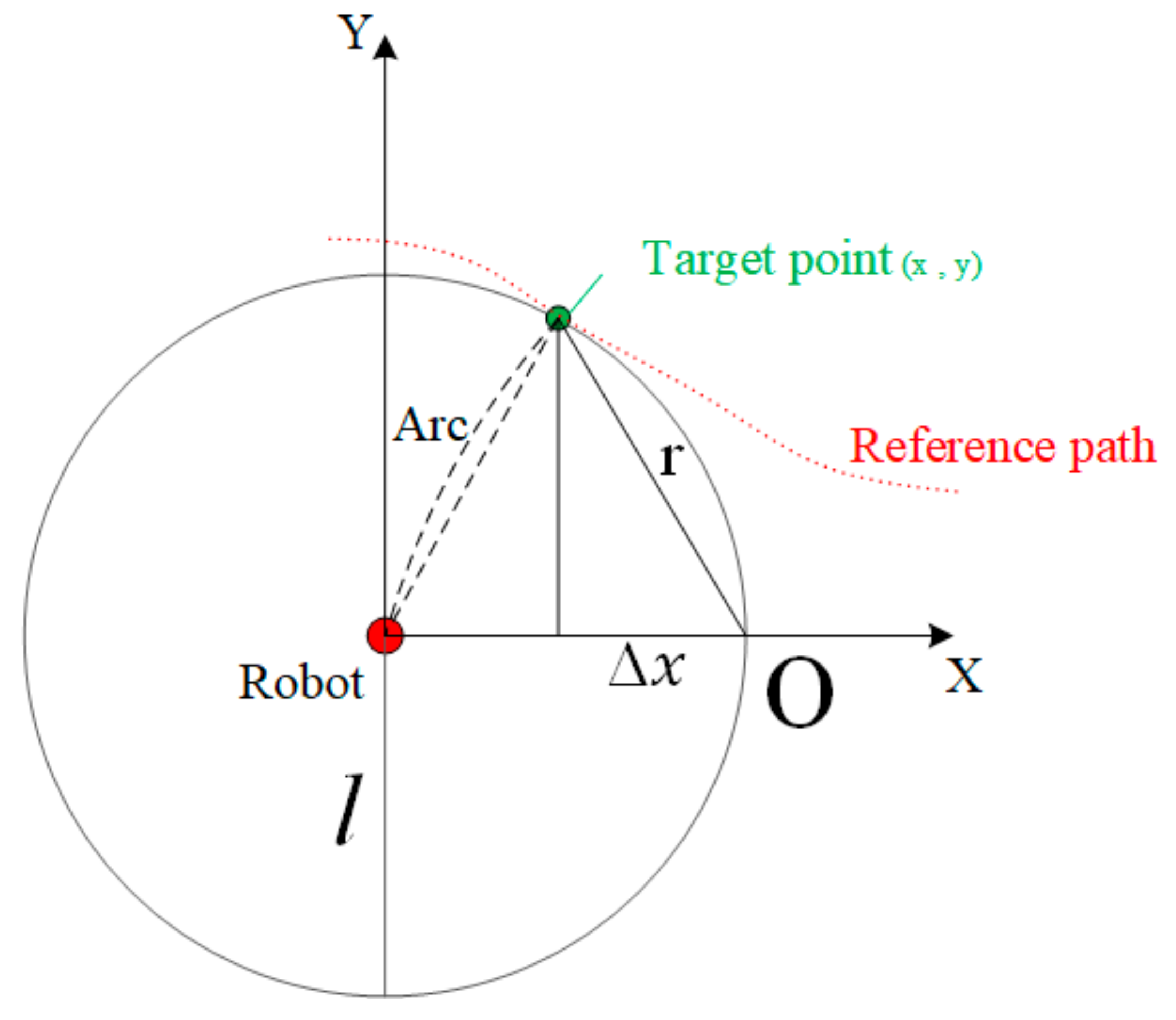
3.2. Path Tracking
- (1)
- Defined the initial position of the robot in the wall coordinate system.
- (2)
- Calculated the Euclidean distance between all points on the reference path and the robot and took the point with the smallest Euclidean distance.
- (3)
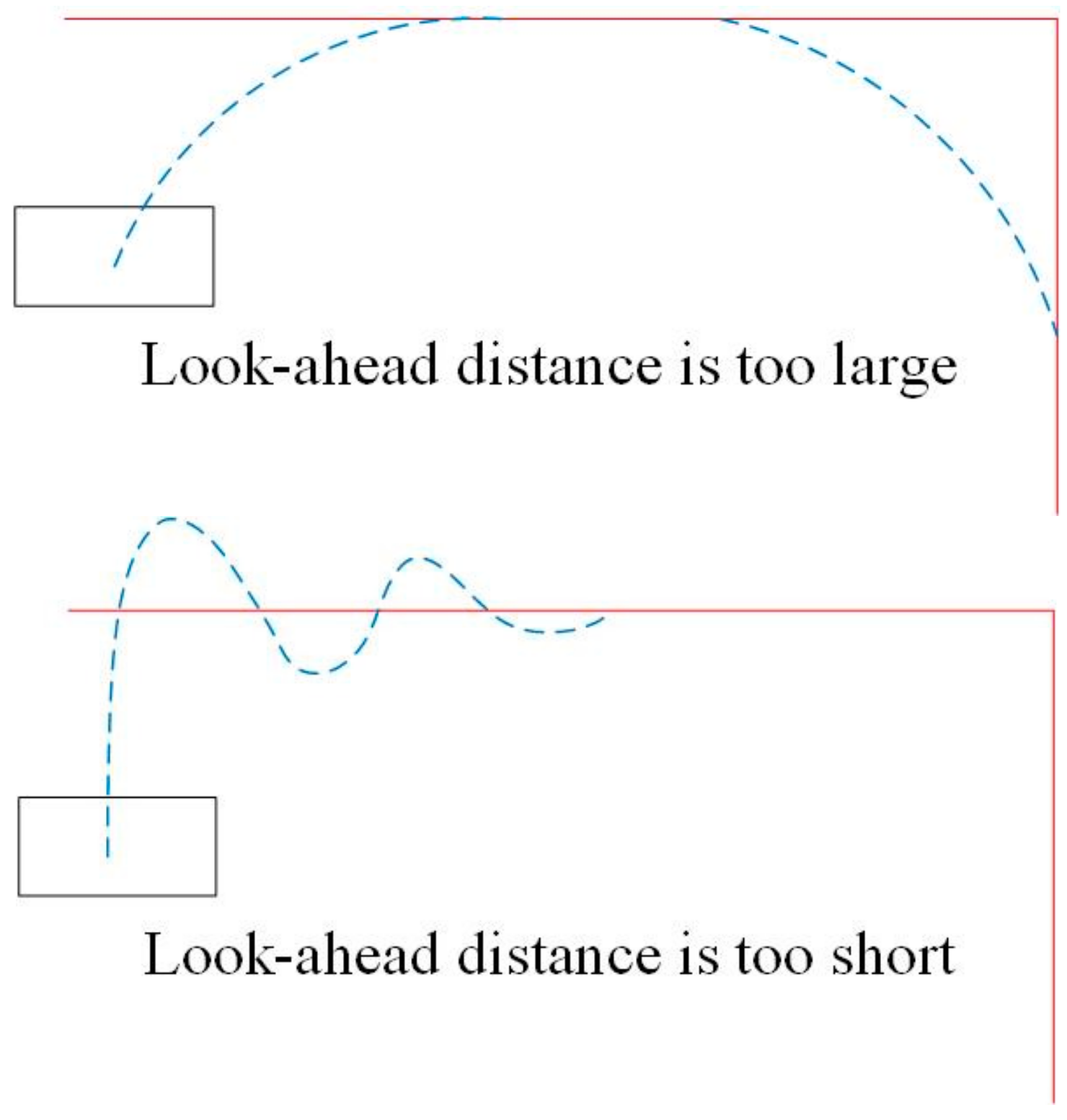
- Determined the look-ahead distance l, start from the point with the smallest Euclidean distance and look for the target point with a distance l from the robot in the forward direction of the path.
- (4)
- The position of the target point in the wall coordinate system was transformed into the robot coordinate system.
- (5)
- The turning radius r was calculated according to Formula (12).
- (6)
- The turning radius was calculated as the linear speed of the wheels on both sides, and the position of the robot was continuously updated.
- (7)
- The robot chased the advancing target point and keep driving on the predetermined path.
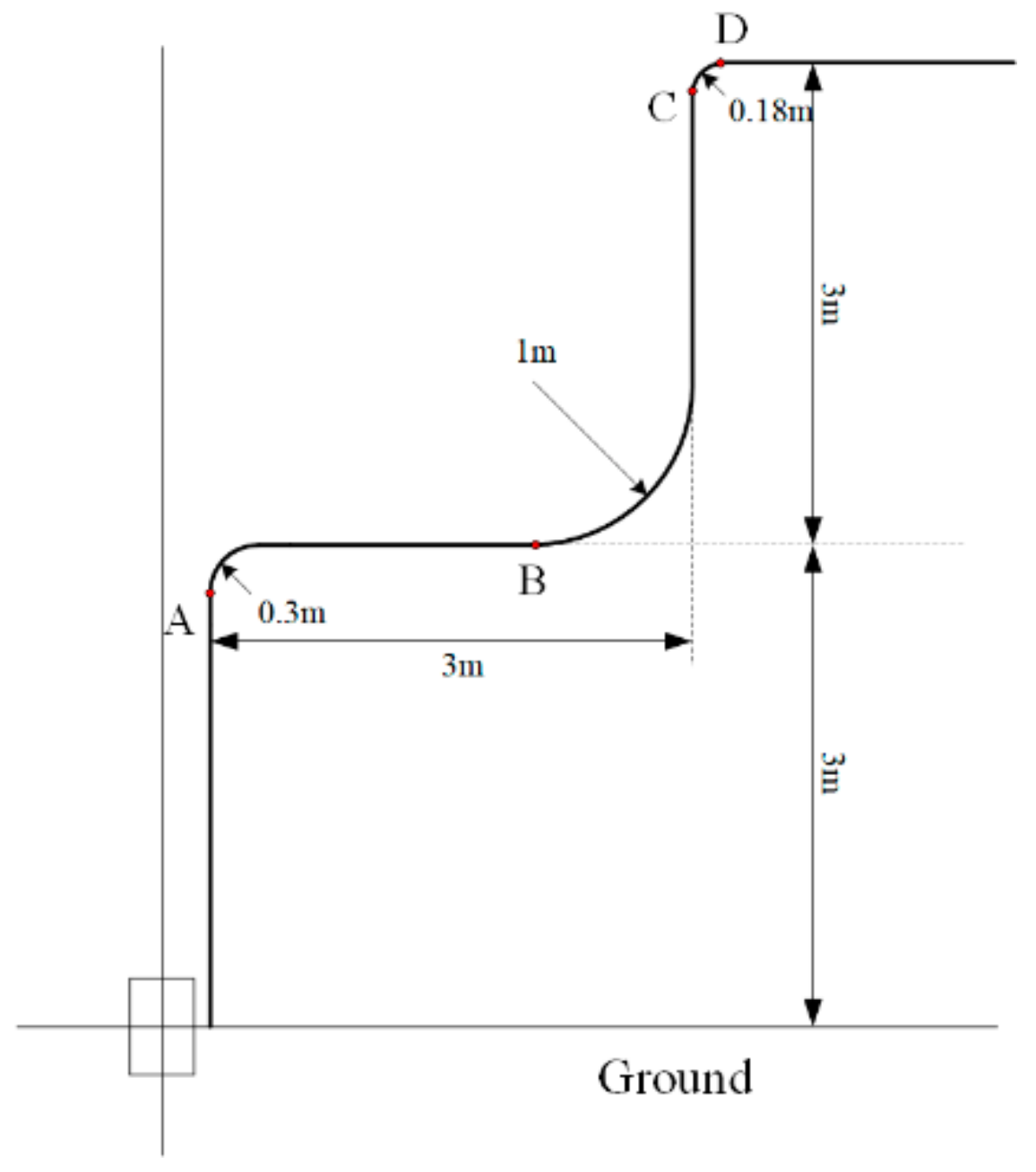
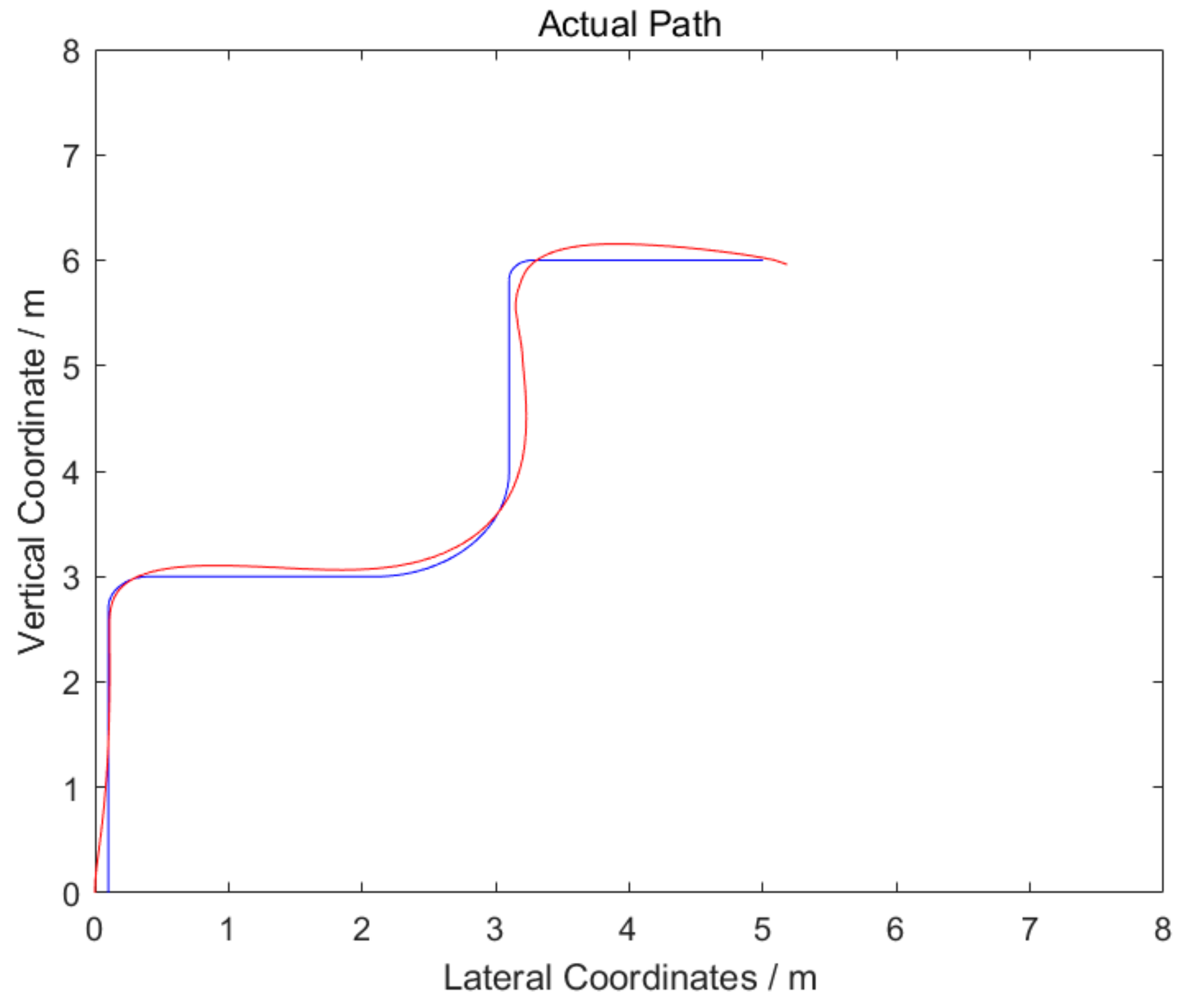
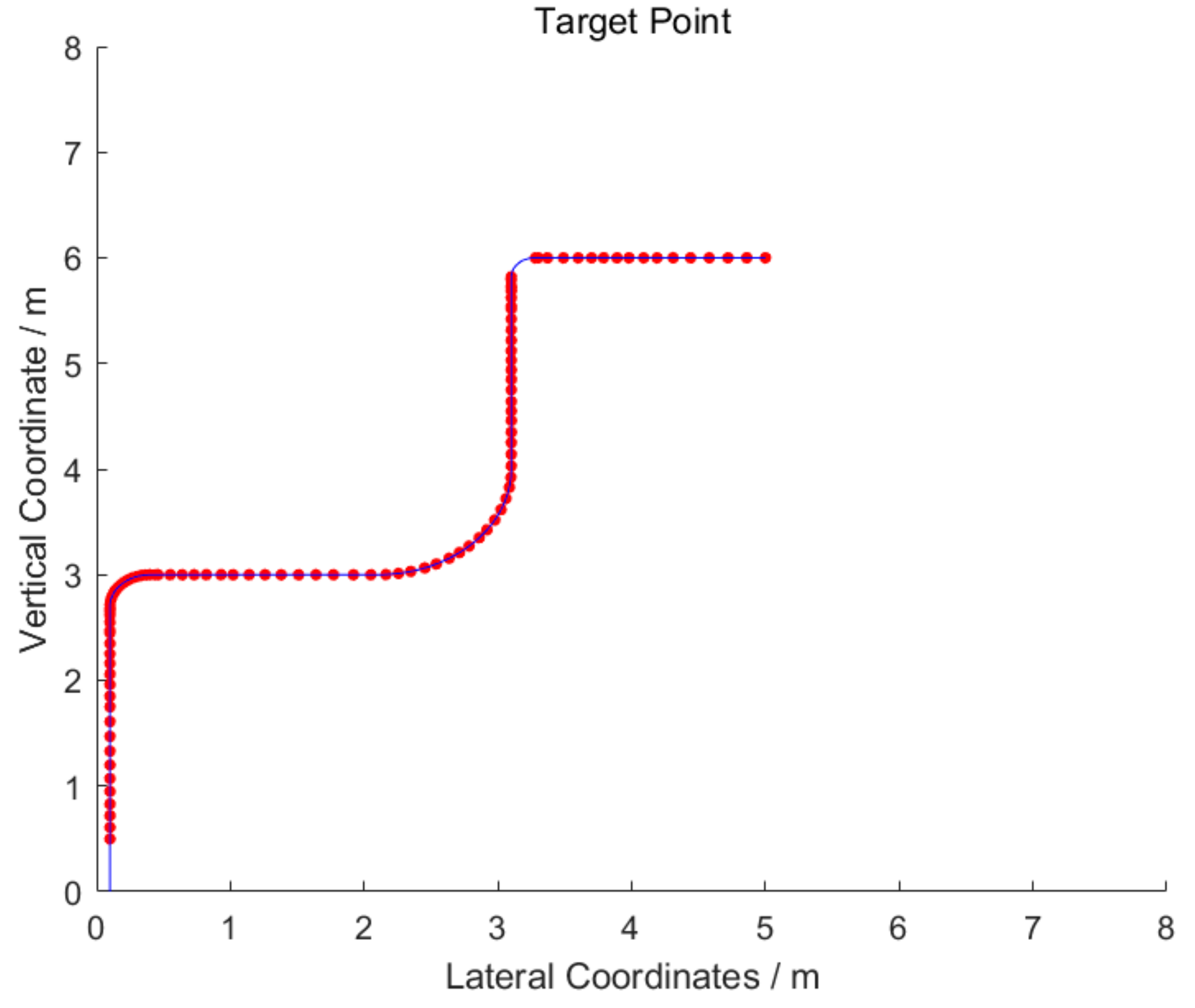
3.3. Simulation and Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Feng, X.; Tian, W.; Wei, R.; Pan, B.; Chen, Y.; Chen, S. Application of a Wall-Climbing, Welding Robot in Ship Automatic Welding. J. Coast. Res. 2020, 106, 609–613. [Google Scholar] [CrossRef]
- Abdulkader, R.E.; Veerajagadheswar, P.; Lin, N.H.; Kumaran, S.; Vishaal, S.R.; Mohan, R.E. Sparrow: A Magnetic Climbing Robot for Autonomous Thickness Measurement in Ship Hull Maintenance. J. Mar. Sci. Eng. 2020, 8, 469. [Google Scholar] [CrossRef]
- Alkalla, M.G.; Fanni, M.A.; Mohamed, A.M.; Hashimoto, S. Tele-operated propeller-type climbing robot for inspection of petrochemical vessels. Ind. Robot 2017, 44, 166–177. [Google Scholar] [CrossRef]
- Huang, H.; Li, D.; Xue, Z.; Chen, X.; Liu, S.; Leng, J.; Wei, Y. Design and performance analysis of a tracked wall-climbing robot for ship inspection in shipbuilding. Ocean Eng. 2017, 131, 224–230. [Google Scholar] [CrossRef]
- Ravindra, S.B.; Pushparaj, M.P.; Saroj, K.P. Experimental investigations on permanent magnet based wheel mechanism for safe navigation of climbing robot. Procedia Comput. Sci. 2018, 133, 377–384. [Google Scholar]
- Jiao, S.; Zhang, X.; Zhang, X.; Jia, J.; Zhang, M. Magnetic, Circuit Analysis of Halbach, Array and Improvement of Permanent, Magnetic Adsorption, Device for Wall-Climbing, Robot. Symmetry 2022, 14, 429. [Google Scholar] [CrossRef]
- Olivier, K. A magnetic climbing robot to perform autonomous welding in the shipbuilding industry. Robot. Comput. Integr. Manuf. 2018, 53, 178–186. [Google Scholar]
- Zhong, Z.; Xu, M.; Xiao, J.; Lu, H. Design and Control of an Omnidirectional Mobile Wall-Climbing Robot. Appl. Sci. 2021, 11, 11065. [Google Scholar] [CrossRef]
- Nagano, K.; Fujimoto, Y. Simplification of Motion, Generation in the Singular, Configuration of a Wheel-Legged, Mobile Robot. IEEJ J. Ind. Appl. 2019, 8, 745–755. [Google Scholar]
- Li, J.; Wang, J.; Wang, S.; Peng, H.; Wang, B.; Qi, W.; Zhang, L.; Su, H. Parallel structure of six wheel-legged robot trajectory tracking control with heavy payload under uncertain physical interaction. Assem. Autom. 2020, 40, 675–687. [Google Scholar] [CrossRef]
- Orozco-Magdaleno, E.C.; Cafolla, D.; Castillo-Castaneda, E.; Carbone, G. Static Balancing of Wheeled-legged Hexapod Robots. Robotics 2020, 9, 23. [Google Scholar] [CrossRef] [Green Version]
- Lee, F.-S.; Lin, C.-I.; Chen, Z.-Y.; Yang, R.-X. Development of a control architecture for a parallel three-axis robotic arm mechanism using CANopen communication protocol. Concurr. Eng. 2021, 29, 197–207. [Google Scholar] [CrossRef]
- Yu, L.; Xiangdong, J.; Canfeng, Z.; Jiaqing, C.; Suxin, H. Welding robot system applied in sub-sea pipeline-installation. Ind. Robot 2015, 42, 83–92. [Google Scholar] [CrossRef]
- Hung, C.-W.; Lee, R.C.; Huang, B.-K.; Yu, S.-T. Multi-Motor Synchronous Control with CANopen. J. Robot. Netw. Artif. Life 2019, 5, 236–240. [Google Scholar] [CrossRef] [Green Version]
- Forsyth, D.; Ponce, J. Computer Vision: A Modern Approach; Prentice Hall: Hoboken, NJ, USA, 2011. [Google Scholar]
- Du, P.; Ma, Z.; Chen, H.; Xu, D.; Wang, Y.; Jiang, Y.; Lian, X. Speed-adaptive motion control algorithm for differential steering vehicle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2020, 235, 672–685. [Google Scholar] [CrossRef]
- Tian, J.; Tong, J.; Luo, S. Differential Steering Control of Four-Wheel Independent-Drive Electric Vehicles. Energies 2018, 11, 2892. [Google Scholar] [CrossRef] [Green Version]
- Hang, P.; Chen, X. Path tracking control of 4-wheel-steering autonomous ground vehicles based on linear parameter-varying system with experimental verification. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2020, 235, 411–423. [Google Scholar] [CrossRef]
- Cui, Q.; Ding, R.; Wei, C.; Zhou, B. Path-tracking and lateral stabilisation for autonomous vehicles by using the steering angle envelope. Veh. Syst. Dyn. 2020, 59, 1672–1696. [Google Scholar] [CrossRef]
- Kuwata, Y.; Teo, J.; Karaman, S.; Fiore, G.; Frazzoli, E.; How, J. Motion, Planning in Complex, Environments Using, Closed-loop Prediction. Guid. Navig. Control Conf. Exhib. 2008, 7166. [Google Scholar]




| Symbol | Explanation | Symbol | Explanation |
|---|---|---|---|
| XOY | Geodetic coordinate system | XSY | Wall coordinate system |
| φ | Included angle | θ | Pose angle |
| ω | Robot angular velocity | Steering angle | |
| Vij | Wheel line speed | C | Geometry center |
| P | Instantaneous rotation center | R | Steering radius |
| 2B | Wheel base on both sides | 2 L | Front and rear wheel distance |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| B | 0.2 m | h | 0.2 m |
| m | 40 kg | Fmagnetic force | 600 N |
| G | 400 N | Vmax | 1 m/s |
| Accelerate | 0.5 m/s2 | Deceleration | 0.5 m/s2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, S.; Pei, X.; Song, H.; Dai, P. Design and Motion Analysis of a Magnetic Climbing Robot Applied to Ship Shell Plate. Machines 2022, 10, 632. https://doi.org/10.3390/machines10080632
Cui S, Pei X, Song H, Dai P. Design and Motion Analysis of a Magnetic Climbing Robot Applied to Ship Shell Plate. Machines. 2022; 10(8):632. https://doi.org/10.3390/machines10080632
Chicago/Turabian StyleCui, Shuwan, Xunyi Pei, Huzhe Song, and Penghui Dai. 2022. "Design and Motion Analysis of a Magnetic Climbing Robot Applied to Ship Shell Plate" Machines 10, no. 8: 632. https://doi.org/10.3390/machines10080632
APA StyleCui, S., Pei, X., Song, H., & Dai, P. (2022). Design and Motion Analysis of a Magnetic Climbing Robot Applied to Ship Shell Plate. Machines, 10(8), 632. https://doi.org/10.3390/machines10080632





