Nonlinear Control of a Hydraulic Exoskeleton 1-DOF Joint Based on a Hardware-In-The-Loop Simulation
Abstract
:1. Introduction
2. HIL Platform of Hydraulic Exoskeleton
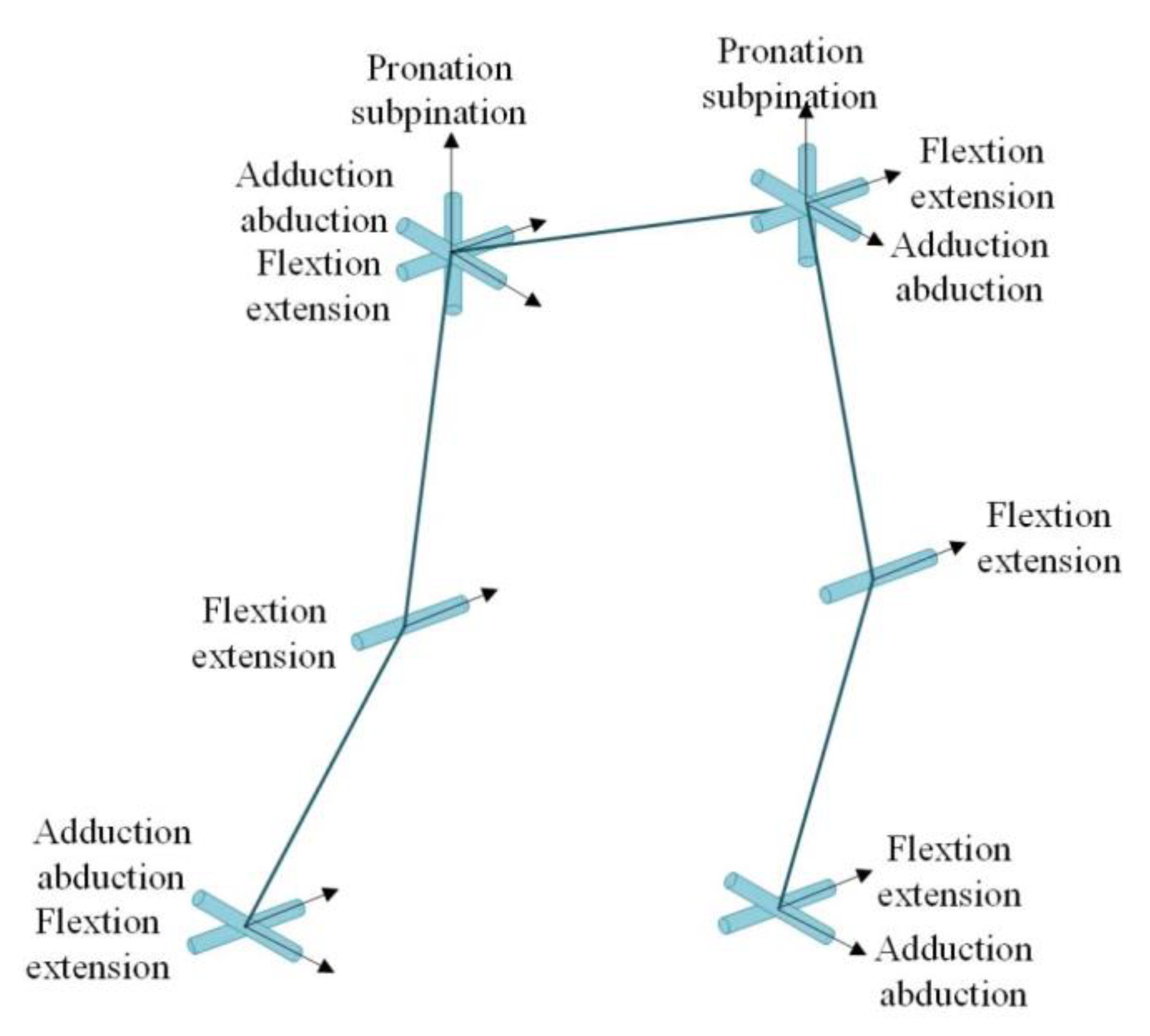
2.1. Mechanical Structure of the Exoskeleton System
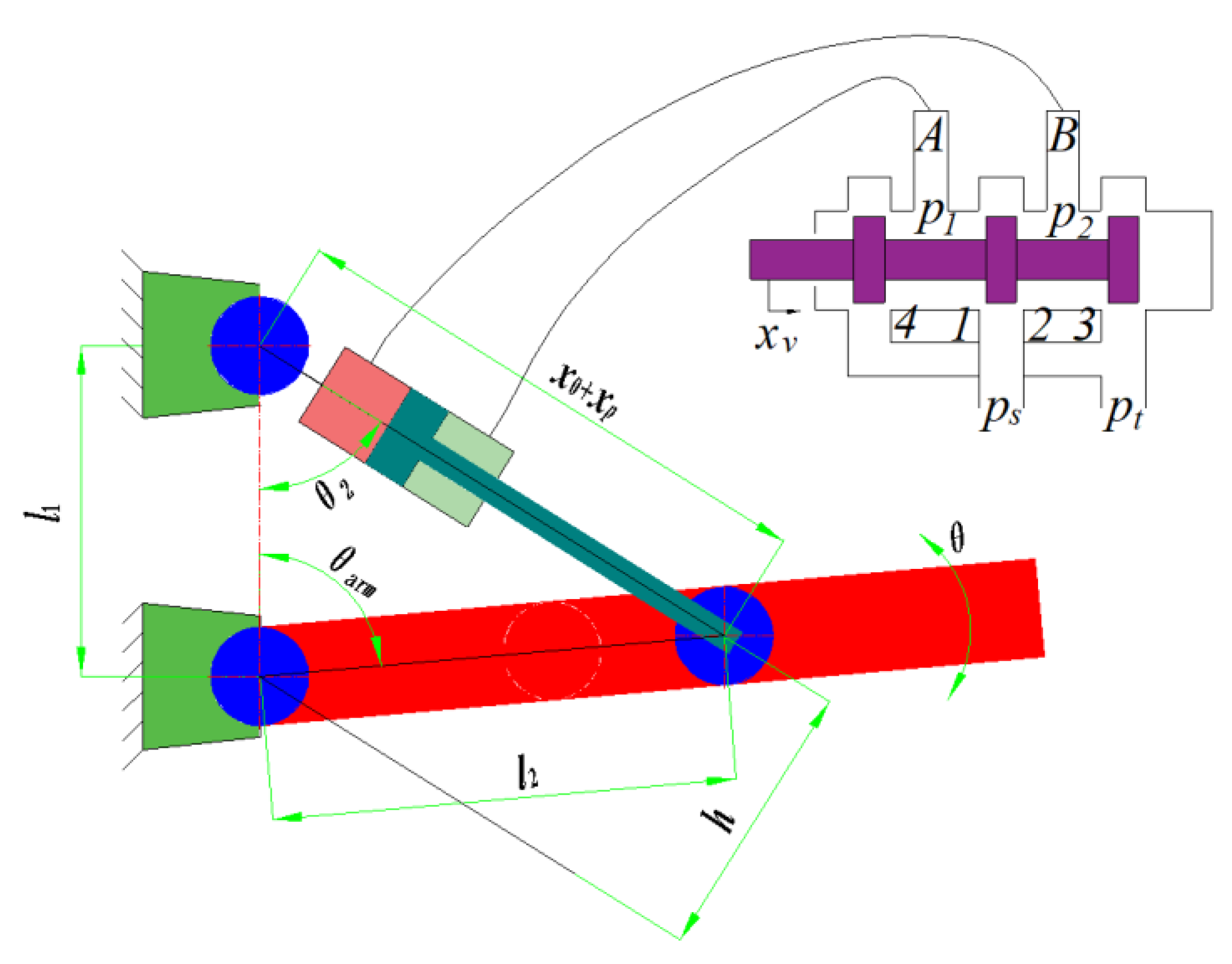
2.2. Joint Dynamic Modelling
2.2.1. Dynamic Model of the Electro-Hydraulic Servo System
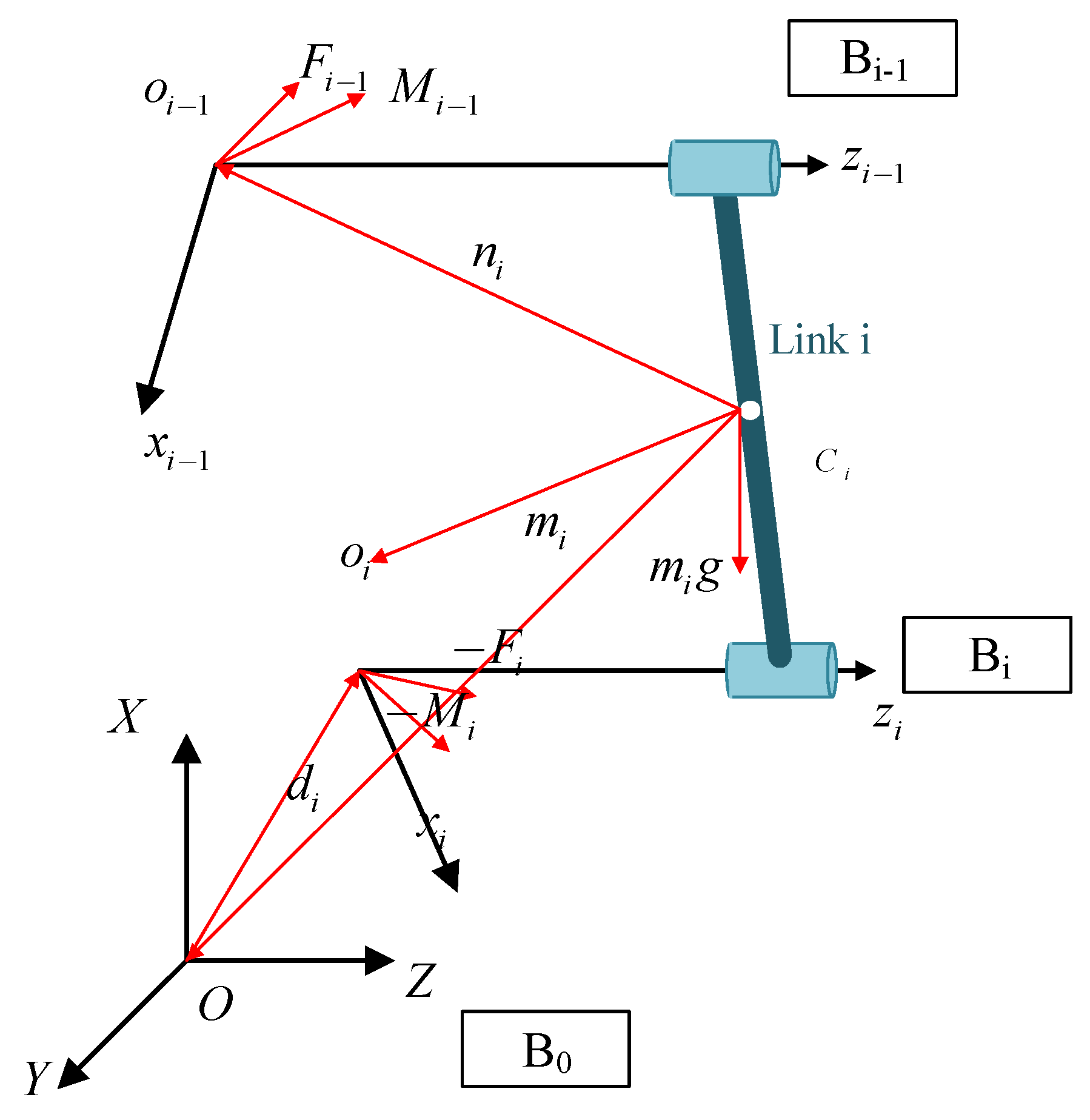
2.2.2. Dynamic Model of the Mechanical System
2.2.3. Overall System Dynamic Equation
2.3. Nonlinear Control Strategies
2.4. Development of the HIL Platform
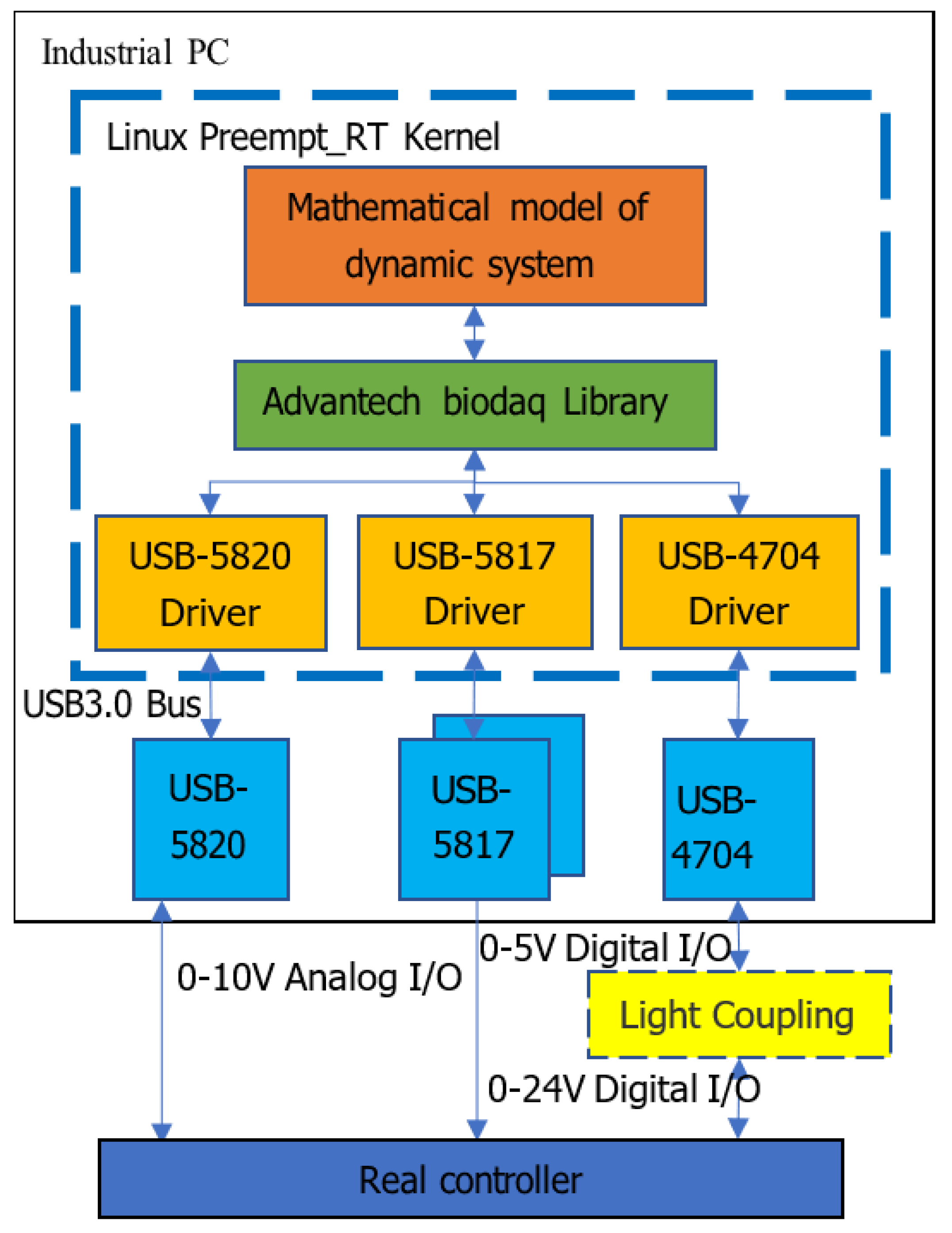
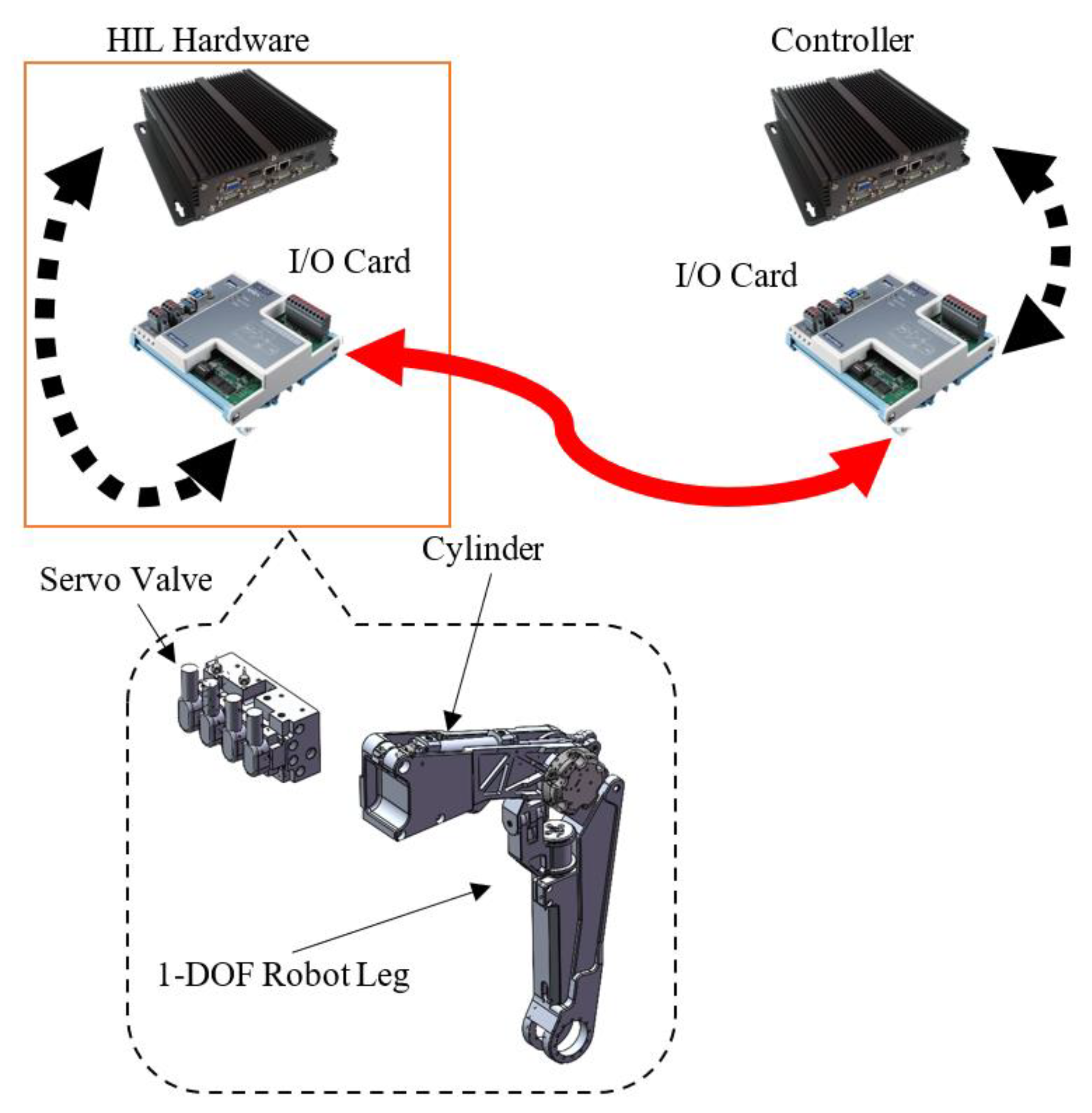
2.4.1. Overall System Architecture
2.4.2. Hardware
2.4.3. Software
- Real-time scheduling and priority;
- Memory lock. Lock all pages mapped to the address space of the calling process to prevent this memory from being paged to the swap area;
- Limit the power-saving state and state conversion of the processor. To prevent the system from going into the power-saving state and to provide the fastest idle state time, the kernel boots with the processor. Select max_cstate = 1 and idle = poll;
- Disable the X window server and network interfaces.
3. HIL Simulation and Experimental Results
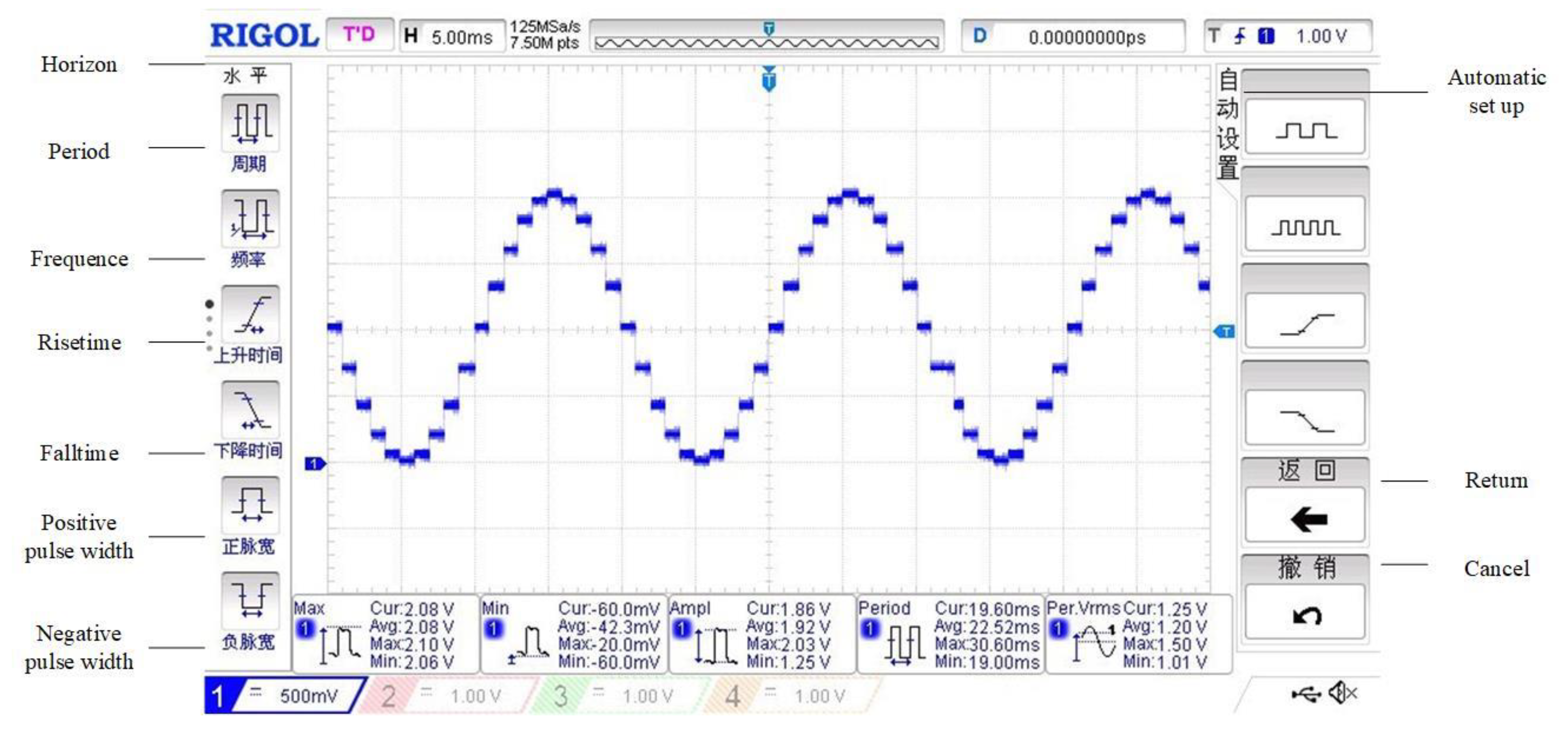
3.1. Real-time Performance Test
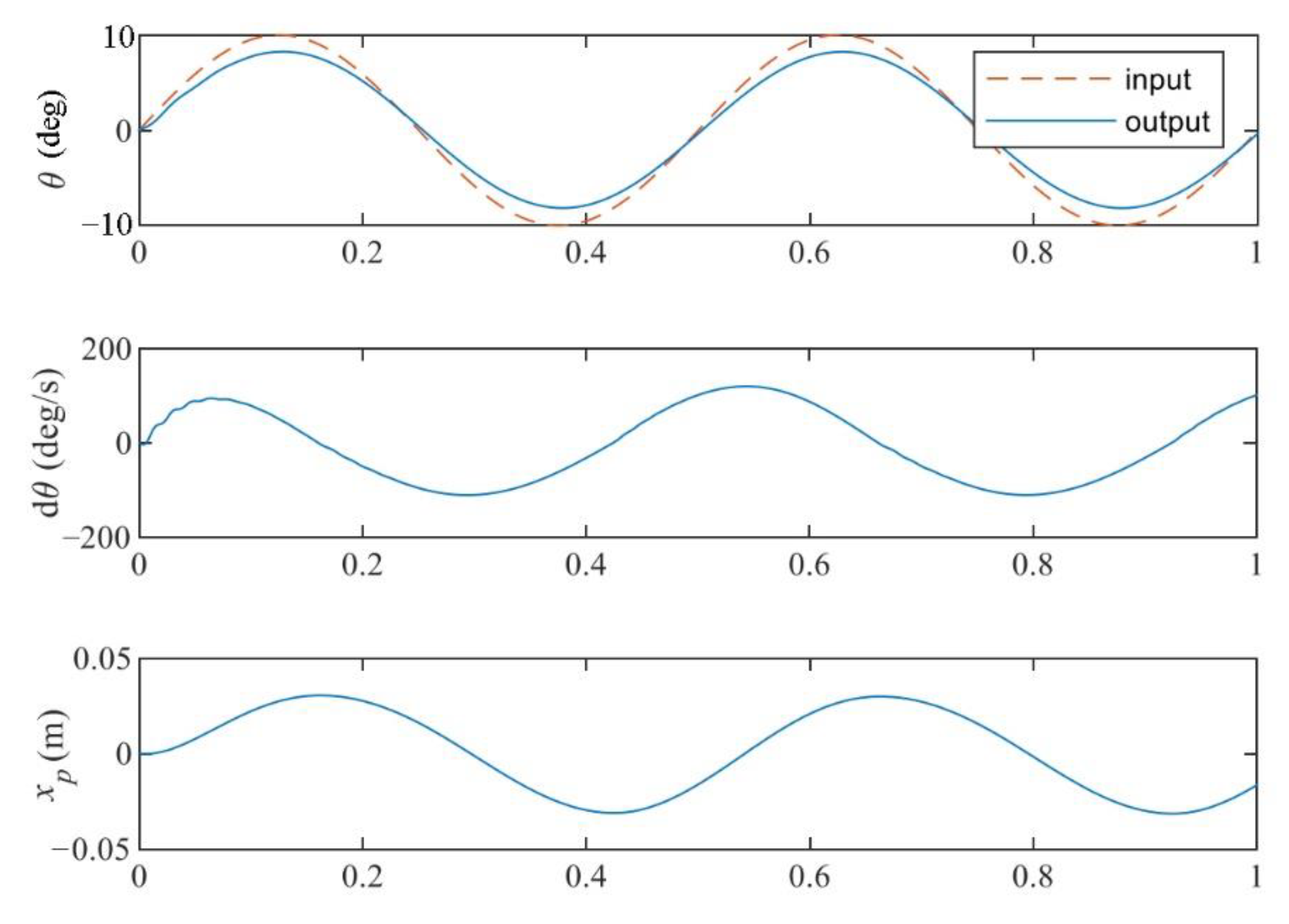
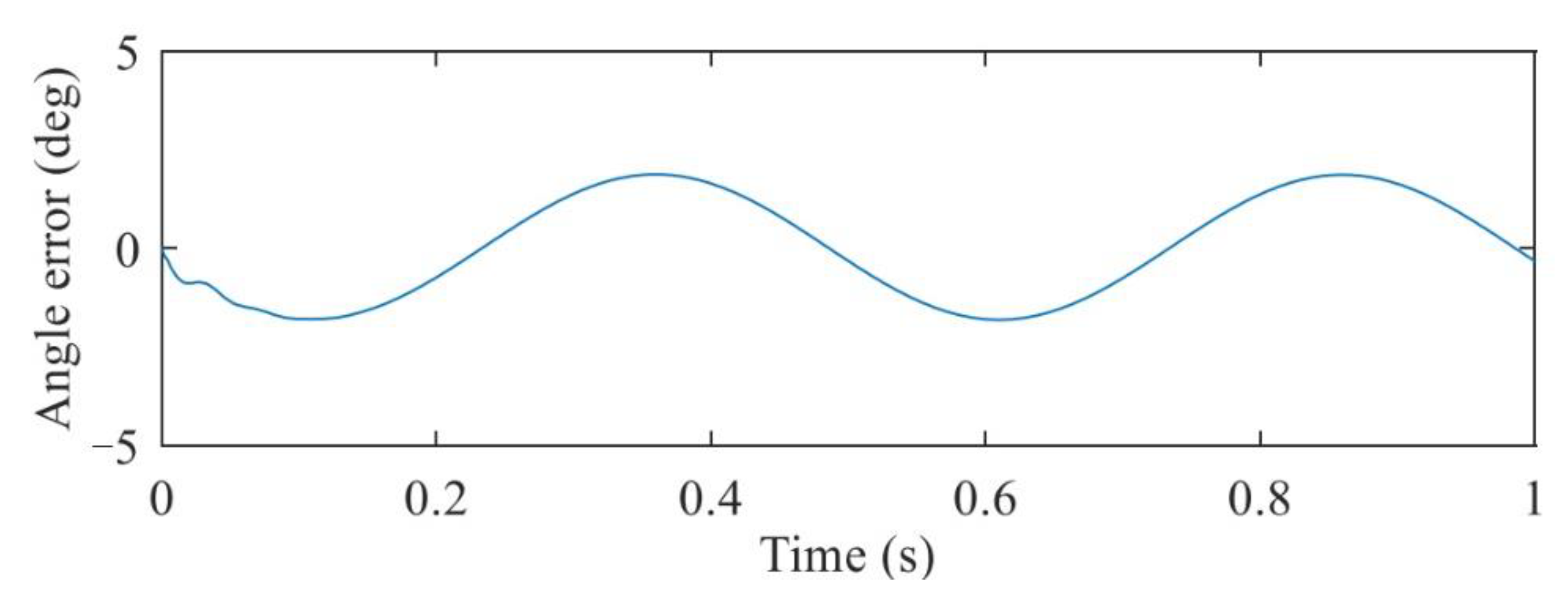
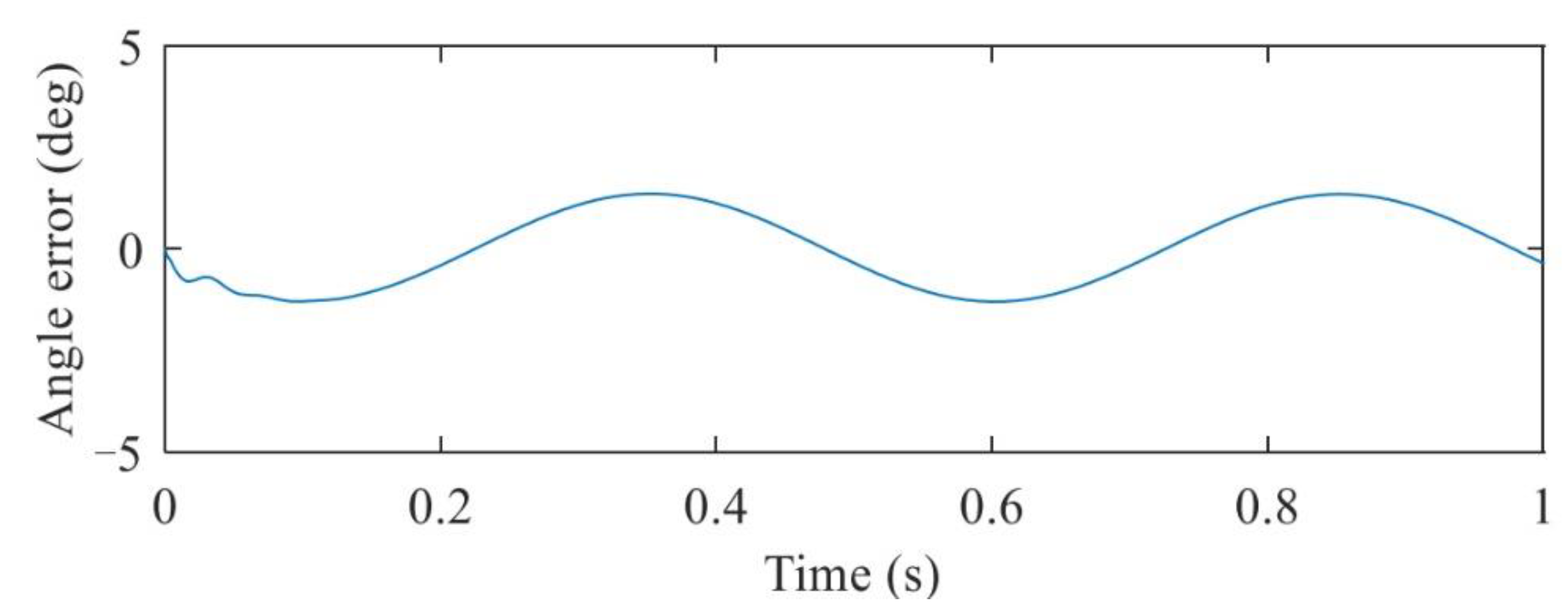
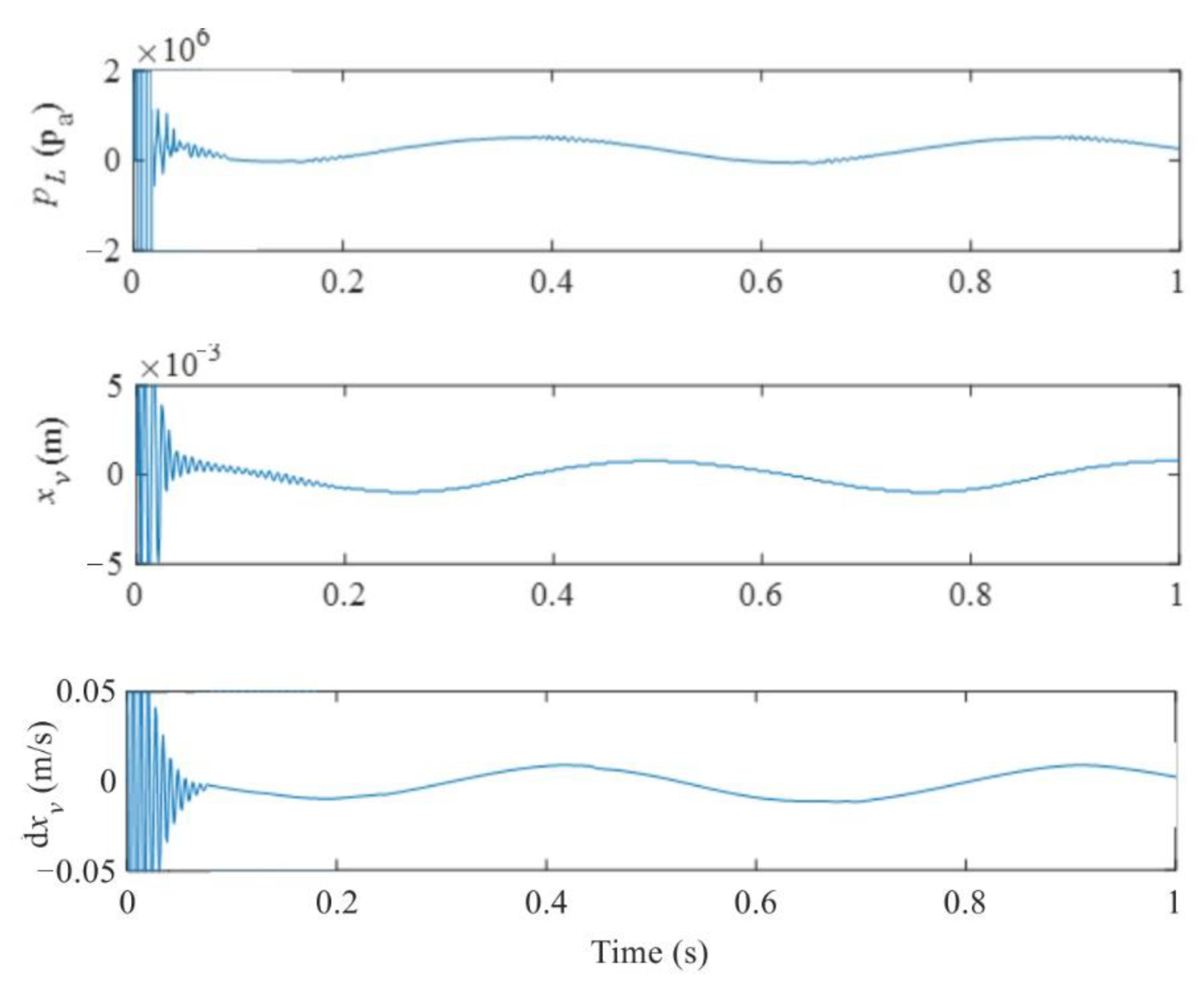
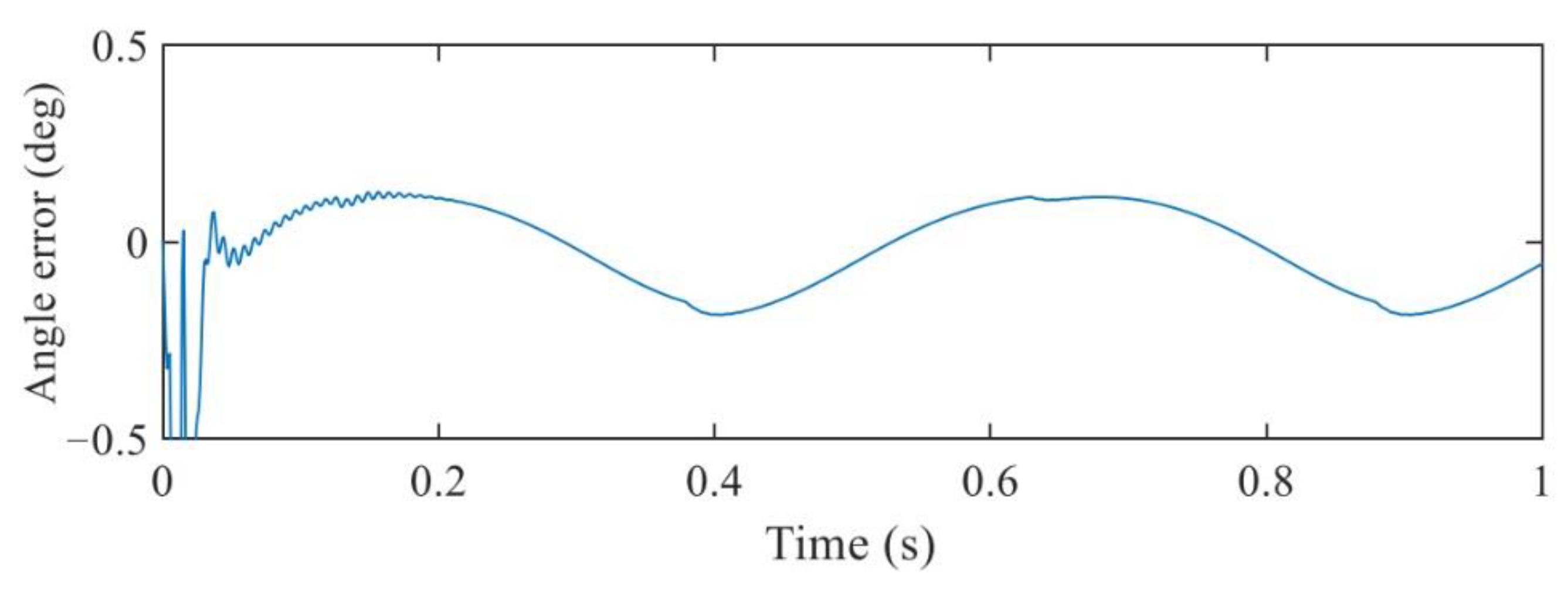
3.2. A 1-DOF Joint HIL Simulation Test
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhu, Y.; Zhang, G.; Zhang, C.; Liu, G.; Zhao, J. Biomechanical modeling and load-carrying simulation of lower limb exoskeleton. Bio-Med. Mater. Eng. 2015, 26, S729–S738. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, L.; Wang, S.; van Asseldonk, E.H.; van der Kooij, H. Actively controlled lateral gait assistance in a lower limb exoskeleton. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 965–970. [Google Scholar]
- Luna, C.O.; Rahman, M.H.; Saad, M.; Archambault, P.; Zhu, W.H. Virtual decomposition control of an exoskeleton robot arm. Robotica 2016, 34, 1587–1609. [Google Scholar] [CrossRef]
- Brahmi, B.; Saad, M.; Rahman, M.H.; Ochoa-Luna, C. Cartesian trajectory tracking of a 7-DOF exoskeleton robot based on human inverse kinematics. IEEE Trans. Syst. Man Cybern. Syst. 2017, 49, 600–611. [Google Scholar] [CrossRef]
- Brahmi, B.; Driscoll, M.; El Bojairami, I.K.; Saad, M.; Brahmi, A. Novel adaptive impedance control for exoskeleton robot for rehabilitation using a nonlinear time-delay disturbance observer. ISA Trans. 2021, 108, 381–392. [Google Scholar] [CrossRef] [PubMed]
- Brahmi, B.; Saad, M.; Ochoa-Luna, C.; Rahman, M.H.; Brahmi, A. Adaptive tracking control of an exoskeleton robot with uncertain dynamics based on estimated time-delay control. IEEE/ASME Trans. Mechatron. 2018, 23, 575–585. [Google Scholar] [CrossRef]
- Brahim, B.; Maarouf, S.; Luna, C.O.; Abdelkrim, B.; Rahman, M.H. Adaptive iterative observer based on integral backstepping control for upper extremity exoskelton robot. In Proceedings of the IEEE 2016 8th International Conference on Modelling, Identification and Control (ICMIC), Algiers, Algeria, 15–17 November 2016; pp. 886–891. [Google Scholar]
- Tschiersky, M.; Hekman, E.E.; Brouwer, D.M.; Herder, J.L.; Suzumori, K. A compact McKibben muscle based bending actuator for close-to-body application in assistive wearable robots. IEEE Robot. Autom. Lett. 2020, 5, 3042–3049. [Google Scholar] [CrossRef] [Green Version]
- Xie, D.; Liu, J.; Zuo, S. Pneumatic Flexible Exoskeleton with Variable Stiffness Based on Wire Driving and Clamping. In Proceedings of the 2019 IEEE 9th Annual International Conference on CYBER Technology in Automation, Control, and Intelligent Systems (CYBER), Suzhou, China, 29 July–2 August 2019; pp. 1215–1218. [Google Scholar]
- Di Natali, C.; Sadeghi, A.; Mondini, A.; Bottenberg, E.; Hartigan, B.; De Eyto, A.; O’Sullivan, L.; Rocon, E.; Stadler, K.; Mazzolai, B.; et al. Pneumatic quasi-passive actuation for soft assistive lower limbs exoskeleton. Front. Neurorobotics 2020, 6, 30. [Google Scholar] [CrossRef] [PubMed]
- Henderson, G.C.; Ueda, J. Pneumatically-powered robotic exoskeleton to exercise specific lower extremity muscle groups in humans. In Proceedings of the 2012 4th IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics (BioRob), Rome, Italy, 24–27 June 2012; pp. 1506–1511. [Google Scholar]
- Zhang, X.; Jiang, W.; Li, Z.; Song, S. A hierarchical Lyapunov-based cascade adaptive control scheme for lower-limb exoskeleton. Eur. J. Control 2019, 50, 198–208. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Zhang, S.; Liu, S.; Xu, K.; Yao, B. Adaptive Backstepping Sliding Mode Control for a Hydraulic Knee Exoskeleton Robot. In Proceedings of the 2020 2nd International Conference on Artificial Intelligence, Robotics and Control, Cairo, Egypt, 12–14 December 2020; pp. 43–48. [Google Scholar]
- Chen, S.; Yao, B.; Zhu, X.; Chen, Z.; Wang, Q.; Zhu, S.; Song, Y. Adaptive robust backstepping force control of 1-dof joint exoskeleton for human performance augmentation. IFAC-PapersOnLine 2015, 48, 142–147. [Google Scholar] [CrossRef]
- Glowinski, S.; Krzyzynski, T.; Bryndal, A.; Maciejewski, I. A kinematic model of a humanoid lower limb exoskeleton with hydraulic actuators. Sensors 2020, 20, 6116. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Zhao, D.; Ma, L.; Zhu, Q.; Huang, D. Backstepping trajectory tracking control of electro-hydraulic actuators of lower limb load exoskeleton. In Proceedings of the IECON 2016-42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 6073–6078. [Google Scholar]
- Yang, J. Design and experiment of the lower extremity exoskeleton. In Proceedings of the 2017 IEEE 2nd Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 25–26 March 2017; pp. 1380–1383. [Google Scholar]
- Yang, Y.; Ma, L.; Huang, D. Development and repetitive learning control of lower limb exoskeleton driven by electrohydraulic actuators. IEEE Trans. Ind. Electron. 2016, 64, 4169–4178. [Google Scholar] [CrossRef]
- Glowinski, S.; Obst, M.; Majdanik, S.; Potocka-Banaś, B. Dynamic model of a humanoid exoskeleton of a lower limb with hydraulic actuators. Sensors 2021, 21, 3432. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Chen, Z.; Yao, B. Precision cascade force control of multi-DOF hydraulic leg exoskeleton. IEEE Access 2018, 6, 8574–8583. [Google Scholar] [CrossRef]
- Liu, T.; Yao, J.; Liu, X.; Li, L. Disturbance rejection control for single-rod electro-hydraulic servo system based on dual-extended-state-observer. In Proceedings of the IECON 2017-43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 3032–3037. [Google Scholar]
- Guo, Q.; Yu, T.; Jiang, D. High-gain observer-based output feedback control of single-rod electro-hydraulic actuator. IET Control. Theory Appl. 2015, 9, 2395–2404. [Google Scholar] [CrossRef]
- Tian, L.; Qian, L.; Chen, L.; Zhang, W. Sliding mode control based on backstepping method for electro-hydraulic single-rod actuator. In Proceedings of the 2015 IEEE International Conference on Information and Automation, Lijiang, China, 8–10 August 2015; pp. 2326–2329. [Google Scholar]
- Wang, J.; Ai, P.; Zhang, J.; Chen, W.; Chen, W. An Adaptive Backstepping Control Method for Lower-Limb Exoskeleton Robot. In Proceedings of the 2020 15th IEEE Conference on Industrial Electronics and Applications (ICIEA), Kristiansand, Norway, 9–13 November 2020; pp. 574–578. [Google Scholar]
- Khamar, M.; Edrisi, M. Designing a backstepping sliding mode controller for an assistant human knee exoskeleton based on nonlinear disturbance observer. Mechatronics 2018, 54, 121–132. [Google Scholar] [CrossRef]
- Sun, J.; Wang, J.; Yang, P.; Geng, Y. Model-free fractional-order adaptive back-stepping prescribed performance control for wearable exoskeletons. Int. J. Intell. Robot. Appl. 2021, 5, 590–605. [Google Scholar] [CrossRef]
- Chen, Z.; Guo, Q.; Xiong, H.; Jiang, D.; Yan, Y. Control and Implementation of 2-DOF Lower Limb Exoskeleton Experiment Platform. Chin. J. Mech. Eng. 2021, 34, 14–30. [Google Scholar] [CrossRef]
- Zaev, E.; Babunski, D.; Tuneski, A.; Rath, G. Hardware-in-the-loop for simulation of hydraulic servo systems and their control. In Proceedings of the IEEE 2017 6th Mediterranean Conference on Embedded Computing (MECO), Bar, Montenegro, 11–15 June 2017; pp. 1–4. [Google Scholar]
- Yong, J.; Gao, F.; Ding, N.; He, Y. Design and validation of an electro-hydraulic brake system using hardware-in-the-loop real-time simulation. Int. J. Automot. Technol. 2017, 18, 603–612. [Google Scholar] [CrossRef]
- Lim, T.H.; Cho, H.C.; Lee, H.S.; Yang, S.Y. Development of Hardware In the Loop System (HILS) for Hydraulic Excavator. In Proceedings of the IEEE 22nd International Symposium on Automation and Robotics in Construction ISARC 2005, Ferrara, Italy, 11–14 September 2015; pp. 11–14. [Google Scholar]
- Karpenko, M.; Sepehri, N. Electrohydraulic force control design of a hardware-in-the-loop load emulator using a nonlinear QFT technique. Control. Eng. Pract. 2012, 20, 598–609. [Google Scholar] [CrossRef]
- Lv, C.; Zhang, J.; Li, Y.; Sun, D.; Yuan, Y. Hardware-in-the-loop simulation of pressure-difference-limiting modulation of the hydraulic brake for regenerative braking control of electric vehicles. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2014, 228, 649–662. [Google Scholar] [CrossRef]
- Manring, N.D.; Fales, R.C. Hydraulic Control Systems; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Jazar, R.N. Theory of Applied Robotics: Kinematics, Dynamics, and Control; Springer Science & Business Media: Berlin, Germany, 2010. [Google Scholar]
- Gungor, G.; Turhan, M.H.; Jamshidifar, H.; Fidan, B. Online estimation and compensation of friction in industrial cable robot manipulation. IFAC-PapersOnLine 2015, 48, 1332–1337. [Google Scholar] [CrossRef]
- Advantech. Available online: https://www.advantech.com.cn/ (accessed on 10 June 2022).
- Preempt_RT. Available online: https://wiki.linuxfoundation.org/realtime/documentation/start/howtos (accessed on 10 June 2022).
- Linjama, M.; Virvalo, T.; Gustafsson, J.; Lintula, J.; Aaltonen, V.; Kivikoski, M. Hardware-in-the-loop environment for servo system controller design, tuning and testing. Microprocess. Microsyst. 2000, 24, 13–21. [Google Scholar] [CrossRef]







| Thread Type | Waveform | Timer Period (ms) | Generated Function Period (ms) | Average Value (ms) | Maximum Value (ms) | Minimum Value (ms) |
|---|---|---|---|---|---|---|
| Single thread | Square wave(sleep function) | 1 | 2 | 2.645 | 4.701 | 2.505 |
| Multithread | Square wave(high-resolution timer) | 1 | 2 | 2.007 | 2.195 | 1.820 |
| Multithread | Square wave(calculated load) | 1 | 2 | 2.010 | 2.495 | 1.945 |
| Thread Type | Waveform | Timer Period (ms) | Generated Function Period(ms) | Average Value (ms) | Maximum Value (ms) | Minimum Value (ms) |
|---|---|---|---|---|---|---|
| Multithread | Square | 1 | 2 | 2.003 | 2.075 | 1.930 |
| Multithread | Square wave (calculated load) | 1 | 2 | 2.000 | 2.035 | 1.940 |
| Single thread | Sine wave (sleep function) | 1 | 5.6 | 5.226 | 7.520 | 3.750 |
| Multithread | Sine wave | 1 | 56 | 56.18 | 56.20 | 54.80 |
| Parameter | Value | Unit | Specification |
|---|---|---|---|
| 0.02 | m | Piston diameter | |
| 0.01 | m | Rod diameter | |
| 0.75 | Area ratio | ||
| 0.625 | Orifice flow coefficient | ||
| 0.01 | m | Valve spool diameter | |
| 0.0314 | m | Valve area gradient | |
| 2.20 × 104 | m3 | Initial volume of piston chamber | |
| 1.65 × 104 | m3 | Initial volume of rod chamber | |
| 628 | rad/s | Natural frequency of valve | |
| 0.7 | Damper of valve | ||
| 0.2 | m/s | Flow gain of valve | |
| 0.14 | m | Cylinder stroke | |
| 870 | kg/m3 | Oil density | |
| 21 | MPa | Supply pressure | |
| 0 | MPa | Return pressure | |
| 7 × 108 | Pa | Elastic modulus of oil | |
| 3.33 × 10−2 | m3/s/A | Servo valve gain | |
| 6.4 | kg | Mass of robot arm | |
| 0.322 | m | Fixed end length 1 | |
| 0.06 | m | Fixed end length 2 | |
| 90 | deg. | Initial angle of robot arm | |
| 9.81 | kg m/s2 | Gravitational acceleration | |
| 0.466 | m | Length of robot arm | |
| 3.02 | kg m2 | Rotational inertia of robot arm | |
| 10 | N | Normal force | |
| 0.5 | s/m | Viscous friction coefficient | |
| 1 | Coulomb friction coefficient | ||
| 1 × 103 | s/m | Steepness of coulomb friction curve |
| Symbol | Value |
|---|---|
| 25 | |
| 265 | |
| 2 |
| Symbol | Value |
|---|---|
| 200 | |
| 80 | |
| 100 | |
| 280 | |
| 80 |
| Symbol | Value |
|---|---|
| 200 | |
| 200 | |
| 400 | |
| 400 | |
| 40 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, Q.; Pei, Z.; Tang, Z. Nonlinear Control of a Hydraulic Exoskeleton 1-DOF Joint Based on a Hardware-In-The-Loop Simulation. Machines 2022, 10, 607. https://doi.org/10.3390/machines10080607
Su Q, Pei Z, Tang Z. Nonlinear Control of a Hydraulic Exoskeleton 1-DOF Joint Based on a Hardware-In-The-Loop Simulation. Machines. 2022; 10(8):607. https://doi.org/10.3390/machines10080607
Chicago/Turabian StyleSu, Qiying, Zhongcai Pei, and Zhiyong Tang. 2022. "Nonlinear Control of a Hydraulic Exoskeleton 1-DOF Joint Based on a Hardware-In-The-Loop Simulation" Machines 10, no. 8: 607. https://doi.org/10.3390/machines10080607
APA StyleSu, Q., Pei, Z., & Tang, Z. (2022). Nonlinear Control of a Hydraulic Exoskeleton 1-DOF Joint Based on a Hardware-In-The-Loop Simulation. Machines, 10(8), 607. https://doi.org/10.3390/machines10080607






