Abstract
The traditional dynamic characteristic analysis of the multi-stage centrifugal pump rotor system is developed assuming the bearing structural parameters with constant values. However, the manufacturing errors will cause the structural parameters to vary around their nominal values and then affect the dynamic characteristics of the bearing-rotor system. Thus, this paper proposes a method for analyzing the dynamic characteristics of the bearing-rotor system with uncertain bearing structural parameters. First, dynamic characteristic coefficients of the sliding bearing are identified to establish the dynamic model of the rotor system, and its dynamic characteristics are analyzed through finite element simulations. Next, the sliding bearing structural parameters are taken as the variables to establish an optimization model, which is solved by the improved particle swarming optimization algorithm to obtain the extreme critical speed of the rotor system. A case study was carried out on a multi-stage centrifugal pump. The obtained extreme values of the critical speeds were close to those calculated using the multiple samples generated by the Monte Carlo method, indicating that the proposed method can provide accurate variation ranges of critical speeds efficiently and lay a theoretical basis for selecting robust operational speeds and designing the rotor system of the multi-stage centrifugal pump.
1. Introduction
Multi-stage centrifugal pump is a key piece of equipment for the fluid transportation, which has been widely used in various industries such as the metallurgy, chemical industry, electric power and so on [1,2,3]. Rapid developments of these industries push the multi-stage centrifugal pump to increase its speed, resulting in safety and stability failures of the rotor system under operational conditions. Once the working speed approximates the critical speed of the rotor system, a resonance will occur and induce severe vibrations, causing deformations of rotor components and affecting safeties of operators [4]. Therefore, several studies have analyzed the dynamic characteristics of the multi-stage centrifugal pump rotor system. Generally, the dynamic model of the rotor system is constructed to predict the corresponding critical speeds, providing an important approach to select the working speeds and ensure the reliable operations of the rotor system [5,6,7].
Since sliding bearing is an important component to support the rotor system of a multi-stage centrifugal pump, its dynamic characteristics can directly affect the dynamic characteristics of the rotor system [8]. Thus, the prerequisite for establishing an accurate dynamic model of the rotor system is studying the dynamic characteristics of the sliding bearing. Many methods have been provided to identify the dynamic characteristic coefficients of the sliding bearing. The equation proposed by O. Reynolds in 1886 lays a theoretical basis of fluid lubricated bearing research, and solving the Reynolds equation is the key problem of analyzing the hydrodynamic characteristics of the sliding bearing [9]. Researchers at home and abroad have proposed a variety of algorithms to obtain the analytical solution of the Reynolds equation. The numerical analysis and the fluid simulation are the mainly used two approaches. In the numerical analysis, the Reynolds equation is generally solved with the aid of the MATLAB software to obtain the oil film pressure and the dynamic characteristic coefficients of the sliding bearing. Li et al. [10] analyzed the transient response of the rotor system and the pressure distribution of oil film flow field by combining the finite element method and finite difference method; the partial differential equation about the disturbance of dynamic characteristic coefficients of the sliding bearing were solved by the numerical integration. Zhou [11] used the bisection and secant method to iteratively calculate the static equilibrium position of the sliding bearing. On that basis, the small parameter method was adopted to solve the dynamic characteristic coefficients of the sliding bearing. In the fluid simulation, the dynamic model of the bearing fluid domain was established with the aid of the fluid simulation software, and the dynamic characteristic coefficients of the sliding bearing were solved by setting the boundary conditions. Hanoca et al. [12] analyzed the influence of oil film thickness on the dynamic characteristics of the sliding bearing using ANSYS Workbench software. The numerical solution of the computational fluid dynamics was compared with the numerical analysis solution of the Reynolds equation. Manshoor et al. [13] investigated the three-dimensional computational fluid dynamics (CFD) analysis on the performance characteristics of a thin film lubricated journal bearing and solved the characteristics of the sliding bearing using three turbulence models with the ANSYS Fluent software.
The aforementioned studies focused on identifying the dynamic characteristics of the sliding bearing with constant structural parameters, and the disturbances of the structural parameters have not been further discussed. Recently, few researchers have investigated the effects of the manufacturing errors of the sliding bearing structural parameters on the dynamic characteristics of the sliding bearing-rotor system. Wei et al. [14] established the dynamic model of the rotor system and analyzed the influences of the dimensional errors of the dynamic viscosity, bearing width, bearing diameter and journal diameter on the friction power loss. Wang et al. [15] numerically studied the influence of the bearing surface waviness on the performance of the aerostatic sliding bearing, and used the finite difference method to solve the Reynolds equation. The obtained dynamic characteristic coefficients were utilized to analyze the influences of bearing surface waviness amplitude on the bearing capacity, stiffness and friction coefficient. Shin et al. [16] studied the influence of the bearing seal surface roughness on the lubrication characteristics and concluded that the small machining error and surface waviness would affect the stability of the rotor system. Song et al. [17] proposed a new algorithm for dealing with the non-triangular matrix based on the periodic boundary conditions of the journal bearing, and then investigated the half frequency whirling motion and critical speed caused by the shape error of the bearing surface. Later, Zoupas et al. [18] analyzed the influences of the manufacturing errors on the minimum oil film thickness, friction torque and maximum pressure of the large tilting pad thrust bearing.
Although effects of the manufacturing errors on the dynamic characteristics of the sliding bearing have already been investigated, how the manufacturing errors further affect the dynamic characteristics of the sliding bearing-rotor system have not been studied. Moreover, many studies have already found that the parameter disturbances of the rotor system can affect its stability and provided theoretical methods to perform the dynamic analysis of rotor system with uncertainty [19,20]. Therefore, this paper presents a method to study the dynamic characteristics of the multi-stage centrifugal pump rotor system, where the structural parameters of the sliding bearing are uncertain because of the manufacture errors. First, the mathematic relationship between the structural parameters and dynamic characteristic coefficients of the sliding bearing is established according to the Reynolds equation. These structural parameters contain the length, clearance ratio, ratio of length to diameter and oil film viscosity coefficient. On that basis, the dynamic model of the multi-stage centrifugal pump rotor system can thus be established to perform the dynamic characteristic analysis. Next, an optimization model is further established to obtain the extreme value of the critical speed of the bearing-rotor system, where the sliding bearing structural parameters are taken as the independent variables. The finite element simulations and the improved particle swarm optimization (PSO) algorithm are combined to solve the optimization model, and the extreme value of the critical speed can be obtained in the variation ranges of the sliding bearing structural parameters.
Henceforth, this paper is organized as follows. The principles of identifying the dynamic characteristic coefficients of the sliding bearing and constructing the dynamic model of the bearing-rotor system are provided in Section 2. In Section 3, an optimization model for obtaining the extreme value of the critical speed of the rotor system is established and solved by the improved PSO algorithm. In Section 4, a case study for illustrating the proposed method is performed on a real multi-stage centrifugal pump rotor system, and variation ranges of the critical speeds are obtained considering uncertain sliding bearing structural parameters. Finally, conclusions from the current research are summarized in Section 5.
2. Dynamic Modeling of the Bearing-Rotor System of a Multi-Stage Centrifugal Pump
The bearing-rotor system of a multi-stage centrifugal pump is described in Figure 1, which is mainly composed of the impeller, rotating shaft and sliding bearing. As an important component supporting the rotor system, the structural parameters and dynamic characteristics of the sliding bearings can directly affect the dynamic characteristics of the rotor system. Thus, the dynamic modeling of the rotor system considering the dynamic characteristics of the sliding bearing is discussed in this section.

Figure 1.
Structure of a real multi-stage centrifugal pump.
2.1. Calculation of the Dynamic Characteristic Coefficients of the Sliding Bearing
The sliding bearing plays the role of supporting the rotating shaft and reducing the friction during the operation of a multi-stage centrifugal pump [21], a typical structure of which is shown in Figure 2.
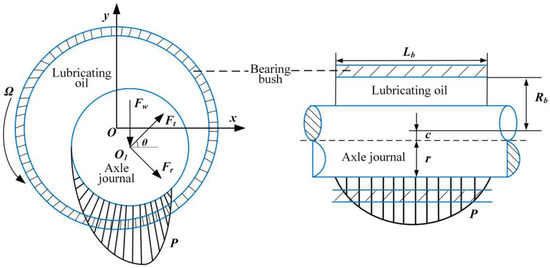
Figure 2.
Description of the sliding bearing structure and its working condition.
According to the bearing fluid lubrication theory, the radial oil film characteristics of the sliding bearing obey the generalized Reynolds equation of fluid mechanics expressed in Equation (1):
where P is the oil film pressure, H is the thickness of oil film, is the bearing radius, η is the oil film viscosity, ρ is the oil film density, φ and z are the circumferential and axial coordinates of the sliding bearing respectively, and vj and vb are the linear velocities of the journal and bearing respectively.
Considering the actual working condition, the bearing bush is assumed to be fixed with the assembling unit as vj =0. Then, Equation (1) can be transformed into the following Equation (2) if the influence of the lubricating fluid medium density is ignored.
Subsequently, is defined when the sliding bearing is in a stable state, and the following dimensionless parameters are introduced into the equation:
where is the dimensionless axial coordinate, ε is the eccentricity, ϕ is the dimensionless clearance ratio, and λ is the dimensionless ratio of length to diameter. Thus, Equation (2) can be further simplified into a dimensionless form as shown in Equation (4):
A five-point difference method is adopted to discretize the partial differential equation in Equation (4), and then the over-relaxation iterative method is used to calculate the oil film pressure. After the oil film pressure distribution of the sliding bearing is obtained, the dynamic characteristic coefficients of the sliding bearing can be solved by the small parameter method. First, the small perturbations of the displacement and velocity are applied at the equilibrium position, and then the dimensionless thickness and pressure of the oil film under the disturbance are written as:
where
where and are the displacements of the oil film pressure in x and y directions, and are the velocities of the oil film pressure in x and y directions, is the thickness of the oil film in a static equilibrium condition, and is the pressure of the oil film pressure in a static equilibrium condition.
The above Equations (5) and (6) are utilized to redescribe Equation (4), and the following dimensionless disturbance equation is obtained after ignoring the high-order term:
Thus, after the , , and are calculated by the integral operation, the dimensionless stiffness and damping coefficients of the sliding bearing can be solved according to Equations (8) and (9), respectively.
where k and c represent the stiffness and damping coefficients, and the subscripts x and y mean the corresponding x and y directions.
According to Equations (1)–(9), the length Lb, clearance ratio φ, ratio of length to diameter λ and oil film viscosity coefficient η are the main factors affecting the stiffness and damping coefficients of the sliding bearing. Then, the Lb, φ, λ and η are taken as the uncertain structural parameters of the sliding bearing in this paper, and the effects of their variations on the dynamic characteristics of the sliding bearing-rotor system of a multi-stage centrifugal pump are studied.
2.2. The Finite Element Modeling of the Multi-Stage Centrifugal Pump Rotor System
The prerequisite to precisely predict the dynamic characteristics of the multi-stage centrifugal pump rotor system is constructing an accurate dynamic model, which can well reflect the complex structure and actual working conditions. In this paper, the ANSYS software is adopted to construct the finite element model of the multi-stage centrifugal pump in the virtual environment. When constructing the finite element model, the small holes, keyways, chamfers on the rotating shaft and impeller are ignored, and the following simplification principles are also considered:
- The centrosymmetric pump shaft is simplified as a circular section beam element, and the parameters such as the element density, elastic modulus and Poisson’s ratio are defined.
- The multiple impellers are equivalent to the centralized mass points by applying the Mass 21 units at their positions. The translational mass and moment of inertia for a Mass 21 unit are set through its six real constants as MASSX, MASSY, MASSZ, IXX, IYY and IZZ.
- The spring-damping element COMBI214 is adopted to simulate the dynamic characteristics of the sliding bearing. The stiffness and damping coefficients identified through the method presented in Section 2.1 are set in the COMBI214 to simulate the support of the rotating pump shaft. The COMBI214 unit has two nodes, and the four stiffness coefficients and four damping coefficients of the sliding bearing are set through K11, K22, K12, K21, C11, C22, C12 and C2. K11 and K22 are the main stiffness values, K12 and K21 are the cross stiffness values, C11 and C22 are the main damping values, and C12 and C21 are the cross damping values.
On the basis, a schematic diagram is provided in Figure 3 to describe the equivalent approach for the multi-stage centrifugal pump rotor system. In Figure 3, the red points mean the Mass 21 units which are used to represent the impellers at these positions, and the COMBI214 spring-damping elements represent the dynamic characteristics of the sliding bearings.
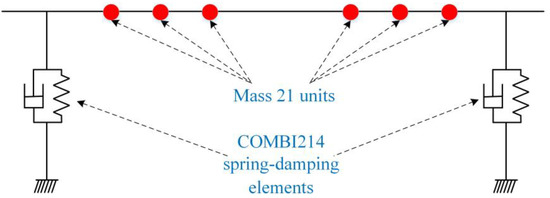
Figure 3.
Description of the equivalent dynamic model for a multi-stage centrifugal pump rotor system.
3. Dynamic Characteristic Analysis of the Multi-Stage Centrifugal Pump Rotor System with Uncertain Sliding Bearing Structural Parameters
The dynamic characteristic analysis of the multi-stage centrifugal pump rotor system mainly focuses on predicting the critical speeds, which can benefit the selections of the operational speeds to avoid the resonance and guarantee the stable operation. However, the manufacturing errors can cause the variations of the sliding bearing structural parameters around their nominal values, and lead to changes of the stiffness and damping coefficients of the sliding bearing. As a consequence, the critical speeds of the multi-stage centrifugal pump rotor system will vary within a certain range. Considering this situation, an optimization model is established in this section to obtain the extreme value of the critical speed within the variation ranges of the sliding bearing structural parameters. The improved particle swarm optimization algorithm is introduced to solve this optimization model based on the co-simulations of the MATLAB and ANSYS. The Monte Carlo algorithm is used to verify the accuracy of the obtained extreme value.
3.1. Establishing an Optimization Model Based on the Critical Speed of the Rotor System
3.1.1. The Design Variables
The length Lb, clearance ratio φ, ratio of length to diameter λ and oil film viscosity coefficient η are the maim structural parameters of the sliding bearing. The manufacturing errors cause the variations of these structural parameters, and then result in uncertain dynamic characteristics of the multi-stage centrifugal pump rotor system. Therefore, these structural parameters of the sliding bearing VS = (Lb, φ, λ, η) are taken as the design variables to obtain robust critical speeds of the rotor system.
3.1.2. The Optimization Objective
The extreme value of the critical speed of the multi-stage centrifugal pump rotor system is defined as the optimization objective. At present, the critical speeds of the multi-stage centrifugal pump rotor system are mainly obtained by establishing the finite element model of the rotor system in simulation software and obtaining the Campbell diagram through the modal analysis. According to Section 2.2, the prerequisite of establishing the finite element model is to obtain the 8 stiffness and damping coefficients, which represents the dynamic characteristics of the sliding bearing. For each combination of sliding bearing structural parameters, its corresponding 8 dynamic coefficients can be calculated by writing and solving the programs of the Reynolds equation in the MATLAB software.
Therefore, in order to establish the direct relationship between the sliding bearing structural parameters and the critical speeds of the rotor system, the ANSYS and MATLAB are combined to compute the critical speeds automatically when the sliding bearing structural parameters change. The co-computations are realized based on the re-development language of ANSYS and the data exchange interface of the ANSYS and MATLAB. The main control program to calculate the 8 dynamic coefficients of the sliding bearing is written in the MATLAB software. The calculated dynamic characteristic coefficients are transferred into the ANSYS software through the ANSYS parametric design language (APDL). Then, the corresponding finite element model of the multi-stage centrifugal pump rotor system can be established. Subsequently, the modal analysis considering the gyroscopic effect is carried out on the finite element model to yield the Campbell diagram shown in Figure 4, where the abscissa represents the speed and the ordinate represents the frequency. The ray from the origin intersects with the other lines, and the intersections stand for the natural frequencies [22]. The natural frequency f and the critical speed n have the following mathematic relationship:
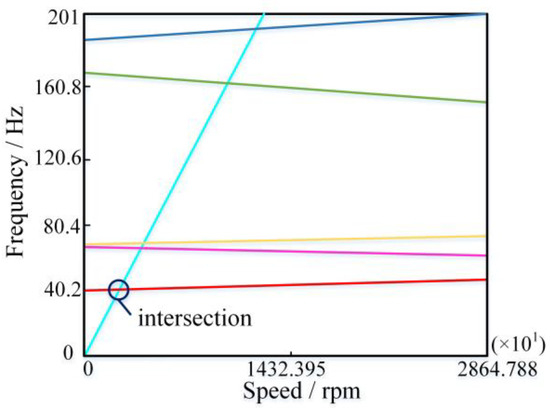
Figure 4.
Description of the Campbell diagram.
Then, the critical speeds output by the ANSYS software are transferred to the MATLAB software for the subsequent analysis.
In summary, the optimization model for obtaining the extreme value of the critical speed of the multi-stage centrifugal pump rotor system is expressed in Equation (11):
3.2. The Improved PSO Algorithm for Solving the Optimization Model
As a numerical optimization algorithm based on the swarm intelligence, PSO algorithm can effectively solve the optimization problem of complex functions [23,24]. Thus, an improved PSO algorithm is introduced to solve the optimization model for obtaining the extreme value of the critical speed in this research. For a PSO algorithm, each particle has two attributes as the position vector and velocity vector. The position represents the direction of flight and the particle flies to a new position according to the velocity vector. Assuming that there are N D-dimensional particles forming a community, the ith particle with the position vector Xi = (, , ···, ) flies to a better position with the velocity vector Vi = (, , ···, ). During the optimization process, the position vector and velocity vector are updated iteratively based on the individual optimal position and the global optimal position described in Equation (12).
where k is the current iteration number, ω is the inertial weight, and are the learning factors, and are the random parameters varying in the range of 0 to 1, means the dth element in the velocity vector of the ith particle, and means the dth element in the position vector of the ith particle, Pbest_id is the dth element in the individual optimal position vector of the ith particle determined by comparing the fitness values, and Gbest_id is the dth element in the global optimal position vector determined by comparing the fitness values of the N particles. The fitness value indicates the superior or inferior of the current particle position, and it can be calculated from the fitness function. Moreover, the inertia weight ω is dynamically modified as expressed in Equation (13), for improving the global and local search ability at different stages of the iterative process.
where kmax is the maximum iteration number, and ωmin and ωmax stand for the defined minimum and maximum inertial weights respectively.
According to the aforementioned theory of the PSO algorithm and the specific optimization problem described in Section 3.1, the sliding bearing structural parameters Vs = (Lb, φ, λ, η) are defined as the position vector of one particle, and the fitness value is the critical speed of the rotor system calculated using the related position vector X. Then, the optimal critical speed of the rotor system can be obtained through the following steps:
- The basic parameters for carrying out the optimization are initialized, including the number of particles, the maximum iteration number, the position and velocity vectors for each particle, the learning factors and the extreme values of the inertial weights.
- In each iteration, the critical speeds corresponding to the position vector of each particle are calculated with the co-simulations of the MATLAB and ANSYS software, and then the individual optimal position for each particle and the global optimal position among all the particles can be determined by comparing the critical speeds.
- After each iteration, the position and velocity vectors for each particle are updated by Equation (12), and these updated vectors are utilized to find better individual and globe optimal positions by repeating the step 2.
- The iteration terminates when the convergence condition is met or the iteration number reaches its maximum value. Then, the fitness value corresponding to the global optimal position is the extreme critical speed within the variation ranges of the sliding bearing structural parameters.
3.3. The Monte Carlo Algorithm for the Validation
The extreme values of the critical speed can be obtained by solving the optimization models according to Section 3.1 and Section 3.2. To verify whether the obtained values belong to local optimums and guarantee their accuracies, the Monte Carlo algorithm is adopted in this paper to generate a large number of sample data within the variation ranges of the independent variables. The Monte Carlo algorithm is a numerical sampling process, belonging to a branch of stochastic mathematics. The algorithm has the characteristic of strong universality, and its calculation accuracy will be improved with the increase of simulation times. Since the repeatedly calculations under a large number of random samples are time-consuming, the Monte Carlo algorithm is mainly used for a verification in practical engineering. A brief introduction of the random variable sampling process in the Monte Carlo method is described as follows [25,26].
The random variable β within the interval [a, b] is assumed to meet the distribution of the probability density function p(β), which has the following normalization condition:
In order to estimate the random variable, the pseudo-random number evenly distributed between 0 and 1 is generated, and then the cumulative distribution function of is expressed in Equation (15).
If a non-decreasing function can be found to describe the mapping relationship between the ξ and β as β = f(ξ), the following probability relationship can be obtained.
Then, the cumulative distribution function in Equation (15) and the probability density function in Equation (16) are combined to yield the following equation.
For Equation (17), its left side is further expressed by the integral of the probability density function, and its right side is substituted by the equation in Equation (15). Then, a following relationship between the β and can be obtained as described in Equation (18).
Thus, a β1 can be obtained by Equation (18) once a random number is generated.
Based on the probability and statistics theory of the Monte Carlo method, its application in validating the accuracy of the optimization model in this research can be concluded as the following steps:
- Taking the sliding bearing structural parameters Lb, φ, λ and η as the random variables, and M random combinations of the structural parameters are generated to calculate the dynamic characteristic coefficients of the sliding bearing.
- These calculated stiffness and damping coefficients are written into the finite element model of the multi-stage centrifugal pump rotor system to predict the corresponding critical speeds.
- The obtained critical speeds of the multiple samples are compared to determine the maximum and minimum values, which are further compared with those calculated by solving the optimization models with the improved PSO algorithm.
4. Case Study and Results Discussion
In this section, the previously presented method was applied to a real multi-stage centrifugal pump to validate its feasibility. Effects of the variations of the sliding bearing structural parameters on the dynamic characteristics of the multi-stage centrifugal pump rotor system were investigated through the co-simulations of the MATLAB and ANSYS. Then, optimization models were established and solved by the improved PSO algorithm to obtain the optimal critical speeds within the variation ranges of the sliding bearing structural parameters. The accuracies of the obtained extreme values of the critical speeds were validated through the Monte Carlo algorithm and the rated speed of the multi-stage centrifugal pump.
4.1. Effects of the Structural Parameters on the Dynamic Characteristics of the Sliding Bearing
The studied sliding bearing is described in Figure 5, and the nominal values of its structural parameters are Lb = 0.45 m, φ = 0.002, λ = 2.04 and η = 0.0016 Pa·s. The nominal values were first used to calculate the stiffness and damping coefficients of the sliding bearing according to the method provided in Section 2.1, and the dynamic characteristic coefficients computed through the programs in the MATLAB virtual environment are provided in Table 1.

Figure 5.
Real structure of the studied sliding bearing.

Table 1.
Dynamic characteristic coefficients of the sliding bearing.
Furthermore, the structural parameters containing the length Lb, clearance ratio φ, ratio of length to diameter λ and oil film viscosity coefficient η were taken as the variables, and the effects of the variations of the structural parameters on the dynamic characteristic coefficients of the sliding bearing were studied following the single variable principle. In Figure 6, the stiffness and damping coefficients of the sliding bearing increase with the increase of the length Lb. In Figure 7, the stiffness and damping coefficients of the sliding bearing decrease with the increase of the clearance ratio φ. In Figure 8, the stiffness and damping coefficients of the sliding bearing increase with the increase of the ratio of the length to diameter λ. In Figure 9, the stiffness and damping coefficients of the sliding bearing increase with the increase of the viscosity coefficient η. Therefore, it is significant to take the uncertain sliding bearing structural parameters into consideration, since their variations can lead to the changes of the dynamic characteristic coefficients.
Figure 6.
Variation tendencies of the dynamic coefficients for different sliding bearing lengths Lb.
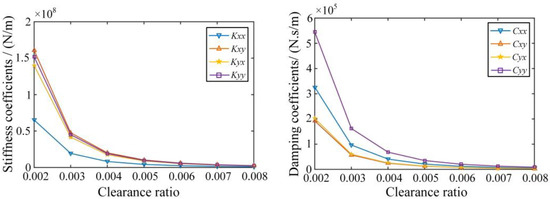
Figure 7.
Variation tendencies of the dynamic coefficients for different clearance ratios φ.
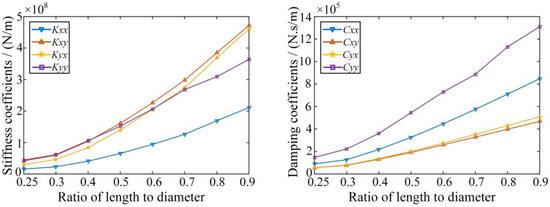
Figure 8.
Variation tendencies of the dynamic coefficients for different ratio of length to diameter λ.
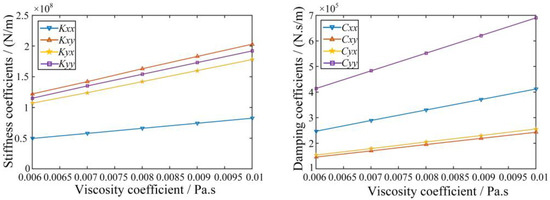
Figure 9.
Variation tendencies of the dynamic coefficients for different viscosity coefficients η.
4.2. Dynamic Characteristic Analysis of the Multi-Stage Centrifugal Pump Rotor System
The specific parameters of the impeller and shaft section of the multi-stage centrifugal pump rotor system are described in Table 2 and Table 3, respectively. One the basis, the beam elements, spring-damping elements and concentrated mass elements were integrated to establish the dynamic model of the multi-stage centrifugal pump rotor system in the ANSYS virtual environment as shown in Figure 10. The 8 stiffness and damping coefficients of each sliding bearing are solved as listed in Table 1, which were written into the corresponding spring-damping elements. Then, the modal analysis was carried out to obtain the Campbell diagram shown in Figure 4 for predicting the critical speeds of the multi-stage centrifugal pump rotor system.

Table 2.
The specific parameters of the impellers.

Table 3.
Dimension parameters of the rotor shaft section.
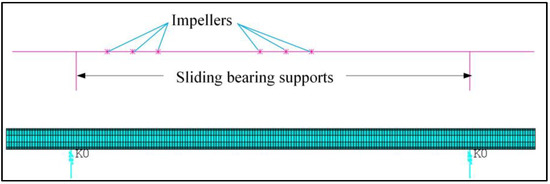
Figure 10.
The finite element model of the multi-stage centrifugal pump rotor system.
Obeying the single variable principle, effects of the variations of the siding bearing length Lb, clearance ratio φ, ratio of length to diameter λ and oil film viscosity coefficient η on the dynamic characteristics of the multi-stage centrifugal pump rotor system were also investigated. The first three critical speeds were selected to represent the dynamic characteristics of the rotor system. In Figure 11, the first three critical speeds increase with the increase of the bearing length Lb, and the first critical speed is more sensitive to the variation of Lb. In Figure 12, the first critical speed decreases with the increase of the clearance ratio φ, and the second and third critical speeds increase with the increase of the clearance ratio φ. In Figure 13, the first two critical speeds increase with the increase of the ratio of length to diameter λ, and the third critical speed decreases with the increase of the ratio of length to diameter λ. However, the variation of λ has slight effects on all the three critical speeds. In Figure 14, all the first three critical speeds increase with the increase of the oil film viscosity coefficient η, and the first critical speed is more vulnerable to the variation of η since it has a greater rate of change.
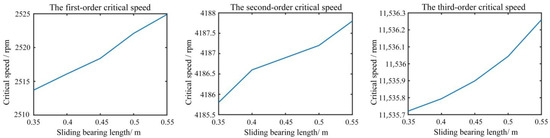
Figure 11.
Influences of the sliding bearing length Lb on the first three critical speeds.
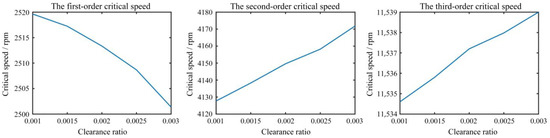
Figure 12.
Influences of the clearance ratio φ on the first three critical speeds.
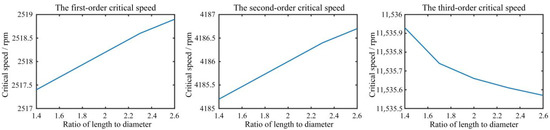
Figure 13.
Influences of the ratio of length to diameter λ on the first three critical speeds.
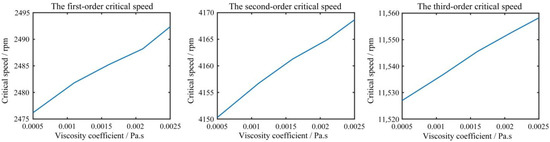
Figure 14.
Influences of the viscosity coefficient η on the first three critical speeds.
4.3. Robust Dynamic Characteristic Analysis of the Rotor System Considering Uncertain Sliding Bearing Structural Parameters
The simulated results in Section 4.2 show that the sliding bearing structural parameters have important impacts on the dynamic characteristics of the multi-stage centrifugal pump rotor system. Thus, it is necessary to take the variations of the sliding bearing structural parameters caused by the manufacturing errors into account when predicting the critical speeds. Therefore, the length Lb, clearance ratio φ, ratio of length to diameter λ and oil film viscosity coefficient η were taken as the independent variable, and the 5% and −5% of the nominal value of each structural parameter were calculated to define the boundary values. Then, the corresponding variation ranges of the sliding bearing structural parameters Lb, φ, λ and η are [0.43 m, 0.47 m], [0.0019, 0.0021], [1.94, 2.14], [0.0015 Pa.s, 0.0017 Pa.s] respectively. Considering the first three critical speeds, 6 optimization models were established for obtaining the minimum and maximum values of each critical speed within the variation ranges of these sliding bearing structural parameters.
To carry out the improved particle swarm optimization algorithm for solving the established optimization models, the number of particles was 80, the maximum number of iterations was 150, the learning factors C1 and C2 were defined as 1.5, respectively, and the maximum and minimum inertia weights were 1.2 and 0.6, respectively. During the optimization process, the MATLAB and ANSYS were combined to calculate the critical speed of each particle. The iterative process for obtaining the maximum value of the first-order critical speed is shown in Figure 15, where the optimal critical speed trends to a stable value after 58 iterative calculations. The finally obtained extreme values of the first three critical speeds are listed in Table 4, and obvious differences between the maximum and minimum values can be observed. Comparing the extreme values in Table 4, the deviations of the first three critical speeds are 54.4 rpm, 39.7 rpm and 13.8 rpm respectively, and the corresponding variation rates are 2.22 %, 1.0% and 0.12%. Thus, the first-order critical speed shows more vulnerable to the variations of the sliding bearing structural parameters.
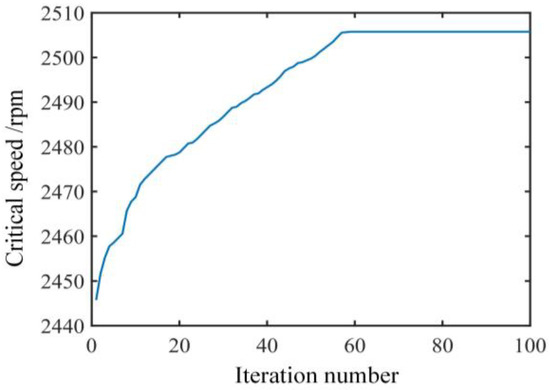
Figure 15.
The convergence curve for the optimization of the first-order critical speed.

Table 4.
The ranges of the critical speeds calculated by different methods.
In all, 106 random combinations of the structural parameters Lb, φ, λ and η were defined by the Monte Carlo method, and the corresponding maximum and minimum values of the first three critical speeds are also listed in Table 4. It can be seen from Table 4 that the maximum error between the extreme critical speeds calculated by the Monte Carlo method and those obtained by solving the optimization model is within 1%, indicating that the improved particle swarm optimization algorithm for obtaining the optimal critical speed can not only improve the calculation efficiency by reducing the number of samples but also have a desired accuracy. Moreover, in the actual operating conditions, the rated working speed of the rotor system of the multi-stage centrifugal pump is 1980 rpm. It is far from the first-order critical speed range [2451.3 rpm, 2505.7 rpm] calculated in this paper, avoiding the resonance and guaranteeing a safe operation.
5. Conclusions
In this paper, a new method was proposed to predict the critical speeds of the multi-stage centrifugal pump with uncertain sliding bearing structural parameters. The structural parameters are taken as the variables to establish an optimization model for obtaining the extreme value of the critical speed, which can be solved by the improved particle swarm optimization algorithm based on the co-simulations of the MATLAB and ANSYS. Therefore, variation ranges of the critical speeds of the focused orders can be obtained, laying a basis for selecting robust speeds that are away from the variation ranges to guarantee the stable operation of the multi-stage centrifugal pump under actual working conditions. The main contributions of this paper include:
- The oil film pressure distribution of the sliding bearing was first solved by combing the finite difference method and the successive over-relaxation method. Then, the small parameter method was used to compute the dynamic characteristic coefficients of the sliding bearing in the virtual environment of the MATLAB. On that basis, effects of the variations of the sliding bearing structural parameters Lb, φ, λ and η on the stiffness and damping coefficients were investigated.
- The beam elements, spring-damping elements and concentrated mass elements were combined to construct the finite element model of the multi-stage centrifugal pump rotor system in the virtual environment of ANSYS. The computed dynamic characteristic coefficients of the sliding bearing were assigned to the spring-damping elements. Moreover, the MATLAB and ANSYS were combined to investigate the effects of the variations of each structural parameter on the first three critical speeds of the rotor system.
- Six optimization models for obtaining the extreme values of the first three critical speeds were established, where the sliding bearing structural parameters Lb, φ, λ and η were taken as the independent variables. These optimization models were solved by the improved PSO algorithm within the variation ranges of the structural parameters, and the maximum and minimum values of each critical speed were obtained. These extreme values were close to those calculated with the 106 random samples generated by the Monte Carlo method. The deviation between the maximum and minimum values of the first-order critical speed is 54.5 rpm, showing the necessity for considering the effects of the manufacturing errors on the dynamic characteristics of the rotor system. Moreover, the actual operational speed is away from the variation range of the first-order critical speed, indicating that the proposed method is promising in selecting robust operational speed of a multi-stage centrifugal pump.
Author Contributions
Conceptualization, L.L., W.M. and Q.W.; methodology, L.L., H.Z. and C.D.; software, L.L., M.H. and C.D.; validation, L.L., M.H. and C.D.; investigation, L.L., H.Z., W.M. and C.D.; resources, L.L., W.M. and C.D.; data curation, L.L., M.H. and C.D.; writing—original draft preparation, L.L and C.D.; writing—review and editing, M.H. and C.D.; supervision, Q.W.; funding acquisition, L.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Sichuan Science and Technology Program, grant number 2022YFG0225 and Opening Foundation of Sichuan Province Engineering Center for Powder Metallurgy, Chengdu University, grant number SC-FMYJ2020-085.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| P | the oil film pressure |
| H | the thickness of oil film |
| Lb | the length of the sliding bearing |
| Rb | the bearing radius |
| η | the oil film viscosity coefficient |
| φ, z | the circumferential and axial coordinates of the sliding bearing respectively |
| vj, vb | the linear velocities of the journal and bearing respectively |
| the dimensionless axial coordinate | |
| ε | the eccentricity |
| ϕ | the dimensionless clearance ratio |
| λ | the dimensionless ratio of length to diameter |
| , | the displacements of the oil film pressure in x and y directions |
| the velocities of the oil film pressure in x and y directions | |
| the thickness of the oil film in a static equilibrium condition | |
| the pressure of the oil film pressure in a static equilibrium condition | |
| kxx, kxy, kyx, kyy | the stiffness coefficients |
| cxx, cxy, cyx, cyy | the damping coefficients |
| n | the critical speed(rpm) |
| Xi, Vi | the position vector and velocity vector of the ith particle |
| , | the dth element in the position vector and the velocity vector of the ith particle respectively |
| , | the dth element in the individual and global optimal position vector of the ith particle |
References
- Wang, C.; Shi, W.; Wang, X.; Jiang, X.; Yang, Y.; Li, W.; Zhou, L. Optimal design of multistage centrifugal pump based on the combined energy loss model and computational fluid dynamics. Appl. Energy 2017, 187, 10–26. [Google Scholar] [CrossRef]
- Yun, L.; Bin, L.; Jie, F.; Rongsheng, Z.; Qiang, F. Research on the transient hydraulic characteristics of multistage centrifugal pump during start-up process. Front. Energy Res. 2020, 8, 76. [Google Scholar] [CrossRef]
- Yang, J.; Pavesi, G.; Liu, X.; Xie, T.; Liu, J. Unsteady flow characteristics regarding hump instability in the first stage of a multistage pump-turbine in pump mode. Renew. Energy 2018, 127, 377–385. [Google Scholar] [CrossRef]
- Zhang, M.; Jiang, Z.-N.; Feng, K. Research on variational mode decomposition in rolling bearings fault diagnosis of the multistage centrifugal pump. Mech. Syst. Signal Process. 2017, 93, 460–493. [Google Scholar] [CrossRef]
- Maleki, A.; Ghorani, M.M.; Haghighi, M.H.S.; Riasi, A. Numerical study on the effect of viscosity on a multistage pump running in reverse mode. Renew. Energy 2019, 150, 234–254. [Google Scholar] [CrossRef]
- Stefanizzi, M.; Torresi, M.; Fornarelli, F.; Fortunato, B.; Camporeale, S. Performance prediction model of multistage centrifugal Pumps used as Turbines with Two-Phase Flow. Energy Procedia 2018, 148, 408–415. [Google Scholar] [CrossRef]
- Suh, S.-H.; Kyung-Wuk, K.; Kim, H.-H.; Cho, M.T.; Yoon, I.S. A Study on Multistage Centrifugal Pump Performance Characteristics for Variable Speed Drive System. Procedia Eng. 2015, 105, 270–275. [Google Scholar] [CrossRef]
- Reynolds, O. On the theory of lubrication and its application to mr. beauchamp tower’s experiments, including an experi-mental determination of the viscosity of olive oil. Philos. Trans. R. Soc. A 1886, 177, 191–203. [Google Scholar]
- Zhou, W.-J.; Qiu, N.; Wang, L.; Gao, B.; Liu, D. Dynamic analysis of a planar multi-stage centrifugal pump rotor system based on a novel coupled model. J. Sound Vib. 2018, 434, 237–260. [Google Scholar] [CrossRef]
- Li, Y.; Ao, L.; Li, L.; Yue, Z. Dynamic Analysis Method of Dynamic Character Coefficient of Hydrodynamic Journal Bearing. J. Mech. Eng. 2010, 46, 52–57. [Google Scholar] [CrossRef]
- Zhou, W. The Dynamic Characteristics Study on Multi-stage Centrifugal Pump Rotor Coupled System. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2016. [Google Scholar]
- Hanoca, P.; Ramakrishna, H. To Investigate the Effect of Oil Film Thickness at the Entrance of the Infinitely Long Slider Bearing Using CFD Analysis. Procedia Eng. 2015, 127, 447–454. [Google Scholar] [CrossRef][Green Version]
- Manshoor, B.; Jaat, M.; Izzuddin, Z.; Amir, K. CFD Analysis of Thin Film Lubricated Journal Bearing. Procedia Eng. 2013, 68, 56–62. [Google Scholar] [CrossRef]
- Wei, Y. Effect of Dimension Error on the Power Loss of the Rotor Bearing System. Master’s Thesis, Guangxi University of Technology, Guangxi, China, 2012. [Google Scholar]
- Wang, X.-K.; Xu, Q.; Wang, B.; Zhang, L.; Yang, H.; Peng, Z. Effect of surface waviness on the static performance of aerostatic journal bearings. Tribol. Int. 2016, 103, 394–405. [Google Scholar] [CrossRef]
- Shin, J.-H.; Kim, K.-W. Effect of surface non-flatness on the lubrication characteristics in the valve part of a swash-plate type axial piston pump. Meccanica 2014, 49, 1275–1295. [Google Scholar] [CrossRef]
- Song, M.; Azam, S.; Jang, J.; Park, S.-S. Effect of shape errors on the stability of externally pressurized air journal bearings using semi-implicit scheme. Tribol. Int. 2017, 115, 580–590. [Google Scholar] [CrossRef]
- Zoupas, L.; Wodtke, M.; Papadopoulos, C.I.; Wasilczuk, M. Effect of manufacturing errors of the pad sliding surface on the performance of the hydrodynamic thrust bearing. Tribol. Int. 2019, 134, 211–220. [Google Scholar] [CrossRef]
- Mao, W. Identification of the key characteristic parameters in dynamics for a sliding bearing-rotor system of high speed spindle. Ph.D. Thesis, Hunan University, Changsha, China, 2015. [Google Scholar]
- Hajžman, M.; Balda, M.; Polcar, P.; Polach, P. Turbine Rotor Dynamics Models Considering Foundation and Stator Effects. Machines 2022, 10, 77. [Google Scholar] [CrossRef]
- El-Sabaa, F.M.; Amer, T.S.; Gad, H.M.; Bek, M.A. On the motion of a damped rigid body near resonances under the influence of harmonically external force and moments. Results Phys. 2020, 19, 103352. [Google Scholar] [CrossRef]
- Fu, C.; Ren, X.; Yang, Y.; Xia, Y.; Deng, W. An interval precise integration method for transient unbalance response analysis of rotor system with uncertainty. Mech. Syst. Signal Process. 2018, 107, 137–148. [Google Scholar] [CrossRef]
- Tang, Z.; Wang, M.; Zhao, M.; Sun, J. Modification and Noise Reduction Design of Gear Transmission System of EMU Based on Generalized Regression Neural Network. Machines 2022, 10, 157. [Google Scholar] [CrossRef]
- Ma, Y.; Yao, M.H.; Liu, H.C.; Tang, Z.G. State of Health estimation and Remaining Useful Life prediction for lithium-ion batteries by Improved Particle Swarm Optimization-Back Propagation Neural Network. J. Energy Storage 2022, 52, 104750. [Google Scholar] [CrossRef]
- Angus, J.R.; Link, A.; Friedman, A.; Ghosh, D.; Johnson, J.D. On numerical energy conservation for an implicit particle-in-cell method coupled with a binary Monte-Carlo algorithm for Coulomb collisions. J. Comput. Phys. 2022, 456, 111030. [Google Scholar] [CrossRef]
- Guo, H.; Zhou, Y.; Liu, H.; Hu, X. Improved Cubature Kalman Filtering on Matrix Lie Groups Based on Intrinsic Numerical Integration Error Calibration with Application to Attitude Estimation. Machines 2022, 10, 265. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).