Composite Fault Diagnosis of Rolling Bearing Based on Chaotic Honey Badger Algorithm Optimizing VMD and ELM
Abstract
:1. Introduction
- Chaotic mapping improved Honey Badger algorithm (CHBA);
- A novel adaptive variational mode decomposition (VMD) is established based on variational mode decomposition;
- A novel adaptive extreme learning machine (ELM) is established based on extreme learning machine.
2. Theoretical Analysis of Algorithm
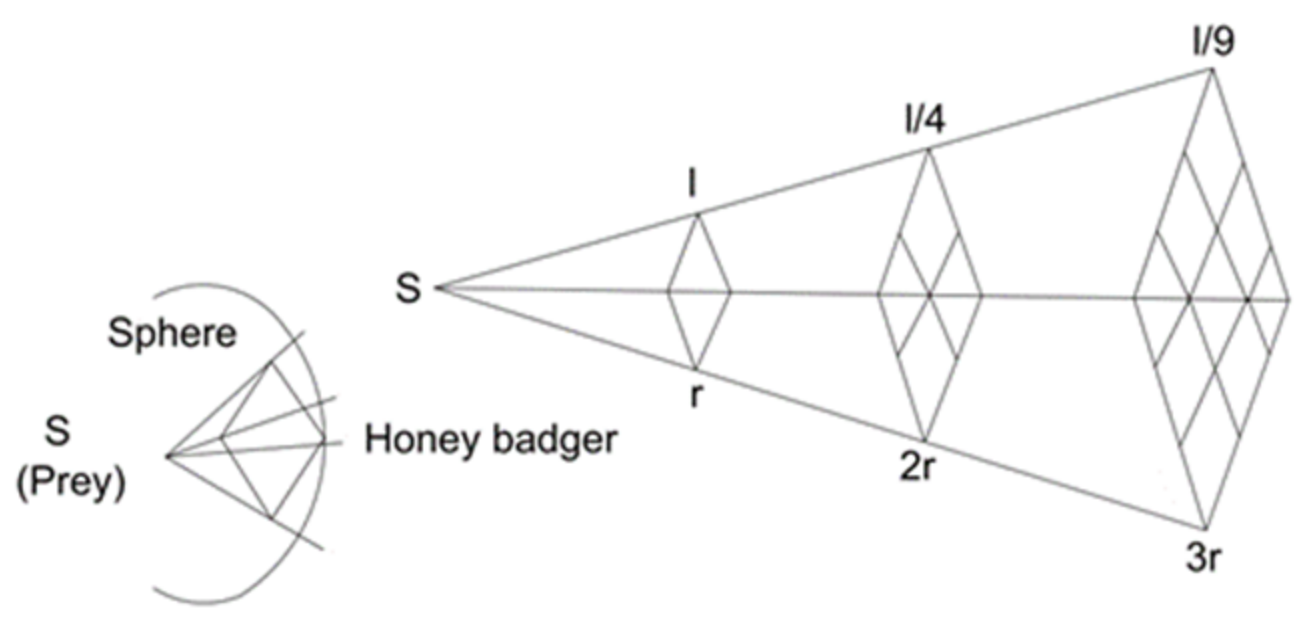
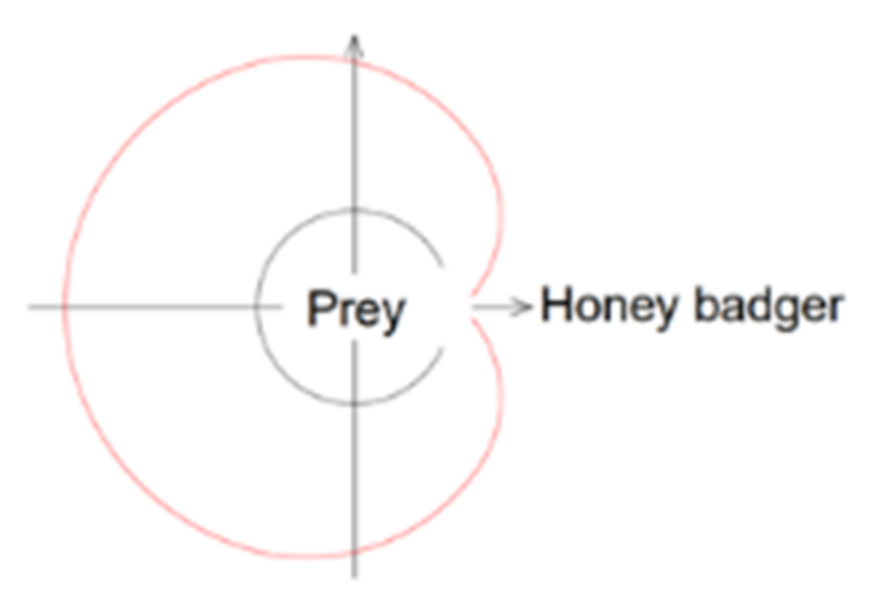
2.1. Introduction to the Honey Badger Algorithm (HBA)
2.2. Variational Modal Decomposition (VMD)
2.3. Extreme Learning Machine (ELM)
3. Proposed Method
3.1. Chaotic Mapping-Improved Honey Badger Algorithm (CHBA)
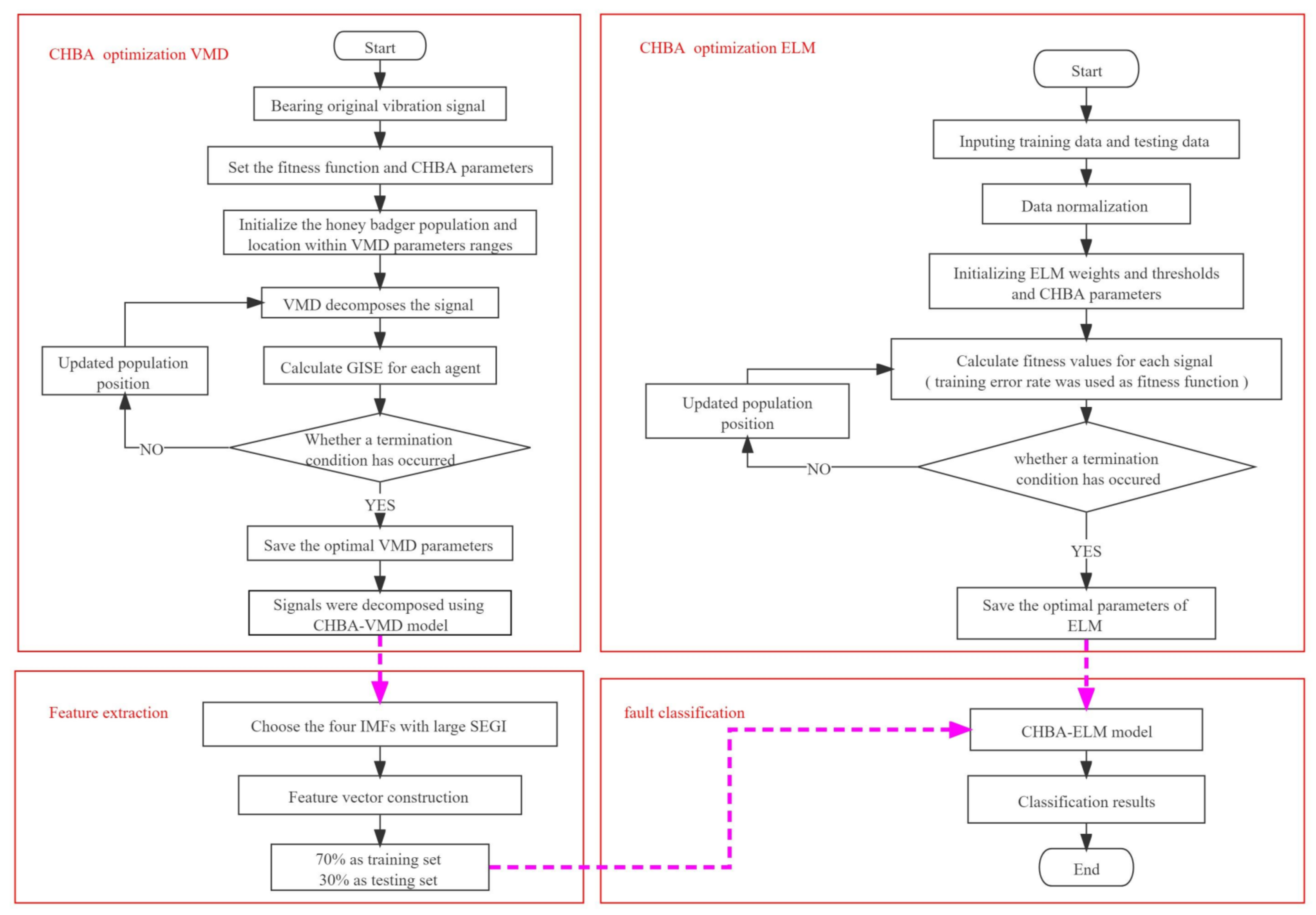
3.2. CHBA Optimizes VMD and ELM
CHBA-VMD Model
3.3. Feature Extraction
3.4. Fault Diagnosis Model
4. Analysis of the Influence of Chaotic Mapping on the Performance of HBA
4.1. Low-Dimensional Single-Objective Test Function
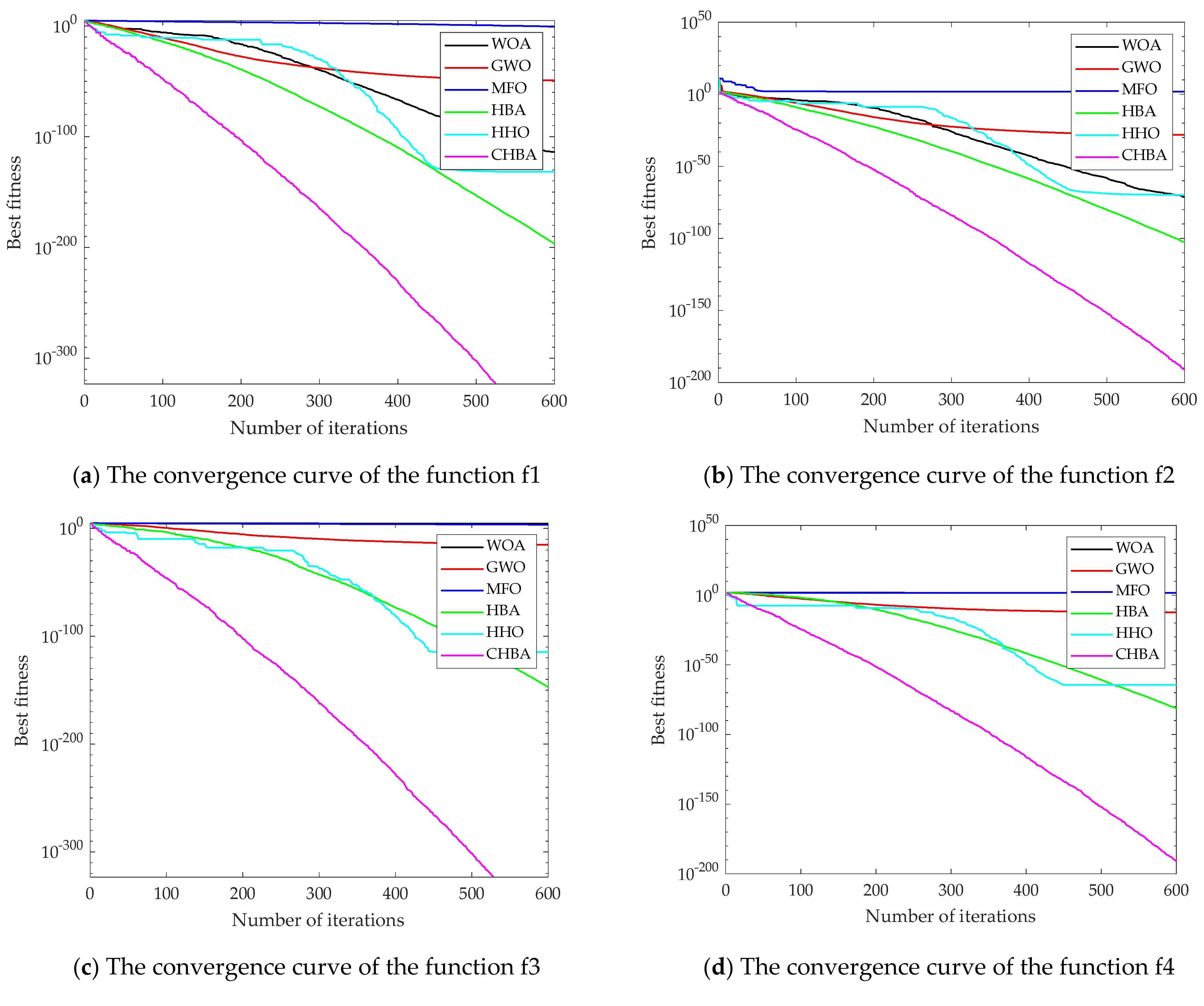
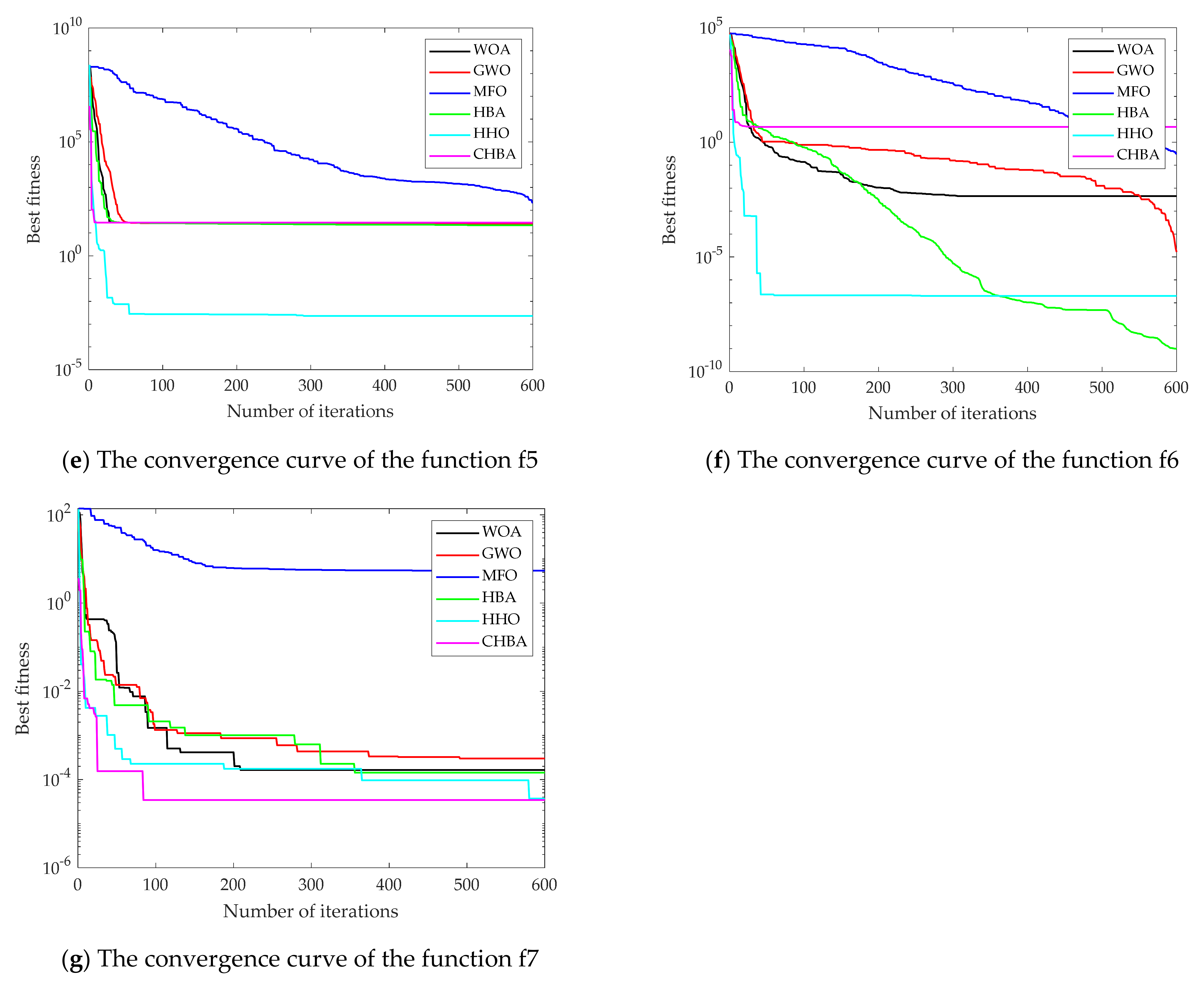
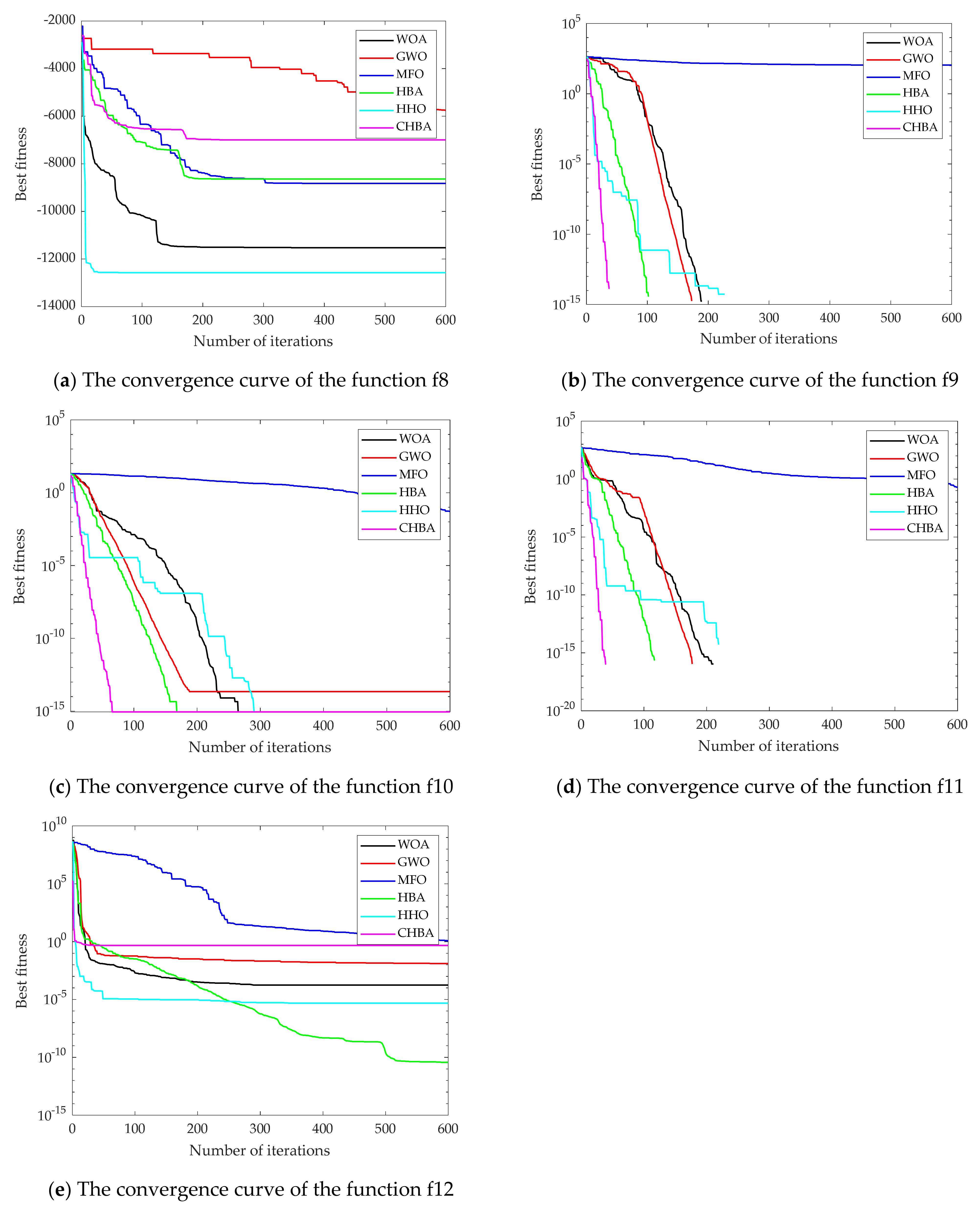
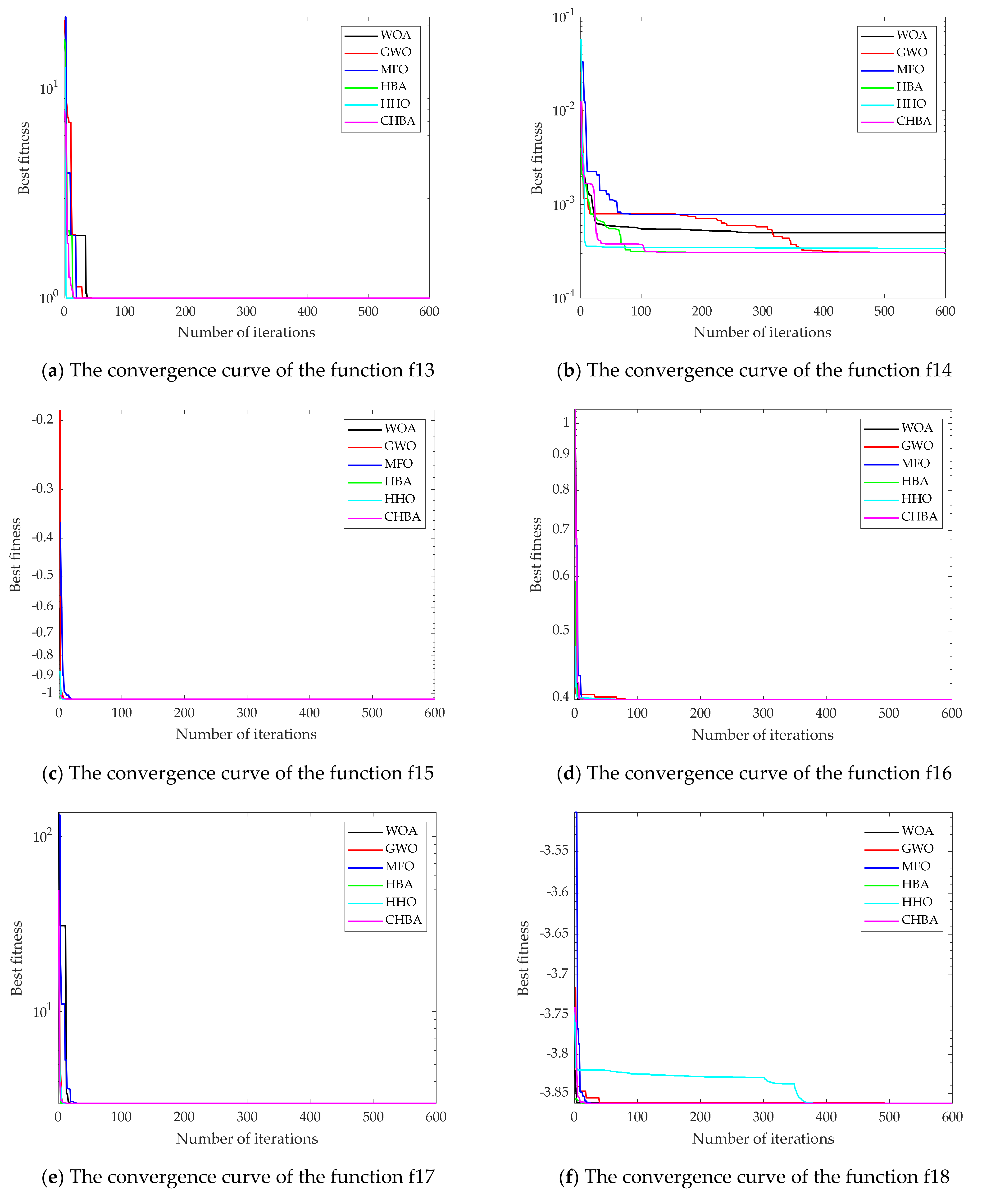
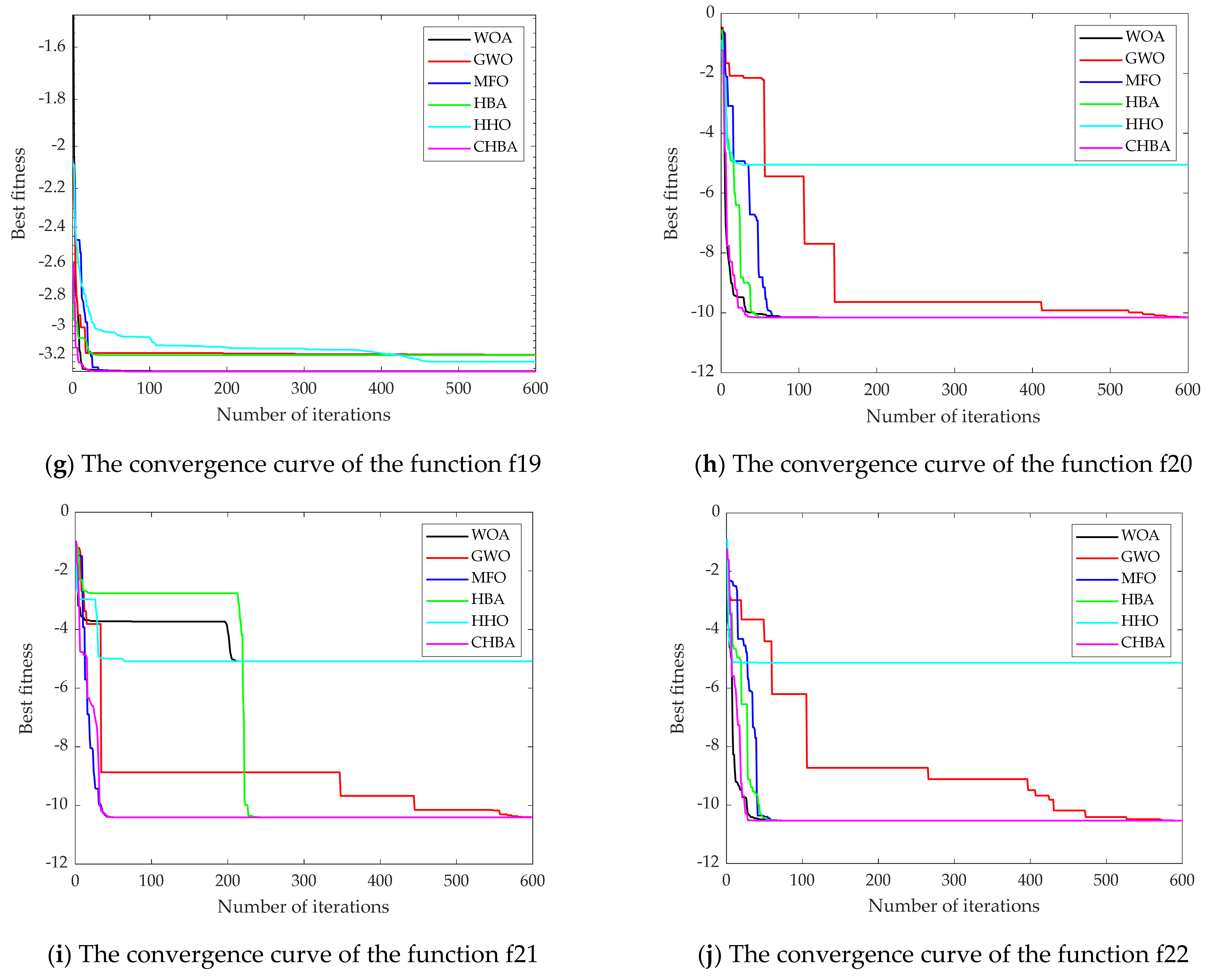
4.1.1. Analysis of Convergence Accuracy and Stability
4.1.2. Analysis of Convergence Speed
4.2. High-Dimensional Multi-Objective Test Function
4.2.1. Analysis of Convergence Accuracy and Stability
4.2.2. Analysis of Convergence Speed
4.3. Low-Dimensional Test Function
4.3.1. Analysis of Convergence Accuracy and Stability
4.3.2. Analysis of Convergence Speed
5. Experimental Study
5.1. Parameter Selection of VMD
5.2. Construction of Fault Feature Vector
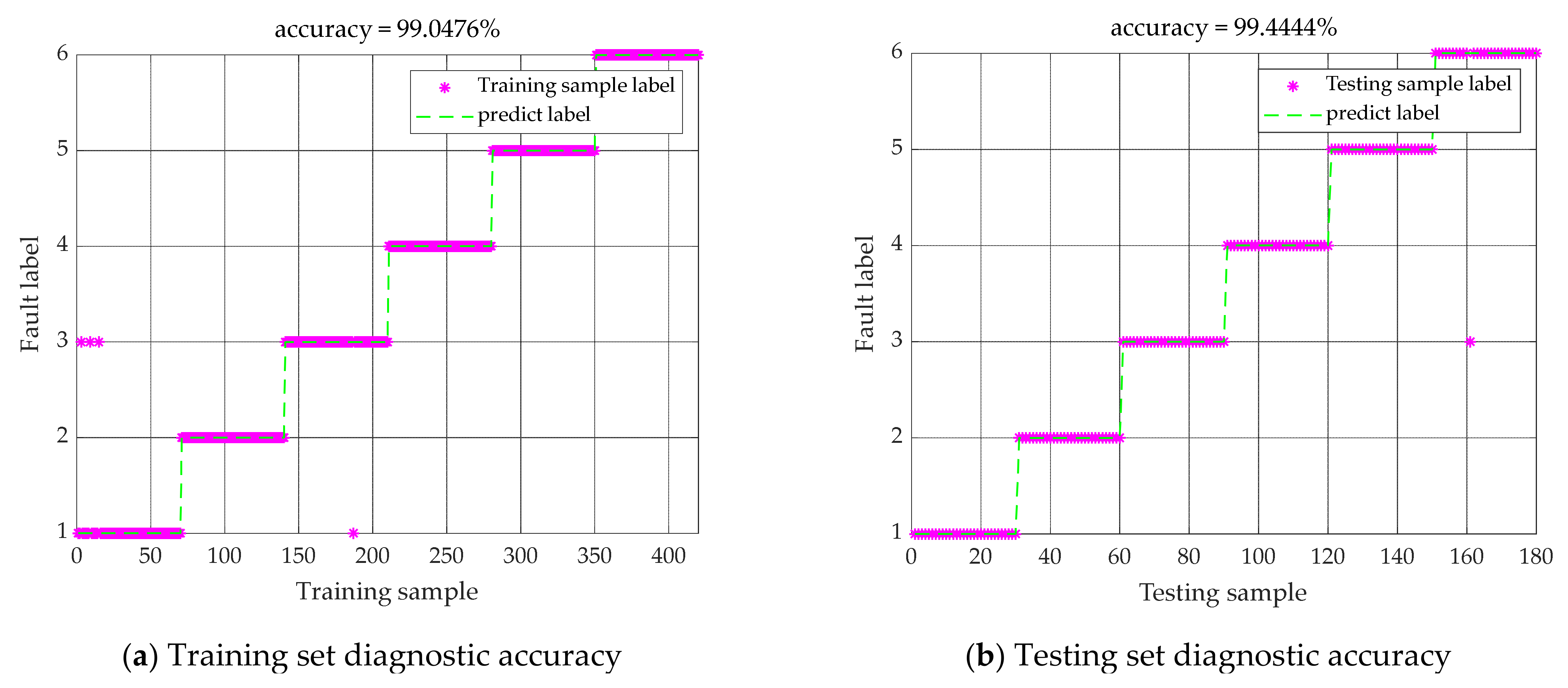
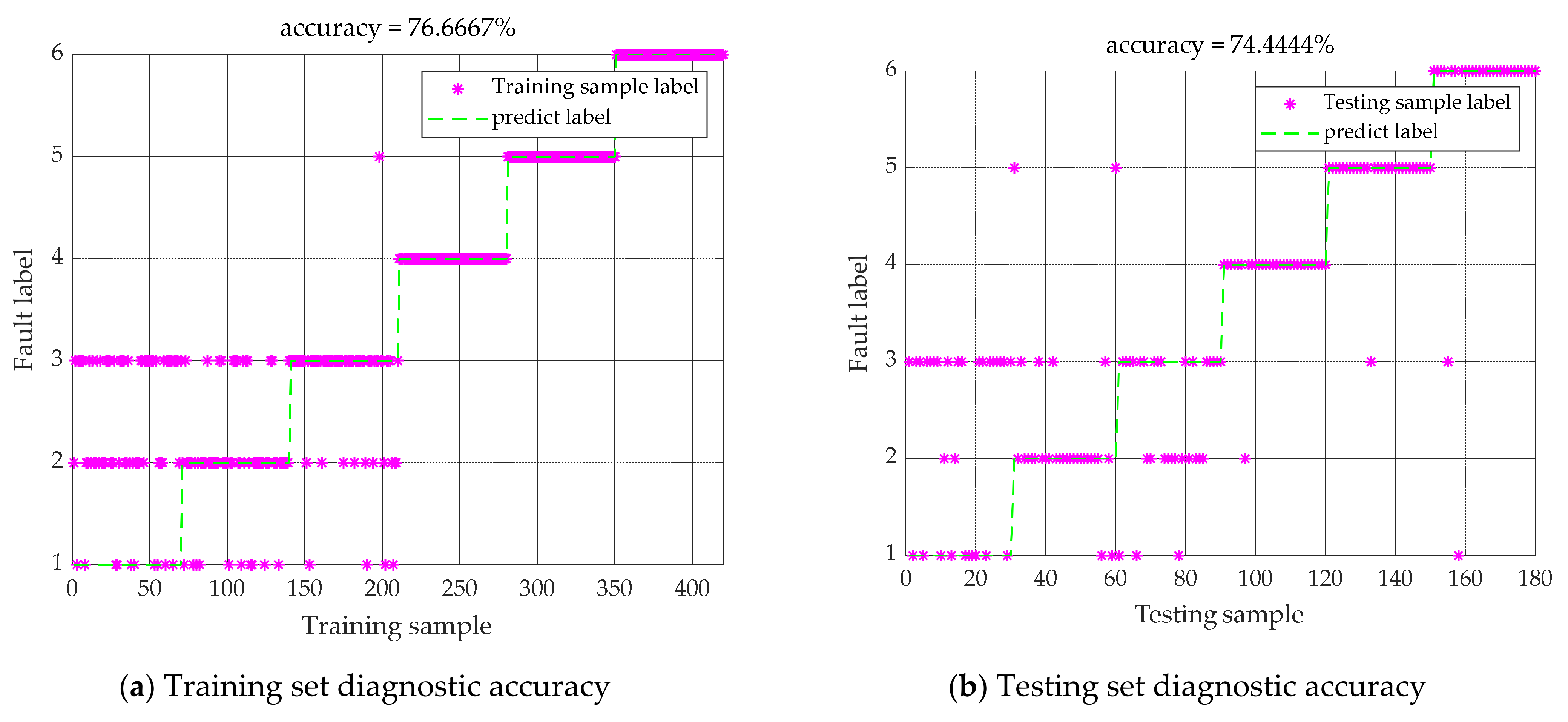
5.3. Classification Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Functions | Value | WOA | GWO | MFO | HBA | HHO | CHBA |
|---|---|---|---|---|---|---|---|
| Ave Std Best | 1.03 × 10−114 5.18 × 10−114 1.59 × 10−123 | 1.05 × 10−49 1.43 × 10−49 3.10 × 10−51 | 1.39 × 10−1 1.20 × 10−1 1.35 × 10−2 | 7.25 × 10−194 02.96 × 10−202 | 1.38 × 10−126 6.68 × 10−126 4.35 × 10−142 | 0 0 0 | |
| Ave Std Best | 2.85 × 10−67 1.51 × 10−66 6.29 × 10−74 | 3.98 × 10−29 2.76 × 10−29 5.63 × 10−30 | 2.28 × 10 1.79 × 10 2.31 × 10−2 | 1.37 × 10−102 3.01 × 10−102 1.71 × 10−105 | 1.65 × 10−65 8.72 × 10−65 2.66 × 10−75 | 1.71 × 10−191 0 3.17 × 10−195 | |
| Ave Std Best | 1.12 × 104 6.99 × 103 1.13 × 103 | 1.63 × 10−14 4.71 × 10−14 5.46 × 10−19 | 1.26 × 104 1.12 × 104 7.75 × 102 | 5.79 × 10−139 3.17 × 10−138 3.80 × 10−154 | 2.49 × 10−106 1.36 × 10−105 2.94 × 10−128 | 0 0 0 | |
| Ave Std Best | 2.09 × 10 2.52 × 10 1.77 × 10−3 | 5.21 × 10−2 2.85 × 10−1 1.71 × 10−13 | 3.78 × 10 1.04 × 10 2.17 × 10 | 2.19 × 10−81 9.54 × 10−81 7.58 × 10−88 | 1.18 × 10−63 4.40 × 10−63 2.15 × 10−70 | 8.00 × 10−190 0 6.11 × 10−196 | |
| Ave Std Best | 2.66 × 10 3.32 × 10−1 2.61 × 10 | 2.61 × 10 4.75 × 10−1 2.51 × 10 | 6.57 × 103 2.27 × 104 2.91 × 10 | 2.05 × 10 6.04 × 10−1 1.93 × 10 | 6.49 × 10−4 8.02 × 10−4 1.14 × 10−5 | 2.89 × 10 4.19 × 10−2 2.88 × 10 | |
| Ave Std Best | 2.59 × 10−3 1.09 × 10−3 6.64 × 10−4 | 2.00 × 10−1 2.22 × 10−1 1.64 × 10−5 | 1.01 × 103 3.08 × 103 2.66 × 10−2 | 4.85 × 10−9 6.46 × 10−9 5.24 × 10−11 | 9.17 × 10−6 1.29 × 10−5 1.12 × 10−8 | 4.55 7.44 × 10−1 3.35 | |
| Ave Std Best | 8.22 × 10−4 8.98 × 10−4 3.12 × 10−5 | 4.99 × 10−4 2.64 × 10−4 9.61 × 10−5 | 2.75 5.85 2.58 × 10−2 | 1.20 × 10−4 9.45 × 10−5 9.77 × 10−6 | 5.59 × 10−5 3.09 × 10−5 6.74 × 10−6 | 2.20 × 10−5 1.80 × 10−5 1.30 × 10−6 | |
| Ave Std Best | −1.18 × 104 1.18 × 103 −1.26 × 104 | −6.50 × 103 6.59 × 102 −7.98 × 103 | −8.84 × 103 7.15 × 102 −1.03 × 104 | −9.27 × 103 1.08 × 103 −1.09 × 104 | −1.26 × 104 2.76 × 10−2 −1.26 × 104 | 1.24 × 104 2.70 × 102 1.15 × 104 | |
| Ave Std Best | 0 0 0 | 0 0 0 | 1.33 × 102 3.99 × 10 5.97 × 10 | 0 0 0 | 0 0 0 | 0 0 0 | |
| Ave Std Best | 4.09 × 10−15 2.53 × 10−15 9.28 × 10−16 | 1.87 × 10−14 3.96 × 10−15 1.51 × 10−14 | 8.43 8.91 5.23 × 10−2 | 8.88 × 10−16 1.00 × 10−31 8.88 × 10−16 | 8.88 × 10−16 1.00 × 10−31 8.88 × 10−16 | 8.88 × 10−16 1.00 × 10−31 8.88 × 10−16 | |
| Ave Std Best | 3.18 × 10−3 1.25 × 10−2 0 | 4.12 × 10−3 7.88 × 10−3 0 | 6.20 2.29 × 10 3.25 × 10−2 | 0 0 0 | 0 0 0 | 0 0 0 | |
| Ave Std Best | 7.59 × 10−4 1.73 × 10−3 1.04 × 10−4 | 1.68 × 10−2 1.02 × 10−2 1.05 × 10−6 | 1.40 1.51 6.53 × 10−3 | 1.77 × 10−9 3.60 × 10−9 3.04 × 10−11 | 5.71 × 10−7 7.98 × 10−7 7.37 × 10−11 | 4.00 × 10−1 1.50 × 10−1 1.77 × 10−1 | |
| Ave Std Best | 9.98 × 10−1 3.39 × 10−16 9.98 × 10−1 | 2.11 2.50 9.98 × 10−1 | 9.98 × 10−1 3.39 × 10−16 9.98 × 10−1 | 9.98 × 10−1 3.39 × 10−16 9.98 × 10−1 | 9.98 × 10−1 3.39 × 10−16 9.98 × 10−1 | 9.82 × 10−1 3.06 × 10−16 9.82 × 10−1 | |
| Ave Std Best | 7.37 × 10−4 4.53 × 10−4 3.08 × 10−4 | 3.68 × 10−3 7.59 × 10−3 3.07 × 10−4 | 9.42 × 10−4 2.64 × 10−4 6.56 × 10−4 | 4.61 × 10−3 8.22 × 10−3 3.07 × 10−4 | 3.21 × 10−4 1.22 × 10−5 3.08 × 10−4 | 3.08 × 10−4 2.26 × 10−6 3.07 × 10−4 | |
| Ave Std Best | −1.03 4.52 × 10−1 −1.03 | −1.03 4.52 × 10−16 −1.03 | −1.03 0 −1.03 | −1.03 0 −1.03 | −1.03 0 −1.03 | −1.03 0 −1.03 | |
| Ave Std Best | 0.398 1.69 × 10−16 0.398 | 0.398 0 0.398 | 0.398 1.13 × 10−16 0.398 | 0.398 1.13 × 10−16 0.398 | 0.398 1.69 × 10−16 0.398 | 0.398 0 0.398 | |
| Ave Std Best | 3 4.52 × 10−16 3 | 3 1.36 × 10−15 3 | 3 4.52 × 10−16 3 | 3 4.52 × 10−16 3 | 3 4.52 × 10−16 3 | 3 4.52 × 10−16 3 | |
| Ave Std Best | −3.86 1.54 × 10−4 −3.86 | −3.72 3.50 × 10−3 −3.86 | −3.86 2.71 × 10−15 −3.86 | −3.86 2.71 × 10−15 −3.86 | −3.86 2.71 × 10−15 −3.86 | −3.86 2.71 × 10−15 −3.86 | |
| Ave Std Best | −3.25 6.18 × 10−2 −3.32 | −3.29 5.20 × 10−2 −3.32 | −3.25 5.92 × 10−2 −3.32 | −3.26 6.40 × 10−2 −3.32 | −3.22 5.71 × 10−2 −3.32 | −3.32 1.09 × 10−4 −3.32 | |
| Ave Std Best | −9.23 2.42 −10.1532 | −9.13 2.07 −10.1532 | −8.64 2.61 −10.1532 | −10.1532 1.81 × 10−15 −10.1532 | −6.58 2.37 −10.1532 | −10.1532 1.81 × 10−15 −10.1532 | |
| Ave Std Best | −9.03 2.56 −10.403 | −10.403 2.77 × 10−4 −10.403 | −9.52 2.00 −10.403 | −5.54 3.56 −10.403 | 5.62 1.61 −10.403 | −10.403 0 −10.403 | |
| Ave Std Best | −8.88 2.82 −10.536 | −9.99 2.06 −10.536 | −9.64 2.04 −10.536 | −6.52 3.88 −10.536 | −5.13 1.83 × 10−4 −5.13 | −10.536 9.03 × 10−15 −10.536 |
References
- Noshirvani, G.; Askari, J.; Fekih, A. A robust fault detection and isolation filter for the pitch system of a variable speed wind turbine. Int. Trans. Electr. Energy Syst. 2018, 28, e2625. [Google Scholar] [CrossRef]
- Huang, N.; Shen, Z.; Long, S.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Amrinder, S.M.; Gurpreet, S.; Jagpreet, S.; Kankar, P.K.; Sukhjeet, S. A novel method to classify bearing faults by integrating standard deviation to refined composite multi-scale fuzzy entropy. Measurement 2020, 154, 107441. [Google Scholar]
- Zheng, J.; Su, M.; Ying, W.; Tong, J.; Pan, Z. Improved uniform phase empirical mode decomposition and its application in machinery fault diagnosis. Measurement 2021, 179, 109425. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Ye, M.; Yan, X.; Jia, M. Rolling Bearing Fault Diagnosis Based on VMD-MPE and PSO-SVM. Entropy 2021, 23, 762. [Google Scholar] [CrossRef] [PubMed]
- Fu, W.; Shao, K.; Tan, J.; Wang, K. Fault Diagnosis for Rolling Bearings Based on Composite Multiscale Fine-Sorted Dispersion Entropy and SVM With Hybrid Mutation SCA-HHO Algorithm Optimization. IEEE Access 2020, 8, 13086–13104. [Google Scholar] [CrossRef]
- Zhang, F.; Sun, W.; Wang, H.; Xu, T. Fault Diagnosis of a Wind Turbine Gearbox Based on Improved Variational Mode Algorithm and Information Entropy. Entropy 2021, 23, 794. [Google Scholar] [CrossRef]
- Li, Y.; Peng, Z. Fault Diagnosis of Rolling Bearing Based on Parameter Adaptive VMD. Noise Vib. Control. 2021, 41, 139–146. [Google Scholar]
- Liang, T.; Lu, H.; Sun, H. Application of Parameter Optimized Variational Mode Decomposition Method in Fault Feature Extraction of Rolling Bearing. Entropy 2021, 23, 520. [Google Scholar] [CrossRef]
- Zhi, L.; Hu, F.; Zhao, C.; Wang, J. Modal parameter estimation of civil structures based on improved variational mode decomposition. Struct. Eng. Mech. 2021, 79, 683–697. [Google Scholar]
- Mganb, C.; Tmh, A.; Om, A. An adaptive variational mode decomposition based on sailfish optimization algorithm and Gini index for fault identification in rolling bearings. Measurement 2020, 173, 108514. [Google Scholar]
- Hashim, F.A.; Houssein, E.H.; Hussain, K.; Mabrouk, M.S.; Al-Atabany, W. Honey Badger Algorithm: New Metaheuristic Algorithm for Solving Optimization Problems. Math. Comput. Simul. 2021, 192, 84–110. [Google Scholar] [CrossRef]
- Wang, C. A sample entropy inspired affinity propagation method for bearing fault signal classification. Digit. Signal Process. 2020, 102, 102740. [Google Scholar] [CrossRef]
- Deng, W.; Yao, R.; Sun, M.; Zhao, H.; Luo, Y.; Dong, C. Study on a novel fault diagnosis method based on integrating EMD, fuzzy entropy, improved PSO and SVM. J. Vibroeng. 2017, 19, 2562–2577. [Google Scholar]
- Hou, J.; Wu, Y.; Gong, H.; Ahmad, A.S.; Liu, L. A novel intelligent method for bearing fault diagnosis based on EEMD permutation entropy and GG clustering. Appl. Sci. 2020, 10, 386. [Google Scholar] [CrossRef] [Green Version]
- Ding, F.; Xia, Y.; Tian, J.; Zhang, X. An AVMD Method Based on Energy Ratio and Deep Belief Network for Fault Identification of Automation Transmission Device. IEEE Access 2021, 9, 150088–150097. [Google Scholar] [CrossRef]
- Zhou, R.; Wang, X.; Wan, J.; Xiong, N. EDM-Fuzzy: An Euclidean Distance Based Multiscale Fuzzy Entropy Technology for Diagnosing Faults of Industrial Systems. IEEE Trans. Ind. Inform. 2021, 17, 4046–4054. [Google Scholar] [CrossRef]
- Udmale, S.S.; Singh, S.K. Bearing Fault Classification Using Wavelet Energy and Autoencoder; Springer Nature: Cham, Switzerland, 2020; Volume 25, pp. 227–238. [Google Scholar]
- Shi, P.; Guo, X.; Han, D.; Fu, R. A sparse auto-encoder method based on compressed sensing and wavelet packet energy entropy for rolling bearing intelligent fault diagnosis. J. Mech. Sci. Technol. 2020, 34, 1445–1458. [Google Scholar] [CrossRef]
- Gao, T.; Yang, J.; Jiang, S. A Novel Incipient Fault Diagnosis Method for Analog Circuits Based on GMKL-SVM and Wavelet Fusion Features. IEEE Trans. Instrum. Meas. 2020, 70, 3502315. [Google Scholar] [CrossRef]
- Song, S.; Qiu, D.; Qin, S. Research on the Fault Diagnosis Method of Mine Fan Based on Sound Signal Analysis. Adv. Civ. Eng. 2021, 9650644. [Google Scholar] [CrossRef]
- Huang, G.B.; Chen, Y.Q.; Babri, H.A. Classification ability of single hidden layer feedforward neural networks. IEEE Trans. Neural Netw. 2000, 11, 799–801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xiao, J.; Zhou, J.; Li, C.; Xiao, H.; Zhang, W.; Zhu, W. Multi-fault classification based on the two-stage evolutionary extreme learning machine and improved artificial bee colony algorithm. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2013, 228, 1797–1807. [Google Scholar] [CrossRef]
- Qin, Y.L.; Liu, J.G.; Wang, Y.Z. Rolling bearing fault diagnosis method based on extreme learning machine. Mod. Mach. Tool Autom. Manuf. Technol. 2016, 5, 103–106. [Google Scholar]
- Wang, T.T.; Wang, Y.; Ji, Z.C. Rolling bearing fault diagnosis based on improved extreme learning machine. J. Syst. Simul. 2018, 30, 4413–4420. [Google Scholar]
- Cheng, H.; Wu, T.; Gu, R.; Jin, Z.; Ma, R.; Qu, H. Rolling bearing fault diagnosis based on composite multiscale permutation entropy and reverse cognitive fruit fly optimization algorithm–Extreme learning machine-ScienceDirect. Measurement 2020, 173, 108636. [Google Scholar]
- Wang, H.; Jing, W.; Li, Y.; Yang, H. Fault Diagnosis of Fuel System Based on Improved Extreme Learning Machine. Neural Process. Lett. 2020, 53, 2553–2565. [Google Scholar] [CrossRef]
- Liu, C.; Tan, J.; Huang, Z. Fault Diagnosis of Rolling Element Bearings Based on Adaptive Mode Extraction. Machines 2022, 10, 260. [Google Scholar] [CrossRef]
- Zhang, C.; Ding, S. A stochastic configuration network based on chaotic sparrow search algorithm. Knowl.-Based Syst. 2021, 220, 106924. [Google Scholar] [CrossRef]
- Dehkordi, A.A.; Sadiq, A.S.; Mirjalili, S.; Ghafoor, K.Z. Nonlinear-based Chaotic Harris Hawks Optimizer: Algorithm and Internet of Vehicles application. Appl. Soft Comput. 2021, 109, 107574. [Google Scholar] [CrossRef]
- Xu, Z.; Yang, H.; Li, J.; Zhang, X.; Lu, B. Comparative Study on Single and Multiple Chaotic Maps Incorporated Grey Wolf Optimization Algorithms. IEEE Access 2021, 9, 77416–77437. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, D.; Wang, Y.; Song, T.; Fan, Y. Hybrid strategy improved whale optimization algorithm. Comput. Eng. Des. 2020, 41, 3397–3404. [Google Scholar]
- Miao, Y.; Wang, J.; Zhang, B.; Li, H. Improvement of kurtosis-guided-grams via Gini index for bearing fault feature identification. Meas. Sci. Technol. 2017, 28, 12. [Google Scholar] [CrossRef]
- Albezzawy, M.N.; Nassef, M.G.; Elsayed, E.S.; Elkhatib, A. Early Rolling Bearing Fault Detection Using A Gini Index Guided Adaptive Morlet Wavelet Filter. In Proceedings of the 10th International Conference on Mechanical and Aerospace Engineering (ICMAE), Brussels, Belgium, 22–25 July 2019; pp. 314–322. [Google Scholar]
- Miao, Y.; Wang, J.; Zhang, B.; Li, H. Practical framework of Gini index in the application of machinery fault feature extraction. Mech. Syst. Signal Processing 2022, 165, 108333. [Google Scholar] [CrossRef]
- Wang, B.; Lei, Y.G.; Li, N.P.; Li, N. A hybrid prognostics approach for estimating remaining useful life of rolling element bearings. IEEE Trans. Reliab. 2018, 69, 401–412. [Google Scholar] [CrossRef]

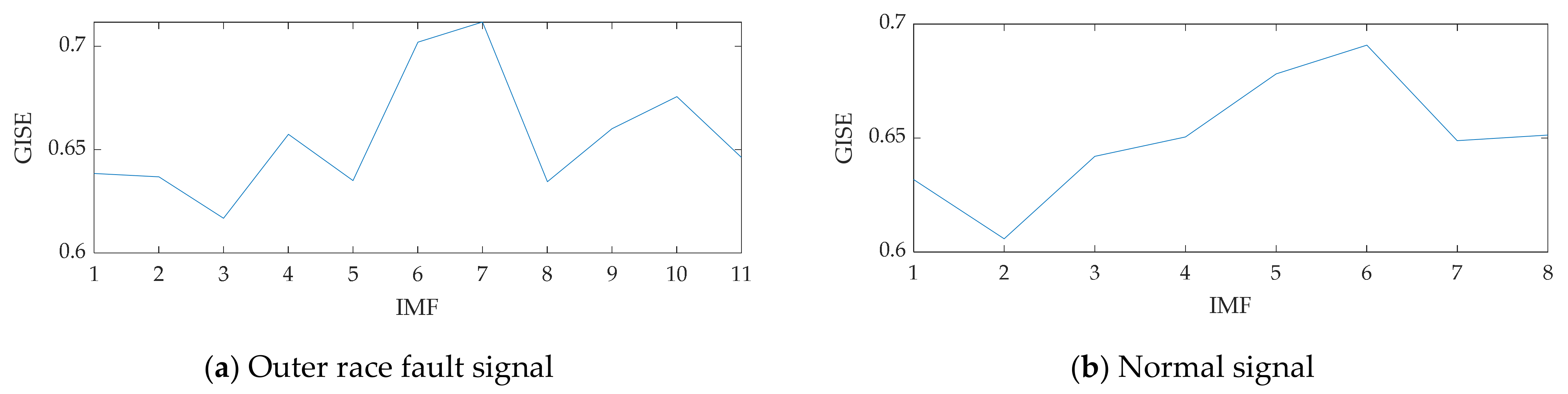
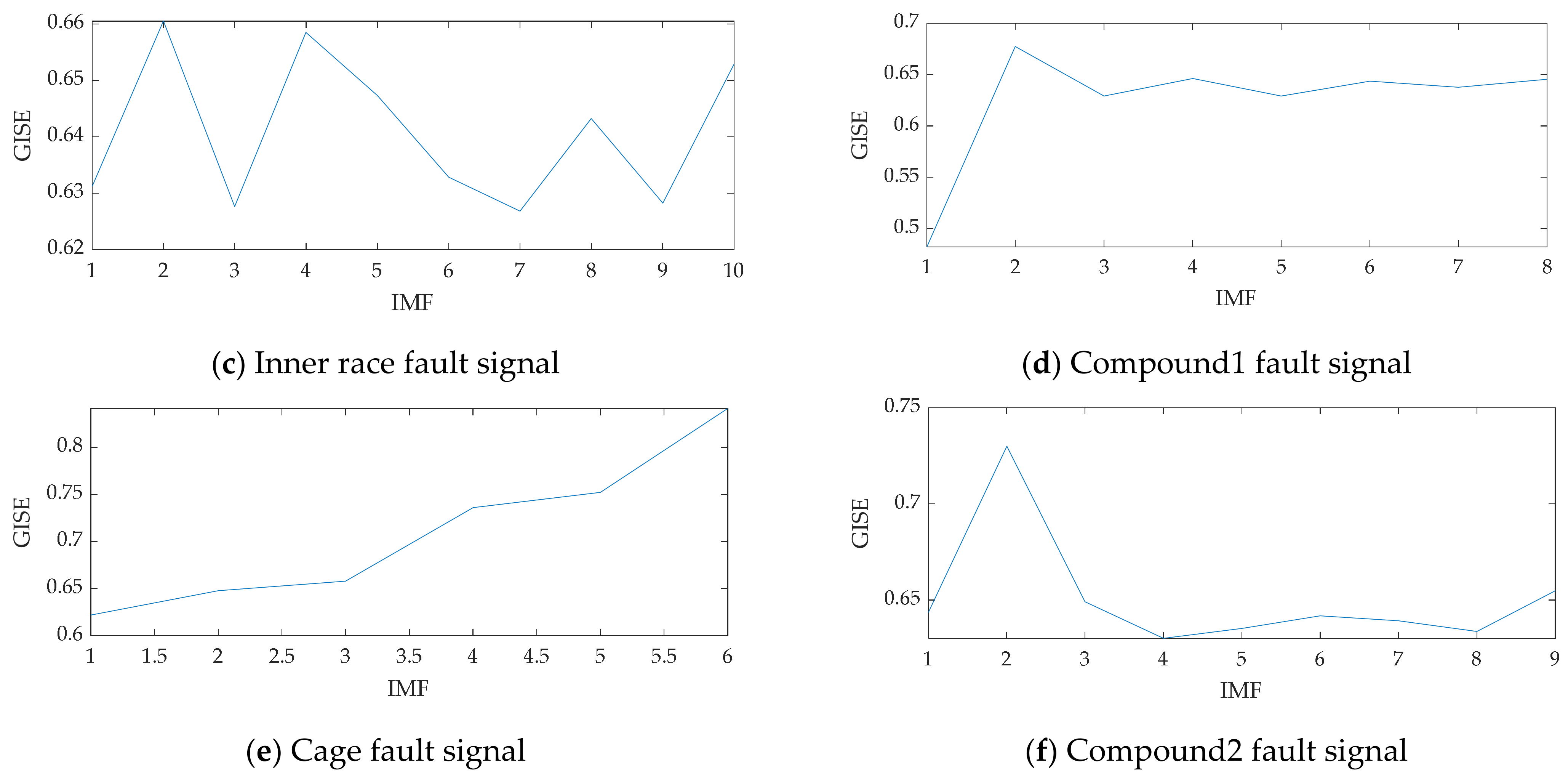
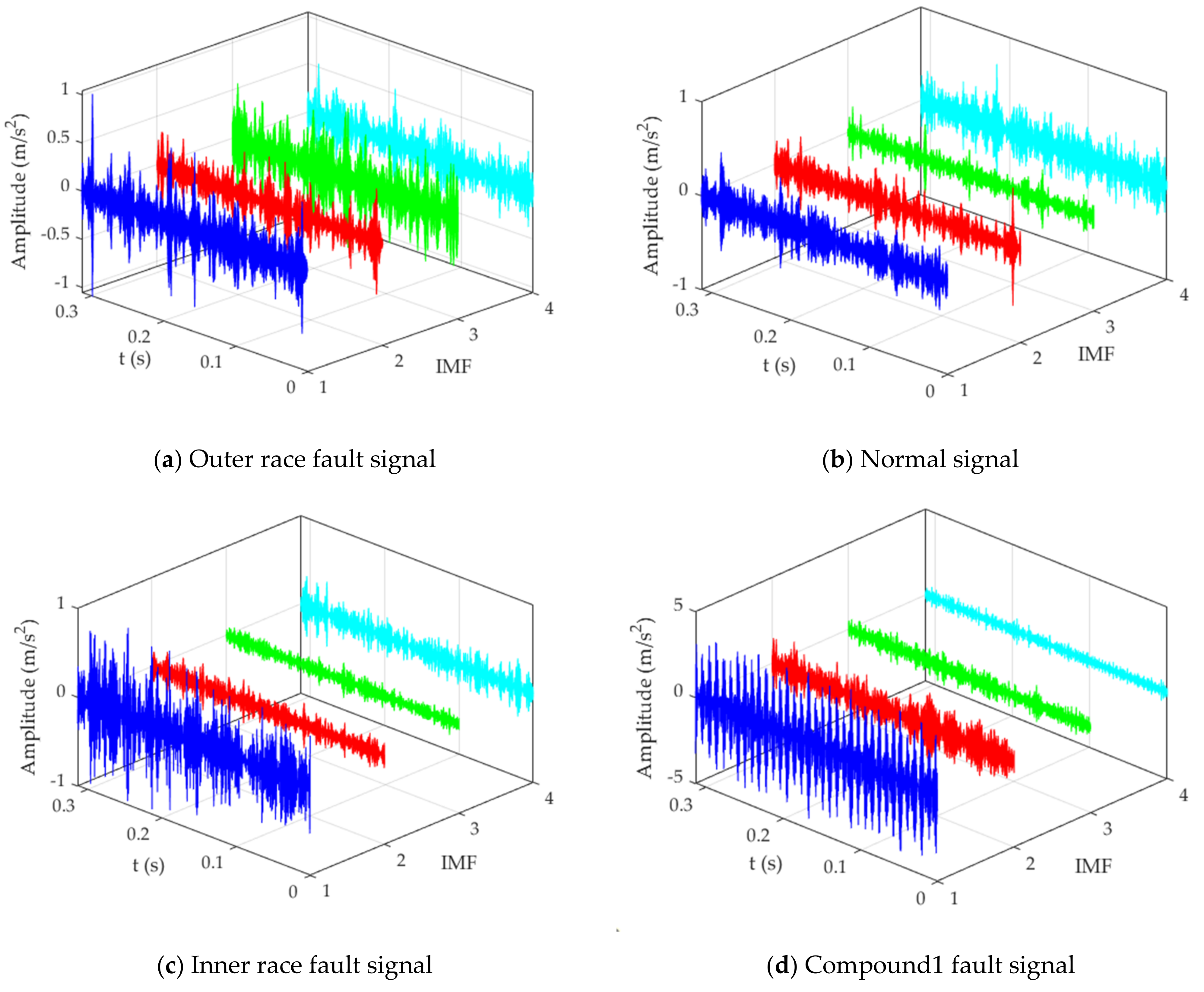
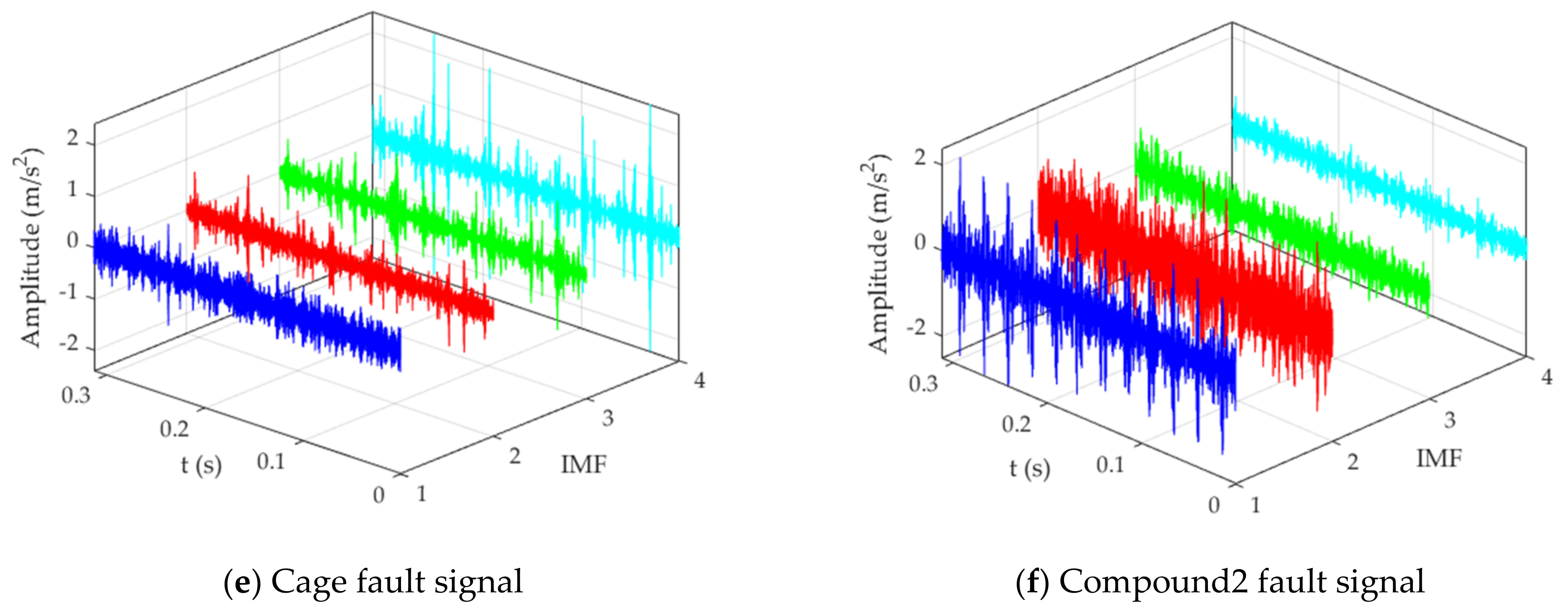
| Name of the Algorithm | Name of the Parameter |
|---|---|
| MFO | Convergence factor a: [−2 −1] |
| WOA | Convergence factor a: [2 0] |
| GWO | Convergence factor a: [2 0] |
| HBA | The ability to get food , constant |
| CHBA | The ability to get food , constant |
| Function | Range | |
|---|---|---|
| [−100,100] | 0 | |
| [−10,10] | 0 | |
| [−100,100] | 0 | |
| [−100,100] | 0 | |
| [−30,30] | 0 | |
| [−100,100] | 0 | |
| [−1.28,1.28] | 0 |
| Function | Range | |
|---|---|---|
| [−500,500] | −418.9829n | |
| [−5.12,5.12] | 0 | |
| [−32,32] | 0 | |
| [−600,600] | 0 | |
| [−50,50] | 0 |
| Function | Dim | Range | |
|---|---|---|---|
| 2 | [−65,65] | 1 | |
| 4 | [−5,5] | 0.003 | |
| 2 | [−5,5] | −1.0316 | |
| 2 | [−5,5] | 0.398 | |
| 2 | [−5,5] | 3 | |
| 3 | [0,1] | −3.86 | |
| 6 | [0,1] | −3.32 | |
| 4 | [0,10] | −10.1532 | |
| 4 | [0,10] | −10.4028 | |
| 4 | [0,10] | −10.5363 |
| Fault Type | K | |
|---|---|---|
| Outer race | 11 | 841 |
| Normal | 8 | 2117 |
| Inner race | 10 | 1474 |
| The inner and outer race | 8 | 328 |
| Cage | 6 | 280 |
| Inner race, outer race, rolling elements and cage | 9 | 265 |
| Algorithm | Accuracy of Training Set (%) | Accuracy of Testing Set (%) | ||||
|---|---|---|---|---|---|---|
| Min | Max | Mean | Min | Max | Mean | |
| BP | 59.52 | 89.76 | 71.24 | 63.89 | 95.56 | 77.77 |
| ELM | 97.00 | 98.67 | 98.33 | 76.33 | 80.33 | 78.17 |
| GWO-ELM | 98.57 | 98.81 | 98.76 | 95.00 | 97.78 | 96.39 |
| HBA-ELM | 95.24 | 98.81 | 97.26 | 96.11 | 99.44 | 97.50 |
| CHBA-ELM | 98.10 | 100.00 | 98.80 | 100.00 | 98.83 | 99.50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, J.; Yu, S.; Cheng, W. Composite Fault Diagnosis of Rolling Bearing Based on Chaotic Honey Badger Algorithm Optimizing VMD and ELM. Machines 2022, 10, 469. https://doi.org/10.3390/machines10060469
Ma J, Yu S, Cheng W. Composite Fault Diagnosis of Rolling Bearing Based on Chaotic Honey Badger Algorithm Optimizing VMD and ELM. Machines. 2022; 10(6):469. https://doi.org/10.3390/machines10060469
Chicago/Turabian StyleMa, Jie, Sen Yu, and Wei Cheng. 2022. "Composite Fault Diagnosis of Rolling Bearing Based on Chaotic Honey Badger Algorithm Optimizing VMD and ELM" Machines 10, no. 6: 469. https://doi.org/10.3390/machines10060469
APA StyleMa, J., Yu, S., & Cheng, W. (2022). Composite Fault Diagnosis of Rolling Bearing Based on Chaotic Honey Badger Algorithm Optimizing VMD and ELM. Machines, 10(6), 469. https://doi.org/10.3390/machines10060469







