Using Pose-Dependent Model Predictive Control for Path Tracking with Bounded Tensions in a 3-DOF Spatial Cable Suspended Parallel Robot

Abstract

This paper proposes the preliminary results on a novel control architecture based on model predictive control (MPC) for cable-driven parallel robots (CDPRs) and applies them to a three degrees of freedom (3-DOF) robot with a suspended configuration, leading to a cable-suspended parallel robot (CSPR). The goal of the control scheme is ensuring accurate path tracking of the reference end-effector path, while imposing a priori positive cable tensions. To handle the nonlinearities characterizing the dynamic model that governs this kind of multibody system and to keep the computational effort low, a position-dependent MPC algorithm with an embedded integrator is designed to compute the optimal cable tensions required to track the end-effector commanded path. Such tensions must belong to the feasible domain defined through a lower bound, which is slightly greater than zero, to ensure that cables pull the end-effector, and an upper bound, to represent the maximum stress that cables can withstand without breaking. The resulting controller is nonlinear, although it performs a local linearization in the prediction at each time step to reduce the computational effort. The optimal tensions are then transformed into the commanded motor torques through the inverse dynamic model of the servomotors driving the winches, since no force measurement is adopted in the controller implementation. The control architecture is designed and numerically validated through a spatial CSPR with lumped end-effector, and driven by three cables (i.e., with a non-redundant configuration). Four different paths are assumed to highlight various features of the proposed controller.

1. Introduction

An emerging technology and area of research in the field of multibody system dynamics is modeling, motion planning, and control of cable-driven parallel robots (CDPRs). In particular, accurate path tracking control is attracting a lot of attention in the literature since CSPRs have a high payload-to-weight ratio and large workspace [1]. On the other hand, it is a non-trivial task due to the positivity constraints on cable tensions, since cables can just pull the load. To face this issue and to exploit all the benefits coming from these multibody systems, optimal design, trajectory planning, and feedback control approaches are commonly studied. As for design, the use of overconstrained or overactuated configurations, together with optimized topologies or force-distribution algorithms, is widely investigated (see, e.g., [2,3,4]). As for motion planning strategies, the literature proposes several techniques to ensure a priori positive and bounded cable tensions along given paths (e.g., [5,6]). On the other hand, from the closed-loop perspective, some standard industrial control schemes, such as PID controllers, have been usually applied to CDPRs, showing acceptable results. In [7], dynamic load carrying capacity of a CDPR is considered with a closed-loop control system based on feedback linearization, which is subsequently converted into a PID control design. In [8], structured and unstructured uncertainties in the robot dynamics are considered with a focus to propose a robust PID controller for fully constrained cable-driven parallel manipulators; experimental outcomes are presented in order to verify the correctness of the proposed control scheme. While standard techniques are simple and require reduced computational effort, they often do not exploit the dynamics model: the model is usually just used for the feedforward actions that support the feedback ones, by means of the inverse dynamics [9]. Additionally, they are not able to embed the positiveness constraints on the cable tensions, as well as bounds on the feasible maximum tensions, into the controller design, leading to the inclusion of a posteriori saturations. This aspect should be avoided since closed-loop systems start to behave as open-loop ones when a posteriori saturations occur and, therefore, accuracy in the tracking response tends to lower, as well as robustness against external disturbances. To overcome these negative aspects, advanced control techniques have to be considered to obtain even better performances.

In this paper, the theory regarding model predictive control (MPC) is exploited and extended with the goal to achieve precise path tracking control in cable suspended parallel robots (CSPRs), i.e., a CDPR where all the cables lie above the end-effector, and therefore tensioning is insured by gravity. Indeed, MPC presents several benefits that make it very appealing for CDPRs in general. The fundamental idea of MPC is to solve an optimal control problem defined by a cost function over a receding horizon and constrained by the system dynamics and by bounds on the control variables. The optimization problem over the future control variables is solved at each time step by exploiting the prediction of the future trajectory of the states and outputs of the system, providing an optimal sequence of the control input which considers the constraints on input and output variables. Therefore, different from the standard industrial controllers mentioned above, constraints are included into the controller design itself. Due to these reasons, MPC is a privileged candidate for motion control of multibody systems in general (see e.g., [10,11]), especially with constrained control input.

Since the very last years, some applications of MPC have been exploited in the field of CDPRs, although just a few works can be found up to now. In [12], CDPRs with redundant cables under input constraints are considered and the controller design is carried on based on the exploitation of both input-output feedback linearization and linear model predictive control concepts; numerical simulation is performed to illustrate the effectiveness of the proposed method. An architecture made by two decoupled subsystems, an in-plane system and an out-plane one, is presented in [13]; based on these decoupled systems, two MPCs are used: the first one is designed to control the lower-cable tensions with the goal to damp out in-plane vibrations, while the second one is exploited to control pendulum torques to eliminate out-plane moving. A workspace-based model predictive control scheme is proposed in [14], which combines online model predictive control with offline workspace analysis. In [15], an experimental application is provided through a redundant CDPR; the control scheme consists of an MPC and an inner feedback control loop made by a PI controller for each motor and a feedforward term based on inverse kinematic that exploits tension measurements to compute the optimal torques of the motors. The idea of MPC has also been adopted in [16] to plan dynamic transition trajectories for a fully actuated CSPR with three DOFs.

In this work, model predictive control concepts are exploited and extended, proposing a two-step control strategy that splits the system into two subsystems and uses them in a sequential approach. In this way, the controller design becomes hugely easier since it does not directly involve the nonlinear model of the CSPR. Additionally, no further measurements of the cable tensions are required, thus simplifying the controller hardware. The first part concerns the subsystem made by the suspended mass to design the feedback MPC algorithm, achieving the positive feasible tensions; in particular, the dynamic matrix of the state-space model is constant, while the input matrix is position-dependent which allows one to handle nonlinearities by updating the model at each time step of the control loop. The input matrix is held constant along the prediction horizon to reduce computational burden, therefore making it a reasonable algorithm for real-time implementations. To better understand the proposed control scheme, it is useful to highlight that position and speed of the suspended mass are considered as the feedback signals and an embedded integrator is adopted into the MPC formulation (MPC-EI) [17] in order to achieve effective tracking responses with zero errors at steady-state conditions. Once the optimal tensions are evaluated, the second part exploits the algebraic dynamic model of the motors and the commanded speed and acceleration to compute the reference motor torques, thanks to an inverse dynamic approach, without requiring measurements of the actual tensions. Numerical assessment of the control performances is performed considering a fully actuated three degrees of freedom cable-suspended robot (i.e., with a point-mass end-effector), controlled by three cables and therefore in a non-redundant configuration, which is a more challenging configuration than redundant ones.

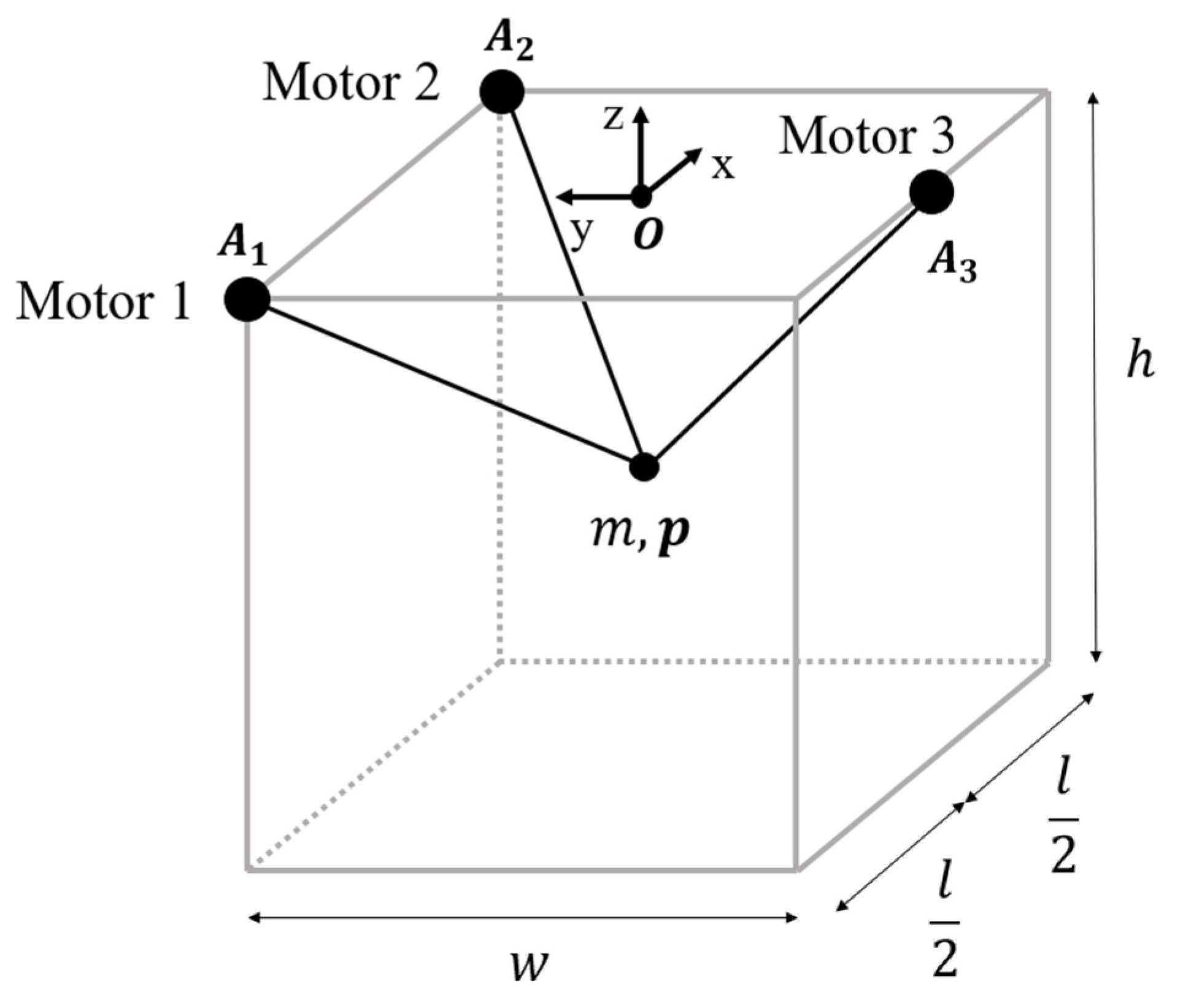
2. Dynamic Model of the Suspended Load

The CSPR investigated in this paper is sketched in Figure 1: it is made by a point-mass end-effector driven by three cables. The control goal is to ensure precise path tracking of the point-mass end-effector, while fulfilling the constraints on the feasible tensions. The dynamics model of such a mass ($m$), in the presence of the control actions exerted by the three cables, is formulated through the following set of ordinary differential equations (ODEs):

$$m\ddot{p}=mg+{\displaystyle \sum _{i=1}^3\left(-T_i\frac{p-A_i}{\Vert p-A_i\Vert }\right)}$$

(1)

$p=[\begin{array}{ccc}x& y& z{]}^T\end{array}$$\in {ℝ}^3$ is the vector of the absolute end-effector positions.

In the whole paper, it is assumed that cables are taut and stiff and with negligible mass; these assumptions are reasonable in several CSPRs with relatively small workspaces and payload, and therefore it is widely assumed in the literature (see, e.g., [18,19,20,21]). The system is fully actuated, since the number of degrees of freedom matches the number of independent control forces. However, control is challenging since the positiveness constraint on $T_i$ reduces the achievable performances compared to traditional parallel manipulators. For this reason, several studies in the literature on CSPRs exploit kinematically redundant mechanisms to simplify motion planning and control [2,4,22,23,24,25,26].

3. Control Design

3.1. Control Architecture

The ODEs in Equation (1) are nonlinear due to the pose-dependent terms $\frac{p-A_i}{\Vert p-A_i\Vert }$. Additional nonlinearities arise if the model with the motor torques as the inputs is considered, due to the pose-dependent Jacobian matrix of the kinematic constraints, and hence of the relation between $\dot{p}\hspace{0.17em}$ and the motor speeds. To handle this nonlinear model without increasing the computational complexity of the control scheme, which would make cumbersome the real-time implementation of the controller, the proposed control architecture is based on a two-step controller. First, as described in Section 3.2, MPC with EI is developed to calculate the positive tensions that make the load track the reference spatial path, by means of the ODEs in Equation (1). Then, as described in Section 3.4, the model in Equation (15) is exploited to translate the desired tension into reference motor torques to be commanded to the current control loops of the three servomotors.

3.2. Model Formulation for Control Design

The second-order model in Equation (1) is, first of all, transformed into a first-order one by introducing the state vector ${\chi }_c={\left[\begin{array}{cc}{\dot{p}}^T& p^T\end{array}\right]}^T$$\in {ℝ}^6$, the control input vector input vector $T={\left[\begin{array}{ccc}{T}_1& T_2& T_3\end{array}\right]}^T$$\in {ℝ}^3,$ and the output $y_c$$\in {ℝ}^3$:

$$\{\begin{array}{lll}{\dot{\chi }}_c(t)& =& A_c\hspace{0.17em}{\chi }_c(t)+B_c\left(p\right)T(t)+B_{gc}\hspace{0.17em}g\\ y_c(t)& =& C_c\hspace{0.17em}{\chi }_c(t)\end{array}$$

(2)

While the dynamic matrix $A_c$$\in {ℝ}^{6\times 6}$ is constant, the control force distribution matrix $B_c\left(p\right)$$\in {ℝ}^{6\times 3}$ is pose-dependent, because of the matrix of the cable unitary vectors $V\left(p\right)$$\in {ℝ}^{3\times 3}$ ($I_3$$\in {ℝ}^{3\times 3}$ is the identity matrix, $0_3$$\in {ℝ}^{3\times 3}$ is the null matrix):

$$\begin{array}{ccc}{A}_c=\left[\begin{array}{cc}{0}_3& 0_3\\ I_3& 0_3\end{array}\right]& & B_c\left(p\right)=\left[\begin{array}{c}-\frac{1}{m}V(p)\\ 0_3\end{array}\right]\end{array}$$

(3)

$B_{gc}$$\in {ℝ}^{6\times 3}$ is the gravity acceleration distribution matrix, while $C_c$$\in {ℝ}^{3\times 6}$ is the output matrix of the continuous-time, state-space model:

$$\begin{array}{ccc}{B}_{gc}=\left[\begin{array}{c}{I}_3\\ 0_3\end{array}\right]& & C_c=\left[\begin{array}{cc}{0}_3& I_3\end{array}\right]\end{array}$$

(4)

Discretizing Equation (2) with a proper sampling time $\Delta t$ transforms the ODEs into a set of difference equations, as required by the MPC theory, with $k$ ($t=k\Delta t$) representing the time variable:

$$\{\begin{array}{ccc}\hfill {\chi }_c(k+1)& =& A_d\hspace{0.17em}{\chi }_c(k)+B_d\left(p\right)T(k)+B_{gd}\hspace{0.17em}g\hfill \\ \hfill y_c(k)& =& C_d\hspace{0.17em}{\chi }_c(k)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hfill \end{array}$$

(5)

The following matrices are introduced: $A_d$$\in {ℝ}^{6\times 6}$, $B_d\left(p\right)$$\in {ℝ}^{6\times 3}$, $B_{gd}$$\in {ℝ}^{6\times 3}$, $C_d$$\in {ℝ}^{3\times 6}$.

The embedding of the integrator is performed by defining the following difference variables:

$$\Delta {\chi }_c(k)={\chi }_c(k)-{\chi }_c(k-1)$$

(6)

$$\Delta T(k)=T(k)-T(k-1)$$

(7)

and the augmented state vector $\chi$$\in {ℝ}^9$:

$$\chi (k)=\left[\begin{array}{c}\Delta {\chi }_c(k)\\ y_c(k)\end{array}\right]$$

(8)

Coherently, the following augmented first-order model is formulated:

$$\{\begin{array}{c}\chi (k+1)=A\hspace{0.17em}\chi (k)+B\left(p\right)\hspace{0.17em}\Delta T(k)\\ \hspace{0.17em}y(k)=C\hspace{0.17em}\chi (k)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\end{array}$$

(9)

with $A$$\in {ℝ}^{9\times 9}$, $B\left(p\right)$$\in {ℝ}^{9\times 3}$, $C$$\in {ℝ}^{3\times 9}$ defined as follows:

$$\begin{array}{ccc}A=\left[\begin{array}{cc}{A}_d& 0_{6\times 3}\\ C_d{A}_d& I_3\end{array}\right]& B\left(p\right)=\left[\begin{array}{c}{B}_d\left(p\right)\\ C_d{B}_d\left(p\right)\end{array}\right]& C=\left[\begin{array}{cc}{0}_{3\times 6}& I_3\end{array}\right]\end{array}$$

(10)

3.3. Calculation of the Optimal Tensions

The computation of the optimal tensions exploits the prediction of the system output over the prediction horizon $N_p$$\in ℝ$. Because of the model nonlinearities, matrix $B_d\left(p\left(k_i\right)\right)$ is updated at each step ($k_i$) of the control loop, based on the pose of the end-effector. $B_d\left(p\left(k_i\right)\right)$ is held constant during all the calculations performed at time step $k_i$, and hence over the prediction horizon to predict the trajectory of the system output.

By assuming a vectorial representation, the predicted output $Y$$\in {ℝ}^{3N_p}$ is:

$$Y=Fx(k_i)+\Phi \left(p\left(k_i\right)\right)\Delta T_{N_c}$$

(11)

where $F$$\in {ℝ}^{3N_p\times 9}$ and $\Phi \left(p\left(k_i\right)\right)$$\in {ℝ}^{3N_p\times 3N_c}$ are defined as:

$$\begin{array}{cc}F=\left[\begin{array}{c}CA\\ C{A}^2\\ ⋮\\ C{A}^{N_p}\end{array}\right]& \Phi \left(p\left(k_i\right)\right)=\left[\begin{array}{cccc}CB\left(p\left(k_i\right)\right)& 0& \cdots & 0\\ CAB\left(p\left(k_i\right)\right)& CB\left(p\left(k_i\right)\right)& \cdots & 0\\ ⋮& ⋮& ⋮& ⋮\\ C{A}^{N_p-1}B\left(p\left(k_i\right)\right)& C{A}^{N_p-2}B\left(p\left(k_i\right)\right)& \cdots & C{A}^{N_p-N_c}B\left(p\left(k_i\right)\right)\end{array}\right]\end{array}$$

(12)

The optimal tensions, $\Delta T_{N_c}$$\in {ℝ}^{3N_c}$, required to track the desired path defined through reference $Y^{des}$$\in {ℝ}^{3N_p}$, are computed by solving the following performance index $J$$\in ℝ$:

$$J={(Y^{des}-Y)}^T{R}_Y(Y^{des}-Y)+\Delta T_{N_c}{}^T{R}_{\Delta T}\Delta T_{N_c}$$

(13)

$R_Y$$\in {ℝ}^{3N_p\times 3N_p}$ and $R_{\Delta T}$$\in {ℝ}^{3N_c\times 3N_c}$ are tuning parameters that should be chosen for trade-off between keeping the error small and, at the same time, the control effort as well. Indeed, low gains usually result in higher robustness and allow tackling unmodeled dynamics and the presence of delay sources (see e.g., [27]).

The reference in the prediction horizon, $Y^{des}$$\in {ℝ}^{3N_p}$, is written as follows:

$$Y^{des}={\left[\begin{array}{cccc}{I}_3& I_3& \cdots & I_3\end{array}\right]}^{T}r(k_i)=F^{des}r(k_i)\hspace{0.17em}\hspace{0.17em},$$

(14)

Matrix $F^{des}$$\in {ℝ}^{3N_p\times 3}$ maps the vector of reference trajectories $r(k_i)$$\in {ℝ}^3$ at each time sample $k_i$. The vector of the control tensions, $\Delta T_{N_c}$$\in {ℝ}^{3N_c}$, includes the future control actions in the control horizon lasting $N_c$$\in ℝ$ samples ($N_c$ is, in practice, the size of the optimal control input vector). Between all the entries of $\Delta T_{N_c}$, just the first three ones are accounted for, which are, in practice, the entries of $\Delta T(k_i)$. In contrast, the other ones are unused since they are the optimal control actions for the future steps, which will be reevaluated in the next time steps (again, through the constrained optimization problem). Starting from $\Delta T(k_i)$, the commanded tensions $T_i{}^{MPC}$ are, finally, computed.

Constraints on the magnitude of the cable tensions are embedded in the control synthesis through lower and upper bounds that represent the minimum and the maximum feasible cable tensions ($T_{\min }$ and $T_{\max }$, respectively): $T_{\min }\le T_i(k)\le T_{\max }$. $T_{\min }$ sets the positiveness tension constraint; $T_{\max }$ represents the maximum stress that cables can withstand to avoid cable failure, or the maximum torque that the motors can exert.

3.4. Calculation of Motor Torques

The optimal tensions $T_i{}^{MPC}$ are transformed into the motor torques $C_{m,i}$ that are commanded to the motor torque (current) inner loops. Since no measurement of the cable tensions is adopted, the inverse dynamic model of each actuator is exploited. By calculating the motor speed and acceleration references, ${\dot{\theta }}_i{}^{ref}(t)$ and ${\ddot{\theta }}_i{}^{ref}(t)$, by means of the inverse kinematics of the reference load trajectory, the $ith$ electric motor is required to exert the following torque $C_{m,i}$:

$$C_{m,i}=J_i{\ddot{\theta }}_i{}^{ref}(t)+r_i{T}_i{}^{MPC}(t)\hspace{0.17em}\hspace{0.17em}+f_{v,i}{\dot{\theta }}_i{}^{ref}(t)+C_i{}^{friction}(t)$$

(15)

$J_i$ is the motor moment of inertia, which comprises the contributions of the rotor and of the drum (with radius $r_i$); $f_{v,i}$ is the viscous friction coefficient, which includes the rotor friction and the reflected contributions of the drum and the pulleys. Finally, other friction terms, such as Coulomb friction, are accounted for by means of $C_i{}^{friction}(t)$.

4. Numerical Results

4.1. Description of the Test Case

The features of the studied CSPR, as well as of the controller, are listed in

Table 1. Parameters of the CSPR and of the controller.

Parameter	Value
$J_{m,1},J_{m,2},J_{m,3}$	$2.6\times {10}^{-5} {\mathrm{kgm}}^2$
$f_{v,1},f_{v,2},f_{v,3}$	$3\times {10}^{-5} \mathrm{Nms}/\mathrm{rad}$
$r_1,r_2,r_3$	$0.036 \mathrm{m}$
$m$	$2.94 \mathrm{kg}$
$T_{\min }; T_{\max }$	$5; 200 \mathrm{N}$
$T_s$	$2\times {10}^{-3} \mathrm{s}$
$N_c; N_p$	$1; 90$
$R_Y; R_{\Delta T}$	$I_{240}; 1\times {10}^{-3} I_3$
$A_1$	${\left[\begin{array}{ccc}-0.89& 0.85& 0\end{array}\right]}^T$
$A_2$	${\left[\begin{array}{ccc}0.89& 0.85& 0\end{array}\right]}^T$
$A_3$	${\left[\begin{array}{ccc}0& -0.85& 0\end{array}\right]}^T$

. Four references have been numerically tested to highlight different features of the proposed control schemes, by developing a multibody simulator in Matlab-Simulink. All the tests have been performed with the same tuning of the controller parameters, to provide a fair validation of the method and to show that the same tuning is suitable for both sharp and smooth motion profiles.

A lower bound of tensions equal to $5\hspace{0.17em}\hspace{0.17em}\mathrm{N}$ has been assumed to impose the cables to always have strictly positive tensions. An upper bound equal to $200\hspace{0.17em}\hspace{0.17em}\mathrm{N}$ has been set to avoid cable failure, by assuming that such a limit is consistent with the motor operating range.

4.2. Test Cases

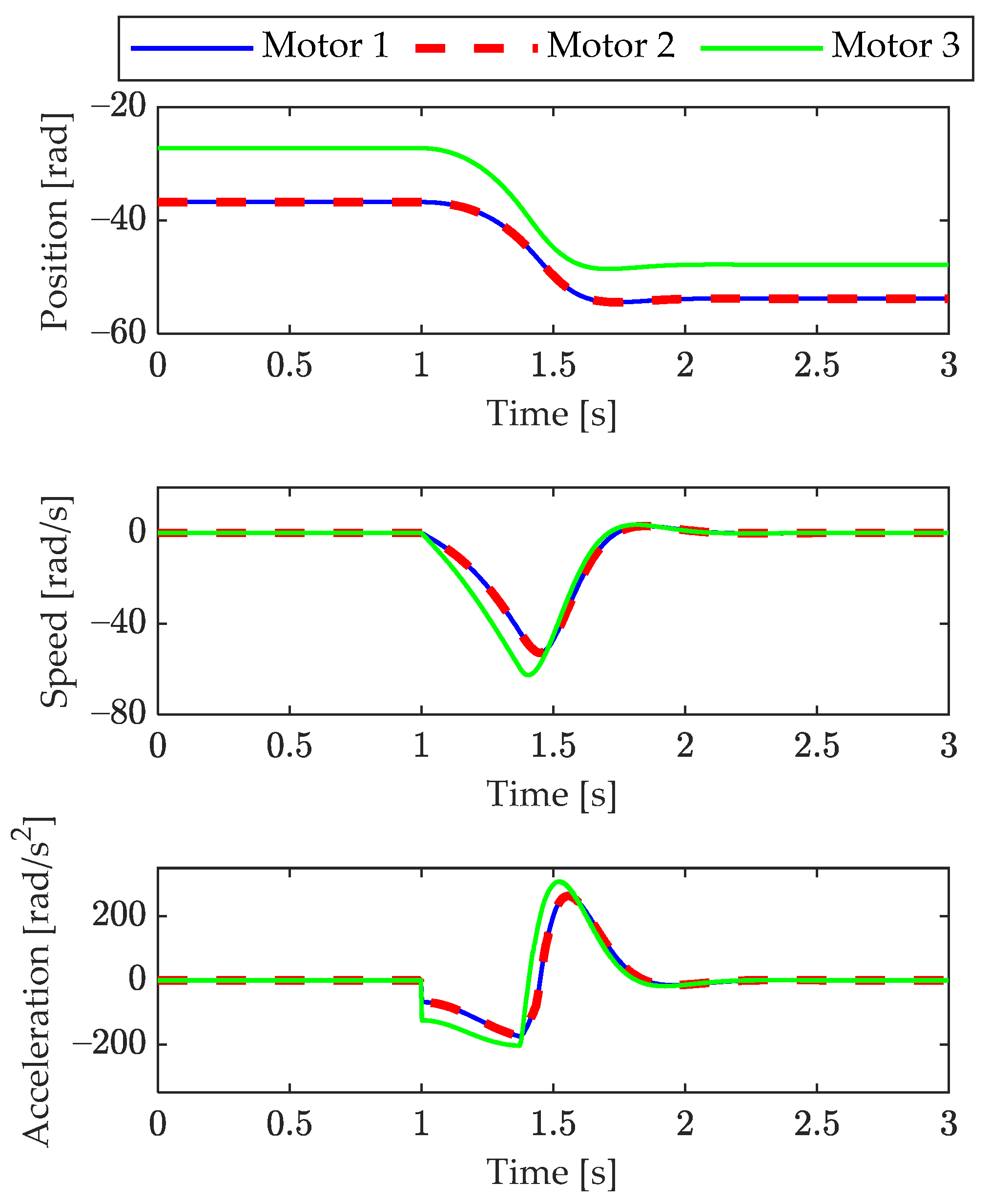
4.2.1. Test 1: Point-to-Point Motion through a Position Step Reference

The first test consists of a descending position step reference (no displacements are required in the x-axis and in the y-axis). This reference is not feasible since it imposes negative infinite speeds and accelerations. For this reason, it is well-known that step references are never used in motion planning of mechatronic systems [28,29,30]. The problem is exacerbated in CSPR since sharp changes of the position references along the z-axis would cause negative tensions, thus leading to slack cables. The inclusion of bounds on the allowable tensions in the control design allows quick reference tracking, as fast as possible, while ensuring that all the cable tensions fulfill the bounds. This aspect is shown in Figure 2 through the time history of the z-axis response and through the cable tensions shown in Figure 3. Figure 2 shows that the controller allows for quick tracking of the reference signal, with a rise time (from $10\%$ to $90\%$ of the final values) equal to $0.35\hspace{0.17em}\hspace{0.17em}\mathrm{s}$, and with a $2\%$ settling time equal to $0.81\hspace{0.17em}\hspace{0.17em}\mathrm{s}$. A small overshoot is obtained by exceeding the steady state value of just $1.95\%$. As for the tensions, it is evident that tracking this reference would require infinite negative values. Thanks to the embedding of the bounds on the feasible input calculation, the commanded ones reach the lower bound of $5\hspace{0.17em}\hspace{0.17em}\mathrm{N}$ and hold them for about $0.4\hspace{0.17em}\hspace{0.17em}\mathrm{s}$. Subsequently, tensions rise to avoid relevant overshoot, without exceeding the upper bound (which could be related both to the cable’s strength and to the motor feasible torques). The embedding of the constraints in the controller design, i.e., the formulation of a constrained optimization problem over the prediction horizon, prevents dangerous overshoots that are often exacerbated by integral windup phenomena.

The temporal evolution of cable tensions reported in Figure 3 can be better understood by looking at the time histories of the motors, whose positions, speeds, and accelerations are displayed in Figure 4: a sharp, although continuous, change of accelerations is obtained at the beginning of the motion up to reaching the tension lower bound. Once the $5\hspace{0.17em}\hspace{0.17em}\mathrm{N}$ tensions are obtained, a smoother motion of the motors is performed to allow for a rapid settling of the end-effector.

The torques exerted by the motors are finally shown in Figure 5: the presence of an upper bound on the feasible tensions allows one to represent upper bounds on the feasible motor torque, and hence to ensure feasibility, also accounting for the features of the motors.

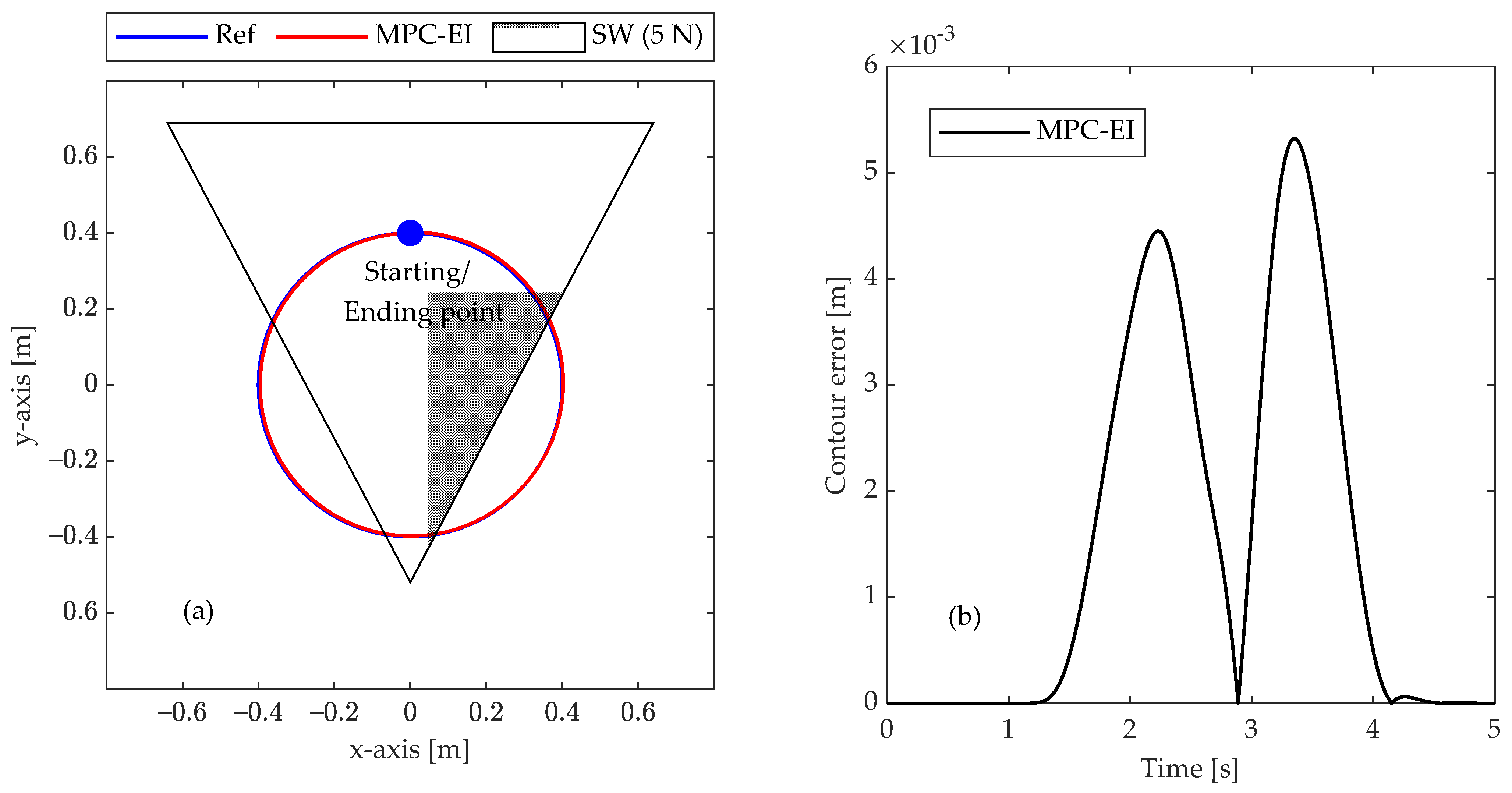
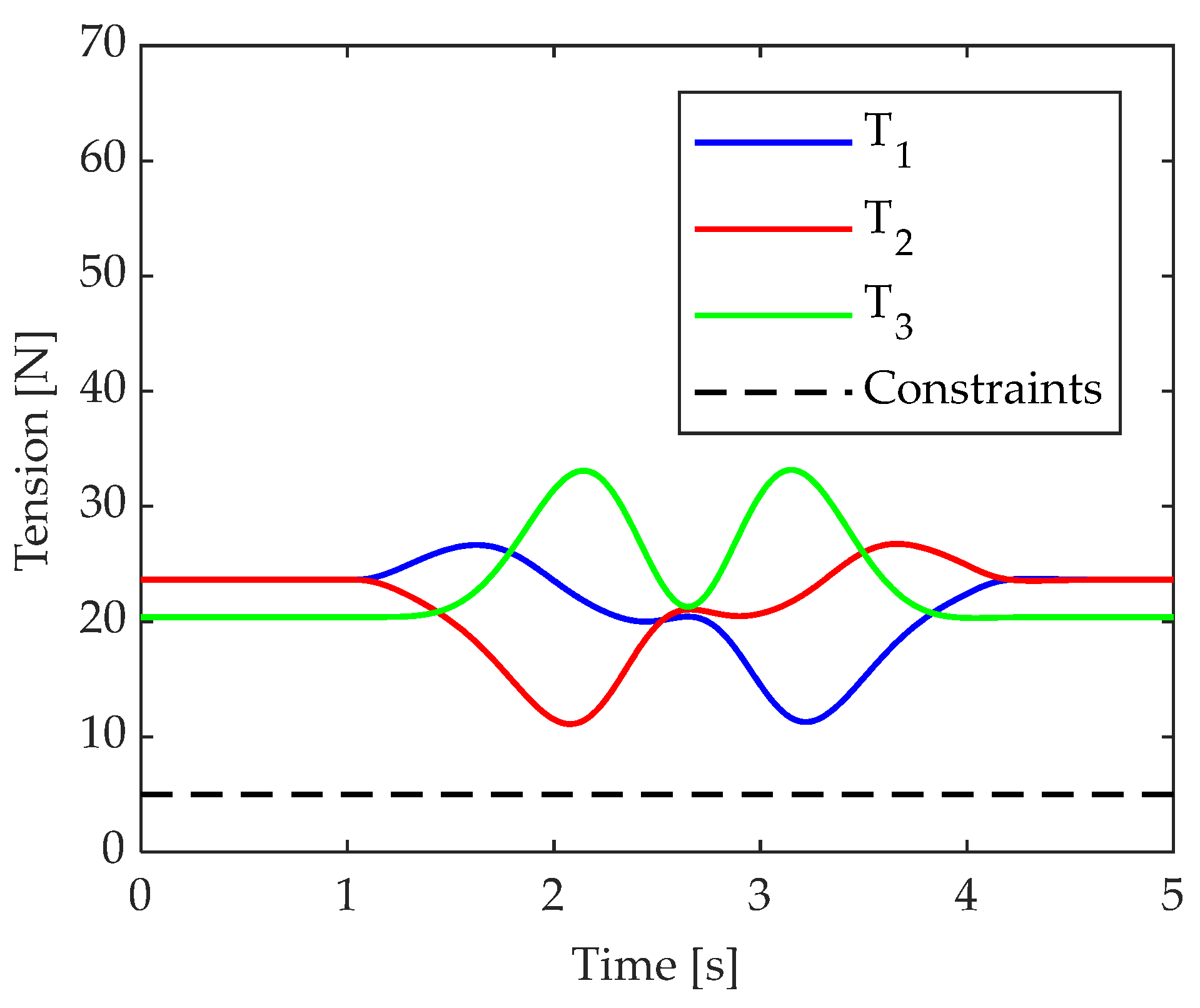
4.2.2. Test 2: Circular Path

The second path is a circular planar reference path, whose radius is $0.4\hspace{0.17em}\hspace{0.17em}\mathrm{m}$, with a motion time of $5\hspace{0.17em}\hspace{0.17em}\mathrm{s}$. A 5th-degree polynomial timing law has been assumed. This test has been chosen since it is a quite common path in the literature. However, it is worth noticing that it goes outside the static workspace (denoted SW in Figure 6) of the studied CSPR; in contrast, it belongs to the dynamic workspace (in the presence of the commanded accelerations).

The path tracking capability is corroborated through Figure 6, which shows the spatial response and the related contour error. Figure 6a clearly shows that reference and actual paths are almost overlapped. A closer look through the analysis of the contour error is shown in Figure 6b. The contour error is defined as the actual difference between the reference spatial path and the actual one, and therefore it is a reliable evaluation of the capability of a controlled system to execute a path. Additionally, it summarizes the error in all the motion directions. Figure 6b corroborates that the proposed control architecture provides very close tracking of the circular path, with a maximum contour of $5.3\times {10}^{-3}\hspace{0.17em}\mathrm{m}$ (i.e., $1.3\%$ of the radius), while the root mean square (RMS) value is $2.3\times {10}^{-3}\hspace{0.17em}\mathrm{m}$ (i.e., $0.57\%$ of the radius).

The optimal cable tensions are finally represented in Figure 7: since this path belongs to the dynamic workspace, although no computation of such a domain is required by the proposed control technique, no tension saturation is obtained.

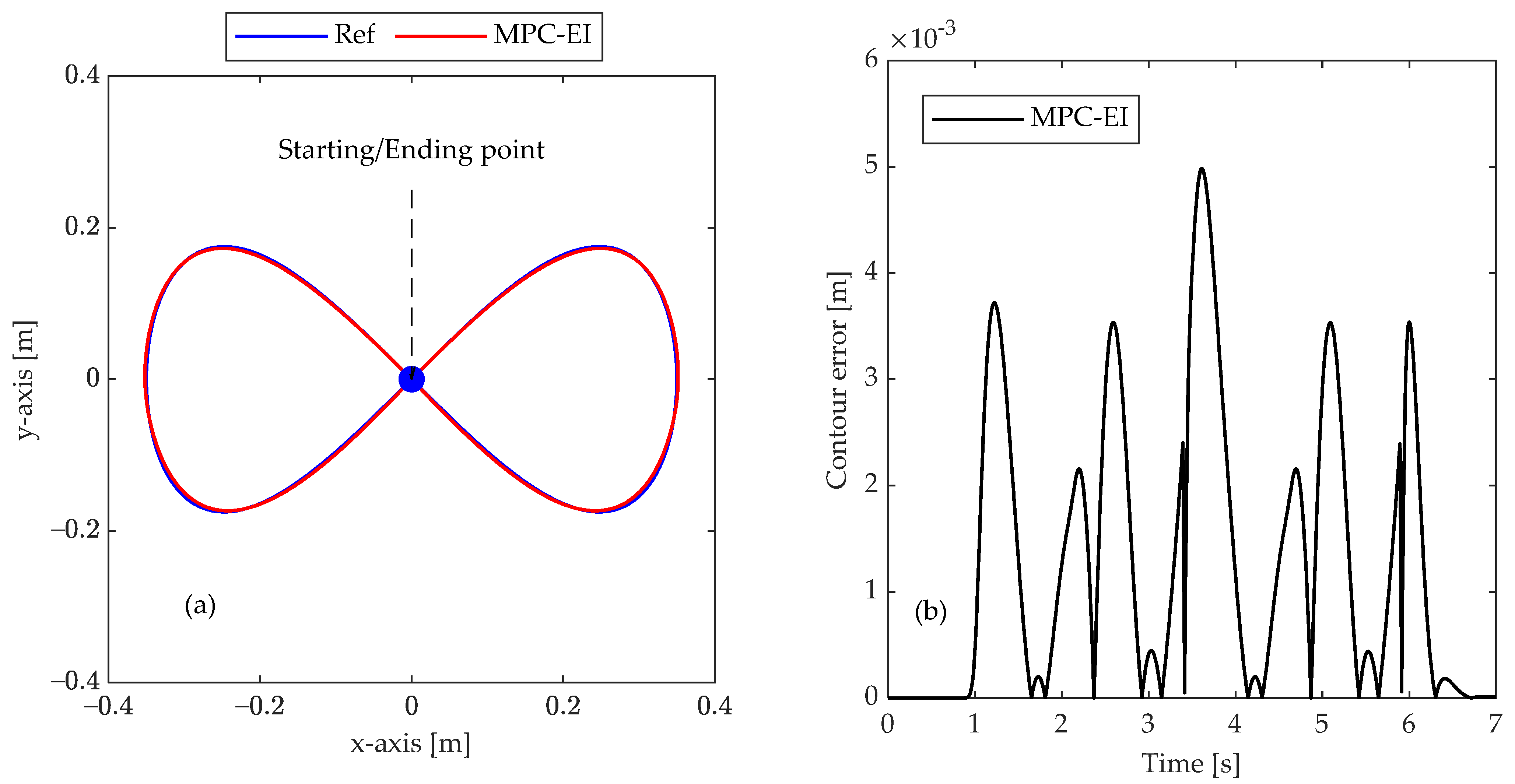
4.2.3. Test 3: Gerono’s Lemniscate Path

The third path is a planar Gerono’s lemniscate, which resembles an “8” shape. The path belongs to the horizontal plane with $z=-0.5\hspace{0.17em}\hspace{0.17em}\mathrm{m}$, and it is defined through the following equation:

$$x{\left(t\right)}^4=\alpha \left(x{\left(t\right)}^2-y{\left(t\right)}^2\right)$$

(16)

with $\alpha =0.35\hspace{0.17em}\hspace{0.17em}\mathrm{m}$ defining the size of the entire path, which spans the following intervals:

$$\begin{array}{c}\hspace{0.17em}\hspace{0.17em}\Delta x=2\alpha \\ \Delta y=\alpha \end{array}$$

(17)

A motion time of $5\hspace{0.17em}\hspace{0.17em}\mathrm{s}$ is chosen to test the closed-loop system under fast dynamics conditions; additionally, two rest time intervals of $1\hspace{0.17em}\hspace{0.17em}\mathrm{s}$ are included both at the beginning and at the end of the test.

This path has been chosen since it goes beyond the dynamic workspace, i.e., some parts cannot be executed without exceeding the lower bound, thus making a severe test case for the proposed control architecture. Despite this limitation, accurate path tracking is obtained, as corroborated by Figure 8. Path tracking is shown in Figure 8a, where the reference and the actual paths are almost overlapped. The analysis of the contour error in Figure 8b reveals that the maximum error is $5\times {10}^{-3}\hspace{0.17em}\mathrm{m}$ (i.e., $1.4\%$ of $\Delta y$ and $0.7\%$ of $\Delta x$). A remarkably smaller average error is obtained, as corroborated by the RMS value equal to $1.8\times {10}^{-3}\hspace{0.17em}\mathrm{m}$ (i.e., $0.5\%$ of $\Delta y$ and $0.7\%$ of $\Delta x$).

The optimal cable tensions are, finally, represented in Figure 9: the commanded tensions reach the lower bound twice. However, due to the inclusion of the constraints in the computation of the optimal tension, no relevant error increases occur.

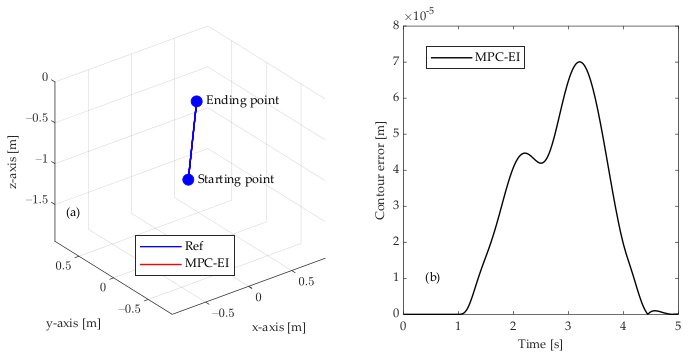
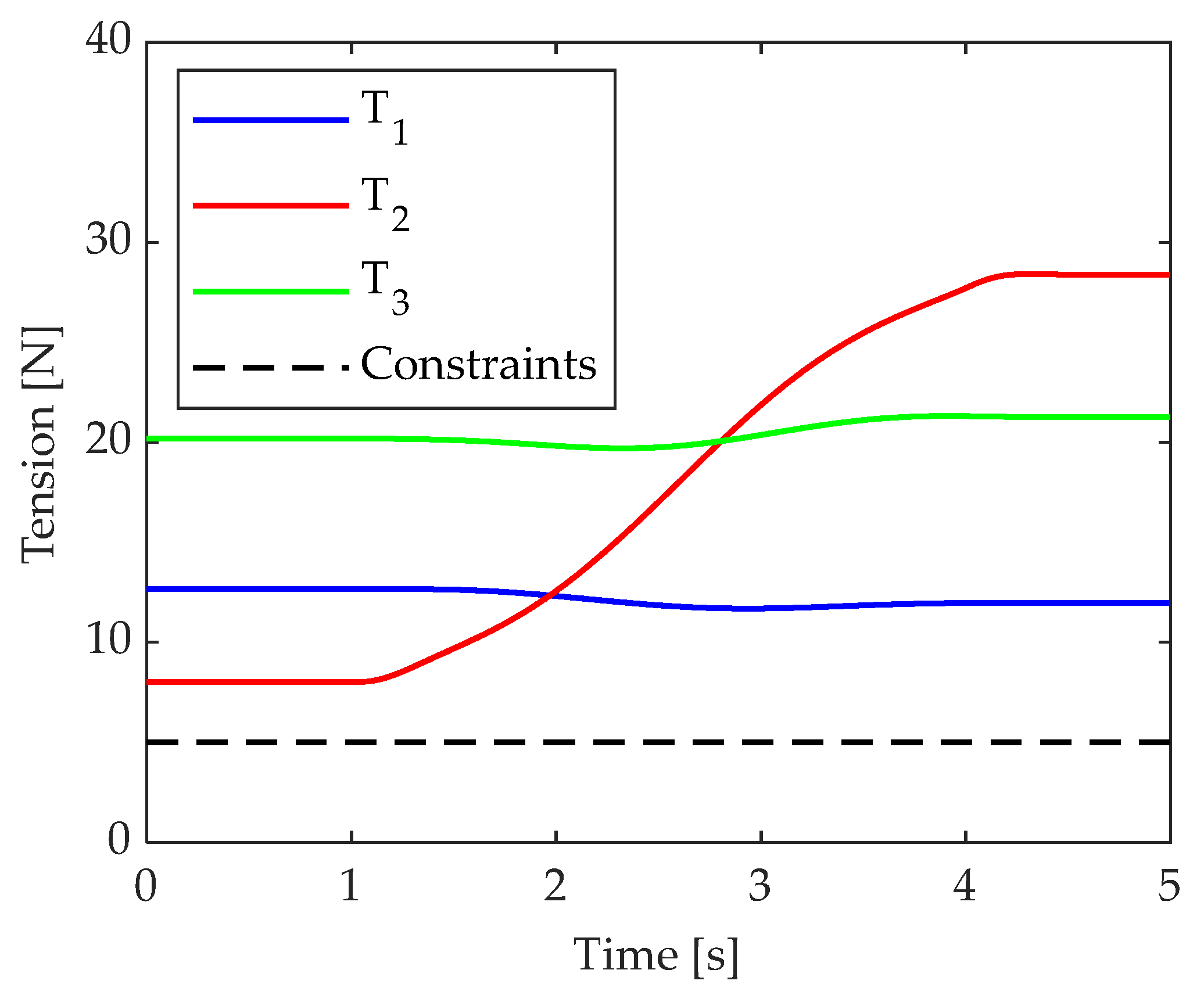
4.2.4. Test 4: Straight Line

The final test is aimed at showing the tracking capability of the proposed controller in the presence of a reference described by a straight line in space, to be executed through a 5th-degree polynomial motion law. The coordinates of the starting point are ${\left[\begin{array}{ccc}-0.1& -0.1& -1\end{array}\right]}^T$ while the ones related to the ending point are ${\left[\begin{array}{ccc}0.4& 0.4& -0.5\end{array}\right]}^T$, thus leading to a $0.866\hspace{0.17em}\hspace{0.17em}\mathrm{m}$ length. The motion time is $3\hspace{0.17em}\hspace{0.17em}\mathrm{s}$; two rest intervals lasting $1\hspace{0.17em}\hspace{0.17em}\mathrm{s}$ are also included at the beginning and after the end, for evaluating the steady state controller response.

The spatial path tracking response is depicted in Figure 10a, which also evaluates contour error in Figure 10b. Once again, reference and actual paths are almost overlapped, with no visible errors; a fair evaluation of the results can be achieved through the analysis of the contour error, which also summarizes the error in all the motion directions. The peak value of the contour error is $7.0\times {10}^{-5}\hspace{0.17em}\mathrm{m}$ (i.e., $0.008\%$ of the path length), which is achieved during the deceleration phase. The RMS value is just $3.4\times {10}^{-5}\hspace{0.17em}\mathrm{m}$ (i.e., $0.004\%$ of the path length).

Finally, the cable tensions commanded by the MPC are shown in Figure 11: no saturation is achieved in this case since this path belongs to the feasible dynamic workspace.

5. Conclusions

This paper proposes the preliminary results on a control scheme for precise path tracking in a spatial CSPR with three degrees of freedom (i.e., with a point-mass as end-effector), driven by three independent cables. Although this is a fully actuated configuration, in the field of cable robots it is more widespread to use redundant configurations to simplify motion planning and control and to dispense with the fact that cables can pull, but not push, the load.

First, a constrained, pose-dependent model predictive control (MPC) with embedded integrator (EI) is exploited to calculate the optimal positive cable tensions to be exerted to ensure precise tracking of the spatial path. The embedding of integrator is exploited to accurately track the path, both in transient and in steady-state conditions. Then, the inverse dynamic model of each motor is adopted to transform these tensions into commanded torques through algebraic calculations. The controller just relies on the measurement exhibited by the encoders of the motor, thus simplifying its hardware implementation.

Four numerical test cases are proposed to show the features and the benefits of the proposed control architecture. The analysis of the contour errors clearly reveals that the developed controller provides high accuracy even in the case of fast trajectories, while fulfilling the boundaries on the feasible cable tensions.

The method has been proposed here through a simple architecture. However, it can be extended to other architecture of CDPRs by proper modification of the underlying dynamic models in Equations (1) and (15).

Due to the simple formulation and thanks to the concept of splitting the system into two subsystems for calculating the optimal tensions and then the optimal torques, a reduced computational effort is required, thus simplifying the real-time implementation.