The Effect of Fit Clearance between Outer Race and Housing on Vibration Characteristics of a Cylindrical Roller Bearing with Localized Defects
Abstract
:1. Introduction
2. Model of a Defective Cylindrical Roller Bearing with Fit Clearance between Outer Race and Housing
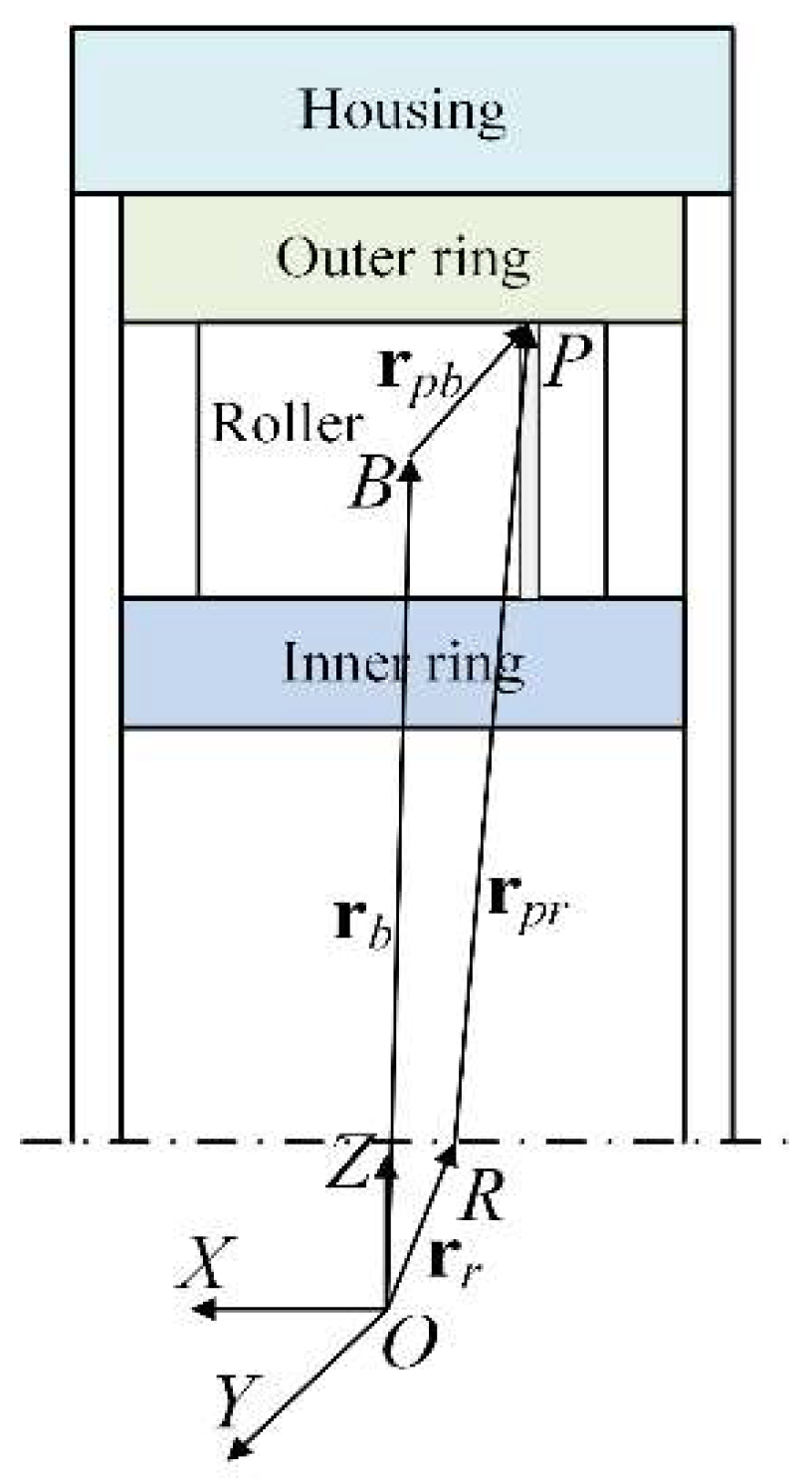
2.1. Interaction between a Roller and Rings
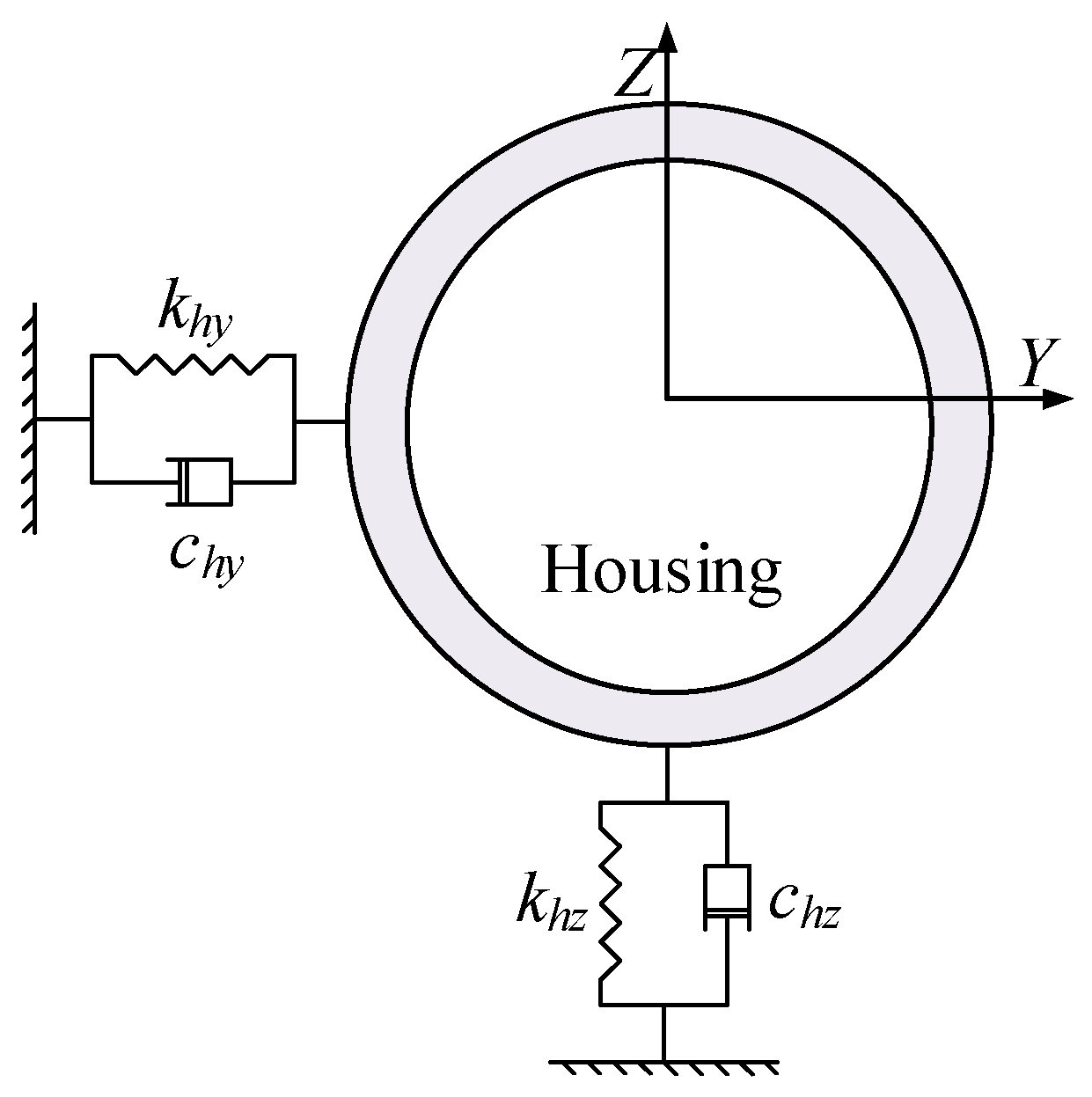
2.2. Interaction between Outer Ring and Housing
2.3. The Model for Localized Defects in the Bearing
2.4. Bearing System Equations
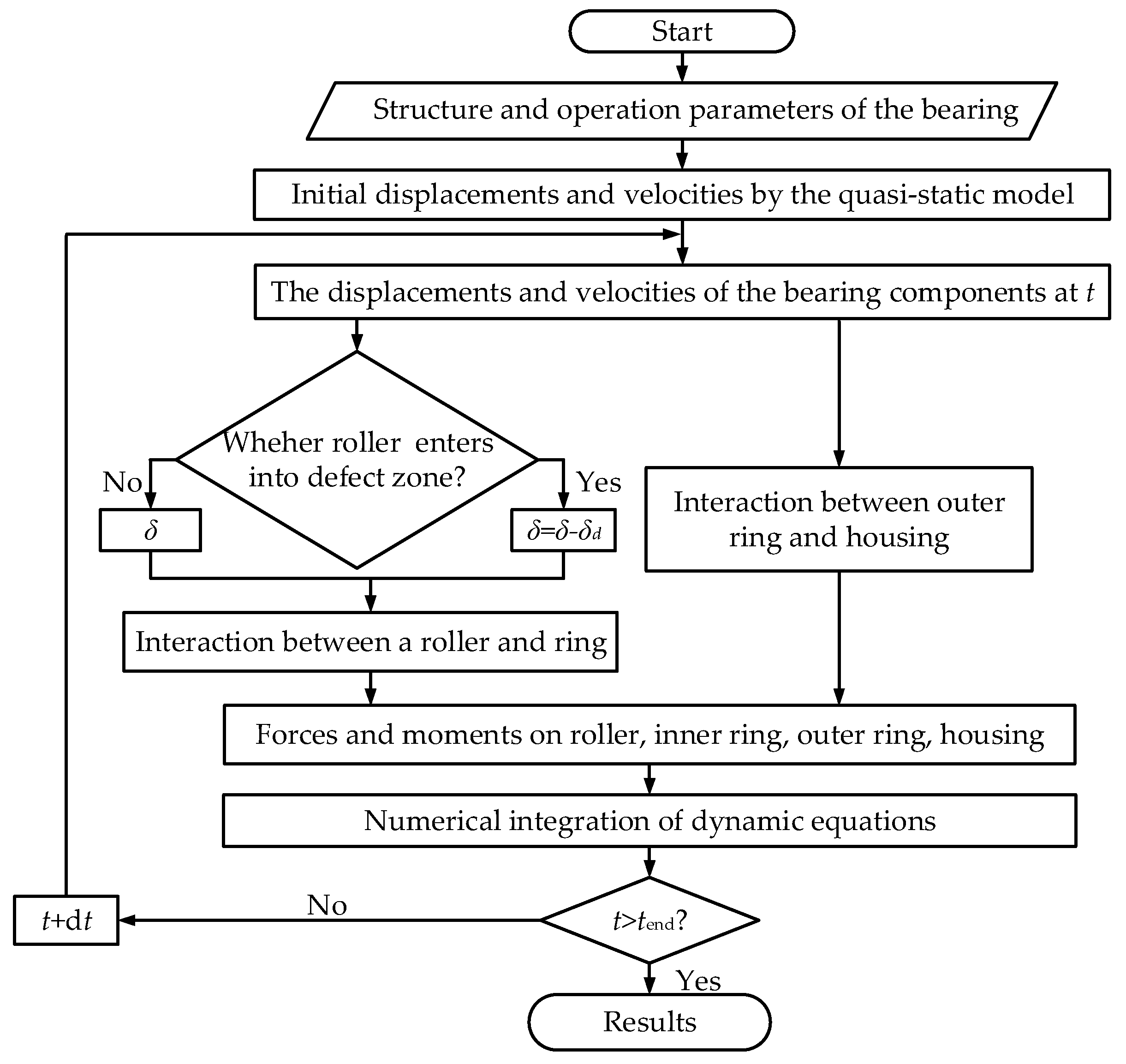
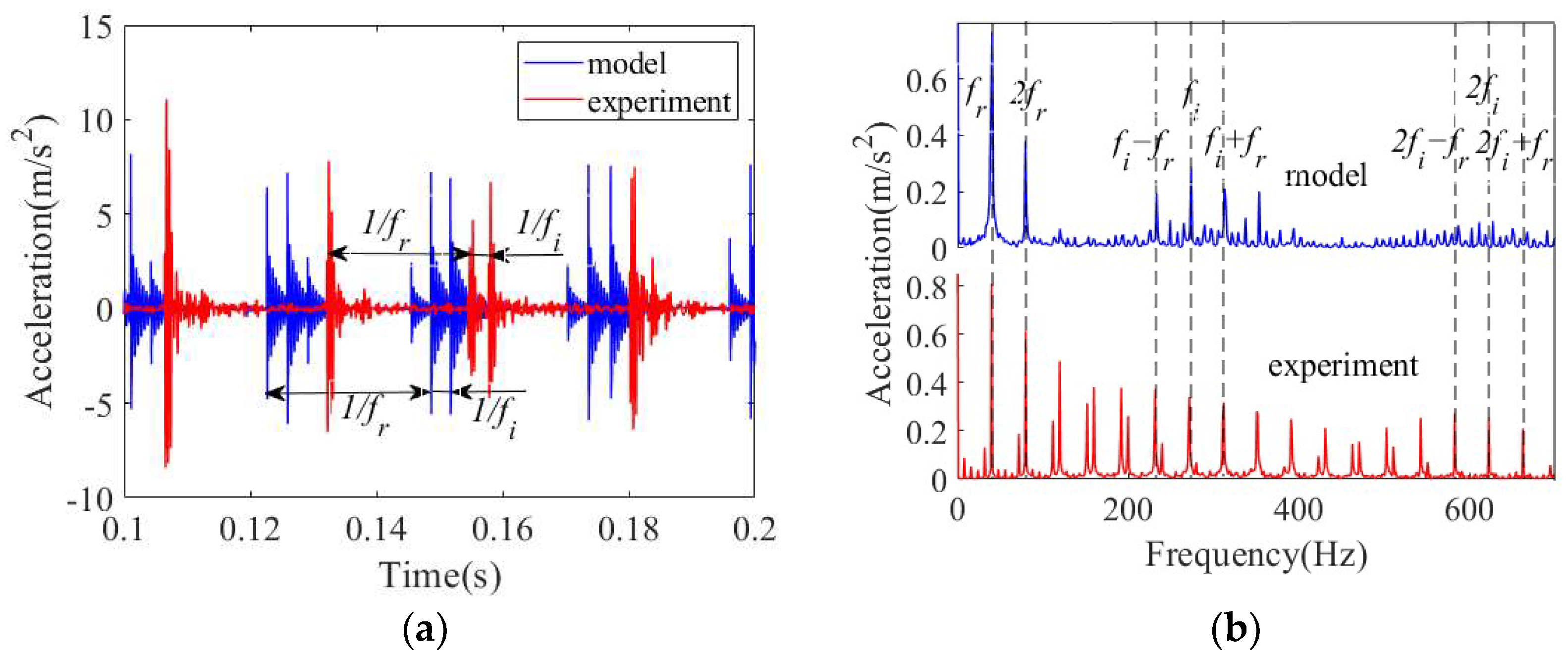
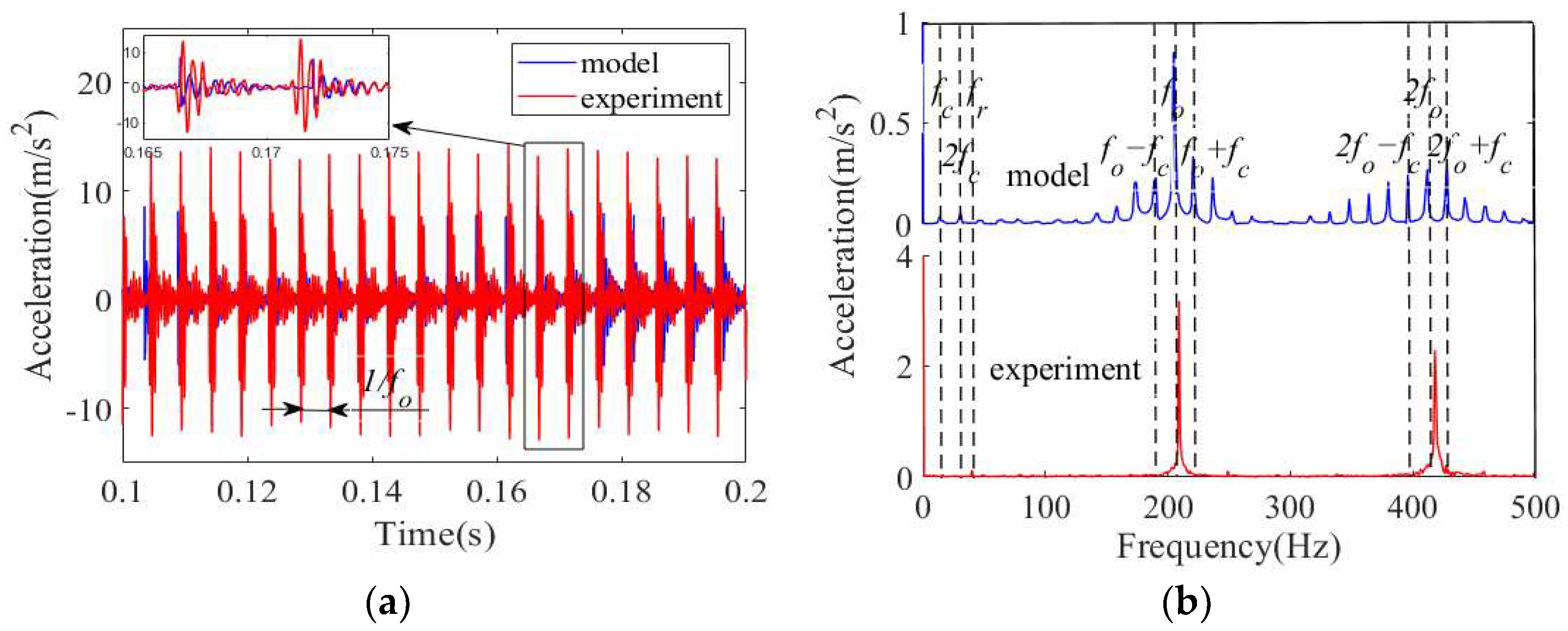
3. Results
4. Discussion
4.1. Vibration Characteristics of a Cylindrical Roller Bearing with Fit Clearance and Inner Ring Defect
4.1.1. Effect of Housing Stiffness
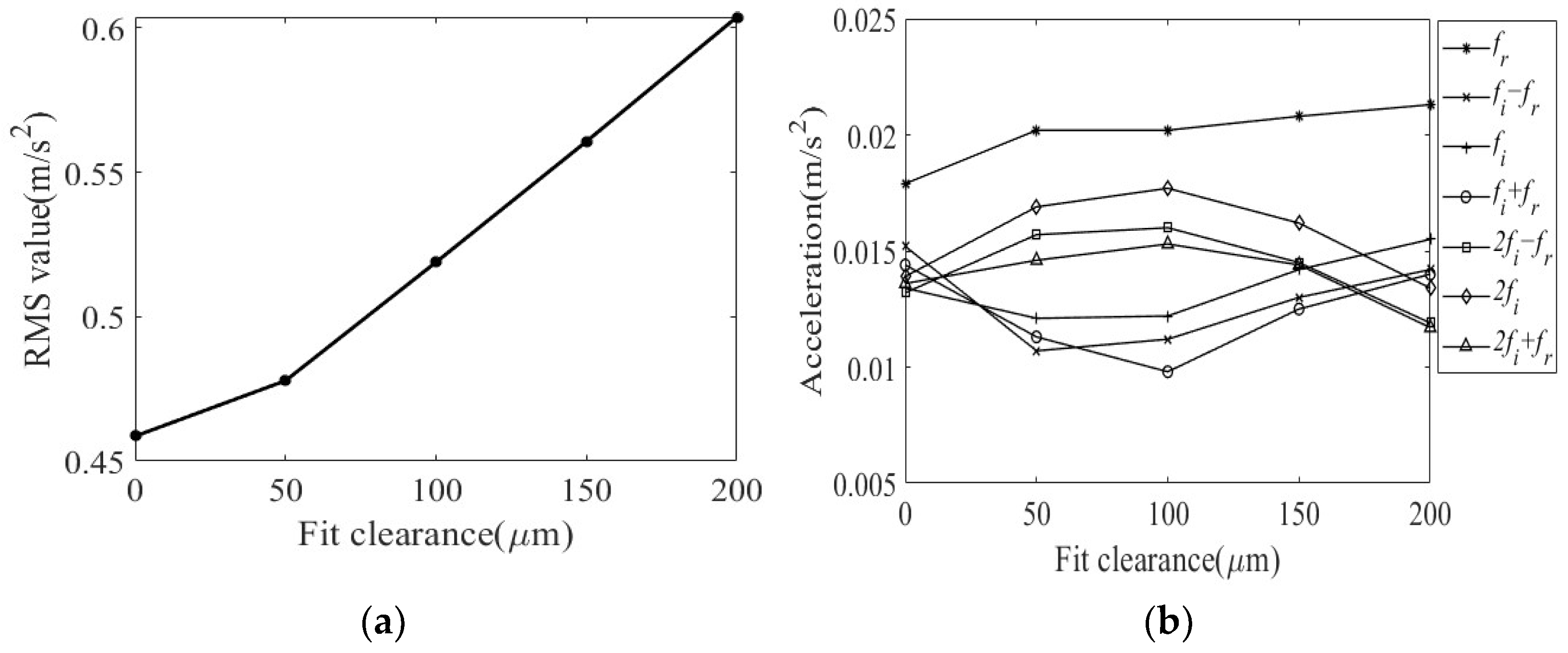
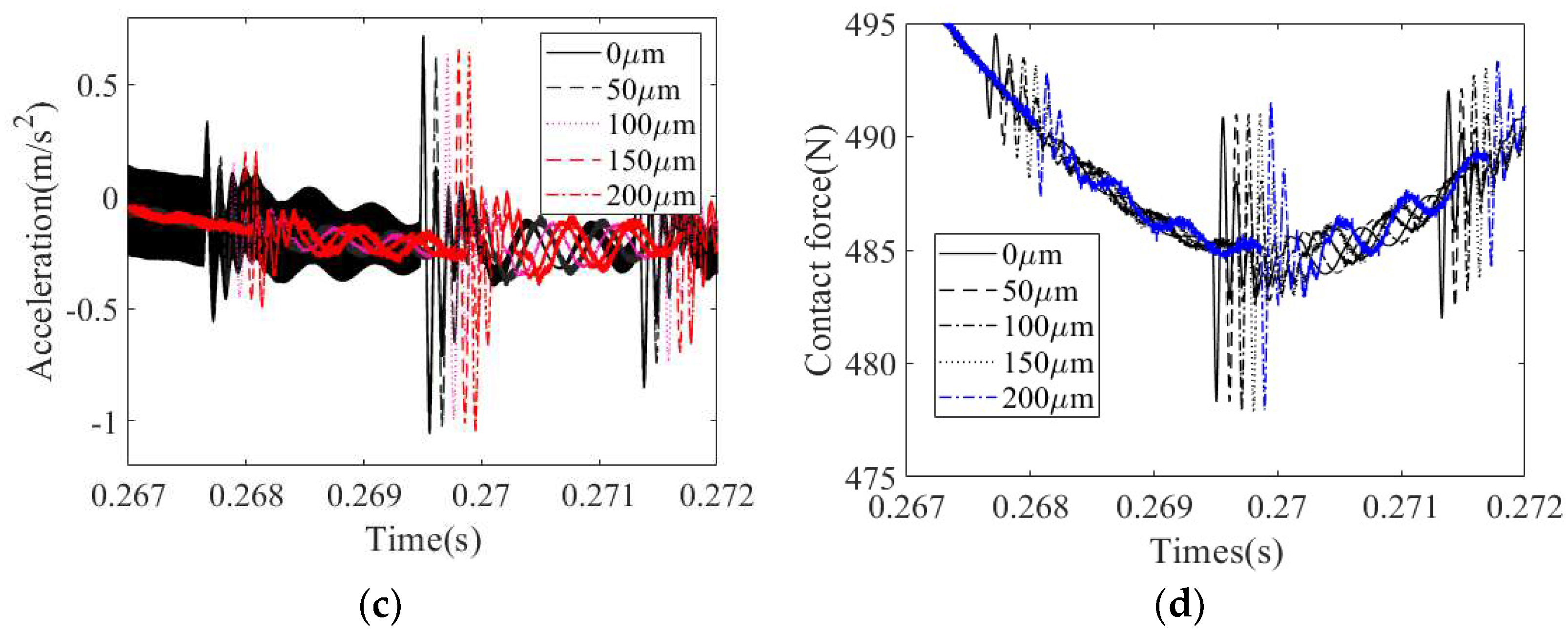
4.1.2. Effect of Fit Clearance
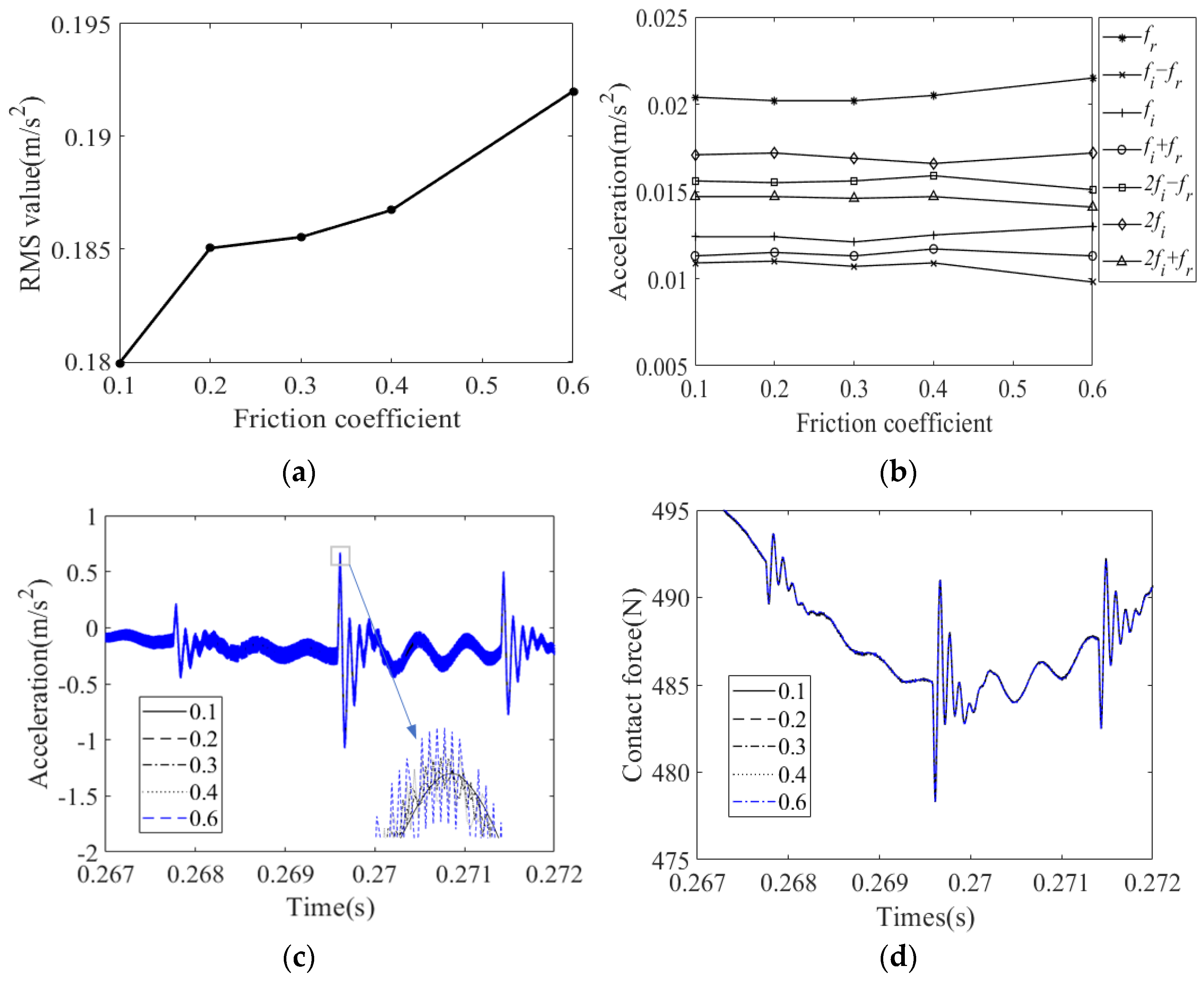
4.1.3. Effect of Friction Coefficient
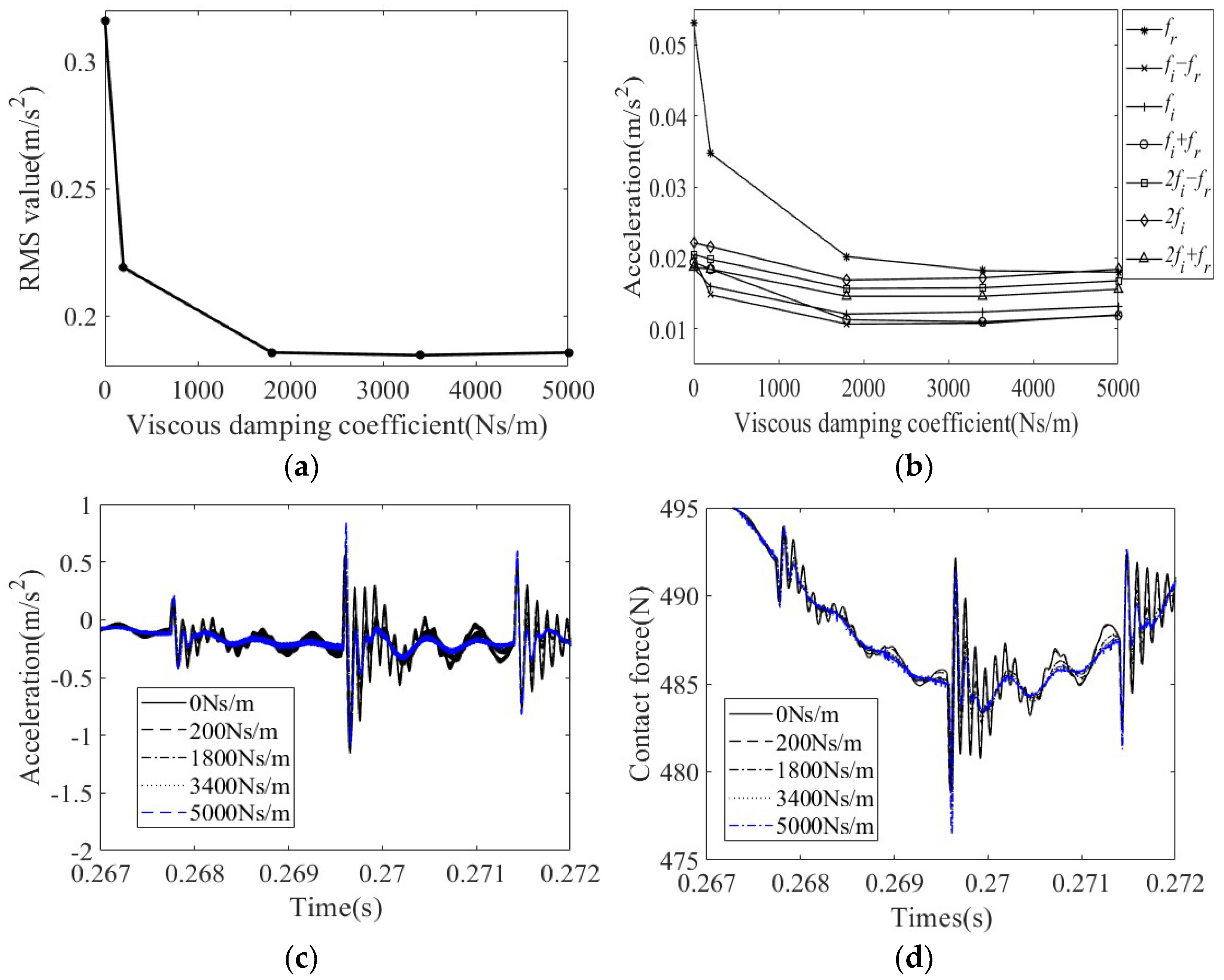
4.1.4. Effect of Viscous Damping
4.1.5. Effect of Phase Difference
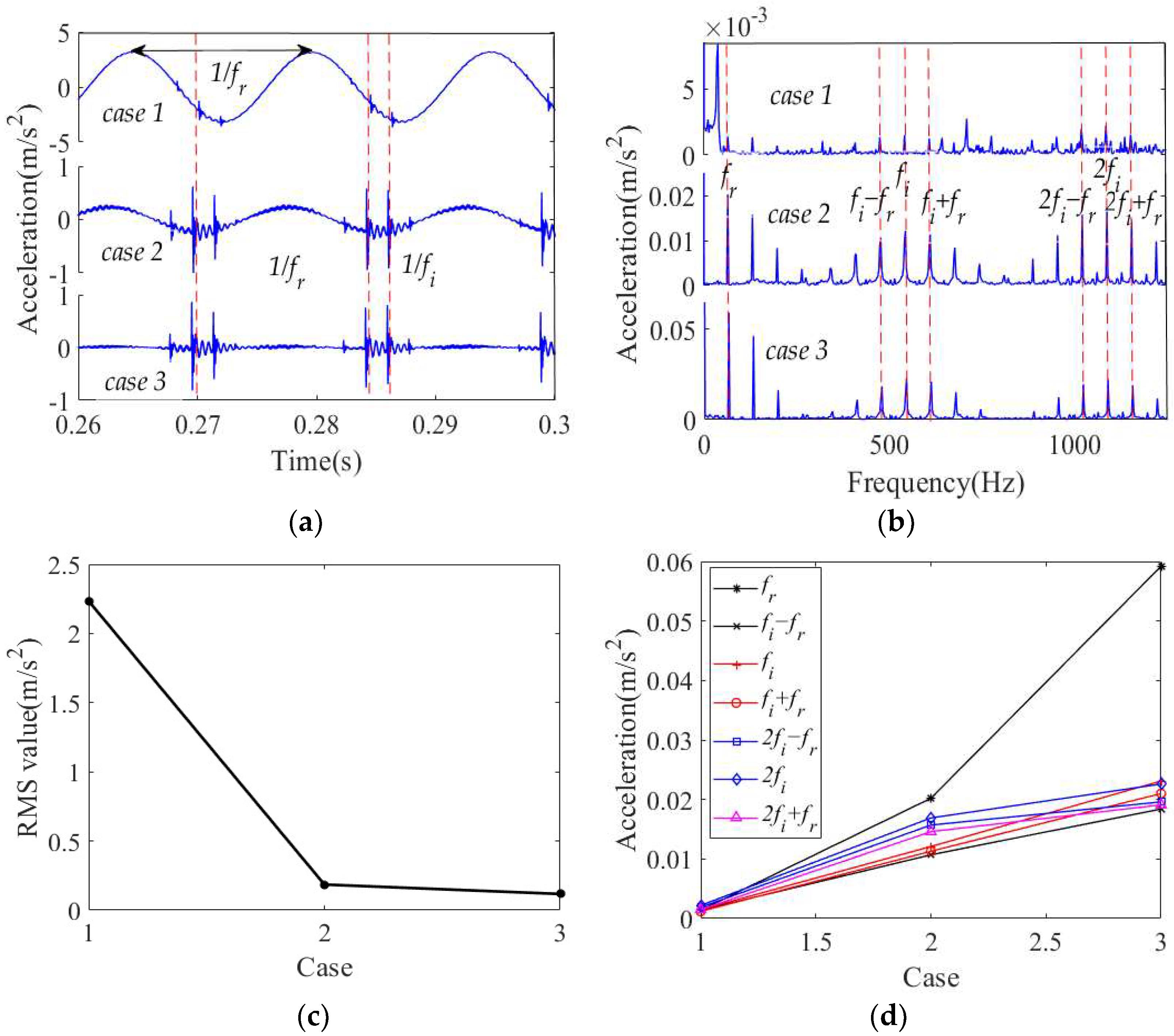
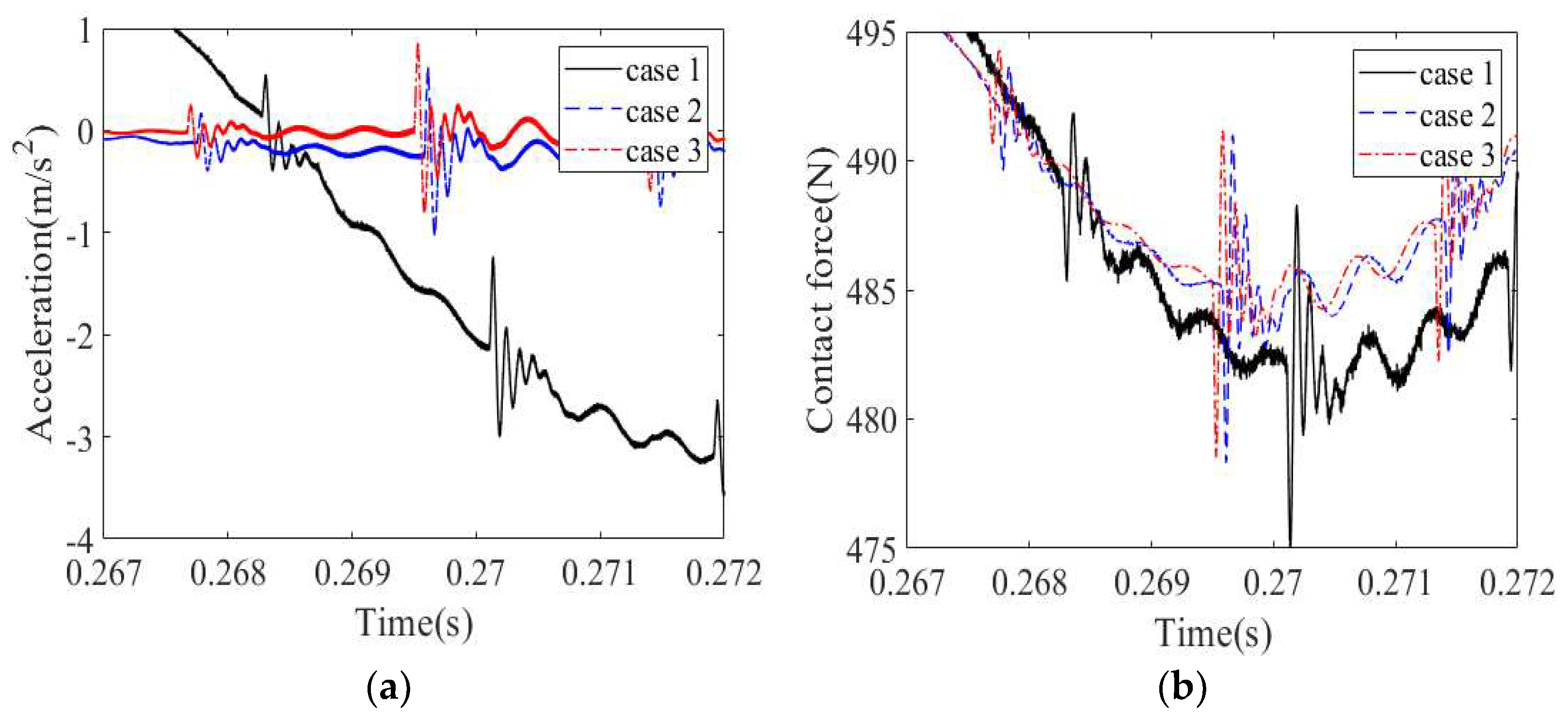
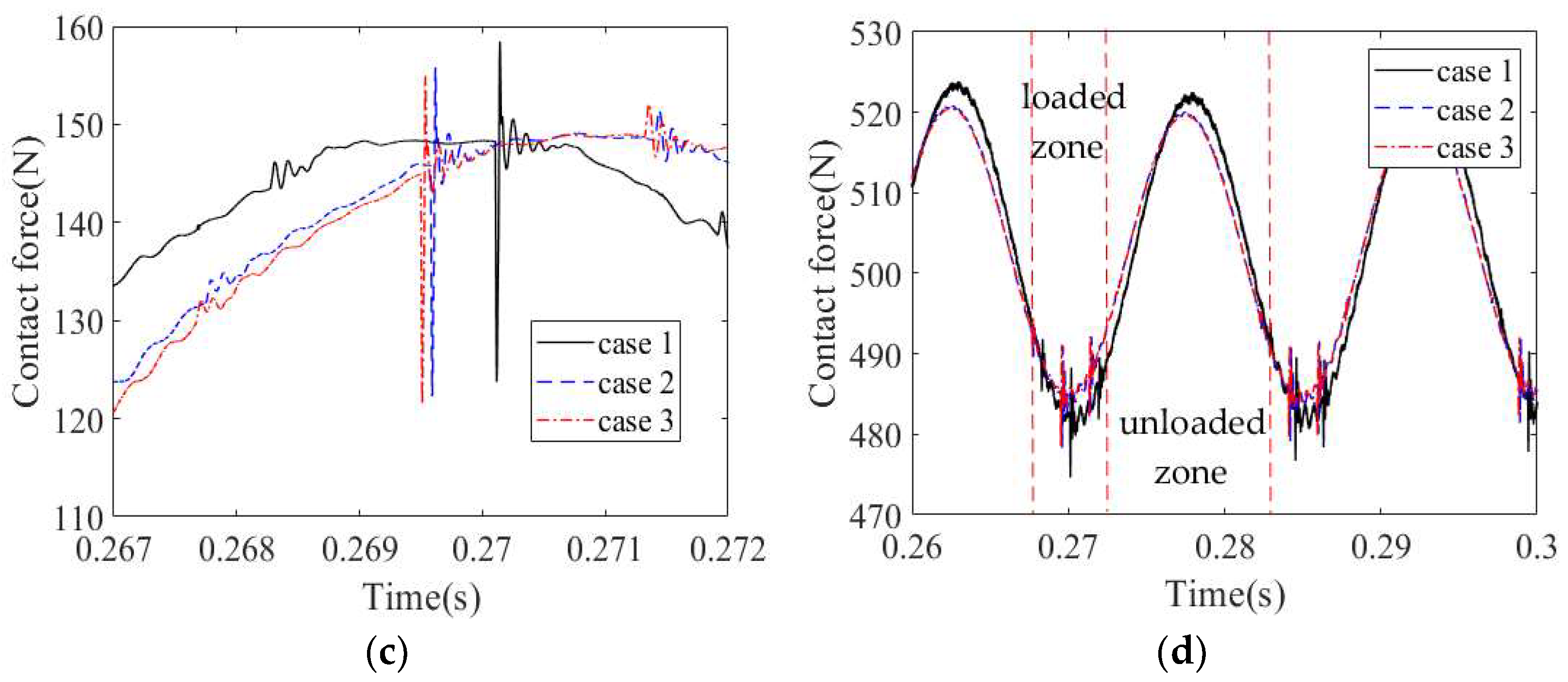
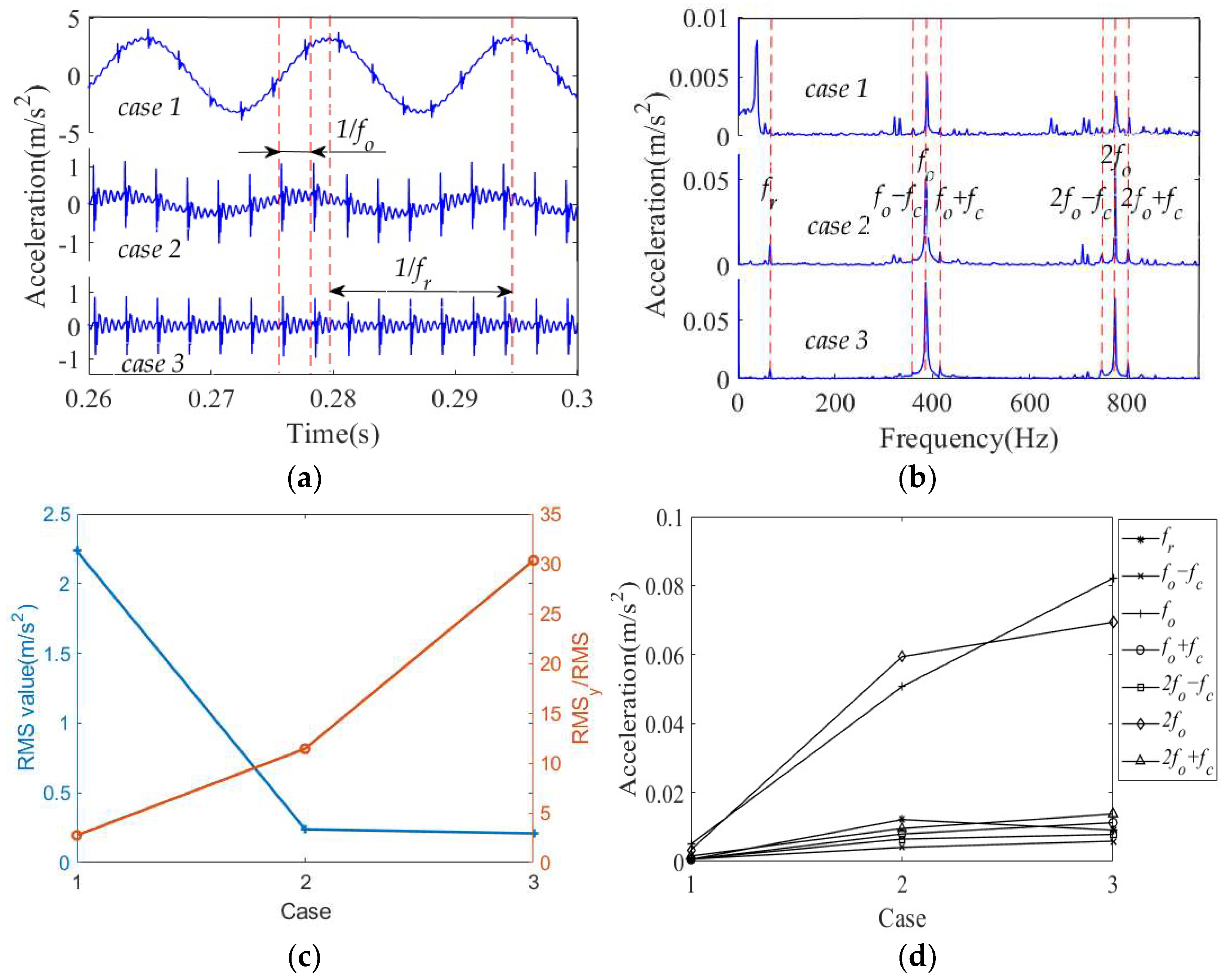
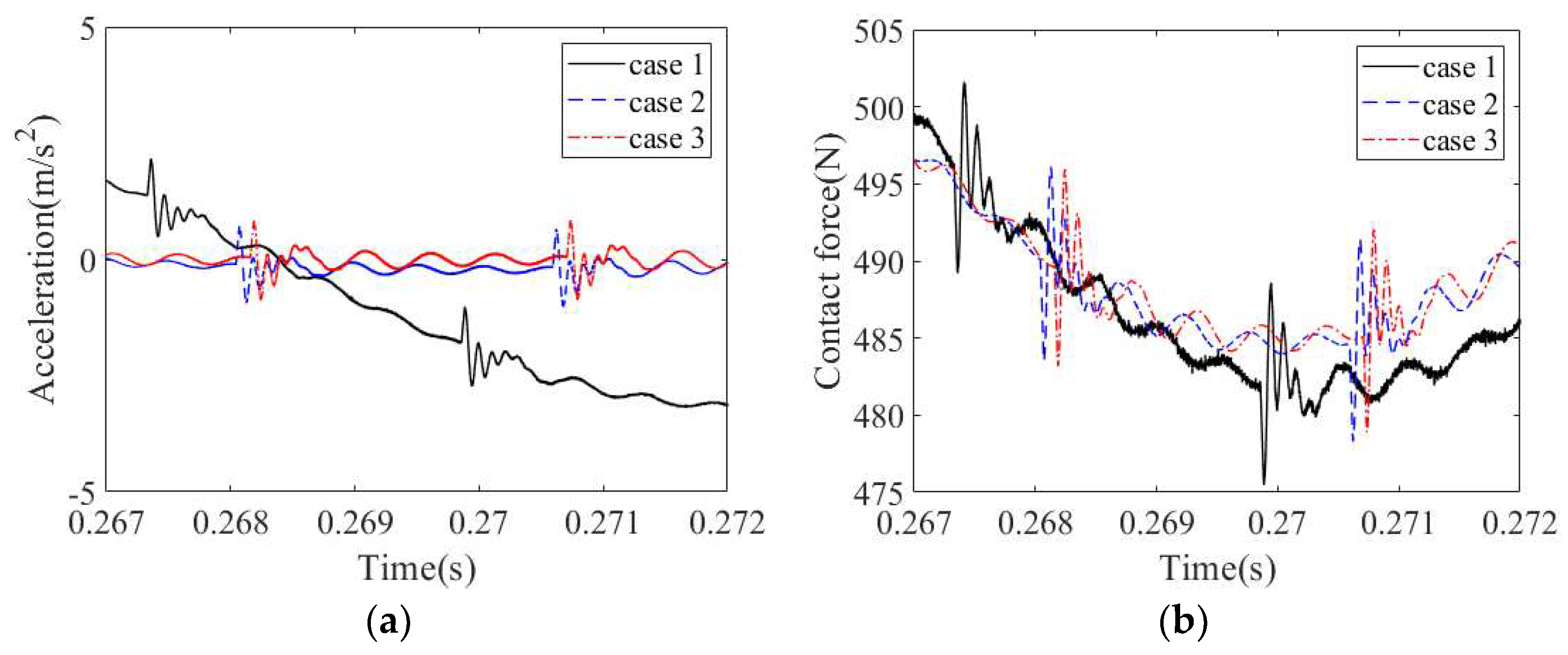
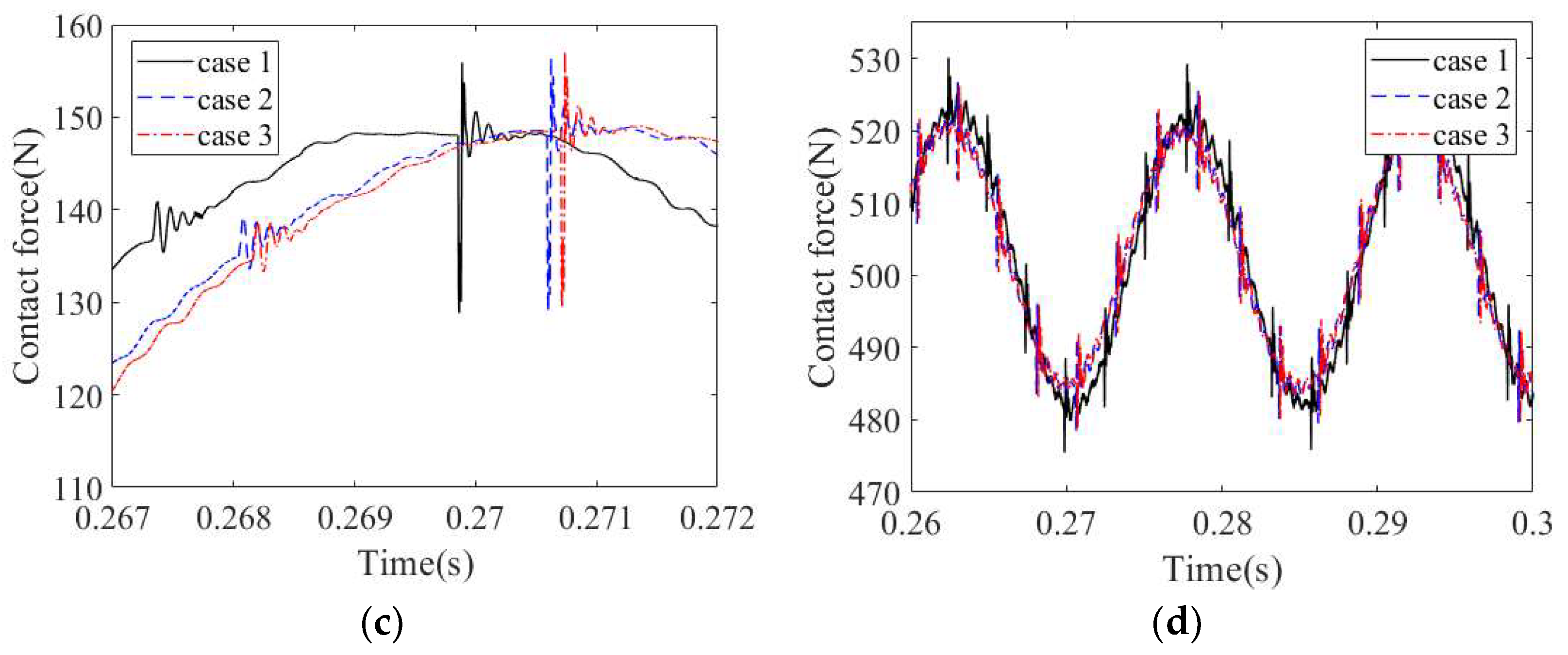
4.2. Vibration Characteristics of a Cylindrical Roller Bearing with Fit Clearance and Outer Ring Defect
4.2.1. Effect of Housing Stiffness
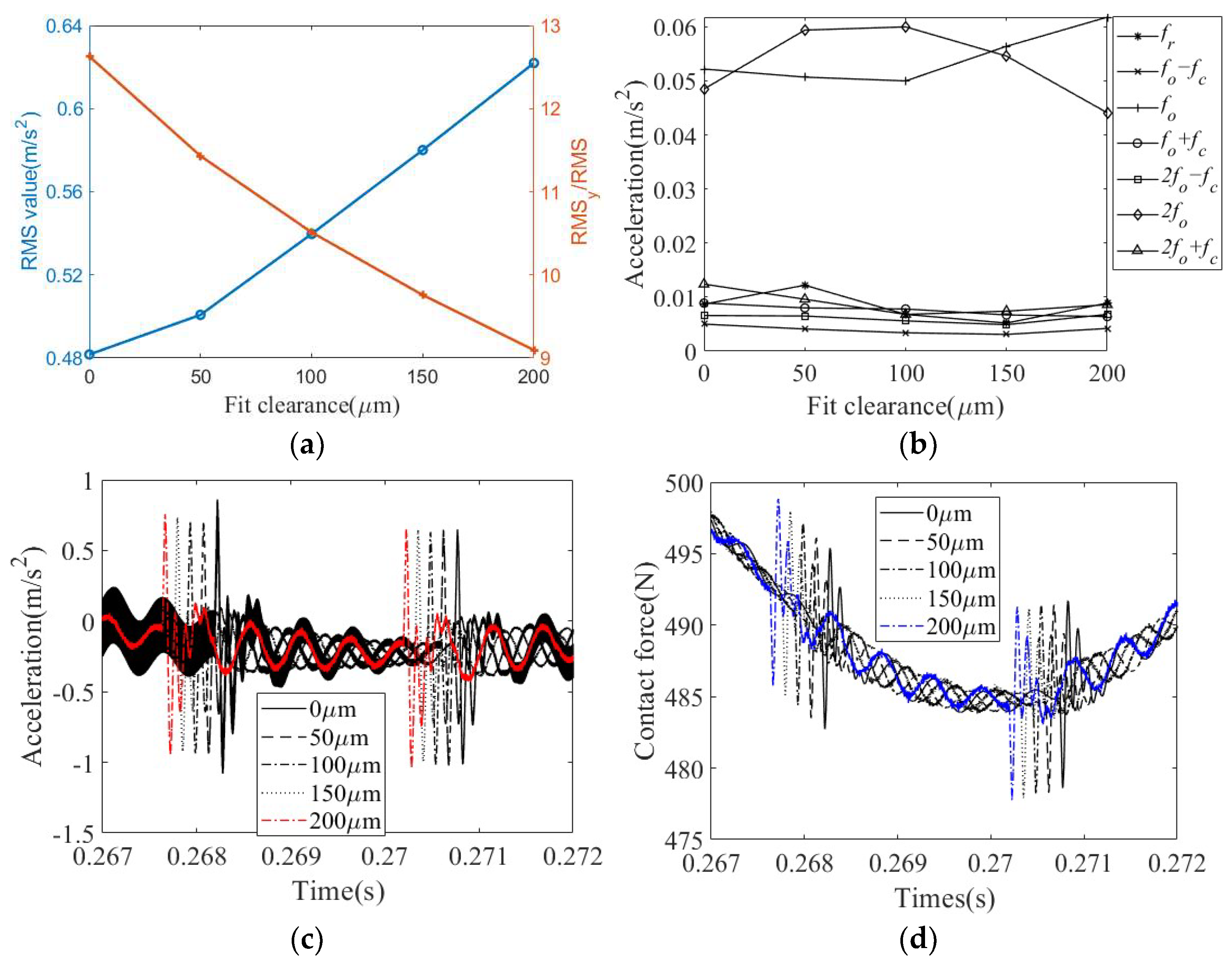
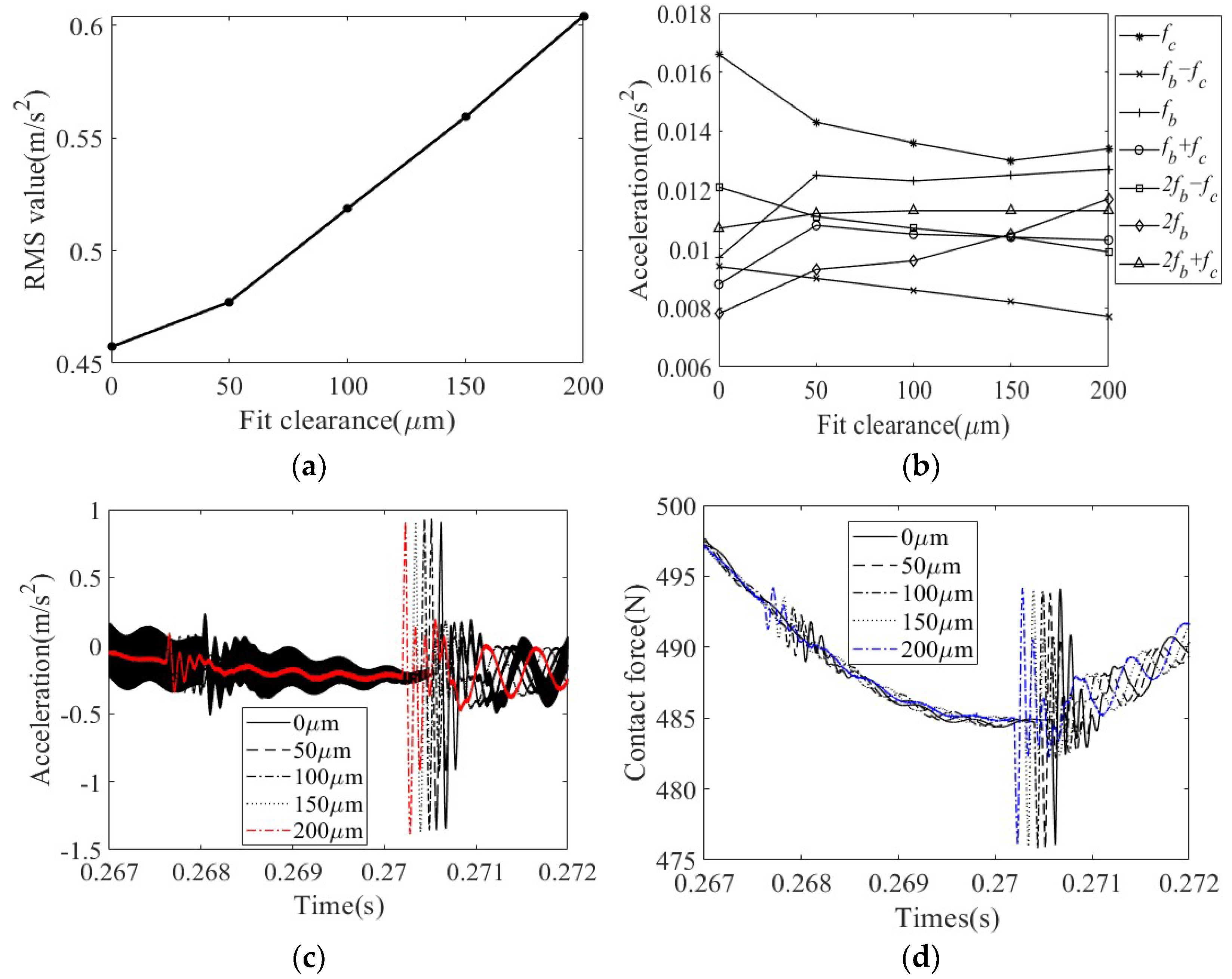
4.2.2. Effect of Fit Clearance
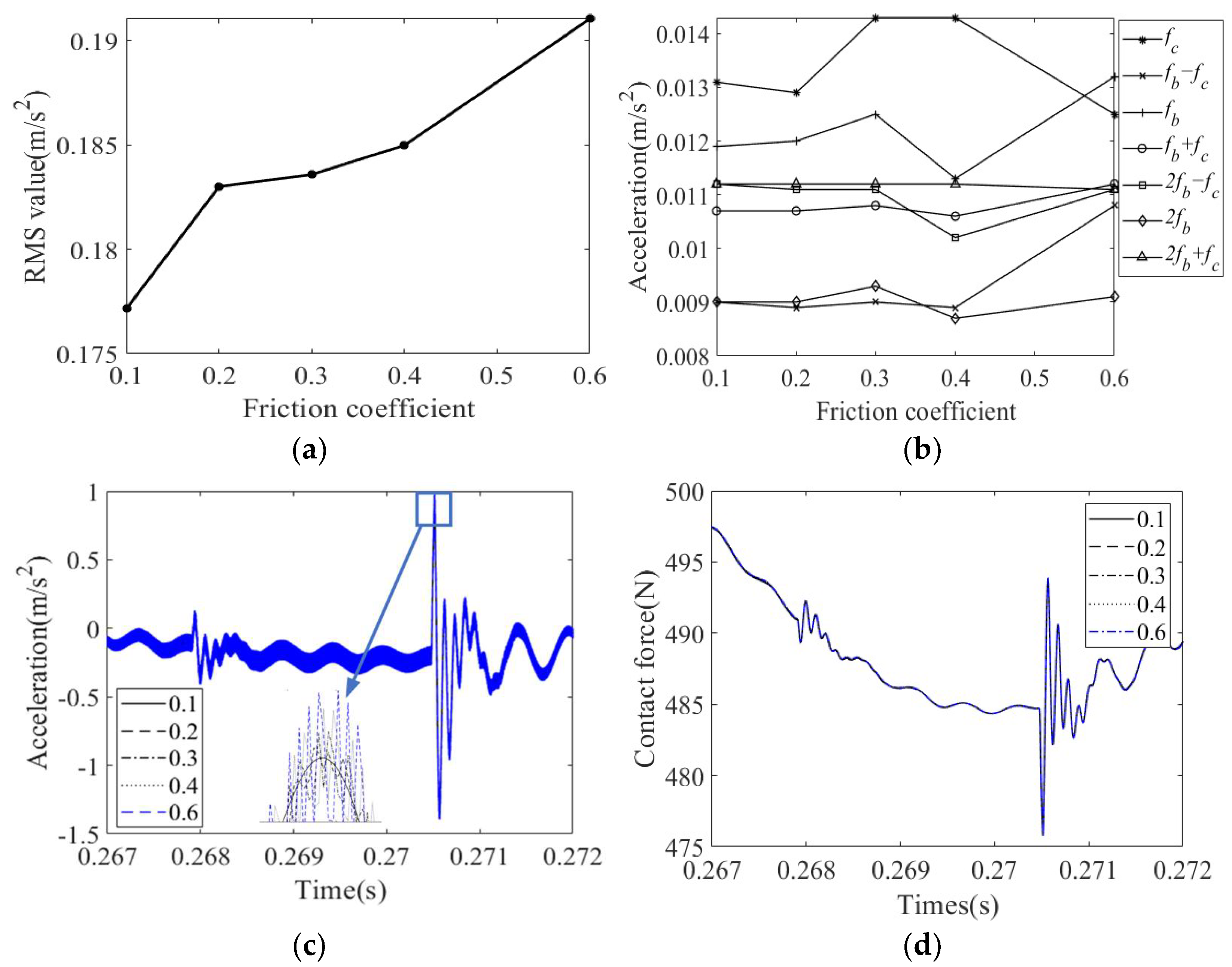
4.2.3. Effect of Friction Coefficient
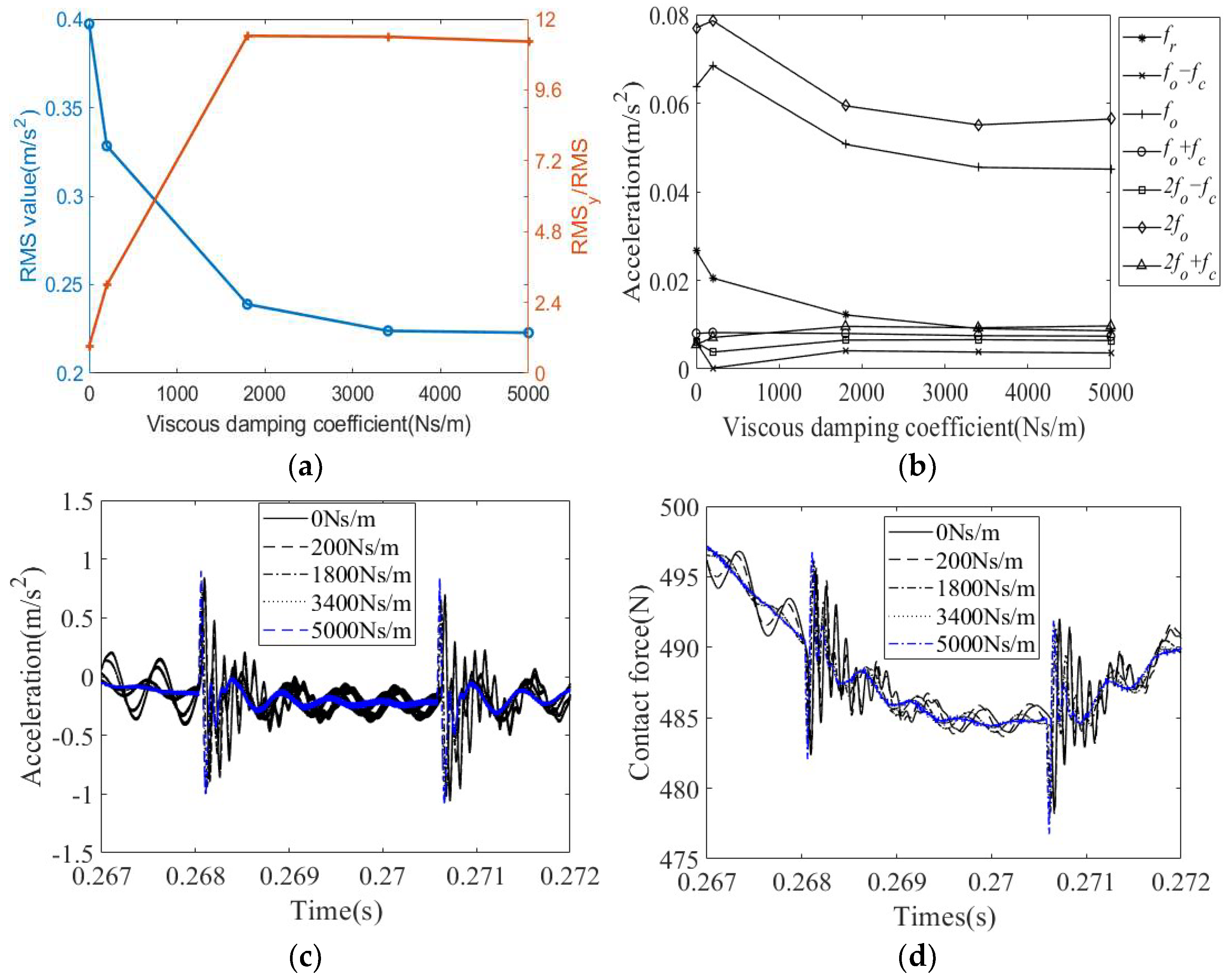
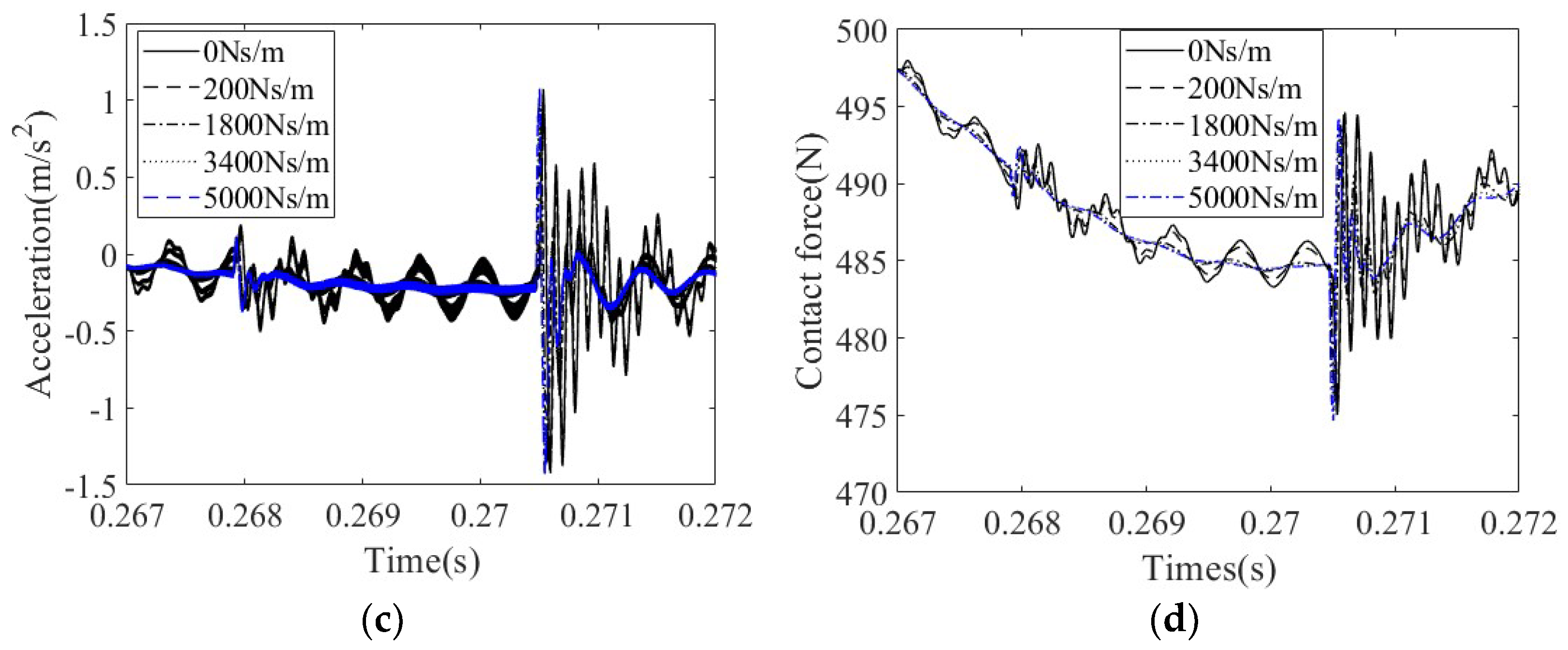
4.2.4. Effect of Viscous Damping
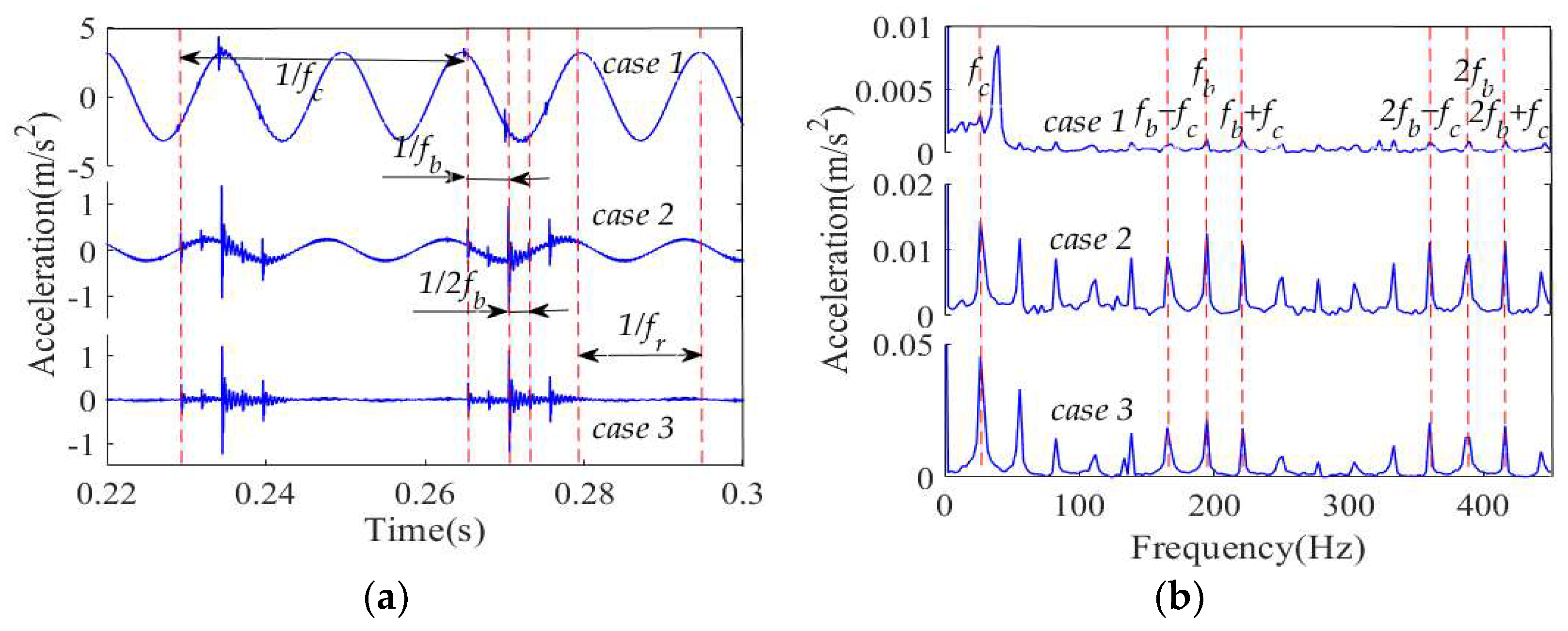
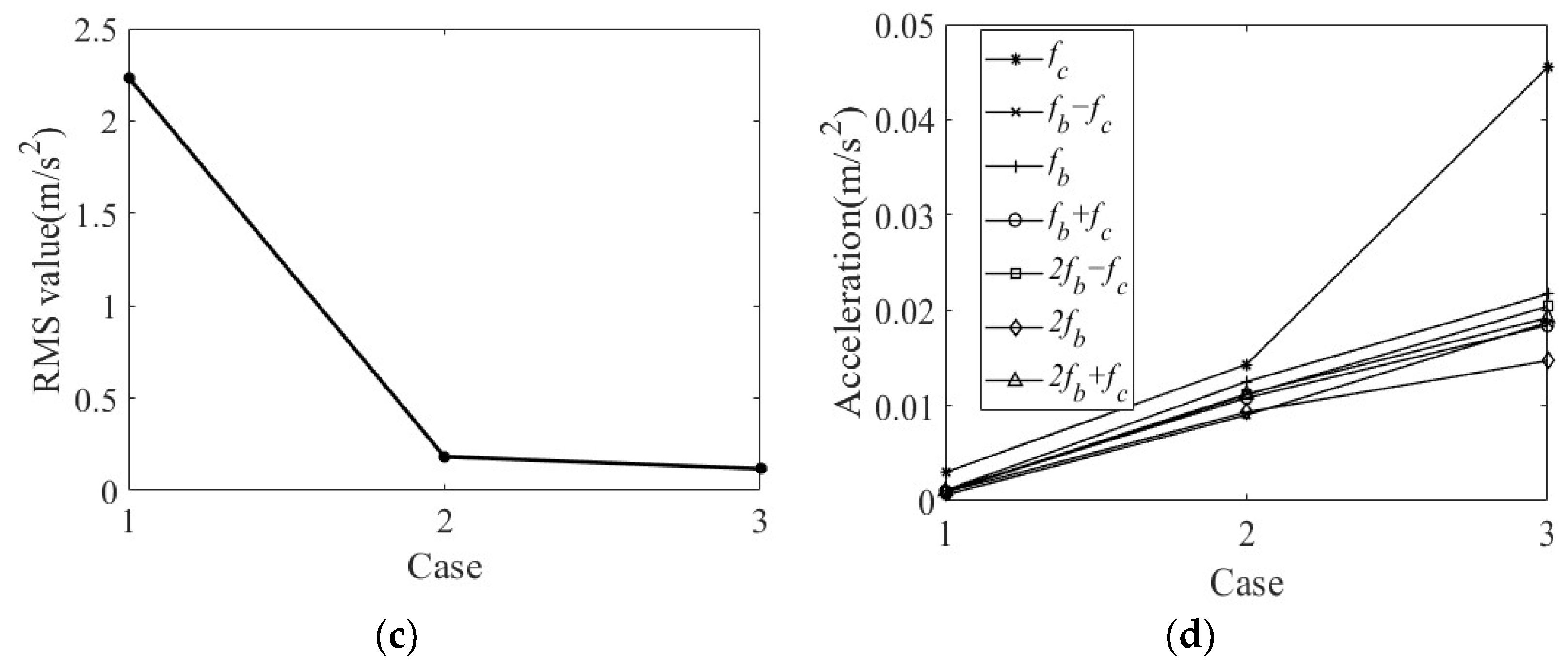
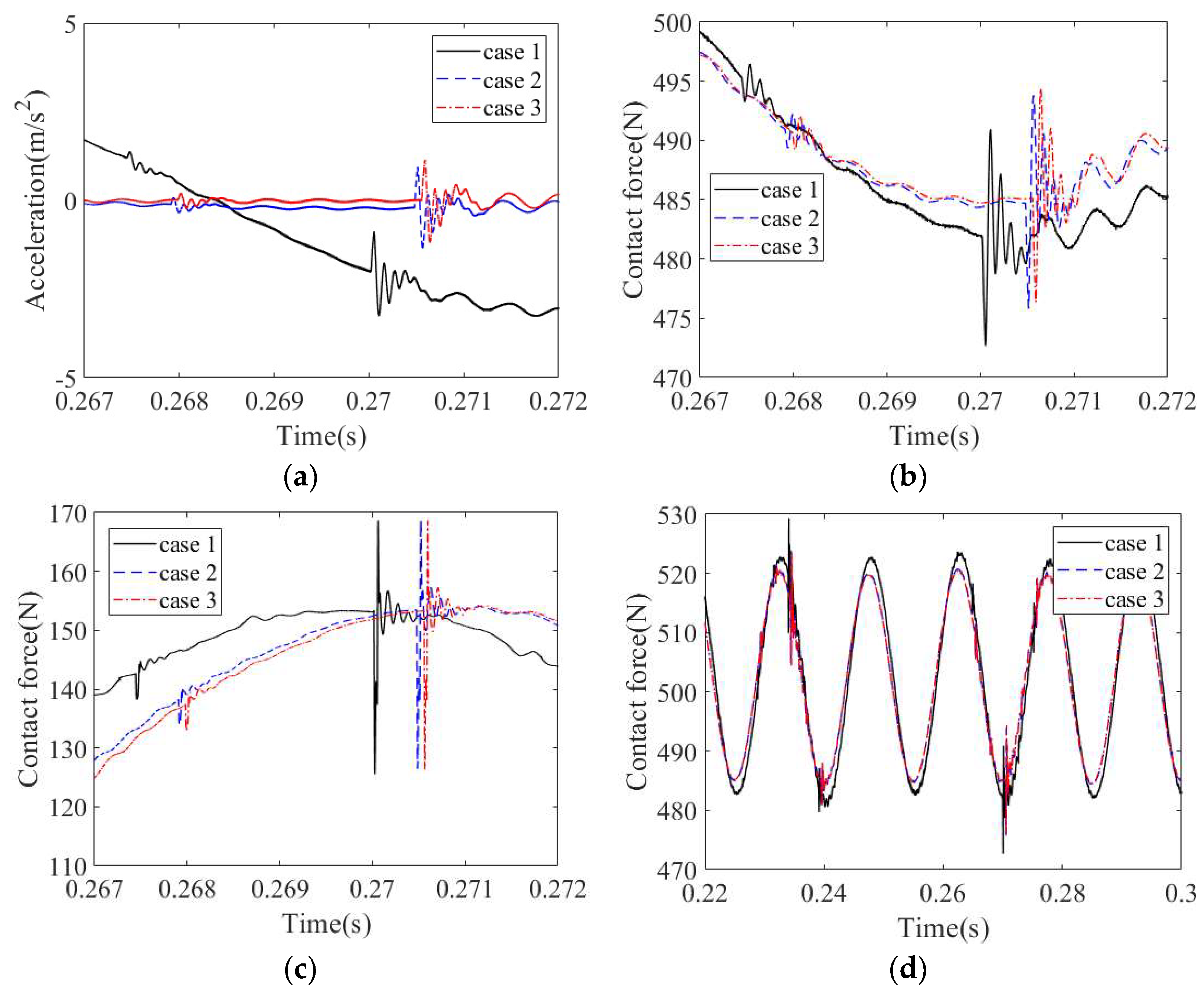
4.2.5. Effect of Defect Location
4.3. Vibration Characteristics of a Cylindrical Roller Bearing with Fit Clearance and Roller Defect
4.3.1. Effect of Housing Stiffness
4.3.2. Effect of Fit Clearance
4.3.3. Effect of Friction Coefficient
4.3.4. Effect of Viscous Damping
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
- (1)
- rotor frequency
- (2)
- cage frequency
- (3)
- defect frequency for outer ring
- (4)
- cage passing inner ring frequency
- (5)
- defect frequency for roller
- (6)
- defect frequency for inner ring
References
- Sun, J.; Wood, R.; Wang, L.; Care, I.; Powrie, H. Wear monitoring of bearing steel using electrostatic and acoustic emission techniques. Wear 2005, 259, 1482–1489. [Google Scholar] [CrossRef]
- Sadeghi, F.; Jalalahmadi, B.; Slack, T.S.; Raje, N.; Arakere, N.K. A Review of Rolling Contact Fatigue. J. Tribol. 2009, 131, 041403. [Google Scholar] [CrossRef]
- Tandon, N.; Choudhury, A. A review of vibration and acoustic measurement methods for the detection of defects in rolling element bearings. Tribol. Int. 1999, 32, 469–480. [Google Scholar] [CrossRef]
- Shao, Y.; Liu, J.; Ye, J. A new method to model a localized surface defect in a cylindrical roller-bearing dynamic simulation. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2013, 228, 140–159. [Google Scholar] [CrossRef]
- Wang, F.; Jing, M.; Yi, J.; Dong, G.; Liu, H.; Ji, B. Dynamic modelling for vibration analysis of a cylindrical roller bearing due to localized defects on raceways. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2014, 229, 39–64. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Shao, Y. A numerical investigation of effects of defect edge discontinuities on contact forces and vibrations for a defective roller bearing. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2016, 230, 387–400. [Google Scholar] [CrossRef]
- Liu, J.; Shi, Z.; Shao, Y. An analytical model to predict vibrations of a cylindrical roller bearing with a localized surface defect. Nonlinear Dyn. 2017, 89, 2085–2102. [Google Scholar] [CrossRef]
- Liu, J. A dynamic modelling method of a rotor-roller bearing-housing system with a localized fault including the additional excitation zone. J. Sound Vib. 2019, 469, 115144. [Google Scholar] [CrossRef]
- Liu, J.; Wang, L. Dynamic modelling of combination imperfects of a cylindrical roller bearing. Eng. Fail. Anal. 2022, 135. [Google Scholar] [CrossRef]
- Liu, J.; Wang, L.; Shi, Z. Dynamic modelling of the defect extension and appearance in a cylindrical roller bearing. Mech. Syst. Signal Process. 2022, 173, 109040. [Google Scholar] [CrossRef]
- Patel, U.A.; Upadhyay, S.H. Theoretical model to predict the effect of localized defect on dynamic behavior of cylindrical roller bearing at inner race and outer race. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2014, 228, 152–171. [Google Scholar] [CrossRef]
- Patel, U.A.; Upadhyay, S.H. An analytical model (7 D.O.F.) for the prediction of the vibration response of cylindrical roller element bearings due to a combined localized defect. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2015, 229, 383–406. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, Y.; Yan, K.; Wang, F.; Hong, J. A novel method to model effects of natural defect on roller bearing. Tribol. Int. 2018, 122, 169–178. [Google Scholar] [CrossRef]
- Tang, H.; Liu, H.; Zhao, Y.; Tian, G.; Xu, Z. Analysis of mechanics around a localized surface defect of cylindrical roller bearing. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2018, 233, 391–403. [Google Scholar] [CrossRef]
- Patel, S.P.; Upadhyay, S.H. Nonlinear analysis of cylindrical roller bearing under the influence of defect on individual and coupled inner–outer race. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2018, 233, 404–428. [Google Scholar] [CrossRef]
- Patel, S.P.; Upadhyay, S.H. Influence of roller defect and coupled roller–inner–outer race defects on the performance of cylindrical roller bearing. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2019, 233, 731–746. [Google Scholar] [CrossRef]
- Patra, P.; Saran, V.H.; Harsha, S.P. Chaotic dynamics of cylindrical roller bearing supported by unbalanced rotor due to localized defects. J. Vib. Control 2020, 26, 1898–1908. [Google Scholar] [CrossRef]
- Niu, L.; Cao, H.; Hou, H.; Wu, B.; Lan, Y.; Xiong, X. Experimental observations and dynamic modeling of vibration characteristics of a cylindrical roller bearing with roller defects. Mech. Syst. Signal Process. 2019, 138, 106553. [Google Scholar] [CrossRef]
- Cao, H.; Su, S.; Jing, X.; Li, D. Vibration mechanism analysis for cylindrical roller bearings with single/multi defects and compound faults. Mech. Syst. Signal Process. 2020, 144, 106903. [Google Scholar] [CrossRef]
- Su, S.; Cao, H.; Zhang, Y. Dynamic modeling and characteristics analysis of cylindrical roller bearing with the surface texture on raceways. Mech. Syst. Signal Process. 2021, 158, 107709. [Google Scholar] [CrossRef]
- Xu, H.; He, D.; Ma, H.; Yu, K.; Zhao, X.; Yang, Y. A method for calculating radial time-varying stiffness of flexible cylindrical roller bearings with localized defects. Eng. Fail. Anal. 2021, 128, 105590. [Google Scholar] [CrossRef]
- Chen, G.; Qu, M. Modeling and analysis of fit clearance between rolling bearing outer ring and housing. J. Sound Vib. 2018, 438, 419–440. [Google Scholar] [CrossRef]
- Shi, H.; Li, Y.; Bai, X.; Wang, Z.; Zou, D.; Bao, Z.; Wang, Z. Investigation of the orbit-spinning behaviors of the outer ring in a full ceramic ball bearing-steel pedestal system in wide temperature ranges. Mech. Syst. Signal Process. 2020, 149, 107317. [Google Scholar] [CrossRef]
- Liu, J.; Shao, Y.; Lim, T.C. Impulse vibration transmissibility characteristics in the presence of localized surface defects in deep groove ball bearing systems. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2013, 228, 62–81. [Google Scholar] [CrossRef]
- Harris, T.A.; Kotzalas, M.N. Advanced Concepts of Bearing Technology, 2nd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2006. [Google Scholar]
- Gupta, P.K. Advanced Dynamics of Rolling Element; Springer-Verlag New York Inc.: New York, NY, USA, 1984. [Google Scholar]
- Shi, H.T.; Liu, Z.M.; Bai, X.T.; Hui, M. Crack location recognition method for full ceramic bearing outer ring. Acta Aeronaut. Astronaut. Sin. 2021, 42. Available online: http://hkxb.buaa.edu.cn/EN/10.7527/S1000-6893.2021.25481 (accessed on 22 April 2022).








| Parameters | Value |
|---|---|
| Pitch diameter dm/mm | 60 |
| Bearing width Lr/mm | 18 |
| Roller number Nb | 14 |
| Roller length Lb/mm | 10 |
| Roller diameter db/mm | 10 |
| Central flat land Lp/mm | 5 |
| Roller corner radius rc/mm | 0.4 |
| Crown radius Rr/mm | 1500 |
| Radial clearance Cr/mm | 0 |
| The unbalanced mass me/kg | 0.02 |
| The unbalanced distance from the rotor center e/mm | 5 |
| Roller mass mb/kg | 0.006 |
| Mass of inner ring and rotor mr/kg | 0.164 |
| Mass of outer ring mor/kg | 1 |
| Mass of housing mh/kg | 8 |
| Axial inertia moment of roller Ib/kgm2 | 7.6 × 10−8 |
| Contact stiffness between outer ring and housing kp/N/m | 1.5 × 107 |
| Parameters | Value |
|---|---|
| Load Fr/N | 500 |
| Input speed wr/r/min | 4000 |
| Frequency | Value |
|---|---|
| Rotor frequency fc/Hz | 66.67 |
| Cage frequency fr/Hz | 27.78 |
| Outer defect frequency fo/Hz | 388.89 |
| Inner defect frequency fi/Hz | 544.44 |
| Roller defect frequency fb/Hz | 194.44 |
| Cage passing inner ring frequency fir/Hz | 38.89 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Ling, X.; Zhang, Z.; Dai, P.; Yan, S.; Wang, L. The Effect of Fit Clearance between Outer Race and Housing on Vibration Characteristics of a Cylindrical Roller Bearing with Localized Defects. Machines 2022, 10, 415. https://doi.org/10.3390/machines10060415
Wang F, Ling X, Zhang Z, Dai P, Yan S, Wang L. The Effect of Fit Clearance between Outer Race and Housing on Vibration Characteristics of a Cylindrical Roller Bearing with Localized Defects. Machines. 2022; 10(6):415. https://doi.org/10.3390/machines10060415
Chicago/Turabian StyleWang, Fengtao, Xin Ling, Zhen Zhang, Peng Dai, Shuping Yan, and Lei Wang. 2022. "The Effect of Fit Clearance between Outer Race and Housing on Vibration Characteristics of a Cylindrical Roller Bearing with Localized Defects" Machines 10, no. 6: 415. https://doi.org/10.3390/machines10060415
APA StyleWang, F., Ling, X., Zhang, Z., Dai, P., Yan, S., & Wang, L. (2022). The Effect of Fit Clearance between Outer Race and Housing on Vibration Characteristics of a Cylindrical Roller Bearing with Localized Defects. Machines, 10(6), 415. https://doi.org/10.3390/machines10060415






