Towards Self-Adaptability of Instrumented Electromagnetic Energy Harvesters
Abstract
:1. Introduction
2. Methods
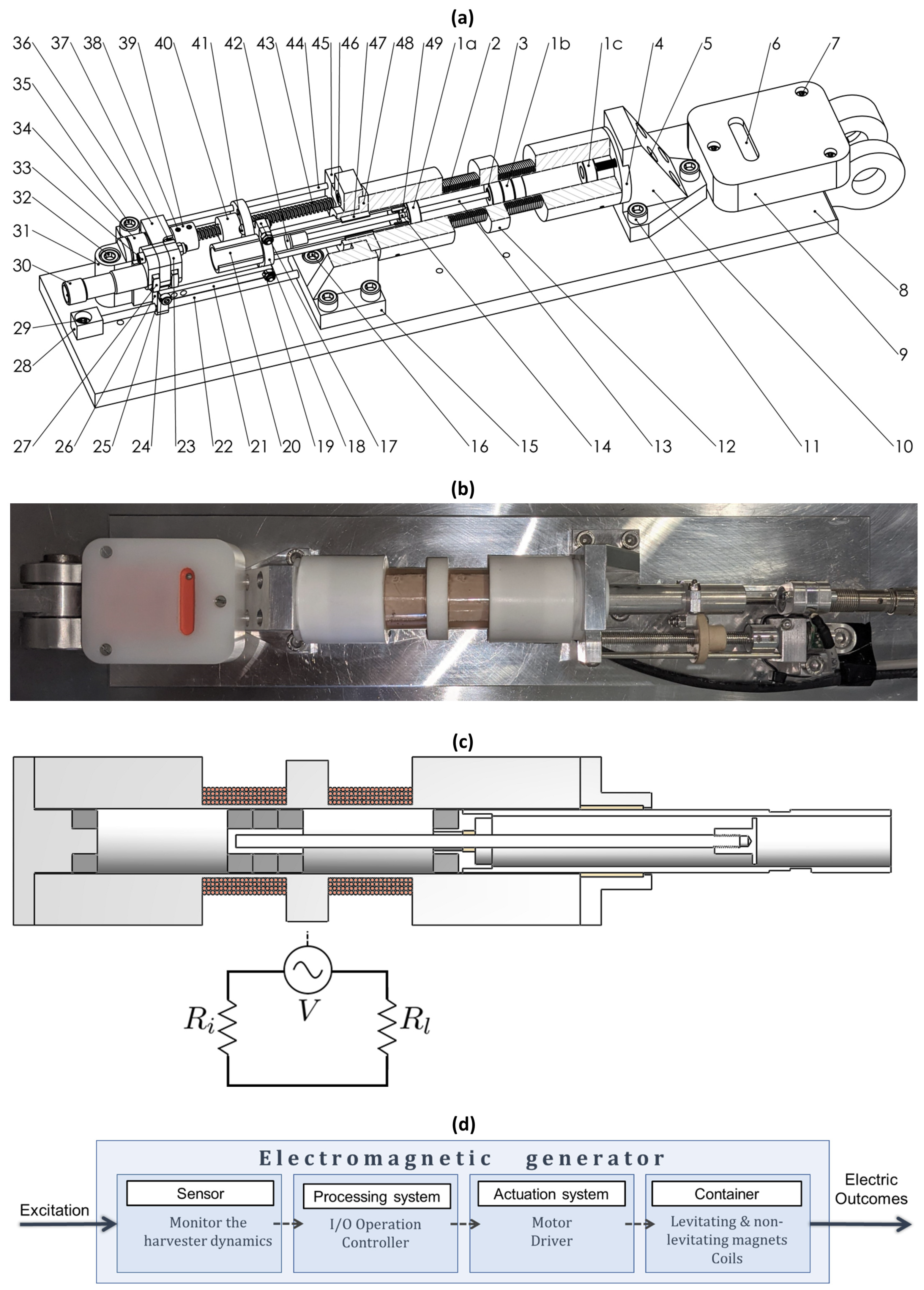
2.1. Electromagnetic Harvester Design
2.2. Mechanical–Electric Transduction Mechanism
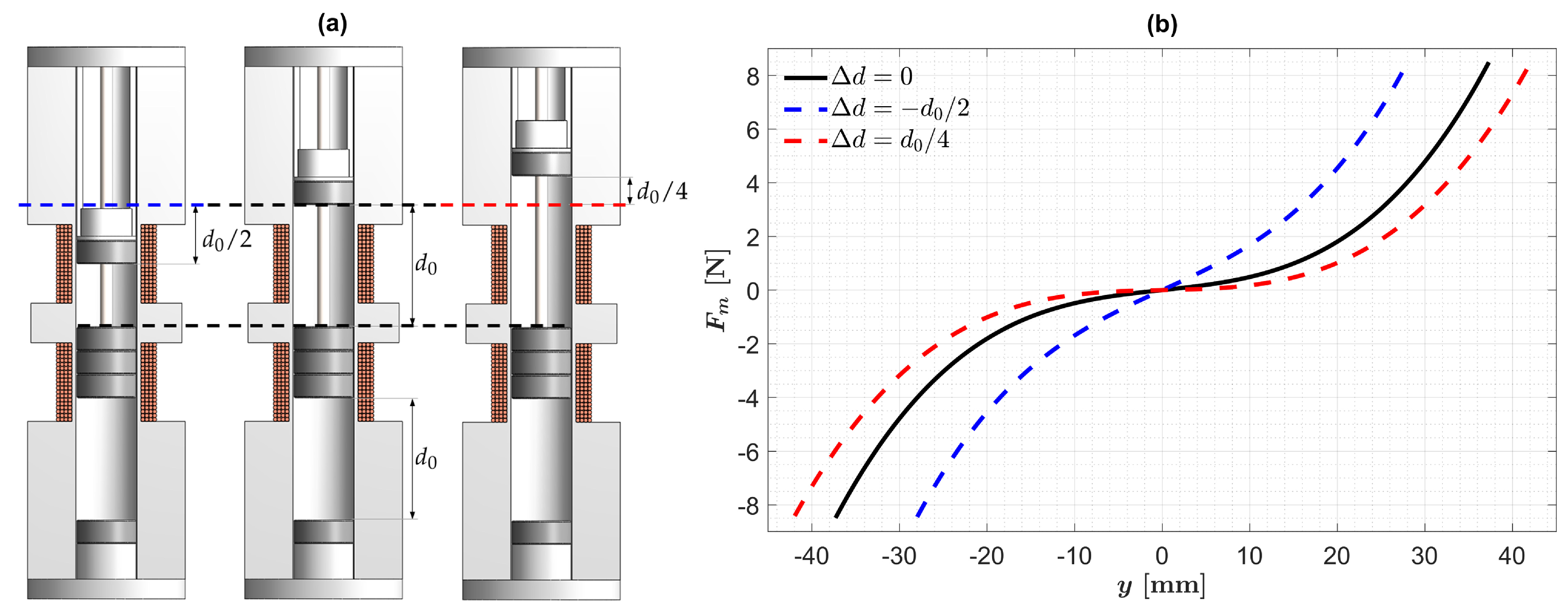
2.3. Length Variation of the Electromagnetic Harvester
2.4. Simulation Details
2.4.1. Details for Identification of Optimal Harvester Lengths
2.4.2. Details Used in Case Studies
2.5. Data Analysis
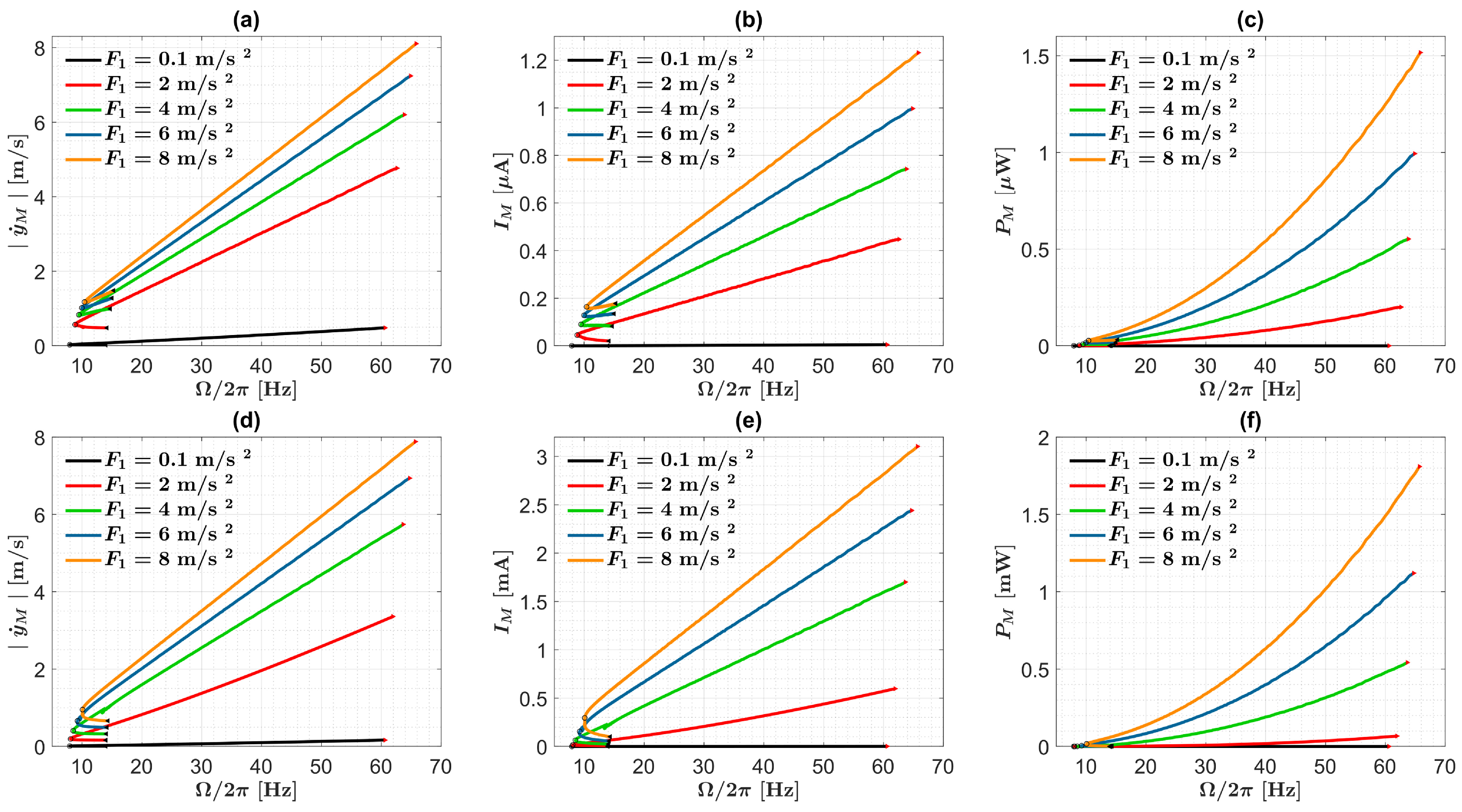
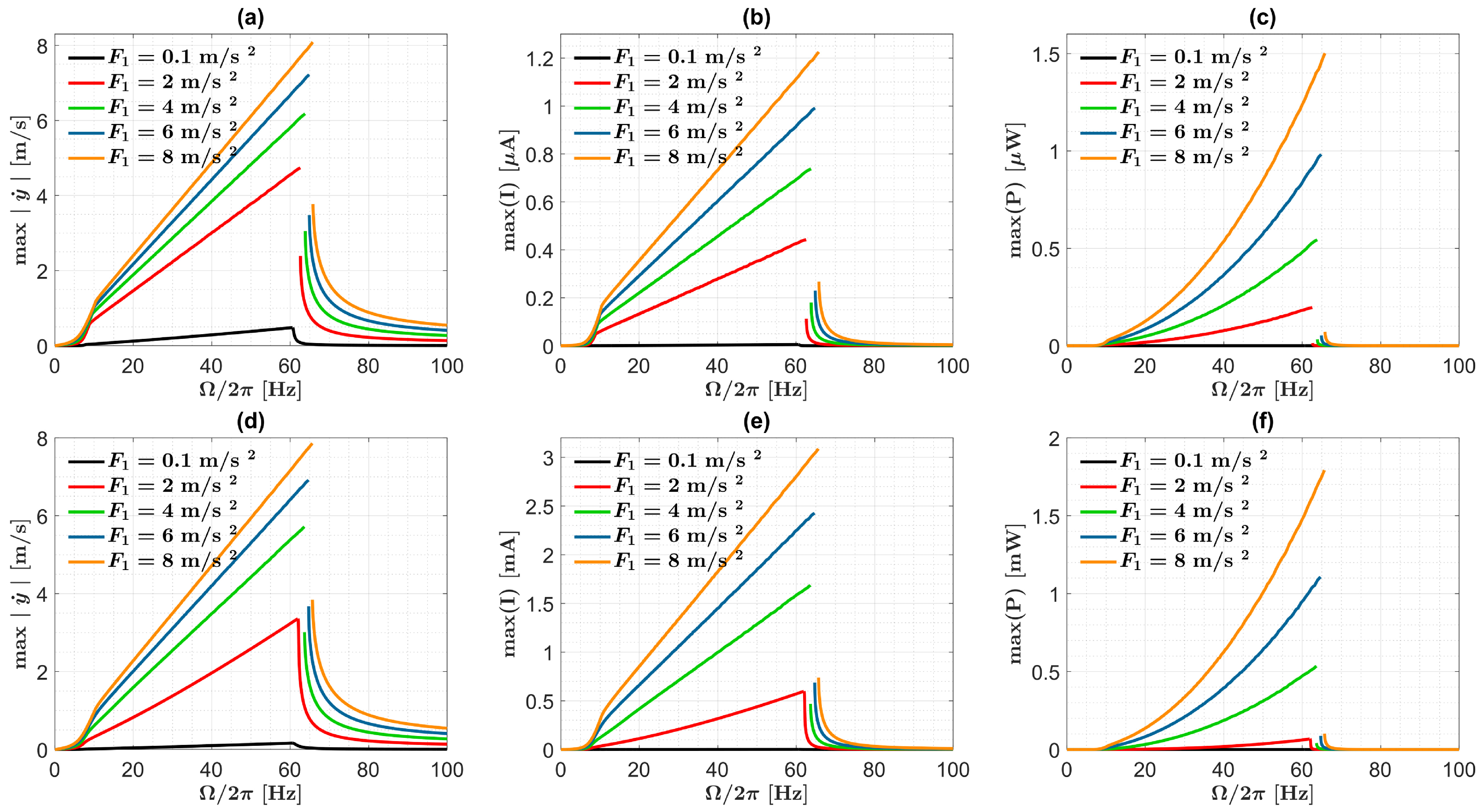
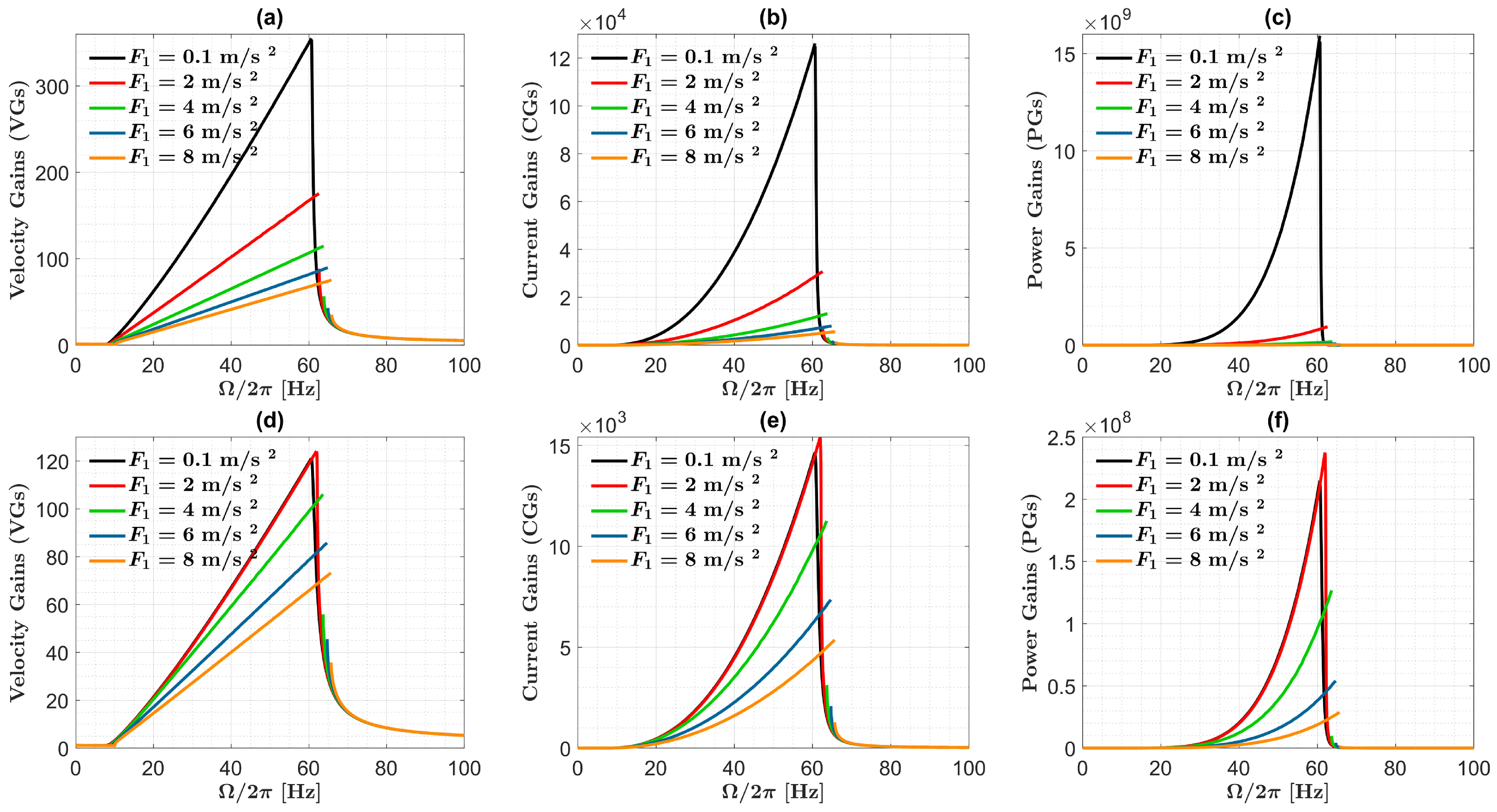
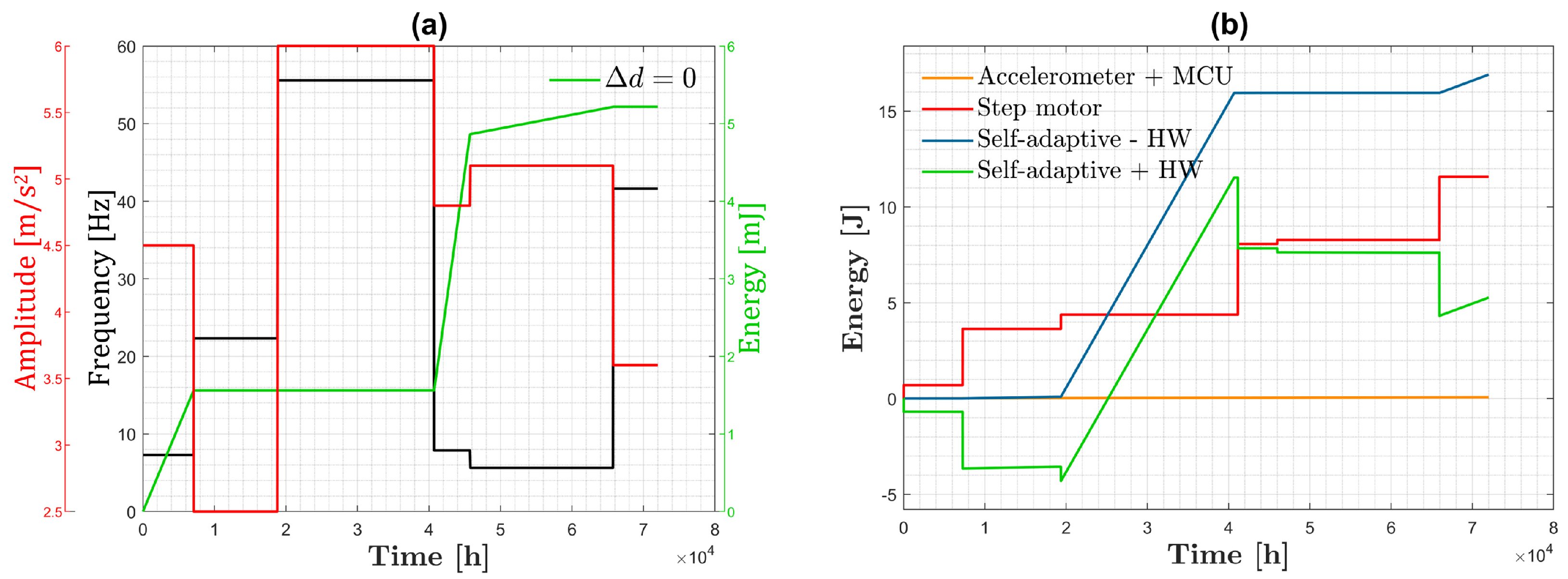
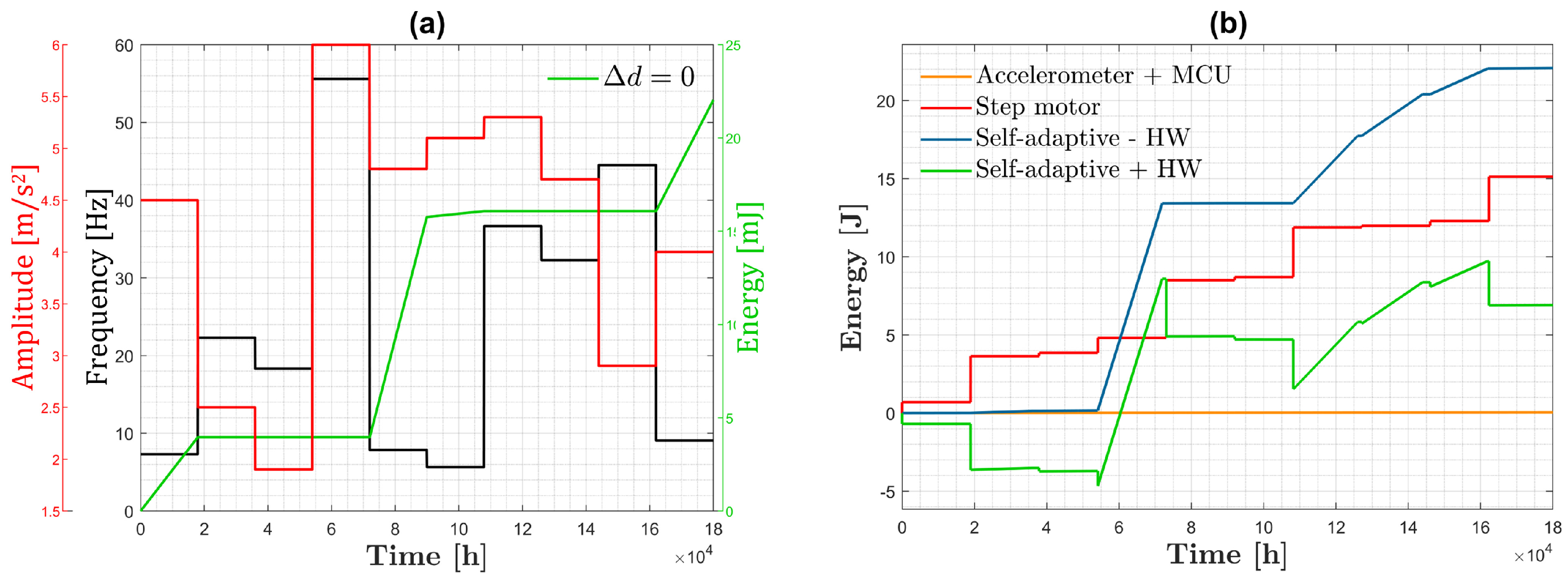
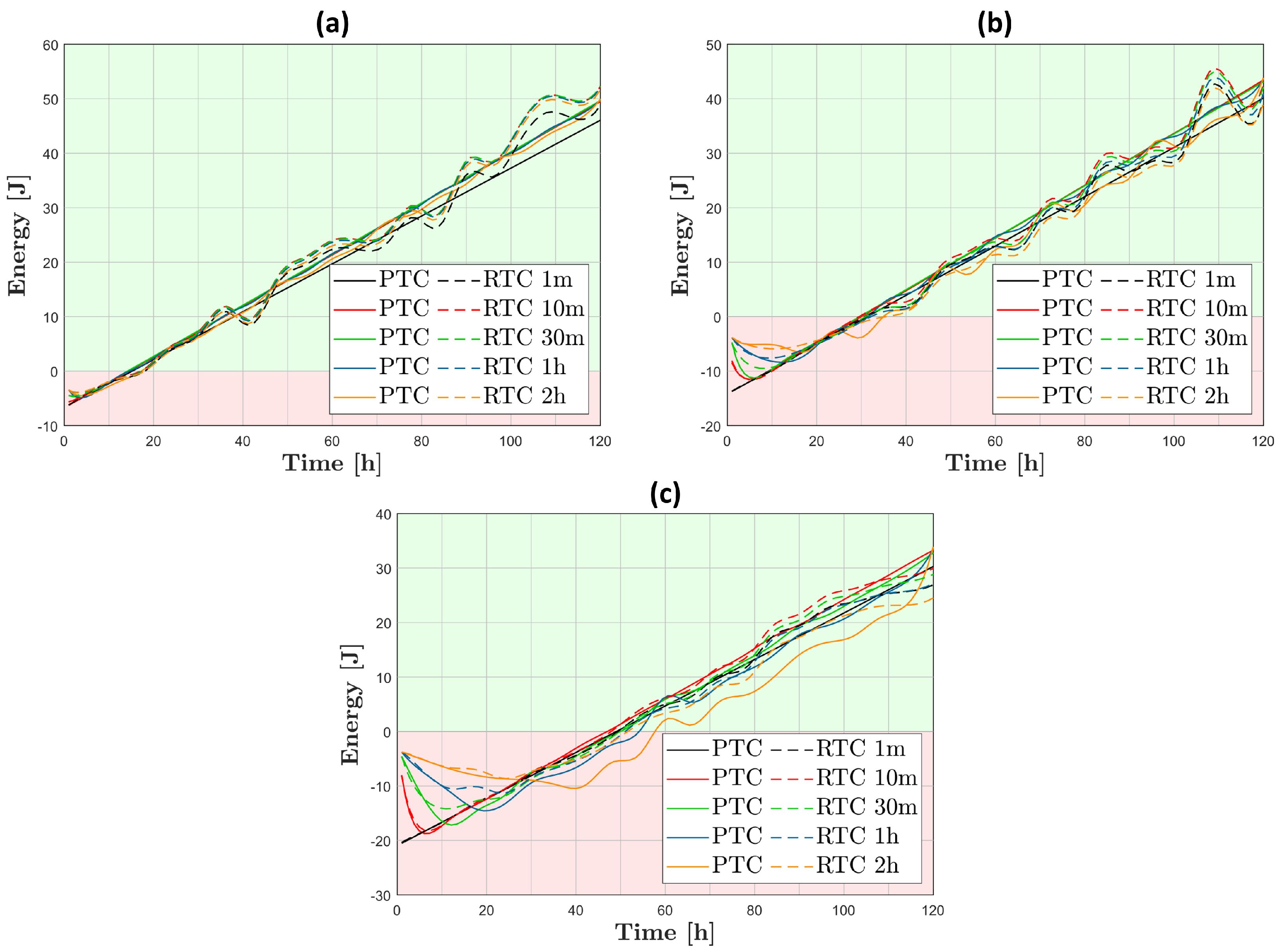
3. Results
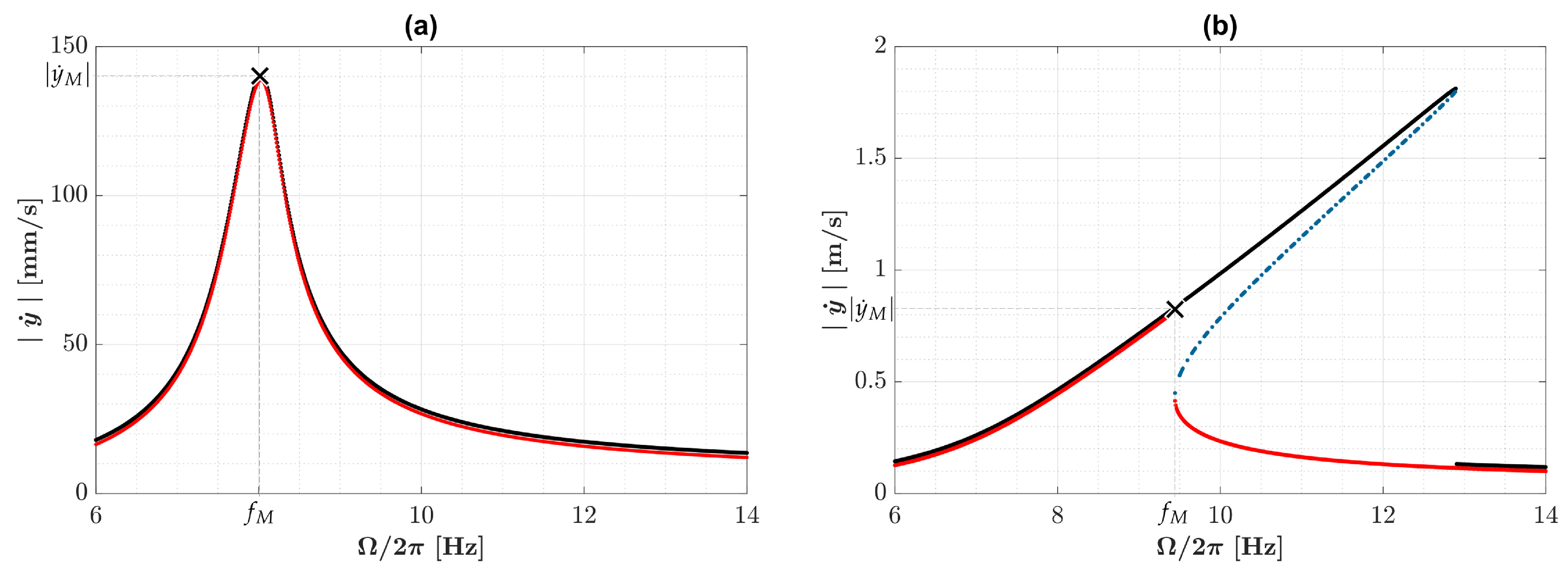
3.1. Identification of Optimal Harvester Lengths and Related Performance Gains
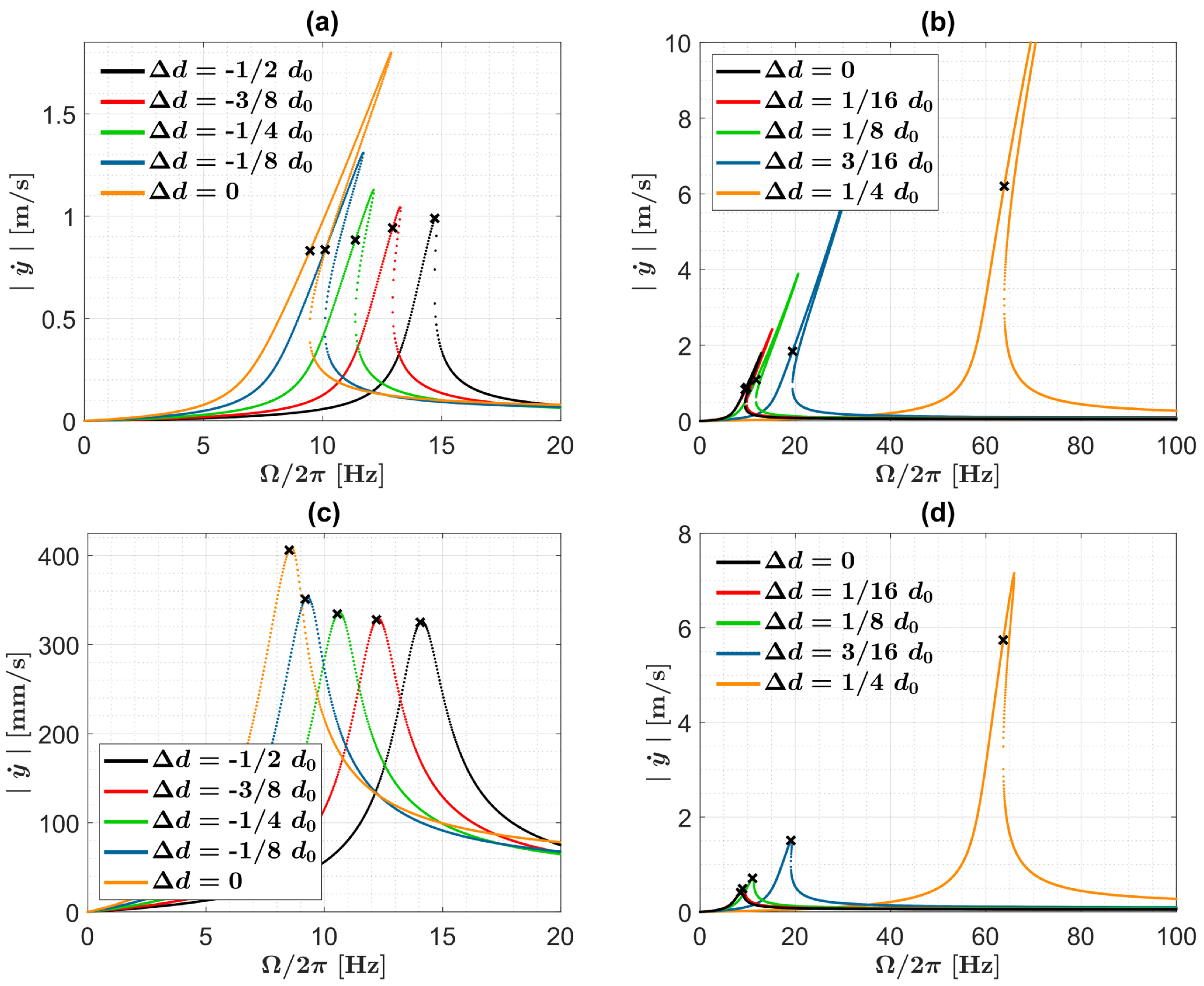
3.2. Case Studies
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PTC | Periodic time changes |
| RTC | Random time changes |
| MCU | Ultra-low-power MSP430 microcontroller |
| HW | Hardware |
| VG | Velocity gain |
| CG | Current gain |
| PG | Power gain |
References
- EIA. International Energy Outlook 2016 whith Projections to 2040; 2016; p. 276. Available online: https://www.osti.gov/biblio/1296780 (accessed on 20 March 2022).
- Larsson, S.; Fantazzini, D.; Davidsson, S.; Kullander, S.; Höök, M. Reviewing electricity production cost assessments. Renew. Sustain. Energy Rev. 2014, 30, 170–183. [Google Scholar] [CrossRef] [Green Version]
- Sovacool, B.K. The intermittency of wind, solar, and renewable electricity generators: Technical barrier or rhetorical excuse? Util. Policy 2009, 17, 288–296. [Google Scholar] [CrossRef]
- Elliott, D. A balancing act for renewables. Nat. Energy 2016, 1, 15003. [Google Scholar] [CrossRef]
- Carneiro, P.; Soares dos Santos, M.P.; Rodrigues, A.; Ferreira, J.A.; Simões, J.A.; Marques, A.T.; Kholkin, A.L. Electromagnetic energy harvesting using magnetic levitation architectures: A review. Appl. Energy 2020, 260, 114191. [Google Scholar] [CrossRef] [Green Version]
- dos Santos, M.P.S.; Ferreira, J.A.F.; Simões, J.A.O.; Pascoal, R.; Torrão, J.; Xue, X.; Furlani, E.P. Magnetic levitation-based electromagnetic energy harvesting: A semi-analytical non-linear model for energy transduction. Sci. Rep. 2016, 6, 18579. [Google Scholar] [CrossRef]
- Dewan, A.; Ay, S.U.; Karim, M.N.; Beyenal, H. Alternative power sources for remote sensors: A review. J. Power Sources 2014, 245, 129–143. [Google Scholar] [CrossRef]
- Beeby, S.P.; Tudor, M.J.; White, N.M. Energy harvesting vibration sources for microsystems applications. Meas. Sci. Technol. 2006, 17, 175–195. [Google Scholar] [CrossRef]
- Teng, X.F.; Zhang, Y.T.; Poon, C.C.Y.; Bonato, P. Wearable medical systems for p-health. IEEE Rev. Biomed. Eng. 2008, 1, 62–74. [Google Scholar] [CrossRef]
- Dos Santos, M.P.; Marote, A.; Santos, T.; Torrão, J.; Ramos, A.; Simões, J.A.; Da Cruz E Silva, O.A.; Furlani, E.P.; Vieira, S.I.; Ferreira, J.A. New cosurface capacitive stimulators for the development of active osseointegrative implantable devices. Sci. Rep. 2016, 6, 30231. [Google Scholar] [CrossRef] [Green Version]
- Soares dos Santos, M.P.; Coutinho, J.; Marote, A.; Sousa, B.; Ramos, A.; Ferreira, J.A.; Bernardo, R.; Rodrigues, A.; Marques, A.T.; Cruz e Silva, O.A.; et al. Capacitive technologies for highly controlled and personalized electrical stimulation by implantable biomedical systems. Sci. Rep. 2019, 9, 5001. [Google Scholar] [CrossRef] [Green Version]
- Peres, I.; Rolo, P.; Ferreira, J.A.F.; Pinto, S.C.; Marques, P.A.A.P.; Ramos, A.; Soares dos Santos, M.P. Multiscale Sensing of Bone-Implant Loosening for Multifunctional Smart Bone Implants: Using Capacitive Technologies for Precision Controllability. Sensors 2022, 22, 2531. [Google Scholar] [CrossRef] [PubMed]
- Alanne, K.; Cao, S. An overview of the concept and technology of ubiquitous energy. Appl. Energy 2019, 238, 284–302. [Google Scholar] [CrossRef]
- Mann, B.P.; Sims, N.D. Energy harvesting from the nonlinear oscillations of magnetic levitation. J. Sound Vib. 2009, 319, 515–530. [Google Scholar] [CrossRef] [Green Version]
- Harne, R.L.; Schoemaker, M.E.; Dussault, B.E.; Wang, K.W. Wave heave energy conversion using modular multistability. Appl. Energy 2014, 130, 148–156. [Google Scholar] [CrossRef]
- Stoutenburg, E.D.; Jacobson, M.Z. Reducing offshore transmission requirements by combining offshore wind and wave farms. IEEE J. Ocean. Eng. 2011, 36, 552–561. [Google Scholar] [CrossRef]
- Berdy, D.F.; Valentino, D.J.; Peroulis, D. Kinetic energy harvesting from human walking and running using a magnetic levitation energy harvester. Sensors Actuators Phys. 2015, 222, 262–271. [Google Scholar] [CrossRef]
- Geisler, M.; Boisseau, S.; Perez, M.; Gasnier, P.; Willemin, J.; Ait-Ali, I.; Perraud, S. Human-motion energy harvester for autonomous body area sensors. Smart Mater. Struct. 2017, 26, 12. [Google Scholar] [CrossRef]
- Masoumi, M.; Wang, Y. Repulsive magnetic levitation-based ocean wave energy harvester with variable resonance: Modeling, simulation and experiment. J. Sound Vib. 2016, 381, 192–205. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.L.; Chen, W.Q. A wideband magnetic energy harvester. Appl. Phys. Lett. 2010, 96, 123507. [Google Scholar] [CrossRef]
- Jang, S.J.; Kim, I.H.; Jung, H.J.; Lee, Y.P. A tunable rotational energy harvester for low frequency vibration. Appl. Phys. Lett. 2011, 99, 134102. [Google Scholar] [CrossRef]
- Zhu, D.; Tudor, M.J.; Beeby, S.P. Strategies for increasing the operating frequency range of vibration energy harvesters: A review. Meas. Sci. Technol. 2010, 21, 29. [Google Scholar] [CrossRef]
- Harne, R.L.; Wang, K.W. A review of the recent research on vibration energy harvesting via bistable systems. Smart Mater. Struct. 2013, 22, 12. [Google Scholar] [CrossRef]
- Nguyen, S.D.; Halvorsen, E. Nonlinear springs for bandwidth-tolerant vibration energy harvesting. J. Microelectromech. Syst. 2011, 20, 1225–1227. [Google Scholar] [CrossRef]
- Siddique, A.R.M.; Mahamud, S.; Heyst, B.V. A comprehensive review on vibration based micro power generators using electromagnetic and piezoelectric transducer mechanisms. Energy Convers. Manag. 2015, 106, 728–747. [Google Scholar] [CrossRef]
- Struwig, M.N.; Wolhuter, R.; Niesler, T. Nonlinear model and optimization method for a single-axis linear-motion energy harvester for footstep excitation. Smart Mater. Struct. 2018, 27, 125007. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Cao, J.; Zhang, N.; Lin, J.; Liao, W.H. Magnetic-spring based energy harvesting from human motions: Design, modeling and experiments. Energy Convers. Manag. 2017, 132, 189–197. [Google Scholar] [CrossRef]

| Parameter | Value | Units |
|---|---|---|
| m | 0.0195 | kg |
| 35.0396 | N/m | |
| 149.0883 | 6.7750 | N/m | |
| 138400 | N/m | |
| 195559 | 110045 | N/m | |
| 37.3 | mm | |
| 7.752 | Vs/m | |
| 188 | ||
| 0.0826 | Ns/m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carneiro, P.M.R.; Ferreira, J.A.F.; Kholkin, A.L.; Soares dos Santos, M.P. Towards Self-Adaptability of Instrumented Electromagnetic Energy Harvesters. Machines 2022, 10, 414. https://doi.org/10.3390/machines10060414
Carneiro PMR, Ferreira JAF, Kholkin AL, Soares dos Santos MP. Towards Self-Adaptability of Instrumented Electromagnetic Energy Harvesters. Machines. 2022; 10(6):414. https://doi.org/10.3390/machines10060414
Chicago/Turabian StyleCarneiro, Pedro M. R., Jorge A. F. Ferreira, Andrei L. Kholkin, and Marco P. Soares dos Santos. 2022. "Towards Self-Adaptability of Instrumented Electromagnetic Energy Harvesters" Machines 10, no. 6: 414. https://doi.org/10.3390/machines10060414
APA StyleCarneiro, P. M. R., Ferreira, J. A. F., Kholkin, A. L., & Soares dos Santos, M. P. (2022). Towards Self-Adaptability of Instrumented Electromagnetic Energy Harvesters. Machines, 10(6), 414. https://doi.org/10.3390/machines10060414








