Prediction of the Comprehensive Error Field in the Machining Space of the Five-Axis Machine Tool Based on the “S”-Shaped Specimen Family
Abstract
:1. Introduction
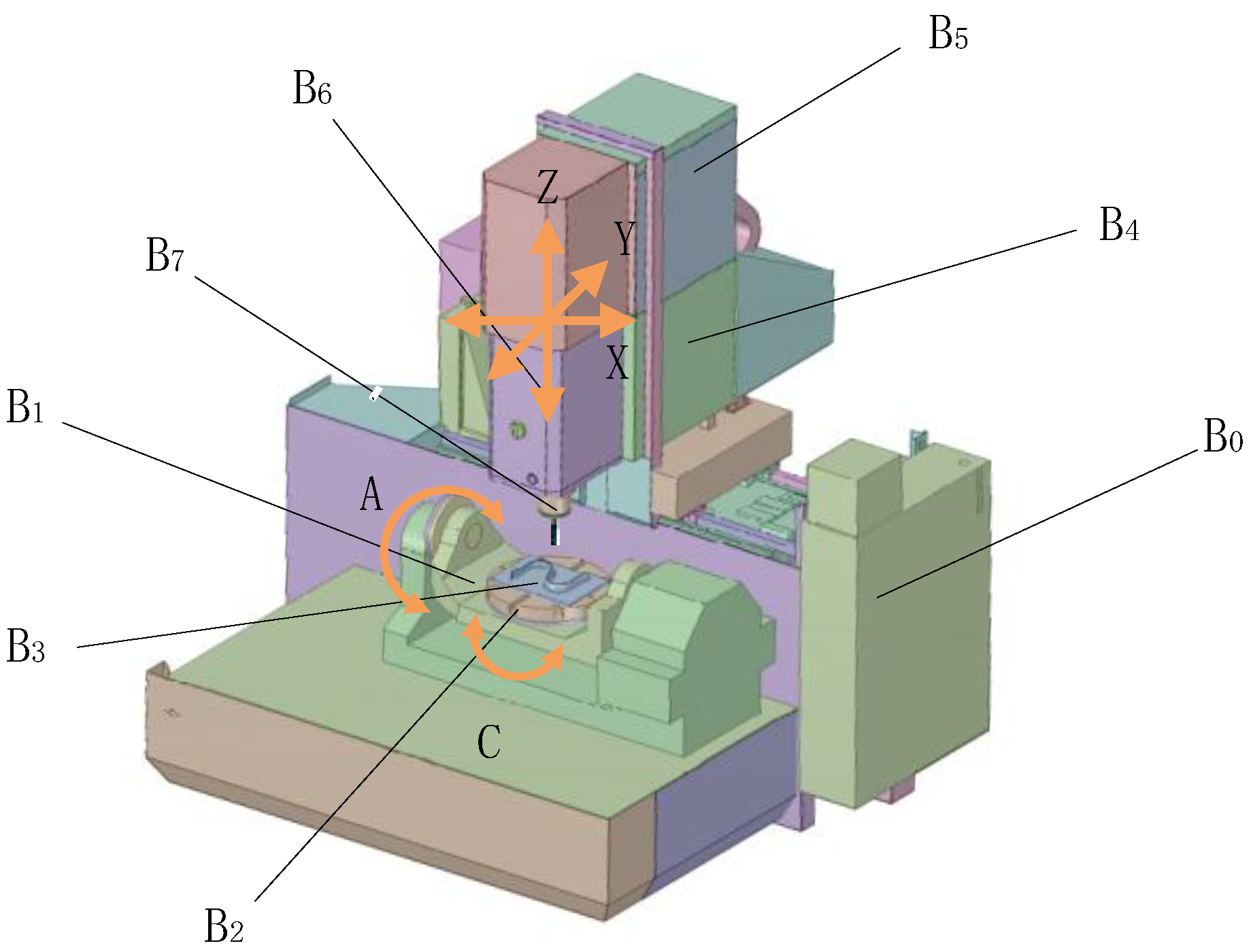
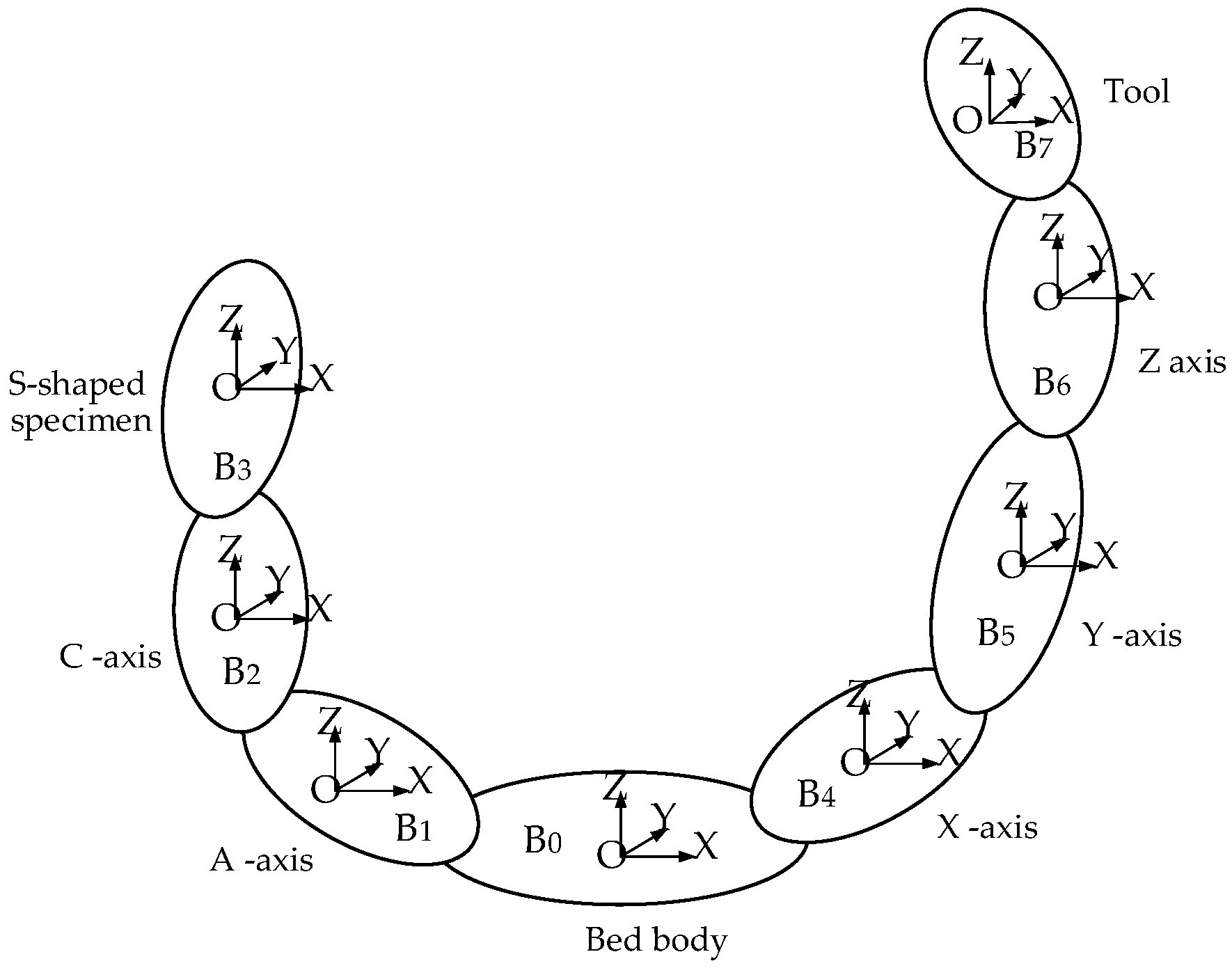
2. Rotating Axis Geometry Error Model
2.1. Rotating Axis Geometric Error Element
2.2. Geometric Model in The Ideal State of the Axis of Rotation
2.3. Geometric Error Model in The Actual State of The Axis of Rotation
3. Geometric Error Identification Based on the “S” Sample Family
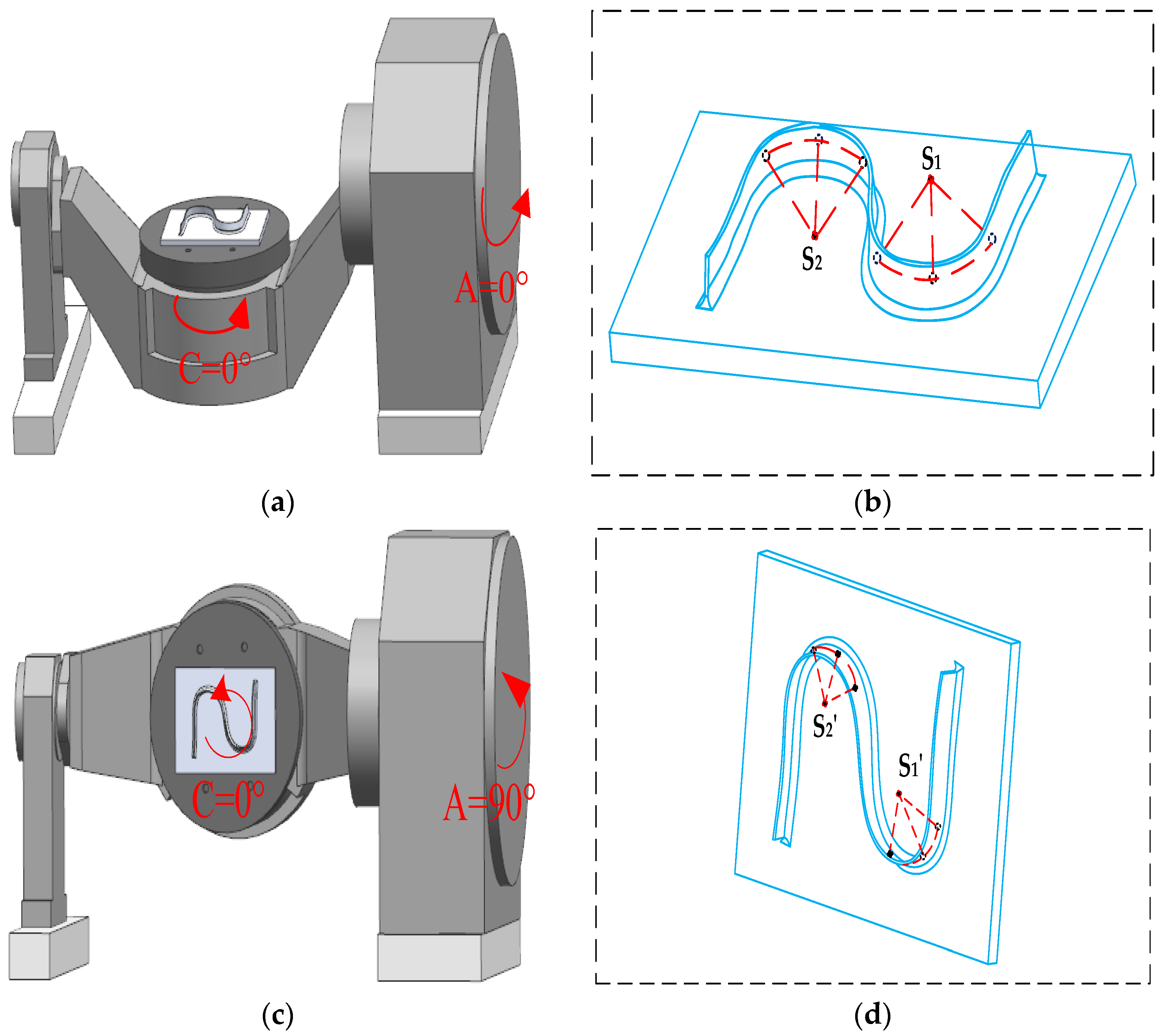
3.1. Geometric Error Identification of the A-axis
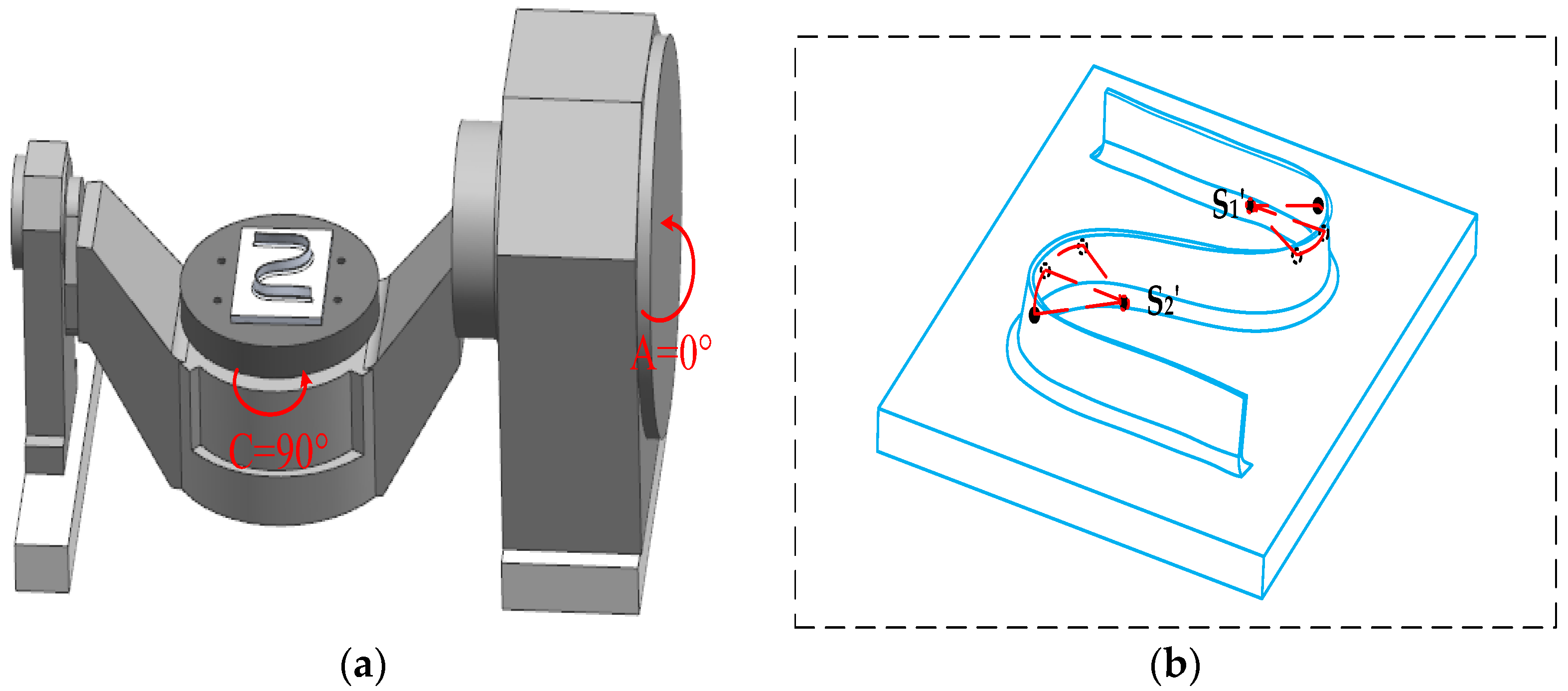
3.2. Geometric Error Identification of Axis C
4. In-Machine Measurement of the Sampling Point Error of S-Shaped Samples
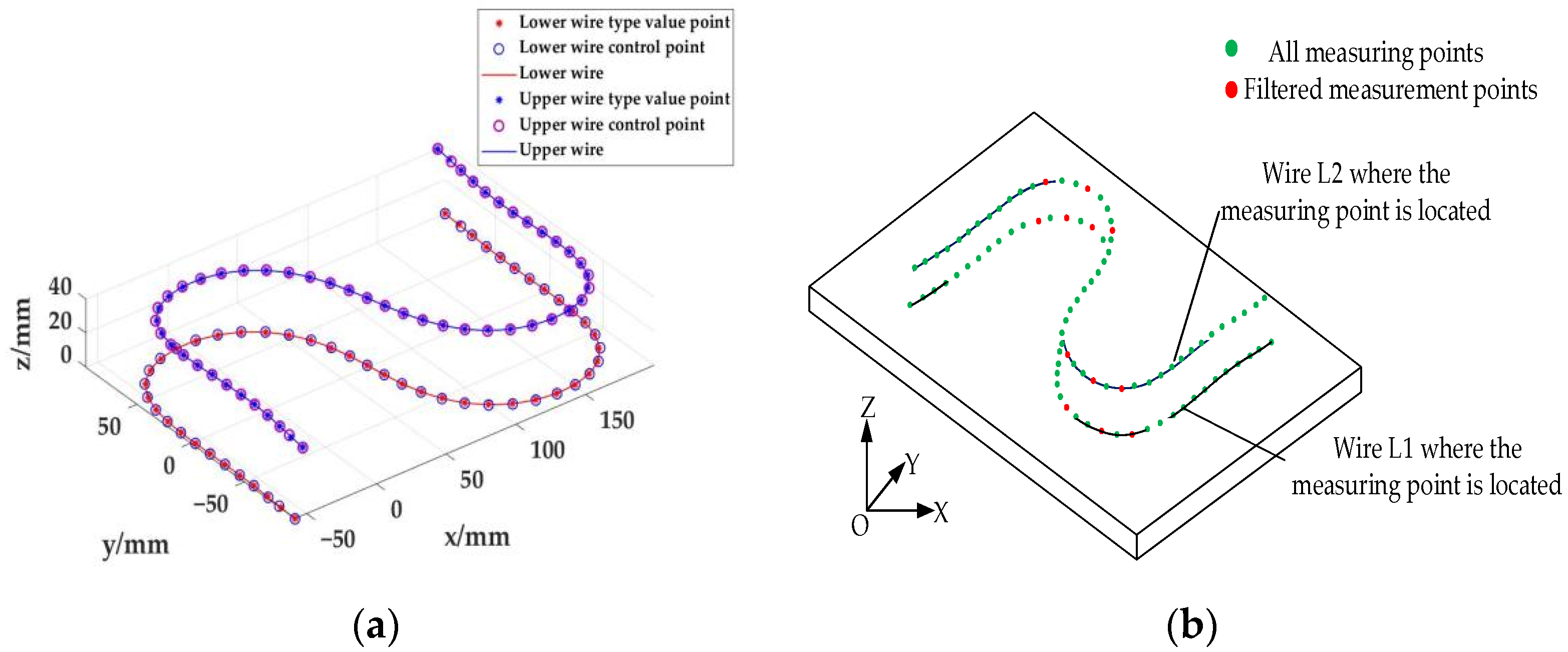
4.1. Mathematical Model of the S-Shaped Sample Family
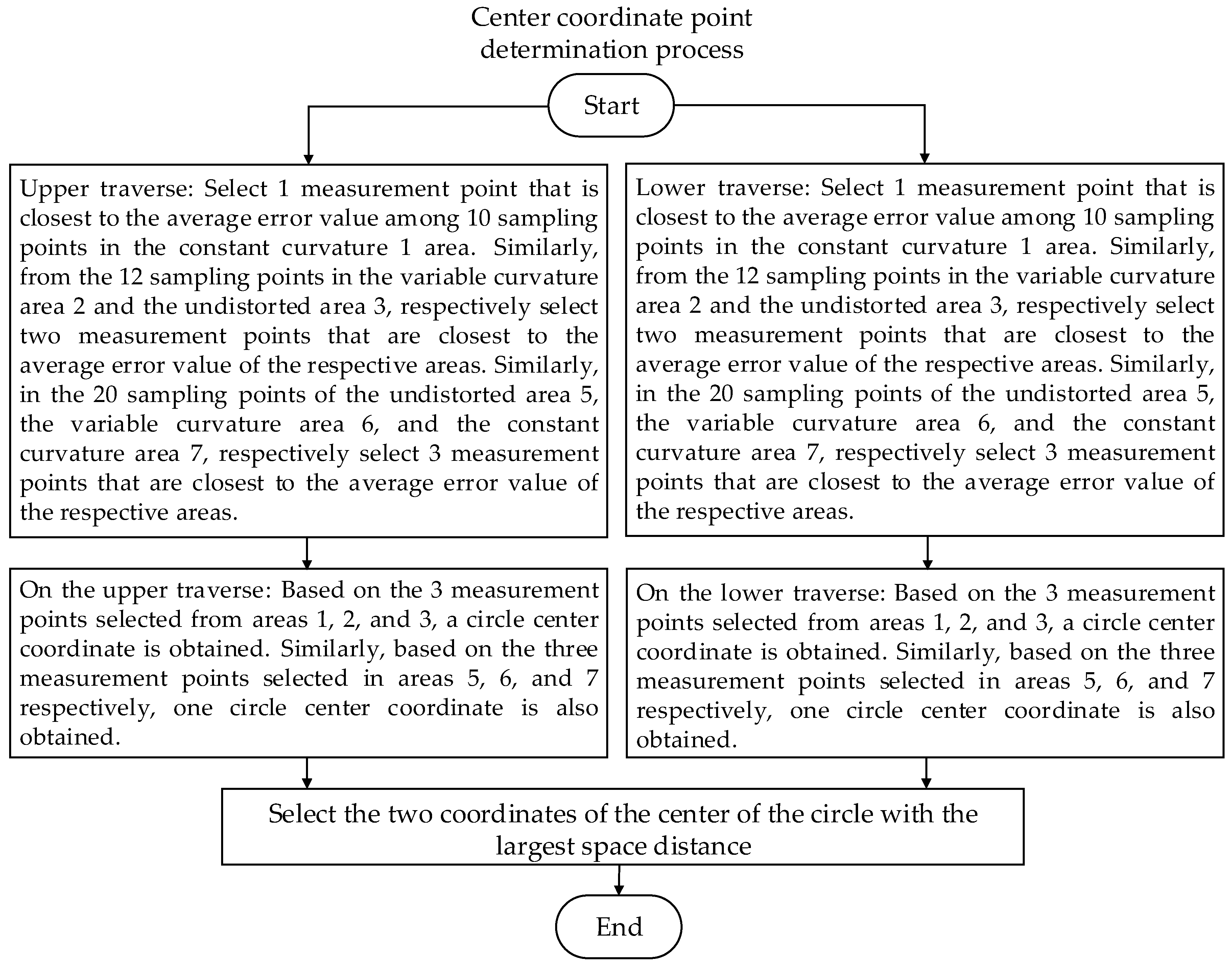
4.2. In-Machine Measurement of Sampling Point Error Based on the S-Shaped Specimen
5. Establishment and Analysis of the Machining Space Comprehensive Error Field
6. Conclusions
- (1)
- Based on the “S”-shaped specimen family, the error mapping relationship between the machining process system and the workpiece is analyzed, and the 12 geometric errors of the two rotation axes are identified by the double-center coordinate values obtained from the sampling points measured on the specimen. A comprehensive error field prediction method for five-axis machine tool machining space based on the “S”-shaped specimen family is proposed. Compared with the position error identification method based on double standard spheres, the geometric error identified by this method is about 90% consistent.
- (2)
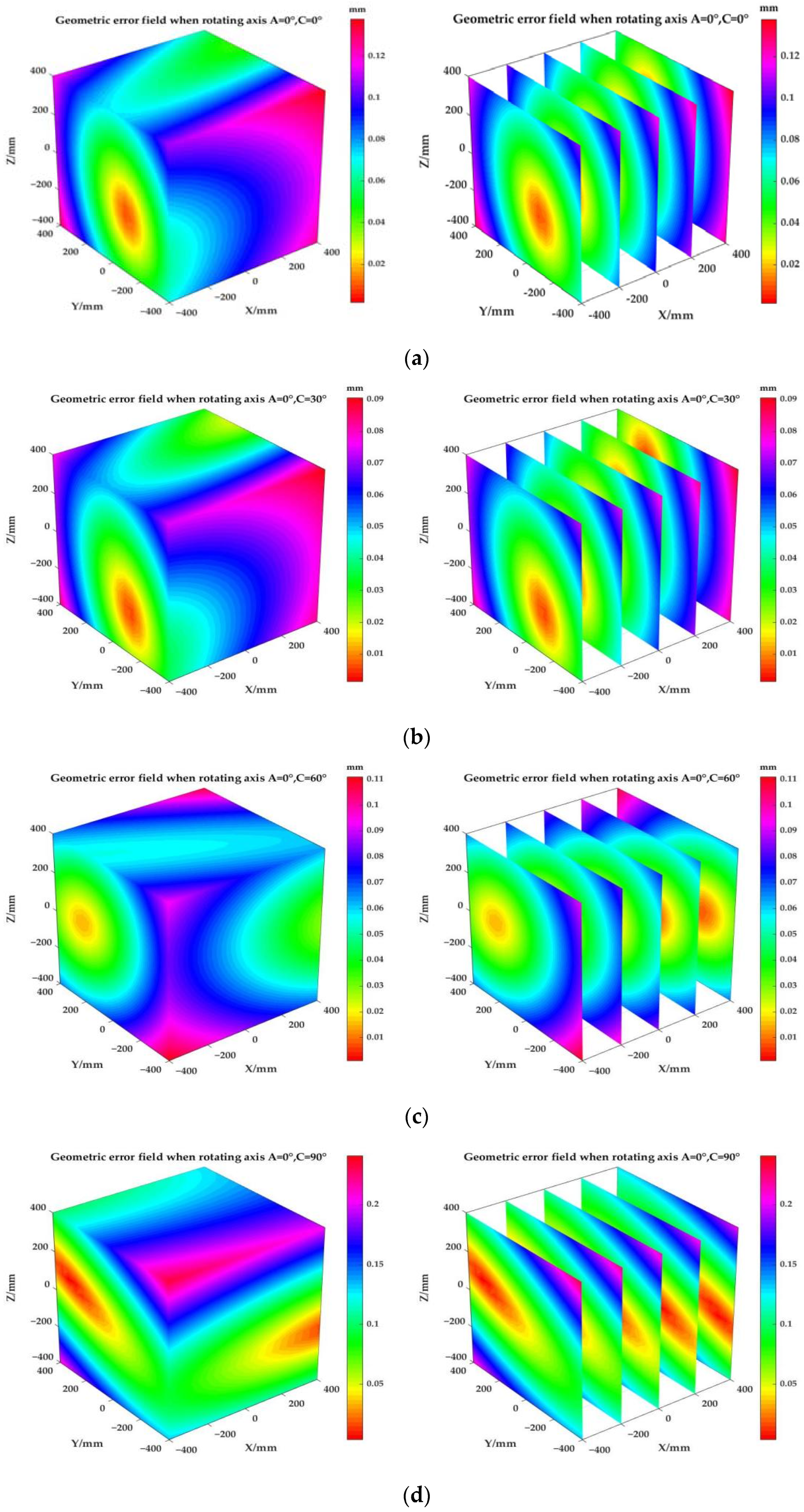
- The five-axis CNC machine rotation axis error field was plotted. As can be seen from the comprehensive error field prediction image, when A = 90° the comprehensive error is smallest at the centre of the processing space, at 0.003 mm, and the internal-to-external error is gradually increasing. The comprehensive error increases with the increase in the rotation angle of the A-axis; therefore, excessive angle rotation of the A-axis should be avoided during processing. The same predictive image by the comprehensive error field can be seen in the A-axis angle. To maintain the constant C-axis angle from 0° to 30°, the angle gradually increased, the machine’s processing comprehensive error gradually increased, therefore excessive angle rotation of the C-axis during processing should also be avoided.
- (3)
- This paper proposes using S-shaped test pieces manufactured by high-precision machine tool processing as a sample of machine geometry error detection, which is cost-effective. However, considering that there are not only geometric errors in the processing of “S” test pieces, but also thermal errors and machine vibration, these factors may make the measurement of geometric errors inaccurate. Therefore, it is necessary to further study the separation and identification of machine tool processing errors in the future.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Qiao, Y.; Chen, Y.; Yang, J. A five-axis geometric errors calibration model based on the common perpendicular line (CPL) transformation using the product of exponentials (POE) formula. Int. J. Mach. Tools Manuf. 2017, 118, 49–60. [Google Scholar] [CrossRef]
- Zhong, G.; Wang, C.; Yang, S. Position geometric error modelling, identification and compensation for large 5-axis machining centre prototype. Int. J. Mach. Tools Manuf. 2015, 89, 142–150. [Google Scholar] [CrossRef]
- Fan, J.; Zhang, Y. A novel methodology for predicting and identifying geometric errors of rotary axis in five-axis machine tools. Int. J. Adv. Manuf. Technol. 2020, 108, 705–719. [Google Scholar] [CrossRef]
- Fu, G.; Gong, H.; Fu, J. Geometric error contribution modelling and sensitivity evaluating for each axis of five-axis machine tools based on POE theory and transforming differential changes between coordinate frames. Int. J. Mach. Tools Manuf. 2019, 147, 103455. [Google Scholar] [CrossRef]
- Wu, C.; Fan, J.; Wang, Q. Prediction and compensation of geometric error for translational axes in multi-axis machine tools. Int. J. Adv. Manuf. Technol. 2018, 95, 3413–3435. [Google Scholar] [CrossRef]
- Liang, R.; Li, W.; Wang, Z. A method to decouple the geometric errors for rotary axis in a five-axis CNC machine. Meas. Sci. Technol. 2020, 31, 085007. [Google Scholar] [CrossRef]
- Zheng, F.; Feng, Q.; Zhang, B. A high-precision laser method for directly and quickly measuring 21 geometric motion errors of three linear axes of computer numerical control machine tools. Int. J. Adv. Manuf. Technol. 2020, 109, 1285–1296. [Google Scholar] [CrossRef]
- Guo, S.; Tang, S.; Jiang, G. Highly efficient and accurate calibration method for the position-dependent geometric errors of the rotary axes of a five-axis machine tool. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2021, 235, 23–33. [Google Scholar] [CrossRef]
- Huang, N.; Jin, Y.; Li, X. Identification of integrated geometric errors of rotary axis and setup position errors for 5-axis machine tools based on machining test. Int. J. Adv. Manuf. Technol. 2019, 102, 1487–1496. [Google Scholar] [CrossRef]
- Maeng, S.; Min, S. Simultaneous geometric error identification of rotary axis and tool setting in an ultra-precision 5-axis machine tool using on-machine measurement. Precis. Eng. 2020, 63, 94–104. [Google Scholar] [CrossRef]
- Meng, F.; Wen, G.L.; Ping, W.L. Tool diameter optimization in S-shaped test piece machining. Adv. Mech. Eng. 2021, 13, 1687814020988414. [Google Scholar] [CrossRef]
- Jiang, Z.; Ding, J.; Song, Z. Modelling and simulation of surface morphology abnormality of ‘S’ test piece machined by five-axis CNC machine tool. Int. J. Adv. Manuf. Technol. 2016, 85, 2745–2759. [Google Scholar] [CrossRef]
- Wang, Q.; Wu, C.; Fan, J. A novel causation analysis method of machining defects for five-axis machine tools based on error spatial morphology of S-shaped test piece. Int. J. Adv. Manuf. Technol. 2019, 103, 3529–3556. [Google Scholar] [CrossRef]
- Guan, L.; Mo, J.; Fu, M. An improved positioning method for flank milling of S-shaped test piece. Int. J. Adv. Manuf. Technol. 2017, 92, 1349–1364. [Google Scholar] [CrossRef]
- Tao, H.; Fan, J.; Wu, C. An optimized single-point offset method for reducing the theoretical error of S-shaped test piece. Int. J. Adv. Manuf. Technol. 2019, 104, 617–629. [Google Scholar] [CrossRef]
- Zhong, Y.J.; Hua, X. A new error measurement method to identify all six error parameters of a rotational axis of a machine tool. Int. J. Mach. Tools Manuf. Des. Res. Appl. 2015, 88, 1–8. [Google Scholar]
- Zhao, L.Q.; Wei, W.; Jing, Z. All position-dependent geometric error identification for rotary axes of five-axis machine tool using double ball bar. Int. J. Adv. Manuf. Technol. 2020, 110, 1351–1366. [Google Scholar]
- Xiang, S.; Altintas, Y. Modelling and compensation of volumetric errors for five-axis machine tools. Int. J. Mach. Tools Manuf. 2016, 101, 65–78. [Google Scholar] [CrossRef]
- Dong, L.C.; Li, L.X.; Shi, W. Geometric Error Identification and Analysis of Rotary Axes on Five-Axis Machine Tool Based on Precision Balls. Appl. Sci. 2019, 10, 100. [Google Scholar] [CrossRef] [Green Version]
- ISO 10791-7: 2014; Test Conditions for Machining Centres—Part 7: Accuracy of Finished Test Piece. ISO—International Organization for Standardization: Geneva, Switzerland, 2014.





| Shaft | Corner Error | Movement Error |
|---|---|---|
| A-axis | ||
| C-axis |
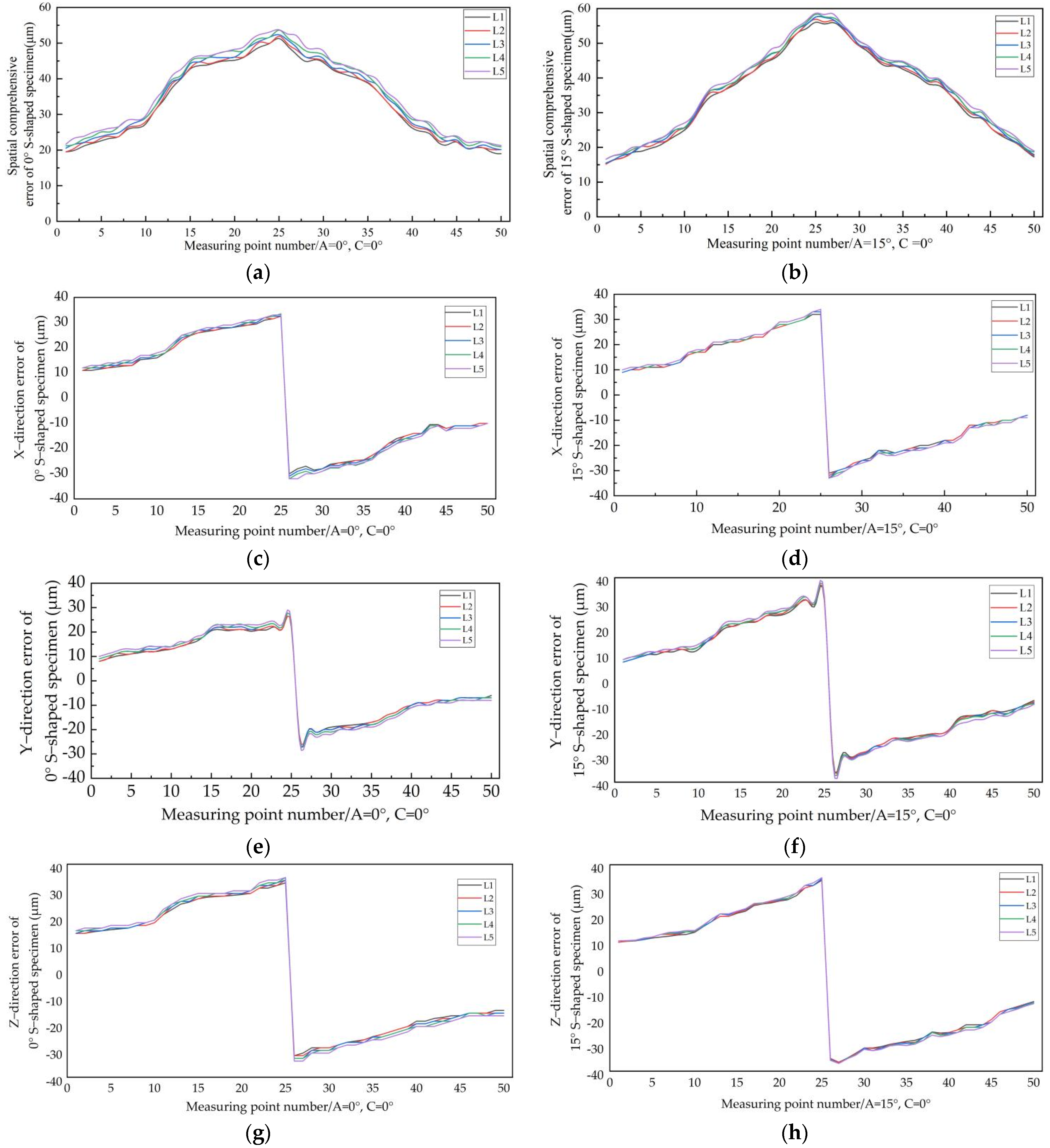
| Curvature Change of Specimen | Constant Curvature | Variable Curvature | No Distortion | Distorted | No Distortion | Variable Curvature | Constant Curvature |
|---|---|---|---|---|---|---|---|
| Measurement point | 1~10① | 11~14② | 15~22③ | 23~30④ | 31~36⑤ | 37~41⑥ | 42~50⑦ |
| Maximum error (μm) | 30 | 43 | 51 | 54 | 45 | 37 | 28 |
| Minimum error (μm) | 20 | 31 | 43 | 45 | 37 | 25 | 19 |
| Mean error (μm) | 25 | 37 | 46 | 49 | 41 | 31 | 22 |
| Curvature Change of Specimen | Constant Curvature | Variable Curvature | No Distortion | Distorted | No Distortion | Variable Curvature | Constant Curvature |
| Measurement point | 1~10① | 11~14② | 15~22③ | 23~30④ | 31~36⑤ | 37~41⑥ | 42~50⑦ |
| Maximum error (μm) | 27 | 38 | 53 | 59 | 49 | 42 | 34 |
| Minimum error (μm) | 15 | 28 | 37 | 49 | 41 | 34 | 17 |
| Mean error (μm) | 21 | 34 | 44 | 55 | 45 | 38 | 25 |
| A-Axis Angle | 0° | 30° | 60° | 90° |
|---|---|---|---|---|
| Compre- Hensive Error | ||||
| 0.004 | 0.008 | 0.003 | 0.003 | |
| 0.122 | 0.127 | 0.167 | 0.217 |
| C-Axis Angle | 0° | 30° | 60° | 90° |
|---|---|---|---|---|
| Compre- Hensive Error | ||||
| 0.004 | 0.003 | 0.004 | 0.004 | |
| 0.122 | 0.084 | 0.111 | 0.234 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, S.; Dong, Z.; Qi, F.; Fan, Z. Prediction of the Comprehensive Error Field in the Machining Space of the Five-Axis Machine Tool Based on the “S”-Shaped Specimen Family. Machines 2022, 10, 408. https://doi.org/10.3390/machines10050408
Wu S, Dong Z, Qi F, Fan Z. Prediction of the Comprehensive Error Field in the Machining Space of the Five-Axis Machine Tool Based on the “S”-Shaped Specimen Family. Machines. 2022; 10(5):408. https://doi.org/10.3390/machines10050408
Chicago/Turabian StyleWu, Shi, Zeyu Dong, Fei Qi, and Zhendong Fan. 2022. "Prediction of the Comprehensive Error Field in the Machining Space of the Five-Axis Machine Tool Based on the “S”-Shaped Specimen Family" Machines 10, no. 5: 408. https://doi.org/10.3390/machines10050408
APA StyleWu, S., Dong, Z., Qi, F., & Fan, Z. (2022). Prediction of the Comprehensive Error Field in the Machining Space of the Five-Axis Machine Tool Based on the “S”-Shaped Specimen Family. Machines, 10(5), 408. https://doi.org/10.3390/machines10050408






