Cascading Failure Analysis of Hierarchical Industrial Wireless Sensor Networks under the Impact of Data Overload
Abstract
:1. Introduction
1.1. Motivation
- Under the influence of harsh industrial environments (such as noise, exhaust gas, dust, and high temperature), industrial wireless sensors pose severe challenges to the survival and stability of the network, which becomes more prone to cascading failures;
- High topology complexity means that the network node layout in the industrial site is more complex, and the coverage is more considerable. Using the simple networking topology (e.g., star topology) is not suitable;
- The real-time performance of data transmission, in some scenarios, requires data to be transmitted at a breakneck speed to reduce the risk of accidents.
1.2. Literature Review
1.2.1. Research Status of IWSNs
1.2.2. Research Status of Cascading Failure
1.3. Our Contribution
- Different from previous cascading failure planar structural models, a parameter-adjustable cascading failure simulation model with hierarchical architecture is established to make its network topology closer to the actual scenario;
- To address the problem that conventional destructibility metrics are not applicable to industrial complex environments, the destructibility measure is optimized by combining communication efficiency and direct connection survivability;
- Aiming at the problem that the allocation strategy of the planar structure is not suitable for the hierarchical structure, we adopt the dynamic capacity allocation methods. Through experiments, the invulnerability of the network can be improved.
- According to the characteristics of cascading failure hierarchical topology, we study the impact of single-hop cluster head node capacity on the network’s re-resistance to damage, to provide a reference for building a higher quality network.
2. Preliminaries
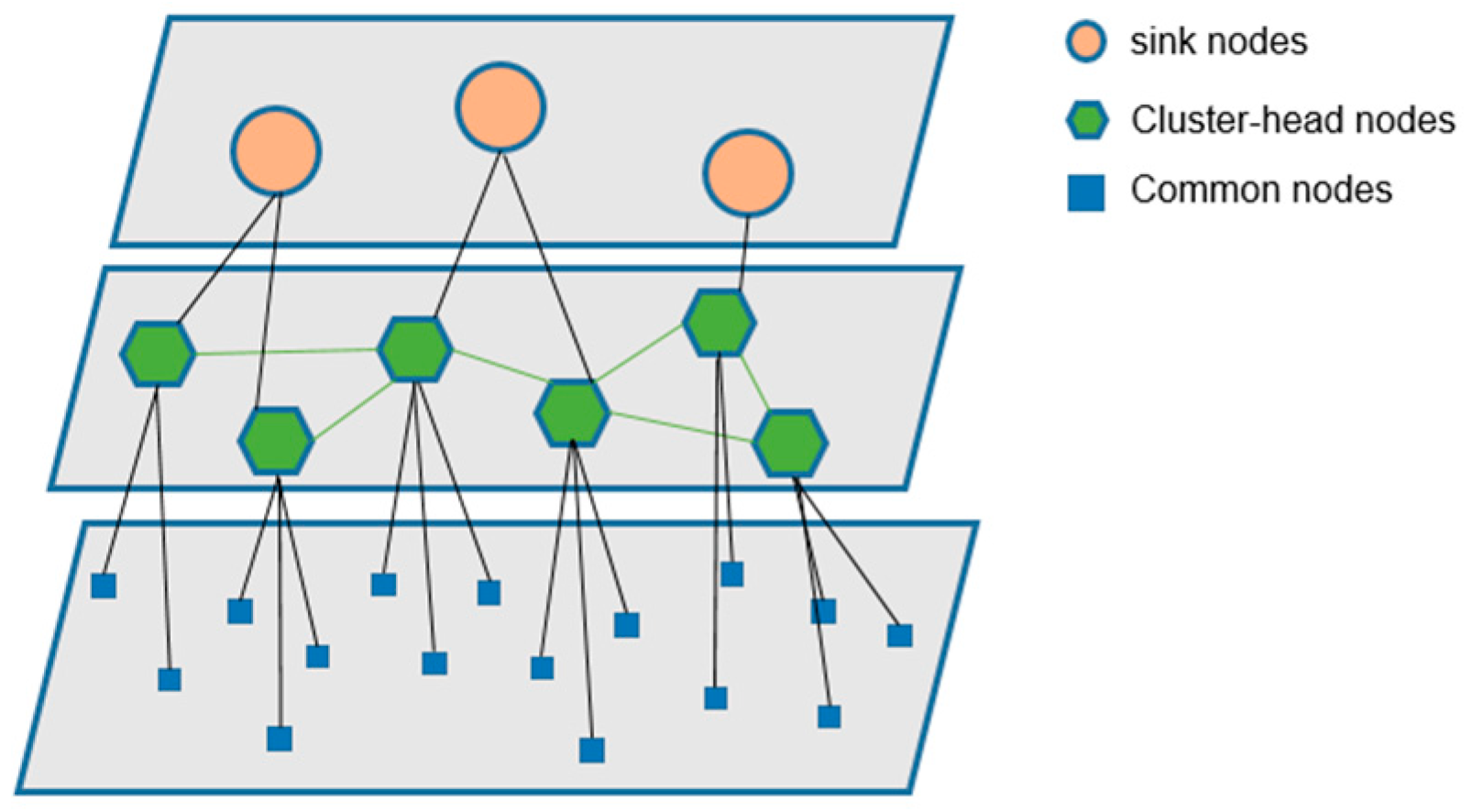
2.1. Hierarchical Topology of IWSNs
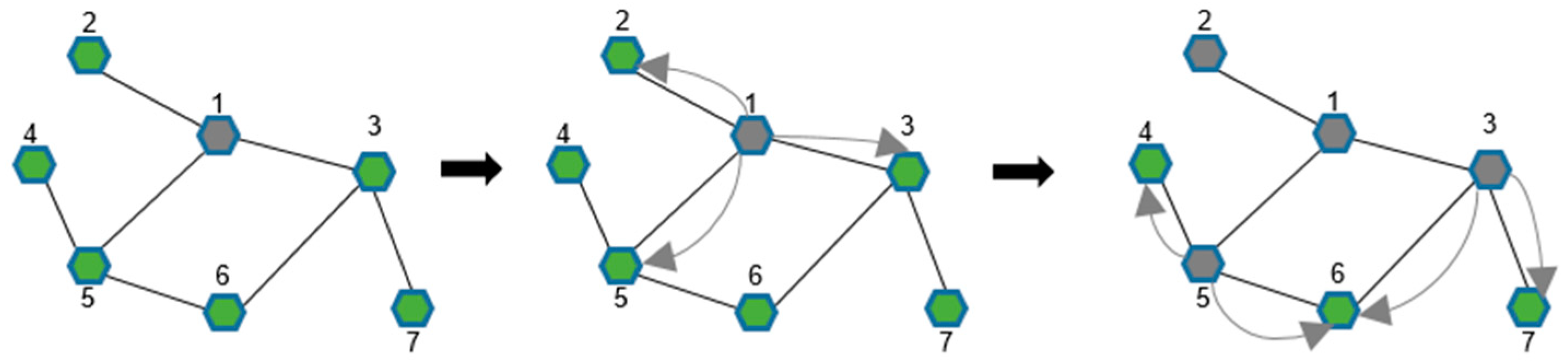
2.2. Cascading Failure Mechanism
2.3. Load-Capacity and Allocation Mechanisms
3. Main Results
3.1. The Improved Evaluation Mechanism of IWSNs
3.2. The Improved Load and Capacity Metrics of IWSNs
3.3. The Improved Dynamic Allocation Method
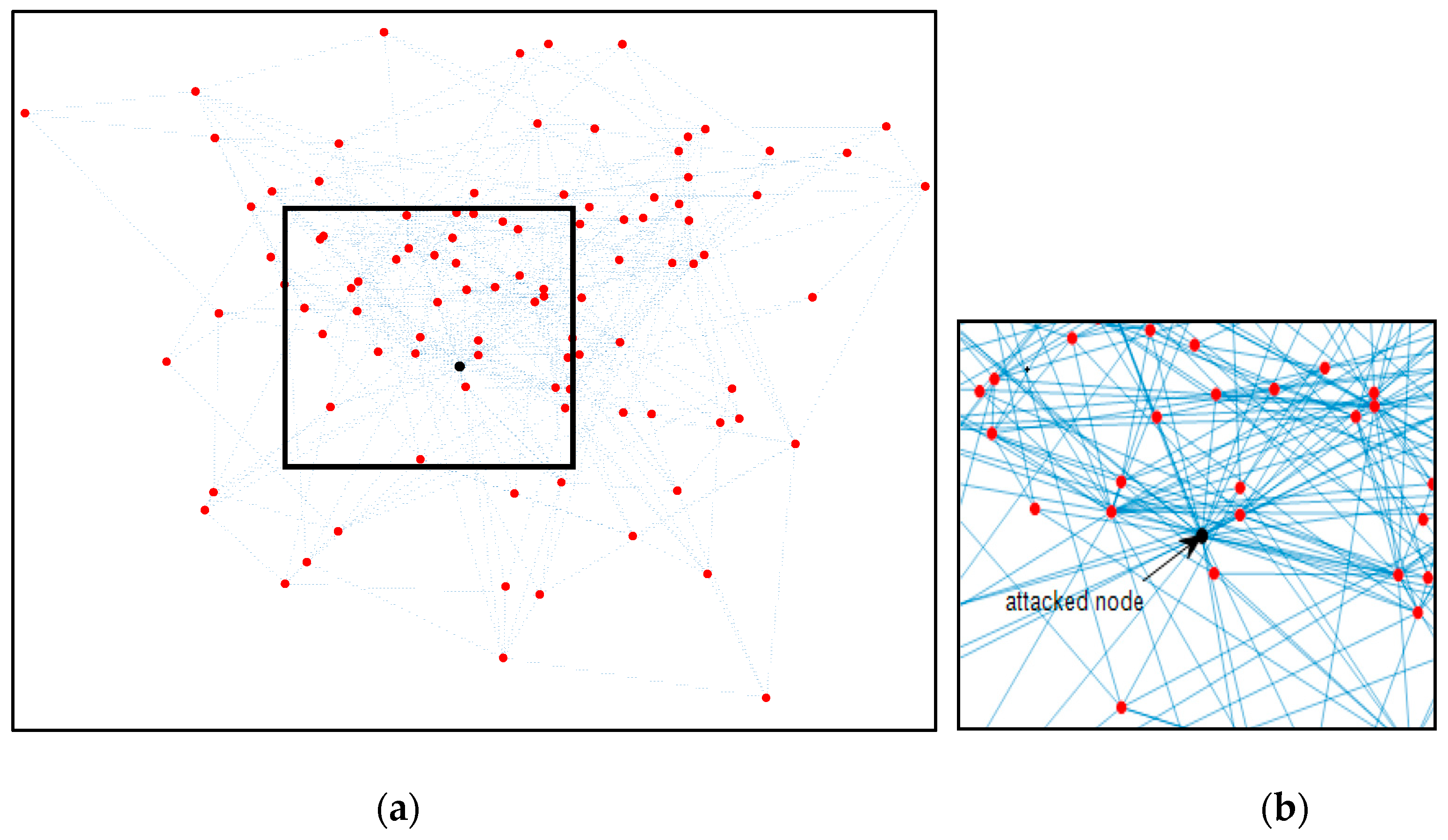
4. Simulations
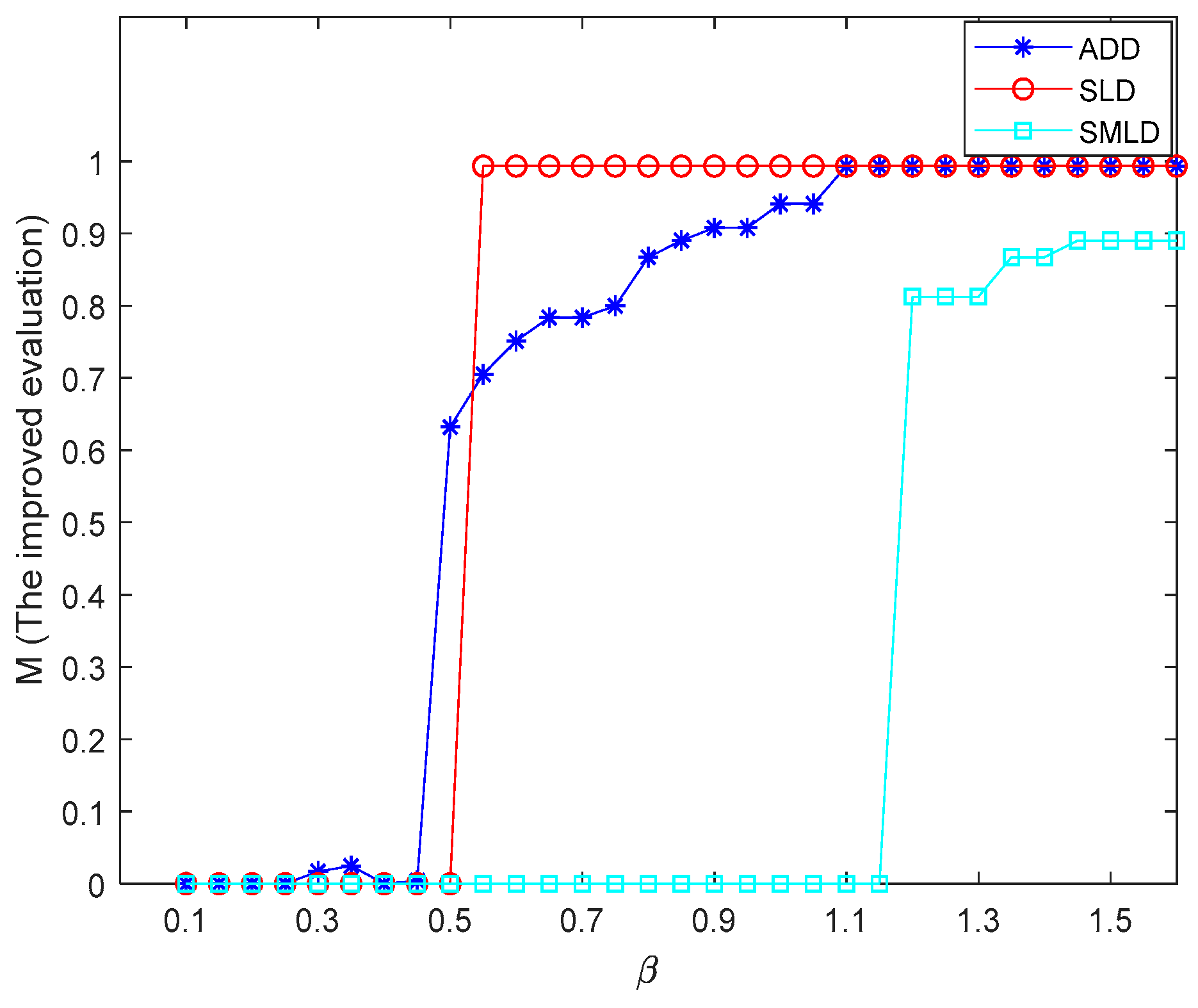
4.1. Comparison of Evaluation Indicators
4.2. Impact of Some Parameters on the Invulnerability Performance
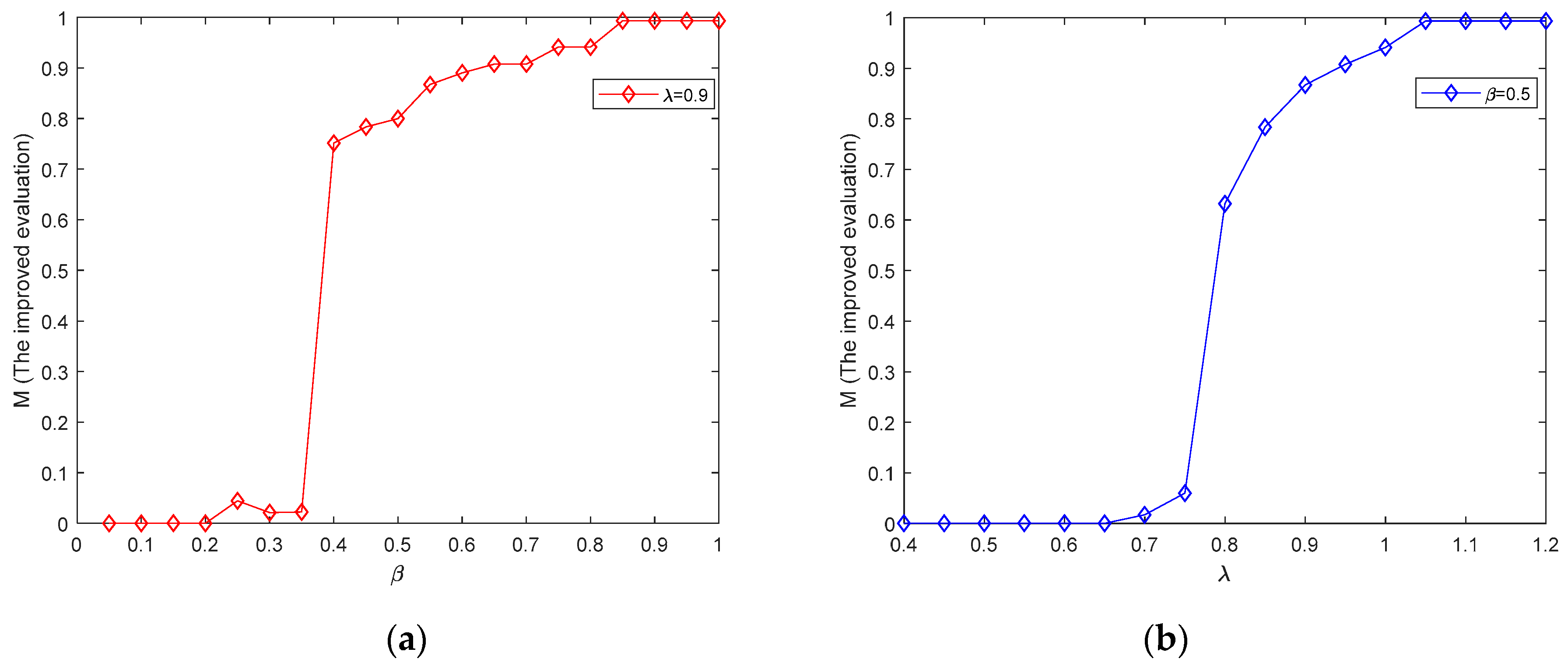
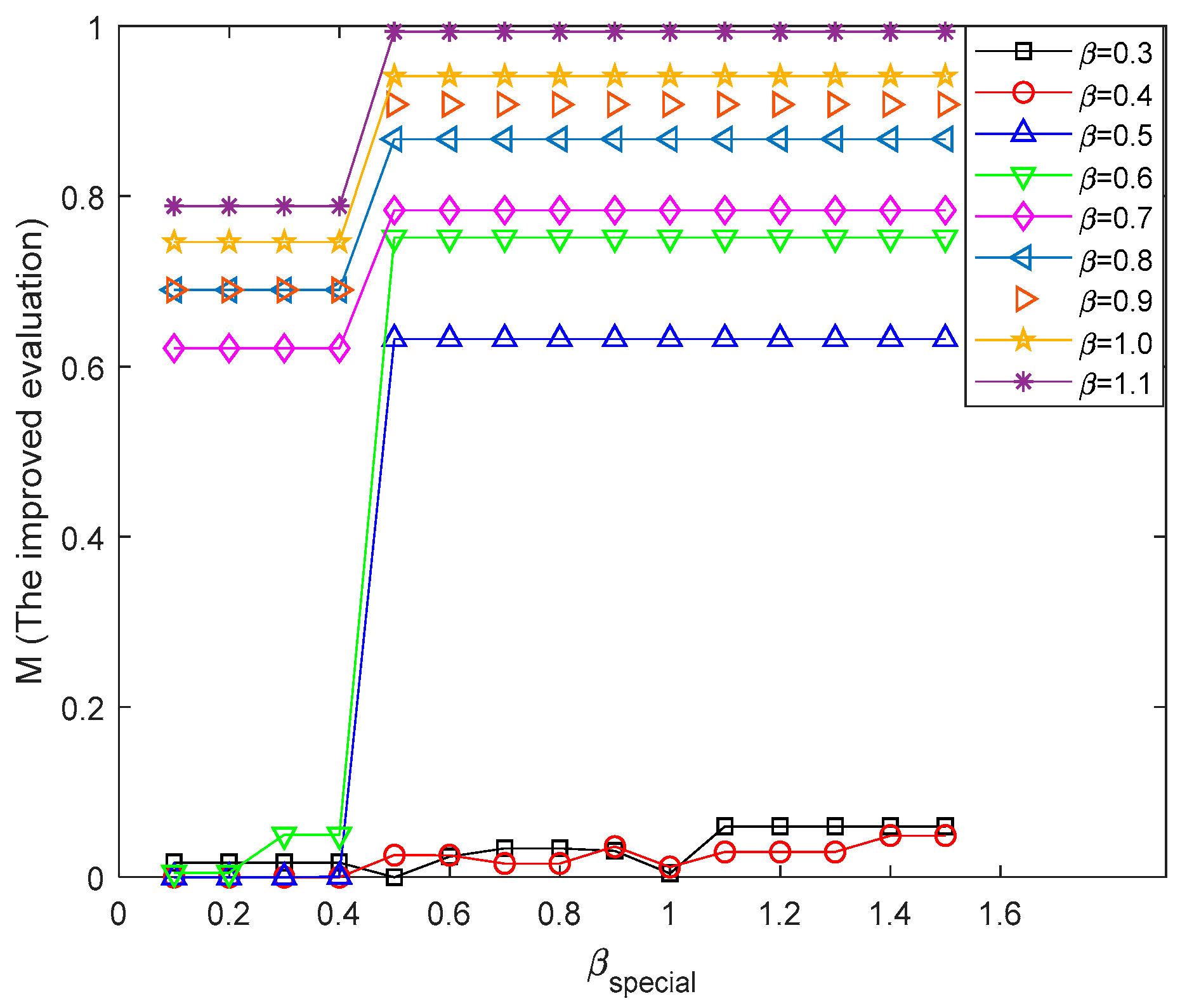
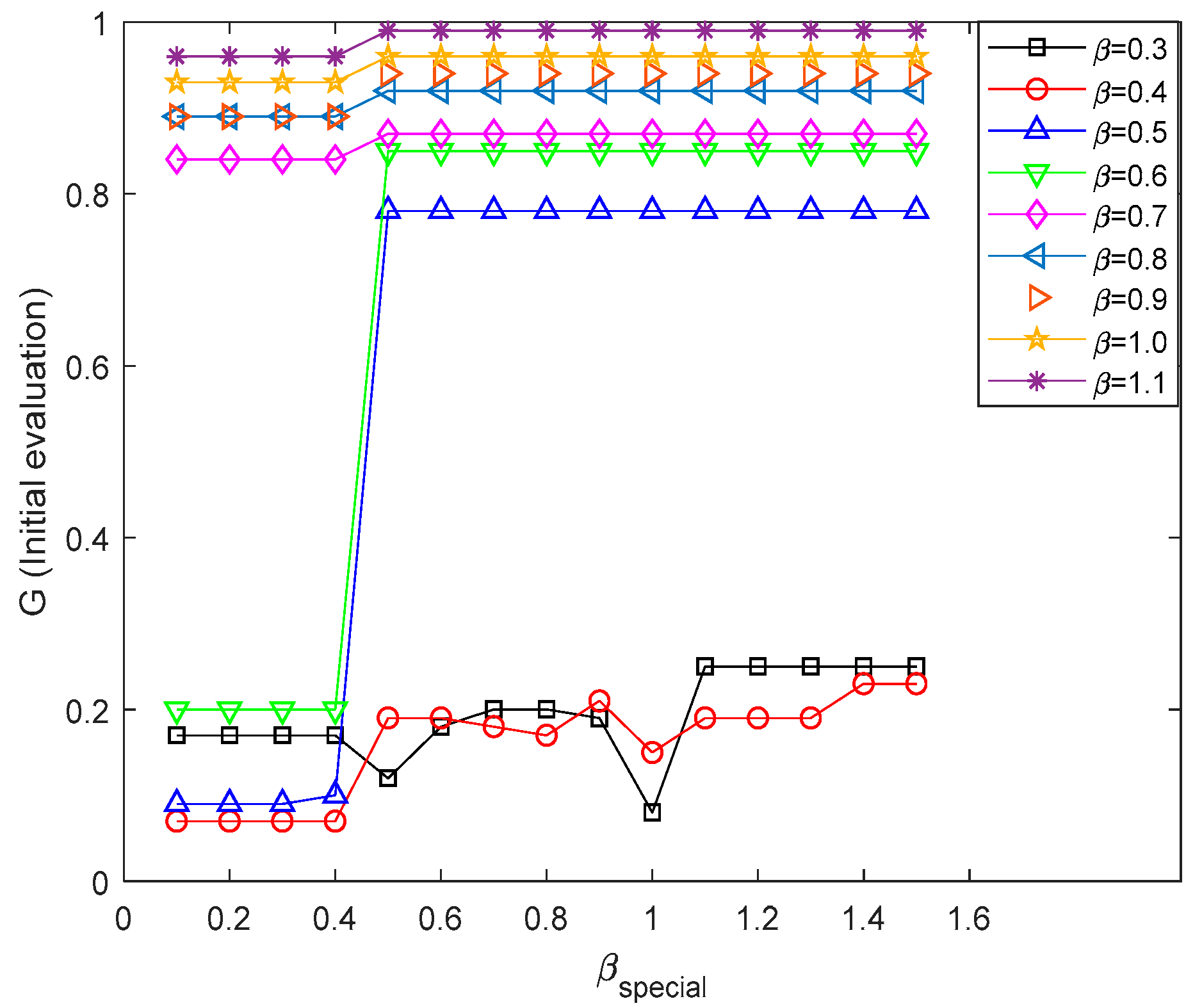
4.2.1. Effect of Capacity Regulation Parameters
4.2.2. Impact of Single-Hop Cluster Head Node Capacity
4.3. Impact of Dynamic Redistribution Strategies on Invulnerability Performance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xing, L. Cascading Failures in Internet of Things: Review and Perspectives on Reliability and Resilience. IEEE Internet Things J. 2020, 8, 44–64. [Google Scholar] [CrossRef]
- Xiao, X.; Roh, B.-M.; Zhu, F. Strength Enhancement in Fused Filament Fabrication via the Isotropy Toolpath. Appl. Sci. 2021, 11, 6100. [Google Scholar] [CrossRef]
- Xiao, X.; Joshi, S. Process planning for five-axis support free additive manufacturing. Addit. Manuf. 2020, 36, 101569. [Google Scholar] [CrossRef]
- Kumarage, H.; Khalil, I.; Tari, Z.; Zomaya, A. Distributed anomaly detection for industrial wireless sensor networks based on fuzzy data modelling. J. Parallel Distrib. Comput. 2013, 73, 790–806. [Google Scholar] [CrossRef]
- Raza, M.; Aslam, N.; Le Minh, H.; Hussain, S.; Cao, Y.; Khan, N.M. A Critical Analysis of Research Potential, Challenges, and Future Directives in Industrial Wireless Sensor Networks. IEEE Commun. Surv. Tutor. 2017, 20, 39–95. [Google Scholar] [CrossRef]
- Jan, B.; Farman, H.; Javed, H.; Montrucchio, B.; Khan, M.; Ali, S. Energy Efficient Hierarchical Clustering Approaches in Wireless Sensor Networks: A Survey. Wirel. Commun. Mob. Comput. 2017, 2017, 6457942. [Google Scholar] [CrossRef] [Green Version]
- Rostami, A.S.; Badkoobe, M.; Mohanna, F.; Keshavarz, H.; Hosseinabadi, A.A.R.; Sangaiah, A.K. Survey on clustering in heterogeneous and homogeneous wireless sensor networks. J. Supercomput. 2018, 74, 277–323. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, Q.; Xu, Y.; Liu, J.; He, C. MPDMAC-SIC: Priority-based distributed low delay MAC with successive interference cancellation for multi-hop industrial wireless networks. Comput. Commun. 2020, 154, 48–57. [Google Scholar] [CrossRef]
- Liu, M.; Yang, K.; Zhao, N.; Chen, Y.; Song, H.; Gong, F. Intelligent Signal Classification in Industrial Distributed Wireless Sensor Networks Based Industrial Internet of Things. IEEE Trans. Ind. Inform. 2020, 17, 4946–4956. [Google Scholar] [CrossRef]
- Borgiani, V.; Moratori, P.; Kazienko, J.F.; Tubino, E.R.R.; Quincozes, S.E. Toward a Distributed Approach for Detection and Mitigation of Denial-of-Service Attacks within Industrial Internet of Things. IEEE Internet Things J. 2020, 8, 4569–4578. [Google Scholar] [CrossRef]
- Cao, B.; Zhao, J.; Lv, Z.; Liu, X.; Kang, X.; Yang, S. Deployment optimization for 3D industrial wireless sensor networks based on particle swarm optimizers with distributed parallelism. J. Netw. Comput. Appl. 2018, 103, 225–238. [Google Scholar] [CrossRef]
- Gholami, M.; Taboun, M.; Brennan, R. An ad hoc distributed systems approach for industrial wireless sensor network management. J. Ind. Inf. Integr. 2019, 15, 239–246. [Google Scholar] [CrossRef]
- Zhong, J.; Zhang, F.; Yang, S.; Li, D. Restoration of interdependent network against cascading overload failure. Phys. A Stat. Mech. Appl. 2019, 514, 884–891. [Google Scholar] [CrossRef]
- Ren, W.; Wu, J.; Zhang, X.; Lai, R.; Chen, L. A Stochastic Model of Cascading Failure Dynamics in Communication Networks. IEEE Trans. Circuits Syst. II Express Briefs 2018, 65, 632–636. [Google Scholar] [CrossRef]
- Shen, Y.; Ren, G.; Ran, B. Cascading failure analysis and robustness optimization of metro networks based on coupled map lattices: A case study of Nanjing, China. Transportation 2021, 48, 537–553. [Google Scholar] [CrossRef]
- Vivek, S. Cascading Failure from Targeted Road Network Disruptions. arXiv 2020, arXiv:2010.09887. [Google Scholar]
- Shen, Y.; Ren, G.; Ran, B. Analysis of cascading failure induced by load fluctuation and robust station capacity assignment for metros. Transp. A Transp. Sci. 2021, 1942304. [Google Scholar] [CrossRef]
- Liao, W.; Salinas, S.; Li, M.; Li, P.; Loparo, K.A. Cascading Failure Attacks in the Power System: A Stochastic Game Perspective. IEEE Internet Things J. 2017, 4, 2247–2259. [Google Scholar] [CrossRef]
- Guo, H.; Zheng, C.; Iu, H.H.-C.; Fernando, T. A critical review of cascading failure analysis and modeling of power system. Renew. Sustain. Energy Rev. 2017, 80, 9–22. [Google Scholar] [CrossRef]
- Zhao, Z. Research on Invulnerability of Wireless Sensor Networks Based on Complex Network Topology Structure. Int. J. Online Eng. 2017, 13, 100. [Google Scholar] [CrossRef] [Green Version]
- Tan, X.; Tang, J.; Yu, L.; Wang, J. A New Energy-Efficient and Fault-Tolerant Evolution Model for Large-Scale Wireless Sensor Networks Based on Complex Network Theory. Int. J. Distrib. Syst. Technol. 2019, 10, 21–36. [Google Scholar] [CrossRef]
- Liu, H.-R.; Dong, M.-R.; Yin, R.-R.; Han, L. Cascading failure in the wireless sensor scale-free networks. Chin. Phys. B 2015, 24, 050506. [Google Scholar] [CrossRef]
- Fu, X.; Yao, H.; Yang, Y. Cascading failures in wireless sensor networks with load redistribution of links and nodes. Ad Hoc Netw. 2019, 93, 101900. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, Z.; Shao, F. Survivability Analysis on a Cyber-Physical System. Machines 2017, 5, 17. [Google Scholar] [CrossRef] [Green Version]
- Guo, Z.; Wang, Y.; Zhong, J.; Fu, C.; Sun, Y.; Li, J.; Chen, Z.; Wen, G. Effect of load-capacity heterogeneity on cascading overloads in networks. Chaos Interdiscip. J. Nonlinear Sci. 2021, 31, 123104. [Google Scholar] [CrossRef]
- Fan, C.; Wang, B.; Tian, J. Cascading failure model in aviation network considering overload condition and failure probability. J. Comput. Appl. 2022, 42, 502. [Google Scholar] [CrossRef]
- Zhong, J.; Sanhedrai, H.; Zhang, F.; Yang, Y.; Guo, S.; Yang, S.; Li, D. Network endurance against cascading overload failure. Reliab. Eng. Syst. Saf. 2020, 201, 106916. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, Z.; Qi, X.; Liu, L. Identify Critical Nodes in Network Cascading Failure Based on Data Analysis. J. Netw. Syst. Manag. 2020, 28, 21–34. [Google Scholar] [CrossRef]
- Potts, M.W.; Sartor, P.A.; Johnson, A.; Bullock, S. A network perspective on assessing system architectures: Robustness to cascading failure. Syst. Eng. 2020, 23, 597–616. [Google Scholar] [CrossRef]
- Lei, W.; Ma, J.; Ma, S. Robustness analysis of scale-free networks against cascading failures with tunable redistribution load parameters. In Proceedings of the 2021 China Automation Congress (CAC), Beijing, China, 22–24 October 2021; pp. 2908–2911. [Google Scholar] [CrossRef]
- Hou, Y.; Xing, X.; Li, M.; Zeng, A.; Wang, Y. Overload cascading failure on complex networks with heterogeneous load redistribution. Phys. A Stat. Mech. Appl. 2017, 481, 160–166. [Google Scholar] [CrossRef]
- Xiao, X.; Joshi, S.; Cecil, J. Critical assessment of Shape Retrieval Tools (SRTs). Int. J. Adv. Manuf. Technol. 2021, 116, 3431–3446. [Google Scholar] [CrossRef]
- Zhang, L.; Xia, J.; Cheng, F.; Qiu, J.; Zhang, X. Multi-Objective Optimization of Critical Node Detection Based on Cascade Model in Complex Networks. IEEE Trans. Netw. Sci. Eng. 2020, 7, 2052–2066. [Google Scholar] [CrossRef]
- Liu, C.; Li, D.; Fu, B.; Yang, S.; Wang, Y.; Lu, G. Modeling of self-healing against cascading overload failures in complex networks. Eur. Lett. 2014, 107, 68003. [Google Scholar] [CrossRef]
- Shen, Y.; Ren, G.; Zhang, N.; Song, G.; Wang, Q.; Ran, B. Effects of mutual traffic redistribution on robustness of interdependent networks to cascading failures under fluctuant load. Phys. A Stat. Mech. Appl. 2020, 560, 125138. [Google Scholar] [CrossRef]
- Qi, X.; Yang, G.; Liu, L. Robustness analysis of the networks in cascading failures with controllable parameters. Phys. A Stat. Mech. Appl. 2020, 539, 122870. [Google Scholar] [CrossRef]
- Liu, X. Atypical Hierarchical Routing Protocols for Wireless Sensor Networks: A Review. IEEE Sensors J. 2015, 15, 5372–5383. [Google Scholar] [CrossRef]
- Ávila, K.; Sanmartin, P.; Jabba, D.; Gómez, J. An analytical Survey of Attack Scenario Parameters on the Techniques of Attack Mitigation in WSN. Wirel. Pers. Commun. 2021, 1–32. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; Dai, H.; Eun, D.Y. Maximization of Robustness of Interdependent Networks Under Budget Constraints. IEEE Trans. Netw. Sci. Eng. 2019, 7, 1441–1452. [Google Scholar] [CrossRef]
- Shi, X.; Deng, D.; Long, W.; Li, Y.; Yu, X. Research on the robustness of interdependent supply networks with tunable parameters. Comput. Ind. Eng. 2021, 158, 107431. [Google Scholar] [CrossRef]
- Fu, X.; Yang, Y. Modeling and analyzing cascading failures for Internet of Things. Inf. Sci. 2021, 545, 753–770. [Google Scholar] [CrossRef]
| Related Literature | Network Structure |
|---|---|
| [20,22,30] | scale-free network |
| [21,28] | Barabási–Albert (BA) network |
| [15,26,39] | reality network |
| [24,39,40] | coupled network |
| Exponential Adjustment Parameter β | Number of Surviving Nodes | Communication Efficiency E (×104) | Comprehensive Evaluation Indicators | ||
|---|---|---|---|---|---|
| M | G | M | G | ||
| 0.1 | 0 | 0 | 0 | 0 | 0 |
| 0.2 | 0 | 5 | 0 | 0 | 0.050 |
| 0.3 | 13 | 17 | 4.91 | 0.017 | 0.170 |
| 0.4 | 0 | 7 | 0 | 0 | 0.070 |
| 0.5 | 78 | 78 | 32.39 | 0.631 | 0.780 |
| 0.6 | 85 | 85 | 35.37 | 0.751 | 0.850 |
| 0.7 | 87 | 87 | 36.05 | 0.784 | 0.870 |
| 0.8 | 92 | 92 | 37.75 | 0.867 | 0.920 |
| 0.9 | 94 | 94 | 38.68 | 0.908 | 0.940 |
| 1.0 | 96 | 96 | 39.28 | 0.941 | 0.960 |
| 1.1 | 99 | 99 | 40.22 | 0.993 | 0.990 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, H.; Wu, Z.; Zhang, X.; Jiang, B.; Gao, Q. Cascading Failure Analysis of Hierarchical Industrial Wireless Sensor Networks under the Impact of Data Overload. Machines 2022, 10, 380. https://doi.org/10.3390/machines10050380
Lv H, Wu Z, Zhang X, Jiang B, Gao Q. Cascading Failure Analysis of Hierarchical Industrial Wireless Sensor Networks under the Impact of Data Overload. Machines. 2022; 10(5):380. https://doi.org/10.3390/machines10050380
Chicago/Turabian StyleLv, Hongchi, Zhengtian Wu, Xin Zhang, Baoping Jiang, and Qing Gao. 2022. "Cascading Failure Analysis of Hierarchical Industrial Wireless Sensor Networks under the Impact of Data Overload" Machines 10, no. 5: 380. https://doi.org/10.3390/machines10050380
APA StyleLv, H., Wu, Z., Zhang, X., Jiang, B., & Gao, Q. (2022). Cascading Failure Analysis of Hierarchical Industrial Wireless Sensor Networks under the Impact of Data Overload. Machines, 10(5), 380. https://doi.org/10.3390/machines10050380







