Practical Obstacle-Overcoming Robot with a Heterogeneous Sensing System: Design and Experiments
Abstract
:1. Introduction
- The robot has a compact construct, a flat upper surface and high load capacity, and it is reliable in different motion modes. It can work for different application scenarios and easily facilitate actuators or load payloads, such as robotic arms.
- A heterogeneous perception system is designed to solve the complex problem of robot motion execution in various scenes.
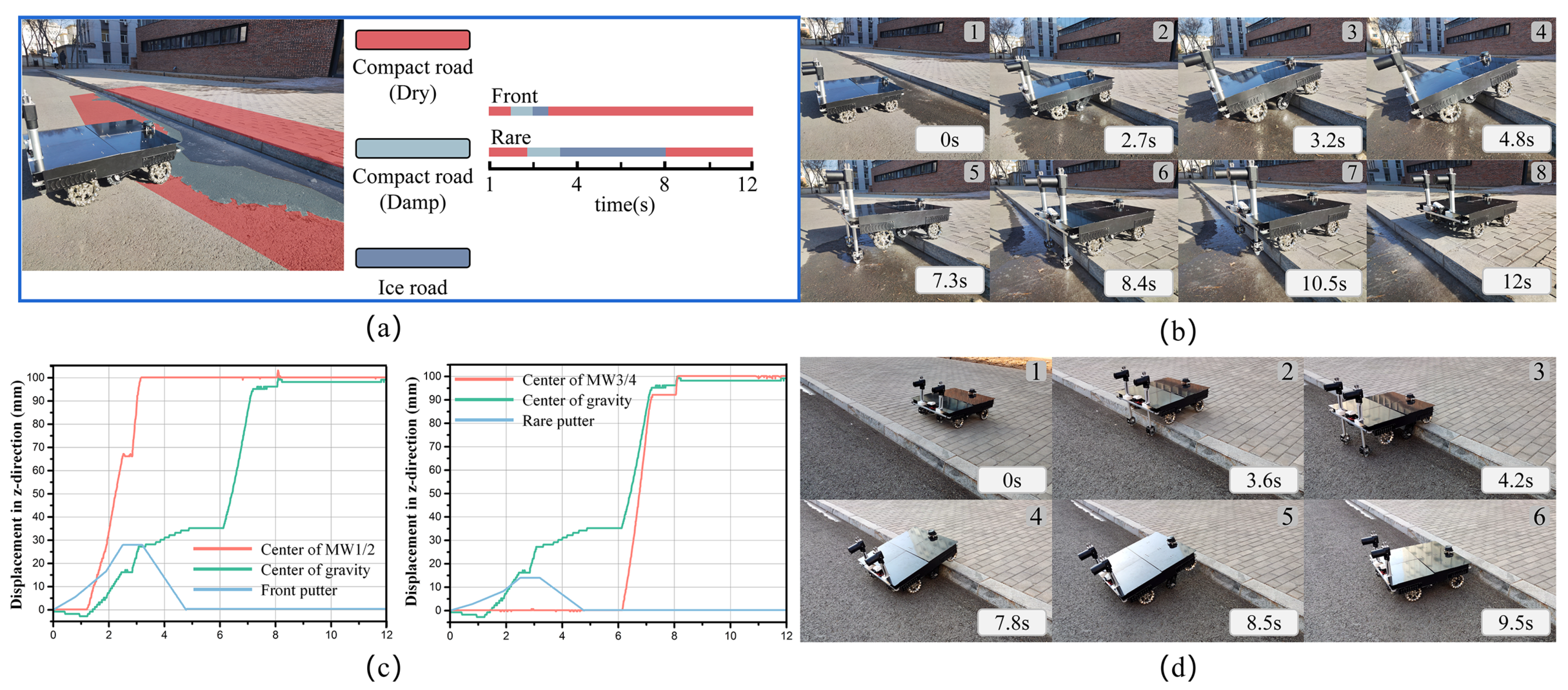
- An overall motion strategy is presented for the robot. The strategy is based on heterogeneous sensing systems and the determination of motion parameters for overcoming obstacles. The robot performs stably using this strategy when overcoming obstacles in complex environments.
2. Related Works
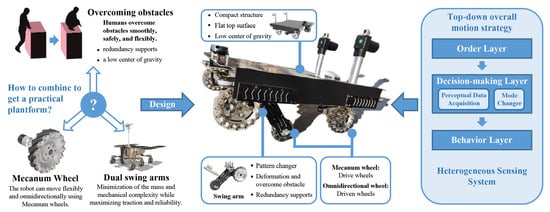
3. Design of Robotic Platform
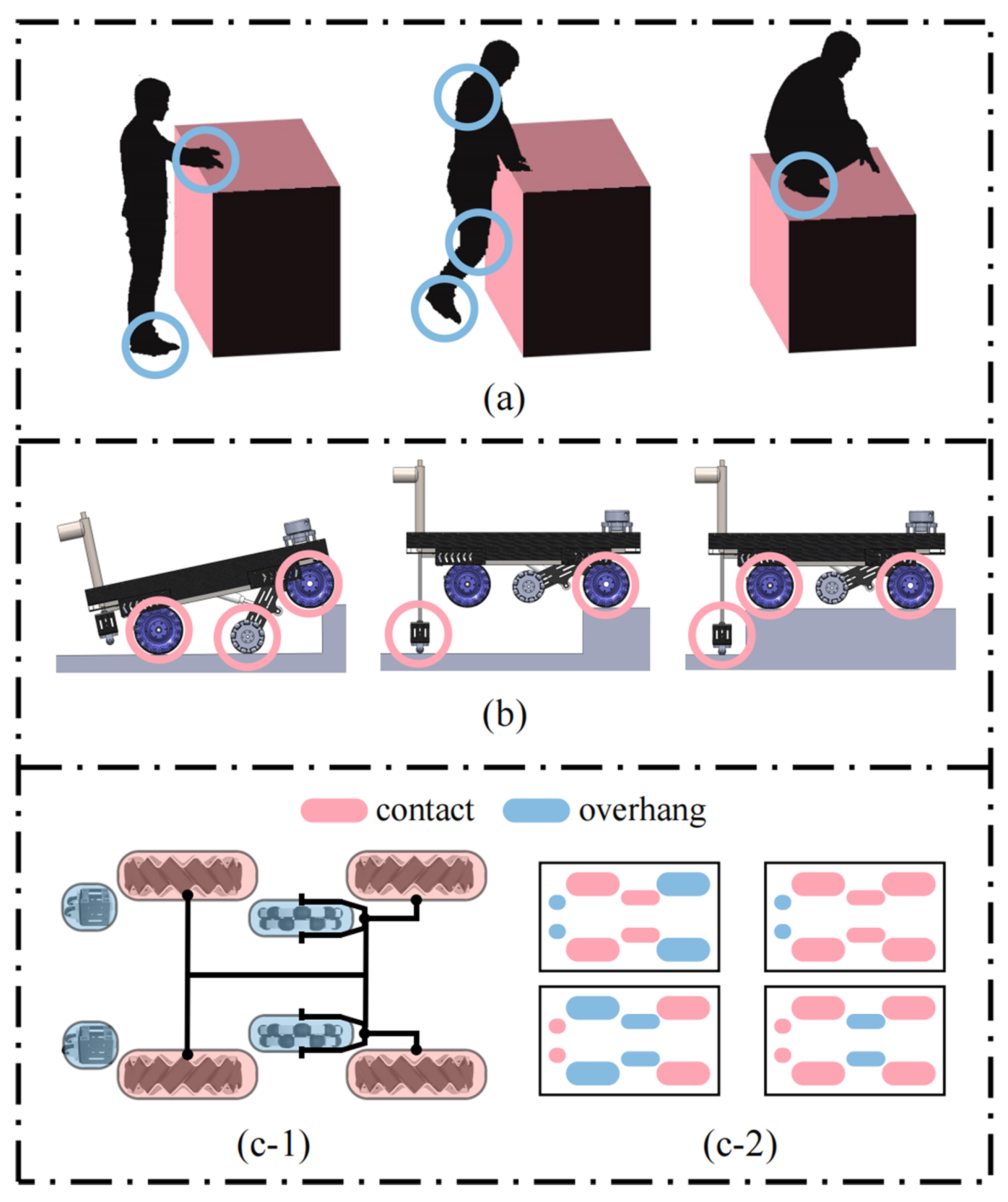
3.1. Design Concept
3.2. Prototype Platform
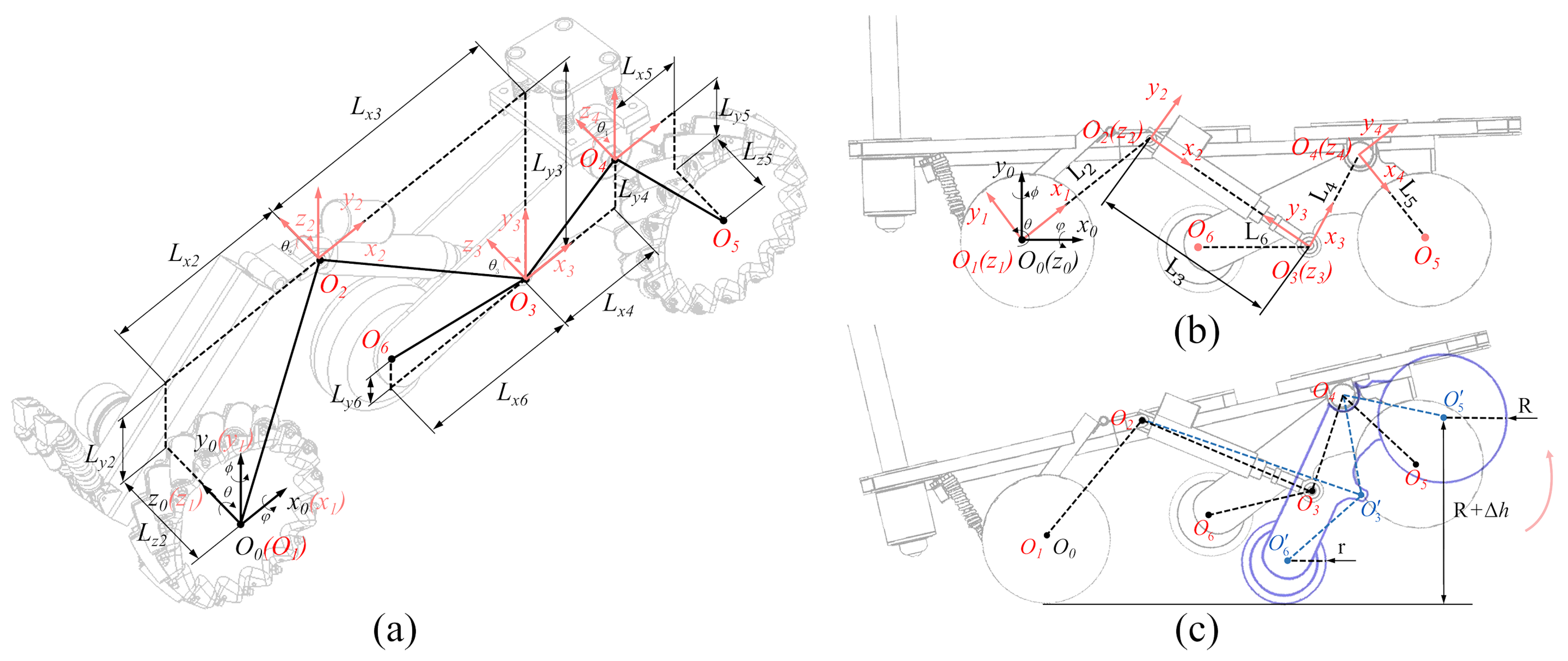
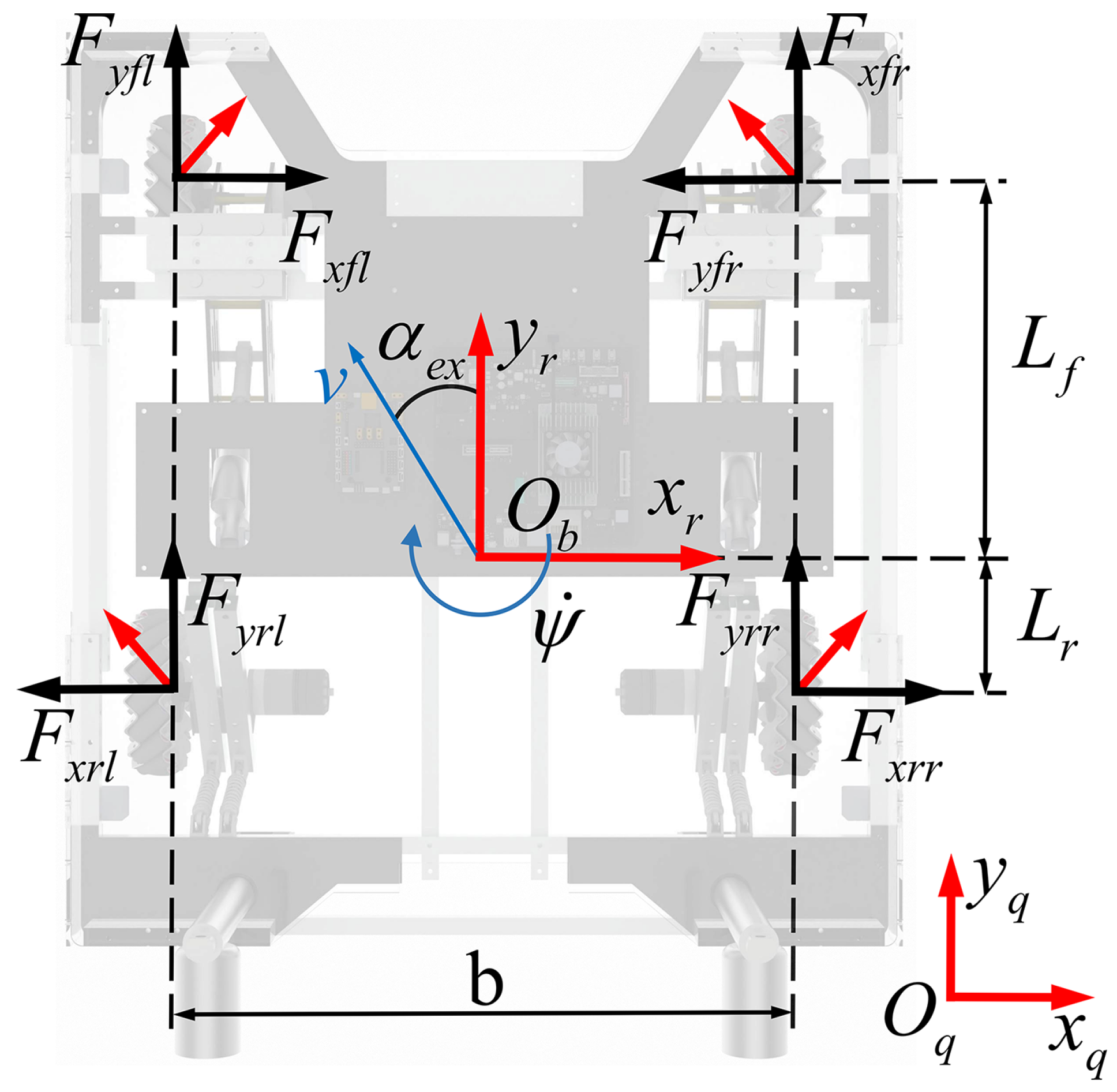
3.3. Modelling
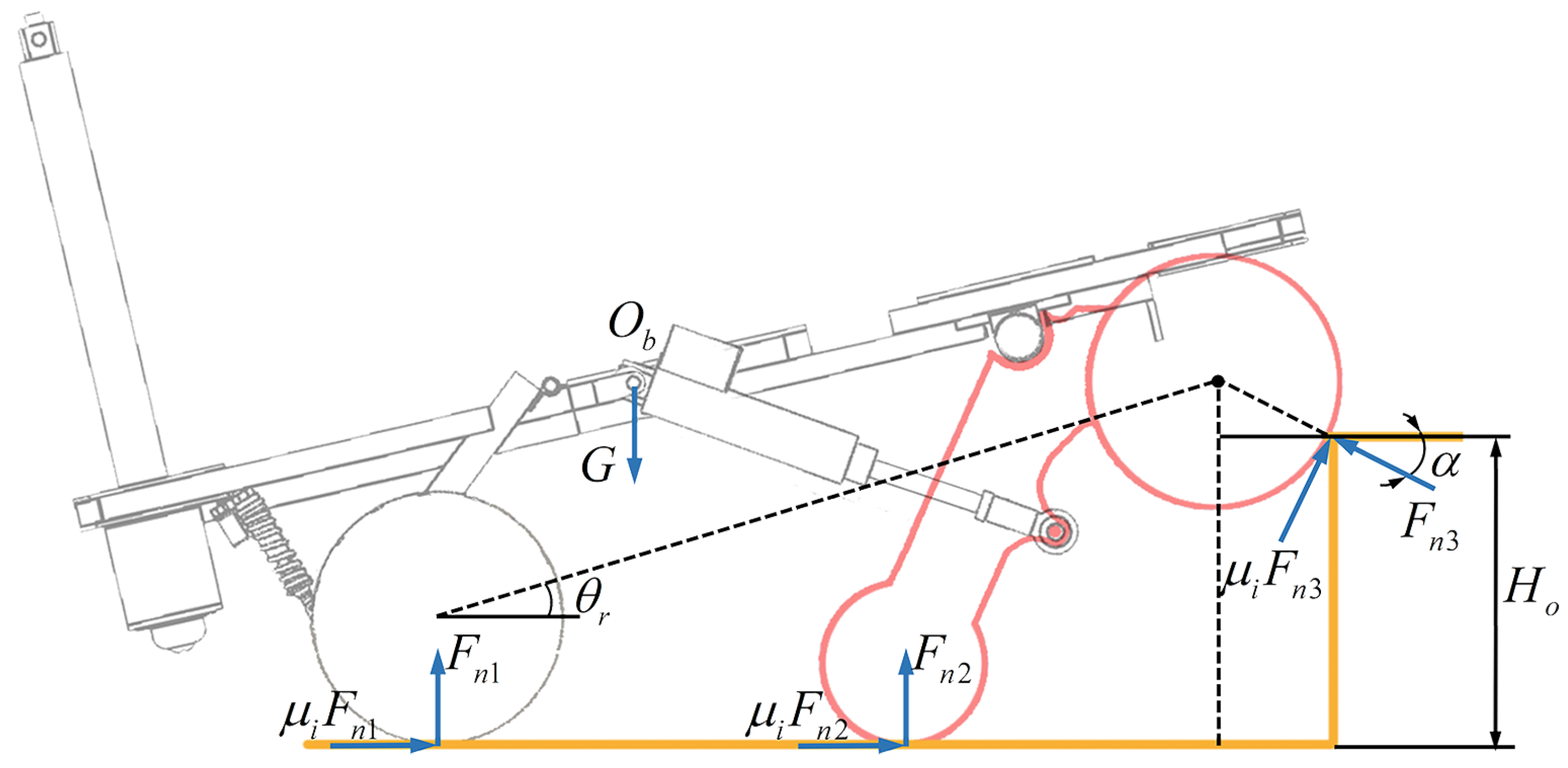
4. Methodology for Overcoming Obstacles
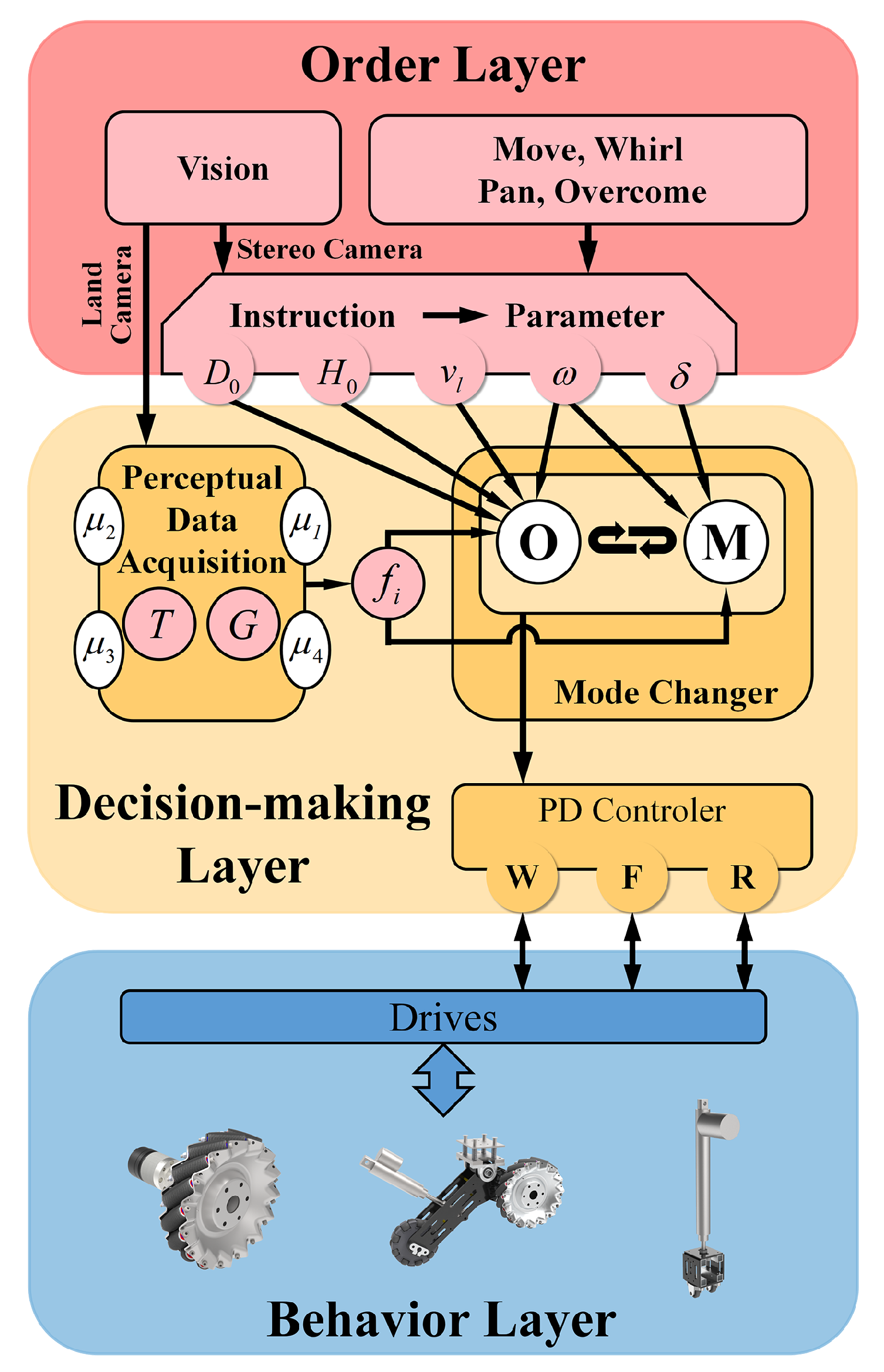
4.1. Heterogeneous Sensing System
4.2. Overall Motion Strategy
5. Experiments and Discussion
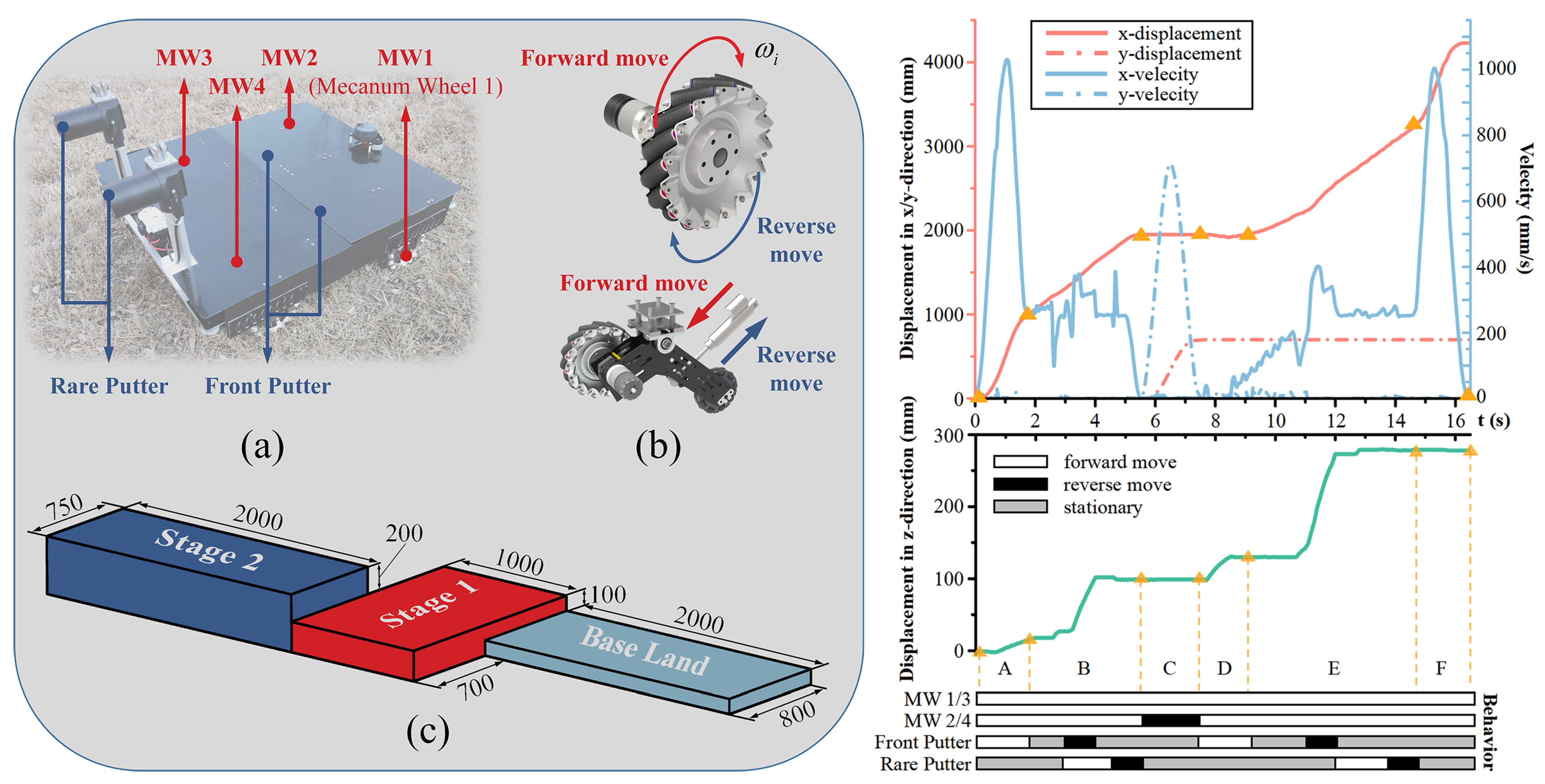
5.1. Simulation of Motion and Continuous Obstacles Overcoming
5.2. Experiments of Overcoming Obstacles
5.3. Discussion and Future Works
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rubio, F.; Valero, F.; Llopis-Albert, C. A review of mobile robots: Concepts, methods, theoretical framework, and applications. Int. J. Adv. Robot. Syst. 2019, 16. [Google Scholar] [CrossRef] [Green Version]
- Kuwada, A.; Wakimoto, S.; Suzumori, K.; Adomi, Y. Automatic pipe negotiation control for snake-like robot. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics, AIM, Xi’an, China, 2–5 July 2008; pp. 558–563. [Google Scholar] [CrossRef]
- Rollinson, D.; Choset, H. Gait-based compliant control for snake robots. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 5138–5143. [Google Scholar] [CrossRef]
- Chen, J.; Liang, Z.; Zhu, Y.; Zhao, J. Improving Kinematic Flexibility and Walking Performance of a Six-legged Robot by Rationally Designing Leg Morphology. J. Bionic Eng. 2019, 16, 608–620. [Google Scholar] [CrossRef]
- Lee, Y.H.; Lee, Y.H.; Lee, H.; Phan, L.T.; Kang, H.; Kim, U.; Jeon, J.; Choi, H.R. Trajectory design and control of quadruped robot for trotting over obstacles. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 4897–4902. [Google Scholar] [CrossRef]
- Park, H.W.; Chuah, M.Y.; Kim, S. Quadruped bounding control with variable duty cycle via vertical impulse scaling. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 3245–3252. [Google Scholar] [CrossRef]
- Park, H.W.; Wensing, P.M.; Kim, S. Jumping over obstacles with MIT Cheetah 2. Robot. Auton. Syst. 2021, 136, 103703. [Google Scholar] [CrossRef]
- Seok, S.; Wang, A.; Chuah, M.Y.; Otten, D.; Lang, J.; Kim, S. Design principles for highly efficient quadrupeds and implementation on the MIT Cheetah robot. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 3307–3312. [Google Scholar] [CrossRef]
- Bajracharya, M.; Ma, J.; Malchano, M.; Perkins, A.; Rizzi, A.A.; Matthies, L. High fidelity day/night stereo mapping with vegetation and negative obstacle detection for vision-in-the-loop walking. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 3663–3670. [Google Scholar] [CrossRef]
- Li, C.; Liu, D.; Liu, B.; Ren, X.; Liu, J.; He, Z.; Zuo, W.; Zeng, X.; Xu, R.; Tan, X.; et al. Chang’E-4 initial spectroscopic identification of lunar far-side mantle-derived materials. Nature 2019, 569, 378–382. [Google Scholar] [CrossRef] [PubMed]
- Grotzinger, J.P.; Crisp, J.; Vasavada, A.R.; Anderson, R.C.; Baker, C.J.; Barry, R.; Blake, D.F.; Conrad, P.; Edgett, K.S.; Ferdowski, B.; et al. Mars Science Laboratory Mission and Science Investigation. Space Sci. Rev. 2012, 170, 5–56. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Yang, W.; Hu, S.; Lin, Y.; Fang, G.; Li, C.; Peng, W.; Zhu, S.; He, Z.; Zhou, B.; et al. Volcanic history of the Imbrium basin: A close-up view from the lunar rover Yutu. Proc. Natl. Acad. Sci. USA 2015, 112, 5342–5347. [Google Scholar] [CrossRef] [Green Version]
- Bosworth, W.; Whitney, J.; Kim, S.; Hogan, N. Robot locomotion on hard and soft ground: Measuring stability and ground properties in-situ. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 3582–3589. [Google Scholar] [CrossRef]
- Rodríguez-Martínez, D.; Van Winnendael, M.; Yoshida, K. High-speed mobility on planetary surfaces: A technical review. J. Field Robot. 2019, 36, 1436–1455. [Google Scholar] [CrossRef]
- Estier, T.; Piguet, R.; Eichhorn, R.; Siegwart, R. Shrimp, a Rover Architecture for Long Range Martian Mission. In Proceedings of the Sixth ESA Workshop on Advanced Space Technologies for Robotics and Automation (ASTRA’2000), Noordwijk, The Netherlands, 5–7 December 2000; pp. 5–7. [Google Scholar]
- Shiroma, N.; Chiu, Y.H.; Min, Z.; Kawabuchi, I.; Matsuno, F. Development and control of a high maneuverability wheeled robot with variable-structure functionality. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 4000–4005. [Google Scholar] [CrossRef]
- Ning, M.; Yu, K.; Zhang, C.; Wu, Z.; Wang, Y. Wheelchair design with variable posture adjustment and obstacle-overcoming ability. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 197. [Google Scholar] [CrossRef]
- Candiotti, J.L.; Daveler, B.J.; Kamaraj, D.C.; Chung, C.S.; Cooper, R.; Grindle, G.G.; Cooper, R.A. A Heuristic Approach to Overcome Architectural Barriers Using a Robotic Wheelchair. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 27, 1846–1854. [Google Scholar] [CrossRef]
- Li, Y.; Dai, S.; Zhao, L.; Yan, X.; Shi, Y. Topological design methods for mecanum wheel configurations of an omnidirectional mobile robot. Symmetry 2019, 11, 1268. [Google Scholar] [CrossRef] [Green Version]
- Şahin, O.N.; Dede, M.İ.C. Investigation of longitudinal friction characteristics of an omnidirectional wheel via LuGre model. Robotica 2021, 39, 1654–1673. [Google Scholar] [CrossRef]
- Karamipour, E.; Dehkordi, S.F.; Korayem, M.H. Reconfigurable Mobile Robot with Adjustable Width and Length: Conceptual Design, Motion Equations and Simulation. J. Intell. Robot. Syst. Theory Appl. 2020, 99, 797–814. [Google Scholar] [CrossRef]
- Rauniyar, A.; Upreti, H.C.; Mishra, A.; Sethuramalingam, P. MeWBots: Mecanum-Wheeled Robots for Collaborative Manipulation in an Obstacle-Clustered Environment Without Communication. J. Intell. Robot. Syst. Theory Appl. 2021, 102, 3. [Google Scholar] [CrossRef]
- Lee, Y.; Yoon, D.; Oh, J.; Kim, H.S.; Seo, T.W. Novel Angled Spoke-Based Mobile Robot Design for Agile Locomotion with Obstacle-Overcoming Capability. IEEE/ASME Trans. Mechatronics 2020, 25, 1980–1989. [Google Scholar] [CrossRef]
- Mo, J.; Yan, Z.; Li, B.; Xi, F.; Li, Y. Study of obstacle-crossing and pitch control characteristic of a novel jumping robot. Sensors 2021, 21, 2432. [Google Scholar] [CrossRef]
- Wang, X.; Ge, H.; Zhang, K.; Chen, Y. System design and analysis of outdoor obstacle surmounting experiments for the robot with foldable wheels. In Proceedings of the 2019 IEEE 3rd Information Technology, Networking, Electronic and Automation Control Conference, ITNEC 2019, Chengdu, China, 15–17 March 2019; pp. 266–270. [Google Scholar] [CrossRef]
- Kim, Y.; Lee, Y.; Lee, S.; Kim, J.; Kim, H.S.; Seo, T.W. STEP: A New Mobile Platform with 2-DOF Transformable Wheels for Service Robots. IEEE/ASME Trans. Mechatronics 2020, 25, 1859–1868. [Google Scholar] [CrossRef]
- Wang, S.; Zou, M.; Dang, Z.; Chen, B.; Zhou, T.; Su, B. Modelling of flexible metal wheels for planetary rover on deformable terrain. Thin-Walled Struct. 2019, 141, 97–110. [Google Scholar] [CrossRef]
- Fuchs, M.; Borst, C.; Giordano, P.R.; Baumann, A.; Kraemer, E.; Langwald, J.; Gruber, R.; Seitz, N.; Plank, G.; Kunze, K.; et al. Rollin’ Justin - Design considerations and realization of a mobile platform for a humanoid upper body. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 4131–4137. [Google Scholar] [CrossRef] [Green Version]
- Lee, D.Y.; Kim, S.R.; Kim, J.S.; Park, J.J.; Cho, K.J. Origami wheel transformer: A variable-diameter wheel drive robot using an origami structure. Soft Robot. 2017, 4, 163–180. [Google Scholar] [CrossRef]
- Choi, J.N.; Jeong, K.; Seo, T.W. Pol-E: Large-obstacle overcoming based on energy conversion method using an elastic link. Int. J. Control Autom. Syst. 2017, 15, 1835–1843. [Google Scholar] [CrossRef]
- Quaglia, G.; Maffiodo, D.; Franco, W.; Appendino, S.; Oderio, R. The Epi.q-1 hybrid mobile robot. Int. J. Robot. Res. 2010, 29, 81–91. [Google Scholar] [CrossRef]
- Cebollada, S.; Payá, L.; Flores, M.; Peidró, A.; Reinoso, O. A state-of-the-art review on mobile robotics tasks using artificial intelligence and visual data. Expert Syst. Appl. 2021, 167, 114195. [Google Scholar] [CrossRef]
- Masehian, E.; Jannati, M.; Hekmatfar, T. Cooperative mapping of unknown environments by multiple heterogeneous mobile robots with limited sensing. Robot. Auton. Syst. 2017, 87, 188–218. [Google Scholar] [CrossRef]
- Yun, S.H.; Park, J.; Seo, J.; Kim, Y.J. Development of an Agile Omnidirectional Mobile Robot with GRF Compensated Wheel-leg Mechanisms for Human Environments. IEEE Robot. Autom. Lett. 2021, 6, 8301–8308. [Google Scholar] [CrossRef]
- Patil, A.K.; Balasubramanyam, A.; Ryu, J.Y.; Chakravarthi, B.; Chai, Y.H. An open-source platform for human pose estimation and tracking using a heterogeneous multi-sensor system. Sensors 2021, 21, 2340. [Google Scholar] [CrossRef]
- Li, T.; Ceccarelli, M.; Luo, M.; Laribi, M.A.; Zeghloul, S. An experimental analysis of overcoming obstacle in human walking. J. Bionic Eng. 2014, 11, 497–505. [Google Scholar] [CrossRef]
- Alakshendra, V.; Chiddarwar, S.S. Adaptive robust control of Mecanum-wheeled mobile robot with uncertainties. Nonlinear Dyn. 2017, 87, 2147–2169. [Google Scholar] [CrossRef]
- Ren, C.; Li, X.; Yang, X.; Ma, S. Extended state observer-based sliding mode control of an omnidirectional mobile robot with friction compensation. IEEE Trans. Ind. Electron. 2019, 66, 9480–9489. [Google Scholar] [CrossRef]
- Guo, K.; Pan, Y.; Yu, H. Composite learning robot control with friction compensation: A neural network-based approach. IEEE Trans. Ind. Electron. 2019, 66, 7841–7851. [Google Scholar] [CrossRef]
- Chassis, T.A. The Automotive Chassis; Biddles, Guildford & Kings Lynn: Guildford, UK, 2001. [Google Scholar] [CrossRef]
- Márton, L.; Van Der Linden, F. Temperature dependent friction estimation: Application to lubricant health monitoring. Mechatronics 2012, 22, 1078–1084. [Google Scholar] [CrossRef]
- Niskanen, A.; Tuononen, A.J. Three three-Axis IEPE accelerometers on the inner liner of a tire for finding the tire-road friction potential indicators. Sensors 2015, 15, 19251–19263. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Khamis, H.; Birznieks, I.; Lepora, N.F.; Redmond, S.J. Tactile Sensors for Friction Estimation and Incipient Slip Detection—Toward Dexterous Robotic Manipulation: A Review. IEEE Sens. J. 2018, 18, 9049–9064. [Google Scholar] [CrossRef] [Green Version]
- Ge, Z.; Liu, S.; Wang, F.; Li, Z.; Sun, J. YOLOX: Exceeding YOLO Series in 2021. arXiv 2021, arXiv:2107.08430. [Google Scholar]

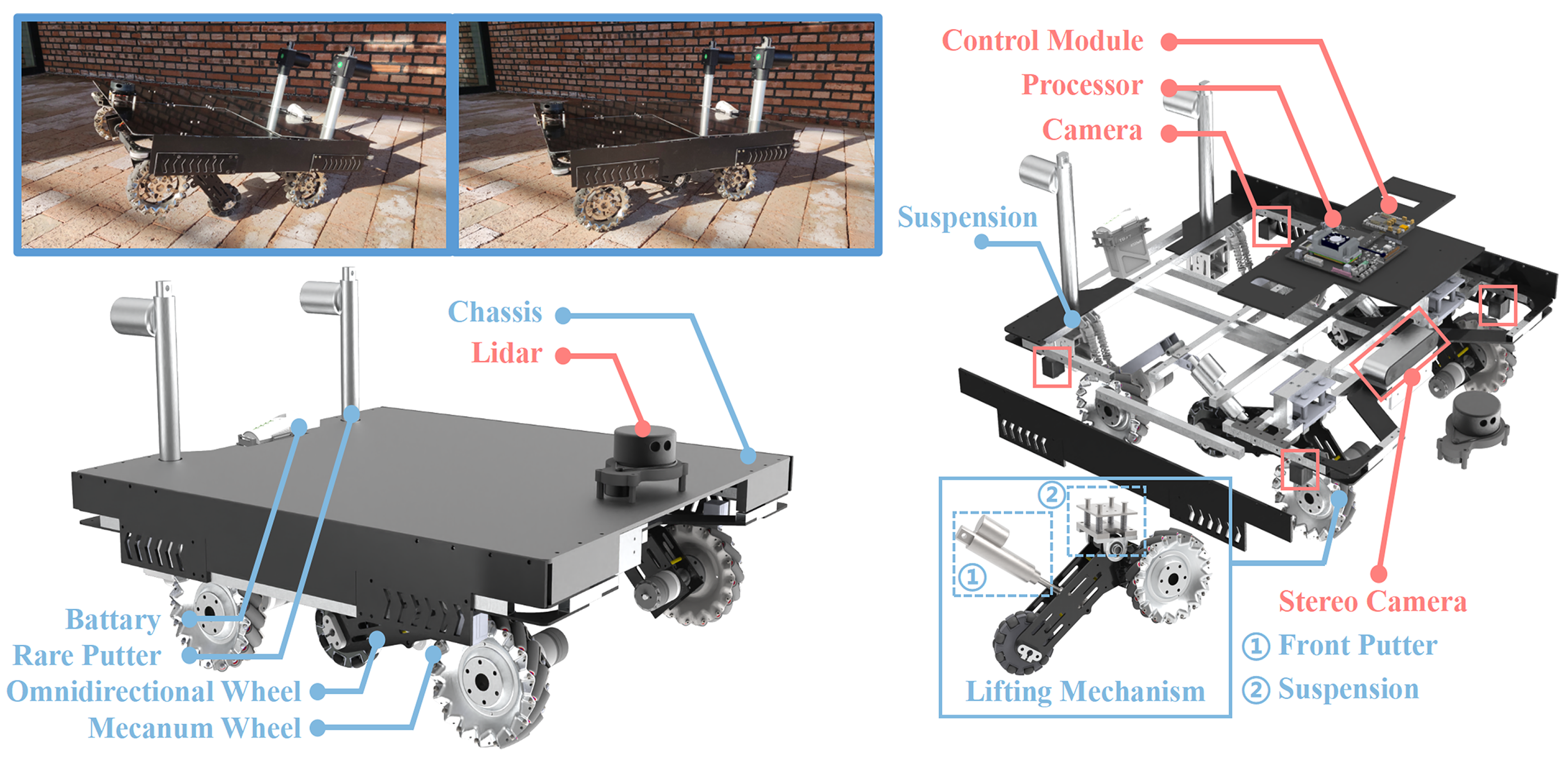

| Width | Body | 700 mm |
| Wheel-to-wheel | 576 mm | |
| Depth | Body | 768 mm |
| Shaft-to-shaft | 465 mm | |
| Height | Body | 564 mm |
| Ground-to-upper | 274 mm | |
| Weight | Total | 18.8 kg |
| Body | 12.5 kg | |
| Swing-arm * | 2.1 kg (×2) | |
| Mecanum Wheel | 0.7 kg (×2) | |
| Battery | 0.7 kg | |
| Payload | Workable load | 30 kg |
| Speed | Max. Average speed | 5.2 m/s |
| Lift Height | Front wheels | 234.4 mm |
| Rare wheels | 220 mm | |
| Wheel actuators | Rotational speed | 4338 deg/s |
| Peak torque | 10.1 Nm | |
| Cont. torque | 6.8 Nm | |
| Reduction | 19:1 | |
| Putter | Load speed | 100 mm/s |
| Battery | 24 V—5.7 Ah | Approx. 40 min work time |
| Condition | Notes | ||
|---|---|---|---|
| Compact road | 0.90–1.00 | 0.70–0.85 | Asphalt, Rubber |
| Brick, Concrete | |||
| Loose road | 0.50–0.70 | 0.45–0.60 | Gravel, Sand |
| Ash, Wasteland | |||
| Snowed road | 0.20–0.30 | 0.20–0.35 | ― |
| Ice road | 0.10–0.60 | 0.05–0.55 | to 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Meng, R.; Yu, J.; Zhao, Z.; Zhang, X. Practical Obstacle-Overcoming Robot with a Heterogeneous Sensing System: Design and Experiments. Machines 2022, 10, 289. https://doi.org/10.3390/machines10050289
Huang Y, Meng R, Yu J, Zhao Z, Zhang X. Practical Obstacle-Overcoming Robot with a Heterogeneous Sensing System: Design and Experiments. Machines. 2022; 10(5):289. https://doi.org/10.3390/machines10050289
Chicago/Turabian StyleHuang, Yuanhao, Ruifeng Meng, Jingyang Yu, Ziqi Zhao, and Xinyu Zhang. 2022. "Practical Obstacle-Overcoming Robot with a Heterogeneous Sensing System: Design and Experiments" Machines 10, no. 5: 289. https://doi.org/10.3390/machines10050289
APA StyleHuang, Y., Meng, R., Yu, J., Zhao, Z., & Zhang, X. (2022). Practical Obstacle-Overcoming Robot with a Heterogeneous Sensing System: Design and Experiments. Machines, 10(5), 289. https://doi.org/10.3390/machines10050289