Investigation of Hydrodynamic Performance and Evolution of the near Wake on a Horizontal Axis Tidal Turbine
Abstract
:1. Introduction
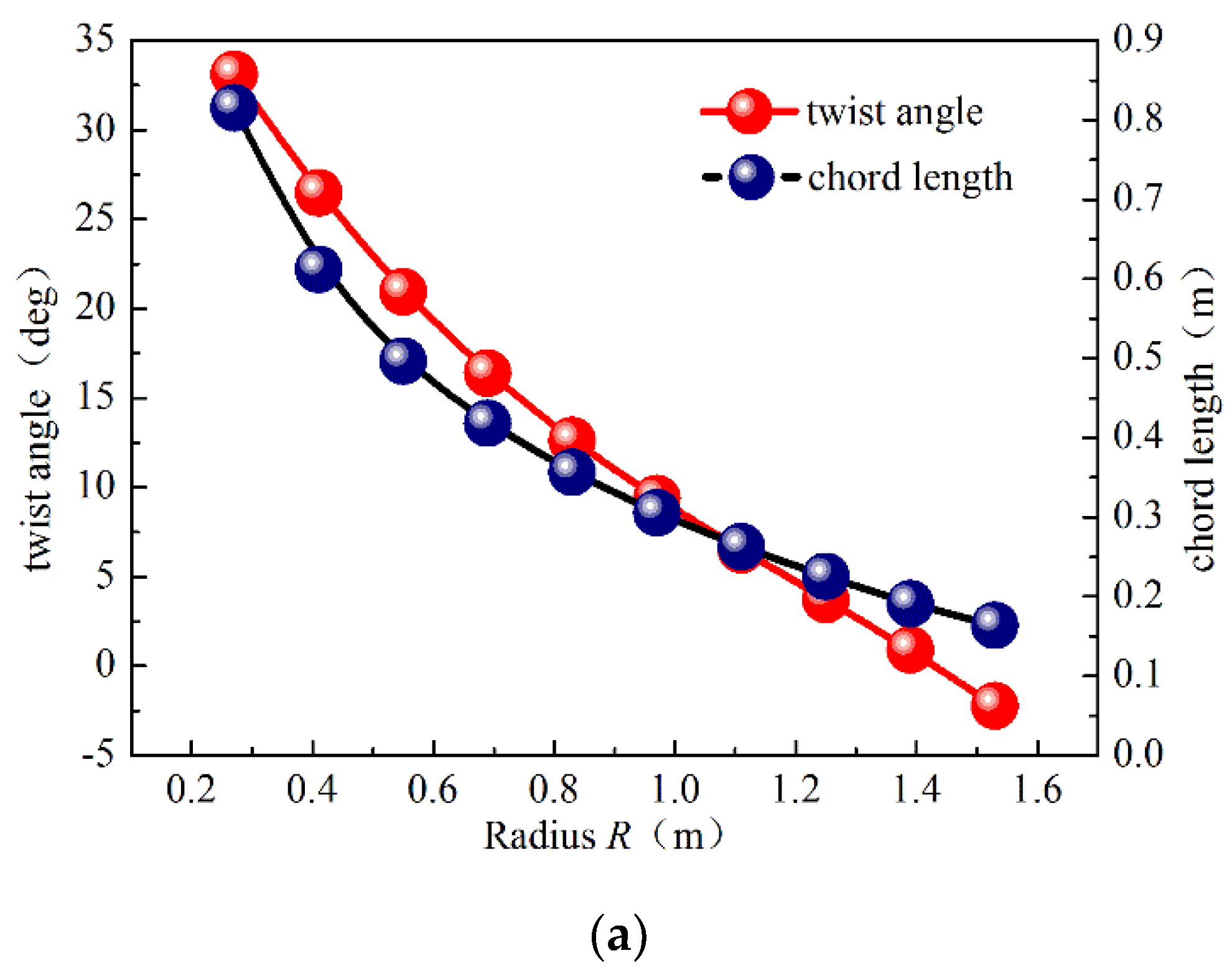
2. Turbine Blade Design
3. Numerical Method
3.1. Large Eddy Simulation
3.2. Computation Domains and Boundary Conditions
3.3. Grid Generation
4. Experimental Arrangement
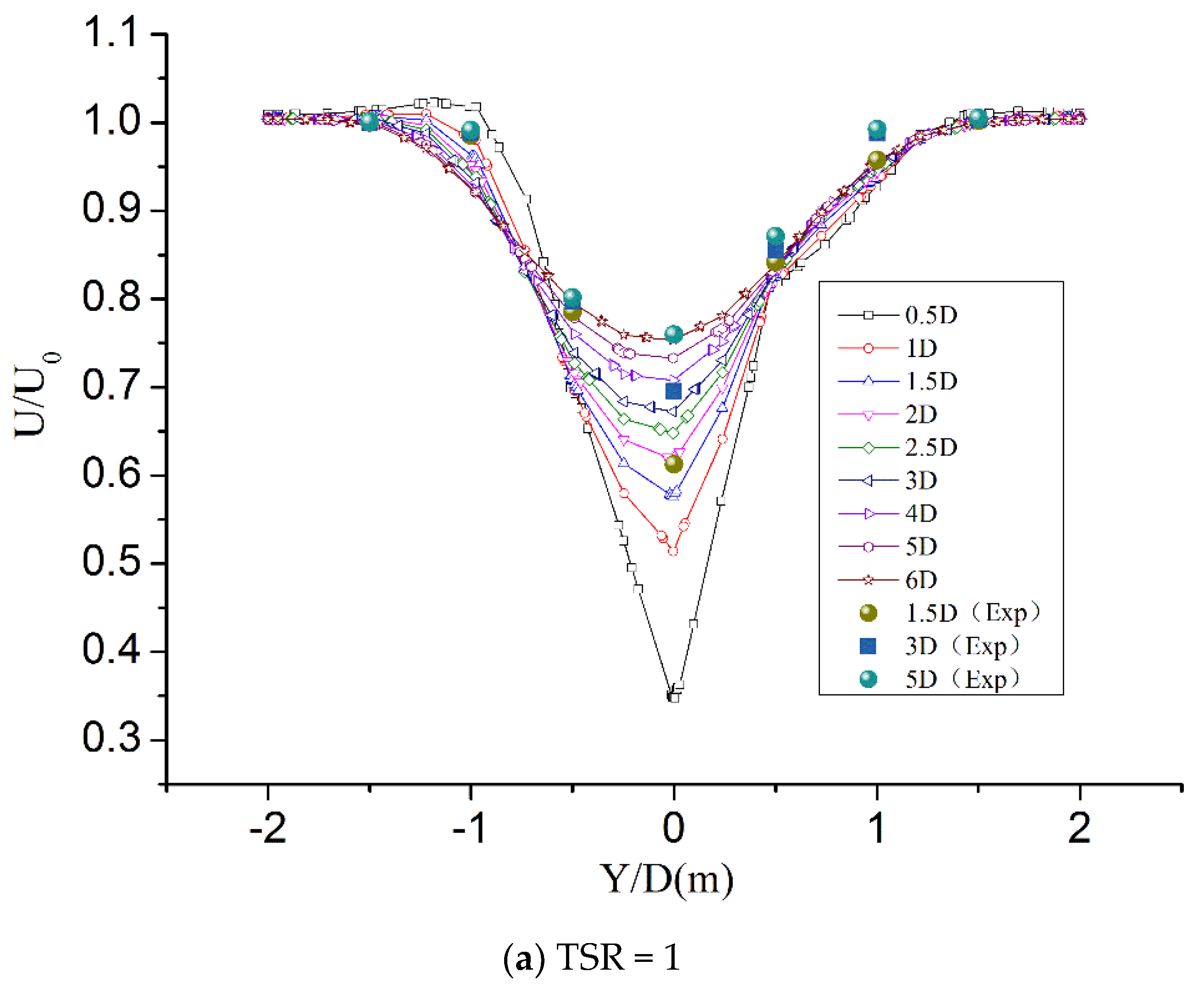
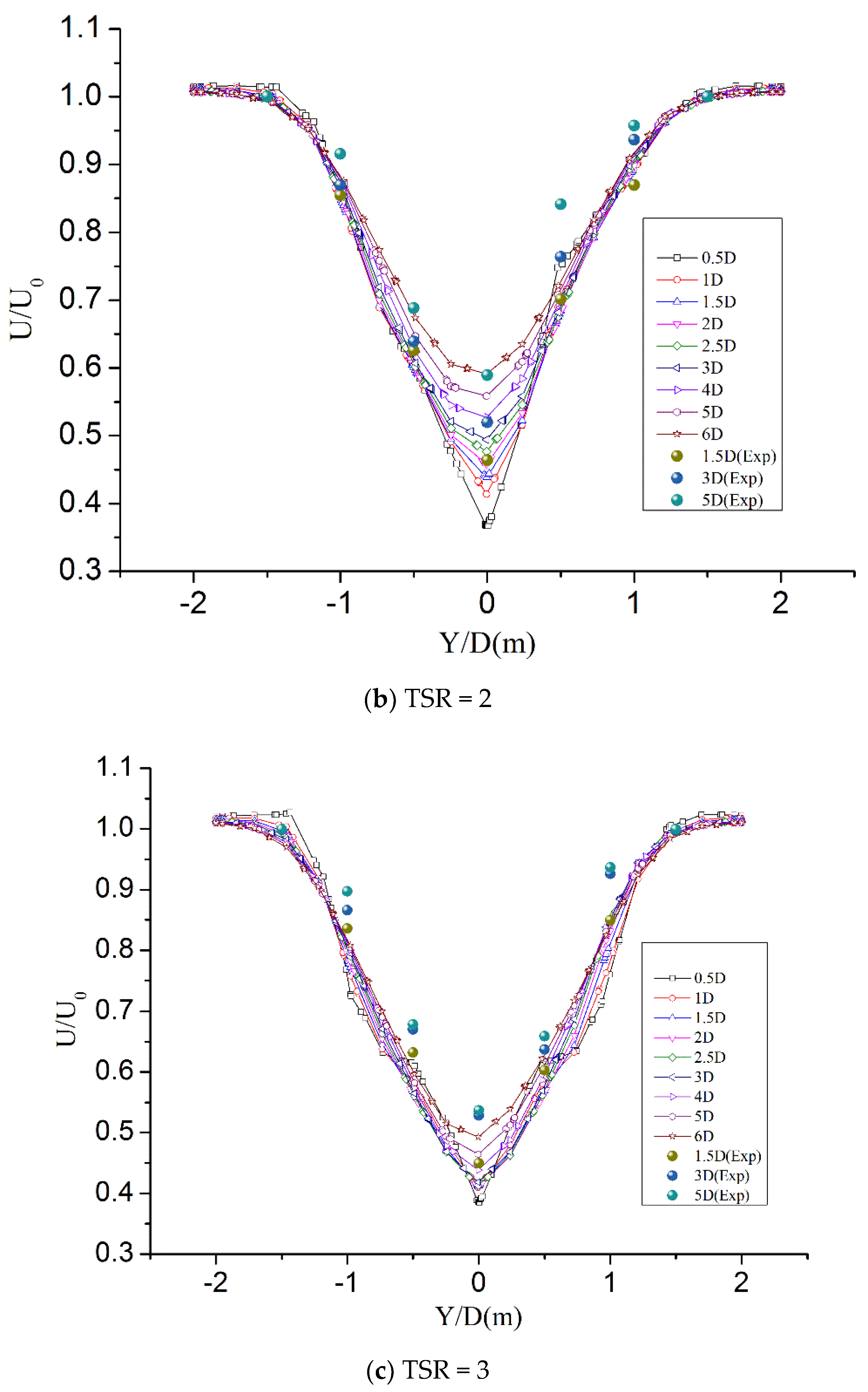
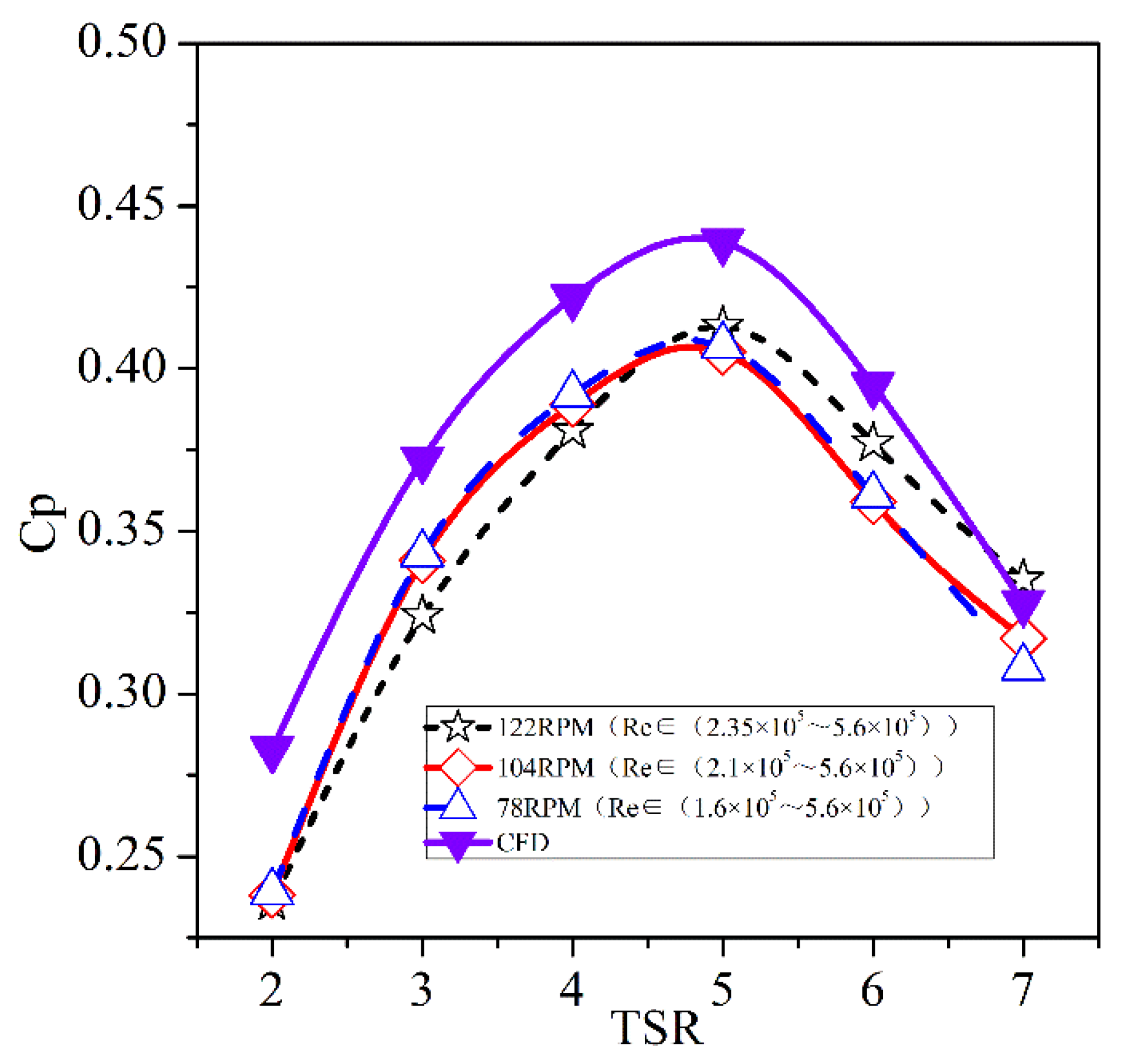
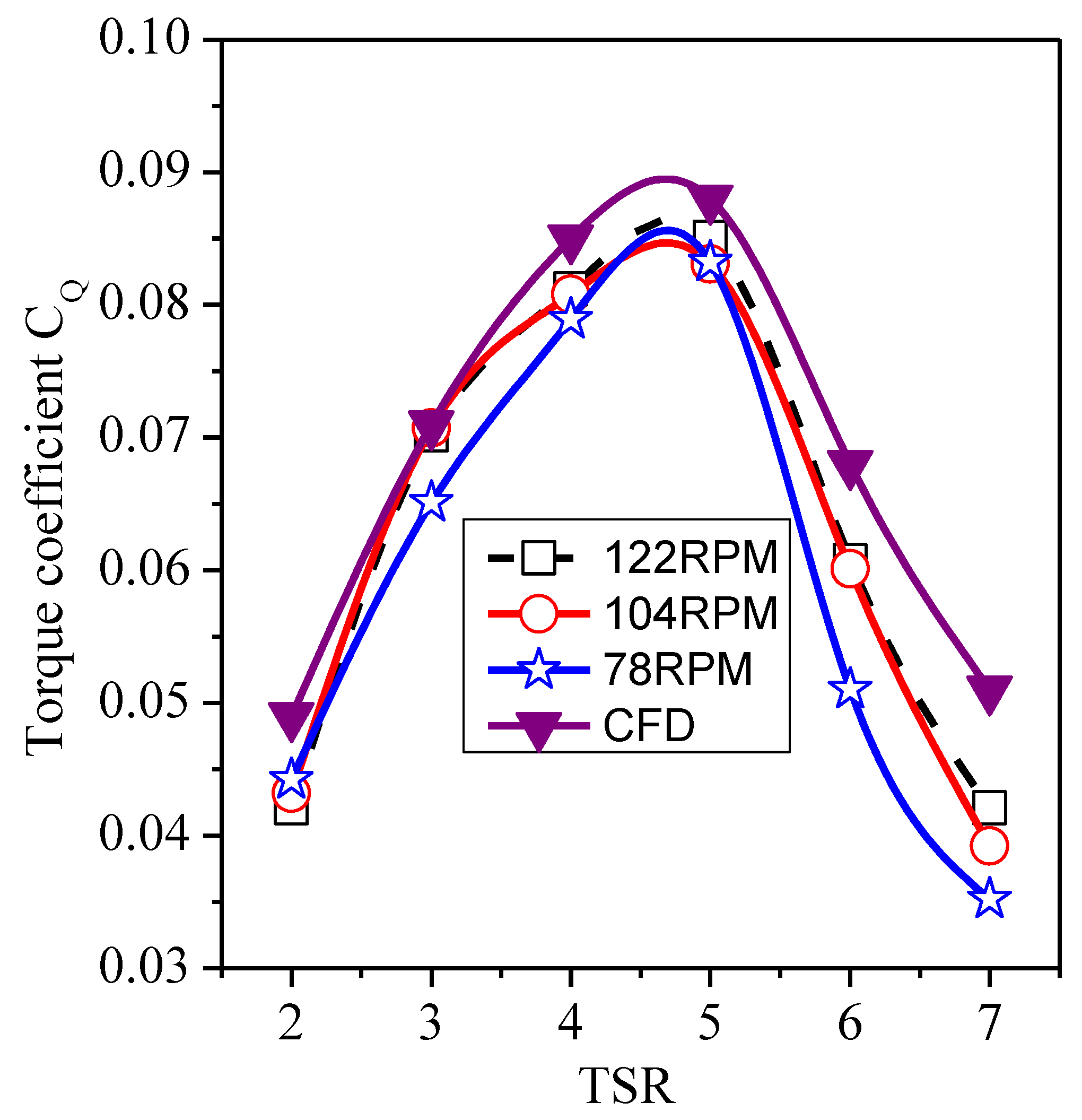
5. Results and Discussion
6. Conclusions
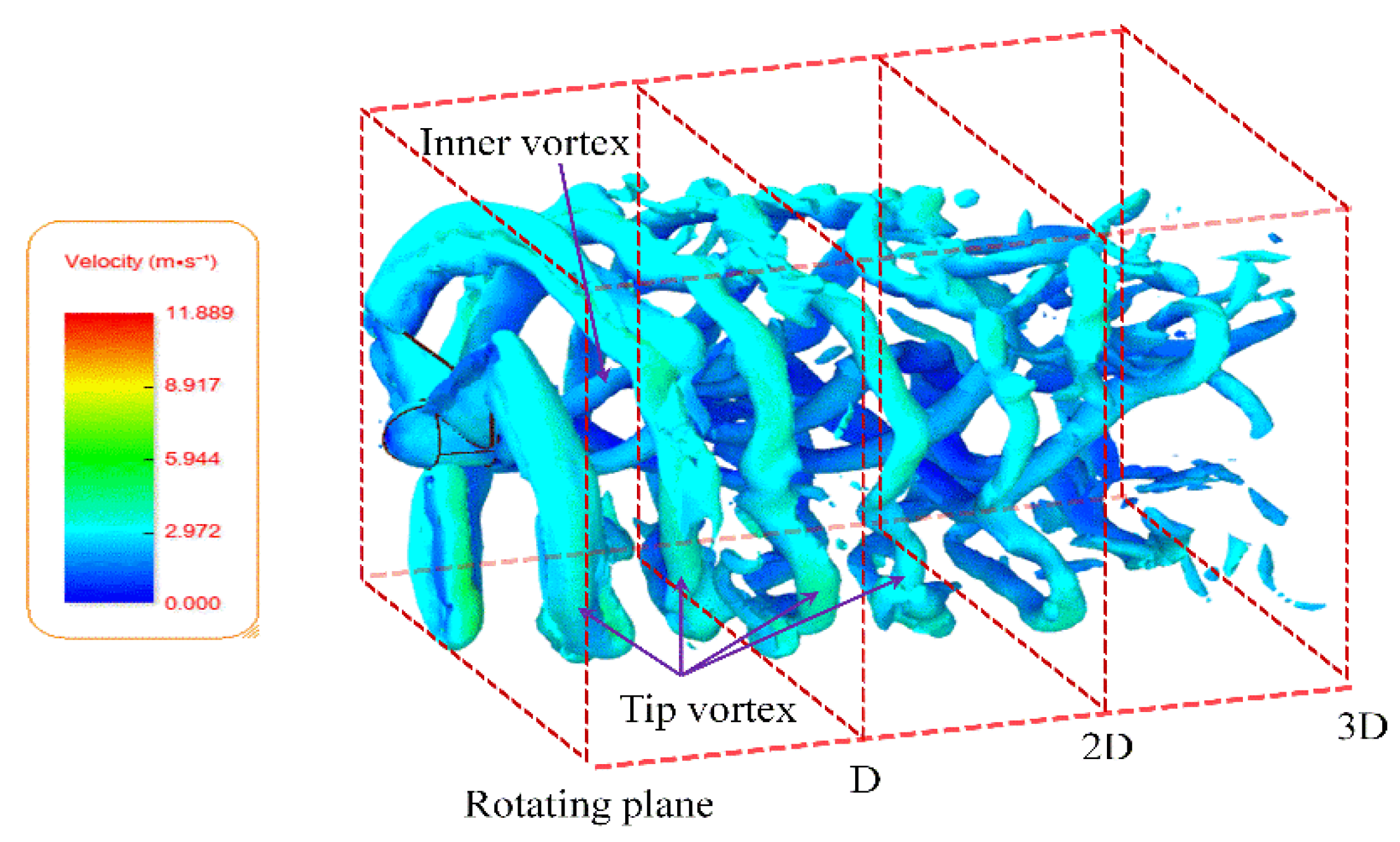
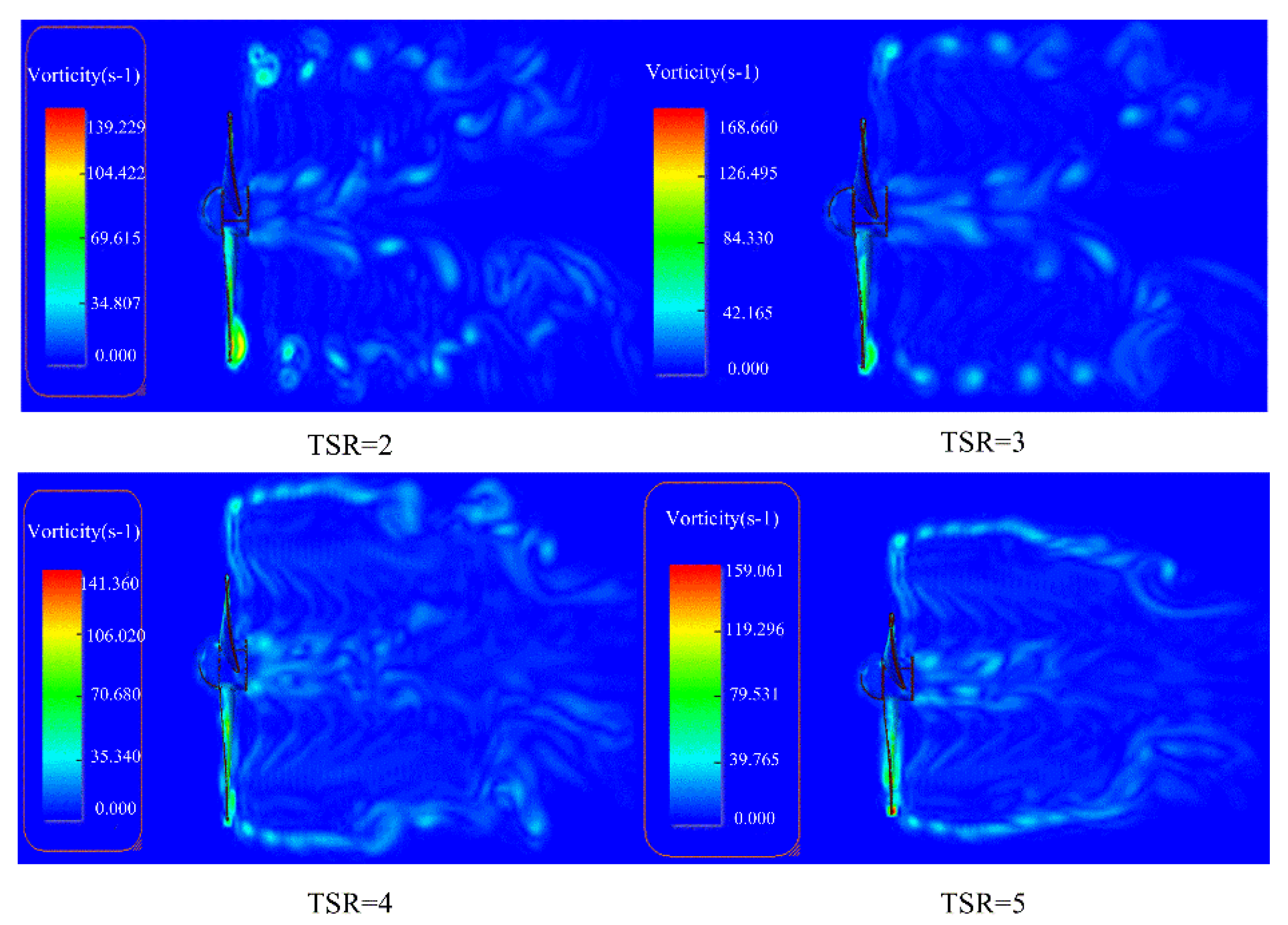
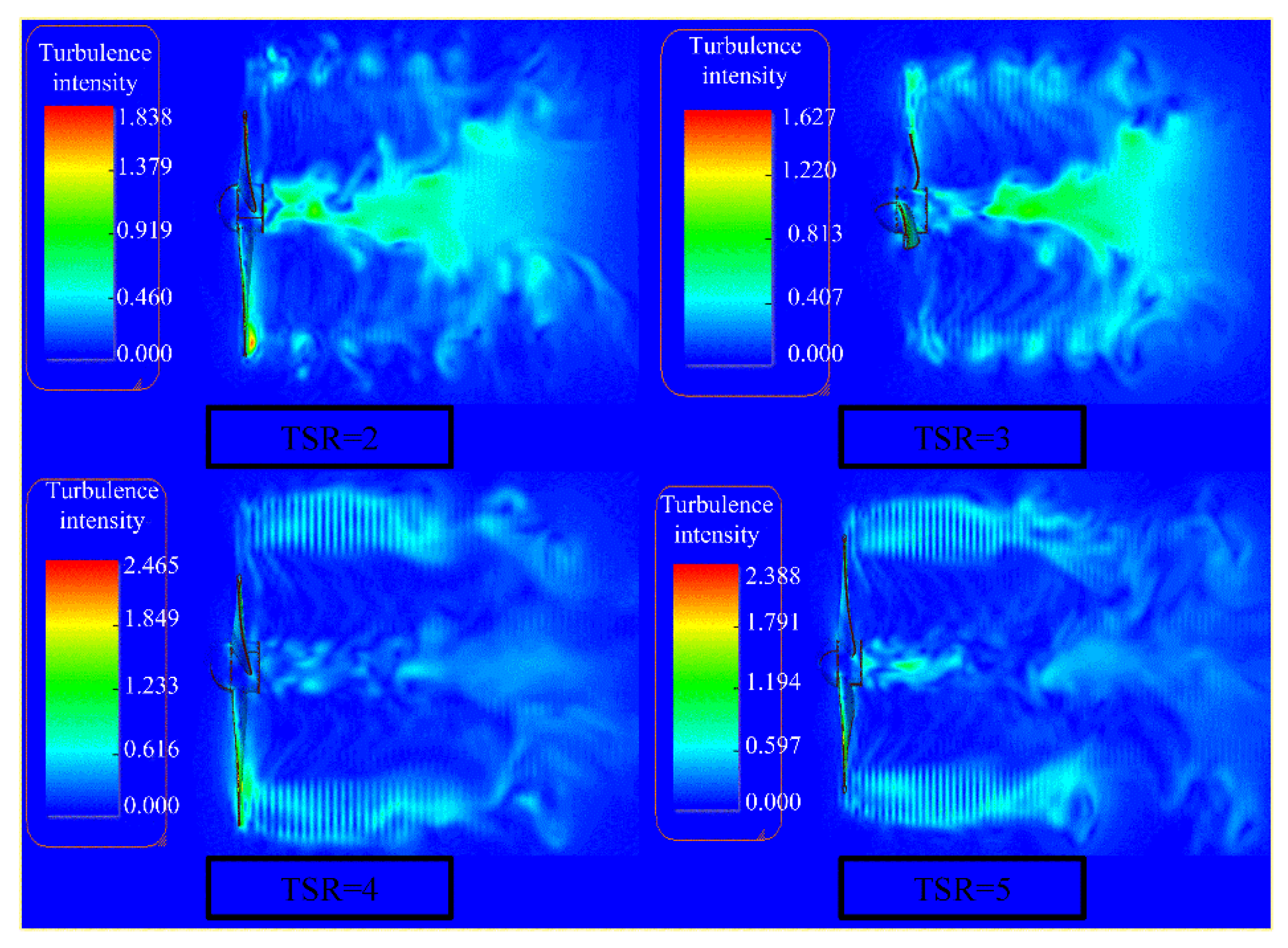
- The numerical simulation and experimental results show that at the downstream position of the turbine, the velocity deficit curve changes with the position, and the velocity deficit at the downstream position of the hub shows a decreasing trend. The velocity deficit also shows a decreasing trend with the direction of blade spanwise. With the increase of TSR, the pitch of the helix formed by tip vortex decreases gradually, and the vortex generated at the root and tip of the blade collapses earlier.
- There is an optimal tip speed ratio range for turbine operation. The parameters such as turbine power and torque predicted by the experimental values are different from those predicted by the numerical simulation, but the trend fits well. Because the water flow around the turbine is limited by the side wall of the water tank, the speed of the water flow is forcibly increased, resulting in the difference between the stress condition of the turbine and the simulation condition. When the tip speed ratio is about 5, the designed turbine power coefficient reaches the maximum.
- In addition, through the comparison between experiment and numerical simulation, it is proved that large eddy simulation (LES) has certain accuracy and advantages in predicting wake vortex trace.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| a | Axial induction factor |
| b | Tangential induction factor |
| B | Number of blades |
| c | Chord length |
| CL | Lift coefficient |
| CD | Drag coefficient |
| CT | Thrust coefficient |
| CN | Torque coefficient |
| f | Prandtl’s tip loss factor |
| CP | Power coefficient |
| V1 | Inflow velocity |
| V0 | Relative inflow velocity |
| Re | Reynolds number |
| α | Angle of attack |
| β | Twist angle |
| θ | Inflow angle |
| ρ | Liquid density |
| Ω | Angular velocity of the rotor |
| r | Local radius |
| R | Radius of whole turbine |
| p | the filtered pressure |
| ui | the filtered ith Cartesian velocity component |
| τij | subgrid scale stress |
| TSR | tip speed ratio |
References
- Alamian, R.; Shafaghat, R.; Amiri, H.A.; Shadloo, M.S. Experimental assessment of a 100 W prototype horizontal axis tidal turbine by towing tank tests. Renew. Energy 2020, 155, 172–180. [Google Scholar] [CrossRef]
- Elie, B.; Oger, G.; Guillerm, P.-E.; Alessandrini, B. Simulation of horizontal axis tidal turbine wakes using a Weakly-Compressible Cartesian Hydrodynamic solver with local mesh refinement. Renew. Energy 2017, 108, 336–354. [Google Scholar] [CrossRef]
- Su, H.; Dou, B.; Qu, T.; Zeng, P.; Lei, L. Experimental investigation of a novel vertical axis wind turbine with pitching and self-starting function. Energy Convers. Manag. 2020, 217, 1–14. [Google Scholar] [CrossRef]
- Noruzi, R.; Vahidzadeh, M.; Riasi, A. Design, analysis and predicting hydrokinetic performance of a horizontal marine current axial turbine by consideration of turbine installation depth. Ocean. Eng. 2015, 108, 789–798. [Google Scholar] [CrossRef]
- Neto, J.X.V.; Junior, E.J.G.; Moreno, S.R.; Ayala, H.V.H.; Mariani, V.C.; Coelho, L.d.S. Wind turbine blade geometry design based on multi-objective optimization using metaheuristics. Energy 2018, 162, 645–658. [Google Scholar] [CrossRef]
- Goundar, J.N.; Ahmed, M.R. Design of a horizontal axis tidal current turbine. Appl. Energy 2013, 111, 161–174. [Google Scholar] [CrossRef]
- Tian, W.; Mao, Z.; Ding, H. Design, test and numerical simulation of a low-speed horizontal axis hydrokinetic turbine. Int. J. Nav. Archit. Ocean Eng. 2018, 10, 782–793. [Google Scholar] [CrossRef]
- Melo, D.B.; Baltazar, J.; de Campos, J.A.C.F. A numerical wake alignment method for horizontal axis wind turbines with the lifting line theory. J. Wind Eng. Ind. Aerodyn. 2018, 174, 382–390. [Google Scholar] [CrossRef]
- UsAr, D.; Bal, Ş. Cavitation simulation on horizontal axis marine current turbines. Renew. Energy 2015, 80, 15–25. [Google Scholar] [CrossRef]
- Lam, W.H.; Chen, L. Equations used to predict the velocity distribution within a wake from a horizontal-axis tidal-current turbine. Ocean Eng. 2014, 79, 35–42. [Google Scholar] [CrossRef]
- Faizan, M.; Badshah, S.; Badshah, M.; AliHaider, B. Performance and wake analysis of horizontal axis tidal current turbineusing Improved Delayed Detached Eddy Simulation. Renew. Energy 2022, 184, 740–752. [Google Scholar] [CrossRef]
- Ebdon, T.; Allmark, M.J.; O’Doherty, D.M.; Mason-Jones, A.; O’Doherty, T.; Germain, G.; Gaurier, B. The impact of turbulence and turbine operating condition on the wakes of tidal turbines. Renew. Energy 2021, 165, 96–116. [Google Scholar] [CrossRef]
- Lin, J.; Lin, B.; Sun, J.; Chen, Y. Wake structure and mechanical energy transformation induced by a horizontal axis tidal stream turbine. Renew. Energy 2021, 171, 1344–1356. [Google Scholar] [CrossRef]
- Gajardo, D.; Escauriaza, C.; Ingram, D.M. Capturing the development and interactions of wakes in tidal turbine arrays using a coupled BEM-DES model. Ocean. Eng. 2019, 181, 71–88. [Google Scholar] [CrossRef] [Green Version]
- Modali, P.K.; Vinod, A.; Banerjee, A. Towards a better understanding of yawed turbine wake for efficient wake steering in tidal arrays. Renew. Energy 2021, 177, 482–494. [Google Scholar] [CrossRef]
- Vinod, A.; Han, C.; Banerjee, A. Tidal turbine performance and near-wake characteristics in a sheared turbulent inflow. Renew. Energy 2021, 175, 840–852. [Google Scholar] [CrossRef]
- Bai, G.; Li, G.; Ye, Y.; Gao, T. Numerical analysis of the hydrodynamic performance and wake field of a horizontal axis tidal current turbine using an actuator surface model. Ocean. Eng. 2015, 94, 1–9. [Google Scholar] [CrossRef]
- Ma, Y.; Lam, W.H.; Cui, Y.; Zhang, T.; Jiang, J.; Sun, C.; Guo, J.; Wang, S.; Lam, S.S.; Hamill, G. Theoretical vertical-axis tidal-current-turbine wake model using axial momentum theory with CFD corrections. Appl. Ocean. Res. 2018, 79, 113–122. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Zhang, Y.; Zhang, J.; Zheng, Y.; Zang, W.; Lin, X.; Fernandez-Rodriguez, E. Experimental study of the wake homogeneity evolution behind a horizontal axis tidal stream turbine. Appl. Ocean Res. 2021, 111, 102644. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, J.; Lin, X.; Wang, R.; Zhang, C.; Zhao, J. Experimental investigation into downstream field of a horizontal axis tidal stream turbine supported by a mono pile. Appl. Ocean Res. 2020, 101, 102257. [Google Scholar] [CrossRef]
- Leroux, T.; Osbourne, N.; Groulx, D. Numerical study into horizontal tidal turbine wake velocity deficit: Quasi-steady state and transient approaches. Ocean Eng. 2019, 181, 240–251. [Google Scholar] [CrossRef]
- Nuernberg, M.; Tao, L. Experimental study of wake characteristics in tidal turbine arrays. Renew. Energy 2018, 127, 168–181. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Lin, B.; Lin, J.; Wang, S. Experimental study of wake structure behind a horizontal axis tidal stream turbine. Appl. Energy 2017, 196, 82–96. [Google Scholar] [CrossRef]
- Ahmadi, M.H.B.; Yang, Z. The evolution of turbulence characteristics in the wake of a horizontal axis tidal stream turbine. Renew. Energy 2020, 151, 1008–1015. [Google Scholar] [CrossRef]
- Ahmadi, M.B. Influence of upstream turbulence on the wake characteristics of a tidal stream turbine. Renew. Energy 2018, 132, 989–997. [Google Scholar] [CrossRef] [Green Version]
- Menon, S.; Yeung, P.K.; Kim, W.W. Effect of sub-grid models on the computed inter-scale energy transfer in isotropic turbulence. Comput. Fluid 1996, 25, 165e180. [Google Scholar] [CrossRef]
- Mcnaughton, J.; Afgan, I.; Apsley, D.D.; Rolfo, S.; Stallard, T.; Stansby, P.K. A simple sliding-mesh interface procedure and its application to the CFD simulation of a tidal-stream turbine. Int. J. Numer. Methods Fluids 2014, 74, 250–269. [Google Scholar] [CrossRef]
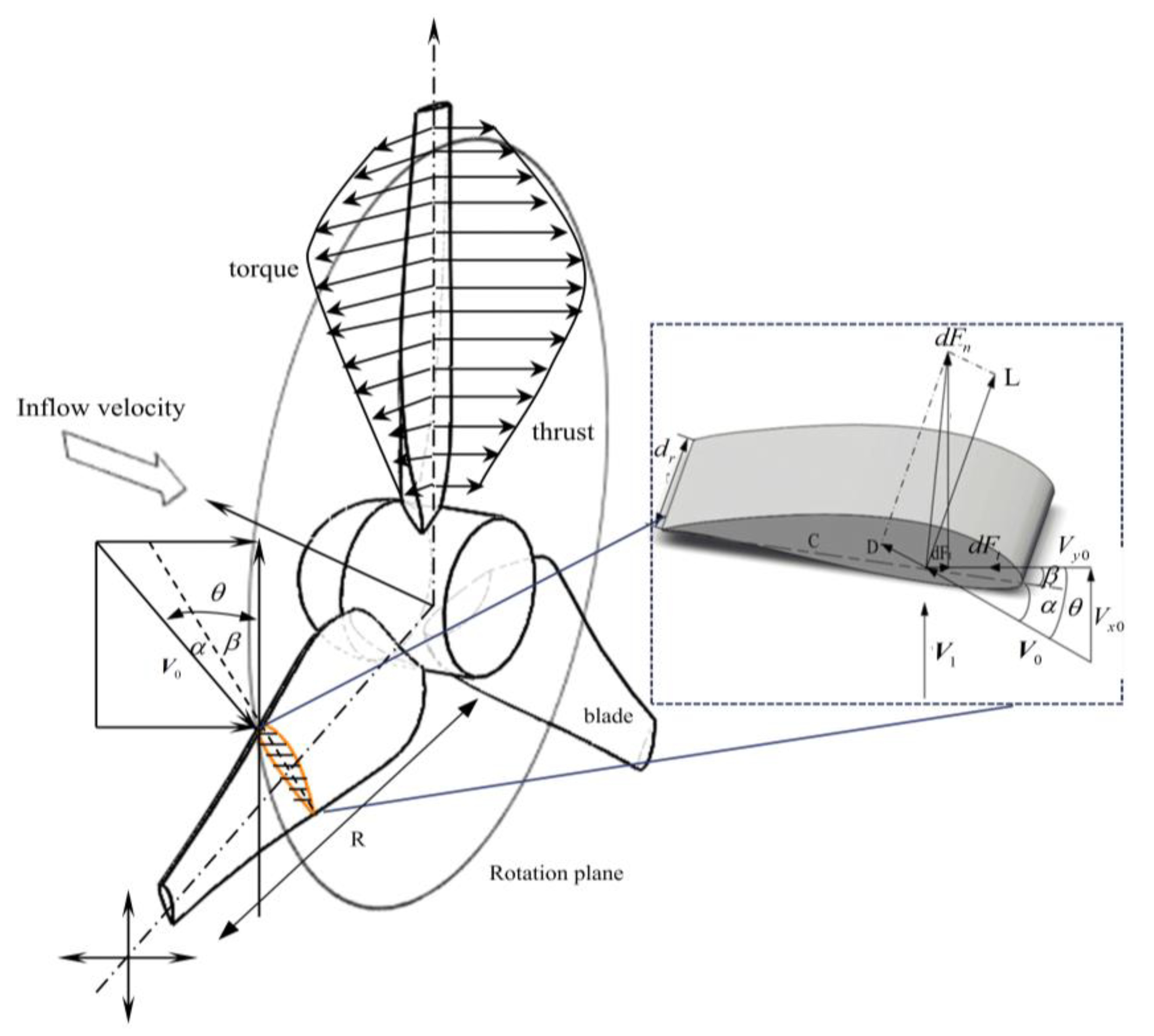
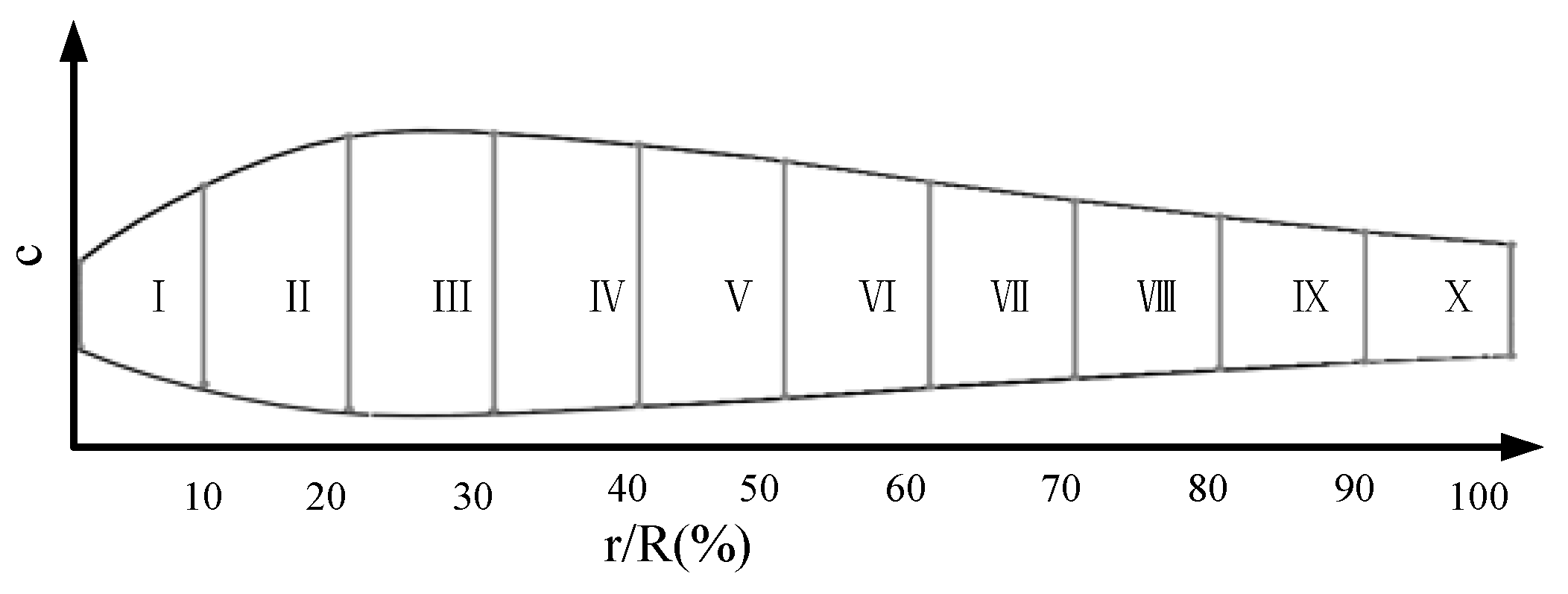
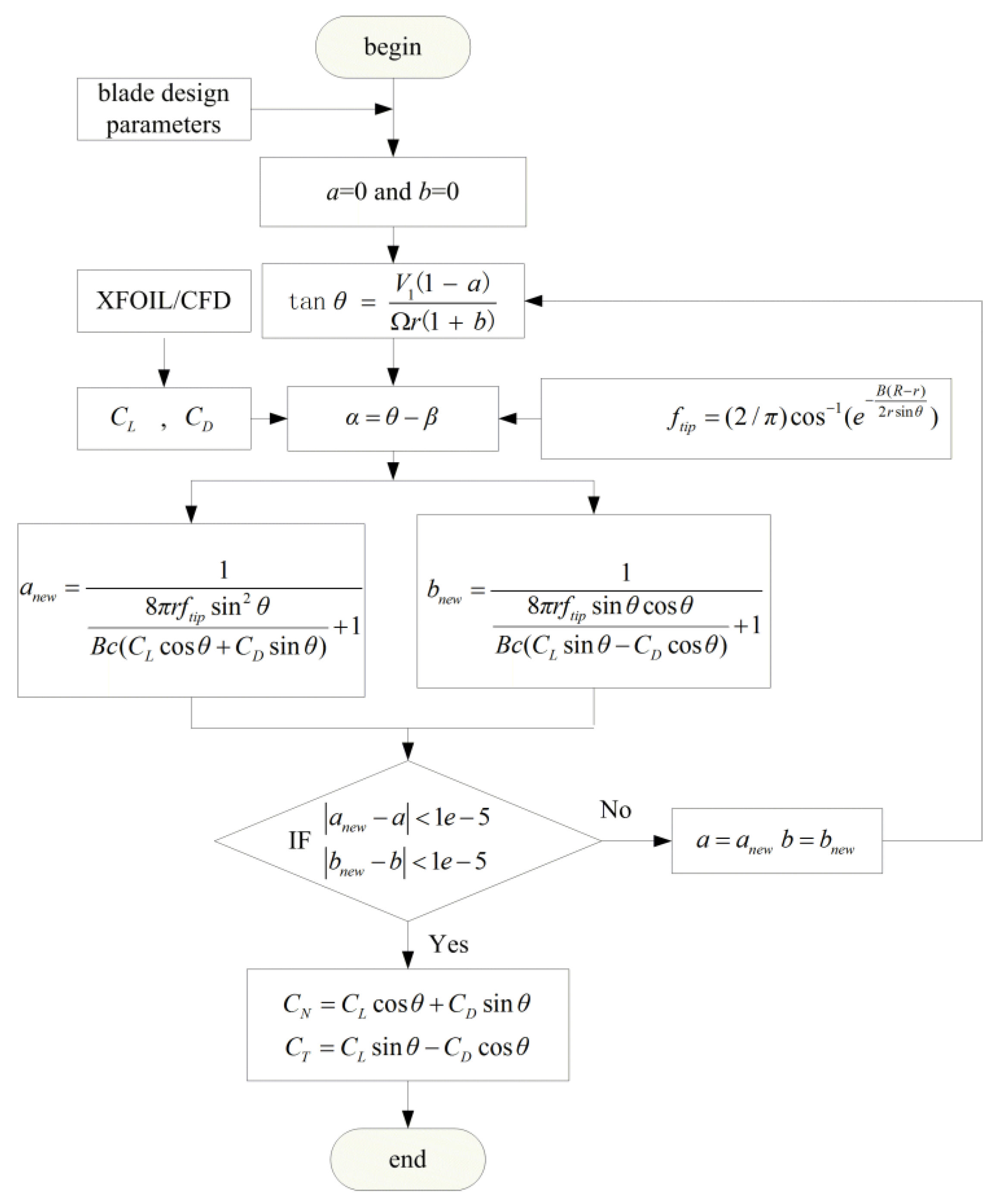





| Classical BEM |
|---|
| Input date: radial position and turbine radius, angular velocity of the rotor, velocity in ambient free stream, number ofblades (r, Ω, V0, B) Divide the blade into 10 sections, and set initial values for a and b (axial and tangential induction factors); Calculate the inflow angle Calculate lift and drag coefficients (CL & CD) according to CFD or experimental data. Calculate the tip loss factorftip (Prandtl). Calculate anew and bnew. Calculate CT, CN |
| Type | Mesh Nodes | Iteration Steps | CT |
|---|---|---|---|
| Case I | 3.43 × 106 | 500 | 0.514 |
| Case II | 3.84 × 106 | 500 | 0.552 |
| Case III | 4.36 × 106 | 500 | 0.557 |
| Project | Parameter | Memos |
|---|---|---|
| Sink size parameter (length, width and height) | 16,000 (mm) × 800 (mm) × 1400 (mm) | |
| Maximum water depth | 1000 mm | |
| Turbine diameter | 600 mm | |
| Dynamic torque sensor measuring range | 0–20 Nm | The error range is 0.1% |
| Incoming flow velocity range | 0.00~1.50 (m/s) | The error range is 1.5% |
| TSR range | 1–6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Z.; Feng, L.; Mao, Y.; Li, D.; Zhang, Y.; Gao, C.; Liu, C.; Fan, M. Investigation of Hydrodynamic Performance and Evolution of the near Wake on a Horizontal Axis Tidal Turbine. Machines 2022, 10, 234. https://doi.org/10.3390/machines10040234
Sun Z, Feng L, Mao Y, Li D, Zhang Y, Gao C, Liu C, Fan M. Investigation of Hydrodynamic Performance and Evolution of the near Wake on a Horizontal Axis Tidal Turbine. Machines. 2022; 10(4):234. https://doi.org/10.3390/machines10040234
Chicago/Turabian StyleSun, Zhaocheng, Long Feng, Yufeng Mao, Dong Li, Yue Zhang, Chengfei Gao, Chao Liu, and Menghao Fan. 2022. "Investigation of Hydrodynamic Performance and Evolution of the near Wake on a Horizontal Axis Tidal Turbine" Machines 10, no. 4: 234. https://doi.org/10.3390/machines10040234
APA StyleSun, Z., Feng, L., Mao, Y., Li, D., Zhang, Y., Gao, C., Liu, C., & Fan, M. (2022). Investigation of Hydrodynamic Performance and Evolution of the near Wake on a Horizontal Axis Tidal Turbine. Machines, 10(4), 234. https://doi.org/10.3390/machines10040234






