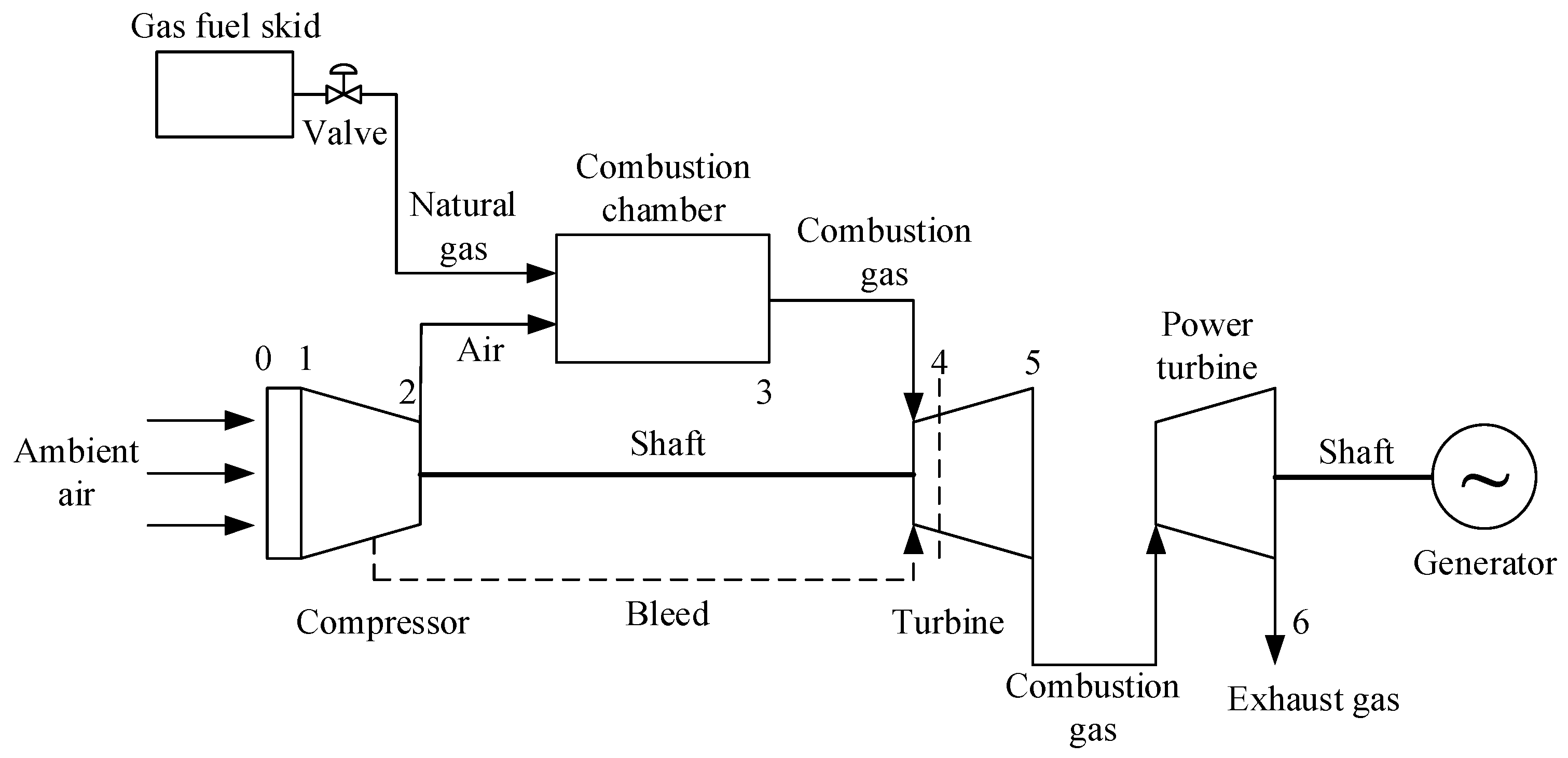
Firstly, this part introduces the original controller of this aero-derivative gas turbine, and the specific inner structure is exhibited in detail. Then, a new neural network technology is introduced and developed as a controller. The working process of this new neural network is illustrated, and the structure determination algorithm which determines the optimal number of hidden layer neurons is given. Finally, the novel integrated control method is designed based on the original controller and the new neural network controller.
3.2. A New Neural Network Controller
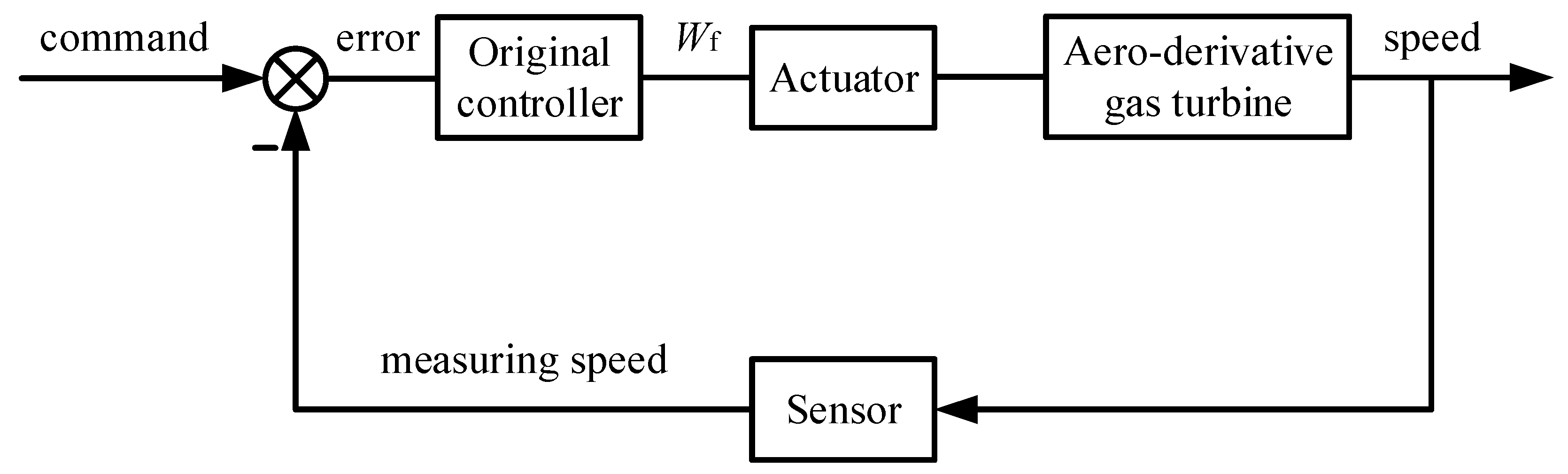
In this part, the neural network technique is employed to develop the controller, and the entire control system of the aero-derivative gas turbine is displayed in
Figure 3. The inputs of the neural network controller (NNM) are speed command and speed error, and the output is the fuel flow rate.
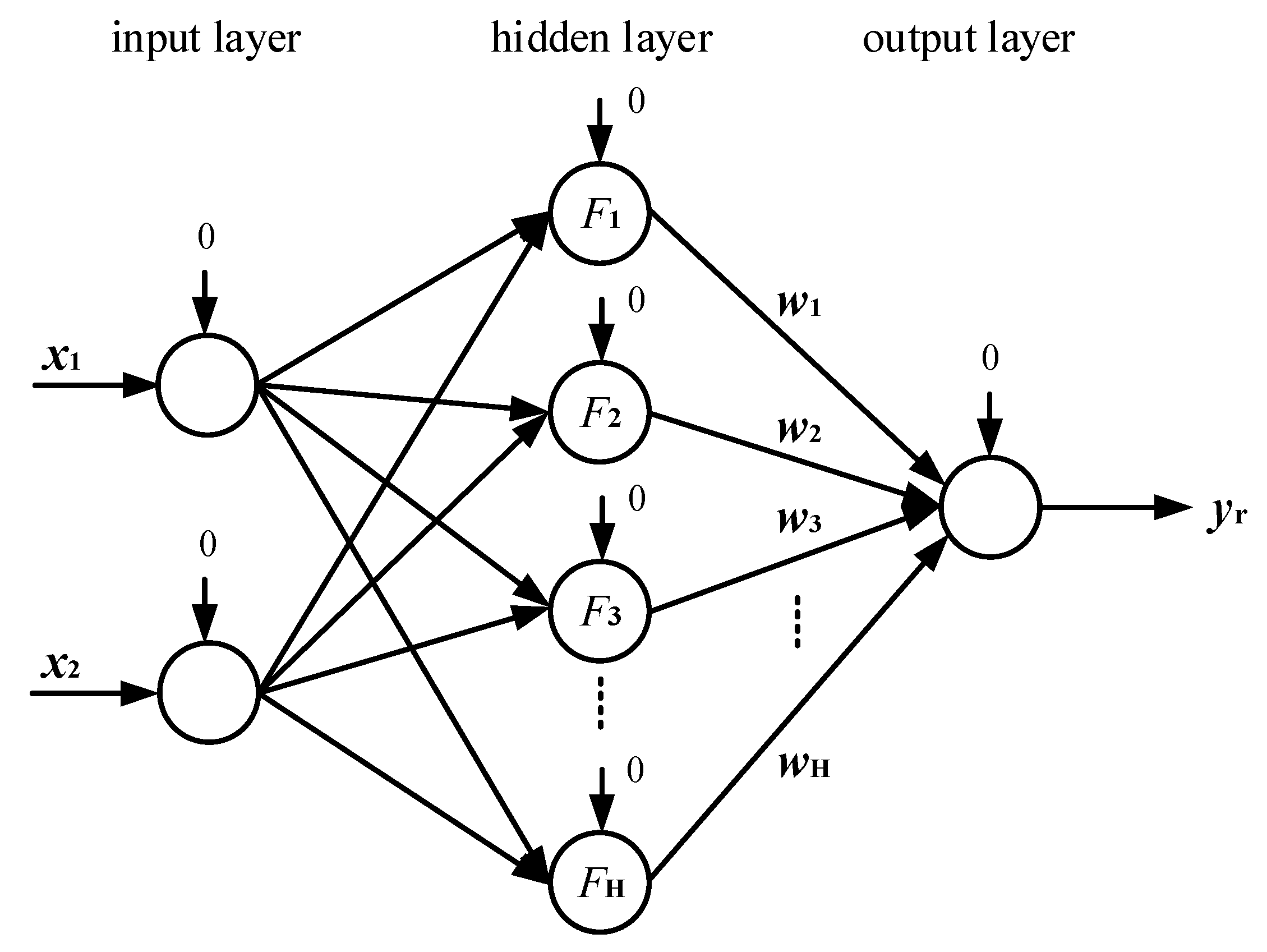
In contrast to common neural networks, the applied network is a new neural network, called a Chebyshev polynomial, a Class 1 neural network, which is proposed by Zhang et al. [
24,
25], and the specific structure is given in
Figure 4. There are three layers, which are the input layer, the hidden layer, and the output layer. Meanwhile, both the input layer and the output layer adopt linear activation functions. The activation function of the hidden layer adopts the Chebyshev polynomial of Class 1. For simplification, the thresholds of all the neurons are set as zero. It utilizes the weight direction determination method to obtain the optimal linking weights between the hidden layer and the output layer, only needing a step calculation, which obviously lowers the calculation time and work. Hence, this new neural network is more easily implemented by the hardware and has enormous potential in engineering application. For the neural network, the two inputs are speed command and speed error, and the output is the fuel flow rate.
In order to comprehend the new Chebyshev polynomial Class 1 neural network in depth, the working process is shown in detail. Similar to the common neural networks, it also contains a signal forward propagation process and an error back propagation process, respectively, illustrated as follows:
- (1)
signal forward propagation process
The activation function of the input layer is linear, and there are two neurons. Hence, the input and output signals of the input layer, respectively, are,
where the superscript (1) denotes the input layer;
k denotes the present time.
In the hidden layer, the input of the
jth neuron is,
where the superscript (2) denotes the hidden layer.
In order to construct the activation function of the hidden layer, it firstly gives the Chebyshev polynomial of Class 1 as follows,
Based on the above polynomial definition, the total number of hidden layer neurons is set as
H = (
H1 + 1)(
H2 + 1), and the activation function of every hidden layer neuron is constructed as follows,
The output of the
jth hidden neuron is,
Because the activation function of the output layer is linear, the corresponding input and output signals, respectively, are,
where the superscript (3) denotes the output layer;
is the linking weight between the
jth hidden neuron and the output neuron at (
k − 1) time.
The batch processing error function is defined as follows,
where
is the error of the
lth desired output and the network output at
k time;
L is the total number of sample data.
- (2)
error back propagation process
In order to minimize the batch processing error function
E(
k), the gradient descent method needs to be adopted to revise the linking weights between the hidden layer and the output layer. The increment of the linking weight between the
jth hidden neuron and the output neuron is given as follows,
where
μ is the learning rate, which is larger than zero.
The specific revision formula of the linking weight between the
jth hidden neuron and the output neuron is,
The training data are the Simulink model data. According to the weight direct determination method, which is proposed by Professor Zhang [
24,
25], the optimal linking weights between the hidden layer and the output layer can be obtained,
where
;
Z is the activated input matrix,
;
is the output of the
jth hidden layer neuron when the
lth sample data is input to the network;
y is the desired output data vector,
;
pinv is used to calculate the pseudo inverse.
In order to determine the optimal number of hidden neurons which may exert a significant influence on the performance of the neural network, the structure determination algorithm, which is an uncertain accuracy method, is employed [
24,
25], and the corresponding flowchart is given in
Figure 5. For the structure determination algorithm, the calculation formula of the half mean square error (
HE) needs to be given as follows:
The specific work process is illustrated as follows:
Step 1. Collect the sample data (xl, yl), l = 1, 2, …, L. Initialize the parameters including the current number of the Chebyshev polynomial of Class 1 p = 2, and the current minimal number pmin = 2. The current minimal half mean square error HEmin is set to be 10, which should be large enough so that the procedure can be smoothly actuated. In the light of the initial structure of the neural network, calculate the half mean square error HE via (43).
Step 2. If HE ≤ HEmin or p ≤ pmin + 1, proceed to step 3. Otherwise, go forward to step 5.
Step 3. According to the current structure of the neural network, calculate the activated input matrix Z, the linking weights w between the hidden layer and the output layer, and HE.
Step 4. If HE ≤ HEmin, actuated HEmin = HE, pmin = p, and wopt = w, and allow p = p + 1, proceed to step 2. Otherwise, directly allow p = p + 1, and proceed to step 2.
Step 5. Save the minimal half mean square error HEmin, the optimal number of hidden layer neurons Hopt = pmin2, and the optimal linking weights wopt.
So far, the complete work process of this new neural network, which includes the signal forward propagation process and the error back propagation process, has been given; the calculation method of the optimal linking weights between the hidden layer and the output layer has been presented, and the structure determination algorithm has also been illustrated. In the subsequent part, the above formulas and algorithm will be employed to design and rectify the new neural network controller of the aero-derivative gas turbine.
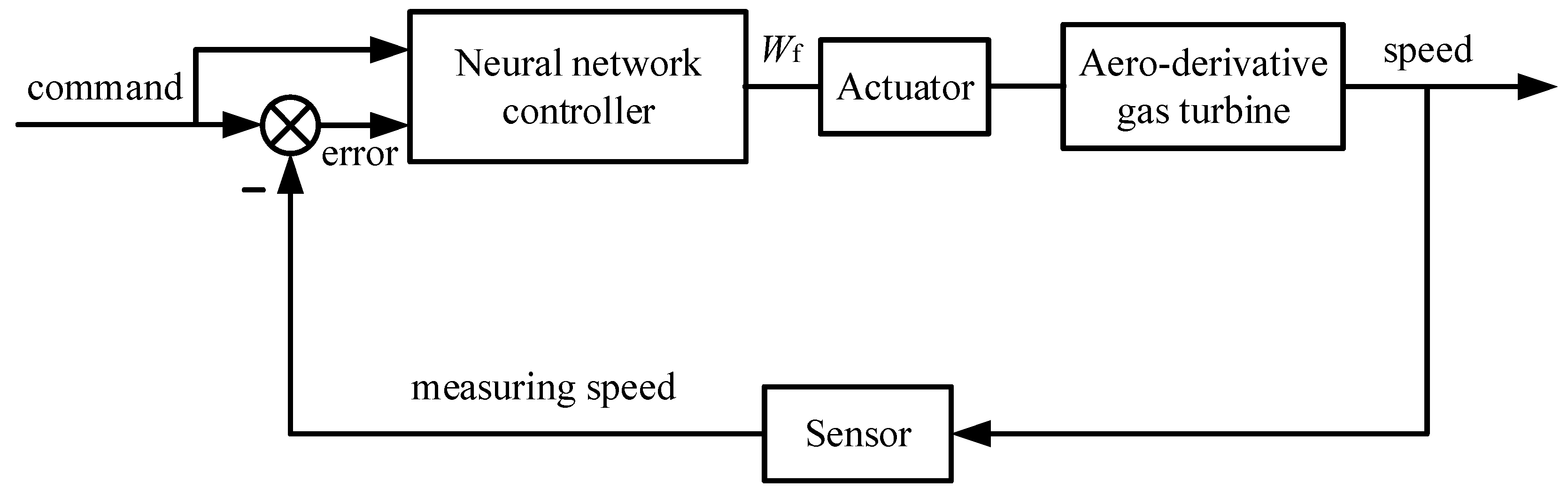
3.3. The Integrated Control Method
The original controller and a new neural network controller have been illustrated in
Section 3.1 and
Section 3.2, respectively. Although the original controller has a rapid response performance, the overshoot is large. Thus, the integrated control method uses the new neural network to decrease the overshoot. By combining the original controller with the new neural network controller, it develops a novel integrated control method, which is shown in
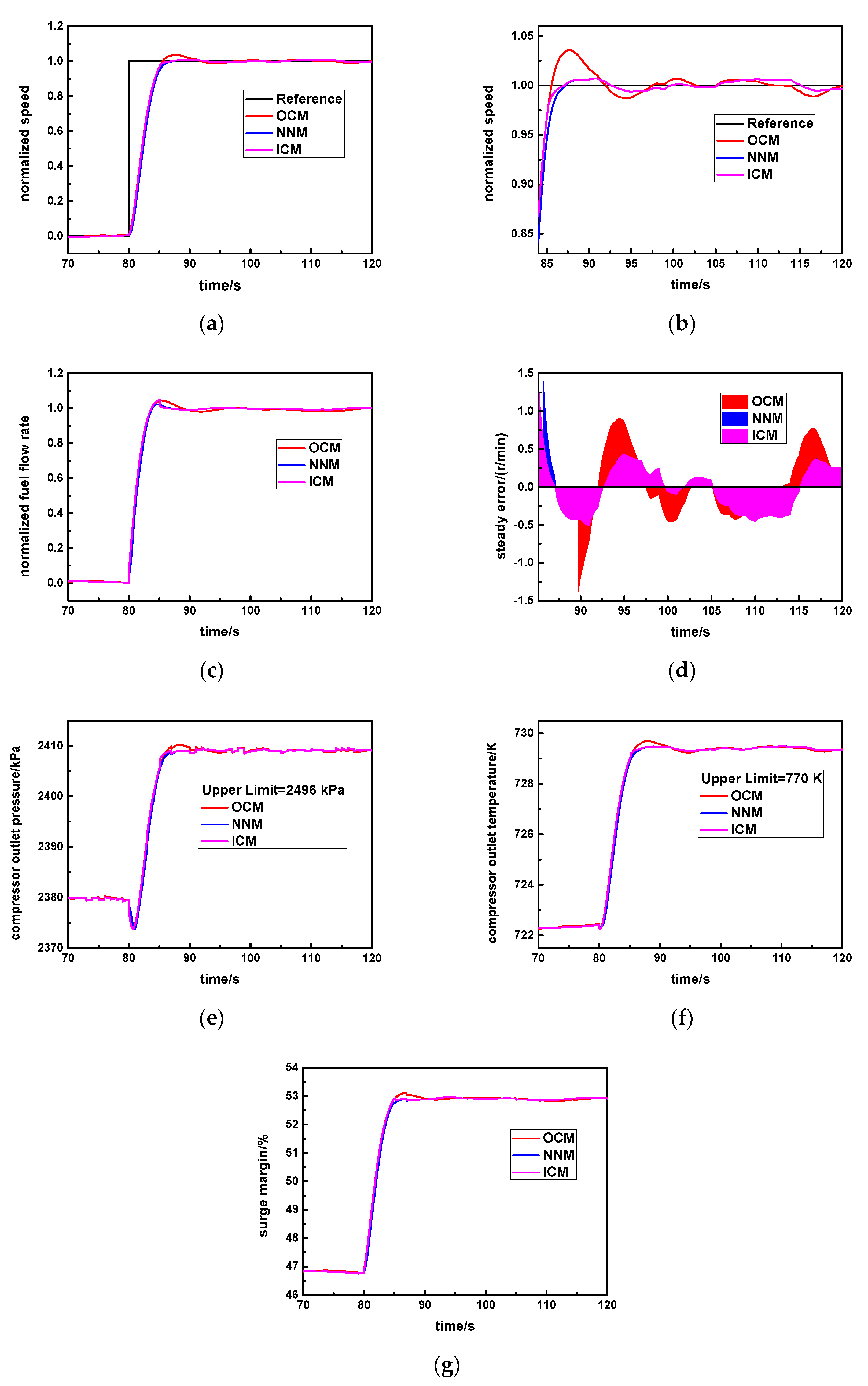
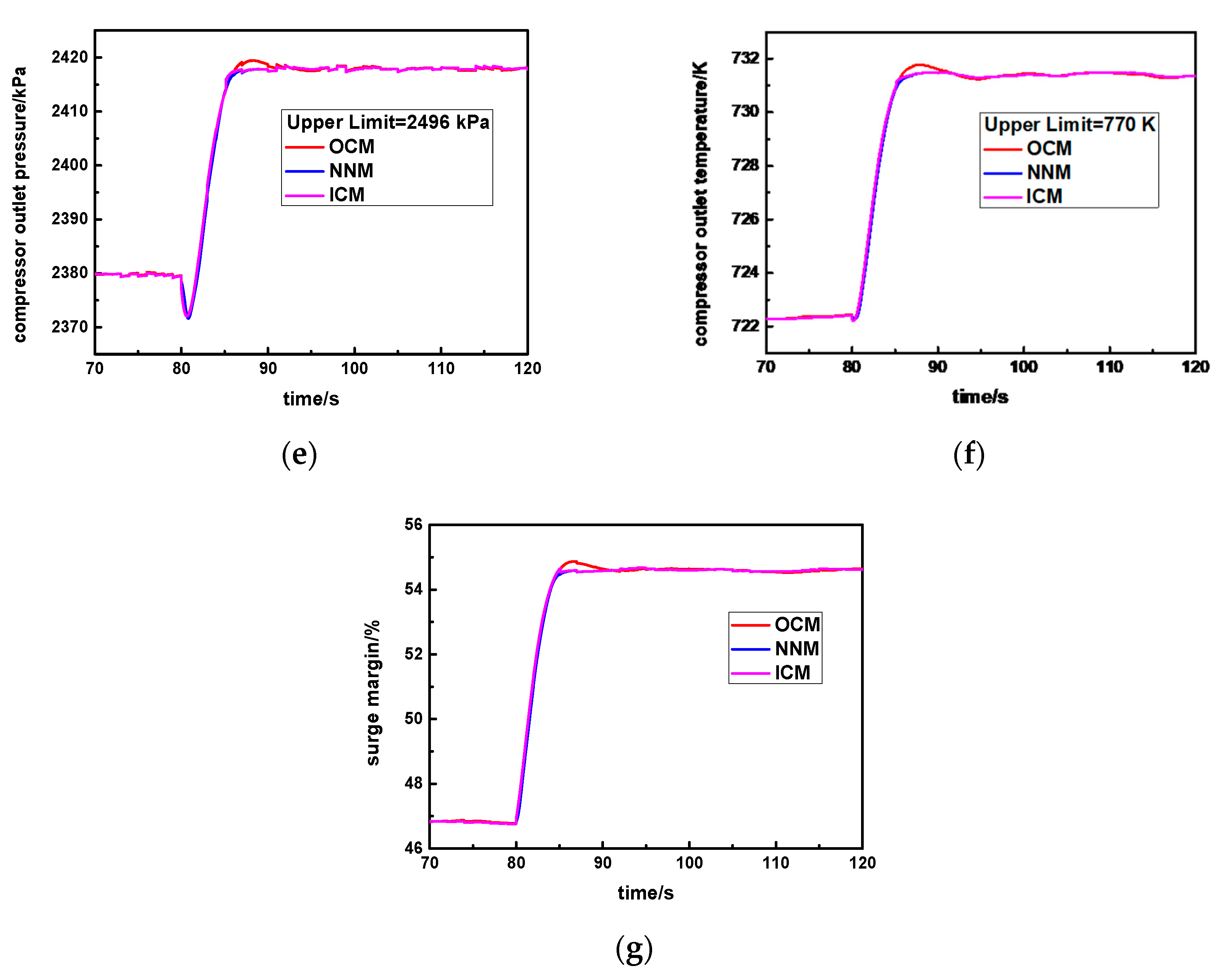
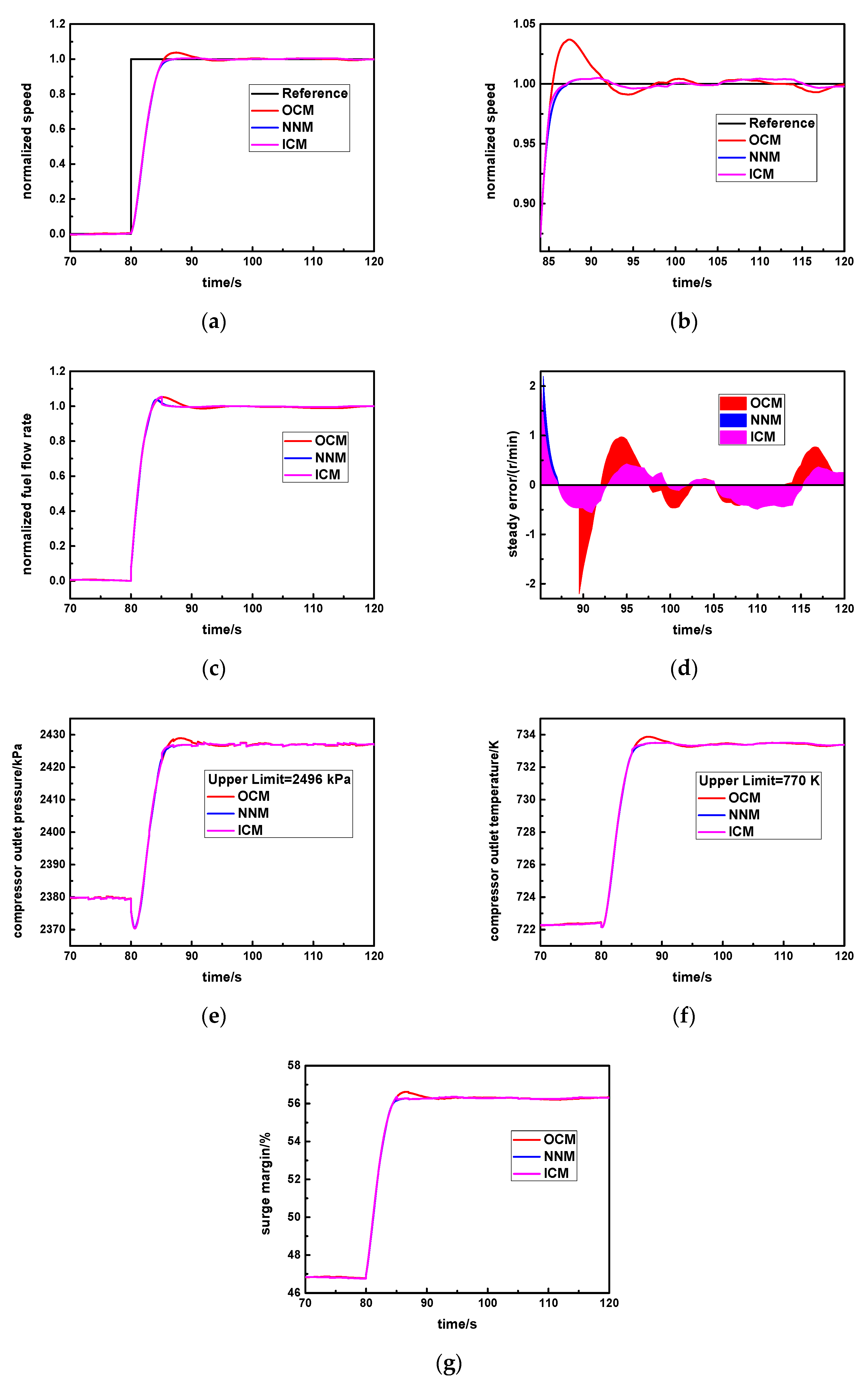
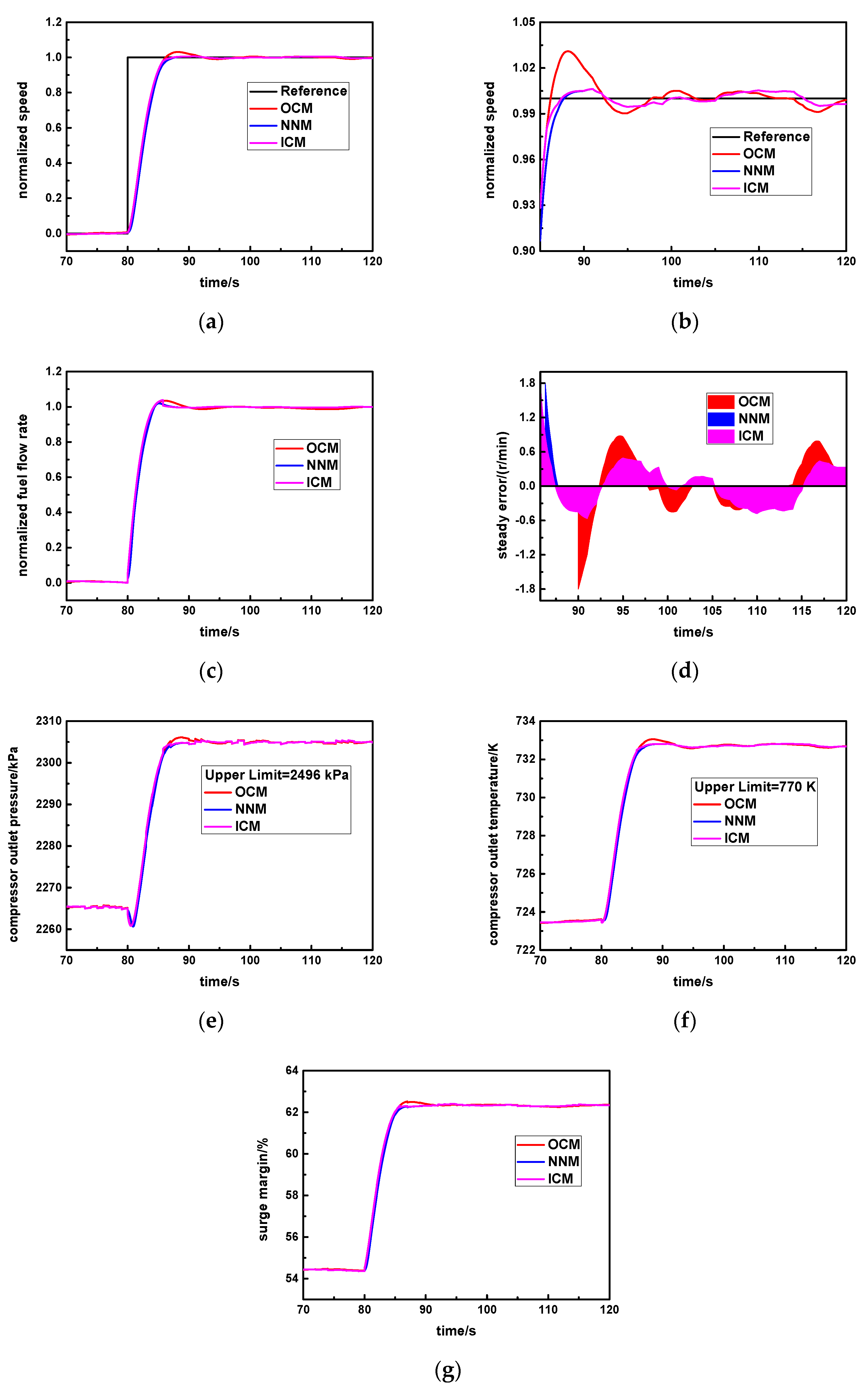
Figure 6. Meanwhile, the OCM is the original controller, and the NNM is the new neural network controller. During the normal step response process, the instant error of the speed step command and the measuring speed continuously change, and the aero-derivative gas turbine will select the specific controller according to the given error threshold
cv. The complete selecting logic is shown as follows:
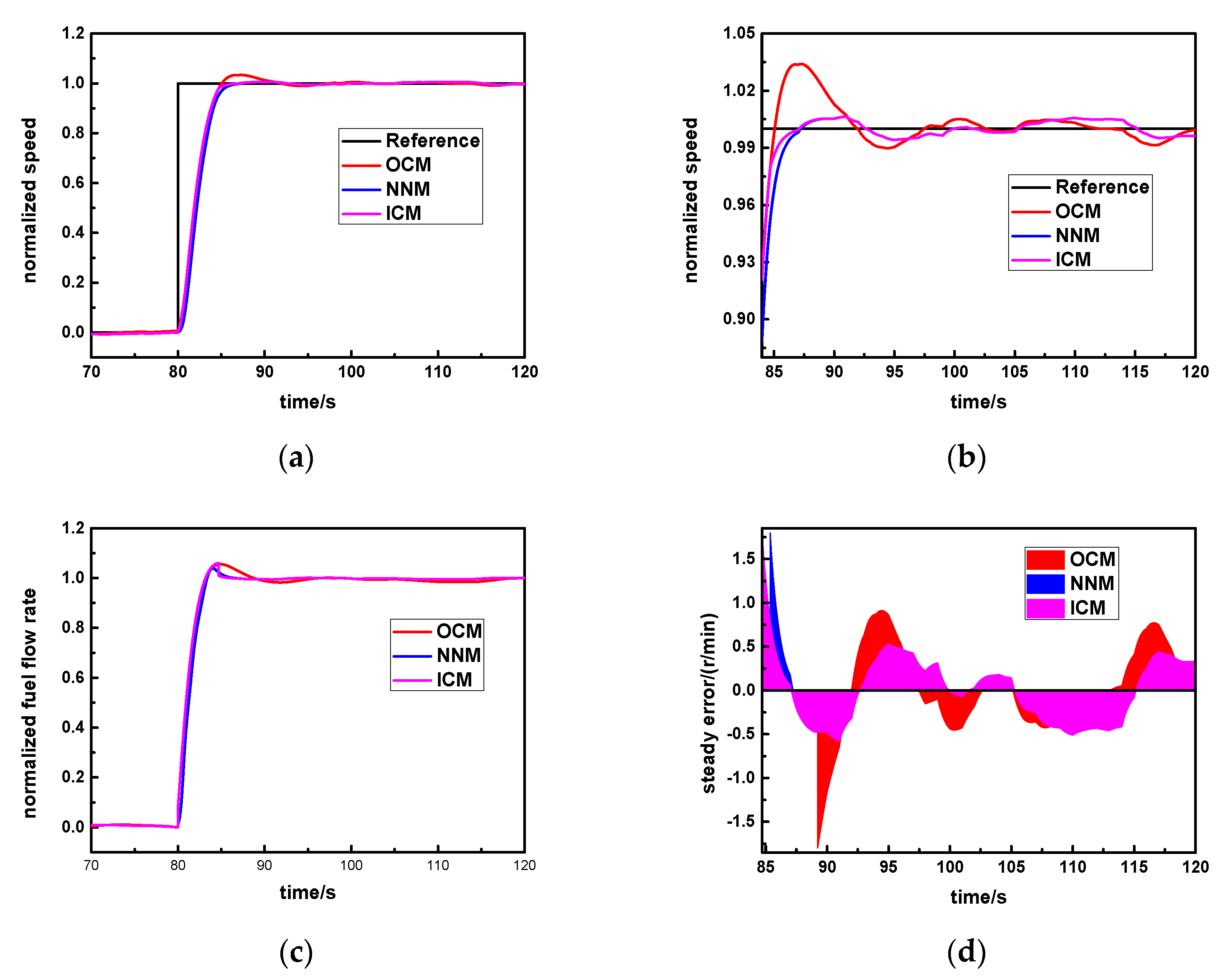
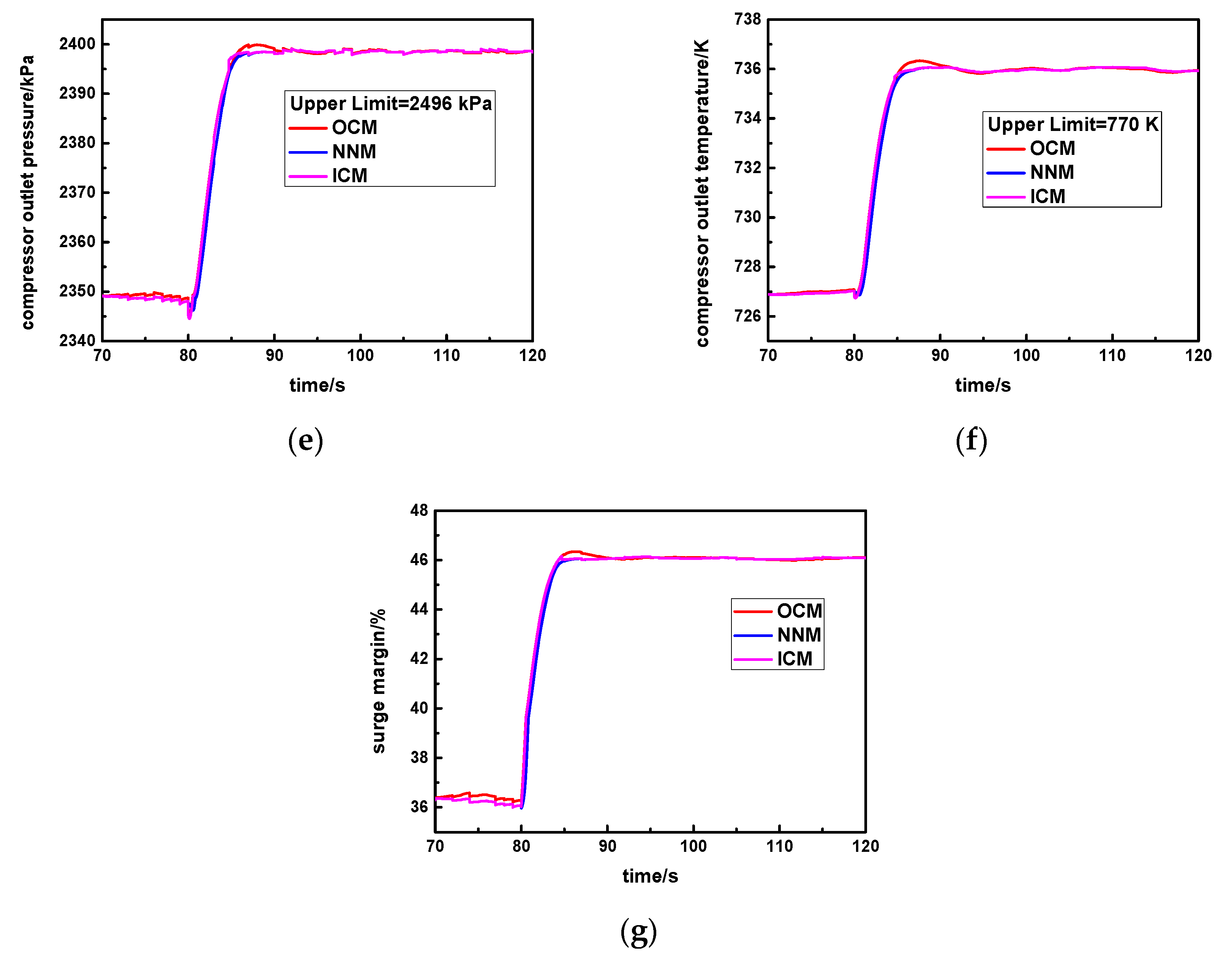
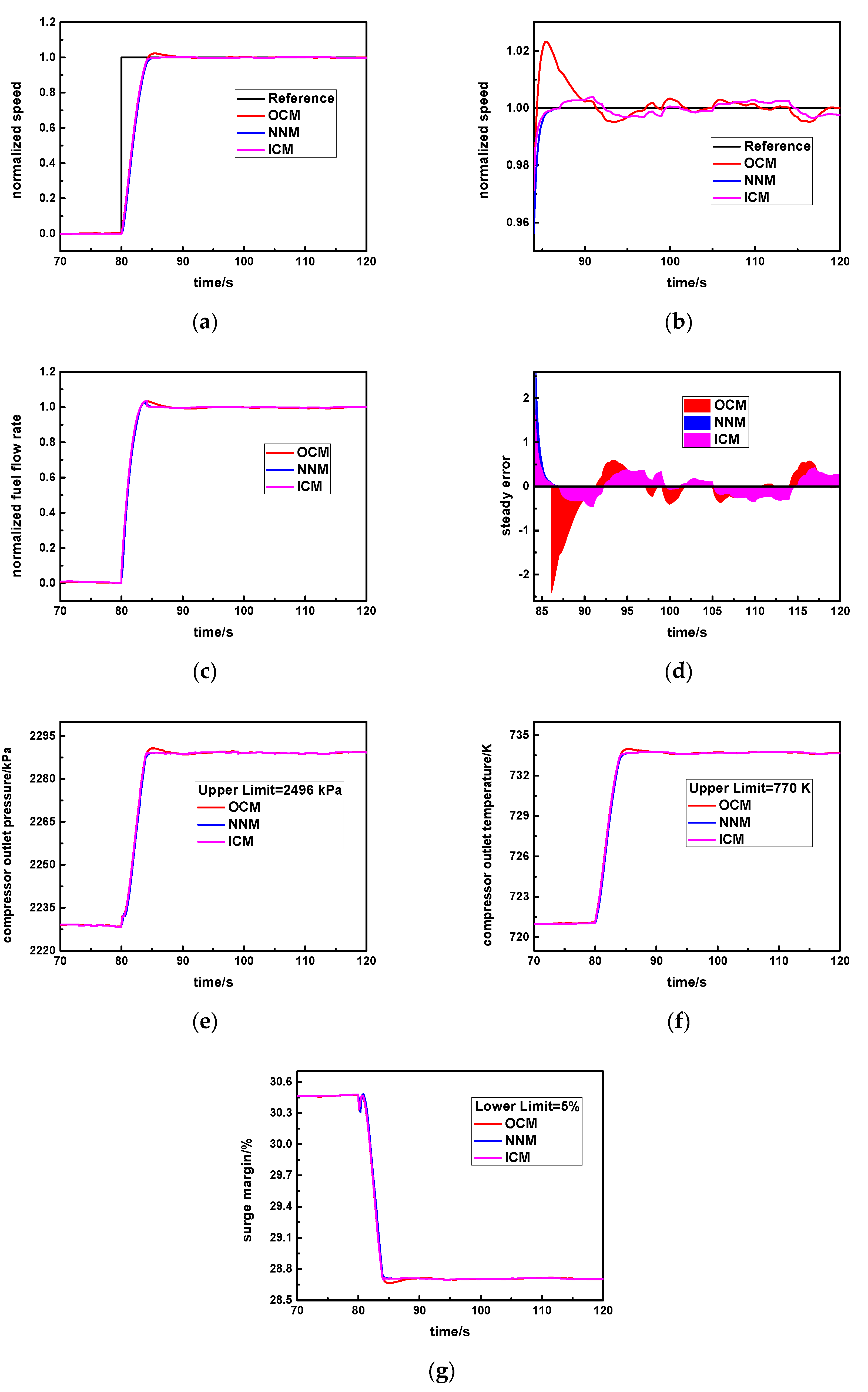
Specifically, cv is set as the standard steady error value. In the early response process, the instant error is larger than cv, and the original controller will be activated (SW = 1) so that response rapidity will be greater. In the steady response stage, the instant error is smaller than or equal to cv, and the new neural network controller will be triggered (SW = 2) so that it is able to obtain higher steady accuracy and avoids the larger overshoot.
In this way, the advantages of the original controller and the new neural network controller can be simultaneously utilized, which is beneficial for realizing the ideal control effect of this aero-derivative gas turbine.
The controlled variable is speed, and the controlling variable is fuel flow rate. For the neural network, the input variables are step command and speed error, and the output variable is fuel flow rate, which is the same as in
Section 3.2.