Abstract
To solve the problem that fault features are difficult to extract and the time-frequency features cannot fully represent the state information, a novel method is proposed in this paper based on the whale optimization algorithm (WOA) and the kernel extreme learning machine (KELM). First, the vibration signals are processed by the ensemble empirical mode decomposition and sample entropy to obtain the feature vectors. Based on this, a KELM model for fault diagnosis is established. Then, the penalty factor and the kernel parameters in the KELM are optimized by WOA to improve the stability and classification accuracy. Taking faults of a ball-screw pair on a linear feed table as a case, the experimental results indicate that the proposed method can effectively extract the fault features of the ball-screw pair, and it can achieve higher classification accuracy, faster convergence speed, and greater convergence precision than the existing fault diagnosis methods.
1. Introduction
1.1. Background
The rotor is an indispensable component in rotating machinery. Since it works under a complex condition of heavy load and high speed for a long time, it is prone to many kinds of faults. Timely fault identification is important to ensure that the equipment operates normally and to improve the manufacturing capability. Faults can be detected by analyzing vibration signals of rotating machinery. Although the vibration signals contain fault information, it is chaotic and mixed with noise. Therefore, the preprocessing step of the original signals is very important. Then the extraction of state information from vibration signals is a key to fault diagnosis [1]. The fault is classified based on the operating state information.
At present, machine learning, deep learning and some other methods are applied to fault diagnosis. For the machine learning model, its early training is particularly important, which requires a relatively large number of training samples to achieve a higher classification accuracy.
1.2. Literature Review
The vibration signals of the ball-screw pair are non-linear and non-stationary under the fault state. Empirical Mode Decomposition (EMD) has a strong self-adaptivity and a high signal-to-noise ratio, which is suitable for analyzing non-linear and non-stationary signals [2,3,4]. In [5,6,7], EMD was adopted to process the original signals to obtain the intrinsic mode function (IMF) components and reduce the noise. By further processing of IMF components, the fault feature information was obtained. EMD can process noisy signals, but serious modal aliasing exists. Wu et al. [8,9] proposed Ensemble Empirical Mode Decomposition (EEMD), which provides a relatively consistent reference by adding multiple groups of different white noise into the original signal. EEMD can effectively suppress the end effect and mode aliasing.
The key to the next step after EEMD is how to extract effective fault features from IMFs. The entropy theory was introduced. The combination of EEMD with singular value entropy was proposed to diagnose bearing faults [10]. Zhang et al. [11] proposed a method that combines EMD with Multipoint Optimal Minimum Entropy Deconvolution (MOMEDA) to extract the fault cycle of the gearbox signals.
The intelligent diagnostic technique provides a more accurate method for fault diagnosis of ball-screws [12,13,14]. Compared with traditional neural networks, the Extreme Learning Machine (ELM) has faster convergence and less error [15], and it has been widely used for machinery fault diagnosis. Huang et al. [16] put forward the Kernel Extreme Learning Machine (KELM), which improves the stability and generalization ability of ELM. It is also found through experiments that KELM, which was used to classify the fault states of rotating machinery, has a higher classification accuracy than ELM [17]. However, the penalty factor and kernel parameters of the KELM are assigned randomly, which easily causes the network structure to fluctuate.
1.3. Contribution
To solve the problem, this paper proposes a method of optimizing KELM for fault diagnosis based on the whale optimization algorithm (WOA). WOA can optimize the penalty factor and kernel parameters of KELM [18,19,20], and it can enhance the stability and generalization ability of the diagnostic model and improve the classification accuracy. Firstly, EEMD is used to decompose the vibration signals to reduce noise and obtain the IMFs. Then, the first IMFs highly correlated with the original signals and containing main fault information are selected, and the sample entropies of the IMFs are calculated to constitute the sample entropy feature vectors. Next, the KELM fault diagnosis model is established, and the sample entropy feature vectors of IMFs are taken as the input of the KELM model. For the random assignment of KELM’s penalty factor and kernel parameter, WOA is used for optimization to obtain the optimal parameters. Finally, the method proposed in this paper is applied to the fault diagnosis of the ball-screw pair to verify its effectiveness.
2. Methods
The framework of the method proposed in this paper is shown in Figure 1. Firstly, vibration signals of the equipment were collected. Secondly, EEMD was used to decompose the vibration signals under different states to reduce noise and obtain IMFs. The first few IMFs which are highly correlated with the original signals and containing the main fault information were chosen to calculate their sample entropies and obtain the feature vectors. Thirdly, as established, WOA was used to optimize the penalty factor and kernel parameters in the KELM fault diagnosis model, and the feature vectors were taken as the input of the WOA-KELM model. Finally, the performance of WOA-KELM was compared with the other KELM models.
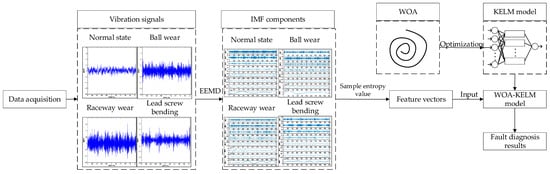
Figure 1.
Framework of the method.
2.1. Vibration Signal Feature Extration Methods
2.1.1. Ensemble Empirical Mode Decomposition (EEMD)
Different from traditional signal processing methods, EMD obtains a series of IMFs by screening non-linear and non-stationary signals. Each IMF contains different time dimensions that represent real physical information of the signal. However, EMD is an empirical method, and it lacks strict mathematical derivation and theoretical support. Thus, there could be problems such as end effect and mode aliasing, which affect the accuracy of decomposition results. Compared to EMD, EEMD adds different random white noise, and the decomposition results are averaged to eliminate the influence of white noise. Meanwhile, EEMD reduces modal aliasing by ensuring the continuity of each modal function in the time domain. The decomposition steps, shown in Figure 2, are as follows:

Figure 2.
EEMD decomposition process.
(1) Add a group of normally distributed sequences of white noise into the original signal and obtain a group of composite signals .
(2) Decompose each composite signal by EMD, and the steps are:
(a) Determine all local maximum and minimum points of , and connect these points with cubic spline interpolation curves to form the upper envelope and lower envelope . Calculate the mean value of the upper and lower envelopes .
(b) Subtract from to obtain the new sequence . If the IMF conditions are met, is taken as the first IMF component of ; otherwise, is taken as the original data to repeat step (a).
(c) The first IMF component is subtracted from to obtain the residual signal . Take as the original data to repeat steps (a) to (b) to obtain the remaining IMFs and the residual signals.
(3) Average the IMF components and the residual signals.
2.1.2. Sample Entropy (SampEn)
The vibration signals were processed by EEMD to obtain IMF components. Each IMF component contains different frequency components and has a different energy distribution in the frequency domain [21]. When a certain part of the ball-screw fails, the frequency distribution and energy distribution of the vibration signal will change. Therefore, by comparing the sample entropy of the IMFs after EEMD decomposition, the complexity of the signal can be measured and the corresponding fault state can be analyzed. The sample entropies of the IMF components of each vibration signal constitute a set of feature vectors that will be used as the input of the KELM model. The higher the complexity of the signal, the greater the entropy.
Denote the discrete time series of length as , and the calculation steps of the sample entropy are as follows:
(1) The time series is reconstructed into -dimensional vectors, i.e.,
(2) Denote the distance between vectors and as , which is the maximum difference between the scalars corresponding to the two vectors, i.e.,
(3) Given the similarity tolerance , denote the number of distances between and less than as . Then, the probability that and match data points under the similarity tolerance can be expressed as:
(4) Increase the dimension by 1 and repeat steps (1) to (3). Since is a finite value in the actual situation, the estimated value of the sample entropy is
2.2. WOA-KELM Model
2.2.1. Kernel Extreme Learning Machine (KELM)
During training, the weight matrix and bias between the input layer and the hidden layer of the ELM are randomly initialized. Only the number of hidden layer neurons and activation functions needs to be set in the training process, and the hidden layer parameters do not need to be adjusted many times. This can improve the training speed [16,17]. However, different hidden layer output matrices and output weights are randomly generated during each training process, which reduces the stability and generalization ability of the ELM model. To address this issue, the kernel function [22] was introduced to map the input samples to the high-dimensional kernel space by using the kernel matrix instead of the random matrix. In this way, the output weight matrix can only be determined by training samples and the kernel function.
According to Mercer’s condition, the kernel matrix is defined as
where is the output matrix of the hidden layer, is the feature mapping function of the hidden layer, is the radial basis function (RBF), and .
Therefore, the output of KELM is
where is the penalty factor, is the identity matrix, and is the expected output matrix.
In this study, 40 groups of the collected data were randomly selected as the training samples and the other 10 groups of data as the testing samples. The training accuracy, testing accuracy, and run time of the KELM, BP, and ELM model are shown in Table 1.

Table 1.
Comparison of different algorithms.
It can be seen from Table 1 that the BP neural network obtained the lowest classification accuracy and had the longest run time. This is because it uses the gradient descent method for learning, which is prone to the problems of local optima and overfitting in the iterative process. ELM and KELM do not have to iterate continuously, so they have lower computational complexity and are less time-consuming than BP neural networks. Additionally, KELM has higher diagnostic accuracy and is less time-consuming than ELM.
2.2.2. Whale Optimization Algorithm (WOA)
Although KELM has certain advantages, the random initialization of the penalty factor and kernel parameter in the training process will affect its stability and accuracy. WOA can optimize the parameters by using a random or optimal search strategy to simulate the three behaviors of humpback whales: surrounding prey along a spiral path from bottom to top, attacking prey with bubble nets, and searching for prey [20]. It is a new heuristic search optimization algorithm with simple operation, few adjustment parameters, and a strong global searching ability.
- (1)
- Surrounding prey
When the prey location is known, humpback whales can identify the prey location and surround the prey. However, for practical problems, the prey location is unknown. Thus, it is assumed that the current optimal solution is the target prey location, and other whales update the location by surrounding the current optimal solution. The location update formula is:
where represents the current iteration times, is the current whale individual position, is the current optimal solution position, and and are coefficient vectors. The calculation formulas of and are
where is the convergence factor. With the increase of the number of iterations, decreases linearly from 2 to 0. and are random variables within , and is the maximum number of iterations.
- (2)
- Bubble net attack
When the coefficient vector falls within , the whales update the position according to the prey, and they randomly appear at any position between the current position and the optimal solution position, showing the local search ability of the WOA. When humpback whales attack the prey with a bubble net, they shrink and surround the prey in a spiral path. The position update model of shrink-wrapping is
The position update model of spiral rise is
where represents the distance between the whale and the current optimal solution, is the shape constant of the logarithmic spiral line, is a random number within , and is a random number within .
- (3)
- Random search
When the coefficient vector does not fall within , the whale is outside the contraction circle and no longer updates the position according to the prey, and it randomly selects other individuals in the population to update the position, showing the global search ability of the WOA. The location update model for this behavior is
where is the position of a randomly selected whale.
2.2.3. Establishment of the WOA-KELM Model
The random initialization of the penalty factor and kernel parameters in KELM will reduce the stability and classification accuracy. Since WOA can determine the optimal parameters within a certain search range, it was adopted in this study to optimize KELM to establish a fault diagnosis model which is WOA-KELM. The establishment of the WOA-KELM model, shown in Figure 3, is described as follows:
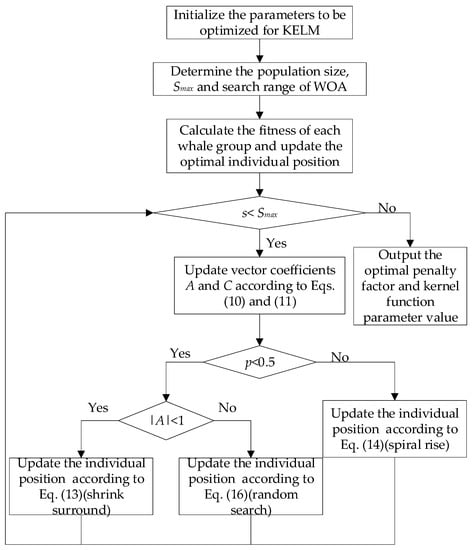
Figure 3.
Process of the WOA-optimization of KELM.
(1) Initialize the position of the whale population vector, that is, initialize the penalty factor and kernel parameters of KELM. Determine the whale population size, the maximum number of iterations , and the parameter search range.
(2) Calculate the fitness of each whale, and update and record the optimal individual position.
(3) If the current number of iterations , directly output the optimal penalty factor and kernel function parameters; otherwise, update the vector coefficients and according to Equations (10) and (11) and determine the value of random number .
(4) If , update the individual whale position according to the spiral rising model shown in Equation (14). If , further determine the value of vector coefficient .
(5) If , update the individual whale position according to the contraction surrounding model shown in Equation (13); otherwise, update the individual whale position according to the random search strategy which is shown in Equation (16).
3. Experiment and Results
3.1. Data Acquisition
Taking the fault diagnosis of the ball-screw pair as an example to verify the effectiveness of the WOA-KELM model. The ball-screw pair has the advantages of stable transmission, high accuracy, and high efficiency. It can accurately position the workbench on the equipment, such as the computer numerical control machine tool and three-coordinate measuring machine. Since the ball-screw pair has a complex structure, it is prone to many kinds of faults. When the equipment operates under high speed and heavy load for a long time, the dynamic load between the ball and the raceway will become large, and the contact surface will be severely worn. In this case, the surface performance will deteriorate rapidly, resulting in wear failure. When the equipment operates at low speed and light load, the dynamic load exerted by the ball on the raceway will become small, and the wear loss will be little. In this case, the bending deformation is the main fault. Therefore, the working condition of the ball-screw pair can be divided into four states: normal state, ball wear, raceway wear, and lead screw bending.
Figure 4 shows the two kinds of fault states of the ball-screw: raceway wear and lead screw bending. As shown in Figure 5a, a linear feed table driven by the ball-screw pair was applied to collect the vibration signal of the ball-screw under the different states including normal, ball wear, raceway wear, and lead screw bending. The forces on the moving table, represented by Fx, Fy, and Fz, will be transmitted onto the ball-screw. A three-axis acceleration sensor was installed on the nut seat to acquire the vibration data, as shown in Figure 5b. The acquisition program was developed containing the functions of starting and stopping data acquisition, starting and stopping data recording, setting the sampling number and sampling rate, and real-time display of the vibration data.

Figure 4.
The fault modes of the ball-screw pair: (a) raceway wear and (b) lead screw bending.

Figure 5.
Vibration signal acquisition on the feed table: (a) alinear feed table driven by the ball-screw and (b) a three-axis acceleration sensor.
In the experiment, the speed of the lead screw was set to 800 r/min; the sampling frequency was set to 1000 Hz, and the sampling time for each state was set to 10 s. The data set was enhanced by overlapping sampling. For a sample length of 2048 and an offset of 162, the vibration signal in each state can generate 50 samples, and the total number of samples was 200.
3.2. Feature Extraction
3.2.1. Extracting Signal Features by EEMD
Time-domain analysis cannot characterize frequency information, and frequency-domain analysis cannot characterize the time point information at a certain frequency. Therefore, the single time-domain or frequency-domain analysis cannot reflect the global information of fault features. EEMD can obtain the change rule of signal and the distribution of signal energy with time and frequency. In this study, EEMD decomposition was performed on the vibration signal of the ball-screw in each state. Since the fault information is usually included in the first few IMF components [23], the energy values of the first eight IMFs were extracted as time-frequency domain features, as shown in Figure 6. Each IMF contains different frequency components and has a different energy distribution.

Figure 6.
The first 8 IMFs decomposed by EEMD: (a) normal, (b) ball wear, (c) raceway wear, and (d) lead screw bending.
3.2.2. Extracting Signal Features by SampEn
The input feature vectors of the KELM model were obtained by calculating the sample entropy of each IMF. They can measure the complexity of the signal and help to analyze the fault state of the ball-screw pair. According to Formula (4), the sample entropy is related to , where is the dimension, is the similarity tolerance, and is the sample length. In this paper, = 2, = 0.2 Std (Std represents the standard deviation of the time series), and . Figure 7 illustrates the sample entropy of the IMFs of the partial vibration data under the four states of the ball-screw pair.

Figure 7.
The sample entropy of the IMFs.
As shown in Figure 7, signals 1–10 are normal signals, 11–20 are ball wear signals, 21–30 are raceway wear signals, and 31–40 are lead screw bending signals. It can be seen that in the first three states, the sample entropy of IMF1 to IMF8 gradually decreased, that is, the signal complexity became lower. Meanwhile, the state information was mainly concentrated in the components of IMF1 and IMF2. In the lead screw bending state, the sample entropy of IMF1 was smaller than that of the last IMF, and the state information was mainly concentrated in the components of IMF2 and IMF3.
3.3. Comparison of the Diagnosis Results of the Models
The fault diagnosis model was trained and tested with the vibration signals of the ball-screw pair under the four states. Following the method introduced in Section 3.1, 200 groups of feature vectors were extracted from the collected vibration signals, of which 160 groups were taken as training samples and 40 groups were taken as test samples. In the WOA, the number of whales was 40, the dimension was 2, and the maximum number of iterations was 100.
The bat algorithm (BA), similar to the WOA, can simulate the mechanism of an animal capturing prey in nature by seeking the optimal solution through the iterative update of its position. The cloud bat algorithm (CBA) is an improvement of BA by using the cloud model. To test the performance of WOA-KELM, under the same parameter settings, training samples, and test samples, the diagnostic results of the WOA-KELM model were compared with those of WOA-ELM, BA-KELM, and CBA-KELM. The optimal accuracy, worst accuracy, and average accuracy in training and testing the four algorithms are shown in Figure 8, and the corresponding iteration curves are shown in Figure 9.

Figure 8.
Diagnostic accuracy of the four methods: (a) training samples and (b) testing samples.

Figure 9.
Iterative curves of the four methods.
Figure 8 and Figure 9 show that the WOA-KELM algorithm performed better than WOA-ELM and BA-KELM in diagnosis accuracy, diagnosis stability, convergence speed, and accuracy. Although there was little difference in the diagnostic accuracy of WOA-KELM and CBA-KELM, WOA-KELM achieved a higher convergence speed than CBA-KELM. Then, the WOA-KELM fault diagnosis model was constructed based on the optimal parameter combination and applied to the test samples. The diagnosis accuracy is shown in Figure 10. It can be seen that WOA-KELM only made a few errors and can correctly diagnose most samples.

Figure 10.
The fault diagnosis results of the WOA-KELM model: (a) training samples and (b) testing samples.
4. Discussion
(1) Considering that the effective features cannot be obtained from a simple time-frequency analysis of the original vibration signals, in this study, the EEMD and SampEn were adopted to extract the vibration signal feature vectors containing the deeper fault information.
(2) Compared with ELM and BP, the KELM model has the advantages of higher diagnosis accuracy and lower execution time.
(3) The random initialization of the penalty factor and kernel parameters of KELM easily affects the diagnosis accuracy. To address this issue, this study adopted WOA to optimize the KELM, and built a fault diagnosis model called WOA-KELM. By simulating the process of a whale hunting prey, the best whale position with the best fitness, that is, the optimal training parameters of KELM, can be obtained.
(4) The proposed method was applied to the fault diagnosis of the ball-screw pair. From the experimental results, it can be observed that compared with the WOA-ELM, BA-KELM, and CBA-KELM, the WOA-KELM achieved higher accuracy, faster convergence speed, and better stability, which indicates that the WOA-KELM can be used as an effective algorithm for fault diagnosis of rotating machinery.
Author Contributions
Conceptualization, R.L.; methodology, R.L.; software, Y.C.; validation, R.L.; formal analysis, R.L. and Y.C.; investigation, Y.C.; resources, R.Z.; data curation, Y.C.; writing—original draft preparation, R.L.; writing—review and editing, R.L. and Y.C.; visualization, R.L. and Y.C.; supervision, R.L. and R.Z.; project administration, R.L.; funding acquisition, R.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This study is supported by the National Key Research and Development Program of China (No. 2018YFB2001300).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No data available.
Conflicts of Interest
The authors declare that there is no conflict of interest regarding the publication of this paper.
Abbreviations
| WOA | Whale Optimization Algorithm |
| KELM | Kernel Extreme Learning Machine |
| EMD | Empirical Mode Decomposition |
| IMF | Intrinsic Mode Function |
| EEMD | Ensemble Empirical Mode Decomposition |
| ELM | Extreme Learning Machine |
| Std | The standard deviation of the time series |
| BA | Bat Algorithm |
References
- Han, C.F.; He, H.Q.; Wei, C.C.; Horng, J.H.; Chiu, Y.L.; Hwang, Y.C.; Lin, J.F. Techniques developed for fault diagnosis of long-range running ball screw drive machine to evaluate lubrication condition. Measurement 2018, 126, 274–288. [Google Scholar] [CrossRef]
- Yang, D.; Liu, S.T.; Xu, G.L.; Wang, X.W. An improved fast adaptive BEMD method based on multi-scale extrema. J. Data Acquis. Processing 2020, 35, 362–372. [Google Scholar]
- Wang, J.; Du, G.; Zhu, Z.; Shen, C.; He, Q. Fault diagnosis of rotating machines based on the EMD manifold. Mech. Syst. Signal Process. 2020, 135, 106443. [Google Scholar] [CrossRef]
- Wei, D.D.; Tang, W.C. A method for constraining the end effect of EMD based on sequential similarity detection and adaptive filter. J. Southeast Univ. 2021, 37, 14–21. [Google Scholar]
- Cheng, J.S.; Yu, D.J.; Yang, Y. Energy operator demodulating approach based on EMD and its application in mechanical fault diagnosis. Chin. J. Mech. Eng. 2004, 40, 115–118. [Google Scholar] [CrossRef]
- Yu, D.J.; Yang, Y.; Cheng, J.S. Fault diagnosis approach for gears based on EMD and SVM. Chin. J. Mech. Eng. 2005, 41, 140–144. [Google Scholar] [CrossRef]
- Cheng, J.S.; Yu, D.J.; Yang, Y. Fault diagnosis of roller bearings based on EMD and SVM. J. Aerosp. Power 2006, 21, 575–580. [Google Scholar]
- Chang, Y.M.; Wu, Z.; Chang, J.; Huang, N.E. Model Validation Based on Ensemble Empirical Mode Decomposition. Adv. Adapt. Data Anal. 2010, 2, 415–428. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Zhang, C.; Zhao, R.Z.; Deng, L.F. Rolling bearing fault diagnosis method based on EEMD singular value entropy. J. Vib. Meas. Diagn. 2019, 39, 353–358; 446–447. [Google Scholar]
- Zhang, X.; Zhao, J.; Ni, X.; Sun, F.; Ge, H. Fault diagnosis for gearbox based on EMD-MOMEDA. Int. J. Syst. Assur. Eng. Manag. 2019, 10, 836–847. [Google Scholar] [CrossRef]
- Zhang, W.; Jia, M.P.; Zhu, L.; Yan, X.A. Comprehensive Overview on Computational Intelligence Techniques for Machinery Condition Monitoring and Fault Diagnosis. Chin. J. Mech. Eng. 2017, 30, 782–795. [Google Scholar] [CrossRef] [Green Version]
- Chen, F.; Yang, Z.; Zhang, Z.C.; Luo, W. Fault diagnosis method of rotating machinery for unlabeled data. J. Jilin Univ. Eng. Ed. 2022, 1–11. [Google Scholar] [CrossRef]
- Zhang, L.Z.; Xu, W.X.; Jing, L.Y.; Tan, J.W. Fault diagnosis of rotating machinery based on EMD-SVD and CNN. J. Vib. Meas. Diagn. 2020, 40, 1063–1070; 1228. [Google Scholar]
- Huang, G.B.; Zhou, H.; Ding, X.; Zhang, R. Extreme Learning Machine for Regression and Multiclass Classification. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2012, 42, 513–529. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, G.B.; Zhu, Q.Y.; SIEW, C.K. Extreme learning machine: A new learning scheme of feedforward neural networks. IEEE Int. Joint Conf. Neural. Netw. 2004, 2, 985–990. [Google Scholar]
- Wang, P.; Wen, Z.; Gao, X.J.; Wen, H.R. Fault diagnosis method of rotating machinery based on the kernel extreme learning machine. Noise Vib. Control 2018, 32, 138–143. [Google Scholar]
- Zhang, P.; Zhang, W.H.; Zhao, X.H.; Wu, X.T.; Liu, N. Application of WOA-VMD algorithm in bearing fault diagnosis. Noise Vib. Control 2021, 41, 86–93; 275. [Google Scholar]
- Huang, G.B.; Ding, X.; Zhou, H. Optimization method based extreme learning machine for classification. Neurocomputing 2010, 74, 155–163. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Yu, W.J.; He, L.; Cui, L.L.; Xu, R.W.; Li, R.B. Outboard abnormal noise source localization method with curved surface projection based on time delay matching and weighting criterion. Acta Acust. 2019, 44, 49–56. [Google Scholar]
- Iosifidis, A.; Tefas, A.; Pitas, I. On the kernel Extreme Learning Machine classifier. Pattern Recognit. Lett. 2015, 54, 11–17. [Google Scholar] [CrossRef]
- Zhang, J.; Gao, R.X. Deep Learning-Driven Data Curation and Model Interpretation for Smart Manufacturing. Chin. J. Mech. Eng. 2021, 34, 65–85. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).