Effect of Assembly Errors on Ground Tooth Surface Deviations for Large-Scale CNC Gear Profile Grinding Machines
Abstract
:1. Introduction
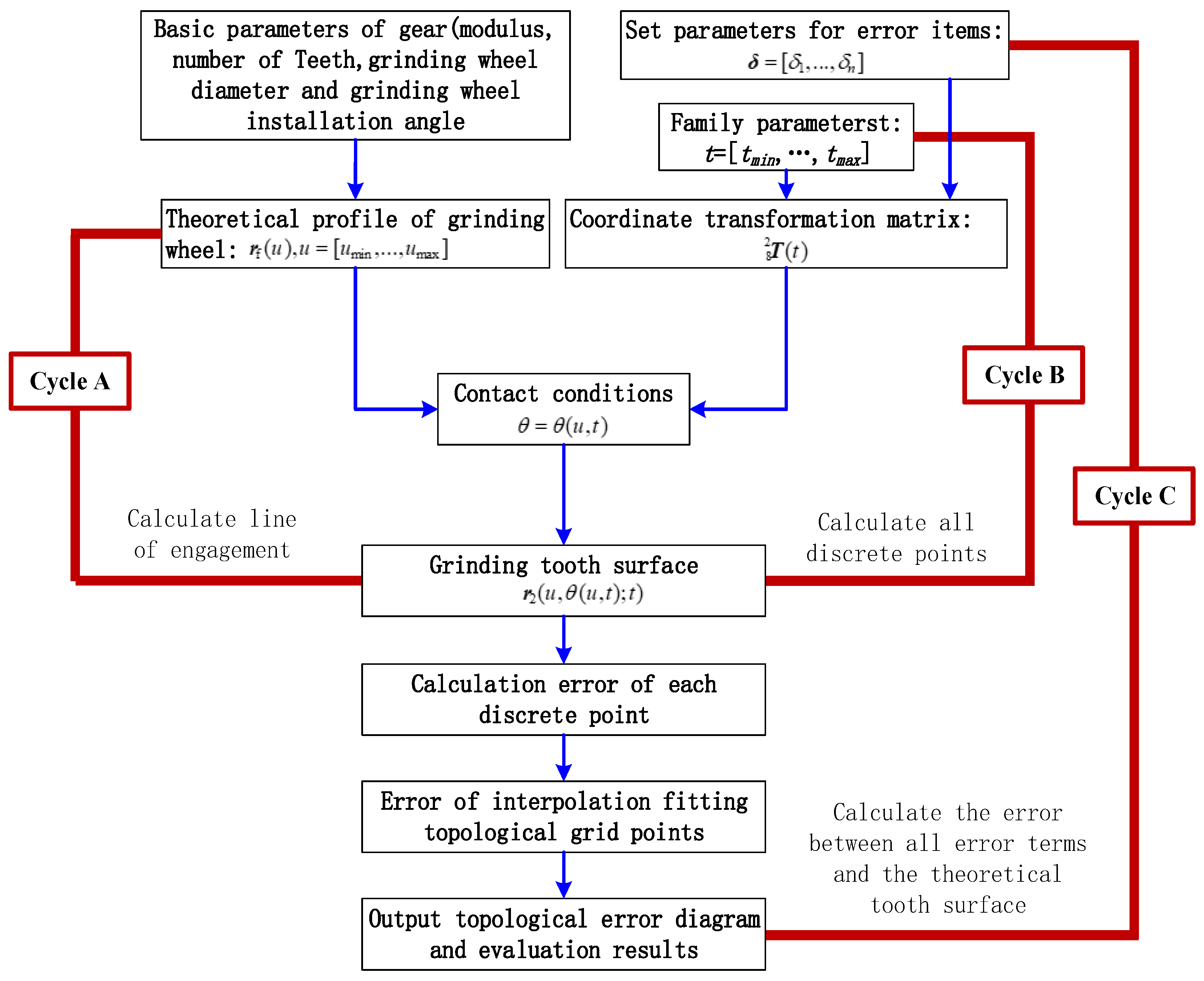
2. Tooth Surface Modeling including Assembly Errors
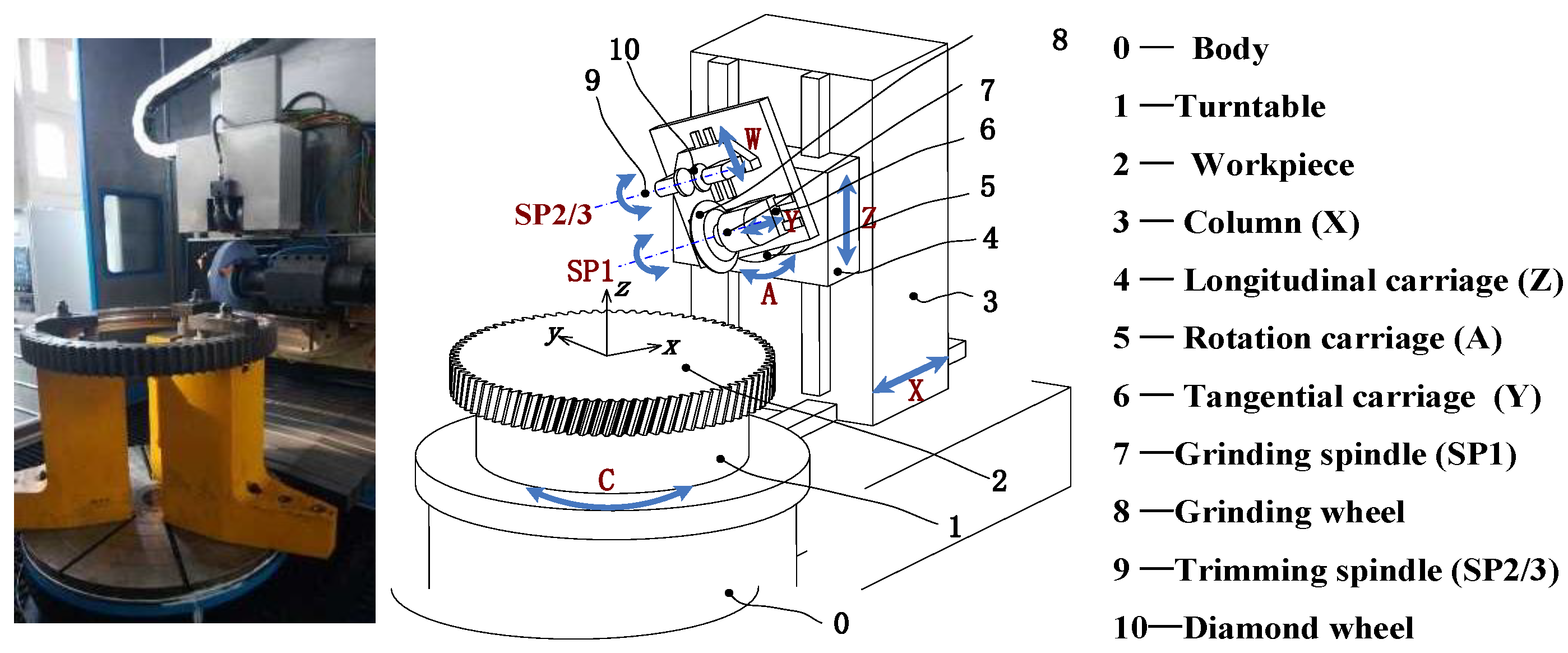
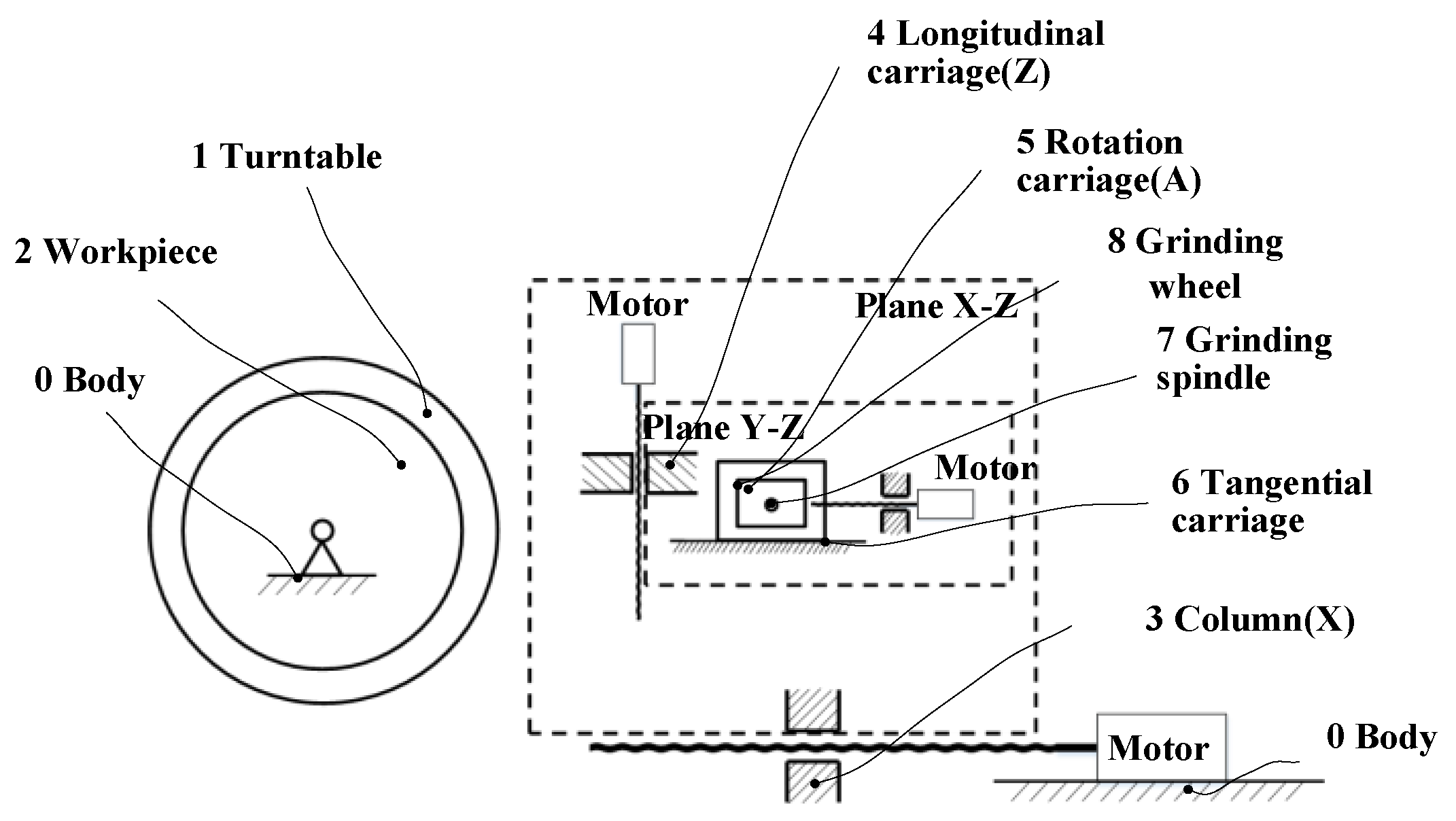
2.1. Assembly Errors of Grinding System
2.2. Modeling of Gear Profile Grinding Motion
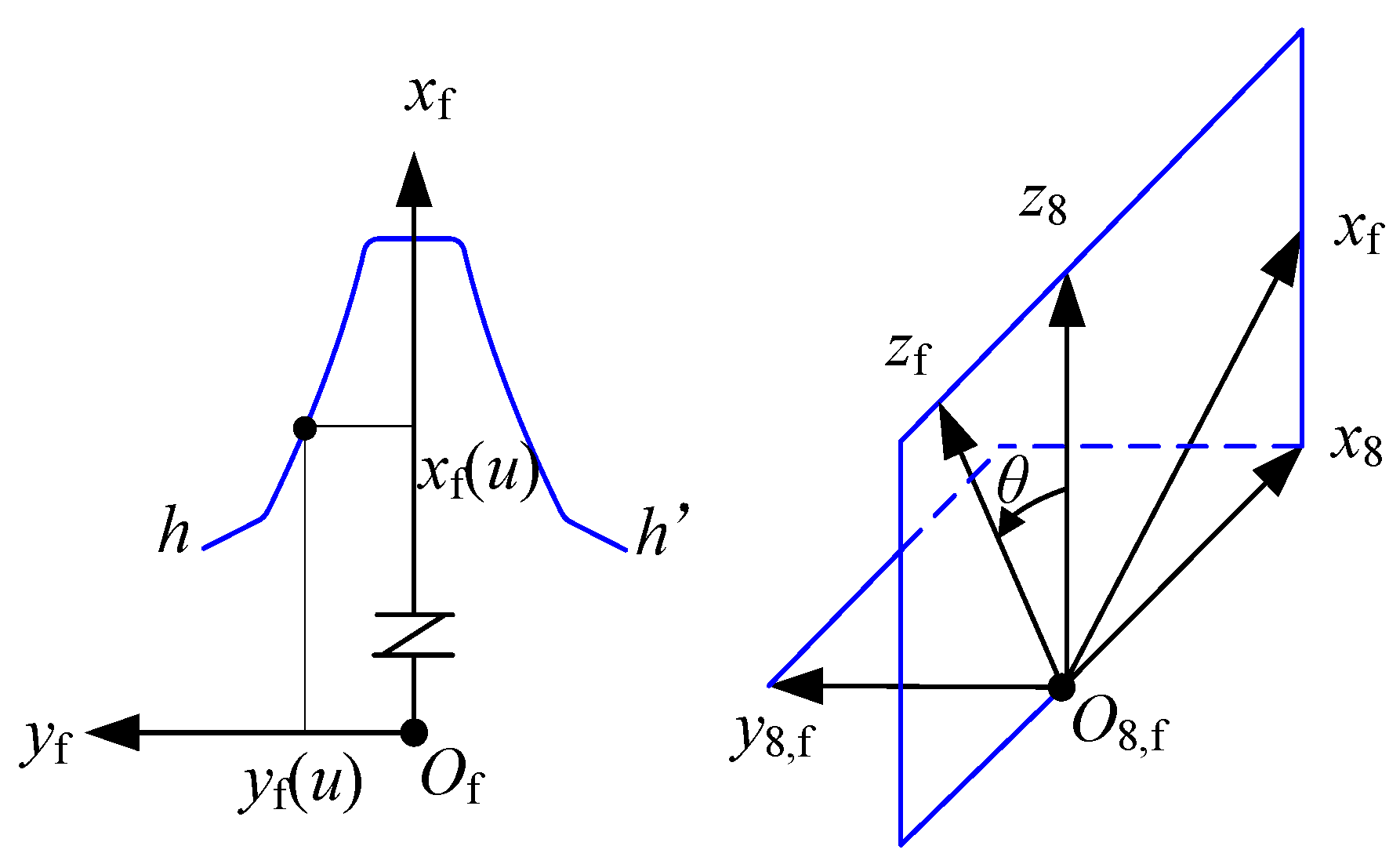
2.3. Tooth Surface Modeling of Gear Profile Grinding
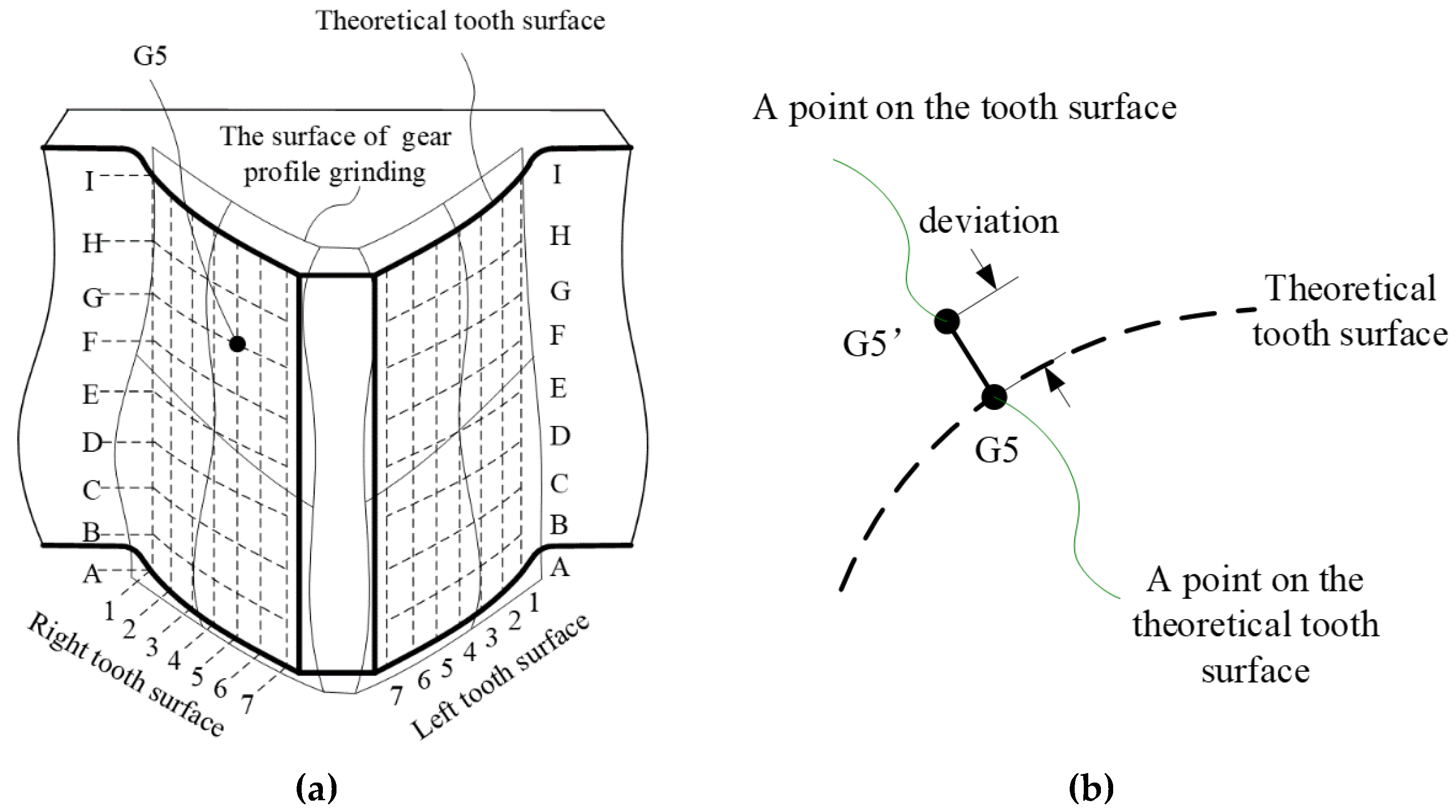
3. Evaluation of Tooth Surface Deviations in Gear Profile Grinding
4. Calculation Analysis and Error Distribution
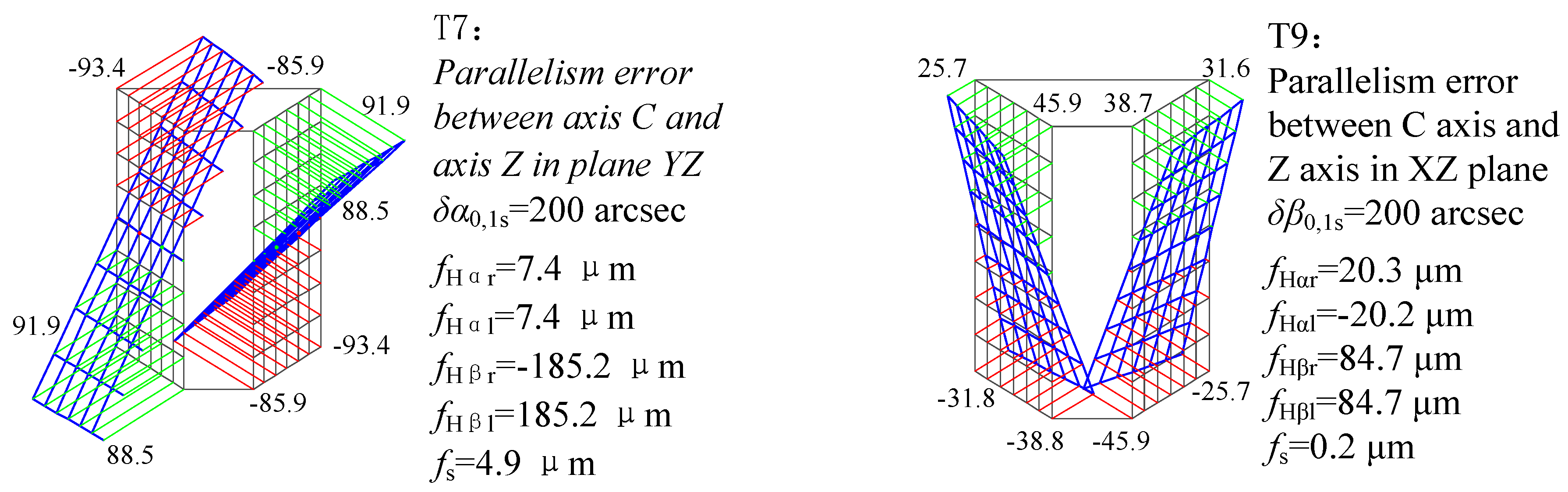
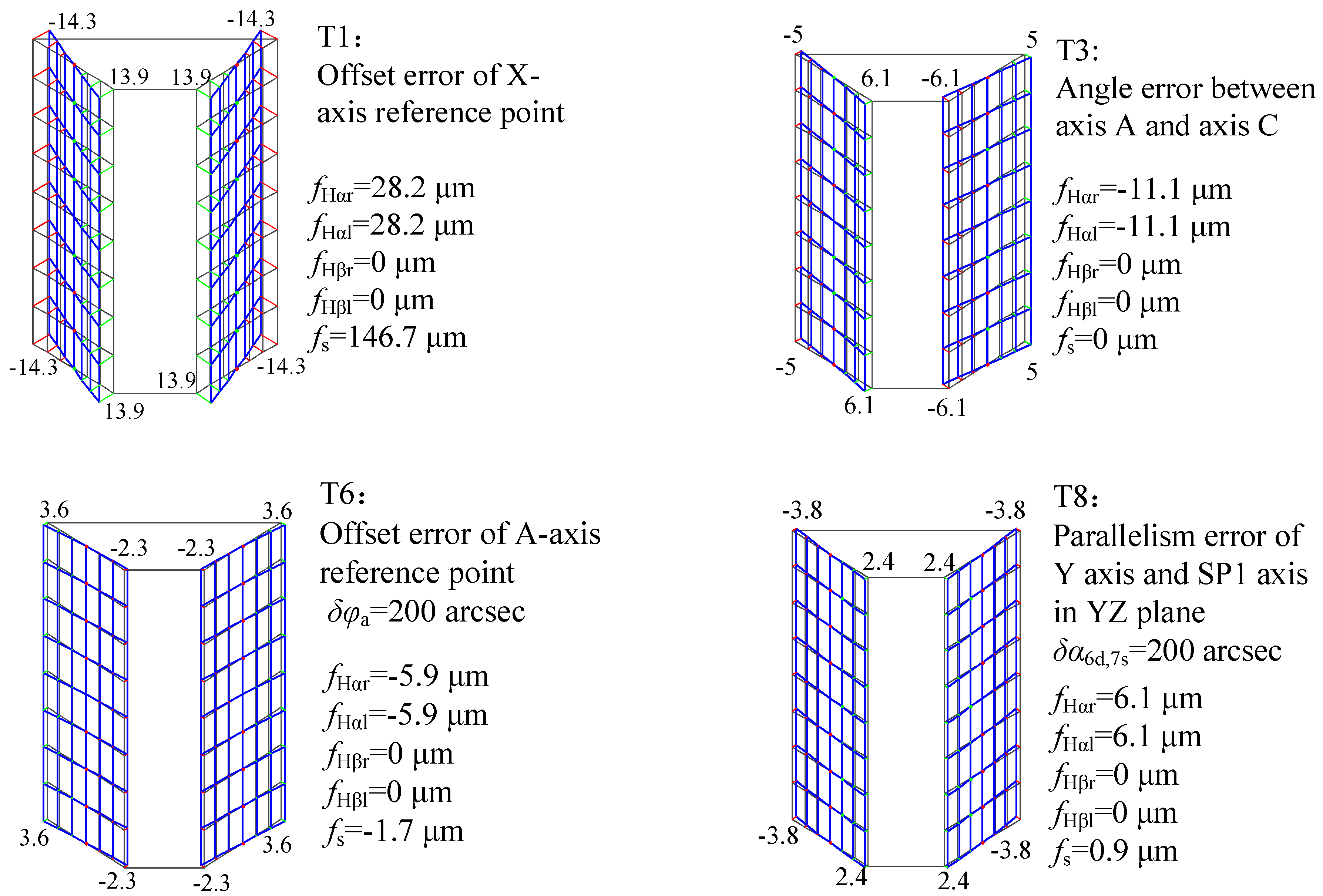
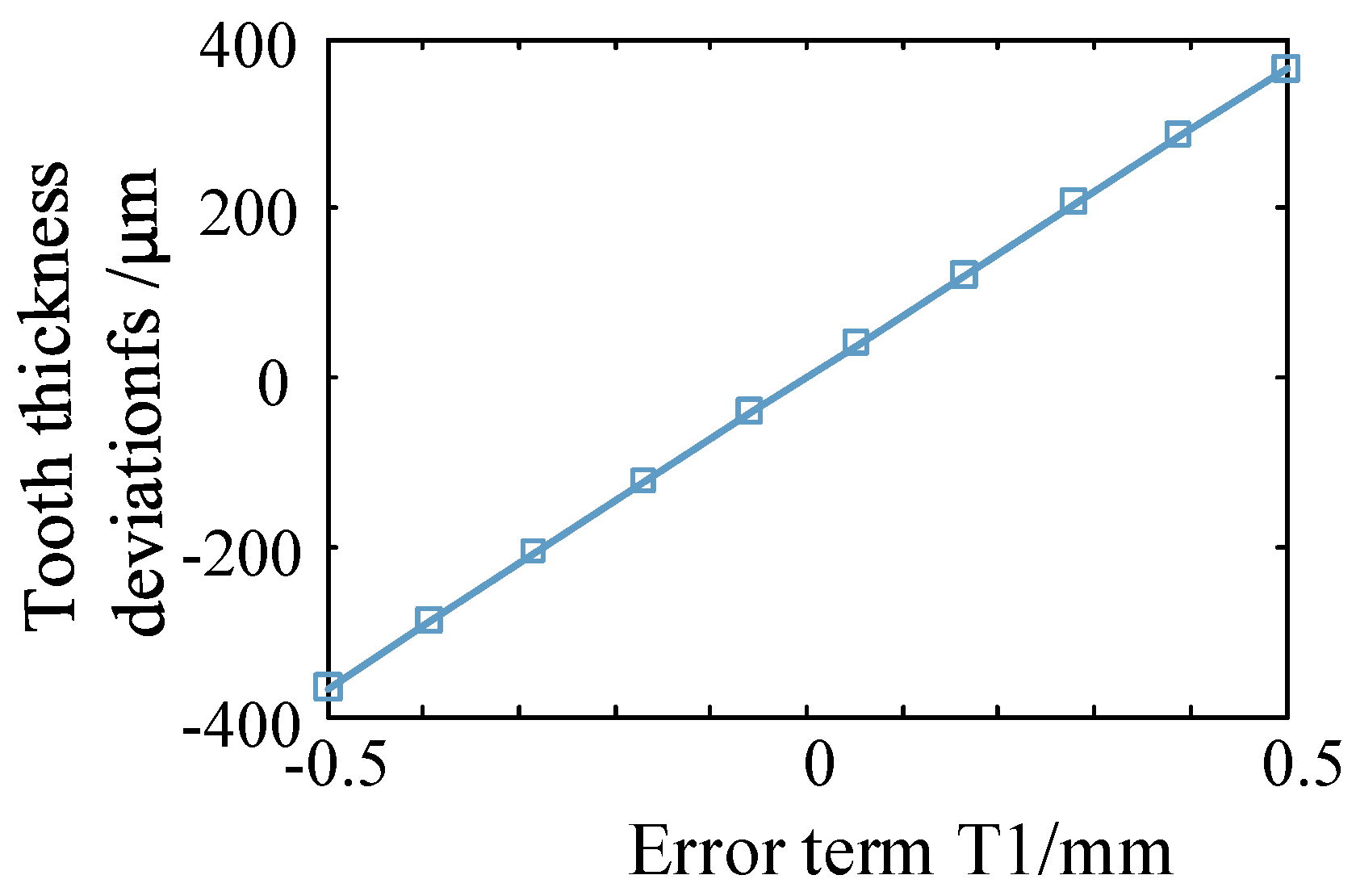
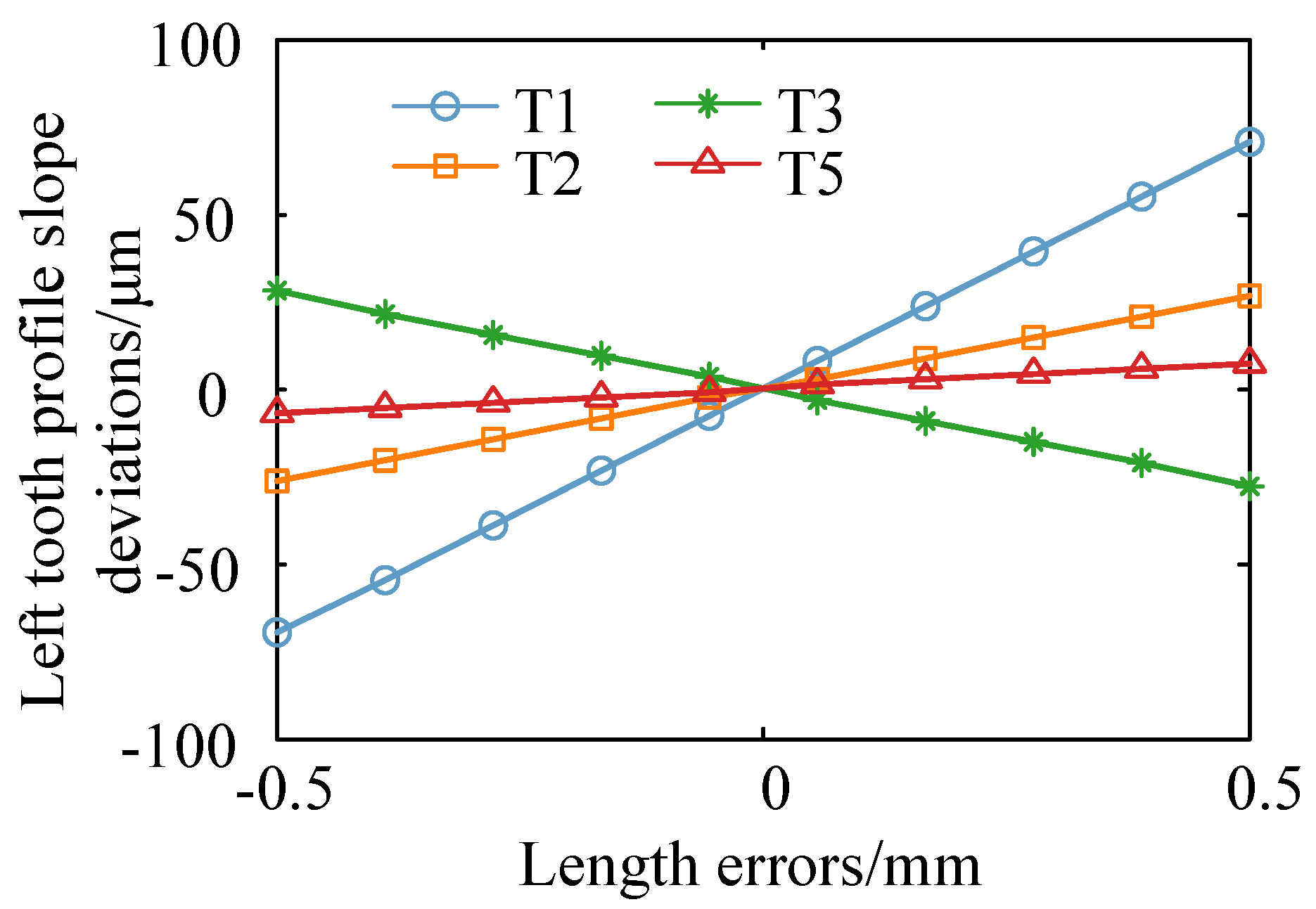
4.1. Single Value Calculation and Analysis
4.2. Multi-Value Computation and Analysis
4.3. Optimized Distribution of Assembly Errors
4.4. Gear Profile Grinding Test
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wegener, K.; Bleicher, F.; Krajnik, P.; Hoffmeister, H.-W.; Brecher, C. Recent developments in grinding machines. CIRP Ann.-Manuf. Technol. 2017, 66, 779–802. [Google Scholar] [CrossRef]
- Wang, K.; Sheng, X.; Kang, R. Volumetric error modelling, measurement, and compensation for an integrated measurement-processing machine tool. Proc. IMechE Part C J. Mech. Eng. Sci. 2010, 224, 2477–2486. [Google Scholar] [CrossRef]
- Heinzel, C.; Wagner, A. Fine finishing of gears with high shape accuracy. CIRP Ann.-Manuf. Technol. 2013, 62, 359–362. [Google Scholar] [CrossRef]
- Rowe, W.B. Principles of Modern Grinding Technology, 3rd ed.; Elsevier: Oxford, UK, 2013. [Google Scholar]
- Araujo, J.B.; Oliveira, J.F. Evaluation of two competing machining processes based on sustainability indicators, in leveraging technology for a sustainable world. In Proceedings of the 19th CIRP Conference on Life Cycle Engineering, Berkeley, CA, USA, 23–25 May 2012. [Google Scholar]
- Litvin, F.L.; Fuentes, A. Gear Geometry and Applied Theory, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Denkena, B.; Preising, D.; Woiwode, S. Gear profile grinding with metal bonded CBN tools. Prod. Eng.-Res. Dev. 2015, 9, 73–77. [Google Scholar] [CrossRef]
- Fong, Z.; Chen, G. Gear flank modification using a variable lead grinding worm method on a computer numerical control gear grinding machine. J. Mech. Des. 2016, 138, 083302-1–083302-10. [Google Scholar] [CrossRef]
- Wu, Y.; Fan, C. Mathematical modeling for screw rotor form grinding on vertical multi-axis computerized numerical control form grinder. J. Manuf. Sci. Eng. 2013, 135, 051020-1–051020-13. [Google Scholar] [CrossRef]
- Chen, G.; Mei, X.; Li, H. Geometric error modeling and compensation for large-scale grinding machine tools with multi-axes. Int. J. Adv. Manuf. Technol. 2013, 69, 2583–2592. [Google Scholar] [CrossRef]
- Zhou, B.; Wang, S.; Fang, C.; Sun, S.; Dai, H. Geometric error modeling and compensation for five-axis CNC gear profile grinding machine tools. Int. J. Adv. Manuf. Technol. 2017, 92, 2639–2652. [Google Scholar] [CrossRef]
- Wang, S.; Zhou, B.; Fang, C.; Sun, S. Research on thermal deformation of large CNC gear profile grinding machine tools. Int. J. Adv. Manuf. Technol. 2017, 91, 577–587. [Google Scholar] [CrossRef]
- Yang, H.; Huang, X.; Guo, E. Analysis and compensation for pitch error in forming manufacturing big gears. Modul. Mach. Tool Autom. Manuf. Tech. 2018, 10, 59–63. [Google Scholar]
- Zhang, H.; Fang, C.; Guo, E.; Huang, X. Accurate lead modification of CNC gear profile grinding based on five-axis motions optimization. Comput. Integr. Manuf. Syst. 2014, 20, 3058–3065. [Google Scholar]
- Guo, E.; Huang, X.-D.; Fang, C.-G.; Yuan, H. Contact lines optimization method for improving tooth-trace modification accuracy of form grinding. Comput. Integr. Manuf. Syst. 2014, 20, 134–141. [Google Scholar]
- Ding, G.; Zhang, S.; Zhao, D.; Zhao, D. Interference study of gear form grinding based on induced normal curvature. Chin. J. Mech. Eng. 2016, 52, 197–204. [Google Scholar] [CrossRef]
- Li, T.; Yan, P.; Yu, G.; Ji, W. Solving the problem of interference of forming grinding wheel based on MATLAB. Tool Eng. 2021, 55, 101–104. [Google Scholar]
- Ding, S.; Huang, X.; Yu, C.; Wang, W. Actual inverse kinematics for location error compensation of five-axis machine tool. Comput. Integr. Manuf. Syst. 2021, 27, 1300–1308. [Google Scholar]
- Zhao, F.; Mei, X.; Jiang, G.; Tao, T.; Shi, J. Molding and characters analysis error of numerical control machine tool. J. Shanghai Jiaotong Univ. 2013, 47, 703–708. [Google Scholar]
- Lee, R.S.; Lin, Y.H. Applying bidirectional kinematics to assembly error analysis for five-axis machine tools with general orthogonal configuration. Int. J. Adv. Manuf. Technol. 2012, 62, 1261–1272. [Google Scholar] [CrossRef]
- Xia, C.; Wang, S.; Sun, S.; Lin, X.; Huang, X. Geometric error to tooth surface error model and identification of crucial errors in five-axis CNC gear profile grinding machines. Comput. Integr. Manuf. Syst. 2020, 26, 1191–1201. [Google Scholar]
- Zhao, W.; Zhang, X.; Lv, D.; Zhang, J. Technical status and strategies for domestic CNC machine tools. Aeronaut. Manuf. Technol. 2016, 9, 16–22. [Google Scholar]
- Sun, Y.; Liu, Y.; Ran, Y.; Zhou, Q. Assembly precision prediction method of numerical control machine tools based on meta-action. Mech. Sci. Technol. Aerosp. Eng. 2017, 36, 1734–1739. [Google Scholar]
- Guo, J.; Li, B.; Hong, J.; Li, X. Assembly adjustment process planning of precision machine tools based on optimal estimation of variation propagation. Chin. J. Mech. Eng. 2020, 56, 172–180. [Google Scholar]
- Wang, Z.; Jiang, X.; Liu, W.; Shi, M.; Yang, S.; Yang, G. Precision prediction and error propagation model of remanufacturing machine tool assembly process. Comput. Integr. Manuf. Syst. 2021, 27, 1300–1308. [Google Scholar]
- Chen, X.; Morgan, M.N. Advances in quality and productivity in precision grinding—A review of selected research. In Proceedings of the ASME 2016 International Manufacturing Science and Engineering Conference, Blacksburg, VA, USA, 27 June–1 July 2016. [Google Scholar]
- Uriarte, L.; Zatarain, M.; Axinte, D.; Yagüe-Fabra, J.; Ihlenfeldt, S.; Eguia, J.; Olarra, A. Machine tools for large parts. CIRP Ann.-Manuf. Technol. 2013, 62, 731–750. [Google Scholar] [CrossRef]
- Hu, W.; Wang, X. Grinding Machines Part3: Profile Grinding Machines Accuracy Inspection; China Machine Press: Beijing, China, 2014. [Google Scholar]
- Bhoskar, T.; Kulkarni, O.K.; Kulkarni, N.K.; Patekar, S.L.; Kakandikar, G.M.; Nandedkar, V.M. Genetic algorithm and its applications to mechanical engineering: A review. Mater. Today 2015, 2, 2624–2630. [Google Scholar] [CrossRef]
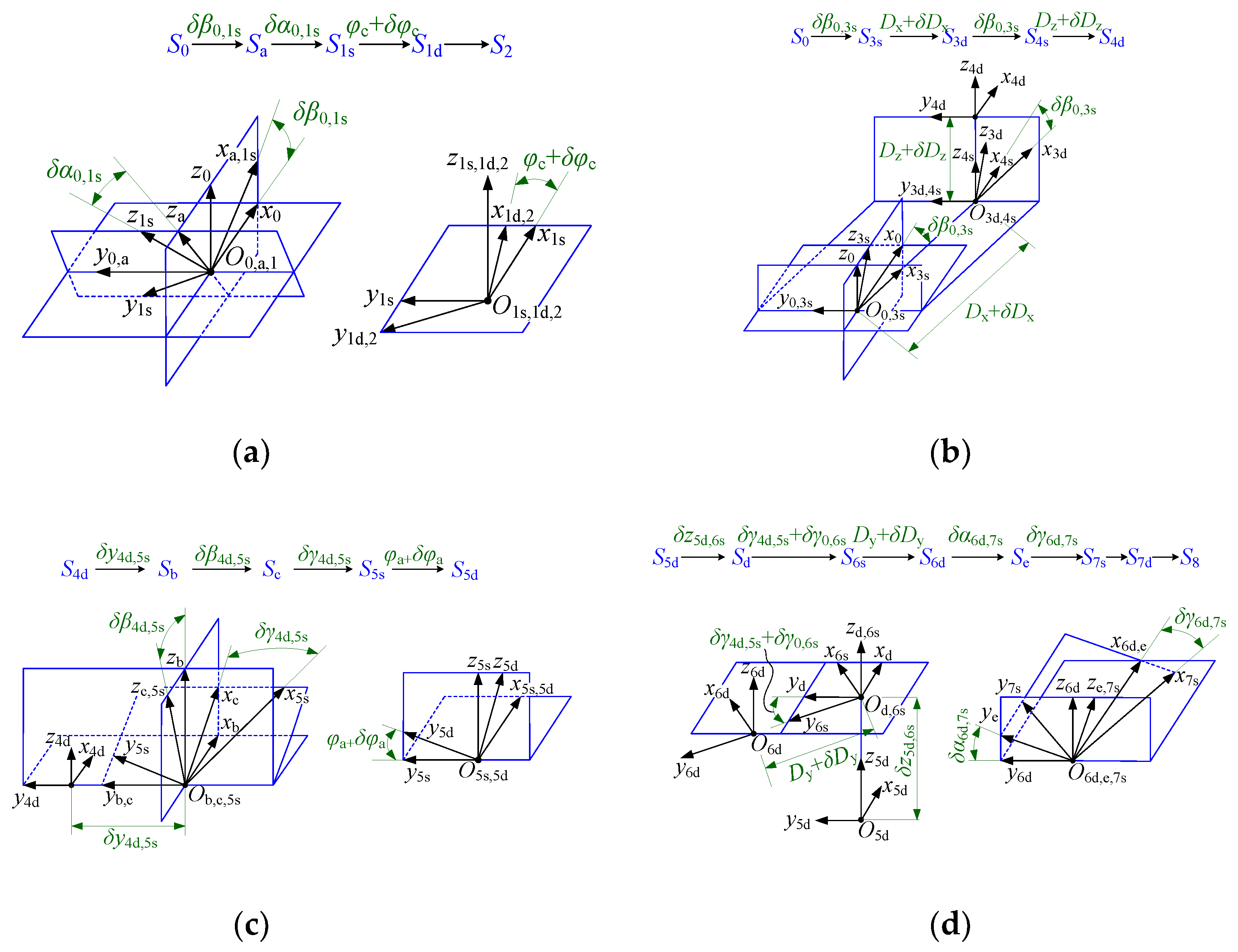
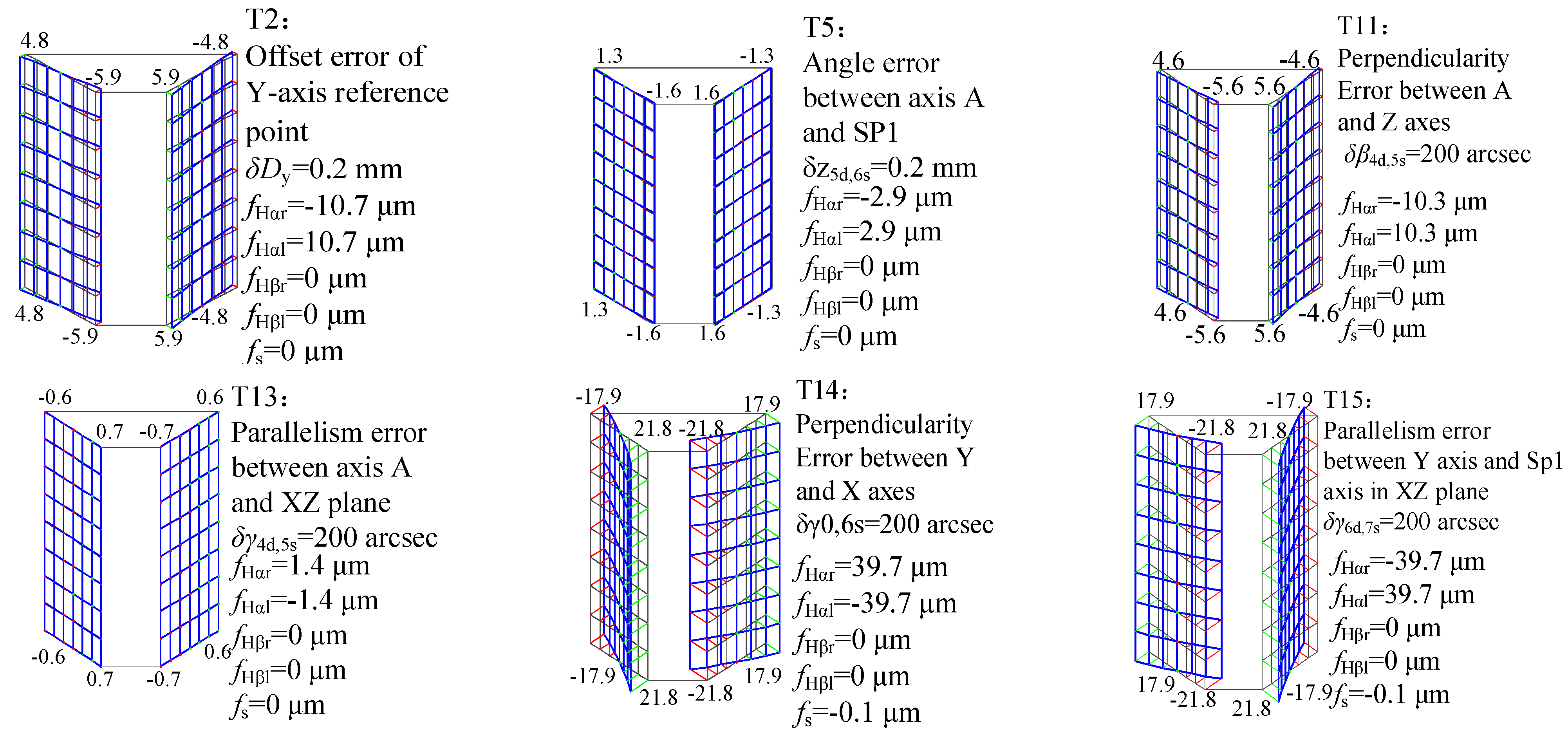
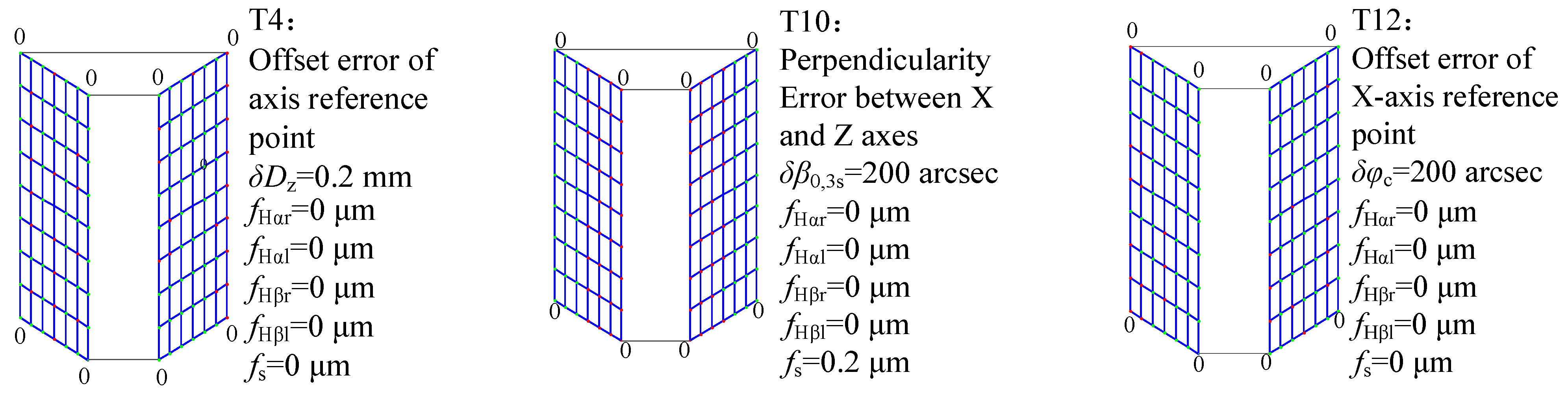
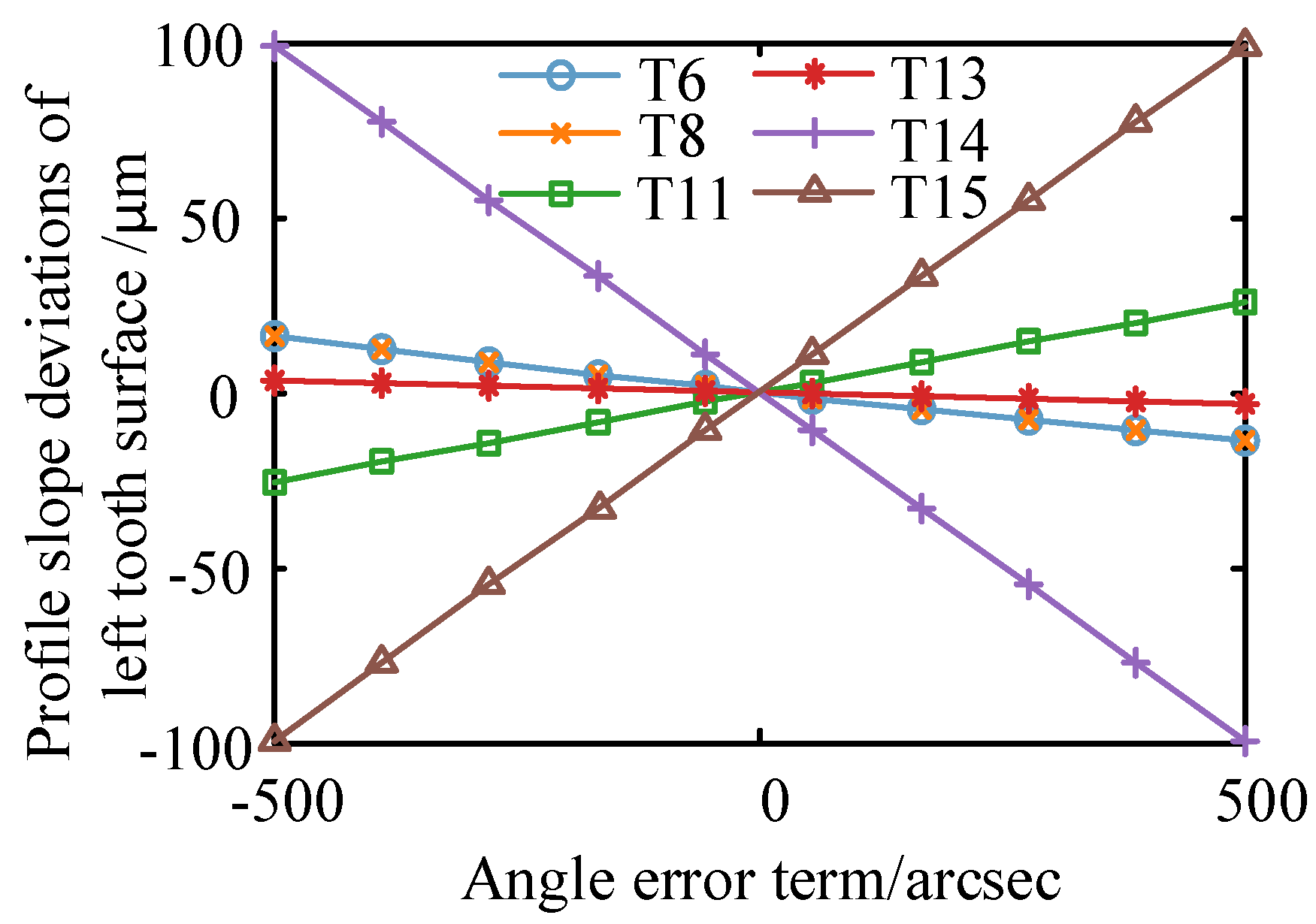
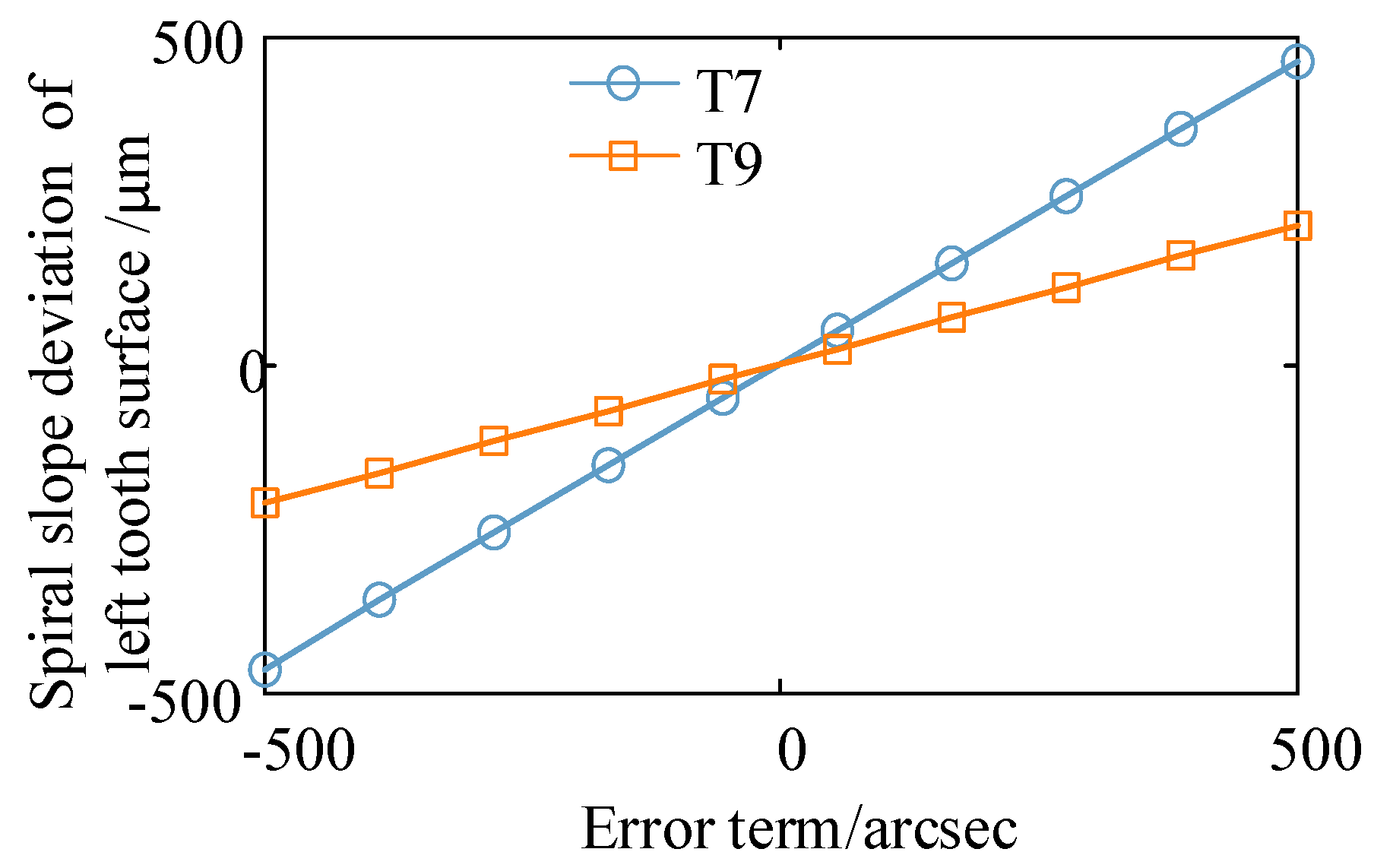
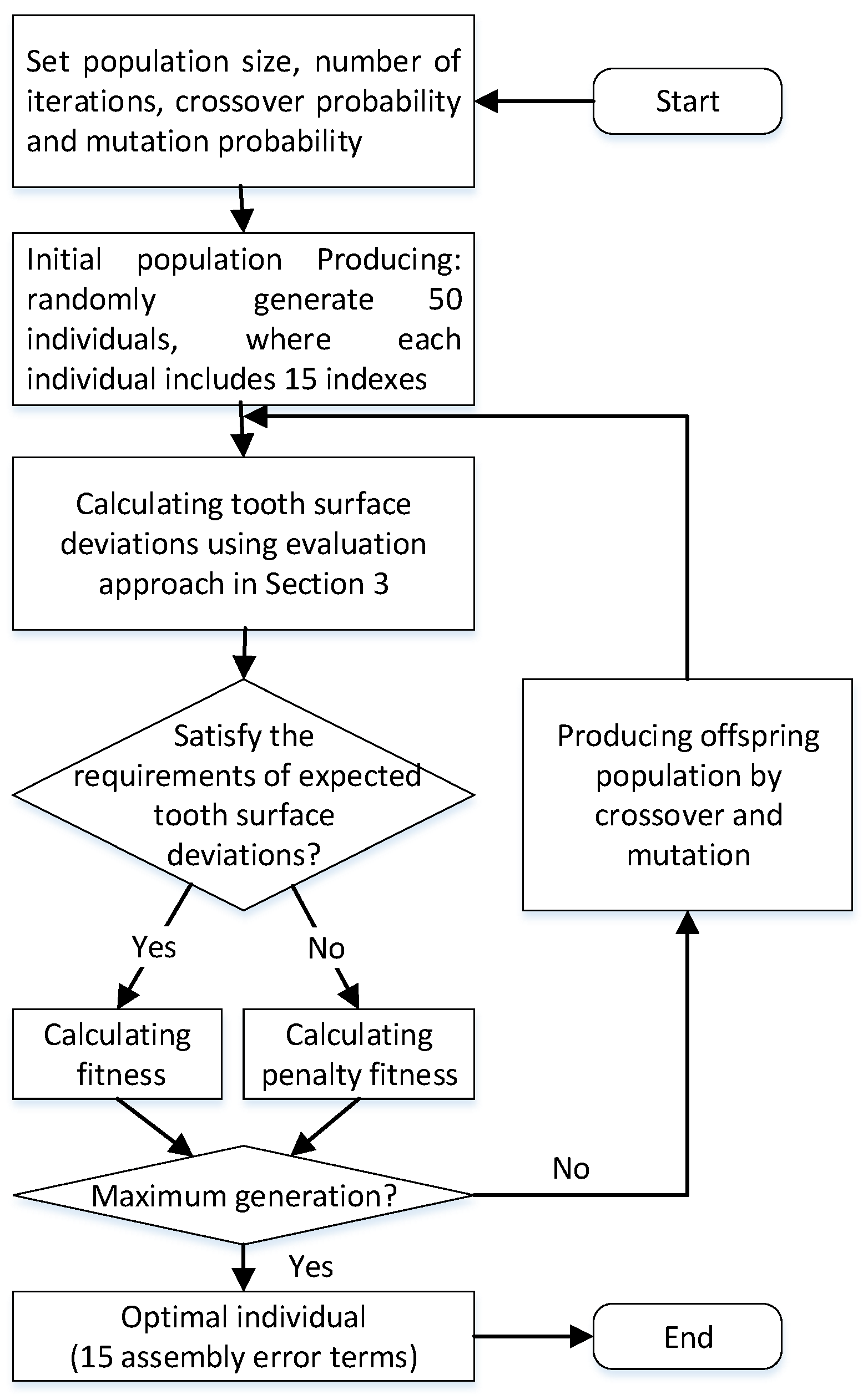

| Number | Symbol | Meaning | Number | Symbol | Meaning |
|---|---|---|---|---|---|
| T1 | δDx | Offset error of the X-axis reference point | T9 | δβ0,1s | Parallelism error between the C axis and the Z axis in the XZ plane |
| T2 | δDy | Offset error of the Y-axis reference point | T10 | δβ0,3s | Perpendicularity error between the X and Z axes |
| T3 | δy4d,5s | Angle error between the axis A and the axis C | T11 | δβ4d,5s | Perpendicularity error between the A and Z axes |
| T4 | δDz | Offset error of the axis reference point | T12 | δφc | Offset error of the X-axis reference point |
| T5 | δz5d,6s | Angle error between the axis A and SP1 | T13 | δγ4d,5s | Parallelism error between axis A and the XZ plane |
| T6 | δφa | Offset error of the A-axis reference point | T14 | δγ0,6s | Perpendicularity error between the Y and X axes |
| T7 | δα0,1s | Parallelism error between the axis C and the axis Z in the plane YZ | T15 | δγ6d,7s | Parallelism error between the Y axis and the SP1 axis in the XZ plane |
| T8 | δα6d,7s | Parallelism error of the Y axis and the SP1 axis in the YZ plane |
| Symbol | Matrix | Symbol | Matrix |
|---|---|---|---|
| Name | Symbol | Unit | Value | Name | Symbol | Unit | Value |
|---|---|---|---|---|---|---|---|
| Module | mn | mm | 14 | Tooth breadth | B | mm | 200 |
| Gear number | z | - | 74 | helix parameter | p | mm | 2001.3983 |
| Pressure angle | αn | deg | 20 | Grinding wheel diameter | dw | mm | 380 |
| Helix angle | β | deg | 15 | Grinding tooth root diameter | dfg | mm | 1040 |
| Modification coefficient | xn | - | 0 | Grinding tooth tip diameter | dag | mm | 1104 |
| Root diameter | df | mm | 1037.55 | Grinding tooth installation angle | γs | deg | 15 |
| Tip diameter | da | mm | 1100.55 | Grinding tooth center distance | Dx | mm | 710 |
| Number | Symbol | Unit | Value | Number | Symbol | Unit | Value |
|---|---|---|---|---|---|---|---|
| T1 | δDx | mm | 0.03 | T9 | δβ0,1s | arcsec | 15 |
| T2 | δDy | mm | 0.05 | T10 | δβ0,3s | arcsec | 50 |
| T3 | δy4d,5s | mm | 0.05 | T11 | δβ4d,5s | arcsec | 10 |
| T4 | δDz | mm | 0.2 | T12 | δφc | arcsec | 20 |
| T5 | δz5d,6s | mm | 0.2 | T13 | δγ4d,5s | arcsec | 20 |
| T6 | δφa | arcsec | 50 | T14 | δγ0,6s | arcsec | 20 |
| T7 | δα0,1s | arcsec | 30 | T15 | δγ6d,7s | arcsec | 20 |
| T8 | δα6d,7s | arcsec | 20 |
| Left Tooth Surface | Right Tooth Surface | ||
|---|---|---|---|
| fHα/μm (Q) | fHβ/μm (Q) | fHα/μm (Q) | fHβ/μm (Q) |
| 7.7 (4) | 7.9 (4) | 8.2 (4) | 7.3 (4) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, W.; He, W.; Zhang, H.; Li, Y. Effect of Assembly Errors on Ground Tooth Surface Deviations for Large-Scale CNC Gear Profile Grinding Machines. Machines 2022, 10, 111. https://doi.org/10.3390/machines10020111
Ding W, He W, Zhang H, Li Y. Effect of Assembly Errors on Ground Tooth Surface Deviations for Large-Scale CNC Gear Profile Grinding Machines. Machines. 2022; 10(2):111. https://doi.org/10.3390/machines10020111
Chicago/Turabian StyleDing, Wenzheng, Wenquan He, Hu Zhang, and Yao Li. 2022. "Effect of Assembly Errors on Ground Tooth Surface Deviations for Large-Scale CNC Gear Profile Grinding Machines" Machines 10, no. 2: 111. https://doi.org/10.3390/machines10020111
APA StyleDing, W., He, W., Zhang, H., & Li, Y. (2022). Effect of Assembly Errors on Ground Tooth Surface Deviations for Large-Scale CNC Gear Profile Grinding Machines. Machines, 10(2), 111. https://doi.org/10.3390/machines10020111





