Study on Dynamic Lubrication Characteristics of the External Return Spherical Bearing Pair under Full Working Conditions
Abstract
:1. Introduction
2. Mathematical Model of the External Return Spherical Bearing Pair under Full Working Conditions
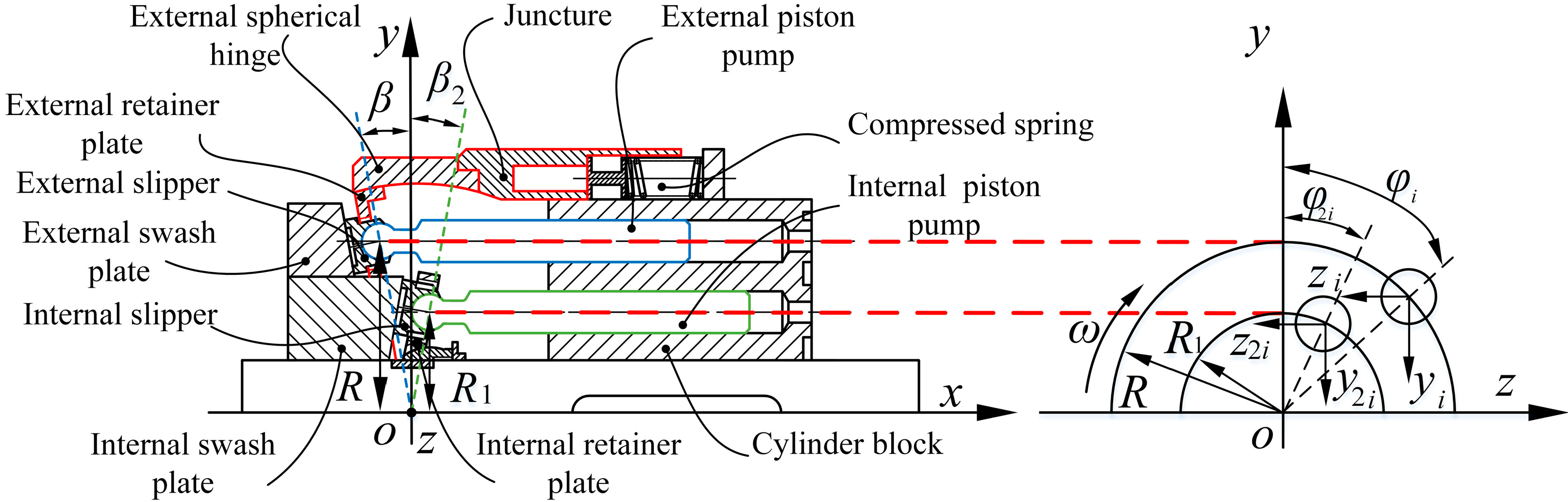
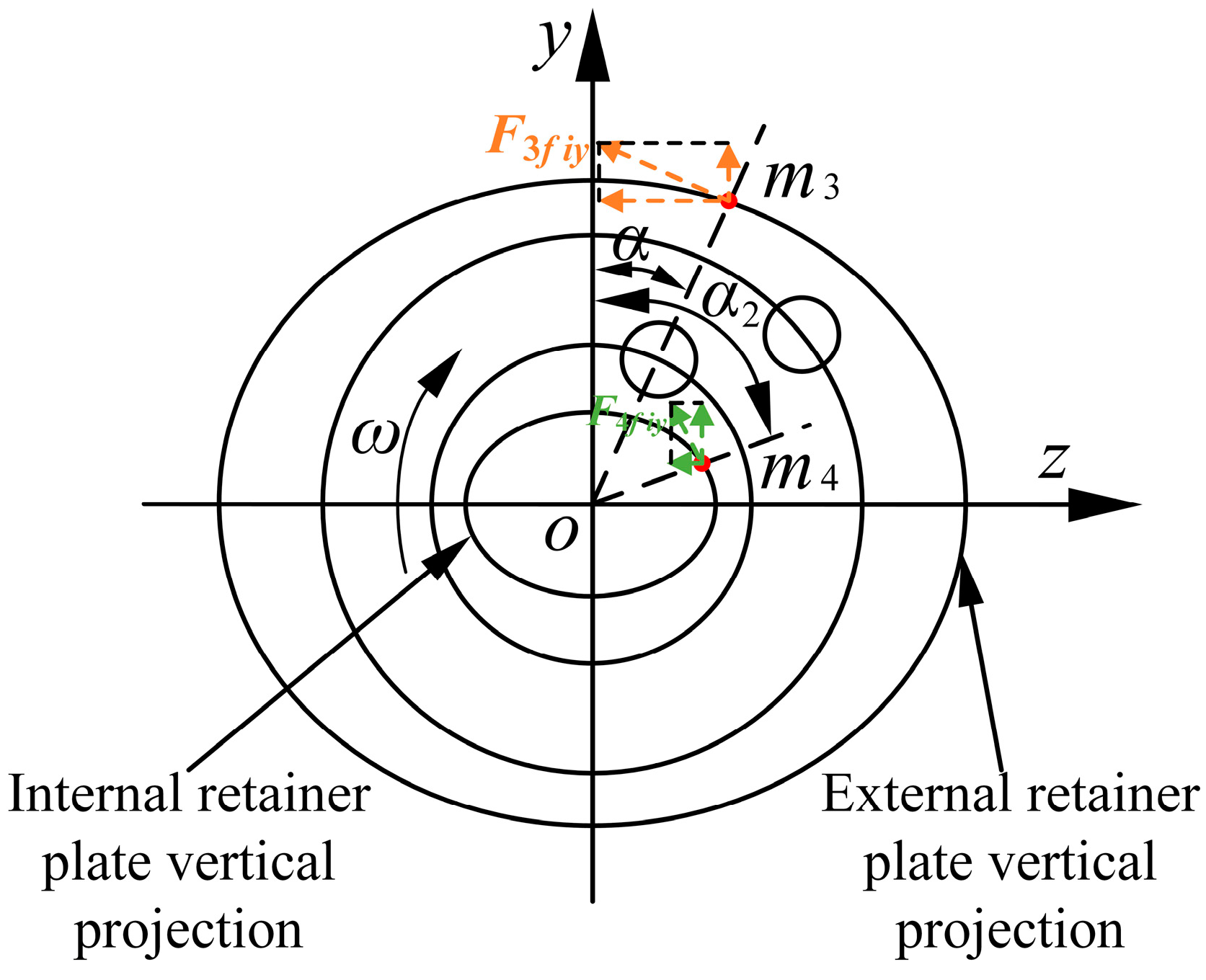
2.1. Kinematic Model of a Balanced Double-Row Axial Piston Pump
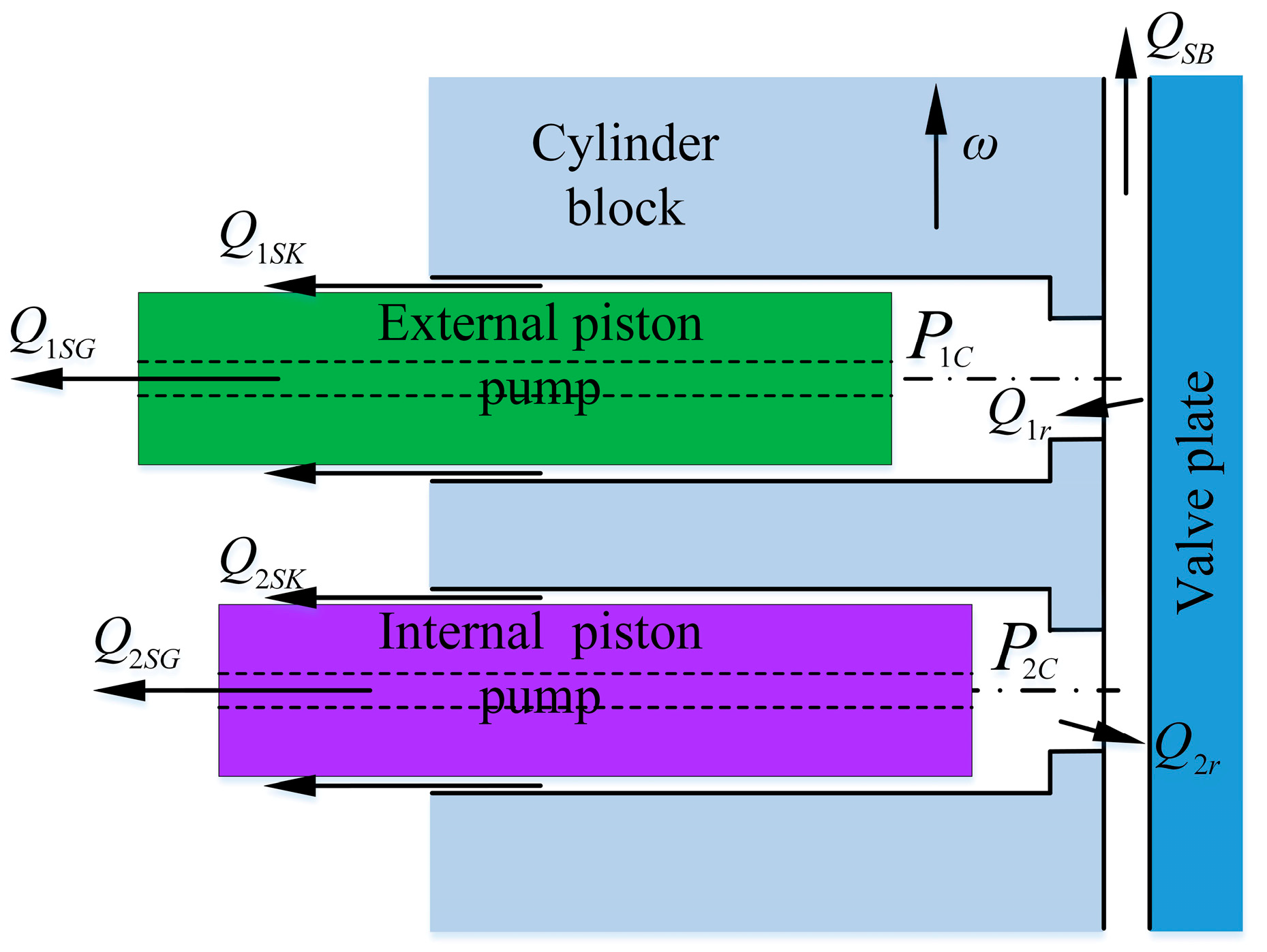
2.2. Oil Pressure Model of the Internal and External Plunger Cavity
2.3. Dynamic Model of an Underconstrained Double-Row Cylinder Block/Juncture
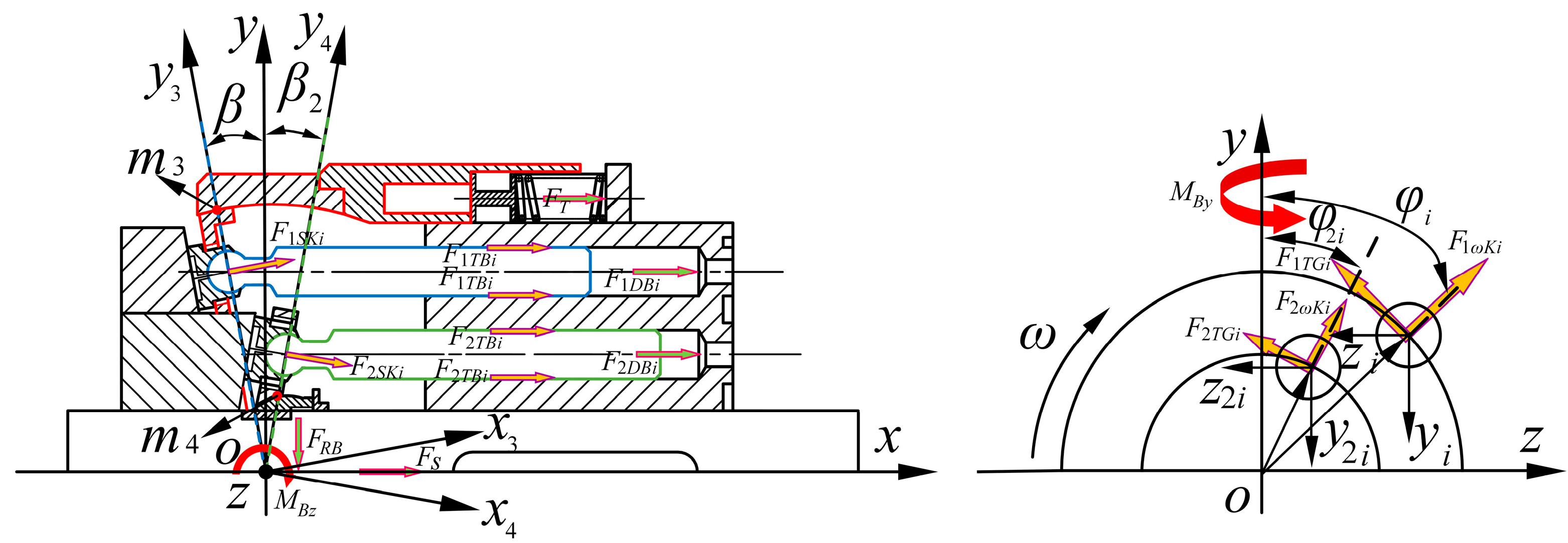
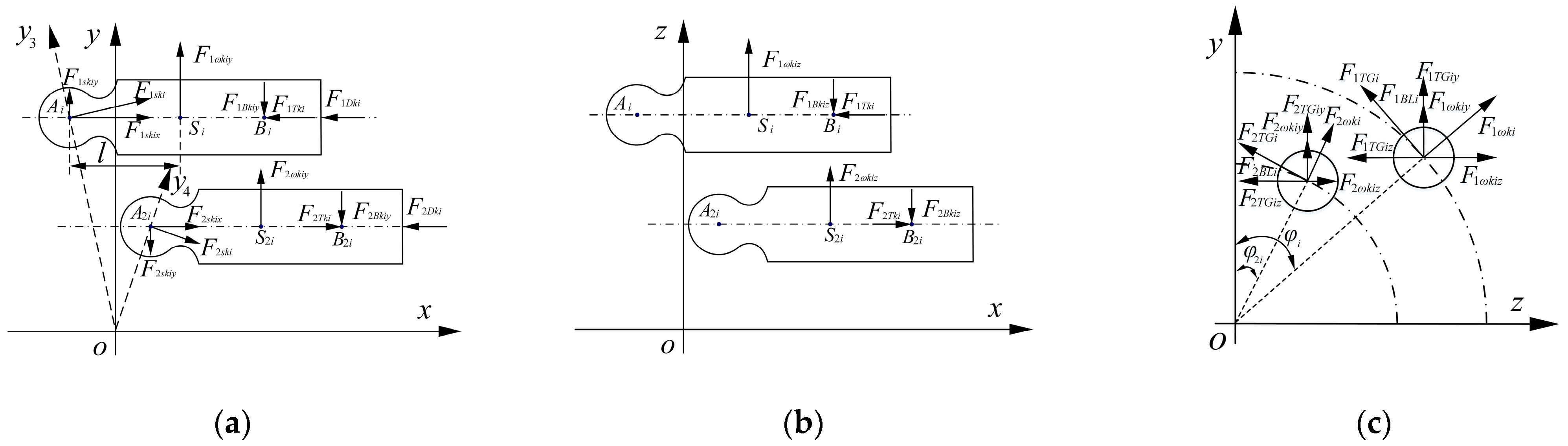
2.3.1. Direct Force Analysis of a Double-Row Cylinder Block
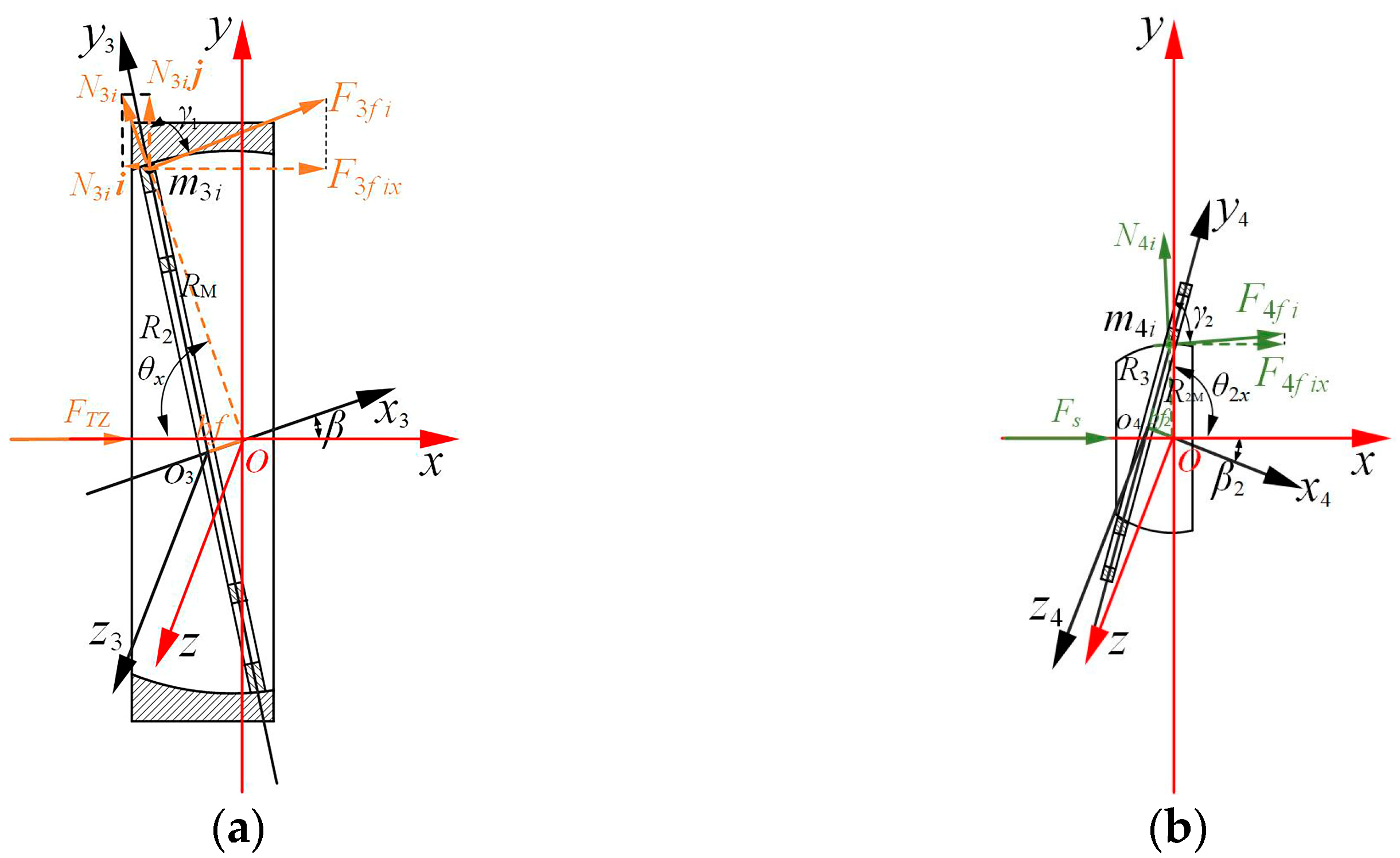
2.3.2. Indirect Force Analysis of a Double-Row Cylinder Block
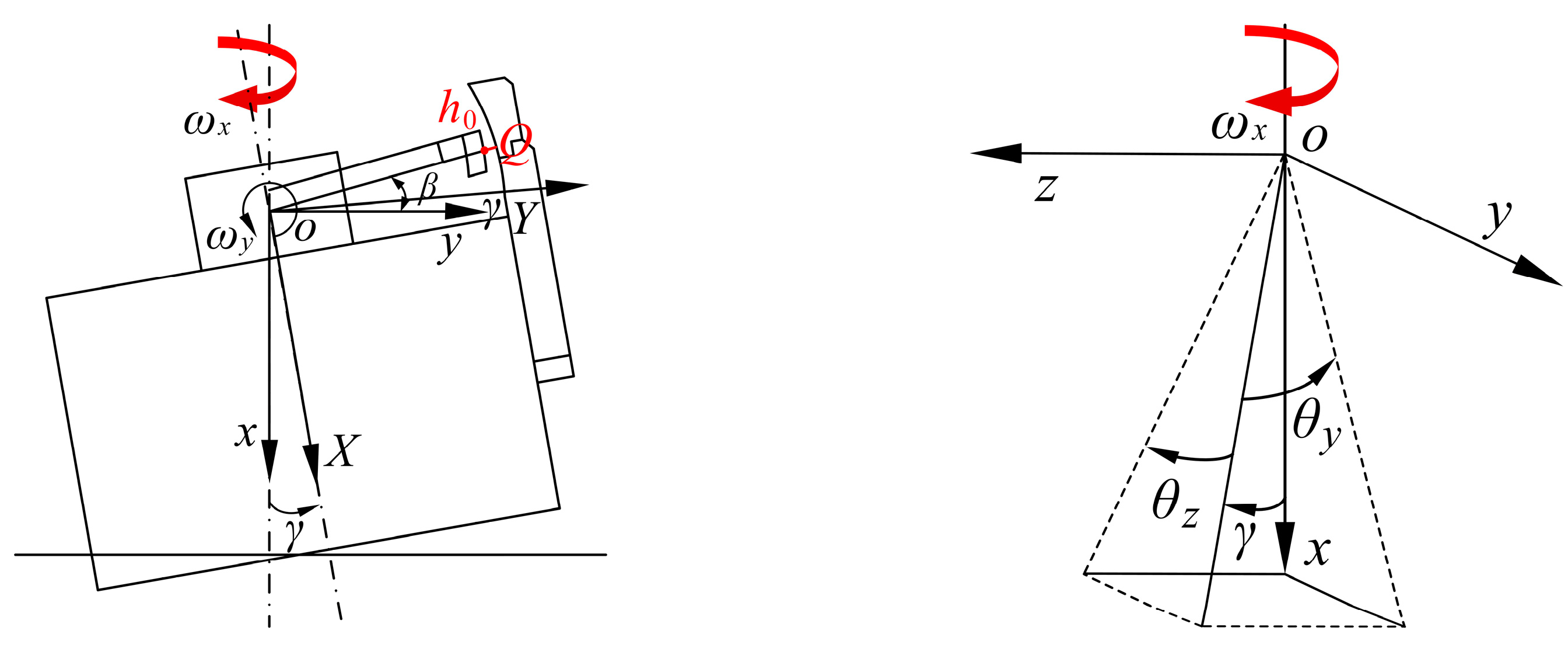
2.4. Tiny Movement Equation of a Double-Row Cylinder Block
2.4.1. Tiny Linear Movement of a Cylinder Block along the x-Axis
2.4.2. Tiny Rotation of a Cylinder Block along with Origin O
2.5. Mixed Fluid Lubrication Model of the External Return Spherical Hinge Pair
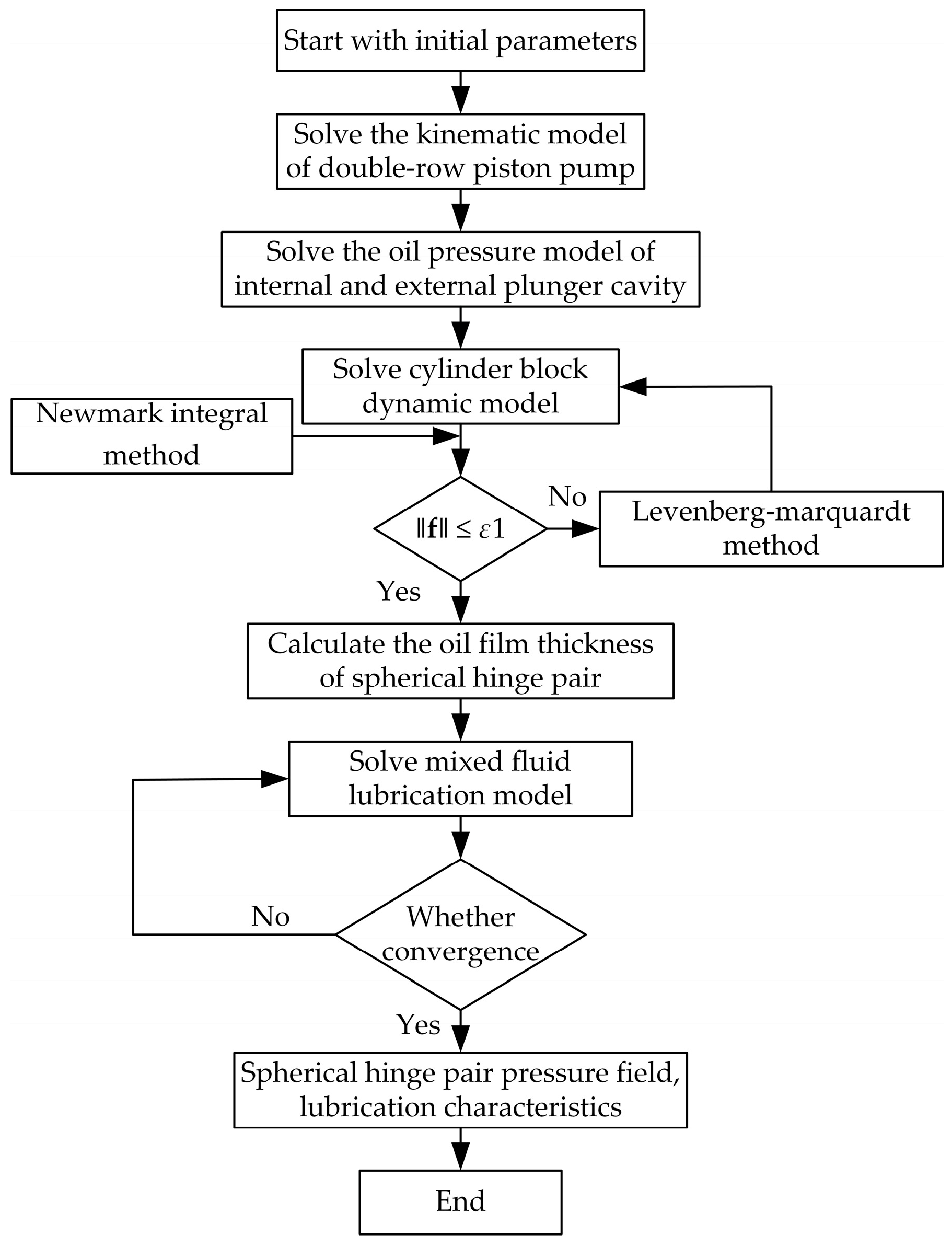
2.6. Mathematical Model Solving
3. Results and Analysis
3.1. Lubrication Characteristics of the External Return Spherical Hinge Pair
3.1.1. Analysis of Oil Film Pressure Characteristics
3.1.2. Influence of Operating Parameters on Oil Film Shape
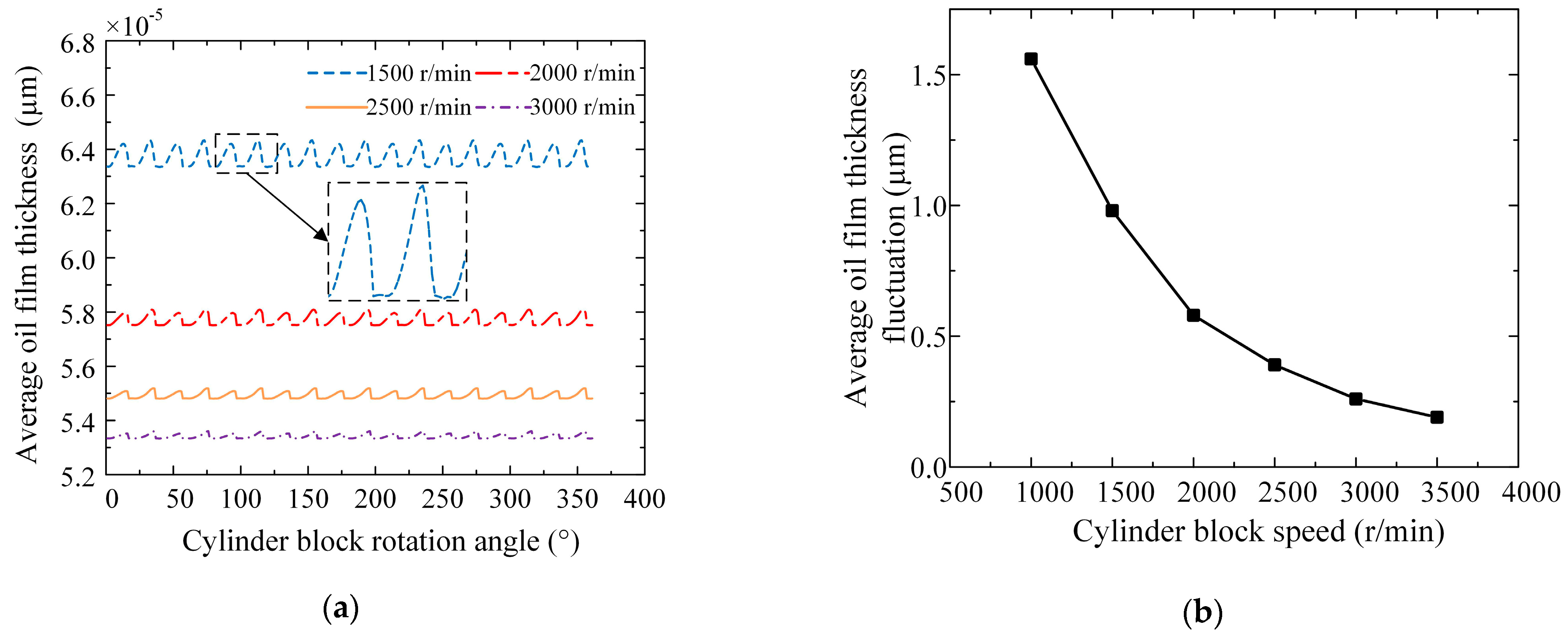
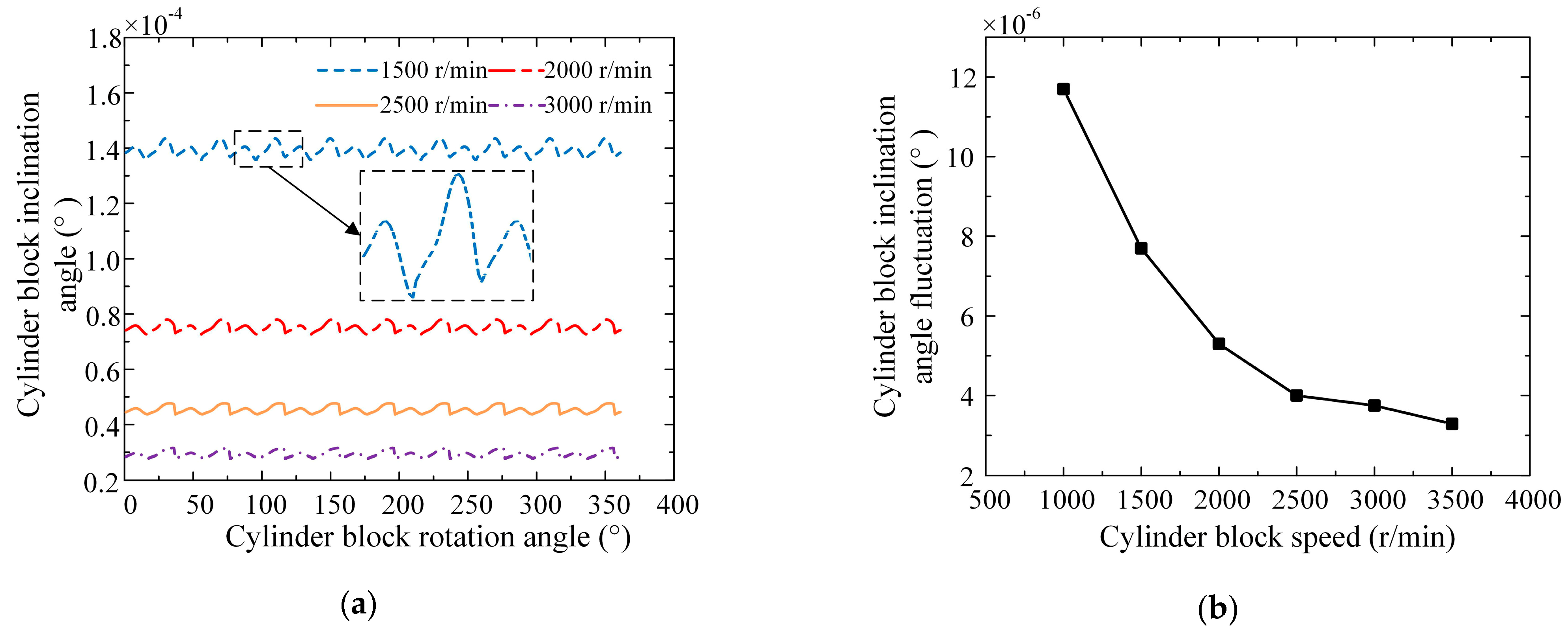
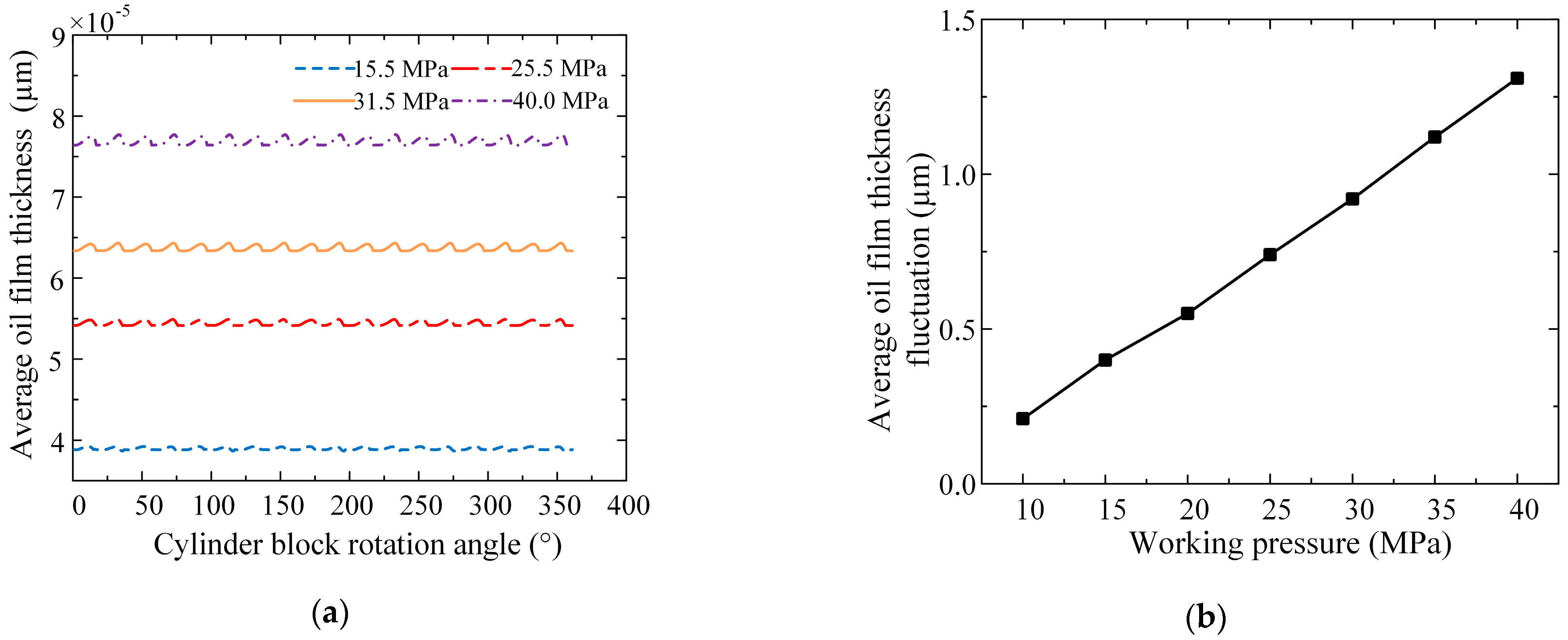
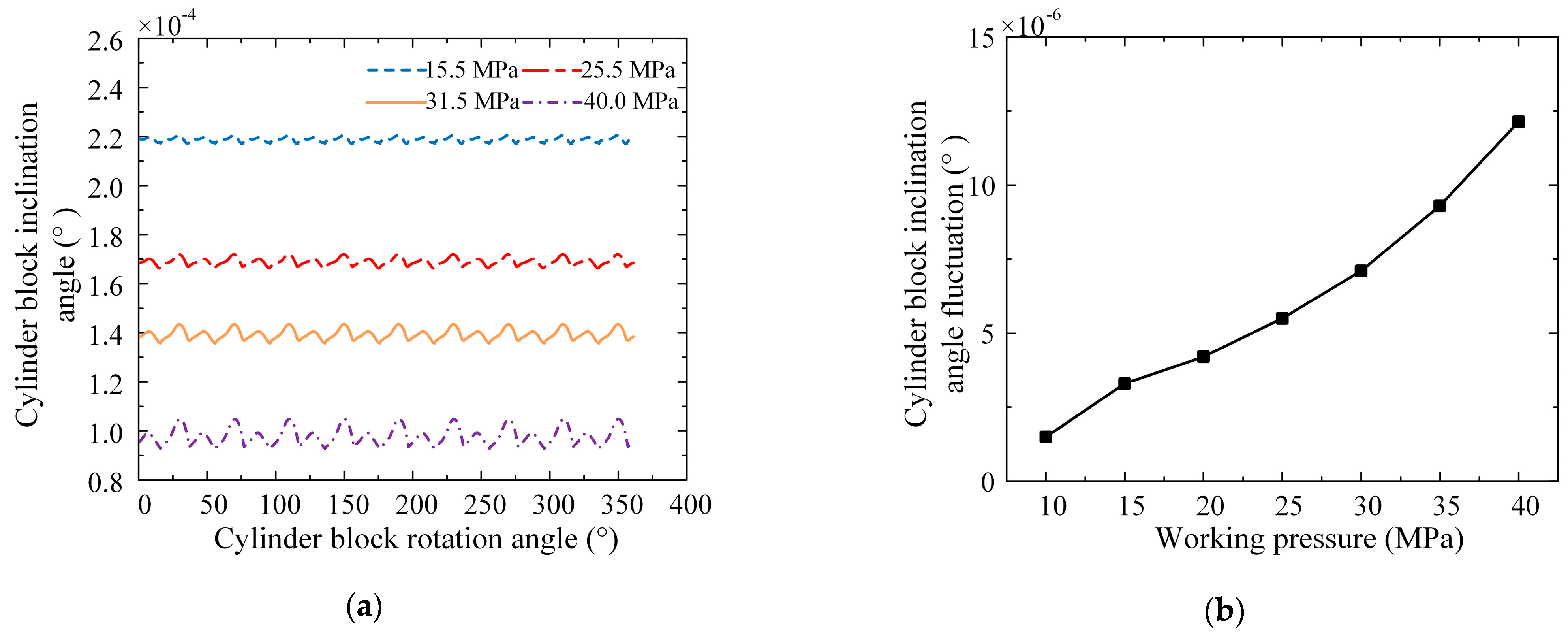
3.1.3. Influence of Operating Parameters on Lubrication Characteristics
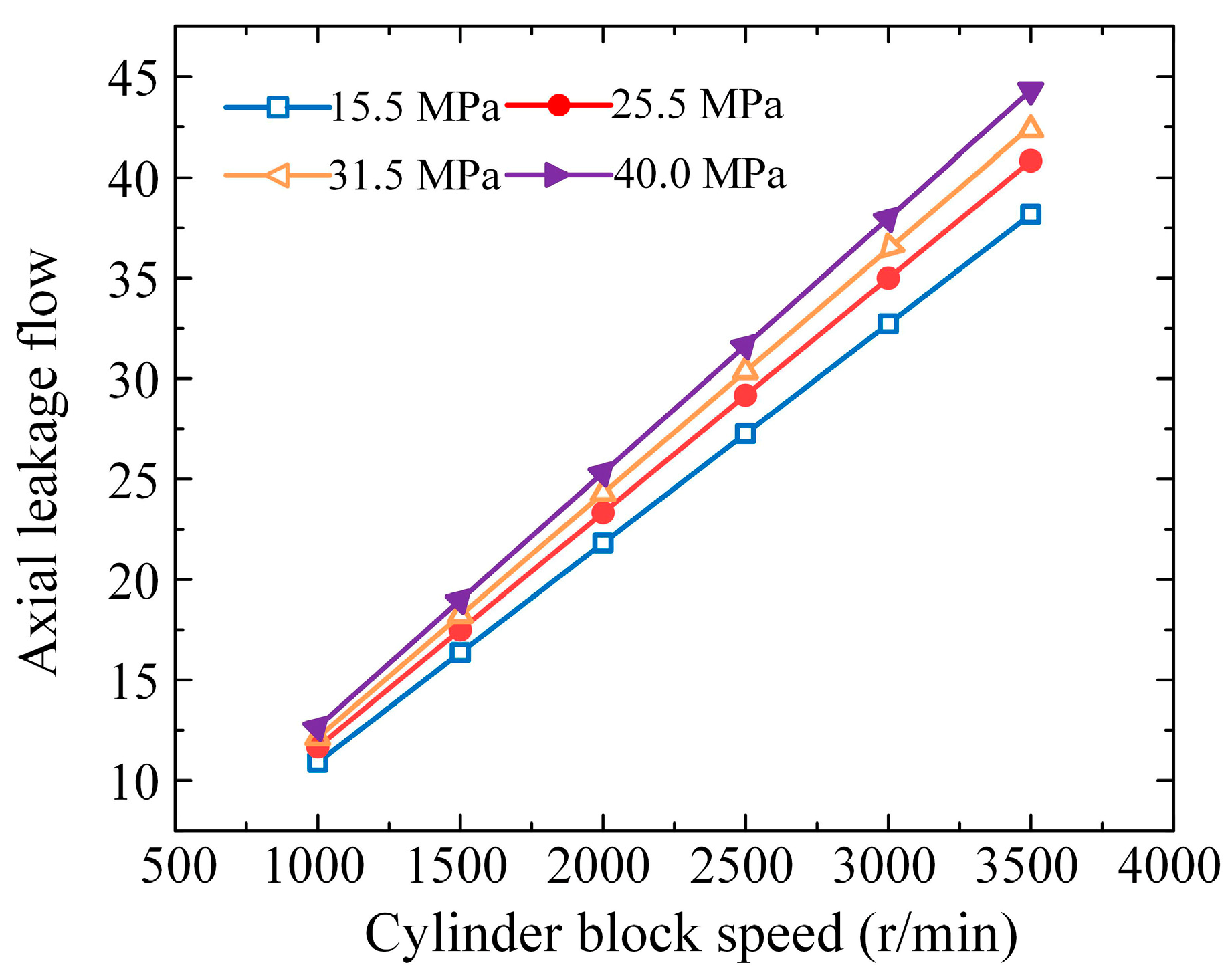
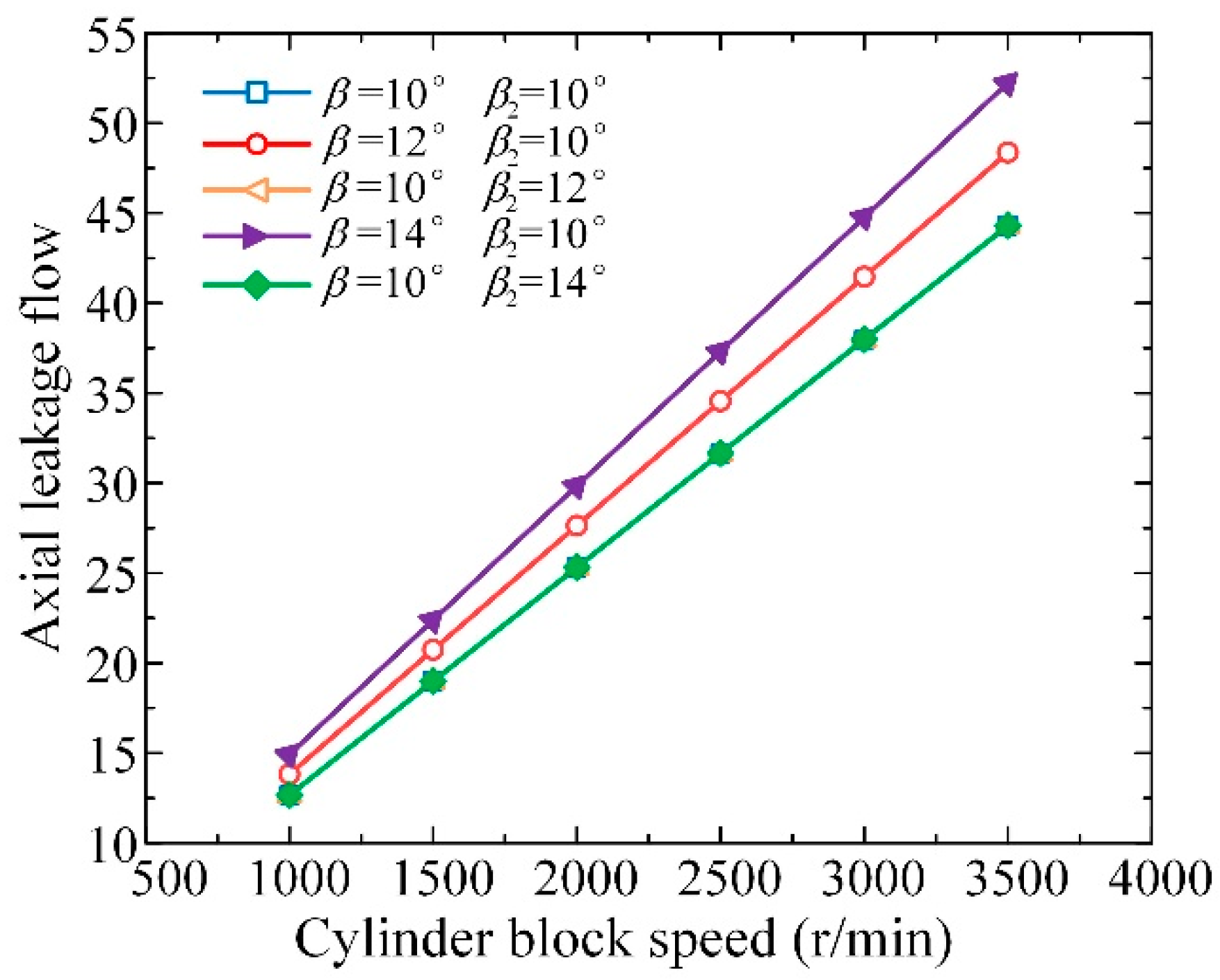
3.2. Friction and Leakage Characteristics of the External Return Spherical Hinge Pair
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| xAi, yAi, zAi | The coordinates of the external row plunger |
| x2Ai, y2Ai, z2Ai | The coordinates of theinternalrow plunger |
| R, R1 | The distribution circle radius of external plunger and the distribution circle radius of internal plunger (m) |
| β, β1 | The inclination of the external swash plate and the inclination of the internal swash plate (°) |
| φi, φ2i | The rotation angle of the external plunger relative to the y-axis and the rotation angle of the internal plunger relative to the y-axis (°) |
| K | The oil volume modulus (Pa) |
| AD | The oil action area of the plunger cavity (m2) |
| N3i | The positive pressure at point m3 (N) |
| N4i | The positive pressure at point m4 (N) |
| ρ5 | The vector equation of the contact point in the external return spherical bearing pair |
| ΔV | The relative motion velocity vector equation of the contact point in the external return spherical bearing pair |
| fs | Coefficient of the sliding friction between the external retainer plate and the external spherical hinge |
| Fφ, Fφ2 | The oil film frictional force of the external return spherical bearing pair and the oil film frictional force of internal return spherical bearing pair (N) |
| τφ1 | Fluid shear stress component of the external return spherical bearing pair (MPa) |
| R2, R3 | The radius of the external retainer plate and the radius of the internal retainer plate (m) |
| bf, bf2 | Deviation distance of external retainer plate and the deviation distance of the internal retainer plate (m) |
| RM | Internal surface radius of the external spherical hinge (m) |
| R2M | External surface radius of the internal spherical hinge (m) |
| xSi, ySi, zSi | The coordinates of the centroid of the external plunger–slipper assembly |
| x2Si, y2Si, z2Si | The coordinates of the centroid of the internal plunger–slipper assembly |
| l | Distance between the center of spherical hinge and the centroid of plunger–slipper assembly (m) |
| ω | Angular velocity of the cylinder block (rad/s) |
| fk | The friction coefficient of the plunger pair |
| RG, rG | The external diameter of the slipper’s sealing belt and the internal diameter of the slipper’s sealing belt (m) |
| It, Ia | The rotational inertia of the cylinder block around the y-axis was 0.191 kg·m2, and the rotational inertia of the cylinder block around the z-axis was 0.0889 kg·m2 |
| AK | The cross-sectional area of the plunger (m2) |
| pe | The drainage pressure of the slipper pair (MPa) |
| p | Pressure of oil film of external spherical hinge pair (MPa) |
| mk | The weight of plunger (kg) |
| mG | The weight of cylinder block (kg) |
| h | The average oil film thickness (m) |
| γ | The tilt angle of cylinder block (°) |
References
- Zhang, J.H.; Chao, Q.; Xu, B.; Pan, M.; Wang, Q.N.; Chen, Y. Novel three-piston pump design for a slipper test rig. Appl. Math. Model. 2017, 52, 65–81. [Google Scholar] [CrossRef] [Green Version]
- Xu, B.; Li, Y.B.; Zhang, B.; Zhang, J.H. Numerical simulation of overturning phenomenon of axial piston pump slipper pair. J. Mech. Eng. 2010, 46, 161–168. [Google Scholar] [CrossRef]
- Li, D.L.; Fang, M.S.; Deng, Y.P.; Liu, Y.S.; Wu, D.F. Study of materials for piston pairs of water hydraulic piston pump. Chin. Hydraul. Pneum. 2017, 11, 12–16. [Google Scholar]
- Wang, D.; Li, Z.Y.; Zhu, Y.Q. Study of the key problems in a water hydraulic piston pump and its applications. Ind. Lubr. Tribol. 2013, 53, 211–216. [Google Scholar]
- Wang, Z.Q.; Xu, Y.F.; Hu, S.; Ji, H.; Yang, J. Research on lubrication mechanism with fluid-solid coupling of port plate pair in swash plate axial piston pump. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2019, 234, 515–529. [Google Scholar] [CrossRef]
- Ji, Z.L. Research on thermal-fluid-structure coupling of valve plate pair in an axial piston pump with high pressure and high speed. Ind. Lubr. Tribol. 2018, 6, 1137–1144. [Google Scholar] [CrossRef] [Green Version]
- Manring, N.D. The relative motion between the ball guide and slipper retainer within an axial-piston swash-plate type hydrostatic pump. J. Dyn. SYST-T ASME 1999, 121, 518–523. [Google Scholar] [CrossRef]
- Chen, C. The Simulation Analysis of Collision Interference on Retainer Plate of Axial Piston Pump and Its Structure Optimizing Design. Master’s Thesis, Lanzhou University of Technology, Lanzhou, China, 2018. [Google Scholar]
- Yang, F.L. The Simulation and Optimum Design on Retainer Plate of Axial Piston Pump Based on Multi-Body Dynamics. Master’s Thesis, Lanzhou University of Technology, Lanzhou, China, 2019. [Google Scholar]
- Wang, G.Z.; Zhang, Z.P.; Liu, H.L.; Ke, J.; Zhang, R. Optimization design of swivel plate for piston pump based on ANSYS Workbench. Mach. Des. Res. 2012, 28, 62–65. [Google Scholar]
- Ji, P.; Yang, F.Y.; Hu, M. Analysis and design of return mechanism of inclined piston pump with conical cylinder block. Chin. Hydraul. Pneum. 2011, 12, 35–38. [Google Scholar]
- Zhang, J.; Hu, L.; Li, X.J.; Shi, W.D. The dynamic characteristic simulation of retainer plate in axial piston pump based on virtual prototype technology. Chin. Hydraul. Pneum. 2016, 3, 86–91. [Google Scholar]
- Wang, T.; Mao, M.; Tang, S.S.; Gai, J.T.; Ji, H. Research on lubrication mechanism of retaining spherical pair of variable displacement axial piston pump. Acta Armamentarii 2017, 38, 11–19. [Google Scholar]
- Wang, T.M.; Liang, B.; Zhao, W.H.; Tao, L.M.; Cui, W.Y. Study on the tribological properties of a self-lubricating spherical plain bearing at a cryogenic and wide temperature range. Sci. Sin. Technol. 2020, 50, 775–785. [Google Scholar] [CrossRef]
- Fang, Y.; Zhang, C.; Chen, X.; Wang, Y.; Tan, Y. A new universal approximate model for conformal contact and non-conformal contact of spherical surfaces. Acta Mech. 2015, 226, 1657–1672. [Google Scholar] [CrossRef]
- Kazama, T.; Tauruno, T.; Sasaki, H. Temperature measurement of tribological parts in swash-plate type axial piston pumps. In Proceedings of the JFPS International Symposium on Fluid Power, Toyama, Japan, 15–18 September 2008; Volume 2008, pp. 341–346. [Google Scholar]
- Lin, J.R.; Teng, M.Y.; Ho, M.H. Effects of non-Newtonian rheology on the film-height history between non-parallel sliding-squeezing surfaces. Proc. Inst. Mech. Eng. Part J-J. Eng. Tribol. 2007, 221, 155–159. [Google Scholar] [CrossRef]
- Lin, Q.Y.; Wei, Z.Y.; Wang, N.; Chen, W. Analysis on the lubrication performances of journal bearing system using computationalfluid dynamics andfluid–Structure interaction considering thermal influence and cavitation. Tribol. Int. 2013, 64, 8–15. [Google Scholar] [CrossRef]
- Mukras, S.; Kim, N.H.; Sawyer, W.G.; Jackson, D.B.; Bergquist, L.W. Numerical integration schemes and parallel computation for wear prediction using finite element method. Wear 2009, 266, 822–831. [Google Scholar] [CrossRef]
- Yacout, A.W.; Ismaeel, A.S.; Kassab, S.Z. The combined effects of the centripetal inertia and the surface roughness on the hydrostatic thrust spherical bearings performance. Tribol. Int. 2007, 40, 522–532. [Google Scholar] [CrossRef]
- Xie, Z.L.; Zhu, W.D. Theoretical and experimental exploration on the micro asperity contact load ratios and lubrication regimes transition for water-lubricated stern tube bearing. Tribol. Int. 2021, 164, 107105. [Google Scholar] [CrossRef]
- Xie, Z.L.; Wang, X.R.; Zhu, W.D. Theoretical and experimental exploration into the fluid structurecoupling dynamic behaviors towards water-lubricated bearingwith axial asymmetric grooves. Mech. Syst. Signal. Pr. 2020, 168, 108624. [Google Scholar] [CrossRef]
- Tang, Z.Q.; Liu, K.; Wang, W.; Liu, X.J. Numerical analysis of grease lubrication for radial spherical plain bearings in rotation and swing motion. Appl. Math. Mech. 2015, 36, 207–219. [Google Scholar]
- Goenka, P.K.; Booker, J.F. Spherical bearings: Static and dynamic analysis via the finite element method. J. Lubr. Technol. 1980, 102, 308–318. [Google Scholar] [CrossRef]
- Wang, Q.C. Kinematics and Friction Lubrication Analysis in the External Return Mechanism of Piston Pump/Motor. Master’s Thesis, Anhui University of Science and Technology, Huainan, China, 2019. [Google Scholar]
- Deng, H.S.; Hu, C.; Wang, Q.C.; Wang, L.; Wang, C.L. Friction and wear analysis of the external return spherical bearing pair of axial piston pump/motor. Mech. Ind. 2020, 21, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Deng, H.S.; Wang, L.; Guo, Y.C.; Zhang, Y.; Wang, C.L. Analysis of the hydrodynamic lubrication characteristics of the external Return spherical bearing pair of an axial piston pump/motor. Math. Probl. Eng. 2020, 2020, 1–14. [Google Scholar] [CrossRef]
- Wang, L.; Deng, H.S.; Gou, Y.C.; Wang, C.L.; Hu, C. Lubrication characteristics of external return spherical hinge pair of axial piston pump or motor under combined action of inclination and offset distance. J. Cent. South. Univ. 2021, 28, 2375–2393. [Google Scholar] [CrossRef]
- Sun, Y.; Jiang, J.H.; Liu, J.L. Piston pump slipper chuck and ball head relative position and friction power consumption. J. South China Univ. Technol. 2011, 39, 82–87. [Google Scholar]
- Xu, L. Study on the Lubrication Characteristics of the Valve Plate Bearing in Hydraulic Axial Piston Pump. Ph.D. Thesis, Beijing Institute of Technology, Beijing, China, 2016. [Google Scholar]



| Parameters | Values |
|---|---|
| Distribution circle radius of external plunger, R (m) | 0.041 |
| Distribution circle radius of internal plunger, R1 (m) | 0.024 |
| Radius of external retainer plate, R2 (m) | 0.0725 |
| Internal surface radius of external spherical hinge, RM (m) | 0.07255 |
| External swash plate inclination, β (°) | 10 |
| Internal swash plate inclination, β2 (°) | 10 |
| Number of single row plungers, z | 9 |
| Deviation distance of external retainer plate, bf (m) | 0.0031 |
| Bulk modulus of oil, K (Pa) | 7 × 108 |
| Calibration spindle speed, n (r/min) | 1500 |
| Weight of the plunger, mk (kg) | 0.15 |
| External diameter of slipper sealing belt, RG (m) | 0.008 |
| Internal diameter of slipper sealing belt, rG (m) | 0.005 |
| Viscosity of lubricating oil, η (Pa·s) | 0.0129 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, H.; Zhu, P.; Hu, C.; He, T. Study on Dynamic Lubrication Characteristics of the External Return Spherical Bearing Pair under Full Working Conditions. Machines 2022, 10, 107. https://doi.org/10.3390/machines10020107
Deng H, Zhu P, Hu C, He T. Study on Dynamic Lubrication Characteristics of the External Return Spherical Bearing Pair under Full Working Conditions. Machines. 2022; 10(2):107. https://doi.org/10.3390/machines10020107
Chicago/Turabian StyleDeng, Haishun, Pengkun Zhu, Cong Hu, and Tao He. 2022. "Study on Dynamic Lubrication Characteristics of the External Return Spherical Bearing Pair under Full Working Conditions" Machines 10, no. 2: 107. https://doi.org/10.3390/machines10020107
APA StyleDeng, H., Zhu, P., Hu, C., & He, T. (2022). Study on Dynamic Lubrication Characteristics of the External Return Spherical Bearing Pair under Full Working Conditions. Machines, 10(2), 107. https://doi.org/10.3390/machines10020107





