Improvement of Steady State Performance of Voltage Control in Switched Reluctance Generator: Experimental Validation
Abstract
:1. Introduction
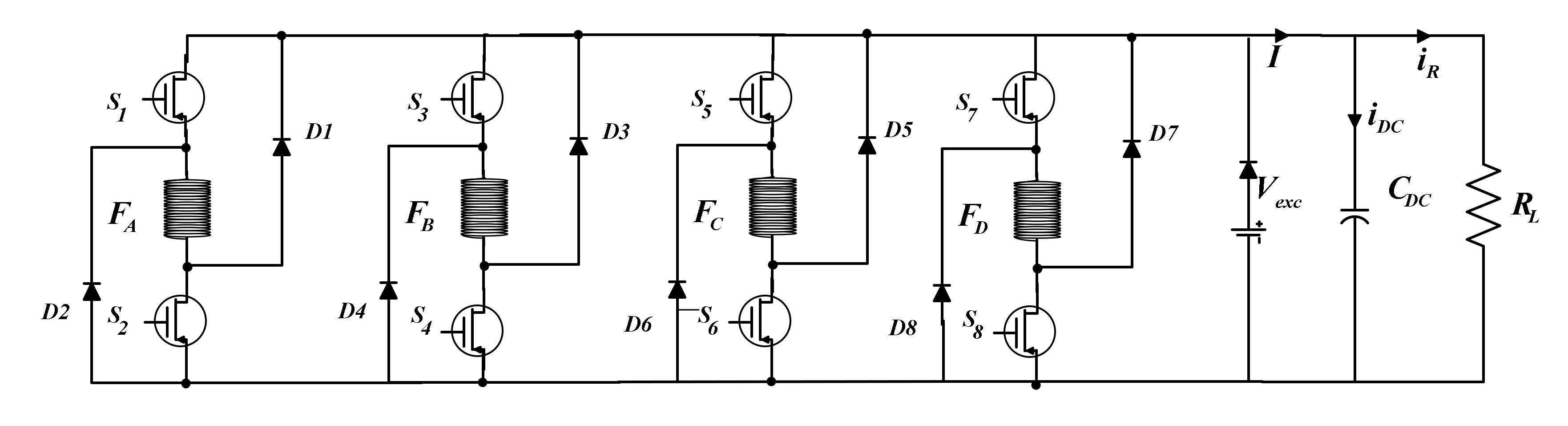
2. Basic Principle of SRG
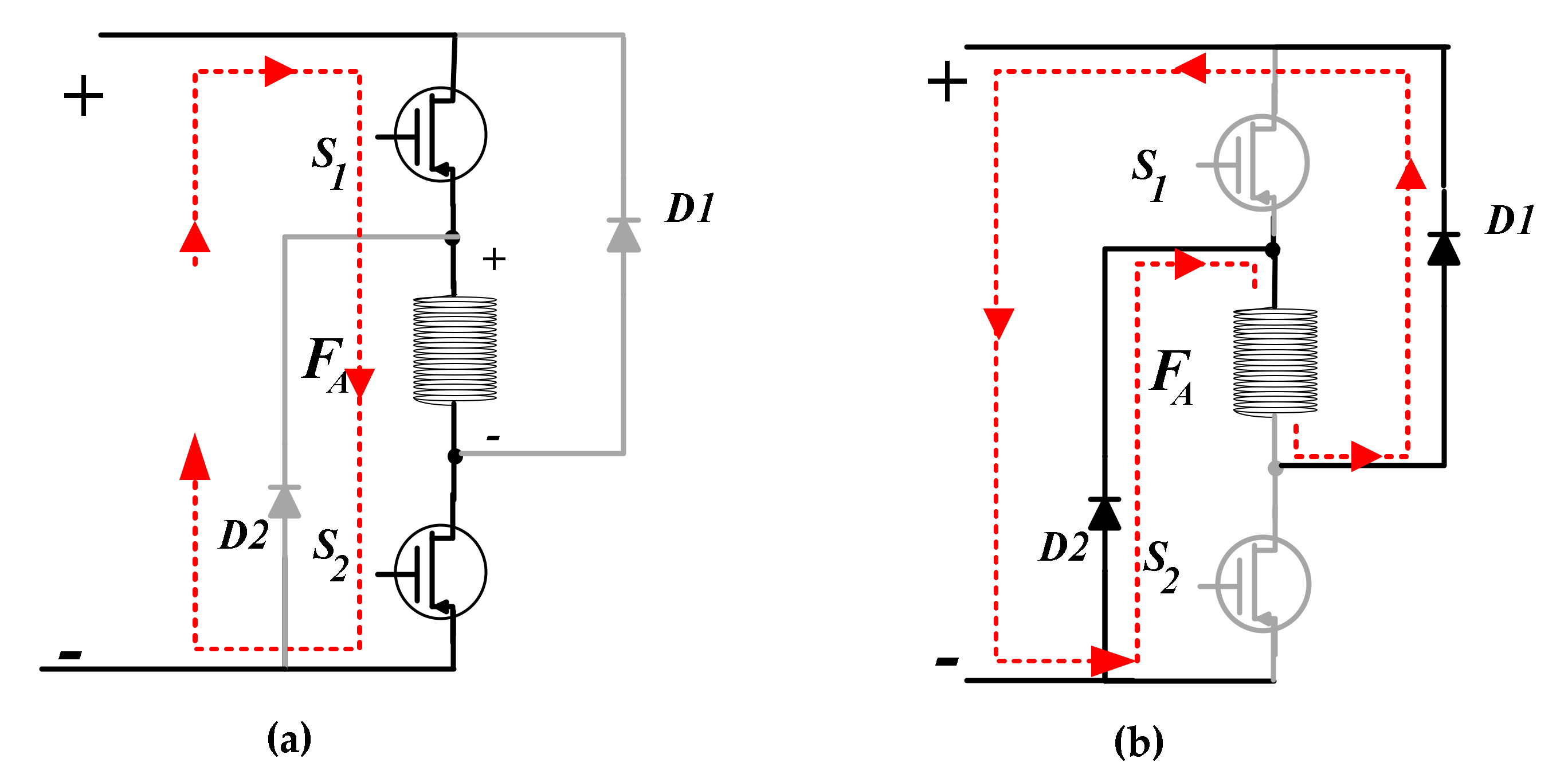
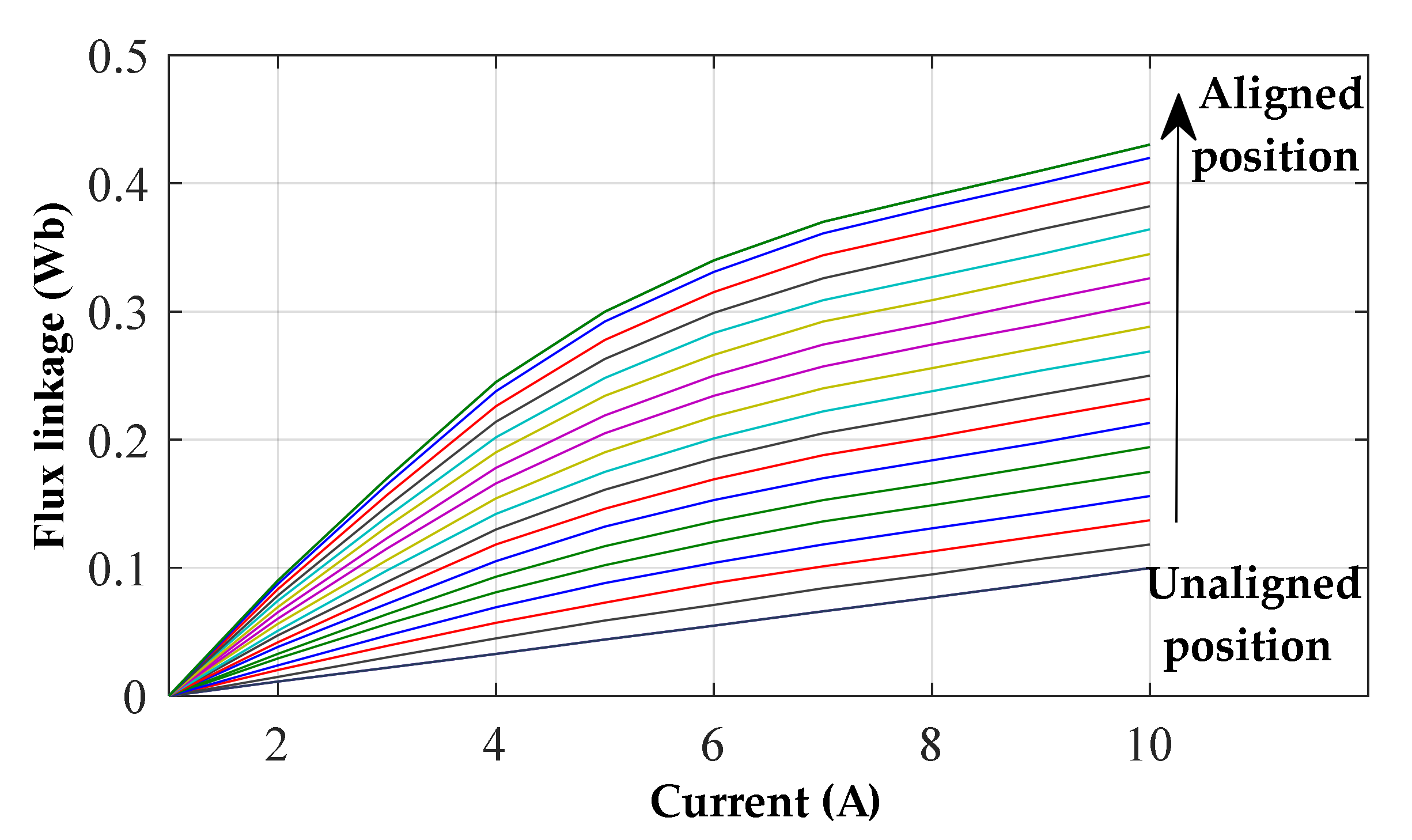
2.1. Analysis of SRG Operation
2.2. Model Simplification and Linearization
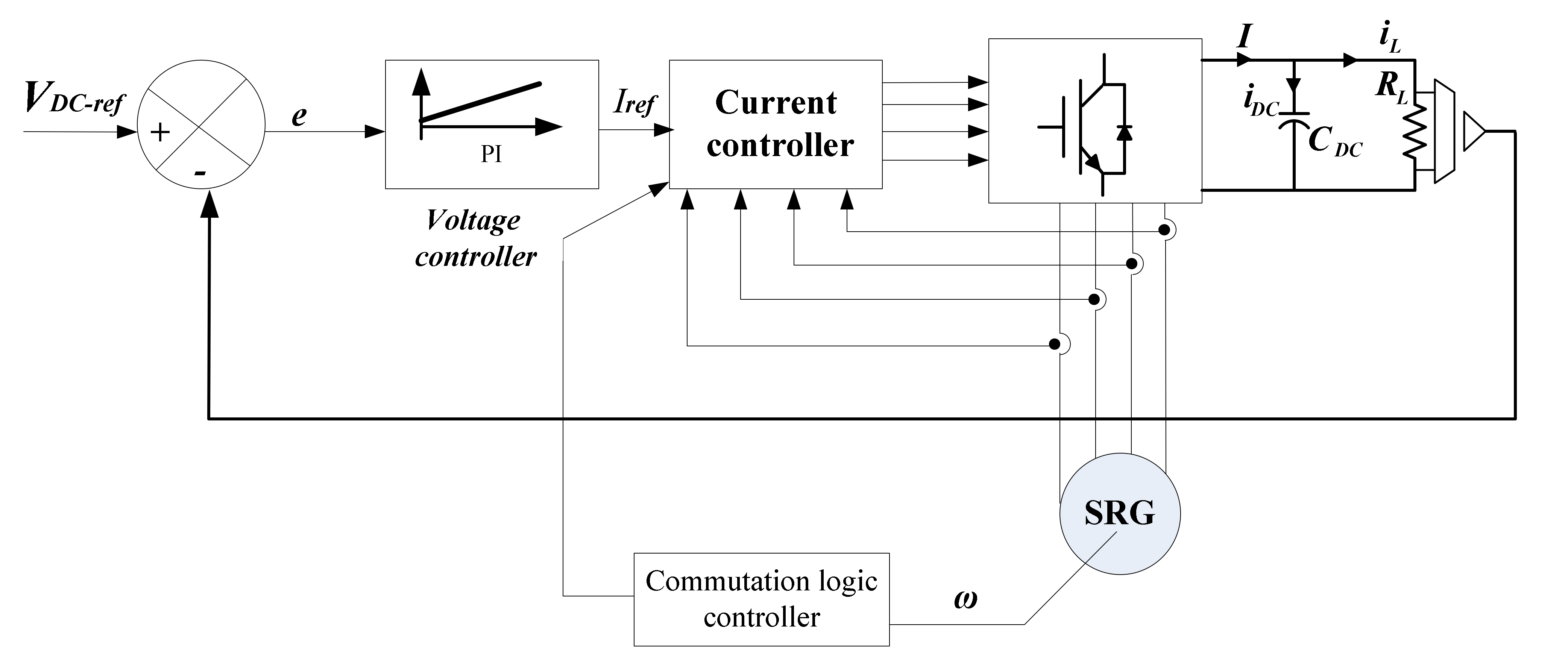
3. SRG Voltage Control
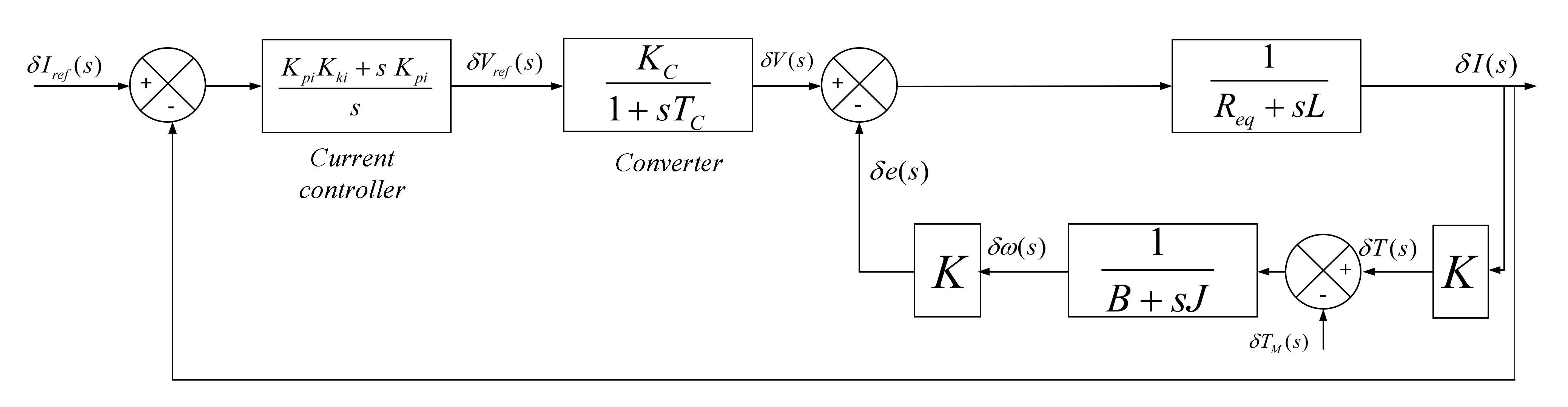
3.1. Control Scheme
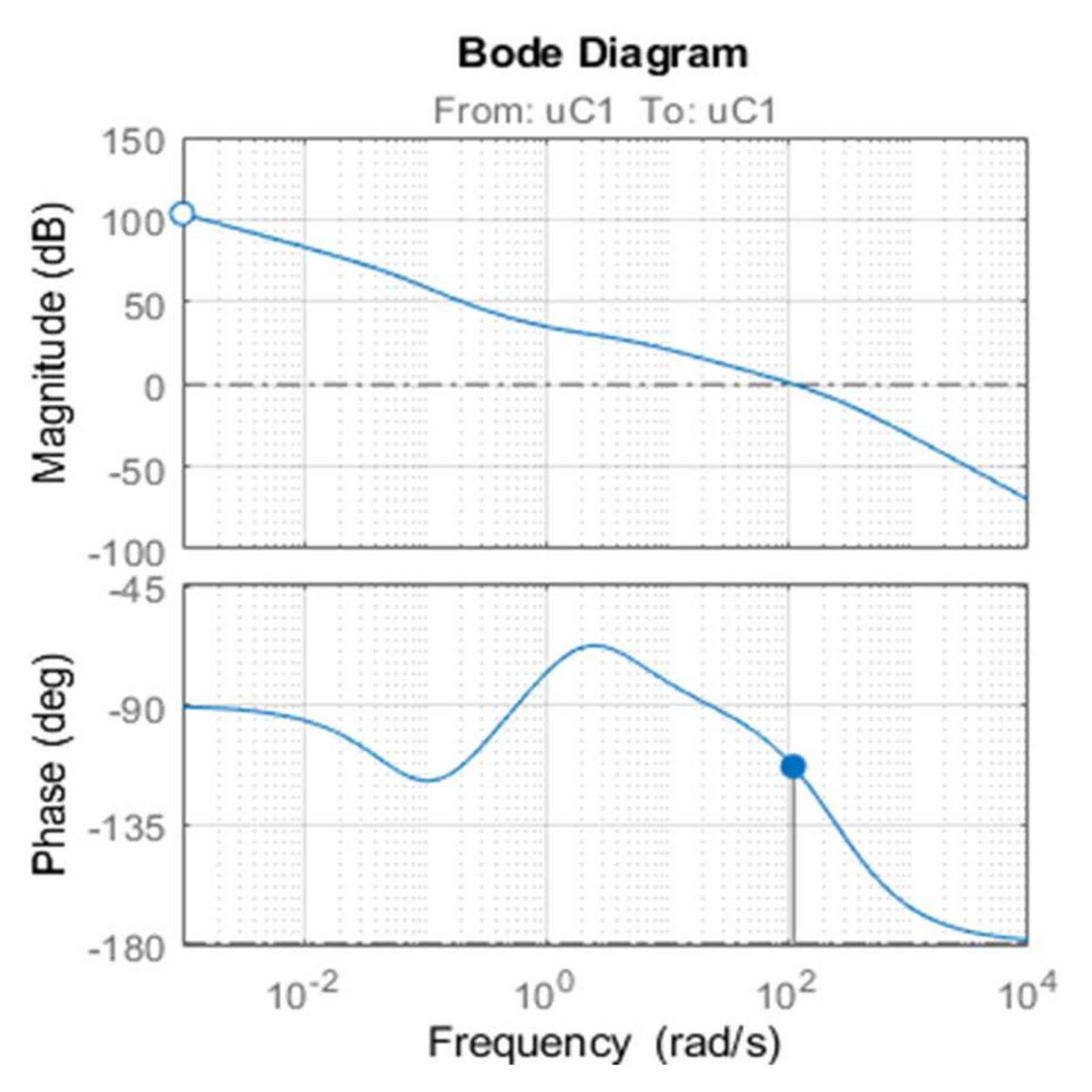
3.2. Synthesis of the Controller
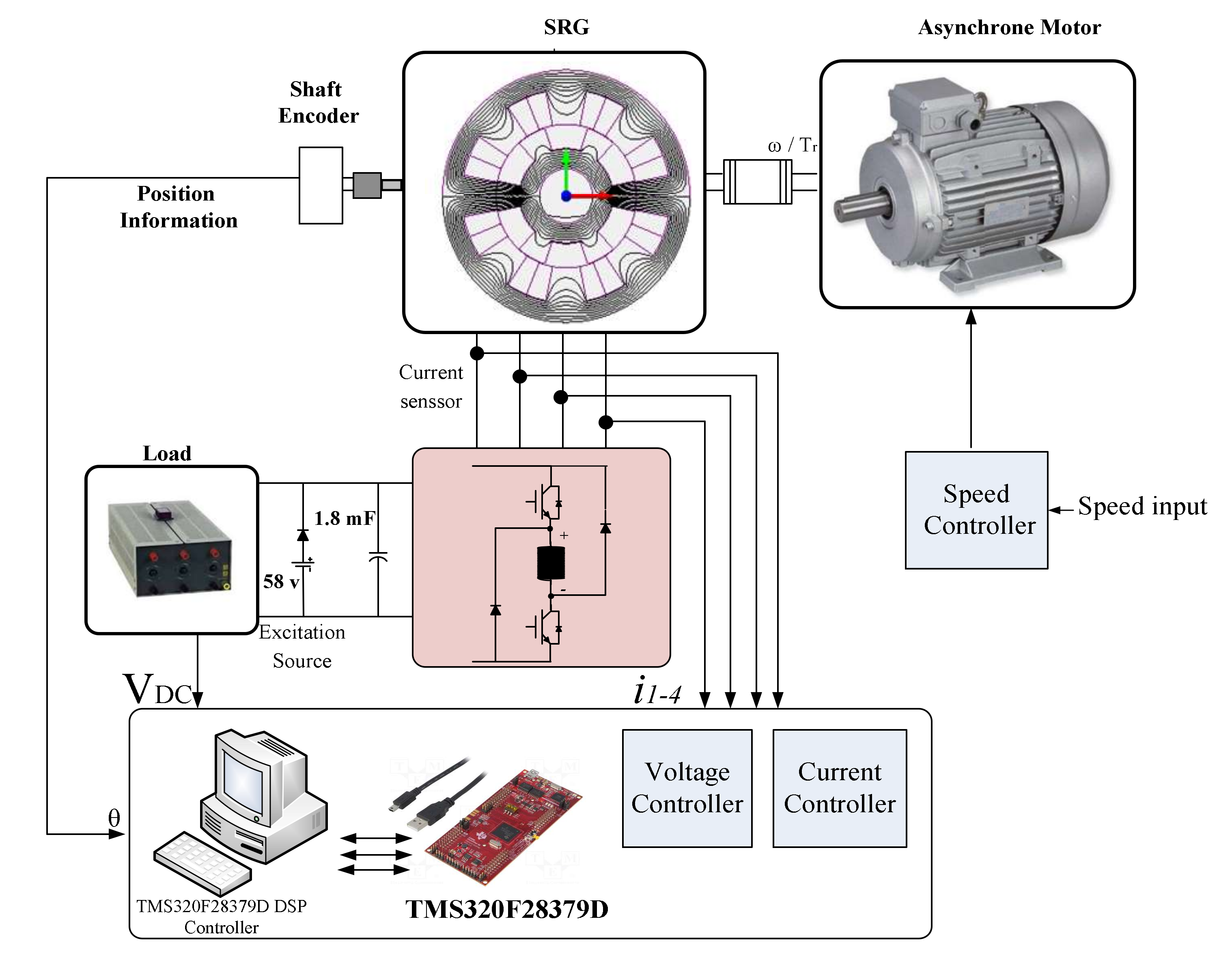
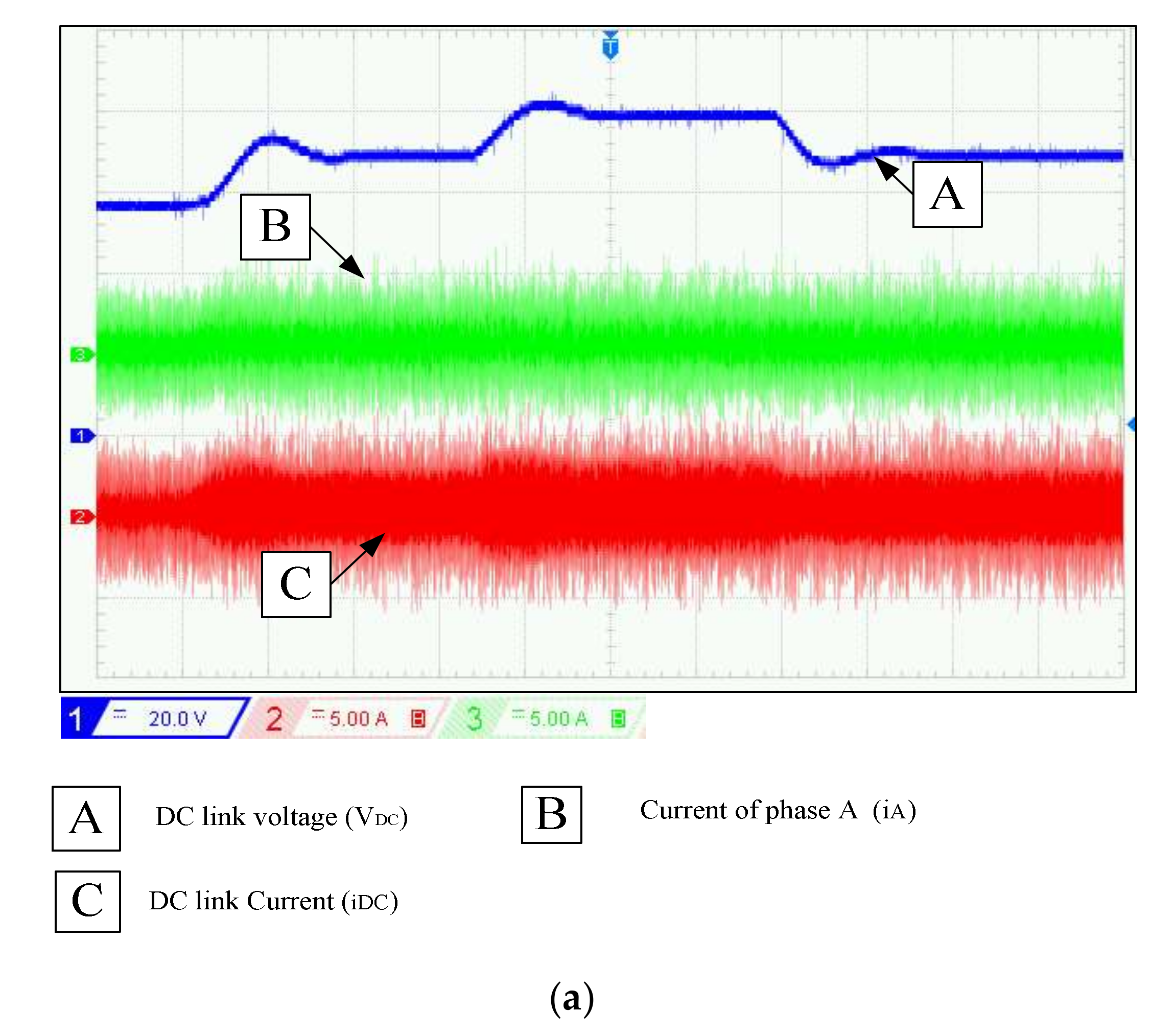
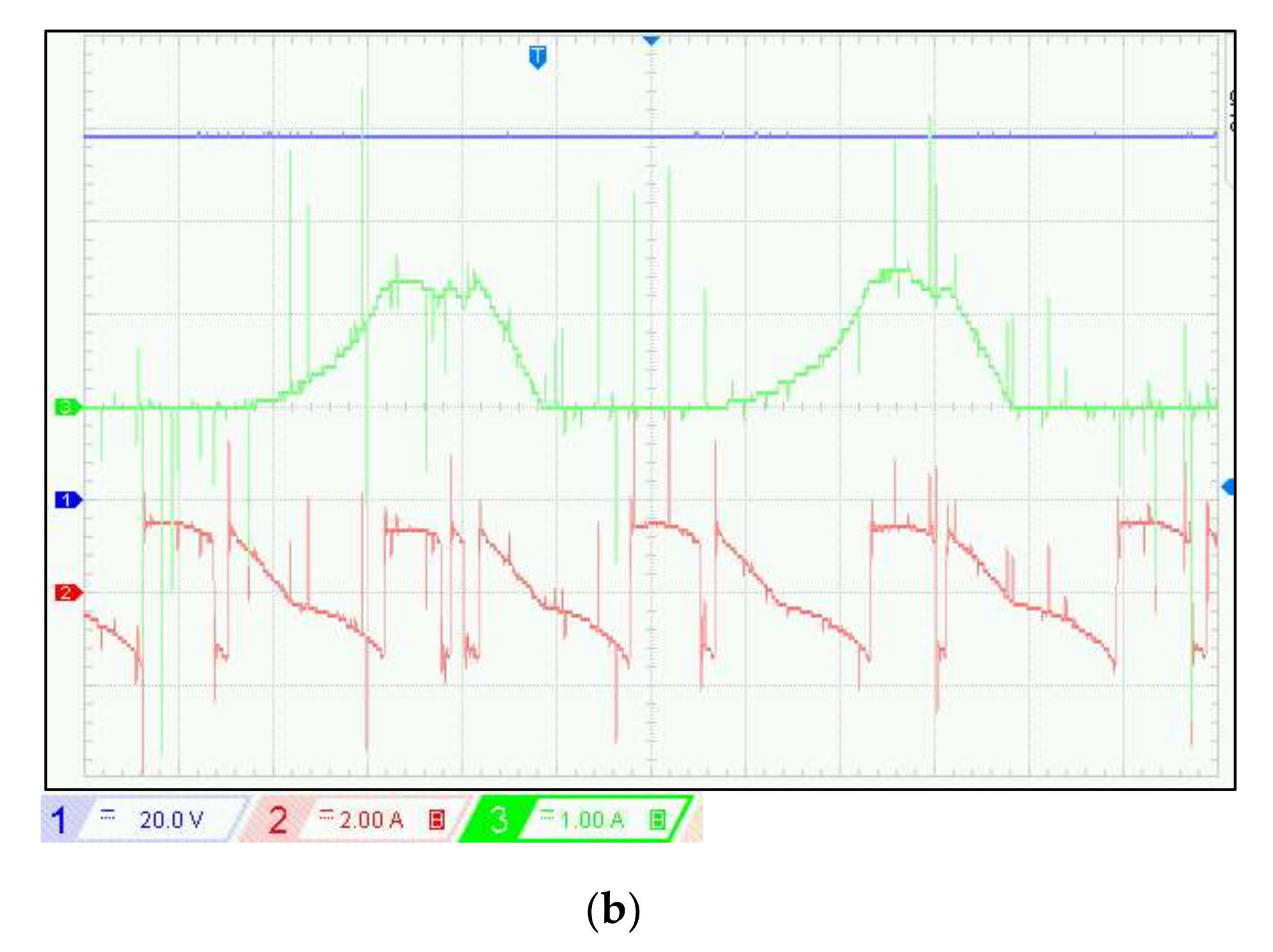
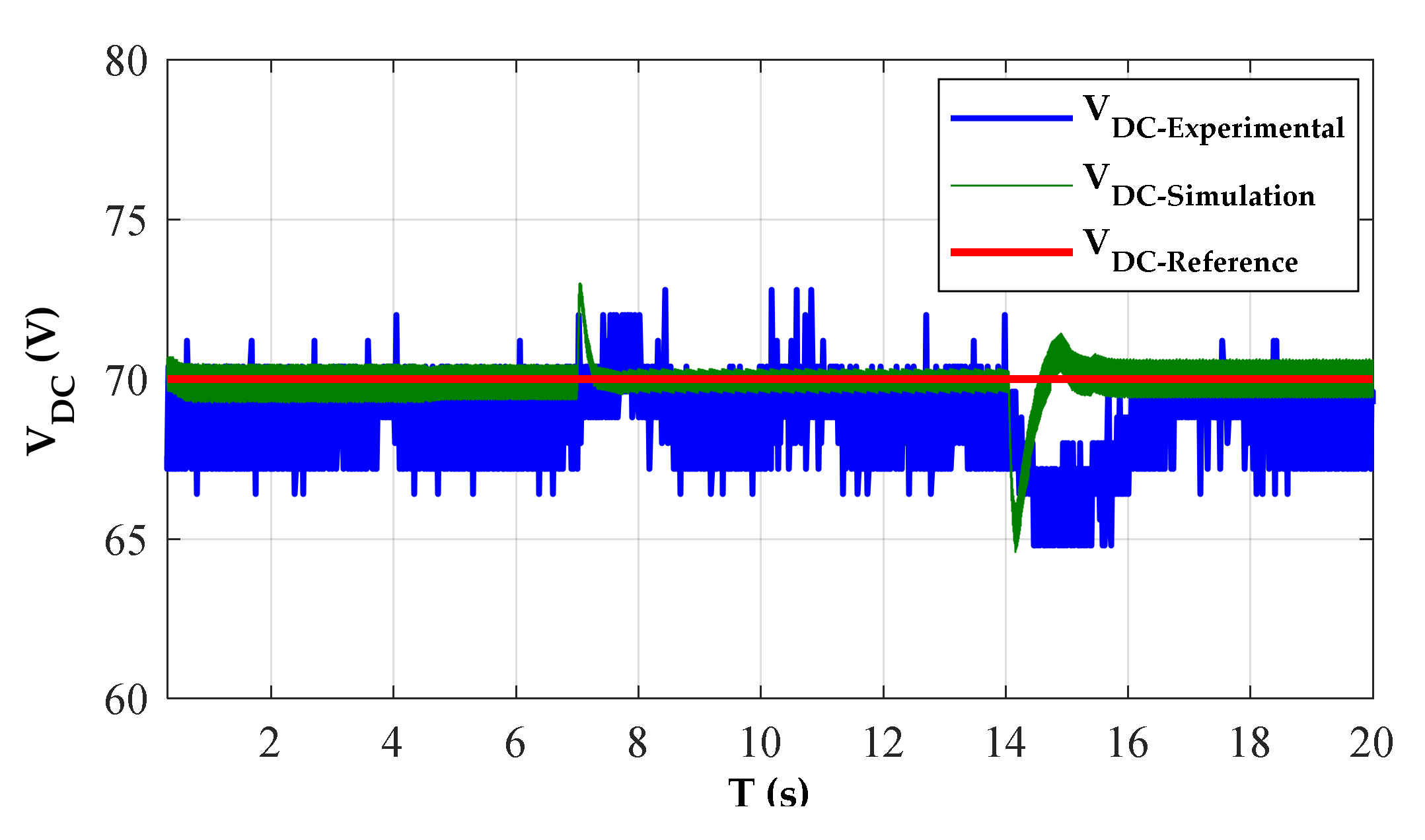
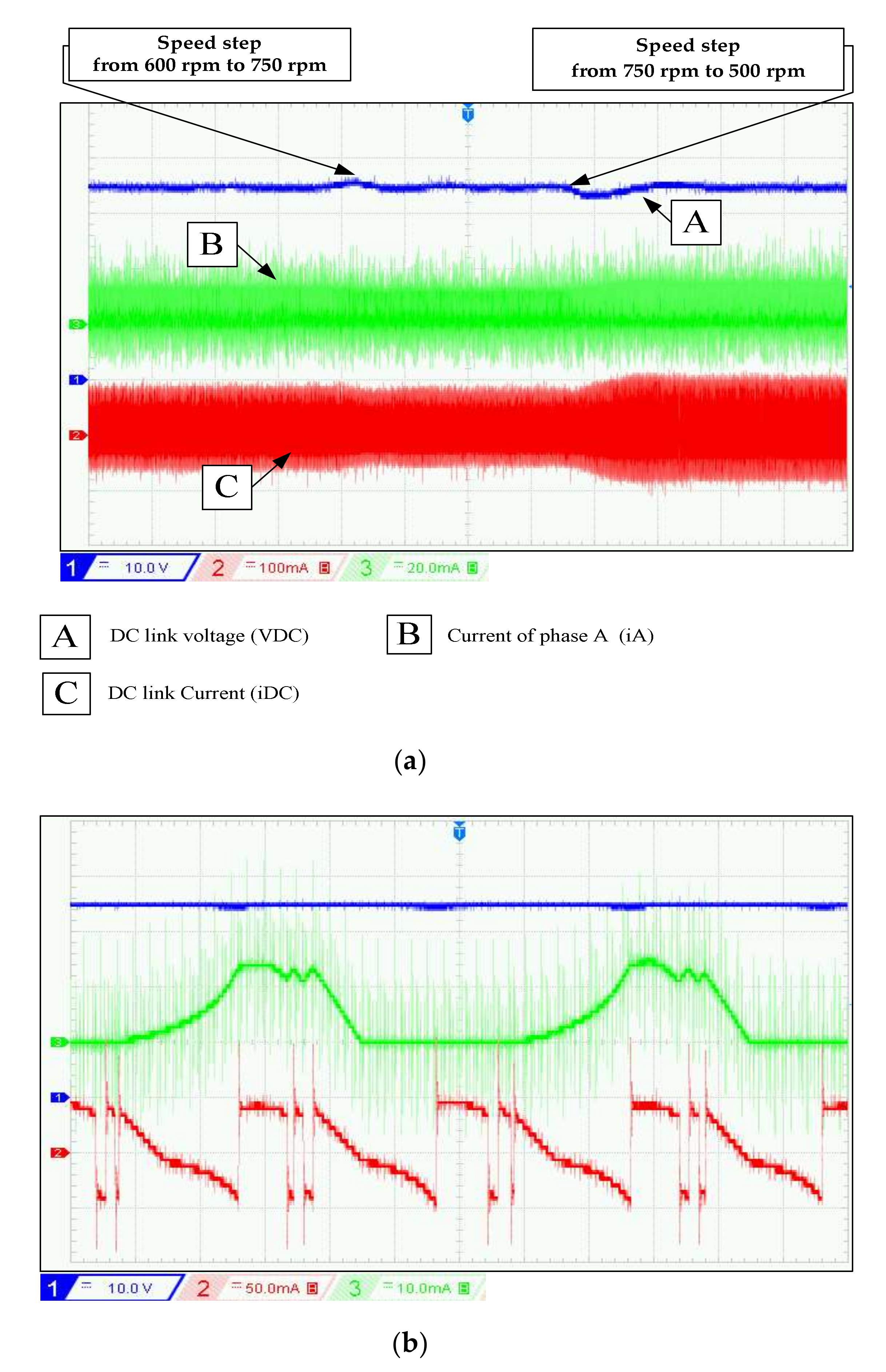
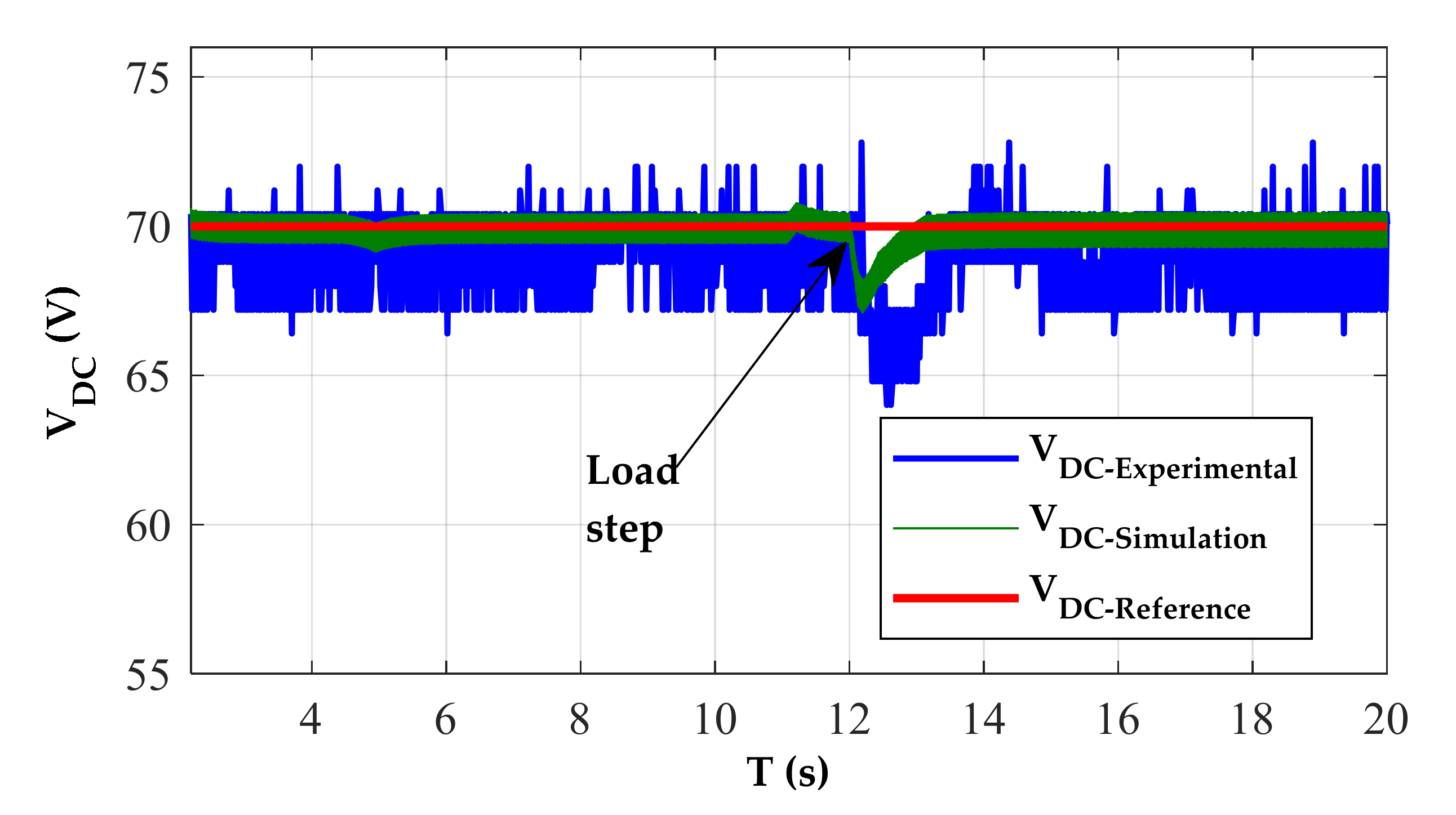
4. Simulation and Experimental Verification
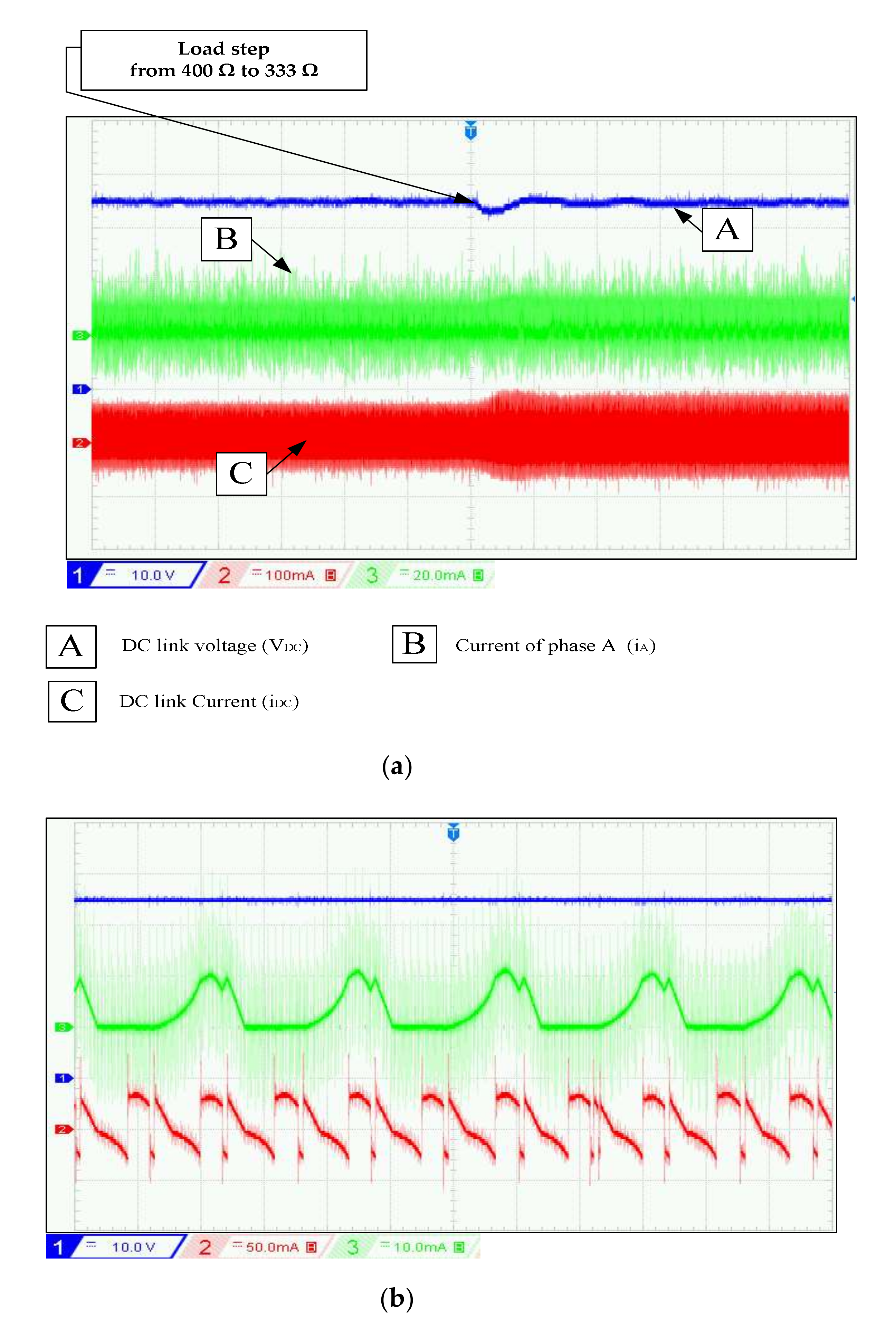
4.1. Experimentation
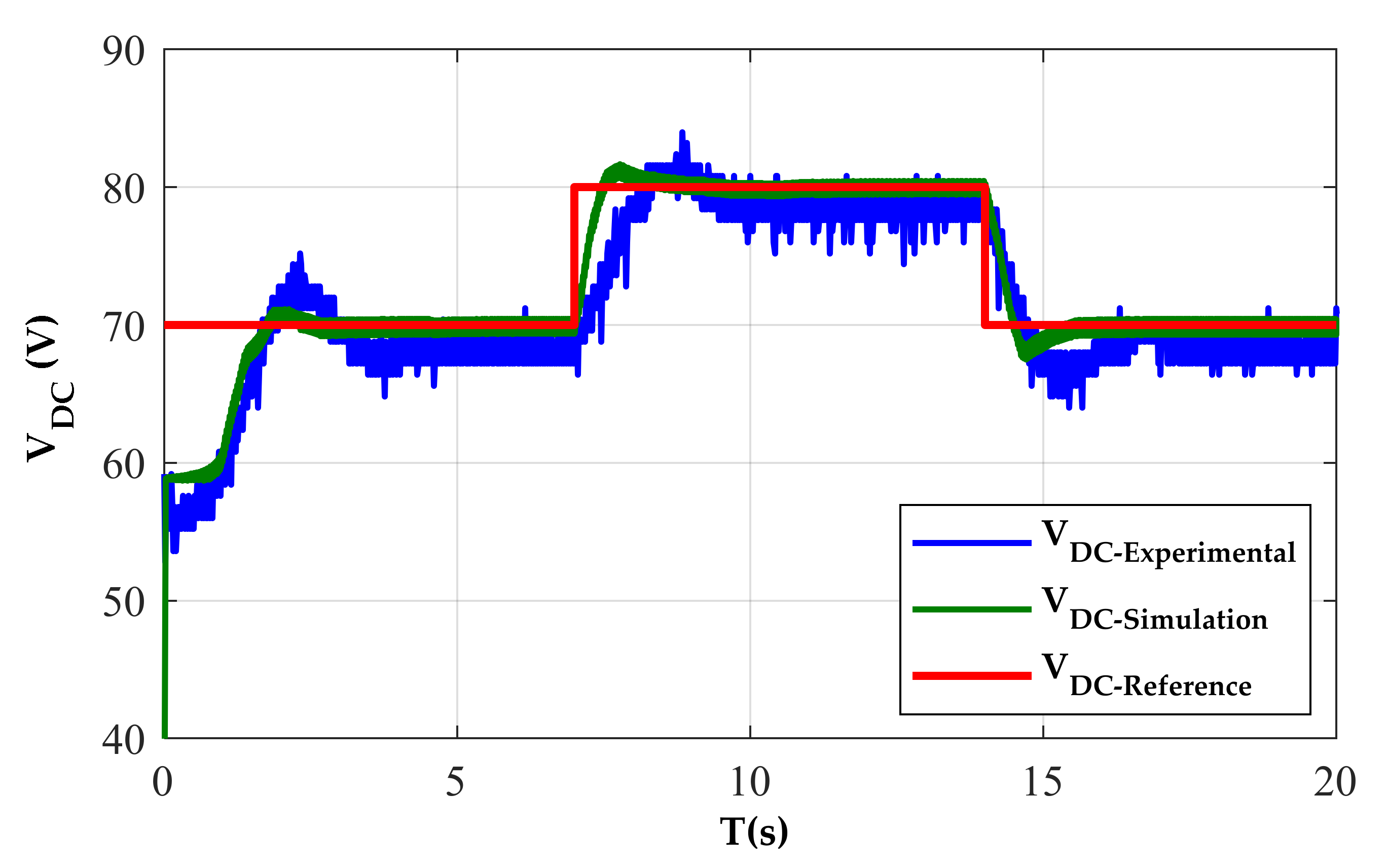
4.2. Discussion of Simulation and Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A
| Characteristics | Values |
|---|---|
| Output power | 250 W |
| Current maximum | 3 A |
| Inductance (aligned position) | 0.14 H |
| Inductance (unaligned position) | 0.021 H |
| Viscous friction | 0.01 Nms |
| Moment of inertia | 0.006 Kgm2 |
| Resistance of phase winding | 5 Ω |
References
- Yu, D.; Hua, Y.; Yu, S.; Zhang, P.; Iu, H.H.C.; Fernando, T. A New Modulation–Demodulation Approach to DC Power-line Data Transmission for SRG-Integrated Microgrid. IEEE Trans. Power. Electron. 2020, 11, 12370–12382. [Google Scholar] [CrossRef]
- Cheng, H.; Wang, L.; Xu, L.; Ge, X.; Yang, S. An Integrated Electrified Powertrain Topology with SRG and SRM for Plug-In Hybrid Electrical Vehicle. IEEE Trans. Ind. Electron. 2020, 10, 8231–8241. [Google Scholar] [CrossRef]
- Mosaad, M.I. Direct power control of SRG-based WECSs using optimised fractional-order PI controller. IET Electr. Power Appl. 2020, 3, 409–417. [Google Scholar] [CrossRef]
- Hong, C.-M.; Chen, C.-H. Enhanced radial fuzzy wavelet neural network with sliding mode control for a switched reluctance wind turbine distributed generation system. Eng. Optim. 2018, 7, 1133–1151. [Google Scholar] [CrossRef]
- Dos Santos Neto, P.J.; dos Santos Barros, T.A.; De Paula, M.V.; Filho, E.R.; Vasquez, J.C.; Guerrero, J.M. Wind Distributed System Based on Switched Reluctance Generator Using a Bidirectional DC-DC Converter with Sliding Mode Control. In Proceedings of the IECON 2019 – 45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019. [Google Scholar] [CrossRef]
- Li, Z.; Yu, X.; Qian, Z.; Wang, X.; Xiao, Y.; Sun, H. Generation Characteristics Analysis of Deflection Type Double Stator Switched Reluctance Generator. IEEE Access. 2020, 8, 196175–196186. [Google Scholar] [CrossRef]
- Kiani, E.; Ganji, B.; Taher, S.A. Model predictive control of switched reluctance generator based on Z-source converter for wind power applications. Int. Trans. Electr. Energy Syst. 2020, 11, 12578. [Google Scholar] [CrossRef]
- Gan, C.; Wu, J.; Sun, Q.; Kong, W.; Li, H.; Hu, Y. A Review on Machine Topologies and Control Techniques for Low-Noise Switched Reluctance Motors in Electric Vehicle Applications. IEEE Access. 2018, 6, 31430–31443. [Google Scholar] [CrossRef]
- Sun, X.; Wu, J.; Wang, S.; Diao, K.; Yang, Z. Analysis of torque ripple and fault-tolerant capability for a 16/10 segmented switched reluctance motor in HEV applications. COMPEL - Int. J. Comput. Math. Electr. Electron. Eng. 2019, 6, 1725–1737. [Google Scholar] [CrossRef]
- Ćalasan, M.P.; Vujičić, V.P. A robust continuous conduction mode control strategy of switched reluctance generator for wind power plant applications. Electr. Eng. 2016, 3, 943–958. [Google Scholar] [CrossRef]
- Dias, R.J.; Silva, C.R.; dos Santos, B.R.; dos Santos Costa, C.; da Silveira, A.F.V.; de Andrade, D.A. Innovations on Design of 6×4 and 6×6 Switched Reluctance Generators for Increasing the Efficiency. IEEE Lat. Am. Trans. 2017, 4, 646–655. [Google Scholar] [CrossRef]
- Namazi, M.M.; Koofigar, H.R.; Ahn, J.W. Active Stabilization of Self-Excited Switched Reluctance Generator Supplying Constant Power Load in DC Microgrids. IEEE Trans. Emerg. Sel. 2021, 3, 2735–2744. [Google Scholar] [CrossRef]
- Roshandel, E.; Namazi, M.M.; Rashidi, A.; Saghaian-Nejad, S.M.; Ahn, J.W. SSC strategy for SRG to achieve maximum power with minimum current ripple in battery charging. IET Electr. Power Appl. 2017, 7, 1205–1213. [Google Scholar] [CrossRef]
- Zan, X.; Cui, M.; Yu, D.; Xu, R.; Ni, K. Improvement of the Response Speed for Switched Reluctance Generation System Based on Modified PT Control. Energies 2018, 8, 2049. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Chen, H.; Cheng, H.; Yan, S.; Abbas, S. An Active Boost Power Converter for Improving the Performance of Switched Reluctance Generators in DC Generating Systems. IEEE Trans. Power Electron. 2020, 5, 4741–4755. [Google Scholar] [CrossRef]
- Chirapo, K.A.C.; Oliveira, A.L.; Sguarezi Filho, A.J.; Pelizari, A.; Di Santo, S.G.; Costa, E.C.M. P+RES Controller Applied to the Direct Power Control of Switched Reluctance Generator. J. Control. Autom. Electr. 2020, 2, 360–366. [Google Scholar] [CrossRef]
- Barros, T.A.; Neto, P.J.; Filho, P.S.N.; Moreira, A.B.; Ruppert, E. Approach for performance optimization of switched reluctance generator in variable-speed wind generation system. Renew. Energy. 2016, 97, 114–128. [Google Scholar] [CrossRef]
- Yahia, H.; Liouane, N.; Dhifaoui, R. Differential evolution method-based output power optimisation of switched reluctance generator for wind turbine applications. IET Renew. Power Gener. 2014, 7, 795–806. [Google Scholar] [CrossRef]
- Dos Santos Barros, T.A.; dos Santos Neto, P.J.; Nascimento Filho, P.S.; Moreira, A.B.; Ruppert Filho, E. An Approach for Switched Reluctance Generator in a Wind Generation System with a Wide Range of Operation Speed. IEEE Trans. Power Electron. 2017, 11, 8277–8292. [Google Scholar] [CrossRef]
- Kushwaha, A.; Kanagaraj, R. Peak-current estimation using simplified current-rise model of switched reluctance generator operating in single-pulse mode. Int. J. Electr. Power Energy. Syst. 2020, 120, 105971. [Google Scholar] [CrossRef]
- Lu, M.Z.; Jhou, P.-H.; Liaw, C.M. Wind Switched-Reluctance Generator Based Microgrid with Integrated Plug-In Energy Support Mechanism. IEEE Trans. Power Electron. 2021, 5, 5496–5511. [Google Scholar] [CrossRef]
- Hancco Catata, E.O.; Dos Santos Neto, P.J.; De Paula, M.V.; Carvalho, J.P.; Barros, T.A.S.; Ruppert, E. In-Loop Adaptive Filters to Improve the Power Quality of Switched Reluctance Generator in WECS. IEEE Access. 2021, 10, 2941–2951. [Google Scholar] [CrossRef]
- Dos Santos Neto, P.J.; dos Santos Barros, T.A.; Catata, E.H.; Ruppert Filho, E. Grid-connected SRG interfaced with bidirectional DC-DC converter in WECS. IEEE Trans. Energy Convers. 2021, 4, 3261–3270. [Google Scholar] [CrossRef]
- Sarker, R.; Sengupta, D.; Datta, A. PWM Control Technique for Switched Reluctance Generator in Variable Speed Applications. In Recent Advances in Power Electronics and Drives; Kumar, J., Jena, P., Eds.; Springer: Berlin, Germany, 2021; pp. 339–350. [Google Scholar] [CrossRef]
- Chen, H.; Xu, D.; Deng, X. Control for power converter of small-scale switched reluctance wind power generator. IEEE Trans. Power Electron. 2020, 4, 3148–3158. [Google Scholar] [CrossRef]
- Takayama, K.; Miki, I. Design of switched reluctance motor to reduce acoustic noise. In Proceedings of the 2016 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Capri, Italy, 22–24 June 2016. [Google Scholar] [CrossRef]
- Sarr, A.; Bahri, I.; Berthelot, E.; Kebe, A.; Diallo, D. Switched Reluctance Generator for Low Voltage DC Microgrid Operation: Experimental Validation. Energies 2020, 12, 3032. [Google Scholar] [CrossRef]
- Krishnan, R. Switched Reluctance Motor Drives, 1st ed.; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Pereira, M.; Araújo, R.E. Analysis and Design of a Speed Controller for Switched Reluctance Motor Drive. U. Porto J. Eng. 2019, 1, 46–58. [Google Scholar]



| Torque Ripple | Variation | Simulation | Measurement |
|---|---|---|---|
| Voltage | 70 V | 1.57% | 4.65% |
| 80 V | 1.25% | 4.04% | |
| 90V | 1.18% | 3.40% | |
| Speed | 500 rpm | 1.85% | 4.65% |
| 600 rpm | 1.67% | 4.64% | |
| 750 rpm | 1.04% | 4.62% | |
| Load resistance | 333 Ω | 1.43% | 4.65% |
| 400 Ω | 1.43% | 4.65% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Touati, Z.; Pereira, M.; Araújo, R.E.; Khedher, A. Improvement of Steady State Performance of Voltage Control in Switched Reluctance Generator: Experimental Validation. Machines 2022, 10, 103. https://doi.org/10.3390/machines10020103
Touati Z, Pereira M, Araújo RE, Khedher A. Improvement of Steady State Performance of Voltage Control in Switched Reluctance Generator: Experimental Validation. Machines. 2022; 10(2):103. https://doi.org/10.3390/machines10020103
Chicago/Turabian StyleTouati, Zeineb, Manuel Pereira, Rui Esteves Araújo, and Adel Khedher. 2022. "Improvement of Steady State Performance of Voltage Control in Switched Reluctance Generator: Experimental Validation" Machines 10, no. 2: 103. https://doi.org/10.3390/machines10020103
APA StyleTouati, Z., Pereira, M., Araújo, R. E., & Khedher, A. (2022). Improvement of Steady State Performance of Voltage Control in Switched Reluctance Generator: Experimental Validation. Machines, 10(2), 103. https://doi.org/10.3390/machines10020103








