Impact of Electric Vehicles on a Power Line with Photovoltaic Power Plants Connected

Abstract

Electric vehicles (EVs) are currently popular, and their number is growing; therefore, they have an impact on the power system. In this paper, the impact of electric vehicles on a power line connected to photovoltaic (PV) power plants regarding the power losses and voltage level is presented. The study is performed for a power line located in Mureș County, Romania, to which two photovoltaic power plants are connected. Three supply options are available for the power line, which supplies 15 loads. The power demand of the loads is determined with the power meters installed at the load premises. Electric vehicles are also considered to be connected in different points along the power line at the buses with the lowest voltage level. The results give the power losses and voltage levels for the case of when the PV power plants and EVs are connected to the power line, compared with the case when the EVs are not connected to the power line. The power losses were 400% higher in the case where the EVs were connected when the power demand was higher, while the voltage level was 2% lower if the EVs were connected.

1. Introduction

In the past years, the number of electric vehicles (EVs) has significantly increased. The European Union, in 2020, sold over 500,000 EVs, while in 2020, Romania sold over 7000 EVs, and over 6000 EVs in 2019 [1]. Currently, these EVs are expensive, but these sales will continue to rise as governments promote them by offering vouchers and tax deductions, and thus various manufacturers claim to produce only EVs by 2030.

EVs can be divided into three categories: hybrid electric vehicles (HEV), plug-in hybrid electric vehicles (PHEV) and battery-powered electric vehicles (BEV). The difference between them is that the PHEV and BEV can be connected to the main power grid in order to be charged [1,2,3,4,5,6]. Of the total EVs sold in Romania, the majority are HEV; however, the PHEV and BEV are gaining more and more ground [1].

The charging of these vehicles can be performed at the user home or at dedicated charging stations. One of the issues related to the charging of EVs is the fact that they have an im-pact on the power grid [2,3,4,5,6,7].

This impact on the power grid was studied by different researchers. In [2,3], different methods of scheduling for PHEV charging and discharging were analyzed; thus, the power grid demand was reduced, and a cost function was optimized. The EVs charging data obtained from smart meters were used to study the impact on a test distribution network in [4] regarding the power demand, voltage levels and charging profile. The power demand, voltage drops and a strategy to optimize the power required by the loads was studied in [5] for the Milan distribution network. Considering fast charging of the EVs, the voltage drop was under 0.5% with reference to the nominal voltage value. The impact of PHEV on the power systems scheduling considering the generation sources and power cost was studied in [6]. The thermal overloads, voltage drops and power losses for a residential distribution network in the United Kingdom with EVs and distributed generation sources were investigated in [7]. The power demand and power losses for a distribution system with a solar power plant and EV parking lot were analyzed in [8]. A power quality analysis regarding frequency, voltage, harmonic distortion and power factor was performed in [9] for a 16 bus system, with high-penetration of EVs and renewable energy sources, in which the voltage drop and frequency were below limits in the case of a high number of EVs. In [10], the effects of EV charging strategies were analyzed for the German power system considering the power generation, power demand, CO₂ emissions and CO₂ prices. The charging patterns of EVs charging were studied in [11] for a residential community considering the power demand, thermal and cooling demand and power cost. The voltage profile, power flow and power losses were studied in [12] for a radial distribution system with EVs and photovoltaic power plants. In [13], the sizing of storage systems and impact of EVs (power losses) was studied considering power demand. Monte Carlo simulations were performed in [14] for a distribution network of different penetration rates of photovoltaic generation sources and EVs in order to determine the power losses. In [15], the power system expansion planning was studied considering different EV charging scenarios. In [16], the voltage profile, harmonic distortion and power demand were studied for an urban distribution network with photovoltaic power plants and PHEV. The impact of EVs on power generation and power demand on Portugal electrical grid was studied in [17], and in [18] for an office building microgrid with photovoltaic sources and a combined heat and power unit. The power losses and voltage levels were determined in [19] for a typical distribution network in the UK considering different EV charging locations and power supplied by distributed generation sources, while in [20], the power losses and voltage levels were determined for a distribution network located on an island considering EV battery charging characteristics. The impact of the integration of charging stations and photovoltaics on voltage quality and voltage stability was studied in [21]. The power demand was studied in [22] considering different levels of penetration, uncontrolled and controlled charging of the EVs and generation scenarios for the renewable energy sources. In [23], a strategy was developed for EVs, thus, the charging costs were minimized, and the power supplied by the renewable energy sources was maximized, which also was evaluated for the impact of the charging strategy on power generation planning. The voltage level, power line loading, and feeder profiles for a distribution system with uncontrolled charging of EVs was studied in [24]. The voltage level was studied in [25] for a distribution system considering uncertainties in the EV charging and power supplied by photovoltaic systems, while in [26], an Irish distribution network considering charging at different stations was studied. The power losses, control and demand response capability, compensator capacity and PV throughput were studied in [27] for a distribution network with a high penetration of photovoltaic power plants and EV charging stations. The voltage profile and power losses were determined in [28] for a distribution network considering different charging scenarios for the EVs. An EV charging and discharging strategy was developed in [29]; thus, the power supplied by residential photovoltaic sources was balanced. In [30], the impact of EVs on high and extra high voltage power grids regarding the voltage level was studied, which had values between allowed limits, nodal prices and greenhouse emissions that were approximately 9% higher.

Other aspects taken into consideration in the EV analyses in [31,32,33,34,35,36] were the power generation from the classic power plants and renewable energy sources (such as photo-voltaic power plants) considering the availability of the sources, the charging cost to be minimum, and the possible required investments in equipment for the power grid to be minimum. Management strategies were studied in [37,38,39,40,41,42,43,44]. In [37,38], a review of the management strategies of EVs was presented considering the power demand of these vehicles, charging patterns or driving conditions. In [39], a fuzzy cloud stochastic framework for the management of power in renewable microgrids with wind, solar or storage was developed, considering a maximum deployment of electric vehicles. In [40], a management strategy was created for a community with residential houses that had a planned grid outage; the power during the outage was supplied to the houses by electric vehicles. In [41], the management of a renewable microgrid considering demand during coordinated and intelligent charging of hybrid electric vehicles was developed, resulting in 2.5% reduction of the total operation cost of the microgrid in the case of the intelligent charging In [42], the management in automated hybrid electric vehicles with flexible torque request was studied, resulting in lower fuel consumption and higher drivability and traffic efficiency. In [43], real-time management of a hybrid electric vehicle was studied such that the battery had a longer life and the fuel economy was higher. In [44], a thermal management of the battery of electric vehicles was developed so that the temperature of the battery was 16% lower. The authors of [45] analyzed the power flow between photovoltaic power plants and EVs, while in [46], the authors analyzed the voltage control of a distribution network with distributed generation units and EVs that were charging. An overview of the configurations and technical requirements for the implementation of vehicle-to-X was presented in [47], while in [48], machine learning algorithms were used in order to determine the state of charge of batteries. In [49], a load frequency control method was developed, while in [50,51,52], the integration of electric vehicles in the power grid was studied considering different options, such as fuel cells and PV power plants. In [53], the charging behavior of electric vehicles was studied, while in [54], an evaluation of the profitability of vehicle-to-home installations, optimal configuration and energy performance was studied, considering different types of homes and storage options. The results showed that vehicle-to-home is profitable for households with short EV absence times, large available areas for PV installation, and high power demand.

This paper is a further study of [55], in which the analyses were performed for a test system with 13 buses for one day. The authors of [55] analyzed the power demand, active power losses and the voltage level in the cases when the EVs were not connected to the system or when they were connected in different charging scenarios. The EVs were connected to a single bus. The charging scenarios considered EVs from different manufacturers, and the charging of the EVs was performed simultaneously or at different hours of the day from home or from charging stations.

The contributions of this paper are:

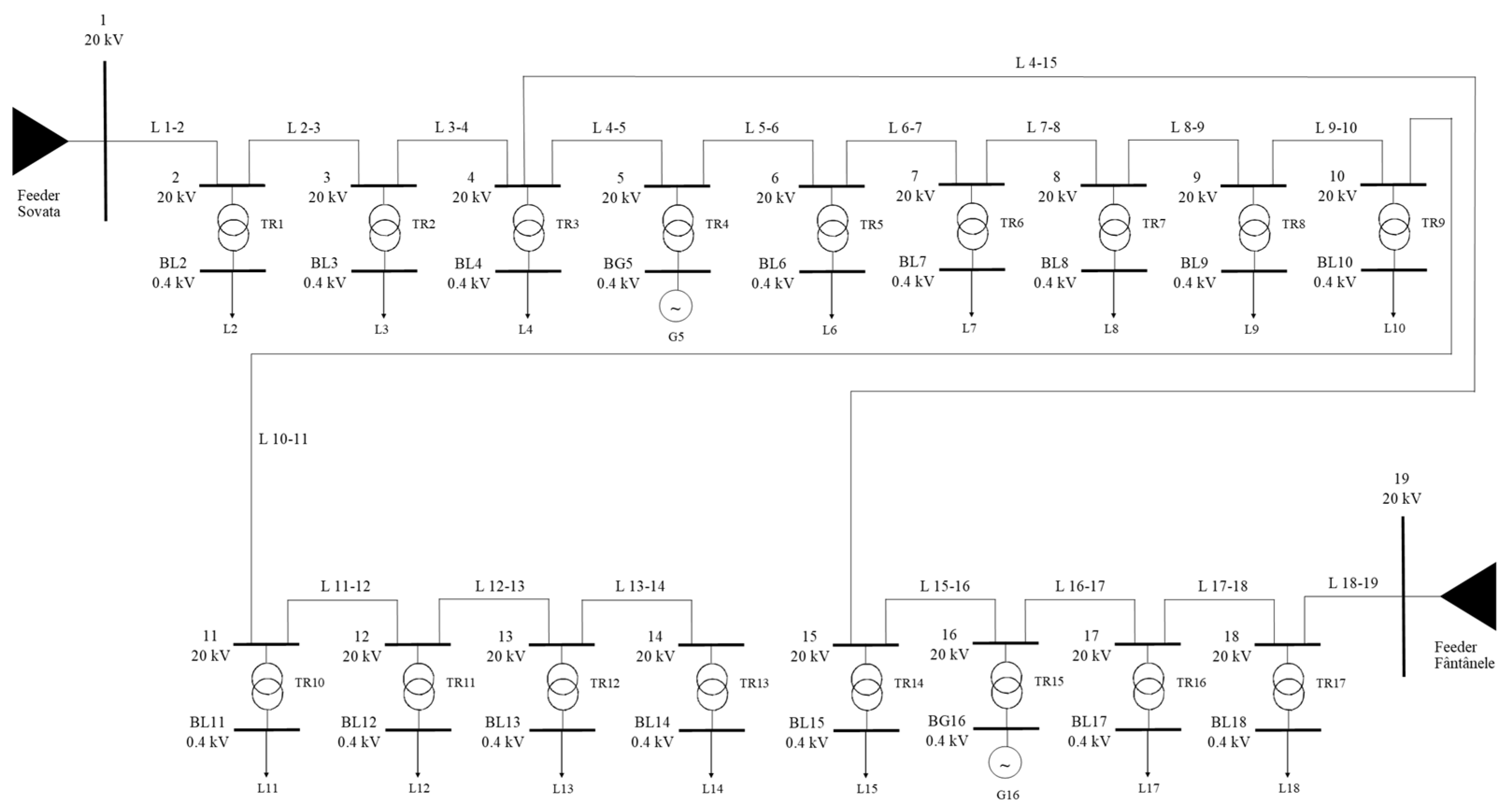
• The study will be performed for a real power line located in the Mureș County, Romania, namely the Sovata–Fântânele power line. Other researchers have considered test systems in most of their studies, while in the cases where real systems have been considered, the approach has been to manage the charging such that the power network is not affected.
• The power line has two and fifteen loads (two photovoltaic (PV) power plants connected in Ghindari and Sângeorgiu de Pădure, respectively). The power supplied by the PV power plants and the power demand of the loads determined with the power meters located at the consumer location will be taken into account in the studies performed.
• The electric vehicles (EVs) were connected in different points (buses) of the power line. Compared to the work of other researchers who considered only one supply option, three supply options for the power line were considered. In addition, two seasons (summer and winter) and different charging scenarios for the EVs were considered, while other researchers had a different approach, i.e., charging was performed in a controlled manner in their studies. The power demand of the EVs will be added to the demand of loads. The analyses will be performed with the NEPLAN software [56], and the results regarding the power losses and voltage level will be obtained.

The paper is structured as follows. Section 2 presents the data of the Sovata–Fântânele power line and of the EVs. Section 3 presents the results and discussion of the results. Section 4 presents the conclusions.

2. Materials and Methods

The load flow analysis, which was performed with the NEPLAN software, is based on the Newton–Raphson method.

The power losses can be determined with the following equations:

ΔS_ik = ΔP_ik + j·ΔQ_ik = S_ik + S_ki

(1)

where ΔS_ik represents the apparent power losses from bus i to bus k in kVA, ΔP_ik represents the active power losses from bus i to bus k in kW, ΔQ_ik represents the reactive power losses from bus i to bus k in kVAr, S_ik represents the apparent power flow from bus i to bus k in kVA, while S_ki represents the apparent power flow from bus k to bus i in kVA. S_ik and S_ki can be expressed as:

S_ik = V_i · (V_i* − V_k*) · Y_ik

(2)

S_ki = V_k · (V_k* − V_i*) · Y_ki

(3)

where V_i represents the voltage at bus i in kV, V_k represents the voltage at bus k in kV, Y_ik and Y_ki represent the non-diagonal components of admittance matrix in S. Y_ik and Y_ki are equal to the admittance of the branch that connects bus i and bus k, considered with the minus sign.

One condition that must be respected according to the technical regulations in Romania is the bus voltage between limits:

V_min ≤ V ≤ V_max

(4)

where V_min represents the bus minimum voltage, which is 0.9 (90%) of the nominal voltage at the respective bus, while V_max represents the bus maximum voltage, which is 1.1 (110%) of the nominal voltage at the respective bus in Romania for networks with voltages below 110 kV. The nominal values for the bus voltage are 20 and 0.4 kV, which represent 1 p.u. depending on the bus; the feeders are connected at 20 kV, while the generators and loads are connected at 0.4 kV. In this paper, the voltage level results will be presented in percent (%) of the nominal voltage.

The one-line diagram for the 20/0.4 kV Sovata–Fântânele power line is presented in Figure 1. The power line is located in Mureș County, Romania.

The power line has 2 feeders, 2 PV power plants and 15 loads. The power line section is 95 mm². Bus 1 and bus 19 are slack buses. The loads represent the communities (villages) that are connected to the power line. The two feeders are located in Sovata and in Fântânele. Thus, the loads connected at the power line can be supplied either from Sovata, from Fântânele, or from Sovata and Fântânele.

The two photovoltaic (PV) power plants located in Ghindari with an installed power of 2.3 MW (G5), and Sângeorgiu de Pădure with an installed power of 2.85 MW (G16), are connected to the power line. The Ghindari PV power plant has 5250 solar panels located on approximately 2.6 acres. The Sângeorgiu de Pădure PV power plant has 13,524 solar panels located on approximately 6.8 acres.

The average power supplied by the PV power plant from Ghindari is 1.2 MW, while average power supplied by the PV power plant from Sângeorgiu de Pădure is 2 MW.

Table 1. Feeder/generator data.

Feeder/Generator Connected at Bus	V (p.u.)	P (kW)
1	1	-
G5	1	1200
G16	1	2000
19	1	-

presents the feeder and PV power plant data.

In the study, we considered the seasons with the highest and lowest output from the PV power plants, namely summer and winter. During these seasons, the power is supplied by the PV power plants, which is presented in Figure 2.

The active and reactive power demand of the loads connected to the power line was measured with the power meters located at the consumer premises.

Table 2. Load data.

Load	Active Power Demand (kW)	Reactive Power Demand (kVAr)
L2	633	475
L3	476	375
L4	56	42
L6	420	315
L7	125	94
L8	56	42
L9	196	147
L10	35	26
L11	196	147
L12	40	30
L13	35	26
L14	56	42
L15	287	215
L17	734	550
L18	1387	1040

presents the load data. In

Table 3. Load scale factor.

Hour (h)	Load Scale Factor for Summer	Load Scale Factor for Winter
1	0.5717	0.7071
2	0.5682	0.7129
3	0.5765	0.7359
4	0.6177	0.7992
5	0.6651	0.8792
6	0.6854	0.9366
7	0.695	0.962
8	0.6989	0.965
9	0.7078	0.9516
10	0.7164	0.9445
11	0.7089	0.9401
12	0.7054	0.9242
13	0.7059	0.9187
14	0.7065	0.9301
15	0.7041	0.9699
16	0.7056	0.9841
17	0.7159	0.9754
18	0.7437	0.9435
19	0.7103	0.8862
20	0.6533	0.7769
21	0.6089	0.7861
22	0.584	0.7446
23	0.5679	0.7228
24	0.5691	0.7096

is presented the load scale factor for summer and winter used to calculate the power demand for a day.

The length of the power line between buses is presented in

Table 4. Length of the power line between buses.

Power Line between Bus and Bus	Length (km)
1–2	8.3
2–3	5.3
3–4	4.3
4–5	0.1
4–15	3.8
5–6	0.1
6–7	4.1
7–8	5.8
8–9	2.6
9–10	4.5
10–11	1.2
11–12	6
12–13	5.6
13–14	2.4
15–16	8.1
16–17	7.6
17–18	7.6
18–19	6.7

.

To this power line, the following PHEV and BEVs are considered: Toyota Prius PHEV, Renault Zoe, Nissan Leaf, BMW i3, Volkswagen e-Golf and Dacia Spring, which represent the models with the highest sales in Romania.

The battery capacity of the selected EVs is presented in

Table 5. Battery capacity of EVs.

Electric Vehicle	Battery Capacity (kWh)
Toyota Prius PHEV	8.8
Renault Zoe	41
Nissan Leaf	40
BMW i3	33.2
Volkswagen e-Golf	35.8
Dacia Spring	26.8

, while

Table 6. Charging time of EVs.

Electric Vehicle	Charging Time at Home (2.3 kW) (h)	Charging Time at Regular 22 kW Charging Station (h)	Charging Time at Fast 50 kW Charging Station (h)
Toyota Prius PHEV	4	3	2
Renault Zoe	19	2	0.75
Nissan Leaf	19	7	0.5
BMW i3	14	3	0.25
Volkswagen e-Golf	16.5	5.25	0.7
Dacia Spring	13.75	5	1

presents the charging time.

Considering the fact that charging at home or at a regular station has a limited impact on the power line due to the lower amount of power that is required during charging over a longer time period, charging will be performed at a fast station, therefore the scenarios that will be considered are:

• charging at a fast station starting at 2:00 (scenario 1);
• charging at a fast station starting at 5:00 (scenario 2);
• charging at a fast station starting at 9:00 (scenario 3);
• charging at a fast station starting at 12:00 (scenario 4);
• charging at a fast station starting at 15:00 (scenario 5);
• charging at a fast station starting at 18:00 (scenario 6);
• charging at a fast station starting at 22:00 (scenario 7).

3. Results and Discussion

The analyses were performed with the NEPLAN software. The simulations performed considered the following:

• power line supplied from Sovata and Fântânele;
• power line supplied from Sovata;
• power line supplied from Fântânele.

It was first performed with no EVs connected, and then with the EVs connected to the buses, with the lowest voltage values considering the charging scenarios.

3.1. EVs Not Connected

The results considering the EVs not connected to the power line are presented in Figure 3 (power losses), Figure 4 (voltage level) and

Table 7. Bus voltages without EVs.

Bus	Bus Voltage Level for Power Line Supplied from Sovata and Fântânele (%)	Bus Voltage Level for Power Line Supplied from Sovata (%)	Bus Voltage Level for Power Line Supplied from Fântânele (%)
BL2	97.73	97.3	95.85
BL3	98.06	97.36	96.46
BL4	99.25	98.34	97.89
BL6	98.19	97.27	96.81
BL7	98.93	98.02	97.57
BL8	99	98.09	97.64
BL9	98.54	97.62	97.17
BL10	98.94	98.03	97.58
BL11	98.47	97.55	97.1
BL12	98.89	97.97	97.52
BL13	98.88	97.97	97.52
BL14	98.82	97.9	97.45
BL15	98.63	97.49	97.42
BL17	97.33	95.2	96.75
BL18	95.33	92.57	95.07

.

It can be observed from Figure 3 that, in the case of the EVs that are not connected, the power losses are lower if the power line is supplied from Sovata and Fântânele. It can be observed from Figure 4 that the voltage level is at 100% for the feeders in the case of the EVs that are not connected if the power line is supplied from Sovata and Fântânele. If the line is supplied from only one feeder, the voltage level is lower. If we compare the voltage level of the buses to which the EVs will be connected in the case of the power line that is supplied from both feeders, the highest voltage level is at bus BL9, while the lowest voltage is at bus BL18.

The EVs will be connected at buses with the lowest voltage levels; therefore, the EVS will be connected simultaneously at buses BL2, BL17 and BL18. Next, 60 EVs (10 pairs of six) will be connected at each of these buses; thus, the power demand will be higher.

3.2. EVs Connected and Charging (Scenario 1)

The results for scenario 1 are presented in

Table 8. Power losses at 2:00 (scenario 1).

Power Losses (kW, kVar)	Power Line Supplied from Sovata and Fântânele	Power Line Supplied from Sovata	Power Line Supplied from Fântânele
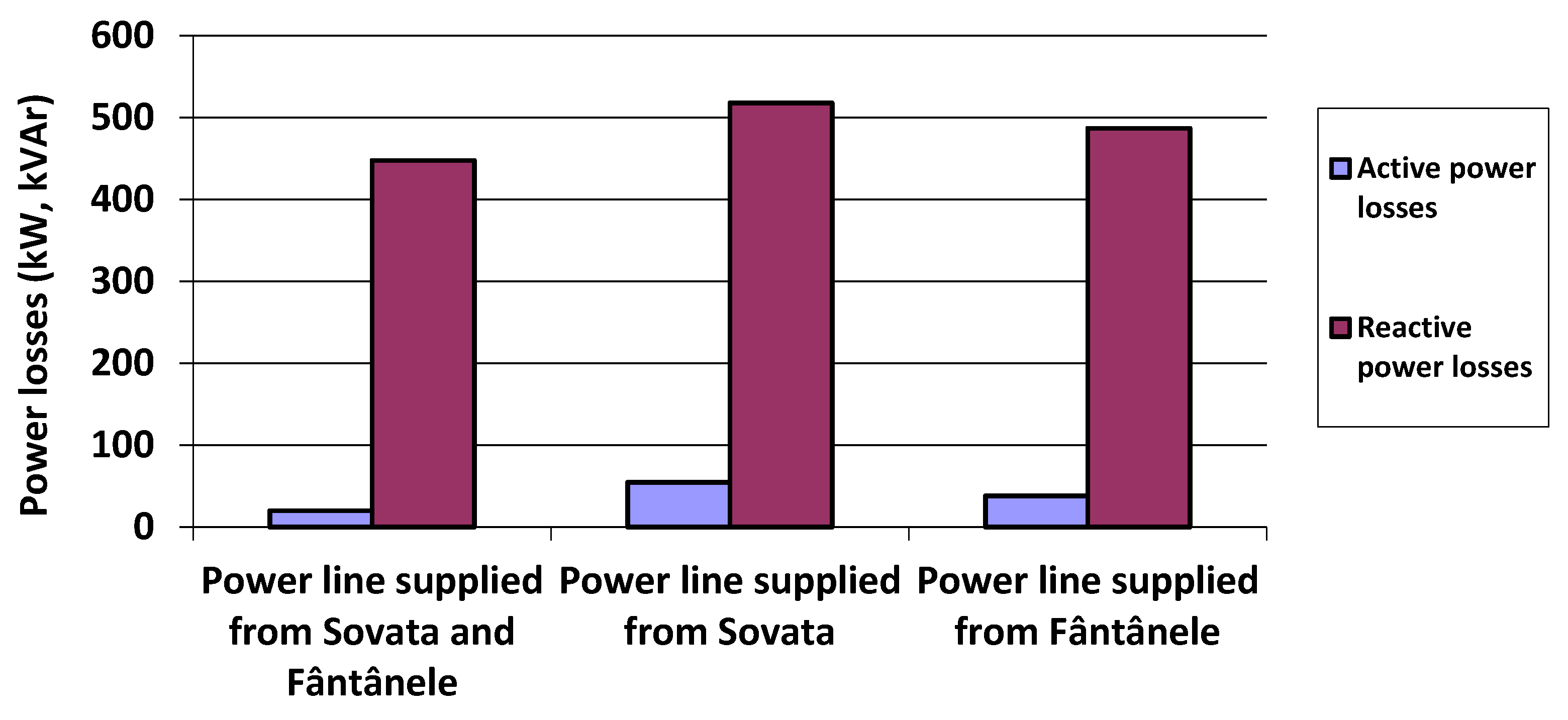
Active power losses with no EVs (summer)	12.18	46.78	39.82
Reactive power losses with no EVs (summer)	83.03	127.34	117.48
Active power losses with EVs (summer)	65.37	338.76	224.98
Reactive power losses with EVs (summer)	766.81	1167.52	990.68
Active power losses with no EVs (winter)	18.79	114.83	61.86
Reactive power losses with no EVs (winter)	128.34	72.93	182.44
Active power losses with EVs (winter)	78.94	409.41	275.11
Reactive power losses with EVs (winter)	883.02	1376.79	1160.25

and

Table 9. Power losses at 3:00 (scenario 1).

Power Losses (kW, kVar)	Power Line Supplied from Sovata and Fântânele	Power Line Supplied from Sovata	Power Line Supplied from Fântânele
Active power losses with no EVs (summer)	12.55	48.21	41.04
Reactive power losses with no EVs (summer)	85.53	131.25	121.05
Active power losses with EVs (summer)	13.19	51.43	43.3
Reactive power losses with EVs (summer)	92.02	141.15	129.63
Active power losses with no EVs (winter)	20.06	78.03	66.14
Reactive power losses with no EVs (winter)	137.12	212.59	195.06
Active power losses with EVs (winter)	20.86	82.43	69.01
Reactive power losses with EVs (winter)	145.21	226.49	205.86

(power losses) and

Table 10. Voltage level at 2:00 (scenario 1).

Bus	Bus Voltage Level for Power Line Supplied from Sovata and Fântânele (%)	Bus Voltage Level for Power Line Supplied from Sovata (%)	Bus Voltage Level for Power Line Supplied from Fântânele (%)
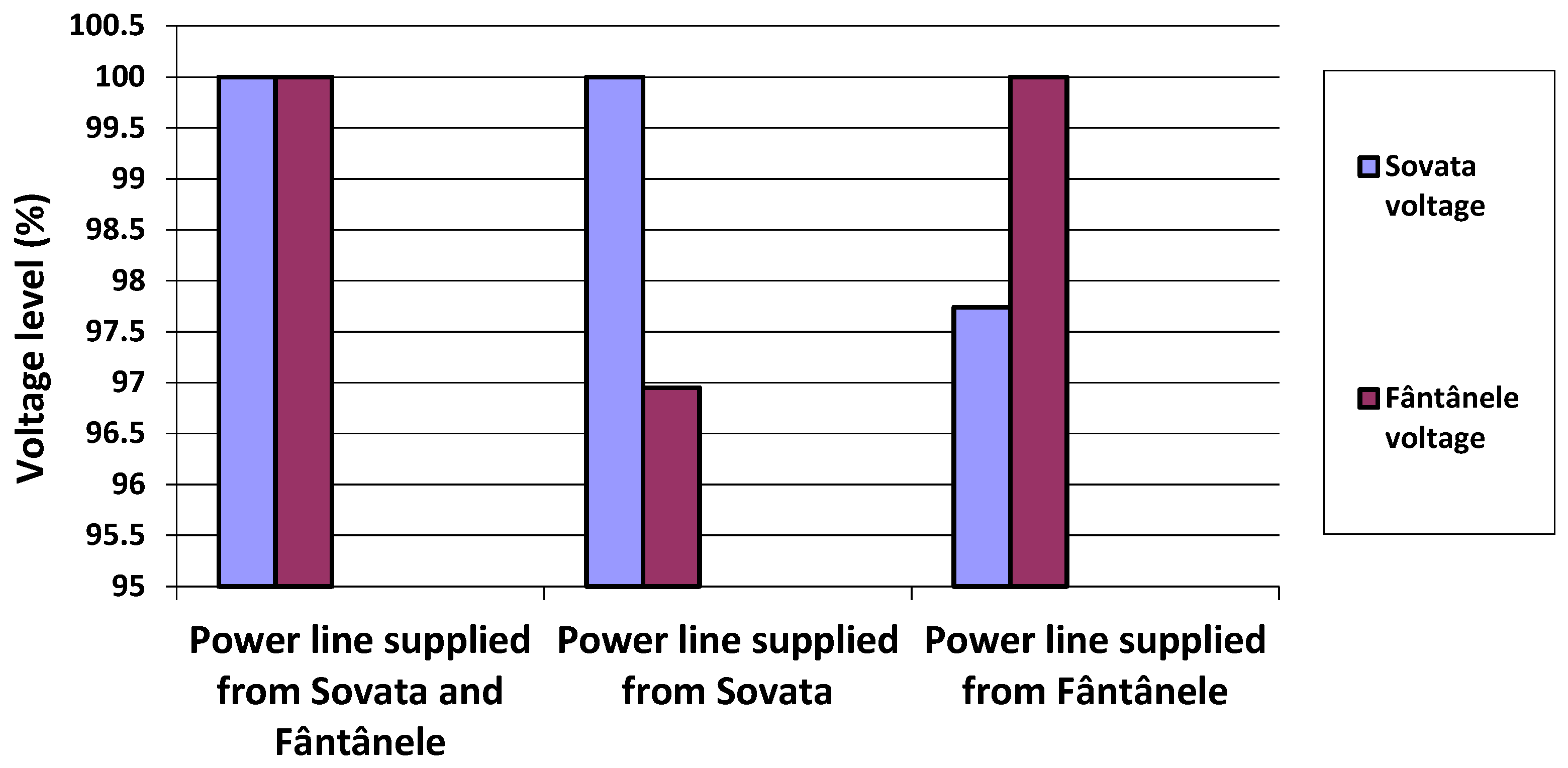
Sovata (no EVs in summer)	100	100	97.46
Fântânele (no EVs in summer)	100	97.15	100
BL2 (no EVs in summer)	98.57	98.11	96.4
BL17 (no EVs in summer)	98.24	96.17	97.5
BL18 (no EVs in summer)	97.32	94.76	96.98
Sovata (EVs in summer)	100	100	94.64
Fântânele (EVs in summer)	100	93.01	100
BL2 (EVs in summer)	97.8	96.63	93.15
BL17 (EVs in summer)	97.15	91.93	95.53
BL18 (EVs in summer)	96.35	89.91	95.61
Sovata (no EVs in winter)	100	100	96.83
Fântânele (no EVs in winter)	100	96.43	100
BL2 (no EVs in winter)	98.22	97.64	95.5
BL17 (no EVs in winter)	97.81	95.21	96.88
BL18 (no EVs in winter)	96.65	93.42	96.22
Sovata (EVs in winter)	100	100	93.94
Fântânele (EVs in winter)	100	92.15	100
BL2 (EVs in winter)	97.42	96.09	92.13
BL17 (EVs in winter)	96.67	90.77	94.83
BL18 (EVs in winter)	95.6	88.28	94.75

and

Table 11. Voltage level at 3:00 (scenario 1).

Bus	Bus Voltage Level for Power Line Supplied from Sovata and Fântânele (%)	Bus Voltage Level for Power Line Supplied from Sovata (%)	Bus Voltage Level for Power Line Supplied from Fântânele (%)
Sovata (no EVs in summer)	100	100	97.42
Fântânele (nos EVs in summer)	100	97.11	100
BL2 (no EVs in summer)	98.55	98.08	96.35
BL17 (no EVs in summer)	98.22	96.11	97.46
BL18 (no EVs in summer)	97.28	94.68	96.94
Sovata (EVs in summer)	100	100	97.36
Fântânele (EVs in summer)	100	97.02	100
BL2 (EVs in summer)	98.54	98.05	96.28
BL17 (EVs in summer)	98.2	96.03	97.43
BL18 (EVs in summer)	97.26	94.59	96.91
Sovata (no EVs in winter)	100	100	96.72
Fântânele (no EVs in winter)	100	96.31	100
BL2 (no EVs in winter)	98.16	97.56	95.35
BL17 (no EVs in winter)	97.74	95.04	96.77
BL18 (no EVs in winter)	96.53	93.19	96.09
Sovata (EVs in winter)	100	100	96.66
Fântânele (EVs in winter)	100	96.22	100
BL2 (EVs in winter)	98.15	97.53	95.28
BL17 (EVs in winter)	97.72	94.96	96.74
BL18 (EVs in winter)	96.51	93.08	96.07

(voltage level).

The power losses in scenario 1 are lower if the power line is supplied from Sovata and Fântânele. If the power line is supplied from one feeder, then the power losses are lower in scenario 1 when the line is supplied from Fântânele. When the EVs are connected and the power line is supplied from both feeders at 2:00, the active power losses are 536.72% higher during summer and 420.11% higher during winter, while at 3:00, the active power losses are 4.7% higher during summer and 3.17% higher during winter. This is caused by power demand of the EVs, which is lower at 3:00. The voltage level is at 100% for the feeders in scenario 1 in the case that the EVs are connected or not and the power line is supplied from Sovata and Fântânele. If the line is supplied from one feeder, then the voltage level is lower. The voltage level of the buses to which the EVs were connected in the case of the power line being supplied from both feeders is between limits. If the power line is supplied from Sovata at 2:00, then the voltage level at bus BL18 drops from 94.76% to 89.91% during summer and from 93.42% to 88.28% during winter, below the regulated limit due to the high distance from the feeder to the load.

3.3. EVs Connected and Charging (Scenario 2)

The results for scenario 2 are presented in

Table 12. Power losses at 5:00 (scenario 2).

Power Losses (kW, kVar)	Power Line Supplied from Sovata and Fântânele	Power Line Supplied from Sovata	Power Line Supplied from Fântânele
Active power losses with no EVs (summer)	16.78	64.49	55.15
Reactive power losses with no EVs (summer)	114.59	176.91	162.67
Active power losses with EVs (summer)	74.96	38.85	260.36
Reactive power losses with EVs (summer)	849.14	1315.17	1105.95
Active power losses with no EVs (winter)	29.01	114.83	96.37
Reactive power losses with no EVs (winter)	198.73	313.99	284.14
Active power losses with EVs (winter)	98.05	511.05	346.57
Reactive power losses with EVs (winter)	1044.15	1676.93	1398.9

and

Table 13. Power losses at 6:00 (scenario 2).

Power Losses (kW, kVar)	Power Line Supplied from Sovata and Fântânele	Power Line Supplied from Sovata	Power Line Supplied from Fântânele
Active power losses with no EVs (summer)	14.89	50.52	40.24
Reactive power losses with no EVs (summer)	120.91	183.36	168.57
Active power losses with EVs (summer)	15.59	53.90	42.59
Reactive power losses with EVs (summer)	128.64	195.46	179.04
Active power losses with no EVs (winter)	33.08	131.72	110.24
Reactive power losses with no EVs (winter)	210.04	360.39	324.98
Active power losses with EVs (winter)	34.13	137.29	114.48
Reactive power losses with EVs (winter)	237.42	377.50	340.96

(power losses) and

Table 14. Voltage level at 5:00 (scenario 2).

Bus	Bus Voltage Level for Power Line Supplied from Sovata and Fântânele (%)	Bus Voltage Level for Power Line Supplied from Sovata (%)	Bus Voltage Level for Power Line Supplied from Fântânele (%)
Sovata (no EVs in summer)	100	100	97.01
Fântânele (no EVs in summer)	100	96.64	100
BL2 (no EVs in summer)	98.32	97.77	96.07
BL17 (no EVs in summer)	97.93	95.48	97.27
BL18 (no EVs in summer)	96.84	93.8	96.71
Sovata (EVs in summer)	100	100	94.14
Fântânele (EVs in summer)	100	92.39	100
BL2 (EVs in summer)	97.53	96.24	92.42
BL17 (EVs in summer)	96.8	91.1	95.03
BL18 (EVs in summer)	95.81	88.75	95
Sovata (no EVs in winter)	100	100	96.04
Fântânele (no EVs in winter)	100	95.52	100
BL2 (no EVs in winter)	97.78	97.05	94.37
BL17 (no EVs in winter)	97.27	93.98	96.1
BL18 (no EVs in winter)	95.8	91.69	95.26
Sovata (EVs in winter)	100	100	93.06
Fântânele (EVs in winter)	100	91.04	100
BL2 (EVs in winter)	96.64	95.41	90.84
BL17 (EVs in winter)	96.07	89.28	93.94
BL18 (EVs in winter)	94.65	86.15	93.66

and

Table 15. Voltage level at 6:00 (scenario 2).

Bus	Bus Voltage Level for Power Line Supplied from Sovata and Fântânele (%)	Bus Voltage Level for Power Line Supplied from Sovata (%)	Bus Voltage Level for Power Line Supplied from Fântânele (%)
Sovata (no EVs in summer)	100	100	97.66
Fântânele (no EVs in summer)	100	97.16	100
BL2 (no EVs in summer)	98.31	97.91	96.38
BL17 (no EVs in summer)	97.94	95.98	97.35
BL18 (no EVs in summer)	96.77	94.25	96.5
Sovata (EVs in summer)	100	100	97.61
Fântânele (EVs in summer)	100	97.09	100
BL2 (EVs in summer)	98.3	97.89	96.33
BL17 (EVs in summer)	97.92	95.91	97.32
BL18 (EVs in summer)	96.75	94.17	96.48
Sovata (no EVs in winter)	100	100	95.76
Fântânele (no EVs in winter)	100	95.2	100
BL2 (no EVs in winter)	97.63	96.84	93.38
BL17 (no EVs in winter)	97.09	93.55	95.83
BL18 (no EVs in winter)	95.5	91.08	94.92
Sovata (EVs in winter)	100	100	95.7
Fântânele (EVs in winter)	100	95.1	100
BL2 (EVs in winter)	97.62	96.81	93.9
BL17 (EVs in winter)	97.06	93.46	95.78
BL18 (Evs in winter)	95.48	90.97	94.89

(voltage level).

The power losses in scenario 2 are lower if the power line is supplied from Sovata and Fântânele. When the EVs are connected and the power line is supplied from both feeders at 5:00, the active power losses are 446.72% higher during summer and 337.98% higher during winter, while at 6:00, the active power losses are 4.7% higher during summer and 3.17% higher during winter. The voltage level is at 100% for the feeders in scenario 2 in the case that the EVs are connected or not, and the power line is supplied from Sovata and Fântânele. If the line is supplied from only one feeder, the voltage level is lower. The lowest voltage level values are when the line is supplied from Sovata. The voltage level of the buses to which the EVs were connected in the case that the power line is supplied from both feeders is between limits in scenario 2. If the power line is supplied from Sovata at 5:00 during summer, then the voltage level at bus BL18 is 88.75% and 1.25% below the regulated limit due to the high distance from the feeder to the load. If the power line is supplied from Sovata at 5:00, then the voltage level at bus BL18 drops from 93.8% to 88.75% during summer, while during winter, the voltage level at bus BL17 drops from 93.98% to 89.28% and bus BL18 drops from 91.69% to 86.15%, therefore below the regulated limits due to high distance from the feeder to the load and the power demand, which is 13.2% higher compared with summer. The voltage at bus BL17 was between limits at 5:00 due to power supplied by the PV power plants.

3.4. EVs Connected and Charging (Scenario 3)

The results for scenario 3 are presented in

Table 16. Power losses at 9:00 (scenario 3).

Power Losses (kW, kVar)	Power Line Supplied from Sovata and Fântânele	Power Line Supplied from Sovata	Power Line Supplied from Fântânele
Active power losses with no EVs (summer)	9.2	27	18.45
Reactive power losses with no EVs (summer)	194.05	227.45	213.86
Active power losses with EVs (summer)	46.56	237.67	134.19
Reactive power losses with EVs (summer)	923.82	1275.15	1092.44
Active power losses with no EVs (winter)	28.56	98.78	77.75
Reactive power losses with no EVs (winter)	232.6	360.66	326.21
Active power losses with EVs (winter)	96.8	462.39	307.14
Reactive power losses with EVs (winter)	1117.97	1789.72	1502.08

and

Table 17. Power losses at 10:00 (scenario 3).

Power Losses (kW, kVar)	Power Line Supplied from Sovata and Fântânele	Power Line Supplied from Sovata	Power Line Supplied from Fântânele
Active power losses with no EVs (summer)	10.39	25.8	18.97
Reactive power losses with no EVs (summer)	255.65	284.37	272.7
Active power losses with EVs (summer)	10.49	26.67	19.14
Reactive power losses with EVs (summer)	262.91	295.45	280.51
Active power losses with no EVs (winter)	26.37	91.63	71
Reactive power losses with no EVs (winter)	228.23	347.86	314.08
Active power losses with EVs (winter)	27.29	96.21	74.08
Reactive power losses with EVs (winter)	238.85	364.87	328.42

(power losses) and

Table 18. Voltage level at 9:00 (scenario 3).

Bus	Bus Voltage Level for Power Line Supplied from Sovata and Fântânele (%)	Bus Voltage Level for Power Line Supplied from Sovata (%)	Bus Voltage Level for Power Line Supplied from Fântânele (%)
Sovata (no EVs in summer)	100	100	98.35
Fântânele (no EVs in summer)	100	97.78	100
BL2 (no EVs in summer)	98.4	98.09	97.03
BL17 (no EVs in summer)	98.1	96.56	97.68
BL18 (no EVs in summer)	96.76	94.79	96.57
Sovata (EVs in summer)	100	100	96.15
Fântânele (EVs in summer)	100	94.29	100
BL2 (EVs in summer)	97.63	96.8	94.39
BL17 (EVs in summer)	97.01	92.95	96
BL18 (EVs in summer)	95.74	90.52	95.27
Sovata (no EVs in winter)	100	100	96.74
Fântânele (no EVs in winter)	100	96.01	100
BL2 (no EVs in winter)	97.66	97.09	94.94
BL17 (no EVs in winter)	97.14	94.35	96.3
BL18 (no EVs in winter)	95.46	91.87	95.08
Sovata (EVs in winter)	100	100	94.4
Fântânele (EVs in winter)	100	92.23	100
BL2 (EVs in winter)	96.83	95.67	92.06
BL17 (EVs in winter)	95.96	90.35	94.45
BL18 (EVs in winter)	94.29	87.03	93.59

and

Table 19. Voltage level at 10:00 (scenario 3).

Bus	Bus Voltage Level for Power Line Supplied from Sovata and Fântânele (%)	Bus Voltage Level for Power Line Supplied from Sovata (%)	Bus Voltage Level for Power Line Supplied from Fântânele (%)
Sovata (no EVs in summer)	100	100	98.57
Fântânele (no EVs in summer)	100	97.98	100
BL2 (no EVs in summer)	98.42	98.14	97.24
BL17 (no EVs in summer)	98.15	96.75	97.78
BL18 (no EVs in summer)	96.75	94.96	96.59
Sovata (EVs in summer)	100	100	98.52
Fântânele (EVs in summer)	100	97.9	100
BL2 (EVs in summer)	98.41	98.12	97.19
BL17 (EVs in summer)	98.13	96.68	97.75
BL18 (EVs in summer)	96.73	94.87	96.56
Sovata (no EVs in winter)	100	100	96.84
Fântânele (no EVs in winter)	100	96.12	100
BL2 (no EVs in winter)	97.69	97.14	95.06
BL17 (no EVs in winter)	97.18	94.47	96.37
BL18 (no EVs in winter)	95.51	92.01	95.14
Sovata (EVs in winter)	100	100	96.79
Fântânele (EVs in winter)	100	96.04	100
BL2 (EVs in winter)	97.68	97.12	95.01
BL17 (EVs in winter)	97.16	94.4	96.34
BL18 (EVs in winter)	95.49	91.92	95.11

(voltage level).

The power losses in scenario 3 are lower if the power line is supplied from Sovata and Fântânele. If the power line is supplied from one feeder, then the power losses are lower in scenario 3 when the line is supplied from Fântânele. When the EVs are connected and the power line is supplied from both feeders at 9:00, the active power losses are 506.08% higher during summer and 338.93% higher during winter, while at 10:00, the active power losses are 1% higher during summer and 1.03% higher during winter. This is caused by the power demand of the EVs, which is lower at 10:00. The voltage level of the buses to which the EVs were connected in the case of the power line that is supplied from both feeders is between limits in scenario 3. If the line is supplied from one feeder, then the voltage level is lower. If the power line is supplied from Sovata at 9:00, then the voltage level at bus BL18 drops from 91.87% to 87.03% during winter, below the regulated limits due to high distance from the feeder to the load.

3.5. EVs Connected and Charging (Scenario 4)

The results for scenario 4 are presented in

Table 20. Power losses at 12:00 (scenario 4).

Power Losses (kW, kVar)	Power Line Supplied from Sovata and Fântânele	Power Line Supplied from Sovata	Power Line Supplied from Fântânele
Active power losses with no EVs (summer)	13.02	27.07	23.21
Reactive power losses with no EVs (summer)	329.38	354.03	346.12
Active power losses with EVs (summer)	36.72	177.89	88.999
Reactive power losses with EVs (summer)	1039.6	1313.58	1152.02
Active power losses with no EVs (winter)	22.88	79.8	60.32
Reactive power losses with no EVs (winter)	219.78	324.88	293.08
Active power losses with EVs (winter)	84.9	412.65	266.01
Reactive power losses with EVs (winter)	1082.77	1687.45	1417.35

and

Table 21. Power losses at 13:00 (scenario 4).

Power Losses (kW, kVar)	Power Line Supplied from Sovata and Fântânele	Power Line Supplied from Sovata	Power Line Supplied from Fântânele
Active power losses with no EVs (summer)	13.16	27.25	23.47
Reactive power losses with no EVs (summer)	332.67	357.33	349.51
Active power losses with EVs (summer)	13.08	27.37	23
Reactive power losses with EVs (summer)	338.45	365.21	356.35
Active power losses with no EVs (winter)	22.79	79.4	60.17
Reactive power losses with no EVs (winter)	216.79	321.16	289.84
Active power losses with EVs (winter)	23.62	83.56	62.93
Reactive power losses with EVs (winter)	227.01	337.22	303.41

(power losses) and

Table 22. Voltage level at 12:00 (scenario 4).

Bus	Bus Voltage Level for Power Line Supplied from Sovata and Fântânele (%)	Bus Voltage Level for Power Line Supplied from Sovata (%)	Bus Voltage Level for Power Line Supplied from Fântânele (%)
Sovata (no EVs in summer)	100	100	98.86
Fântânele (no EVs in summer)	100	98.26	100
BL2 (no EVs in summer)	98.5	98.25	97.56
BL17 (no EVs in summer)	98.26	97.05	97.96
BL18 (no EVs in summer)	96.84	95.3	96.71
Sovata (EVs in summer)	100	100	96.7
Fântânele (EVs in summer)	100	94.82	100
BL2 (EVs in summer)	97.74	96.99	94.96
BL17 (EVs in summer)	97.17	93.5	96.32
BL18 (EVs in summer)	95.82	91.1	95.43
Sovata (no EVs in winter)	100	100	97.03
Fântânele (no EVs in winter)	100	96.32	100
BL2 (no EVs in winter)	97.77	97.24	95.3
BL17 (no EVs in winter)	97.28	94.72	96.52
BL18 (no EVs in winter)	95.63	92.32	95.28
Sovata (EVs in winter)	100	100	94.72
Fântânele (EVs in winter)	100	92.59	100
BL2 (EVs in winter)	96.94	95.84	92.46
BL17 (EVs in winter)	96.11	90.78	94.7
BL18 (EVs in winter)	94.48	87.57	93.82

and

Table 23. Voltage level at 13:00 (scenario 4).

Bus	Bus Voltage Level for Power Line Supplied from Sovata and Fântânele (%)	Bus Voltage Level For Power Line Supplied from Sovata (%)	Bus Voltage Level for Power Line Supplied from Fântânele (%)
Sovata (no EVs in summer)	100	100	98.87
Fântânele (no EVs in summer)	100	98.26	100
BL2 (no EVs in summer)	98.5	98.26	97.56
BL17 (no EVs in summer)	98.26	97.06	97.97
BL18 (no EVs in summer)	96.84	95.3	96.71
Sovata (EVs in summer)	100	100	98.82
Fântânele (EVs in summer)	100	98.19	100
BL2 (EVs in summer)	98.49	98.23	97.51
BL17 (EVs in summer)	98.24	96.99	97.94
BL18 (EVs in summer)	96.82	95.22	96.68
Sovata (no EVs in winter)	100	100	97.04
Fântânele (no EVs in winter)	100	96.33	100
BL2 (no EVs in winter)	97.78	97.26	95.32
BL17 (no EVs in winter)	97.3	94.74	96.54
BL18 (no EVs in winter)	95.66	92.36	95.31
Sovata (EVs in winter)	100	100	96.99
Fântânele (EVs in winter)	100	96.26	100
BL2 (EVs in winter)	97.77	97.23	95.26
BL17 (EVs in winter)	97.28	94.66	96.5
BL18 (EVs in winter)	95.64	92.27	95.29

(voltage level).

The power losses in scenario 4 are lower if the power line is supplied from Sovata and Fântânele. When EVs are connected and the power line is supplied from both feeders at 12:00, the active power losses are 282.02% higher during summer and 371.06% higher during winter, while at 13:00, the active power losses are 1% lower during summer and 1.03% higher during winter due to the power demand and power supplied by the PV power plants. The voltage level is at 100% for the feeders in scenario 4 in the case that the EVs are connected or not, and the power line is supplied from Sovata and Fântânele. If the line is supplied from only one feeder, then the voltage level is lower in scenario 4. The voltage level of the buses to which the EVs were connected in the case of the power line that is supplied from both feeders is between limits. If the power line is supplied from Sovata at 12:00 during summer, then the voltage level at bus BL18 drops from 92.32% to 87.575, below the regulated limits due to high distance from the feeder to the load.

3.6. EVs Connected and Charging (Scenario 5)

The results for scenario 5 are presented in

Table 24. Power losses at 15:00 (scenario 5).

Power Losses (kW, kVar)	Power Line Supplied from Sovata and Fântânele	Power Line Supplied from Sovata	Power Line Supplied from Fântânele
Active power losses with no EVs (summer)	10.6	24.99	19.08
Reactive power losses with no EVs (summer)	266.14	292.67	282.26
Active power losses with EVs (summer)	39.59	198.67	104.04
Reactive power losses with EVs (summer)	983	1284.37	1114.78
Active power losses with no EVs (winter)	29.13	101.05	79.08
Reactive power losses with no EVs (winter)	241.65	373.36	337.12
Active power losses with EVs (winter)	97.65	467.11	309.3
Reactive power losses with EVs (winter)	1136.48	1818.74	1524.67

and

Table 25. Power losses at 16:00 (scenario 5).

Power Losses (kW, kVar)	Power Line Supplied from Sovata and Fântânele	Power Line Supplied from Sovata	Power Line Supplied from Fântânele
Active power losses with no EVs (summer)	9.17	26.4	18.12
Reactive power losses with no EVs (summer)	198.67	231.02	217.76
Active power losses with EVs (summer)	9.4	27.83	18.76
Reactive power losses with EVs (summer)	206	240.65	226.11
Active power losses with no EVs (winter)	32.11	110.85	88.12
Reactive power losses with no EVs (winter)	251.16	394.73	357.09
Active power losses with EVs (winter)	33.16	116.04	91.67
Reactive power losses with EVs (winter)	262.37	413.14	372.55

(power losses) and

Table 26. Voltage level at 15:00 (scenario 5).

Bus	Bus Voltage Level for Power Line Supplied from Sovata and Fântânele (%)	Bus Voltage Level for Power Line Supplied from Sovata (%)	Bus Voltage Level for Power Line Supplied from Fântânele (%)
Sovata (no EVs in summer)	100	100	98.67
Fântânele (no EVs in summer)	100	98.08	100
BL2 (no EVs in summer)	98.46	98.2	97.36
BL17 (no EVs in summer)	98.2	96.88	97.86
BL18 (no EVs in summer)	96.82	95.12	96.67
Sovata (EVs in summer)	100	100	96.49
Fântânele (EVs in summer)	100	94.62	100
BL2 (EVs in summer)	97.7	96.92	94.75
BL17 (EVs in summer)	97.12	93.3	96.21
BL18 (EVs in summer)	95.8	90.9	95.38
Sovata (no EVs in winter)	100	100	96.69
Fântânele (no EVs in winter)	100	95.95	100
BL2 (no EVs in winter)	97.62	97.04	94.86
BL17 (no EVs in winter)	97.09	94.26	96.23
BL18 (no EVs in winter)	95.37	91.71	94.98
Sovata (EVs in winter)	100	100	94.35
Fântânele (EVs in winter)	100	92.15	100
BL2 (EVs in winter)	96.78	95.61	91.97
BL17 (EVs in winter)	95.9	90.24	94.38
BL18 (EVs in winter)	94.19	86.84	93.48

and

Table 27. Voltage level at 16:00 (scenario 5).

Bus	Bus Voltage Level for Power Line Supplied from Sovata and Fântânele (%)	Bus Voltage Level for Power Line Supplied from Sovata (%)	Bus Voltage Level for Power Line Supplied from Fântânele (%)
Sovata (no EVs in summer)	100	100	98.38
Fântânele (no EVs in summer)	100	97.81	100
BL2 (no EVs in summer)	98.41	98.1	97.07
BL17 (no EVs in summer)	98.11	96.6	97.7
BL18 (no EVs in summer)	96.77	94.83	96.59
Sovata (EVs in summer)	100	100	98.33
Fântânele (EVs in summer)	100	97.74	100
BL2 (EVs in summer)	98.4	98.08	97.02
BL17 (EVs in summer)	98.09	96.53	97.67
BL18 (EVs in summer)	96.76	94.75	96.57
Sovata (no EVs in winter)	100	100	96.56
Fântânele (no EVs in winter)	100	95.8	100
BL2 (no EVs in winter)	97.57	96.97	94.69
BL17 (no EVs in winter)	97.02	94.08	96.13
BL18 (no EVs in winter)	95.29	91.49	94.88
Sovata (EVs in winter)	100	100	96.51
Fântânele (EVs in winter)	100	95.72	100
BL2 (EVs in winter)	97.55	96.94	94.64
BL17 (EVs in winter)	97	94	96.09
BL18 (EVs in winter)	95.27	91.4	94.85

(voltage level).

The power losses in scenario 5 are lower if the power line is supplied from Sovata and Fântânele. When the EVs are connected and the power line is supplied from both feeders at 15:00, the active power losses are 274.81% higher during summer and 335.22% higher during winter, while at 16:00, the active power losses are 1.02% higher during summer and 1.03% higher during winter. The voltage level is at 100% for the feeders in scenario 5 in the case that the EVs are connected or not, and the power line is supplied from Sovata and Fântânele. If the line is supplied from only one feeder, the voltage level is lower. The voltage level of the buses to which the EVs were connected in the case of the power line that is supplied from both feeders is between limits. If the power line is supplied from Sovata at 15:00 during summer, then the voltage level at bus BL18 drops from 91.71% to 86.84%, below the regulated limit due to high distance from the feeder to the load.

3.7. EVs Connected and Charging (Scenario 6)

The results for scenario 6 are presented in

Table 28. Power losses at 18:00 (scenario 6).

Power Losses (kW, kVar)	Power Line Supplied from Sovata and Fântânele	Power Line Supplied from Sovata	Power Line Supplied from Fântânele
Active power losses with no EVs (summer)	14.26	49.03	36.95
Reactive power losses with no EVs (summer)	145.2	207.63	189.67
Active power losses with EVs (summer)	67.71	333.63	212.43
Reactive power losses with EVs (summer)	914.26	1387.95	1175.29
Active power losses with no EVs (winter)	33.59	133.84	111.98
Reactive power losses with no EVs (winter)	230.35	366.22	330.1
Active power losses with EVs (winter)	106.11	554.54	377.12
Reactive power losses with EVs (winter)	1111.02	1805.03	1499.43

and

Table 29. Power losses at 19:00 (scenario 6).

Power Losses (kW, kVar)	Power Line Supplied from Sovata and Fântânele	Power Line Supplied from Sovata	Power Line Supplied from Fântânele
Active power losses with no EVs (summer)	14.93	50.97	39.89
Reactive power losses with no EVs (summer)	129.71	193.4	177.25
Active power losses with EVs (summer)	15.61	54.32	42.18
Reactive power losses with EVs (summer)	137.69	205.74	187.93
Active power losses with no EVs (winter)	29.5	116.83	98.01
Reactive power losses with no EVs (winter)	202.06	319.46	288.97
Active power losses with EVs (winter)	30.48	122.04	101.6
Reactive power losses with EVs (winter)	212.04	335.46	302.38

(power losses) and

Table 30. Voltage level at 18:00 (scenario 6).

Bus	Bus Voltage Level for Power Line Supplied from Sovata and Fântânele (%)	Bus Voltage Level for Power Line Supplied from Sovata (%)	Bus Voltage Level for Power Line Supplied from Fântânele (%)
Sovata (no EVs in summer)	100	100	97.66
Fântânele (no EVs in summer)	100	97.1	100
BL2 (no EVs in summer)	98.2	97.8	96.27
BL17 (no EVs in summer)	97.82	95.81	97.23
BL18 (no EVs in summer)	96.51	93.93	96.23
Sovata (EVs in summer)	100	100	95.41
Fântânele (EVs in summer)	100	93.52	100
BL2 (EVs in summer)	97.43	96.47	93.55
BL17 (EVs in summer)	96.71	92.09	95.5
BL18 (EVs in summer)	95.46	89.52	94.9
Sovata (no EVs in winter)	100	100	95.73
Fântânele (no EVs in winter)	100	95.16	100
BL2 (no EVs in winter)	97.61	96.82	93.93
BL17 (no EVs in winter)	97.06	93.5	95.79
BL18 (no EVs in winter)	95.46	91.01	94.88
Sovata (EVs in winter)	100	100	92.71
Fântânele (EVs in winter)	100	90.6	100
BL2 (EVs in winter)	96.75	95.15	90.33
BL17 (EVs in winter)	95.84	88.68	93.6
BL18 (EVs in winter)	94.27	85.29	93.23

and

Table 31. Voltage level at 19:00 (scenario 6).

Bus	Bus Voltage Level for Power Line Supplied from Sovata and Fântânele (%)	Bus Voltage Level for Power Line Supplied from Sovata (%)	Bus Voltage Level for Power Line Supplied from Fântânele (%)
Sovata (no EVs in summer)	100	100	97.64
Fântânele (no EVs in summer)	100	97.11	100
BL2 (no EVs in summer)	98.26	97.86	96.31
BL17 (no EVs in summer)	97.88	95.89	97.28
BL18 (no EVs in summer)	96.65	94.09	96.38
Sovata (EVs in summer)	100	100	97.59
Fântânele (EVs in summer)	100	97.04	100
BL2 (EVs in summer)	98.25	97.83	96.26
BL17 (EVs in summer)	97.87	95.81	97.25
BL18 (EVs in summer)	96.64	94.01	96.36
Sovata (no EVs in winter)	100	100	96.01
Fântânele (no EVs in winter)	100	95.48	100
BL2 (no EVs in winter)	97.77	97.02	94.33
BL17 (no EVs in winter)	97.25	93.93	96.07
BL18 (no EVs in winter)	95.76	91.62	95.22
Sovata (EVs in winter)	100	100	95.94
Fântânele (EVs in winter)	100	95.39	100
BL2 (EVs in winter)	97.75	96.99	94.26
BL17 (EVs in winter)	97.23	93.84	96.03
BL18 (EVs in winter)	95.74	91.51	95.19

(voltage level).

The power losses in scenario 6 are lower if the power line is supplied from Sovata and Fântânele. When EVs are connected and the power line is supplied from both feeders at 18:00, the active power losses are 474.82% higher during summer and 315.89% higher during winter, while at 19:00, the active power losses are 1.04% higher during summer and 1.03% higher during winter. The voltage level is at 100% for the feeders in scenario 6 in the case of the EVs that are connected or not, and the power line is supplied from Sovata and Fântânele. If the line is supplied from only one feeder, the voltage level is lower. The voltage level of the buses to which the EVs were connected in the case that the power line is supplied from both feeders is between limits. If the power line is supplied from Sovata at 18:00 during summer, then the voltage level at bus BL18 drops from 93.93% to 89.52% during summer and from 91.01% to 86.84% during winter, while for bus BL17, the voltage level drops from 93.5% to 88.68% during winter, below the regulated limit due to high distance from the feeder to the load.

3.8. EVs Connected and Charging (Scenario 7)

The results for scenario 7 are presented in

Table 32. Power losses at 22:00 (scenario 7).

Power Losses (kW, kVar)	Power Line Supplied from Sovata and Fântânele	Power Line Supplied from Sovata	Power Line Supplied from Fântânele
Active power losses with no EVs (summer)	12.89	49.53	42.15
Reactive power losses with no EVs (summer)	87.82	134.83	124.32
Active power losses with EVs (summer)	66.87	346.54	230.52
Reactive power losses with EVs (summer)	779.79	1190.62	1009.52
Active power losses with no EVs (winter)	20.56	80.02	67.8
Reactive power losses with no EVs (winter)	140.52	218	199.96
Active power losses with EVs (winter)	82.39	427.51	287.9
Reactive power losses with EVs (winter)	912.21	1430.28	1203.18

and

Table 33. Power losses at 23:00 (scenario 7).

Power Losses (kW, kVar)	Power Line Supplied from Sovata and Fântânele	Power Line Supplied from Sovata	Power Line Supplied from Fântânele
Active power losses with no EVs (summer)	12.17	46.73	39.78
Reactive power losses with no EVs (summer)	82.95	127.21	117.36
Active power losses with EVs (summer)	12.8	49.9	42.02
Reactive power losses with EVs (summer)	89.34	136.95	125.8
Active power losses with no EVs (winter)	19.34	75.11	63.69
Reactive power losses with no EVs (winter)	132.09	204.6	187.82
Active power losses with EVs (winter)	20.13	79.18	66.54
Reactive power losses with EVs (winter)	140.14	217.07	198.55

(power losses) and

Table 34. Voltage level at 22:00 (scenario 7).

Bus	Bus Voltage Level for Power Line Supplied from Sovata and Fântânele (%)	Bus Voltage Level For Power Line Supplied from Sovata (%)	Bus Voltage Level for Power Line Supplied from Fântânele (%)
Sovata (no EVs in summer)	100	100	97.39
Fântânele (no EVs in summer)	100	97.07	100
BL2 (no EVs in summer)	98.53	98.05	96.3
BL17 (no EVs in summer)	98.19	96.06	97.43
BL18 (no EVs in summer)	97.24	94.61	96.9
Sovata (EVs in summer)	100	100	94.56
Fântânele (EVs in summer)	100	92.91	100
BL2 (EVs in summer)	97.76	96.57	93.03
BL17 (EVs in summer)	97.09	91.8	95.45
BL18 (EVs in summer)	96.26	89.72	95.51
Sovata (no EVs in winter)	100	100	96.68
Fântânele (no EVs in winter)	100	96.26	100
BL2 (no EVs in winter)	98.14	97.53	95.29
BL17 (no EVs in winter)	97.71	94.98	96.73
BL18 (no EVs in winter)	96.49	93.1	96.04
Sovata (EVs in winter)	100	100	93.77
Fântânele (EVs in winter)	100	91.94	100
BL2 (EVs in winter)	97.33	95.97	91.89
BL17 (EVs in winter)	96.56	90.49	94.66
BL18 (EVs in winter)	95.42	87.88	94.55

and

Table 35. Voltage level at 23:00 (scenario 7).

Bus	Bus Voltage Level for Power Line Supplied from Sovata and Fântânele (%)	Bus Voltage Level for Power Line Supplied from Sovata (%)	Bus Voltage Level for Power Line Supplied from Fântânele (%)
Sovata (no EVs in summer)	100	100	97.46
Fântânele (no EVs in summer)	100	97.15	100
BL2 (no EVs in summer)	98.57	98.11	96.4
BL17 (no EVs in summer)	98.24	96.18	97.5
BL18 (no EVs in summer)	97.32	94.77	96.99
Sovata (EVs in summer)	100	100	97.4
Fântânele (EVs in summer)	100	97.06	100
BL2 (EVs in summer)	98.56	98.08	96.34
BL17 (EVs in summer)	98.23	96.09	97.46
BL18 (EVs in summer)	97.31	94.67	96.96
Sovata (no EVs in winter)	100	100	96.78
Fântânele (no EVs in winter)	100	96.38	100
BL2 (no EVs in winter)	98.19	97.6	95.44
BL17 (no EVs in winter)	97.78	95.14	96.83
BL18 (no EVs in winter)	96.6	93.32	96.17
Sovata (EVs in winter)	100	100	96.72
Fântânele (EVs in winter)	100	96.29	100
BL2 (EVs in winter)	98.18	97.58	95.37
BL17 (EVs in winter)	97.76	95.05	96.8
BL18 (EVs in winter)	96.58	93.22	96.14

(voltage level).

The power losses in scenario 7 are lower if the power line is supplied from Sovata and Fântânele. When EVs are connected and the power line is supplied from both feeders at 22:00, the active power losses are 518.77% higher during summer and 400.72% higher during winter, while at 23:00, the active power losses are 1.05% higher during summer and 1.04% higher during winter. The voltage level is at 100% for the feeders in scenario 7 in the case of the EVs that are connected or not, and the power line is supplied from Sovata and Fântânele. If the line is supplied from only one feeder, the voltage level is lower. The voltage level of the buses to which the EVs were connected in the case of the power line that is supplied from both feeders is between limits. If the power line is supplied from Sovata at 22:00, then the voltage level at bus BL18 drops from 94.61% to 89.72% during summer and from 93.1% to 87.88% during winter, below the regulated limits due to high distance from the feeder to the load.

If the results are compared, the lowest power losses for summer and winter considering the EVs connected are in scenario 4, when the PV power plants supply the highest amount of power.

The lowest voltage considering the EVs connected is when the power line is supplied only from Sovata, in most cases at bus BL18 during summer and at buses BL17 and BL18 during winter the voltage, in which it was below the minimum limit of 0.36 kV.

The power supplied by the photovoltaic power plants helps maintain the power losses and voltage levels at corresponding values.

In [55], for the test system with 13 buses, the differences between the power losses were approximately 2% higher in the worst scenarios when the EVs were charging compared with the EVs not charging (not connected), and 0.2% higher in the best scenario when the EVs were charging compared with the EVs charging. Regarding the voltage level, it was also between regulated limits, and it was approximately 0.5% lower in the worst scenario when the EVs were charging compared with the EVs not charging, and 0.1% lower in the best scenario when the EVs were charging compared with the EVs charging.

Thus, if we compare the power losses and voltage level from this paper and those from [55], the differences are significant, the voltage level in this paper is 6% lower in the worst case and is below the regulated limits.

4. Conclusions

Electric vehicles are becoming an important part of everyday life in Romania and everywhere on Earth, with their numbers increasing year after year. Currently, there are three categories of electric vehicles: hybrid, plug-in hybrid and battery-powered, of which only the latter two need to be connected to the main grid such that they can charge. The charging of electric vehicles has an impact on the power system—an impact that can refer to the extra power demand required by these vehicles, power losses, voltage levels, CO₂ emissions or investments required in order to upgrade the power system.

In this paper, we studied and presented the impact of electric vehicles regarding the power losses and voltage levels for a real power line with photovoltaic power plants connected.

First, the power losses and voltage levels were determined for the cases of when the electric vehicles were not connected to the power line. Second, 180 electric vehicles were connected to the power line via buses with the lowest voltage such that the power demand of the respective bus was higher. Considering the fact that the power line has three supply options, namely from both feeders and only from one feeder, the analyses were performed for two seasons (summer and winter), taking into account the power demand for these seasons, compared with the work of other researchers that considered only one supply option. In all cases, if the power line was supplied from the two feeders, the voltage was between the minimum and maximum limits. In the case that the power line was supplied from the feeder in Sovata, the voltage level at the buses farthest from the feeder was in most cases below the regulated limits with approximately 6% in the worst case. The voltage level was higher for summer compared with winter. The power losses were also lower in the case of the power line that was supplied from both feeders. The power losses were lower during summer.

Considering the power line supplied from both feeders, in the cases when the electric vehicles were connected to the three buses and in the case when the electric vehicles were not connected, the power losses were approximately 400% higher in the case of the EVs that were connected and in which the power demand was higher. In addition, the voltage level was slightly lower if the EVs were connected.