Multi-Objective Optimization of the Geometry of a Non-Pneumatic Tire for Three-Dimensional Stiffness Adaptation
Abstract
1. Introduction
2. Numerical Model of NPT
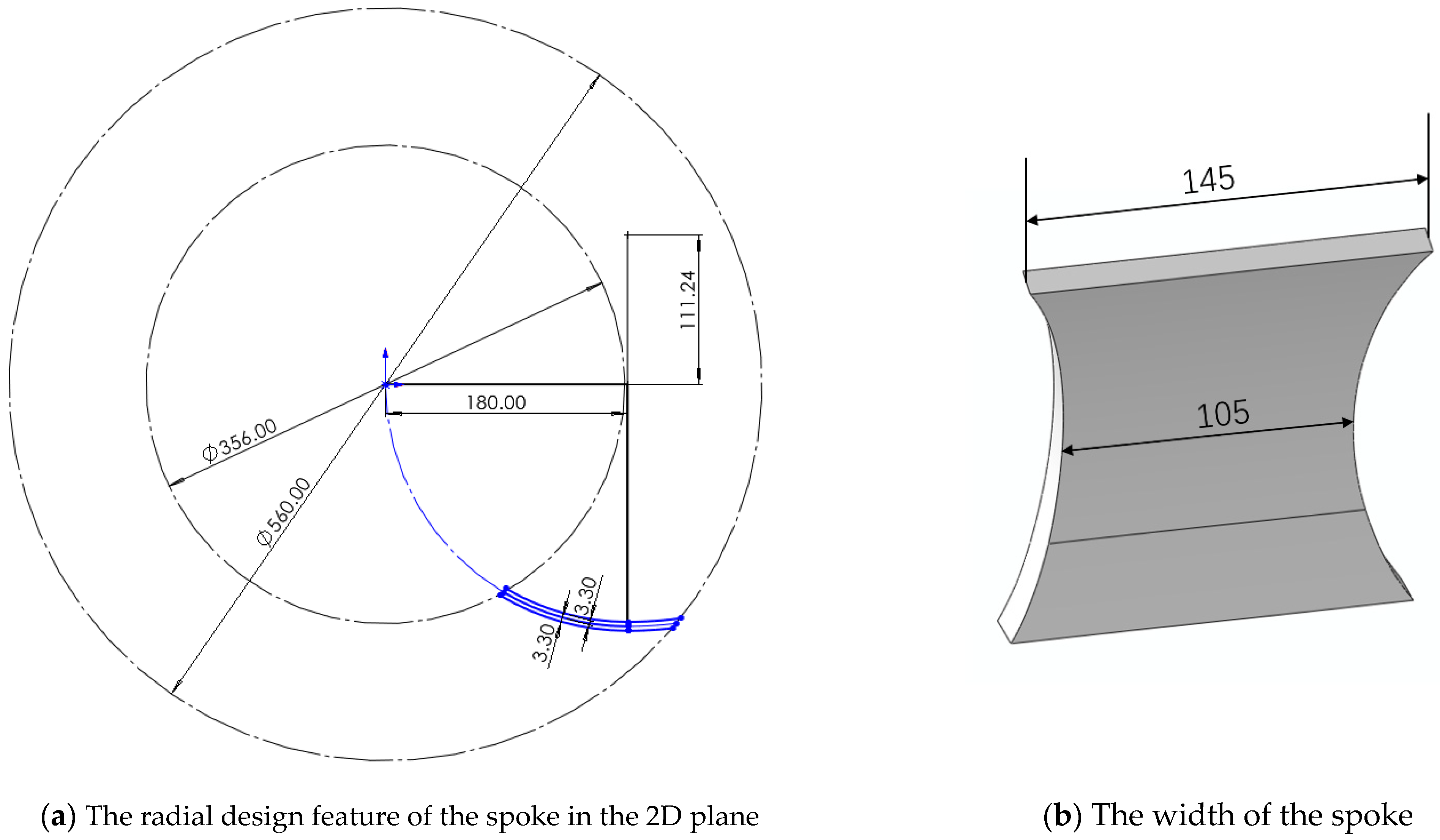
2.1. CAD Models
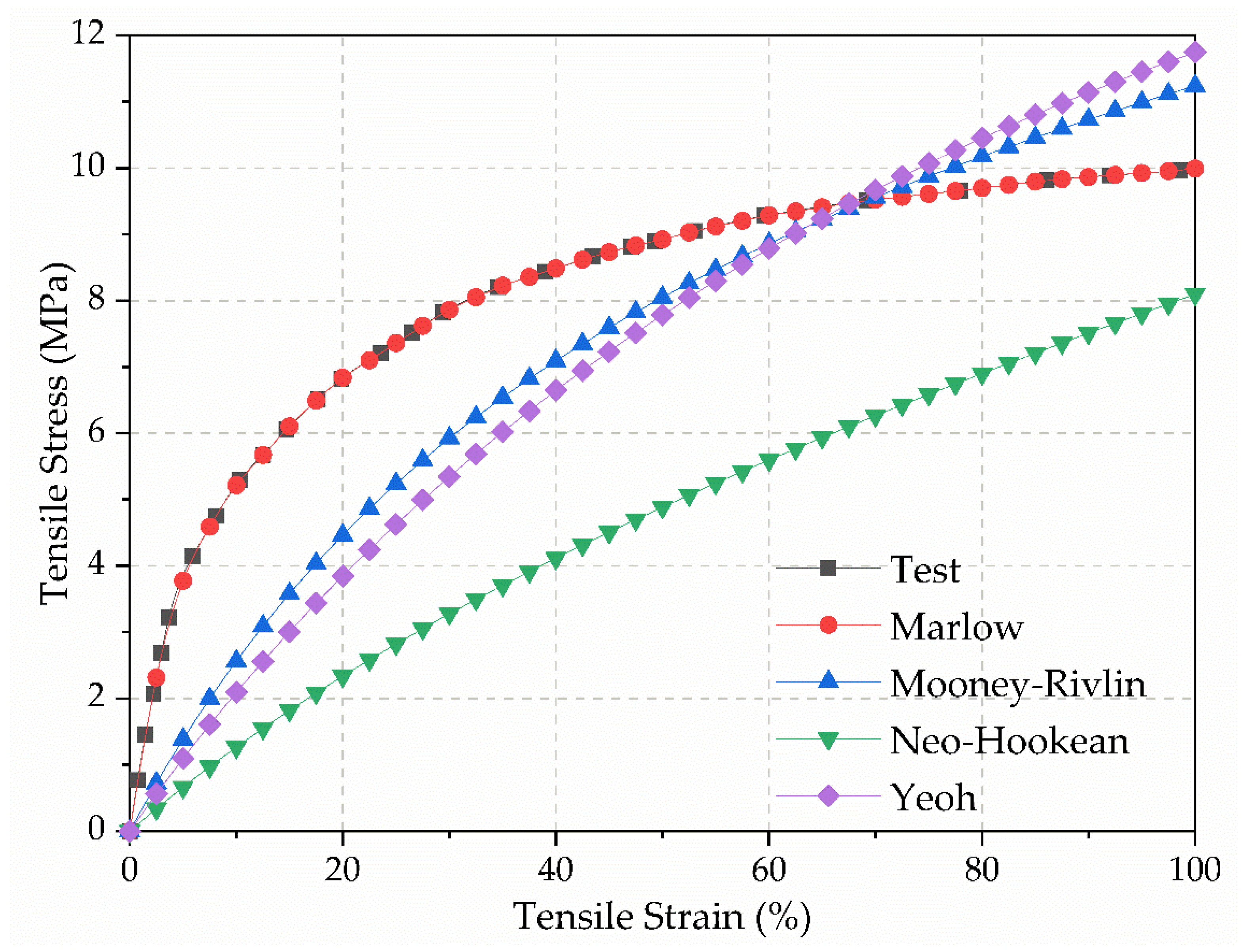
2.2. Material Properties of NPT
2.3. FEA Simulation Details
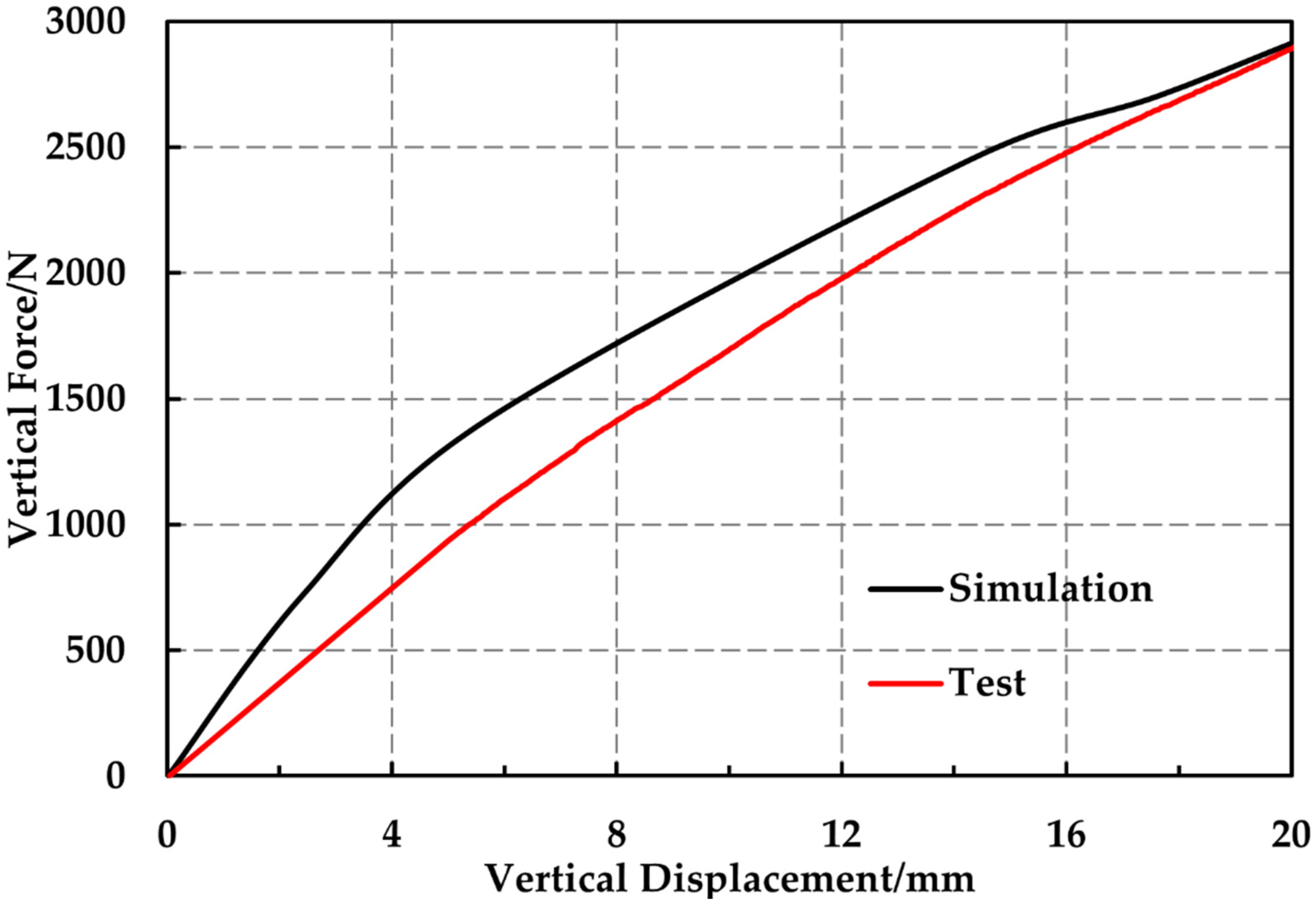
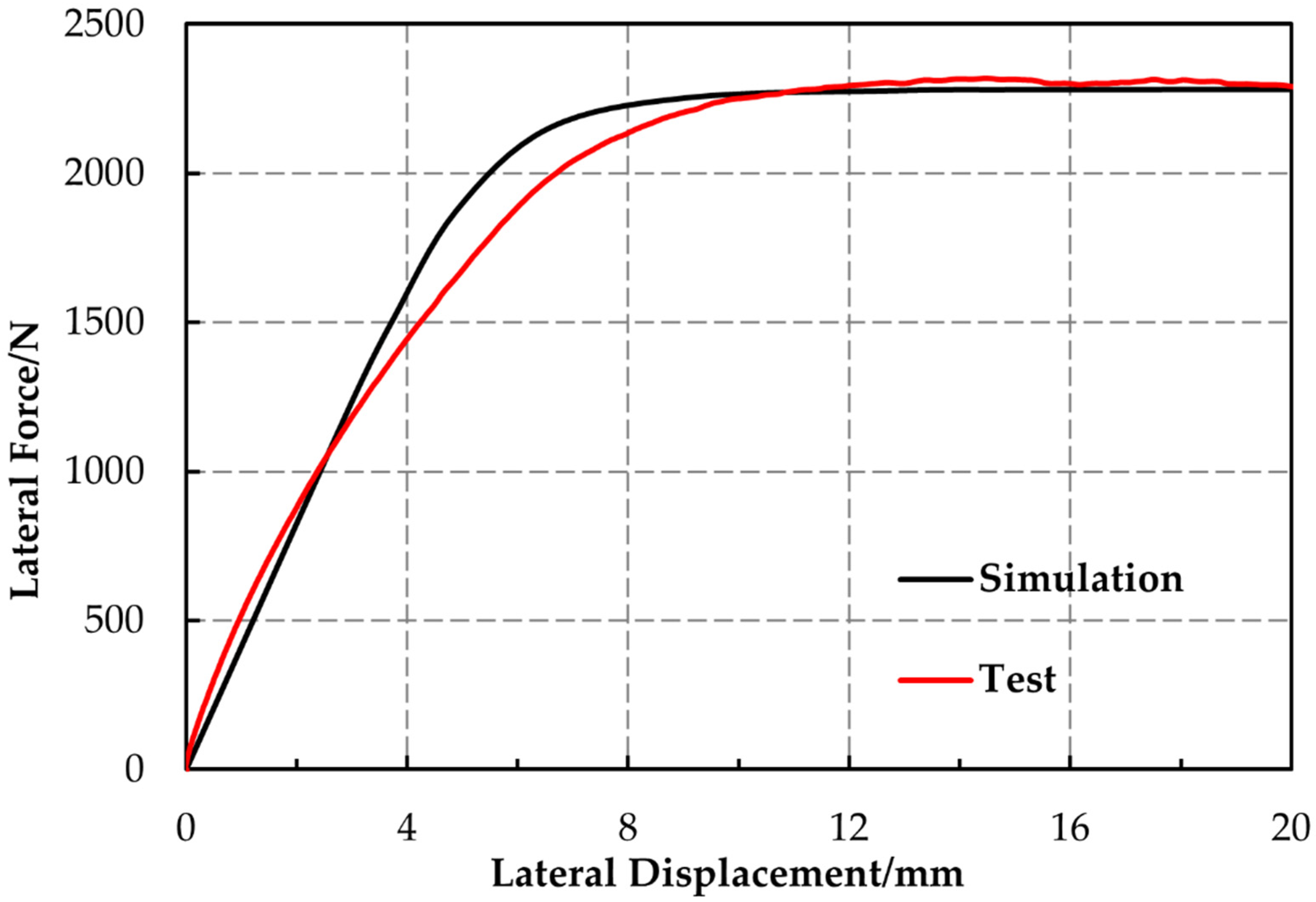
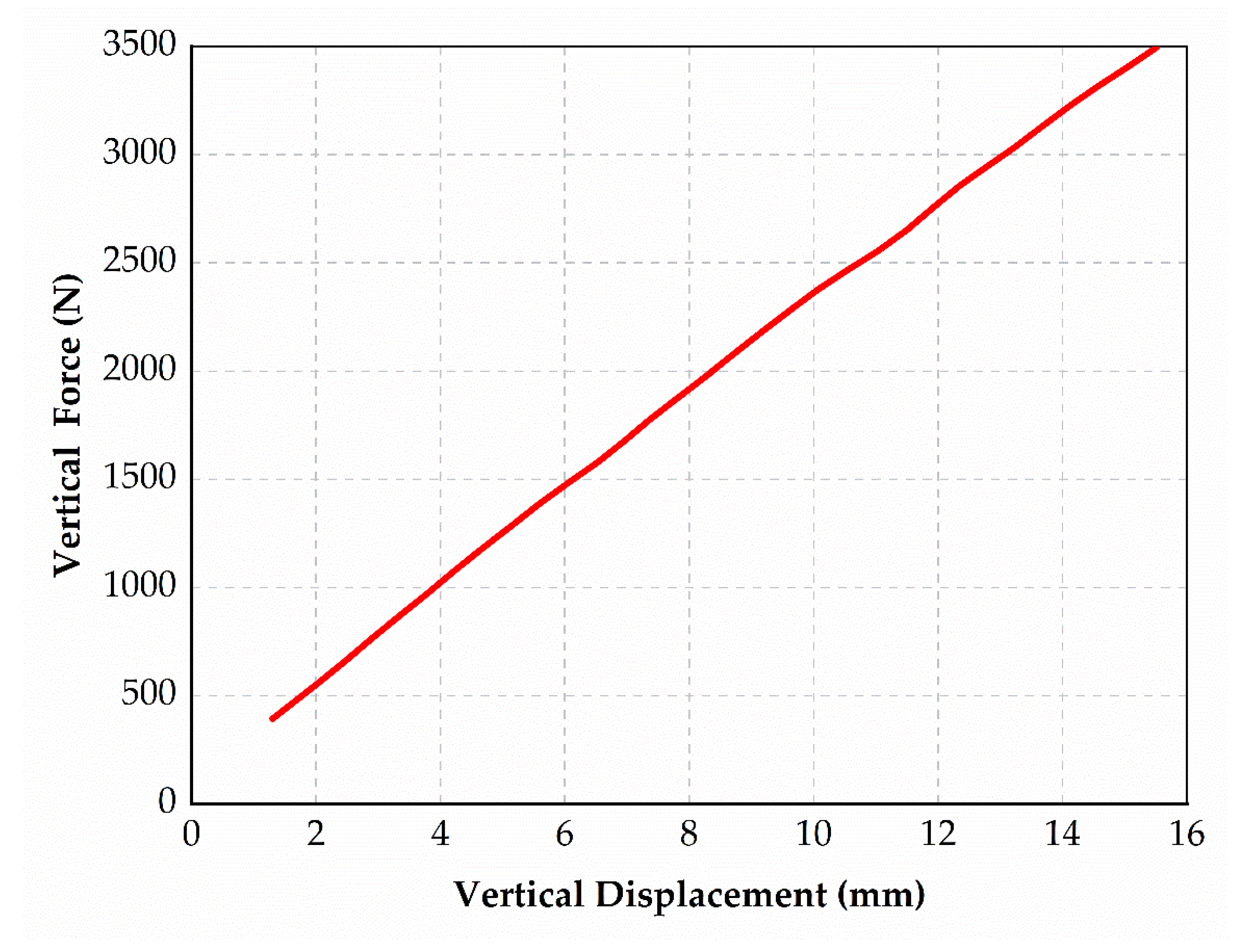
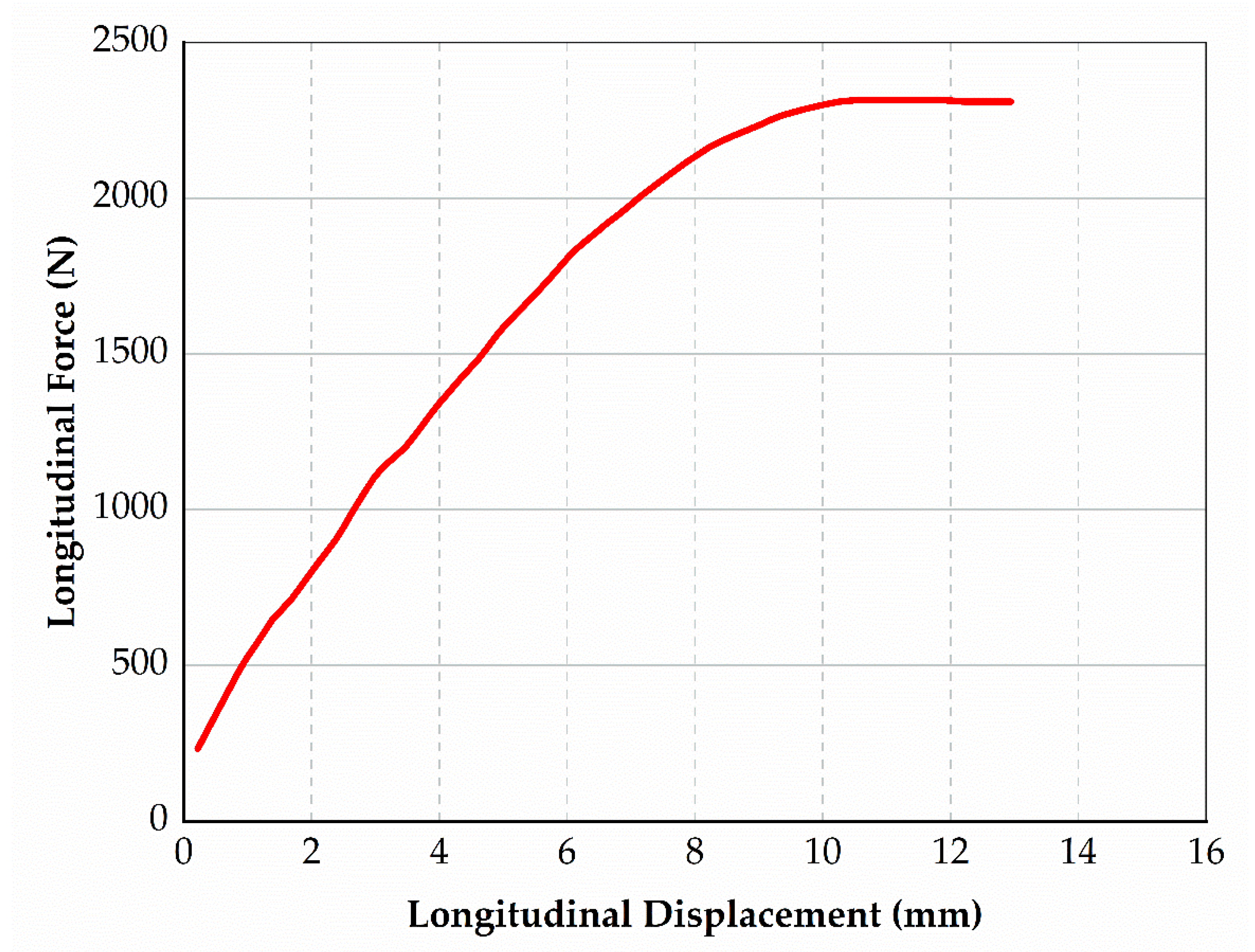
2.4. Experimental Verification
3. Parametric Studies of Geometry
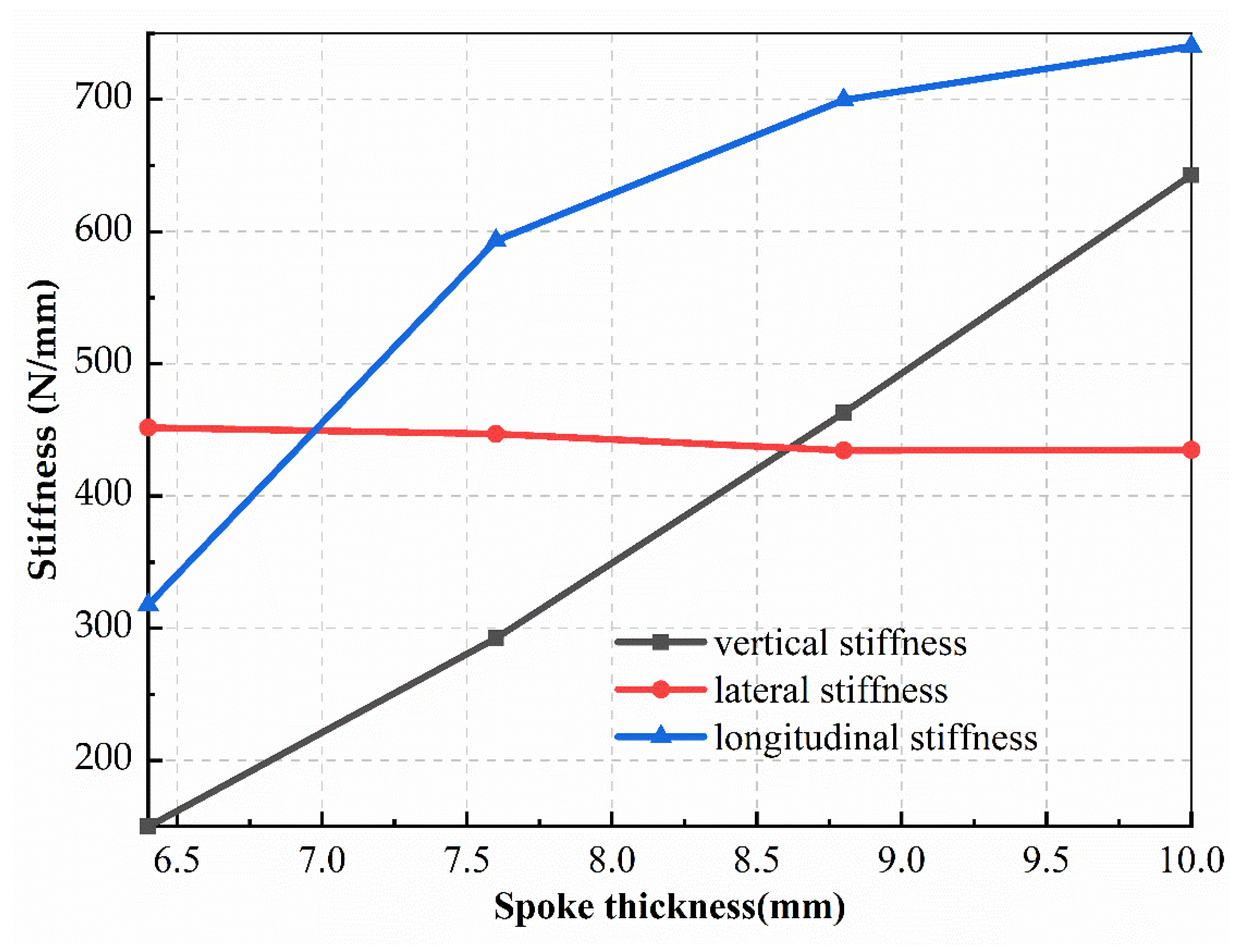
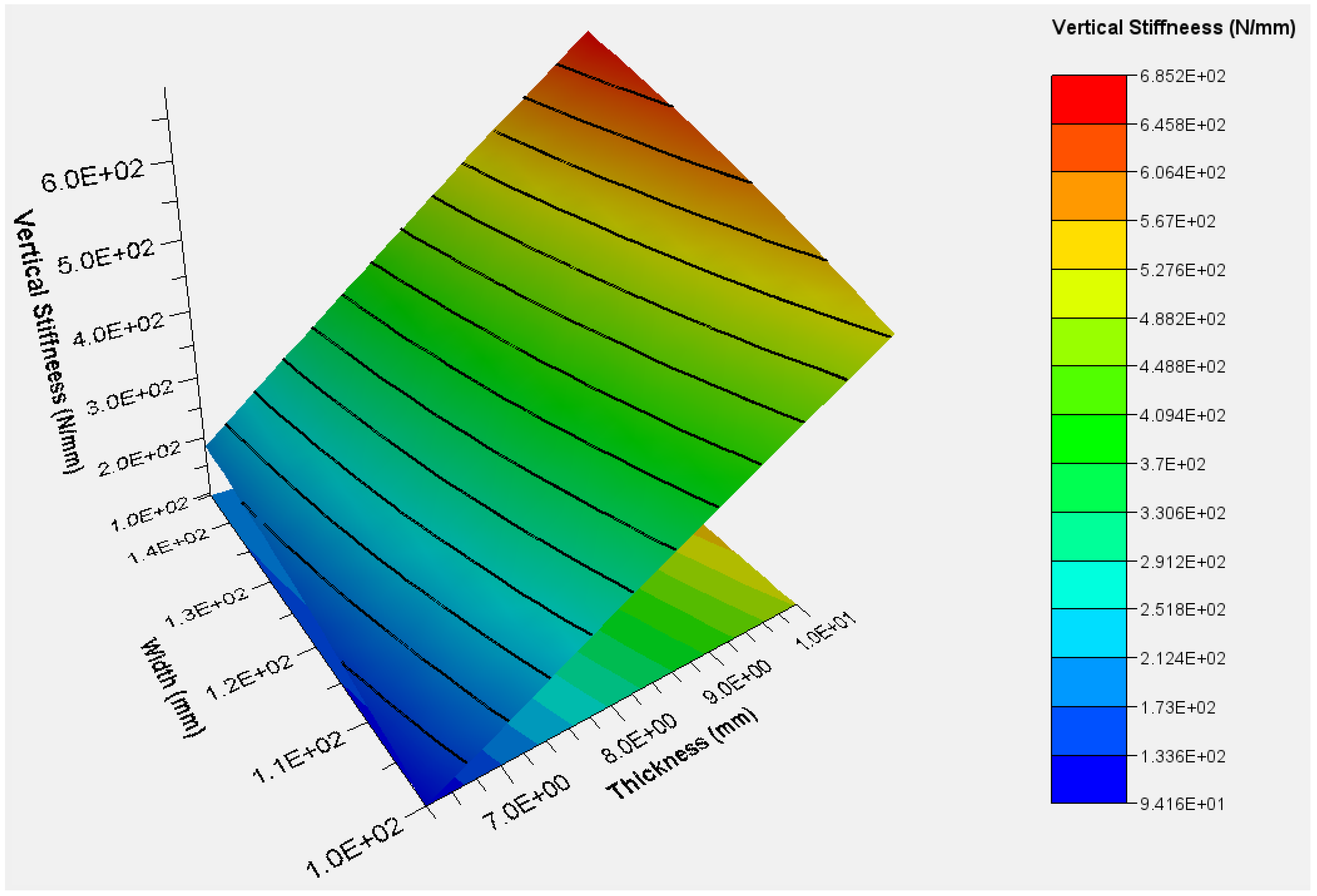
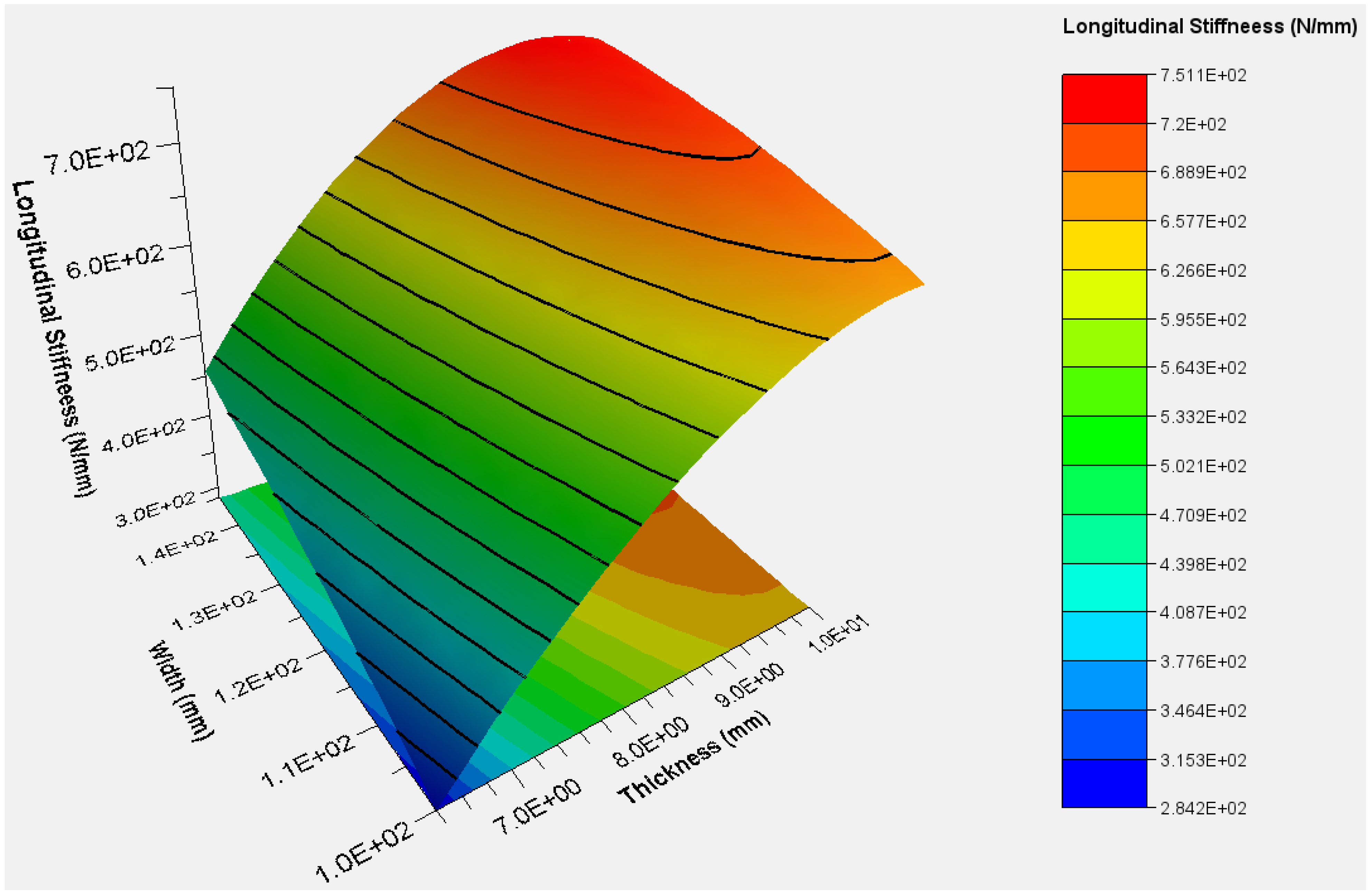
3.1. Effects of Spoke Thickness on Three-Dimensional Stiffnesses of FS-NPT
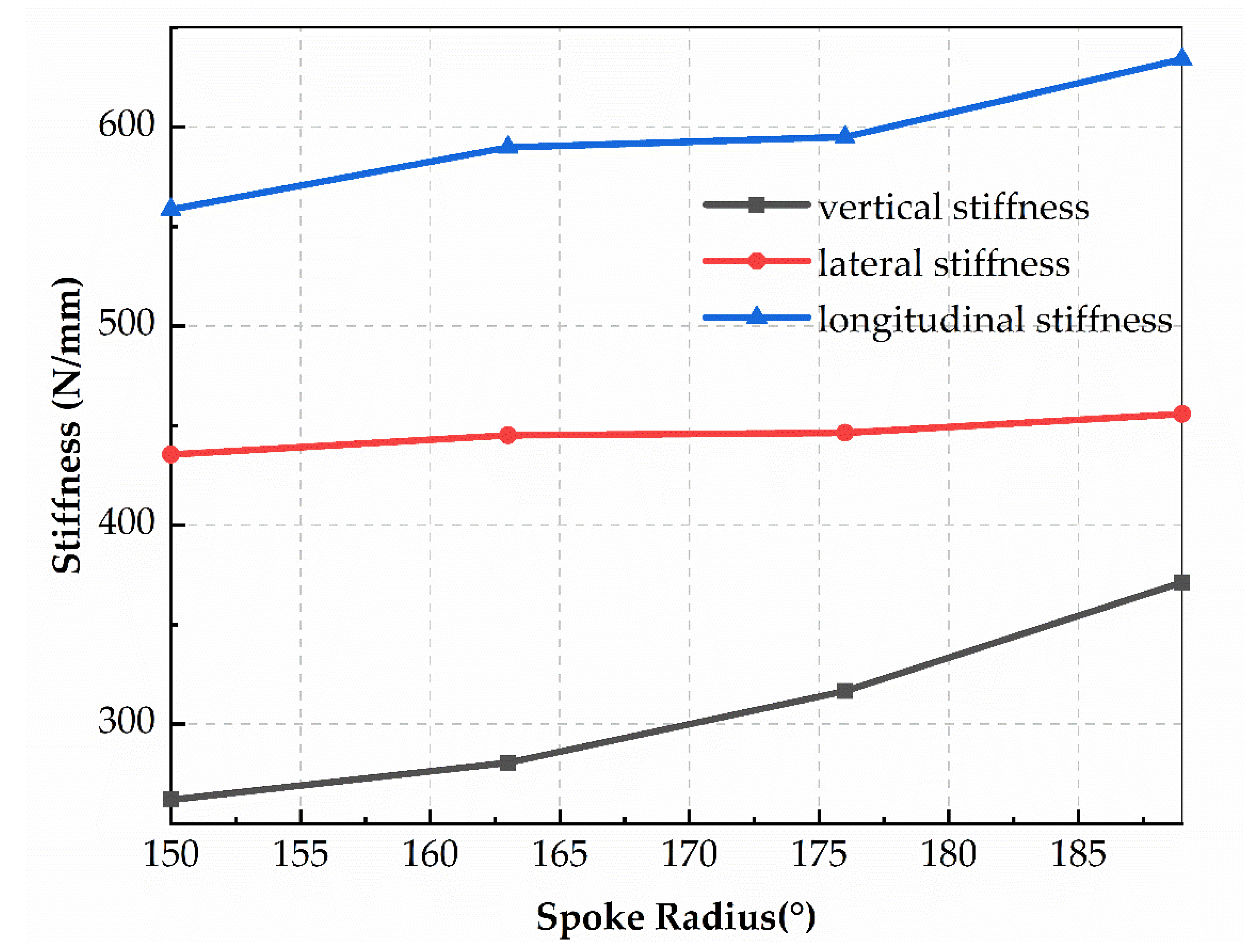
3.2. Effects of Spoke Radius on Three-Dimensional Stiffnesses of FS-NPT
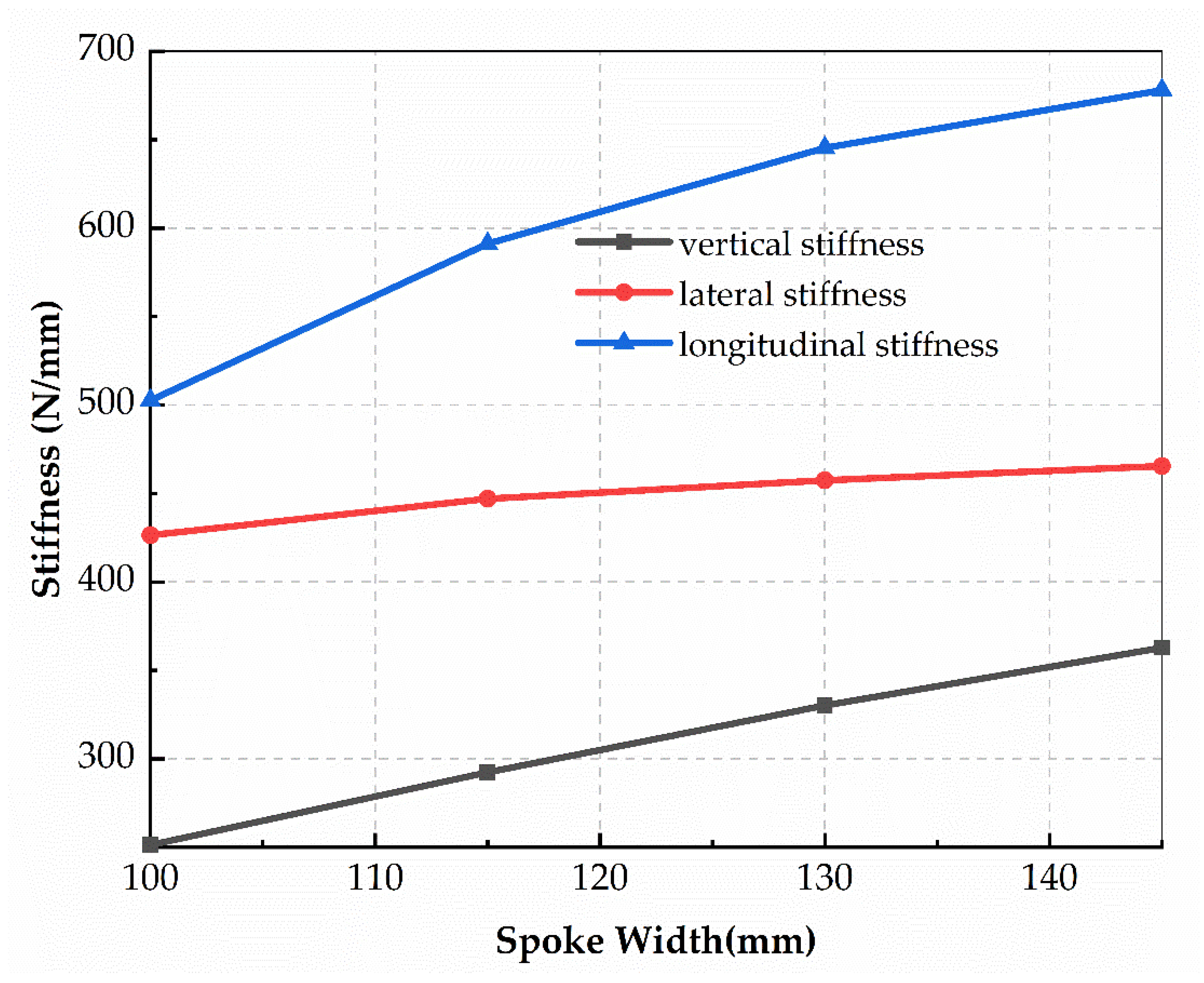
3.3. Effects of Spoke Width on Three-Dimensional Stiffnesses of FS-NPT
4. Optimization with Design of Experiments and Sensitivity Analysis
4.1. Optimization Problem Statement
4.2. Design of Experiments and Design Sensitivity Study
4.3. Response Surface Model (RSM)
4.4. Optimization Algorithms
5. Conclusions and Future Work
- The parametric study showed that variation in all three design parameters had no considerable effect on the lateral stiffness. The lateral stiffness kept nearly independent and was not coupled with the other two stiffnesses.
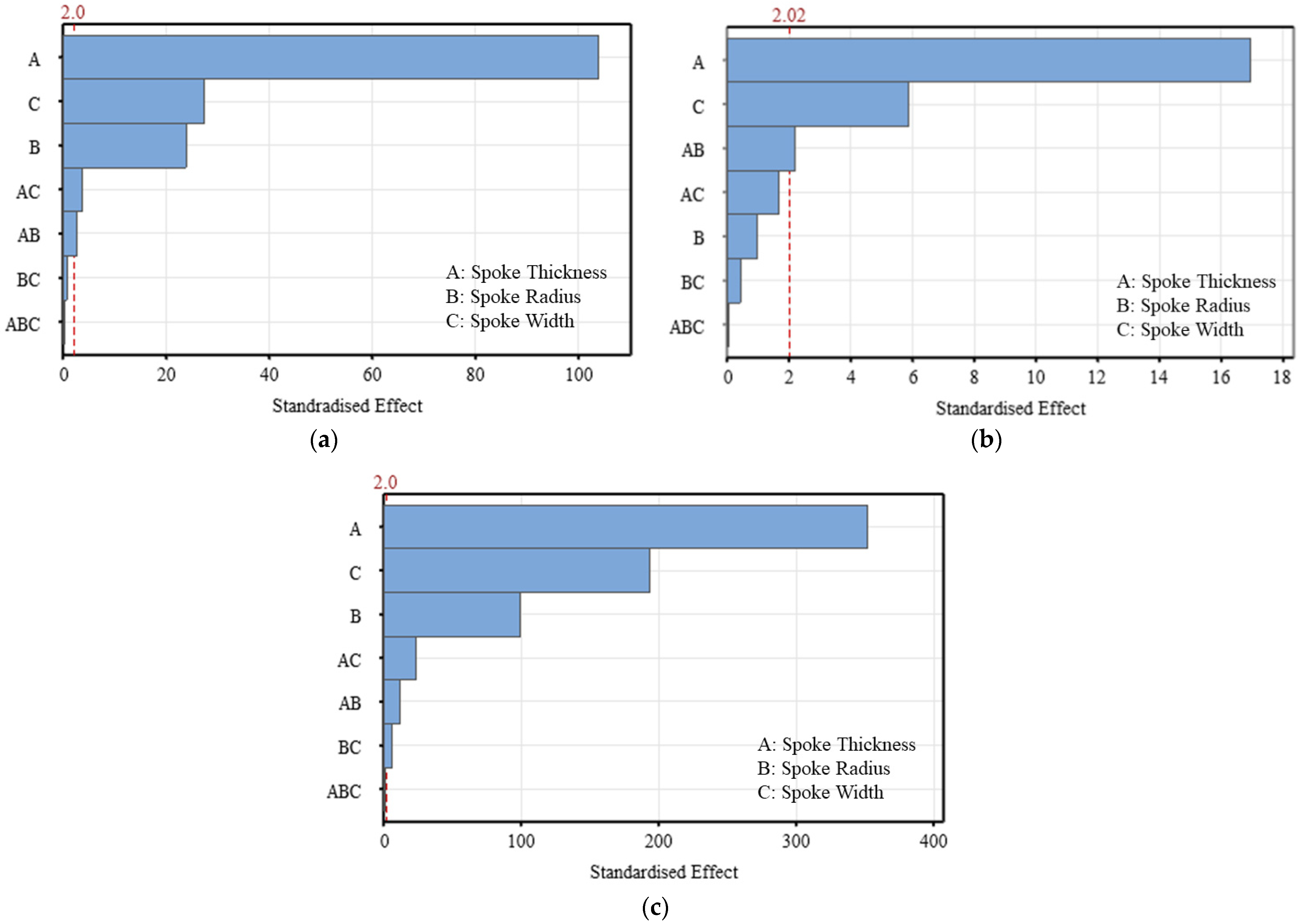
- The sensitivity analysis with the DOE and Pareto charts demonstrated that the spoke thickness was the most important design parameter regarding vertical stiffness, longitudinal stiffness, and weight. The spoke radius had no potential effect on the longitudinal stiffness of the NPT.
- Optimized geometric parameters were found: a spoke thickness of 6.87 mm, a spoke radius of 182.09°, and a spoke width of 101.30 mm under a constraint on weight. The optimization result was completely consistent with the stiffness target, and the error rate was less than 1%.
- Vertical stiffness and longitudinal stiffness were coupled to a certain extent, but the predetermined goals were achieved by different design variables affecting them to different degrees. The optimization results indicated that the FS-NPT has a large stiffness design range. The different stiffness targets were achieved by adjusting different combinations of design variables, and the tire mass did not increase significantly.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Yoo, S.; Uddin, M.S.; Heo, H.; Ju, J.; Kim, D.M.; Choi, S.J. Deformation and heat generation in a nonpneumatic tire with lattice spokes (No. 2015-01-1512). SAE Technical Paper, 14 April 2015; p. 9. [Google Scholar] [CrossRef]
- Narasimhan, A.; Ziegert, J.; Thompson, L. Effects of material properties on static load-deflection and vibration of a non-pneumatic tire during high-speed rolling. SAE Int. J. Passeng. Cars-Mech. Syst. 2011, 4, 59–72. [Google Scholar] [CrossRef]
- Rhyne, T.B.; Cron, S.M. Development of a non-pneumatic wheel. Tire Sci. Technol. 2006, 34, 150–169. [Google Scholar] [CrossRef]
- Gibert, J.M.; Ananthasayanam, B.; Joseph, P.F.; Rhyne, T.B.; Cron, S.M. Deformation Index–Based Modeling of Transient, Thermo-mechanical Rolling Resistance for a Nonpneumatic Tire. Tire Sci. Technol. 2013, 41, 82–108. [Google Scholar] [CrossRef]
- Zhao, Y.; Du, X.; Lin, F.; Wang, Q.; Fu, H. Static stiffness characteristics of a new non-pneumatic tire with different hinge structure and distribution. J. Mech. Sci. Technol. 2018, 32, 3057–3064. [Google Scholar] [CrossRef]
- Gasmi, A.; Joseph, P.F.; Rhyne, T.B.; Cron, S.M. Development of a two-dimensional model of a compliant non-pneumatic tire. Int. J. Solids Struct. 2012, 49, 1723–1740. [Google Scholar] [CrossRef]
- Narasimhan, A. A Computational Method for Analysis of Material Properties of a Non-Pneumatic Tire and Their Effects on Static Load-Deflection, Vibration, and Energy Loss from Impact Rolling over Obstacles. Master’s Thesis, Clemson University, Clemson, SC, USA, August 2010. Available online: https://tigerprints.clemson.edu/all_theses/1003 (accessed on 1 August 2022).
- Dhrangdhariya, P.; Soumyadipta, M.; Beena, R. Effect of spoke design and material nonlinearity on non-pneumatic tire stiffness and durability performance. arXiv 2021, arXiv:2103.03637. [Google Scholar] [CrossRef]
- Wu, T.; Li, M.; Zhu, X.; Lu, X. Research on non-pneumatic tire with gradient anti-tetrachiral structures. Mech. Adv. Mater. Struct. 2021, 28, 2351–2359. [Google Scholar] [CrossRef]
- Rugsaj, R.; Suvanjumrat, C. Proper Radial Spokes of Non-Pneumatic Tire for Vertical Load Supporting by Finite Element Analysis. Int. J. Automot. Technol. 2019, 20, 801–812. [Google Scholar] [CrossRef]
- Xu, T.; Zhang, B. The Invention Relates to a High Speed and High Load Non-Pneumatic Tire and a Preparation Method Thereof. Patent CN 111152600B, 2019. [Google Scholar]
- Li, C.; Ji, A.; Cao, Z. Stressed Fibonacci spiral patterns of definite chirality. Appl. Phys. Lett. 2007, 90, 164102. [Google Scholar] [CrossRef]
- Paul, B.G. Pattern formation in shoots: A likely role for minimal energy configurations of the tunica. Int. J. Plant Sci. 1992, 153, S59–S75. [Google Scholar]
- Lee, W.S.; Su, T.T. Mechanical properties and microstructural features of aisi 4340 high-strength alloy steel under quenched and tempered conditions. J. Mater. Process. Technol. 1999, 87, 198–206. [Google Scholar] [CrossRef]
- Fang, K.T.; Li, R.; Sudjianto, A. Design and Modeling for Computer Experiments; Chapman and Hall/CRC: New York, NY, USA, 2005. [Google Scholar]
- Barrentine, L.B. An Introduction to Design of Experiments: A Simplified Approach; American Society for Quality: Milwaukee, WI, USA, 1999. [Google Scholar]
- Myers, R.H.; Montgomery, D.C.; Anderson-Cook, C.M. Response Surface Methodology: Process and Product Optimization Using Designed Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Granville, V.; Krivanek, M.; Rasson, J.-P. Simulated annealing: A proof of convergence. IEEE Trans. Pattern Anal. Mach. Intell. 1994, 16, 652–656. [Google Scholar] [CrossRef]
- Coello, C.A.C.; Lechuga, M.S. MOPSO: A proposal for multiple objective particle swarm optimization. In Proceedings of the 2002 Congress on Evolutionary Computation. CEC’02 (Cat. No. 02TH8600), Honolulu, HI, USA, 12–17 May 2002; Volume 2, pp. 1051–1056. [Google Scholar]
- Boggs, P.T.; Tolle, J.W. Sequential quadratic programming for large-scale nonlinear optimization. J. Comput. Appl. Math. 2000, 124, 123–137. [Google Scholar] [CrossRef]






| Material | Density (kg/m3) | Neo-Hookean Strain Energy Potential | |
|---|---|---|---|
| Coefficients C10 | Coefficients D1 | ||
| Tread rubber | 1100 | 0.0833 | 1.242384 |
| Material | Density (kg/m3) | Young’s Modulus, E (GPa) | Poisson’s Ratio, ν - |
|---|---|---|---|
| High-strength steel, ANSI 4340 | 7800 | 210 | 0.29 |
| Stiffness (N/mm) | Vertical Stiffness | Lateral Stiffness | Longitudinal Stiffness |
|---|---|---|---|
| Test | 146.45 | 367.92 | 338.52 |
| Simulation | 149.75 | 400.00 | 333.33 |
| Error | 2.25% | 8.72% | 1.53% |
| No | Thickness (mm) | Radius (°) | Width (mm) | Vertical Stiffness (N/mm) | Longitudinal Stiffness (N/mm) | Weight (kg) |
|---|---|---|---|---|---|---|
| 1 | 9.34 | 153.98 | 125.71 | 549.53 | 724.10 | 17.67 |
| 2 | 9.05 | 175.47 | 130.31 | 589.68 | 717.05 | 17.13 |
| 3 | 7.94 | 174.67 | 127.55 | 413.18 | 644.16 | 16.26 |
| 4 | 7.28 | 186.61 | 126.63 | 374.13 | 601.33 | 15.57 |
| 5 | 8.60 | 177.86 | 117.45 | 489.42 | 725.02 | 16.35 |
| 6 | 8.90 | 176.27 | 104.59 | 477.29 | 649.71 | 16.13 |
| 7 | 8.53 | 162.73 | 123.88 | 456.85 | 694.45 | 16.80 |
| 8 | 8.75 | 165.92 | 138.57 | 534.93 | 734.53 | 17.38 |
| 9 | 8.02 | 157.96 | 145.00 | 420.62 | 690.83 | 17.16 |
| 10 | 7.36 | 150.00 | 110.10 | 235.97 | 513.61 | 15.75 |
| 11 | 7.14 | 172.29 | 103.67 | 231.04 | 472.56 | 15.05 |
| 12 | 7.06 | 182.63 | 140.41 | 345.47 | 598.87 | 15.82 |
| 13 | 8.31 | 189.00 | 122.96 | 522.89 | 691.40 | 16.13 |
| 14 | 9.56 | 165.12 | 129.39 | 609.95 | 745.13 | 17.70 |
| 15 | 8.68 | 188.20 | 109.18 | 522.24 | 673.71 | 15.95 |
| 16 | 8.97 | 178.65 | 144.08 | 619.86 | 713.83 | 17.45 |
| 17 | 6.40 | 179.45 | 128.47 | 215.18 | 446.84 | 15.10 |
| 18 | 9.41 | 155.57 | 139.49 | 598.77 | 723.84 | 18.19 |
| 19 | 6.84 | 185.82 | 106.43 | 242.90 | 465.59 | 14.76 |
| 20 | 9.27 | 161.14 | 101.84 | 465.71 | 678.22 | 16.54 |
| 21 | 8.09 | 184.22 | 136.73 | 496.81 | 687.78 | 16.46 |
| 22 | 8.16 | 167.51 | 100.00 | 338.66 | 587.28 | 15.65 |
| 23 | 7.87 | 181.84 | 102.76 | 352.48 | 600.10 | 15.34 |
| 24 | 7.43 | 151.59 | 132.14 | 298.89 | 589.85 | 16.44 |
| 25 | 7.80 | 173.08 | 141.33 | 419.32 | 658.35 | 16.57 |
| 26 | 9.93 | 170.69 | 105.51 | 594.52 | 701.78 | 16.93 |
| 27 | 7.72 | 168.31 | 113.78 | 326.73 | 584.79 | 15.80 |
| 28 | 9.63 | 173.88 | 118.37 | 620.46 | 705.32 | 17.16 |
| 29 | 6.91 | 156.37 | 143.16 | 267.94 | 552.42 | 16.23 |
| 30 | 7.58 | 181.04 | 115.61 | 350.61 | 599.80 | 15.55 |
| 31 | 6.77 | 170.69 | 137.65 | 253.65 | 525.59 | 15.72 |
| 32 | 7.65 | 163.53 | 133.06 | 363.25 | 632.23 | 16.40 |
| 33 | 8.24 | 157.16 | 107.35 | 357.35 | 623.34 | 16.14 |
| 34 | 10.00 | 180.24 | 135.82 | 740.63 | 708.95 | 17.92 |
| 35 | 9.12 | 187.41 | 134.90 | 656.96 | 718.51 | 17.09 |
| 36 | 9.78 | 169.10 | 142.24 | 694.54 | 768.17 | 18.24 |
| 37 | 9.85 | 161.94 | 116.53 | 590.47 | 715.02 | 17.51 |
| 38 | 6.62 | 160.35 | 131.22 | 206.38 | 487.11 | 15.62 |
| 39 | 6.47 | 154.78 | 119.29 | 159.84 | 374.98 | 15.29 |
| 40 | 9.49 | 185.02 | 122.04 | 651.35 | 691.80 | 16.97 |
| 41 | 7.50 | 158.76 | 121.12 | 307.92 | 583.29 | 16.03 |
| 42 | 8.31 | 150.80 | 120.20 | 389.01 | 650.34 | 16.76 |
| 43 | 7.21 | 159.55 | 100.92 | 210.99 | 466.40 | 15.20 |
| 44 | 9.71 | 183.43 | 108.27 | 615.93 | 670.59 | 16.65 |
| 45 | 9.19 | 152.39 | 111.02 | 481.31 | 680.89 | 17.04 |
| 46 | 6.55 | 177.06 | 114.69 | 197.43 | 427.28 | 14.90 |
| 47 | 6.69 | 164.33 | 111.94 | 184.18 | 413.80 | 15.11 |
| 48 | 8.46 | 153.18 | 133.98 | 452.12 | 688.84 | 17.29 |
| 49 | 8.82 | 166.71 | 112.86 | 472.98 | 679.73 | 16.55 |
| 50 | 6.99 | 169.90 | 123.88 | 257.51 | 515.68 | 15.55 |
| Optimization/ Validation | Spoke Thickness (mm) | Spoke Radius (°) | Spoke Width (mm) | Vertical Stiffness (N/mm) | Longitudinal Stiffness (N/mm) | Weight (kg) |
|---|---|---|---|---|---|---|
| ASA | 6.87 | 182.09 | 101.30 | 218.00 | 444.00 | 14.69 |
| MOPSO | 6.91 | 177.24 | 104.05 | 216.86 | 453.89 | 14.85 |
| NLPQL | 7.00 | 171.97 | 100 | 201.22 | 443.88 | 14.85 |
| Optimization/ Validation | Spoke Thickness (mm) | Spoke Radius (°) | Spoke Width (mm) | Vertical Stiffness (N/mm) | Longitudinal Stiffness (N/mm) | Weight (kg) |
|---|---|---|---|---|---|---|
| ASA | 6.87 | 182.09 | 101.30 | 218.00 | 444.00 | 14.69 |
| FEA | 6.87 | 182.09 | 101.30 | 216.30 | 444.92 | 14.67 |
| Error % | 0.79% | 0.21% | 0.14% |
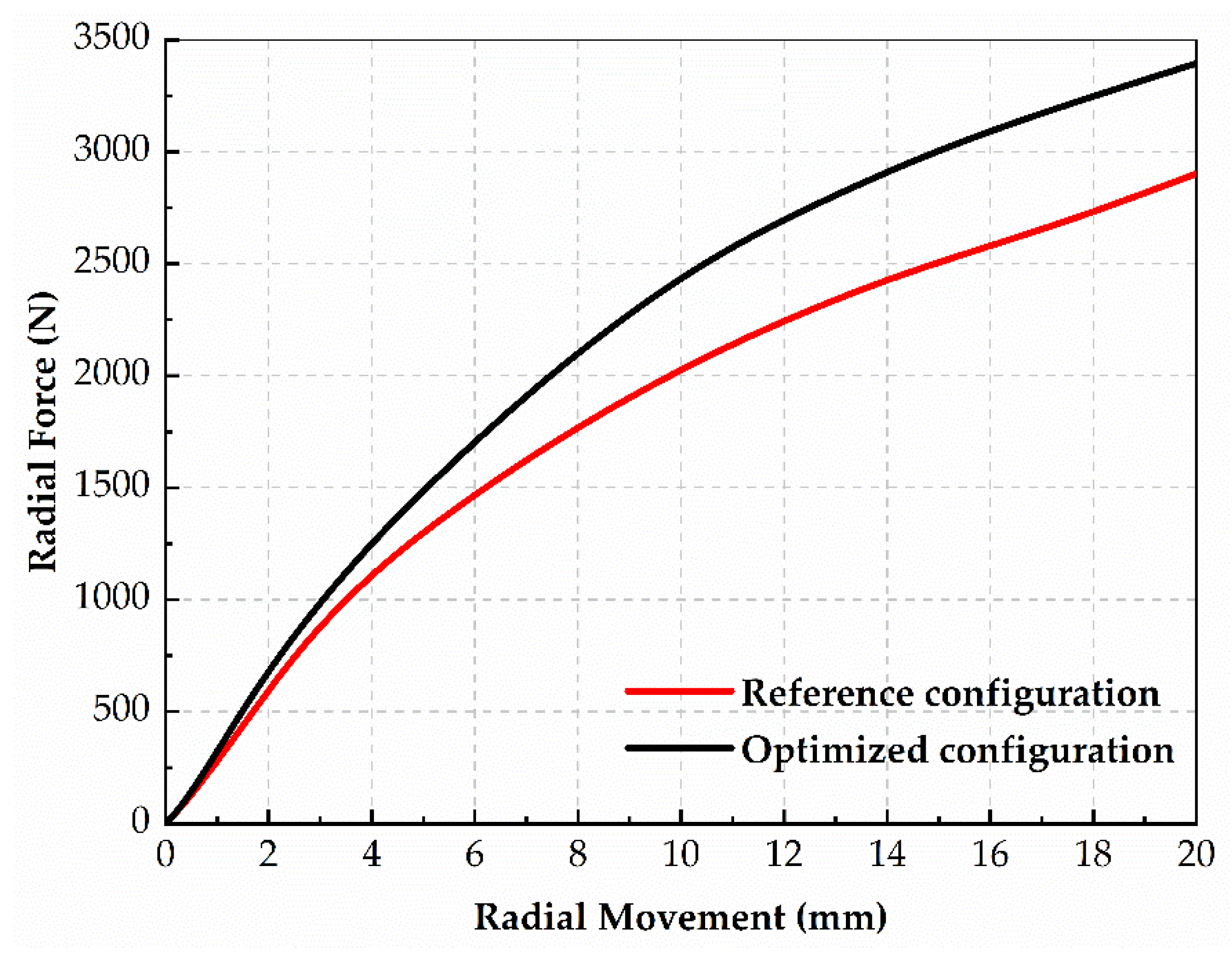
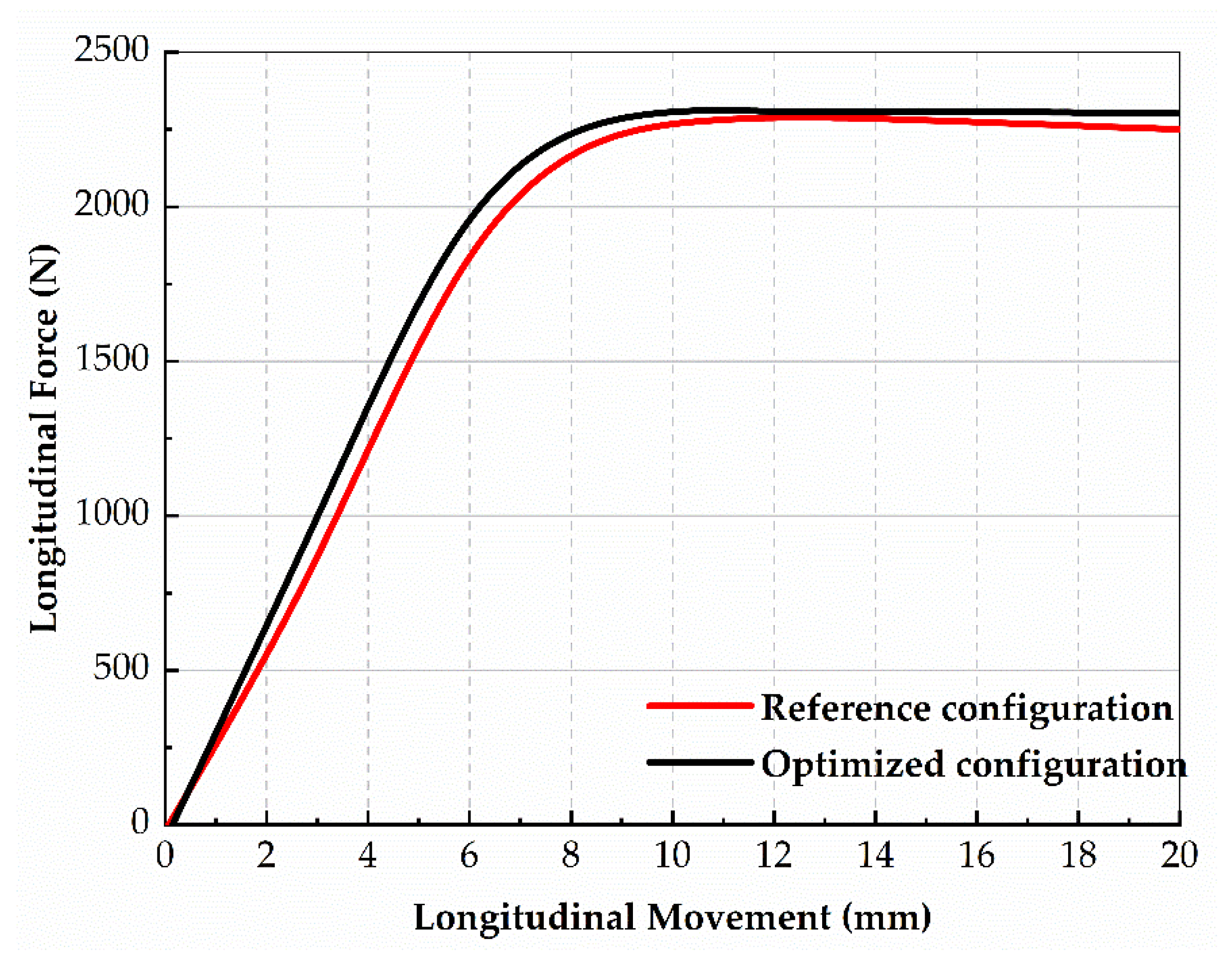
| Configuration | Spoke Thickness (mm) | Spoke Radius (°) | Spoke Width (mm) | Vertical Stiffness (N/mm) | Longitudinal Stiffness (N/mm) | Weight (kg) |
|---|---|---|---|---|---|---|
| Reference | 6.6 | 180 | 105 | 149.75 | 338.52 | 14.65 |
| Optimized | 6.87 | 182.09 | 101.30 | 216.30 | 444.92 | 14.67 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Xu, T.; Zhu, L.; Gao, F. Multi-Objective Optimization of the Geometry of a Non-Pneumatic Tire for Three-Dimensional Stiffness Adaptation. Machines 2022, 10, 1183. https://doi.org/10.3390/machines10121183
Liu X, Xu T, Zhu L, Gao F. Multi-Objective Optimization of the Geometry of a Non-Pneumatic Tire for Three-Dimensional Stiffness Adaptation. Machines. 2022; 10(12):1183. https://doi.org/10.3390/machines10121183
Chicago/Turabian StyleLiu, Xiaoyu, Ting Xu, Liangliang Zhu, and Fei Gao. 2022. "Multi-Objective Optimization of the Geometry of a Non-Pneumatic Tire for Three-Dimensional Stiffness Adaptation" Machines 10, no. 12: 1183. https://doi.org/10.3390/machines10121183
APA StyleLiu, X., Xu, T., Zhu, L., & Gao, F. (2022). Multi-Objective Optimization of the Geometry of a Non-Pneumatic Tire for Three-Dimensional Stiffness Adaptation. Machines, 10(12), 1183. https://doi.org/10.3390/machines10121183






