MFPointNet: A Point Cloud-Based Neural Network Using Selective Downsampling Layer for Machining Feature Recognition
Abstract
1. Introduction
2. Literature Review
2.1. Traditional Feature Recognition Methods
2.2. Deep Learning-Based Feature Recognition Methods
3. Machining Feature Dataset Creation
3.1. Overview
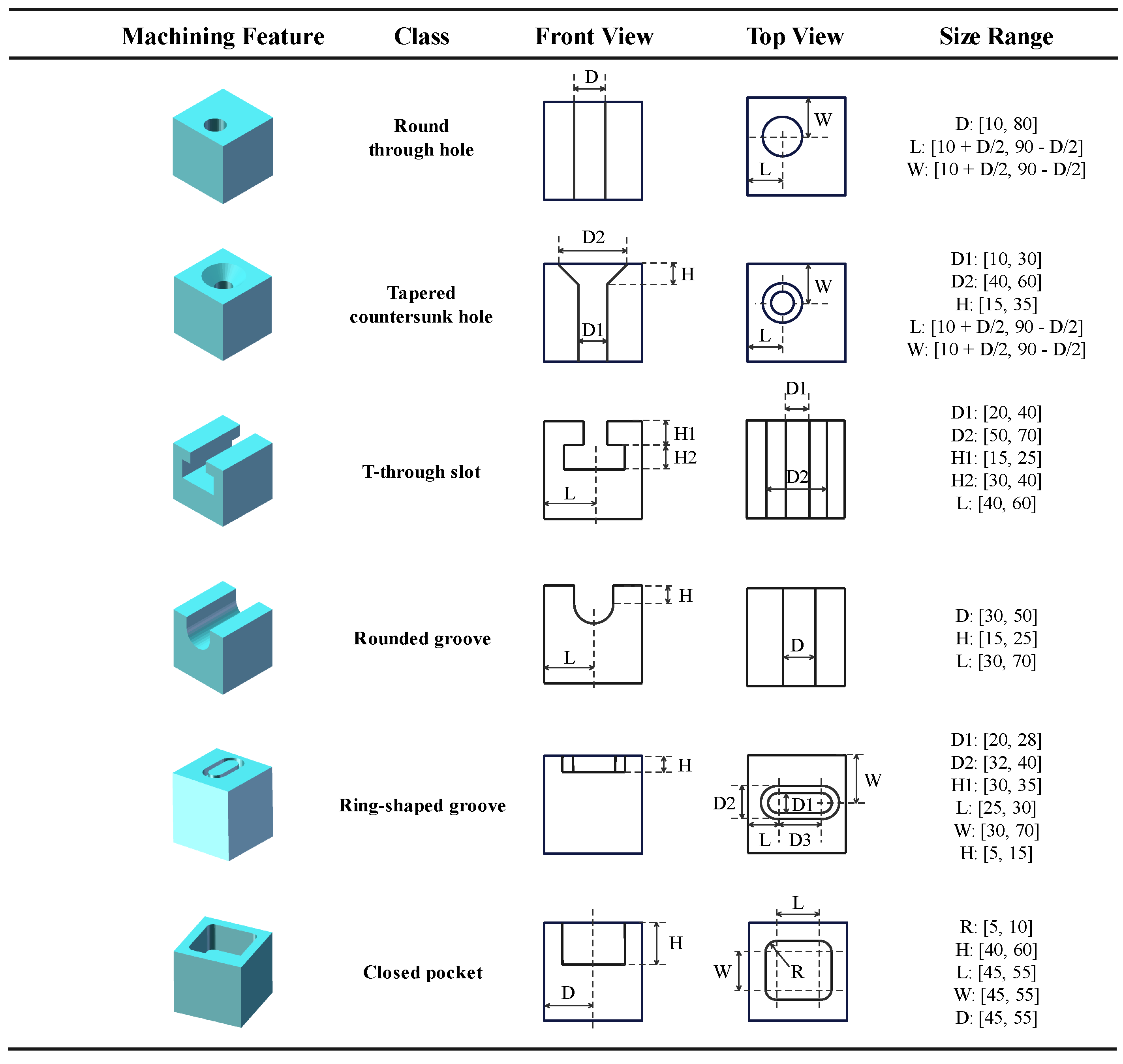
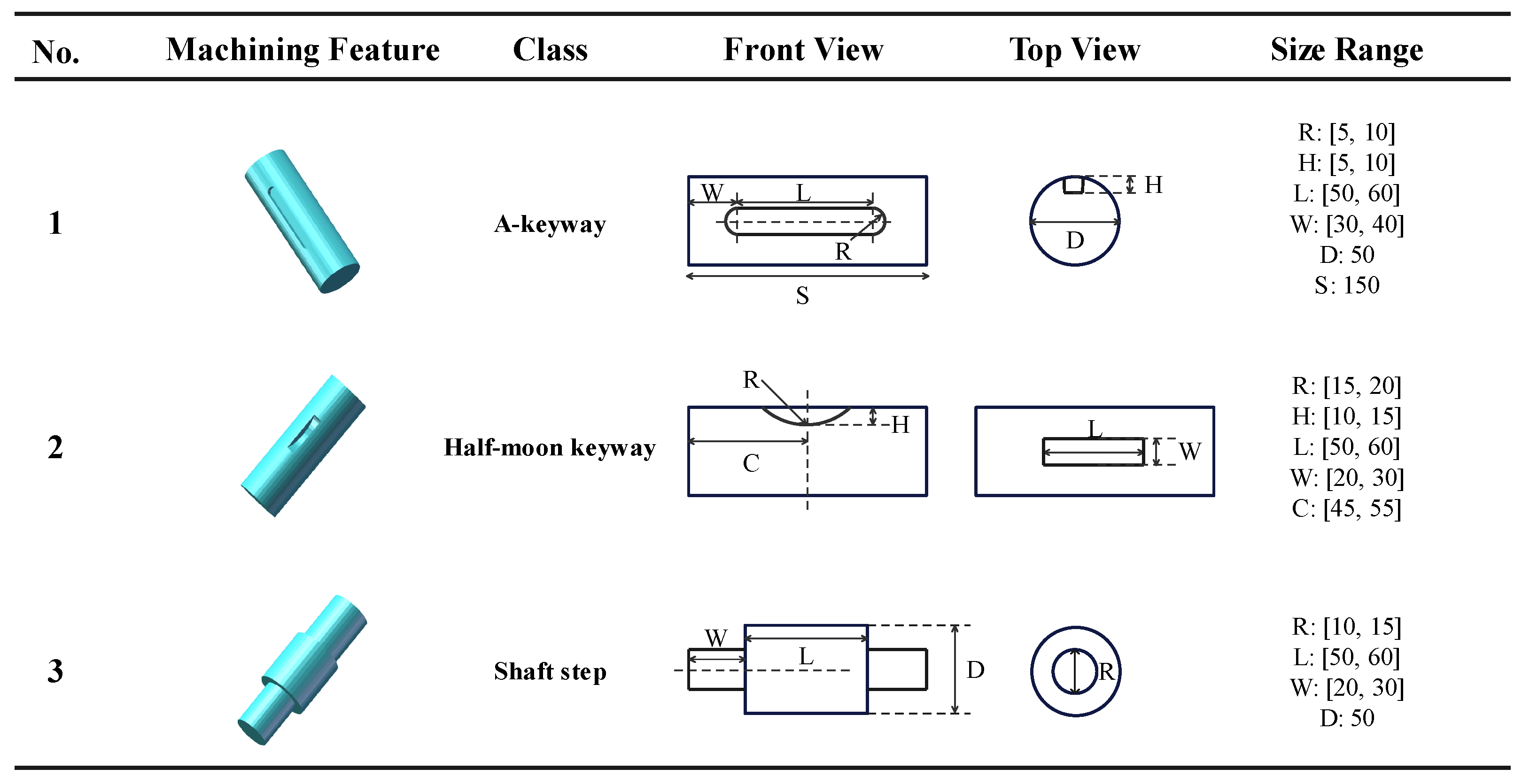
3.2. Definition and Types of Machining Feature
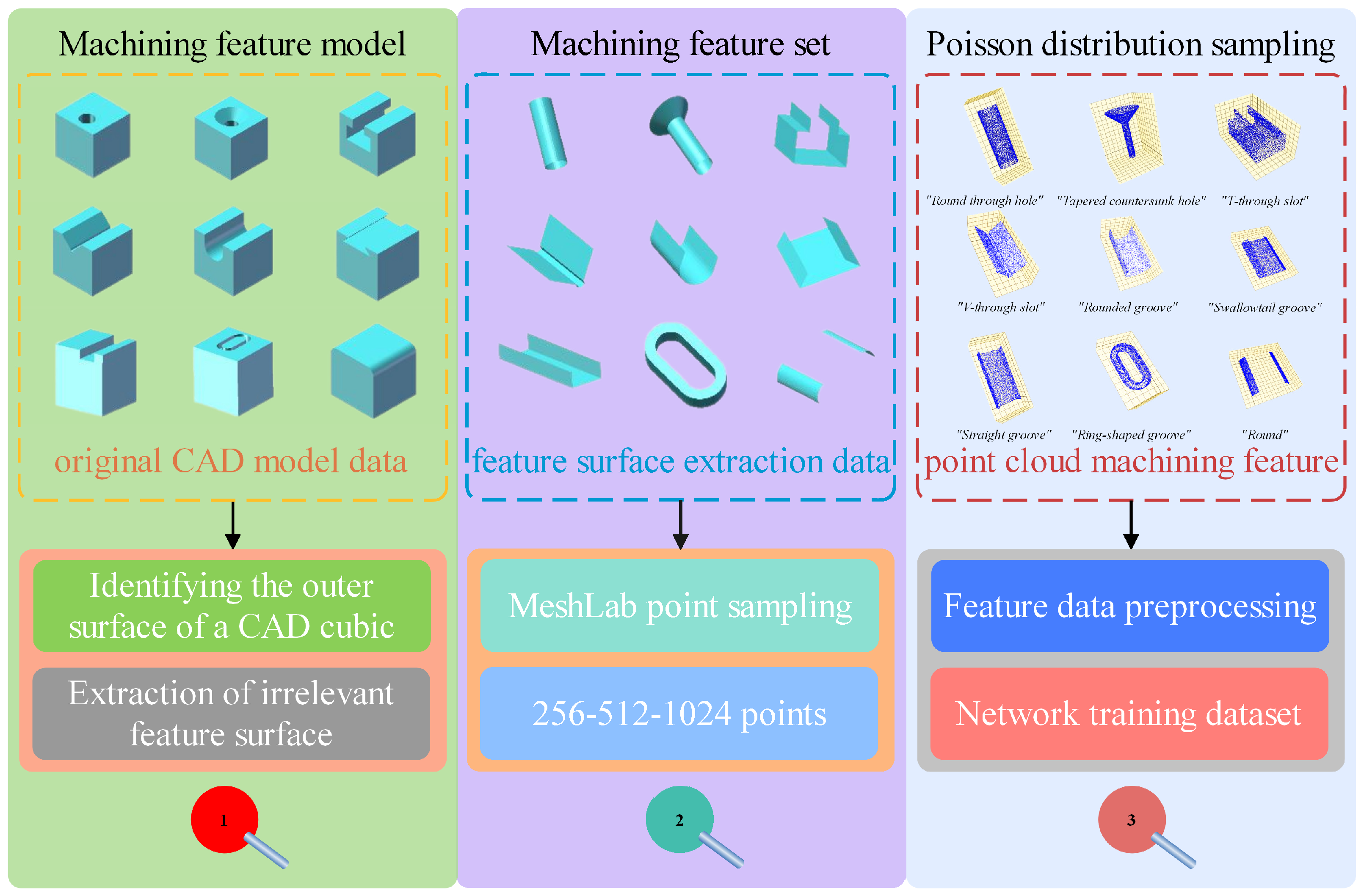
3.3. Point Cloud Feature Dataset
3.3.1. Extraction of Machining Feature Surface Point Sets
| Algorithm 1 The process of machining feature surface set extraction. |
|
3.3.2. Poisson-Disk Sampling
3.3.3. Feature Data Pre-Processing
3.4. Multi-Machining Feature Dataset
4. MFPointNet for Machining Feature Recognition
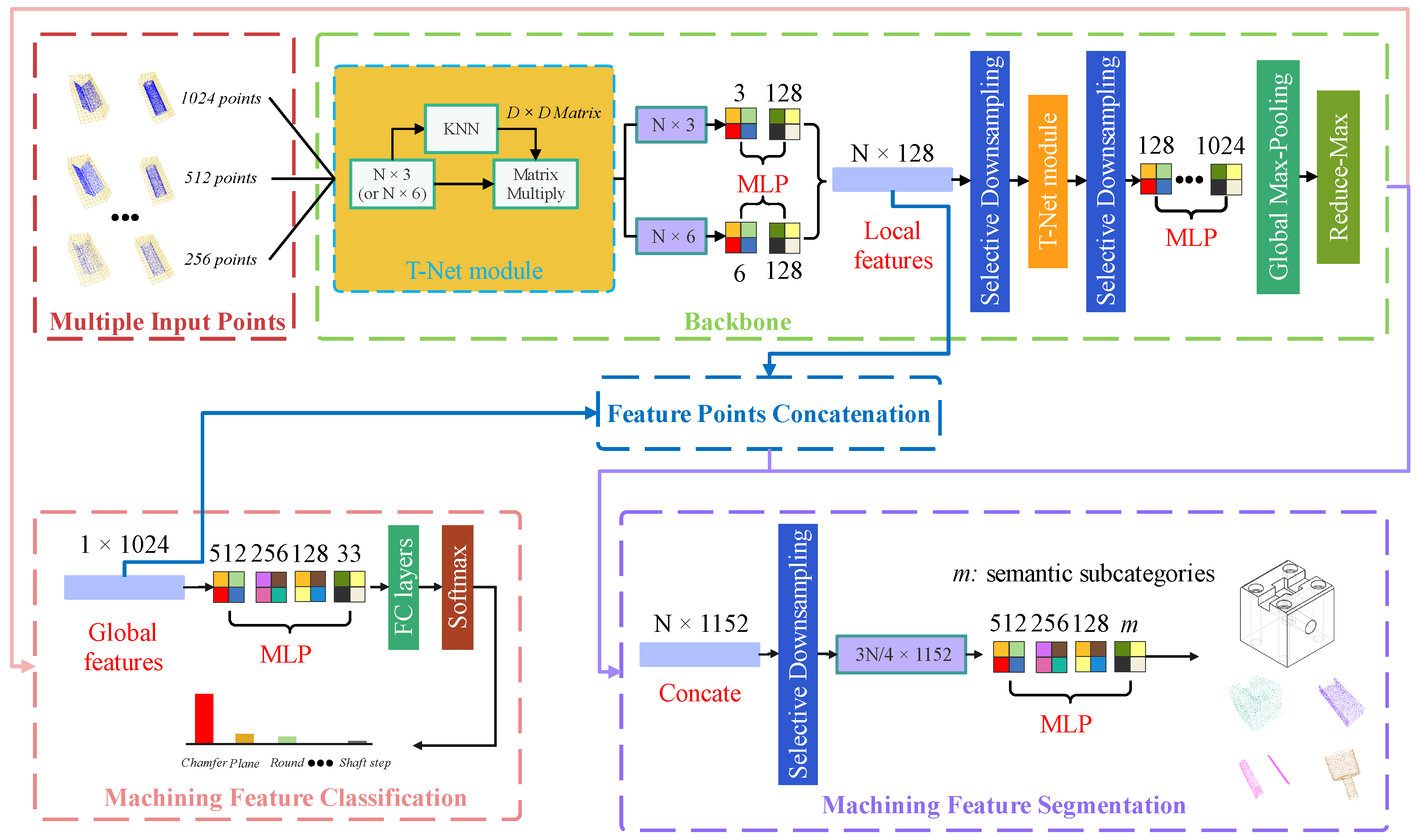
4.1. Single-Machining Feature Recognition
4.1.1. The Selective Downsampling Layer (SDL)
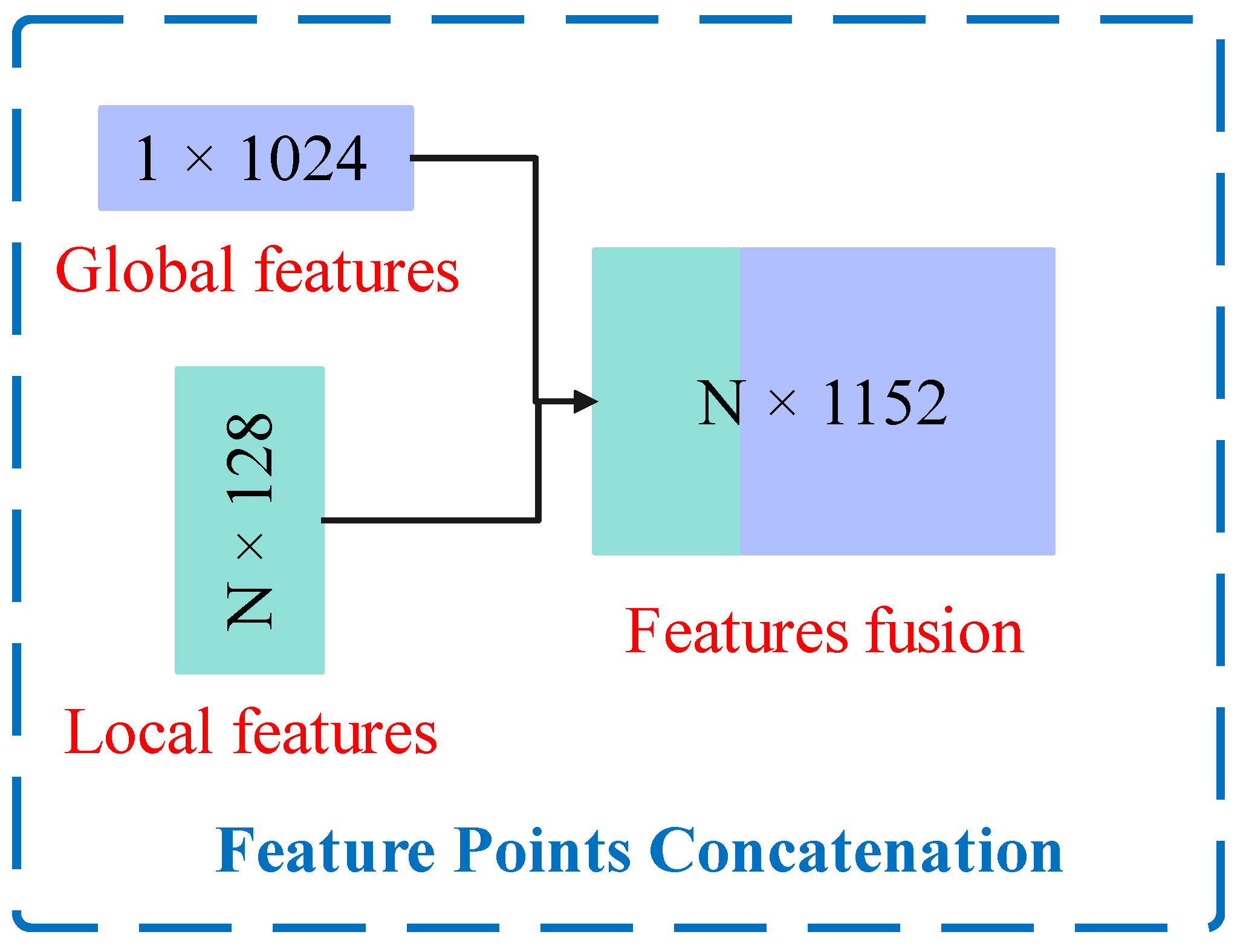
4.1.2. The Architecture of the MFPointNet
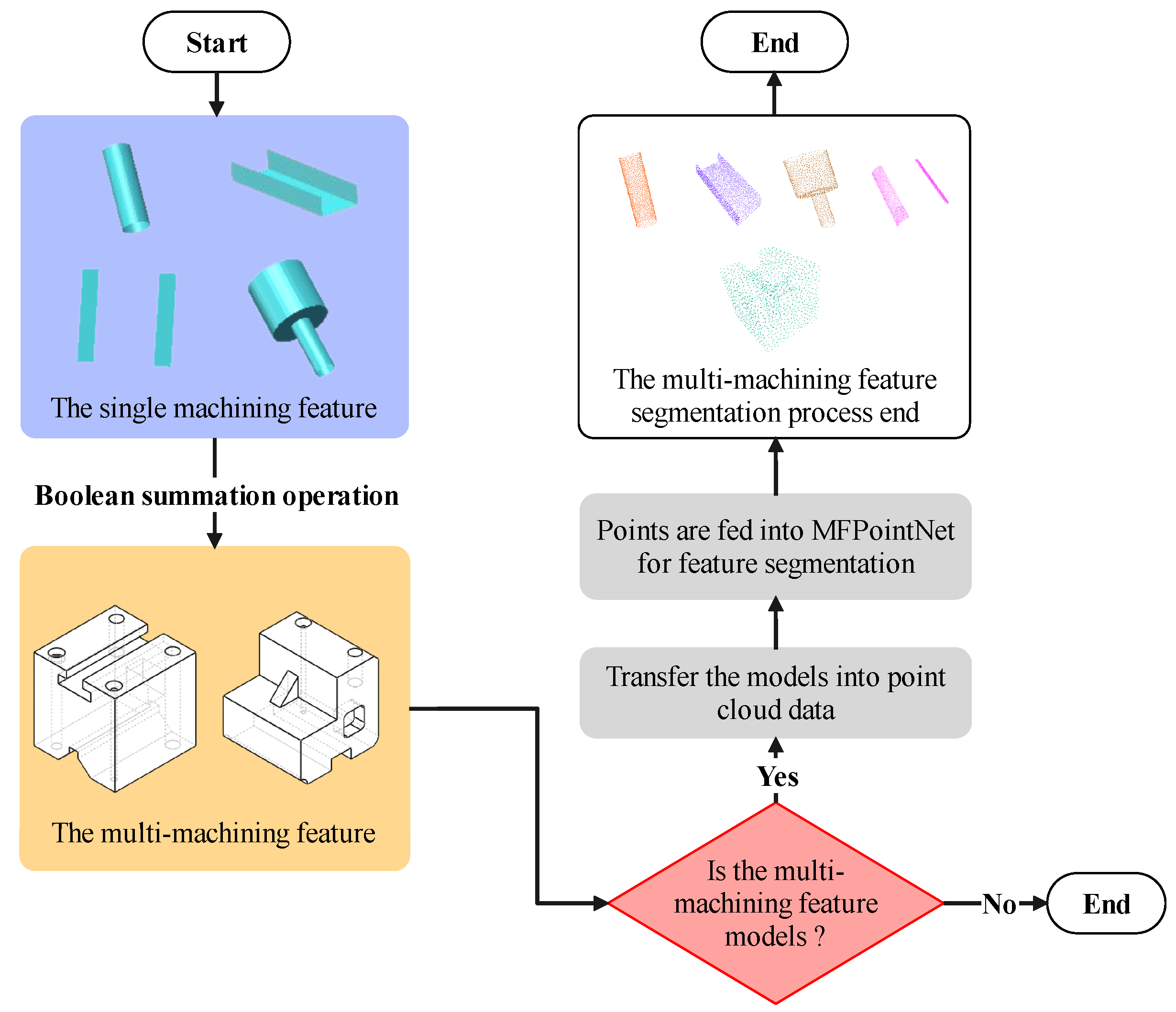
4.2. The Procedure of Multi-Machining Feature Recognition
5. Experimental Results and Discussion
5.1. Single-Machining Feature Recognition
5.1.1. The MFPointNet Experimental Results
5.1.2. Comparative Experiments of Effect on Input Point Number with Other Point Cloud-Based Networks
5.1.3. Comparative Experiments of Effect on Input Normal Vectors with Other Point Cloud-Based Networks
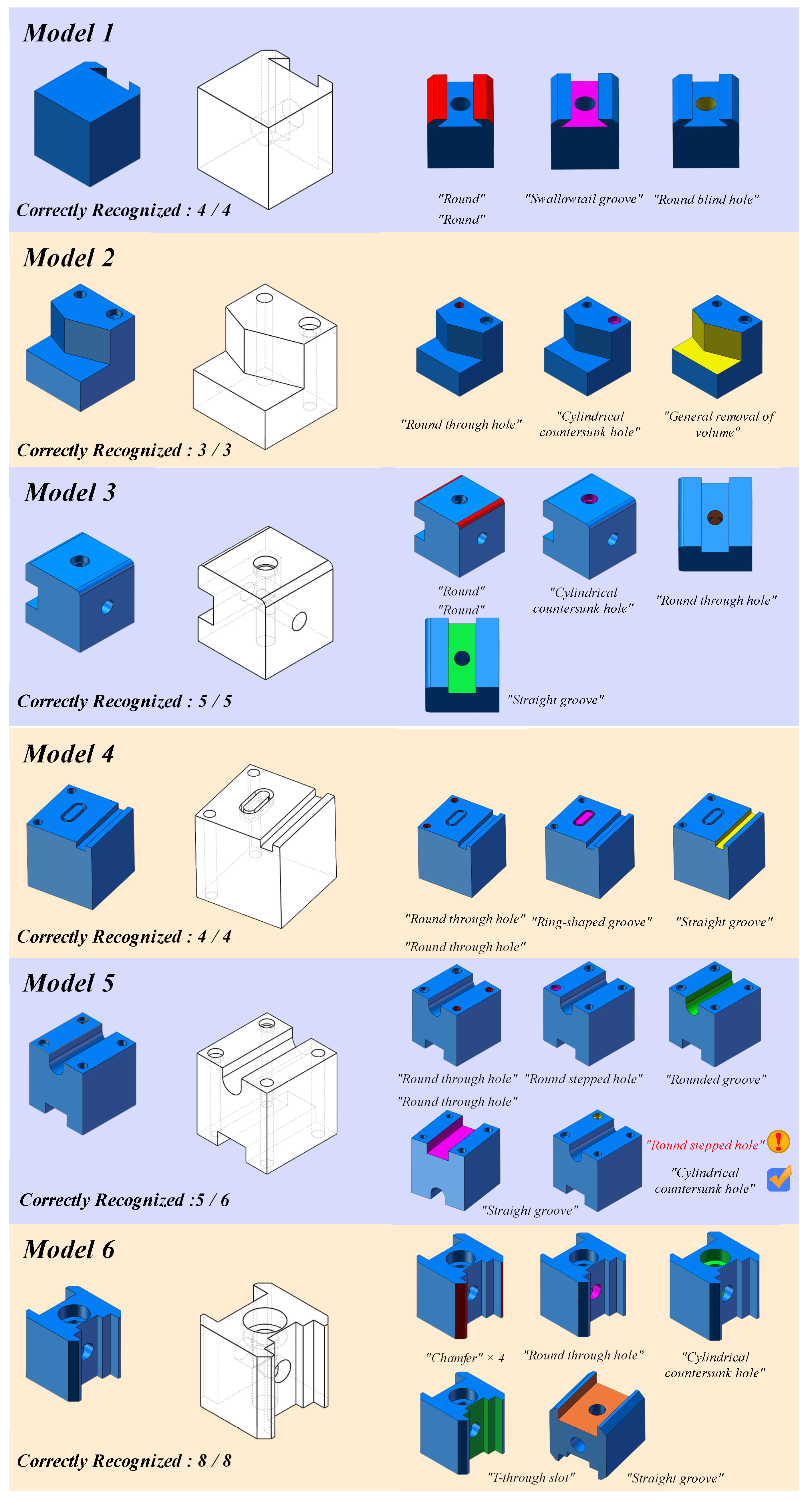
5.2. Multi-Machining Feature Recognition
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
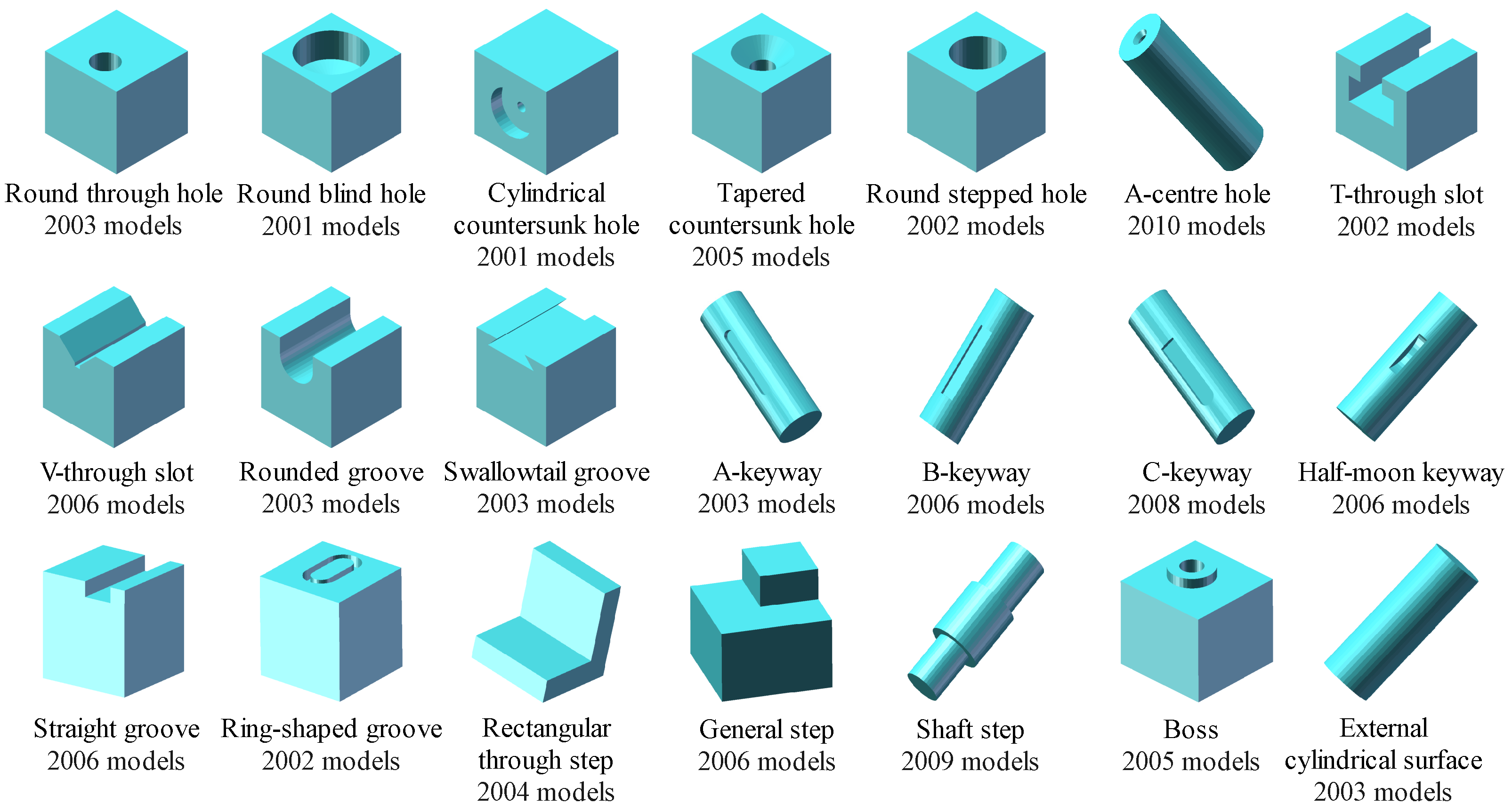
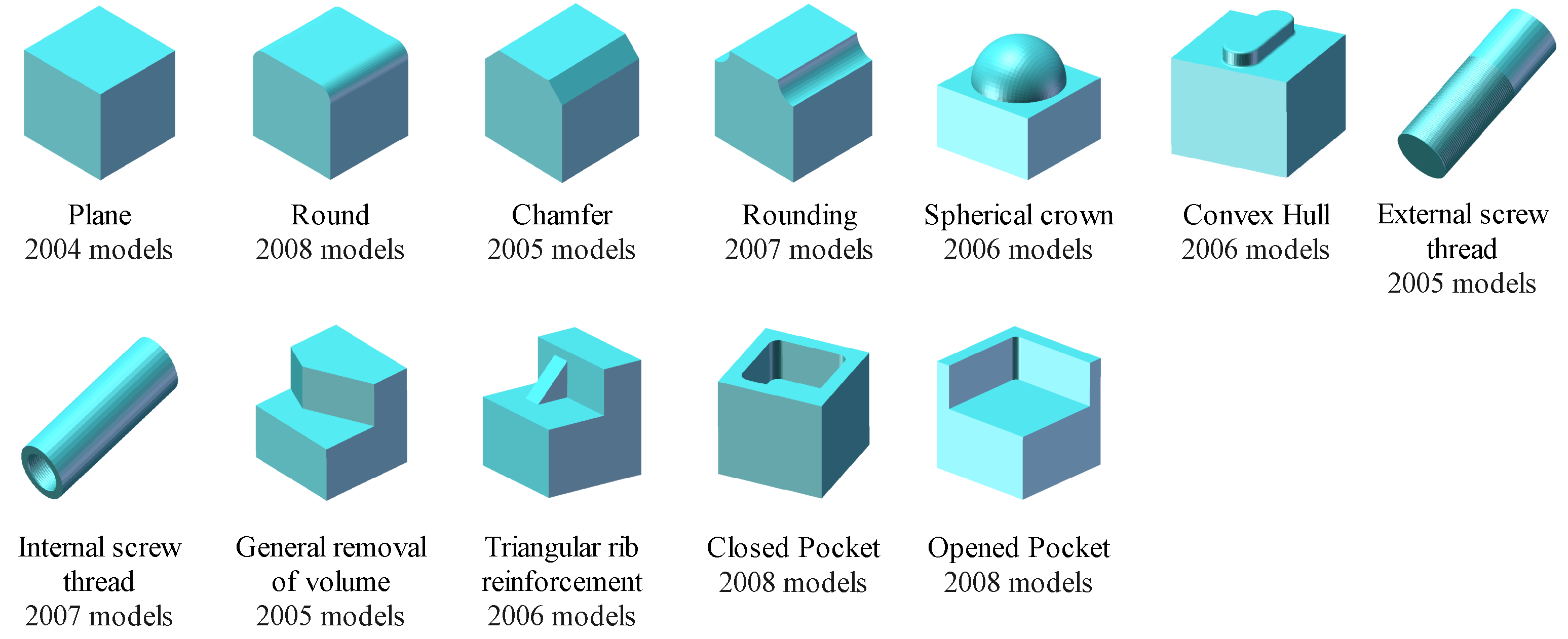
Appendix B

Appendix C
Appendix D
References
- Ding, S.; Feng, Q.; Sun, Z.; Ma, F. MBD Based 3D CAD Model Automatic Feature Recognition and Similarity Evaluation. IEEE Access 2021, 9, 150403–150425. [Google Scholar] [CrossRef]
- Shi, Y.; Zhang, Y.; Xia, K.; Harik, R. A critical review of feature recognition techniques. Comput.-Aided Des. Appl. 2020, 17, 861–899. [Google Scholar] [CrossRef]
- Deng, L.; Yu, D. Deep learning: Methods and applications. Found. Trends Signal Process. 2014, 7, 197–387. [Google Scholar] [CrossRef]
- Fougères, A.J.; Ostrosi, E. Intelligent agents for feature modelling in computer aided design. J. Comput. Des. Eng. 2018, 05, 19–40. [Google Scholar] [CrossRef]
- Zhao, P.; Sheng, B. Recognition method of process feature based on delta-volume decomposition and combination strategy. J. South China Univ. Technol. (Natural Sci. Ed.) 2011, 39, 30–35. (In Chinese) [Google Scholar]
- Han, J.H.; Requicha, A.A.G. Integration of feature based design and feature recognition. Comput. Aided Des. Appl. 1997, 29, 393–403. [Google Scholar] [CrossRef]
- Zehtaban, L.; Roller, D. Automated rule-based system for Opitz feature recognition and code generation from STEP. Comput.-Aided Des. Appl. 2016, 13, 309–319. [Google Scholar] [CrossRef]
- Zhang, Y.; Luo, X.; Zhang, B.; Zhang, S. Semantic approach to the automatic recognition of machining features. Int. J. Adv. Manuf. Technol. 2017, 89, 417–437. [Google Scholar] [CrossRef]
- Woo, Y.; Wang, E.; Kim, Y.S.; Rho, H.M. A hybrid feature recognizer for machining process planning systems. CIRP Ann. 2005, 54, 397–400. [Google Scholar] [CrossRef]
- Wu, M.C.; Lit, C.R. Analysis on machined feature recognition techniques based on B-rep. Comput.-Aided Des. 1996, 28, 603–616. [Google Scholar] [CrossRef]
- Sakurai, H.; Gossard, D.C. Recognizing shape features in solid models. IEEE Comput. Graph. Appl. 1990, 10, 22–32. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. In Proceedings of the Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Li, Y.; Bu, R.; Sun, M.; Wu, W.; Di, X.; Chen, B. Pointcnn: Convolution on x-transformed points. In Proceedings of the Advances in Neural Information Processing Systems 31: Annual Conference on Neural Information Processing Systems 2018, NeurIPS 2018, Montréal, QC, Canada, 3–8 December 2018; Volume 31. [Google Scholar]
- Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic graph cnn for learning on point clouds. ACM Trans. Graph. TOG 2019, 38, 1–12. [Google Scholar] [CrossRef]
- Yao, X.; Wang, D.; Yu, T.; Luan, C.; Fu, J. A machining feature recognition approach based on hierarchical neural network for multi-feature point cloud models. J. Intell. Manuf. 2022, 1–12. [Google Scholar] [CrossRef]
- Keller, J.M.; Gray, M.R.; Givens, J.A. A fuzzy k-nearest neighbor algorithm. IEEE Trans. Syst. Man Cybern. 1985, 4, 580–585. [Google Scholar] [CrossRef]
- Nezhadarya, E.; Taghavi, E.; Razani, R.; Liu, B.; Luo, J. Adaptive hierarchical down-sampling for point cloud classification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 12956–12964. [Google Scholar]
- Tolstikhin, I.O.; Houlsby, N.; Kolesnikov, A.; Beyer, L.; Zhai, X.; Unterthiner, T.; Dosovitskiy, A. Mlp-mixer: An all-mlp architecture for vision. Adv. Neural Inf. Process. Syst. 2021, 34, 24261–24272. [Google Scholar]
- Joshi, S.; Chang, T.C. Graph-based heuristics for recognition of machined features from a 3D solid model. Comput. Aided Des. 1988, 20, 58–66. [Google Scholar] [CrossRef]
- Gao, S.; Shah, J.J. Automatic recognition of interacting machining features based on minimal condition subgraph. Comput. Aided Des. 1998, 30, 727–739. [Google Scholar] [CrossRef]
- Yeo, C.; Cheon, S.; Mun, D. Manufacturability evaluation of parts using descriptor-based machining feature recognition. Int. J. Comput. Integr. Manuf. 2021, 34, 1196–1222. [Google Scholar] [CrossRef]
- Xu, T.; Li, J.; Chen, Z. Automatic machining feature recognition based on MBD and process semantics. Comput. Ind. 2022, 142, 103736. [Google Scholar] [CrossRef]
- Shi, Y.; Zhang, Y.; Harik, R. Manufacturing feature recognition with a 2D convolutional neural network. CIRP J. Manuf. Sci. Technol. 2020, 30, 36–57. [Google Scholar] [CrossRef]
- Dimov, S.S.; Brousseau, E.B.; Setchi, R. A hybrid method for feature recognition in computer-aided design models. Proc. Inst. Mech. Eng. 2007, 221, 79–96. [Google Scholar] [CrossRef]
- Cao, W.; Robinson, T.; Hua, Y. Graph representation of 3D CAD models for machining feature recognition with deep learning. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Virtual, 17–19 August 2020; Volume 84003. [Google Scholar]
- Verma, A.K.; Rajotia, S. A hint-based machining feature recognition system for 2.5 D parts. Int. J. Prod. Res. 2008, 46, 1515–1537. [Google Scholar] [CrossRef]
- Fu, M.W.; Ong, S.K.; Lu, W.F.; Lee, I.B.H.; Nee, A.Y. An approach to identify design and manufacturing features from a data exchanged part model. Comput. Aided Des. 2003, 35, 979–993. [Google Scholar] [CrossRef]
- Nasr, E.S.A.; Kamrani, A.K. A new methodology for extracting manufacturing features from CAD system. Comput. Ind. Eng. 2006, 51, 389–415. [Google Scholar] [CrossRef]
- Li, H.; Huang, Y.; Sun, Y.; Chen, P. Hint-based generic shape feature recognition from three-dimensional B-rep models. Adv. Mech. Eng. 2015, 7, 1687814015582082. [Google Scholar] [CrossRef]
- Gong, L.; Xue, X.; Wang, T.; Wu, T.; Zhang, H.; Meng, Z. Machining Hole Feature Recognition Method and Application for Manufacturability Check. In Proceedings of the 6th International Conference on Virtual and Augmented Reality Simulations, Brisbane, Australia, 22–27 June 2014; pp. 76–84. [Google Scholar]
- Kataraki, P.S.; Abu Mansor, M.S. Auto-recognition and generation of material removal volume for regular form surface and its volumetric features using volume decomposition method. Int. J. Adv. Manuf. Technol. 2017, 90, 1479–1506. [Google Scholar] [CrossRef]
- Zubair, A.F.; Abu Mansor, M.S. Auto-recognition and part model complexity quantification of regular-freeform revolved surfaces through delta volume generations. Eng. Comput. 2020, 36, 511–526. [Google Scholar] [CrossRef]
- Kim, B.C.; Mun, D. Stepwise volume decomposition for the modification of B-rep models. Int. J. Adv. Manuf. Technol. 2014, 75, 1393–1403. [Google Scholar] [CrossRef]
- Kwon, S.; Mun, D.; Kim, B.C.; Han, S.; Suh, H.-W. B-rep model simplification using selective and iterative volume decomposition to obtain finer multi-resolution models. Comput. Aided Des. 2019, 112, 23–34. [Google Scholar] [CrossRef]
- Woo, Y.; Sakurai, H. Recognition of maximal features by volume decomposition. Comput. Aided Des. 2002, 34, 195–207. [Google Scholar] [CrossRef]
- Gupta, M.K.; Swain, A.K.; Jain, P.K. A novel approach to recognize interacting features for manufacturability evaluation of prismatic parts with orthogonal features. Int. J. Adv. Manuf. Technol. 2019, 105, 343–373. [Google Scholar] [CrossRef]
- Verma, A.K.; Rajotia, S. A hybrid machining Feature Recognition system. Int. J. Manuf. Res. 2009, 4, 343–361. [Google Scholar] [CrossRef]
- Rameshbabu, V.; Shunmugam, M.S. Hybrid feature recognition method for setup planning from STEP AP-203. Robot. Comput.-Integr. Manuf. 2009, 25, 393–408. [Google Scholar] [CrossRef]
- Jong, W.R.; Lai, P.J.; Chen, Y.W.; Ting, Y.H. Automatic process planning of mold components with integration of feature recognition and group technology. Int. J. Adv. Manuf. Technol. 2015, 78, 807–824. [Google Scholar] [CrossRef]
- Guo, L.; Zhou, M.; Lu, Y.; Yang, T.; Yang, F. A hybrid 3D feature recognition method based on rule and graph. Int. J. Comput. Integr. Manuf. 2021, 34, 257–281. [Google Scholar] [CrossRef]
- Al-wswasi, M.; Ivanov, A. A novel and smart interactive feature recognition system for rotational parts using a STEP file. Int. J. Adv. Manuf. Technol. 2019, 104, 261–284. [Google Scholar] [CrossRef]
- Sunil, V.B.; Agarwal, R.; Pande, S.S. An approach to recognize interacting features from B-Rep CAD models of prismatic machined parts using a hybrid (graph and rule based) technique. Comput. Ind. 2010, 61, 686–701. [Google Scholar] [CrossRef]
- Zhang, Z.; Jaiswal, P.; Rai, R. Featurenet: Machining feature recognition based on 3D convolution neural network. Comput. Aided Des. 2018, 101, 12–22. [Google Scholar] [CrossRef]
- Ghadai, S.; Balu, A.; Sarkar, S.; Krishnamurthy, A. Learning localized features in 3D CAD models for manufacturability analysis of drilled holes. Comput. Aided Geom. Des. 2018, 62, 263–275. [Google Scholar] [CrossRef]
- Ning, F.; Shi, Y.; Cai, M.; Xu, W. Part machining feature recognition based on a deep learning method. J. Intell. Manuf. 2021, 2021, 1–13. [Google Scholar] [CrossRef]
- Peddireddy, D.; Fu, X.; Shankar, A.; Wang, H.; Joung, B.G.; Aggarwal, V.; Jun, M.B.G. Identifying manufacturability and machining processes using deep 3D convolutional networks. J. Manuf. Process. 2021, 64, 1336–1348. [Google Scholar] [CrossRef]
- Lee, H.; Lee, J.; Kim, H.; Mun, D. Dataset and method for deep learning-based reconstruction of 3D CAD models containing machining features for mechanical parts. J. Comput. Des. Eng. 2022, 9, 114–127. [Google Scholar] [CrossRef]
- Lee, J.; Lee, H.; Mun, D. 3D convolutional neural network for machining feature recognition with gradient-based visual explanations from 3D CAD models. Sci. Rep. 2022, 12, 14864. [Google Scholar] [CrossRef] [PubMed]
- Yeo, C.; Kim, B.C.; Cheon, S.; Lee, J.; Mun, D. Machining feature recognition based on deep neural networks to support tight integration with 3D CAD systems. Sci. Rep. 2021, 11, 22147. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Zhang, Y.; He, K.; Li, D.; Xu, X.; Gong, Y. Intelligent feature recognition for STEP-NC-compliant manufacturing based on artificial bee colony algorithm and back propagation neural network. J. Manuf. Syst. 2022, 62, 792–799. [Google Scholar] [CrossRef]
- Shi, Y.; Zhang, Y.; Baek, S.; De Backer, W.; Harik, R. Manufacturability analysis for additive manufacturing using a novel feature recognition technique. Comput. Aided Des. Appl. 2018, 15, 941–952. [Google Scholar] [CrossRef]
- Shi, P.; Qi, Q.; Qin, Y.; Scott, P.J.; Jiang, X. A novel learning-based feature recognition method using multiple sectional view representation. J. Intell. Manuf. 2020, 31, 1291–1309. [Google Scholar] [CrossRef]
- Shi, P.; Qi, Q.; Qin, Y.; Scott, P.J.; Jiang, X. Intersecting machining feature localization and recognition via single shot multibox detector. IEEE Trans. Ind. Inform. 2020, 17, 3292–3302. [Google Scholar] [CrossRef]
- Shi, P.; Qi, Q.; Qin, Y.; Scott, P.J.; Jiang, X. Highly interacting machining feature recognition via small sample learning. Robot. Comput.-Integr. Manuf. 2022, 73, 102260. [Google Scholar] [CrossRef]
- Colligan, A.R.; Robinson, T.T.; Nolan, D.C.; Hua, Y. Point Cloud Dataset Creation for Machine Learning on CAD Models. Comput. Aided Des. Appl. 2021, 18, 760–771. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, S.; Zhang, Y.; Liang, J.; Wang, Z. Machining feature recognition based on a novel multi-task deep learning network. Robot. Comput.-Integr. Manuf. 2022, 77, 102369. [Google Scholar] [CrossRef]
- Worner, J.M.; Brovkina, D.; Riedel, O. Feature recognition for graph-based assembly product representation using machine learning. In Proceedings of the 2021 21st International Conference on Control, Automation and Systems (ICCAS), Jeju, Republic of Korea, 12–15 October 2021; pp. 629–635. [Google Scholar]
- Liu, C.; Li, Y.; Li, Z. A machining feature definition approach by using two-times unsupervised clustering based on historical data for process knowledge reuse. J. Manuf. Syst. 2018, 49, 16–24. [Google Scholar] [CrossRef]
- Sharma, R.; Gao, J.X. Implementation of STEP Application Protocol 224 in an automated manufacturing planning system. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2002, 216, 1277–1289. [Google Scholar] [CrossRef]
- Bowers, J.; Wang, R.; Wei, L.-Y.; Maletz, D. Parallel Poisson disk sampling with spectrum analysis on surfaces. ACM Trans. Graph. TOG 2010, 29, 1–10. [Google Scholar] [CrossRef]
- Corsini, M.; Cignoni, P.; Scopigno, R. Efficient and flexible sampling with blue noise properties of triangular meshes. IEEE Trans. Vis. Comput. Graph. 2012, 18, 914–924. [Google Scholar] [CrossRef]
- Cignoni, P.; Callieri, M.; Corsini, M.; Dellepiane, M.; Ganovelli, F.; Ranzuglia, G. Meshlab: An open-source mesh processing tool. In Proceedings of the Eurographics Italian Chapter Conference, Salerno, Italy, 2–4 July 2008; pp. 129–136. [Google Scholar]
- Brands, S. Rapid demonstration of linear relations connected by boolean operators. In Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Konstanz, Germany, 11–15 May 1997; pp. 318–333. [Google Scholar]
- Odena, A.; Dumoulin, V.; Olah, C. Deconvolution and checkerboard artifacts. Distill 2016, 1, e3. [Google Scholar] [CrossRef]
- Gardner, M.W.; Dorling, S.R. Artificial neural networks (the multilayer perceptron)—A review of applications in the atmospheric sciences. Atmos. Environ. 1998, 32, 2627–2636. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. In Proceedings of the Advances in Neural Information Processing Systems 32: Annual Conference on Neural Information Processing Systems 2019, NeurIPS 2019, Vancouver, BC, Canada, 8–14 December 2019; Volume 32. [Google Scholar]



| Model Definition | Number of Feature Types | Feature Categories | Intersecting Degrades |
|---|---|---|---|
| Model 1 | 3 | 02 + 10 + 24 | slight |
| Model 2 | 3 | 01 + 03 + 30 | slight |
| Model 3 | 4 | 01 + 03 + 15 + 23 | slight |
| Model 4 | 4 | 01 + 01 + 15 + 16 | slight |
| Model 5 | 5 | 01 + 03 + 05 + 09 + 15 | moderate |
| Model 6 | 5 | 01 + 03 + 07 + 15 + 24 | moderate |
| Model 7 | 6 | 01 + 03 + 05 + 15 + 23 + 32 | high |
| Model 8 | 7 | 01 + 02 + 03 + 04 + 07 + 08 + 30 | high |
| Model 9 | 8 | 02 + 04 + 15 + 23 + 24 + 25 + 30 + 31 | high |
| Input Point Numbers | Using Normal Vectors | Training Epoch Number | Average Epoch Time | Total Training Time | Training Model Size | Network Parameters | Overall Classification Accuracy |
|---|---|---|---|---|---|---|---|
| 256 | No | 185 | 470.9 s | 24.20 h | 0.1067 G | 5.2118M | 96.88% |
| 512 | No | 188 | 474.8 s | 24.79 h | 0.1435 G | 98.09% | |
| 1024 | No | 190 | 490.4 s | 25.88 h | 0.2172 G | 98.93% | |
| Yes | 189 | 488.8 s | 25.66 h | 0.2188 G | 99.60% |
| Methods | Input Point Numbers | Network Parameters | Overall Accuracy | Mean Class Accuracy |
|---|---|---|---|---|
| PointNet [12] | 256 | 3.469674M | 96.41% | 96.12% |
| PointNet++ [13] | 1.745569M | 96.82% | 96.58% | |
| PointCNN [14] | 0.275449M | 94.42% | 94.04% | |
| DGCNN [15] | 1.810849M | 95.02% | 94.88% | |
| MFPointNet | 5.211882M | 96.88% | 96.20% | |
| PointNet [12] | 512 | 3.469674M | 97.33% | 96.95% |
| PointNet++ [13] | 1.745569M | 98.35% | 97.99% | |
| PointCNN [14] | 0.275449M | 96.37% | 95.96% | |
| DGCNN [15] | 1.810849M | 97.75% | 97.01% | |
| MFPointNet | 5.211882M | 98.09% | 97.23% | |
| PointNet [12] | 1024 | 3.469674M | 98.05% | 97.09% |
| PointNet++ [13] | 1.745569M | 98.34% | 97.20% | |
| PointCNN [14] | 0.275449M | 98.89% | 97.75% | |
| DGCNN [15] | 1.810849M | 98.59% | 97.56% | |
| MFPointNet | 5.211882M | 98.93% | 97.99% |
| Methods | Input Point Numbers | Training Epoch Number | Average Epoch Time | Total Training Time | Model Complexity Size |
|---|---|---|---|---|---|
| PointNet [12] | 256 | 184 | 200.9 s | 10.27 h | 0.11393 G |
| PointNet++ [13] | 178 | 430.8 s | 21.30 h | 1.02956 G | |
| PointCNN [14] | 174 | 746.4 s | 36.08 h | 0.04760 G | |
| DGCNN [15] | 190 | 190.8 s | 10.07 h | 0.62470G | |
| MFPointNet | 185 | 470.9 s | 24.20 h | 0.10676 G | |
| PointNet [12] | 512 | 165 | 199.8 s | 9.16 h | 0.22484 G |
| PointNet++ [13] | 196 | 441.3 s | 24.03 h | 2.09457 G | |
| PointCNN [14] | 179 | 2127.7 s | 105 h | 0.06665 G | |
| DGCNN [15] | 175 | 194.0 s | 9.43 h | 1.24821 G | |
| MFPointNet | 188 | 474.8 s | 24.79 h | 0.14359 G | |
| PointNet [12] | 1024 | 200 | 200.2 s | 11.12 h | 0.44704 G |
| PointNet++ [13] | 199 | 447.2 s | 24.72 h | 4.01569 G | |
| PointCNN [14] | 188 | 7340.8 s | 383.35 h | 0.10476 G | |
| DGCNN [15] | 185 | 199.8 s | 10.27 h | 2.49523 G | |
| MFPointNet | 194 | 490.4 s | 26.43 h | 0.21725 G |
| Methods | Input Point Numbers | Using Normal Vectors | Network Parameters | Overall Accuracy | Mean Class Accuracy |
|---|---|---|---|---|---|
| PointNet [12] | 1024 | No | 3.469674M | 98.05% | 97.09% |
| PointNet++ [13] | 1.745569M | 98.34% | 97.20% | ||
| PointCNN [14] | 0.275449M | 98.89% | 97.75% | ||
| DGCNN [15] | 1.810849M | 98.59% | 97.56% | ||
| MFPointNet | 5.211882M | 98.93% | 97.99% | ||
| PointNet [12] | 1024 | Yes | 3.470058M | 99.94% | 98.56% |
| PointNet++ [13] | 1.746049M | 99.96% | 98.79% | ||
| PointCNN [14] | 0.280056M | 99.03% | 98.09% | ||
| DGCNN [15] | 1.820042M | 99.54% | 98.23% | ||
| MFPointNet | 5.211882M | 99.80% | 98.55% |
| Methods | Input Point Numbers | Using Normal Vectors | Training Epoch Number | Average Epoch Time | Total Training Time | Model Complexity Size |
|---|---|---|---|---|---|---|
| PointNet [12] | 1024 | No | 200 | 200.2 s | 11.12 h | 0.44704 G |
| PointNet++ [13] | 199 | 447.2 s | 24.72 h | 4.01569 G | ||
| PointCNN [14] | 188 | 7340.8 s | 383.35 h | 0.10476 G | ||
| DGCNN [15] | 185 | 199.8 s | 10.27 h | 2.49523 G | ||
| MFPointNet | 194 | 490.4 s | 26.43 h | 0.21725 G | ||
| PointNet [12] | 1024 | Yes | 147 | 200.5 s | 8.19 h | 0.44664 G |
| PointNet++ [13] | 189 | 448.2 s | 23.53 h | 4.02960 G | ||
| PointCNN [14] | 191 | 7336.6 s | 389.25 h | 0.11257 G | ||
| DGCNN [15] | 190 | 200.1 s | 10.56 h | 2.50613 G | ||
| MFPointNet | 189 | 488.8 s | 25.66 h | 0.21885 G |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, R.; Wu, H.; Peng, Y. MFPointNet: A Point Cloud-Based Neural Network Using Selective Downsampling Layer for Machining Feature Recognition. Machines 2022, 10, 1165. https://doi.org/10.3390/machines10121165
Lei R, Wu H, Peng Y. MFPointNet: A Point Cloud-Based Neural Network Using Selective Downsampling Layer for Machining Feature Recognition. Machines. 2022; 10(12):1165. https://doi.org/10.3390/machines10121165
Chicago/Turabian StyleLei, Ruoshan, Hongjin Wu, and Yibing Peng. 2022. "MFPointNet: A Point Cloud-Based Neural Network Using Selective Downsampling Layer for Machining Feature Recognition" Machines 10, no. 12: 1165. https://doi.org/10.3390/machines10121165
APA StyleLei, R., Wu, H., & Peng, Y. (2022). MFPointNet: A Point Cloud-Based Neural Network Using Selective Downsampling Layer for Machining Feature Recognition. Machines, 10(12), 1165. https://doi.org/10.3390/machines10121165







