Type Synthesis of 4-DOF Non-Overconstrained Parallel Mechanisms with Symmetrical Structures
Abstract
1. Introduction
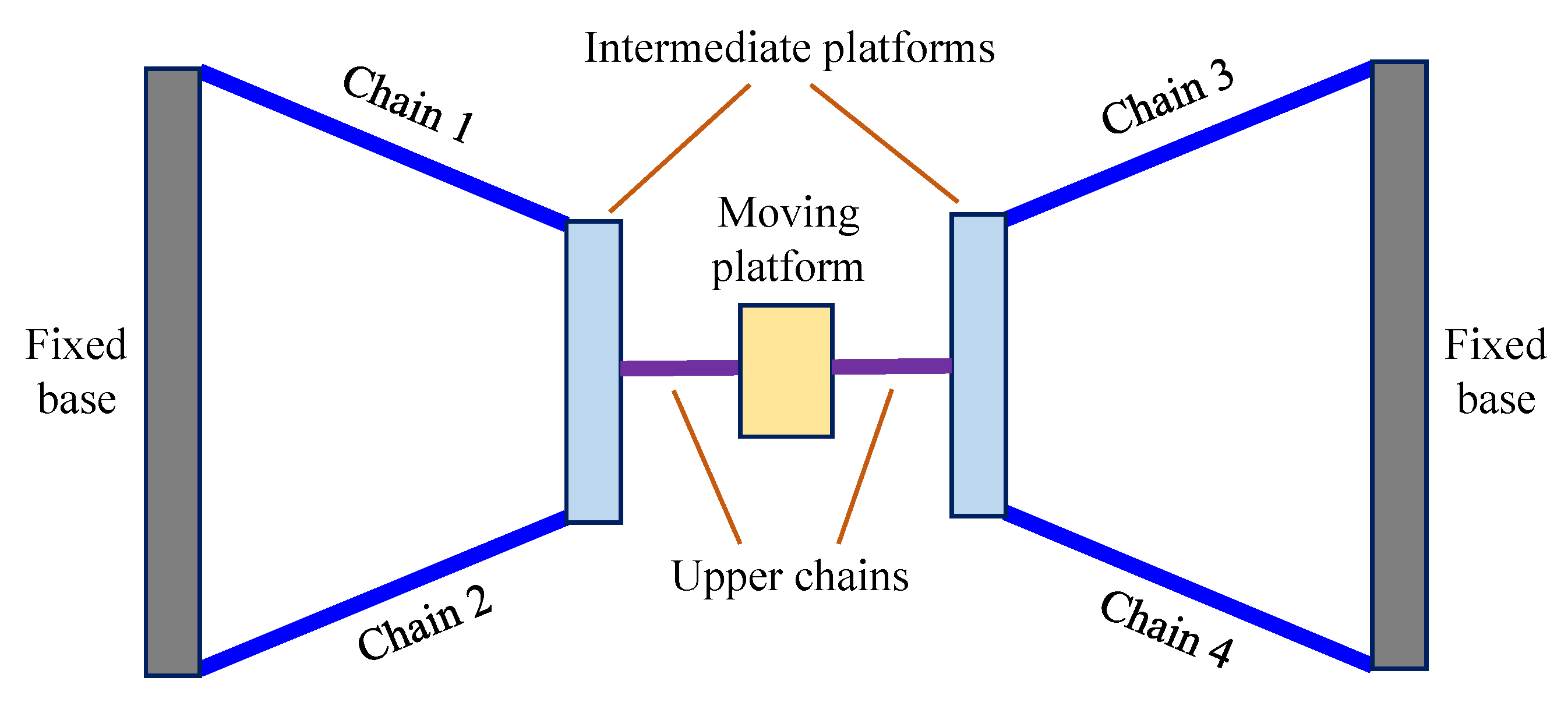
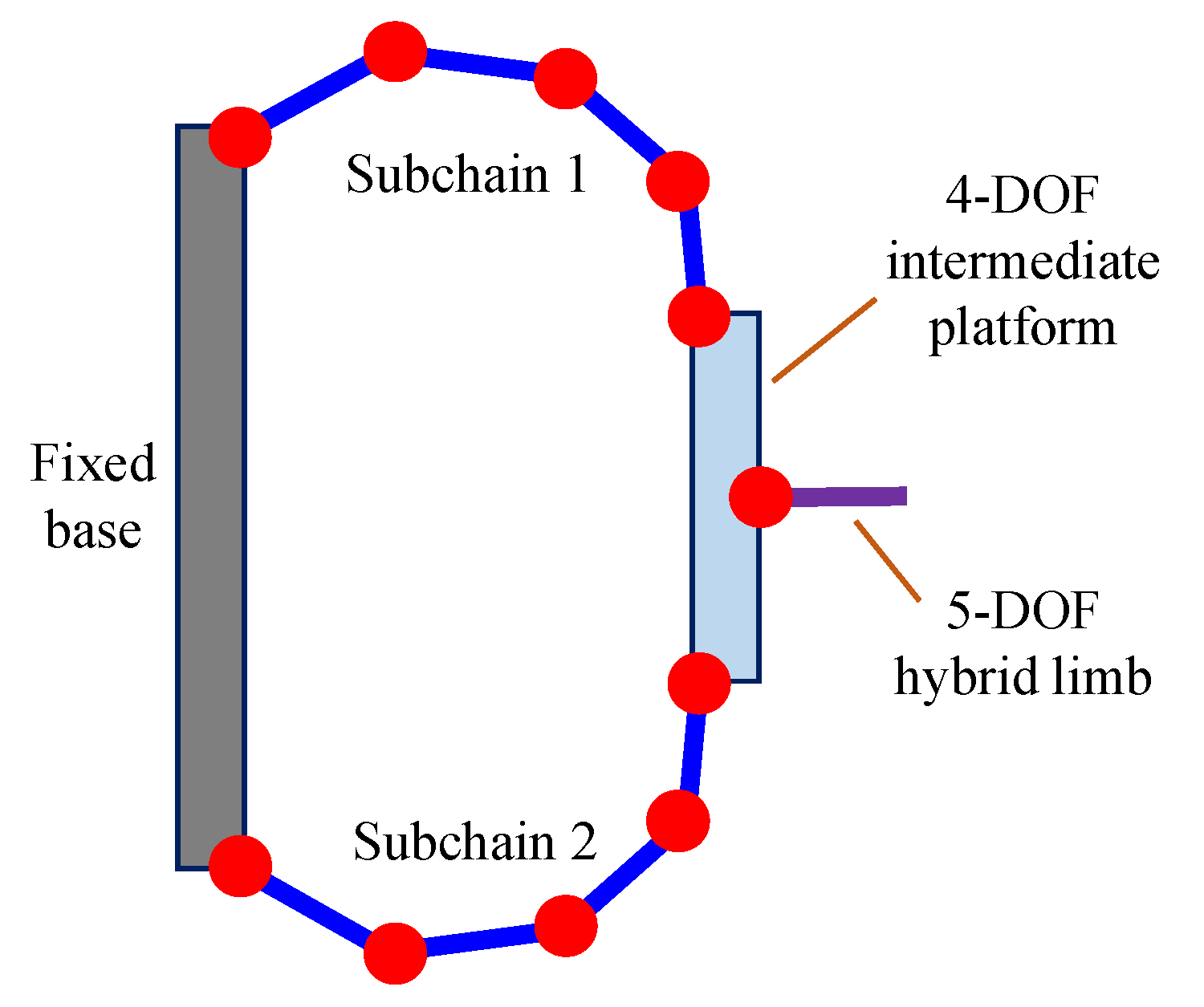
2. Topological Structure of 4-DOF PMs
3. Construction of Hybrid Limbs
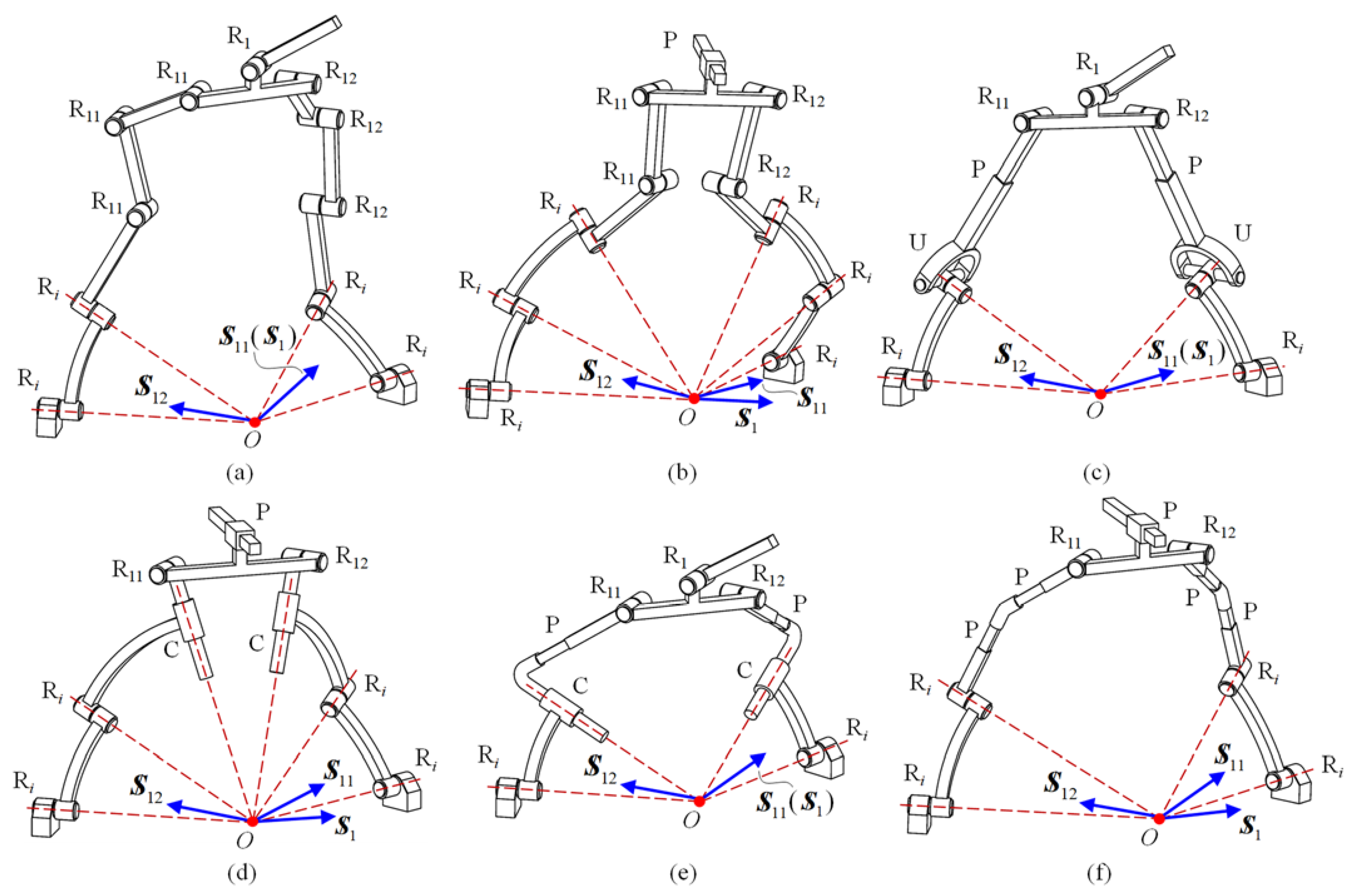
3.1. Synthesis of F-Hybrid Limbs
3.2. Synthesis of C-Hybrid Limbs
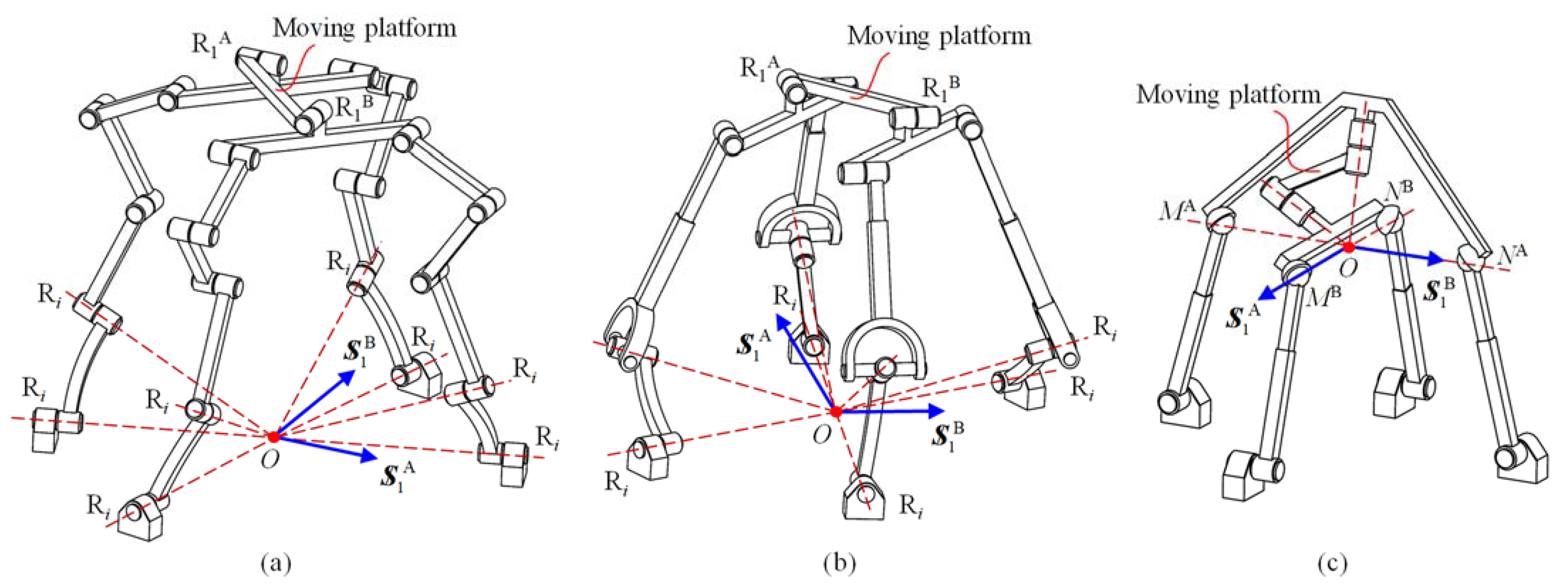
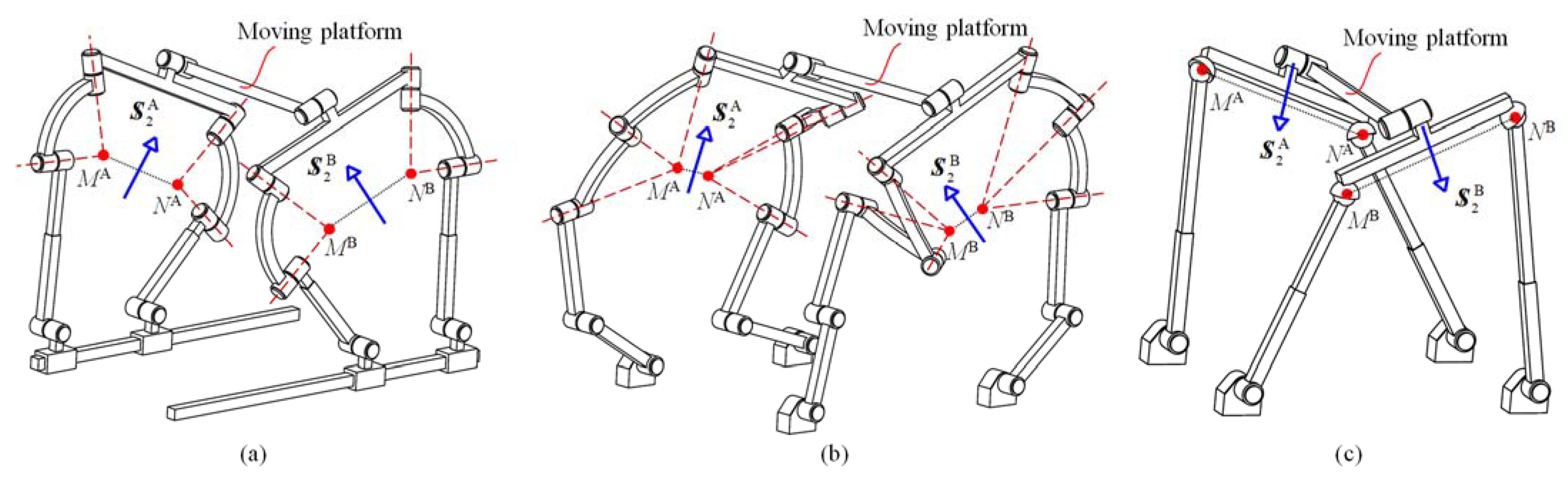
4. Construction of 4-DOF PMs
4.1. 3R1T Non-Overconstrained PMs
4.2. 2R2T Non-Overconstrained PMs
4.3. 1R3T Non-Overconstrained PMs
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pierrot, F.; Reynaud, C.; Fournier, A. DELTA: A simple and efficient parallel robot. Robotica 1990, 8, 105–109. [Google Scholar] [CrossRef]
- Gasparetto, A.; Scalera, L. From the Unimate to the Delta robot: The early decades of Industrial Robotics. In Explorations in the History and Heritage of Machines and Mechanisms; Springer: Berlin/Heidelberg, Germany, 2019; pp. 284–295. [Google Scholar]
- Hunt, K.H. Structural kinematics of in-parallel-actuated robot-arms. J. Mech. Transm. Autom. Des. 1983, 105, 705–712. [Google Scholar] [CrossRef]
- Ma, Y.; Tian, Y.; Song, Y. A Screw Theory-Based Approach for Conservative Stiffness Mapping of 3-PRS Parallel Mechanism. In 2022 WRC Symposium on Advanced Robotics and Automation (WRC SARA); IEEE: Beijing, China, 2022; pp. 19–24. [Google Scholar]
- Pierrot, F.; Krut, S.; Nabat, V. Four-Dof PKM with articulated travelling-plate. In Proceedings of the Parallel Kinematics Seminar, Chemnitz, Germany, 25–26 April 2006; pp. 25–26. [Google Scholar]
- Liu, Y.; Kong, M.; Wan, N.; Ben-Tzvi, P. A Geometric Approach to Obtain the Closed-Form Forward Kinematics of H4 Parallel Robot. J. Mech. Robot. 2018, 10, 051013. [Google Scholar] [CrossRef]
- Fang, Y.; Tsai, L.W. Structure synthesis of a class of 4-DoF and 5-DoF parallel manipulators with identical limb structures. Int. J. Robot. Res. 2002, 21, 799–810. [Google Scholar] [CrossRef]
- Tsai, L.W. Systematic enumeration of parallel manipulators. In Parallel Kinematic Machines; Springer: London, UK, 1999; pp. 33–49. [Google Scholar]
- Huang, Z.; Li, Q.C. General methodology for type synthesis of symmetrical lower-mobility parallel manipulators and several novel manipulators. Int. J. Robot. Res. 2002, 21, 131–145. [Google Scholar] [CrossRef]
- Huang, Z.; Li, Q.C. Type Synthesis of Symmetrical Lower-Mobility Parallel Mechanisms Using the Constraint-Synthesis Method. Int. J. Robot. Res. 2003, 22, 59–79. [Google Scholar] [CrossRef]
- Kong, X.; Gosselin, C.M. Type synthesis of 3T1R 4-DOF parallel manipulators based on screw theory. IEEE Trans. Robot. Autom. 2004, 20, 181–190. [Google Scholar] [CrossRef]
- Kong, X.; Gosselin, C.M. Type synthesis of 5-DOF parallel manipulators based on screw theory. J. Robot. Syst. 2005, 22, 535–547. [Google Scholar] [CrossRef]
- Kong, X.; Gosselin, C.M. Type synthesis of 4-DOF SP-equivalent parallel manipulators: A virtual chain approach. Mech. Mach. Theory 2006, 41, 1306–1319. [Google Scholar] [CrossRef]
- Meng, X.; Gao, F.; Wu, S.; Ge, Q.J. Type synthesis of parallel robotic mechanisms: Framework and brief review. Mech. Mach. Theory 2014, 78, 177–186. [Google Scholar] [CrossRef]
- Xie, F.; Li, T.; Liu, X. Type synthesis of 4-DOF parallel kinematic mechanisms based on Grassmann line geometry and atlas method. Chin. J. Mech. Eng. 2013, 26, 1073–1081. [Google Scholar] [CrossRef]
- Xie, F.; Liu, X.J. Design and development of a high-speed and high-rotation robot with four identical arms and a single platform. J. Mech. Robot. 2015, 7, 041015. [Google Scholar] [CrossRef]
- Li, Q.; Hervé, J.M.; Ye, W. Geometric Method for Type Synthesis of Parallel Manipulators; Springer: Singapore, 2020. [Google Scholar]
- Zhao, T.S.; Dai, J.S.; Huang, Z. Geometric Analysis of Overconstrained Parallel Manipulators with Three and Four Degrees of Freedom. JSME Int. J. Ser. C 2002, 45, 730–740. [Google Scholar] [CrossRef][Green Version]
- Guo, S.; Wang, C.; Qu, H.; Fang, Y. A novel 4-RRCR parallel mechanism based on screw theory and its kinematics analysis. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2013, 227, 2039–2048. [Google Scholar] [CrossRef]
- Amine, S.; Masouleh, M.T.; Caro, S.; Wenger, P.; Gosselin, C.M. Singularity Conditions of 3T1R Parallel Manipulators With Identical Limb Structures. J. Mech. Robot. 2012, 4, 011011. [Google Scholar] [CrossRef]
- Masouleh, M.T.; Gosselin, C.; Husty, M.; Walter, D.R. Forward kinematic problem of 5-RPUR parallel mechanisms (3T2R) with identical limb structures. Mech. Mach. Theory 2011, 46, 945–959. [Google Scholar] [CrossRef]
- Cao, W.; Ding, H. A method for solving all joint reactions of 3R2T parallel mechanisms with complicated structures and mul-tiple redundant constraints. Mech. Mach. Theory 2018, 121, 718–730. [Google Scholar] [CrossRef]
- Zhu, S.-J.; Huang, Z. Eighteen fully symmetrical 5-DoF 3R2T parallel manipulators with better actuating modes. Int. J. Adv. Manuf. Technol. 2007, 34, 406–412. [Google Scholar] [CrossRef]
- Dai, J.S.; Huang, Z.; Lipkin, H. Mobility of overconstrained parallel mechanisms. J. Mech. Des. 2006, 128, 220–229. [Google Scholar] [CrossRef]
- Fang, Y.; Tsai, L.W. Enumeration of a class of overconstrained mechanisms using the theory of reciprocal screws. Mech. Mach. Theory 2004, 39, 1175–1187. [Google Scholar] [CrossRef]
- Gan, D.; Dai, J.S. Geometry constraint and branch motion evolution of 3-PUP parallel mechanisms with bifurcated motion. Mech. Mach. Theory 2013, 61, 168–183. [Google Scholar] [CrossRef]
- Zhang, K.; Dai, J.S.; Fang, Y. Constraint analysis and bifurcated motion of the 3PUP parallel mechanism. Mech. Mach. Theory 2012, 49, 256–269. [Google Scholar] [CrossRef]
- Ruggiu, M.; Kong, X. Mobility and kinematic analysis of a parallel mechanism with both PPR and planar operation modes. Mech. Mach. Theory 2012, 55, 77–90. [Google Scholar] [CrossRef]
- Kong, X.; Yu, J. Type Synthesis of Two-Degrees-of-Freedom 3-4R Parallel Mechanisms With Both Spherical Translation Mode and Sphere-on-Sphere Rolling Mode. J. Mech. Robot. 2015, 7, 041018. [Google Scholar] [CrossRef]
- Krut, S.; Benoit, M.; Ota, H.; Pierrot, F. I4: A new parallel mechanism for Scara motions. In 2003 IEEE International Conference on Robotics and Automation (Cat. No. 03CH37422); IEEE: Taipei, Taiwan, 2003; Volume 2, pp. 1875–1880. [Google Scholar]
- Guo, S.; Fang, Y.; Qu, H. Type synthesis of 4-DOF nonoverconstrained parallel mechanisms based on screw theory. Robotica 2012, 30, 31–37. [Google Scholar] [CrossRef]
- Sun, T.; Song, Y.; Gao, H.; Qi, Y. Topology Synthesis of a 1-Translational and 3-Rotational Parallel Manipulator with an Articulated Traveling Plate. J. Mech. Robot. 2015, 7, 31015. [Google Scholar] [CrossRef]
- He, J.; Gao, F.; Meng, X.; Guo, W. Type synthesis for 4-DOF parallel press mechanism using GF set theory. Chin. J. Mech. Eng. 2015, 28, 851–859. [Google Scholar] [CrossRef]
- Murray, R.C.; Ophaswongse, C.; Agrawal, S.K. Design of a wheelchair robot for active postural support. J. Mech. Robot. 2019, 11, 020911. [Google Scholar] [CrossRef]
- Wang, G.; Wang, L. Dynamics investigation of spatial parallel mechanism considering rod flexibility and spherical joint clearance. Mech. Mach. Theory 2019, 137, 83–107. [Google Scholar] [CrossRef]
- Song, Y.; Gao, H.; Sun, T.; Dong, G.; Lian, B.; Qi, Y. Kinematic analysis and optimal design of a novel 1T3R parallel manipulator with an articulated travelling plate. Robot. Comput. Manuf. 2014, 30, 508–516. [Google Scholar] [CrossRef]
- Gan, D.; Dai, J.S.; Dias, J.; Umer, R.; Seneviratne, L. Singularity-Free Workspace Aimed Optimal Design of a 2T2R Parallel Mechanism for Automated Fiber Placement. J. Mech. Robot. 2015, 7, 041022. [Google Scholar] [CrossRef]



| Limb Type | Limb with Single-DOF Joints | Limb with Composite Joints |
|---|---|---|
| [5R-5R]-R | [RiRiRiR11R11-RiRiRiR12R12]-R1 | [RiRiUR11-RiRiUR11]-R1 |
| [RiRiR11R11R11-RiRiR12R12R12]-R1 | [RiUR11R11-RiUR11R11]-R1 | |
| [5R-5R]-P | [RiRiRiR11R11-RiRiRiR12R12]-P | [RiRiUR11-RiRiUR11]-P |
| [RiRiR11R11R11-RiRiR12R12R12]-P | [RiUR11R11-RiUR11R11]-P | |
| [4R1P-4R1P]-R | [RiRiRiR11P-RiRiRiR12P]-R1 | [RiRiUP-RiRiUP]-R1 |
| [RiRiRiPR11-RiRiRiPR12]-R1 | [RiRiCR11-RiRiCR12]-R1 | |
| [RiRiR11R11P-RiRiR12R12P]-R1 | [RiUR11P-RiUR12P]-R1 | |
| [RiRiR11PR11-RiRiR12PR12]-R1 | [RiUPR11-RiUPR12]-R1 | |
| [RiRiPR11R11-RiRiPR12R12]-R1 | [RiCR11R11-RiCR12R12]-R1 | |
| [4R1P-4R1P]-P | [RiRiRiR11P-RiRiRiR12P]-P | [RiRiUP-RiRiUP]-P |
| [RiRiRiPR11-RiRiRiPR12]-P | [RiRiCR11-RiRiCR12]-P | |
| [RiRiR11R11P-RiRiR12R12P]-P | [RiUR11P-RiUR12P]-P | |
| [RiRiR11PR11-RiRiR12PR12]-P | [RiUPR11-RiUPR12]-P | |
| [RiRiPR11R11-RiRiPR12R12]-P | [RiCR11R11-RiCR12R12]-P | |
| [3R2P-3R2P]-R | [RiRiRiPP-RiRiRiPP]-R1 | [RiRiCP-RiRiCP]-R1 |
| [RiRiR11PP-RiRiR12PP]-R1 | [RiUPP-RiUPP]-R1 | |
| [RiRiPPR11-RiRiPPR12]-R1 | [RiCPR11-RiCPR12]-R1 | |
| [RiRiPR11P-RiRiPR12P]-R1 | [RiCR11P-RiCR12P]-R1 | |
| [3R2P-3R2P]-P | [RiRiRiPP-RiRiRiPP]-P | [RiRiCP-RiRiCP]-P |
| [RiRiR11PP-RiRiR12PP]-P | [RiUPP-RiUPP]-P | |
| [RiRiPPR11-RiRiPPR12]-P | [RiCPR11-RiCPR12]-P | |
| [RiRiPR11P-RiRiPR12P]-P | [RiCR11P-RiCR12P]-P |
| Limb Type | Limb with Single-DOF Joints | Limb with Composite Joints |
|---|---|---|
| [5R-5R]-R | [R1R1RMRMRM-R1R1RNRNRN]-RO [R1R1R1RMRM-R1R1R1RNRN]-RO | [R1URMRM-R1URNRN]-RO [R1R1URM-R1R1URN]-RO [R1R1S-R1R1S]-RO |
| [4R1P-4R1P]-R | [R1PRMRMRM-R1PRNRNRN]-RO [PR1RMRMRM-PR1RNRNRN]-RO [PR1R1RMRM-PR1R1RNRN]-RO [R1PR1RMRM-R1PR1RNRN]-RO [R1R1PRMRM-R1R1PRNRN]-RO | [R1CRMRM-R1CRNRN]-RO [PURMRM-PURNRN]-RO [PR1URM-PR1URN]-RO [R1PURM-R1PURN]-RO [R1R1CRM-R1R1CRN]-RO [R1PS-R1PS]-RO [PR1S-PR1S]-RO |
| [3R2P-3R2P]-R | [PPRMRMRM-PPRNRNRN]-RO [PPR1RMRM-PPR1RNRN]-RO [R1PPRMRM-R1PPRNRN]-RO [PR1PRMRM-PR1PRNRN]-RO | [PCRMRM-PCRNRN]-RO [PPURM-PPURN]-RO [R1PCRM-R1PCRN]-RO [PR1CRM-PR1CRN]-RO [PPS-PPS]-RO |
| Limb Type | Limb with Single-DOF Joints | Limb with Composite Joints |
|---|---|---|
| [5R-5R]-R | [R1R1RMRMRM-R1R1RNRNRN]-RMN [R1R1R1RMRM-R1R1R1RNRN]-RMN | [R1URMRM-R1URNRN]-RMN [R1R1URM-R1R1URN]-RMN [R1R1S-R1R1S]-RMN |
| [5R-5R]-P | [R1R1RMRMRM-R1R1RNRNRN]-P [R1R1R1RMRM-R1R1R1RNRN]-P | [R1URMRM-R1URNRN]-P [R1R1URM-R1R1URN]-P [R1R1S-R1R1S]-P |
| [4R1P-4R1P]-R | [R1PRMRMRM-R1PRNRNRN]-RMN [PR1RMRMRM-PR1RNRNRN]-RMN [PR1R1RMRM-PR1R1RNRN]-RMN [R1PR1RMRM-R1PR1RNRN]-RMN [R1R1PRMRM-R1R1PRNRN]-RMN | [R1CRMRM-R1CRNRN]-RMN [PURMRM-PURNRN]-RMN [PR1URM-PR1URN]-RMN [R1PURM-R1PURN]-RMN [R1R1CRM-R1R1CRN]-RMN [R1PS-R1PS]-RMN [PR1S-PR1S]-RMN |
| [4R1P-4R1P]-P | [R1PRMRMRM-R1PRNRNRN]-P [PR1RMRMRM-PR1RNRNRN]-P [PR1R1RMRM-PR1R1RNRN]-P [R1PR1RMRM-R1PR1RNRN]-P [R1R1PRMRM-R1R1PRNRN]-P | [R1CRMRM-R1CRNRN]-P [PURMRM-PURNRN]-P [PR1URM-PR1URN]-P [R1PURM-R1PURN]-P [R1R1CRM-R1R1CRN]-P [R1PS-R1PS]-P [PR1S-PR1S]-P |
| [3R2P-3R2P]-R | [PPRMRMRM-PPRNRNRN]-RMN [PPR1RMRM-PPR1RNRN]-RMN [R1PPRMRM-R1PPRNRN]-RMN [PR1PRMRM-PR1PRNRN]-RMN | [PCRMRM-PCRNRN]-RMN [PPURM-PPURN]-RMN [R1PCRM-R1PCRN]-RMN [PR1CRM-PR1CRN]-RMN [PPS-PPS]-RMN |
| [3R2P-3R2P]-P | [PPRMRMRM-PPRNRNRN]-P [PPR1RMRM-PPR1RNRN]-P [R1PPRMRM-R1PPRNRN]-P [PR1PRMRM-PR1PRNRN]-P | [PCRMRM-PCRNRN]-P [PPURM-PPURN]-P [R1PCRM-R1PCRN]-P [PR1CRM-PR1CRN]-P [PPS-PPS]-P |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, W.; Li, Q.; Chai, X. Type Synthesis of 4-DOF Non-Overconstrained Parallel Mechanisms with Symmetrical Structures. Machines 2022, 10, 1123. https://doi.org/10.3390/machines10121123
Ye W, Li Q, Chai X. Type Synthesis of 4-DOF Non-Overconstrained Parallel Mechanisms with Symmetrical Structures. Machines. 2022; 10(12):1123. https://doi.org/10.3390/machines10121123
Chicago/Turabian StyleYe, Wei, Qinchuan Li, and Xinxue Chai. 2022. "Type Synthesis of 4-DOF Non-Overconstrained Parallel Mechanisms with Symmetrical Structures" Machines 10, no. 12: 1123. https://doi.org/10.3390/machines10121123
APA StyleYe, W., Li, Q., & Chai, X. (2022). Type Synthesis of 4-DOF Non-Overconstrained Parallel Mechanisms with Symmetrical Structures. Machines, 10(12), 1123. https://doi.org/10.3390/machines10121123





