Rigid-Body Guidance Synthesis of Noncircular Gear-Five-Bar Mechanisms and Its Application in a Knee Joint Rehabilitation Device
Abstract
1. Introduction
2. Materials and Methods
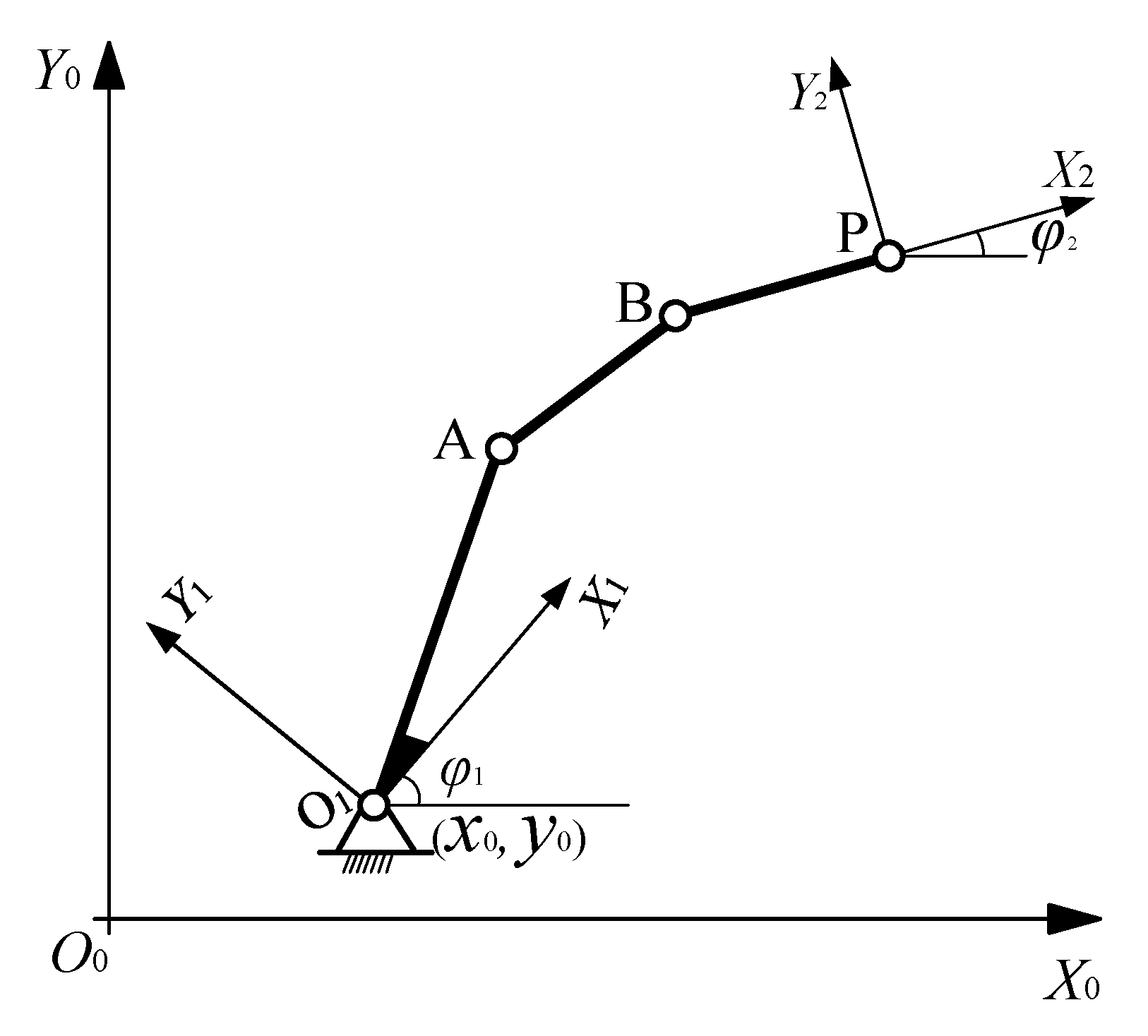
2.1. Introduction to Kinematic Mapping
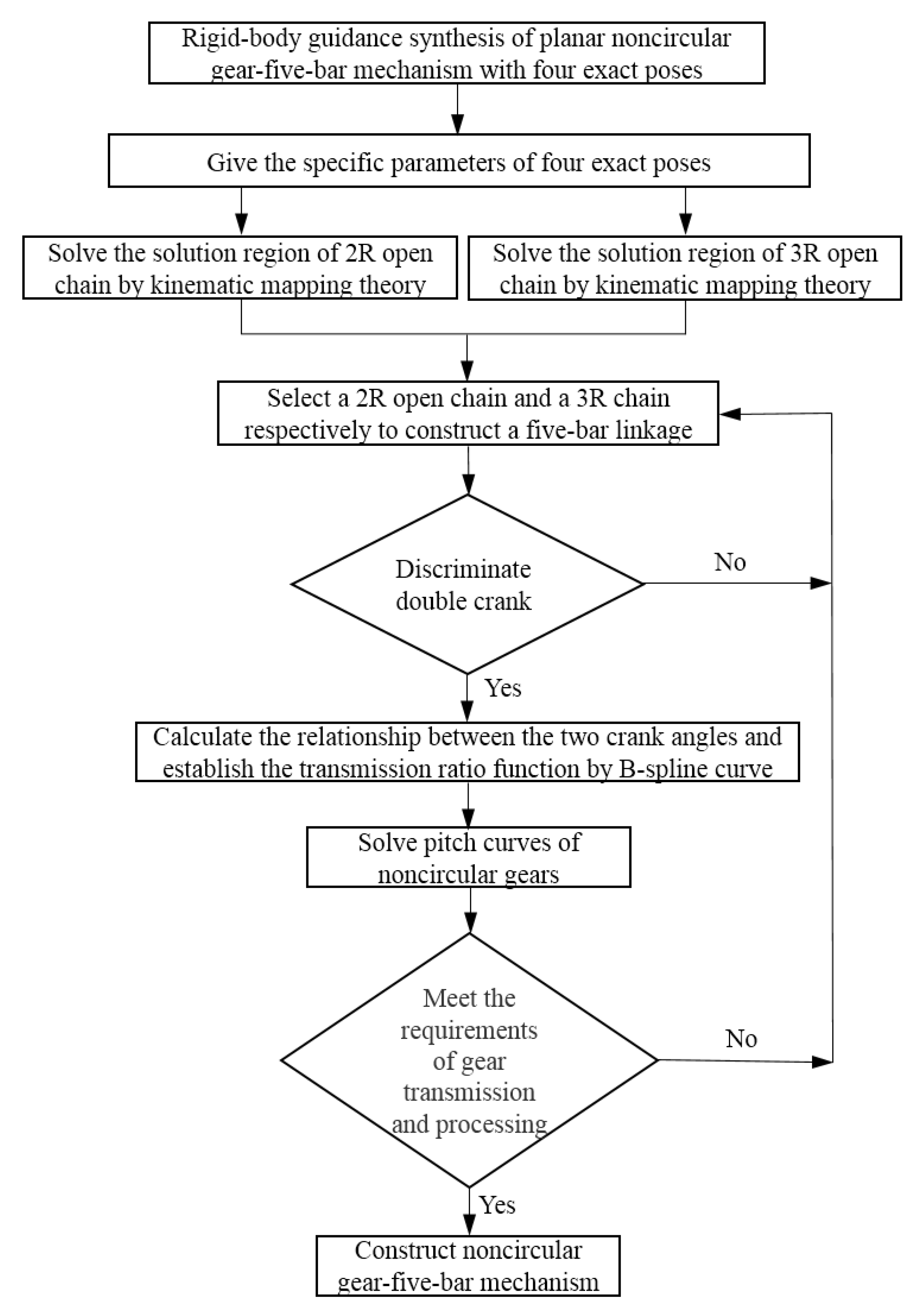
2.2. Rigid-Body Guidance of Noncircular Gear-Five-Bar Mechanism with Four Exact Pose Constraints
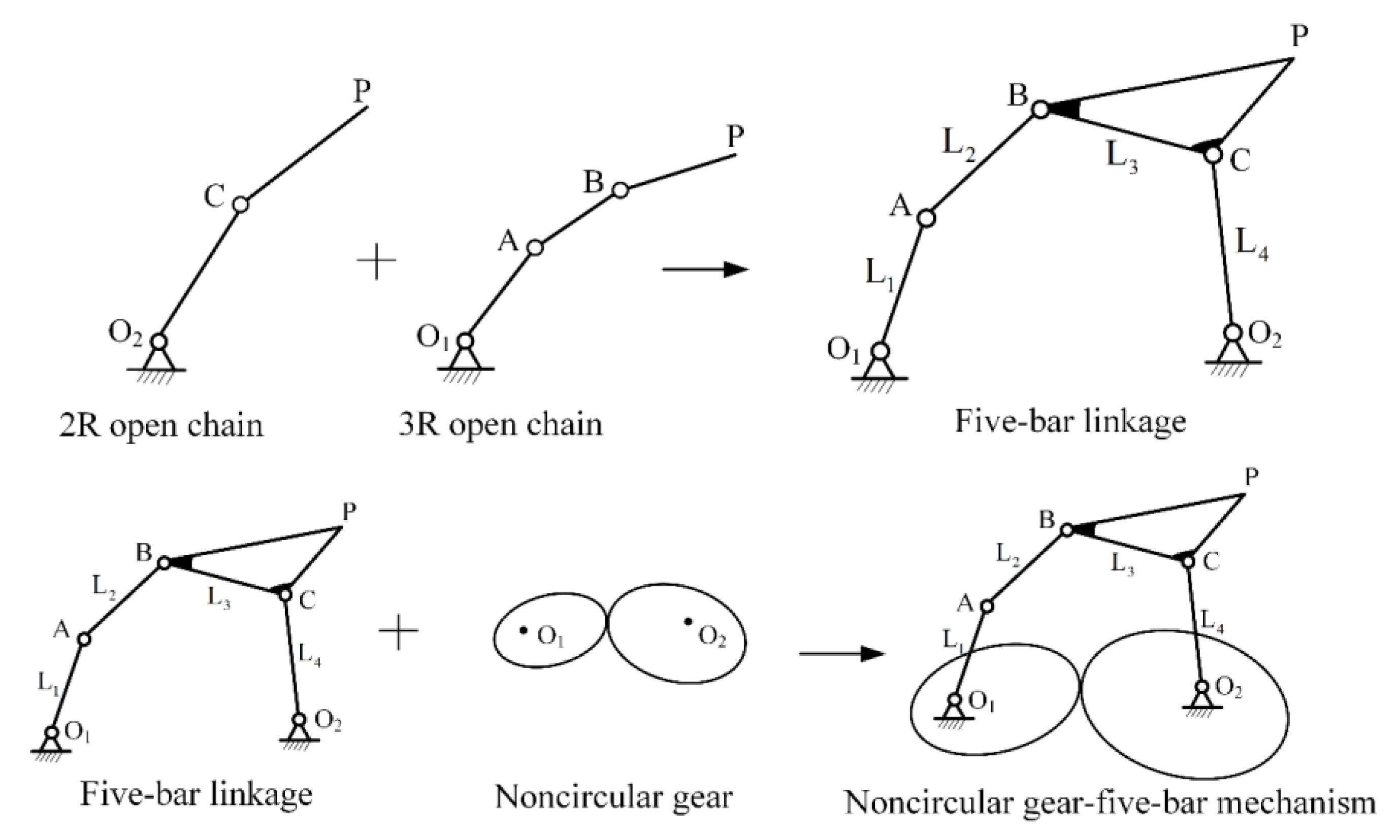
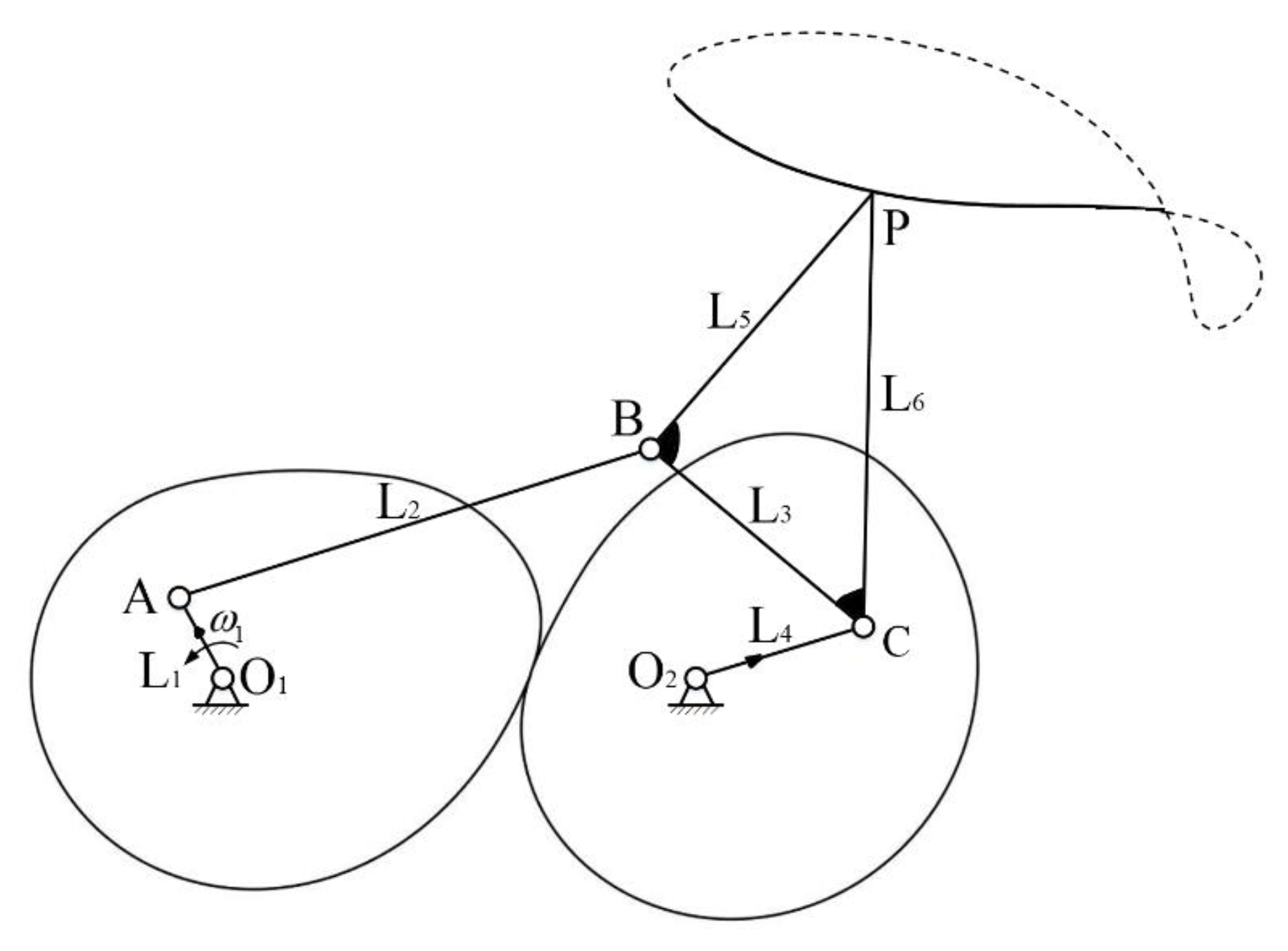
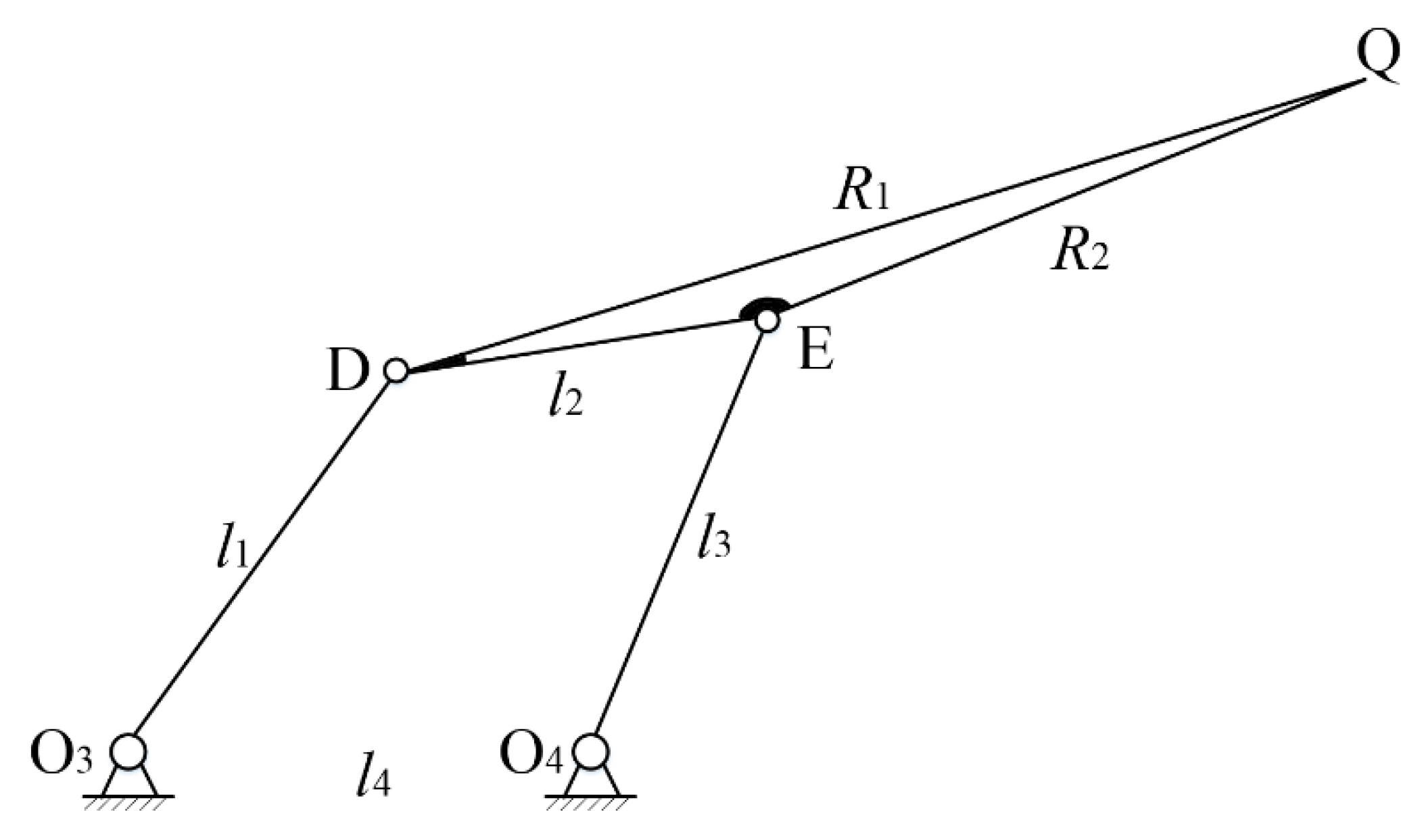
2.2.1. Synthesis of Five-Bar Linkages
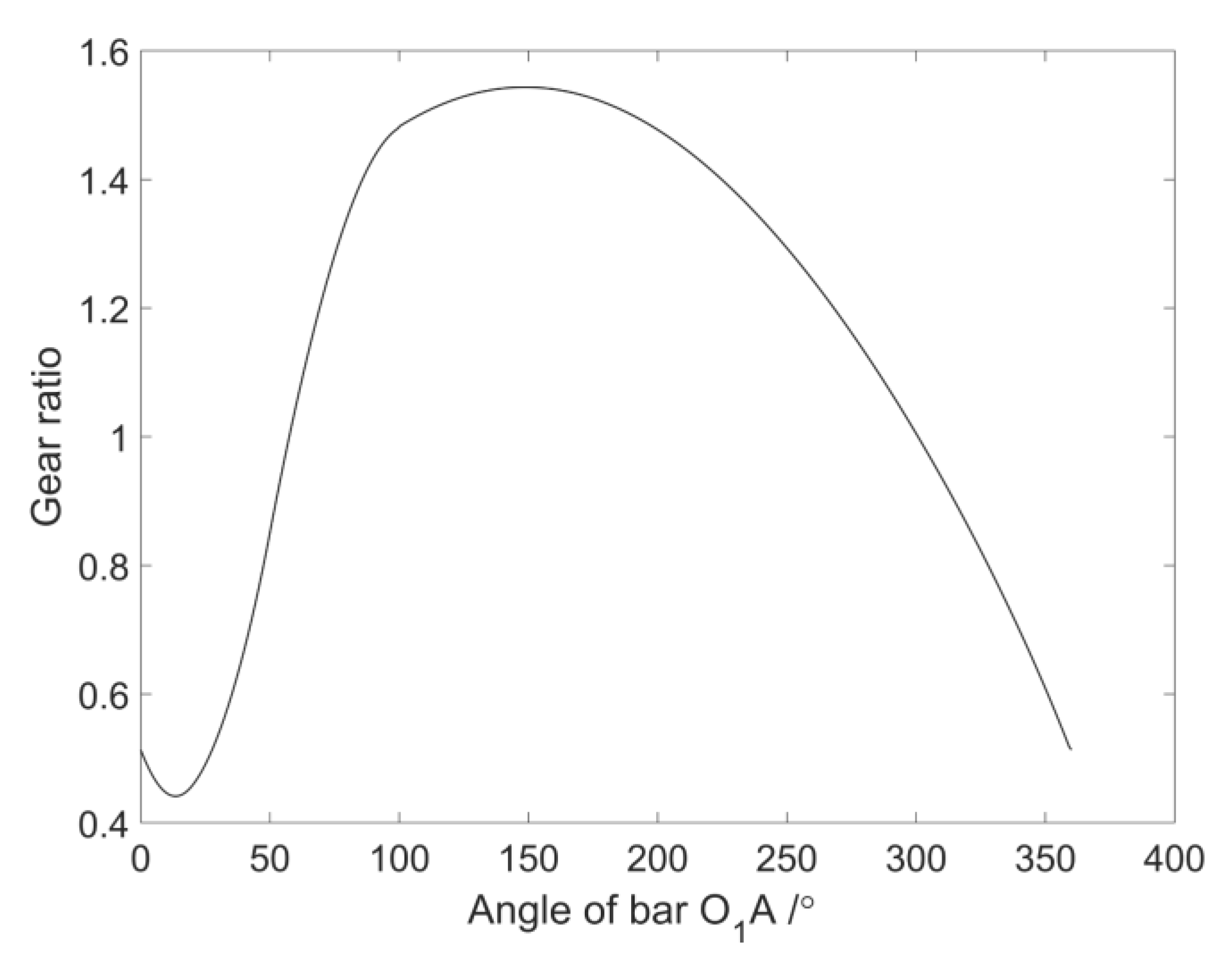
2.2.2. Modeling of Noncircular Gears
3. Results and Discussion
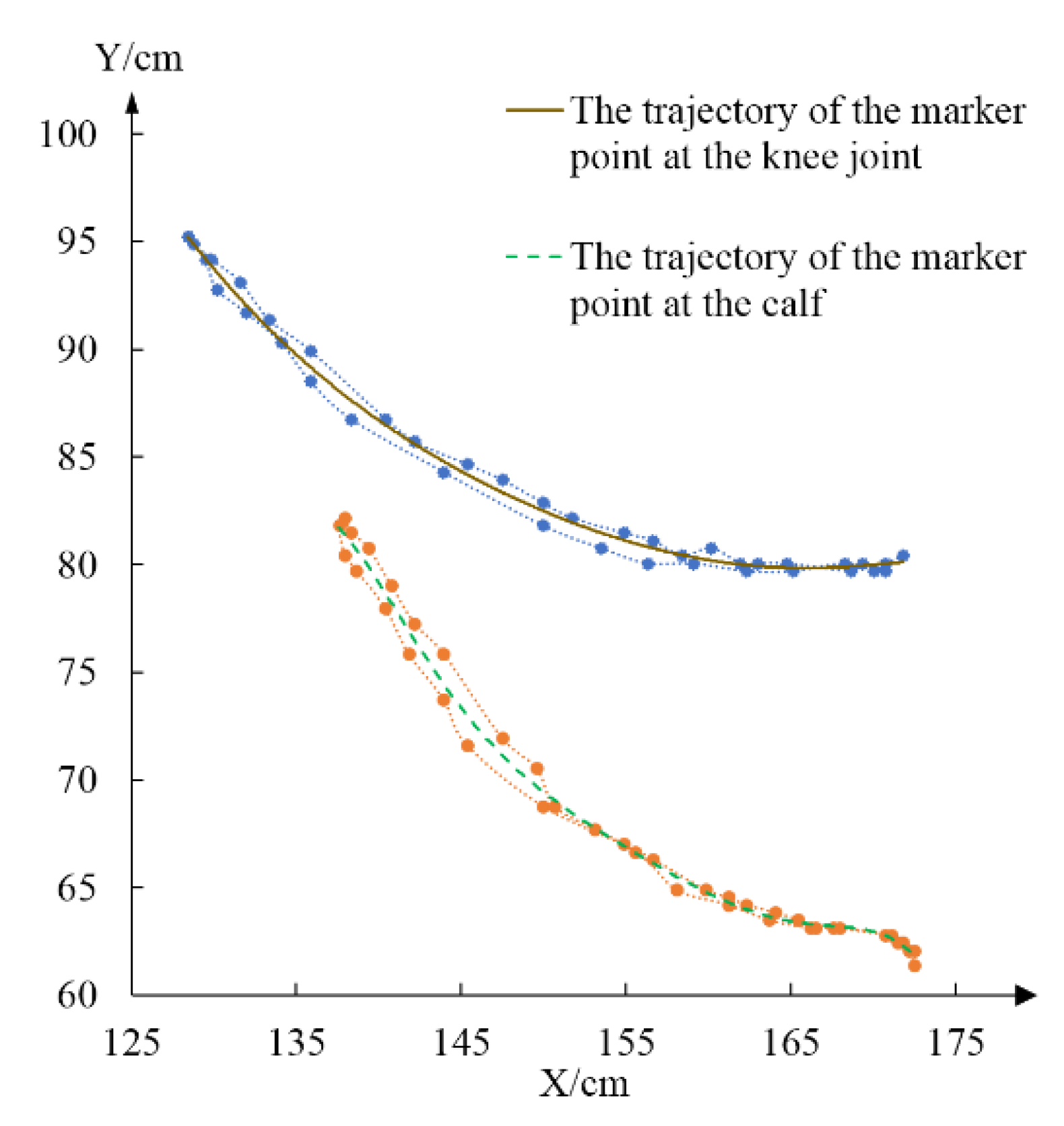
3.1. Acquisition of Knee Joint Motion Data
3.2. Synthesis of Noncircular Gear-Five-Bar Mechanism
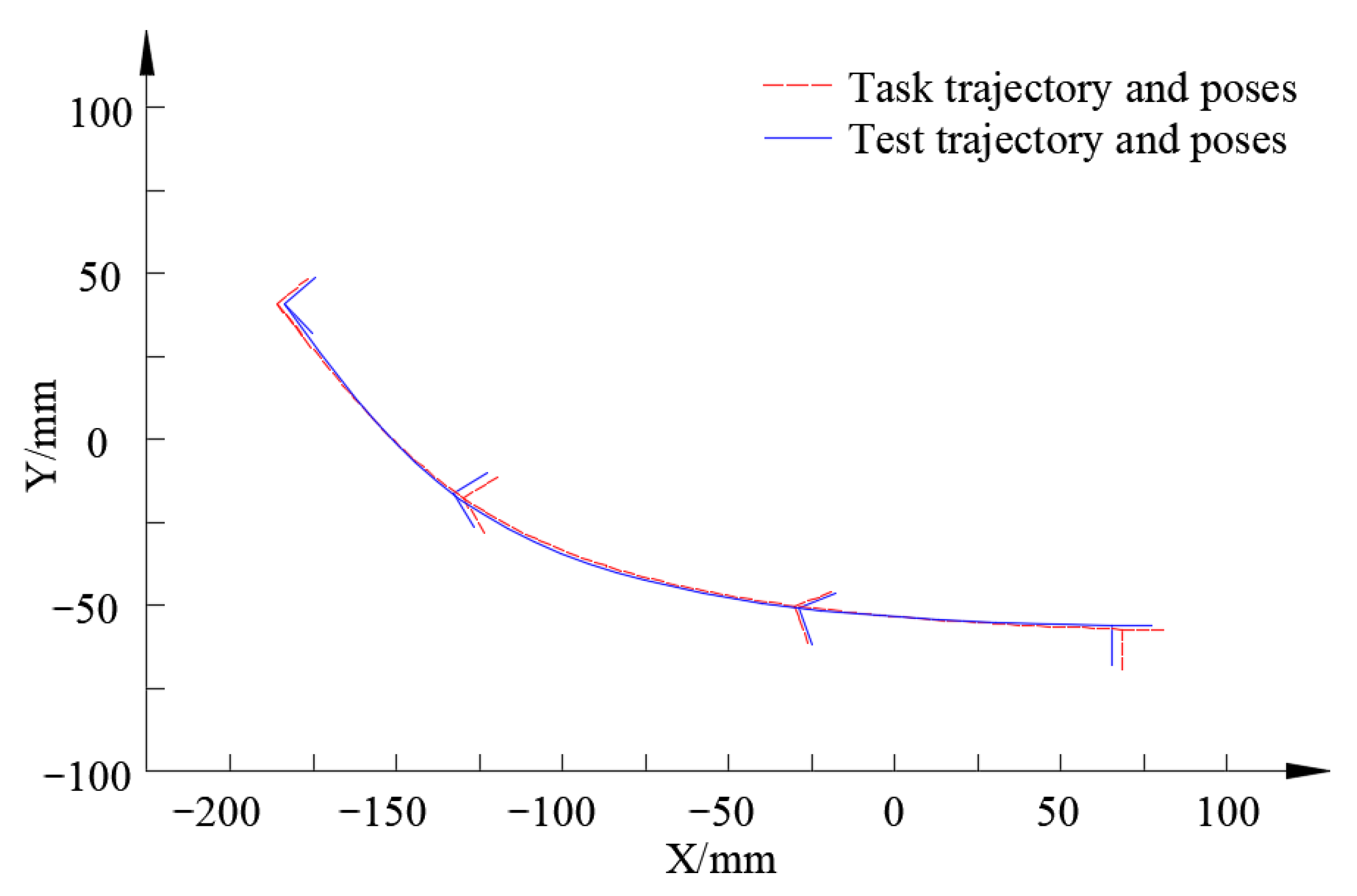
3.3. Structural Design and Test of Rehabilitation Device
- (1)
- Place a high-speed camera in a suitable position and adjust the height of the camera to ensure that the camera is perpendicular to the knee joint of the human body.
- (2)
- The subject stands normally, with the right leg attached to the exoskeleton with a black flexible strap, and the right foot on the pedal. Set an obvious marker point on the knee joint and calf of the subject, and ensure that the end of the noncircular gear-five-bar mechanism (point P) coincides with the marker point of the knee joint.
- (3)
- Fix the waist of the human body to the back with a black flexible strap.
- (4)
- The motor controller is used to control the forward and reverse rotation of the motor, and the rotation angle is 78°, so that the right lower limb swings back and forth with the test bench.
- (5)
- Turn on the high-speed camera to record the movement of the lower limb with the test bench.
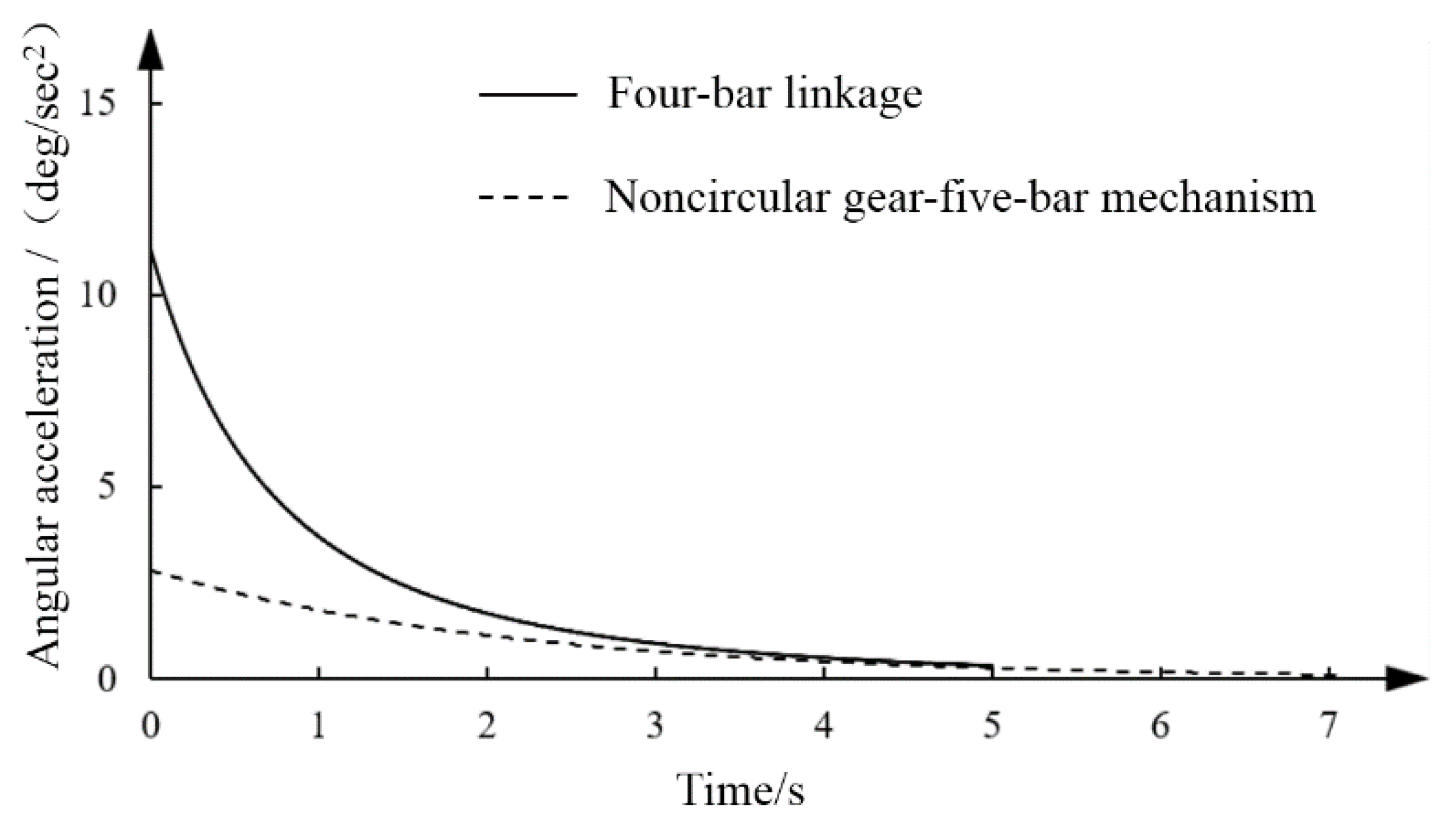
3.4. Discussion
4. Conclusions
- (1)
- In this paper, the research object of rigid-body guidance synthesis is extended to the noncircular gear-five-bar combined mechanism. The noncircular gear-five-bar mechanism is regarded as the combination of a 2R open chain, a 3R open chain and a pair of noncircular gears, and a rigid-body guidance synthesis method of the noncircular gear-five-bar mechanism based on kinematic mapping is proposed.
- (2)
- Based on the four exact task poses required for knee joint rehabilitation, a noncircular gear-five-bar mechanism is synthesized and applied to exoskeleton knee joint rehabilitation. The structure design, prototype development and tests of the rehabilitation device are carried out. The test results show that the device can drive the lower limb for rehabilitation training, and the knee joint can pass through the given four task poses, which verifies the correctness of the proposed rigid-body guidance synthesis method.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Burmester, L. Lehrbuch der Kinematik; Verlag Von Arthur Felix: Leipzig, Germany, 1888. [Google Scholar]
- Han, J.Y.; Qian, W.X. On the solution of region-based planar four-bar motion generation. Mech. Mach. Theory. 2009, 44, 457–465. [Google Scholar] [CrossRef]
- Deshpande, S.; Purwar, A. A task-driven approach to optimal synthesis of planar four-bar linkages for extended Burmester problem. J. Mech. Robot. 2017, 9, 061005. [Google Scholar] [CrossRef]
- Ge, Q.J.; Zhao, P.; Purwar, A.; Li, X.Y. A novel approach to algebraic fitting of a pencil of quadrics for planar 4R motion synthesis. J. Comput. Inf. Sci. Eng. 2012, 12, 041003. [Google Scholar] [CrossRef]
- Ge, Q.J.; Purwar, A.; Zhao, P.; Deshpande, S. A task-driven approach to unified synthesis of planar four-bar linkages using algebraic fitting of a pencil of G-manifolds. J. Comput. Inf. Sci. Eng. 2017, 17, 031011. [Google Scholar] [CrossRef]
- Qian, W.X.; Han, J.Y. Solution region analysis and synthesis method of 4-position rigid-body guidance. Chin. J. Eng. 2008, 30, 1163–1168. [Google Scholar]
- Han, J.Y.; Cai, Y.J. Solution-region synthesis method of single-degree-of-freedom planar six-bar mechanisms for robotic fingers. Trans. Chin. Soc. Agric. Mach. 2018, 49, 367–373. [Google Scholar]
- Cui, G.Z.; Han, J.Y.; Yang, T. The synthesis method of eight-bar linkage based on solution region synthesis theory. J. Northeastern. Univ. (Nat. Sci.) 2015, 36, 1010–1014. [Google Scholar]
- Shao, Y.X.; Xiang, Z.X.; Liu, H.T.; Li, L.L. Conceptual design and dimensional synthesis of cam-linkage mechanisms for gait rehabilitation. Mech. Mach. Theory 2016, 104, 31–42. [Google Scholar] [CrossRef]
- Sun, Y.X.; Ge, W.J.; Zheng, J.; Dong, D.B. Design and evaluation of a prosthetic knee joint using the geared five-bar mechanism. IEEE Trans. Neural. Syst. Rehabil. Eng. 2015, 23, 1031–1038. [Google Scholar] [CrossRef]
- Modler, K.H.; Lovasz, E.C.; Bär, G.F.F.; Neumann, R. General method for the synthesis of geared linkages with non-circular gears. Mech. Mach. Theory 2009, 44, 726–738. [Google Scholar] [CrossRef]
- Mundo, D.; Gatti, G.; Dooner, D.B. Optimized five-bar linkages with non-circular gears for exact path generation. Mech. Mach. Theory 2009, 44, 751–760. [Google Scholar] [CrossRef]
- Shih, A.J.; Yan, H.S. Synthesis of a single-loop overconstrained six revolute joint spatial mechanism for two-position cylindrical rigid body guidance. Mech. Mach. Theory 2002, 37, 61–73. [Google Scholar] [CrossRef]
- Shirazi, K.H. Synthesis of an 8S5R mechanism in four-point rigid body guidance problem using Maple. Mech. Mach. Theory 2008, 43, 285–296. [Google Scholar] [CrossRef]
- Sun, J.W.; Wang, P.; Liu, W.R.; Chu, J.K. Wavelet characteristic parameter method of a planar four-bar mechanism motion generation synthesis. Chin. Mech. Eng. 2018, 29, 688–695. [Google Scholar]
- Sun, J.W.; Liu, Q.; Chu, J.K. Motion generation of RCCC mechanism using numerical atlas. Mech. Based Des. Struc. Mach. 2017, 45, 62–75. [Google Scholar] [CrossRef]
- Chung, W.Y. Synthesis and analysis of spatial CS-3SS mechanism for body guidance. Proc. Inst. Mech. Eng. Part C-J. Mech. Eng. Sci. 2015, 229, 2455–2466. [Google Scholar] [CrossRef]
- Zhao, P.; Li, X.Y.; Zhu, L.H.; Zi, B. A novel motion synthesis approach with expandable solution space for planar linkages based on kinematic-mapping. Mech. Mach. Theory 2016, 105, 164–175. [Google Scholar] [CrossRef]
- Zhao, P.; Wang, Y.; Zhu, L.H.; Li, X.Y. A frame-independent comparison metric for discrete motion sequences. Proc. Inst. Mech. Eng. Part C-J. Mech. Eng. Sci. 2020, 234, 1764–1774. [Google Scholar] [CrossRef]
- Cui, G.Z.; Han, J.Y. The solution region-based synthesis methodology for a 1-DOF eight-bar linkage. Mech. Mach. Theory 2016, 98, 231–241. [Google Scholar] [CrossRef]
- Ravani, B.; Roth, B. Motion synthesis using kinematic mappings. ASME J. Mech. Transm. Autom. Des. 1983, 105, 460–467. [Google Scholar] [CrossRef]
- Li, X.Y.; Ge, X.; Purwar, A.; Ge, Q.J. A unified algorithm for analysis and simulation of planar four-bar motions defined with R- and P-joints. J. Mech. Robot. 2015, 7, 011014. [Google Scholar] [CrossRef]
- Purwar, A.; Deshpande, S.; Ge, Q.J. MotionGen: Interactive design and editing of planar four-bar motions for generating pose and geometric constraints. J. Mech. Robot. 2017, 9, 024504. [Google Scholar] [CrossRef]
- Zhao, P.; Li, X.Y.; Purwar, A.; Ge, Q.J. A task-driven unified synthesis of planar four-bar and six-bar linkages with R- and P-joints for five-position realization. J. Mech. Robot. 2016, 8, 061003. [Google Scholar] [CrossRef]
- Zhao, P.; Ge, X.; Zi, B.; Ge, Q.J. Planar linkage synthesis for mixed exact and approximated motion realization via kinematic mapping. J. Mech. Robot. 2016, 8, 051004. [Google Scholar] [CrossRef]
- Yu, C.N.; Ye, J.; Jia, J.M.; Zhao, X.; Chen, J.N. Design, synthesis, and experiment of foot-driven lower limb rehabilitation mechanisms. J. Mech. Robot. 2022, 14, 021001. [Google Scholar] [CrossRef]
- Liao, H.Y.; Kong, J.Y.; Li, J.; Tang, B. The types of 5-bar linkage with two-degree of freedom and their differentiation. J. Hubei Univ. Technol. 2006, 21, 4–6. [Google Scholar]
- Mao, Z.Y.; Liu, Z.J. A trajectory planning method for cubic uniform B-spline curve. Chin. Mech. Eng. 2010, 21, 2569–2572. [Google Scholar]
- Wang, F. Quasi-cubic B-spline curve and its application. Adv. Appl. Math. 2020, 9, 1255–1262. [Google Scholar] [CrossRef]
- Huang, Z.C.; Lan, Z.H. Design of transmission ratio function of non-circular gears with closed pitch curve. J. Mech. Trans. 2011, 35, 30–33. [Google Scholar]
- Sun, L.; Wang, Z.F.; Wu, C.Y.; Zhang, G.F. Novel approach for planetary gear train dimensional synthesis through kinematic mapping. Proc. Inst. Mech. Eng. Part C-J. Mech. Eng. Sci. 2019, 234, 273–288. [Google Scholar] [CrossRef]
- Irawan, A.P.; Halim, A.; Kurniawan, H. Hybrid robot climbing system design. IOP Conf. Ser Mater. Sci. Eng. 2017, 237, 012006. [Google Scholar] [CrossRef]
- Li, J.F.; Huang, X.Q.; Tao, C.J.; Wang, S.; Ji, R. Configuration synthesis and structure design of knee rehabilitation exoskeleton. J. Harbin Eng. Univ. 2017, 38, 625–632. [Google Scholar]
- Li, S. Design and Research of a Wearable Lower Limb Rehabilitation Robot. Master’s Thesis, Yanshan University, Qinhuangdao, China, 2021. [Google Scholar]




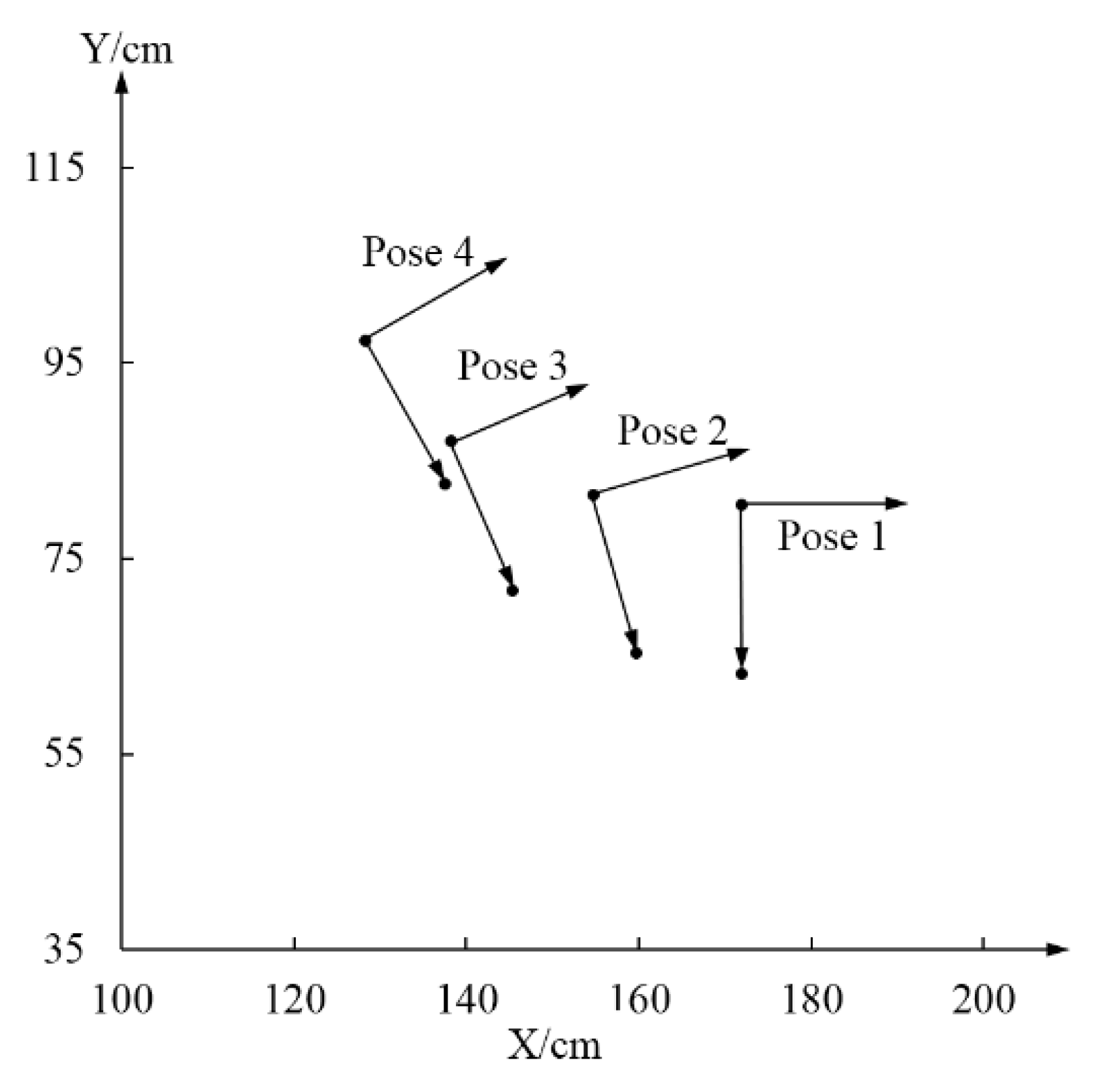
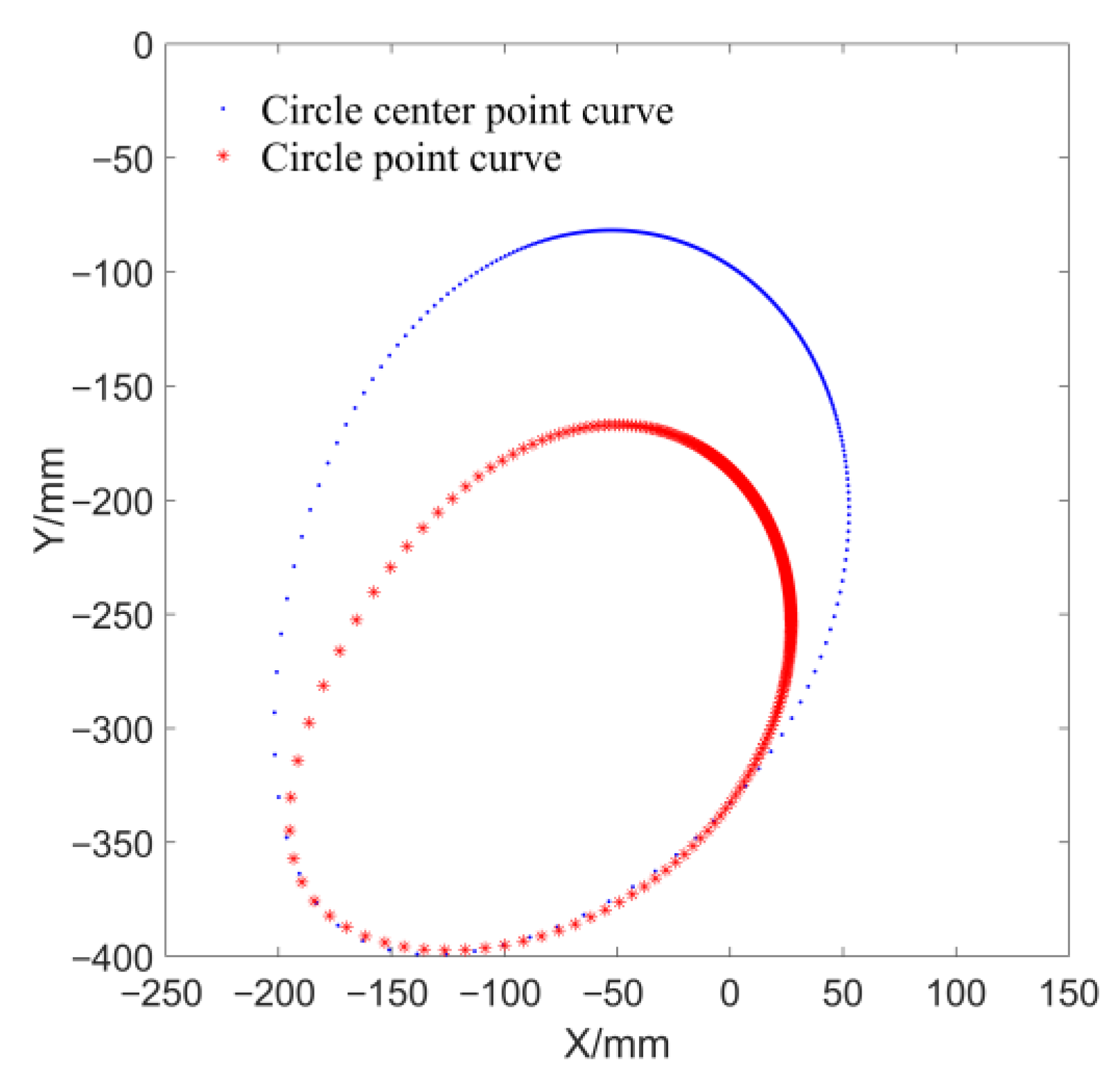
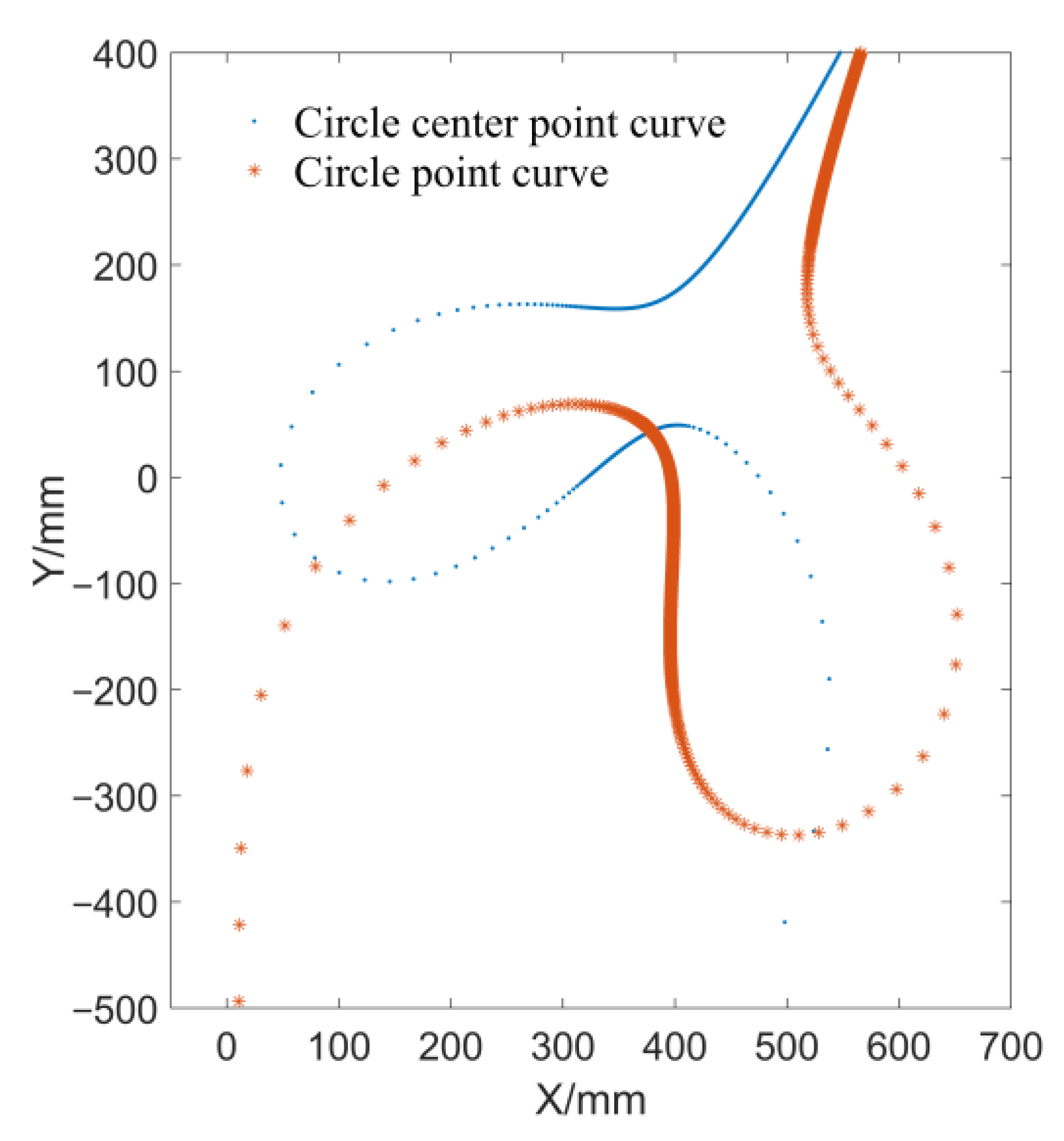
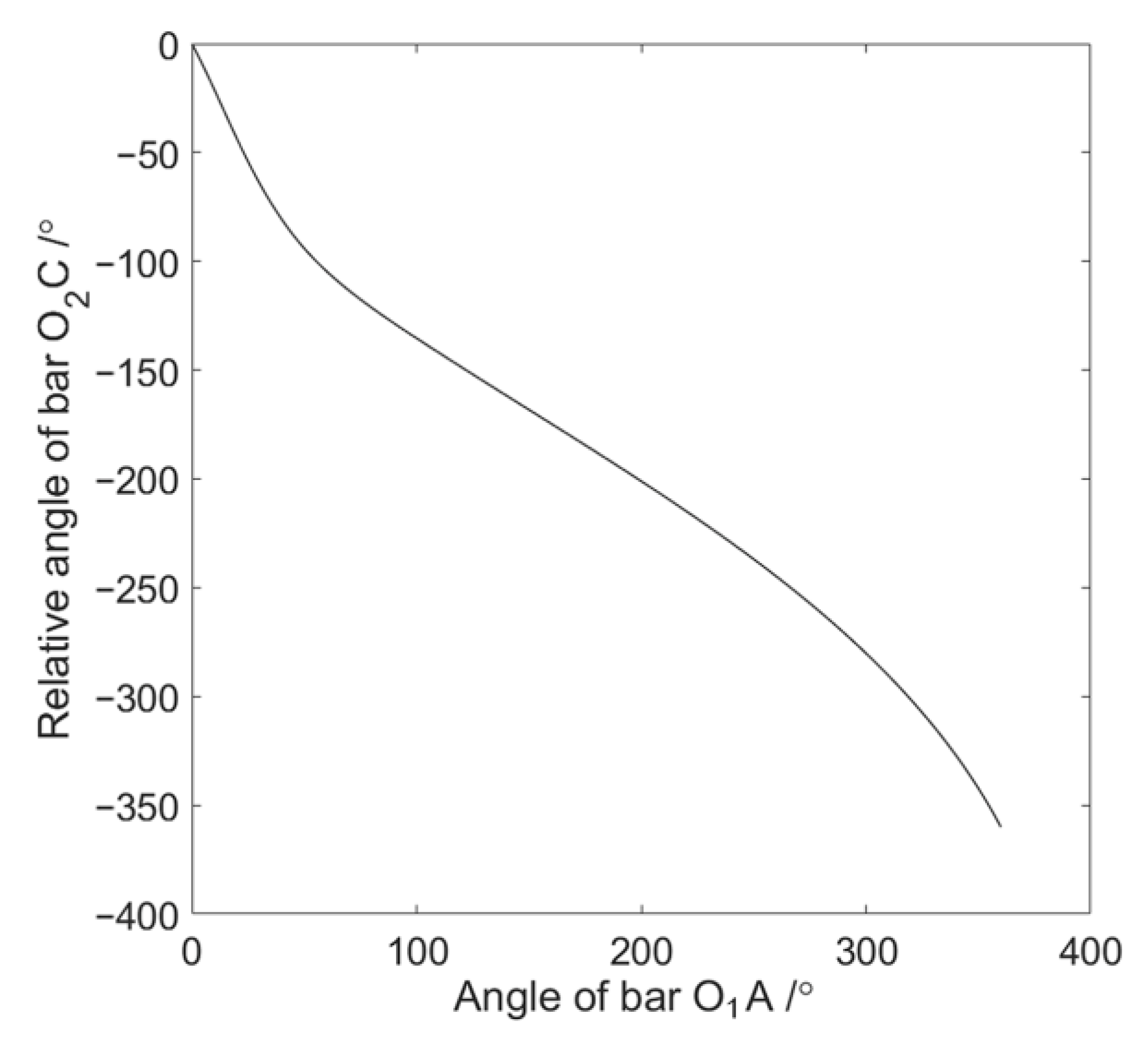





| Number | X-Coordinate (mm) | Y-Coordinate (mm) | Posture (°) |
|---|---|---|---|
| 1 | 68.70 | −57.22 | 0 |
| 2 | −30.15 | −50.10 | 20 |
| 3 | −129.82 | −17.71 | 31 |
| 4 | −185.83 | 40.84 | 40 |
| Number | Theoretical Coordinates (mm) | Actual Coordinates (mm) | Position Error (mm) | Theoretical Posture Angle (°) | Actual Posture Angle (°) | Angle Error (°) |
|---|---|---|---|---|---|---|
| 1 | (68.70, −57.22) | (66.41, −55.87) | 2.66 | 0 | 0.07 | 0.07 |
| 2 | (−30.15, −50.10) | (−29.00, −50.81) | 1.35 | 20 | 21.16 | 1.16 |
| 3 | (−129.82, −17.71) | (−132.88, −16.43) | 3.32 | 31 | 31.98 | 0.98 |
| 4 | (−185.83, 40.84) | (−183.45, 40.75) | 2.38 | 40 | 42.13 | 2.13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, C.; Yao, K.; Zong, Y.; Ye, J.; Chen, J. Rigid-Body Guidance Synthesis of Noncircular Gear-Five-Bar Mechanisms and Its Application in a Knee Joint Rehabilitation Device. Machines 2022, 10, 1110. https://doi.org/10.3390/machines10121110
Yu C, Yao K, Zong Y, Ye J, Chen J. Rigid-Body Guidance Synthesis of Noncircular Gear-Five-Bar Mechanisms and Its Application in a Knee Joint Rehabilitation Device. Machines. 2022; 10(12):1110. https://doi.org/10.3390/machines10121110
Chicago/Turabian StyleYu, Chennan, Kun Yao, Yanyu Zong, Jun Ye, and Jianneng Chen. 2022. "Rigid-Body Guidance Synthesis of Noncircular Gear-Five-Bar Mechanisms and Its Application in a Knee Joint Rehabilitation Device" Machines 10, no. 12: 1110. https://doi.org/10.3390/machines10121110
APA StyleYu, C., Yao, K., Zong, Y., Ye, J., & Chen, J. (2022). Rigid-Body Guidance Synthesis of Noncircular Gear-Five-Bar Mechanisms and Its Application in a Knee Joint Rehabilitation Device. Machines, 10(12), 1110. https://doi.org/10.3390/machines10121110





