Design and Application of Non-Circular Gear with Cusp Pitch Curve
Abstract
1. Introduction
2. Design Principle of VIIVC-CTF
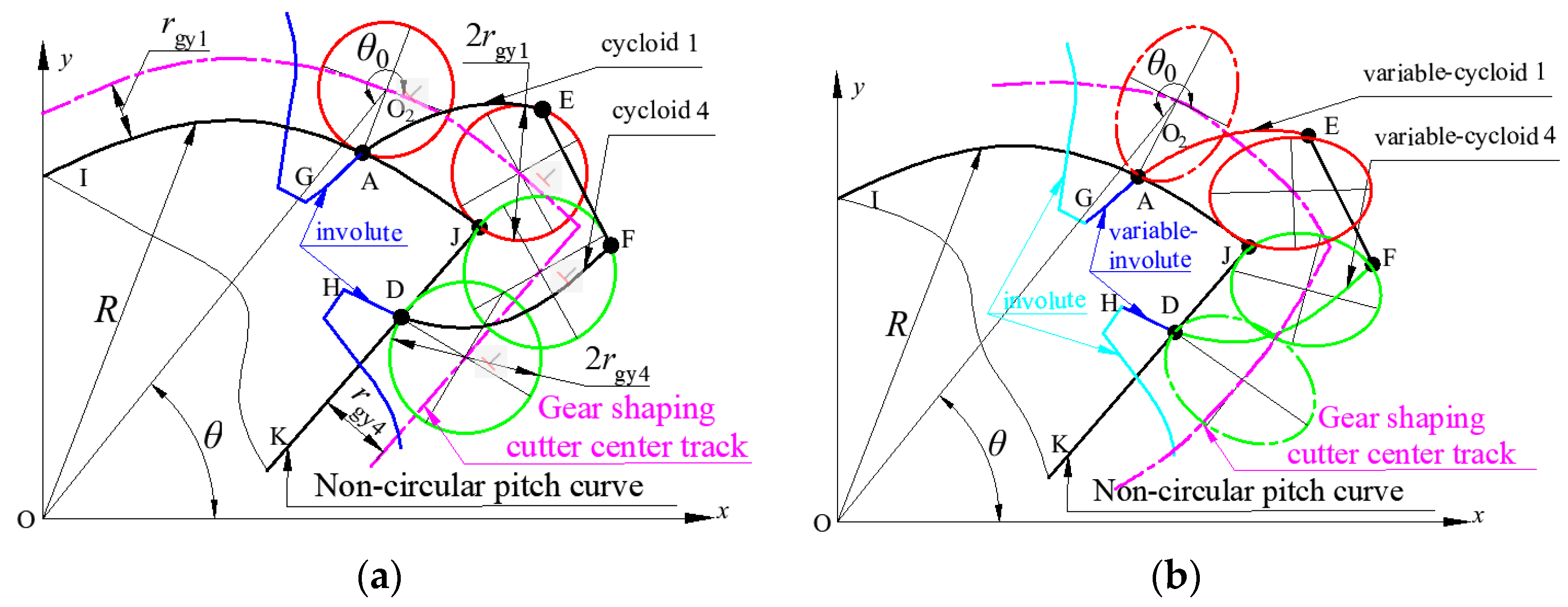
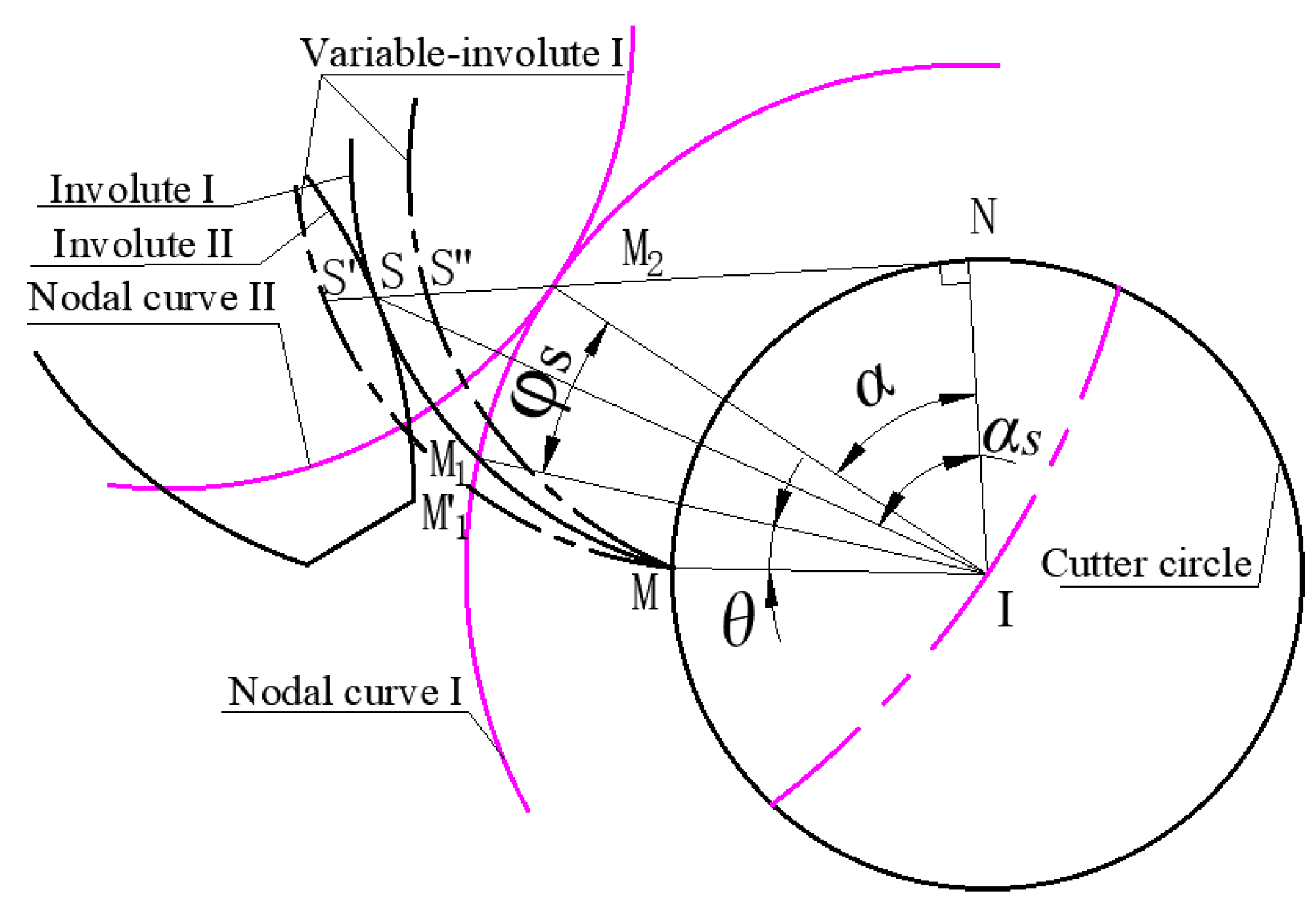
2.1. Variable-Involute Tooth Profile of Non-Circular Gear with Incomplete Pitch Curve
2.2. Incomplete Cycloid Tooth Profile of Non-Circular with Incomplete Pitch Curve
2.3. Design of Non-Circular Gear Transmission Mechanism with Cusp Pitch Curve
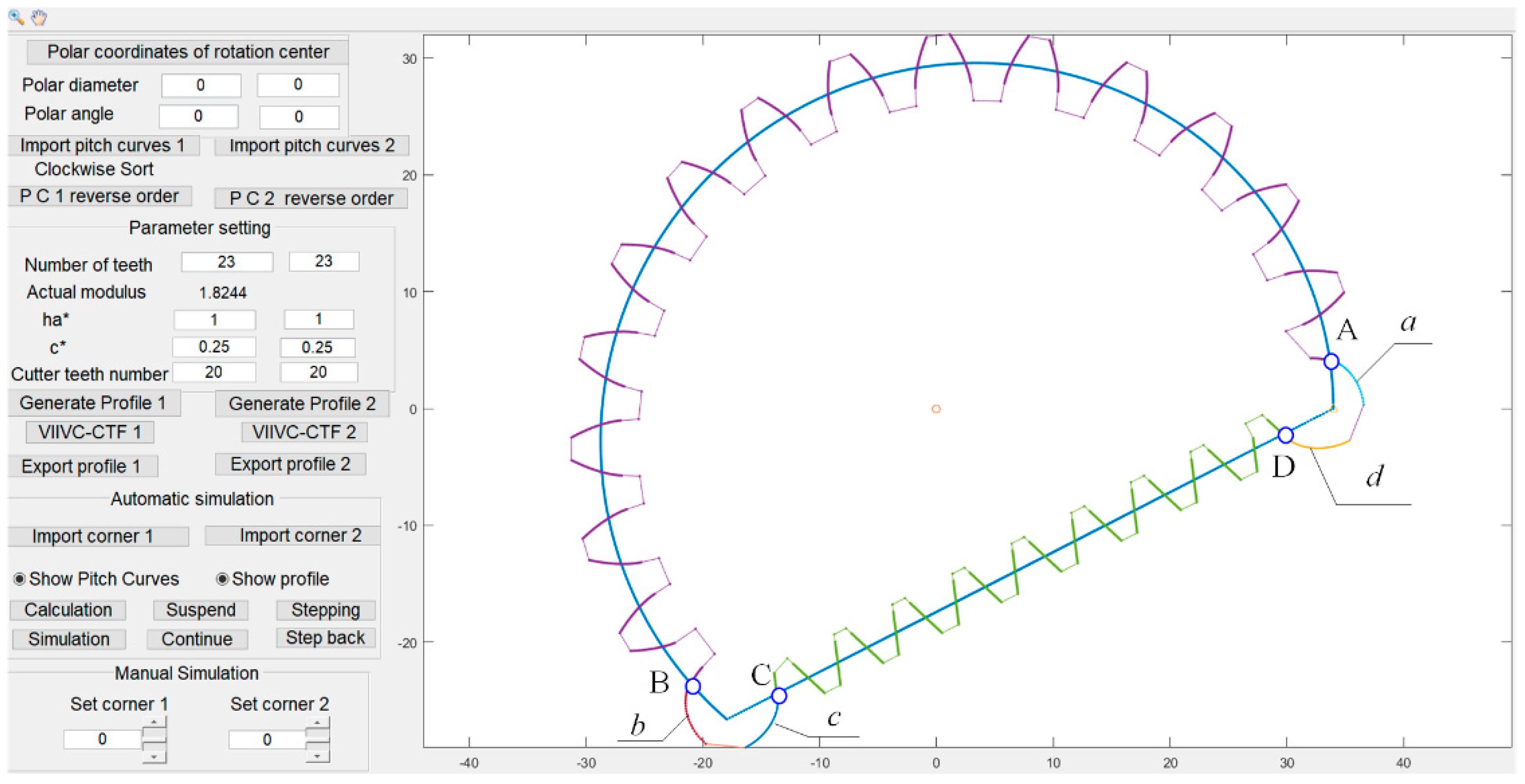
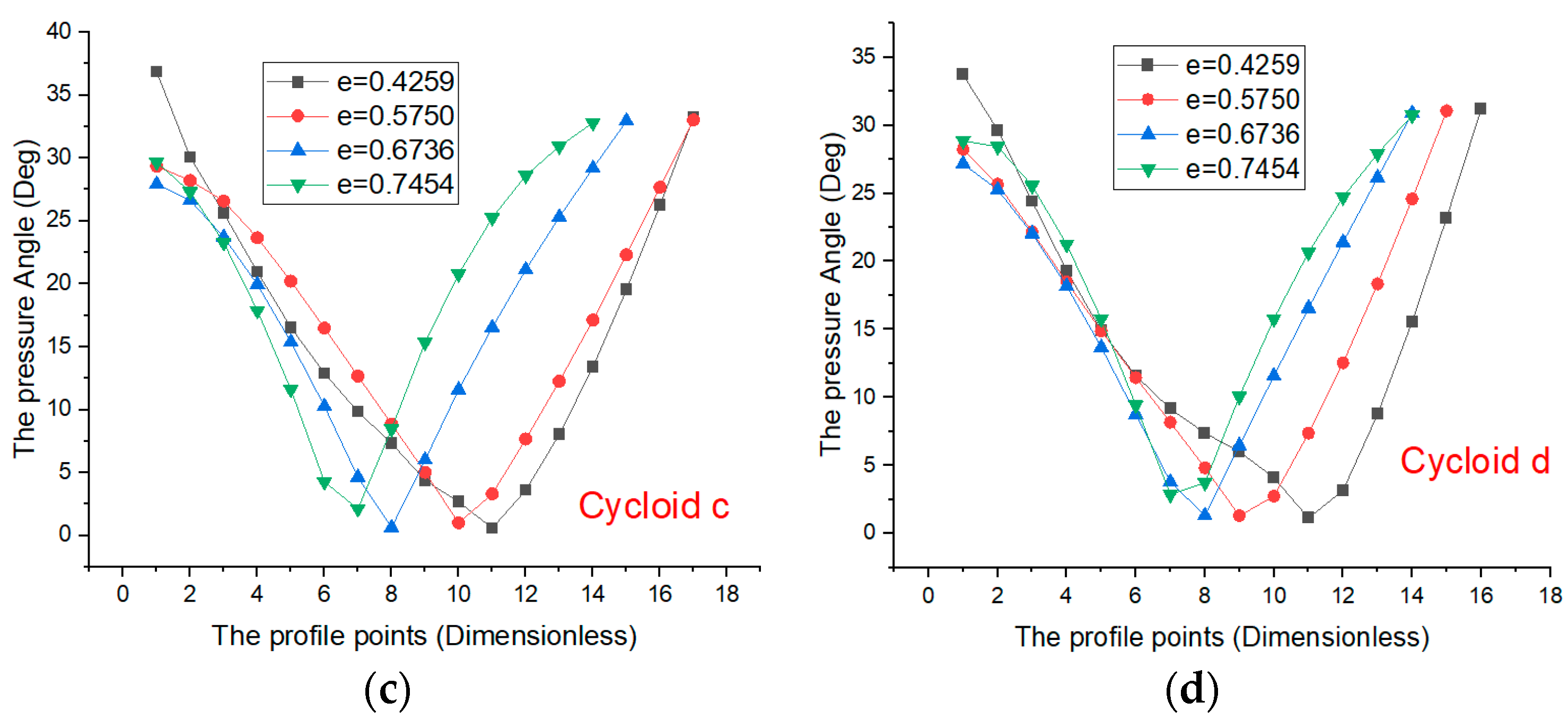
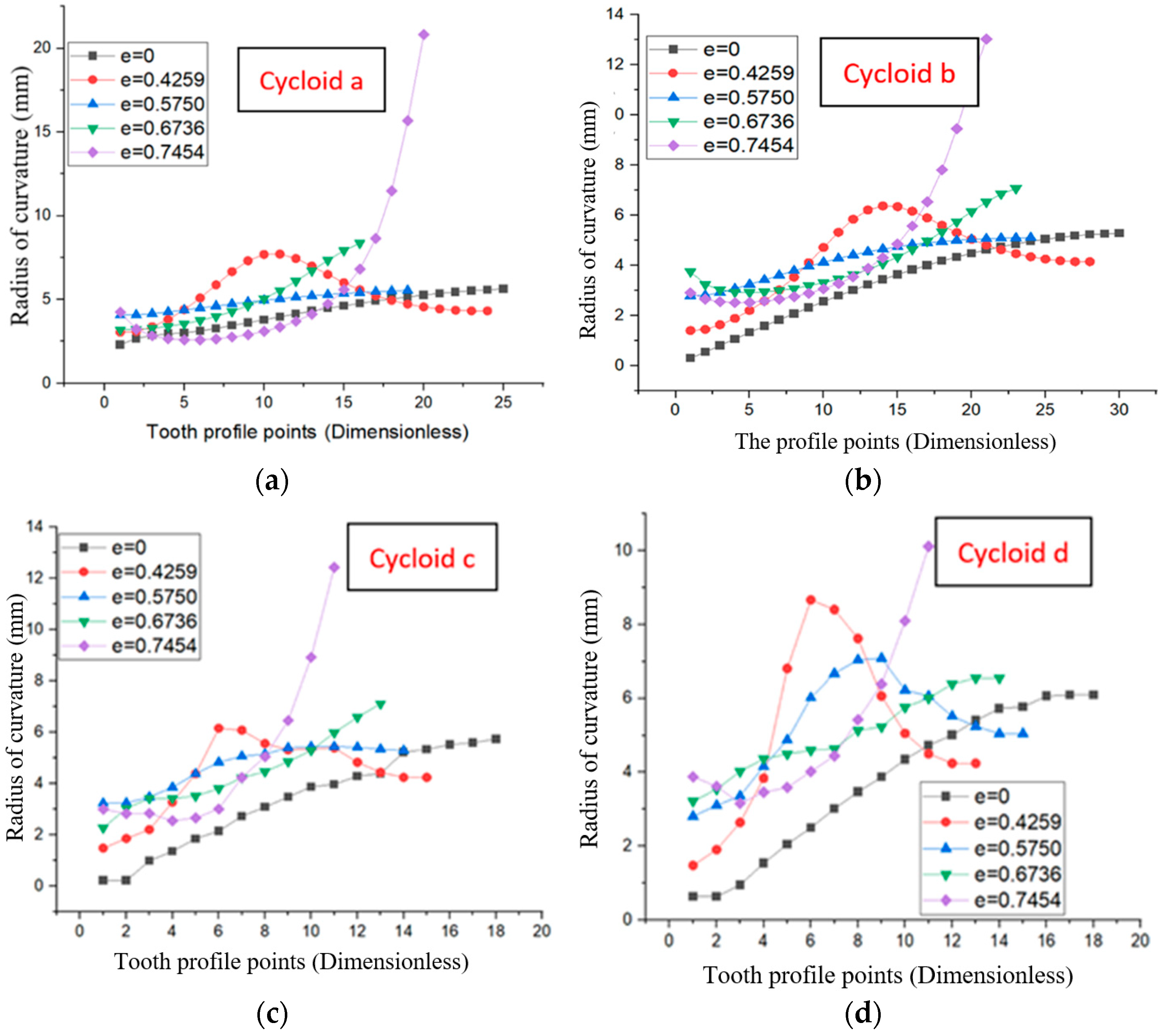
3. Tooth Profile Characteristic of a Non-Circular Gear with the VIIVC-CTF
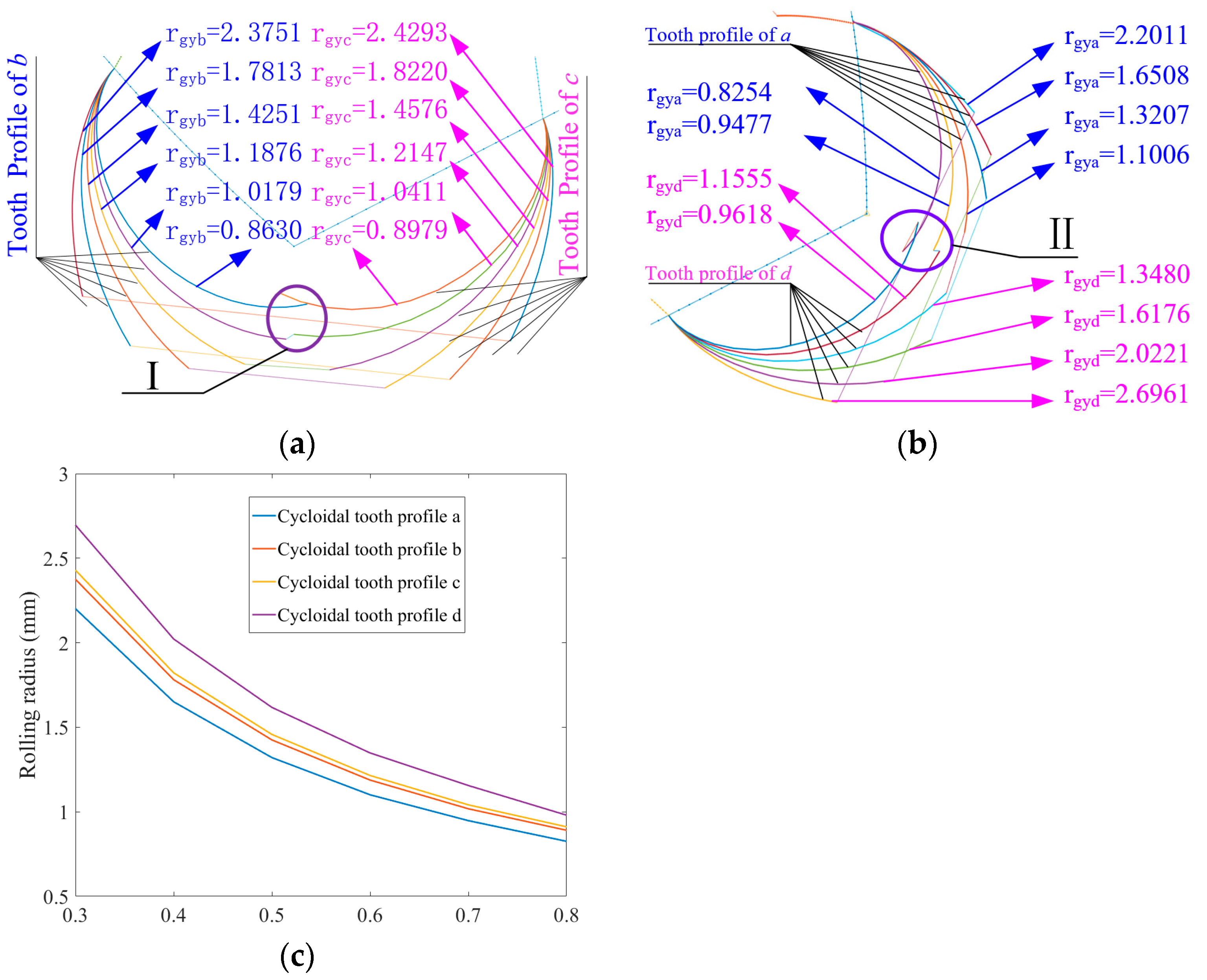
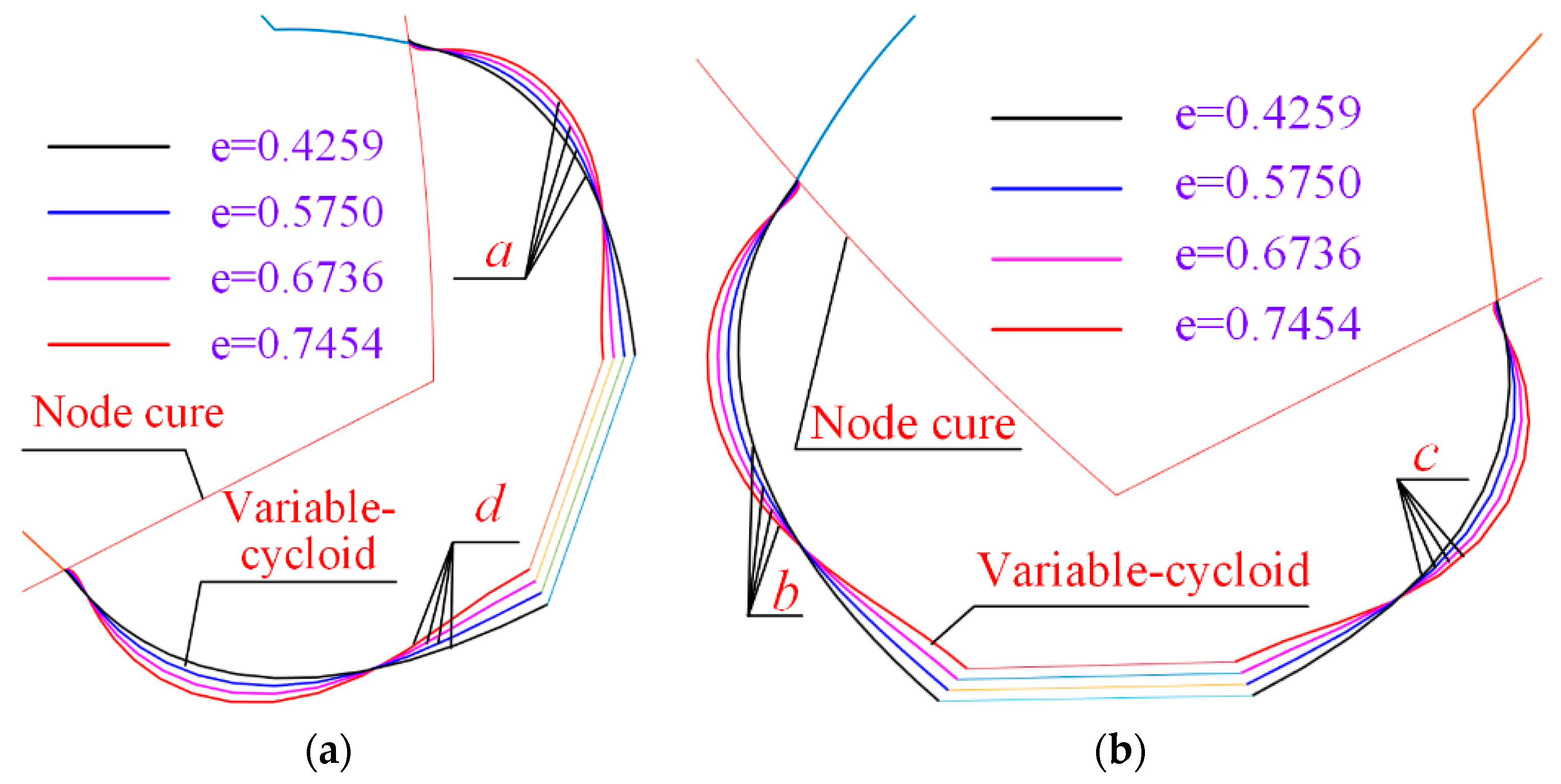
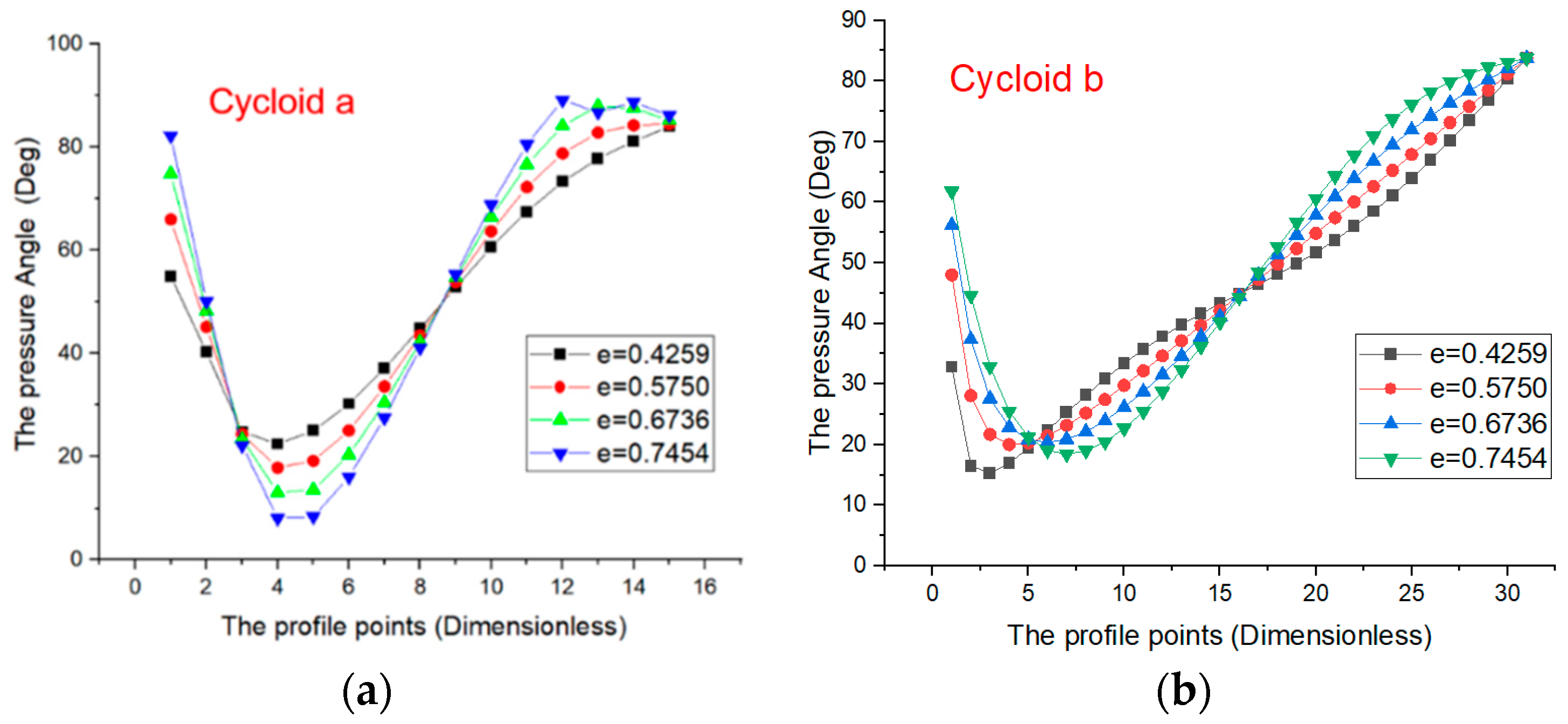
3.1. Tooth Profile Shape on Incomplete Cycloid Tooth Profile Based on Rolling Radius
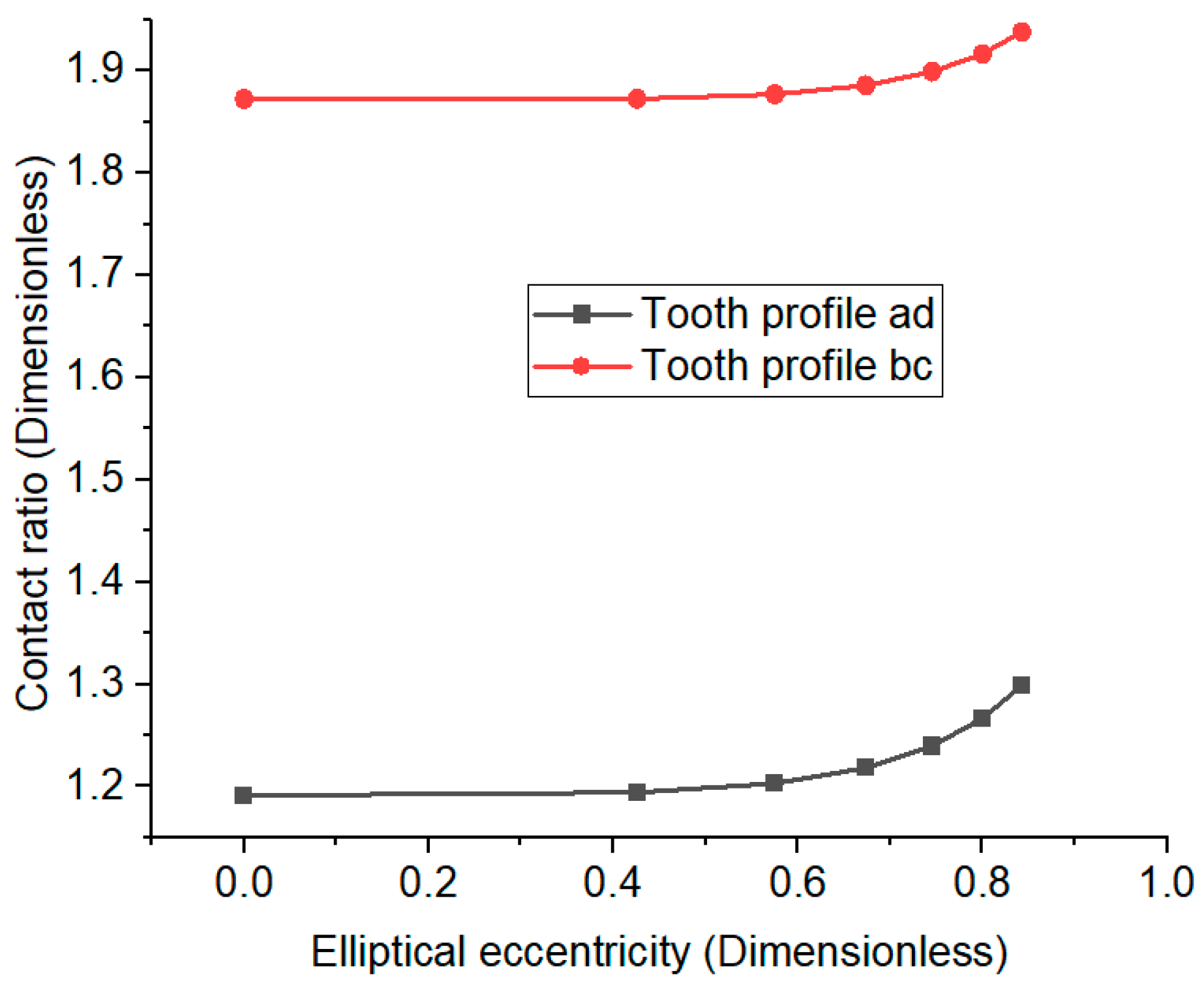
3.2. Contact Ratio of VIIVC-CTF
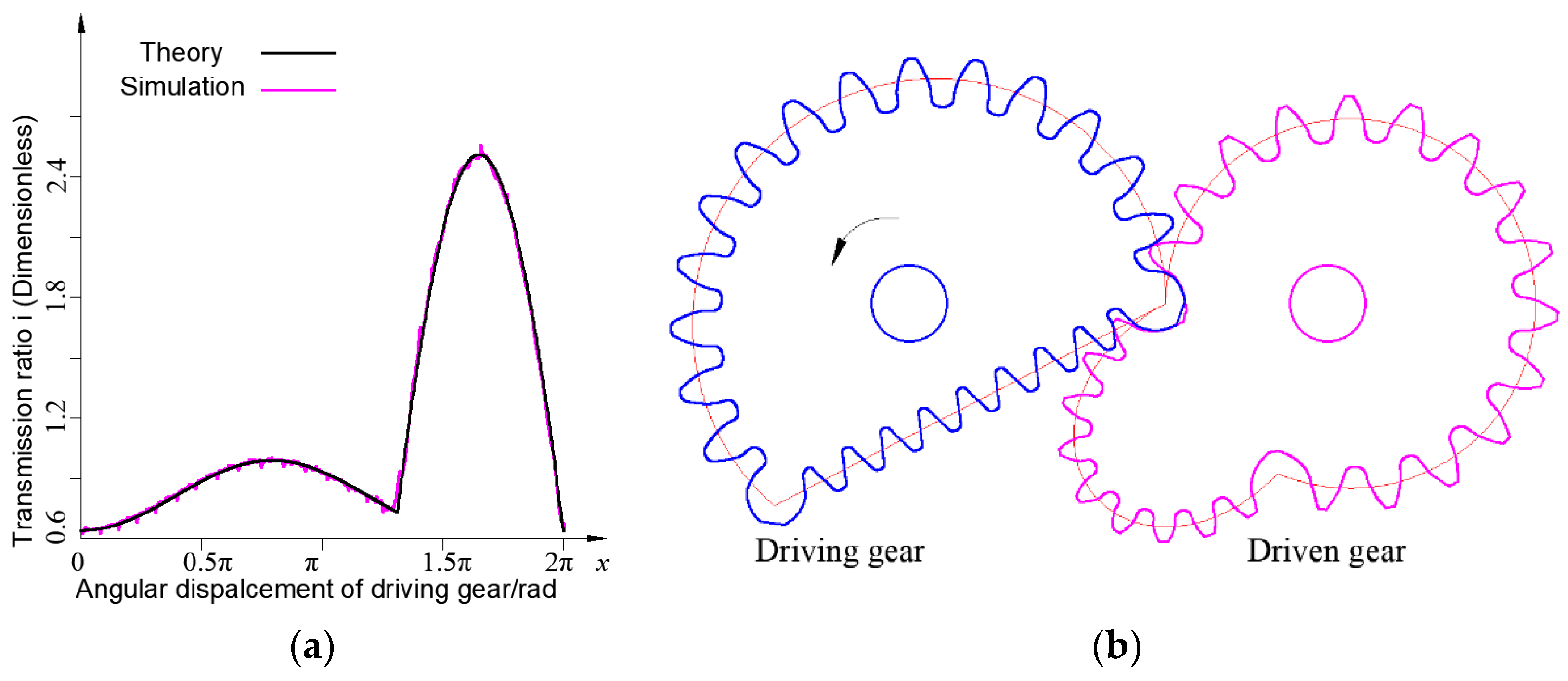
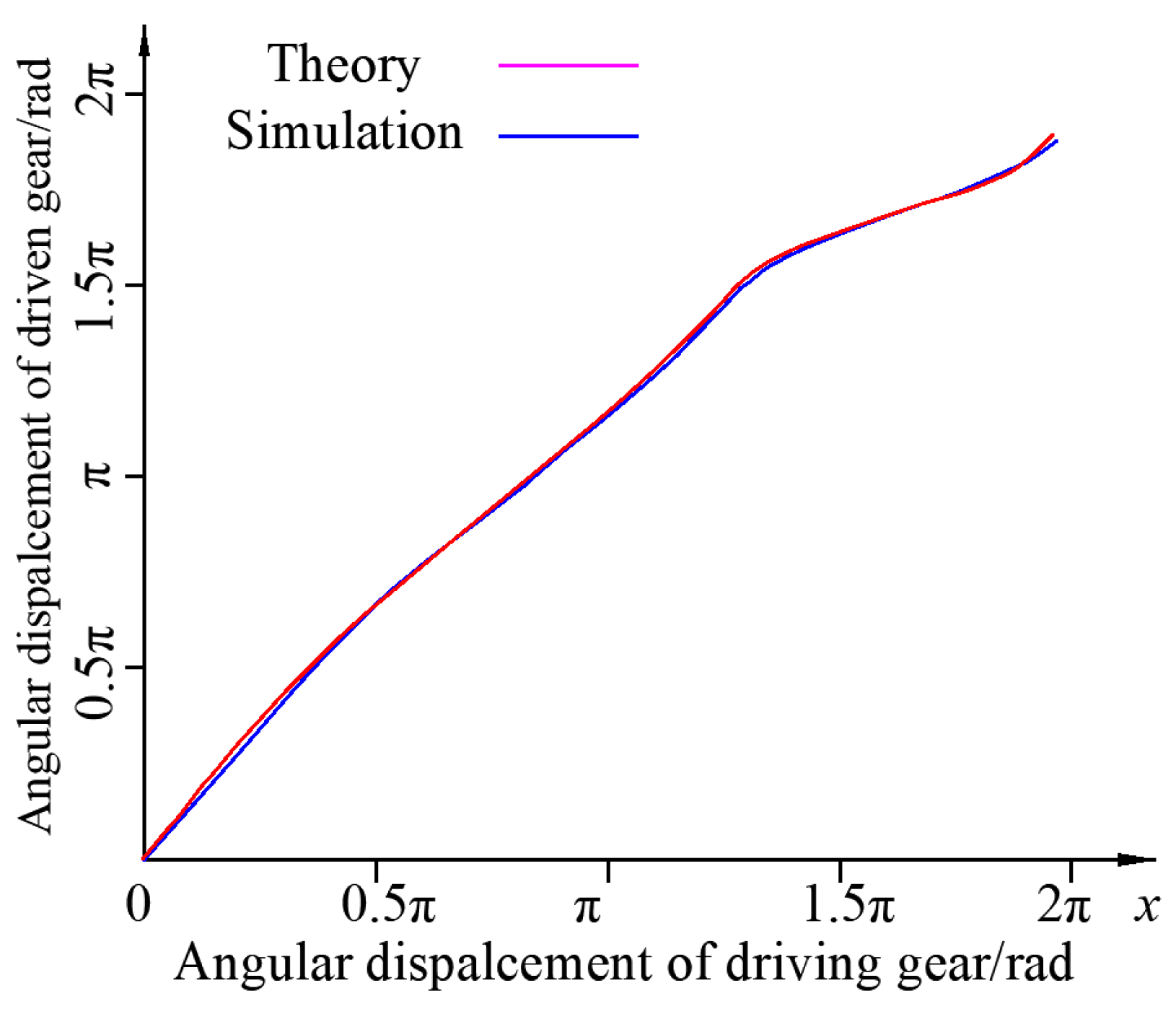
4. Transmission Characteristics of VIIVC-CTF
4.1. Tooth Profile Characteristic of VIIVC-CTF
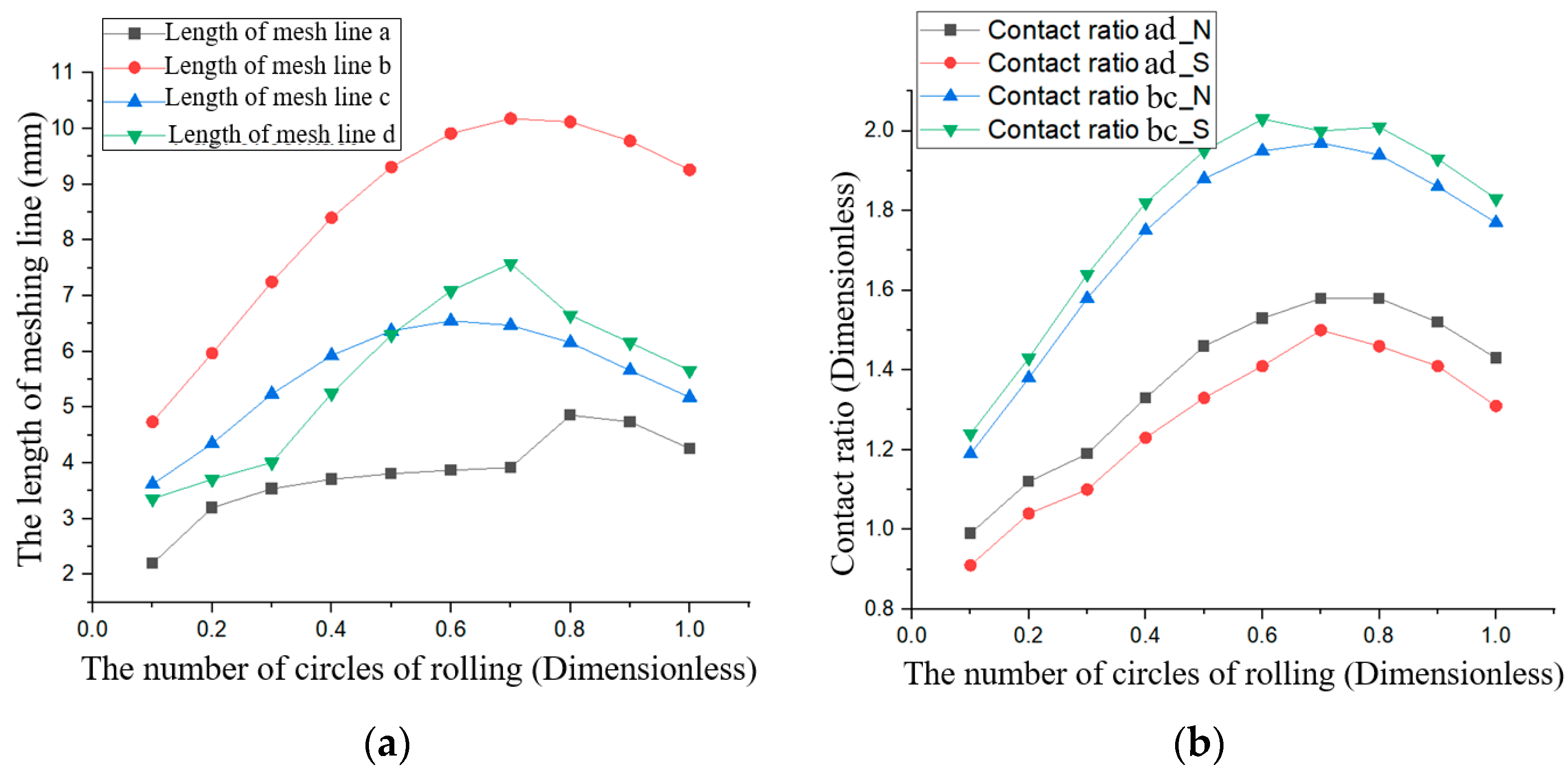
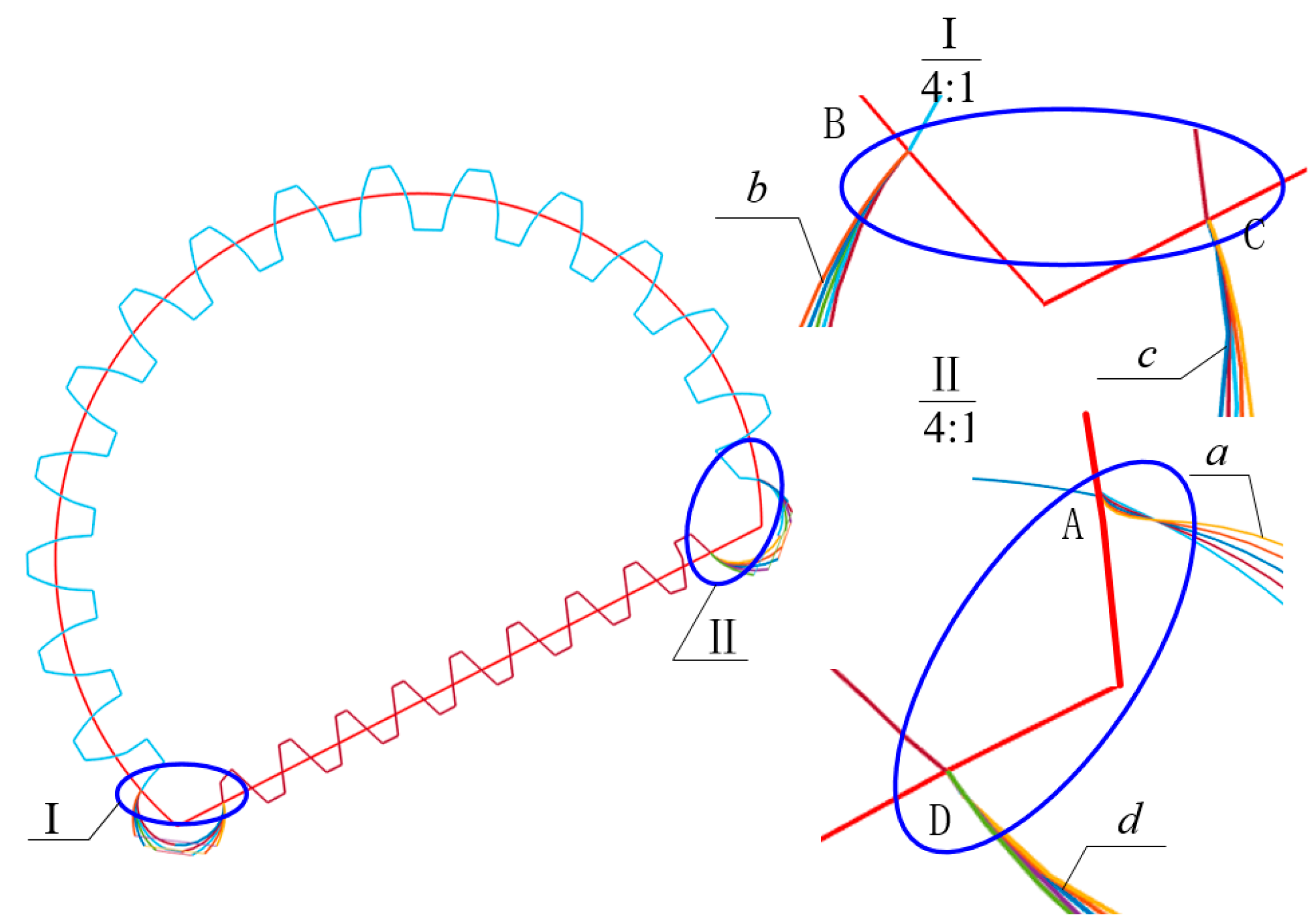
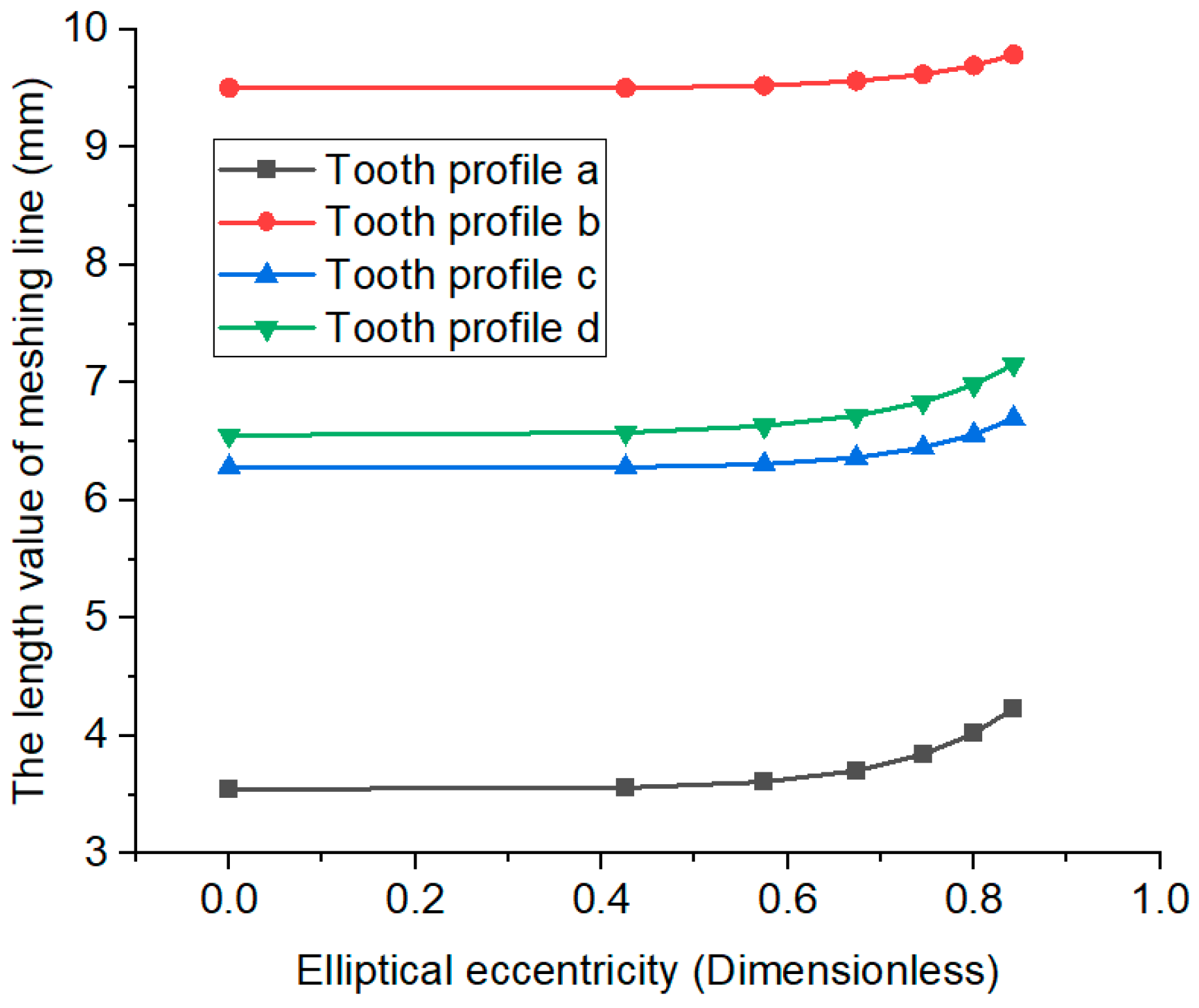
4.2. The Meshing Line and Contact Ratio of VIIVC-CTF
5. Virtual Test of Non-Circular Gear Transmission Mechanism
6. Application and Experiment of VIIVC-CTF
6.1. Application of VIIVC-CTF in Seedling Pick-Up Mechanism with Non-Circular Gears
6.2. Seedling Picking Experiment
7. Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, J.; Liu, Q.Q.; Yang, S.R.; Li, H.X.; Qang, Z.L.; Li, Q. Geometric Design and Analysis of Novel Asymmetrical Rotors for Roots Vacuum Pumps. J. Mech. Des. 2020, 142, 1–6. [Google Scholar] [CrossRef]
- Choi, T.H.; Kim, M.S.; Lee, G.S.; Jung, S.Y.; Bae, J.H.; Kim, C.B. Design of Rotor for Internal Gear Pump Using Cycloid and Circular-Arc Curves. J. Mech. Des. 2012, 134, 011005. [Google Scholar] [CrossRef]
- Chen, Q.; Xu, F.; Liu, P.; Fan, H. Research on Fractal Model of Normal Contact Stiffness between two spheroidal joint surfaces considering friction factor. Tribol. Int. 2016, 97, 253–264. [Google Scholar] [CrossRef]
- He, S.X.; He, Y.B.; Chen, Y.C.; Dai, Q.S.; Liu, X. Research on Contact Stiffness of Cycloid-pin Gear based on Monte Carlo Method. J. Mech. Transm. 2021, 45, 28–32. [Google Scholar]
- Chung, W.J.; Park, J.H.; Yoo, H.G.; Park, Y.J.; Kim, S.C.; Sohn, J.; Lee, G.H. Improved analytical model for calculating mesh stiffness and transmission error of helical gears considering trochoidal root profile. Mech. Mach. Theory 2021, 163, 104386. [Google Scholar] [CrossRef]
- Yang, J.; Lin, T.J.; He, Z.Y.; Chen, M. Novel Calculation method for Dynamic Excitation of modified double-helical gear transmission. Mech. Mach. Theory 2022, 167, 104467. [Google Scholar] [CrossRef]
- Sun, Z.; Chen, S.Y.; Hu, Z.H.; Tao, X. Improved Mesh Stiffness Calculation model of comprehensive modification gears considering actual manufacturing. Mech. Mach. Theory 2022, 167, 104470. [Google Scholar] [CrossRef]
- Choi, C.H.; Ahn, H.J.; Park, Y.J.; Lee, G.H.; Kim, S.C. Influence of Gear tooth Addendum and Dedendum on the helical gear optimization considering mass, efficiency and transmission error. Mech. Mach. Theory 2021, 166, 104476. [Google Scholar] [CrossRef]
- Benaïcha, Y.; Perret-Liaudet, J.; Beley, J.D.; Rigaud, E.; Thouverez, F. On a Flexible Multibody Modelling approach using FE-based contact formulation for describing gear transmission error. Mech. Mach. Theory 2022, 167, 104505. [Google Scholar] [CrossRef]
- Korta, J.A.; Mundo, D. Multi-objective Micro-geometry Optimization of gear tooth supported by response surface methodology. Mech. Mach. Theory 2017, 109, 278–295. [Google Scholar] [CrossRef]
- Kim, S.C.; Moon, S.G.; Sohn, J.H.; Park, Y.J.; Choi, C.H.; Lee, G.H. Macro Geometry Optimization of a Helical Gear pair for mass, efficiency, and transmission error. Mech. Mach. Theory 2020, 144, 103634. [Google Scholar] [CrossRef]
- Zheng, F.Y.; Guo, X.D.; Zhang, M.D. Non-uniform flank rolling measurement for shaped noncircular gears. Measurement 2018, 116, 207–215. [Google Scholar] [CrossRef]
- Zheng, F.Y.; Hua, L.; Han, X.H. The mathematical model and mechanical properties of variable center distance gears based on screw theory. Mech. Mach. Theory 2016, 101, 116–139. [Google Scholar] [CrossRef]
- Lin, C.; Wang, Y.T. Principle and Design of Noncircular Pin-Cycloid Gear Transmission. J. Northeast. Univ. (Nat. Sci.) 2014, 35, 1190–1194. [Google Scholar]
- Hou, Y.J.; Lin, C. Kinematic Analysis and Experimental Verifcation of an oval noncircular bevel gears with rotational and axial translational motions. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 60. [Google Scholar] [CrossRef]
- Vivet, M.; Tamarozzi, T.; Desmet, W.; Mundo, D. On the Modelling of gear alignment errors in the tooth contact analysis of spiral bevel gears. Mech. Mach. Theory 2021, 155, 104065. [Google Scholar] [CrossRef]
- Dooner, D.B.; Vivet, M.; Mundo, D. Deproximating Tredgold’s Approximation. Mech. Mach. Theory 2016, 102, 36–54. [Google Scholar] [CrossRef]
- Litvin, F.L.; Gonzalez-Perez, I.; Yukishima, K.; Fuentes, A.; Hayasaka, K. Design, Simulation of Meshing, and contact stresses for an improved worm gear drive. Mech. Mach. Theory 2007, 42, 940–959. [Google Scholar] [CrossRef]
- Liu, P.; Zhao, H.; Huang, K.; Chen, Q.; Xiong, Y.T. Research on Normal Contact Stiffness of Micro-segments Gear Based on Improved Fractal Model. J. Mech. Eng. 2018, 54, 114–122. [Google Scholar] [CrossRef]
- Xiong, Y.S.; Han, G.Z.; Huang, K.; Zhao, H. Research on the Nonlinear Dynamics of Micro-segment Gear System with Time-Varying Friction Coefficient. J. Mech. Eng. 2021, 57, 113–127. [Google Scholar]
- Chen, Y.Z.; Zhu, A.S.; Lü, Y.L. Study on the Meshing Characteristic of Parallel Axis Line Gear. J. Mech. Transm. 2018, 42, 1–6. [Google Scholar]
- Krawiec, P.; Grzelka, M.; Kroczak, J.; Domek, G.; Kołodziej, A. A proposal of measurement methodology and assessment of manufacturing methods of nontypical cog belt pulleys. Measurement 2019, 132, 182–190. [Google Scholar] [CrossRef]
- Krawiec, P.; Domek, G.; Warguła, Ł.; Waluś, K. The application of the optical system ATOS II for rapid prototyping methods of non-classical models of cogbelt pulleys. In Proceedings of the MATEC Web of Conferences, Sklené Teplice, Slovak Republic, 5–8 September 2017; p. 01010. [Google Scholar]
- Medvecká-Beňová, S. Designing pitch curves of non-circular gears. Sci. J. Sil. Univ. Technol. 2018, 99, 105–114. [Google Scholar] [CrossRef]
- Maláková, S.; Urbanský, M.; Fedorko, G.; Molnár, V.; Sivak, S. Design of Geometrical Parameters and Kinematical Characteristics of a Non-circular Gear Transmission for Given Parameters. Appl. Sci. 2021, 11, 1000. [Google Scholar] [CrossRef]
- Cristescu, A.; Cristescu, B.; Andrei, L. Finite element analysis of multispeed noncircular gears. Appl. Mech. Mater. 2015, 808, 246–251. [Google Scholar]
- Niculescu, M.; Andrei, L. Using noncircular gears for the unloading door kinematics modification. In Proceedings of the MATEC Web of Conferences, Iasi, Romania, 24–27 May 2017; Volume 112, p. 6013. [Google Scholar]
- Nezir, E.; Nihat, Y.; Fatih, E.; Bahadır, K.; Burak, Ş. Non-circular gear design, elliptical gears as example. In Proceedings of the Ejons VI–International Conference on Mathematics Engineering Natural & Medical Sciences, Adana, Turkey, 14–16 November 2019; pp. 624–641. [Google Scholar]
- Yu, G.H.; Yu, J.P.; Tong, J.H.; Ye, B.L.; Zheng, S.Y. Design a Conjugate Concave-convex Non-circular Gear Mechanism. China Mech. Eng. 2016, 27, 2155–2159, 2165. [Google Scholar]
- Yu, G.H.; Yu, T.F.; Ye, B.L. Design of a Rotary Plug Seedling Pick-up Mechanism. J. Mech. Eng. 2015, 51, 67–76. [Google Scholar] [CrossRef]
- Yu, G.H.; Tong, Z.P.; Sun, L. Novel Gear Transmission Mechanism with Twice Unequal Amplitude transmission Ratio. J. Mech. Des. 2019, 141, 092304. [Google Scholar] [CrossRef]
- Liu, J.G.; Tong, Z.P.; Yu, G.H.; Zhao, X.; Zhou, H.L. Design of a Noncircular gear Mechanism with Twice Unequal Amplitude Transmission Ratio. J. Mech. Robot. 2022, 14, 054501. [Google Scholar] [CrossRef]
- Liu, J.G.; Tong, Z.P.; Yu, G.H.; Zhao, X.; Zhou, H.L. Non-circular gear transmission mechanism with Variable-Involute and Variable-Cycloid composite tooth profile. J. Mech. Sci. Technol. 2022, 36, 2445–2459. [Google Scholar] [CrossRef]
- Wu, X.T. Gear Meshing Principle; Machine Press: Beijing, China, 2009. [Google Scholar]


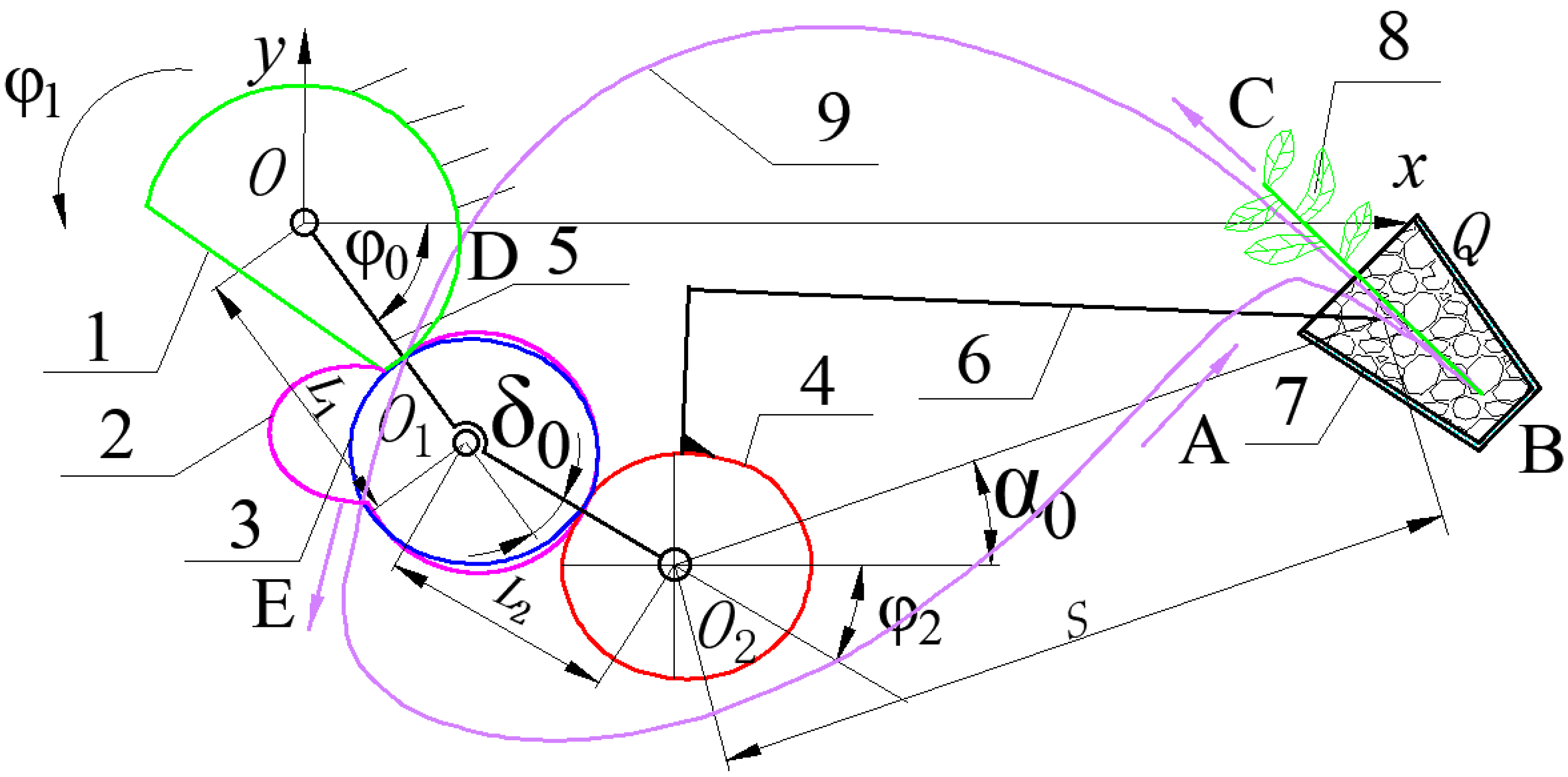




| Symbol | Meaning | Symbol | Meaning |
|---|---|---|---|
| S | Distance from the rotation center of the planet gear to the tip of the seedling needle | φ0 | Angle of rotation of the second-stage planetary carrier relative to the first-stage planetary carrier |
| L1, L2 | Distance of the center of the first and second gear transmission | α0 | Installation position of the seedling picking arm relative to the planet carrier |
| φ1 | Angular displacement of planet gear relative to planet carrier | δ0 | Initial installation position of the planet carrier |
| φ2 | Angle of the planet carrier |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.-G.; Tong, Z.-P.; Yu, G.-H.; Zhao, X.; Zhou, H.-L. Design and Application of Non-Circular Gear with Cusp Pitch Curve. Machines 2022, 10, 985. https://doi.org/10.3390/machines10110985
Liu J-G, Tong Z-P, Yu G-H, Zhao X, Zhou H-L. Design and Application of Non-Circular Gear with Cusp Pitch Curve. Machines. 2022; 10(11):985. https://doi.org/10.3390/machines10110985
Chicago/Turabian StyleLiu, Jian-Gang, Zhi-Peng Tong, Gao-Hong Yu, Xiong Zhao, and Hai-Li Zhou. 2022. "Design and Application of Non-Circular Gear with Cusp Pitch Curve" Machines 10, no. 11: 985. https://doi.org/10.3390/machines10110985
APA StyleLiu, J.-G., Tong, Z.-P., Yu, G.-H., Zhao, X., & Zhou, H.-L. (2022). Design and Application of Non-Circular Gear with Cusp Pitch Curve. Machines, 10(11), 985. https://doi.org/10.3390/machines10110985





