Abstract
Due to the high center of gravity of distributed drive electric buses, it is crucial to enhance their stability and sliding mode control (SMC) is an effective method to enhance vehicle yaw stability. However, the traditional SMC needs to know the upper limits of the interference term in advance and select a better switching gain to obtain a better control effect, which is impossible for vehicle control. To solve the existing problems, an improved adaptive nonsingular fast terminal sliding mode (ANFTSM) control is presented to enhance the stability of distributed drive electric bus. An uncertainty term is introduced as a switching term in the sliding mode variable and the switching gain in the controller is obtained by parameter adaptation without knowing any uncertainty information. In addition, to enhance the stability of the vehicle in real-time, an adaptive neuro fuzzy inference system (ANFIS) for the weighting factor in the sliding surface is adjusted. A co-simulation of Matlab/Simulink–TruckSim is performed to verify the effectiveness of the algorithm under two typical conditions. The results indicate that the proposed control can follow the ideal value better which improves handling stability and chattering is weaker. Furthermore, the proposed control requires fewer control actions, and also reduces the motor torque variation.
1. Introduction
The traditional fuel vehicles will cause serious environmental pollution; as people become more aware of environmental protection, pure electric vehicles have attracted extensive attention from society [1]. Distributed drive electric vehicles offer the strengths of independent and controllable four wheels, a compact structure and flexible torque control [2], and their handling stability has always been a key topic of research. Especially, the research on the handling stability of distributed drive bus is of great significance due to its characteristics of large vehicle mass, a long wheelbase and high center of gravity. Direct yaw moment control (DYC) is achieved by independently controlling the drive torque distributed over the different wheels, which is a typical approach to enhancing vehicle handling stability [3]. In the analysis of vehicle lateral stability, the most commonly used methods are the phase plane method and Lyapunov theory, and other methods can be classified into one category [4,5].
In DYC, control parameters need to be selected first. Yaw rate and sideslip angle are key parameters to describe vehicle motion state, and most studies chose either of them or both of them [6,7]. To generate the reference yaw rate, a precise estimation of tire road friction coefficients is essential [8,9]. However, In the absence of additional sensors, the road friction coefficient is hard to use to evaluate accurately. Moreover, even if the road friction coefficient is accurately estimated, additional yaw moments maybe occur, which will affect vehicle performance. The majority of current DYCs rely on measurements of yaw rate and sideslip angle. Of these, sideslip angle has been proven to be well observed [10,11]. Zhang et al. [12] designed an observer for sideslip angle on the electric ground vehicle (EGV), and then proposed an optimal observer design method; simulations have verified the performance of the designed observer. Boada et al. [13] combined an unscented Kalman filter (UKF) and ANFIS to estimate the sideslip angle. The advantage of this estimation is to directly measure the signal of the vehicle sensor. The results showed that the presented method based on ANFIS–UKF is effective.
At present, plenty of research has been conducted on DYC by many scholars. Different control methods have been applied to DYC, such as LQR control [14], model predictive control [15,16,17] and robust control [18]. SMC has the advantages of high control accuracy, a simple structure and strong anti-interference. So, SMC has become one of the most common direct yaw moment controls. Peng et al. [19] employed the SMC method to track the ideal yaw rate and Xu et al. [20] designed a controller based on SMC to track the reference slip rate. In addition, Liu et al. [21] proposed an additional yaw moment controller based on SMC with yaw angle, yaw rate and lateral displacement as control variables, using a bilateral regulation method. The simulation results showed that the presented SMC strategy achieved good results. However, the chattering phenomenon exists in SMC, and many scholars put forward improvement methods for the chattering phenomenon of sliding mode. Zhang et al. [22] and Guo et al. [23] designed a controller based on fuzzy sliding mode control (FSMC). Furthermore, Lin et al. [24] proposed an adaptive FSMC to achieve DYC, which adjusted the weight factor of sideslip angle and yaw rate in real-time through fuzzy control, and finally obtained the optimal direct yaw moment. Compared with traditional SMC, FSMC is not only effective in maintaining the stability of the vehicle, but also significantly reducing the chattering phenomenon. However, the above studies did not take into account the model’s inaccuracy and external interference. Fu et al. [25] introduced an adaptive sliding mode method for DYC. The method used variable control gain to adapt to the change of sideslip angle in the front and rear wheels. Li et al. [26] proposed an adaptive sliding mode control method using the Lyapunov method to ensure vehicle stability and the convergence of adaptive speed. Asiabar et al. [27] proposed an adaptive SMC method, in which the modified yaw momentum was obtained through adaptive control of unknown parameters, so that the yaw rate could be tracked to the expected value and the sideslip angle could be kept within a certain range.
Ferrara et al. [28] designed a new second-order sliding mode control algorithm based on adaptive optimization for uncertain nonlinear systems. Ding et al. [29] further presented a second-order sliding mode control for chattering problems existing in traditional SMC. To avoid the excessive gain of the derived controller, the nonlinear disturbance observer was combined with the derived controller and a composite control scheme was proposed. Compared with the first order discontinuous sliding mode controller, the second order sliding mode controller has a better control effect. Zhang et al. [30] proposed an adaptive second-order sliding mode (ASOSM) controller based on the backstepping method. ASOSM requires fewer control actions due to the existence of adaptive law. Ding et al. [31] proposed a new adaptive terminal sliding mode (ANTSM) control method, which can automatically search for the minimum control gain in the presence of external disturbance.
State estimation has been less studied in DYC. The nonlinearity of the tire has not been considered, although the estimation of the sideslip angle has been researched; considering these problems, the actual sideslip angle was first identified and estimated using a sliding mode observer, and a method for simultaneous control of yaw rate and sideslip angle is proposed. The ANFTSM control method is used to eliminate chattering and interference caused by modeling errors, parameter uncertainties and external uncertainties. In addition, the ANFIS algorithm was introduced to adjust the weight factor of sliding mode surface in real time. Co-simulation results were obtained by Trucksim (Mechanical Simulation Corporation, CA, USA) and Matlab/Simulink (The Mathworks, Inc., Natick, MA, USA) co-simulation. Compared with the SMC process and control results, the effectiveness of the control method developed was analyzed in detail. The DYC problem of distributed drive electric buses was solved effectively.
The structure is as follows: Section 2 establishes a 2-DOF reference model and a 7-DOF vehicle dynamics model. Section 3 introduces the design of the controller in detail, including the design of a sideslip angle observer, the design of the upper ANFTSM controller, adjustment of weight factor of sliding surface and method of distributing the lower controller generalized yaw moment. In Section 4, Matlab/Simulink–Trucksim is used for the co-simulation experiment, and the simulation results are discussed and analyzed. Section 5 concludes the results.
2. Bus Dynamic Models
In this section, a 2-DOF dynamic model is used to derive the ideal yaw rate and sideslip angle. The 2-DOF vehicle model does not reflect the dynamics of the individual wheels of vehicle, therefore it cannot be applied to the subsequent strategy control. Meanwhile, the additional yaw moment needs to be distributed to each wheel. Therefore, a 7-DOF distributed drive electric bus dynamics model is presented as well.
2.1. 2-DOF Bus Model
The distributed drive electric bus model is a complex system with strong coupling and nonlinear characteristics. there are many modeling methods. The 2-DOF model is a common method for analyzing vehicle handling and stability. In the linear 2-DOF reference model, the lateral and yaw motions of the vehicle are considered, ignoring the influence of the suspension, which can reflect the important dynamic characteristics of the vehicle stability.
The 2-DOF model can describe the lateral motion and yaw motion of the distributed drive electric bus model as demonstrated in Figure 1. The equation of the 2-DOF model is as follows:
where m is vehicle mass; is the vehicle velocity; denotes the sideslip angle; is the steering angle at the front wheel; denotes the vehicle yaw rate; a and b represent the distances from the center of gravity to the front and rear axle, with L = a + b; and are respectively the equivalent cornering stiffness of the front and rear axles; indicates the vehicle rotational inertia around the Z-axis.
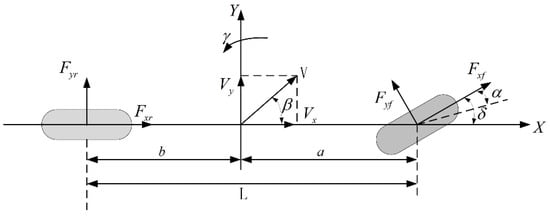
Figure 1.
The 2-DOF model.
When the vehicle is at a steady state,, , the desired yaw rate and the desired sideslip angle are obtained by the Equation (1). The desired yaw rate and desired sideslip angle are described in Equations (2) and (3):
where k denotes the stability factor, represents desired yaw rate, and represents desired sideslip angle.
Under the condition of considering road constraints, Equation (5) is obtained:
where is the lateral acceleration; μ is road friction coefficient.
According to and shown in Equation (5), the values are small, accounting for about 15% of the total lateral acceleration [8], so the upper limit of the desired yaw rate can be described in Equation (6):
To sum up, the relationship of desired yaw rate is shown in Equation (7):
In general, the maximum sideslip angle is not more than 10 degrees under good road friction conditions. When the sideslip angle of the bus is larger than 10 degrees, the vehicle will lose controllability and stability. Under the condition of poor road friction, such as snow or ice-covered road, the sideslip angle is less than 4 degrees. When the sideslip angle of the bus is larger than 4 degrees, the vehicle will lose controllability and stability. Therefore, the sideslip angle is limited by road friction conditions and satisfies the Equation (8):
In summary, the desired sideslip angle is shown in Equation (9):
2.2. 7-DOF Bus Model
This section introduces the 7-DOF model, which provides a detailed description of the vehicle dynamics. The nonlinear dynamic model with 7-DOF is shown in Figure 2.

Figure 2.
The 7-DOF model.
The following are some assumptions for the 7-DOF model:
- (1)
- The road surface is flat and has no influence on the vertical movement of the wheels. The wheel movement caused by the dynamic load on the road surface is ignored.
- (2)
- It ignores air resistance and ramp resistance.
- (3)
- It neglects the effects of torsional vibrations and pendulum vibrations, etc.
- (4)
- The front steering wheel angles of both sides are the same when the vehicle is turning.
The dynamic equations are Equations (10)–(13):
The equation of longitudinal motion is:
The equation of lateral motion is:
The equation of yaw movement is:
The rotating motion of the wheels is:
During the movement of the vehicle, the vertical load on the tires is influenced by the state of motion of the vehicle and is transferred between the axles. Load transfer then occurs from axle to axle. The vertical load on the wheel is calculated by the following equation:
where denotes the tire lateral force, denotes the longitudinal force of the tire; Fzij is the vertical load; ωij is angular velocities of wheel; i represents the front or rear axle, and j represents the left or right tire. is the front wheel base and is the rear wheel base; h is the height of the vehicle center of mass; ax is longitudinal acceleration; is the additional yaw moment applied to the center of gravity; is a bounded concentrated disturbance, including system uncertainty and external disturbance; Jw is the wheel moment of inertia with respect to the rotating axis; represents the driving torque; represents the braking moment; rw represents the wheel radius.
2.3. Tire Model
This paper uses the magic formula for the non-linear modeling of tires because of its high accuracy and ease of use, which makes it particularly suitable for the analysis of vehicle dynamics. The general expression of the magic formula is Equation (15):
where Y represents the output of the magic formula, the longitudinal force, lateral force and return moment; X is the input to the magic formula, representing the longitudinal slip rate or side-slip angle of the tire; is the horizontal drift of the curve; denotes the vertical drift of the curve; B, C, D and E are the curve correction factors of the magic formula, representing the stiffness factor, curve shape factor, peak factor and curve curvature factor, respectively.
The longitudinal force of the tire in pure rolling is described as follows:
Factors of longitudinal force:
The lateral force of the tire during pure steering is described as follows:
Factors of lateral force:
In Equations (16) and (17), s is the longitudinal slip rate and is the side-slip angle of the tire. The parameters and can be calibrated through tire force tests; the results are illustrated in Table 1.

Table 1.
The parameters of the tire.
The tire formula above does not reflect the effect of the road adhesion coefficient on tire forces. To modify it, the modified expression is as follows [32]
Equations (16) and (17) calculate the longitudinal and lateral forces under pure slip and pure sideways deflection conditions, whereas normally there is both slip and sideways deflection during the operation of the tire, i.e., a combined condition. In this case, the longitudinal and lateral forces of the tire and lateral forces need to be calculated according to the generalized displacement proposed in the literature [33].
The equivalent joint generalized displacement is as follows:
The responses of longitudinal force and lateral force of the tire under combined working conditions are as follows:
where Xx is the input when the tire is purely rolling; Xy is the input during pure steering; X* is input at generalized displacement.
3. Controller Design
The overall controller structure is shown in Figure 3, which adopts a hierarchical control structure, including a three-layer structure. One is the sideslip angle observer, which is used to make accurate observation of the sideslip angle for subsequent control. Then, there is the core decision layer, which mainly applies the sliding mode variable structure of ANFIS combined with the ANFTSM algorithm to calculate the additional yaw moment. Finally, a torque distribution controller is needed to distribute the additional yaw torque to the individual wheels.
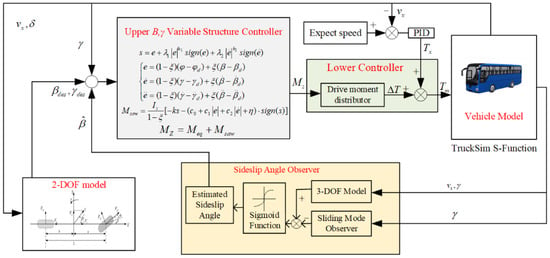
Figure 3.
Structure of overall controller.
3.1. Sliding Mode Observer Design
The 7-DOF vehicle model is simplified into a 3-DOF model with only longitudinal, lateral and yaw motion, namely Equations (10)–(12), which are sorted into Equation (22).
The sideslip angle is defined in Equation (23):
According to Equations (22) and (23), the state equation and observation equation of the nonlinear system are established, as shown in Equation (24).
represents the state vector; represents the control volume, ; C is the coefficient matrix.
According to the principle of the sliding mode observer [34], the sliding mode state observer is designed as:
where H and K denote respectively the damping coefficient matrix and robust control coefficient of the sliding mode observer; ; .
According to Equations (24) and (25), it can be obtained:
As required , .
To reduce system chattering caused by the sign function, the saturation function can be used instead.
3.2. Upper Controller Design
To design the controller, a sliding surface needs to be selected first. The purpose of the control is for the yaw rate and sideslip angle to follow their target values; according to the strategy of ANFTSM, the sliding surface can be considered as Equation (27):
where , , , and sign() are the signum function; e denotes the error, which is defined as:
where is the weight factor of sideslip angle and yaw angle; φ is the yaw angle.
Substituting Equation (28) into Equation (27), the derivative of Equation (29) can be obtained:
Rearranging Equation (12), we can obtain:
where is the yaw moment applied by the controller, whose expression is Equation (31):
where w(t) is a bounded concentrated disturbance, including system uncertainty and external disturbance, whose expression is Equation (32):
when , it can be obtained by Equations (29)–(31):
The equivalent yaw moment is described as Equation (35):
To decrease the impact of uncertainties and external disturbances on the control performance, the parameters of the upper bound on the indeterminacy of the system are evaluated using an adaptive switching law, which can be denoted as Equations (36) and (37):
The overall law design for ANFTSM control of direct yaw moment is shown in Equation (38):
To illustrate the stability of the control system, the analysis is performed using Lyapunov’s theory and the process is as follows [35].
Proof.
First, defining Lyapunov function as Equation (39):
Then, the following Equation (40) can be obtained by taking the derivative of V:
Substituting Equation (29) into Equation (40), the following equation can be obtained:
By further substituting Equation (38) in Equation (41), the above formula can be rewritten as:
Considering the adaptive updating laws shown in Equation (37), Equation (42) can be rewritten as:
Combining the above equations, the system Lyapunov function satisfies:
From the above analysis, it is clear that the system state can converge gradually to zero along the sliding surface in finite time, which proves the robustness of the control system. □
3.3. ANFIS Controller
To make the proposed algorithm have a better effect under different working conditions of the vehicle, the weight factor of sideslip angle and yaw rate needs to be adjusted online in real-time. In other words, the constant ξ needs to be adjusted in real time. Therefore, an ANFIS is proposed for the adjustment of ξ.
ANFIS is a kind of artificial neural network that is based on the Takagi–Sugeno fuzzy inference system [36]. ANFIS implements fuzzification, fuzzy inference and anti-fuzzification using neural network modeling. The neural network itself can automatically update the rules from the input and output sample data by training and learning, thus forming an adaptive neuro-fuzzy inference system and adjusting the fuzzy rules by training and learning. Figure 4 depicts the structure diagram.
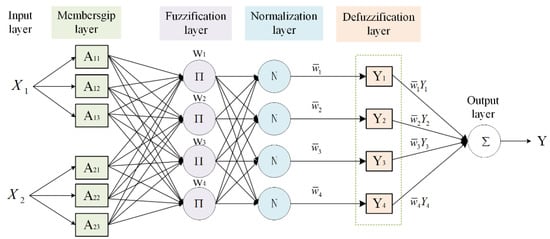
Figure 4.
Structure of the ANFIS controller.
The difference between the sideslip angle and the yaw angle from their ideal values are used as inputs and the weight factor ξ is used as output. At the end of training, the trained ANFIS network can map the input to the output and feed the weight factor ξ into the ANFTSM controller.
3.4. Lower Controller Design
The needs to be allocated into the torque input of wheels to realize the DYC of the vehicle. Therefore, it is worth establishing a torque distribution controller which fully considers the actual constraints such as ground attachment and motor output.
When the rolling resistance of the tire is not considered, the rotational dynamics of the wheel are described as Equation (45):
The output torque is restricted by the maximum motor torque. It is described as Equation (46):
The longitudinal force of the tire is constrained by the road friction coefficient and the vertical load of the tire; it is described as Equation (47):
According to the Equation (46) and (47), it can be concluded that to make the tire work within the friction limit, and to not cause the tire to slip strongly due to excessive torque input, which seriously worsens the stress of the tire, the torque output of the motor should meet the Equation (48) constraints:
where is driving torque; is driving force; represents the maximum motor output torque; is road friction coefficient; denotes vertical load.
For smaller additional longitudinal force and to improve the stability margin for each wheel, to reduce the failure rate without increasing the complexity of the controller and to enable the system to respond quickly, the form of equal proportional torque distribution is adopted; that is, the torque correction of each wheel is considered equal. It is described as Equation (49):
where is the torque assigned by the wheel; D is wheel base.
In addition to determining the torque assigned to each wheel, the lower controller also needs to determine the torque direction as to whether each wheel should be driven or braked. This requires the analysis of the current steering state of the vehicle, which is the driver’s operating intention. The front wheel angle δ and yaw rate deviation are used to judge whether the vehicle is understeering or oversteering, thereby determining the direction of each torque, in addition, preventing the vehicle from being too sensitive to state deviation and preventing the controller from working intensively. The threshold value of yaw rate deviation is set, so that only when the deviation between the actual yaw rate and the ideal yaw rate of the vehicle reaches the set threshold value can the controller take effect. The exact allocation rules are shown in Table 2.

Table 2.
Torque distribution rules.
4. Simulation Results and Analysis
To confirm the effectiveness of the presented method, a co-simulation by TruckSim (2019.1)–Matlab (R2016b)/Simulink is applied. TruckSim (2019.1) software is used for numerical simulation, and the tour bus with four-wheel independent drive in TruckSim is used for simulation. The vehicle parameters used are described in Table 3.

Table 3.
Main vehicle parameters.
To assess the control performance of the algorithm, simulations of sine and fishhook conditions were performed and the root mean square error (RMSE) values during each simulation were used to verify the control performance in tracking ideal value; RMSE is described as following Equation (50):
where rref (t) is the ideal value, r(t) is the real value.
4.1. Sine Condition
The detailed simulation conditions are as follows: the initial speed of the vehicle is 80 km/h, which is essentially constant; the steering wheel angle is a sinusoidal condition with a maximum steering angle of 180 deg, as shown in Figure 5; the road friction coefficient is 0.85.
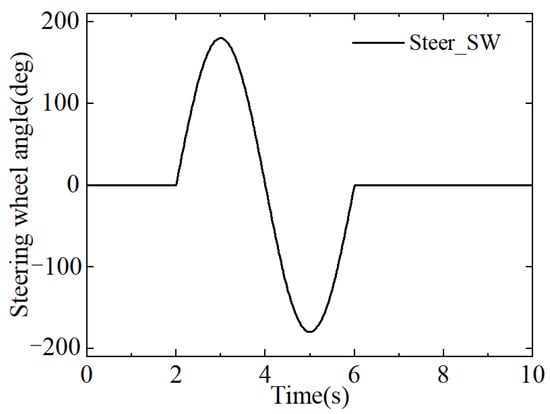
Figure 5.
Steering wheel angle in sine condition.
From Figure 6a, the true value of sideslip angle was generated by TruckSim software. It is evident that the sideslip angle observed by the non-linear sliding mode observer is pretty close to the true value, with a maximum error of no more than 0.3 deg, which indicates a good observation effect that is satisfactory. This can provide a basis for subsequent yaw stability control.
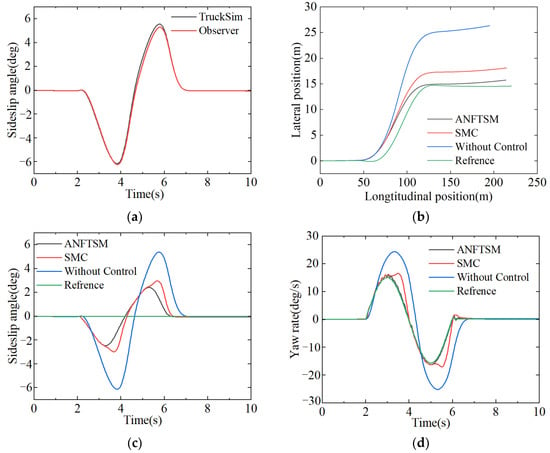
Figure 6.
Sine wave response test results. (a) Estimation of sideslip angle; (b) vehicle track; (c) sideslip angle; (d) yaw rate.
From the simulation results, the ANFTSM controller designed is effective. From Figure 6b, it can be observed that under the action of the ANFTSN controller, the track of the vehicle follows the target track fabulously, while vehicles without control cannot drive along the target path. In addition, the sideslip angle is shown in Figure 6c. It can be seen that no matter which control is adopted, the sideslip angle cannot always be kept at zero. From Table 4 and Figure 6a, when there is no control, the sideslip angle fluctuates the most, and its maximum value is 5.39 deg, as can be seen in Figure 7b. From Figure 7, the RMSEs of ANFTSM and SMC are 1.03 deg and 1.29 deg, respectively, relative to the ideal sideslip angle, and the RMSE of ANFTSM is reduced by 20.2% relative to SMC.

Table 4.
Objective performance indicators of the sine wave tests.
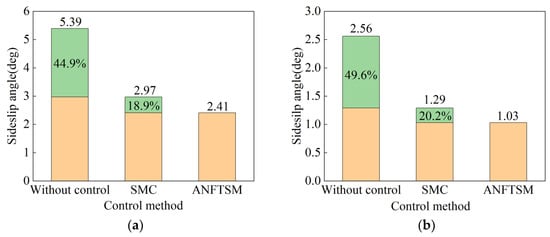
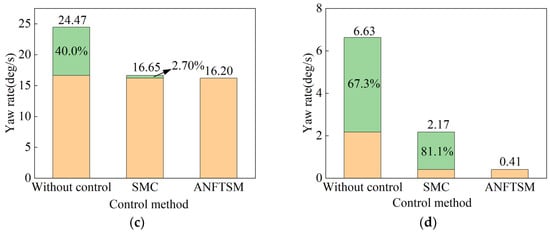
Figure 7.
Objective performance index of sinusoidal test. (a) Maximum sideslip angle; (b) RMSE of sideslip angle; (c) maximum yaw rate; (d) RMSE of yaw rate.
From Figure 6d, the yaw rate controlled by ANFTSM and SMC is closest to the ideal value, but the effect of the SMC controller is not as good as that of the ANFTSM controller, and a chattering phenomenon occurs. As can be seen from Table 4 and Figure 7c, the maximum yaw rate controlled by ANFTSM is 16.2 deg/s. This is 2.7% lower than the SMC control maximum of 16.65 deg/s. This shows that chattering can be reduced under ANFTSM control. From Figure 7d, the RMSE between ANFTSM’s actual yaw rate and ideal yaw rate decreases by 81.1% compared with the RMSE under SMC control, which indicates that the yaw rate under ANFTSM control can track the ideal yaw rate with a small error.
Without control, accidents such as rollovers maybe occur when the driver suddenly increases the steering wheel angle of the distributed drive electric bus during a turn, which increases the sideslip angle. However, the control method of the ANFTSM yaw rate of the vehicle and sideslip angle can track its ideal value very well, and also reduce the chattering and response speed faster when compared with traditional sliding mode control, improving vehicle handling stability and the distributed drive electric bus safety.
4.2. Fishhook Condition
The detailed simulation conditions of fishhook condition are as follows: the initial vehicle speed is 80 km/h, which remains unchanged; the steering wheel angle is up to 180 deg, as shown in Figure 8; the road friction coefficient is 0.85.

Figure 8.
Steering wheel angle in fishhook condition.
Based on the estimated effect of the sliding mode observer for the fishhook condition, Figure 9a, it can be seen that the observation error increases compared to the sinusoidal condition, but is within 2 degrees of the error. This is because the fishhook condition is more extreme and has a higher value of sideslip angle, which can be considered to have higher accuracy.
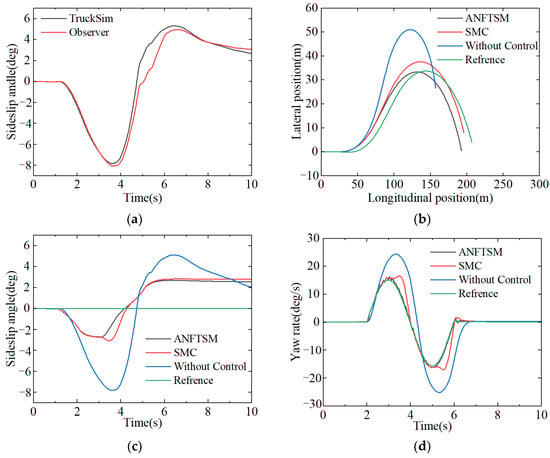
Figure 9.
Fishhook response test results. (a) Estimation of sideslip angle; (b) vehicle track; (c) sideslip angle; (d) yaw rate.
The vehicle path is described in Figure 9b. It can be noticed that when there is no control, the vehicle path deviates severely from the target path, thereby making the driver unable to control the direction of the vehicle and reducing vehicle stability. The common sliding mode control and ANFTSM control can track the target track well. Among them, ANFTSM control has a smaller deviation from target trajectory than SMC, and can promote tracking effects and control accuracy.
The sideslip angle is depicted in Figure 9c which indicates that in the absence of control, the fluctuation range of the sideslip angle is the largest, while both SMC and ANFTSM control can suppress the fluctuation of the sideslip angle. It can be seen from Table 5 that the maximum sideslip angle under the control of ANFTSM is 2.10 deg. The maximum sideslip angle under SMC control is 2.29 deg. Figure 10a indicates that the maximum sideslip angle under the control of ANFTSM decreases by 5.0% and 8.3% compared with SMC respectively. These results indicate that ANFTSM control has a better control effect than sliding mode control, with a smaller chattering effect and a smaller maximum sideslip angle. However, neither sliding mode control nor ANFTSM control can make the sideslip angle always be zero without fluctuation. This is because the lateral force of the tire cannot be controlled directly, but it can be changed by controlling the longitudinal force of each tire, which makes it difficult to achieve precise control of the lateral force. Therefore, the sideslip angle is restrained in the stability zone and cannot be zero.

Table 5.
Objective performance indicators of the fishhook tests.

Figure 10.
Objective performance index of fishhook test. (a) Maximum sideslip angle; (b) RMSE of sideslip angle; (c) maximum yaw rate; (d) RMSE of yaw rate.
The yaw rate is illustrated in Figure 9d. It can be viewed that in the absence of control, the yaw rate seriously deviates from the ideal yaw rate, and accidents such as tail slashings may occur in extreme cases. From Table 5, it can see that the maximum yaw rate without control is 25.06 deg/s, and the maximum yaw rate under SMC is 16.87 deg/s. The maximum yaw rate at ANFTSM is 16.45 deg/s. From Figure 10c, it can be noted that ANFTSM’s maximum yaw rate is reduced by 2.5% compared to SMC. The above shows that ANFTSM control has smaller chattering control and a better effect. As shown in Table 5, RMSE without control is 6.97 deg/s, RMSE under SMC is 1.71 deg/s, and RMSE under ANFTSM is 0.57 deg/s. From Figure 10d, it can be seen that RMSE under the control of ANFTSM decreased by 66.7% compared with SMC. It can be concluded that the ANFTSM control can follow the expected yaw rate well and the control effect is remarkable.
According to the results, it can be concluded that when the steering wheel rotation speed changes, the yaw rate and sideslip angle will produce drastic fluctuations. the traditional sliding mode control and ANTFSM control effectively improve the vehicle stability, but the traditional SMC can’t adjust the rate of change, and is more sensitive to interference and chattering. When the ANFTSM controller can switch the to the adaptive sliding mode surface, this reduces the chattering, follows the ideal value better and maintains the stability of the vehicle.
5. Conclusions
A distributed drive electric bus stability control method based on ANFTSM was proposed which uses a 2-DOF vehicle model as the reference model. A nonlinear sliding mode observer is used based on estimating the sideslip angle, which takes into account the uncertainty of external disturbances and the existence of jitter and other problems in traditional SMC. Traditional SMC is very sensitive to external interference, which will lead to a sudden increase of control variables and chattering phenomenon. The control of the ANFTSM designed can automatically adjust the gain switching term to maintain continuous discrete symbol function in the presence of external interference, and avoid the problems associated with traditional SMC. In addition, the real-time adjustment of the sliding surface also increases the real-time stability of the vehicle.
Two kinds of conditions of the simulation results indicate that for ANFTSM control compared with traditional SMC, the trajectory and yaw rate of the vehicle can better follow the target value. In addition, the sideslip angle decreased and was limited to a small range, and the RMSE relative to the traditional sliding mode control has been reduced, which shows that the controller has a good tracking control effect and effectively improves the safety of the vehicle. Compared with the traditional sliding mode control, the maximum yaw rate of ANFTSM control is reduced by 2.5% and 2.7% in sinusoidal and fishhook conditions respectively. The maximum sideslip angle decreases by 18.9% and 5.0% respectively. The results show that the ANFTSM control has superior performance in the closed-loop robustness of parameter uncertainties and external perturbations, and can reduce chattering. The results also show that the stability of a distributed drive electric bus is improved significantly by using ANFTSM control.
Author Contributions
Conceptualization, H.Z. and F.Z.; methodology, H.Z.; software, H.Z., L.S and G.G.; validation, F.Z., Y.Z. and L.S.; formal analysis, H.Z.; investigation, F.Z.; resources, F.Z.; data curation, H.Z. and F.Z.; writing—original draft preparation, H.Z.; writing—review and editing, H.Z. and F.Z.; visualization, H.Z.; supervision, F.Z.; project administration, F.Z.; funding acquisition, F.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Fundamental Research Funds for the Central Universities (ZQN-074) and National Key Research and Development Program of China (2021YFB2500704).
Data Availability Statement
Not applicable.
Acknowledgments
We would like to thank Xiamen King Long United Automotive Industry Co. Ltd., especially Liang Su and Gang Gong, for helping the authors collect and organize literature and it provides guidance to build the dynamic model.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Su, L.; Wang, Z.; Chen, C. Torque vectoring control system for distributed drive electric bus under complicated driving conditions. Assem. Autom. 2022, 42, 1–18. [Google Scholar] [CrossRef]
- Wang, J.; Yang, B.; Wang, Q.; Ni, J. Review on Vehicle Drive Technology of Torque Vectoring. Jixie Gongcheng Xuebao/J. Mech. Eng. 2020, 56, 92–104. [Google Scholar] [CrossRef]
- Medina, A.; Bistue, G.; Rubio, A. Comparison of Typical Controllers for Direct Yaw Moment Control Applied on an Electric Race Car. Vehicles 2021, 3, 127–144. [Google Scholar] [CrossRef]
- Sakhnevych, A.; dell’Annunziata, G.N.; Russo, R. On the Vehicle Stability and Maneuverability Domain Definition for Automated Vehicles. In Advances in Italian Mechanism Science; Mechanisms and Machine Science; Springer: Cham, Switzerland, 2022; pp. 331–345. [Google Scholar]
- Huang, Y.; Liang, W.; Chen, Y. Stability Regions of Vehicle Lateral Dynamics: Estimation and Analysis. J. Dyn. Syst. Meas. Control 2021, 143, 051002. [Google Scholar] [CrossRef]
- Lenzo, B.; Sorniotti, A.; Gruber, P.; Sannen, K. On the experimental analysis of single input single output control of yaw rate and sideslip angle. Int. J. Automot. Technol. 2017, 18, 799–811. [Google Scholar] [CrossRef]
- Tchamna, R.; Youn, I. Yaw rate and side-slip control considering vehicle longitudinal dynamics. Int. J. Automot. Technol. 2013, 14, 53–60. [Google Scholar] [CrossRef]
- Her, H.; Koh, Y.; Joa, E.; Yi, K.; Kim, K. An Integrated Control of Differential Braking, Front/Rear Traction, and Active Roll Moment for Limit Handling Performance. IEEE Trans. Veh. Technol. 2016, 65, 4288–4300. [Google Scholar] [CrossRef]
- Qi, Z.; Taheri, S.; Wang, B.; Yu, H. Estimation of the tyre–road maximum friction coefficient and slip slope based on a novel tyre model. Veh. Syst. Dyn. 2015, 53, 506–525. [Google Scholar] [CrossRef]
- Chindamo, D.; Lenzo, B.; Gadola, M. On the vehicle sideslip angle estimation: A literature review of methods, models, and innovations. Appl. Sci. 2018, 8, 355. [Google Scholar] [CrossRef]
- Zhang, B.; Du, H.; Lam, J.; Zhang, N.; Li, W. A Novel Observer Design for Simultaneous Estimation of Vehicle Steering Angle and Sideslip Angle. IEEE Trans. Ind. Electron. 2016, 63, 4357–4366. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, G.; Wang, J. Sideslip Angle Estimation of An Electric Ground Vehicle via Finite-frequency H∞ Approach. IEEE Trans. Transp. Electrif. 2016, 2, 200–209. [Google Scholar] [CrossRef]
- Boada, B.L.; Boada, M.J.L.; Diaz, V. Vehicle sideslip angle measurement based on sensor data fusion using an integrated ANFIS and an Unscented Kalman Filter algorithm. Mech. Syst. Signal Process. 2016, 72–73, 832–845. [Google Scholar] [CrossRef]
- Wang, Z.; Montanaro, U.; Fallah, S.; Sorniotti, A.; Lenzo, B. A gain scheduled robust linear quadratic regulator for vehicle direct yaw moment Control. Mechatronics 2018, 51, 31–45. [Google Scholar] [CrossRef]
- Nahidi, A.; Kasaiezadeh, A.; Khosravani, S.; Khajepour, A.; Chen, S.-K.; Litkouhi, B. Modular integrated longitudinal and lateral vehicle stability control for electric vehicles. Mechatronics 2017, 44, 60–70. [Google Scholar] [CrossRef]
- Ren, B.; Chen, H.; Zhao, H.; Yuan, L. MPC-based yaw stability control in in-wheel-motored EV via active front steering and motor torque distribution. Mechatronics 2016, 38, 103–114. [Google Scholar] [CrossRef]
- Li, S.; Wang, G.; Zhang, B.; Yu, Z.; Cui, G. Vehicle Yaw Stability Control at the Handling Limits Based on Model Predictive Control. Int. J. Automot. Technol. 2020, 21, 361–370. [Google Scholar] [CrossRef]
- Jin, X.; Yin, G.; Zeng, X.; Chen, J. Robust gain-scheduled output feedback yaw stability control for in-wheel-motor-driven electric vehicles with external yaw-moment. J. Frankl. Inst. 2018, 355, 9271–9297. [Google Scholar] [CrossRef]
- Peng, H.; Wang, W.; An, Q.; Xiang, C.; Li, L. Path Tracking and Direct Yaw Moment Coordinated Control Based on Robust MPC With the Finite Time Horizon for Autonomous Independent-Drive Vehicles. IEEE Trans. Veh. Technol. 2020, 69, 6053–6066. [Google Scholar] [CrossRef]
- Xu, W.; Wang, D.; Li, Y. The lateral stability control of vehicles based on sliding mode method. In Proceedings of the 2014 IEEE International Conference on Information and Automation (ICIA), Hailar, China, 28–30 July 2014; pp. 1312–1317. [Google Scholar]
- Liu, Z.; Qiao, Y.; Chen, X. A Novel Control Strategy of Straight-line Driving Stability for 4WID Electric Vehicles Based on Sliding Mode Control. In Proceedings of the 2021 5th CAA International Conference on Vehicular Control and Intelligence (CVCI), Tianjin, China, 29–31 October 2021; pp. 1–6. [Google Scholar]
- Zhang, H.; Liang, J.; Jiang, H.; Cai, Y.; Xu, X. Stability Research of Distributed Drive Electric Vehicle by Adaptive Direct Yaw Moment Control. IEEE Access 2019, 7, 106225–106237. [Google Scholar] [CrossRef]
- Guo, L.; Ge, P.; Sun, D. Fuzzy-Sliding Mode Control based Yaw Stability Control Algorithm for Four-in-wheel-motor Drive Electric Vehicle. In Proceedings of the 2019 3rd Conference on Vehicle Control and Intelligence (CVCI), Hefei, China, 21–22 September 2019; pp. 1–6. [Google Scholar]
- Lin, J.; Zou, T.; Zhang, F.; Zhang, Y. Yaw Stability Research of the Distributed Drive Electric Bus by Adaptive Fuzzy Sliding Mode Control. Energies 2022, 15, 1280. [Google Scholar] [CrossRef]
- Fu, C.; Hoseinnezhad, R.; Li, K.; Hu, M. A novel adaptive sliding mode control approach for electric vehicle direct yaw-moment control. Adv. Mech. Eng. 2018, 10, 1687814018803179. [Google Scholar] [CrossRef]
- Li, S.T.; Liu, H.; Zhao, D.; Li, Q.Y.; Tian, Y.T.; Wang, D.J.; Yu, D.L. Adaptive Sliding Mode Control of Lateral Stability of Four Wheel Hub Electric Vehicles. Int. J. Automot. Technol. 2020, 21, 739–747. [Google Scholar] [CrossRef]
- Asiabar, A.N.; Kazemi, R. A direct yaw moment controller for a four in-wheel motor drive electric vehicle using adaptive sliding mode control. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2019, 233, 549–567. [Google Scholar] [CrossRef]
- Ferrara, A.; Incremona, G.P.; Regolin, E. Optimization-based adaptive sliding mode control with application to vehicle dynamics control. Int. J. Robust Nonlinear Control 2019, 29, 550–564. [Google Scholar] [CrossRef]
- Ding, S.; Liu, L.; Zheng, W.X. Sliding Mode Direct Yaw-Moment Control Design for In-Wheel Electric Vehicles. IEEE Trans. Ind. Electron. 2017, 64, 6752–6762. [Google Scholar] [CrossRef]
- Zhang, L.; Ding, H.; Shi, J.; Huang, Y.; Chen, H.; Guo, K.; Li, Q. An Adaptive Backstepping Sliding Mode Controller to Improve Vehicle Maneuverability and Stability via Torque Vectoring Control. IEEE Trans. Veh. Technol. 2020, 69, 2598–2612. [Google Scholar] [CrossRef]
- Ding, S.; Liu, L.; Park, J.H. A novel adaptive nonsingular terminal sliding mode controller design and its application to active front steering system. Int. J. Robust Nonlinear Control 2019, 29, 4250–4269. [Google Scholar] [CrossRef]
- Jagt, P.V.D.; Parsons, A.W. Road Surface Correction o f Tire Test Data. Veh. Syst. Dyn. 1996, 25, 147–165. [Google Scholar] [CrossRef]
- Sakhnevych, A. Multiphysical MF-based tyre modelling and parametrisation for vehicle setup and control strategies optimisation. Veh. Syst. Dyn. 2021, 60, 3462–3483. [Google Scholar] [CrossRef]
- Chen, Y.; Ji, Y.; Guo, K. A reduced-order nonlinear sliding mode observer for vehicle slip angle and tyre forces. Veh. Syst. Dyn. 2014, 52, 1716–1728. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, X.; Han, F. On nonsingular terminal sliding-mode control of nonlinear systems. Automatica 2013, 49, 1715–1722. [Google Scholar] [CrossRef]
- Jang, J.S.R. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).