Abstract
In order to improve the performance of magnetorheological dampers under impact load, a double-rod magnetorheological damper is designed in this paper, and its multi-physical field coupling model is established. The performance of a double-rod magnetorheological damper under impact conditions is characterized from the aspects of viscosity, velocity, peak pressure, impact energy consumption and viscous damping force ratio. The research contents include: a comparison of dynamic characteristics such as the viscosity, velocity and pressure of the magnetorheological damper under impact conditions and low-speed vibration; the influence of temperature on the mechanical performance parameters of the magnetorheological damper, such as peak pressure, impact energy dissipation and viscous damping force ratio, under impact load; and the establishment of a peak sensitivity function to study the influence of three key structural parameters on the magnetic flux density and impact energy dissipation at the damper damping channel. On the basis of the above theoretical research, an impact test of the processed double-rod magnetorheological damper prototype under different excitation currents is carried out. The results show that the viscosity distribution of the damping channel activation region (i.e., the region where the magnetorheological effect occurs after energization) of the magnetorheological damper under impact is disordered, the region of the structural flow in the semi-solid state is small and the influence of the Coulomb damping force is greatly weakened. When the current is 0.5 A, the viscous damping force accounts for 91.2%, and the viscous damping force plays a major role in buffering energy absorption. With an increase in working temperature, the effect of the Coulomb damping force decreases, and the peak pressure and impact energy consumption of the MR damper decrease greatly. With increasing excitation current, this reduction is further increased. The influence of gap height, piston diameter and effective length on magnetic flux density and impact energy dissipation is determined via the peak sensitivity function. When the change in the structural parameters ∆α is 30%, the change in the piston diameter has the greatest influence on the peak sensitivity of the magnetic flux density, and the peak sensitivity index of the magnetic flux density reaches 25%. The change in clearance height has the greatest influence on the impact energy consumption, and the peak sensitivity index of the impact energy consumption reaches 115%. This shows that the magnetic flux density is most affected by the piston diameter, and the impact energy consumption is most affected by the clearance height. The test results show that the test pressure peak-change curve is consistent with the simulation pressure peak-change curve, and the pressure peak error between the two is within 10%.
1. Introduction
As an intelligent magnetic material, the apparent viscosity of magnetorheological fluid can change greatly under the action of an external magnetic field and quickly return to its free-flow state after removal of the magnetic field. The characteristics of magnetorheological fluid are effectively applied in the field of vibration damping and impact resistance. A buffer designed with magnetorheological fluid can control the damping force by controlling the current. At present, magnetorheological dampers are widely used in the fields of industry, vehicles, civil engineering and weapon equipment [1,2,3,4,5,6,7,8].
In the field of magnetorheological damper structure design, Ebrahim Yarali et al. [9] used the characteristics of magnetorheological fluid to make a prototype of a double-barrel magnetorheological damper with double magnetic components, and carried out a damping force measurement test. In addition, a general evolutionary process was given using a neural network algorithm. The derived damping force evolution had high performance in predicting the response of the magnetorheological damper in other currents. Nguyen Q H [10] proposed a compact magnetorheological damper. Its performance was studied via finite element analysis, and its prevention was verified using experiments. Li Yongtao [11] designed a two-channel magnetorheological damper, and realized the coupling between the magnetic field and the flow field in ANSYS through UDF; moreover, they studied the performance of the magnetorheological damper under high-speed impact using a multi-physical field coupling model, and verified the simulation model through an artillery impact test.
Computational fluid dynamics (CFD) has been widely used to study fluid flow behavior, and there are also many scholars who have studied the hydrodynamic behavior of magnetorheological dampers via CFD. Wael Elsaady et al. [12] first realized the coupling between the magnetic field and flow field through a combination of COMSOL Multiphysics and Fluent, and obtained a series of research results for single-phase incompressible and multiphase compressible models. D Case et al. [13] used the small magnetorheological damper on a medical prosthesis, and the accuracy of the simulation results was verified by experiments. Gurubasavaraju et al. [14] used experimental and calculation methods, using ANSYS CFX to model a magnetorheological damper, and realized coupling through ANSYS CFX command language (CCL). Z Parlak et al. [15] used the finite element method, electromagnetic field analysis method and magnetorheological fluid computational fluid dynamics analysis method to study and optimize the target damping force and maximum magnetic fluid density of a magnetorheological damper and obtained the optimal value of the design parameters. Huang Tengyi et al. [16] simulated a magnetorheological damper in COMSOL Multiphysics and determined the influence of structural parameters on damping force under low-speed vibration. Liu Xinyun [17] also used a combination of COMSOL Multiphysics and Fluent to study a magnetorheological damper designed via the implicit dynamic boundary, and the simulation results showed an obvious temperature-rise phenomenon. Wael Elsaady et al. [18] used the FFE and CFD methods to study the effect of bubbles in dampers. Kemari M [19] studied a single-tube mixed-model magnetorheological damper via experimental and CFD methods. The results showed that the numerical results were in good agreement with the experimental data. Hu Guoliang et al. [20] established a multiphysics coupling model using COMSOL to study the dynamic performance of magnetorheological dampers under vibration conditions. Yu Zhenhuan et al. [21] used ADINA to establish a magneto-flow coupling model, and used an ADINA solid model, a magnetic field module and a CFD model to establish multiple single physical models, respectively. The three-field coupling conditions were set and finite element analysis was conducted to obtain the distribution of the magnetic field and the structural stress field inside the magnetorheological damper. Zhang Yutong et al. [22] conducted mechanical modeling of a magnetorheological damper, established a multi-field coupling simulation model of the flow field, structure field and electromagnetic field of the magnetorheological damper in ADINA, and studied the dynamic characteristics and influencing factors of the magnetorheological damper.
Regarding the effect of temperature on magnetorheological damper performance, Feng Zhimin et al. [23] obtained the viscosity–temperature characteristics of magnetorheological fluid using an experimental method and explored the influence of temperature on damping force under low-speed vibration via a CFD method. Stephen G [24] experimentally studied the temperature characteristics of magnetorheological fluid and obtained an influence curve of temperature on the viscosity and yield stress of magnetorheological fluid. Michael McKee [25] studied the influence of temperature on the hydrodynamic properties of MR Fluid, and the results showed that the shear yield stress of MR Fluid remained unchanged within the test range, while the plastic viscosity and volume modulus of MR Fluid decreased with increasing temperature. Zarana L et al. [26] studied the influence of temperature on the material properties of MR Fluid, and the results showed that the magnetization, coercivity and shear viscosity of magnetic particles in the MR Fluid decreased significantly with increasing temperature. Feng Zhimin et al. [27] obtained the viscosity and temperature characteristics of MR Fluid through experiments, and explored the influence of temperature on damping force under low-speed vibration via the CFD method. Aiming to determine the impact of a buffering target, Zheng Jiajia et al. [28] proposed a multi-stage independent magnetorheological buffer, and proposed a magnetic-flow-temperature multi-physical field model based on the inverse Jiles–Atherton (J–A) hysteresis model. The model can describe the multi-physical field transient characteristics of magnetorheological dampers under sinusoidal and step excitation currents and impact load.
According to existing research, it can be seen that the properties of magnetorheological dampers under low-speed vibration and the damping force, pressure, and other traditional performance indicators of magnetorheological dampers under impact conditions were introduced. The influence of temperature on the output damping force and the viscosity temperature characteristics of the MR Fluid were mainly studied. The performance indicators of magnetorheological dampers include the output damping force, dynamic adjustable coefficient, peak pressure, energy absorption capacity, etc. To date, we have not found comprehensive studies on the impact of mechanical properties (such as pressure, viscosity, viscous damping force, energy absorption ratio and temperature) on the viscous damping force energy consumption ratio under impact conditions, or the influence of the three structural parameters of piston diameter, effective length and gap height on the magnetic flux density at the damping channel of magnetorheological dampers, and their impact energy consumption.
In view of the above problems, in this paper, a double-rod-type magnetorheological damper is designed to analyze the static magnetic field of the double-rod-type magnetorheological damper. Additionally, a multi-field coupling model of the magnetorheological damper is established for multiphysics simulation to study the mechanical properties of the double-rod magnetorheological damper under impact conditions; these include a comparison of dynamic characteristics such as the viscosity, velocity and pressure of the magnetorheological damper under impact conditions and low-speed vibration, the influence of temperature on mechanical properties such as the peak pressure, impact energy dissipation and viscous damping force ratio of the magnetorheological damper under impact load, and the influence of three key structural parameters on magnetic flux density and impact energy dissipation at the damper damping channel. Based on the above research, an impact test of the double-rod magnetorheological damper prototype under different excitation currents is carried out, so as to provide a basis for the optimal design of magnetorheological dampers and provide a new scheme for the improvement of magnetorheological damper performance.
2. Design of Magnetorheological Damper
2.1. Structure Design
One new type of magnetorheological damper with a double-outlet bar is designed, and it is applied to a mine car in inclined shaft production in this paper. A mine car is the main means of transport in the production of inclined shafts in a mine. When the mine car runs on the roadway, it is usually connected with several carriages in front and behind for operation. When the speed of the rear car is higher than the speed of the front car or the front car is braking, an impact collision will occur between the carriages, so it is necessary to install anti-impact devices between two adjacent carriages as a buffer. When the speed of the front and rear cars is inconsistent, it can effectively slow down the impact force of the car. A schematic diagram of the structure and installation of the dual-outlet magnetorheological damper is shown in Figure 1a.
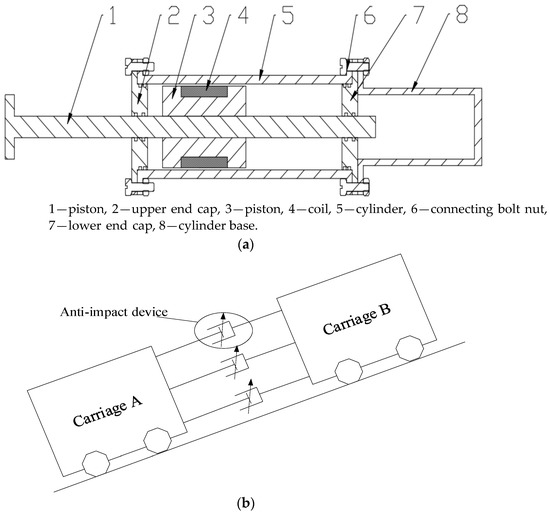
Figure 1.
Schematic diagram of structure and installation of double-rod magnetorheological damper. (a) Structure schematic diagram of a double-bar magnetorheological damper; (b) installation diagram of anti-impact device.
It can be seen from Figure 1b that three anti-impact devices are installed in parallel between the two carriages. There is a double-bar magnetorheological damper in the impact-resistance device. The inclination angle of the inclined shaft used in this design is 30°. Considering the technical parameters of the mine car, the inclination angle of the inclined shaft and the installation quantity of the anti-impact device, the design parameters of the magnetorheological damper are determined. The specific parameters are as follows: the impact mass is 200 kg, the maximum stroke is 60 mm, the maximum working pressure is 10 MPa, and the maximum working current is 4 A.
The structure parameters of the piston are shown in Figure 2. The main values of these parameters are shown in Table 1.
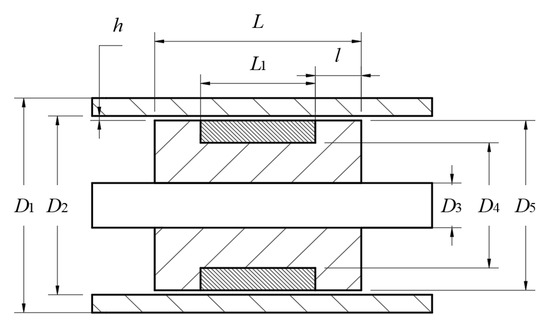
Figure 2.
Structure dimension diagram of a piston.

Table 1.
The specific structure size of the magnetorheological damper.
According to the traditional magnetic circuit design method, it is necessary to calculate the effective length and flux area of each part of the magnetic conduction region, and then, calculate the reluctance of each part. Finally, the number of turns of the coil required for the magnetic circuit design is calculated by the total reluctance of the magnetic conduction circuit. This design method is more complicated. In this paper, a simplified design method for the design calculation is adopted; the magnetorheological damper piston magnetic circuit design formula is:
In the formula, is the number of turns of the excitation coil; is the current; is the total magnetic flux of the loop; is the average length of magnetic circuit; is the permeability of the magnetorheological fluid; is the permeability of the magnetic core material; is the average cross-sectional area of the magnetic core material region; is the average cross-sectional area at the damping channel; is the magnetoresistance of the core material; is the total magnetoresistance of the damping channel.
Since is much smaller than and is much larger than , when = , with simplification of the above formula, the following result can be obtained:
The above formula is the relationship between the coil turns and the gap height , in other words, the gap height, the maximum working current and the magnetic induction intensity of the magnetorheological fluid can determine the number of coil turns required for the magnetic circuit design of the magnetorheological damper. By simplifying the magnetic circuit, when the coil current is 4 A, there are 170 coil turns.
2.2. Characteristics of Magnetorheological Fluid
The magnetorheological fluid used in this paper is MRF132DG from the Lord Corporation (Cary, NC, USA). Its main components are carbonyl iron powder, silicone oil and additives. In this paper, it is assumed that the magnetorheological fluid is incompressible. When the magnetorheological fluid is affected by the magnetic field, the carbonyl iron powder in the magnetorheological fluid will rapidly form a chain structure, which will greatly enhance the yield shear stress of the magnetorheological fluid. According to the experimental data [15], the shear yield stress of MRF132DG is fitted as Formula (3), and the specific material properties of the magnetorheological fluid and 45# carbon steel are shown in Figure 3 and Table 2.
where is the shear yield stress of MRF132DG and is the magnetic flux density.
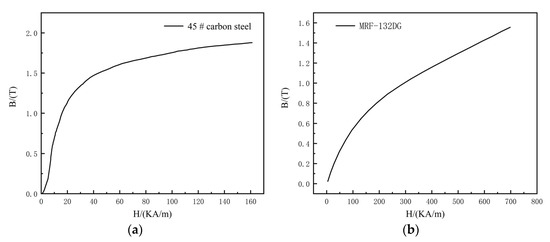
Figure 3.
B-H curve of 45# carbon steel and magnetorheological fluid. (a) 45#carbon steel; (b) MRF-132DG.

Table 2.
Properties of Magnetorheological Fluid and 1045 Structural Steel.
Stephen G et al. [24] tested the temperature stability of LORD-132DG through experiments, and obtained influence curves of temperature on the viscosity and yield stress of Magnetorheological Fluid under different current conditions; these are shown in Figure 4.
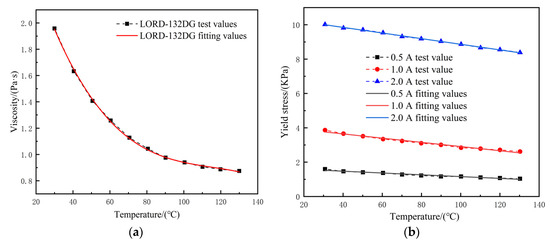
Figure 4.
Influence of temperature on viscosity and yield stress of Magnetorheological Fluid. (a) Influence of temperature on the viscosity of Magnetorheological Fluid; (b) effect of temperature on yield stress of Magnetorheological Fluid.
Polynomial fitting was performed on the test data in Figure 4 so as to obtain the fitting formula of the influence of temperature on the viscosity and yield stress of Magnetorheological Fluid under different current conditions, which is shown in Formula (4).
where is the temperature of the magnetorheological fluid, is the yield stress of the magnetorheological fluid and I is the working current.
3. Multi-Physical Field Coupling Analysis
3.1. Static Magnetic Field Analysis
According to the designed magnetorheological damper, COMSOL Multiphysics is used to solve the static electromagnetic field in this paper. A two-dimensional axisymmetric model is established, including 3266 domain elements and 407 boundary elements. A grid independence test is carried out using encryption. The encrypted grid includes 12,272 domain e lements and 700 boundary elements. The results of the grid independence analysis of the current FE model are shown in Figure 5; the two simulation results show that the magnetic flux densities at the damping channel are almost equal, which proves that the grid used in this paper is sufficient to meet the calculation requirements.
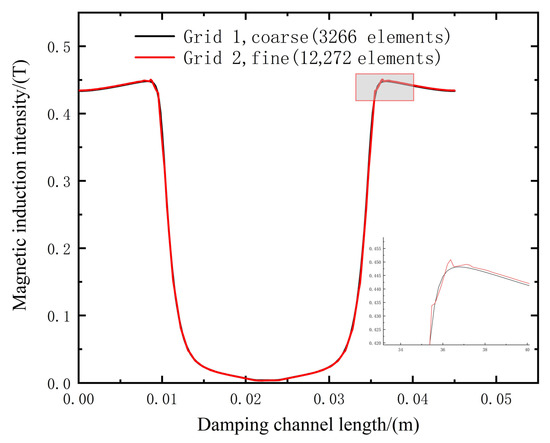
Figure 5.
Grid independence analysis of the current FE model.
Since magnetorheological fluid and 45# carbon steel are nonlinear magnetic materials, their relative permeability cannot be directly defined. Therefore, it is necessary to import the B-H curve of nonlinear magnetic materials into COMSOL Multiphysics and select its constitutive model as a B-H curve; the B-H curve of magnetorheological fluid and 45# carbon steel is shown in Figure 3.
A steady-state solver is used to solve the problem. The excitation current is 0–2 A, and the magnetic flux density curves at the damping channel under different currents are shown in Figure 6. It can be seen that the magnetic flux density in the activation region increases gradually with increasing current. When the working current is 0.5 A, the average magnetic flux density in the activation region is 0.105 T, and when the current increases to 2 A, the magnetic flux density reaches 0.45 T. It can be seen from the magnetic field contours in Figure 7 that the magnetic flux density distribution in the activation region on both sides is relatively uniform, and most of the magnetic flux occurs through the damping channel, which shows that the magnetic circuit design of the magnetorheological damper is reasonable.
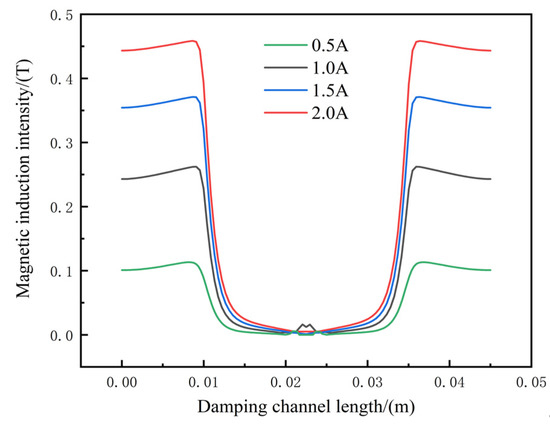
Figure 6.
Magnetic flux density curves of different currents’ damping channels.
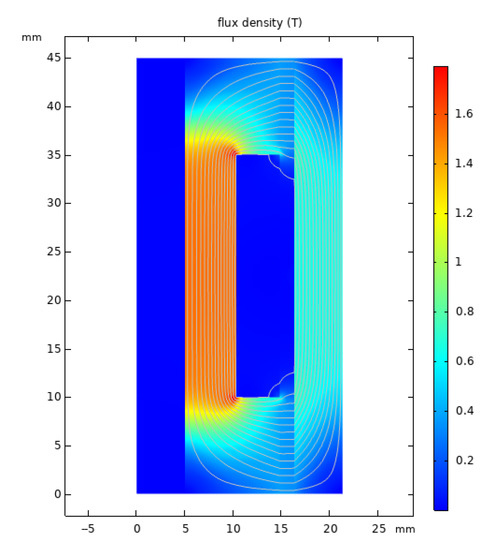
Figure 7.
Magnetic flux density and magnetic line distribution at 2 A.
3.2. CFD Dynamic Simulation Model
3.2.1. Constitutive Model
In the previous section, we obtained the magnetic flux density distribution at the damping channel through the magnetic field finite element and determined the corresponding yield stress distribution through Formula (3). Now, we need to determine the constitutive model of magnetorheological fluid to connect the yield stress and non-Newtonian viscosity. In this paper, the hyperbolic tangent function model used in References [12,13,17] is used to define the non-Newtonian function viscosity, and its function expression is:
and are viscosity growth control factors, which are 0.03 and 0.1, respectively; is the zero-field viscosity; and is the shear rate.
α and can control the viscosity growth rate of magnetorheological fluid at a very low shear rate. When α and are 0.03 and 0.1, respectively, the viscosity of the magnetorheological fluid at a low shear rate can be reduced.
3.2.2. Dynamic Grid Technology
The dynamic mesh model can be used to simulate the problem of the flow field shape changing with time due to boundary motion. A dynamic mesh [30,31,32] must be used to simulate the piston motion to realize automatic updating of the grid in the process of piston motion to ensure the quality of the grid in the calculation process. The dynamic mesh updating method in Fluent mainly includes the dynamic layering method, local reconstruction method and spring smoothing method. The local reconstruction and spring smoothing methods adopted in this paper can ensure the quality and accuracy of the grid in the calculation process.
All boundaries of the magnetorheological damper fluid domain are divided into a moving wall, a deforming wall, a central axis, a bottom wall and a top wall, where the top wall is set to the free outlet boundary condition, and the remaining boundary conditions are set to the solid. The fluid domain boundary needs to be set in the dynamic mesh model. According to the structural characteristics of the magnetorheological damper, the boundary between the two ends of the piston is defined as a rigid body, and the velocity is applied via UDF. A moving boundary diagram is shown in Figure 8. The two boundaries that contact the moving boundary need to be defined as deforming walls, and the other boundaries are defined as the wall.
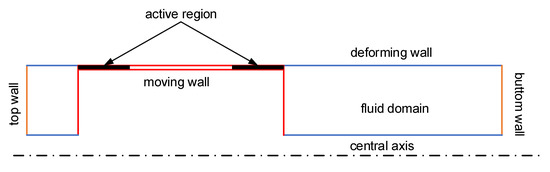
Figure 8.
Diagram of moving boundaries.
3.2.3. Magnetic-Flow Coupling Analysis Method
In this paper, the unidirectional coupling between the magnetic field and the flow field is realized via the yield stress Formula (3) fitted using the experimental data, and the constitutive model Formula (5) defined by the non-Newtonian function of the magnetorheological fluid. The magnetic flux density distribution at the damping channel is obtained via static magnetic field analysis, and then, the yield stress at the corresponding position is determined by the fitting function Formula (3). By means of the hyperbolic tangent constitutive model, the viscosity distribution at the corresponding position can be obtained. In this paper, the non-Newtonian viscosity region is only defined in the active region in the damping channel, and the rest of the calculation domain is the Newtonian fluid domain. The UDF file is written in c language, and the viscosity expression is defined using the DEFINE_PROPERTY macro. The non-Newtonian fluid domain is obtained using the THREAD_ID macro. Formulas (3) and (5) are written into the non-Newtonian viscosity expression of magnetorheological fluid, so the definition of non-Newtonian region viscosity is completed. The two variables “yield stress and shear rate” are needed in the constitutive model. The yield stress is determined using the static magnetic field finite element and Formula (3), and the shear rate is read directly using the C_STRAIN_RATE_MAG (c, t) macro in the UDF.
The coupling method used in this paper is shown in Figure 9.
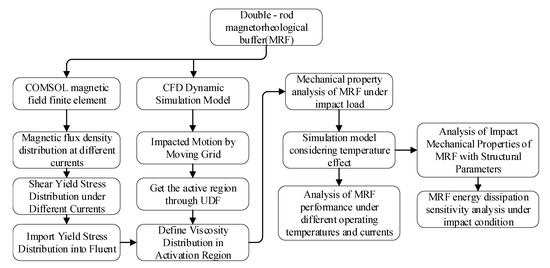
Figure 9.
Diagram of magnetic field and flow field coupling technology.
4. Multiphysics Simulation of Magnetorheological Damper
4.1. Impact Load versus Quasi-Static Simulation
4.1.1. Quasi-Static Simulation Analysis
The piston motion and excitation current are defined by writing the UDF, with a movement speed of 0.1 m/s and 0.5 m/s, and the excitation current is changed from 0 A to 2 A. The damping force of the magnetorheological damper under low-speed vibration is shown in Figure 10. The output damping force is stable and controllable when the excitation current is changed from 0 A to 2 A.
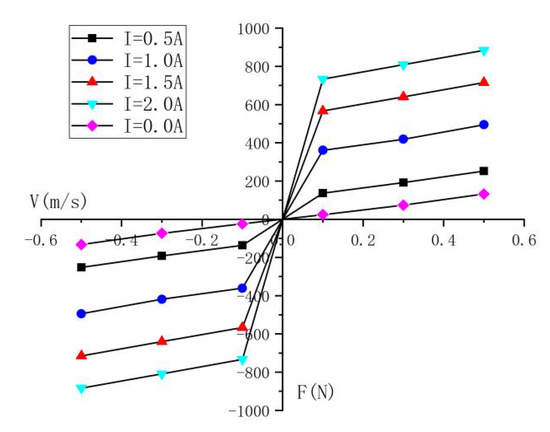
Figure 10.
Output of damping force under low-speed vibration.
Viscosity and velocity nephograms at the damping channel under a constant velocity motion of 0.1 m/s and 0.5 m/s are shown in Figure 11 and Figure 12. When the velocity is 0.1 m/s, it can be seen that the damping channel activation area viscosity distribution is uniform, the activation area basically has regular structure flow, the viscosity of the two sides near the wall’s shear rate has a larger decrease, and the velocity of the non-activation area in the middle of the damping channel is higher; moreover, there will be an obvious backflow phenomenon because the high-viscosity area at both ends of the blocking effect leads to liquid backflow. When the velocity is 0.5 m/s, the viscosity distribution nephogram is different to when the velocity is 0.1 ms, and the structure flow of the activation area is not regular. When the current is higher, the viscosity distribution of the right activation area is not uniform and the inlet of the viscosity is lower. Because the current is higher, the shear yield stress is larger, so it can barely form a structure flow. When the current is reduced to 0.5 A, it can be found that the right inlet of the viscous flow and the damping channel structure of the flow are not increased.

Figure 11.
The viscosity distribution in the damping channel when the current is 0.5 A, 1 A, 1.5 A and 2 A at different velocities. (1) velocity = 0.1 m/s.; (2) velocity = 0.5 m/s. (a) the current is 0.5 A; (b) the current is 1 A; (c) the current is 1.5 A; (d) the current is 2 A.

Figure 12.
Velocity contours and velocity contour distribution in damping channel when the current is 0.5 A, 1 A, 1.5 A and 2 A at different velocities. (1) velocity = 0.1 m/s; (2) velocity = 0.5 m/s. (a) the current is 0.5 A; (b) the current is 1 A; (c) the current is 1.5 A; (d) the current is 2 A.
4.1.2. Simulation Analysis of Impact Conditions
A two-dimensional axisymmetric model based on a pressure-based solver is used in the simulation, and the initial temperature is 30 °C. Due to the large change in internal pressure in the impact process, PRESTO pressure interpolation is used to solve to get courant to 50, whereby the time step is 10−4 s, and the simulation time is 0.023 s. The impact velocity curve obtained from the test (Figure 13) is compiled via UDF to define the impact motion of the piston. The excitation current used in this simulation is 2 A.
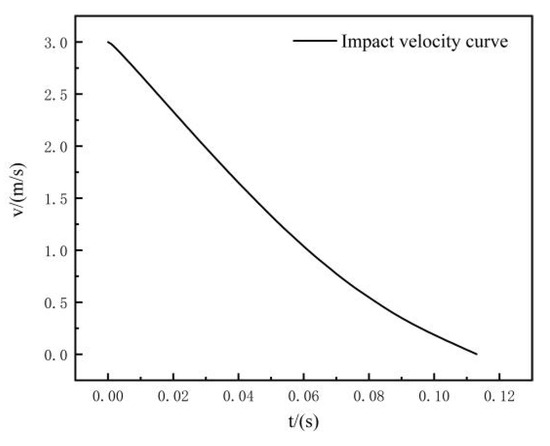
Figure 13.
Impact velocity curve.
After the simulation, the post-processing file generated by Fluent is imported into tecplot for processing. The pressure, velocity and viscosity contours in the early and middle stages of the impact conditions are shown in Figure 14.
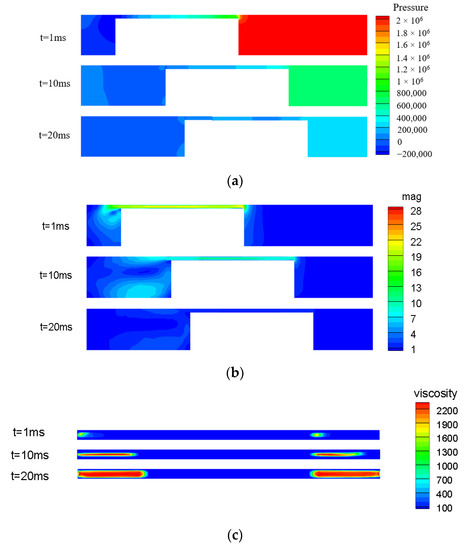
Figure 14.
Pressure, velocity and viscosity contours at different times under impact conditions. (a) Pressure contours; (b) velocity contours; (c) viscosity contours.
As shown in the above charts, the impact velocity is larger and the pressure peak appears in the high-pressure cavity at 1 ms; moreover, the flow velocity of the magnetorheological fluid at the damping access point can reach more than 20 m/s. The flow velocity in the middle of the damping channel is significantly higher and a backflow phenomenon occurs. An obvious eddy current appears in the left low-pressure cavity. At this time, the viscosity distribution of the damping channel activation area is disordered, and the structural flow area is small. With the impact energy consumption at 10 ms, the impact velocity decreases, and the pressure of the high-pressure cavity decreases significantly below 10 m/s. The low-pressure cavity has a large eddy current. At this time, the viscosity of the magnetorheological fluid near the central line in the damping channel is larger. The impact velocity decreases to 0.2 m/s at 20 ms, and the flow velocity and pressure of the high-pressure cavity are greatly reduced.
4.1.3. Proportion of Viscous Damping Energy Absorption
There is a big difference between the energy absorption effect of the viscous damping force of the magnetorheological damper under impact load and low-speed vibration conditions. Now, the energy consumption ratio of the viscous damping force is defined and analyzed using indicators.
is the proportion of energy consumed by the viscous damping force; is the energy consumption of the damping force when no current passes; is the energy consumption of the damping force when a current passes.
The energy consumption proportion of viscous damping force under shock conditions and low-speed vibration is shown in Figure 15. Firstly, the energy consumption proportion of the viscous damping force increases with increasing motion speed under low-speed vibration. When the current is 0.5 A and the movement speed is 0.5 m/s, the energy consumption proportion reaches 52.6%. This means that speed increasing and current reducing will also increase the role of the viscous damping force. When a shock condition is simulated, it can be seen that the viscous damping force occupies the dominant position. When the current is 0.5 A, the proportion reaches 91.2%. At this time, the viscous damping force plays a major role in energy buffering and absorbing, and the role of the Coulomb damping force is greatly weakened.
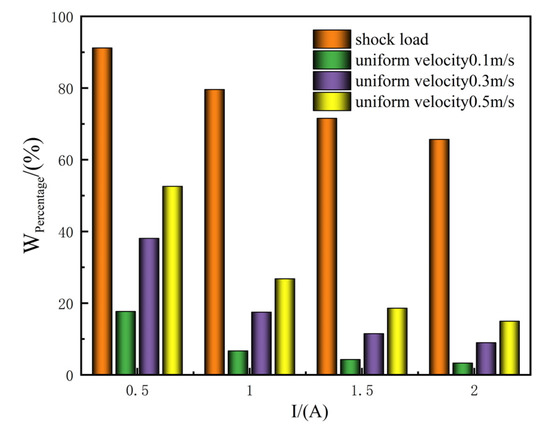
Figure 15.
Impact energy consumption ratio of viscous damping force under low-velocity vibration and impact conditions.
Through the comparative simulation of low-speed vibration and impact conditions, it can be found that the area of semi-solid structural flow formed with increasing current under low-speed conditions increases, and its shape is more regular. Under high-speed motion or impact conditions, with increasing flow rate in the damping channel and the pressure difference between the two sides of the cavity, the area of semi-solid structural flow formed by the activation zone in the channel will be smaller, so it is difficult to form a more regular structural flow in the early and middle stages of the impact; this results in significant weakening of the role of the Coulomb damping force under impact conditions, and viscous damping force plays a major role in energy absorption.
4.2. Effect of Temperature on Mechanical Properties of Magnetorheological Damper under Impact Load
In reference [16], the viscosity–temperature characteristics of MRF-132DG the magnetorheological fluid were obtained via an experimental method, and the parametric fitting is shown in Figure 3. In our study, Formula (4) was written into the viscosity expression of the magnetorheological fluid using the user-defined function (UDF), and a numerical simulation was carried out for the specific impact conditions shown in Figure 13 to study the effect of temperature on the mechanical properties of the magnetorheological damper under impact conditions.
The working chamber pressure and piston stroke curves of the two sets of CFD simulation models with and without viscosity–temperature characteristics are shown in Figure 16. It can be seen that the pressure difference between the two groups is large in the initial stage of the impact, and the pressure difference between the two groups decreases in the middle and late stages of the impact. The pressure curves of the two groups are almost coincident at the end of the impact. This is because the flow velocity in the damping channel is higher in the initial stage of the impact, and the shear rate of the magnetorheological fluid is larger. The temperature rise in the damping channel is significantly lower than that in the damping channel, resulting in a difference in pressure. In the later stage of the impact, the flow velocity in the damping channel is greatly reduced, the shear rate of the magnetorheological fluid is smaller, and the temperature rise in the channel is smaller.
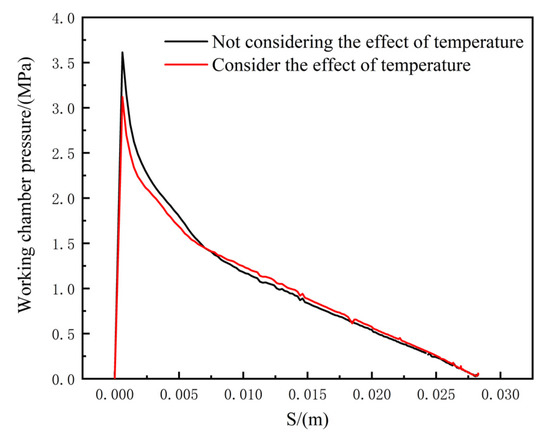
Figure 16.
Curves of working chamber pressure and piston stroke considering the viscosity–temperature characteristics of magnetorheological fluids.
It can be seen that the temperature has a certain influence on the mechanical properties of the magnetorheological damper under impact load through the above two sets of models. So, we simulate the magnetorheological damper when the excitation current is changed from 0 A to 2 A and working temperature is changed from 10 °C to 50 °C, respectively, so as to study the mechanical properties of the magnetorheological damper under different currents and working temperatures. In this paper, the magnetic flux density at the damping channel under different currents is obtained via finite element analysis of the electromagnetic field. Now, the obtained magnetic flux density is calculated using the constitutive model of magnetorheological fluid to obtain the viscosity of the magnetorheological fluid under different currents, and the simulation is carried out according to the above coupling mode. The pressure displacement curves obtained are shown in Figure 17.
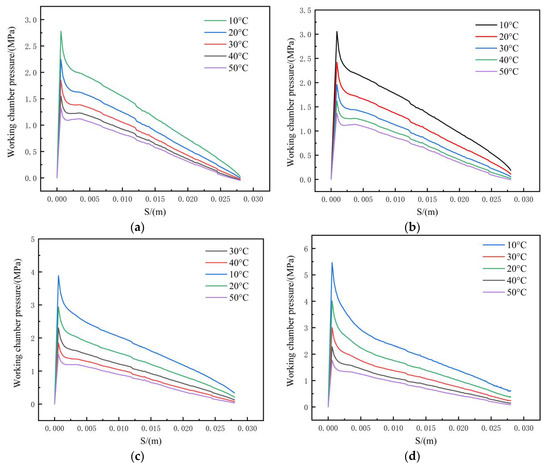
Figure 17.
Curves of working chamber pressure and piston displacement when the current is 0 A, 0.5 A, 1 A and 2 A. (a) Working chamber pressure at 0 A; (b) working chamber pressure at 0.5 A; (c) working chamber pressure at 1 A; (d) working chamber pressure at 2 A.
The obtained curve of working chamber pressure and piston displacement under impact load is similar to the impact velocity curve shown in Figure 13. The peak pressure appears at the maximum impact velocity in the initial stage, and then, the pressure of the high-pressure cavity decreases slowly with decreasing impact velocity. The peak pressure, energy absorption capacity and viscous damping force energy absorption ratio are affected by temperature. The peak pressure impact energy absorption capacity decreases with increasing temperature, and the viscous damping force ratio is the opposite. In order to better study temperature’s influence on the peak pressure, impact energy absorption and viscous damping force energy absorption ratio, the pressure data are analyzed and a curve is obtained, which is shown in Figure 18, Figure 19 and Figure 20.
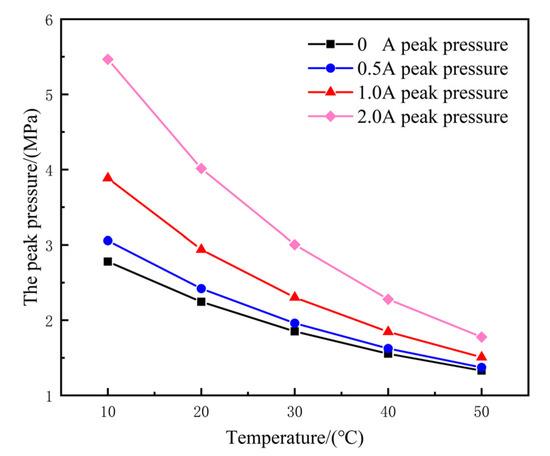
Figure 18.
Effect of temperature on peak pressure under impact conditions.
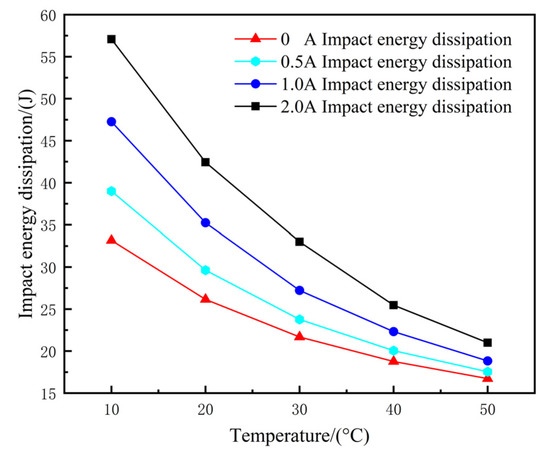
Figure 19.
Effect of temperature on impact energy dissipation under impact condition.
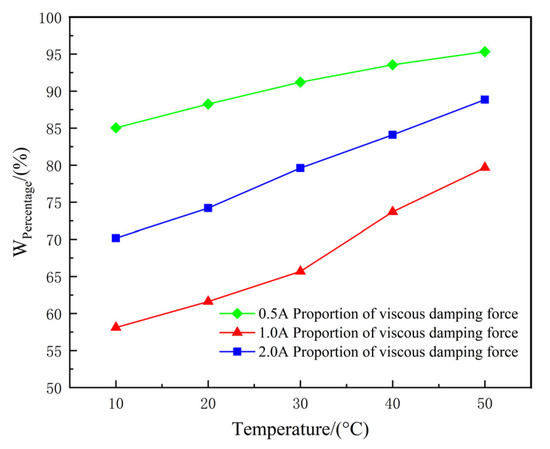
Figure 20.
Effect of temperature on viscous damping ratio under impact conditions.
To a certain extent, the peak pressure can reflect the energy absorption capacity of the magnetorheological damper under impact load, so it is necessary to study the change in peak pressure at different operating temperatures. The above figure shows the influence of temperature on peak pressure. It can be seen that the peak pressure decreases with increasing temperature in Table 3; this is because the viscosity of the magnetorheological fluid decreases with increasing temperature when the current is 0 A. Additionally, the temperature drops from 10 °C to 50 °C, the peak pressure drops by 52% and the change rate of the peak pressure is 0.036. When the excitation current increases to 2 A, the peak pressure decreases by 67% and the peak pressure change rate is 0.092. Therefore, with increasing excitation current, the influence of temperature on the peak pressure is more obvious.

Table 3.
Effect of temperature on peak pressure.
The impact energy dissipation under the same impact conditions with different currents and temperatures are shown in Figure 19. It can be seen that the energy absorbed by the magnetorheological damper under impact conditions is greatly affected by temperature. It can be seen in Table 4, when the working temperature is from 10 to 50 °C and the excitation current is from 0 A to 2 A, the change rate of the impact energy dissipation increases from 0.41 to 0.9, and the percentage of energy dissipation decreases from 49.6% to 63.2%. This shows that with increasing excitation current, the temperature has a more significant impact on the performance of the magnetorheological damper under impact conditions, and the decrease in the impact energy dissipation is greater. This is because the viscosity of the magnetorheological fluid in the activated area of the damping channel is larger and the temperature is more sensitive to its influence when the excitation current is higher. Therefore, it is necessary to consider the influence of the working temperature on the performance of the magnetorheological damper.

Table 4.
Impact energy dissipation affected by temperature.
The shock energy consumption data with excitation currents from 0 A to 2 A are processed to obtain the curve of the viscous damping force shock energy consumption ratio versus temperature, which is shown in Figure 20. It can be seen that the viscous damping force shock energy consumption ratio increases significantly with increasing temperature when the excitation current passes through. This is because the Coulomb damping force is greatly affected by temperature and the apparent viscosity decreases obviously, while the zero-field viscosity of the magnetorheological fluid is less affected by temperature. Therefore, the Coulomb damping force decreases with increasing working temperature, and the viscous damping force plays a major role in energy absorption.
Through the above analysis, it can be seen that the viscosity–temperature characteristics of magnetorheological fluid have a great influence on its mechanical properties under impact load. As the temperature increases, the Coulomb damping force decreases, and the viscous damping force plays a major role in energy absorption. Additionally, with increasing temperature, the peak pressure and impact energy consumption of the magnetorheological damper are greatly reduced, and with increasing excitation current, this reduction further increases.
4.3. Effect of Structural Parameters on Impact Performance of the Magnetorheological Damper
In order to study the influence of piston structural parameters on buffer performance, three structure parameters, which include the piston diameter, effective length and clearance height, are now taken as the research objects, and the variation in structural parameters is defined as ∆α. Firstly, the corresponding geometric models are established in COMSOL Multiphysics so as to study the influence of structural parameters on the magnetic flux density at the damping channel.
is the amount of change in the structural parameters; is the size of the structure after change; and is the size of initial structure.
4.3.1. Effects of Structural Parameters
As shown in Figure 21, when the structural parameters change, the average magnetic flux density of the active region of the damping channel is effectively activated. When the gap height and effective length increase by 50%, the magnetic flux density of the damping channel decreases by 17.5% and 16.8%, respectively. On the contrary, when the gap height and effective length decrease by 50%, the magnetic flux density increases by 32% and 12%, respectively. This is because an increase in the gap height and effective length will increase the magnetoresistance of the damping channel, and then, reduce its magnetic flux density, and the gap height has a more significant impact on the magnetoresistance. When the piston diameter increases by 50%, the magnetic flux density of the damping channel increases by only 10.3%, and the magnetic flux density decreases by 40% when the piston diameter decreases. At this time, the reluctance at the central shaft end increases significantly due to the reduction in the cross-sectional area at the central shaft end, and the magnetic circuit design is unreasonable.
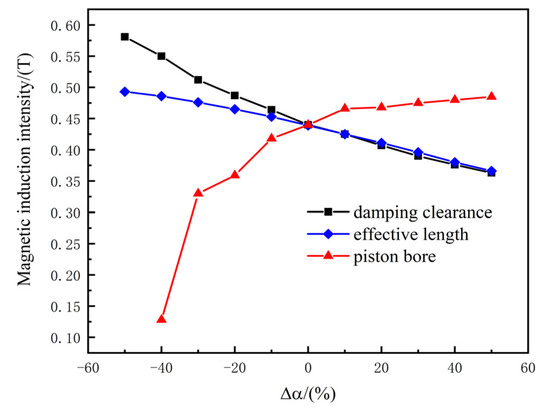
Figure 21.
Effect of structural parameters on magnetic flux density at damping channel.
A static magnetic field stimulation is used to obtain the magnetic flux density of the activated area when the structural parameters change. The corresponding magnetic flux density is written into Fluent through UDF to carry out a dynamic simulation of the impact. As shown in Figure 22, the impact energy consumption of the structure changes. When the piston diameter increases by 50%, the impact energy consumption increases by 64%. It can be seen that the piston diameter has a significant impact on the impact performance of the magnetorheological damper. Increasing the piston diameter can effectively increase its energy absorption capacity. When the gap height increases by 50%, the impact energy consumption decreases by 59%. Additionally, the impact energy consumption level increases by 367% when the gap height decreases by 50%. The gap height reducing can greatly increase the energy absorption capacity of the magnetorheological damper, but when the gap height is too small, it will lead to poor flowability. The change in effective length has little effect on impact energy dissipation. When the effective length increases and decreases by 50%, the change in impact energy dissipation is 9.8% and 20%, respectively. It can be seen that the effect of effective length changing on impact energy dissipation is far less than that of clearance height and piston diameter changing. This is because the purpose of increasing the effective length is to increase the effect of the Coulomb damping force, but the viscous damping force plays a major role in energy absorption under impact conditions. The effect of effective length changing on impact energy dissipation is not obvious, which is consistent with the conclusion in Section 3.1.
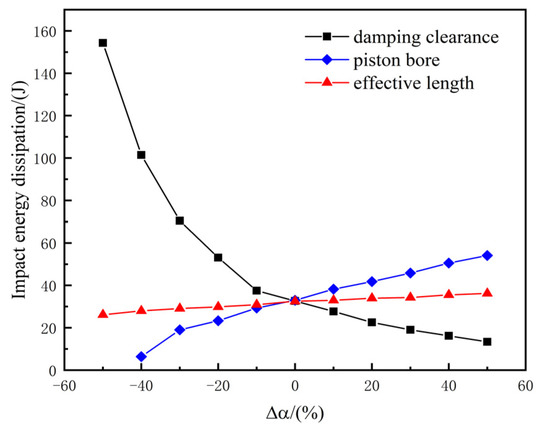
Figure 22.
Effect of structural parameters on impact energy dissipation.
4.3.2. Sensitivity Analysis of Structural Parameters
To better analyze the influence of structural parameters on the magnetic flux density and impact energy dissipation, the sensitivity function [23,33] is used for quantitative analysis. When the structure changes to ∆α, the maximum variation of the magnetic flux density in the active region of the damping channel ΔT and the percentage of T0 at the initial parameter are defined as the peak sensitivity of the magnetic flux density, which is expressed by s1; the expression is:
The peak sensitivity function of impact energy dissipation is also defined and expressed as s2; the expression is:
By defining two peak sensitivity functions, the influence of ∆α on the flux density and impact energy dissipation can be quantitatively analyzed, and then, the influence on the impact performance of the magnetorheological damper can be obtained. According to the formula, the peak sensitivity indexes of each structural parameter change of 10%, 20% and 30% are calculated, respectively, and the results are shown in Figure 23.
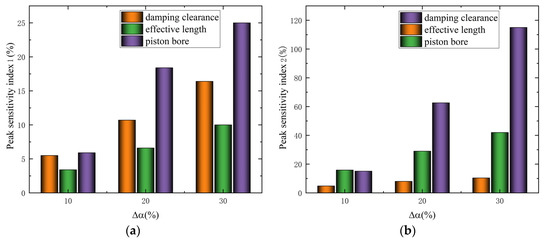
Figure 23.
Peak sensitivity index of magnetic flux density and impact energy consumption. (a) Peak sensitivity index 1 (peak sensitivity index of magnetic induction intensity); (b) peak sensitivity index 2 (peak sensitivity index of impact energy consumption).
As shown in Figure 23a, the proportion of the peak sensitivity indexes of clearance height and piston diameter are relatively high. With increasing structural parameter change, the change in the sensitivity index of the piston diameter is more obvious. When ∆α is 30%, the peak sensitivity index reaches 25%. That is to say changing the piston diameter will have a great influence on the magnetic flux density in the activation area of the damping channel of the magnetorheological damper. Additionally, changing the effective length has little influence on it. Therefore, the two parameters of clearance height and piston diameter should be emphatically considered in the design of the magnetic circuit.
The peak sensitivity of impact energy dissipation is shown in Figure 23b. When ∆α is 10%, the peak sensitivity indexes of the piston diameter and clearance height are slightly higher. When ∆α increases to 20%, the peak sensitivity index of clearance height is up to 62.6%, while the other two indexes are 29% and 8%, respectively. When ∆α increases to 30%, the index of clearance height is up to 115%, and the other two indexes increase slightly by 42% and 10.4%, respectively. This indicates that the clearance height and piston diameter have a great influence on the impact energy dissipation of the MR buffer when the structural change is small. When ∆α is large, the clearance height plays an absolute leading role, and the effective length index maintains a low proportion; this indicates that the change in effective length has little influence on the impact energy dissipation under impact load.
5. Experimental Verification
To verify the results of the simulation analysis, a test system was built to conduct an impact test and the test results were compared with the simulation data. The impact test bench is shown in Figure 24, which mainly includes a lifting device, an impact loading module, a data acquisition module and a power supply device.

Figure 24.
Impact test bench. (a) A diagram of the whole test system; (b) local detail diagram of test system.
The principle of the test system is to fix the magnetorheological damper on the bottom of the impact loading module, use the electromagnetic washing plate of the lifting device to pull the counterweight slider to a certain height, and then, cut off the power to make it fall freely so as to cause impact. The piston rod of the magnetorheological damper drives the piston downward after being impacted. At this time, the pressure and displacement data are collected by the pressure sensor and displacement sensor installed on the magnetorheological damper, and then, the displacement data are differentially calculated to obtain the movement speed of the piston rod during the impact.
The prototype of the double-barrel magnetorheological damper is manufactured according to the dimensions in Table 1. The magnetorheological fluid is LORD-132DG. The material used in the damper prototype is 45# carbon steel, and the material used in the coil part is copper core enameled wire. The parts and the assembled prototype are shown in Figure 25.

Figure 25.
Prototype of double-rod magnetorheological damper.
An impact test of the magnetorheological damper studied in this paper is carried out, and the true motion speed curve of the piston rod obtained from the test is fitted and compiled using UDF in Fluent. The simulated pressure curve is compared with the test curve directly obtained from the impact test, as shown in Figure 26.
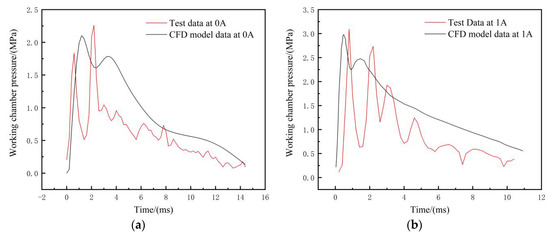
Figure 26.
Comparison of test and simulation data. (a) Data comparison at 0 A; (b) data comparison at 1 A.
From Figure 26, it can be seen that the peak pressure of the working chamber measured in the test at 0 A is 2.25 MPa and the peak pressure obtained by the CFD simulation model is 2.06 MPa, and the peak pressure of the working chamber measured in the test at 1 A is 3.09 MPa and the peak pressure obtained by the CFD simulation model is 2.98 MPa. As seen in the figure, the peak pressure simulation time is slightly earlier than in the test data, the peak pressure in the simulation results is slightly smaller than in the test results, and the test pressure curve has more fluctuations than the simulation pressure curve. This is because the simulation model is more idealized, and the friction and the small structure at the inlet and outlet are not considered. Additionally, some errors are generated during the test process.
The research focus of this paper is the peak value of the pressure curve, and the results show the consistency of the test and simulation trends. The maximum error of the pressure peak in both cases is kept within 10%, which verifies that the multi-physical simulation model established in this paper can effectively reflect the mechanical properties of a real magnetorheological damper.
6. Conclusions
- (1)
- Under impact conditions, the viscosity distribution of the damping channel activation region of the magnetorheological damper is disordered, the region of the structural flow in the semi-solid state is small and the influence of the Coulomb damping force is greatly weakened. When the current is 0.5 A, the viscous damping force accounts for 91.2%, and the viscous damping force plays a major role in buffering and absorbing energy.
- (2)
- With increasing working temperature, the effect of the Coulomb damping force is weakened, and the viscous damping force plays a major role in energy absorption. The peak pressure and impact energy consumption of the magnetorheological damper are greatly reduced. Additionally, this reduction is further increased with increasing excitation current.
- (3)
- The influence of gap height, piston diameter and effective length on magnetic flux density and impact energy dissipation is determined by the peak sensitivity function. When the change in the structural parameters ∆α is 30%, the change in piston diameter has the greatest influence on the peak sensitivity of the magnetic flux density, and the peak sensitivity index of the magnetic flux density reaches 25%. The change in clearance height has the greatest influence on the impact energy consumption, and the peak sensitivity index of the impact energy consumption reaches 115%. This shows that the magnetic flux density is most affected by the piston diameter, and the impact energy consumption is most affected by the clearance height. In the later optimization design of the damper structure, the above parameters can be used as optimization variables by using the NSGA-II algorithm or other multi-objective optimization algorithms to optimize the design.
- (4)
- Because the simulation model is more idealized, the friction and the small structure at the inlet and outlet are not considered. The results show that the maximum error of peak pressure is less than 10% in both cases. It can be assumed that this result shows the consistency of the test and simulation trends, which can help us verify that the multi-physical simulation model established in this paper can better reflect the mechanical properties of a real magnetorheological damper.
Author Contributions
Research planning, structure design and funding acquisition, C.W.; methodology and simulation model research, J.Z. and H.S.; physical testing and supervision, G.L. and X.W.; writing—original draft, J.Z. and X.W.; writing—review and editing, C.W. and G.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Key R&D Plan of Shandong Province (major scientific and technological innovation project) (2020CXGC011502), the Shandong Provincial Key Research and Development Project (2019SDZY01), the National Natural Science Foundation of China (51974170) and the National Natural Science Foundation of China (52274132).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data were curated by the authors and are available upon request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Saleh, M.K.; Nejatpour, M.; Acar, H.Y.; Lazoglu, I. A new magnetorheological damper for chatter stability of boring tools. J. Mater. Process. Technol. 2021, 289, 116931. [Google Scholar] [CrossRef]
- Hu, G.; Yi, F.; Tong, W.; Yu, L. Development and evaluation of an magnetorheological damper with enhanced effective gap lengths. IEEE Access 2020, 8, 156347–156361. [Google Scholar] [CrossRef]
- Christie, M.D.; Sun, S.; Deng, L.; Ning, D.H.; Du, H.; Zhang, S.W.; Li, W.H. A variable resonance magnetorheological-fluid-based pendulum tuned mass damper for seismic vibration suppression. Mech. Syst. Signal Process. 2019, 116, 530–544. [Google Scholar] [CrossRef]
- Li, C.; Wang, J. A gun recoil system employing a magnetorheological fluid damper. Smart Mater. Struct. 2012, 21, 105003. [Google Scholar] [CrossRef]
- Zhu, S.; Liu, X. Design and performance analysis of magnetorheological fluid damper for aircraft nose landing gear. Mach. Tool Hydraul. 2019, 47, 65–68+98. [Google Scholar]
- Du, X.; Gan, B.; Jian, X.; Fu, B.; Liu, C.; Liao, C. Design theory and drop impact test of magnetorheological mud buffer considering wall slip. J. Vib. Shock. 2021, 40, 201–208. [Google Scholar]
- Li, Z. Study on Enhancing Efficiency of Radial Flow Magnetorheological Buffer Device; Chongqing University: Chongqing, China, 2018. [Google Scholar]
- Cheng, M.; Chen, Z.; Kyongsol, K.; Jiao, Y. Design and analysis of a multistage serpentine magnetorheological damper. J. Eng. Des. 2017, 24, 350–358. [Google Scholar]
- Yarali, E.; Mohammadi, A.; Mafakheri, S.; Baghani, M.; Adibi, H. Mathematical modeling and experimental evaluation of a prototype double-tube magnetorheological damper. SN Appl. Sci. 2019, 1, 1341. [Google Scholar] [CrossRef]
- Nguyen, Q.H.; Choi, S.B.; Lee, Y.S.; Han, M.S. Optimal design of high damping force engine mount featuring MR valve structure with both annular and radial flow paths. Smart Mater. Struct. 2013, 22, 5024. [Google Scholar] [CrossRef]
- Li, Y. Simulation and Control of Magnetorheological Damper; Nanjing University of Science and Technology: Nanjing, China, 2019. [Google Scholar]
- Elsaady, W.; Oyadiji, S.O.; Nasser, A. A one-way coupled numerical magnetic field and CFD simulation of viscoplastic compressible fluids in magnetorheological dampers. Int. J. Mech. Sci. 2020, 167, 105265. [Google Scholar] [CrossRef]
- Case, D.; Taheri, B.; Richer, E. Dynamical modeling and experimental study of a small-scale magnetorheological damper. IEEE/ASME Trans. Mechatron. 2014, 19, 1015–1024. [Google Scholar] [CrossRef]
- Gurubasavaraju, T.M.; Kumar, H.; Mahalingam, A. An approach for characterizing twin-tube shear-mode magnetorheological damper through coupled FE and CFD analysis. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 139. [Google Scholar] [CrossRef]
- Parlak, Z.; Engin, T.; Çall, I. Optimal design of magnetorheological damper via finite element analyses of fluid dynamic and magnetic field. Mechatronics 2012, 22, 890–903. [Google Scholar] [CrossRef]
- Huang, T.; Zhou, J.; Xu, Y.; Meng, F. Modeling of magnetorheological damper based on multi-field coupling analysis and influence of structural parameters. J. Zhejiang Univ. (Eng. Sci. Ed.) 2020, 10, 2001–2008. [Google Scholar]
- Liu, X.; Wu, D.; Ma, J. Mechanical performance analysis of magnetorheological damper based on magnetic field FE and CFD. Trans. Chin. Soc. Agric. Mach. 2020, 8, 25. [Google Scholar]
- Elsaady, W.; Oyadiji, S.O.; Nasser, A. Study of failure symptoms of a single-tube magnetorheological damper using an FEA-CFD approach. J. Intell. Mater. Syst. Struct. 2021, 32, 1391–1419. [Google Scholar] [CrossRef]
- Kemerli, M.; Engin, T. Numerical analysis of a monotube mixed-mode magnetorheological damper by using a new rheological approach in CFD. Rheol. Acta 2021, 60, 77–95. [Google Scholar] [CrossRef]
- Hu, G.; Deng, Y.; Yu, L.; Li, G. Multiphysics coupling simulation and dynamic performance analysis of magnetorheological damper. Magn. Mater. Devices 2020, 51, 14–21+66. [Google Scholar]
- Yu, Z. Multi-Field Coupling Analysis and Control System of Magnetorheological Semi-Active Shock Absorber; Jilin University: Changchun, China, 2014. [Google Scholar]
- Zhang, Y. Multi-Field Coupling Analysis and Dynamic Characteristics of Magnetorheological Damper; Yanshan University: Qinhuangdao, China, 2016. [Google Scholar]
- Feng, Z.; Sun, J.; Zhao, H.; Zhang, G.; Wang, L.; Li, H. Dynamics simulation modeling and test of MR Damper under temperature effect. Trans. Chin. Soc. Agric. Mach. 2018, 49, 382–388. [Google Scholar]
- Sherman, S.G.; Powell, L.A.; Becnel, A.C.; Wereley, N.M. Scaling temperature-dependent rheology of magnetorheological fluids. J. Appl. Phys. 2015, 117, 17C751. [Google Scholar] [CrossRef]
- Michael, M.; Faramarz, G.; Wang, X.J. Effects of temperature on performance of compressible magnetorheological fluid suspension systems. J. Intell. Mater. Syst. Struct. 2018, 29, 41–51. [Google Scholar]
- Zarana, L.; Ramesh, V.U. Temperature dependence quasi-static measurements on a magnetorheological fluid having plate-like iron particles as dispersed phase. J. Intell. Mater. Syst. Struct. 2016, 27, 1329–1336. [Google Scholar]
- Hu, H.; Yin, B.; Feng, Z.; Zhang, L. Bouc-wen model of magnetorheological damper considering temperature effect. Ship Eng. 2016, 38, 45–49. [Google Scholar]
- Zheng, J. Research on Key Technology of Impact Resistant Multistage Independent Magnetorheological Buffer; Nanjing University of Science and Technology: Nanjing, China, 2016. [Google Scholar]
- LORD Corporation. Magneto-Rheological (MR) Technological Hydrocarbon-Based Magnetorheological Fluid MRF-132DG Product Bulletin; LORD Corporation: Cary, NC, USA, 2005. [Google Scholar]
- Li, L.; Zou, M.; Ren, S.; Qiao, Y.; Sun, D. Flow field analysis of three-dimensional Lello pump based on FLUENT dynamic mesh technology. J. Chang. Univ. (Nat. Sci. Ed.) 2021, 33, 57–61. [Google Scholar]
- Guan, Z.; Ruan, W.; Tong, Y.; Hao, L.; Meng, W.; Shu, D. Numerical simulation of airborne external weapon separation based on FLUENT software platform. J. Rocket. Guid. 2020, 40, 119–122+134. [Google Scholar]
- Jing, J.; Liu, M.; Li, Y.; Nie, W. Research on buffer characteristics of hydraulic cylinder based on CFD dynamic mesh simulation technology. Fluid Transm. Control. 2015, 3, 37–39. [Google Scholar]
- An, C.; Ma, J.; Wang, J.; Quan, L. Magnetorheological damper output damping force sensitivity analysis. Mech. Electr. Eng. 2018, 35, 1137–1144. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).