Abstract
SLAM (Simultaneous Localization and Mapping) based on lidar is an important method for UGV (Unmanned Ground Vehicle) localization in real time under GNSS (Global Navigation Satellite System)-denied situations. However, dynamic objects in real-world scenarios affect odometry in SLAM and reduce localization accuracy. We propose a novel lidar SLAM algorithm based on LOAM (Lidar Odometry and Mapping), which is popular in this field. First, we applied elevation maps to label the ground point cloud. Then we extracted convex hulls in point clouds based on scanlines as materials for dynamic object clustering. We replaced these dynamic objects with background point cloud to avoid accuracy reduction. Finally, we extracted feature points from ground points and non-ground points, respectively, and matched these feature points frame-to-frame to estimate ground robot motion. We evaluated the proposed algorithm in dynamic industrial park roads, and it kept UGV maximum relative position error less than 3% and average relative position error less than 2%.
1. Introduction
With the advancement of technology, intelligent robots have gradually entered people’s lives. Normal work of intelligent robots is inseparable from their positioning. Usually, the positioning problem of a robot is solved by the GNSS positioning system [1,2]. However, in scenarios such as weak satellite signals or signals indoors, the GNSS system alone cannot achieve high-precision positioning. In 2020, the China Association for Science and Technology pointed out that achieving high-precision positioning and navigation when satellite signals are unavailable has become an urgent engineering and technical problem to be solved. To complete positioning in an environment where a satellite signal is rejected is usually to use sensors such as the wheel speedometer and inertial navigation to calculate the position of the robot by using its motion information [3]. However, the wheel speedometer has high requirements for the model accuracy of the robot, and robot mileage estimation based on the wheel speedometer cannot guarantee high accuracy due to possible road surface unevenness and slippage during the robot’s movement. Although inertial navigation is not affected by the model or the environment, drift of data is amplified in the process of quadratic integration and cannot be corrected independently. Based on the reasons above, the multi-sensor fusion positioning method has gradually entered the field of vision. Commonly used sensors include monocular, stereo, RGB-D cameras, lidar, millimeter-wave radar, UWB (ultra-wideband) [4], etc. Using these sensors, multi-sensor positioning systems such as VO (visual odometry), VIO (visual inertial odometry) and LIO (lidar inertial odometry) have been developed. Because of adoption of multi-sensor fusion methods supplemented by various filtering algorithms, data errors of the sensors themselves are eliminated and positioning accuracy is greatly improved.
SLAM is a means of using a variety of sensors to achieve high-precision, real-time positioning and mapping for robot navigation [5]. At first, SLAM was mainly used in the positioning of small indoor robots. The indoor environment could be mapped with 2D single-line lidar and analyzed with post-processing. Today, SLAM is able to perform 3D analyses of the surrounding environment, and implementation methods are mainly divided into visual SLAM and lidar SLAM [6]. Visual SLAM, which is undergoing rapid development, relies on the advancement of image-processing technology, with mature visual feature points and descriptor extraction methods as well as many vision-based deep neural networks. Among them, the ORB (oriented FAST and rotated BRIEF)-SLAM3 [7] algorithm, which is suitable for monocular, binocular and RGB-D cameras for back-end mileage estimation using cluster adjustment, has become the master of visual SLAM algorithms and has been widely used for reference by other visual SLAM algorithms. In terms of using natural language processing, Rosinol et al. summarized previous experience and established the Kimera [8] open-source SLAM library based on the DBoW2 [9] word bag library. McCormac combined semantic information and convolutional neural networks to propose the SemanticFusion [10] algorithm, which performed well on the NYUv2 [11] dataset and maintained a running speed of 25 Hz. Because lidar SLAM has experienced the process of developing from 2D to 3D, Google open-sourced Cartographer [12], an algorithm based on graph optimization for 2D/3D, in 2016. This algorithm does not include PCL, g2o, etc., which are huge code bases and have simple architecture suitable for lightweight and low-cost robots such as home robots. Zhang et al. proposed the LOAM [13] algorithm, in which only single-line lidar was used to realize the mapping of the 3D environment, in 2014. It is still widely admired today and maintains the third position on the rank of dataset KITTI (Karlsruhe Institute of Technology and Toyota Technological Institute) [14]. Its framework is used by many researchers as a basis for building algorithms. For example, Lego-LOAM [15] is suitable for lightweight robots, I-LOAM [16] provides loop-closure detection and echo-accuracy information and SA-LOAM [17] provides semantic information. Ding et al. proposed the Deepmapping [18] algorithm using deep neural networks combined with traditional algorithms, which made mapping more accurate but sacrificed real-time performance of the algorithm.
Although the SLAM algorithm has been successfully applied in clear situations and simple scenes, odometer estimation accuracy is reduced in complex scenes with many dynamic objects. Mainstream odometer estimation method is based on feature point matching within static world assumption [19]; feature points extracted from dynamic objects are treated as static feature points. These dynamic points influence the matching result. Removing the influence of dynamic objects has become the goal of current SLAM algorithm development [20,21].
The most popular method of removing influence caused by dynamic objects is identifying and marking dynamic objects and removing feature points on marked parts [22,23,24]. There are mainly two methods to identify dynamic objects: traditional methods based on geometric information and neural network methods based on semantic information. These methods have different degrees of improvement for lidar SLAM.
In 2020, Yangzi Cong et al. used UGV as an experimental platform, first filtering out the ground point cloud, then roughly segmenting suspected dynamic objects using traditional clustering methods, using Kalman filter to identify and track suspected point clouds and using probabilistic map assistance to complete tracking and mapping [25]. Compared with Lego-LOAM, which is applied to similar unmanned platforms but does not remove dynamic objects, the result of Yang’s method was better. However, compared with the algorithm that uses semantic information for dynamic object processing, effect of dynamic object recognition was worse, and positioning accuracy was also lower. In 2021, Feiya Li et al. proposed a method to establish an initial vehicle model based on shape characteristics of the vehicle, and constructed and removed sparse points based on the boundary line formed by residual points [26]. Identification and tracking of vehicles were completed through calculation of confidence level of the vehicle model and adaptive threshold, which provided a new idea for dealing with dynamic objects. In 2019, on the basis of Suma, Xieyuanli Chen et al. used the RangeNet++ network to semantically label point clouds and proposed the Suma++ algorithm [27]. For each row of point cloud semantic segmentation, the same semantics were searched and filled in the whole. A dynamic information removal module was added to the Suma framework, and map information was used to identify the dynamic point cloud of this frame. At the same time, semantic constraints were added to the ICP(Iterative Closet Point) algorithm to improve robustness of the algorithm with singular values. However, the algorithm could not identify dynamic objects in the first observation, and required two frames of information for comparison. In 2021, Shitong Du et al. fused semantic information to propose S-ALOAM [28], labeling dynamic objects in the preprocessing stage and removing dynamic objects and singularities. Feature extraction was performed on point clusters with the same semantic label according to geometric rules. The odometer node roughly estimated the motion matrix and performed transformation correction. At the mapping node, dynamic objects were eliminated again, with semantic constraints, to complete laser point cloud mapping. However, it took a lot of time to recognize through semantic tags, which affected the real-time performance of the algorithm. In summary, processing dynamic objects can improve positioning accuracy of the SLAM algorithm and improve the mapping effect. However, whether it is the traditional method or the method using the neural network, it is difficult to maintain a fast running speed while ensuring a high recognition rate of dynamic objects. It is necessary to propose a new SLAM algorithm that can not only ensure the recognition rate of dynamic objects to ensure positioning accuracy, but also ensure running speed of the algorithm to ensure real-time performance of the algorithm.
2. Materials and Methods
In order to solve the problem of accuracy of odometer motion estimation decrease due to the large number of pedestrians and vehicles in the city, and at the same time to ensure real-time performance of the algorithm, this paper proposes a lidar SLAM algorithm in dynamic scenes. It realizes the labeling of ground point cloud data, removes the point cloud of dynamic objects and repairs the removed blank area according to the adjacent point cloud. Inertial navigation data was introduced to eliminate motion distortion of original point cloud data and, at the same time, considering the difference in feature types of the point cloud in ground and non-ground areas, classification features were extracted and features were matched according to category in the odometer estimation stage. In the motion estimation stage, a weight factor was introduced to reduce the influence of possible noise feature points, and motion trajectory estimation results were re-corrected in the mapping stage to improve accuracy of the algorithm.
The main flow of the algorithm was as Figure 1:
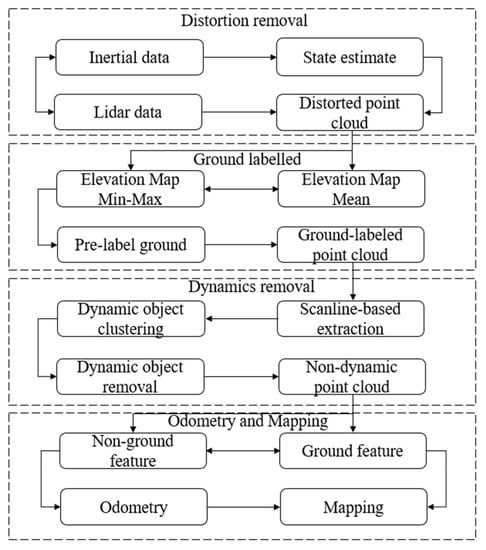
Figure 1.
Algorithm flow.
In this paper, the inertial navigation coordinate system of the starting position of robot motion was selected as the world coordinate system. In the solution process, the lidar coordinate system was set as the {L} coordinate system, the inertial navigation coordinate system was set as the {B} coordinate system and the world coordinate system was set as the {W} coordinate system. When movement started, .
2.1. Distortion Removal
The lidar point cloud acquisition process took a long time for each frame and the point cloud was distorted due to movement of the robot itself during the acquisition process. Using inertial navigation data helped correct for nonlinear distortions that occurred during acquisition. Since acquisition frequency of inertial navigation was much higher than that of lidar, a circular buffer was used to store inertial navigation data, and data of the two sensors were matched according to the timestamp. There were no inertial navigation data at the corresponding time of some lidar points, and the motion state of these lidar points was obtained by linear interpolation of the inertial navigation motion state according to acquisition time of these lidar points. Acquisition time could be calculated from number of lidar lines and horizontal angles .
where represents the number of the bottommost line of lidar, represents the number of the topmost line of lidar, represents the starting timestamp of this frame, and represent time parameters of lidar and represents horizontal angle resolution of lidar.
The number of lidar lines and horizontal angles of lidar points could be calculated from point coordinate , the topmost vertical angle and the bottommost vertical angle .
The state of motion was calculated through integration of acceleration and angular acceleration provided by inertial navigation data. Assuming that the robot moved at a uniform speed during the point cloud acquisition process, motion distortion in {W} was calculated according to the difference between the estimated state in {W} at current moment as well as the uniform motion estimation result, which was calculated from the beginning of the frame to the current moment with estimated state in {W} and speed at the beginning of this frame in {W}.
The nonlinear motion distortion was eliminated through subtraction of the respective distortion from the lidar point.
2.2. Ground Labeling
The ground point cloud was identified to separate objects from the background, which facilitated feature extraction. Lidar points were divided into different grids according to the X and Y coordinates, lidar scanning range and grid resolution , The point cloud was projected to the XOY plane of the world coordinate system, where function ‘floor’ means rounding down of the input.
For each grid , it was necessary to calculate average height of all lidar points’ height in the grid and height difference between the highest point and the lowest point , then establish an elevation map mean (mean map) and an elevation map min-max (difference map).
where function calculates the total number of lidar points.
For each grid in the mean map, it was necessary to calculate gradient in the four neighborhoods and select the maximum gradient as the gradient of the grid. The gradient and of every grid were compared with the threshold and . A grid where both parameters were greater than threshold was identified as an object; where both were less, it was identified as a ground grid. Other grids were pended.
Through the breadth-first search (BFS) algorithm, the four neighborhoods of the ground grid were searched for clustering and multiple ground planes were obtained after clustering. The plane with the largest area among the multiple planes was identified as the ground. The average height difference between other planes and the ground was calculated and difference was compared with the threshold . A grid with a height difference from the ground that was less than the threshold was identified as ground and a grid with a height difference from the ground that was greater than the threshold was identified as ‘other planes.’
The undetermined grid was traversed and voxelized. First, the undetermined grid was divided into small grids with smaller resolutions: and . Vertical bars were established within each small grid according to the highest point and the lowest point of the small grid; the vertical bars were divided into voxels using voxel resolution . Voxels that contained points were retained and those that did not contain points were removed. Voxels were clustered and the group of voxels with the lowest height was taken as the ground part of the grid. In comparison of these low-voxel groups with the determined ground grid, the voxel group where mean heights were within the range of above or below ground height could be identified as ground voxel groups, and points contained in the voxel groups were identified for the ground point cloud.
2.3. Dynamics Removal
According to number of lines , horizontal angle and coordinates, the point cloud was projected into the range image according to Equation (6).
Since the intensity of some lidar points was lower than the receiving threshold, some information could not be received, resulting in missing point clouds. Each missing point cloud was classified and filled in and its range given value; when the range difference between the two boundary points or the sequence number difference was small enough, the linear interpolation value of boundary range was used as a range to fill in missing point positions. After filling was completed, Equation (6) was used to calculate its three-dimensional coordinates inversely. Then the backward difference was used to calculate the first derivative of the range of point , where , were, respectively, the range of points and . Forward difference was used to calculate the second derivative of the range of point , where is the range of points .
The first derivative of range image was traversed from upper left to lower right; the coordinates of the pixel in image whose first derivative was less than the negative value were recorded. Next, the second derivative of range image was traversed from this pixel in the row to find the point cloud segment whose second derivative was continuously positive and whose length was greater than or equal to so as to extract an arc-shaped convex hull (shown in Figure 2) in the point cloud of dynamic objects (generally including pedestrians and vehicles).
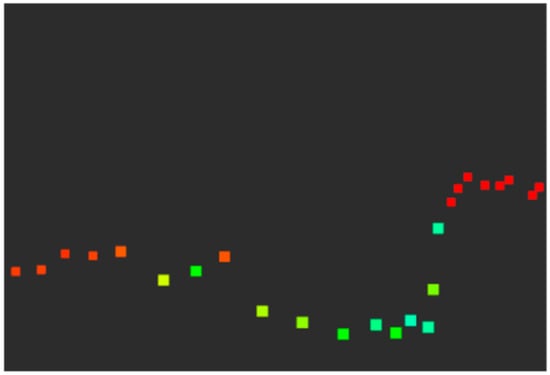
Figure 2.
Convex hull. Some convex hulls that meet segment conditions are segmented from the raw point cloud.
Depth difference between the two ends of the point cloud convex hull was calculated to judge whether this difference was less than or equal to . The angle γ was calculated between the two end points and the outer point of the adjacent segment, as shown in Figure 3.
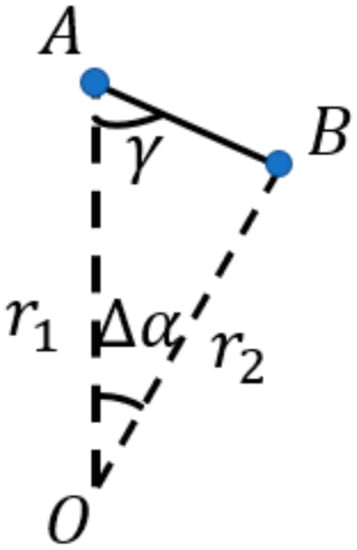
Figure 3.
Angle γ, where A, B, and represent the end point, the adjacent point and their range, respectively. O represents lidar; represents horizontal angle resolution of lidar.
This angle could more stably represent the degree of depth variation of adjacent laser spots, and the angle of the segmented point cloud should have been less than or equal to the threshold value . The calculation method is as in Equation (7).
The point cloud segment that satisfied the above conditions was taken as segment , which represents the first segment of scanline . Considering that the length of the point cloud segment representing a pedestrian’s leg was short and the point cloud of this kind of segment often appeared in the last several lines, was reduced for segmenting by the line to adapt to this feature. Pseudocode for this process is shown in Algorithm 1.
| Algorithm 1: Segment |
 |
Segments were clustered for dynamic object recognition. The complete point cloud of a dynamic object needed to be composed of multiple segments across the scanlines, so it was necessary to follow the sequence of the scanlines and check . Segments were clustered according to two criteria. The first criterion was centroid Euclidean distance difference , which ensured that the distance between the two segments was close enough and isolated segments could not form a dynamic object point cloud. The centroid was calculated from the points within the segment.
where represents number of points within the segment. The second criterion was principal component analysis result of the segment point cloud. Create covariance matrix for all the points contained in the segment, the eigenvector and the eigenvalue were calculated, with the eigenvalue and the eigenvector corresponding in turn. For principal component analysis results of the two adjacent segments and , Equation (9) needed to be satisfied:
Point cloud segments that met the criteria were clustered to obtain the complete point cloud of dynamic objects. The pseudocode of this algorithm is shown in Algorithm 2.
| Algorithm 2: Cluster |
 |
After clustering was completed, the object point cloud could be identified; those with a number of crossing lines larger than the number of segment points were identified as pedestrians and those with a number of crossing lines smaller than the number of segment points were identified as vehicles. According to the serial number of the point cloud of the dynamic object, range was modified to 0 in the range image to eliminate dynamic point clouds.
After the dynamic point cloud was eliminated, there was a vacancy in the corresponding position. These missing points were repaired to improve feature point extraction and mapping. First, the second derivative , and the first derivative , were taken; the first derivative of the endpoint of the vacant segment , was calculated. Then, according to the first derivative and the range of the outer endpoints on both sides , , the range of the inner endpoints , of the vacant segment was calculated. Next, the first derivative and range with the same second derivative toward the inner vacant segment were calculated according to the sequence. The repair of the vacant segment started from both sides and closed in the middle to complete the repair.
Figure 4 shows the process result of the pedestrian point cloud, in which red points represent the pedestrian point cloud and yellow points are the point cloud of the repaired part.
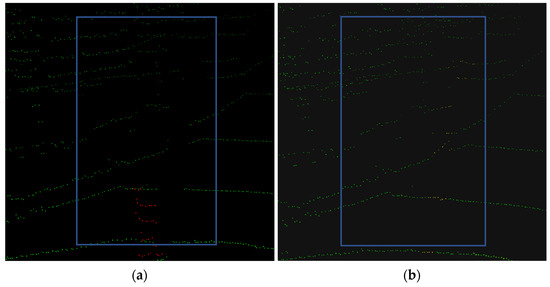
Figure 4.
Pedestrian recognition and repairing. (a) Pedestrian points labeled with red. (b) Points without pedestrians, filled in with yellow.
2.4. Odometry and Mapping
The odometry and mapping process mainly included three parts: feature extraction, odometry and mapping. The LOAM algorithm extracted feature points by calculating curvature and divided the feature points into two types: planar points and edge points. It then matched feature points according to classification. On this basis, we applied ground information for feature extraction. First, the feature extraction strategy was selected according to whether it belonged to the ground. For non-ground areas, in order to ensure uniform distribution of feature points, each scanline was divided into multiple parts according to number of points. The curvature of points in each part was compared with the threshold; those larger than the threshold of edge points were selected as edge points, and those smaller than the threshold of planar points were selected as planar points. The number of edge points and planar points that could be extracted from each part could not exceed the threshold. For the ground area, the planar points were still extracted uniformly, but considering that the ground was relatively flat, extraction density decreased. Because the edge points of the ground were mostly rough ground, the extraction did not consider uniform distribution and only selected several edge points with the largest curvature. In this way, four types of point were extracted: ground edge points, ground planar points, non-ground edge points and non-ground planar points. In odometry and mapping, feature points of each classification were only matched with points of the same classification.
3. Experimental Section
We used a certain type of 8W4AUGV (eight wheel, four arm unmanned ground vehicle, shown in Figure 5) as an experimental platform to conduct experiments on a road in an industrial park. The ground recognition rate, dynamic object recognition rate and localization accuracy of the algorithm were tested by experiments.

Figure 5.
An 8 wheel, 4 arm unmanned ground vehicle.
3.1. Experimental Setup
3.1.1. Experimental Environment
This algorithm mainly solved the problem of dynamic scene localization and mapping, so a scene with more dynamic objects was selected. Selecting a main road with many pedestrians in the industrial park verified recognition effect of the algorithm on dynamic objects. The main way of driving for unmanned vehicles is proceeding straight and turning. Therefore, a main road section with a length of about 150 m was selected for the straight driving test, and a bent section with a length of about 50 m was selected for the turning test. The experiment was carried out during the work and rest period of the park, when there were many pedestrians on both sides of the road. The unmanned vehicle traveled at a speed of 20 km/h, and motion distortion was more obvious while we ensured the safety of the experiment. There were green belts, street trees and workshops on both sides of the road. Those green belts and street trees affected the ground recognition algorithm and tested the efficiency of the ground recognition algorithm. The workshop simulated buildings around the actual application scene of unmanned vehicles.
3.1.2. Experimental Equipment
We used the VLP-16 to collect the point cloud by 360°, horizontally scanning at 16 various vertical angles in the range (−15°, 15°), which worked in the frequency of 10 Hz; about 20,000 points were collected in each frame. Inertial and ground truth data came from WIS-3000: an integrated navigation unit that integrates inertial navigation data and RTK-GNSS (Real Time Kinematic Global Navigation Satellite System) data. WIS-3000 could ensure output accuracy of latitude, longitude and altitude information at the centimeter level. Its output frequency was 50 Hz. The experimental equipment is as Figure 6.

Figure 6.
Experimental equipment.
The hardware configuration was Intel Core i5-9300H and GTX-1660Ti, the development environment was the Ubuntu18.04 system and ROS system architecture was used for development.
3.2. Ground Recognition Rate
In order to compute recognition rate and running speed of the ground recognition module of this algorithm, 100 typical frames of point cloud data were chosen from the experimental data and our ground recognition algorithm was executed on them. Those 100 frames of point data were manually marked as ground point or non-ground point in advance. The number of ground points recognized by our algorithm running on the data was counted and compared with the actual value to judge recognition effect. The selected point cloud was about 17,000 points per frame. Sensitivity and specificity were calculated using the number of ground points correctly identified (TP), non-ground points correctly identified (FN), ground points not correctly identified (TN) and non-ground points not correctly identified (FP) for quantitative analysis.
According to Equation (9), the higher the sensitivity, the better the recognition effect; the lower the specificity, the better the recognition effect. According to statistics, our algorithm had a sensitivity of 93.7% for ground recognition, a specificity of 1.3% and a running speed of 9.41 ms in this dataset. Ground recognition results are shown in Figure 7.

Figure 7.
Ground recognition. Red points represent the ground point; green points represent the rest.
3.3. Dynamic Object Recognition Rate
In order to quantitatively describe the efficiency of the recognition algorithm for dynamic objects and the repair algorithm to reconstruct the environmental point cloud, 100 frames of point clouds were taken from the experimental data and the algorithm was executed on that data. We evaluated our recognition algorithm by counting successfully marked point clouds in every frame and computing average recognition rate. The point cloud marked as dynamic objects, with rate of coinciding with actual dynamic points marked manually more than 75%, was recognized successfully marked. According to statistics, the recognition rate of this algorithm for dynamic objects is 72.5%.
The evaluation norm for the repair algorithm was the geometric error between the repaired point cloud and the corresponding actual objects, as shown in the Figure 8.

Figure 8.
Repaired point cloud. (a) Point cloud. (b) Actual object. The yellow dots in (a) represent the repaired background point cloud after removal of dynamic objects. (b) represents the actual background of the frame data. The yellow point restores the spherical flowerbed in the green belt, and the geometric error, calculated through comparison of the circle equation of the real object and the point cloud, is about 4.3%. Taking into account the selection of the plane where the circle is located, the accuracy of the measuring tool and other factors, it was considered that the repair algorithm could restore the object accurately.
Similar objects with clear geometric features, such as road signs, curbs and the ground, were also included. The results show that the repair algorithm can restore the environment accurately and retain the characteristics of the static environment.
3.4. Localization Accuracy
3.4.1. Evaluation Criteria
The relative pose error could be calculated from the absolute pose error. The absolute pose error represents the difference between the estimation pose change of lidar in the world coordinate system calculated with the algorithm during the point cloud collection process of the frame and the pose change given by the GNSS as the ground truth value.
where represents absolute position error in frame, represents absolute attitude error in frame, and . The relative position error represents the ratio of the absolute error of the algorithm’s estimated value of lidar’s pose change in the world coordinate system to the true value and true pose change during the frame point cloud collection process. Relative attitude error represents the ratio of absolute attitude change and position absolute error in deg/m:
where represents relative position error and represents relative attitude error. There is an average relative pose error for the entire motion process:
where represents the number of frames of all point cloud sets in the whole movement process, represents the relative position error of the frame and represents the relative attitude error of the frame. The cumulative position error represented the absolute error between the final unmanned vehicle position and the ground truth value, which was calculated by Equation (10), and the final position was involved in the calculation. As to the running speed of algorithm, we counted the time used by the algorithm to run each stage of the ground recognition stage, the dynamic object recognition stage and the overall algorithm, respectively. The test data set consisted of 100 frames of point cloud data with obvious features extracted from each scene, and average running speed of the 100 frames of data was taken as the result.
3.4.2. Data Analysis
A map of the actual scene is shown in Figure 9a,b.
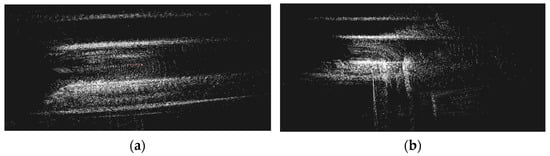
Figure 9.
Mapping of actual scene. (a) Map of straight road. (b) Map of bent road.
According to the aforementioned criteria, the statistical results of the experimental data are as Table 1, Table 2 and Table 3:

Table 1.
Absolute and relative position error.

Table 2.
Relative attitude error.

Table 3.
Running time.
Statistical results show that the algorithm can achieve high-precision positioning and mapping functions while ensuring real-time performance. Compared with LOAM, our algorithm reduced average relative position errors by 50.7% on straight roads and 52.6% on bent roads. Our algorithm also reduced average relative attitude errors by 6.5% on straight roads and 18.6% on bent roads.
4. Conclusions and Future Work
Aiming at the problems of low positioning accuracy and poor mapping effect of lidar SLAM in dynamic scenes, the authors of this paper carried out a series of research on laser point cloud ground recognition, dynamic object recognition and elimination, localization and mapping, then established a laser point cloud suitable for dynamic scenes. Lidar SLAM algorithm improved the performance of SLAM algorithm in practical applications.
In this paper, a light and fast lidar SLAM algorithm is proposed. Compared with classical LOAM, our algorithm reduced relative position error and relative attitude error obviously (51.6% and 12.5% in the average of straight and bent roads, respectively) within the same running time in a dynamic scene. The algorithm uses a lightweight and embedded object recognition method in the front end to efficiently process the original point cloud so that the processed point cloud features are obvious, which ensures positioning accuracy and facilitates subsequent processing of mapping. A dynamic object recognition algorithm is proposed based on the point cloud harness: using the derivative to represent the point cloud feature. The second derivative should be explicitly used to grow the repaired point cloud from both sides. According to the processing results of the dynamic point cloud, it can be concluded that the algorithm can effectively identify the dynamic point cloud and restore background points occluded by dynamic objects according to the surrounding environment. A processing method of extracting feature points for ground and non-ground classification is proposed. Not only are feature points extracted separately according to categories, but methods for selecting feature points for ground and non-ground categories are different. The proposed algorithm should make feature point extraction more accurate and feature point matching more efficient.
This paper has the following room for improvement: First, the recognition scheme for dynamic objects still needs to be improved. Optimizing the recognition of dynamic objects that are not representative but still appear at different distances and resolutions remains a challenge. It is possible to consider the fusion of millimeter-wave radar to assist in dynamic object recognition and tracking as well as conduct experiments in more dynamic scenarios. Second, the structure of the current algorithm is simple enough to fully meet real-time requirements. The parameters of the process algorithm can be modified, the number of iterations can be increased and the algorithm accuracy can be improved. Other optimization methods can also be introduced in the back end to further improve the accuracy of the algorithm.
Author Contributions
Conceptualization, J.L.; methodology, J.L.; software, J.L.; resources, J.H.; writing, J.L.; supervision, J.H.; experiment and data analysis, J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
We are particularly grateful to Wu from Sunward Corporation, China, for providing the experiment platform and place. Finally, we express our gratitude to all the people and organizations that have helped with this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jurišica, L.; Duchoň, F. High Precision GNSS Guidance for Field Mobile Robots. Int. J. Adv. Robot. Syst. 2012, 9, 169. [Google Scholar] [CrossRef]
- Zabalegui, P.; De Miguel, G.; Pérez, A. A review of the evolution of the integrity methods applied in GNSS. IEEE Access 2020, 8, 45813–45824. [Google Scholar] [CrossRef]
- Moussa, M.; Moussa, A.; El-Sheimy, N. Steering angle assisted vehicular navigation using portable devices in GNSS-denied environments. Sensors 2019, 19, 1618. [Google Scholar] [CrossRef] [PubMed]
- Zahran, S.; Mostafa, M.M.; Masiero, A. Micro-Radar and UWB Aided UAV Navigation in GNSS Denied Environment. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 42, 469–476. [Google Scholar] [CrossRef]
- Wu, C.; Yu, S.; Chen, L. An Environmental-Adaptability-Improved RatSLAM Method Based on a Biological Vision Model. Machines 2022, 10, 259. [Google Scholar] [CrossRef]
- Zou, Q.; Sun, Q.; Chen, L. A comparative analysis of LiDAR SLAM-based indoor navigation for autonomous vehicles. IEEE Trans. Intell. Transp. Syst. 2022, 23, 6907–6921. [Google Scholar] [CrossRef]
- Campos, C.; Elvira, R.; Rodríguez, J.J.G. ORB-SLAM3: An Accurate Open-Source Library for Visual, Visual–Inertial, and Multimap SLAM. IEEE Trans. Robot. 2021, 37, 1874–1890. [Google Scholar] [CrossRef]
- Rosinol, A.; Abate, M.; Chang, Y. Kimera: An open-source library for real-time metric-semantic localization and mapping. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 1689–1696. [Google Scholar]
- Galvez, L. Bags of Binary Words for Fast Place Recognition in Image Sequences. IEEE Trans. Robot. A Publ. IEEE Robot. Autom. Soc. 2012, 28, 1188–1197. [Google Scholar] [CrossRef]
- Mccormac, J.; Handa, A.; Davison, A. SemanticFusion: Dense 3D semantic mapping with convolutional neural networks. In Proceedings of the International Conference on Robotics and Automation, Singapore, 29 May–3 June 2017; pp. 4628–4635. [Google Scholar]
- Silberman, N.; Hoiem, D.; Kohli, P. Indoor segmentation and support inference from rgbd images. In Proceedings of the European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 746–760. [Google Scholar]
- Hess, W.; Kohler, D.; Rapp, H. Real-time loop closure in 2D LIDAR SLAM. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 1271–1278. [Google Scholar]
- Zhang, J.; Singh, S. LOAM: Lidar Odometry and Mapping in Real-time. In Robotics: Science and Systems; University of California: Berkeley, CA, USA, 2014; Volume 2. [Google Scholar]
- Geiger, A.; Lenz, P.; Stiller, C. Vision meets robotics: The kitti dataset. Int. J. Robot. Res. 2013, 32, 1231–1237. [Google Scholar] [CrossRef]
- Shan, T.; Englot, B. Lego-loam: Lightweight and ground-optimized lidar odometry and mapping on variable terrain. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 4758–4765. [Google Scholar]
- Park, Y.S.; Jang, H.; Kim, A. I-LOAM: Intensity Enhanced LiDAR Odometry and Mapping. In Proceedings of the 2020 17th International Conference on Ubiquitous Robots (UR), Kyoto, Japan, 22–26 June 2020; pp. 455–458. [Google Scholar]
- Li, L.; Kong, X.; Zhao, X. SA-LOAM: Semantic-aided LiDAR SLAM with Loop Closure. In Proceedings of the IEEE International Conference on Robotics and Automation, Xi’an, China, 30 May–5 June 2021; pp. 7627–7634. [Google Scholar]
- Ding, L.; Feng, C. DeepMapping: Unsupervised map estimation from multiple point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 8650–8659. [Google Scholar]
- Cui, L.; Ma, C. SOF-SLAM: A semantic visual SLAM for dynamic environments. IEEE Access 2019, 7, 166528–166539. [Google Scholar] [CrossRef]
- Xiao, L.; Wang, J.; Qiu, X. Dynamic-SLAM: Semantic monocular visual localization and mapping based on deep learning in dynamic environment. Robot. Auton. Syst. 2019, 117, 1–16. [Google Scholar] [CrossRef]
- Liu, Y.; Miura, J. RDS-SLAM: Real-time dynamic SLAM using semantic segmentation methods. IEEE Access 2021, 9, 23772–23785. [Google Scholar] [CrossRef]
- Yu, C.; Liu, Z. DS-SLAM: A semantic visual SLAM towards dynamic environments. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 1168–1174. [Google Scholar]
- Sun, Y.; Liu, M. Improving RGB-D SLAM in dynamic environments: A motion removal approach. Robot. Auton. Syst. 2017, 89, 110–122. [Google Scholar] [CrossRef]
- Dang, X.; Rong, Z.; Liang, X. Sensor fusion-based approach to eliminating moving objects for SLAM in dynamic environments. Sensors 2021, 21, 230. [Google Scholar] [CrossRef]
- Cong, Y.; Chen, C.; Li, J.; Wu, W.; Li, S. Mapping without dynamic: Robust lidar-slam for ugv mobile mapping in dynamic environments. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 43, 515–520. [Google Scholar] [CrossRef]
- Li, F.; Fu, C.; Wang, S.; Zhu, Y. Lidar-based vehicle detection for dynamic SLAM applications. In Proceedings of the 2021 International Conference on Control, Automation and Information Sciences (ICCAIS), Xi’an, China, 14–17 October 2021; pp. 674–678. [Google Scholar]
- Chen, X.; Milioto, A.; Palazzolo, E.; Giguere, P. Suma++: Efficient lidar-based semantic slam. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 4530–4537. [Google Scholar]
- Du, S.; Li, Y.; Li, X. LiDAR Odometry and Mapping Based on Semantic Information for Outdoor Environment. Remote Sens. 2021, 13, 2864. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).