Joint Optimization Strategy of Condition-Based Maintenance and Spare Parts Ordering for Nonlinear Degraded Equipment under Imperfect Maintenance
Abstract
:1. Introduction
- (1)
- (2)
- (3)
- Based on RUL information, a multi-objective joint optimization strategy is established to reasonably maintain and order spare parts, reduce the operation cost of nonlinear degradation equipment and improve availability.
2. Problem Description
- (1)
- How to find a widely applicable transformation relation to solve the problem of nonlinear degradation data modeling;
- (2)
- Under the premise that the probability of successful imperfect maintenance activities is known, how to determine and analyze the number of imperfect maintenance activities to achieve the purpose of prolonging the life of degraded equipment;
- (3)
- How to reduce the cost of equipment loss per unit time while meeting the availability requirements of degraded equipment.
3. Nonlinear Degradation Modeling and RUL Prediction
4. Joint Optimization Model of Conditional Maintenance and Spare Parts Ordering
- (1)
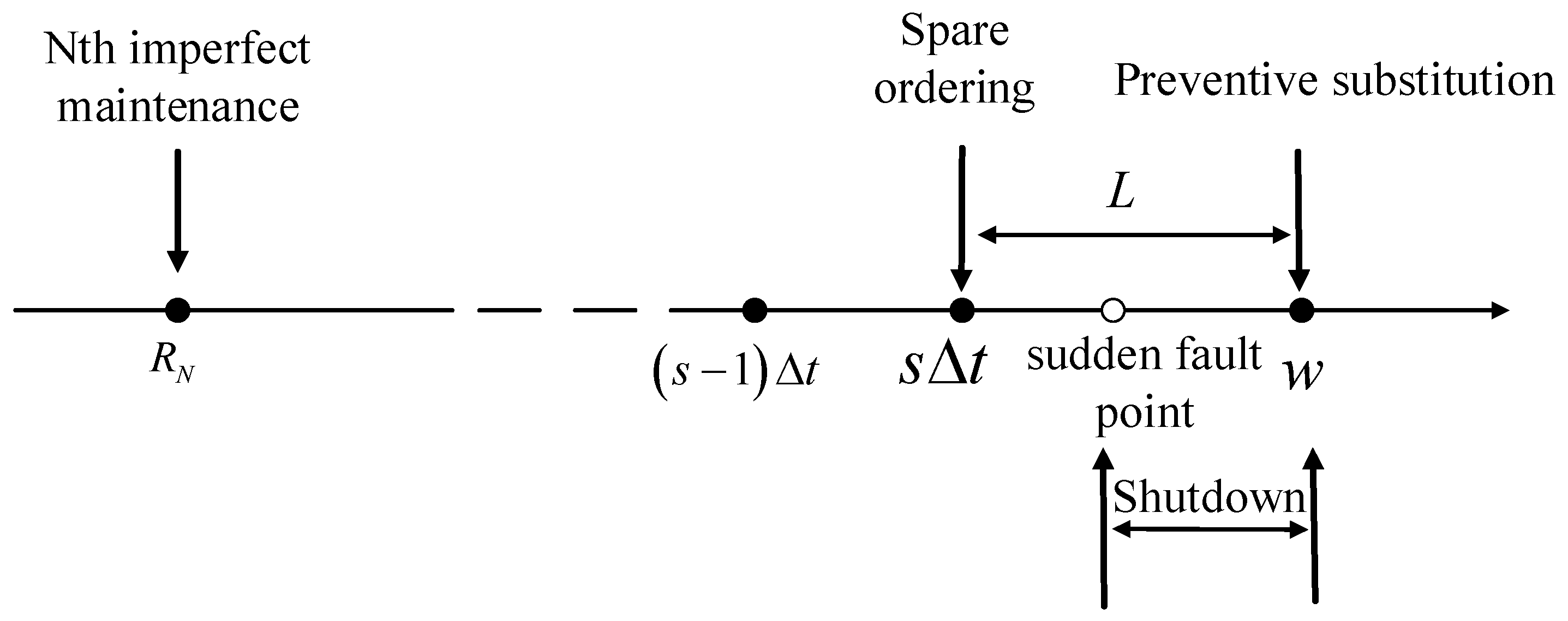
- After imperfect maintenance activities, the equipment fails between the spare parts ordering and the expected failure time, and the standby spare parts need to be replaced.
- (2)
- After imperfect maintenance activities, the equipment normally fails at the expected failure time, which requires the replacement of spare parts without shutdown;
- (3)
- After imperfect maintenance activities, the equipment fails before the expected spare parts ordering time, which requires emergency spare parts ordering and replacement of downtime spare parts;
- (4)
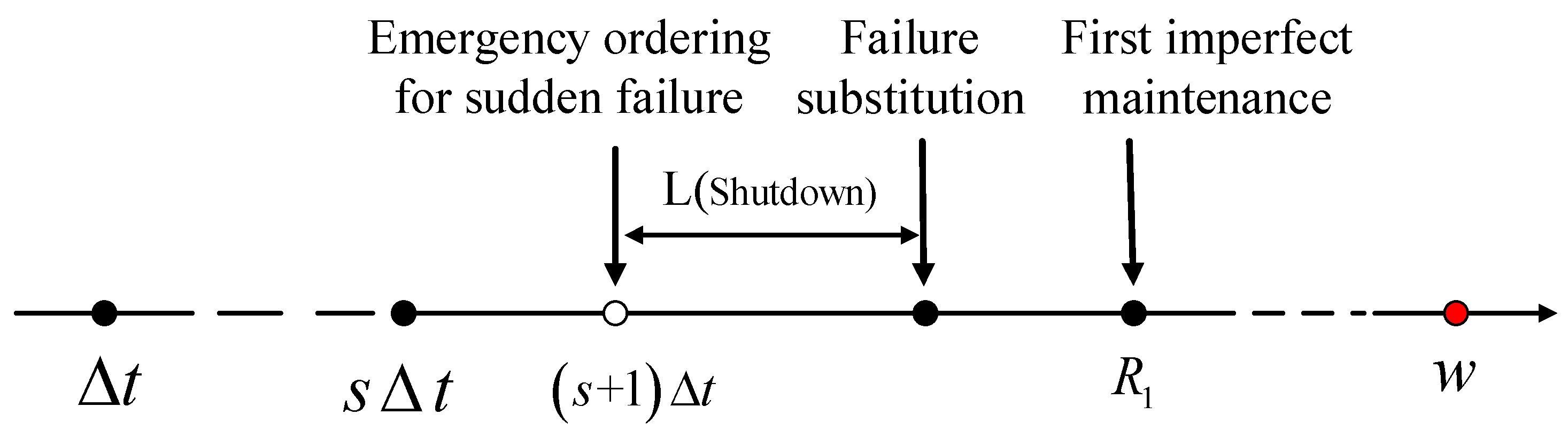
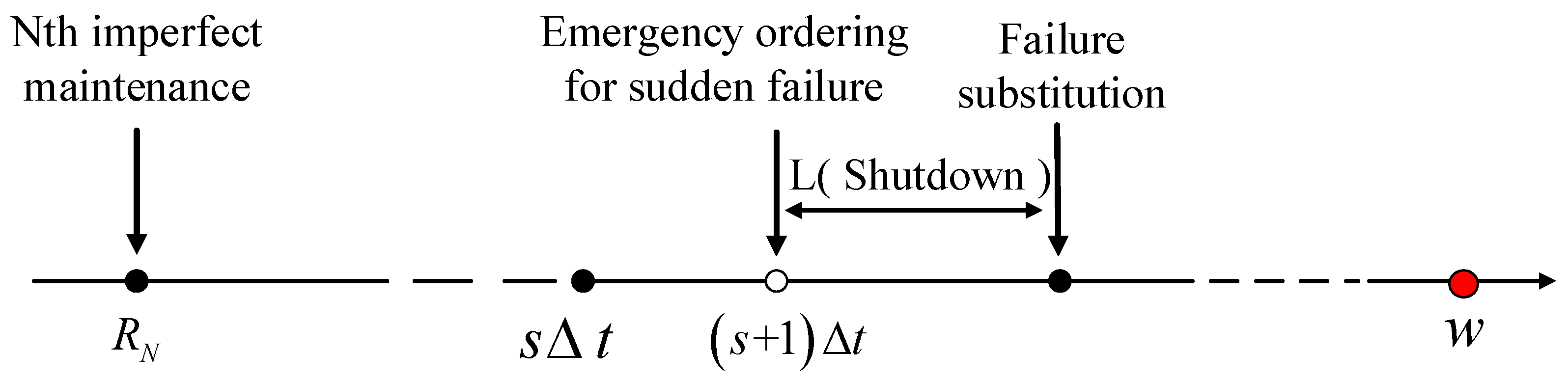
- Without imperfect maintenance of equipment, sudden failure occurs. At this time, emergency spare parts ordering and shutdown spare parts replacement are needed.
- (1)
- During the life cycle, the cost of each test is , the cost of preventive maintenance is , the cost of preventive replacement is , the cost of invalid replacement is , the cost of expected spare parts is , the cost of emergency ordering spare parts for sudden failure is , the downtime cost caused by the inability to replace spare parts is , and the spare parts order time is ;
- (2)
- The detection time and spare parts replacement time are ignored;
- (3)
- The downtime cost per unit time is certain;
- (4)
- Considering the cost relationship in engineering practice, let , .
4.1. Number of Imperfect Maintenance Activities
4.2. Preventive Replacement and Spare Parts Ordering
4.3. Failure Substitution and Spare Parts Ordering
5. Discussion on Experimental Analysis
5.1. Initialization of Parameters
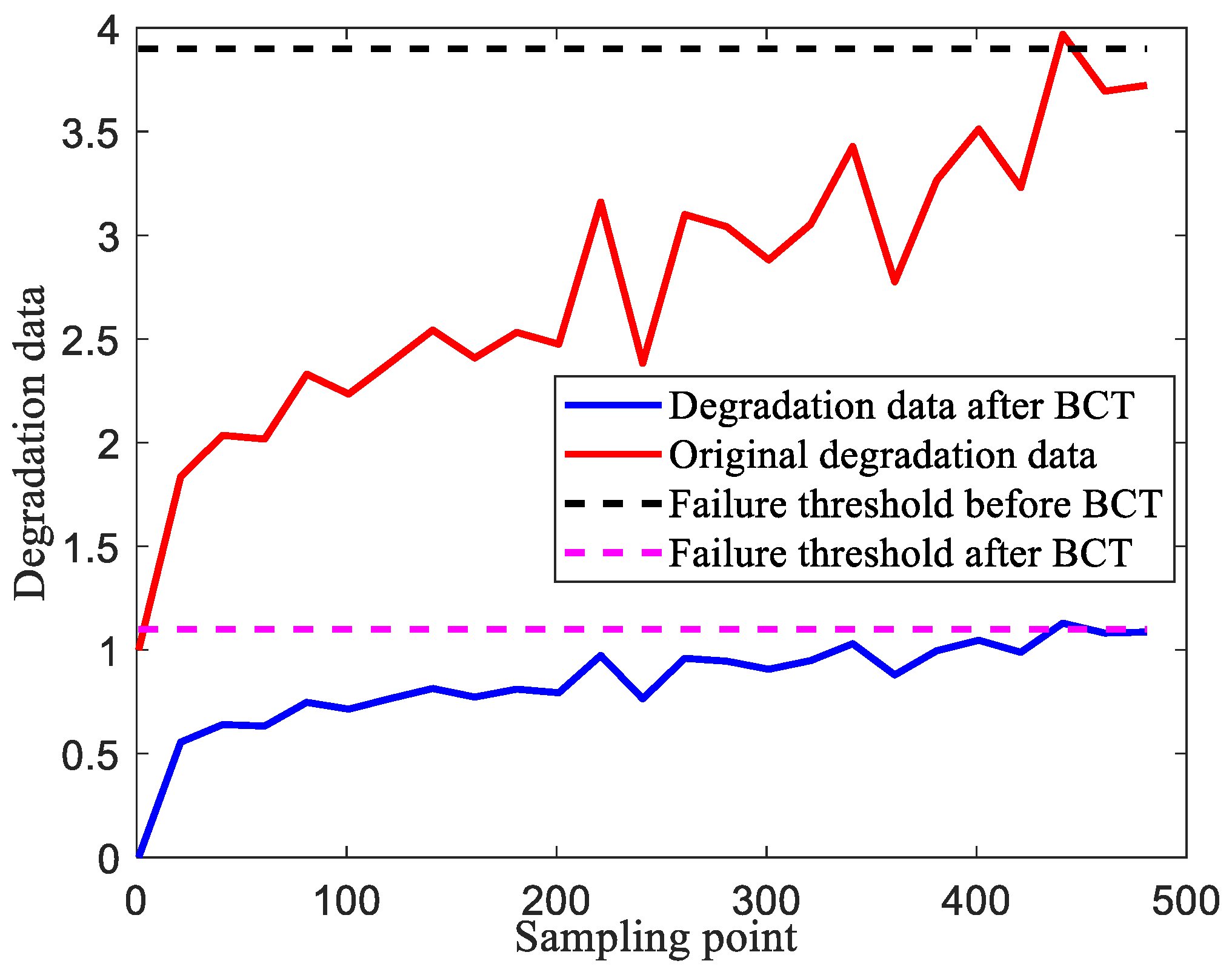
5.2. Simulation Verification
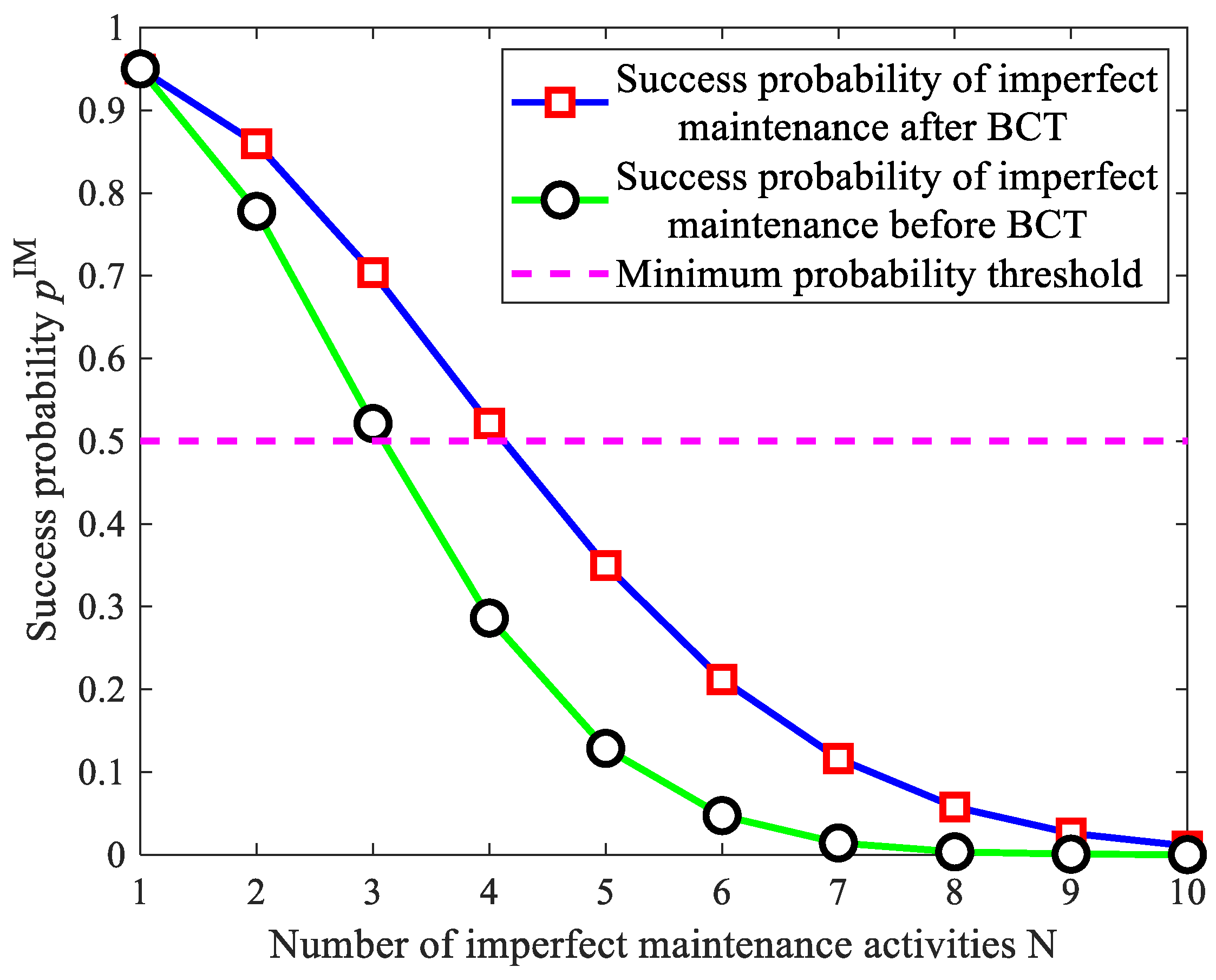
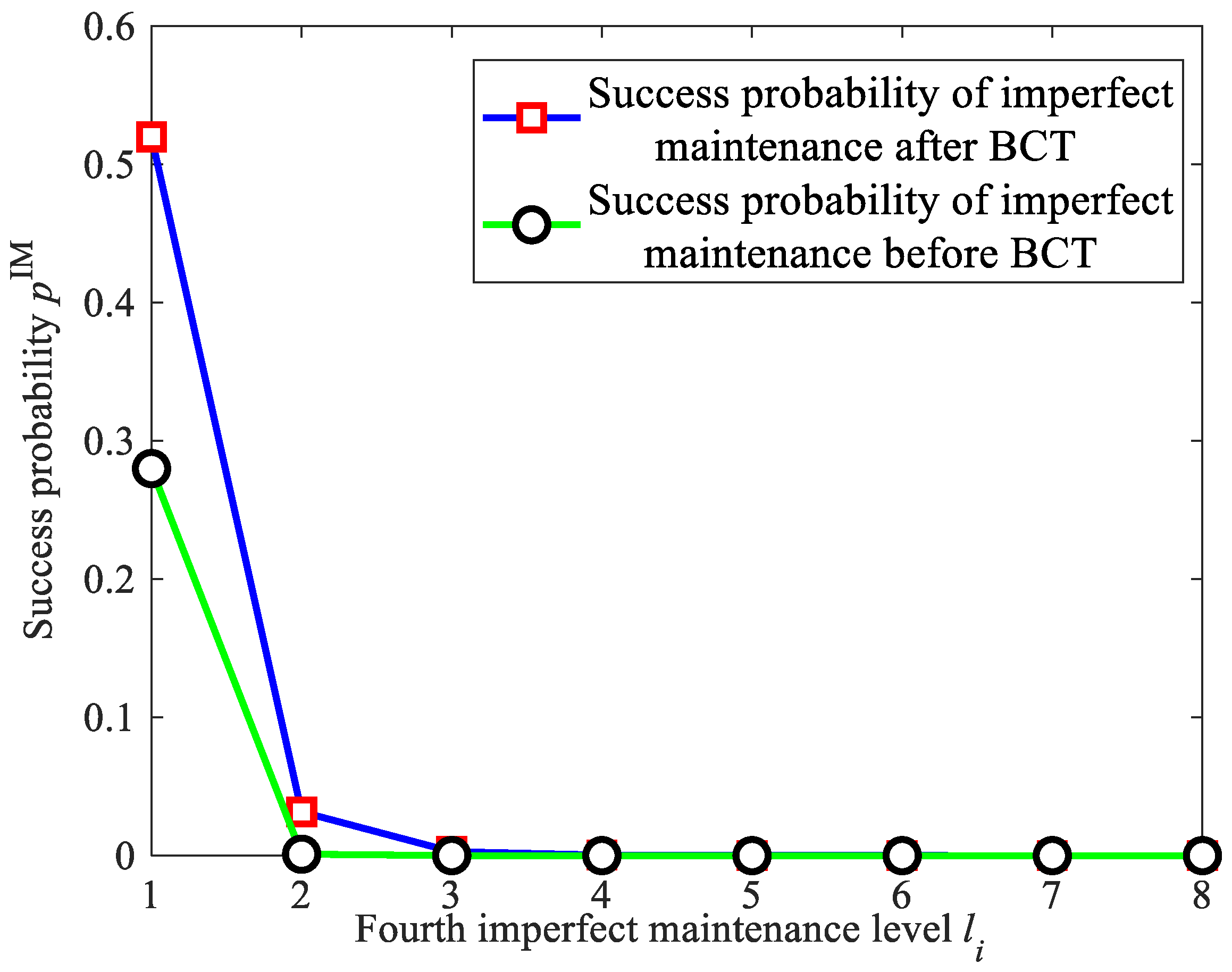
5.2.1. Determination of the Number of Imperfect Maintenances
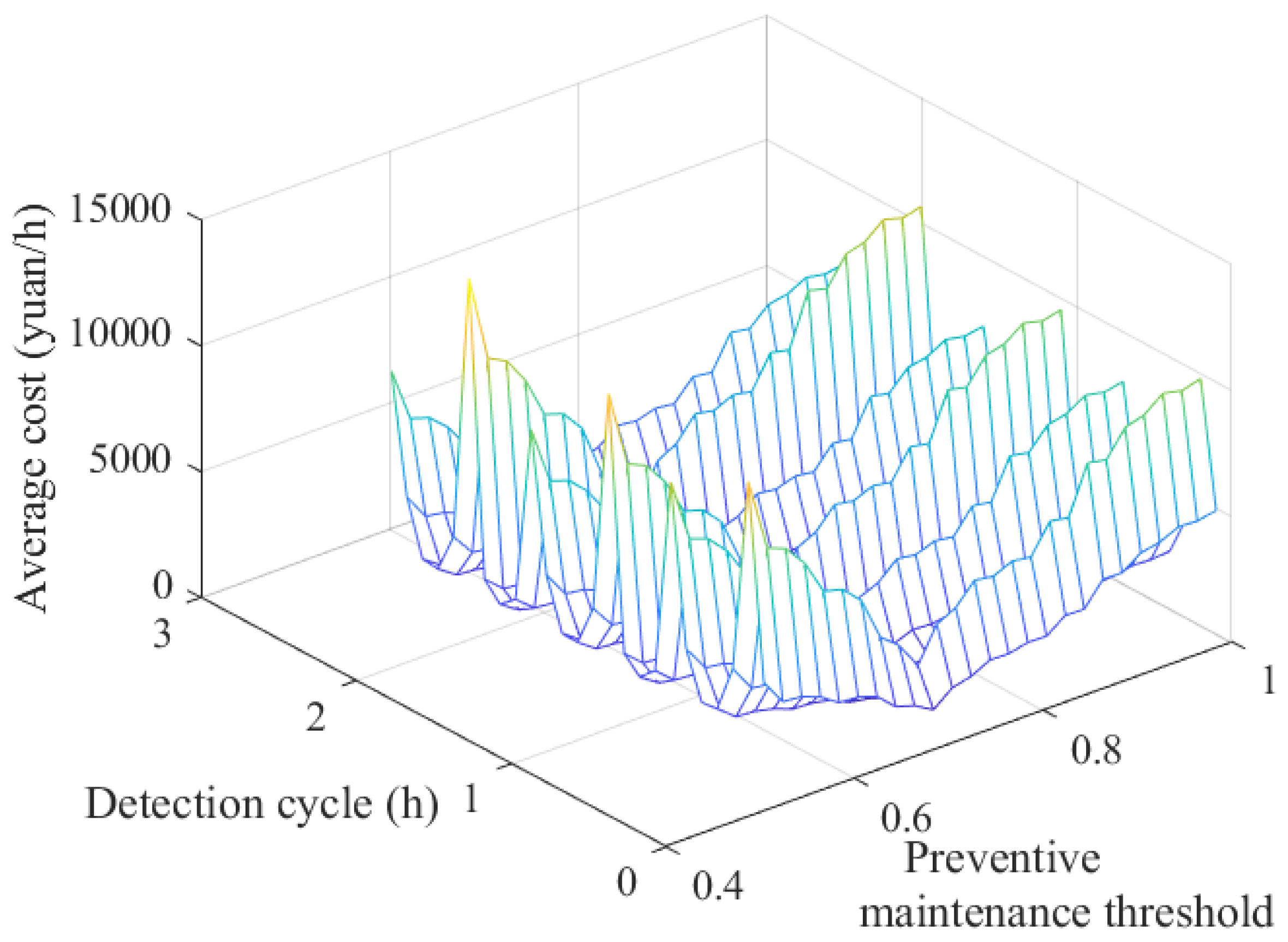
5.2.2. Minimum Average Cost under Constraints
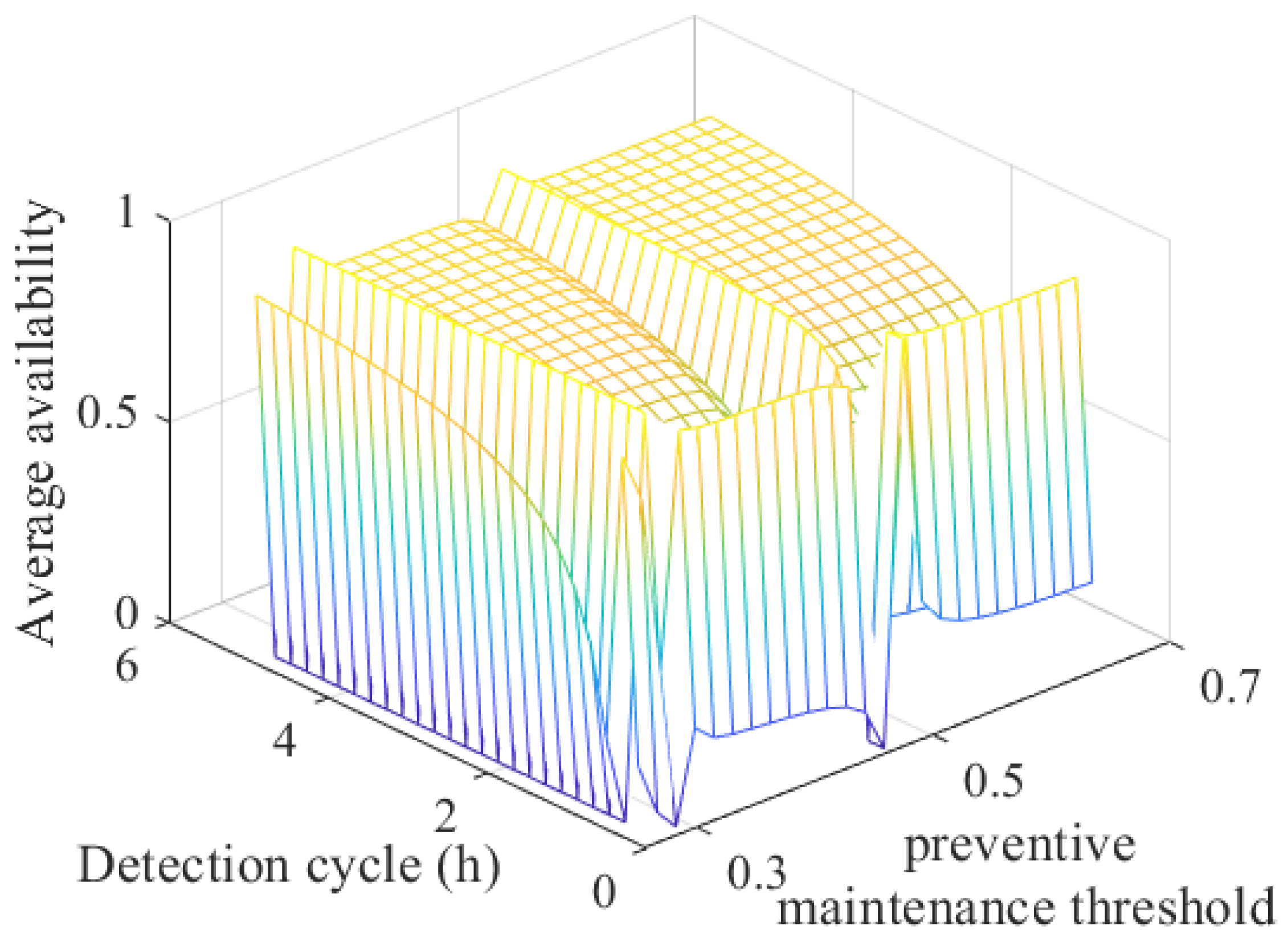
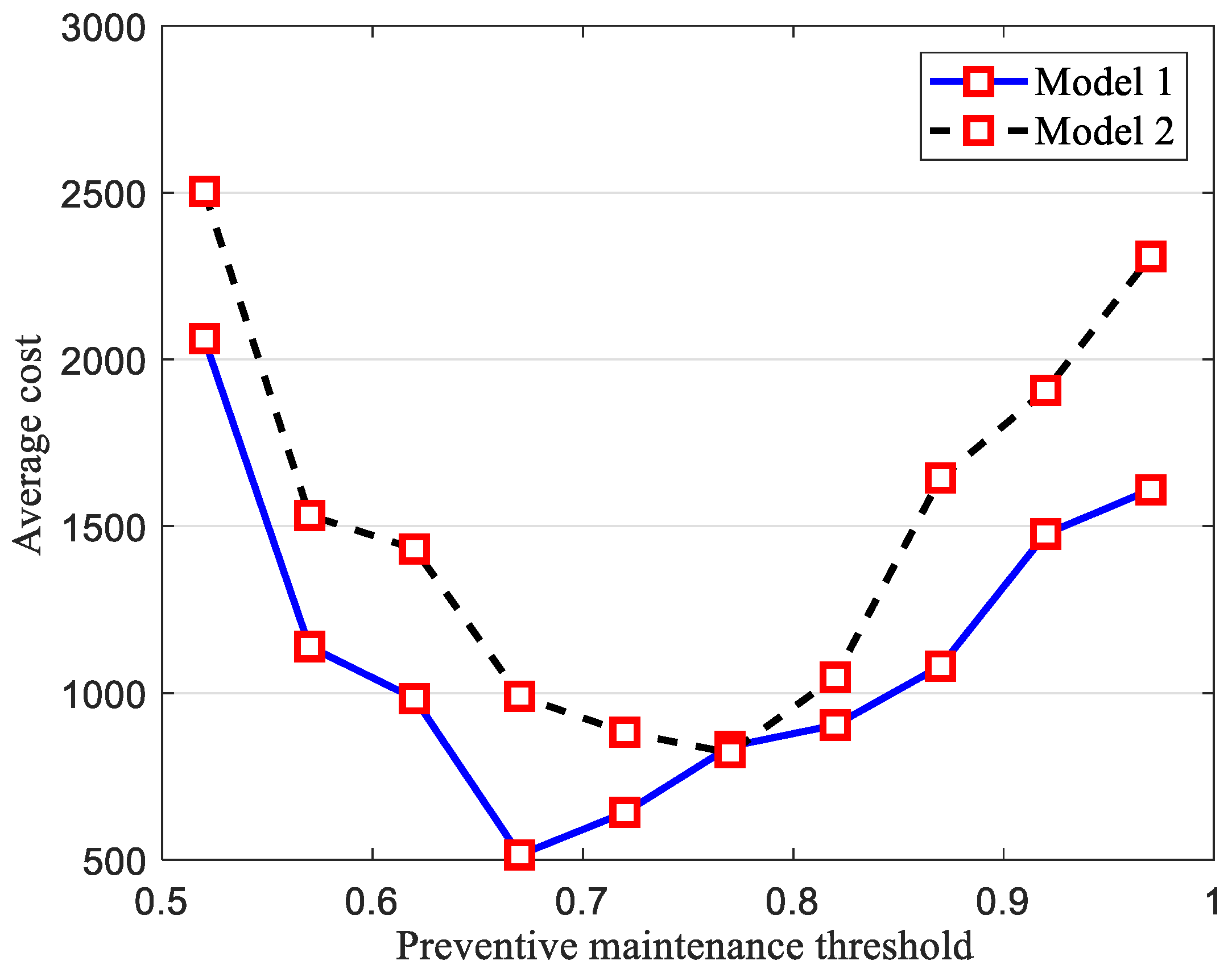
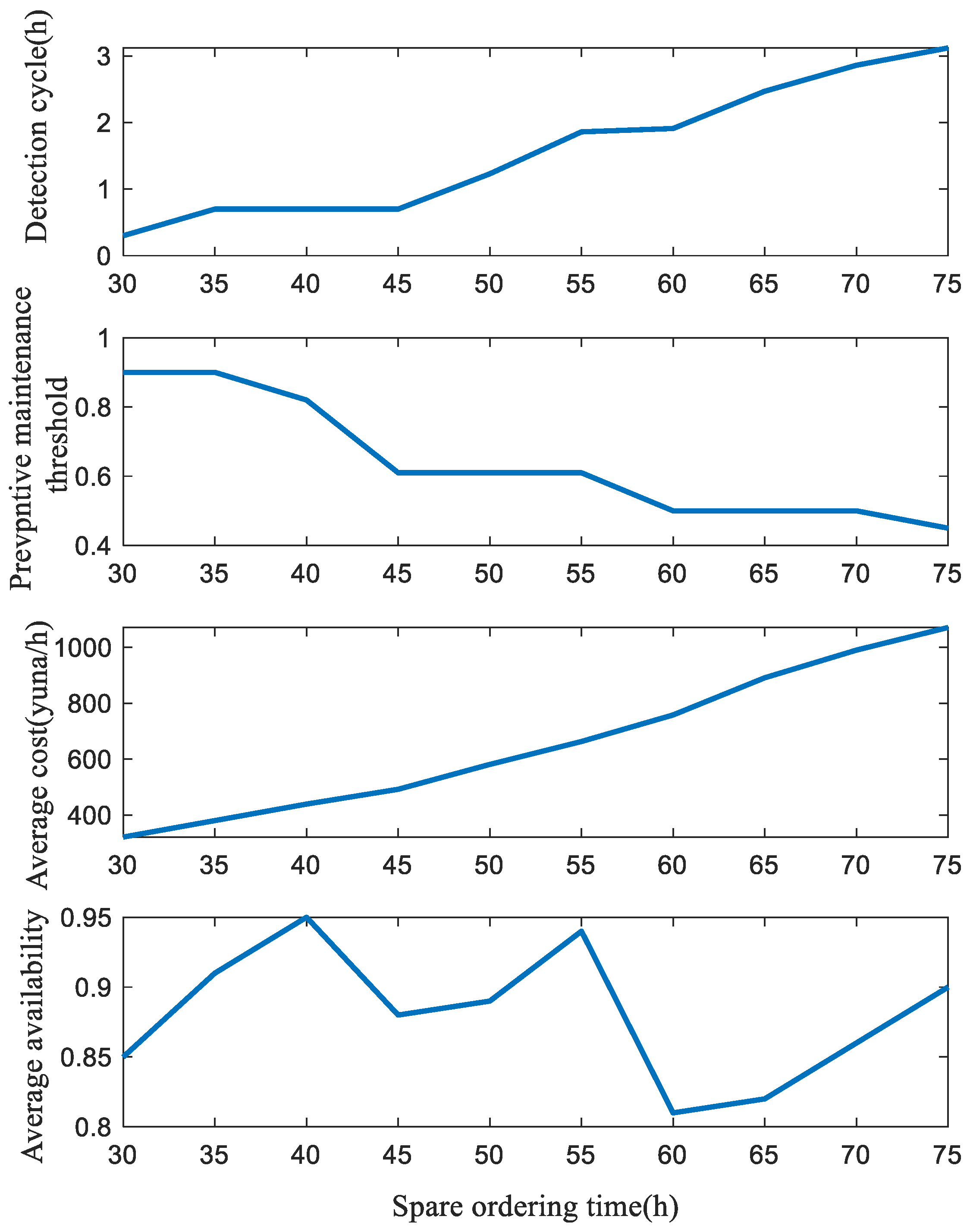
5.2.3. Comparative Experiments and Sensitivity Analysis
6. Conclusions
- (1)
- In this paper, the maintenance strategy of similar nonlinear degradation equipment was studied. In engineering practice, the research goal can be multivariate and systematic. Thus, it is necessary to construct a multivariate nonlinear degradation model and consider the uncertainty of imperfect maintenance activities of multivariate systems.
- (2)
- Considering the influence of parameters such as detection cost and maintenance cost on the joint optimization model, the joint optimization model can be optimized by combining decision variables.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Si, X.; Li, T.; Zhang, Q.; Hu, X. An Optimal Condition-based replacement method for systems with observed degradation signals. IEEE Trans. Reliab. 2018, 67, 1281–1293. [Google Scholar] [CrossRef]
- Chen, C.; Lu, N.; Jiang, B. Condition-based maintenance optimization for continuously monitored degrading systems under imperfect maintenance actions. J. Syst. Eng. Electron. 2020, 31, 841–851. [Google Scholar]
- Yan, T.; Lei, Y.; Wang, B.; Han, T.; Si, X.; Li, N. Joint maintenance and spare parts inventory optimization for multi-unit systems considering imperfect maintenance actions. Reliab. Eng. Syst. Saf. 2020, 202, 106994. [Google Scholar] [CrossRef]
- Zhang, X.; Zeng, J. Joint Optimization of Condition-based Preventive Maintenance and Spare Parts Provisioning Policy for Equipment Maintenance. J. Mech. Eng. 2015, 51, 150–158. [Google Scholar] [CrossRef]
- Cai, J.; Xiao, L.; Li, X. Joint optimization of maintenance decision and spare parts inventory based on Wiener process. Syst. Eng. Electron. 2016, 38, 1854–1859. [Google Scholar]
- Jiang, Y.; Guo, T.; Zhou, D. Joint decision on replacement time and spare ordering time based on remaining useful life prediction. CIESC J. 2015, 66, 284–290. [Google Scholar]
- Lu, N.; Chen, C.; Jiang, B.; Xing, Y. Latest Progress on Maintenance Strategy of Complex System: From Condition-based Maintenance to Predictive Maintenance. Acta Autom. Sin. 2021, 47, 1–17. [Google Scholar]
- Pei, H.; Hu, C.; Si, X.S.; Zhang, Z.; Du, D. Remaining Life Prediction Information-based Maintenance Decision Model for Equipment Under Imperfect Maintenance. Acta Autom. Sin. 2018, 44, 719–729. [Google Scholar]
- Deep, A.; Zhou, S.; Veeramani, D. A data-driven recurrent event model for system degradation with imperfect maintenance actions. IISE Trans. 2022, 54, 271–285. [Google Scholar] [CrossRef]
- Xu, J.; Liang, Z.; Li, Y. Generalized condition-based maintenance optimization for multi-component systems considering stochastic dependency and imperfect maintenance. Reliab. Eng. Syst. Saf. 2021, 211, 107592. [Google Scholar] [CrossRef]
- Wang, X.; Gaudoin, O.; Doyen, L.; Bérenguer, C.; Xie, M. Modeling multivariate degradation processes with time-variant covariates and imperfect maintenance effects. Appl. Stoch. Model. Bus. Ind. 2020, 37, 592–611. [Google Scholar] [CrossRef]
- Sofiene, D.; Mohamed, N. An improved imperfect maintenance strategy for multiperiod randomly failing equipment with stochastic repair times. J. Qual. Maint. Eng. 2022, 28, 491–505. [Google Scholar]
- Zhang, N.; Yu, C.; Xie, F. The time-scaling t-ransformation technique for optimal control problems with time-varying time-delay switched systems. J. Oper. Res. Soc. China 2020, 8, 581–600. [Google Scholar] [CrossRef]
- Yang, Z.; Teng, W.; Duan, Z.; Zhang, J. Reducing forecast errors by logarithmic transformations for complex time series. In Proceedings of the 2012 2nd International Conference on Consumer Electronics, Communications and Networks (CECNet), Yichang, China, 21–23 April 2012; pp. 2761–2764. [Google Scholar]
- Pang, G.; Liu, J.; Liu, J.; Guo, Y.; Yian, X. Study on the decision considering imperfect maintenance of multiple components based on the exponential distribution. J. Phys. Conf. Ser. 2020, 1437, 012098. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, Y.; Cai, Z.; Wang, L.; Xiang, H. Optimal replacement strategy considering equipment remaining useful lifetime prediction information under the influence of uncertain failure threshold. J. Natl. Univ. Def. Technol. 2021, 43, 145–154. [Google Scholar]
- Wu, F.; Niknam, S.A.; Kobza, J.E. A cost effective degradation-based maintenance strategy under imperfect repair. Reliab. Eng. Syst. Saf. 2015, 144, 234–243. [Google Scholar] [CrossRef]
- Zhou, S.; Tang, Y.; Xu, A. A generalized Wiener process with dependent degradation rate and volatility and time-varying mean-to-variance ratio. Reliab. Eng. Syst. Saf. 2021, 216, 107895. [Google Scholar] [CrossRef]
- Zhang, C.; Qi, F.; Zhang, N.; Li, Y.; Huang, H. Maintenance policy optimization for multi-component systems considering dynamic importance of components. Reliab. Eng. Syst. Saf. 2022, 226, 108705. [Google Scholar] [CrossRef]
- Li, T.; Si, X.; Liu, X.; Pei, H. Data-model interactive remaining useful life prediction technologies for stochastic degrading devices with big data. Acta Autom. Sin. 2021, 48, 2119–2141. [Google Scholar]
- Wu, Y.; Yang, Z.; Wang, J.; Chen, X.; Hu, W. Optimizing opportunistic preventive maintenance strategy for multi-unit system of CNC lathe. J. Mech. Sci. Technol. 2022, 36, 145–155. [Google Scholar]
- Box, G.; Cox, D.R. An analysis of transformations. J. R. Stat. Soc. Ser. B Methodol. 1964, 78, 211–252. [Google Scholar] [CrossRef]
- Guo, C.; Wang, W.; Guo, B.; Si, X. A maintenance optimization model for mission-oriented systems based on Wiener degradation. Reliab. Eng. Syst. Saf. 2013, 111, 183–194. [Google Scholar] [CrossRef]
- Pang, Z.; Pei, H.; Li, T.; Hu, C.; Si, X. Remaining useful lifetime prognostic approach for stochastic degradation equipment considering imperfect maintenance activities. J. Mech. Eng. 2022, 58, 1–16. [Google Scholar]
- Si, X.; Wang, W.; Hu, C.; Hu, C.; Chen, M.; Zhou, D. A Wiener process based degradation model with a recursive filter algorithm for remaining useful life estimation. Mech. Syst. Signal Process. 2013, 35, 219–237. [Google Scholar] [CrossRef]


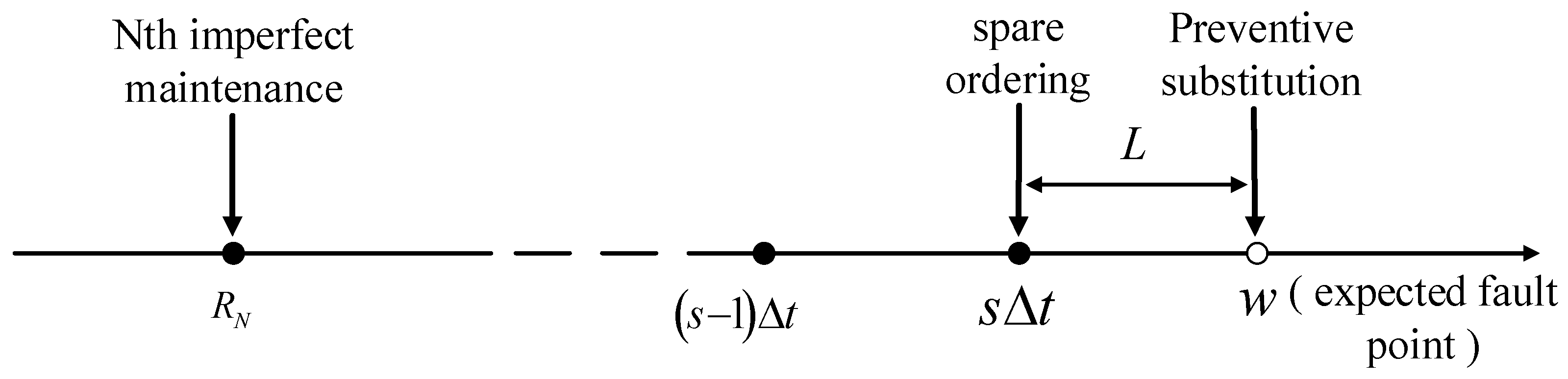
| Parameter | |||||||
| Cost (dollars) | 6000 | 3000 | 500 | 100 | 4000 | 5000 | 1000 |
| Parameter | ||||||
| Set value | 0.9 | 0.5 | 20 (h) | 10 | 0.9 | 10 |
| Parameter | ||||||
| Set value | 0.2 | 0.0001 | 0.001 | −0.3 | 2 | 5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, B.; Si, X.; Pei, H.; Zhang, J.; Li, H. Joint Optimization Strategy of Condition-Based Maintenance and Spare Parts Ordering for Nonlinear Degraded Equipment under Imperfect Maintenance. Machines 2022, 10, 1041. https://doi.org/10.3390/machines10111041
Yang B, Si X, Pei H, Zhang J, Li H. Joint Optimization Strategy of Condition-Based Maintenance and Spare Parts Ordering for Nonlinear Degraded Equipment under Imperfect Maintenance. Machines. 2022; 10(11):1041. https://doi.org/10.3390/machines10111041
Chicago/Turabian StyleYang, Baokui, Xiaosheng Si, Hong Pei, Jianxun Zhang, and Huiqing Li. 2022. "Joint Optimization Strategy of Condition-Based Maintenance and Spare Parts Ordering for Nonlinear Degraded Equipment under Imperfect Maintenance" Machines 10, no. 11: 1041. https://doi.org/10.3390/machines10111041
APA StyleYang, B., Si, X., Pei, H., Zhang, J., & Li, H. (2022). Joint Optimization Strategy of Condition-Based Maintenance and Spare Parts Ordering for Nonlinear Degraded Equipment under Imperfect Maintenance. Machines, 10(11), 1041. https://doi.org/10.3390/machines10111041






