Abstract
A three-dimensional vehicle-axle box bearing coupling model is established. The model can calculate the contact force in three directions and obtain the dynamic response of axle box bearing under the real vehicle running environment. The load distribution on the double row tapered roller bearing and the vehicle is analyzed, and the co-simulation is conducted by comprehensively considering the force transmission between vehicle and bearing. Taking into account the great impact of defects on the bearing, three different types of bearing defects are added into the model, respectively. The simulation results verify the effectiveness of the model. The model is also verified by using the rolling and vibrating test rig of single wheelset. It is concluded that the simulation results show good agreement with experimental results. The influence of track irregularity on the system motion state is studied by using axis trajectory and vibration RMS (Root Mean Square value). The results show that the influence of track irregularity and wheel flat scar on axle box bearing cannot be ignored. The RMS of acceleration will change greatly due to the existence of defects. Wheel flat scar will greatly interfere with the extraction of bearing defect, but it can be selected at high speed and low frequency to monitor the existence of wheel flat scar, and select low speed and high frequency to monitor the existence of bearing defect. The research results are helpful to the detection of wheel flat scar and axle box bearing defect.
1. Introduction
Axle box bearing is a key component of a high-speed train bogie. It bears high-frequency alternating loads during operation, including radial force, axial force and continuous impact vibration. When the vehicle is running, the performance of axle box bearing is an important factor affecting the safe operation of trains; the failure of axle box bearing occurs on multiple types of EMUs, fatigue spalling of inner ring, outer ring and rollers are major defect forms [1]. These failures will cause economic losses to a certain extent. However, up to now, we have not fully mastered the key research and development technology of high-speed train axle box bearings [2]. Therefore, it is of great engineering significance and economic value to conduct in-depth research on axle box bearings.
Analysis on the bearing dynamic model experiences a long period. Many experts and scholars have done a lot of work on traditional bearings and have obtained many achievements. Jones [3] first proposed the bearing quasi-static model, which can define the load and position of each rolling element, as well as the displacement of inner ring relative to its outer ring, this innovation work laid the foundation of bearing dynamics. After that, Walters [4] established a dynamic model considering the rolling element for the first time and analyzed the vibration characteristics of the bearing when it moved at high speed. Using this model, the displacement and speed of the rolling element at any time can be calculated. Harris [5] added inertia force and moment on the basis of Walters’s model and considered the slip of inner and outer raceways, which made the dynamic research of rolling bearings more accurate. Gupta [6,7,8] studied the non-equilibrium dynamics of rolling bearing cage and obtained the motion state of the cage and rolling elements under the conditions of static load, non-equilibrium load and radial load, respectively. Since then, many scholars have studied the dynamic performance of rolling bearings in various aspects. Kogan et al. [9] proposed a three-dimensional bearing dynamic model that can simulate various bearing faults. By using this model, the bearing with axial deformation of the outer ring was simulated and tested, and the effectiveness of the model was verified through experiments. Tong and Hong [10] established a 5-DOF tapered roller bearing model and studied its characteristics under combined load and high speed. It was concluded that the radial displacement and moment load are almost linear, while the axial displacement and moment load are nonlinear and gradually decrease with the increase of load. Shi and Liu [11] established an improved dynamic equation of cylindrical roller bearing, considered the interaction of various components of the bearing, and evaluated the influence of radial load, axle speed and clearance on bearing vibration, respectively. Yang et al. [12] established a mechanical analysis model of the double row tapered roller bearing, studied its resistance torque, contact load and fatigue life under different loads. It was concluded that external radial, thrust loads and angular misalignment often lead to a significant reduction in bearing fatigue life, while the speed tends to increase it. Liu [13] established a axle box bearing model, discussed the distribution law of internal load when the bearing bore radial and axial loads at the same time. It can be found that with the increase of the radial load, the contact load of the double row rollers will also increase, while when the axial load increased, the contact load of one row of rollers increased and that of the other row decreased.
When the bearing fails, some methods are needed to extract the fault. In the process of fault diagnosis, the bearing vibration data is collected and analyzed to achieve effective and preventive maintenance of the bearing at the same time. Many scholars have carried out a lot of research in this direction. Eren et al. [14] proposed a real-time fault diagnosis method of induction bearing based on machine learning. They adopted an adaptive 1D Convolutional Neural Network classifier, which can automatically learn the best features from the original bearing vibration data. Its structure was simple and compact with high accuracy. The validity and feasibility of this method were verified by experimental data. Entezami et al. [15] introduced several signal processing technologies in detail, and summarized the latest development of axle box bearing condition monitoring system. The authors though that the number of monitoring systems applied to axle box bearing was relatively limited, and their technology and performance still had a large space for development. Amini et al. [16] proposed a customized onboard AE condition monitoring system to monitor defective railway bearings. Through a large number of experiments and field data, it has been proved that acoustic emission signal envelope analysis can effectively monitor bearing fault in the real world conditions. Papaeliasa et al. [17] introduced a novel condition monitoring system based on high-frequency acoustic emission and vibration analysis. Its method was simple and cost less and its effectiveness was proved by experimental data under actual conditions. Fan et al. [18] proposed a statistical condition monitoring and fault diagnosis method based on tunable Q-factor wavelet transform, constructed the Shewhart control charts on multiscale wavelet coefficients and proved the effectiveness and superiority of the method. Yi et al. [19] used three EEMD-based steady-state indexes to characterize the stable state of the bearing, which proved that the proposed state detection and fault diagnosis methods can effectively identify different bearing faults.
The above research has proposed many effective methods. However, they only focus on the condition monitoring and diagnosis of bearings, but cannot explain the cause of bearing failure from the mechanism, as well as the process of bearing performance degradation and the mechanism of failure degradation. These problems can be studied from the perspective of dynamic analysis.
Therefore, in order to study the failure mechanism of bearing, many scholars have used dynamic models to conduct in-depth analysis of high-speed train axle box bearing. Yang et al. [20] established a rotor-bearing system model with local defects in the raceway, and analyzed the influence of resonance characteristics and rotor eccentric excitation on the motion state of the system. Tu et al. [21] established the explicit dynamic finite element model of the bearing, and studied the contact characteristics between the rolling element and the fault, as well as the fault characteristics in the bearing vibration signal. Luo et al. [22] established a 4-DOF rolling bearing model with inner and outer rings composite fault, and studied the vibration response characteristics of the defect-ball-defect model. Liu et al. [23] respectively added outer ring fault, inner ring fault and roller fault to the bearing rotor system of high-speed train, obtained the vibration response of the system under variable speed conditions. It was concluded that the vibration acceleration amplitude of the bearing outer ring was positively correlated with the axle speed of the bearings. Du et al. [24] established a 3-DOF dynamic model of double tapered roller axle box bearing of high-speed train, and analyzed the change law of contact stress at the defect position of each element under different fault degrees. Liu [25] established a dynamic model of the rotor-bearing pedestal system, took into account the excitation of the contact area caused by the fault and the complex contour of the outer raceway etc. The results showed that the additional excitation zone of the inner raceway was larger than that of the outer raceway, and it will decrease with the increase of the roller load. Patel and Upadhyay [26] presented a nonlinear dynamic model of a cylindrical roller bearing-rotor system with 9 degrees of freedom and established a combined defect model. The nonlinear dynamic analysis of the model can predict the behavior of the bearing-rotor system. Singh et al. [27] established a dynamic model of rolling bearing with outer raceway defects. The finite element software package, LS-DYNA, was used for numerical solution, and the dynamic contact force between the rolling element and the raceway was analyzed in depth. Petersen et al. [28] studied the defective double row bearing model and proposed a method to calculate the radial load distribution under different stiffness. It was helpful to understand the variable stiffness excitation in defective bearings, and can be used in the research of other nonlinear defective bearing models. Sawalhi and Randall [29] studied the acceleration signal generated when the rolling body entered and exited the peeling defect. Two signal enhancement methods were analyzed, and the entrance and exit of the defect area were simulated.
It can be found that the above research only separates the bearing model for analysis and discussion, ignoring its coupling with the carbody, bogie, wheelset and other systems, which makes the research results deviate from the actual situation to a certain extent. To solve this problem, some scholars have proposed a series of more complete bearing coupling systems on the basis of bearing model research. Wang et al. [30] established a vehicle bearing coupling model, studied the thermal characteristics of the bearing when the track is uneven. In addition, the key influencing factors of the bearing operating temperature were analyzed. Wang et al. [31] established a coupling dynamic model of axle box bearing and vehicle-track system, considered the dynamic performance of axle box bearing under complex dynamic excitation. Liu et al. [32] established the locomotive-track space coupling dynamics model in which the dynamic effect of traction power transmission was considered. The dynamic characteristics of motor bearings at the driving end and non driving end were studied, the results showed that the loaded region of the motor bearing at the driving end is larger than that at the non-driving end. Ma et al. [33] established a 17-DOF vertical dynamic model, including carbody, bogie, axle box bearing and wheelset, discussed the changes of vehicle dynamic performance and vibration characteristics during the early fault evolution of axle box bearing. Some scholars have also studied the axle box bearing fault model based on the coupling model. Niu [34] established a vehicle dynamics simulation model, analyzed the vibration characteristics of the axle box under different bearing defects. In addition, the influence of different excitation types on the vibration characteristics of the bearing was analyzed. Liu et al. [35] established a dynamic calculation model of vehicle with early defects in axle box bearing and analyzed the impact of bearing defects on the vertical vibration characteristics of vehicle. Liu and Du [36] established a vehicle model considering bearings, analyzed the impact of bearing defects on the dynamic performance of high-speed train. Wang et al. [37] established a longitudinal and vertical dynamic model of railway vehicle considering the inner and outer raceway faults of axle box bearing. The change of bearing fault index with the degree of damage was calculated. It can be found that the longitudinal vibration characteristics were suitable for inner ring fault identification, and the vertical vibration characteristics were suitable for outer ring fault identification. Lu et al. [38] established a coupling model of railway vehicle and axle box bearing with defects. The theoretical rolling trajectory of roller passing through the defect was analyzed and deduced. It was concluded that the location of defect points on the outer raceway affected the intensity of defect impact.
As the vehicle affected by various external excitation factors, such as turnout, track joint, track irregularity and wheel wear; some scholars have discussed the vehicle dynamic response under external excitation. Cheli and Corradi [39] studied the influence of track irregularity on vehicle vibration, and the results showed that the vibration caused by track irregularity had a great impact on vehicle comfort. Based on the time-varying nonlinear contact load of axle box bearing, Li et al. [40] established a vehicle-track space coupling dynamic model to study the vibration characteristics of the vehicle under the track irregularity. Liu and Zhai [41] studied the wheel rail interaction caused by polygonal wheel at high speed, it was shown that the vertical wheel rail contact force would fluctuate greatly under the polygonal wheel. Wu et al. [42] calculated the influence of wheel polygon wear order on wheel rail force and analyzed the influence of wear parameters on vibration response of vehicle components. Yang et al. [43] analyzed the measured vibration acceleration signal of the gearbox line; the results showed that the wheel rail excitation frequency may cause resonance with the gearbox structure. Liu et al. [44] established an elastic vehicle-track model, it can be found that the flat scar excitation had a great impact on the vertical vibration of the axle box. Chudzikiewicz et al. [45] put forward new indexes for evaluating railway track quality and carried out a field test and an evaluation of the results through the Rail Vehicle’s and Rail Track Monitoring System. The results showed that the proposed method can effectively monitor the track state. Bogacz and Frischmuth [46] studied the rolling motion of a polygonized railway wheel on the rail, analyzed the variation of contact point velocity under wheel polygon. The authors studied the contact point and vertical acceleration trajectories of rigid and viscoelastic models, respectively, and the results showed that the latter description was more accurate. Bogacz and Kurnik [47] established a wheel-tire mechanical model to study the motion stability of railway wheel and evaluated the influence of the beam curvature and residual stress on the phase velocity and its critical value.
Axle box bearing are also affected by external excitation. Wang et al. [48] studied the influence of wheel polygon wear and nonlinear wheel rail force on the contact force between rollers and raceway; the results showed that the influence of high-order wheel polygon wear on the force was more significant than that of low-order wheel polygon wear. Liu et al. [49] analyzed the dynamic response and slip phenomenon of motor bearing under irregularities; the results showed that locomotive vibration caused by track irregularity and gear meshing will lead to alternating loads, result in high dynamic contact and friction between rollers and raceways. Zha et al. [50] studied the impact of flat scar impact on the bearing outer ring force; it was concluded that the impact load in the loaded zone was larger than that in the unloaded zone, which was distributed symmetrically. The closer to the symmetry axis, the greater the impact load on the raceway.
However, in the above study, the coupling relationship between vehicle and axle box bearing does not consider the spatial transmission characteristics of force, the model is mostly solved by a lot of differential equation, which simplifies the internal force of the vehicle and has low calculation efficiency. At the same time, most of the coupling models focus on the vehicle, and there is less research on the axle box bearing itself. Furthermore, the research on the influence of external excitation factors on axle box bearing is very limited, especially in the analysis of vibration characteristics when the bearing with defects. To address these problems, an improved vehicle-bearing coupling modeling method is proposed in this paper. By combining Universal Mechanism (UM) with MATLAB/Simulink, the coupling between the vehicle and the bearing is realized, and the internal forces of the vehicle and wheel rail contact are fully considered. This model can realize fast calculation and conveniently apply external excitation. In addition, the bearing outer ring fault, inner ring fault and roller fault are added to the coupling model, respectively. The model is simulated and analyzed under the actual running conditions, and verified by the rolling and vibrating test rig of single wheelset. Since the vibration of the axle box bearing is closely related to the movement of the vehicle and the rail, makes use of the advantage of the coupling model, the paper studies the dynamic responses of the axle box bearing under the impact of track irregularity and wheel flat scar, analyzes the dynamic performance of the bearing with defects and summarizes some bearing vibration laws. The vibration mechanism of axle box bearing under external excitation is revealed in time and frequency domain so as to provide some reference for the research of fault diagnosis of axle box bearing under real vehicle running environment.
2. Establishment of Vehicle-Bearing Coupling Model
2.1. High-Speed EMU Model
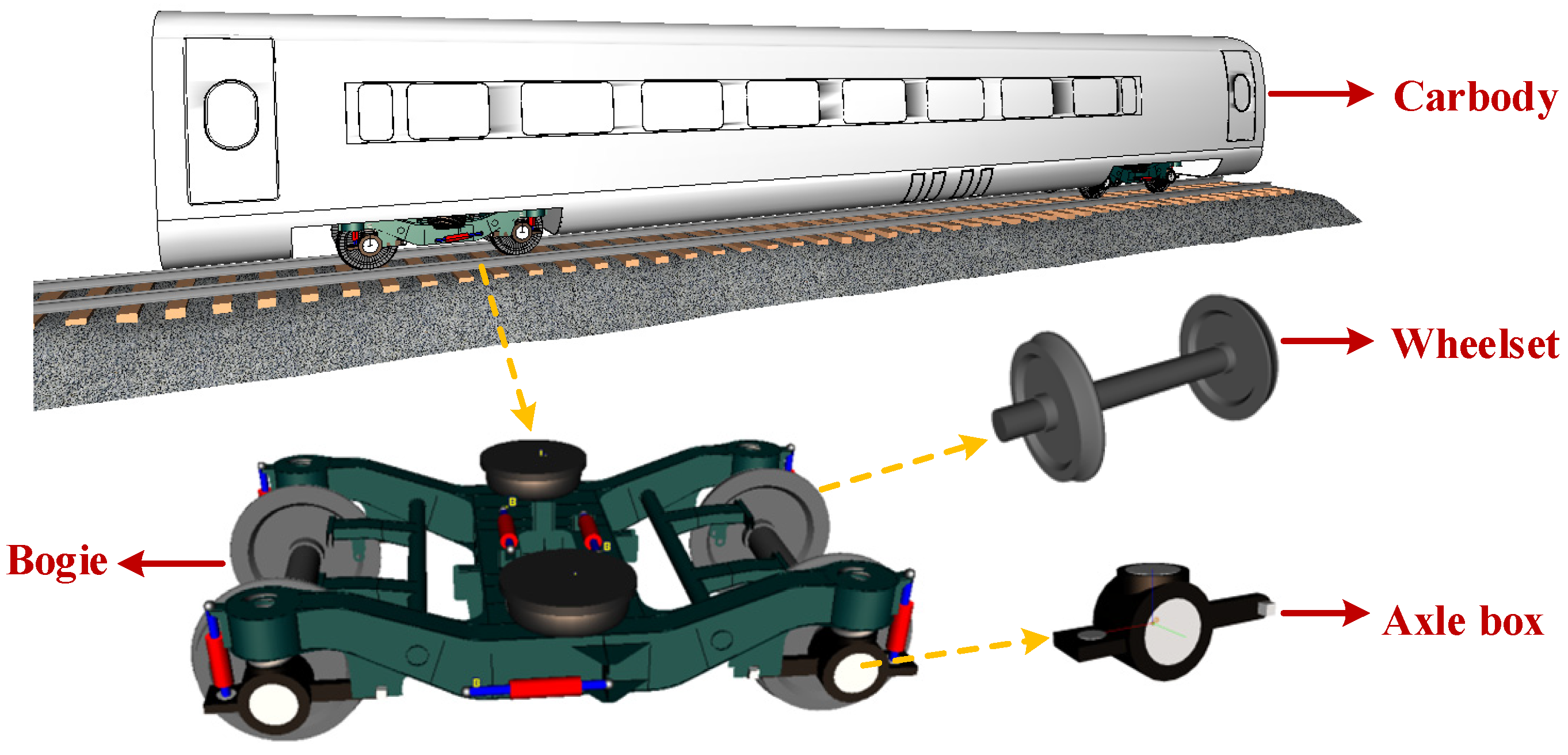
In the paper a vehicle model of a high-speed EMU is established through the multi-body dynamics simulation software, Universal Mechanism (UM), as shown in Figure 1. The model includes 1 carbody, 2 bogies, 4 wheelsets and 8 axle boxes. The carbody, bogie and wheelset have 6 degrees of freedom, respectively, and the axle box has 3 degrees of freedom (translation in X, Y and Z directions). In the process of modeling, all structural components are regarded as rigid bodies without considering their elastic deformation.
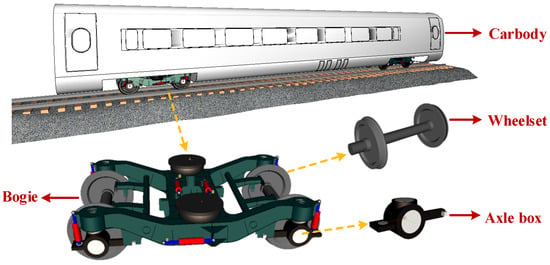
Figure 1.
Dynamic model of the high-speed train.
In the vehicle model, the primary suspension includes 4 axle box positioning devices, 4 coil springs and 4 vertical dampers etc. The secondary suspension includes 2 air springs, 4 yaw dampers, lateral stops, traction rods, and anti-rolling torsion bars, etc.
2.2. Axle Box Bearing Model
In this paper, the dynamic model of double row tapered roller bearing is established through MATLAB/Simulink in which the displacement of inner ring, outer ring and rollers in X, Y and Z directions are considered. For the convenience of research, the modeling process simplifies the whole bearing motion system as follows:
- (1)
- Regardless of the stiffness and damping of elastohydrodynamic lubrication, the nonlinear factors in the system include the nonlinear contact force between the roller and the outer raceway, the roller and the inner raceway, the roller and inner ring flange, and the radial clearance between rollers and the raceways;
- (2)
- The outer ring is fixed, the inner ring and the wheel axle rotate around the Z axis synchronously. At the same time, without considering slipping or creeping, the motion of rollers is supposed as pure rolling.
2.2.1. Force Balance of Tapered Roller Bearing
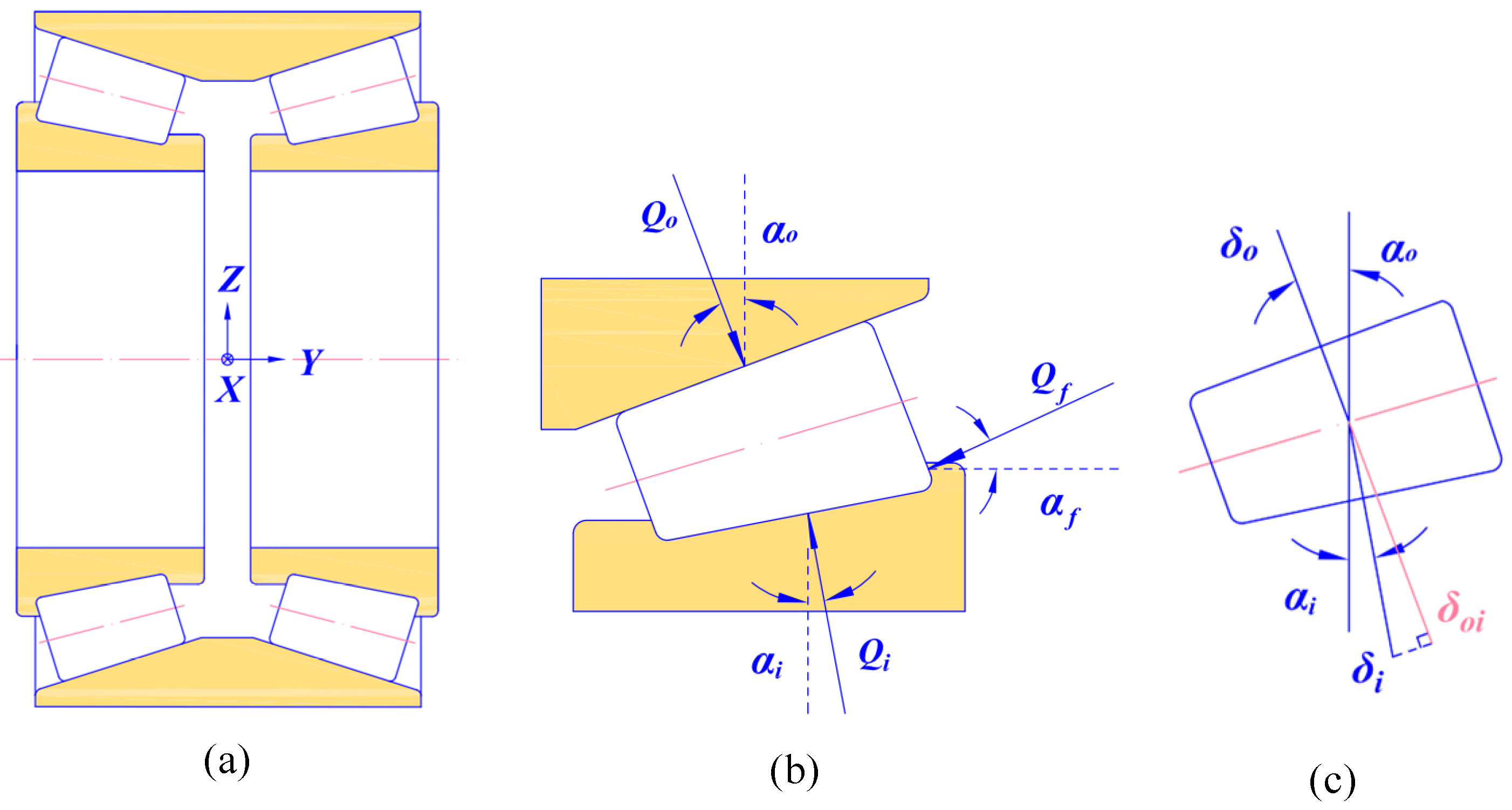
The tapered roller bearing, composed of outer ring, inner ring, rolling elements and cage, has a complex behavior. Its raceway is conical and has strong bearing capacity, which can bear the combined radial and axial load. The basic structure of double row tapered roller bearings is shown in Figure 2a. Take out a roller for analysis, as shown in Figure 2b. Qi represents the contact force between the roller and inner raceway, Qo represents the contact force between the roller and outer raceway, Qf represents the contact force between the roller and the inner ring flange, αi, αo and αf are their contact angles, respectively. When the roller is in equilibrium, its forces satisfy the following balance equation:
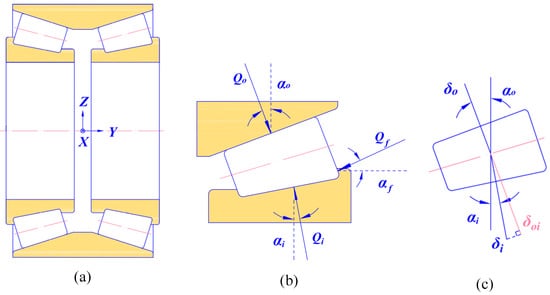
Figure 2.
Schematic diagram of double row tapered roller bearing: (a) bearing structure; (b) force balance diagram of single roller; (c) displacement projection relation.
The contact load Qo of the outer raceway is used as the reference variable, it can be obtained from Equation (1) that:
where ci and cf can be expressed as:
From the above derivation, the relationship between the three contact forces is obtained. If Qo is calculated, Qi and Qf can be solved by using the balance Equation (2).
2.2.2. Relationship between Force and Displacement
The contact between the tapered roller and the raceway is linear contact. Based on the Hertz contact theory, Palmgren [51] gave an empirical formula for calculating the elastic approach:
where Q represents the roller force and l represents the roller length. E and v represent the elastic modulus and Poisson’s ratio, respectively. For steel bearings, their values can be taken as:
So Equation (4) can be derived as:
The deformation of the roller in contact with the inner and outer raceways can be obtained by:
Due to the different contact angles of the inner and outer raceways, the total contact deformation of the roller cannot be obtained by directly adding the deformation of the two raceways. Take the contact deformation of the outer raceway as a reference, and project the contact deformation of the inner raceway to the normal direction of the outer raceway, then the total contact displacement of the roller in the normal direction can be obtained, as shown in Figure 2c. It can be deduced as:
Substituting Equation (6) into Equation (7) to get:
The expression of contact force between roller and outer raceway can be obtained:
where Kne represents the total stiffness coefficient at the contact of the outer raceway:
2.2.3. Bearing Load Distribution Calculation
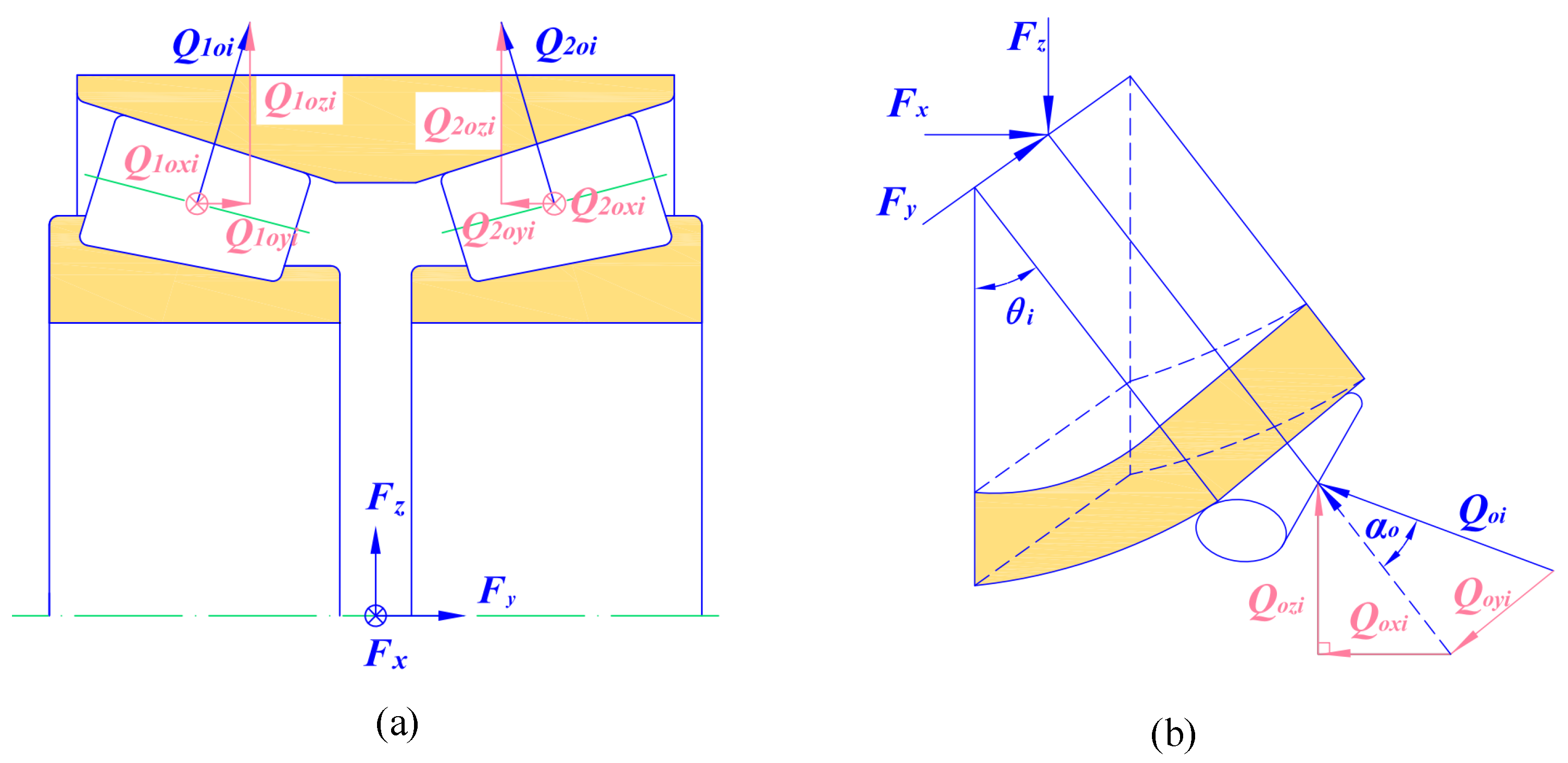
When the bearing is loaded in X, Y and Z directions, the inner ring will displace relative to the outer ring, which are δx, δy and δz, respectively. From the stress analysis of tapered roller bearing, it can be seen that there is only one contact load Qo between the roller and the outer raceway. Therefore, the roller-inner ring system can be studied as a whole part, as shown in Figure 3. In this way, the contact force between each roller and the outer raceway Qoi are decomposed in the three directions of X, Y and Z, and then superimposed to balance with the external load.
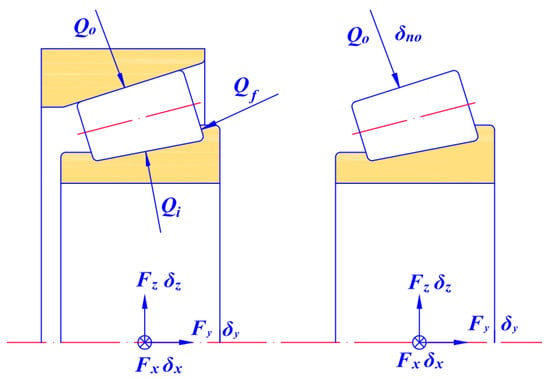
Figure 3.
Contact diagram of single row bearing.
Suppose at time t, the position angle of the roller i is θi, it can be obtained by:
where ωc is the rotation angular speed of the cage, and N is the number of single row rollers. It can be expressed as:
where n and ωs is the rotational angular speed of the wheel axle, the units are r/min and rad/s, respectively. In order to be consistent with the vehicle coordinate system, take X and Z directions as the radial direction of the bearing, and the Y direction as the axial direction. As the rotation of the axle and the effect of the radial clearance, the radial deformation of each roller is different. Set the radial clearance at the roller i as hi, when the bearing bears radial load, the radial contact deformation produced by the roller i can be expressed as:
When the bearing bears axial load, the axial displacement components of all rollers are the same. At this time, the contact deformation of each roller is δy.
The contact deformation in three directions is projected to the normal direction of the outer raceway, respectively, and the total contact deformation between the roller i and the outer raceway can be obtained as follows:
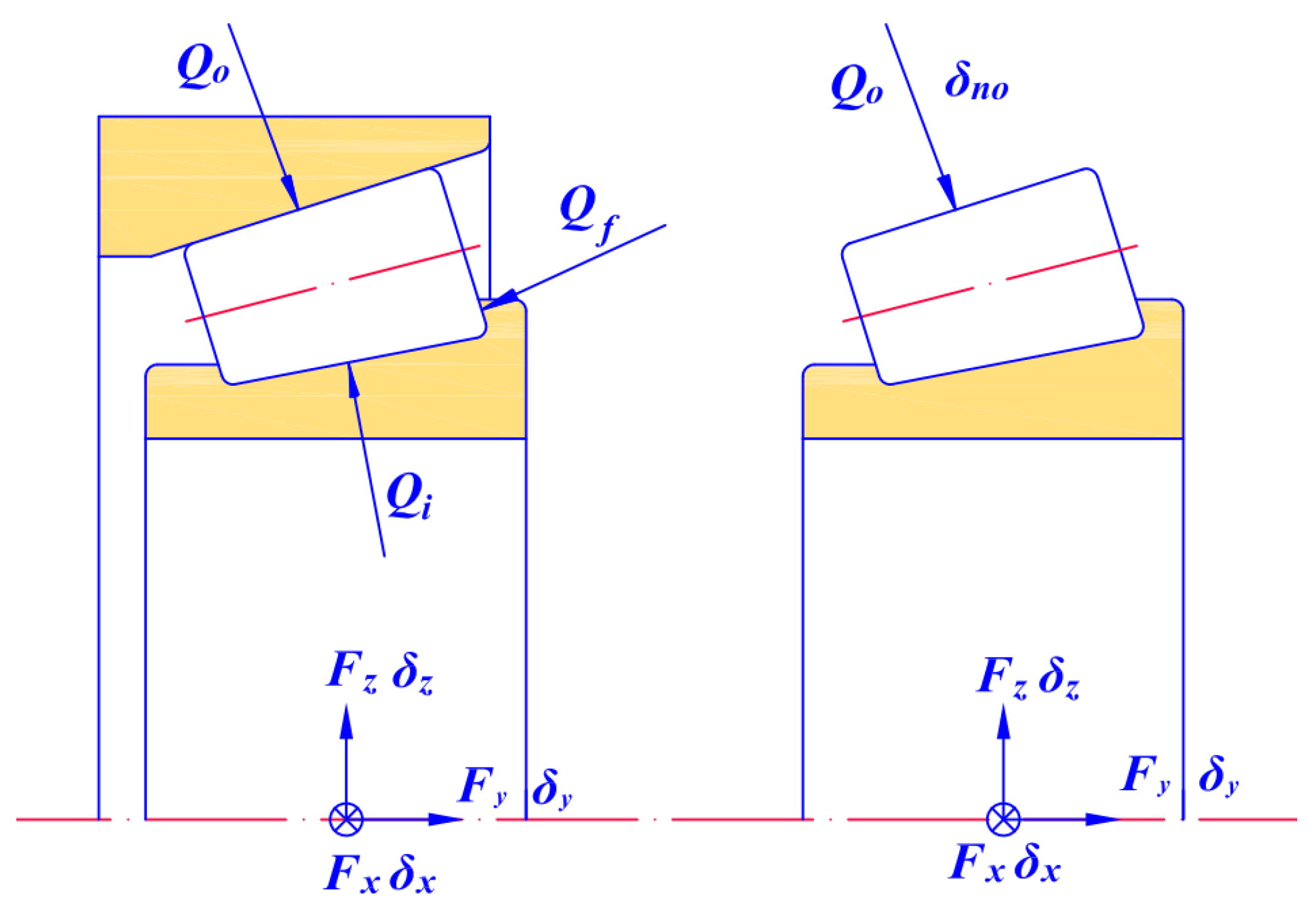
The double row tapered roller bearing located in the axle box of the train adopts the back-to-back installation method. It is defined that in each row of bearings, the displacement that increases the roller load is positive, and the displacement that decreases the roller load is negative. The absolute value of displacement and corresponding load of bearings in the second row is the same as that in the first row, but the direction is different. The force on the outer raceway is shown in Figure 4a; for two rows of rollers, the radial displacement is the same as the direction of the load, and the axial displacement is opposite to that. The balance equation of double row bearing can be obtained by superimposing the corresponding loads of two rows of rollers.
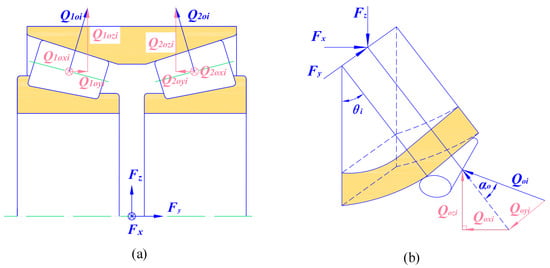
Figure 4.
Contact force analysis of double row tapered roller bearing: (a) contact force between rollers and outer raceway; (b) decomposition of contact force.
The contact deformation of each row of rollers along the normal direction can be obtained by:
2.2.4. Bearing Balance Equation
According to the force of tapered roller bearing and the load displacement relationship between rollers and raceways, the overall balance equation of bearing can be established. Taking the force analysis of the outer raceway as an example, under the external load in the X, Y and Z directions, the roller will produce contact deformation. From the above analysis of the relationship between force and displacement, it can be seen that the contact force between the roller and the outer raceway is expressed as:
Then, the contact force between the roller and the inner raceway Qii and the contact force between the roller and the inner ring flange Qfi can be obtained through Equation (2).
As shown in Figure 4b, form the balance equation of force, the components of Qoi in the X, Y and Z directions can be expressed as:
The balance equation of the bearing can be obtained by balancing the internal contact force of the bearing with the external force. They are nonlinear equations with three relative displacements as variables, and the contact load of each roller can be obtained. Then, the total contact force between the roller and the outer raceway in the X, Y and Z directions can be expressed as:
Similarly, the total contact loads of the roller and the inner race raceway Fi, the roller and the inner ring flange Ff, and their components in the X, Y and Z directions can be obtained.
2.2.5. Bearing Defect Model
As the bearing rotates at high speed, when the bearing slips or overloads, it may cause wear on the surface. Once the wear intensifies, it will gradually evolve into defects on the inner raceway, outer raceway and rollers surface, such as peeling, pitting or cracking, which will cause hidden dangers to the operation safety of the bearing.
The excitation generated by the roller at the defect can be divided into two cases, which are related to the size of the defect. One is that the width of the defect is smaller than the diameter of the roller, and the roller only contacts the edge of the defect. Take the outer ring defect as an example, as shown in Figure 5a,b, in this case, the bearing will generate impact excitation. The other is that the width of the defect is larger than the diameter of the roller, at this time, the roller will not only contact the edge of the defect, but also sink into the bottom of the defect to contact it, as shown in Figure 5c. In this case, the bearing will not only generate impact excitation but also harmonic excitation.
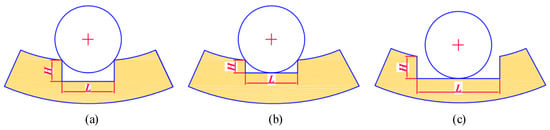
Figure 5.
Bearing defect type: (a) defect width less than the roller diameter without contact the bottom; (b) defect width less than the roller diameter and contact the bottom; (c) the defect width greater than the roller diameter.
In fact, when the early defect of rolling bearing occurs, its area is generally small, therefore, this paper only studies the case that the defect width is smaller than the roller diameter.
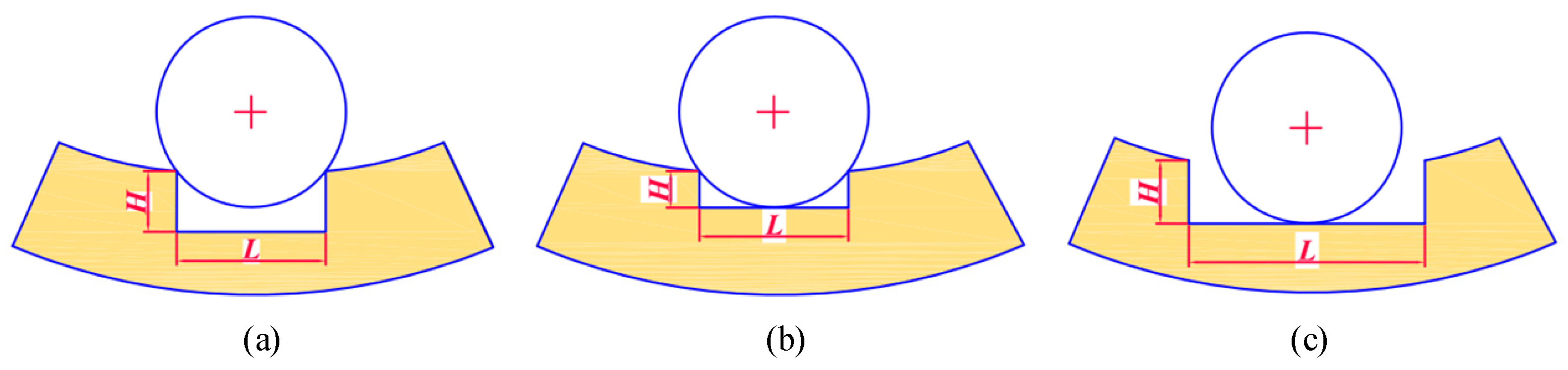
When the roller rolls over the defect, a certain amount of deformation H0 will be released, which will change the contact deformation between the roller and the raceway. At this time, Equation (14) can be transformed into:
where λ is a switching value.
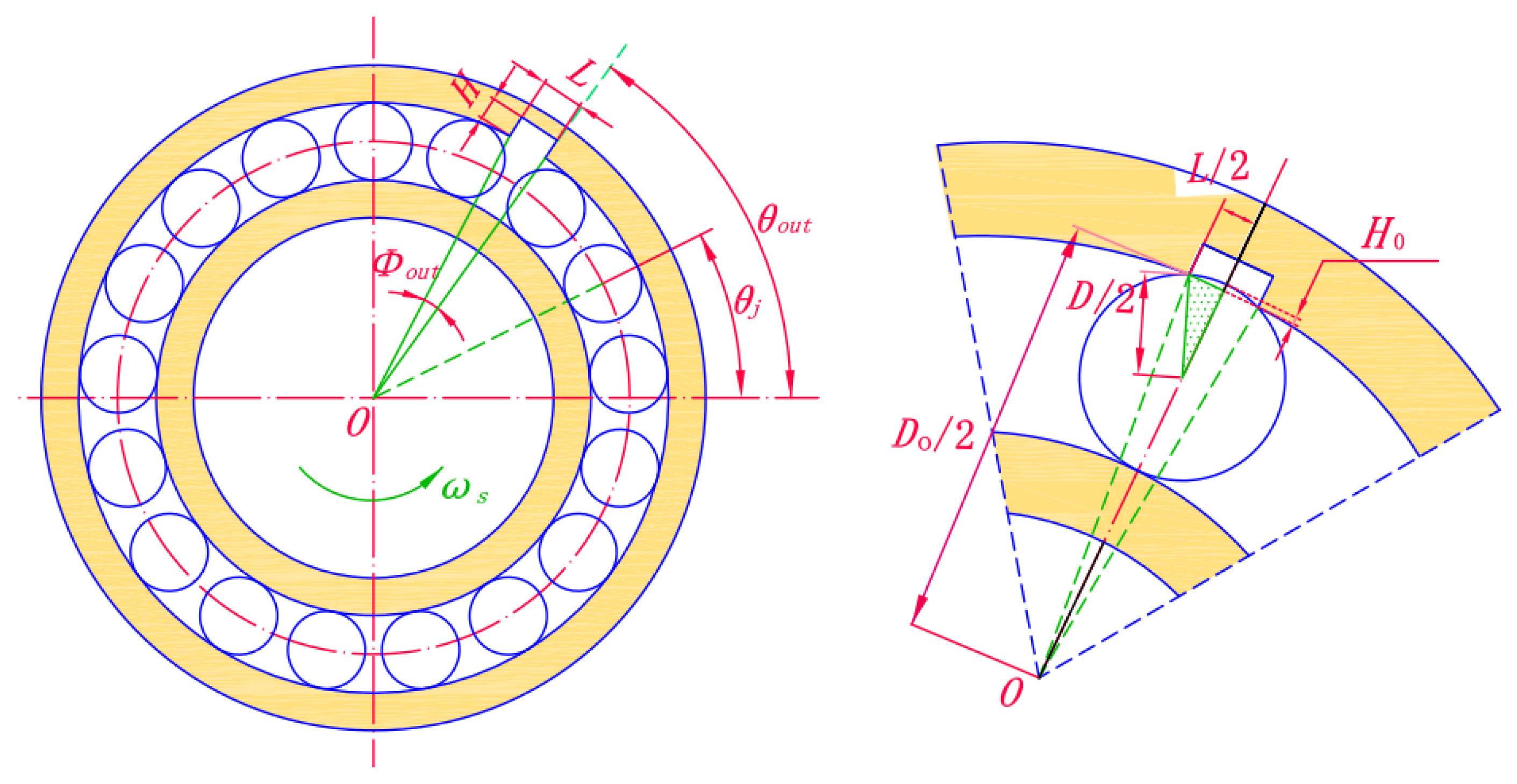
When there is a defect on the outer raceway, as shown in Figure 6, the maximum value of H0 can be expressed as:
where D is the roller diameter. The deformation H0 can be calculated by:
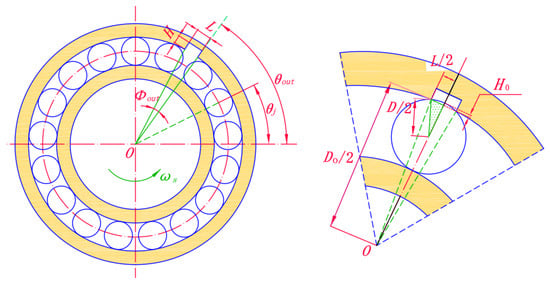
Figure 6.
Schematic diagram of outer raceway defect.
The parameter λ can be expressed as:
where Φout is the defect angle and Dout is the diameter of the outer ring.
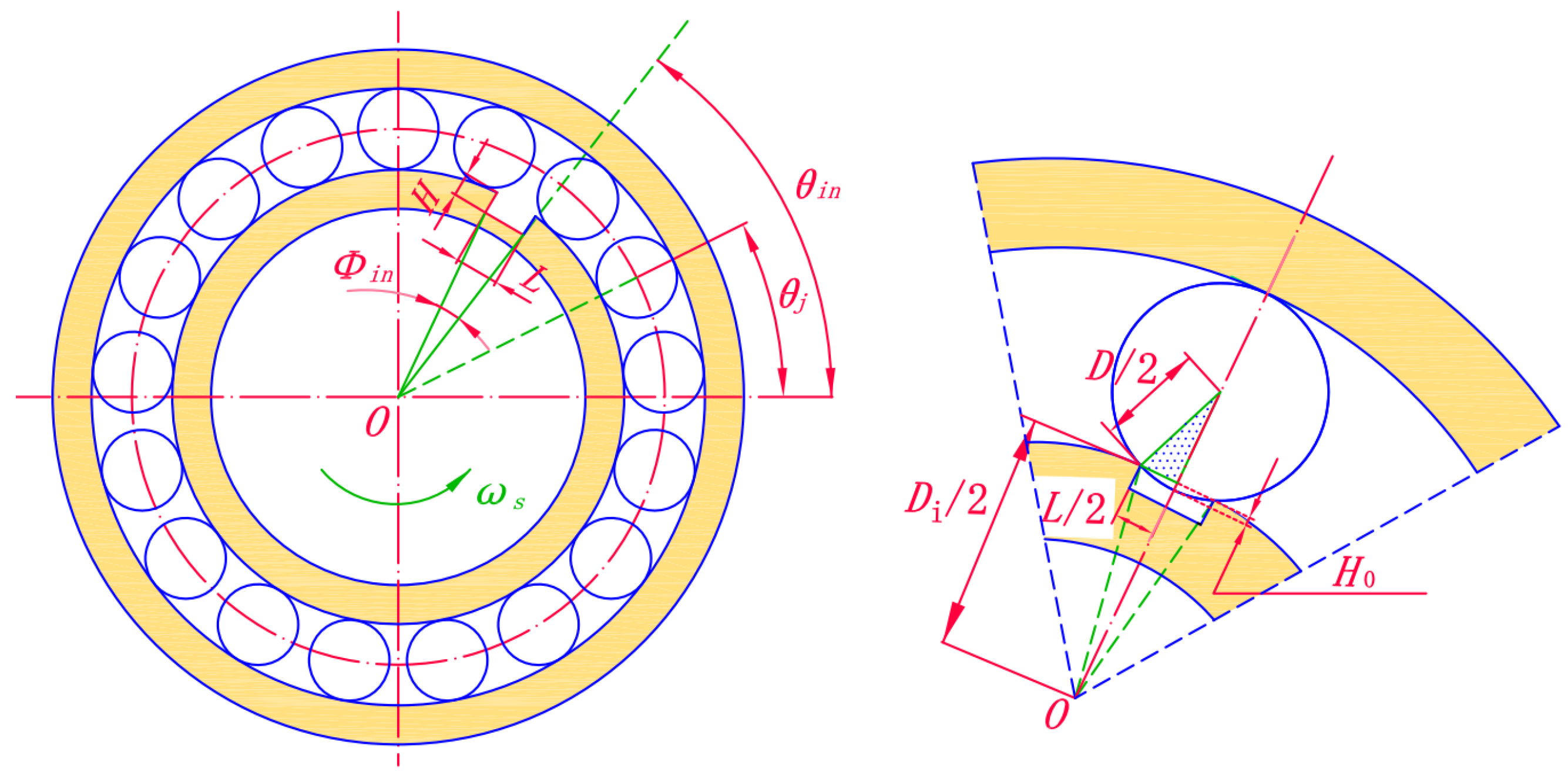
When there is a defect on the inner raceway, as shown in Figure 7, the position of the defect changes at all times since the inner ring rotates with the axle. The maximum value of H0 can be expressed as:
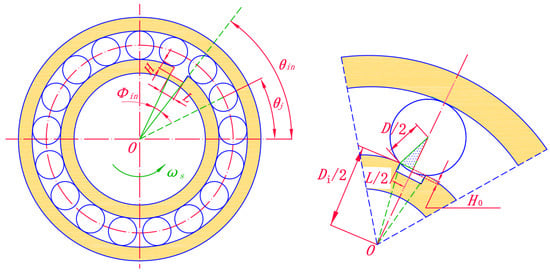
Figure 7.
Schematic diagram of inner raceway defect.
At this time, H0 can be calculated by:
The parameter λ can be expressed as:
where Φin is the defect angle and Din is the diameter of the inner ring.
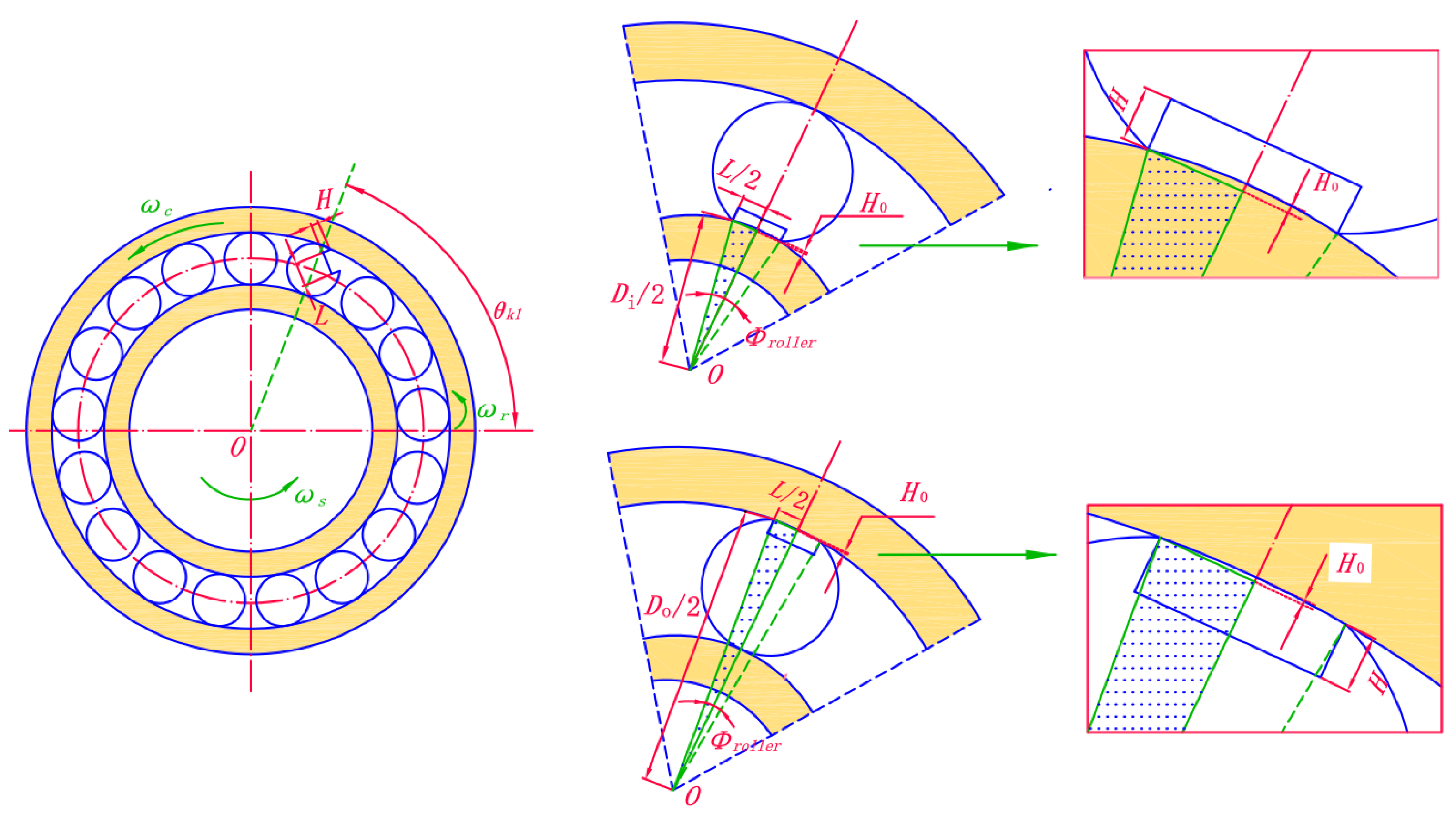
When there is a defect on the roller, the impact will occur both when the defect position contacts the outer or the inner raceway; the contact condition is shown in Figure 8. Assuming that the roller k is defective, so at time t, the roller rotates with the cage and its position can be expressed as:
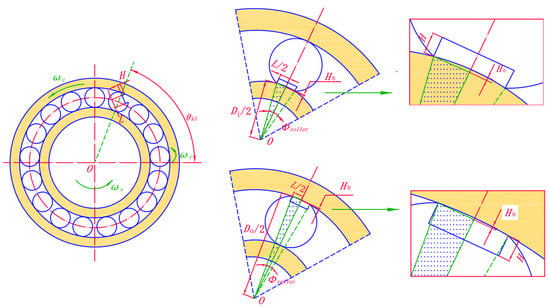
Figure 8.
Schematic diagram of roller defect.
In addition, the defect will also rotate with the roller itself, and the location of the defect can be expressed as:
where ωr is the rotation speed of the roller, it can be calculated as follows:
When the defect of the roller contacts with the inner raceway, the maximum deformation released by the inner ring can be obtained by:
When the defect of the roller contacts with the outer raceway, the maximum deformation released by the outer ring can be obtained by:
At this time, the deformation H0 can be calculated by:
The parameter λ can be expressed as:
where Φroller is the defect angle.
2.3. Vehicle-Bearing Coupling Model
The movement and internal action of each component of axle box bearing are very complex. In this paper, when the bearing model is coupled with the vehicle model, the bearing model is simplified by considering the contact between the roller and the inner raceway, the contact between the roller and the outer raceway, and the contact between the roller and the inner ring flange. As the contact between the bearing inner ring and the axle is an interference fit, so the two are considered as a whole for research. The contact between the bearing outer ring and the axle box is also an interference fit, and the two are also studied as a whole part.
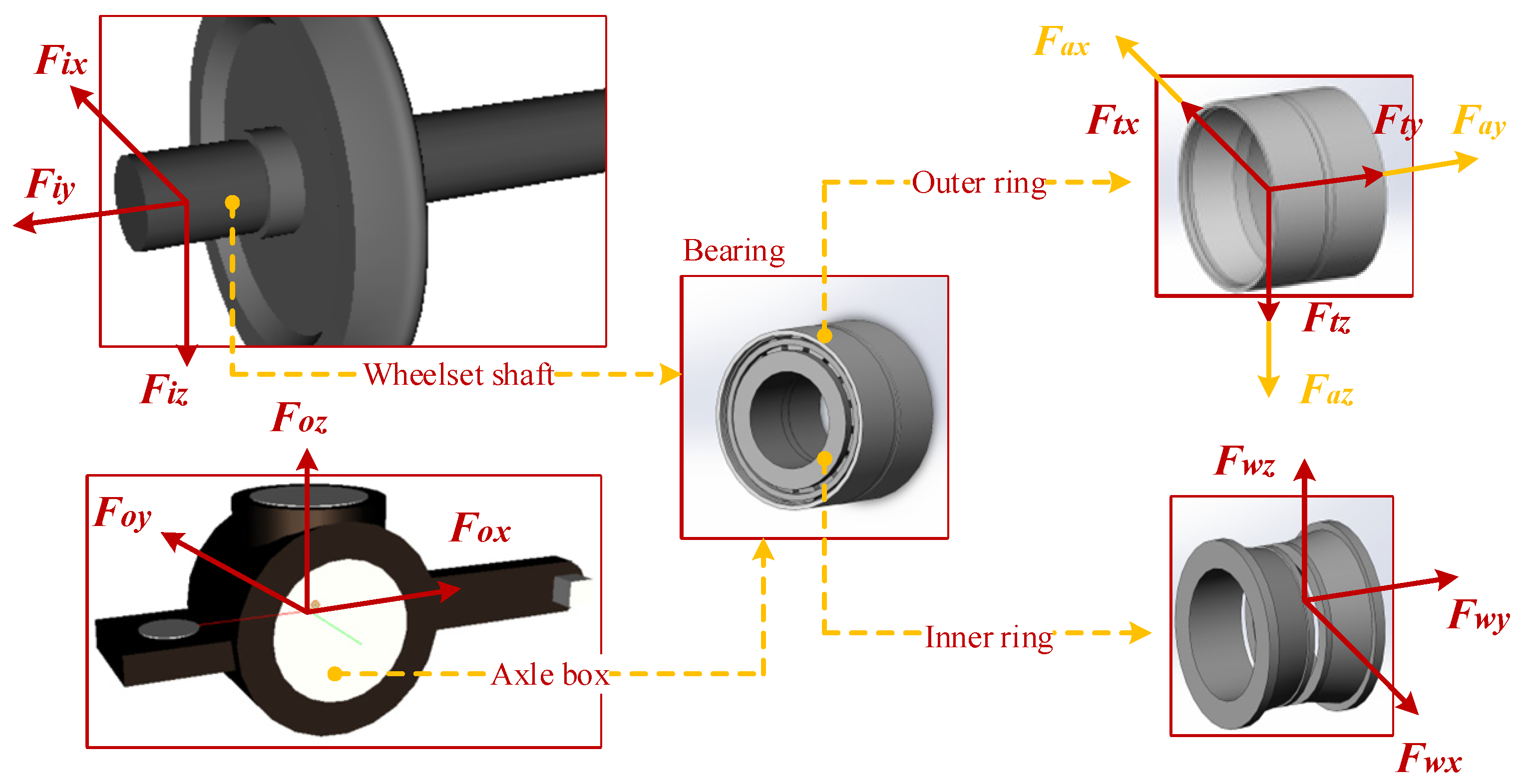
The inner ring and outer ring of the bearing are coupled with the vehicle through the interaction of forces. The bogie frame is connected to the axle box through the primary suspension and the node point of rotaty arm. On the one hand, the force generated by the primary suspension (Ft) and the node point of rotaty arm (Fa), respectively, exert on the outer ring of the bearing through the axle box. The wheel-rail force (Fw) is generated by the contact between the wheelset and track exerts on the inner ring of the bearing through the axle. On the other hand, the contact force generated by the roller-outer raceway (Fo) exerts on the axle box of the vehicle model through the outer ring. The contact force is generated by the roller-inner raceway (Fi) and the contact force generated by the roller-inner ring flange (Ff) exert on the wheelset of the vehicle model through the inner ring. In this way, the coupling of bearing model and vehicle model is realized through the transmission of forces, which is shown in Figure 9.
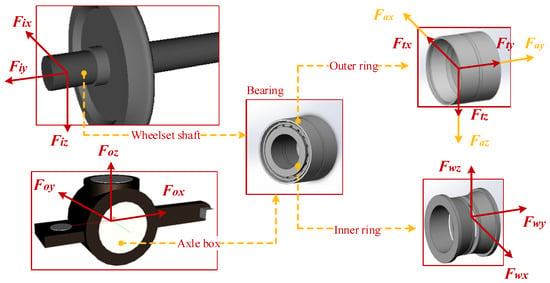
Figure 9.
Coupling relationship between vehicle and bearing.
The corresponding relationship between the vehicle and the bearing coordinate system can be expressed as: the longitudinal direction of the vehicle corresponds to the X direction of the bearing; the lateral direction of the vehicle corresponds to the Y direction of the bearing; and the vertical direction of the vehicle corresponds to the Z direction of the bearing.
Based on the above analysis, the force exerted by the vehicle on the outer ring of the bearing is the force of the primary suspension and the node point of rotaty arm, the force exerted by the vehicle on the inner ring of the bearing is the wheel-rail force. The motion equations of each element of the bearing can be given by Newton’s second law.
Motion equation of bearing outer ring:
Motion equation of bearing inner ring:
Motion equation of bearing rollers:
The characteristic frequency of each element of the bearing can be obtained by:
where R represents the wheel radius, fs, fc, fvc, froller, fout and fin represent the axle rotation frequency (ARF), cage rotation frequency (CRF), VC vibration frequency (VCF), roller fault characteristic frequency (FCFR), outer ring fault characteristic frequency (FCFO) and inner ring fault characteristic frequency (FCFI), respectively.
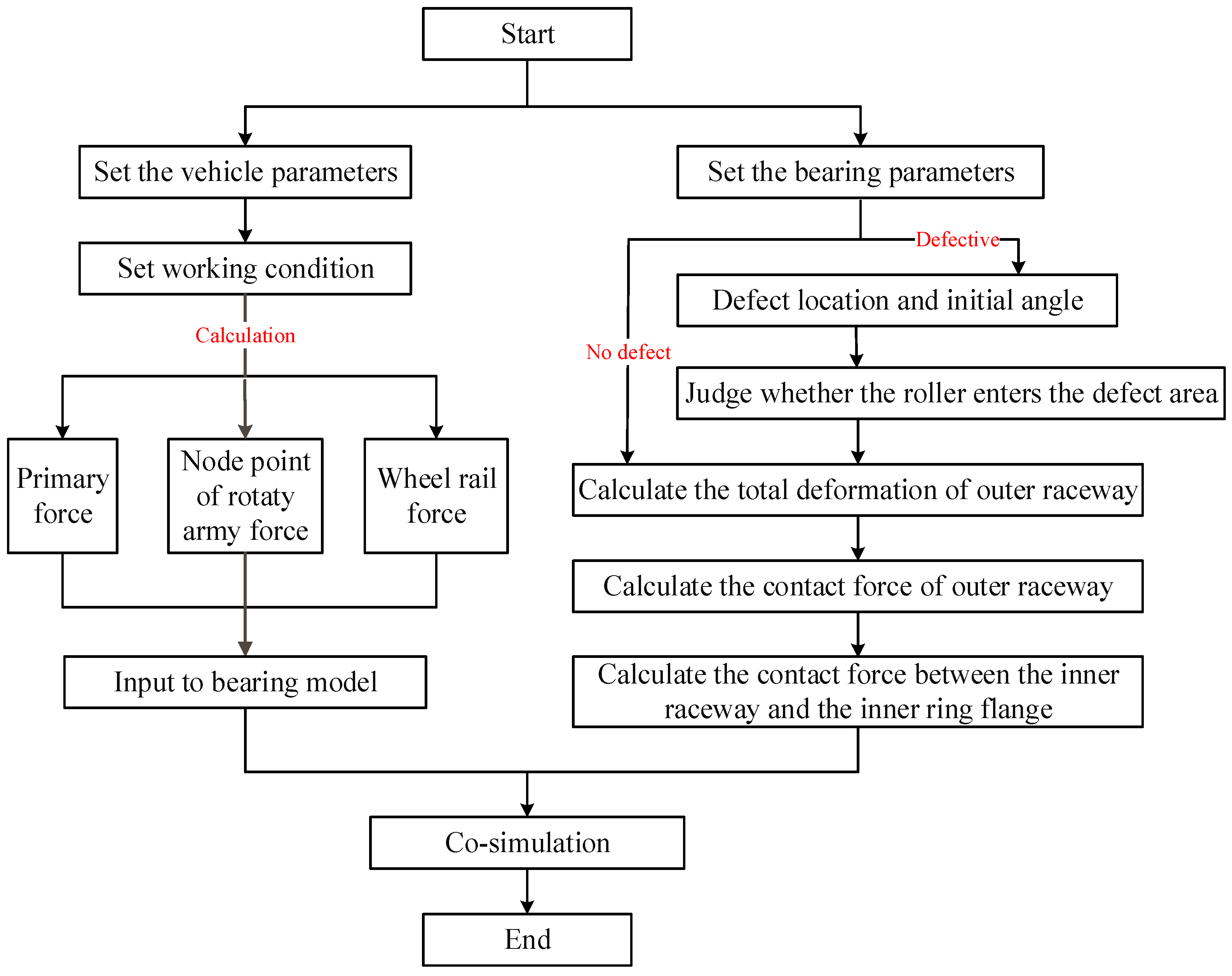
3. Co-Simulation and Model Verification
During the co-simulation of UM and MATLAB/Simulink, the vehicle model is output as an s-function to realize the data exchange between the two models. The calculation process is shown in Figure 10; the parameters of double row tapered roller bearing are shown in Table 1.
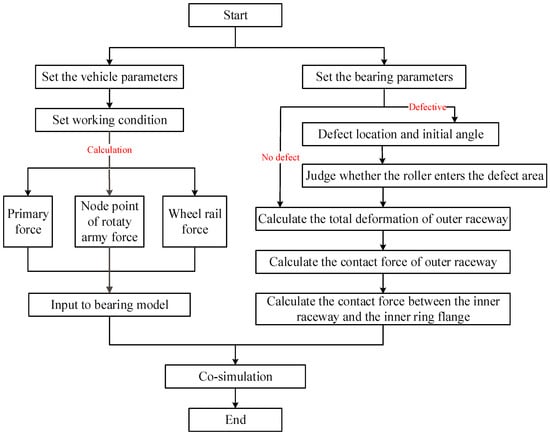
Figure 10.
Flow chart of co-simulation solution.

Table 1.
Structural parameters of double row tapered roller bearings.
In the simulation, the vehicle runs straight, the wheel tread is S1002CN new tread, and the rail is CN_ Rail_ 60 profile. Set the running speed of the vehicle to 200 km/h. In this paper, all the bearing faults used in the simulation are through groove faults, with a width of 1 mm and a depth of 1 mm. The characteristic frequency of the bearing at this time is shown in Table 2.

Table 2.
Characteristic frequency of bearing.
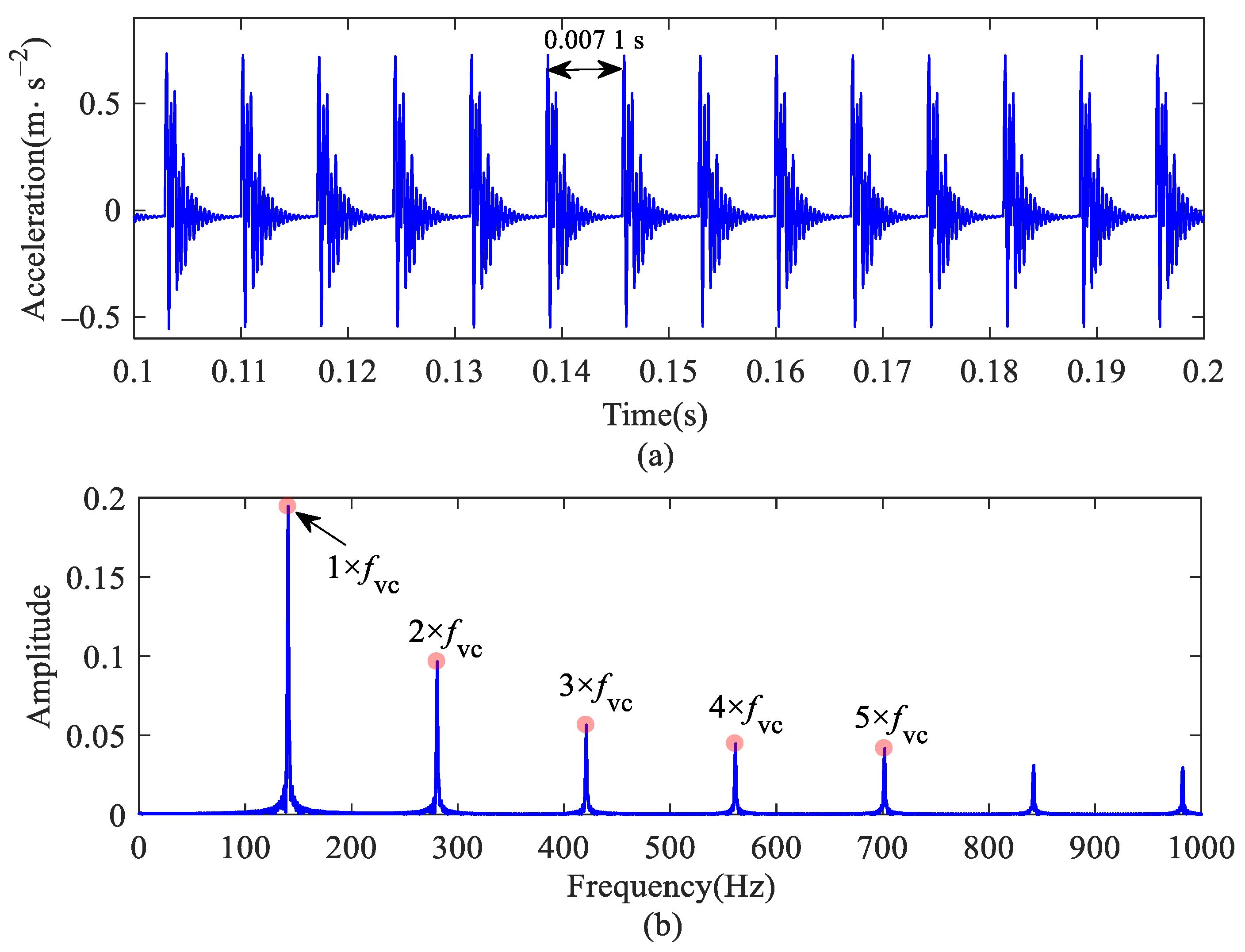
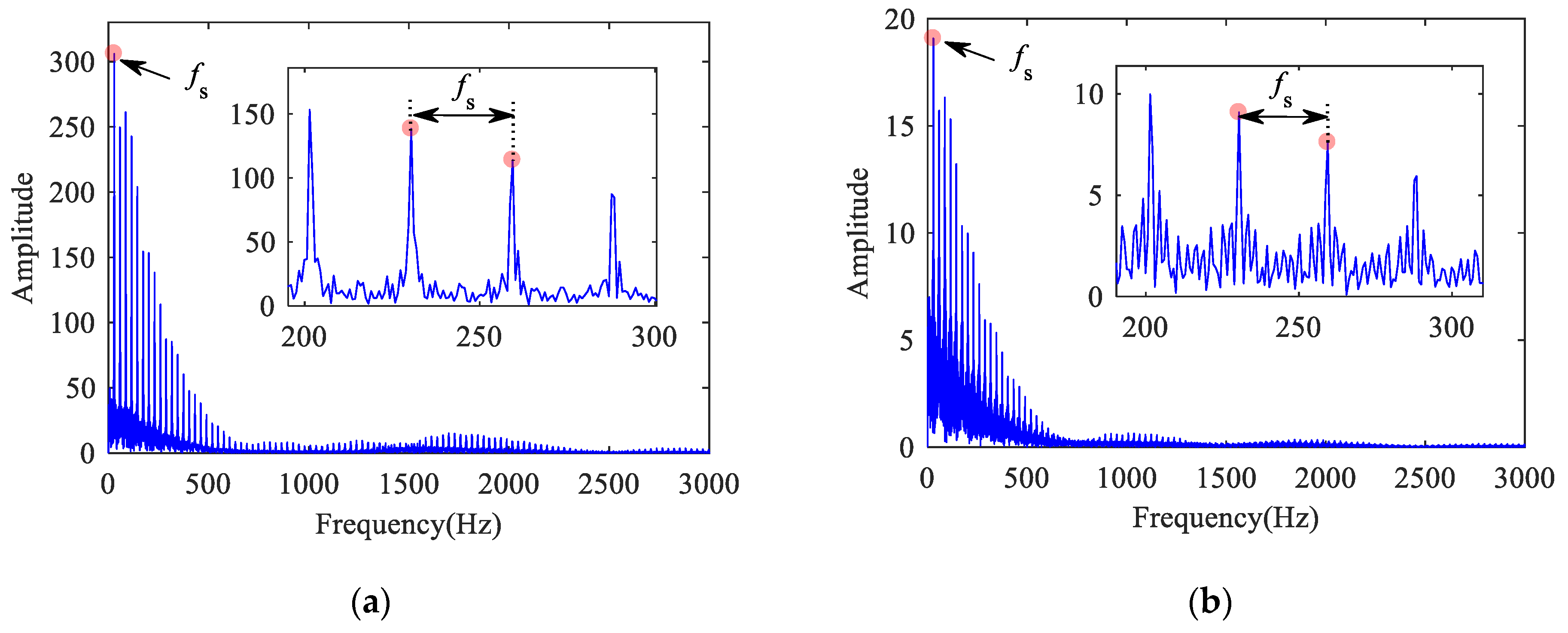
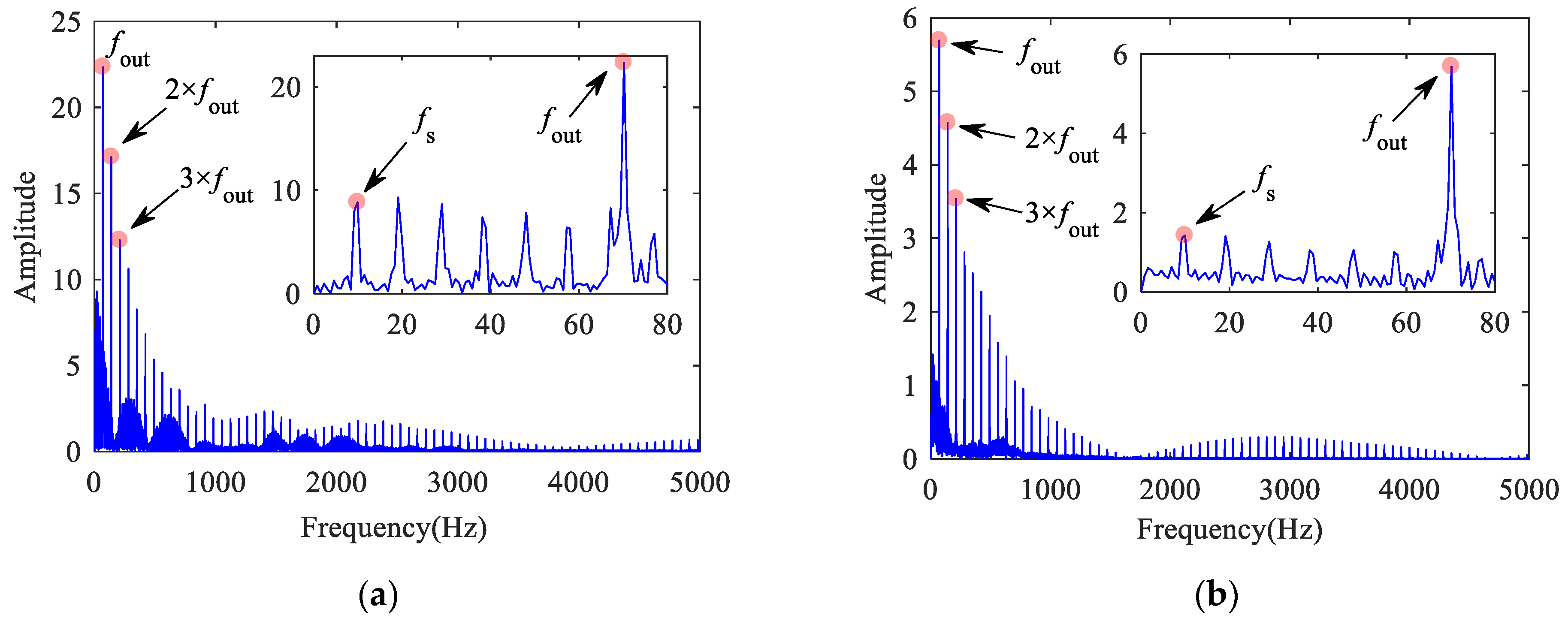
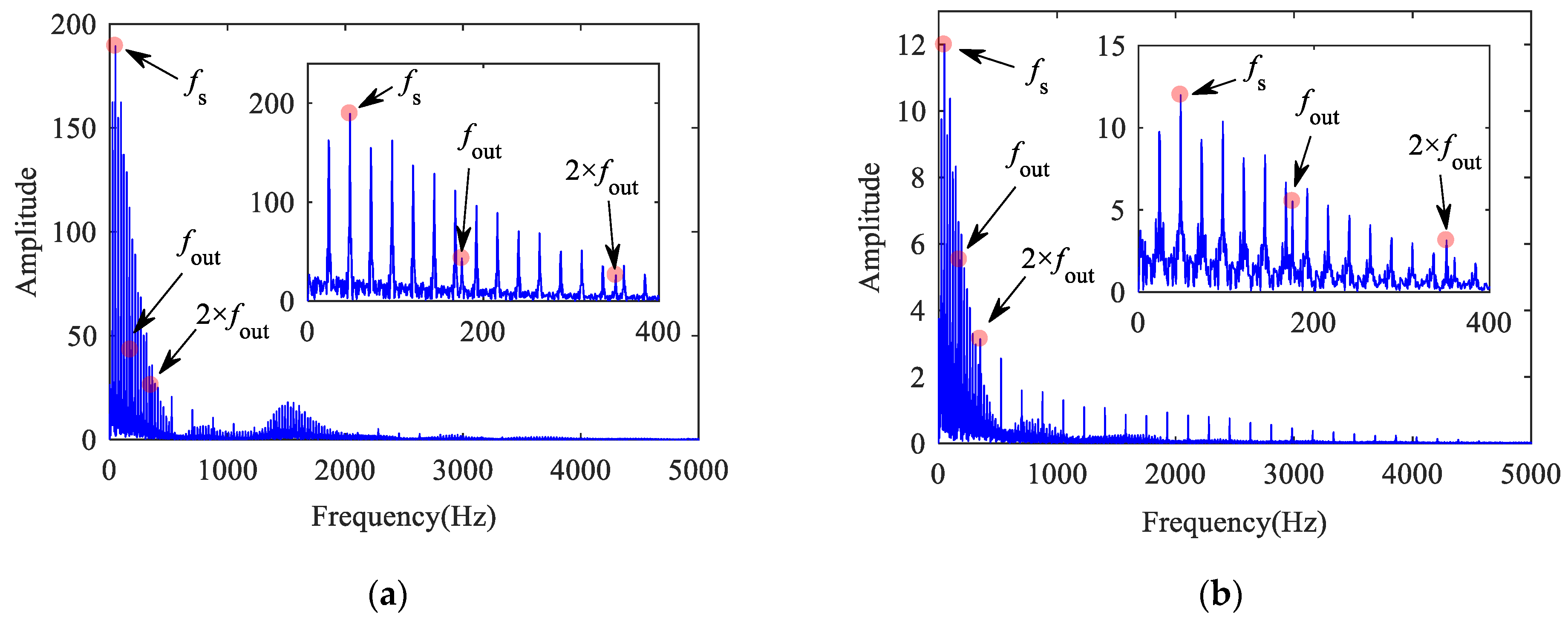
Figure 11 shows the vibration acceleration of a normal bearing without track irregularity. The periodic shock signal generated by VC vibration can be seen from the figure, and the shock period is T = 0.0071 s. The VCF can be clearly observed in the frequency spectrum, which is 140.4 Hz (approximately 1/T); the double-frequency can also be observed, and the value is consistent with the theoretical result.
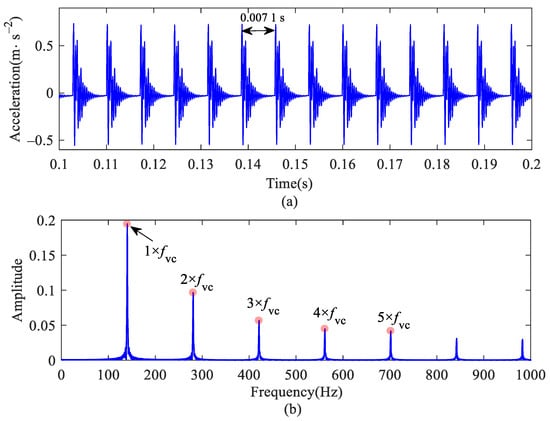
Figure 11.
Outer ring vertical acceleration of normal bearing: (a) time histories; (b) frequency spectrum.
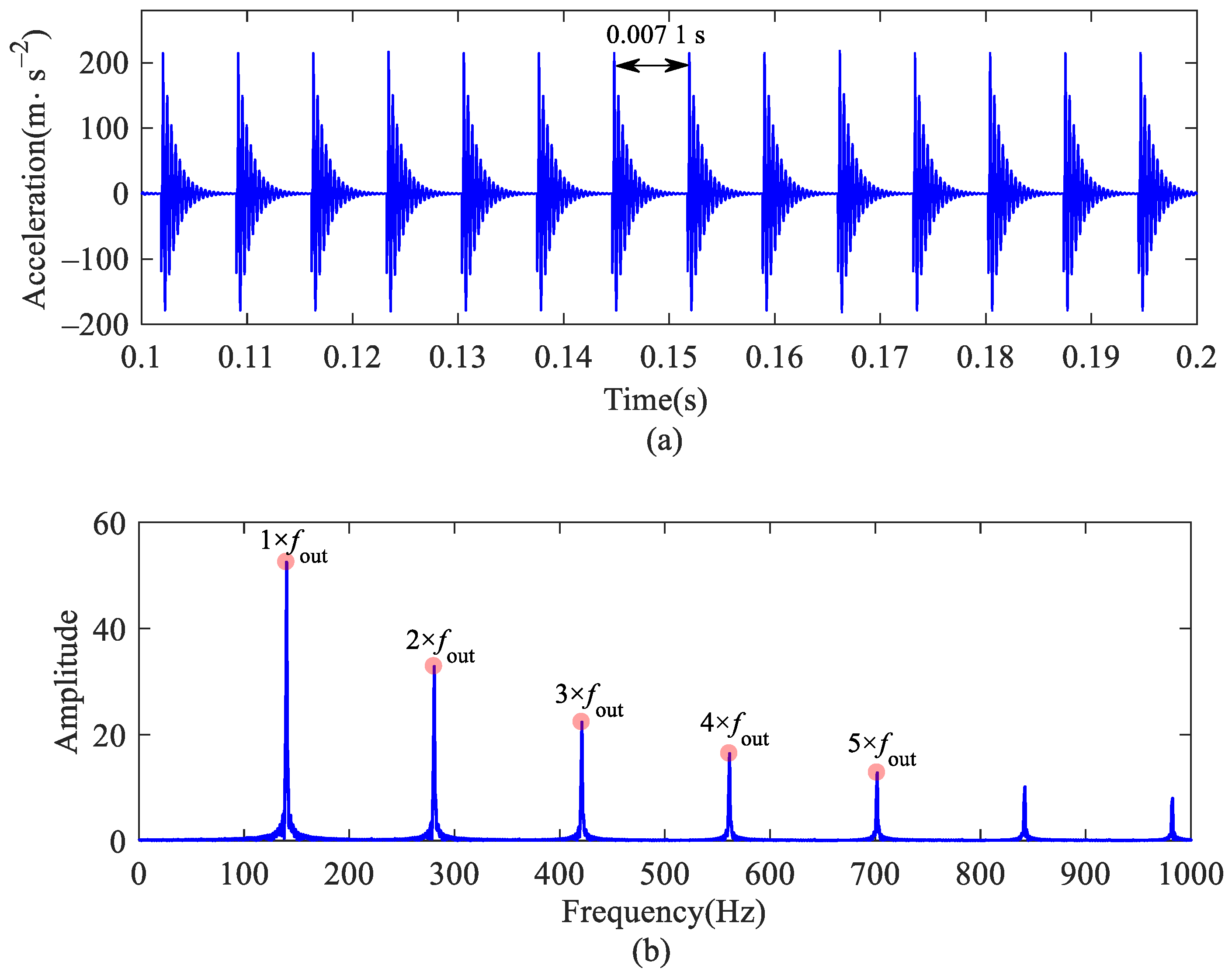
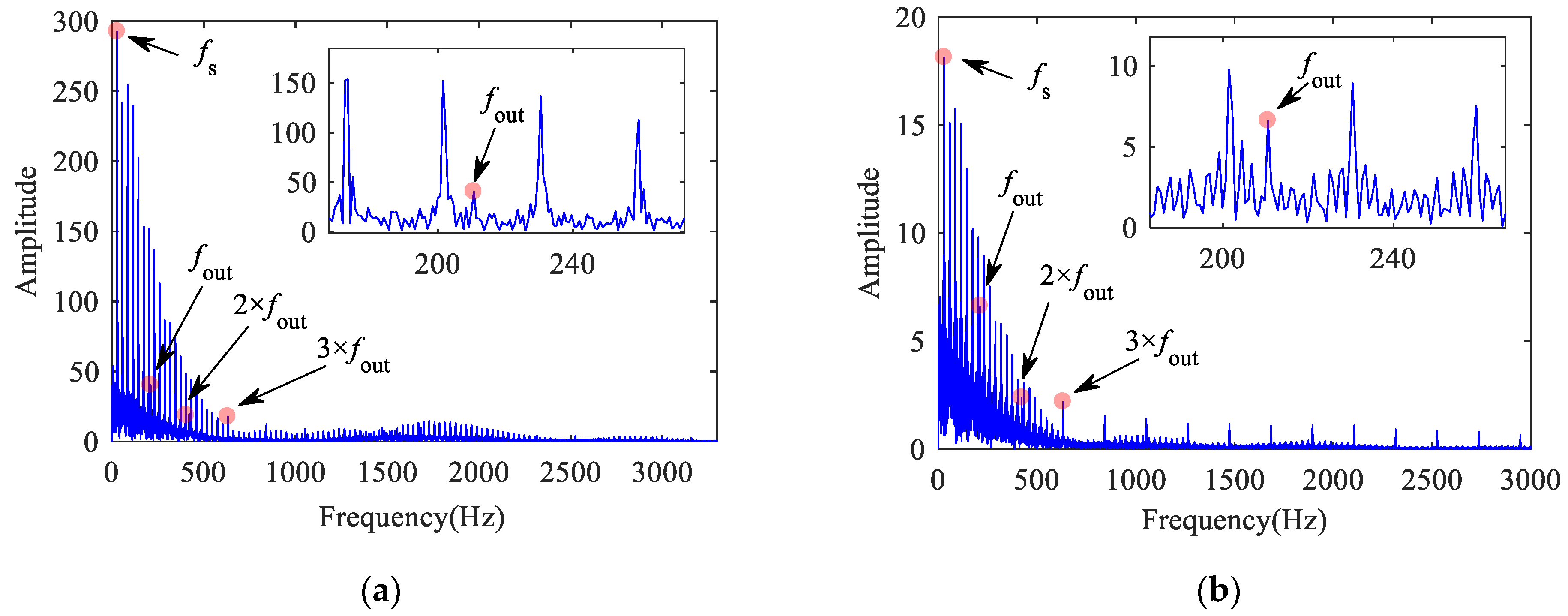
Figure 12 shows the vibration acceleration of a bearing with outer raceway defect. The period caused by defect is T = 0.0071 s, and the FCFO is 140.4 Hz (approximately 1/T).
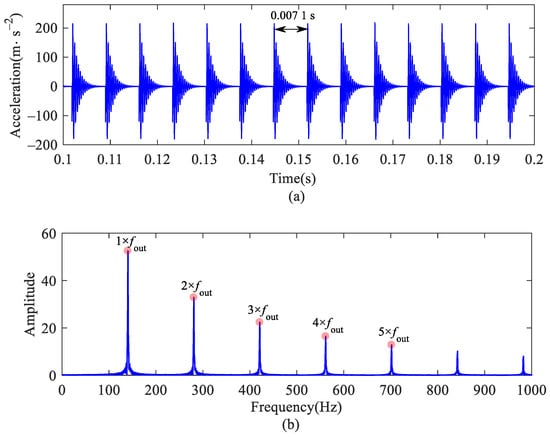
Figure 12.
Outer ring vertical acceleration of bearing with outer raceway defect: (a) time histories; (b) frequency spectrum.
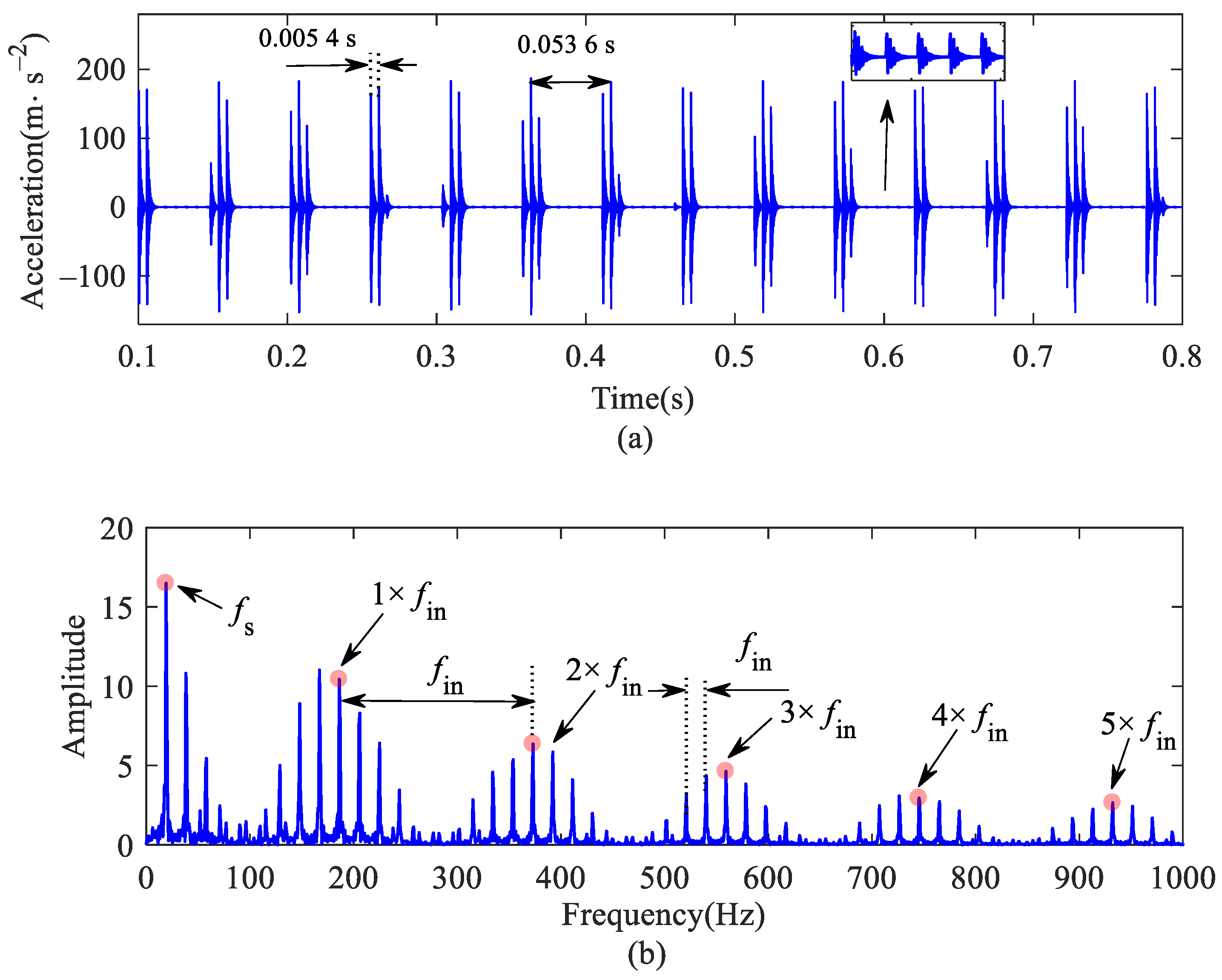
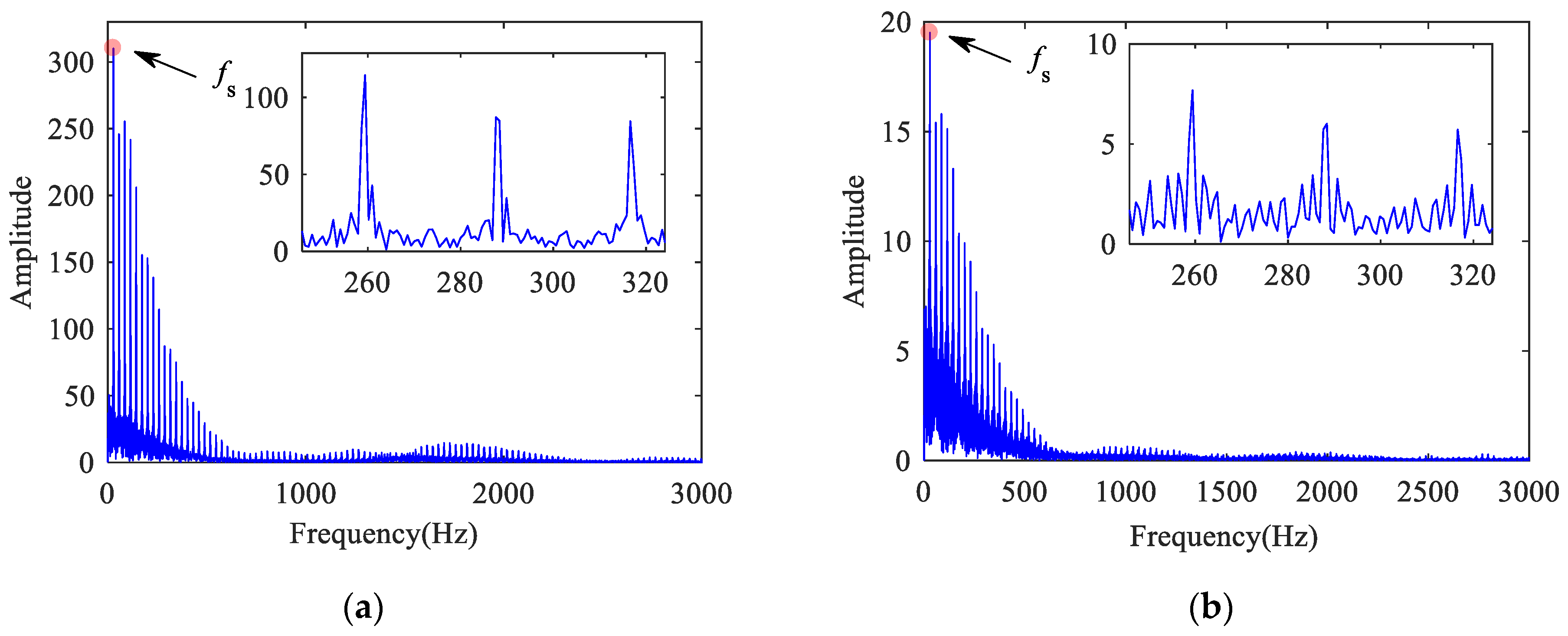
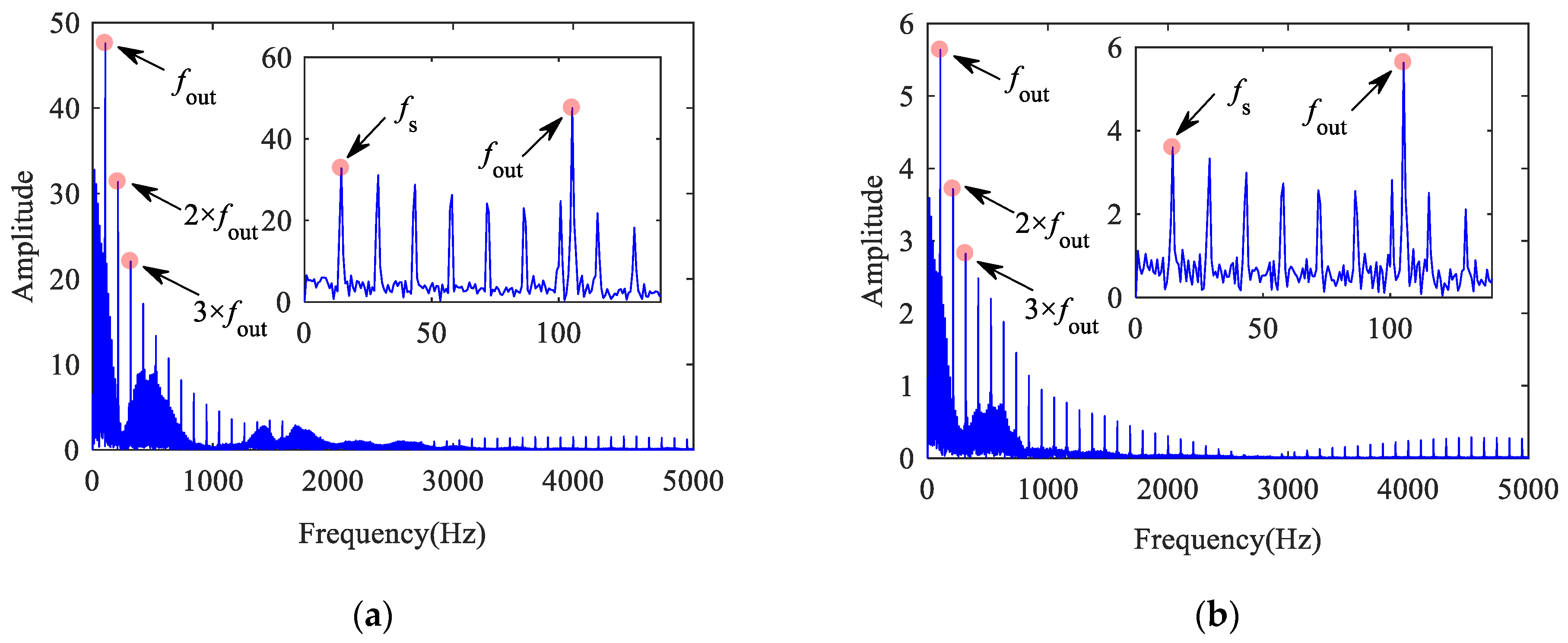
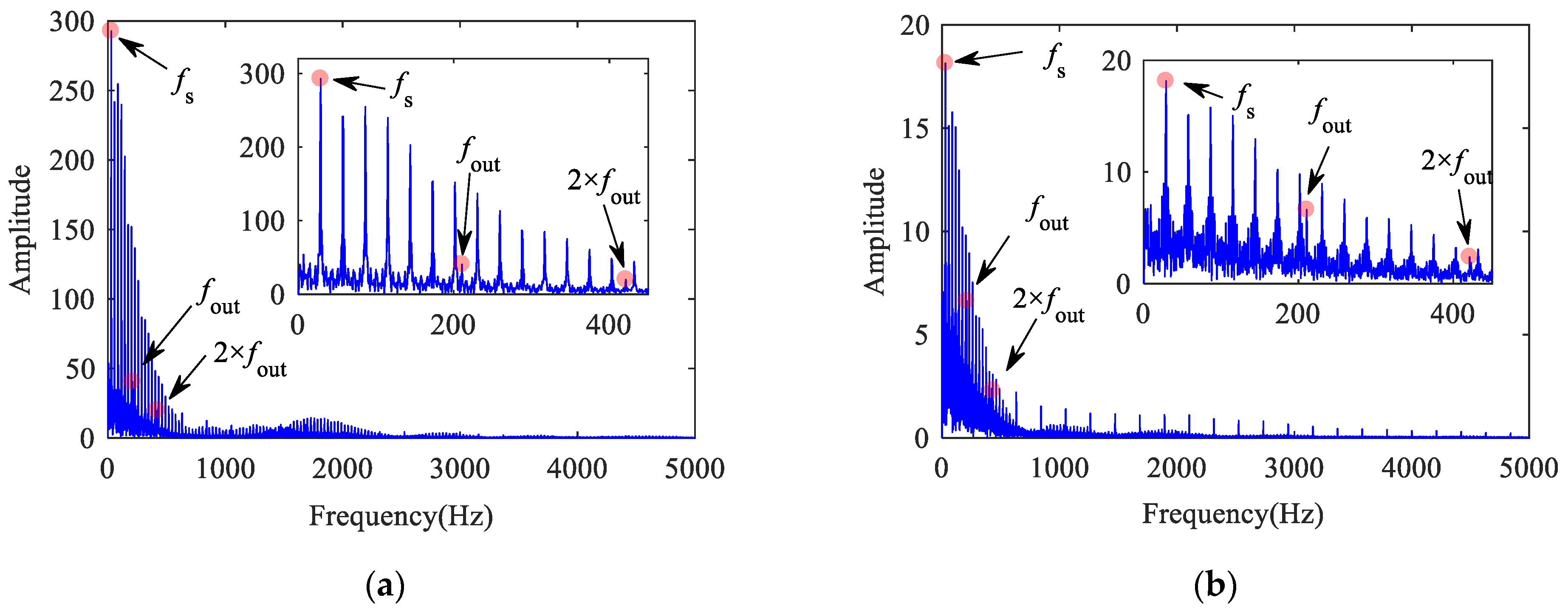
Figure 13 shows the vibration acceleration of a bearing with inner raceway defect. The impact period caused by defect is T = 0.0054 s, and the FCFI is 186.2 Hz (approximately 1/T). As the inner raceway defect rotates with the axle, its impact effect is modulated by the ARF, and the rotation period is T = 0.0536 s.
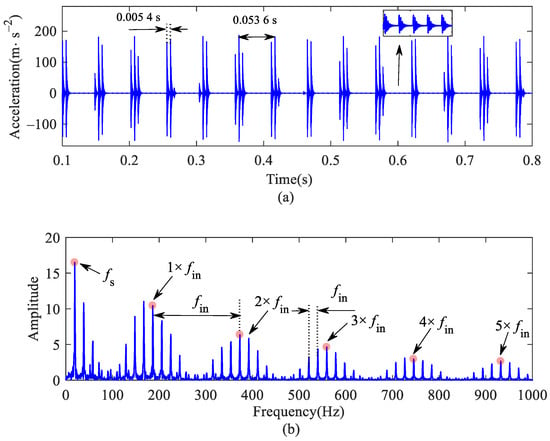
Figure 13.
Outer ring vertical acceleration of bearing with inner raceway defect: (a) time histories; (b) frequency spectrum.
In Figure 13b, some sidebands can be observed on both sides of FCFI and its double-frequency, which the amplitude gradually attenuates. The interval between sidebands is approximately 19.1 Hz (approximately 1/T), which is equal to the ARF exactly.
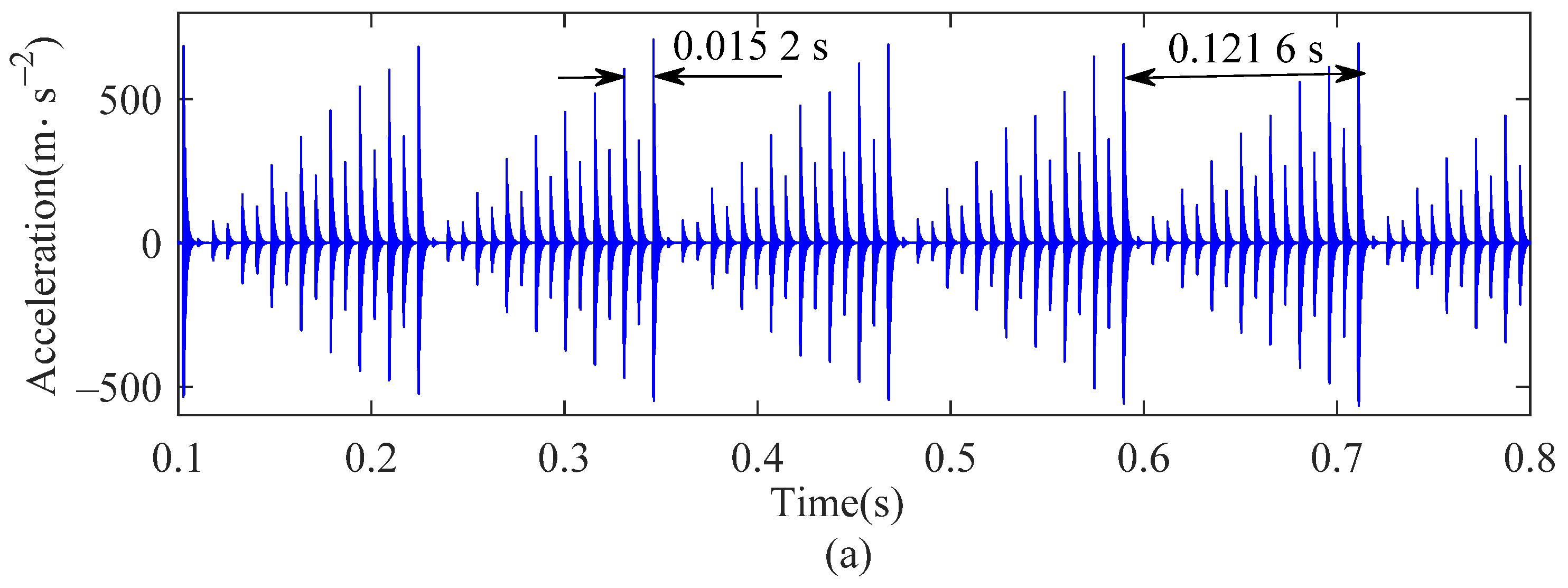
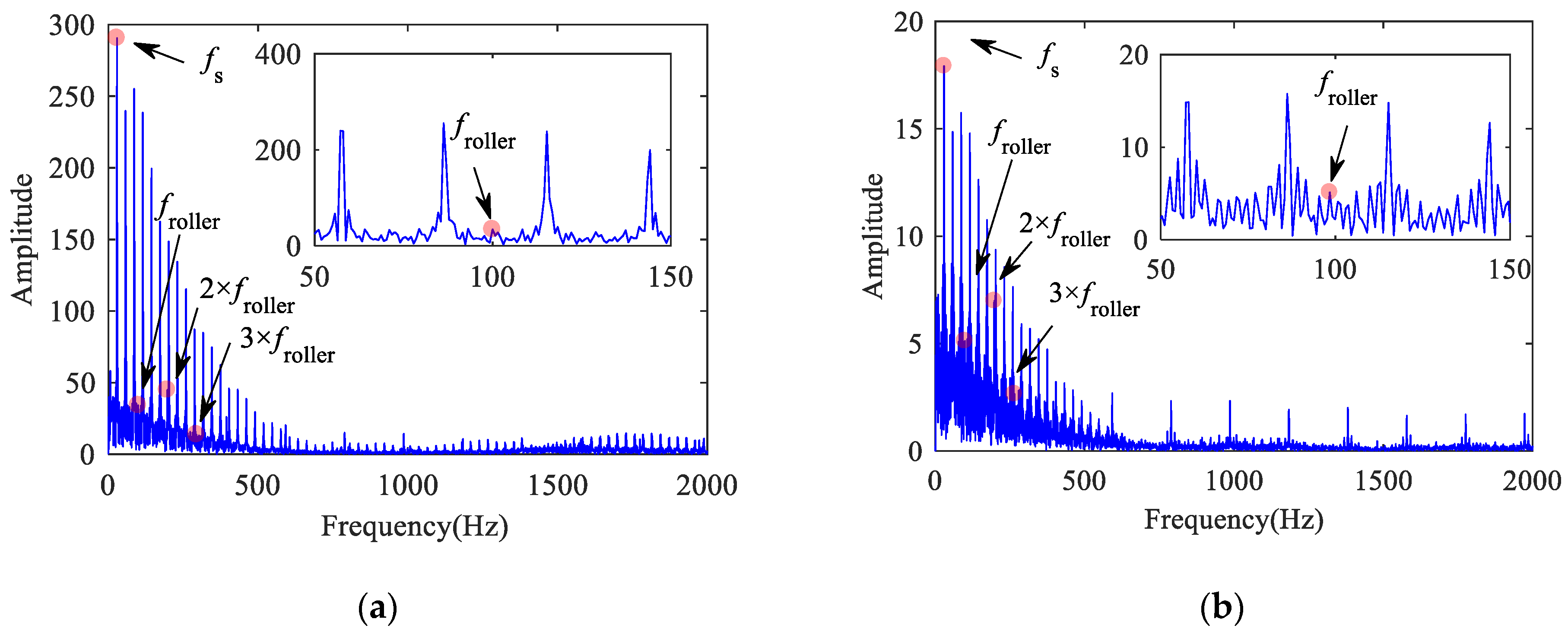
Figure 14 shows the acceleration and its spectrum diagram when the roller has a defect. The impact period caused by roller defect is T = 0.0152 s, and the FCFR is 65.79 Hz (approximately 1/T). As the roller rotates with the cage, the magnitude of the impact generated by the fault is modulated by the cage frequency. It can be seen that its period is T = 0.1216 s in Figure 14a. As shown in Figure 14b, a sideband with gradually decreasing amplitude can be observed on both sides of the FCFR and its double-frequency; the interval is approximately 8.3 Hz (approximately 1/T), which is equal to the CFR.
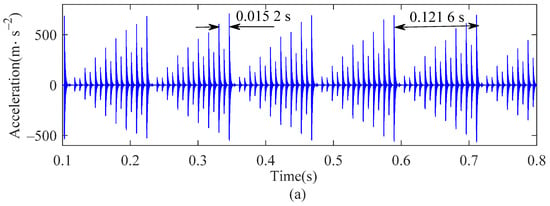
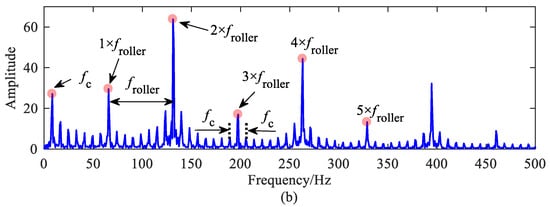
Figure 14.
Outer ring vertical acceleration of bearing with roller defect: (a) time histories; (b) frequency spectrum.
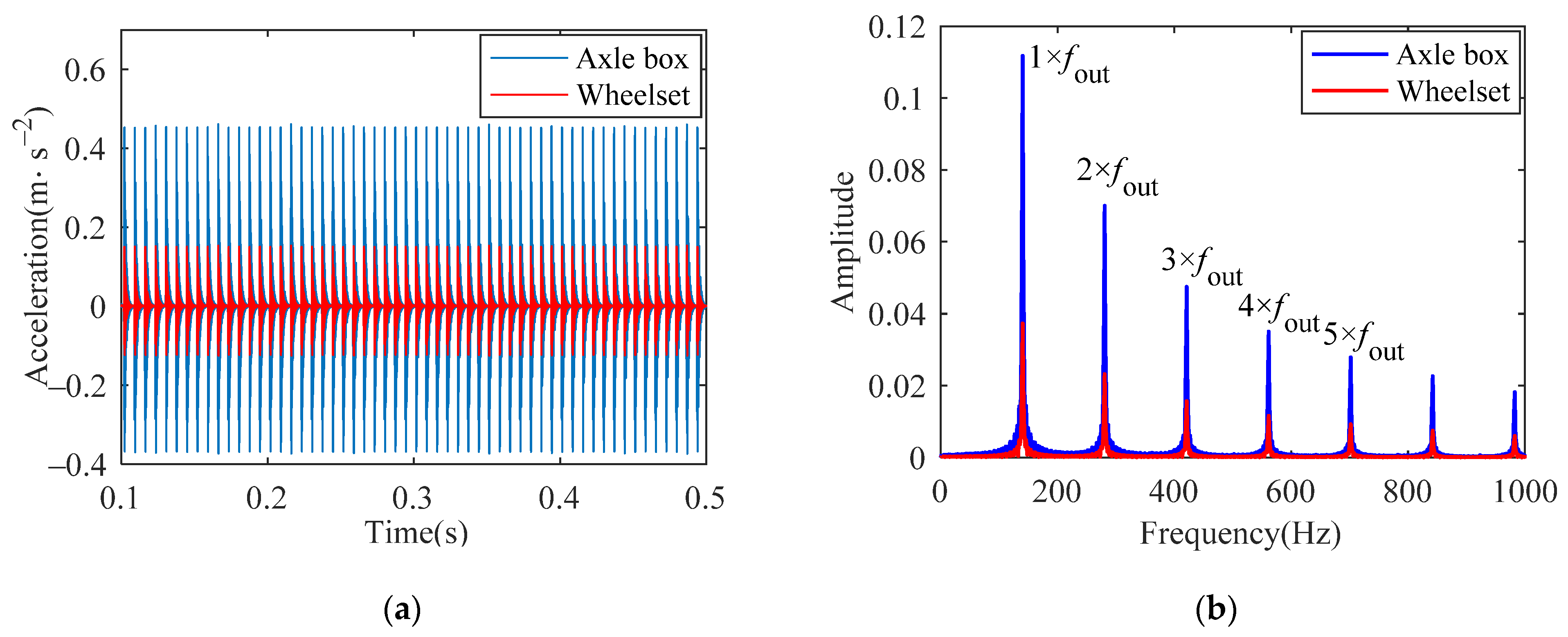
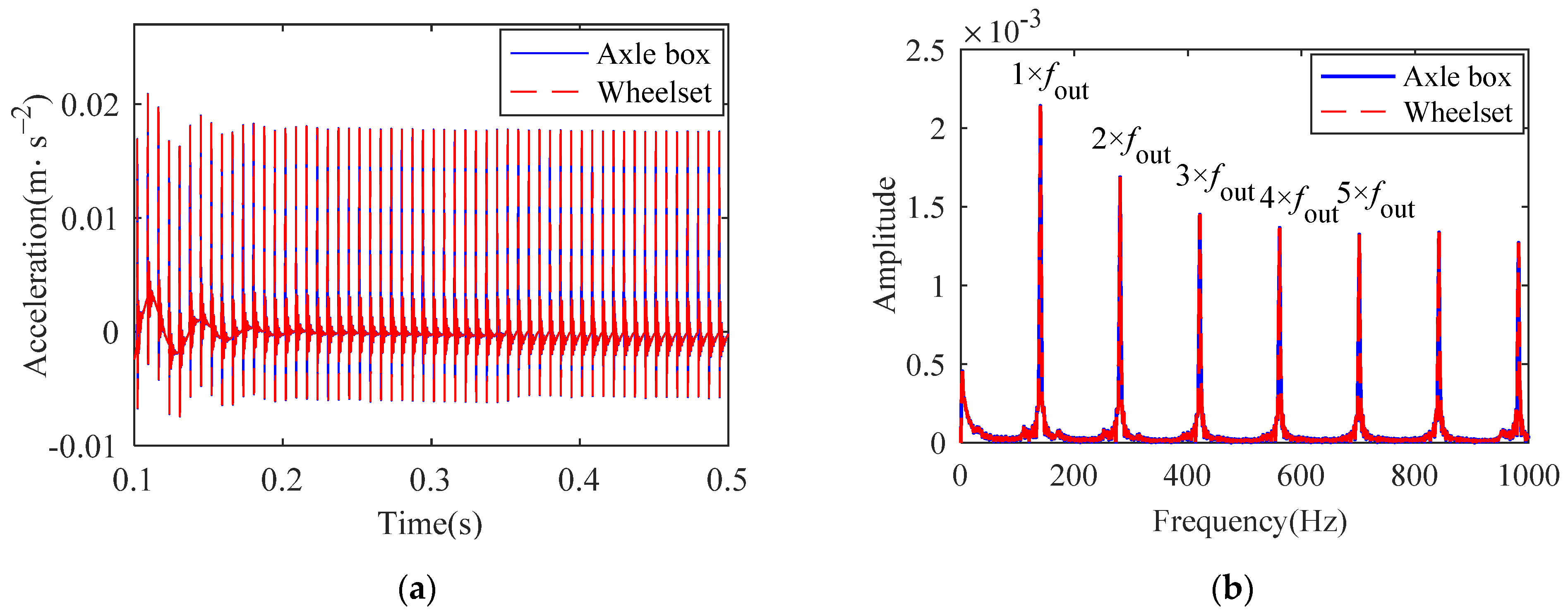
When the outer raceway of the bearing has a defect, the vertical and lateral acceleration of the axle box and wheelset are shown in Figure 15 and Figure 16. A small amplitude vibration can be seen in the vertical and lateral directions. It is indicated that when the vehicle and the bearing are coupled together, the vibration of the bearing is transmitted to the vehicle. In addition, the FCFO can be detected in both the horizontal and vertical directions in the frequency spectrum, which further verifies the effectiveness of the coupling model.
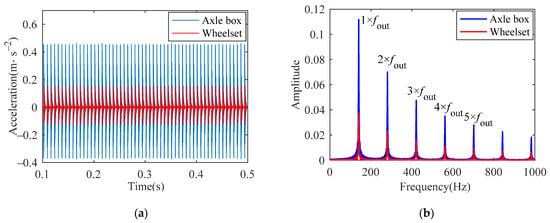
Figure 15.
Vertical acceleration of axle box and wheelset: (a) time histories; (b) frequency spectrum.
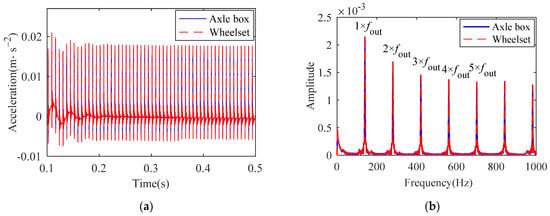
Figure 16.
Lateral acceleration of axle box and wheelset: (a) time histories; (b) frequency spectrum.
The above analysis shows that the vehicle-bearing coupling model established in this paper can reflect the vibration characteristics of the system and can be used for the simulation analysis of vehicle and bearing system.
4. Model Validation by Experiment
In order to further verify the correctness of the model established in the paper, experiments are carried out on the rolling and vibrating test rig of single wheelset. The test rig is mainly composed of actuator, reaction frame, wheelset, hydraulic station, rail wheel and its exciter, etc. It is a multi-purpose test-bed to simulate the operation of high-speed train, which can be used to study the vibration transmission characteristics of wheelsets, gears, axle boxes, bearings and other systems. It can carry out vibration test, traction braking test, lateral stability test, etc. It can be loaded through the action of horizontal and vertical actuators to simulate abnormal wheel-rail contact conditions, such as track irregularity, wheel polygon, rail corrugation, etc. The maximum axle load of the test rig is 25 t, the maximum torque is 5000 N∙m, the maximum running speed is 500 km/h, and the excitation frequency range is 0–500 Hz. The site layout of the test is shown in Figure 17.

Figure 17.
Site layout of the test: (a) rolling and vibrating test rig of single wheelset; (b) ensor arrangement.
The objects of this experiment are three kinds of bearings with faults in different positions. The inner raceway and outer raceway of the bearing used in the experiment are processed into through groove faults, with a width of 1 mm and a depth of 1 mm. The roller is processed as a pitting fault. Set the running speed as 200 km/h. The wheel is subject to sinusoidal excitation in which the axial loading amplitude is 1 mm; the vertical loading amplitude is 2 mm, and the loading frequency is 5 Hz. Select appropriate positions at the left and right axle boxes as measuring points to collect their lateral and vertical acceleration signals. Set the sampling frequency to 25.6 kHz and the sampling time to 60 s. The correctness of the model is verified by comparing the experimental results with the simulation results.
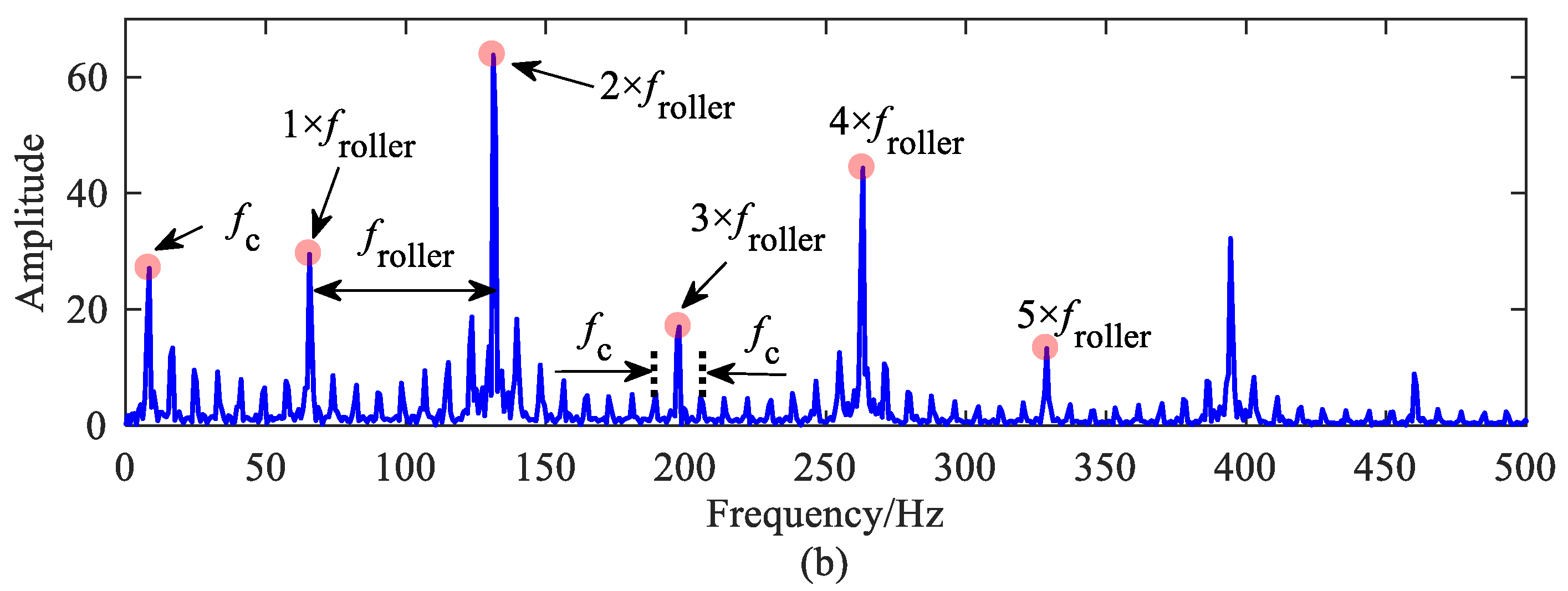
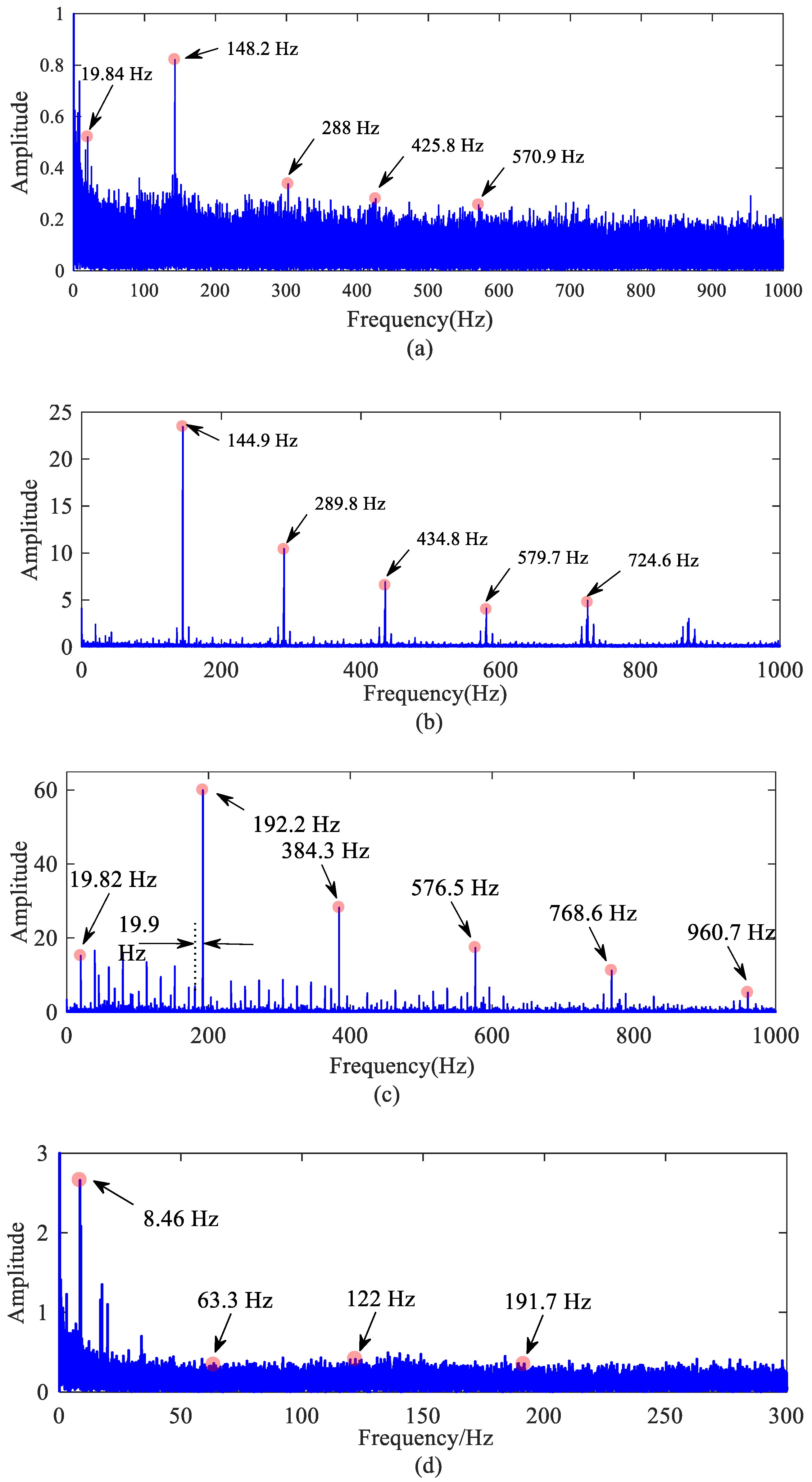
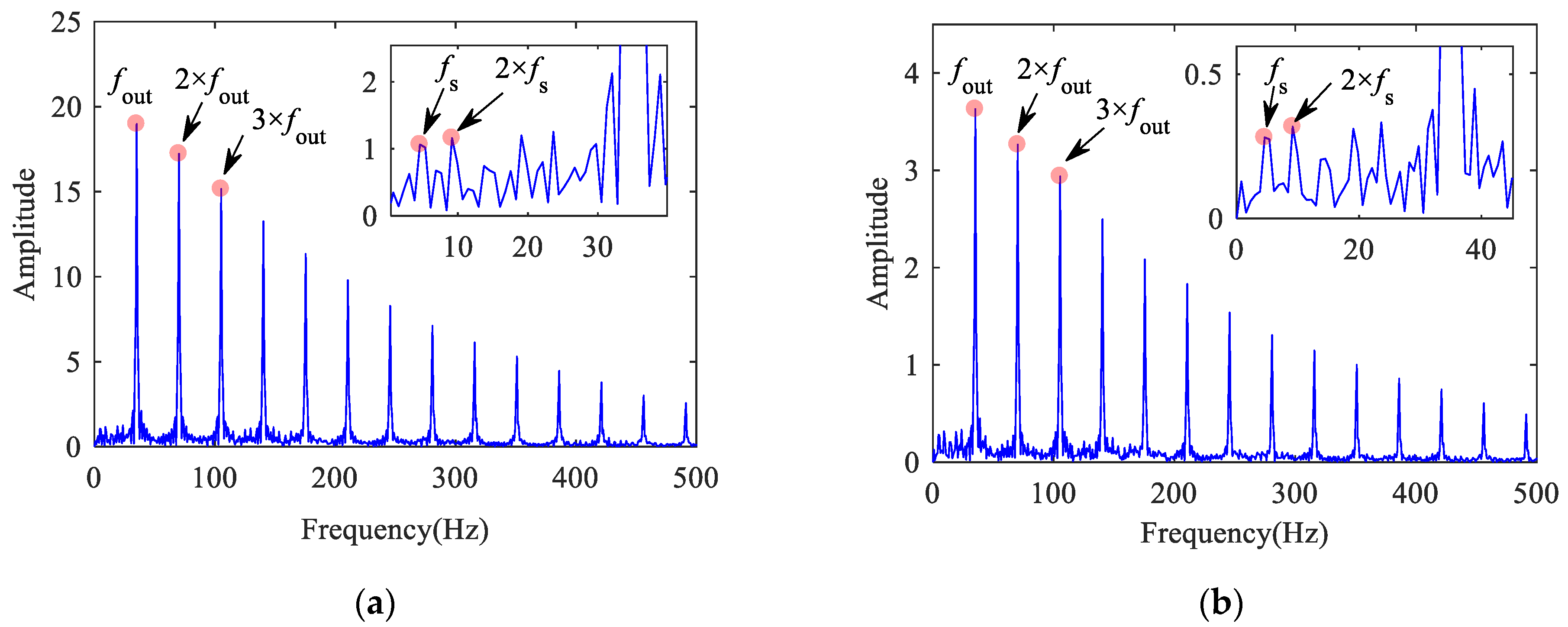
Figure 18 shows the frequency spectrum of the vertical vibration acceleration of the outer ring. The bearing characteristic frequency and its double-frequency can be found in the figure, but perhaps because the size of the roller fault processing is not large enough, the FCFR is not obvious. The comparison between the experimental results and the simulation results is listed in Table 3, and the errors are within a reasonable range, which further proves the correctness of the model established in this paper.
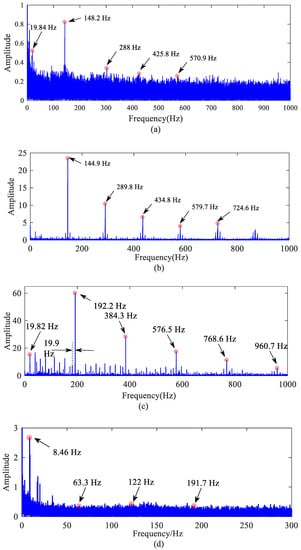
Figure 18.
Frequency spectrum of outer ring vertical acceleration: (a) normal bearing; (b) bearing with outer raceway fault; (c) bearing with inner raceway fault; (d) bearing with roller fault.

Table 3.
Comparisons between the theoretical and simulation results.
5. Track Irregularity Spectrum and Wheel Flat Scar Model
When the train runs on the track, it will be affected by various external disturbances, resulting in relatively strong vibration. The vibration will transmitted upward through the wheel rail interface [52], which will have a certain impact on the vibration of the axle box bearing. Therefore, how the vibration amplitude and frequency characteristics change needs further analysis and discussion. In order to analyze the axle box bearing more accurately and comprehensively, the paper will study the vibration of the bearing under the wheel rail excitation.
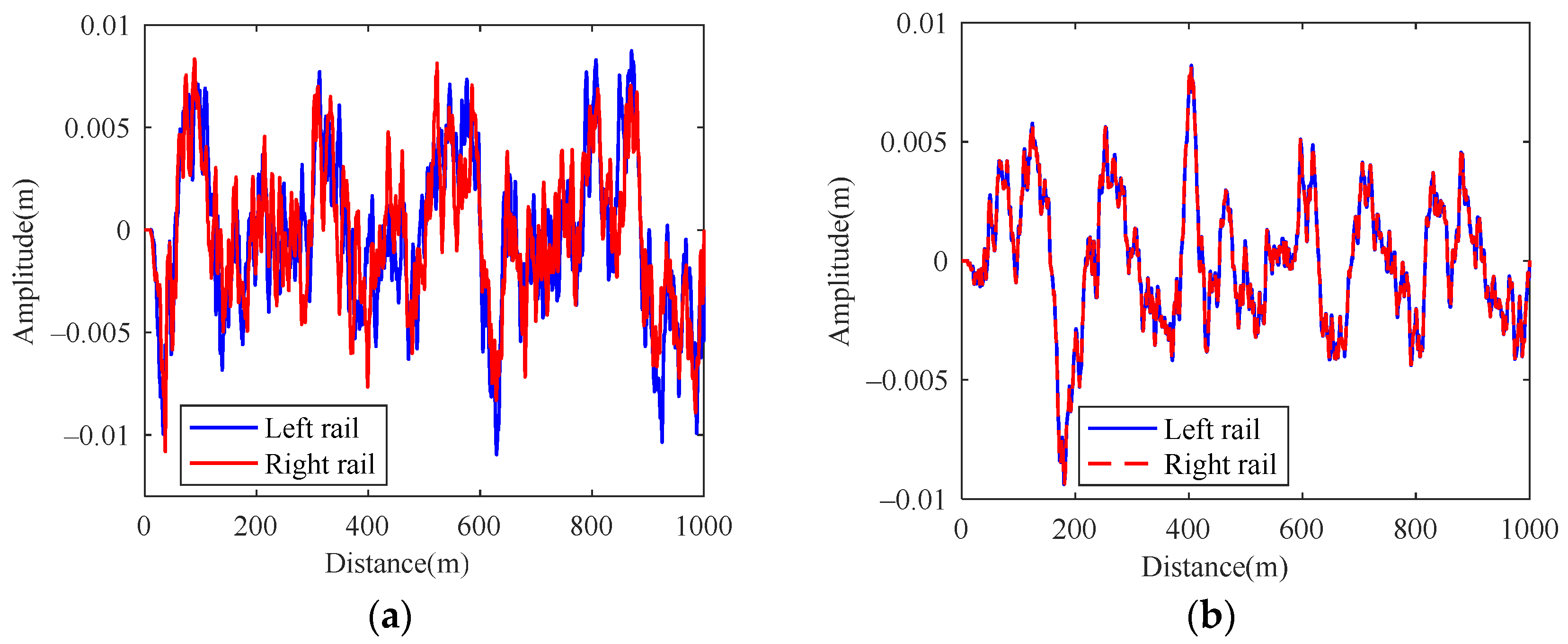
Track irregularity is one of the main factors of vehicle vibration, which is an unavoidable track excitation. Various track irregularities can be directly added to the vehicle for simulation in UM. In the paper, the German high interference track spectrum is selected as an input, which comes from the calculation of UM internal program, as shown in Figure 19.
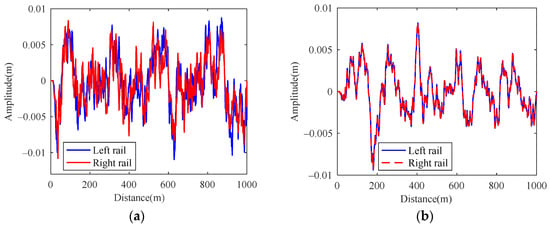
Figure 19.
Track irregularity spectrum: (a) vertical; (b) horizontal.
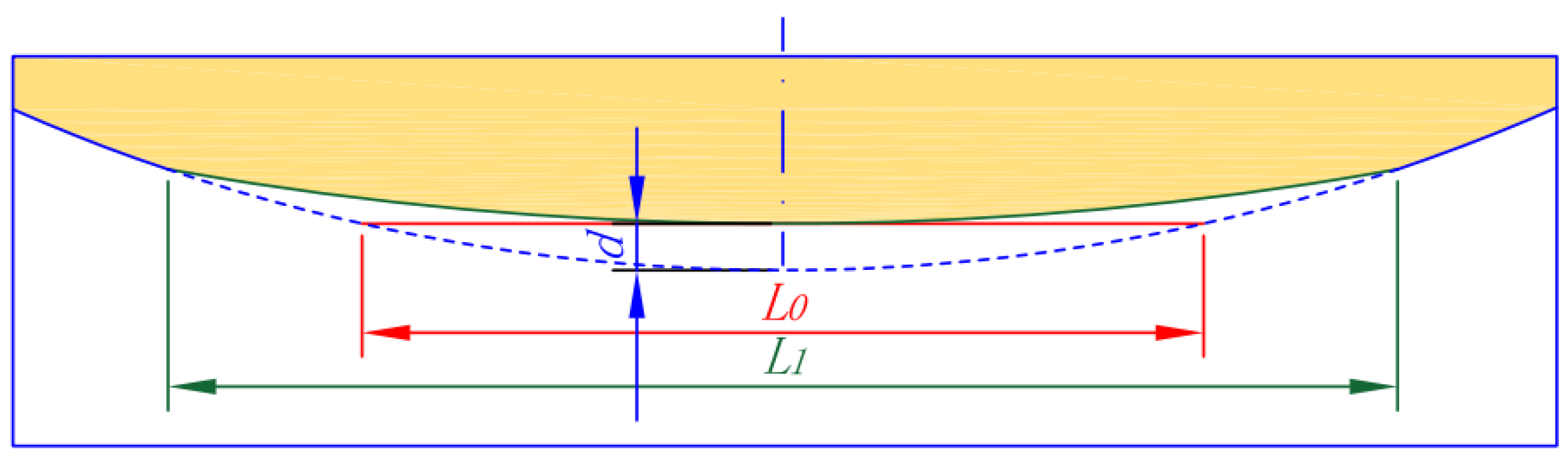
Wheel defects will increase the impact of wheel rail and affect the safety of vehicle and rail. Wheel flat scar is a common wheel shape defect, which will cause a special type of intermittent pulse excitation source at the wheel rail contact interface [53]. Flat scars can be divided into new and old ones. Once a new flat scar is formed, it will produce an acute angle and become an old flat scar after wheel tread wear and plastic deformation. As shown in Figure 20, L0 is the length of the new flat scar, L1 is the minimum length of the old flat scar that guarantees the convex form of the wheel, and d is the depth of them. The geometric dimension of flat scar is determined by Equations (41)–(43) in UM.
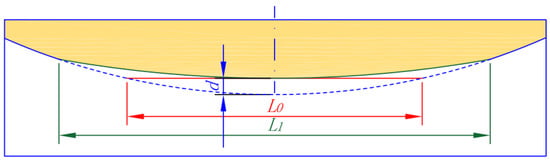
Figure 20.
Schematic diagram of new flat scar and old flat scar.
6. Dynamic Response of Bearing under Track Irregularity
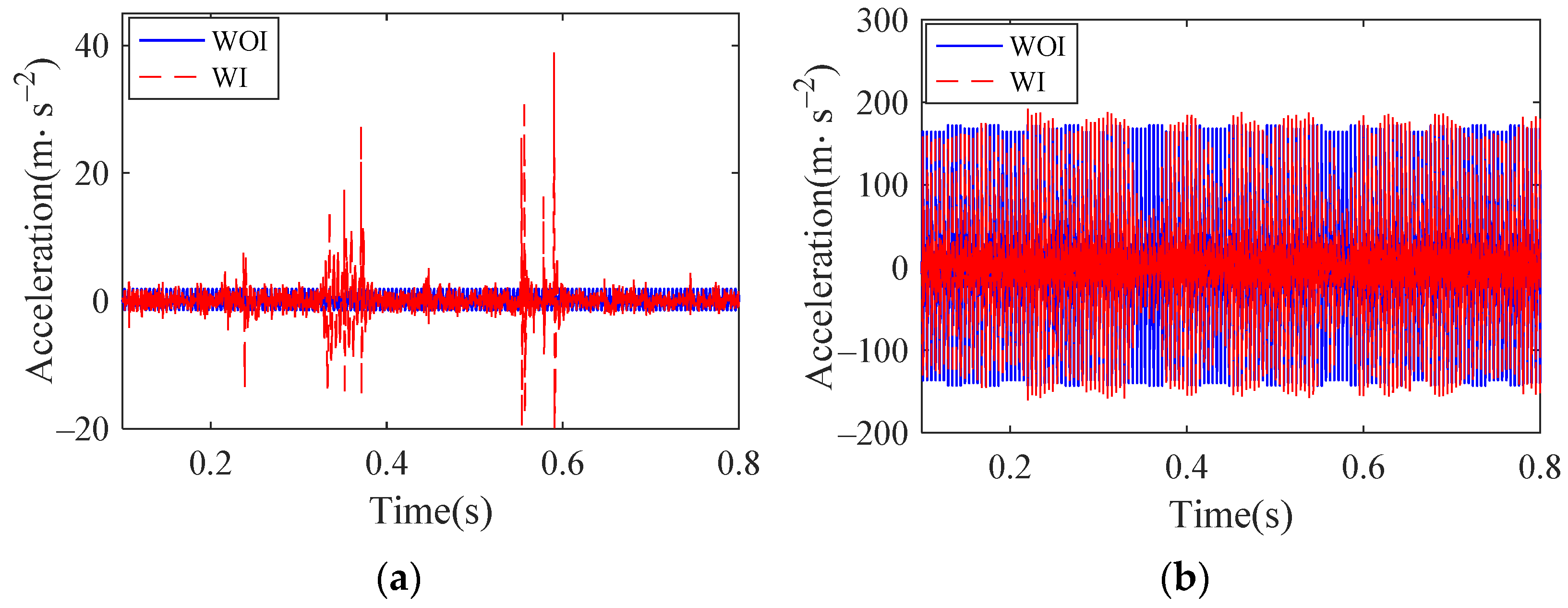
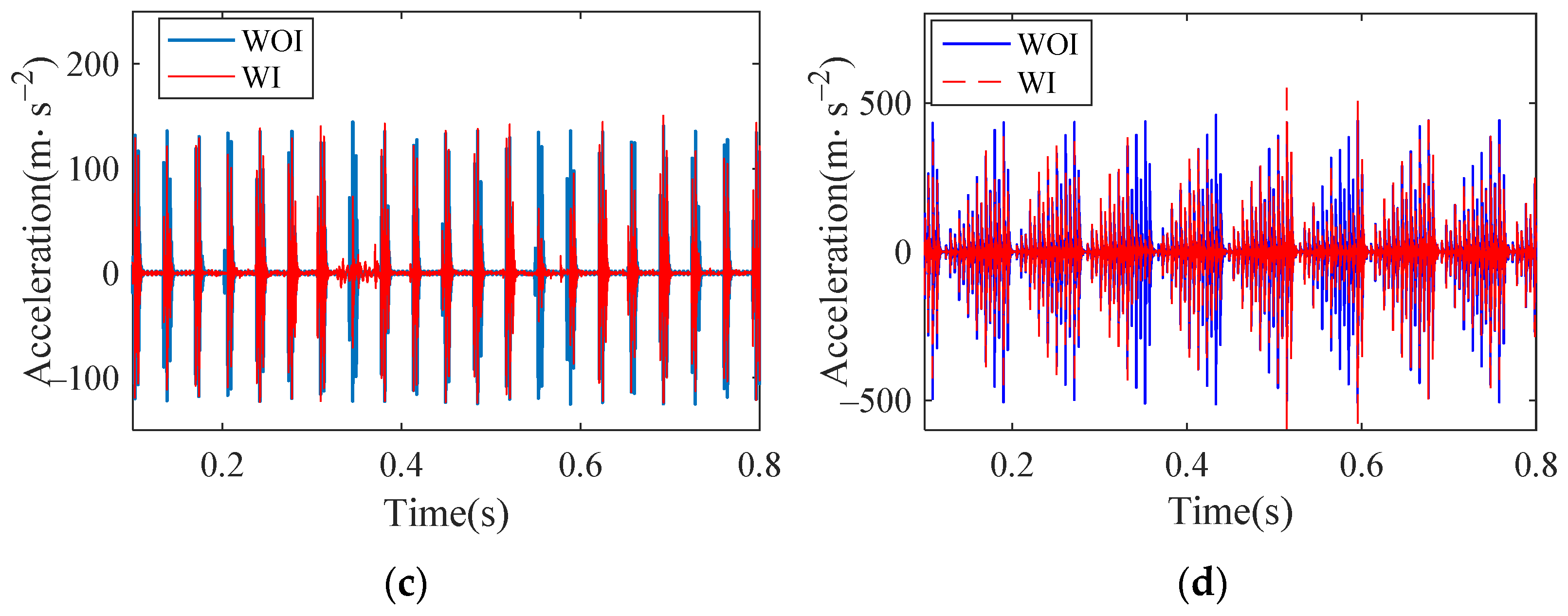
Set the vehicle speed to 300 km/h, take the German high interference track spectrum as an input, simulate the normal bearing and the bearings with outer raceway, inner raceway and roller defects, respectively. The results of the vertical acceleration of the outer ring are shown in Figure 21, where WOI represents without irregularity and WI represents with irregularity (same as blew). Through the comparison of track irregularity and non track irregularity, it can be seen that the vertical acceleration of normal bearing changes greatly, while the acceleration of defective bearings change slightly. Extract the maximum acceleration amplitude of normal bearing and defective bearing, respectively, and make quantitative analysis, as shown in Table 4. It can be seen from the comparison results that the maximum amplitude of normal bearing has changed greatly under the condition of track irregularity, while that of defective bearings has changed little. This is because the vibration of the normal bearing is slight, and the track irregularity will cause its amplitude to fluctuate greatly, while the defective bearing will produce large vibration under the effect of the defect, which causes the effect of track irregularity to not be obvious. This is because the vibration of the normal bearing is slight, and the track irregularity will cause its amplitude to greatly fluctuate. The defective bearing will produce a large vibration under the effect of the defect, which causes the effect of track irregularity to be not obvious.
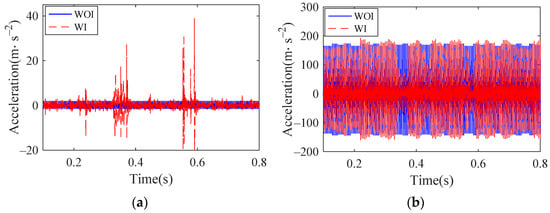
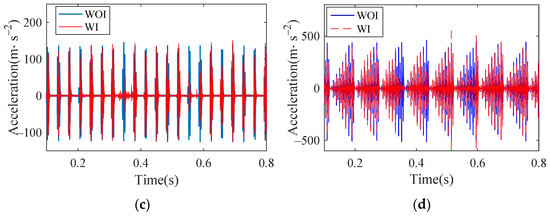
Figure 21.
Time histories of outer ring vertical acceleration: (a) normal bearing; (b) bearing with outer raceway defect; (c) bearing with inner raceway defect; (d) bearing with roller defect.

Table 4.
Comparison before and after input track irregularity.
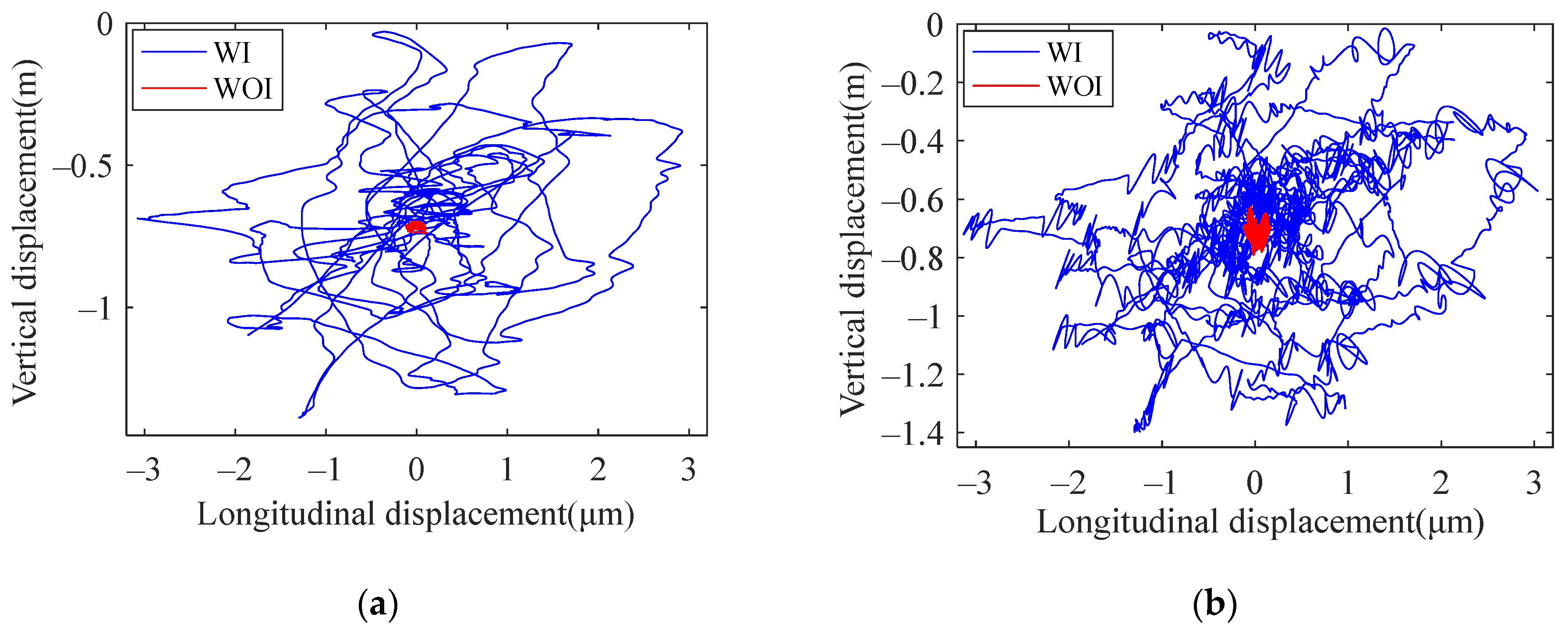
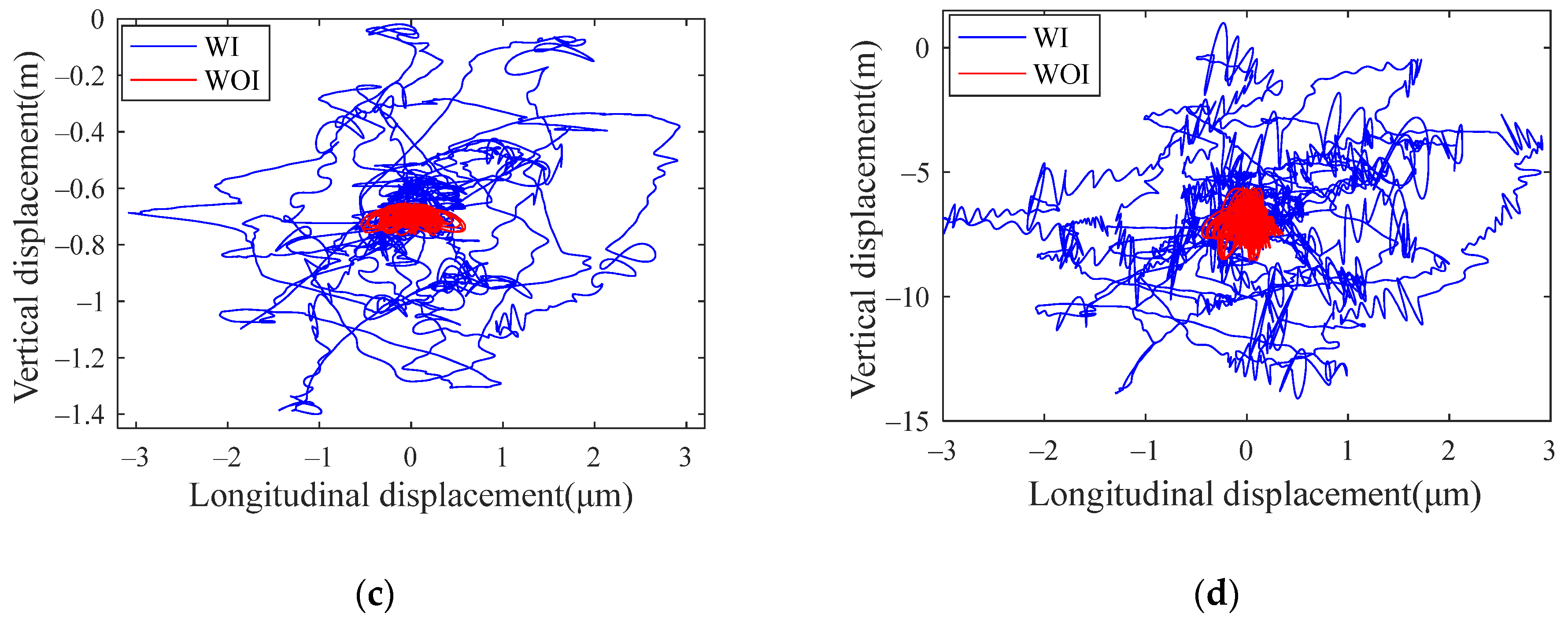
Figure 22 shows the comparison of the axis trajectory under four conditions with and without track irregularity. It can be seen that the axis trajectory changes greatly under the action of track irregularity, whether it is a normal bearing or a defective bearing. So, it can be further explained that the impact of track irregularity on system vibration cannot be ignored. Therefore, through the vehicle-bearing coupling model established in the paper, the study can be closer to the real running environment of axle box bearing.
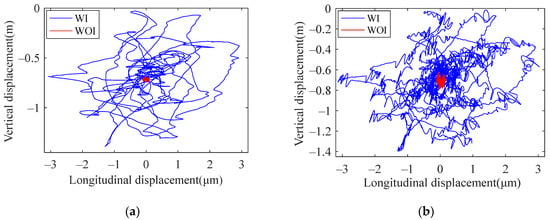
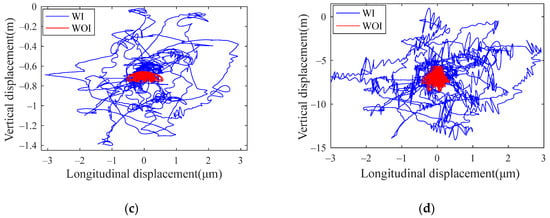
Figure 22.
Axis track of bearing outer ring: (a) normal bearing; (b) bearing with outer raceway fault; (c) bearing with inner raceway fault; (d) bearing with roller fault.
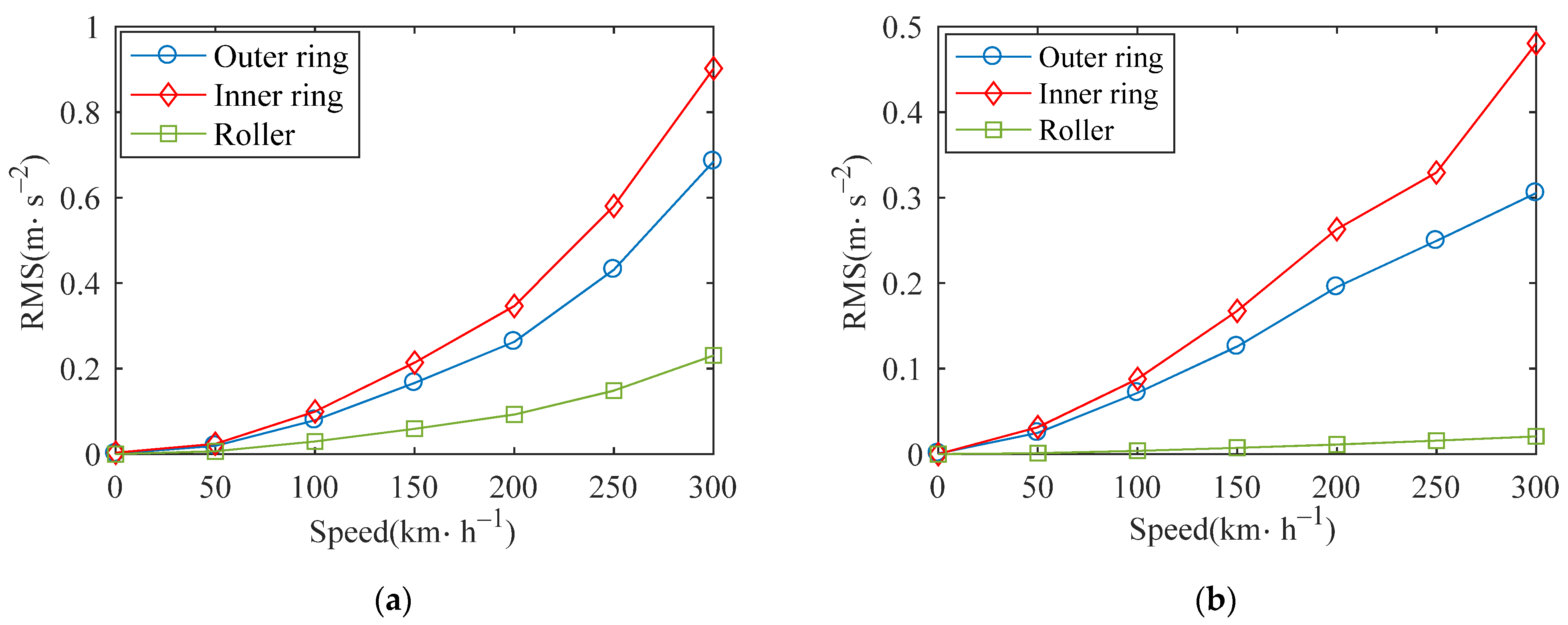
In order to study the influence of speed on the vibration of each element of the bearing, the vehicle-bearing system at different speeds under the action of track irregularity is simulated. Figure 23 shows the RMS values of the vertical and lateral accelerations of the outer ring, inner ring and roller, respectively. It can be seen that with the increase of speed, the RMS values of the three elements gradually increase, the value of the inner ring is the largest, and the value of the roller is the smallest. It is indicated that the vibration of the inner ring is relatively intense, followed by the outer ring and roller in this state.
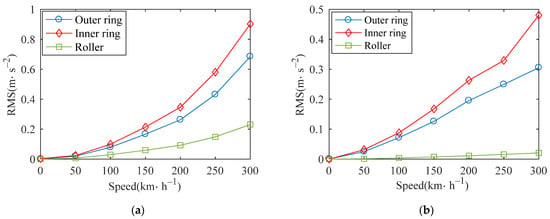
Figure 23.
RMS of outer ring acceleration of normal bearing: (a) vertical; (b) lateral.
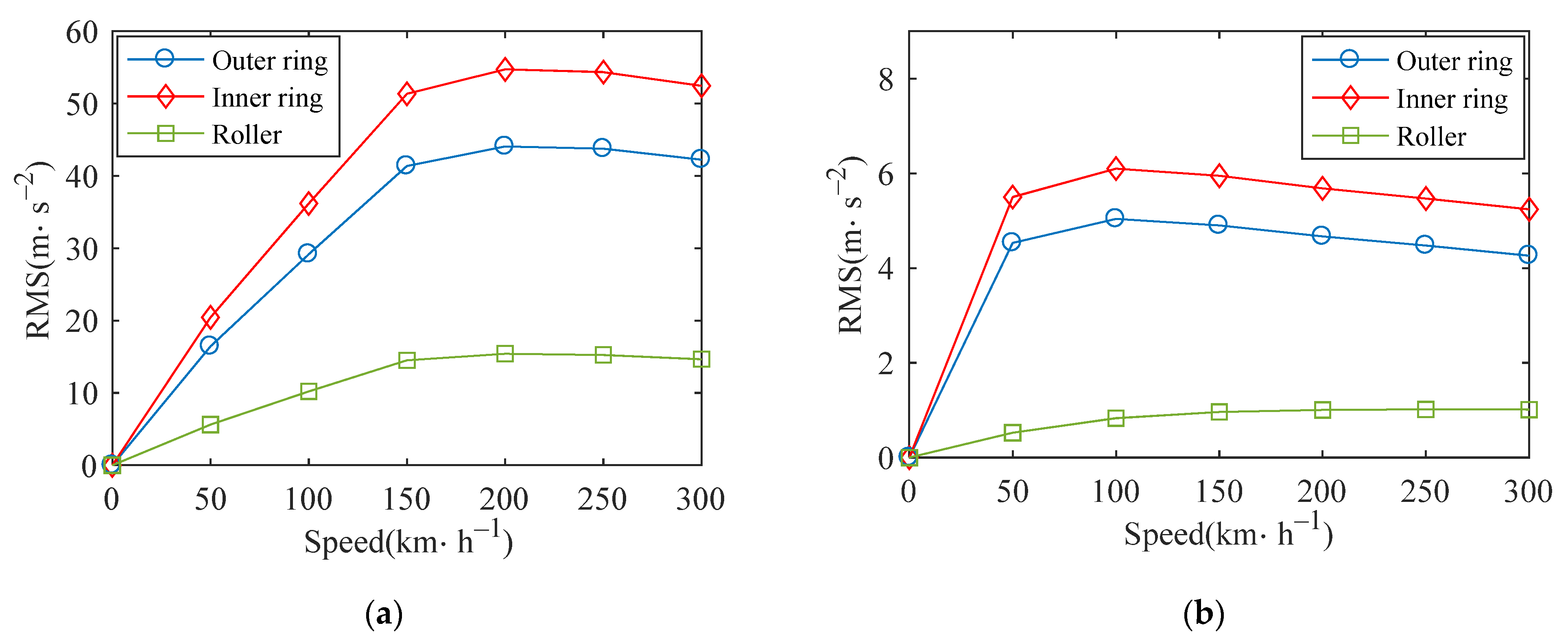
When the outer raceway of the bearing has a defect, the RMS values is shown in Figure 24. With the increase of speed, the RMS value of each element gradually increase and tend to be stable. It may be that in the process of speed increasing, the defect causes relatively large vibration of each element of the bearing. Under the current fault size, the acceleration of the bearing gradually reaches a maximum value and stops when it reaches a certain value. When the speed is higher (200–300 km/h), the RMS of acceleration decreases slightly, possibly because the speed reflects the quickness and slowness of the movement, while the acceleration reflects the change of the speed. When the speed reaches a certain value, the change of speed will be relatively stable, so the corresponding acceleration value will decrease slightly.
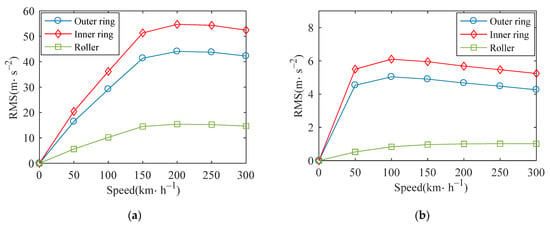
Figure 24.
RMS of outer ring acceleration of bearing with outer raceway fault: (a) vertical; (b) lateral.
The RMS of the defective bearings is greater than that of the normal bearing, because the vibration of the outer ring will increase under the effect of the defect, which will correspondingly increase the RMS of the defective bearings. Compared with normal bearing, the RMS has changed greatly, so it is necessary to further analyze the bearing with defects.
Normal bearing and bearings with inner raceway, outer raceway and roller defects are simulated respectively. Figure 25 shows the variation of RMS values of vertical and lateral acceleration of outer ring under four conditions. As the speed increases, the RMS value shows a gradually increasing trend from the overall situation. When the bearing is normal, the RMS value of the outer ring increases approximately linearly. When the inner ring and outer ring of the bearing have defects, the RMS values increase rapidly and gradually tend to be stable. When the roller has defect, the RMS value increases rapidly at low speed, and gradually tends to be stable at high speed. It can be found that the dynamic response of bearing shows different characteristics when the defect in different components.
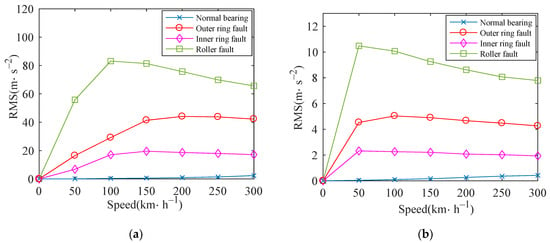
Figure 25.
RMS of outer race acceleration: (a) vertical; (b) lateral.
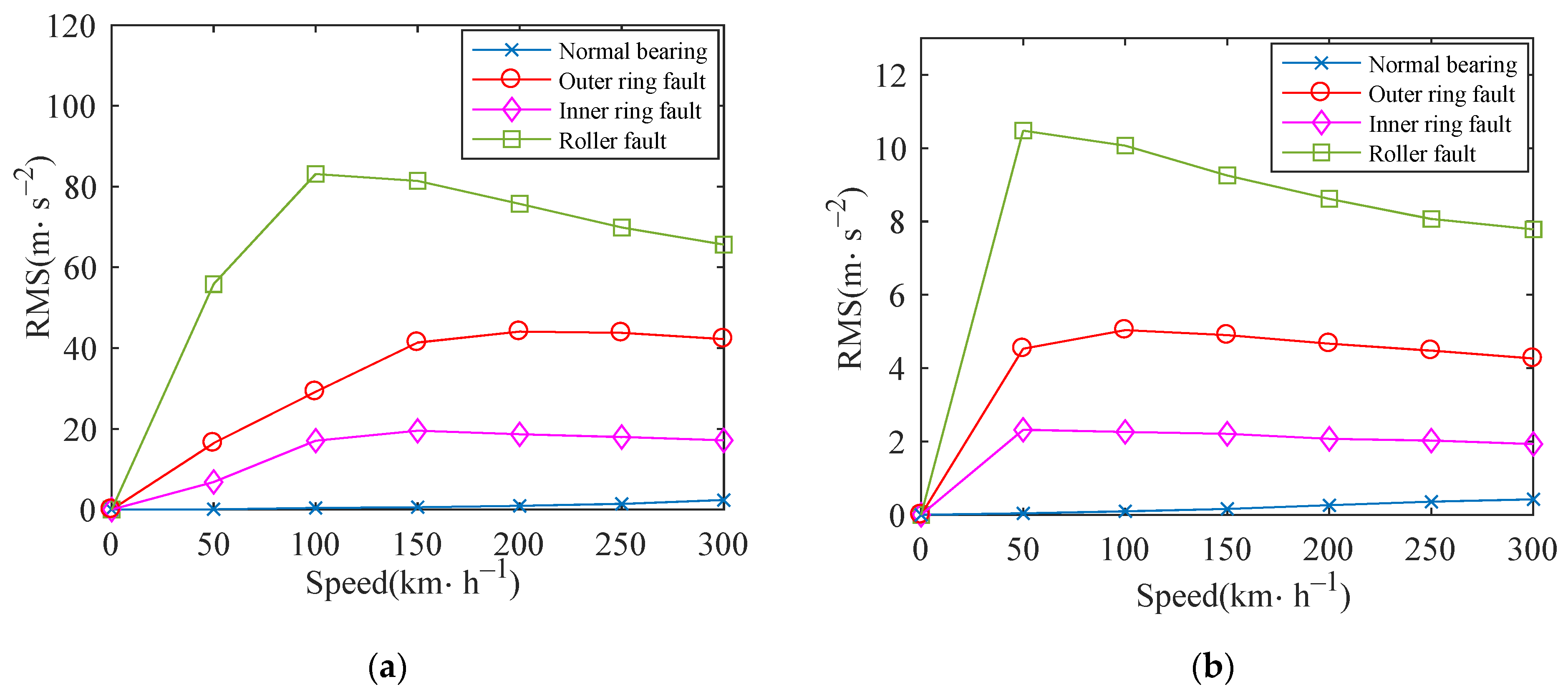
Figure 26 shows the RMS values of the vertical and horizontal contact forces between the roller and the outer raceway in four cases. The RMS values of the vertical contact forces are relatively close and stable, and that of the lateral contact forces have little difference, which gradually increase with the increase of speed and tend to be stable.
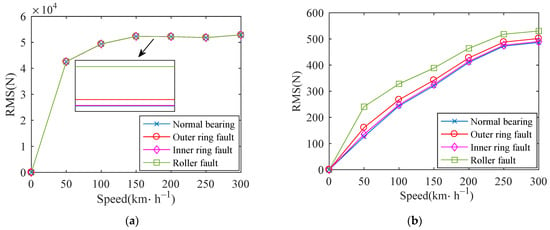
Figure 26.
RMS of outer raceway contact force: (a) vertical; (b) lateral.
Based on the above analysis, by comparing the vibration responses under different defects, it can be concluded that when the defect location appears on the roller, the impact on the vibration of the bearing is greater, followed by the defect located in the outer ring, and the impact is minimal when the defect is located in the inner ring.
7. Dynamic Response of Bearing under Flat Scar Impact
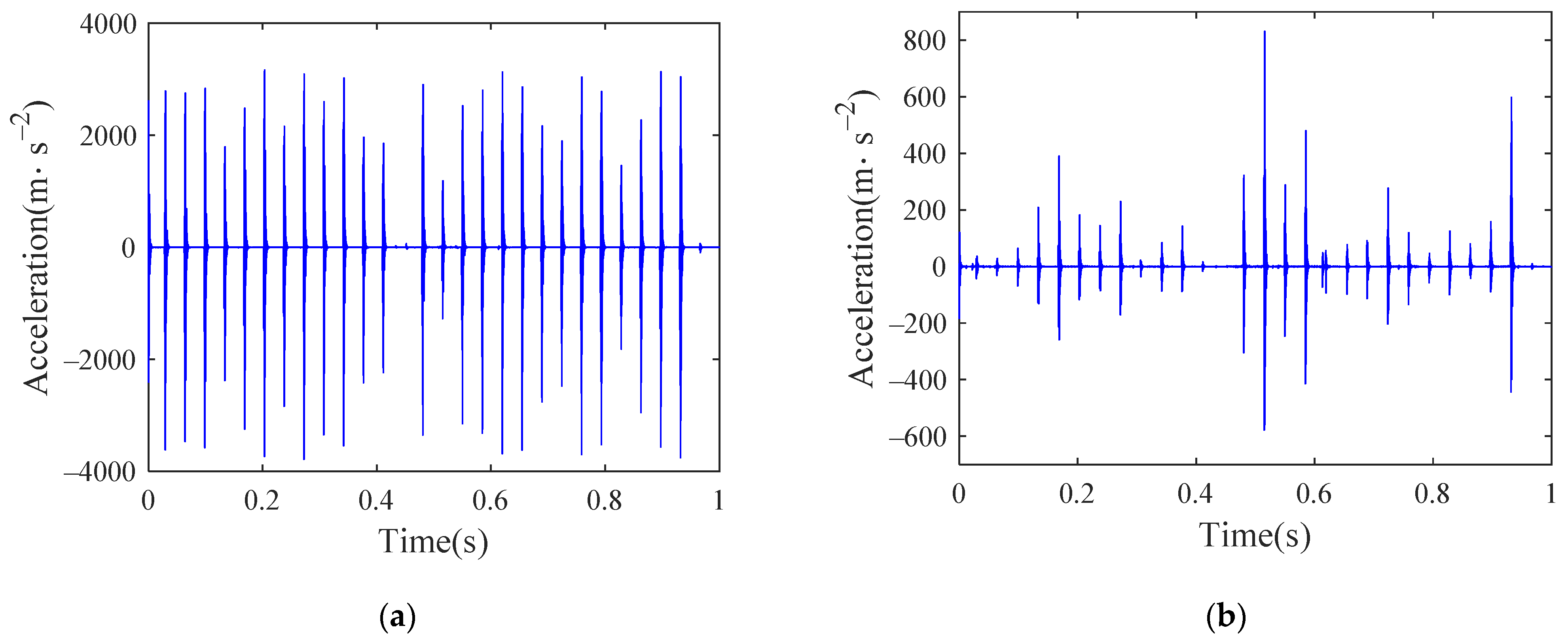
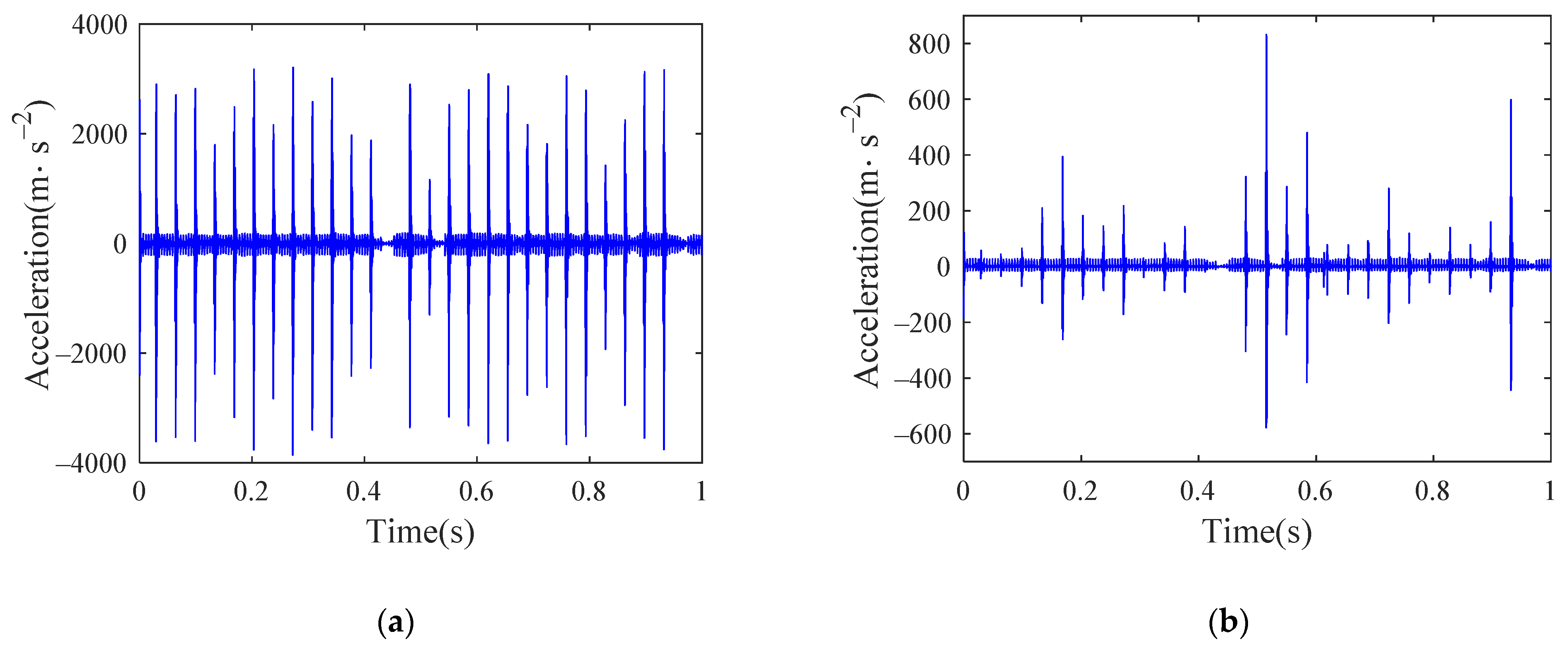
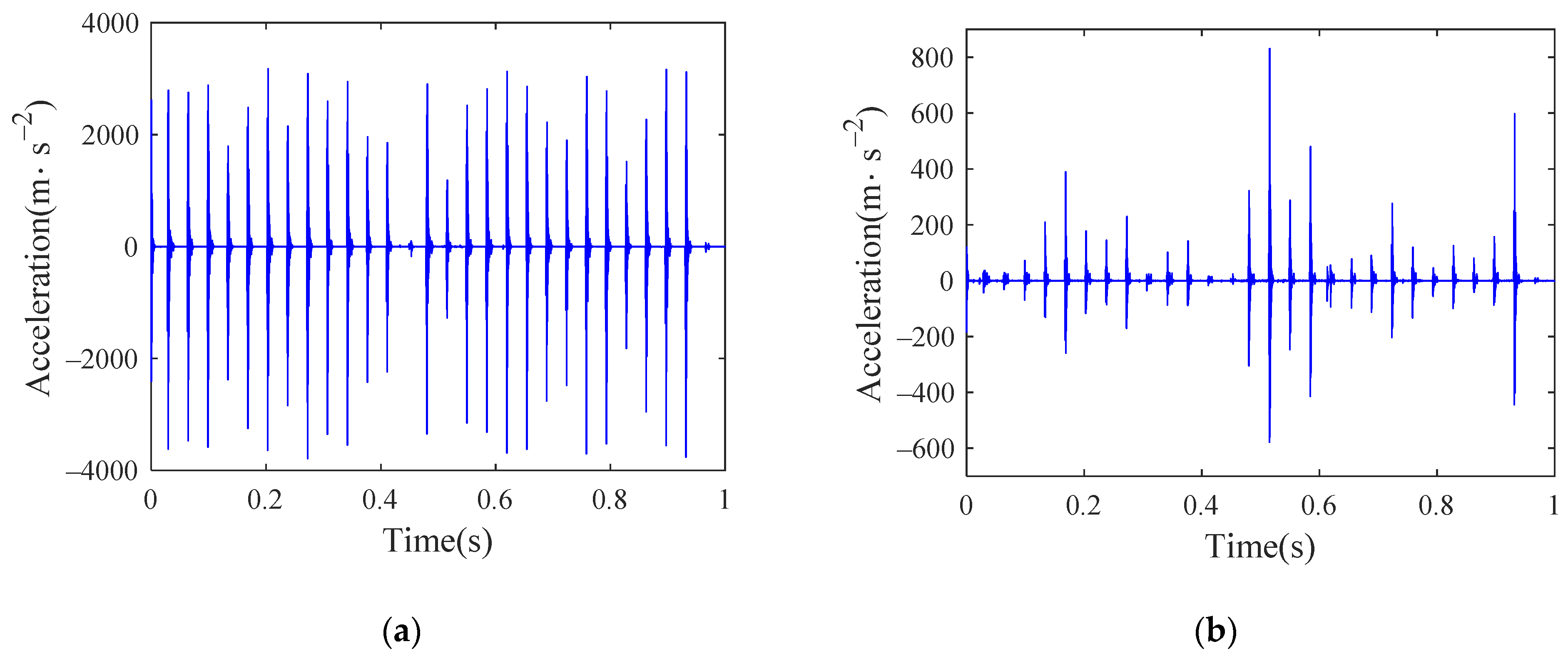
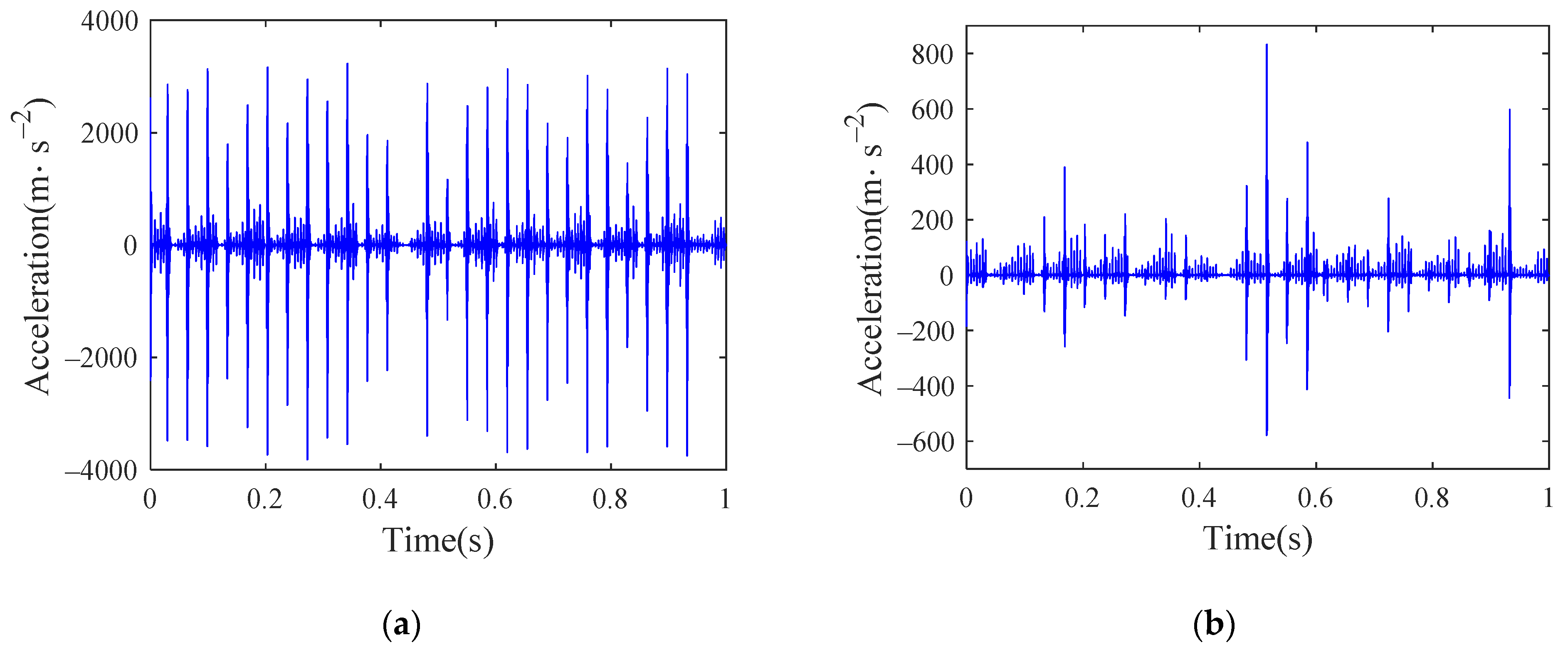
As the new flat scar exists for a relatively short time, this paper only considers the influence of the old flat scar in the study. Take the flat scar height as 0.1 mm, the length of the old flat scar after long-term wear is set to 90 mm. Set the vehicle speed as 300 km/h and input the German high interference track spectrum. The time history of the acceleration of the inner ring under four conditions are shown in Figure 27, Figure 28, Figure 29 and Figure 30. As the inner ring is connected with the axle, it is the bearing element most directly disturbed by the wheel and rail, so the response of the inner ring is selected for analysis. The results show that when the vehicle is running at a high speed, the flat scar impact will have a great impact on the bearing vibration in both the lateral and vertical directions. Judging from the amplitude change of acceleration, the bearing vibration caused by flat scar impact is far greater than that caused by bearing defects, which indicates that it may be difficult to detect the bearing defects when the wheel set has a flat scar.
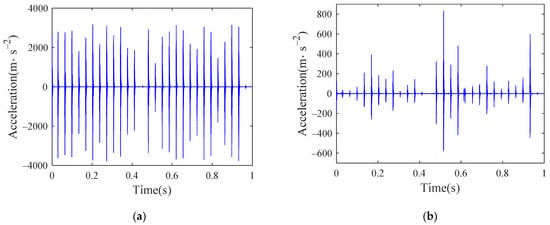
Figure 27.
Time history of inner ring acceleration of normal bearing: (a) vertical; (b) lateral.
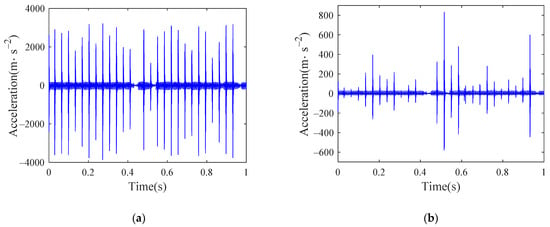
Figure 28.
Time history of inner ring acceleration of bearing with outer raceway defect: (a) vertical; (b) lateral.
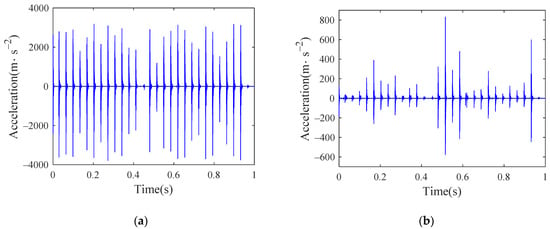
Figure 29.
Time history of inner ring acceleration of bearing with inner raceway defect: (a) vertical; (b) lateral.
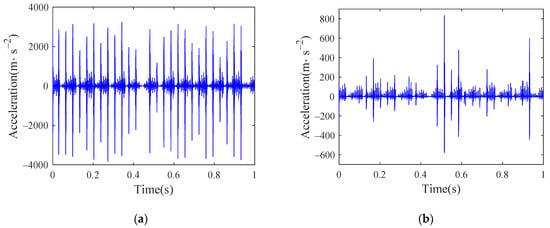
Figure 30.
Time history of inner ring acceleration of bearing with roller defect: (a) vertical; (b) lateral.
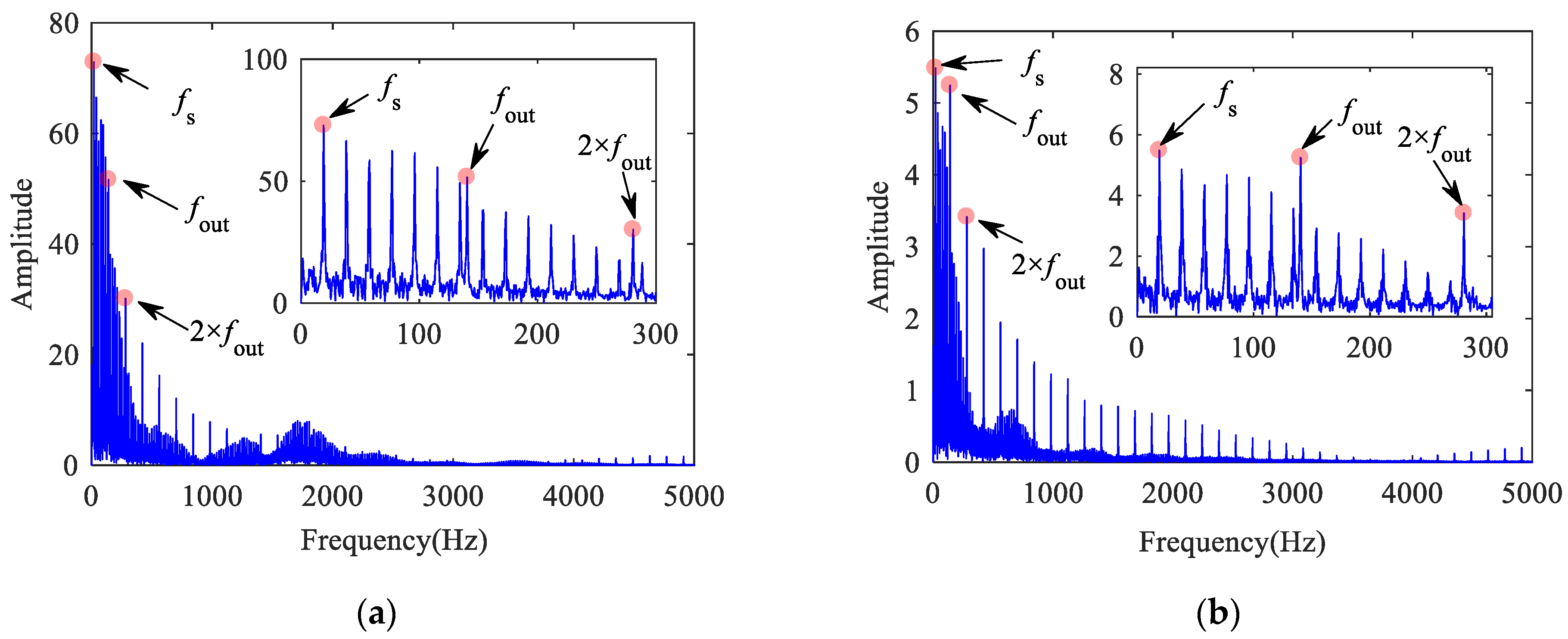
The contact frequency between the flat scar and the rail is equal to the SFR [37]. Figure 31, Figure 32, Figure 33 and Figure 34 show the frequency characteristics of the inner ring acceleration in four cases. In the low frequency section of 0–600 Hz, there are obvious SFR and its double-frequency. When the bearing defect exists, the FCFO and FCFR can be found in Figure 32 and Figure 34, respectively, but the FCFI cannot be found in Figure 33. In addition, the fault characteristic frequency of the bearing in the low frequency section will be covered by the SFR, while that in the high frequency section will gradually appear, especially in the lateral direction. Therefore, when there is flat scar on the wheel with high vehicle speed, it is difficult to detect the inner raceway defect. In addition, it may be relatively easier to detect the bearing defect by selecting the lateral direction and the high frequency section.
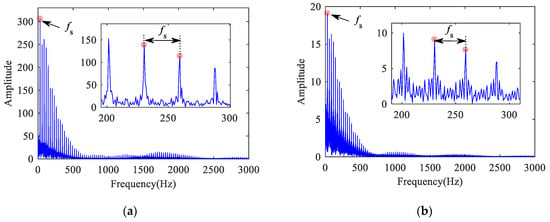
Figure 31.
Frequency spectrum of inner ring acceleration of normal bearing: (a) vertical; (b) lateral.
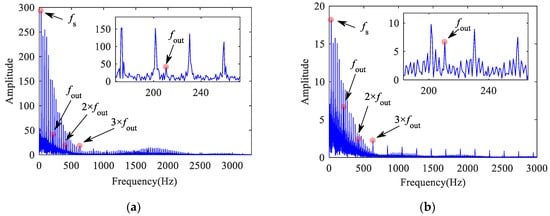
Figure 32.
Frequency spectrum of inner ring acceleration of bearing with outer raceway defect: (a) vertical; (b) lateral.
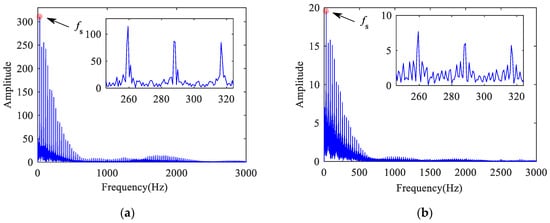
Figure 33.
Frequency spectrum of inner ring acceleration of bearing with inner raceway defect: (a) vertical; (b) lateral.
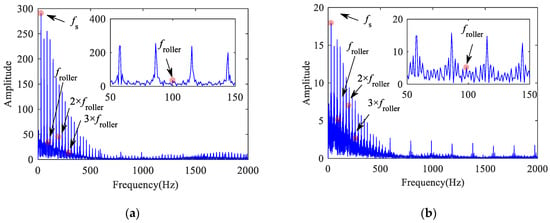
Figure 34.
Frequency spectrum of inner ring acceleration of bearing with roller defect: (a) vertical; (b) lateral.
In order to further explore the vibration law of the faulty bearing with flat scar impact, the frequency characteristics of the inner ring acceleration of the bearing with outer ring defect at different speeds are analyzed. As shown in Figure 35, Figure 36, Figure 37, Figure 38, Figure 39 and Figure 40, when the vehicle speed is 50–150 km/h, it can be found that the SFR is not obvious, but there are obvious FCFO and its double-frequency, especially at a lower speed. When the vehicle speed is 200 km/h, the amplitude of SFR begins to exceed that of FCFO, the FCFO is obvious in the lateral direction but not very obvious in the vertical direction. When the vehicle speed is 250 km/h–300 km/h, the presence of FCFO is weak.
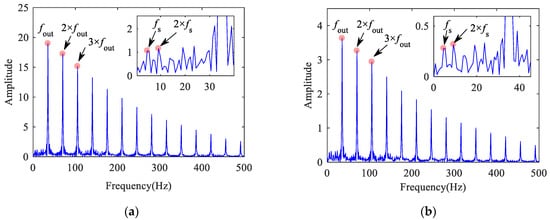
Figure 35.
Inner ring acceleration at speed of 50 km/h: (a) vertical; (b) lateral.
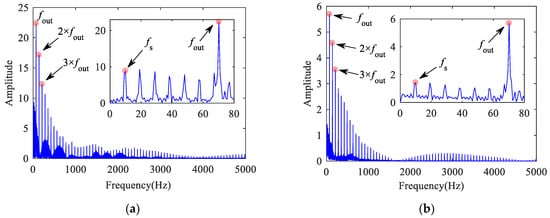
Figure 36.
Inner ring acceleration at speed of 100 km/h: (a) vertical; (b) lateral.
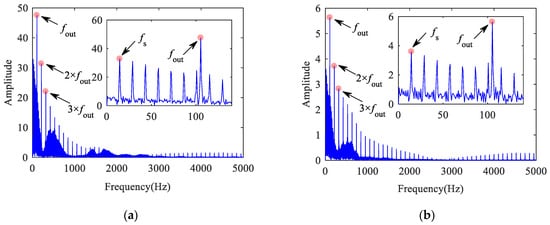
Figure 37.
Inner ring acceleration at speed of 150 km/h: (a) vertical; (b) lateral.
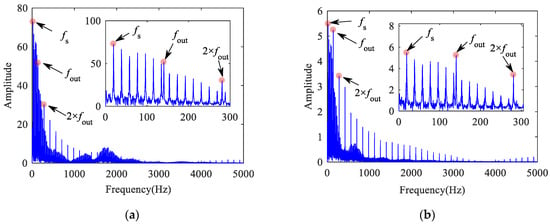
Figure 38.
Inner ring acceleration at speed of 200 km/h: (a) vertical; (b) lateral.
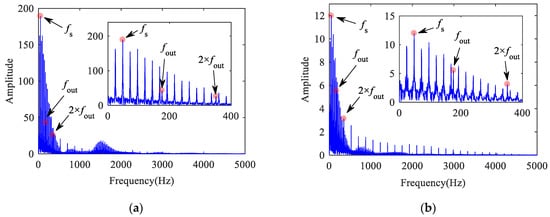
Figure 39.
Inner ring acceleration at speed of 250 km/h: (a) vertical; (b) lateral.
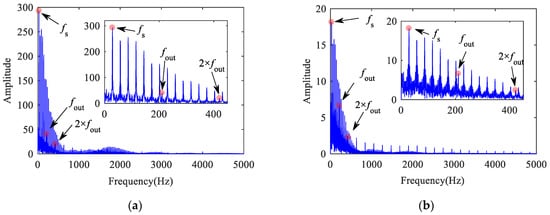
Figure 40.
Inner ring acceleration at speed of 300 km/h: (a) vertical; (b) lateral.
It can be seen from the overall trend that the growth rate of the SFR caused by the flat scar excitation is greater than that of the FCFO caused by the bearing out ring defect with the gradual increase of the speed. The SFR is easily detected in the range of 0–2200 Hz in the vertical direction and 0–1000 Hz in the horizontal direction. The FCFO in the lateral direction is obvious. When the speed exceeds 200 km/h, the influence of bearing defect is greater than that of flat scar. When the speed is in the range of 100–200 km/h, it is relatively easier to distinguish the impact caused by wheel flat scar and that caused by bearing defect.
From the above analysis, it can be concluded that when worn wheel flat scar and bearing outer raceway defect coexist, wheel flat scar is relatively easier to detect in the low frequency section. The higher the speed, the easier it is to detect. The bearing defect is relatively easier to detect in the high frequency section. The lower the speed, the easier it is to detect, especially in the lateral direction with low speed.
8. Conclusions
This paper establishes a three-dimensional dynamic model of a high-speed train-axle box bearing coupling system and adds the defects of outer raceway, inner raceway and roller to the model, respectively. The model is verified by simulation and experiment, which fully proves the effectiveness of the model established in the paper. The coupling model is applied to analyze the vibration response of the bearing. Based on the above analysis, some important conclusions can be drawn, which are as follows.
Through the co-simulation of MATLAB/Simulink and UM software and base on the force coupling between vehicle and bearing, the dynamic model of high-speed train-axle box bearing coupling system is established. The model can easily and efficiently solve the dynamic response of vehicle and bearing components, which lays a good foundation for further analysis and research into them.
- (1)
- The inner raceway defect, outer raceway defect and roller defect models are added to the vehicle bearing coupling system, respectively. The corresponding vibration responses are obtained by model simulation. The effectiveness of the model is verified by the comparison between the simulation and the experimental results;
- (2)
- Considering the real running conditions, the influence of track irregularity on normal bearing and defective bearings are analyzed. The results show that the track irregularity has a greater impact on the acceleration amplitude of normal bearing, and a smaller impact on that of defective bearings. However, whether the bearing is defective or not, its axis trajectory will change greatly, which shows that the influence of wheel rail excitation on axle box bearing cannot be ignored. This conclusion further reflects the superiority of the model proposed in this paper in analyzing the influence of actual factors on dynamic response of bearing;
- (3)
- The vibration characteristics of the system under different train speeds are studied. The results show that with the increase of train speed, the RMS value of each element of normal bearing increases gradually. When the bearing has defects, the RMS values gradually increase but tend to be stable. When the roller has a defect, the vibration of the bearing is relatively intense, followed by outer raceway defect and inner raceway defect;
- (4)
- When there is a flat scar on the wheel, it may have a great impact on the vibration of the bearing. When the worn wheel flat scar and bearing defect exist at the same time, wheel flat scar is relatively easier to detect in the low frequency section, and bearing defect is relatively easier to detect in the high frequency section, but it is difficult to detect the inner raceway defect. It is possible to obtain better results by selecting the lateral direction to detect the bearing defect when the speed is low enough. The defect of the outer ring and rollers of the bearing are relatively easy to detect, while that of the inner ring is relatively difficult. When the speed is in the range of 100–200 km/h, the impact caused by wheel flat scar and bearing fault may be easier distinguished.Based on the establishment of the three-dimensional vehicle-bearing coupling model, the paper focuses on the dynamic analysis of the bearing with early defects and that other defect types still need to be further explored and verified. The research conclusion of this paper may be helpful to the detection of bearing defect and wheel flat scar.
Author Contributions
Conceptualization, methodology, validation, and writing—review and editing, Q.M.; project administration, Y.L. (Yingying Liao) and Y.L. (Yongqiang Liu); supervision, S.Y.; data curation, B.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the, National Key R&D Program (Grant No. 2020YFB2007700), National Natural Science Foundation of China (Grant No. 11790282; 12032017; 12002221 and 11872256), S&T Program of Hebei (Grant No. 20310803D), Natural Science Foundation of Hebei Province (Grant No. A2020210028) and Graduate Innovation Funding Program of Hebei Education Department (Grant No. CXZZBS2022119).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhao, H.; Yang, X.; Tang, J.; Ma, W. Fault Analysis of Axle Box Bearings for High Speed Railway EMUs. Bearing 2022, 7, 1–8. [Google Scholar]
- Wang, X.; Hou, Y.; Sun, S.; Li, Q.; Ren, Z. Advances in key mechanical parameters for reliability assessment of high-speed train bearings. Chin. J. Theor. Appl. Mech. 2021, 53, 19–34. [Google Scholar]
- Jones, A.B. A general theory for elastically constrained ball and radial roller bearings under arbitrary load and speed conditions. J. Basic Eng. 1960, 82, 309–320. [Google Scholar] [CrossRef]
- Walters, C.T. The dynamics of ball bearings. J. Lubr. Technol. 1971, 93, 1–10. [Google Scholar] [CrossRef]
- Harris, T.A. An analytical method to predict skidding in thrust-loaded, angular-contact ball bearings. J. Lub. Technol. 1971, 93, 17. [Google Scholar] [CrossRef]
- Gupta, P.K. Advanced Dynamics of Rolling Elements; Springer: New York, NY, USA, 1984. [Google Scholar]
- Gupta, P.K. Cage unblance and wear in roller bearings. Wear 1991, 147, 105–118. [Google Scholar] [CrossRef]
- Gupta, P.K. Dynamic loads and cage wear in high-speed rolling bearings. Wear 1991, 147, 119–134. [Google Scholar] [CrossRef]
- Kogan, G.; Klein, R.; Kushnirsky, A.; Bortman, J. Toward a 3D dynamic model of a faulty duplex ball bearing. Mech. Syst. Signal Process. 2015, 54–55, 243–258. [Google Scholar] [CrossRef]
- Tong, V.C.; Hong, S.W. Characteristics of tapered roller bearing subjected to combined radial and moment loads. Int. J. Precis. Eng. Manuf. Green Technol. 2014, 1, 323–328. [Google Scholar] [CrossRef]
- Shi, Z.; Liu, J. An improved planar dynamic model for vibration analysis of a cylindrical roller bearing. Mech. Mach. Theory 2020, 153, 103994. [Google Scholar] [CrossRef]
- Yang, L.; Xu, T.; Xu, H.; Wu, Y. Mechanical behavior of double-row tapered roller bearing under combined external loads and angular misalignment. Int. J. Mech. Sci. 2018, 142, 561–574. [Google Scholar] [CrossRef]
- Liu, D. Research on Fatigue Life and Reliability of High-Speed Train Axle Box Bearing. Ph.D. Dissertation, Beijing Jiaotong University, Beijing, China, 2017. [Google Scholar]
- Eren, L.; Ince, T.; Kiranyaz, S. A Generic Intelligent Bearing Fault Diagnosis System Using Compact Adaptive 1D CNN Classifier. J. Signal Process. Syst. 2019, 91, 179–189. [Google Scholar] [CrossRef]
- Entezami, M.; Roberts, C.; Weston, P.; Stewart, E.; Amini, A.; Papaelias, M. Perspectives on railway axle bearing condition monitoring. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2020, 234, 17–31. [Google Scholar] [CrossRef]
- Amini, A.; Entezami, M.; Papaelias, M. Onboard detection of railway axle bearing defects using envelope analysis of high frequency acoustic emission signals. Case Stud. Nondestruct. Test. Eval. 2016, 6, 8–16. [Google Scholar] [CrossRef]
- Papaelias, M.; Amini, A.; Huang, Z.; Vallely, P.; Dias, D.C.; Kerkyras, S. Online condition monitoring of rolling stock wheels and axle bearings. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2016, 230, 709–723. [Google Scholar] [CrossRef]
- Fan, W.; Xue, H.; Yi, C.; Xu, Z. TQWT-assisted statistical process control method for condition monitoring and fault diagnosis of bearings in high-speed rail. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2021, 235, 230–240. [Google Scholar] [CrossRef]
- Yi, C.; Wang, D.; Fan, W.; Tsui, K.-L.; Lin, J. EEMD-based steady-state indexes and their applications to condition monitoring and fault diagnosis of railway axle bearings. Sensors 2018, 18, 704. [Google Scholar] [CrossRef]
- Yang, R.; Zhang, Z.; Chen, Y. Analysis of vibration signals for a ball bearing-rotor system with raceway local defects and rotor eccentricity. Mech. Mach. Theory 2022, 169, 104594. [Google Scholar] [CrossRef]
- Tu, W.; Yang, J.; Yu, W.; Luo, Y. Contact characteristic and vibration mechanism of rolling element bearing in the process of fault evolution. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2021, 235, 19–36. [Google Scholar] [CrossRef]
- Luo, W.; Yan, C.; Yang, J.; Liu, Y.; Wu, L. Vibration response of defect-ball-defect of rolling bearing with compound defects on both inner and outer races. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2021; Volume 1207, p. 012006. [Google Scholar]
- Liu, Y.; Wang, B.; Zhang, B.; Yng, S. Establishment of dynamic model for axle box bearing of high-speed trains under variable speed conditions. Chin. J. Mech. Eng. 2022, 35, 47. [Google Scholar] [CrossRef]
- Du, Z.; Zhen, G.; Tian, R. Simulation analysis of dynamic features of axle box bearing fault of high speed EMU. J. Railw. Technol. Superv. 2021, 49, 31–36+41. [Google Scholar]
- Liu, J. A dynamic modelling method of a rotor-roller bearing-housing system with a localized fault including the additional excitation zone. J. Sound Vib. 2020, 469, 115144. [Google Scholar] [CrossRef]
- Patel, U.K.A.; Upadhyay, S.H. Nonlinear dynamic response of cylindrical roller bearing-rotor system with 9 degree of freedom model having a combined localized defect at inner–outer races of bearing. Tribol. Trans. 2017, 60, 284–299. [Google Scholar] [CrossRef]
- Singh, S.; Köpke, U.G.; Howard, C.Q.; Petersen, D. Analyses of contact forces and vibration response for a defective rolling element bearing using an explicit dynamics finite element model. J. Sound Vib. 2014, 333, 5356–5377. [Google Scholar] [CrossRef]
- Petersen, D.; Howard, C.; Sawalhi, N.; Ahmadi, A.M.; Singh, S. Analysis of bearing stiffness variations, contact forces and vibrations in radially loaded double row rolling element bearings with raceway defects. Mech. Syst. Signal Process. 2015, 50, 139–160. [Google Scholar] [CrossRef]
- Sawalhi, N.; Randall, R.B. Vibration response of spalled rolling element bearings: Observations, simulations and signal processing techniques to track the spall size. Mech. Syst. Signal Process. 2011, 25, 846–870. [Google Scholar] [CrossRef]
- Wang, T.; Wang, Z.; Song, D.; Zhang, W.; Li, J. Effect of track irregularities of high-speed railways on the thermal characteristics of the traction motor bearing. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2021, 235, 22–34. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, W.; Yin, Z.; Cheng, Y.; Huang, G.; Zou, H. Effect of vehicle vibration environment of high-speed train on dynamic performance of axle box bearing. Veh. Syst. Dyn. 2019, 57, 543–563. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Z.; Wang, K.; Zhai, W. Dynamic modelling of traction motor bearings in locomotive-track spatially coupled dynamics system. Veh. Syst. Dyn. 2021, 60, 2686–2715. [Google Scholar] [CrossRef]
- Ma, X.; Liu, J.; Shi, W. Dynamic characteristics of high-speed railway vehicle with axle box bearing faults. IOP Conf. Ser. Mater. Sci. Eng. 2019, 563, 032023. [Google Scholar]
- Niu, Z. Vibration Characteristics and Experimental Study of Axle Box System of High Speed Train. Ph.D. Thesis, Jilin University, Jilin, China, 2019. [Google Scholar]
- Liu, G.; Zeng, J.; Luo, R. Vibration performance of high-speed vehicles with axle box bearing defects. J. Vib. Shock. 2016, 35, 37–42. [Google Scholar]
- Liu, J.; Du, S. Dynamic Analysis of a High-Speed Railway Train with the Defective Axle Bearing. Int. J. Acoust. Vib. 2020, 25, 525–531. [Google Scholar] [CrossRef]
- Wang, J.; Yang, J.; Bai, Y.; Zhao, Y.; He, Y.; Yao, D. A comparative study of the vibration characteristics of railway vehicle axle box bearings with inner/outer race faults. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2021, 235, 1035–1047. [Google Scholar] [CrossRef]
- Lu, Z.; Wang, X.; Yue, K.; Wei, J.; Yang, Z. Coupling model and vibration simulations of railway vehicles and running gear bearings with multitype defects. Mech. Mach. Theory 2021, 157, 104215. [Google Scholar] [CrossRef]
- Cheli, F.; Corradi, R. On rail vehicle vibrations induced by track unevenness: Analysis of the excitation mechanism. J. Sound Vib. 2011, 330, 3744–3765. [Google Scholar] [CrossRef]
- Li, T.; Sun, W.; Meng, Z.; Huo, J.; Dong, J.; Wang, L. Dynamic investigation on railway vehicle considering the dynamic effect from the axle box bearings. Adv. Mech. Eng. 2019, 11, 1687814019840503. [Google Scholar] [CrossRef]
- Liu, X.; Zhai, W. Analysis of vertical dynamic wheel/rail interaction caused by polygonal wheels on high-speed trains. Wear 2014, 314, 282–290. [Google Scholar] [CrossRef]
- Wu, Y.; Han, J.; Liu, J.; Liang, S.; Jin, X. Effect of high-speed train polygonal wheels on wheel/rail contact force and bogie vibration. J. Mech. Eng. 2018, 54, 37–46. [Google Scholar] [CrossRef]
- Yang, G.; Li, G.; Liu, Z.; Wang, W. Vibration characteristics analysis of gearbox housing system of high-speed train subjected to wheel-rail excitation. J. China Railw. Soc. 2017, 39, 46–52. [Google Scholar]
- Liu, G.; Zeng, J.; Pingbo, W.U. Vibration characteristic analysis of vehicle systems due to wheel flat. J. Mech. Eng. 2020, 56, 182–189. [Google Scholar]
- Chudzikiewicz, A.; Bogacz, R.; Kostrzewski, M.; Konowrocki, R. Condition monitoring of railway track systems by using acceleration signals on wheelset axle-boxes. Transport 2018, 33, 555–566. [Google Scholar] [CrossRef]
- Bogacz, R.; Frischmuth, K. On dynamic effects of wheel-rail interaction in the case of Polygonalisation. Mech. Syst. Signal Process. 2016, 79, 166–173. [Google Scholar] [CrossRef]
- Bogacz, R.; Kurnik, W. On some rotor-dynamical phenomena of high-speed trains. Arch. Appl. Mech. 2015, 85, 1343–1352. [Google Scholar] [CrossRef]
- Wang, Z.; Allen, P.; Mei, G.; Wang, R.; Yin, Z.; Zhang, W. Influence of wheel-polygonal wear on the dynamic forces within the axle-box bearing of a high-speed train. Veh. Syst. Dyn. 2019, 58, 1385–1406. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Z.; Zhai, W.; Wang, K. Dynamic investigation of traction motor bearing in a locomotive under excitation from track random geometry irregularity. Int. J. Rail Transp. 2022, 10, 72–94. [Google Scholar] [CrossRef]
- Zha, H.; Ren, Z.; Xu, N. Impact characteristics of axle box bearing due to wheel flat scars. J. Traffic Transp. Eng. 2020, 20, 165–173. [Google Scholar]
- Palmgren, A. Ball and Roller Bearing Engineering; SKF Industries Inc.: Philadelphia, PA, USA, 1959. [Google Scholar]
- Ren, Z.; Liu, Z. Vibration and frequency domain characteristics of high speed EMU. J. Mech. Eng. 2013, 49, 1–7. [Google Scholar] [CrossRef]
- Zhai, W. Dynamic effect of wheel flats in railway. Roll. Stock. 1994, 7, 1–5. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).