A Vision-Based Underwater Formation Control System Design and Implementation on Small Underwater Spherical Robots
Abstract
:1. Introduction
2. Related Works
3. Underwater Spherical Robot Platform Set up
3.1. Electronic System
3.2. Motion Control System Design
4. Underwater Visual System
4.1. Relative Positioning Principle
4.2. Underwater Camera Calibration
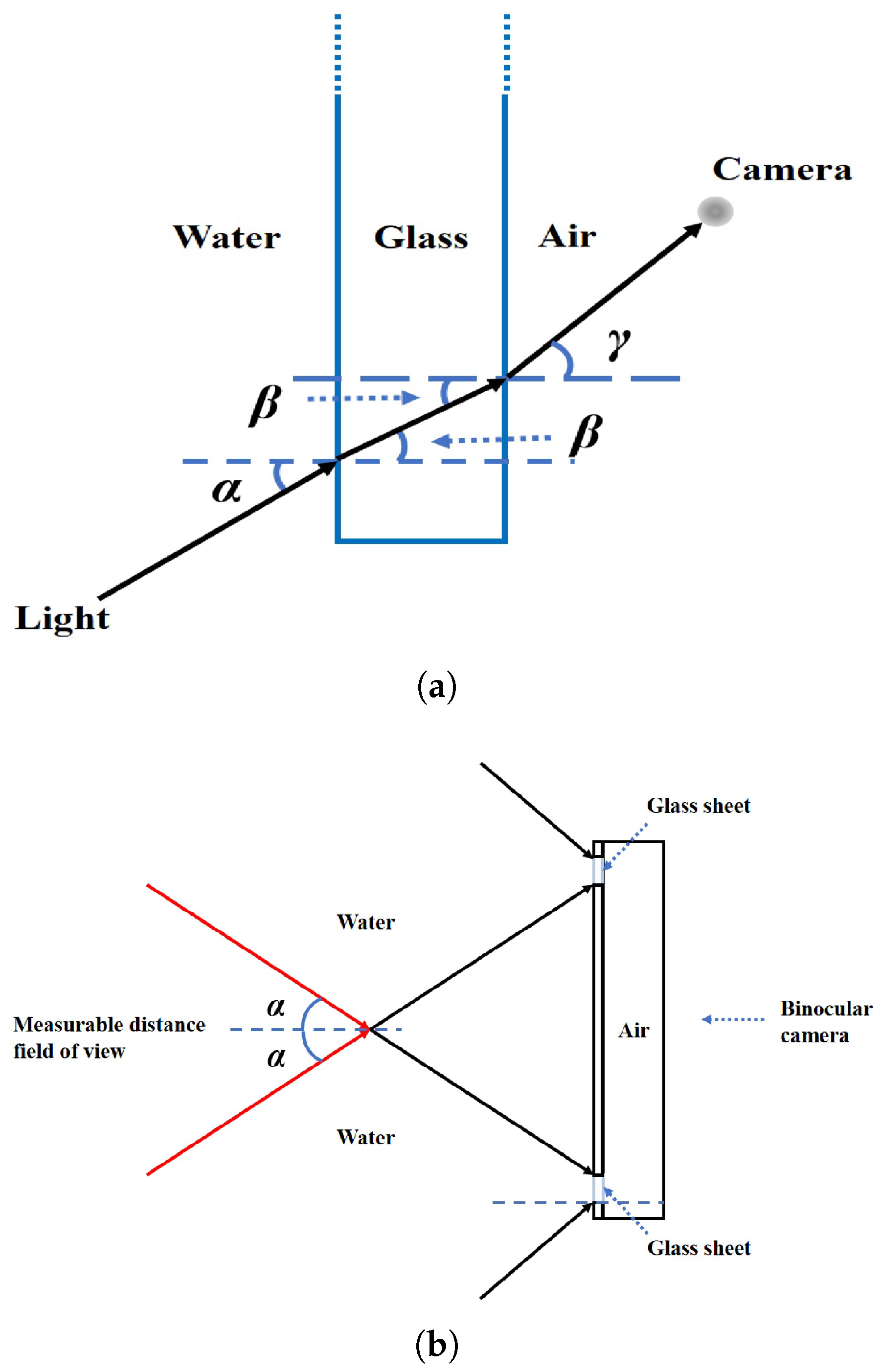
4.3. Analysis of Binocular Field of View
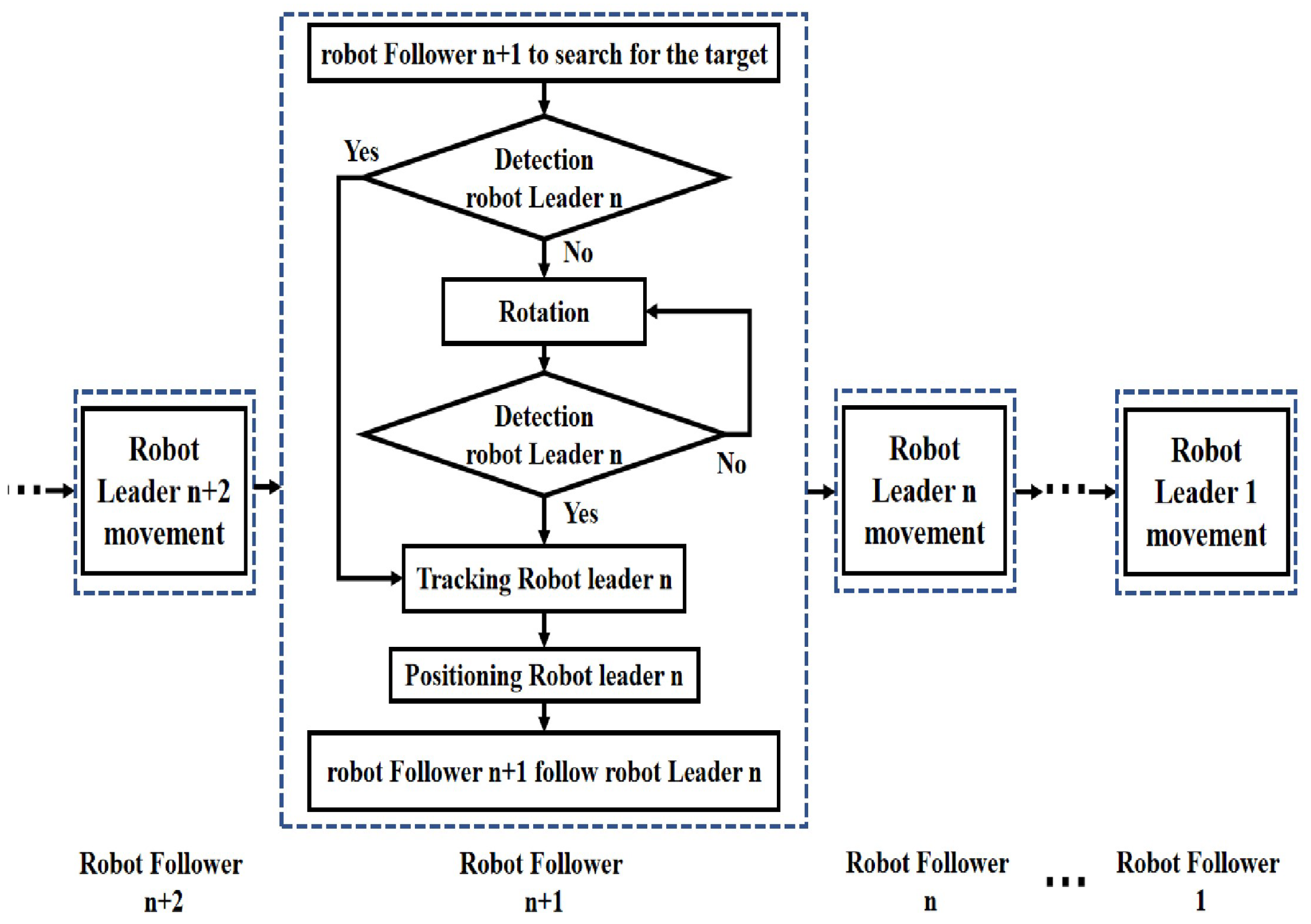
5. Multi-Robot Formation Control System Design
5.1. Formation Structure Design
5.2. Modelling and Control of the Vision-Based Formation System
6. Experiments
6.1. Underwater Motion Control Experiment
6.1.1. Linear Motion of a Single Robot
6.1.2. Rotation Motion of a Single Robot
6.2. Underwater Visual System Experiment
Underwater Camera Calibration Experiment
6.3. Underwater Formation Experiments
6.3.1. Underwater Vision-Based Ranging Experiment
6.3.2. Dynamic Straight-Line Formation Experiment
6.3.3. “V-Type Escort” Formation Experiment
6.3.4. “Round-Up Hunting” Formation Experiment
7. Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yuh, J.; West, M. Underwater robotics. Adv. Robot. 2001, 15, 609–639. [Google Scholar] [CrossRef]
- Sivčev, S.; Coleman, J.; Omerdić, E.; Dooly, G.; Toal, D. Underwater manipulators: A review. Ocean. Eng. 2018, 163, 431–450. [Google Scholar] [CrossRef]
- Sahoo, A.; Dwivedy, S.; Robi, P. Advancements in the field of autonomous underwater vehicle. Ocean. Eng. 2019, 181, 145–160. [Google Scholar] [CrossRef]
- Wu, Y.; Low, K.H.; Lv, C. Cooperative path planning for heterogeneous unmanned vehicles in a search-and-track mission aiming at an underwater target. IEEE Trans. Veh. Technol. 2020, 69, 6782–6787. [Google Scholar] [CrossRef]
- Saback, R.; Conceicao, A.; Santos, T.; Albiez, J.; Reis, M. Nonlinear model predictive control applied to an autonomous underwater vehicle. IEEE J. Ocean. Eng. 2020, 45, 799–812. [Google Scholar] [CrossRef]
- Zhou, Z.; Liu, J.; Yu, J. A survey of underwater multi-robot systems. IEEE/CAA J. Autom. Sin. 2021, 1, 1–18. [Google Scholar] [CrossRef]
- Connor, J.; Champion, B.; Joordens, M.A. Current algorithms, communication methods and designs for underwater swarm robotics: A review. IEEE Sens. J. 2020, 1, 153–169. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, Y.; Wen, J.; Li, K.; Yang, G. An Application of Improved RANSAC Algorithm in Visual Positioning. In Proceedings of the 2019 IEEE 8th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 24–26 May 2019; pp. 1358–1362. [Google Scholar] [CrossRef]
- Cui, R.X.; Ge, S.Z.S.; How, B.V.E.; Choo, Y.S. Leader-follower formation control of underactuated autonomous underwater vehicles. Ocean. Eng. 2010, 37, 1491–1502. [Google Scholar] [CrossRef]
- Wang, J.Q.; Wang, C.; Wei, Y.J.; Zhang, C.J. Sliding mode based neural adaptive formation control of underactuated AUVs with leader-follower strategy. Appl. Ocean. Res. 2020, 94, 101971. [Google Scholar] [CrossRef]
- Makavita, C.; Jayasinghe, S.; Nguyen, H.; Ranmuthugala, D. Experimental study of command governor adaptive control for unmanned underwater vehicles. IEEE Trans. Control Syst. Technol. 2019, 27, 332–345. [Google Scholar] [CrossRef]
- Beard, R.W.; Lawton, J.; Hadaegh, F.Y. A coordination architecture for spacecraft formation control. IEEE Trans. Control Syst. Technol. 2001, 9, 777–790. [Google Scholar] [CrossRef]
- Fiorelli, E.; Leonard, N.E.; Bhatta, P.; Paley, D.A.; Bachmayer, R.; Fratantoni, D.M. Multi-AUV control and adaptive sampling in Monterey Bay. IEEE J. Ocean. Eng. 2006, 31, 935–948. [Google Scholar] [CrossRef]
- An, R.; Guo, S.; Yu, Y.; Li, C.; Awa, T. Task Planning and Collaboration of Jellyfish-inspired Multiple Spherical Underwater Robots. J. Bionic Eng. 2022, 3, 643–656. [Google Scholar] [CrossRef]
- Balch, T.; Arkin, R.C. Behavior-based formation control for multirobot teams. IEEE Trans. Robot. Autom. 1998, 14, 926–939. [Google Scholar] [CrossRef]
- dell’Erba, R. Swarm robotics and complex behaviour of continuum material. Contin. Mech. Thermodyn. 2019, 31, 989–1014. [Google Scholar] [CrossRef]
- Hadi, B.; Khosravi, A.; Sarhadi, P. A review of the path planning and formation control for multiple autonomous underwater vehicles. J. Intell. Robot. Syst. 2021, 101, 67. [Google Scholar] [CrossRef]
- Shojaei, K.; Chatraei, A. Robust platoon control of underactuated autonomous underwater vehicles subjected to nonlinearities, uncertainties and range and angle constraints. Appl. Ocean. Res. 2021, 110, 102594. [Google Scholar] [CrossRef]
- Chen, Y.L.; Ma, X.W.; Bai, G.Q.; Sha, Y.; Liu, J. Multi-autonomous underwater vehicle formation control and cluster search using a fusion control strategy at complex underwater environment. Ocean. Eng. 2020, 216, 108048. [Google Scholar] [CrossRef]
- Liu, H.; Wang, Y.; Lewis, F.L. Robust Distributed Formation Controller Design for a Group of Unmanned Underwater Vehicles. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 1215–1223. [Google Scholar] [CrossRef]
- Gao, Z.; Guo, G. Velocity free leader-follower formation control for autonomous underwater vehicles with line-of-sight range and angle constraints. Inf. Sci. 2019, 486, 359–378. [Google Scholar] [CrossRef]
- Liang, H.; Fu, Y.; Gao, J.; Cao, H. Finite-time velocity-observed based adaptive output-feedback trajectory tracking formation control for underactuated unmanned underwater vehicles with prescribed transient performance. Ocean. Eng. 2021, 233, 109071. [Google Scholar] [CrossRef]
- Xiang, X.; Jouvencel, B.; Parodi, O. Coordinated formation control of multiple autonomous underwater vehicles for pipeline inspection. Int. J. Adv. Robot. Syst. 2010, 1, 3. [Google Scholar] [CrossRef]
- Cao, X.; Guo, L. A leader–follower formation control approach for target hunting by multiple autonomous underwater vehicle in three-dimensional underwater environments. Int. J. Adv. Robot. Syst. 2019, 4, 1729881419870664. [Google Scholar] [CrossRef]
- He, S.; Wang, M.; Dai, S.L.; Luo, F. Leader–follower formation control of USVs with prescribed performance and collision avoidance. IEEE Trans. Ind. Inform. 2018, 15, 572–581. [Google Scholar] [CrossRef]
- Lin, J.; Miao, Z.; Zhong, H.; Peng, W.; Wang, Y.; Fierro, R. Adaptive image-based leader–follower formation control of mobile robots with visibility constraints. IEEE Trans. Ind. Electron. 2020, 68, 6010–6019. [Google Scholar] [CrossRef]
- Han, Z.; Guo, K.; Xie, L.; Lin, Z. Integrated relative localization and leader–follower formation control. IEEE Trans. Autom. Control 2018, 64, 20–34. [Google Scholar] [CrossRef]
- Gao, Z.; Guo, G. Fixed-time leader-follower formation control of autonomous underwater vehicles with event-triggered intermittent communications. IEEE Access 2018, 6, 27902–27911. [Google Scholar] [CrossRef]
- Ai, X.; Yu, J. Flatness-based finite-time leader–follower formation control of multiple quadrotors with external disturbances. Aerosp. Sci. Technol. 2019, 92, 20–33. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, T.; Zhang, T.; Zhou, F.; Cen, N.; Li, T.; Xie, G. Global vision-based formation control of soft robotic fish swarm. Soft Robotics 2021, 3, 310–318. [Google Scholar] [CrossRef]
- Zheng, L.; Guo, S.; Piao, Y.; Gu, S.; An, R. Collaboration and Task Planning of Turtle-Inspired Multiple Amphibious Spherical Robots. Micromachines 2020, 11, 71. [Google Scholar] [CrossRef]
- He, Y.; Zhu, L.; Sun, G.; Dong, M. Study on formation control system for underwater spherical multi-robot. Microsyst. Technol. 2019, 4, 1455–1466. [Google Scholar] [CrossRef]
- Campos, R.; Gracias, N.; Ridao, P. Underwater multi-vehicle trajectory alignment and mapping using acoustic and optical constraints. Sensors 2016, 3, 387. [Google Scholar] [CrossRef] [PubMed]
- Millán, P.; Orihuela, L.; Jurado, I.; Rubio, F.R. Formation control of autonomous underwater vehicles subject to communication delays. IEEE Trans. Control Syst. Technol. 2013, 2, 770–777. [Google Scholar] [CrossRef]
- Das, B.; Subudhi, B.; Pati, B.B. Adaptive sliding mode formation control of multiple underwater robots. Arch. Control Sci. 2014, 4, 515–543. [Google Scholar] [CrossRef]
- Qi, X.; Cai, Z. Three-dimensional formation control based on nonlinear small gain method for multiple underactuated underwater vehicles. Ocean. Eng. 2018, 4, 515–543. [Google Scholar] [CrossRef]
- Fukuda, T. Cyborg and Bionic Systems: Signposting the Future. Cyborg Bionic Syst. 2020, 2020, 1310389. [Google Scholar] [CrossRef]
- Shi, Q.; Gao, J.; Wang, S.; Quan, X.; Jia, G.; Huang, Q.; Fukuda, T. Deveopment of a Small-Sized Quadruped Robotic Rat Capable of Multimodal Motions. IEEE Trans. Robot. 2022, 1–17. [Google Scholar] [CrossRef]
- Shi, Q.; Gao, Z.; Jia, G.; Li, C.; Huang, Q.; Ishii, H.; Takanishi, A.; Fukuda, T. Implementing Rat-Like Motion for a Small-Sized Biomimetic Robot Based on Extraction of Key Movement Joints. IEEE Trans. Robot. 2021, 3, 747–762. [Google Scholar] [CrossRef]
- Namiki, A.; Yokosawa, S. Origami folding by multifingered hands with motion primitives. Cyborg Bionic Syst. 2021, 2021, 9851834. [Google Scholar] [CrossRef]
- Wang, Y.; Li, W.; Togo, S.; Yokoi, H.; Jiang, Y. Survey on Main Drive Methods Used in Humanoid Robotic Upper Limbs. Cyborg Bionic Syst. 2021, 2021, 9817487. [Google Scholar] [CrossRef]
- Shi, L.; Bao, P.; Guo, S.; Chen, Z.; Zhang, Z. Underwater Formation System Design and Implement for Small Spherical Robots. IEEE Syst. J. 2022. [Google Scholar] [CrossRef]
- Lin, X.; Guo, S. Development of a spherical underwater robot equipped with multiple vectored water-jet-based thrusters. J. Intell. Robot. Syst. 2012, 3, 307–321. [Google Scholar] [CrossRef]
- Xing, H.; Shi, L.; Hou, X.; Liu, Y.; Hu, Y.; Xia, D.; Li, Z.; Guo, S. Design, modeling and control of a miniature bio-inspired amphibious spherical robot. Mechatronics 2021, 77, 102574. [Google Scholar] [CrossRef]
- Shi, L.; Hu, Y.; Su, S.; Guo, S.; Xing, H.; Hou, X.; Liu, Y.; Chen, Z.; Li, Z.; Xia, D. A fuzzy PID algorithm for a novel miniature spherical robots with three-dimensional underwater motion control. J. Bionic Eng. 2020, 5, 959–969. [Google Scholar] [CrossRef]
- Xing, H.; Guo, S.; Shi, L.; Hou, X.; Liu, Y.; Liu, H. Design, modeling and experimental evaluation of a legged, multi-vectored water-jet composite driving mechanism for an amphibious spherical robot. Microsyst. Technol. 2020, 2, 475–487. [Google Scholar] [CrossRef]
- He, Y.; Guo, S.; Shi, L.; Xing, H.; Chen, Z.; Su, S. Motion characteristic evaluation of an amphibious spherical robot. Int. J. Robot. Autom. 2019, 3. [Google Scholar] [CrossRef]
- Guo, S.; He, Y.; Shi, L.; Pan, S.; Xiao, R.; Tang, K.; Guo, P. Modeling and experimental evaluation of an improved amphibious robot with compact structure. Robot. Comput.-Integr. Manuf. 2018, 51, 37–52. [Google Scholar] [CrossRef]
- He, Y.; Zhu, L.; Sun, G.; Qiao, J.; Guo, S. Underwater motion characteristics evaluation of multi amphibious spherical robots. Microsyst. Technol. 2019, 2, 499–508. [Google Scholar] [CrossRef]
- Xing, H.; Guo, S.; Shi, L.; He, Y.; Su, S.; Chen, Z.; Hou, X. Hybrid locomotion evaluation for a novel amphibious spherical robot. Appl. Sci. 2018, 2, 156. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Guo, S.; Yue, C. Preliminary concept of a novel spherical underwater robot. Int. J. Mechatron. Autom. 2015, 1, 11–21. [Google Scholar] [CrossRef]
- Xing, H.; Liu, Y.; Guo, S.; Shi, L.; Hou, X.; Liu, W.; Zhao, Y. A Multi-Sensor Fusion Self-Localization System of a Miniature Underwater Robot in Structured and GPS-Denied Environments. IEEE Sens. J. 2021, 23, 27136–27146. [Google Scholar] [CrossRef]
- Shi, L.; Guo, S.; Mao, S.; Yue, C.; Li, M.; Asaka, K. Development of an amphibious turtle-inspired spherical mother robot. J. Bionic Eng. 2013, 4, 446–455. [Google Scholar] [CrossRef]
- Li, M.; Guo, S.; Hirata, H.; Ishihara, H. Design and performance evaluation of an amphibious spherical robot. Robot. Auton. Syst. 2015, 64, 21–34. [Google Scholar] [CrossRef]
- Hou, X.; Guo, S.; Shi, L.; Xing, H.; Liu, Y.; Liu, H.; Hu, Y.; Xia, D.; Li, Z. Hydrodynamic analysis-based modeling and experimental verification of a new water-jet thruster for an amphibious spherical robo. Sensors 2019, 19, 259. [Google Scholar] [CrossRef] [PubMed]
- dell’Erba, R. Distance estimations in unknown sea underwater conditions by power LED for robotics swarms. Contin. Mech. Thermodyn. 2021, 33, 97–106. [Google Scholar] [CrossRef]
- dell’Erba, R. The distances measurement problem for an underwater robotic swarm: A semi-experimental trial, using power LEDs, in unknown sea water conditions. Contin. Mech. Thermodyn. 2020, 2020, 1–9. [Google Scholar] [CrossRef]
- Suryendu, C.; Subudhi, B. Formation control of multiple autonomous underwater vehicles under communication delays. IEEE Trans. Circuits Syst. II Express Briefs 2020, 12, 3182–3186. [Google Scholar] [CrossRef]
- Wu, Y.; Ta, X.; Xiao, R.; Wei, Y.; An, D.; Li, D. Survey of underwater robot positioning navigation. Appl. Ocean. Res. 2019, 90, 101845. [Google Scholar] [CrossRef]
- Desai, J.P.; Ostrowski, J.; Kumar, V. Controlling formations of multiple mobile robots. In Proceedings of the 1998 IEEE International Conference on Robotics and Automation (Cat. No.98CH36146), Leuven, Belgium, 20–20 May 1998. [Google Scholar]
- Das, A.K.; Fierro, R.; Kumar, V.; Ostrowsky, J.P.; Spletzer, J.; Taylor, C. A vision-based formation control framework. IEEE Trans. Robot. Autom. 2002, 5, 813–825. [Google Scholar] [CrossRef] [Green Version]
- Mariottini, G.L.; Pappas, G.; Prattichizzo, D.; Daniilidis, K. Vision-based localization of leader-follower formations. In Proceedings of the 44th IEEE Conference on Decision and Control, Seville, Spain, 15 December 2005; pp. 635–640. [Google Scholar]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 11, 1330–1334. [Google Scholar] [CrossRef] [Green Version]
- Heikkila, J.; Silven, O. Controlling formations of multiple mobile robots. In Proceedings of the 1997 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Santa Barbara, CA, USA, 23–25 June 1998. [Google Scholar]
- Zheng, B.; Zheng, H.; Zhao, L.; Gu, Y.; Sun, L.; Sun, Y. Underwater 3D target positioning by inhomogeneous illumination based on binocular stereo vision. In Proceedings of the IEEE 2012 Oceans-Yeosu, Yeosu, Korea, 21–24 May 2012; pp. 1–4. [Google Scholar]
- Tu, D.; Xu, Z.; Liu, C. The Influence of Active Projection Speckle Patterns on Underwater 3d Measurement Based on Binocular Stereo Vision. 2022. Available online: http://dx.doi.org/10.2139/ssrn.4107116 (accessed on 21 September 2022).































| Parameters | Camera 1 | Camera 2 |
|---|---|---|
| Internal Matrix | ||
| Rotation Matrix | ||
| Translation Vector |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, P.; Shi, L.; Chen, Z.; Guo, S. A Vision-Based Underwater Formation Control System Design and Implementation on Small Underwater Spherical Robots. Machines 2022, 10, 877. https://doi.org/10.3390/machines10100877
Bao P, Shi L, Chen Z, Guo S. A Vision-Based Underwater Formation Control System Design and Implementation on Small Underwater Spherical Robots. Machines. 2022; 10(10):877. https://doi.org/10.3390/machines10100877
Chicago/Turabian StyleBao, Pengxiao, Liwei Shi, Zhan Chen, and Shuxiang Guo. 2022. "A Vision-Based Underwater Formation Control System Design and Implementation on Small Underwater Spherical Robots" Machines 10, no. 10: 877. https://doi.org/10.3390/machines10100877
APA StyleBao, P., Shi, L., Chen, Z., & Guo, S. (2022). A Vision-Based Underwater Formation Control System Design and Implementation on Small Underwater Spherical Robots. Machines, 10(10), 877. https://doi.org/10.3390/machines10100877








