Design and Characteristic Analysis of Magnetostrictive Vibration Harvester with Double-Stage Rhombus Amplification Mechanism

Abstract

Vibration energy harvesting is a new alternative to lithium battery power for low-power devices, attempting to recover wasted or lost vibration energy to generate electricity. Magnetostrictive-based energy harvesting exploits the coupling properties of the Villari and Faraday electromagnetic induction effects to achieve mechanical–magnetic–electric energy conversion. In order to better apply to the actual vibration environment, such as buses, and improve the ability to capture low-frequency vibration energy, a double-stage rhombus vibration energy harvesting device, based on Terfenol-D rods, was developed. By establishing an analytical model of the force amplification ratio of the harvesting device, the design is optimized using the Single-Objective Genetic Algorithm, and the safety and pre-magnetization layout methods are analyzed by Finite Element Analysis. The output characteristics of the prototype, including the output voltage frequency response under low-frequency regular excitation and random excitation, the effect of external resistance, and the vibration energy capture performance under random excitation, are investigated in detail through experiments. The results of the experiments showed that the peak output power of the fabricated prototype was 1.056 mW at 30 Hz operating frequency, the energy harvesting capability reached 41.4 μW/N, and the peak open circuit voltage and output power were 2.92 V and 266 mW, respectively, under random excitation. Practical application test results showed that the peak voltage generated was 1.06–1.51 V when the excitation level was 2.2–4.9 m/s². The comparative study indicates that the output performance of the proposed double-stage rhombus magnetostrictive vibration energy harvesting system is a great improvement over the proposals of existing literature.

1. Introduction

Currently, with the advent of the Internet of Things era, the power consumption of wireless communication systems and sensor nodes, etc. has reduced from mW to μW [1], and, currently, lithium batteries, etc. are still their main power source. Considering the randomness of the installation location of microelectronic devices, it is particularly difficult to replace lithium batteries, and the use of batteries has the disadvantage of harming the environment and running counter to the concept of environmental protection. Therefore, harvesting of wasted mechanical energy in an environmentally friendly manner has become a hot research topic [2,3,4]. Vibration energy harvesting attempts to recover wasted or lost vibration energy to generate electricity [5], and research can address practical problem areas, such as human health monitoring [6], powering wireless sensor networks [7,8,9], wireless transceivers [10], and medical watches [11]. The motivation for the current research is to develop an energy harvester that captures the vibration energy generated by bus seats to power the low-power indicators and radio equipment on board.

As vehicles that transport passengers, buses provide not only vibrational energy, but also body movement energy. It has been reported that harvesting devices can capture the vibration energy of moving vehicles [12]. However, the existing vibration energy harvesting mechanisms work in a single mode, i.e., they capture the vibration energy in the environment or the motion energy of the human body, respectively. In fact, public vehicles and the environment are coupled to each other and exhibit different patterns of movement [13]. For example, bus seats are subjected to both mechanical vibration and pressure, and these excitations are generated by the bus environment and the passengers, respectively. Therefore, the harvester captures the above two types of energy to energize self-powered devices, which would effectively solve the shortcomings of traditional battery power.

Current vibration energy harvesting techniques are classified into electrostatic [14], electromagnetic [15], piezoelectric [16], and magnetostrictive [17], depending on the harvesting principle. Electrostatic energy harvesting is based on a variable capacitor structure consisting of an external voltage source or a voltage source biased pre-charged electret material. IMEC and Panasonic jointly developed a new type of MEMS vibration energy harvester based on a corrugated SiO₂-Si₃N₄ electret [18], and an integrated tire pressure monitoring system (TPMS). The actual power generation in automobile tires is about 10–50 μW, enough to meet the power supply requirements of the TPMS module. The advantage of electrostatic energy harvesting is that it is easy to integrate with micro-mechanical systems. However, the structure is complex and the stability of the device is poor. Electromagnetic vibration acquisition utilizes the Faraday electromagnetic induction effect, where energy capture depends on the relative motion between the coil and the magnet. Teng Lin et al. [19] designed an efficient electromagnetic energy harvester (MMR) for railroad transportation, which is designed to capture energy from track deflections caused by overtaking trains to power trackside equipment, such as warning signals, wireless communication, and track health monitoring. Tests have shown that the MMR has an energy harvesting capacity of 10–100 W and an efficiency of 74%. The electromagnetic type is technically mature and remains the key power generation method. However, its large size and low harvesting efficiency still face great challenges in the application of MEMS.

The piezoelectric and magnetostrictive types have commonalities in the principles of harvesting and conversion, both of which are achieved through the inherent properties of smart materials. Compared with traditional energy harvesting methods, smart materials can achieve higher energy conversion performance at low frequencies [20]. Piezoelectric energy harvesting utilizes the piezoelectric effect of materials to directly convert mechanical energy into electrical energy [21,22]. Piezoelectric materials are popular materials for vibration energy harvesting because of their moderate electromechanical coupling coefficients and good compatibility with MEMS. Feng Qian et al. [23] proposed a human walking piezoelectric energy harvester (PEH) based on a double-stage amplification mechanism for mounting at the heel of a shoe, which can obtain 204.7 mW of peak power and 12.8 mW of average power. Shihao Wen et al. [24] designed a new piezoelectric energy harvester based on an integrated multi-stage force amplification framework, which integrates a multi-stage amplification mechanism, and the peak output power exceeds 50.8 mW after matching resistors. The above literature shows that the piezoelectric type has good convertibility, simple structure, and scalability. However, piezoelectric materials have inherent limitations, depolarization and susceptibility to aging, and low energy density [25]. This hinders its application in real-world environments. In addition, commonly used piezoelectric materials are brittle and cannot withstand excessive strains, and the capacitive characteristics result in high internal resistance. Magnetostrictive materials (MSMs), as new international smart materials, have electromechanical coupling coefficients of up to 75% and high energy density in low frequency states. The MSM-based vibration energy harvesting uses the Villari effect of the MSM to convert mechanical energy into magnetic energy, and then an external pick-up coil converts the magnetic energy into electrical energy, according to the Faraday electromagnetic induction effect. Compared with piezoelectric energy harvesting, MSM energy harvesting has the advantage of not having the shortcomings of depolarization and easy aging, which eliminates the limitation that means piezoelectric materials cannot withstand large strains. Compared to electrostatic and electromagnetic types, MSM energy harvesting does not require moving parts, which contributes to reduced mass and size, and is suitable for harsh environments. However, existing magnetostrictive energy harvesters are mostly based on external stresses acting directly on the MSM [26,27,28], which cannot change the direction of the stresses. In addition, the pick-up coil of the harvester is bulky and the bias magnetic field needs to be applied to increase the energy conversion efficiency, which increases the size of the harvester, which is where the magnetostrictive harvester falls short. However, the use of an amplifying mechanism to drive MSM energy harvesting technology would fill the gap in this field.

In order to harvest low-frequency vibrational energy from the environment, many scholars have worked on developing energy harvesting devices for low frequencies; however, the output performance has been disappointing. When a bus is moving, the armrests and seats etc. produce low frequency vibrations. Zhenjing Li et al. designed a piezoelectric energy storage armrest with vibration and pressure excitation [13], which could obtain 150 μW and 15 mW maximum power under low frequency sinusoidal and random excitation. Obviously, the output power of the piezoelectric energy harvester at low frequencies is not high, and the output performance at low frequencies is greatly affected by the capacitive characteristics of the piezoelectric material. However, MSM has a small resistance value and a high output power density at low frequencies. Brian J. Rosenberg et al. applied magnetostrictive rods to the wave energy harvesting process to develop the Triton wave energy converter (WEC), which has solved the power supply problem in real life [29]. Therefore, the rod-shaped MSM can solve the problem of insufficient energy harvesting performance at low frequencies. The energy harvester developed in this paper is used to harvest low-frequency vibration energy from bus seats to power the bus’s own low-power electronics. Terfenol-D, which is usually cylindrical or rectangular, is the most typical commercial MSM in TbDyFe, with an energy conversion coefficient of up to 70% [20], maximum magnetostriction of 1500 ppm, and compressive strength of 750 MPa. With maximum room temperature magnetostriction and high compressive strength, Terfenol-D is used as the core power generation material in this paper.

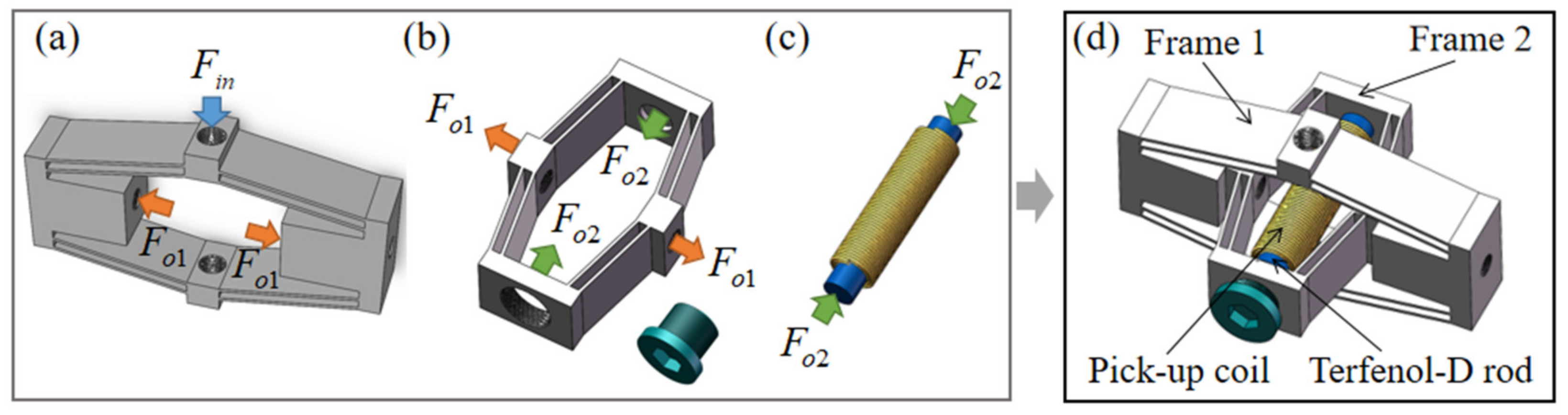
To this end, this paper designs a double-stage rhombus energy harvesting system based on Terfenol-D rods, which can harvest not only the vibration energy of the seats while the bus is moving, but also the pressure energy generated by the passengers. Considering the small vibration force of the seat, in order to fully improve the utilization of vibration energy, a double-stage rhombus amplification mechanism is used to drive the Terfenol-D rod to capture energy. The model of the double-stage rhombus amplification mechanism was designed in a limited physical space, and the Finite Element Analysis (FEA) studied the whole motion process of the mechanism and the characteristic parameters of the mechanism. The pre-magnetization layout for the optimal output performance of the harvesting device was studied and analyzed, and, finally, the output performance of the double-stage rhombus magnetostrictive energy harvesting system was carefully investigated and the sustained power generation capability of the fabricated prototype verified.

2. Structural Design of a Double-Stage Rhombus Magnetostrictive Vibration Energy Harvesting Device

The harvesting device captures the vibrational energy in the environment through the coupling property of Villari and Faraday electromagnetic effect to realize the conversion of mechanical energy–magnetic energy–electrical energy. The double-stage rhombus magnetostrictive vibration energy harvesting device consists of two modules, the force amplification module and the energy conversion core module, as shown in Figure 1d. The force amplification is performed by a double-stage rhombus amplification mechanism, the structure of which includes a first stage (Frame 1) and a second stage (Frame 2) frame [30], as shown in Figure 1a,b. The amplification mechanism fully amplifies the weak vibrations of the environment to maximize the harvesting energy, while avoiding the effects of complexity and instability from the perspective of amplification mechanism selection and frame connection. The energy conversion is performed by a magnetostrictive section, with a structure consisting of a Terfenol-D rod and a pick-up coil [31], as shown in Figure 1c.

2.1. Overall Structure Design and Implementation Principle

The double-stage rhombus energy harvesting device based on Terfenol-D rods consists of two parts: a double-stage rhombus mechanical structure for amplifying the vibration force, which relies on the deflection deformation of the bridge-type beam to transfer and amplify the vibration force; and an energy conversion core part of mechanical–magnetic–electric energy, which relies on the coupling property between Villari and Faraday electromagnetic induction effect to realize the energy conversion.

The realization principle of harvesting vibration energy is as follows: the double-stage rhombus amplifying mechanism captures the external vibration energy, i.e., the top of the first stage of the amplifying mechanism is subjected to a vertical downward load force, as shown in F_in of Figure 1a, and the direction is rotated by 90° after being transmitted by the bridge-type beam, as shown in F_o1 of Figure 1a, i.e., and the output end of the first stage is subjected to a horizontal pull force as shown in F_o1 of Figure 1b. The second stage is rigidly connected to the first stage, and the second stage is subjected to horizontal tension, which is transmitted by the bridge-type beam and becomes pressure, as shown in F_o2 of Figure 1b, pressing the two ends of the second stage toward the center. As a result, a compressive force is generated at the ends of the second stage frame, and this compressive force acts directly on the ends of the Terfenol-D rods, as shown in F_o2 of Figure 1c. The pressure causes deformation of the energy conversion core Terfenol-D rod, and, thus, Terfenol-D rod undergoes the Villari effect [32], the internal magnetization intensity and magnetic field distribution changes, converting mechanical energy to magnetic field energy, and, due to the external distribution pick-up coil of the Terfenol-D rod, the change of magnetization intensity and magnetic field distribution causes the Faraday electromagnetic induction effect. Thus, generating induced electric potential, converting magnetic field energy to electric field energy, and realizing the conversion of mechanical energy–magnetic energy–electric energy, and, finally, converting vibration energy to electric energy.

In this paper, the mechanical frame is made of highly elastic AL7075 alloy material, which has a large deformation limit. The mechanical properties of AL7075 alloy are listed in

Table 1. AL7075 mechanical characteristics.

Mechanical Characteristics	Density (kg/m3)	Poisson’s Ratio	Young’s Modulus (GPa)	Tensile Yield Strength (MPa)
Value	2810	0.33	71.7	503

. MSM chose Terfenol-D, which has a high energy conversion coefficient, and the main material properties are measured by specialized institutions and are listed in

Table 2. Terfenol-D material properties.

Material Properties	Value
Magnetostriction coefficient	≤1500 × 10−6 (240 kA/m; 5~10 MPa)
Young’s modulus	(2.5~3.5) × 1010 N/m2
Compressive strength	≥750 MPa
Tensile strength	≥28 MPa
Density	9.25 g/cm3
Energy density	14~25 kJ/m3
Relative permeability	3~15
Operating temperature	−40~150 °C
Response range of frequency	1~40 KHz

.

2.2. Design of Double-Stage Rhombus Amplification Mechanism Frame

The amplifying mechanism frame is mainly divided into the convex frame studied by W. Zhou et al. [33] and the concave frame studied by P. Liu et al. [34], and the main difference between the two is the different principles of action, where the convex and concave frames act as tension and pressure at the two ends of the Terfenol-D rod when equal forces F_in are applied at the input end [30], as shown in Figure 2a,b, respectively. When the convex frame is subjected to the same force as the concave frame, the mechanical deformation produced by the concave frame is larger, and most of the energy is stored at the deformation surface of the mechanism, and, according to the law of energy conservation, the energy loss actually transferred to the Terfenol-D rod increases. On the contrary, the convex frame has small deformation and large amplification ratio, so higher energy conversion efficiency and safety factor can be obtained. The safety factor is the ratio of yield stress to allowable stress; theoretically, a safety factor greater than 1 meets safety requirements.

Considering the design of the double-stage amplified frame in this paper, the characteristic parameters are different from those of a single convex or concave frame, so a 3-D model of the double-stage convex and concave frames with the same parameters was established, and the characteristic parameters are listed in

Table 3. Selected characteristic parameters and analytical results for different double-stage frames.

Characteristic Parameters	Double-Stage Convex Frame	Double-Stage Concave Frame
Dimension: L × W × H (mm)	56 × 44 × 42	56 × 44 × 42
Beam deflection (mm)	1.2014	1.7014
Maximum stress (MPa)	283.35	371.84
Support reaction force (N)	1214.2	779.3
Amplification ratio-FEA	12.14	7.79
Safety factor	1.78	1.35

. The results of stress analysis for the two frames are shown in Figure 2c,d. The maximum stress was mostly concentrated at the corner of the beam-block joint, where the fatigue damage was likely to occur [35,36]. The results of the stress analysis showed that the double-stage concave frame was subjected to a significantly higher maximum stress than the double-stage convex frame. Therefore, in order to obtain a higher energy transfer efficiency and safety factor, the double-stage amplification framework continued to be studied using a convex framework.

2.3. Beam Design of Double-Stage Rhombus Amplification Mechanism Frame

The beam types of double-stage rhombus frames are also divided into different types, the most commonly used being the hinge beam, studied by L. Wang et al. [37], and the bridge-type beam, studied by Wen. S et al. [30]. The notched hinge beam proposed by L. Wang et al. aims to reduce the stiffness of the bridge-type beam and, thus, improve the force amplification ratio and energy transfer efficiency. The structure and stress analysis of the bridge-type beam and hinge beam are shown in Figure 3. The results of the stress analysis showed that the stresses in the bridge-type beam were relatively uniformly distributed, while the stresses in the hinge beam all concentrated at the notch where the beam was connected to the block. Considering that the amplifying mechanism needs to bear a large force, but the stress concentration of the hinge beam may not lead to a sufficiently high safety factor, the bridge-type beam was chosen as the beam type of the amplifying mechanism, to fully ensure the overall safety of the amplifying mechanism.

In addition, the number of bridge-type girders is also an important factor affecting the amplification ratio and safety. For the traditional bridge-type amplification mechanism, the number of beams is mostly single, and the limit of bearing tensile pressure is low, which limits its application. Moreover, repeated forces over a long period of time are bound to increase the probability of fatigue damage [38]. The number of beams should firstly meet the safety requirements and, secondly, make the amplification ratio as large as possible. We determined the more suitable number of beams by the method of simulation analysis. Considering the practical application and manufacturing, the distance between adjacent beams was controlled within 2 mm, and a force of 400 N was applied to the input end. The stress analysis results of the amplification mechanism with different beam numbers are shown in Figure 4.

Table 4. Partial characteristics and analytical results of single-stage rhombus frames with different number of beams.

Characteristic Parameters	One-Beam	Two-Beam	Three-Beam	Four-Beam
Dimension: L × W × H (mm)	44 × 18 × 10	44 × 22 × 10	44 × 26 × 10	44 × 30 × 10
Maximum stress (MPa)	467.12	273.21	243.89	237.76
Support reaction force (N)	2514.7	2039.0	1960.4	1888.4
Amplification ratio-FEA	6.29	5.10	4.90	4.72
Safety factor	1.08	1.84	2.06	2.1156

summarizes the characteristic parameters of single-stage rhombus frames with different numbers of beams. The results showed that the maximum stress of single-stage rhombus frame was inversely proportional to the number of beams, and increasing the number of beams could improve the safety factor, but the force amplification ratio decreased and the physical size increased. In addition, the one-beam structure had higher stresses and lower safety factors, while the stresses of the remaining three structures did not differ significantly. Since the single-stage amplification frame with two-beam had a larger amplification ratio and smaller size, the rhombus frame form with two-beam was used in this paper.

2.4. Comparison of Characteristic Parameters of Double-Stage Rhombus Amplification Mechanism with Different Numbers of Beams

In order to compare the characteristic parameters of the conventional one-beam and modified two-beam double-stage rhombus amplification mechanisms, a force of 100 N was applied to the input, and the amplification ratio of the amplification mechanism was defined as the ratio between the output force and the input force. The stress analysis and safety factors obtained from the simulation are shown in Figure 5, and the characteristic parameters are summarized in

Table 5. Partial characteristics and analysis results of the double-stage rhombus amplification mechanism with different numbers of beams.

Characteristic Parameters	One-Beam Double-Stage Rhombus Amplification Mechanism	Two-Beam Double-Stage Rhombus Amplification Mechanism
Dimension: L × W × H (mm)	60 × 4 2 × 34	60 × 42 × 34
Maximum stress (MPa)	484.57	189.99
Support reaction force (N)	2178.0	1365.4
Amplification ratio-FEA	21.78	13.65
Safety factor	1.0380	2.6475
Beam deflection (mm)	2.4942	0.9127

. Thinner and longer beams enhanced the amplification ratio, but increased the deformation of the frame material, with the maximum stresses concentrated at the beam-block joints. Therefore, comparing the characteristic parameters of one-beam and two-beam double-stage rhombus, it was concluded that the safety factor of the two-beam double-stage rhombus amplification mechanism met the design requirements and was more suitable as the mechanical structure of the energy harvesting device in this paper.

3. Model Analysis of Force Amplification Ratio of Double-Stage Rhombus Amplification Mechanism

In this section, a theoretical model of the force amplification ratio of a single rhombus frame is established, and the force amplification ratio of a double-stage rhombus amplification mechanism is analyzed by theoretical calculation. The theoretical model of amplification ratio can not only obtain the force amplification ratio and prove the feasibility of the amplification mechanism, but also provides a theoretical analysis model for the subsequent optimization of structural parameters. Analytical modeling of amplifying mechanisms based on the bridge-type beam is less common, and the specific theory is similar to the Euler-Bernoulli beam theory of Q. Xu et al. [39], and the energy method of S. Wen et al. [38]. Considering the bisymmetric characteristics of the rhombus frame in this paper, a quarter frame was selected for analysis in the modeling process, and the structural model of the bridge-type beam and the mechanical analysis model are shown in Figure 6. Considering the bridge-type beam as an elastic beam and the other members as rigid bodies, the two-beam model can be simplified into an equivalent one-beam model AB. The initial force application plane is 1, the input force is $F_i$, the plane of one end of the output force is 2, and the output force is $F_o$, as shown in Figure 6a. Considering that the side block has a certain influence on the force transmission, it is taken as the key force analysis object, as shown in Figure 6d. The elastic direct influence amplification ratio of the frame material is considered, so this paper used Euler-Bernoulli beam theory [30] and focused on the effect of deformation of the bridge-type beam on the transfer of the acting forces. Based on the analysis of the force amplification ratio of a single rhombus amplification frame, the expression of the theoretical description of the force amplification ratio with a double-stage rhombus amplification mechanism was, finally, derived.

First, a vertical upward force $F_i$ is applied in plane 1, and the two-beam are simplified to a one-beam model, as in Figure 6b, where the initial force is the $F_i$ at the end point B of the bridge-type beam, which is amplified by the bridge-type beam to produce a horizontal output force $F_o$. Decompose $F_i$ and $F_o$ into $F_n$ and $F_l$ in the vertical beam direction and along the beam direction, as shown in Figure 6c. According to the force analysis, $F_n$ and $F_l$ can be expressed as the following equation [30]:

$$F_n=F_i\cos \theta -F_{\mathrm{o}}\sin \theta$$

(1)

$$F_l=F_i\sin \theta +F_{\mathrm{o}}\cos \theta$$

(2)

$\theta$ is the inclination angle of the beam with respect to the horizontal direction.

The force analysis of the simplified beam AB is carried out, and according to the balance of moments applied to beam AB, as shown in Figure 6b, it is obtained that [30]:

$$2M_r=F_{\mathrm{o}}{l}_y-F_i{l}_x=F_{\mathrm{o}}{l}_{beam}\sin \theta -F_i{l}_{beam}\cos \theta$$

(3)

$M_{\mathrm{r}}$ indicates the moment applied to the bridge-type beam, $l_y$ and $l_x$ are the vertical and horizontal dimensions of the bridge-type beam, and $l_{beam}$ is the length of the bridge-type beam AB.

The moment $M(x)$ at endpoint B can be expressed as:

$$M(x)=F_{n}x+M_r,0\le x\le l_{beam}$$

(4)

The deflection deformation of the bridge-type beam is shown in Figure 6c, and the deformation of the beam is calculated according to Euler-Bernoulli beam theory as follows [30]:

$$\frac{d^2{W}_{\mathrm{b}}}{d{x}^2}=\frac{M(x)}{E_{frame}{I}_b}$$

(5)

$$I_b=\frac{b_{beam}{t}^3{}_{beam}}{12}$$

(6)

$E_{frame}$ is the modulus of elasticity of the frame material, $W_{\mathrm{b}}$ is the deflection of the bridge-type beam with respect to the neutral axis, $I(x)$ is the moment of inertia of the area of the frame, and $I(b)$ is the moment of inertia of the area of the beam.

According to Figure 6c, it can be seen that there exists a fixed boundary of AB. Considering the limit value of AB, i.e., $x=l_{beam}$, the deflection of the bridge-type beam can be calculated by bringing Equation (4) into Equation (5) as follows [38]:

$$W_b(l_{beam})=\frac{F_n{l}_{beam}{}^3}{6E_{frame}{I}_b}+\frac{M_r{l}^2{}_{beam}}{2E_{frame}{I}_b}$$

(7)

Simplifying Equation (7) yields:

$$W_b(l_{beam})=\frac{-F_n{l}_{beam}{}^3}{12E_{frame}{I}_b}$$

(8)

According to the moment balance of the side block, as shown in Figure 6d, the horizontal deformation of the side block can be expressed as [38]:

$$x_1(l_{block})=\frac{F_o{l}^3{}_{block}}{3E_{frame}{I}_{block}}$$

(9)

Area moment of inertia of the side block $I_{block}$:

$$I_{block}=\frac{b_{block}{t}^3{}_{block}}{12}$$

(10)

The deformation of a bridge-type beam subjected to a tensile force $F_l$ in the direction of the beam can be expressed as [38]:

$$\Delta l_b=\frac{F_l{l}^2{}_{beam}}{E_{frame}{A}_{\mathrm{b}}}$$

(11)

In the above equation, $A_{\mathrm{b}}$ is the cross-sectional area of the bridge-beam material.

Similarly, since the output end of the rhombus frame remains rigidly connected to the end face of the Terfenol-D rod, the support reaction force generated at one end of the Terfenol-D rod is equal in magnitude to the force $F_o$ acting at the output end of the rhombus frame. The deformation of the Terfenol-D rod in the axial direction can be expressed as:

$$\Delta x_D=\frac{F_o{l}^2{}_D}{E_D{A}_{\mathrm{D}}}$$

(12)

In the above equation, $E_D$ and $A_{\mathrm{D}}$ are the Young’s modulus and cross-sectional area of the Terfenol-D material, respectively.

According to the compatibility condition theorem, the total deformation in the horizontal X-direction is equal to zero, and the deformation relation can be obtained as follows [30]:

$$W_b\sin \theta =\Delta x_D+\Delta l_b\cos \theta +x_1(l_{block})$$

(13)

Bringing Equations (1), (9), (11) and (12) into Equation (13) yields the equation:

$$\frac{-F_n{l}_{beam}{}^3}{12E_{frame}{I}_b}\sin \theta =\frac{F_o{l}^2{}_D}{E_D{A}_{\mathrm{D}}}+\frac{F_l{l}^2{}_{beam}}{E_{frame}{A}_{\mathrm{b}}}\cos \theta +\frac{F_o{l}^3{}_{block}}{3E_{frame}{I}_{block}}$$

(14)

The force amplification ratio is the ratio between the output force and the input force, i.e., $F_o/F_i$. According to Equation (14), an equation containing $F_o$ and $F_i$ can be established, and by solving this equation an expression for the force amplification ratio of a single rhombus frame can be obtained as follows:

$$n=\frac{F_o}{F_{\mathrm{i}}}=\frac{E_D{A}_D{I}_{block}{l}^2{}_{beam}\sin \theta \cos \theta (12I_b+A_{\mathrm{b}}{l}_{beam})}{E_D{A}_D{A}_{\mathrm{b}}{I}_{block}{l}^3{}_{beam}{\sin }^2\theta -12l^2{}_D{E}_{frame}{I}_b{A}_{\mathrm{b}}{I}_{block}-12l^2{}_{beam}{E}_D{A}_{\mathrm{D}}{I}_b{I}_{block}{\cos }^2\theta -4l^3{}_{block}{E}_D{A}_D{I}_b{A}_{\mathrm{b}}}$$

(15)

Considering the elastic deformation of the actual frame material, the loss of energy during the deformation of the bridge-type beam, and the tightness of the two frame screw connections, the efficiency of the input force transfer inevitably reduces, resulting in the force amplification ratio ($n_1\times n_2$) of frame 1 and frame 2 not being equal to the force amplification ratio ($n$) of the double-stage rhombus amplification mechanism [30]. Therefore, the transfer efficiency $\eta$ is introduced, i.e., the ratio between the actual and theoretical Terfenol-D rod-branch reaction forces, and the energy lost is taken into account to finally derive the force amplification ratio of the double-stage rhombus amplification mechanism:

$$n=\eta \times n_1\times n_2$$

(16)

4. Optimization of Structural Parameters and Simulation Analysis of Mechanical Characteristics of a Double-Stage Rhombus Energy Harvesting Device

4.1. Dimensional Parameters Analysis and Structure Optimization

In this section, the theoretical model of the amplification ratio of the double-stage rhombus amplification mechanism is derived, based on the previous section, and the mechanism’s dimensional parameters, affecting the amplification ratio, are optimized by combining the objective genetic algorithm. Optimization of the double-stage frame has been accomplished in the literature [36,37,39], but these authors only considered the thickness of the bridge-type beam and the horizontal tilt angle as design variables, and analysis of other parameters that affect the mechanism amplification ratio is lacking. The parameter optimization of the single bridge-type amplification mechanism was studied in the literature in [40], but the results did not include the model’s inference process and overall parameter optimization. Therefore, it is necessary to optimize the energy harvesting device with more systematic dimensional parameters for a higher force amplification ratio and safety factor.

In order to determine the sensitive interval of dimensional parameters affecting the magnification ratio, a trend analysis of the magnification ratio versus dimensional parameters was performed for frames 1 and 2. The influencing factors of the magnification ratio included both the bridge-type beam and the side block. On the one hand, the length $l_{beam}$ and thickness $t_{beam}$ of the bridge-type beam, and, on the other hand, the length $l_{block}$ and thickness $t_{block}$ of the side blocks, as shown in Figure 6. The design goal of the amplification mechanism is to amplify the input force as much as possible so that the Terfenol-D rod obtains optimal output performance. The maximum force amplification ratio of a single rhombus frame was taken as the target, the size range of the frame was set, and the theoretical model of the force amplification ratio was analyzed using a GA, so that the sensitivity distribution of the size parameter to the amplification ratio, and the trend of the amplification ratio versus the size parameter, could be obtained. By analyzing the sensitivity distribution, as shown in Figure 7, it was found that the length and thickness of the bridge-type beam played a dominant role in the amplification ratio. The trend of amplification ratio and size parameters showed that the longer the length and the smaller the thickness of the bridge-type beams of frames 1 and 2, the larger the force amplification ratio. The smaller the length and the larger the thickness of the side blocks of frames 1 and 2, the larger the force amplification ratio, as shown in Figure 8. Based on the analysis of the dimensional parameters of the single rhombus frame, a sensitive range of values for the influence amplification ratio was determined. However, the interaction between frames 1 and 2 had to be considered, as it might inhibit the amplification effect of the mechanism as a whole. Therefore, the overall double-stage rhombus energy harvesting device was considered below and its optimization was analyzed, based on GA, to obtain the exact values of the optimal dimensional parameters.

Since the deformation of the bridge-type beam directly influences the transfer efficiency, combined with the results of the optimization analysis of a single rhombus frame, it was found that the longer and thinner the beam, the greater the force amplification ratio of the frame, which agreed with the existing literature [30]. Therefore, considering the geometric size limitation of the double-stage rhombus energy harvesting device, and analyzing the trend of the amplification ratio, the lengths of the bridge-type beams of frames 1 and 2 were set to 24–26 mm and 15–17 mm, respectively, and the thicknesses were set to 0.5–0.7 mm. The angle $\theta$ between the bridge-type beam and the horizontal direction determines the magnitude of the tension force on the side block. $\theta$ varies in the range of 0–90°, and the force on the side block decreases with the increase of $\theta$. However, $\theta$ cannot take extreme values, and $\theta$ was set to 9–13° with reference to the analysis results. The length and thickness of the side block directly affects the output force. When the side block is subjected to the force of the bridge-type beam, the longer the length and the smaller the thickness of the side block, the greater the deformation of the frame around the point of action and the more energy is lost. Considering the size limitation, the length of the side block was set to 8–12 mm and the thickness was set to 3–5 mm. The width of the bridge-type beam b meets the dimensional requirements of the amplifying mechanism, and the width of the bridge-type beam is appropriately increased to reduce the excessive deformation of the bridge-type beam. To avoid unnecessary energy loss, $b$ was set to 11–13 mm in combination with the mass factor of the frame system. In order to avoid the interaction between the objectives of the Multi-Objective Genetic Algorithm (MOGA), which affects the stability of the model and causes inaccurate results for the objective of maximizing the amplification ratio, the Single-Objective Genetic Algorithm (SOGA) was applied to optimize the double-stage rhombus energy harvesting device. Finally, the force amplification ratio was set as the optimization objective of the double-stage rhombus energy harvesting device with the following optimized design:

• Optimization method: Single-Objective Genetic Algorithm (SOGA)
• Objective: Maximum force amplification ratio or maximum output force
• Design variables:

$l_{1beam}$, $b_{1beam}$, $t_{1beam}$, ${\theta }_{1beam}$, $l_{1block}$, $t_{1block}$,

$l_{2beam}$, $b_{2beam}$, $t_{2beam}$, ${\theta }_{2beam}$, $l_{2block}$, $t_{2block}$.

• subject to:

(1) Safety factor > 2;

(2) $l_{1beam}$ ∈ [24:0.1:26] mm;

(3) $l_{2beam}$ ∈ [15:0.1:17] mm;

(4) $b_{1beam}$, $b_{2beam}$ ∈ [11:0.1:13] mm;

(5) $t_{1beam}$, $t_{2beam}$ ∈ [0.5:0.05:0.7] mm;

(6) ${\theta }_{1beam}$, ${\theta }_{2beam}$ ∈ [9:0.1:13] °;

(7) $l_{1block}$, $l_{2block}$ ∈ [8:0.1:12] mm;

(8) $t_{1block}$, $t_{2block}$ ∈ [3:0.1:5] mm.

The SOGA optimization started from 800 initial samples, the number of iterations N was set to 80, 100 samples were generated for each iteration, and 5 candidate points were selected to find the optimal size parameter combination. The optimization process is shown in Figure 9. The sensitivity results of the amplification ratio of the double-stage rhombus amplification mechanism with respect to the optimized parameters are shown in Figure 10, from which it can be seen that the beam length and beam thickness of both frames were the most sensitive to the amplification ratio, followed by the inclination angle of the beam. In addition, the sensitivity of the dimensional parameters of frame 1 to the amplification ratio was stronger than that of frame 2. The optimized size ranges and the obtained optimized values are listed in

Table 6. Range of dimensional parameters and optimization results of the double-stage rhombus amplification mechanism.

	Frame 1			Frame 2
Design Variables	Parameters	Scope	Value	Parameters	Scope	Value
Beam length (mm)	$l_{1beam}$	[24:26]	25.5	$l_{2beam}$	[15:17]	16
Beam width (mm)	$b_{1beam}$	[11:13]	12	$b_{2beam}$	[11:13]	12
Beam thickness (mm)	$t_{1beam}$	[0.5:0.7]	0.55	$t_{2beam}$	[0.5:0.7]	0.60
Beam inclination angle (°)	${\theta }_{1beam}$	[9:13]	10	${\theta }_{2beam}$	[9:13]	12
Side block length (mm)	$l_{1block}$	[8:12]	8	$l_{2block}$	[8:12]	10
Side block thickness (mm)	$t_{1block}$	[3:5]	4	$t_{2block}$	[3:5]	3.8

.

4.2. Simulation Study of Structural Properties

The 3-D model of the double-stage rhombus energy harvesting device was established, based on the optimized value of SOGA, and the structural characteristics of the harvesting device were studied by FEA, in addition to analyzing whether its safety factor met the requirements. Constraints were set using FEA software. The bottom end of the harvesting device was fixed, and a vertical downward force of 100 N was applied to its top end. The Terfenol-D rod and frame were divided into element size using a hexahedral mesh (element size 0.4 mm) and a tetrahedral mesh (element size 0.5 mm), respectively, and the support reaction force was used as the output parameter for the FEA solution. The stress analysis of a single rhombus frame and the safety factor of a double-stage rhombus energy harvesting device are shown in Figure 11. The results showed that the maximum stress of frames 1 and 2 was much smaller than the yield stress of AL7075 material, and the safety factor of 2.5531 was much larger than 2 for the double-stage rhombus energy harvesting device, which showed that the optimized value of the harvesting device met the safety requirements.

The characteristic parameters of the single rhombus frame and the double-stage rhombus energy harvesting device are listed in

Table 7. Characteristic parameters of a single rhombus frame.

Characteristic Parameters	Frame 1	Frame 2
Dimension: L × W × H (mm)	64 × 34 × 12	44 × 28 × 12
Maximum stress (MPa)	197.01	155.08
Support reaction force (N)	545.64	427.44
Amplification ratio-Theory	5.82	4.56
Amplification ratio-FEA	5.45	4.27
Safety factor	2.71	2.82

and

Table 8. Characteristic parameters of the double-stage rhombus energy harvesting device.

Characteristic Parameters	Double-Stage Rhombus Energy Harvesting Device
Dimension: L × W × H (mm)	64 × 48 × 34
Support reaction force (N)	1603.1
Amplification ratio-Theory	18.60
Amplification ratio-FEA	16.03
Beam deflection-FEA (mm)	2.1
Safety factor	2.5531
Mass (g)	44.22

. Its theoretical value was calculated as 18.60, based on the amplification ratio expression in Section 3, which was similar to the optimized value of 16.03. Comparing the values of force amplification ratios for a single rhombus and a double-stage rhombus frame, it was found that the amplification ratio of the double-stage rhombus frame was lower than the product of the amplification ratios of the single rhombus frame. The reason might have been that the connection constraint setting between the individual rhombus frames had some inhibiting effect on their amplification capacity. In addition, the interaction between individual rhombus frames also reduced the overall force amplification ratio, which indirectly confirmed that the overall optimization was closer to the real situation.

5. Comprehensive Analysis of the Output Characteristics of a Double-Stage Rhombus Energy Harvesting Device

The double-stage rhombus harvesting device was tested on the experimental bench with different loads and excitation frequencies, and the experimental test principle is shown in Figure 12. The double-stage rhombus energy harvesting device was sandwiched between the force sensor and the fixed fixture, and the other end of the force sensor was connected to the shaker, so that the vibration force generated by the shaker was delivered to the harvesting device, which completed the conversion of mechanical energy–magnetic energy–electrical energy. The force hammer was used as the vibration source for random excitation tests. In addition, the displacement sensor measured the time-varying input displacement of the harvesting device, and the charge signal collected by the force sensor was delivered to the charge amplifier, which converted the charge into a voltage signal. The voltage signals output from the harvesting device, the charge amplifier, and the displacement sensor were recorded by the three channels of the oscilloscope. A comprehensive analysis of the output characteristics of a double-stage rhombus energy harvesting device was performed by varying the load force and excitation frequency.

5.1. Prototype Fabrication of a Double-Stage Rhombus Energy Harvesting Device

The fabricated prototype and experimental system of a double-stage rhombus energy harvesting device, based on a Terfenol-D rod, is shown in Figure 13. The size of the Terfenol-D rod, produced by Nanfang Rare Earth Metal Materials Co., Ltd. (Huizhou, China), was Φ 8 mm × 26 mm, and the pick-up coil was made of copper enameled wire from Liu’an Yuanhang Electronic Technology Co., Ltd. (Liuan, China), with a wire diameter specification of 0.21 mm and a resistance value of 8.7 Ω when the number of turns was 500. The dimensions of the double-stage rhombus frame required precision, so it was manufactured by the wire-cutting method. To investigate the output characteristics of the harvesting device under sinusoidal excitation, a function generator from United Energy Electronics (Suzhou, China) excited a sinusoidal excitation signal and then sent the signal to a broadband power amplifier to drive a shaker (Suzhou, China). The output of the shaker was connected to a pull-press bi-directional force transducer (Suzhou, China), and the auxiliary fixture was fixed to the experimental bench. The input of the Terfenol-D rod-based harvesting device prototype was connected to the force transducer, and the bottom end was kept rigidly connected to the auxiliary fixture. Meanwhile, the laser displacement sensor (MTI Instruments INC, Albany, NY, USA) measured the time-varying input displacement of the harvesting device. To investigate the output characteristics of the harvesting device under transient excitation, the bottom end of the harvesting device remained rigidly connected to the fixture. The force hammer (Suzhou, China) applied transient excitation to the input of the harvesting device, and the charge amplifier (Suzhou, China) was connected to the force hammer to convert the output charge signal into a voltage signal. The laser displacement sensor, charge amplifier and harvesting device output voltage signals were recorded by three different channels of a digital fluorescent oscilloscope (Tektronix, Tektronix Inc., Beaverton, OR, USA). The digital multimeter was used to measure the resistance of the pick-up coil. In addition, a variable resistance box (Shanghai, China) was used as an external load resistor to test the output power characteristics of the harvesting device.

5.2. Force Amplification Ratio Test of the Prototype of the Double-Stage Rhombus Energy Harvesting Device

The large mechanical deformation of the double-stage rhombus energy harvesting device prototype might affect the actual force amplification ratio, i.e., the input force might not be fully delivered to the Terfenol-D rod. Therefore, the force amplification ratio of the double-stage rhombus energy harvesting device prototype was tested. By measuring the output voltage of the harvesting device prototype and the Terfenol-D rod when working alone, the difference in slope between the two fitted curves was the force amplification ratio of the prototype, and the curve fit is shown in Figure 14. The results showed that the slope of the voltage versus force fitting curve of the harvesting device prototype was 15.5 times that of the Terfenol-D rod, which was closer to the 16.03 times of the previous FEA results. Therefore, the large deformation of the harvesting device under transient excitation did not affect the amplification ratio too much. In addition, actual manufacturing tolerances and assembly errors, and the setting of FEA connection constraints, etc., could cause differences between theoretical and actual magnification ratios.

5.3. Effect of Pre-Magnetization on the Output Characteristics of the Harvesting Device

The double-stage rhombus energy harvesting device works mainly by using the Villari effect of MSM. Much literature has shown that the pre-magnetized magnetic field has a direct effect on the Villari effect [41,42], so it was inferred that the pre-magnetization might have an effect on the output characteristics of the harvesting device in this paper. According to the available literature [43], both mechanical stress and magnetic field rotate the magnetic domains inside the Terfenol-D rod, and several domain states are shown in Figure 15. The initial state of the magnetic domains is haphazard, and the separate magnetic field makes the domains parallel to the direction of the magnetic field. The magnetic field and mechanical stress work together. When the mechanical stress dominates, the magnetic domains are distributed perpendicular to the stress, and, at this time, the domains have zero magnetization. As the stress decreases, the stress and the magnetic field together rotate the domains by a certain angle, and when the stress decreases to a certain value, the magnetic field plays a dominant role and rotates the domains. The existing literature [43] shows that more magnetic domains rotated generates more magnetic energy. When the Terfenol-D rod was subjected to a certain mechanical stress in this paper, it was necessary to study the pre-magnetization layout for the optimal output performance of the harvesting device, in light of the demand that the pre-magnetized magnetic field should maximize the energy conversion efficiency. Permanent magnets were used to provide a pre-magnetization field for the device, and five different pre-magnetization positions and layouts were selected for the experiments. In addition, a control group, without a pre-magnetized magnetic field, was designed.

The pre-magnetized magnetic field layout method and no pre-magnetization are shown in Figure 16. The magnet is indicated by the symbol P-M1 when arranged on a single side of the radial direction of the Terfenol-D rod, by the symbol P-M2 when arranged on both sides of the radial direction of the Terfenol-D rod, and by the symbol P-M3 when arranged on both sides of the axial direction of the Terfenol-D rod. Each of the above layouts used two disc-shaped permanent magnets of the same size, with Φ 10 mm × 1 mm. P-M4 and P-M5 were extensions of the P-M3 arrangement, in terms of the number of magnets, with the number of permanent magnets on each side of the Terfenol-D rod being 2 and 3, respectively. The coercive force of each permanent magnet was 780–836 KA/m, the remanent magnetization was 1.08–1.12 T, and the maximum magnetic energy area was 223–239 kJ/m³.

The magnetic field intensity distribution of the Terfenol-D rod, using FEA to study the above five pre-magnetization layouts, is shown in Figure 17. It can be seen that the highest magnetic field strength of the Terfenol-D rod with P-M3 layout was higher than those of P-M1 and P-M2, while the magnetic field strength of P-M3, P-M4, and P-M5 increased sequentially with increase in the number of permanent magnet blocks, and the higher magnetic field strength would motivate more magnetic domains. When the Terfenol-D rod was excited by external mechanical stress, the angle of magnetic domain deflection would be greatly enlarged, so the Villari effect of MSM strongly changed the magnetic properties of the Terfenol-D rod, and it was inferred that the vibrational energy capture performance of the harvesting device would also be enhanced [41].

The output voltages of the harvesting device under five magnetic field layouts and without pre-magnetization are shown in Figure 18. The experiments were performed at a 30 Hz sine operating frequency of the harvesting device. The results showed that the layout of different pre-magnetized magnetic fields led to large differences in the output voltage and that the voltage increased with increasing excitation force. When the pre-magnetization was in the P-M3 layout, the output voltage reached 230 mV, which was as much as 13 times higher than without pre-magnetization. However, the output voltage of the harvesting device in the P-M5 layout was not higher than that of P-M4, while the output voltage in the P-M3 pre-magnetization layout was lower than that of P-M4. It has been well demonstrated that a single increase in the pre-magnetization field does not consistently improve the output characteristics of the harvesting device, and it has been corroborated that an excessive magnetic field strength increases the resistance to domain rotation, making the domains less susceptible to deflection and leading to a reduction in the induced voltage generated by the pick-up coil [44]. In this paper, a P-M4 pre-magnetization layout would be used for subsequent studies. The above study showed that the pre-magnetized magnetic field had a significant effect on the output characteristics of the Terfenol-D rod-based harvesting device, and, additionally, the results were related to the pre-magnetization layout. The detailed effect of the pre-magnetized magnetic field on the Villari effect of Terfenol-D rod requires more detailed modeling, including the exact value of the magnetic field strength and the form in which the pre-magnetized field is provided, which will be addressed in future studies.

5.4. Harvesting Performance of the Harvesting Device under Sinusoidal Excitation

Since the frequency of ambient vibration is low and the form of vibration is not determined, it is important to ensure that the operating frequency of the harvesting device is the same as the ambient vibration to maximize the vibration harvesting capacity of the harvesting device. The purpose of this section is to identify the sinusoidal operating frequency of the energy harvesting system and to obtain the relationship between the output voltage and power and the external load to optimize the output performance of the energy harvesting system, in terms of operating frequency and load conditions. The experiments tested the excitation force and output voltage at 25, 30 and 35 Hz, respectively, and the peak excitation force was maintained between 20–30 N, as shown in Figure 19. Since the rigid connection between the harvesting device and the vibration output was not absolutely tight, the frame’s ability to resist external forces changed during compression, so the measured force signal was not sinusoidal. The results showed that the voltage output of the harvesting device at 30 Hz was significantly higher than at 25 Hz, while the output voltage at 35 Hz was not higher than at 30 Hz, and the output voltage curve at 30 Hz excitation frequency was smoother. According to the existing literature, [13], wherein driving bus low-frequency characteristics were collected, the frequency of sinusoidal vibration in the vehicle is near 30.5 Hz. With this in mind, and to further determine the operating frequency of the harvesting device, the frequency range of 25–35 Hz was selected, keeping the excitation force constant, and the output voltage was measured every 0.5 Hz using the point measurement analysis method. The output voltage curve for 25–35 Hz is shown in Figure 20. The curves show that the output voltage of the harvesting device increased and then decreased in the frequency range of 25–35 Hz, reaching a maximum at 30 Hz. Therefore, the sine experimental test results showed that the optimal output performance of the harvesting device was obtained at 30 Hz operating frequency.

To investigate the effect of load resistance on the output power, the digital multimeter measured the resistance value of the pick-up coil as 8.7 Ω. Figure 21a shows the output power of the energy harvesting device under different resistive loads, corresponding to the force input signal, as in Figure 21b. In order to avoid the failure of the harvesting device due to excessive input displacement, the time-varying displacement of its operating process was measured using a laser displacement sensor, as shown in Figure 21c, and the peak input displacement of 0.80 mm was much smaller than the maximum input displacement of the harvesting device of 4.42 mm. From the output power image, the output power was at its maximum when the load resistance matched the internal resistance of the pick-up coil. In practical applications, the internal resistance of the microelectronic components is similar to the pick-up coil resistance, so the harvesting device can easily obtain higher output power, i.e., higher power at both ends of the microelectronic components. If the actual microelectronic component resistance produces a change, the size parameter of the pick-up coil can be controlled to maximize the output power. At 30 Hz operating frequency with an external impedance load of 8 Ω, the open circuit output voltage peaked at over 250 mV, while the maximum output power was 1.056 mW. The maximum input force in this experiment was 25.5 N, and the energy harvesting capacity was about 41.4 μW/N. Future work will consider the use of MSM stacks as core power generation materials to produce a higher ratio between output voltage and applied force.

5.5. Harvesting Performance of Harvesting Device under Random Excitation

In order to fully utilize the application range of the double-stage rhombus energy harvesting device, the output characteristics under random excitation were investigated in conjunction with the existence of many irregular vibration sources in real situations. In the experiments, the bottom end of the harvesting device was kept rigidly connected to the experimental bench, and a random transient excitation was applied to the input via a force hammer. The force hammer comes with a force sensor connected to a charge amplifier, and the real-time force and output voltage images measured by the oscilloscope are shown in Figure 22a,c. The results showed that the harvesting device produced 2.92 V and 2.35 V peak output voltages under 50 N transient loading force. In addition, it was found that the energy harvesting device could generate large output power, and output power of 266 mW and 174 mW could be obtained by connecting load resistors matching the internal resistance, as shown in Figure 22b. Moreover, the elastic deformation of the mechanism was a constant and repeated process until the bridge-type beam became completely stationary, and the process generated a constant decay of the output voltage peak. However, the recovery force of elastic deformation was much smaller compared to the compression force, but the number of deformations experienced was higher. Considering this from the perspective of energy conservation, the input energy at this time was transformed into the energy of the mechanical deformation of the double-stage rhombus energy harvesting device.

We present a rough comparison of piezoelectric and magnetostrictive harvesters in

Table 9. Comparison of performance parameters with existing harvesters.

Characteristic Parameters	Proposed Harvester	Multi-Stage Harvester [24]	Harvester [47]	Double-Stage Harvester [23]
Dimension: L × W × H (mm)	64 × 48 × 34	53 × 39.2 × 25	45 × 30 × 24	68 × 98 × 24
Safety factor	2.5531	1.98	-	1.55
Amplification ratio-Theory	16.03	17.90	-	9.0
Harvested voltage (V)	2.92	26.39	3.55	-
Peak output power (mW)	266	34.81	0.20	204.70
Matching Resistance (Ω)	8.7	2 × 104	1.2 × 105	3 × 103
Normalized power density (mW/cm3)	2.547	0.670	0.02	1.278

. Obviously, in terms of safety and amplification ratio, the harvester in this article performed better. In order to evaluate the working performance of the harvester in detail, the normalized power density was introduced and defined as the power/volume of the harvester [45,46], thus, quantifying the efficiency of different harvesters. In contrast to piezoelectric harvesters, magnetostrictive harvesters exhibited a higher normalized power density. In addition, the magnetostrictive energy harvester had a small matching resistance, while the piezoelectric harvester had a large matching resistance, and even though it generated a high voltage, the power was still less than that of the magnetostrictive harvester.

5.6. Practical Application Tests of the Harvesting Device

The vibration capture performance of the double-stage rhombus energy harvesting device was tested by simulating the process of stress on a bus seat. The harvesting device was installed at the backrest of the seat and the acceleration sensor was fixed to the side of frame 2 to capture the acceleration characteristics of the seat subjected to human back vibration. The experimental setup and output characteristics are shown in Figure 23. The results showed that when the harvesting device was subjected to the pressure of the seat, the acceleration was positive, and the output voltage was also positive at this time, and increased with the acceleration, and, then, gradually decayed after reaching the peak. When the seat returned to its original state due to elasticity, the acceleration changed to the opposite direction, and the output voltage became negative. Unlike the transient force applied by the hammer in the random test experiment, when the transient force in the random test was applied to the harvesting device, the output voltage amplitude decreased gradually, due to the elasticity of the frame material. In practical applications, the force is always present throughout the work of the harvesting device, which reduces the portion of mechanical energy lost due to the elastic action of the material.

6. Conclusions

A double-stage rhombus vibration energy harvesting system, based on the Terfenol-D rod, was designed and fabricated using the coupling between the Villari of MSM and Faraday electromagnetic induction effect. It consists of a force amplification module and an energy conversion core module, which is used to harvest the low-frequency vibration energy generated by a bus seat during the bus driving process. The operating frequency of the harvesting device was studied by the point measurement method, and it was found that the harvesting device had the strongest harvesting capacity at a sinusoidal operating frequency of 30 Hz. In studying matching the load resistance, the maximum power of the harvesting device was found to occur at 8 Ω, which approximately equaled the resistance of the pick-up coil. Pre-magnetization has a significant impact on harvesting capacity, and the analysis determined the pre-magnetization layout with the strongest harvesting capacity. The above studies of operating frequency, matching resistance and pre-magnetization sufficiently improved the output performance of the harvesting device. Experimental studies showed that by applying sinusoidal excitation to the harvesting device, it produced an output power of 1.056 mW at an operating frequency of 30 Hz and an input force of 25.5 N. A random excitation was applied to the harvesting device, which corresponded to an open-circuit voltage of 2.92 V and power of 266 mW, respectively, at an input force of 50 N. Combining the test results of practical applications, i.e., excitation levels of 2.2–4.9 m/s² corresponding to peak voltages of 1.02–1.51 V, it was concluded that the output performance in the above two states was sufficient to power the low-power electronics on the bus. In the future, a double-stage rhombus magnetostrictive vibration energy harvesting platform with circuitry and pre-magnetization system modeling will be developed to further improve the harvesting capability and practical performance.